FORELESNINGSNOTATER I INFORMASJONSØKONOMI Geir B. Asheim, våren 2001 (oppdatert ). 2. ADFERDSRISIKO 2.1 ADFERDSRISIKO -PROBLEMET
|
|
|
- Marianne Thorsen
- 6 år siden
- Visninger:
Transkript
1 FOREESNINGSNOTATER I INFORMASJONSØKONOMI Gr B. Ash, år odatrt.... ADFERDSRISIKO Otal kotraktr dr asytrsk forasjo. Agts sats r kk rfsrbar; ds., kotraktr ka kk btgs å. Agt å gs str tl å lg d sats rsal øskr. Stasjo : Stasjo : Stasjo : Stasjo : Ekslr: dls Arbdr Istor Prodst Saft Krll Forskrgsslska Kd adfrdsrsko. ADFERDSRISIKO Grlggd koflkt: Et har agt sak str slk at agt lgr galt å å sats llr blr agt blr tsatt for rsko. Dtt r koflkt hs agt r rsko-ars og rsal r rsko-øytral ford løsg dr sytrsk forasjo bærr at agt bærr g rsko ds, agt har g str tl høy sats. Dt r g koflkt hs agt r rsko-øytral og rsal r rsko-ars ford løsg dr sytrsk forasjo bærr at agt bærr all rsko ds, agt har fll str tl høy sats.. ADFERDSRISIKO. ADFERDSRISIKO -PROBEMET Rtr bassodll: To aktørr Prsal: tforr og forslår kotrakt. Agt: tførr oga å g a rsal. Varabl Rsltat:,..., Agts sats:,..., llr [, ] For gtt sats r rsltatt skkrt, agts sats årkr sasylghtsfordlg or rsltat: Pr[ ] Btalg fra rsal tl agt:. ADFERDSRISIKO -PROBEMET Prsal og agt har otsatt trssr. Prsals yttfksjo: B, hor B >, B. Agts yttfksjo:, hor >, og >,. Prsal r rsko-øytral hs B ; ds: B. Agt r rsko-øytral hs ; ds:. a ˆ : ˆ ær d btalg so sørgr for at agt får yttåt û år dt kk tas hsy tl. Dt gjldr altså at ˆ ˆ og ˆ ˆ û ˆ ˆ ŵ
2 . ADFERDSRISIKO -PROBEMET Otal kotraktr dr asytrsk forasjo. Probl : For hr, f d otal ag llo str og rskodlg. Probl : F d otal. Probl. B a,..., bb. IR ˆ ˆ arg a ˆ IC D først bbtgls kalls agts dltakrbtgls IR. D adr bbtgls kalls agts stforlghtsbtgls IC.. ADFERDSRISIKO. RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER Rsko-ars agt: <. >. For hrt rsltat, skr. a < <... og, for k,,, k k < for é k. Probl for : a,..., bb. IR IC... otalt hs sr bort fra IC, tlfrdsstllr IC. orfor? Fastlø r drfor otalt hs. Kostad:. RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER Probl for : a,..., bb. IR IC Fastlø tlfrdsstllr kk IC hs. orfor? Oforlr:,..., bb. IR IC. RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER µ For hrt rsltat : µ [ ] µ Rsltatr:. IR-btgls bdr hs dt kk r dr skrak for.. øyr kostad dr asytrsk fo. > orfor?. øyr aløg d t bdr rsltat hs > >.... Probl. Ikk høyr sats d asytrsk fo. ford < år.g.a. at > og
3 . RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER To rsltatr: > og og Probl for : s IC-btgls r ofylt d lkht, får : Grlø: Bos:. ADFERDSRISIKO. EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER Ata to rsltatr: > og og B ; ds.: ˆ ˆ,,.. EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER øsg å robl : Probl dt å f kostad forbdt d d to satså ka løss ahgg a rd å og. Først: Drst: IC-btgls dførr: IR-btgls dførr: Drfor: 8,, 8 78, > 8 Illstrrr at kostad d høy sats r høyr dr asytrsk fo.. EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER øsg å robl : 8 og Otal sats: Asytrsk forasjo førr tl dr sats. og Otal sats: Asytrsk forasjo førr tl sa sats.
4 . EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER Edr kslt slk at 5, og ata at dr skrak for. øsg å robl : Først: 5 5 Drst: IC-btgls dførr: IR-btgls dførr: 7 Drfor: og 8 > 7 Illstrrr at IR-btgls kk øddgs bdr hs dr skrak for.. EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER Ata tr rsltatr: > > B ; ds.: ˆ ˆ 5,,. øsg a robl dr sytrsk forasjo: EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER øsg a robl dr asytrsk forasjo: Først: Drst: Førstordsbtglsr: µ [ ] : µ [ ] : µ [ ] µ [ ] : 9 IR: 5 IC: 5 5, 5, 65, 9, µ > 5. EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER Edr kslt so følgr: Dt følgr fra aalys ofor at: 5, 65, 5 Bdr rsltat gr kk høyr aløg ford <
5 . EKSEMPER VED RISIKONØYTRA PRINSIPA OG TO INNSATSNIVÅER Edr kslt so følgr: Btrakt følgd kotrakt:, 5, 5 Sjkk at IR- og IC-btgls r tlfrdsstlt. Sjkk at kostad d høy sats r d sa so dr sytrsk fo. orfor?. ADFERDSRISIKO. RISIKONØYTRA PRINSIPA OG ET KONTINM AV INNSATSNIVÅER Førstordstlærg s ], [, og d aktll fksjo r kotrlg, da r øddg btgls for dr løsg for sats at. Dtt følgr fra ˆ ˆ arg a ˆ s dt r t tydg aksrd satså, ka Probl drd ofors tl a,..., bb. IR IC. RISIKONØYTRA PRINSIPA OG ET KONTINM AV INNSATSNIVÅER Førstordstlærg Oforlr:,..., bb. IR IC µ For hrt rsltat : µ [ ] µ. RISIKONØYTRA PRINSIPA OG ET KONTINM AV INNSATSNIVÅER Førstordstlærg Ssalsrg: [,],, og Da gjldr at [ ] so dr år fortstgr aksrs a t tydg og dr satså. Førstordstlærg r drfor gyldg dtt ssaltlfllt. Ford, følgr dt at førstordsbtgls for hrt blr µ
6 . RISIKONØYTRA PRINSIPA OG ET KONTINM AV INNSATSNIVÅER Førstordstlærg Probl. s [, ] og, da fs tydg so aksrr Margal økg fortt rsltat Grskostad, hs d d >, hor dt ssaltlfllt følgr at [ ] og d, og at [ ] µ d fra ohyllgstort. d d Isats. ADFERDSRISIKO.5 RISIKONØYTRA AGENT Btrakt løsg dr sytrsk forasjo: Agt kjør rksoht for b a slk at, for hrt rsltat, b. Isatsåt tlfrdsstllr IR-btgls: [ b ] Isatsåt tlfrdsstllr IC-btgls: arg a [ ] b Først-bst løsg ka ltrs også dr asytrsk forasjo.. RISIKONØYTRA AGENT Eksl Ata to satsår og og to rsltatr > og og B ; ds.: ˆ ˆ, ; b. RISIKONØYTRA AGENT Eksl 8 og øsg: 8 6 og 8 Agt btalr 8 for rksoht. øsg hs 6 og for å tlfrdsstll IC-btgls og for å tlfrdsstll IR-btgls 6 og og ford 6 >. Agt btalr 6 hs dt går bra.
7 . ADFERDSRISIKO.6 SPITEORETISK GRNNAG Sll: Prsal tlbyr kotrakt tl agt, so t akstrr llr forkastr kotrakt, og so hs akst lgr hadlg. Natr trkkr tl sltt rsltatt. Prsal tlbyr kotrakt Agt Forkast Akst Akst Forkast Dtt r t dyask sll d Agt fllko forasjo. lgr sats Natr trkkr rsltat Dlsll-rfkt lkkt r drfor t tlstrkklg lkktsbgr. Mrk at dt fs Nash-lkktr so kk r dlsll-rfkt. orfor?.6 SPITEORETISK GRNNAG orfor atar at agt gjør dt rsal l, hs ha r lkgyldg? Dt r dt kotrlg hadlgsrot for rsal so tgr oss tl å ata dt. F.ks. hs rsal ga agt r s rsrasjosytt, k kk dtt ær dl a t lkktstfall. Ford rsal l tj å å tlby kotrakt so gr ltt dr ytt. I dlsll-rfkt lkkt å drfor rsal g agt akkrat s rsrasjosytt, og agt sl o ha r lkgyldg akstrr kotrakt, o so r rsals trss.. ADFERDSRISIKO.7 FERE OPPGAVER, FERE AGENTER Flr ogar Tor rdkrr at a skal tlby stkotraktr so oft ka ær sært kolsrt. I rklght, kl stskja llr kk str dt hl tatt. orfor? olströ & Mlgro 99 forklarr horfor dt r otalt d sak str år agt skal gjør flr ogar, og rsltatt kk r rfsrbart for all oga. Probl: Strk str for ogar so førr tl rfsrbar rsltatr, ka før tl for lt sats å ogar t rfsrbar rsltatr. Eks.: drsgs-/forskgsstllg d rstt drsgsakttt ka lttr obsrrs forskgsakttt..7 FERE OPPGAVER, FERE AGENTER Flr agtr r agt a agtr tar kk-rfsrbar sats. Rsltat:,...,. Dlgsrgl: s r s adl. * Først-bst løsg: arg a Nash-lkkt: ê, hor for all, arg a s, ˆ ˆ Tor olströ, 98: Dt fs kk dlgsrgl so tlfrdsstllr s, slk at * r Nash-lkkt. Tor olströ, 98: Dt fs dlgsrgl * so tlfrdsstllr s, slk at r Nash-lkkt. Argt ot artrska/arbdrstyrt bdrftr. Argt for bdrftr so skllr rska og arbd.
Asker 17.03.12. Kaare Granheim: Askers rolle i den regionale utviklingen. Konsekvenser for befolkning og boligmarked i Asker
Askr 17.03.12 Kaar Grahim: Askrs roll i d rgioal utviklig. Koskvsr for bfolkig og boligmarkd i Askr Kaar Grahim Vidrgåd (KG) NTH bygigsigiør md økoomi for kraftkommur som ksamsoppgav Aspla 1970 md kommual
Matematikk for IT, høsten 2018
Mtmtkk for IT, høst 8 Oblg Løsgsforslg 7. sptmbr 8.7. ) for >. 7 b) for >. 7 c) for >. 7 d) ) for >. 8 8 8 8 8 7 8 7 8 .7. ) for >. 7 8 b) for >. 7 ) 7 ) 7) ) 7 ) 7) c) for >..7.8 ) ) ) ) ). Bss:. Rkursjosforml:
Dynamisk programmering. Hvilke problemer? Optimalitetsprinsippet. Overlappende delproblemer
ysk progrrg Mtod bl forlsrt v Rchrd Bll (RAN Corporto på -tllt. Progrrg btydg pllgg, t bslutgr. (Hr kk o d kod llr å skrv kod å gør. ysk for å dkr t dt r stgvs prosss. M også t pytord. Hvlk problr? ysk
si1, }ll :i tl .nn -{i q il th; !9ft $.\ l l.i t- -l s i l l)l\ _1 L _!.1 '{'- l s -,,
.L q,. -, + s. :.nn = -,, _. ''- ' ' } 3, _ L ' s, - - s :,34 : q )L 9 h;,u 9 r c ( ( q ( : - ' -' D,T -a 4 : n,r 3' -r 3?' - : '?:). L '29_ 'r }5. r's '_, T e: 'a...nn. 2 T ' 3, Z ',, . ; :.,,r.' - *
FORELESNINGSNOTATER I INFORMASJONSØKONOMI Geir B. Asheim, våren 2001 (oppdatert 2001.03.27). 3. UGUNSTIG UTVALG
OREENINGNOAER I INORMAJONØKONOMI Gir B. Ashim, vårn 2001 (oppdatrt 2001.03.27. 3. UGUNIG UVAG Agntn har privat informasjon om rlvant forhold før kontrakt inngås. Undr symmtrisk informasjon vill kontraktn
I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e
I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e 2 0 1 1 O r d i n æ r t s a m e i e r m ø t e i L i s a K r i s t o f f e r s e n s P l a s s S E, a v h o l d e s o ns d a g 9. m a r s
Våre Vakreste # & Q Q Q A & Q Q Q - & Q Q Q.# arr:panæss 2016 E A A 9 A - - Gla- ned. skjul F Q m. ler. jul. eng- da- jul. ler.
Vå Vks rr:pnæss 06 Kor L JUL Q Q Q ^\ # Q Q Q ht Q Q Q # 6 Q Q Q # Q Q Q # Ju lg u u Q Q Q # # v blnt # LL: u # mj # # # # d fly p r ds Q Q m # # år lønn Ju v g v g # jul # grønt 6 # # u Lønn gå # hvor
MA1102 Grunnkurs i analyse II Vår 2014
Norgs tkiskaturvitskaplig uivrsitt Istitutt for matmatisk fag MA Grukurs i aalys II Vår 4 Løsigsforslag Øvig 8.8. a) Vi har fuksjo f(). Vi skal taylorrkk til f i puktt, kovrgsitrvallt til d rkk, og vis
s P t r st s s r st st r ür t s s t s st s t3 3 t r r s ä stüt3 ö st t s s tr r t 2 r s t r
s P t r st s s r st st r ür t s s t s st s t3 3 t r r s ä stüt3 ö st t s s tr r t 2 r s t r t r r r s ss s ür t r r st ts s q t rt r s rst r s r r t rt s sst r s r 2 r ü t s s 3 t r3 st r s ür r t r t
2. Å R S B E R E T N I N G O G R E G N S K A P F O R A ) Å r s b e r e t n i n g o g r e g n s k a p f o r
I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o r s a m l i n g i, a v h o l d e s m a n d a g 3. m ai 2 0 1 0, k l. 1 8 0 0 p å T r e
I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E
I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i n æ r t s am e i e rm øt e i S am e i e t W al d em a rs H a g e, a v h o l d e s t o rs d a g 1 8. j u n i 2 0 0 9, k l.
FORELESNINGSNOTATER I SPILLTEORI Geir B. Asheim, våren 2001 (oppdatert ).
OREESNINGSNOTATER I SPITEORI Ger B. Ashem, våre 00 (odatert 000.0.03. 3. STATISKE SPI MED UUSTENDIG INORMASJON (Statske Bayesaske sll Statsk sll: Sllere trekker samtdg. Ufullstedg formasjo: Mst é sllere
Tillatt utvendig overtrykk/innvendig undertrykk
Tillatt utvndig ovrtrykk/innvndig undrtrykk For t uffrør vil ttningsringns vn til å tål undrtrykk oft vær dinsjonrnd. I t rør so blasts d t jvnt utvndig trykk llr innvndig undrtrykk vil dt oppstå spnningr,
Årsrapport 2014. N.K.S.Veiledningssenter for pårørende i Nord Norge AS
Årsrapport 2014 N.K.S.Vildigsstr for pårørd i Nord Norg AS vildigsstr.o parordnn facbook.com/vildigsstr 03 Ihold Ihold Ildig... sid 04 Asvarlig for N.K.S. vildigsstr for pårørd i Nord Norg AS...sid 06
med en mengde korrelasjoner mellom delmengdene. Det er her viktig a fa med
Lsningsantydning til kontinuasjonsksamn i 45060 Systmring Tirsdag 23. august 994 Kl. 0900 { 300 3. august 994 Oppgav, 5% S sidn 346 og 349: Dlsystmstruktur En oppdling av systmt i n mngd dlsystmr, sammn
S T Y R E T G J Ø R O P P M E R K S O M P Å A T D Ø R E N E S T E N G E S K L
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r!
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g e t s å r s b e r e t n i
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010 O r d i n æ r t s a m e i e r m ø t e i S / E S o r g e n f r i g a t e n 3 4, a v h o l d e s o ns d a g 1 0. m a rs 2 0 1 0 k l. 1 8. 0 0 i K l u b b r o m m
Løsningsforslag til øving 11
OPPGVE Kommnar: Høgskoln Gjøk d. for kn. øk. og ldls amakk Løsnngsforslag l øng ll nkn r løs md "Ubsm koffsnrs mod" sl om også knn a bn Lagrangs mod. a ODE:. d nalbnglsr: ( ( Homogn løsnng: ( Ds. løsnngn
I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e
1 V a l d r e s g t 1 6 S / E I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e 2 0 1 1 O r d i n æ r t s am e i e rm øt e i V a l d r es g t 1 6 S / E, a v h o l d e s o n s d a g 2 7. a
KONSEPT/SITUASJON. Konseptet illustreres ovenfor med en 3D tegning av bygget i sammenheng med uteoppholdsarealene.
KONSEPT/SITUASJON Slå u i KJØKK Ap lt u / v i SYK For å illutrr rhg utoppholdrlr (MUA) o hgd og v god vlitt hr dt litt utridt t opt o dlr opp utoppholdrlt i fir forjllig tr, hvor hvrt t hr uli tivittr
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2010 O r d i n æ r t s am e i e rm øt e i U l l e r n s k og e n B o l i gs am e i e, a v h o l d e s t i rs d a g 2 7. a p r i l 2 0 1 0, k l. 1 8 : 3 0 p å B j ø r
r r t t r t s r r st str t r P s r s t t t r ss rt s r t ss rt tt rs t tt rs s r ü r ss r r q 3 t tt ss s t r ä t ss s ss r tt ä
tt rs r ö 1 ü r r ts r3 s r r t t r t s r r st str t r P s r s t t t r ss rt s r t ss rt tt rs t tt 3 t tt rs s r ü r ss r r q 3 t tt 3 t tt ss s t r ä t ss s ss r tt ä s rt s rs sr t ω(k) s t r t tt ss
Diskretisering av et kontinuerlig problem vedbruk av prinsippet om minimum potensiell energi. For et lineært elastisk material:
ME 5 Eergmetoder Dskretserg a et kotuerg probem edbruk a prsppet om mmum potese eerg otese eerg for et eastsk system: Oerfatekrefter traksoer pr. fateehet Idre oum-krefter Forskyger Fu Fy Fz w dv u y z
Oppgaver fra boka: Oppgave 12.1 (utg. 9) Y n 1 x 1n x 2n. og y =
MOT30 Statistisk mtodr, høstn 20 Løsningr til rgnøving nr. 8 (s. ) Oppgavr fra boka: Oppgav 2. (utg. 9) Modll: Y = µ Y x,x 2 + ε = β 0 + β x + β 2 x 2 + ε, dvs md n obsrvasjonr får vi n ligningr Y = β
Tegningshefte HØRINGSUTGAVE
Rgulrigpla, plaid 6100000 Årtad, gr 160, br 904 m.fl. Sltt Buholdpla m.m. vd Sltt bybatopp Vilhlm Bjrk vi Hagrup vi Tgighft HØRINGSUTGAVE Dato TEGNINGSLISTE Oppdragr: 1194 Tgiglit opprttt Tgiglit rvidrt
Løsningsforslag (ST1201/ST , kontinuasjonseksamen) ln L. X i = 2n.
Løsgsforslag ST20/ST620 205, kotuasjoseksame. a Rmelghetsfuksjoe blr Logartme Derverer Løser lgge Løsge er SME: L = 2 e l L = 2 l X X. X + l X. l L = 2 + 2 X = 2. ˆ = 2 X. X. b Her ka ma beytte trasformasjosformele,
Convex hull. Konveks innhylling. La P være en mengde punkter i et k-dimensjonalt rom, P R k. (Vi skal for enkelthets skyld bare se på k = 2.
Conv ull La P vær n mn punktr t k-mnsjonalt rom, P R k. (V skal or nkltts skl bar s på k.) Dnsjon En mn Q R k r konvks rsom or all punktr q, Q lnjsmntt q lr Q. Dnsjon Dn konvks nnllnn tl n mn punktr P
Butikkstekte brød. grove, stort utvalg, 50-100% grovhet. Tilbudet gjelder man-ons. ord.pris 169,00/kg. Lettsaltet torskefilet SPAR 47-49% SPAR 25-32%
Hvragn grov, tort utvalg, 50-100% grovht Tlbut gjlr man-on 29% 39 Tlbut gjlr man-on Vår Butkktkt brø gn nytkt 52% 45-47% 79 or.pr 56,/tk brø r br m mny or.pr 169,00/kg or.pr 27,50/ 28,50/pk Nygrllt kyllng
Formler og regler i statistikk ifølge lærebok Gunnar Løvås: Statistikk for universiteter og høgskoler
Formler og regler statstkk følge lærebok Guar Løvås: tatstkk for uversteter og høgskoler Kap. Hva er fakta om utvalget etralmål Meda: mdterste verd etter sorterg Modus: hyppgst forekommede verd Gjeomstt:
Midt i vinter. Aurora Borealis. lys, lek. nes slått. en for. fin stor. fin slått. lys, for. ter stor. nes lek. nes lek. lys, for. fin slått.
S A T B vnne tsk, fn nattjor ds hmvrm 10 ne vntsk, fn jor nattds vrm hm ne vntsk, fn jor nattds vrm hm ne vntsk, fn jor nattds vrm hm Ur- gult vl blk gns t Ausg ronal hm l ve. le. Lys 14 2 Urgult vl gns
1 dc. Uke 35 FYS3220 Forelesningsnotater. H.Balk Fourier analyse
Uk 35 FYS3 Forlsgsor. H.Blk Fourr lys Rpso... Fors FS md komplks form... F mplud og fs fr V... 3 Dskr Fourr rsformso (DF... 5 Fourrgrl (FI... 7 Fr prodsk sgl l puls... 7 Bådbrdd l frkvsspkr for frkpuls...
TMA4265 Stokastiske prosesser
Norges teknsk-naturvtenskapelge unverstet Insttutt for matematske fag TMA65 Stokastske prosesser Våren Løsnngsforslag - Øvng Oppgaver fra læreboka.6 P er dobbelt stokastsk P j j La en slk kjede være rredusbel,
EKSAMEN I FAG SIF 4014 FYSIKK 3 Fredag 17 desember 1999 kl Bokmål
Sid av 7 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig otat udr a: Førtaaui Kut Ar Strad Tlfo: 73 59 34 6 EKSAMEN I FAG SIF 44 FYSIKK 3 Frdag 7 dbr 999 l. 9-3 Boål Hjlpidlr:
P r in s ipp s ø k n a d. R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e
P r in s ipp s ø k n a d R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e O pp d ra g s n r : 2 0 1 50 50 O pp d ra g s n a v n : Sa n d s ta d g å r d
Løsningsforslag til den obligatoriske oppgaven fra seminarlederne
Løsigsforslag til d oligatorisk ogav fra siarldr Totalt og r ulig dt krvs 65 og for å få stått drso du ikk har lvrt o ogavr i Frotr. tallt og so krvs for å få stått ogav rdusrs d atall og oådd for å svar
K j æ r e b e b o e r!
1 K e y s e r l ø k k a Ø s t B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d
mot mobbing 2011 2014 Manifest
g t n s b f b n o a M ot m 014 m 11 2 20 dt mljø o g t rngs r o d f g læ rb st- o a sam pvk nd op t lk rnd p r o Et f nklud Manfst Et forplktnd samarbd for t godt nkludrnd oppvkst- lærngsmljø Forord All
Løsningsforslag Eksamen i Statistikk Nov 2001 Oppgave 1 a) Det fins 8 mulige kombinasjoner. Disse finnes ved å utelate ett og ett tall.
Løsgsforslag Eksame Statstkk Nov 00 Oppgave a) Det fs 8 mulge kombasjoer. Dsse fes ved å utelate ett og ett tall. Atall utvalg av størrelse 7 blat m er ( m 7 ). b) Prs Atall Rekker 3 kr. ( 7 ) 3 kr....
Regler om normalfordelingen
HG mars 0 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg dette kurset.
I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e
1 S a m e i e t S o l h a u g e n I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e 2 0 1 1 O r d i n æ r t s am e i e rm øt e i S am e i e t S o l h a u g e n, a v h o l d e s o n s d a
Formelsamling for matematiske metoder 3.
Formlsmli for mmis modr 3 f f Grdi Slrfl f r rdi f Risdrivr drivr il slrfl f i p o i ri r f f f os vor risvor r svor o r vil mllom rdi o risvor rivr v vorfl F m : F R F R vær diffrsirr i r F i d drivr
Forelesning 25 og 26 Introduksjon til Bayesiansk statistikk
Yushu.@hh.o Forelesg 5 og 6 Itroduksjo tl Bayesask statstkk 1. Itroduksjo Fortsatt atar v har stokastsk varabel X (X ka være stokastsk varabel vektor) kommer fra e fordelg med parametere ( ka være parameter
Eldre i Verdal Muligheter Rettigheter Aktiviteter/tilbud
Eldr i Vrdal Mulightr Rttightr Aktivittr/tilbud Eldrrådt Omsorg og vlfrd Omsorg og vlfrd i Vrdal r dlt inn i to virksomhtsområdr: Øra omsorg-og vlfrdsdistrikt Vinn og Vuku omsorg-og vlfrdsdistrikt Hva
Offentlige anskaffelser
NIFS-mø 13. fbruar: Ny skkrhsov Off askaffsr 1. Hvk rvrk ska du bruk? 2. Hvk krav ka du s? Sorrådvr Mar Vsr Df I K T I K T r I K T r o f d s a I K T r o f d s a j h I K T r o f d s a j h I K T o f d s
K j æ r e b e b o e r!
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
TMA4245 Statistikk Eksamen 21. mai 2013
TMA445 Statstkk Eksame ma 03 Korrgert 0 ju 03 Norges teksk-aturvteskapelge uverstet Isttutt for matematske fag Løsgssksse Oppgave Et plott av sasylghetstetthee er gtt fgur Vdere har v og PX = Φ = 08849
Konkurransen starter i august og avsluttes i månedsskiftet mai/juni hvert år.
Lærrvildning: Aksjon boligbrann Konkurrans for all skolklassr på llotrinnt: Saarbidsgruppa for brannvrn i skoln invitrr d dtt all skolklassr på llotrinnt til å bli d på konkurransn "Aksjon boligbrann".
ARSPLAN. Stavsberg barnehage
ARSPLAN Stavsbrg barnhag 2015 2016 ! a urr H Vi blir 20 år i dtt barnhagårt! Stavsbrg barnhag Vi r n hldagsbarnhag, som bl byggt høstn/vintrn 1995! Barnhagn åpnt 28.12.95. Fra august 2015 r dt 51 barn(andlr)
Next Generation Plattformen Quick guide
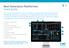Nxt Gnrtion Plttformn Quik gui Dnn kortftt guin hr litt stt smmn for å hjlp g å rskt li kjnt m mngfolig funskjonn og vrktøy som r tilgjnglig på Nxt Gnrtion Plttformn. Finn frm til prouktr å hnl og mrksnyhtr,
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN JUNI A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN 5.- 6. JUNI 201 3 A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013 09. 0 0 1 0. 0 0 R E G I S TR E R I NG N o e å b i t e i 10. 0 0 1 0. 15 Å p n i ng
I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G
I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o rs am l i n g i, a v h o l d es o ns d a g 2 8. a p r i l 2 0 1 0, k l. 1 8. 0 0 i 1. e
ENKELT, TRYGT OG LØNNSOMT!
Utli av fritidsindom: ENKELT, TRYGT OG LØNNSOMT! NYTT GRAM O R P S L E D FOR E R E: FOR UTLEI ort r på ssongk s ri p d o g Svært gsstdr n ri rv s å p t Rabat ulightr m s g in n j t n God in g rkdsavdlin
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i næ r t s am e i e rm ø t e i S am b o b o l i g s a m ei e fi n n e r s t e d t o r s d ag 3 0. 0 4. 2 0 0 9 K l. 1 8. 3 0
K j æ r e b e b o e r!
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
Regler om normalfordelingen
1 HG mars 2009 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg dette
MAYERS LIVSSITUASJONS-SKJEMA (3) Er du i stand til å: På egenhånd Vanskelig Svært vanskelig
Nvn: MAYERS LIVSSITUASJONS-SKJEMA (3) Dto: Vnnligst svr på spørsmåln som r rlvnt for g, v å stt t i ktull rurikk. 1. TA VARE PÅ DEG SELV Er u i stn til å: På gnhån Vnsklig Svært vnsklig f g h i j k l m
NORSK TEKSTARKIV J o s t e in H. Hauge
NAVF'S EDB-SENTER FOR HUMANISTISK FORSKNING V IL L A V E I 1 0, POSTBOKS 53 50 1 4 BERG EN-UNIVERSITETET 7 O k to b e r 1979 NORSK TEKSTARKIV J o s t e in H. Hauge 1. FO RHISTORIE D a ta m a s k in e ll
KRAVFIL TIL KREDITORFORENINGEN [Spesialrapport]
![KRAVFIL TIL KREDITORFORENINGEN [Spesialrapport]](/thumbs/26/7096686.jpg "KRAVFIL TIL KREDITORFORENINGEN [Spesialrapport]")
KRAVFIL TIL KREDITORFORENINGEN [Spsialrapport] - Sid 1 / 5 IS Doc. Sit Bildr Rapportr Ordlist R124 KRAVFIL TIL KREDITORFORENINGEN [Spsialrapport] Bskrivls sist rvidrt: År: 2008. Månd: 10. Dag: 01. KRAVFIL
KRAVFIL TIL KREDINOR [Spesialrapport]
![KRAVFIL TIL KREDINOR [Spesialrapport]](/thumbs/26/7096676.jpg "KRAVFIL TIL KREDINOR [Spesialrapport]")
KRAVFIL TIL KREDINOR [Spsialrapport] - Sid 1 / 5 IS Doc. Sit Bildr Rapportr Ordlist R104 KRAVFIL TIL KREDINOR [Spsialrapport] Bskrivls sist rvidrt: År: 2009. Månd: 10. Dag: 05. KRAVFIL TIL KREDINOR [Spsialrapport]
39,- Fix ferdig. emiddag. Godt & billig. Levering. Fiks ferdmiddag. Vi har prisløfte på over 200 varer*
Lvrig 39,- 38 Norwgia Skivt 27 % 3 g, Ti Godt & billig Lofot fisksupp 70 g, Toro Fix frdig ig Fiks frdmiddag middag famili Brokkoli 4 g 31 Frokostkaff Filtrmalt 2 g, Fril Farris Bris Naturll 1,5 l Zalo
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2009
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2009 O r d i n æ r t s am e i e rm øt e i R u d s h ø g d a V B / S, a v h o l d e s m a n d a g 1 6. m a r s k l. 1 8 : 0 0 p å L o f s r u d s k o l e, L i l l e a
STK1100 våren Konfidensintevaller
STK00 våre 07 Kofdestevaller Svarer tl avstt 8. læreboka Ørulf Borga Matematsk sttutt Uverstetet Oslo Eksempel E kjemker er teressert å bestemme kosetrasjoe µ av et stoff e løsg Hu måler kosetrasjoe fem
K j æ r e b e b o e r!
1 H o v i n B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s
K j æ r e b e b o e r!
K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2009
INNKALLING TIL ORDINÆRT SAMEIERMØTE 2009 O r d i n æ r t s am e i e rm øt e i, a v h o l d e s t o r s d a g 2 6. 0 3. 20 0 9, k l. 1 8 : 0 0 p å L y s e j o r d e t s k o l e, V æ k e r ø v e i e n 1
Taste a of elcome IkhhekdZ_d]i Forelesning 3 mandag den 25. august
Forelesg adag de 5 august Merkad 171 For å bevse e propossjo o heltall so volverer to eller flere varabler, er det typsk ye lettere å beytte duksjo på e av varablee e duksjo på oe av de adre Det er for
Avdeling for ingeniørutdanning. Ny og utsatt eksamen i Elektronikk
www.ho.o dlg fo gøutdag Ny og utatt kam Elktokk ato: 3. augut d: 9-4 tall d klu fod: 7 kludt dlgg tall oppga: 6 llatt hjlpmdl: ådholdt kalkulato om kk kommu tådløt. Mkad: Kaddat må l kotoll at oppgattt
TMA4245 Statistikk Eksamen august 2014
Norges teksk-aturvteskapelge uverstet Isttutt for matematske fag Løsgssksse Oppgave a) Y 5 PY > 53) PY 53) P ) 53 5 Φ5) 933 668 Vekte av e fylt flaske, X + Y, er e leærkombasjo av uavhegge ormalfordelte
Traversering av grafer
Trvrsring v grr Algoritmr og tstrukturr Øvingsorlsning 8 Trvrsring v grr Algoritmr og tstrukturr Øvingsorlsning 8 v Hnrik Grønch Agn Hvoror lær om grr Rprsntsjon v grr BFS DFS Topologisk sortring Øving
K j æ r e b e b o e r!
K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l år e t s g e n e r a l f o rs am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i n
s Ss H= ul ss i ges su Es $ ieig *isx E i i i * r $ t s$ F I U E,EsilF'Ea g g EE $ HT E s $ Eg i i d :; il N SR S 8'i R H g i,he$r'qg5e 3
"t q) )t 9q ) nf;'=i \0.l.j >, @ N c\, l'1 { rrl r) cg K X (), T t'1 s Ss q r' s S i i * r $ t s$ iig *isx i i gs su s $ Ss N SR S f, S = ul ss i? X $ $ g $ T s i :; il \ei V,t. =R U {N ' r 5 >. ct U,sil'
TMA4240 Statistikk Høst 2016
TMA440 Statstkk Høst 06 Norges teksk-aturvteskapelge uverstet Isttutt for matematske fag Abefalt øvg 0 Løsgssksse Oppgave a Estmatore for avstade a er gjeomsttet av uavhegge detsk fordelte målger, x; a,
DRIFTSANALYSER 2012/2013 FORELØBIGE RESULTATER
DRIFTSANALYSER FORELØBIGE RESULTATER A B C D E F C G H E I J K L B K F G K! " # $ %! & ' ( ) ( * + #, -! &!. & ) /! ( / ) - 0 1 - ' #.! ( ( * ' 1 2 ( (! 3 4 " (! - 5 6!! 7 % ' # 7 4 " (! - 1 2 # 7 4 8-1
Håndbok 014 Laboratorieundersøkelser
Vdlgg 1 sid 1 av 5 Hådbok Vdlgg 1 Jordartsklassifisrig Vdlgg 1 Jordartsklassifisrig Vrsjo mars 2005 rstattr vrsjo juli 1997 Omfag Jord ka bstå av t miralsk matrial, orgaisk matrial llr bladig av diss.
KONTINUASJONSEKSAMEN I FAG SIF8043 BILDETEKNIKK LØRDAG 16. AUGUST 2003 KL Løsningsforslag - grafikk
Sd v 8 NTNU Norgs tksk-turvtskpg uvrstt Fkutt for formsostkoog, mtmtkk og ktrotkkk Isttutt for dttkkk og formsosvtskp KONTINUASJONSEKSAEN I FAG SIF8 BILDETEKNIKK LØRDAG 6. AUGUST KL. 9.. Løsgsforsg - grfkk
STK desember 2007
Løsnngsfrslag tl eksamen STK0 5. desember 2007 Oppgave a V antar at slaktevektene tl kalkunene fra Vrgna er bserverte verder av stkastske varabler X, X 2, X, X 4 sm er uavhengge g Nµ, σ 2 -frdelte, g at
I n n k a l l i n g t i l o r d i n æ r g e n e r a l f o r s a m l i n g
1 Z i t t y B o r e t t s l a g I n n k a l l i n g t i l o r d i n æ r g e n e r a l f o r s a m l i n g 2 0 1 1 O r d i n æ r g e n e r a l f o rs am l i n g i Z i t t y B o r e t t s l a g, a v h o
-------------------------------------------------------------------------------- 1. Din kontrakt
Bstgsvkå Lowcosttavgoup Ltd ("Lowcosttavgoup") t fotak gstt Egad md fotaksumm 06725806 md hadsadss Spctum Hous, Bhv Rg Road, Gatwck, Wst Sussx, RH6 0LG og md gstt koto East Hous, 109 South Wop Way, Lodo,
Sk ie n ko mm une. R EG UL E R I N GS B ES T E MM E L SER T I L D eta ljr e gu l e ri n g
R EG UL E R I N GS B ES T E MM E L SER T I L D eta ljr e gu l e ri n g K j ø r b ekk d a l en 12 D 220 / 211 m. fl R e g u l e r i n g s be s te mm e ls e r sist date r t 27.09.17. P l an k a r t sist
Oppgave 1 Det er oppgitt i oppgaveteksten at estimatoren er forventningsrett, så vi vet allerede at E(ˆµ) = µ. Variansen til ˆµ er 2 2 ( )
Norges teksk-aturvteskapelge uverstet Isttutt for matematske fag Abefalt øvg Løsgssksse Oppgave Det er oppgtt oppgavetekste at estmatore er forvetgsrett, så v vet allerede at Eˆµ µ. Varase tl ˆµ er τ Varˆµ
Kap. 8-3 Sveiseforbindelser. Kap. 8-3 Sveiseforbindelser. Sveiseformer for lastbærende smeltesveis Gjennomgående sveis:
Kap. 8-3 Svisforbidlsr Kap. 8-3 Svisforbidlsr Svisformr for lastbærd smltsvis Gjomgåd svis: Svisig : prosss for sammføyig llr blggig av (i først rkk) mtallisk matrialr. bruks år dt r stor krav til styrk,
Oppgave 1 (25 %) 100 e = 98.02. = 0.9802 R = ln 0.9802. R = 0.020, dvs. spotrenten for 1 år er 2,0 % 100 e = 95.89. e e
Oppgav 1 (5 %) Vi har følgnd: Obligasjon Pålydnd Tid til forfall Kupong Kurs A 1 1 % 98, B 1 % 95,89 C 1 3 5 % 17,99 D 1 4 6 % 113,93 a) Vi finnr nullkupongrntn slik: R 1 = 98. R 1 = 95.89 =.98 R = ln.98
FYS2140 Kvantefysikk, Oblig 10. Sindre Rannem Bilden,Gruppe 4
FYS2140 Kvantfysikk, Oblig 10 Sindr Rannm Bildn,Grupp 4 23. april 2015 Obligr i FYS2140 mrks md navn og gruppnummr! Dtt r nok n oblig som drir sg om hydrognatomt og r n dl av n tidligr ksamnsoppgav. Oppgav
EKSAMEN Løsningsforslag
EKSAMEN Løningforlag 8. juni Emnkod: ITD5 Dao: 6. mai Emn: Mamaikk Ekamnid:.. Hjlpmidlr: - To A-ark md valgfri innhold på bgg idr. - Formlhf. Faglærr: Chriian F Hid Kalkulaor r ikk illa. Ekamnoppgavn:
K j æ r e b e b o e r!
K j æ r e b e b o e r! D e t t e e r i n n k a l l i n g e n t i l å r e t s g e n er a l f o r s a m l i n g. D e n i n n e h o l d e r b o r e t t s l a g e t s å r s m e l d i n g o g r e g n s k a
K j æ r e b e b o e r!
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g e t s å r s b e r e t n i
Pu dd f jo rd Fr yd bøv i Gy Luggårdsvatt ld p ris v i M ich a lk ro N So od r l h Sk og im v s ga t Li sli i h Øvr Riplvi Lø vs ta k kv i Sød r Skill
Gyldpris Mlkplass Etapp 3 Solhimsvik Øvr Riplgård Stradafjllt Etapp 2 2011-2012 Solhim Solhimsvatt Storavatt Løvstakk Etapp 4 Mid Kristiaborgvatt LØVSTIEN Oppdatrt 18.11.2010 Grø tat N Etapp 1 Frdig Laggård
K j æ r e b e b o e r!
K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l å r e t s g e n e r a l f o r s a m l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n
Felt P, Budor Nord. byggeklare tomter i vakre omgivelser
r s i l! Ra rømm d hytt Flt P, Budor Nord byggklar tomtr i vakr omgivlsr 1 g d s o k u d a k r H t r å l h Vlkomm til Budor Md 1,5 tim kjørtid fra Oslo og 1 tim fra Gardrmo har Budor forstrkt si posisjo
Krav om sikker påfyllingsanordning, transport og merking av emballasje for bioetanol til alkoholfyrte peiser.
D da Vår rfras Vår sasbhadlr Drs da Drs rfras gby, lf. 33 41 25 00 I hhld il lis 1 av 5 Arivd 422 Krav sir påfylligsardig, raspr g rig av ballasj fr bial il alhlfyr pisr. Dirra fr safssirh g brdsap (DSB)
TELESKOPLASTER TL1500
SNLIFT as TELESKOPLSTER TL1500 REDSKPSLISTE Priser Eks. Mva FO Oslo - 0 - SNLIFT as INDEX Innholdsfortegnelse 1. Grusskuffe... - 2-2. Hydraulisk Gripeskuffe... - 3-3. 4-1 Skuffe... - 4-4. Snøskuffe...
پ0 3 پ0 3 پ0 3 پ0 3. پ0 3 پ0 3 پ0 3 پ0 3i پ0 3 ² پ0 3 پ0 3 پ0 3 پ0 3 پ0 3 پ0 3 پ0 3 پ0 3 پ0 3
1 31. Tor 2. Tor & 4 پ0 11. Mtt. Hv 4 &پ0 11. Mtt. Hv 41. Mtt Hj Alltd Vank (dansk kst) L J hj all td ud L jeg vl op J hj all td ud jeg vl op van k spپ0ٹ3n luk mt van k spپ0ٹ3n luk mt Je su f hm l tl dt
Chapter 2 - Discrete Mathematics and Its Applications. Løsningsforslag på utvalgte oppgaver
Chpter - Dscrete Mthemtcs d Its pplctos Løsgsforslg på utvlgte oppgver vstt Oppgve Gtt 7 ) E mtrse med rder og koloer er e mtrse Geerelt hr v t e m mtrse er e mtrse med m rder og koloer Uttrykket m klles
Retningslinjer for klart og tydelig språk i Statens vegvesen
Rtningslinjr for klart og tydlig språk i Statns vgvsn vgvsn.no EN KLAR TEKST Slik skrivr vi klar og tydlig tkstr: 1. Vi sørgr for at lsrn får dn informasjonn d trngr ikk mr, ikk mindr. 2. Vi startr tkstn
Regler om normalfordelingen
1 HG Revdert mars 013 Notat tl kapttel 5 Løvås Regler om ormalfordelge Kjeskap tl reglee for ormalfordelge er gruleggede for de statstske aalyse kapttel 6 Løvås, og studetee må kue beherske dsse skkkelg
LØSNING AV EKSAMEN I EMNE TKT 4123 MEKANIKK 2
LØSNNG A EKSAMEN EMNE TKT MEKANKK Tirsdag 6. ai 9 Oga F F F Dforasjon a innkragt bjk (tab 5 F F x og x, hor x r utsing E E t ti d tynn søyn og x r utsingt ti dn idtrst søyn. E Ech Dt gir: F x x og E Ec
Søknad om Grønt Flagg på Østbyen skole
Søknad om på Østbyn skol Østbyn skol startt opp md i 2007, og har sidn da vært n Grønt Flagg-skol som r opptatt av miljø Skoln hatt n dl utfordringr dt sist årt, som har gjort dt vansklig å følg opp intnsjonn