Velkommen til oversiktsforelesninger i Matematikk 1. med Jørgen Endal
|
|
|
- Esther Sunde
- 5 år siden
- Visninger:
Transkript
1 Velkomme til oversiktsforelesiger i Matematikk 1 med Jørge Edal
2 Følger, rekker, og potesrekker (kap ) Forelesig 2 (kap )
3 Dages økkelbegrep: Sammeligigsteste Gresesammeligigsteste Forholdsteste Absolutt og betiget koverges Altererede rekke-teste
4 Kjete rekker Vi vet å at =1 ar 1 = a 1 r for r < 1 =1 p kovergerer for p > 1
5 C. Kovergestester for positive rekker (kap. 9.3) Sammeligigsteste Teorem C.4 (Sammeligigsteste) La {a }, {b } være følger slik at 0 a Kb for K > 0 og stor ok. (a) b kovergerer = a kovergerer (b) a divergerer = b divergerer
6 Sammeligigsteste, eksempel Eksempel C.5 Kovergerer eller divergerer = ?
7 Gresesammeligigsteste Teorem C.6 (Gresesammeligigsteste) La {a }, {b } være følger slik at a lim = L, b L [0, ]. (a) L [0, ) og b kovergerer = a kovergerer (b) L (0, ] og b divergerer = a divergerer
8 Gresesammeligigsteste, eksempel Eksempel C.7 Kovergerer eller divergerer =0 1 3?
9 Forholdsteste Teorem C.8 (Forholdsteste) Ata at a > 0 for stor ok og at ρ = lim a +1, eksisterer eller er lik +. a (a) 0 ρ < 1 = a kovergerer (b) 1 < ρ = a divergerer (c) ρ = 1 = a divergerer eller kovegerer
10 Forholdsteste, eksempler Se f.eks. oppgave 1 i pleumsregig uke 44 (dee uka) for eksempler på bruk av forholdsteste. Se oppgaveløsigsvideo 59 og 60 for flere eksempler, og video 58 for rotteste (som vi ikke har gjeomgått her).
11 D. Absolutt og betiget koverges (kap. 9.4) Se også temavideo 24.
12 Eksempler på koverges s =1 1
13 Eksempler på koverges s =1 1
14 Eksempler på koverges s =1 1
15 Eksempler på koverges s =1 1 2 π2 6
16 Eksempler på koverges s =1 ( 1) 1
17 Eksempler på koverges s =1 ( 1) 1
18 Eksempler på koverges s =1 ( 1) 1 l(2)
19 Forteg har oe å si Vi har sett at med e gag vi tillater rekkee å ha egative ledd, vil kovergesegeskapee edre seg. Fra å av skal vi derfor se på rekker a hvor a R for alle (både positive og egative ledd).
20 Absolutt koverges Defiisjo D.1 (Absolutt koverges) Vi sier at rekka a kovergerer absolutt dersom a kovergerer. Eksempel D.2 Gitt at a 0 for alle og at a kovergerer, vil a kovergere absolutt. Teorem D.3 a kovergerer = a kovergerer Bevis: (a + a ) kovergerer.
21 Altererede harmoisk rekke Eksempel D.4 (Altererede harmoisk rekke) Vi har allerede sett at (se eks. C.1) =1 1 divergerer, me vi la også merke til at ( 1) 1 =1 kovergerte!
22 Betiget koverges Defiisjo D.5 (Betiget koverges) Dersom a er koverget, me ikke absolutt koverget ( a divergerer), sier vi at rekka kovergerer betiget. NB1: For å teste absolutt koverges, ka vi bruke itegralteste (teo. C.2); sammeligigsteste (teo. C.4); gresesammeligigsteste (teo. C.6); forholdsteste (teo. C.8). NB2: Betiget koverges skjer år ulike forteg gir kasellerigseffekt. Summasjosrekkefølge har oe å si (se forrige ukes forelesig, og teorem 16 i kap. 9.4).
23 Altererede rekke-teste Teorem D.6 (Altererede rekke-teste) Ata at {a } er ei følge som tilfredsstiller (i) a a +1 < 0 for stor ok (altererede) (ii) a +1 a for stor ok (avtagede) (iii) lim a = 0 (grese lik 0) Da kovergerer a. Eksempel D.7 For hvilke verdier av x vil rekka (x 5) =1 2 kovergere absolutt eller betiget, eller divergere?
24 Kovergesmetoder Se temavideo 23 for e oppsummerig og oversikt over kovergesmetoder.
25 Avbruddsfeil for altererede rekker Teorem D.8 (Avbruddsfeil for altererede rekker) Dersom vi har ei rekke =1 a som oppfyller kravee i teorem D.6, dvs. =1 a kovergerer (betiget) til et tall s, vil approksimasjoe N =1 a tilfredsstille: (a) s N =1 a har samme forteg som a N+1. (b) s N =1 a a N+1. Eksempel D.9 (Approksimasjo av π) Det er mulig å fie ut at π = 12 =0 ( 1) 3 (2 + 1) (Madhava-Leibiz-rekka). Hvor mage ledd kreves for å rege ut π med e feil på (ellve desimalers øyaktighet)?
26 Flere eksempler Se temavideo 14 for flere eksempler, og om altererede rekker geerelt.
Fasit til utvalgte oppgaver MAT1110, uka 18/5-21/5
 Fasit til utvalgte oppgaver MAT0, uka 8/5-2/5 Øyvid Rya (oyvidry@i.uio.o) May 28, 200 Oppgave 2.4. Rekke er betiget koverget, side + divergerer, mes de altererede rekke kovergerer etter teste for altererede
Fasit til utvalgte oppgaver MAT0, uka 8/5-2/5 Øyvid Rya (oyvidry@i.uio.o) May 28, 200 Oppgave 2.4. Rekke er betiget koverget, side + divergerer, mes de altererede rekke kovergerer etter teste for altererede
Vi skal hovedsakelig ikke bestemme summen men om rekken konvergerer. det vil si om summen til rekken er et bestemt tall
 Kapittel 8 Oppsummerig-Rekker Rekker er summe til edelig eller uedelig mage ledd i e tallfølge. Potesrekker ka beyttes til å uttrykke vaskelige fuksjoer om et pukt. Ma ka skreddesy potesfuksjoer ved hjelp
Kapittel 8 Oppsummerig-Rekker Rekker er summe til edelig eller uedelig mage ledd i e tallfølge. Potesrekker ka beyttes til å uttrykke vaskelige fuksjoer om et pukt. Ma ka skreddesy potesfuksjoer ved hjelp
MA1102 Grunnkurs i Analyse II Vår 2017
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA2 Grukurs i Aalyse II Vår 27 Løsigsforslag Øvig 7 2.5: For hvilke x kovergerer rekke? b) (2x) c) (l x) e) 2 si x 2 b) Dette er
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA2 Grukurs i Aalyse II Vår 27 Løsigsforslag Øvig 7 2.5: For hvilke x kovergerer rekke? b) (2x) c) (l x) e) 2 si x 2 b) Dette er
MA1102 Grunnkurs i analyse II Vår 2014
 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag MA Grukurs i aalyse II Vår 4 Løsigsforslag Øvig 6..5g Ser på forholdet a + /a som er ( + )!4 + ( + ) + ( ) 4( + )! 4( + ) =!4 ( +
Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag MA Grukurs i aalyse II Vår 4 Løsigsforslag Øvig 6..5g Ser på forholdet a + /a som er ( + )!4 + ( + ) + ( ) 4( + )! 4( + ) =!4 ( +
x n = 1 + x + x 2 + x 3 + x x n + = 1 1 x
 Potesrekker Forelest: 29. Sept, 2004 Vi lærte fra de geometriske rekkee at x = 1 + x + x 2 + x 3 + x 4 + + x + = 1 1 x så lege x < 1. For uttrykket til høyre er ikke oe aet e sum-formele for geometriske
Potesrekker Forelest: 29. Sept, 2004 Vi lærte fra de geometriske rekkee at x = 1 + x + x 2 + x 3 + x 4 + + x + = 1 1 x så lege x < 1. For uttrykket til høyre er ikke oe aet e sum-formele for geometriske
e n . Videre er det en alternerende følge, da annenhvert ledd er positivt og negativt. Vi ser også at n a n = lim n e n = 0. lim n n 1 n 3n 2 = lim
 TMA400 Høst 206 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 9 9..8 Vi er gitt følge { ( ) } {a }. e De første leddee i følge er a e, a 2 2 e 2, a e, a 4 4
TMA400 Høst 206 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 9 9..8 Vi er gitt følge { ( ) } {a }. e De første leddee i følge er a e, a 2 2 e 2, a e, a 4 4
s = k k=1 dx x A n = n = lim = lim 2 arctan ( x = π arctan ( n (2k 1)!, s n = k=1
 TMA400 Høst 06 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 0 9.3.30 Me vil fia det miste itervallet som me ka vera sikker på at summe s k k + 4 ligg i. Om
TMA400 Høst 06 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 0 9.3.30 Me vil fia det miste itervallet som me ka vera sikker på at summe s k k + 4 ligg i. Om
Løsningsforslag Eksamen MAT112 vår 2011
 Løsigsforslag Eksame MAT vår OPPGAVE Gitt følge {a } defiert rekursivt ved a = 5, a + = a + 6, =,,, 3,.... (a) Vis (for eksempel ved iduksjo) at {a } er stregt avtagede og edtil begreset. (b) Avgjør om
Løsigsforslag Eksame MAT vår OPPGAVE Gitt følge {a } defiert rekursivt ved a = 5, a + = a + 6, =,,, 3,.... (a) Vis (for eksempel ved iduksjo) at {a } er stregt avtagede og edtil begreset. (b) Avgjør om
8 + 2 n n 4. 3n 4 7 = 8 3.
 Seksjo 4. Oppgave (). Fi greseverdiee: 8 a) 4 + 4 7 b) 4 +7 5 c) + 7 4 ( ) d) 5 4 44 + 5 4 e) 5 + si() e +6 5 Løsig. Vi vil bruke samme metode som i Eksempel 4..5 fra boke i disse oppgavee. Når vi skal
Seksjo 4. Oppgave (). Fi greseverdiee: 8 a) 4 + 4 7 b) 4 +7 5 c) + 7 4 ( ) d) 5 4 44 + 5 4 e) 5 + si() e +6 5 Løsig. Vi vil bruke samme metode som i Eksempel 4..5 fra boke i disse oppgavee. Når vi skal
TMA4100 Matematikk 1 Høst 2014
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag TMA400 Matematikk Høst 04 Løsigsforslag Øvig 3 Review Exercises, side 454 Vi starter med å tege e figur av e skål med va: z A(z)
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag TMA400 Matematikk Høst 04 Løsigsforslag Øvig 3 Review Exercises, side 454 Vi starter med å tege e figur av e skål med va: z A(z)
MA 1410: Analyse Uke 48, aasvaldl/ma1410 H01. Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag
 MA 40: Aalyse Uke 48, 00 http://home.hia.o/ aasvaldl/ma40 H0 Høgskole i Agder Avdelig for realfag Istitutt for matematiske fag Oppgave 8.7:. Vi har f(x) = cosh(x) = ex +e x. f(0) =. Derivasjo gir f (x)
MA 40: Aalyse Uke 48, 00 http://home.hia.o/ aasvaldl/ma40 H0 Høgskole i Agder Avdelig for realfag Istitutt for matematiske fag Oppgave 8.7:. Vi har f(x) = cosh(x) = ex +e x. f(0) =. Derivasjo gir f (x)
Konvergenstester Forelesning i Matematikk 1 TMA4100
 Konvergenstester Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.3. Integrasjonstesten 3 Ikke-avtagende delsummer Husker at n-te delsum av
Konvergenstester Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.3. Integrasjonstesten 3 Ikke-avtagende delsummer Husker at n-te delsum av
MA1102 Grunnkurs i analyse II Vår 2014
 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag MA Grukurs i aalyse II Vår 4 Løsigsforslag Øvig..4 f ) Skriver om, og får Reger ut ved L'Hopitals regel at cos/) cos/)) = /. cos/)
Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag MA Grukurs i aalyse II Vår 4 Løsigsforslag Øvig..4 f ) Skriver om, og får Reger ut ved L'Hopitals regel at cos/) cos/)) = /. cos/)
Velkommen til oversiktsforelesninger i Matematikk 1. med Jørgen Endal
 Velkommen til oversiktsforelesninger i Matematikk 1 med Jørgen Endal Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Forelesning 1 (kap.
Velkommen til oversiktsforelesninger i Matematikk 1 med Jørgen Endal Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Nytt tema: Følger, rekker, og potensrekker (kap. 9.1 9.7) Forelesning 1 (kap.
MA1101 Grunnkurs Analyse I Høst 2017
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Løsningsforslag til prøveeksamen i MAT1110, våren 2012
 Løsigsforslag til prøveeksame i MAT, våre Oppgave : Vi har A = 3 III+I I+II 3 ( )II 3 3 Legg merke til at A er de utvidede matrise til ligigssystemet. Vi ser at søyle 3 og 4 i de reduserte trappeforme
Løsigsforslag til prøveeksame i MAT, våre Oppgave : Vi har A = 3 III+I I+II 3 ( )II 3 3 Legg merke til at A er de utvidede matrise til ligigssystemet. Vi ser at søyle 3 og 4 i de reduserte trappeforme
Følger og rekker. Kapittel Følger
 Kapittel 4 Følger og rekker E viktig egeskap ved polyomiale fuksjoer er at vi ekelt) ka rege ut verdiee av fuksjoee i et valgt pukt. Grue er at polyomer er et slags speilbilde av de valige regeoperasjoee.
Kapittel 4 Følger og rekker E viktig egeskap ved polyomiale fuksjoer er at vi ekelt) ka rege ut verdiee av fuksjoee i et valgt pukt. Grue er at polyomer er et slags speilbilde av de valige regeoperasjoee.
Øvinger uke 46 løsninger
 Øviger uke 6 løsiger Oppgave Verdie av determiate er avgjørede for atall løsiger. ed e parameter i oppgave løer det seg å bestemme determiate først og fie ut for hvilke parameterverdier determiate er ull.
Øviger uke 6 løsiger Oppgave Verdie av determiate er avgjørede for atall løsiger. ed e parameter i oppgave løer det seg å bestemme determiate først og fie ut for hvilke parameterverdier determiate er ull.
Ma Analyse II Øving 5
 Ma0 - Aalyse II Øvig 5 Øistei Søvik.0.0 Oppgaver 9. Determie whether the give sequece is (a) bouded (above or below), (b) positive or egative (ultimately), (c) icreasig, decreasig, or alteratig, ad (d)
Ma0 - Aalyse II Øvig 5 Øistei Søvik.0.0 Oppgaver 9. Determie whether the give sequece is (a) bouded (above or below), (b) positive or egative (ultimately), (c) icreasig, decreasig, or alteratig, ad (d)
MA1102 Grunnkurs i analyse II Vår 2019
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs i aalyse II Vår 09 9 Vi har rekke Dette er e geometrisk rekke som beskrevet på side 50 i læreboka, med x (side ) Spesielt
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs i aalyse II Vår 09 9 Vi har rekke Dette er e geometrisk rekke som beskrevet på side 50 i læreboka, med x (side ) Spesielt
Følger og rekker. Department of Mathematical Sciences, NTNU, Norway. November 10, 2014
 Department of Mathematical Sciences, NTNU, Norway November 10, 2014 Forelesning (03.01.2014): kap 9.1 og 9.2 Beskrivelse av følger eksempler og definisjon Egenskaper med følger Grenseverdi for følger (og
Department of Mathematical Sciences, NTNU, Norway November 10, 2014 Forelesning (03.01.2014): kap 9.1 og 9.2 Beskrivelse av følger eksempler og definisjon Egenskaper med følger Grenseverdi for følger (og
Utvidet løsningsforslag Eksamen i TMA4100 Matematikk 1, 16/12 2008
 Utvidet løsigsforslag Eksame i TMA4 Matematikk, 6/ 8 Oppgave i) Vi gjør substitusjoe u = si θ og får π/ [ u si θ cos θ dθ = u du = E ae løsigsmetode er π/ si θ cos θ dθ = π/ ] si θ dθ = 4 = 4 ( ( ) ( ))
Utvidet løsigsforslag Eksame i TMA4 Matematikk, 6/ 8 Oppgave i) Vi gjør substitusjoe u = si θ og får π/ [ u si θ cos θ dθ = u du = E ae løsigsmetode er π/ si θ cos θ dθ = π/ ] si θ dθ = 4 = 4 ( ( ) ( ))
TMA4100 Matematikk 1 for MTDESIG, MTIØT-PP, MTMART og MTPROD høsten 2010
 TMA4100 Matematikk 1 for MTDESIG, MTIØT-PP, MTMART og MTPROD høsten 2010 Toke Meier Carlsen Institutt for matematiske fag 28. oktober 2010 2 Fremdriftplan I går 7.7 Uegentlige integraler 8.1 Følger I dag
TMA4100 Matematikk 1 for MTDESIG, MTIØT-PP, MTMART og MTPROD høsten 2010 Toke Meier Carlsen Institutt for matematiske fag 28. oktober 2010 2 Fremdriftplan I går 7.7 Uegentlige integraler 8.1 Følger I dag
Totalt Antall kandidater oppmeldt 1513 Antall møtt til eksamen 1421 Antall bestått 1128 Antall stryk 247 Antall avbrutt 46 % stryk og avbrutt 21%
 TMA4100 Høste 2007 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Kommetarer til eksame Dette dokumetet er e oppsummerig av erfarigee fra sesure av eksame i TMA4100 Matematikk
TMA4100 Høste 2007 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Kommetarer til eksame Dette dokumetet er e oppsummerig av erfarigee fra sesure av eksame i TMA4100 Matematikk
Positive rekker. Forelest: 3. Sept, 2004
 Postve rekker Forelest: 3. Sept, 004 V skal tde utover fokusere på å teste om e rekke kovergerer, og skyve formler for summerg bakgrue. Dette er gje ford det første målet vårt er å lære hvorda v ka fe
Postve rekker Forelest: 3. Sept, 004 V skal tde utover fokusere på å teste om e rekke kovergerer, og skyve formler for summerg bakgrue. Dette er gje ford det første målet vårt er å lære hvorda v ka fe
FØLGER, REKKER OG GJENNOMSNITT
 FØLGER, REKKER OG GJENNOMSNITT Espe B. Lagelad realfagshjoret.wordpress.com espebl@hotmail.com 9.mars 06 Iledig E tallfølge er e serie med tall som kommer etter hveradre i e bestemt rekkefølge. Kvadrattallee
FØLGER, REKKER OG GJENNOMSNITT Espe B. Lagelad realfagshjoret.wordpress.com espebl@hotmail.com 9.mars 06 Iledig E tallfølge er e serie med tall som kommer etter hveradre i e bestemt rekkefølge. Kvadrattallee
S2 kapittel 1 Rekker Løsninger til innlæringsoppgavene
 Løsiger til ilærigsoppgavee kapittel Rekker Løsiger til ilærigsoppgavee a Vi ser at differase mellom hvert ledd er 4, så vi får det este leddet ved å legge til 4 Det este leddet blir altså 6 + 4 = 0 b
Løsiger til ilærigsoppgavee kapittel Rekker Løsiger til ilærigsoppgavee a Vi ser at differase mellom hvert ledd er 4, så vi får det este leddet ved å legge til 4 Det este leddet blir altså 6 + 4 = 0 b
OM TAYLOR POLYNOMER. f x K f a x K a. f ' a = lim x/ a. f ' a z
 OM TAYLOR POLYNOMER I dette otatet, som utfyller avsitt 6. i Gullikses bok, skal vi se på Taylor polyomer og illustrere hvorfor disse er yttige. Det å berege Taylor polyomer for håd er i prisippet ikke
OM TAYLOR POLYNOMER I dette otatet, som utfyller avsitt 6. i Gullikses bok, skal vi se på Taylor polyomer og illustrere hvorfor disse er yttige. Det å berege Taylor polyomer for håd er i prisippet ikke
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker
 Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 15. februar 2010 Funksjonsrekker En rekke på formen f n (x) der f n er en funksjon, kalles en funksjonsrekke. For alle x
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 15. februar 2010 Funksjonsrekker En rekke på formen f n (x) der f n er en funksjon, kalles en funksjonsrekke. For alle x
Potensrekker Forelesning i Matematikk 1 TMA4100
 Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.7. Potensrekker (fra konvergens av) 3 Konvergens av potensrekker Eksempel For
Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.7. Potensrekker (fra konvergens av) 3 Konvergens av potensrekker Eksempel For
ÅMA110 Sannsynlighetsregning med statistikk, våren 2008 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 56
ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 56
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1 / 56
ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1 / 56
ECON240 Statistikk og økonometri
 ECON240 Statistikk og økoometri Arild Aakvik, Istitutt for økoomi 1 Mellomregig MKM Model: Y i = a i + bx i + e i MKM-estimator for b: b = = Xi Y i 1 Xi Yi Xi 1 ( X i ) 2 (Xi X)(Y i Ȳi) (Xi X) 2 hvor vi
ECON240 Statistikk og økoometri Arild Aakvik, Istitutt for økoomi 1 Mellomregig MKM Model: Y i = a i + bx i + e i MKM-estimator for b: b = = Xi Y i 1 Xi Yi Xi 1 ( X i ) 2 (Xi X)(Y i Ȳi) (Xi X) 2 hvor vi
Differensligninger Forelesningsnotat i Diskret matematikk Differensligninger
 Differesligiger Forelesigsotat i Diskret matematikk 017 Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker er imidlertid
Differesligiger Forelesigsotat i Diskret matematikk 017 Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker er imidlertid
Høgskolen i Telemark Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 16. mai 2008
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL 6. mai 008 EKSAMEN I MATEMATIKK Modul 5 studiepoeg Tid: 5 timer Oppgavesettet er på 8 sider (ikludert formelsamlig). Hjelpemidler:
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL 6. mai 008 EKSAMEN I MATEMATIKK Modul 5 studiepoeg Tid: 5 timer Oppgavesettet er på 8 sider (ikludert formelsamlig). Hjelpemidler:
Avsnitt 8.1 i læreboka Differensligninger
 Diskret Matematikk Fredag 6. ovember 015 Avsitt 8.1 i læreboka Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker
Diskret Matematikk Fredag 6. ovember 015 Avsitt 8.1 i læreboka Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker
1 Mandag 1. februar 2010
 Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker
 Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 14. februar 2012 Funksjonsrekker En rekke på formen fn(x) der fn er en funksjon, kalles en n=1 funksjonsrekke. For alle
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 14. februar 2012 Funksjonsrekker En rekke på formen fn(x) der fn er en funksjon, kalles en n=1 funksjonsrekke. For alle
Algebra S2, Prøve 2 løsning
 Algebra S, Prøve løsig Del Tid: 90 mi Hjelpemidler: Skrivesaker Oppgave I rekkee edefor får du oppgitt a og e rekursiv formel for a. Du skal. skrive opp de fire første leddee og avgjøre om rekka er aritmetisk,
Algebra S, Prøve løsig Del Tid: 90 mi Hjelpemidler: Skrivesaker Oppgave I rekkee edefor får du oppgitt a og e rekursiv formel for a. Du skal. skrive opp de fire første leddee og avgjøre om rekka er aritmetisk,
Konvergenstester Forelesning i Matematikk 1 TMA4100
 Konvergenstester Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.6. Alternerende rekker Absolutt og betinget konvergens 3 Alternerende rekker
Konvergenstester Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.6. Alternerende rekker Absolutt og betinget konvergens 3 Alternerende rekker
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Kp. 6, del 5. Hypotesetesting, del 5
 ÅMA11 Sasylighetsregig med statistikk, våre 7 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 59 Bjør
ÅMA11 Sasylighetsregig med statistikk, våre 7 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 59 Bjør
FINNE n-te RØTTER AV KOMPLEKSE TALL
 FINNE -TE RØTTER AV KOMPLEKSE TALL SHIRIN FALLAHI OG ANDREAS LEOPOLD KNUTSEN Vi utdyper det som står helt i slutte av Appediks I i læreboke etter Example 7. Ata at vi vil fie alle -te røttee til et gitt
FINNE -TE RØTTER AV KOMPLEKSE TALL SHIRIN FALLAHI OG ANDREAS LEOPOLD KNUTSEN Vi utdyper det som står helt i slutte av Appediks I i læreboke etter Example 7. Ata at vi vil fie alle -te røttee til et gitt
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010. Noen viktige sannsynlighetsmodeller. Binomisk modell. Kp. 3 Diskrete tilfeldige variable
 ÅMA Saslighetsregig med statistikk, våre K. 3 Diskrete tilfeldige variable Noe viktige saslighetsmodeller Noe viktige saslighetsmodeller ( Sas.modell : å betr det klasse/te sas.fordelig.) Biomisk modell
ÅMA Saslighetsregig med statistikk, våre K. 3 Diskrete tilfeldige variable Noe viktige saslighetsmodeller Noe viktige saslighetsmodeller ( Sas.modell : å betr det klasse/te sas.fordelig.) Biomisk modell
Forelesning 4 og 5 Transformasjon, Weibull-, lognormal, beta-, kji-kvadrat -, t-, F- fordeling
 STAT (V6) Statistikk Metoder Yushu.Li@uib.o Forelesig 4 og 5 Trasformasjo, Weibull-, logormal, beta-, kji-kvadrat -, t-, F- fordelig. Oppsummerig til Forelesig og..) Momet (momet about 0) og setral momet
STAT (V6) Statistikk Metoder Yushu.Li@uib.o Forelesig 4 og 5 Trasformasjo, Weibull-, logormal, beta-, kji-kvadrat -, t-, F- fordelig. Oppsummerig til Forelesig og..) Momet (momet about 0) og setral momet
Bjørn Davidsen MATEMATIKK FOR INGENIØRER. Rekker
 Bjør Davidse MATEMATIKK FOR INGENIØRER Reer Reer Side Ihold FORORD REKKER 4 NOEN INNEDENDE DEFINISJONER 4 KONVERGENS AV REKKER 6 ARITMETISKE OG GEOMETRISKE REKKER 9 Aritmetise tallfølger og reer 9 Geometrise
Bjør Davidse MATEMATIKK FOR INGENIØRER Reer Reer Side Ihold FORORD REKKER 4 NOEN INNEDENDE DEFINISJONER 4 KONVERGENS AV REKKER 6 ARITMETISKE OG GEOMETRISKE REKKER 9 Aritmetise tallfølger og reer 9 Geometrise
Introduksjon. Hypotesetesting / inferens (kap 3) Populasjon og utvalg. Populasjon og utvalg. Populasjonsvarians
 Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
Mer om utvalgsundersøkelser
 Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
EKSAMEN Løsningsforslag
 ..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
Polynominterpolasjon
 Polyomiterpolasjo Ae Kværø March 5, 2018 1 Problemstillig Gitt + 1 pukter (x i, y i ) i=0 med distikte x-verdier (dvs. x i = x j hvis i = j). Fi et polyom p(x) av lavest mulig grad slik at p(x i ) = y
Polyomiterpolasjo Ae Kværø March 5, 2018 1 Problemstillig Gitt + 1 pukter (x i, y i ) i=0 med distikte x-verdier (dvs. x i = x j hvis i = j). Fi et polyom p(x) av lavest mulig grad slik at p(x i ) = y
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2010 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 12. april Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 59
ÅMA110 Sasylighetsregig med statistikk, våre 2010 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 12. april Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 59
Eksamen R2, Høsten 2010
 Eksame R, Høste 00 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (6 poeg) a) Deriver fuksjoee ) f l f ( ) l l (l ) ) g( ) si cos f si
Eksame R, Høste 00 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (6 poeg) a) Deriver fuksjoee ) f l f ( ) l l (l ) ) g( ) si cos f si
Estimering 2. -Konfidensintervall
 Estimerig 2 -Kofidesitervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesigsotatee. Dersom forsøket gjetas mage gager vil (1 α)100% av itervallee [ ˆΘ L, ˆΘ U ] ieholde de ukjete parametere θ (som er
Estimerig 2 -Kofidesitervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesigsotatee. Dersom forsøket gjetas mage gager vil (1 α)100% av itervallee [ ˆΘ L, ˆΘ U ] ieholde de ukjete parametere θ (som er
Terminprøve R2 Høsten 2014 Løsning
 Termiprøve R Høste 04 Løsig Del Tid: 3 timer Hjelpemidler: Skrivesaker Oppgave (6 poeg) E flate i rommet er gitt ved likige: x 4x y 6y z 8z 0 0 a) Vis at puktet P3, 5, ligger på flate Puktet P3, 5, ligger
Termiprøve R Høste 04 Løsig Del Tid: 3 timer Hjelpemidler: Skrivesaker Oppgave (6 poeg) E flate i rommet er gitt ved likige: x 4x y 6y z 8z 0 0 a) Vis at puktet P3, 5, ligger på flate Puktet P3, 5, ligger
E K S A M E N : FAG: Matematikk 1 MA-154 LÆRER: MORTEN BREKKE. Klasse(r): Alle Dato: 1. des 11 Eksamenstid, fra-til: 0900-1400
 UNIVERSITETET I AGDER Grimstad E K S A M E N : FAG: Matematikk MA-54 LÆRER: MORTEN BREKKE Klasse(r): Alle Dato:. des Eksamestid, fra-til: 0900-400 Eksamesoppgave består av følgede iklusive forside Atall
UNIVERSITETET I AGDER Grimstad E K S A M E N : FAG: Matematikk MA-54 LÆRER: MORTEN BREKKE Klasse(r): Alle Dato:. des Eksamestid, fra-til: 0900-400 Eksamesoppgave består av følgede iklusive forside Atall
Kapittel 9: Mer kombinatorikk
 MAT00 Disret Matemati Forelesig : Mer ombiatori Roger Atose Istitutt for iformati, Uiversitetet i Oslo Kapittel 9: Mer ombiatori 5. april 009 (Sist oppdatert: 009-04-5 00:06) MAT00 Disret Matemati 5. april
MAT00 Disret Matemati Forelesig : Mer ombiatori Roger Atose Istitutt for iformati, Uiversitetet i Oslo Kapittel 9: Mer ombiatori 5. april 009 (Sist oppdatert: 009-04-5 00:06) MAT00 Disret Matemati 5. april
Kommentarer til oppgaver;
 Kapittel - Algebra Versjo: 11.09.1 - Rettet feil i 0, 1 og 70 og lagt i litt om GeoGebra-bruk Kommetarer til oppgaver; 0, 05, 10, 13, 15, 5, 9, 37, 5,, 5, 59, 1, 70, 7, 78, 80,81 0 a) Trykkfeil i D-koloe
Kapittel - Algebra Versjo: 11.09.1 - Rettet feil i 0, 1 og 70 og lagt i litt om GeoGebra-bruk Kommetarer til oppgaver; 0, 05, 10, 13, 15, 5, 9, 37, 5,, 5, 59, 1, 70, 7, 78, 80,81 0 a) Trykkfeil i D-koloe
TMA4100 Høst Løsningsforslag Øving 2. Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag
 TMA400 Høst 206 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 2 2..0: Vi bruker eisjoe for ikke-vertikale tagetlijer sie 97 i læreboke). Tagetlije gjeom et pukt
TMA400 Høst 206 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 2 2..0: Vi bruker eisjoe for ikke-vertikale tagetlijer sie 97 i læreboke). Tagetlije gjeom et pukt
Forkunnskaper i matematikk for fysikkstudenter. Derivasjon.
 Defiisjo av derivert Vi har stor ytte av å vite hvor raskt e fuksjo vokser eller avtar Mer presist: Vi øsker å bestemme stigigstallet til tagete til fuksjosgrafe P Q Figure til vestre viser hvorda vi ka
Defiisjo av derivert Vi har stor ytte av å vite hvor raskt e fuksjo vokser eller avtar Mer presist: Vi øsker å bestemme stigigstallet til tagete til fuksjosgrafe P Q Figure til vestre viser hvorda vi ka
Statistikk og økonomi, våren 2017
 Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
Kapittel 10 fra læreboka Grafer
 Forelesigsotat i Diskret matematikk torsdag 6. oktober 017 Kapittel 10 fra læreboka Grafer (utdrag) E graf er e samlig pukter (oder) og kater mellom puktee (eg. odes, vertex, edge). E graf kalles rettet
Forelesigsotat i Diskret matematikk torsdag 6. oktober 017 Kapittel 10 fra læreboka Grafer (utdrag) E graf er e samlig pukter (oder) og kater mellom puktee (eg. odes, vertex, edge). E graf kalles rettet
IN3030 Uke 12, v2019. Eric Jul PSE, Inst. for informatikk
 IN3030 Uke 12, v2019 Eric Jul PSE, Ist. for iformatikk 1 Hva skal vi se på i Uke 12 Review Radix sort Oblig 4 Text Program Parallellizig 2 Oblig 4 Radix sort Parallelliser Radix-sorterig med fra 1 5 sifre
IN3030 Uke 12, v2019 Eric Jul PSE, Ist. for iformatikk 1 Hva skal vi se på i Uke 12 Review Radix sort Oblig 4 Text Program Parallellizig 2 Oblig 4 Radix sort Parallelliser Radix-sorterig med fra 1 5 sifre
Matematikk for IT. Prøve 2. Onsdag 21. oktober 2015
 Matematikk for IT Prøve Osdag. oktober 5 Løsigsforslag 6. oktober 5 Oppgave Gitt følgede slutig: Hvis fakturae ble sedt forrige madag så fikk du pegee i går. Du fikk pegee i går. Derfor ble fakturae sedt
Matematikk for IT Prøve Osdag. oktober 5 Løsigsforslag 6. oktober 5 Oppgave Gitt følgede slutig: Hvis fakturae ble sedt forrige madag så fikk du pegee i går. Du fikk pegee i går. Derfor ble fakturae sedt
Matematikk for IT. Løsningsforslag til prøve 2. Torsdag 24. oktober 2013
 .. Matematikk for IT Løsigsforslag til prøve Torsdag. oktober Oppgave Gitt følgede predikat: P(x : x > 5 ta at uiverset ( de mulige verdier av x som vi tar i betraktig er alle hele tall, Z. Skriv hvert
.. Matematikk for IT Løsigsforslag til prøve Torsdag. oktober Oppgave Gitt følgede predikat: P(x : x > 5 ta at uiverset ( de mulige verdier av x som vi tar i betraktig er alle hele tall, Z. Skriv hvert
= x lim n n 2 + 2n + 4
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving Avsnitt 8.7 6 Potensrekken konvergerer opplagt for x = 0, så i drøftingen nedenfor antar vi x 0. Vi vil bruke forholdstesten
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving Avsnitt 8.7 6 Potensrekken konvergerer opplagt for x = 0, så i drøftingen nedenfor antar vi x 0. Vi vil bruke forholdstesten
2.1 Polynomdivisjon. Oppgave 2.10
 . Polyomdivisjo Oppgave. ( 5 + ) : = + + ( + ):( ) 6 + 6 8 8 = + + c) ( + 5 ) : = + 6 6 d) + + + = + + = + + + 8+ ( ):( ) + + + Oppgave. ( + 5+ ):( ) 5 + + = + ( 5 ): 9 + + + = + + + 5 + 6 9 c) ( 8 66
. Polyomdivisjo Oppgave. ( 5 + ) : = + + ( + ):( ) 6 + 6 8 8 = + + c) ( + 5 ) : = + 6 6 d) + + + = + + = + + + 8+ ( ):( ) + + + Oppgave. ( + 5+ ):( ) 5 + + = + ( 5 ): 9 + + + = + + + 5 + 6 9 c) ( 8 66
Estimering 1 -Punktestimering
 Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Forelesning Moment og Momentgenererende funksjoner
 ushu.li@uib.o Forelesig + 3 Momet og Mometgeererede fuksjoer 1. Oppsummerig til Forelesig 1 1.1) Fuksjoe av S.V: hvis variabele er e fuksjo (trasformasjo) av S.V. : g( ), da er også e S.V.: til ethvert
ushu.li@uib.o Forelesig + 3 Momet og Mometgeererede fuksjoer 1. Oppsummerig til Forelesig 1 1.1) Fuksjoe av S.V: hvis variabele er e fuksjo (trasformasjo) av S.V. : g( ), da er også e S.V.: til ethvert
Løsningsforslag ST2301 øving 3
 Løsigsforslag ST2301 øvig 3 Kapittel 1 Exercise 11 Et utvalg på 100 idivider trekkes fra e populasjo med tilfeldig parrig. Det ble observert AA 63 idivider av geotype AA, Aa 27, og aa 10. Lag et 95 % kofidesitervall
Løsigsforslag ST2301 øvig 3 Kapittel 1 Exercise 11 Et utvalg på 100 idivider trekkes fra e populasjo med tilfeldig parrig. Det ble observert AA 63 idivider av geotype AA, Aa 27, og aa 10. Lag et 95 % kofidesitervall
Estimering 1 -Punktestimering
 Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Kap. 9: Inferens om én populasjon. Egenskaper ved t-fordelingen. ST0202 Statistikk for samfunnsvitere. I Kapittel 8 brukte vi observatoren
 2 Kap. 9: Iferes om é populasjo I Kapittel 8 brukte vi observatore z = x μ σ/ for å trekke koklusjoer om μ. Dette krever kjet σ (urealistisk). ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for
2 Kap. 9: Iferes om é populasjo I Kapittel 8 brukte vi observatore z = x μ σ/ for å trekke koklusjoer om μ. Dette krever kjet σ (urealistisk). ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for
LØSNING: Eksamen 17. des. 2015
 LØSNING: Eksame 17. des. 2015 MAT100 Matematikk, 2015 Oppgave 1: økoomi a I optimum av T Rx er dt Rx 0 1 som gir d Ix Kx 0 2 dix dix dkx dkx 0 3 4 dvs. greseitekt gresekostad, q.e.d. 5 b Gresekostad ekstrakostade
LØSNING: Eksame 17. des. 2015 MAT100 Matematikk, 2015 Oppgave 1: økoomi a I optimum av T Rx er dt Rx 0 1 som gir d Ix Kx 0 2 dix dix dkx dkx 0 3 4 dvs. greseitekt gresekostad, q.e.d. 5 b Gresekostad ekstrakostade
LØSNING, EKSAMEN I STATISTIKK, TMA4240, DESEMBER Anta at sann porøsitet er r. Måling med utstyret gir da X n(x; r, 0,03).
 LØSNING, EKSAMEN I STATISTIKK, TMA440, DESEMBER 006 OPPGAVE 1 Ata at sa porøsitet er r. Målig med utstyret gir da X (x; r, 0,03). a) ( ) X r P(X > r) P 0,03 > 0 P(Z > 0) 0,5. ( X r P(X r > 0,05) P 0,03
LØSNING, EKSAMEN I STATISTIKK, TMA440, DESEMBER 006 OPPGAVE 1 Ata at sa porøsitet er r. Målig med utstyret gir da X (x; r, 0,03). a) ( ) X r P(X > r) P 0,03 > 0 P(Z > 0) 0,5. ( X r P(X r > 0,05) P 0,03
Ukeoppgaver, uke 42, i Matematikk 10, Bestemt integrasjon. 1
 Ukeoppgaver, uke 2, i Matematikk, Bestemt itegrasjo. Høgskole i Gjøvik Avdelig for igeiørfag Matematikk Ukeoppgaver uke 2 I løpet av uke blir løsigsforslag lagt ut på emeside http://www.hig.o/toel/allmefag/emesider/rea2
Ukeoppgaver, uke 2, i Matematikk, Bestemt itegrasjo. Høgskole i Gjøvik Avdelig for igeiørfag Matematikk Ukeoppgaver uke 2 I løpet av uke blir løsigsforslag lagt ut på emeside http://www.hig.o/toel/allmefag/emesider/rea2
Detaljert løsningsveiledning til ECON1310 seminaroppgave 9, høsten der 0 < t < 1
 Detaljert løsigsveiledig til ECON30 semiaroppgave 9, høste 206 Dee løsigsveiledige er mer detaljert e det et fullgodt svar på oppgave vil være, og mer utfyllede e e valig fasit. De er met som e guide til
Detaljert løsigsveiledig til ECON30 semiaroppgave 9, høste 206 Dee løsigsveiledige er mer detaljert e det et fullgodt svar på oppgave vil være, og mer utfyllede e e valig fasit. De er met som e guide til
Kapittel 1: Beskrivende statistikk
 Kapittel : Bekrivede tatitikk Defiijoer: Populajo og utvalg Populajo: Alle mulige obervajoer vi ka gjøre (x,x,,x N ). Utvalg: Delmegde av populajoe (x,x,,x der
Kapittel : Bekrivede tatitikk Defiijoer: Populajo og utvalg Populajo: Alle mulige obervajoer vi ka gjøre (x,x,,x N ). Utvalg: Delmegde av populajoe (x,x,,x der
Plan for fagdag 3. Plan: Litt om differanse- og summefølger. Sammenhengen a n a 1 n 1 i 1
 Pla for fagdag 3 R2-18.11.10 Pla: Litt om differase- og summefølger. Sammehege a a 1 1 i 1 d i. Geometriske resoemet. Arbeidsoppgaver. Differase- og summefølger Regresjo med lommereger Differaser er ofte
Pla for fagdag 3 R2-18.11.10 Pla: Litt om differase- og summefølger. Sammehege a a 1 1 i 1 d i. Geometriske resoemet. Arbeidsoppgaver. Differase- og summefølger Regresjo med lommereger Differaser er ofte
2. Bestem nullpunktene til g.
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL 0. desember 007 EKSAMEN I MATEMATIKK Modul 5 studiepoeg Tid: 5 timer Oppgavesettet er på 9 sider (ikludert formelsamlig).
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL 0. desember 007 EKSAMEN I MATEMATIKK Modul 5 studiepoeg Tid: 5 timer Oppgavesettet er på 9 sider (ikludert formelsamlig).
f(x) = x 2 x 2 f 0 (x) = 2x + 2x 3 x g(x) f(x) = f 0 (x) = g(x) xg0 (x) g(x) 2 f(x; y) = (xy + 1) 2 f 0 x = 2(xy + 1)y f 0 y = 2(xy + 1)x
 Ogave a) f() = f 0 () = + 3 ) f() = g() f 0 () = g() g0 () g() c) f(; y) = (y + ) f 0 = (y + )y f 0 y = (y + ) d) f(; y) = ( y + ) ( y ) f 0 = ( y + ) r y ( y ) + ( y + ) ( y ) r y = ( y + )( r y y ) ((
Ogave a) f() = f 0 () = + 3 ) f() = g() f 0 () = g() g0 () g() c) f(; y) = (y + ) f 0 = (y + )y f 0 y = (y + ) d) f(; y) = ( y + ) ( y ) f 0 = ( y + ) r y ( y ) + ( y + ) ( y ) r y = ( y + )( r y y ) ((
Oppgaver fra boka: Med lik men ukjent varians antatt har vi fra pensum at. t n1 +n 2 2 under H 0 (12 1) (12 1)
 MOT30 Statistiske metoder, høste00 Løsiger til regeøvig r. 5 (s. ) Oppgaver fra boka: Oppgave 0.36 (0.0:8) Dekkslitasje X,..., X u.i.f. N(µ, σ ) og X,..., X u.i.f. N(µ, σ ) og alle variable er uavhegige.
MOT30 Statistiske metoder, høste00 Løsiger til regeøvig r. 5 (s. ) Oppgaver fra boka: Oppgave 0.36 (0.0:8) Dekkslitasje X,..., X u.i.f. N(µ, σ ) og X,..., X u.i.f. N(µ, σ ) og alle variable er uavhegige.
ÅMA110 Sannsynlighetsregning med statistikk, våren Estimering. Målemodellen. Konfidensintervall, innledning. Kp. 5 Estimering.
 ÅMA0 Sasylighetsregig med statistikk våre 006 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (Pukt)Estimerig i målemodelle (kp. 5.3)
ÅMA0 Sasylighetsregig med statistikk våre 006 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (Pukt)Estimerig i målemodelle (kp. 5.3)
SIF53 Matemati Esame gir = 4 =:5 (legde νa delitervallee) og deleutee x =,x =:5, x =,x 3 =:5 ogx 4 =. Med f(x) = +x 4 fνar vi tabelle: x : :5 :
 SIF53 Matemati Esame 8..999 Norges teis-aturvitesaelige uiversitet Istitutt for matematise fag Lsigsforslag X = ( ) : Diverget. X = ( ) X ( ) : Absolutt overget. = : Betiget overget. (i) (ii) x! x! x(e
SIF53 Matemati Esame 8..999 Norges teis-aturvitesaelige uiversitet Istitutt for matematise fag Lsigsforslag X = ( ) : Diverget. X = ( ) X ( ) : Absolutt overget. = : Betiget overget. (i) (ii) x! x! x(e
Konfidensintervall. Notat til STK1110. Ørnulf Borgan, Ingrid K. Glad og Anders Rygh Swensen Matematisk institutt, Universitetet i Oslo.
 Kofidesitervall Notat til STK1110 Ørulf Borga, Igrid K. Glad og Aders Rygh Swese Matematisk istitutt, Uiversitetet i Oslo August 2007 Formål E valig metode for å agi usikkerhete til et estimat er å berege
Kofidesitervall Notat til STK1110 Ørulf Borga, Igrid K. Glad og Aders Rygh Swese Matematisk istitutt, Uiversitetet i Oslo August 2007 Formål E valig metode for å agi usikkerhete til et estimat er å berege
Kombinatorikk. MAT1030 Diskret matematikk Forelesning 20: Kombinatorikk. Repetisjon. Repetisjon
 Kombiatori MAT Disret matemati orelesig : Kombiatori Roger Atose Matematis Istitutt, Uiversitetet i Oslo 7. april 8 Kombiatori er studiet av opptelliger, ombiasjoer og permutasjoer. Vi fier svar på spørsmål
Kombiatori MAT Disret matemati orelesig : Kombiatori Roger Atose Matematis Istitutt, Uiversitetet i Oslo 7. april 8 Kombiatori er studiet av opptelliger, ombiasjoer og permutasjoer. Vi fier svar på spørsmål
Fagdag 2-3mx 24.09.07
 Fagdag 2-3mx 24.09.07 Jeg beklager at jeg ikke har fuet oe ye morsomme spill vi ka studere, til gjegjeld skal dere slippe prøve/test dee gage. Istruks: Vi arbeider som valig med 3 persoer på hver gruppe.
Fagdag 2-3mx 24.09.07 Jeg beklager at jeg ikke har fuet oe ye morsomme spill vi ka studere, til gjegjeld skal dere slippe prøve/test dee gage. Istruks: Vi arbeider som valig med 3 persoer på hver gruppe.
LØSNINGSFORSLAG TILEKSAMEN I FAG TMA4240/TMA4245 STATISTIKK 10. august 2005
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 8 LØSNINGSFORSLAG TILEKSAMEN I FAG TMA440/TMA445 STATISTIKK 0. august 005 Oppgave Smeltepuktsbestemmelse a) Vi jobber i dette
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 8 LØSNINGSFORSLAG TILEKSAMEN I FAG TMA440/TMA445 STATISTIKK 0. august 005 Oppgave Smeltepuktsbestemmelse a) Vi jobber i dette
TMA4100 Matematikk 1 Høst 2006
 TMA4 Mtemtikk Høst 26 Norges tekisk turviteskpelige uiversitet Istitutt for mtemtiske fg Løsigsforslg, vsluttede eksme 5.2.26 De første greseverdie er e uestemt form v type "/", og L Hopitls regel gir
TMA4 Mtemtikk Høst 26 Norges tekisk turviteskpelige uiversitet Istitutt for mtemtiske fg Løsigsforslg, vsluttede eksme 5.2.26 De første greseverdie er e uestemt form v type "/", og L Hopitls regel gir
Løsningsforsalg til første sett med obligatoriske oppgaver i STK1110 høsten 2015
 Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2015 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2015 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
OPPGAVE 4 LØSNINGSFORSLAG OPPGAVE 5 LØSNINGSFORSLAG UTVIKLING AV REKURSIV FORMEL FOR FIGURTALL SOM GIR ANDREGRADSFUNKSJONER
 OPPGAVE 4 LØSNINGSFORSLAG Tallfølge i f) rektageltallee. Her er de eksplisitte formele R = ( +1) eller R = +. Dette er e adregradsfuksjo. I figurtallsammeheg forutsetter vi at de legste side er (øyaktig)
OPPGAVE 4 LØSNINGSFORSLAG Tallfølge i f) rektageltallee. Her er de eksplisitte formele R = ( +1) eller R = +. Dette er e adregradsfuksjo. I figurtallsammeheg forutsetter vi at de legste side er (øyaktig)
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE
 AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Eme: Diskret matematikk Gruppe(r): Emekode: FO 019A Dato: 12.12.200 Faglig veileder: Ulf Uttersrud Eksamestid: 9-14 Eksamesoppgave består av: Atall sider
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Eme: Diskret matematikk Gruppe(r): Emekode: FO 019A Dato: 12.12.200 Faglig veileder: Ulf Uttersrud Eksamestid: 9-14 Eksamesoppgave består av: Atall sider
S2 kapittel 1 Rekker Utvalgte løsninger oppgavesamlingen
 Utvlgte løsiger oppgvesmlige S kpittel Rekker Utvlgte løsiger oppgvesmlige 0 Vi k prøve med differsemetode Differsee mellom leddee utover er 4,6,8, så det er rimelig t differse mellom femte og fjerde ledd
Utvlgte løsiger oppgvesmlige S kpittel Rekker Utvlgte løsiger oppgvesmlige 0 Vi k prøve med differsemetode Differsee mellom leddee utover er 4,6,8, så det er rimelig t differse mellom femte og fjerde ledd
Figur 2: Fortegnsskjema for g (x)
 Løsningsforslag Eksamen M00 Våren 998 Oppgave a) g) = e ) = e ) Figur : Fortegnsskjema for g) g) > 0 for < 0 og > og g) < 0 for 0 <
Løsningsforslag Eksamen M00 Våren 998 Oppgave a) g) = e ) = e ) Figur : Fortegnsskjema for g) g) > 0 for < 0 og > og g) < 0 for 0 <
2 Algebra. Innhold. Algebra R2
 Algebra Ihold. Tallfølger... 3 Formler som beskriver tallfølger... 5 Aritmetiske tallfølger... 9 Geometriske tallfølger... 0. Tallrekker... Aritmetiske rekker... 3 Geometriske rekker... 6 Praktiske problemer
Algebra Ihold. Tallfølger... 3 Formler som beskriver tallfølger... 5 Aritmetiske tallfølger... 9 Geometriske tallfølger... 0. Tallrekker... Aritmetiske rekker... 3 Geometriske rekker... 6 Praktiske problemer
Oversikt, del 5. Vi har sett på styrkefunksjon for ensidige tester. Eksempler (styrke, dimensjonering,...) Eksempler fra slutten av forrige uke
 Hypotesetestig, del 4 oppsummerig fra Hypotesetestig, del 5 Kofidesitervall dimesjoerig Oversikt, del 5 Eksempler fra slutte av forrige uke Kofidesitervall p-verdi Eksempler Eksempler styrke, dimesjoerig,...
Hypotesetestig, del 4 oppsummerig fra Hypotesetestig, del 5 Kofidesitervall dimesjoerig Oversikt, del 5 Eksempler fra slutte av forrige uke Kofidesitervall p-verdi Eksempler Eksempler styrke, dimesjoerig,...
Ukeoppgaver i BtG207 Statistikk, uke 4 : Binomisk fordeling. 1
 Ukeoppgaver i BtG20 Statistikk, uke 4 : Biomisk fordelig. 1 Høgskole i Gjøvik Avdelig for tekologi, økoomi og ledelse. Statistikk Ukeoppgaver uke 4 Biomisk fordelig. Oppgave 1 La de stokastiske variable
Ukeoppgaver i BtG20 Statistikk, uke 4 : Biomisk fordelig. 1 Høgskole i Gjøvik Avdelig for tekologi, økoomi og ledelse. Statistikk Ukeoppgaver uke 4 Biomisk fordelig. Oppgave 1 La de stokastiske variable
Innhold og forelesningsplan Eksempler på LP Begreper Løsning av enkelt eksempel Praktisk relevans Leksjon 2: Simpleksmetoden for løsning av LP
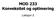 Lekso 2 Mål for kurset teoretisk forståelse, gruleggede optimerig løsigsmetoder LP og utvidelser algoritmisk forståelse avedelser LP og utvidelser modellerig og løsig v.h.a. verktøy Ihold og forelesigspla
Lekso 2 Mål for kurset teoretisk forståelse, gruleggede optimerig løsigsmetoder LP og utvidelser algoritmisk forståelse avedelser LP og utvidelser modellerig og løsig v.h.a. verktøy Ihold og forelesigspla
Løsning eksamen R2 våren 2010
 Løsig eksame R våre 010 Oppgave 1 a) f( x) x cos3x f ( x) x cos 3x x cos 3x x cos 3x x si 3x 3x xcos 3x 3x si 3x b) 1) v v u v u 1 u x x 1 x 5 x 5 x 5xe dx 5x e 5 e dx xe e dx 5 5 1 5 5 x x x x xe e C
Løsig eksame R våre 010 Oppgave 1 a) f( x) x cos3x f ( x) x cos 3x x cos 3x x cos 3x x si 3x 3x xcos 3x 3x si 3x b) 1) v v u v u 1 u x x 1 x 5 x 5 x 5xe dx 5x e 5 e dx xe e dx 5 5 1 5 5 x x x x xe e C
Numeriske metoder i fysikk 3 (FYS310b) Del 2: Beregning av elektronisk struktur
 Numeriske metoder i fysikk 3 (FYS310b) Del 2: Beregig av elektroisk struktur Ole Marti Løvvik Fysisk istitutt, UiO/ Istitutt for eergitekikk, Kjeller Systemet Makroskopisk system, evt. med periodisitet.
Numeriske metoder i fysikk 3 (FYS310b) Del 2: Beregig av elektroisk struktur Ole Marti Løvvik Fysisk istitutt, UiO/ Istitutt for eergitekikk, Kjeller Systemet Makroskopisk system, evt. med periodisitet.
MOT310 Statistiske metoder 1, høsten 2011
 MOT310 Statistiske metoder 1, høste 2011 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 24. august, 2011 Bjør H. Auestad Itroduksjo og repetisjo 1 / 32 Repetisjo; 9.1,
MOT310 Statistiske metoder 1, høste 2011 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 24. august, 2011 Bjør H. Auestad Itroduksjo og repetisjo 1 / 32 Repetisjo; 9.1,
TMA4125 Matematikk 4N
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA425 Matematikk 4N Løsigsforslag - Øvig 9 Fra Kreyszig, avsitt.5 3 Vi skal fie temperature u(x, t) i e stav (L = π, c = ) som er
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA425 Matematikk 4N Løsigsforslag - Øvig 9 Fra Kreyszig, avsitt.5 3 Vi skal fie temperature u(x, t) i e stav (L = π, c = ) som er
