Pytagoreiske tripler og Fibonacci-tall
|
|
|
- Tine Hedda Berge
- 4 år siden
- Visninger:
Transkript
1 Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a f.k.) og Leonado Pisano (a ), som skulle bli kjent unde navnet Fibonai, va begge lidenskapelig opptatt av tall. Og begge gunnet ove fobindelsen mellom geometi og tallmønste. Fibonais tallfølge 32,, 2, 3, 5, 8, 3, 2, 34, 55, 89, 44, 233, Johan F. Aanes Pof. emeitus ved NTNU johana@math.ntnu.no femkomme ved at hvet tall e summen av de to foegående, botsett fa de to føste. Foholdet mellom et tall og dets fogjenge i denne følgen vil ettehvet næme seg det gylne stts fohold ( ),. Dette e også foholdet mellom diagonal og side i en egulæ femkant, som va pytagoeenes symbol. Vi vet ikke om pytagoeene kjente til Fibonais tallfølge og dens mekvedige foekomst i natuens fome, som i gankongle og sneglehus. Men Fibonaitallene hadde utvilsomt passet godt i dees filosofi som gikk ut på at «Alt e tall». De hevdet at tallene og dees innbydes fohold ommet foklaingen på alle uvesets hemmelighete. Det gylne stt kjente de imidletid godt. Histoien fotelle at Pytagoas hustu Teano skal ha abeidet med det (Eves, 983). Det e likevel en annen og ikke så kjent fobindelse mellom Pytagoas og Fibonai vi skal ta fo oss he. Vi skal se at det e en næ sammenheng mellom pytagoeeiske tiple og Fibonai-tallene. Pytagoeiske tiple Et pytagoeisk tippel e et tippel av natulige tall (a, b, ) hvo a 2 + b 2 = 2. Tiplet e pimitivt hvis a og b e uten felles fakto. Kjente eksemple på slike e (3, 4, 5) og (5, 2, 3). Det finnes uendelig mange pimitive pytagoeiske tiple. Alleede fo 3500 å siden, lenge fø Pytagoas, kjente babylonene en metode fo hvodan de kunne finnes, se fo eksempel Eves (ibid.). Det som beskives hos Eves e «standadmetoden», som fotsatt finnes i de fleste tekste som behandle pytagoeiske tiple. I denne atikkelen skal vi se at det finnes en geometisk femgangsmåte som e me visuell og vel så enkel. Vi skal også vise hvodan standadmetoden enkelt kan utledes av denne geometiske metoden, og hvodan Fibonais tallekke e en annen nøkkel til konstuksjon av pytagoeiske tiple. Pytagoeiske tekante Et pytagoeisk tippel bestemme sidene i en pytagoeisk tekant, som selvsagt e ettvinklet, hvo hypotenusen ha lengde lik. La væe adius i den innskevne sikel i en slik tekant,
2 C C x a Q O a Q O R B P b A B P b y A Figu Figu 2 hvo hjønene e betegnet med A, B, C og sentet i sikelen med O (se figu ). Aealet F av tekanten DABC e summen av aealene av tekantene DABO, DBCO og DCAO, slik at F = ab= a+ b+ 2 2 ( ) En liten utegng gi ab ab( a+ b ) = = a + b ( a+ b) ab( a+ b ) = = ( a+ b ) a + 2ab+ b 2 nå vi huske at 2 = a 2 + b 2. Denne fomelen medføe at bli et helt tall. Fo hvis a og b begge e like tall bli også 2 = a 2 + b 2 et like tall, som medføe at også må væe like, og påstanden følge i dette tilfellet. Hvis a e odde og b e like så bli 2 odde og demed odde, slik at a + b igjen bli like og påstanden følge også he. Den siste muligheten e at både a og b e odde tall. Vi skal imidletid se nedenfo at det ikke kan skje. I et pytagoeisk tippel må minst ett av tallene a og b væe et like tall. Med katete på 3 og 4 og hypotenus lik 5 få vi =, mens tiplet (5, 2, 3) gi = 2. Det e natulig å spøe om det e ande pytagoeiske tekante som passe med disse adiene. Fo = e svaet nei, hvis vi se bot fa ombytting av katetene. Hvis = 2 vil tiplet (6, 8, 0) også gi en tekant som passe. Men dette tiplet e ikke pimitivt, så det finnes bae ett pimitivt pytagoeisk tippel, (5, 2, 3) som gi = 2. En geometisk metode fo å konstuee pytagoeiske tiple At adius i den innskevne sikel i en pytagoeisk tekant ha lengde lik et helt tall e inteessant nok, men det e ikke slutten på histoien. Det e he den begynne. La oss spøe: Fo en gitt adius med heltallig lengde, hvilke mulige valg av pytagoeiske tiple ha vi? Elle, fomulet på en litt annen måte: Hvilke pytagoeiske tekante kan omskives en sikel med gitt heltallig adius? Det e imelig klat at fo å besvae spøsmålet må vi finne uttykk fo sidene a, b, som involvee. Vi gå løs på dette poblemet med utgangspunkt i figu 2. La oss gå ut fa at (a, b, ) e et pytagoeisk tippel slik at e et helt tall. Kvadatet i figu 2 ha side lik 2 og støelsene x og y e bestemt ved ligngene a = x + 2, b = y + 2. Det e klat at x og y bli hele tall. Av figuen se vi at CQ = CR = x + og AP = AR = y +, slik at = (x + ) + (y + ) = x + y + 2. Siden (a, b, ) e et pytagoeisk tippel må da (x + 2) 2 + (y + 2) 2 = (x + y + 2) 2. Utegng av begge side gi x 2 + 4x y 2 + 4y tangenten 2/202 33
3 = x 2 + y xy + 4x + 4y. Dette edusee seg til den enkle ligngen xy = 2 2. Siden x og y e hele tall må minst ett av tallene ha 2 som fakto. Anta fo eksempel at x = 2z slik at a = 2 + 2z = 2( + z), som vise at a e et like tall. Analogt, hvis y e et like tall må b væe et like tall. Vi kan defo foeløpig konkludee med at i et pytagoeisk tippel må minst ett av tallene a og b væe et like tall, som vi sa ovenfo. Men det e også klat at hvis tiplet e pimitivt, så må det ande tallet væe odde. Vi vil i fotsettelsen anta at x = 2z, noe vi tygt kan gjøe, eventuelt ved å døpe om de to katetene a og b. Det gi oss ligngen zy = 2. Poduktet zy e defo en faktoiseing av 2, men vi påstå, uten å agumentee fo det he, at hvis z og y e uten felles fakto, så få vi også en faktoiseing av. Da må z = n 2 og y = k 2, slik at = nk, de k og n e hele tall uten felles fakto. Sette vi dette inn i uttykkene fo a, b og ovenfo få vi a = 2nk + 2n 2, b = 2nk + k 2, = 2nk + 2n 2 + k 2. Demed ha vi uttykt alle de te sidene i tekanten ved hjelp av en faktoiseing av! Legg meke til at fodi vi ha antatt at a e et like tall, så e b odde, som medføe at også k e odde. Omvendt, hvis vi state med to tall n og k som ikke ha noen felles fakto, hvo k e odde, og la a, b og væe gitt ved fomlene ovenfo, så e (a, b, ) et pimitivt pytagoeisk tippel. Den endelige konklusjonen e defo at alle pimitive pytagoeiske tiple kan skives på fomen ovenfo. Fo en gitt adius må vi finne alle faktoiseinge = nk de n og k e uten felles fakto og k e odde. Hvo mange pytagoeiske tekante kan omskives en sikel med gitt adius? Ved å la væe lik, 2, 3, få vi geneet alle mulige tiple på denne måten. Gjennom faktoiseingen av ha vi god kontoll på hvo 34 mange og hvilke tekante som vil foekomme fo hve adius. La oss se på noen eksemple.. = 3 gi to mulighete: k =, n = 3 og k = 3, n =. Det gi de to tiplene (24, 7, 25) og (8, 5, 7). 2. = 4 gi en mulighet: k =, n = 4 (k skal væe odde) som gi tiplet (40, 9, 4). 3. = 8: k =, n = 8 og k = 9, n = 2 (k = 3 kan ikke bukes, da bli 3 en fakto i n). 4. = 60: Pøv selv! Som vi se vil antallet av pimitive tiple vaiee stekt med adien til den innskevne sikelen. E fo eksempel et odde pimtall få vi bae to mulighete: k =, n = og k =, n =. Me geneelt må det væe slik at antallet pimitive pytagoeiske tiple fo en gitt adius vil væe bestemt av antallet odde faktoe k i som ikke ha felles fakto med n (de = kn). Dette kan vi edusee til et spøsmål om hvilke ulike odde pimfaktoe (faktoe som e pimtall) som finnes i. Anta nemlig at det foekomme m ulike odde pimtall p, p 2,, p m i faktoiseingen av, slik at = 2 n0 p n p m nm, de n 0 e et helt tall 0, og n i e et natulig tall fo i =, 2,, m. Tallet k kan da bygges opp ved å velge ut en, to elle flee, opp til alle av faktoene p i, og ta poduktet av dem. Fo hve pimtallspotens p i velge vi om den skal væe med som fakto i elle ikke. Dette gi oss m valg, hvet med to altenative. Til sammen gi det 2 m valgmulighete. Siden k og skal væe pimiske må hele pimtalls potensen p i væe med enten i k elle n. Konklusjonen e altså: Hvis ha m ulike pimfaktoe så finnes det nøyaktig 2 m pimitive pytagoiske tekante som kan omskives en sikel med adius. Fo = 60 ha vi to odde pimfaktoe, 3 og 5, og demed 2 2 = 4 pimitive tiple. La oss avslutte med et eksempel som vise situasjonen ganske geneelt. Fo = =
4 ha vi 4 ulike odde pimfaktoe: 3, 5, 7,, og få 2 4 = 6 pimitive tiple. Ta vi fo eksempel k = = 7425 og n = 2 7 = 4 få vi a = = b = = = = , Et pytagoeisk tippel som kanskje ikke ligge helt opp i dagen. Standadmetoden Fa fomlene fo a, b og få vi ved en liten omegng a = 2n(n + k), b = 2nk + k 2 = (n + k) 2 n 2, = 2nk + 2n 2 + k 2 = (n + k) 2 + n 2 Sette vi he m = n + k få vi a = 2mn, b = m 2 n 2, = m 2 + n 2 som e de vanlige fomlene fo et pytagoeisk tippel (a, b, ) uttykt ved paametene m og n. He e m > n og det e ikke vanskelig å se at de ikke kan ha noen felles fakto. Nå vi vaiee m og n unde disse betingelsene få vi alle mulige pimitive pytagoeiske tiple. Dette e enkle fomle, men vi miste ovesikten ove hvo de tilhøende tekantene ligge i landskapet. Fibonai-tallene som nøkkel til pytagoeiske tiple La p og q væe to vilkålige tall som følge ettehveande i Fibonais tallfølge, fo eksempel p = 2 og q = 34. De to neste tallene e da p + q = 55 og q + (p + q) = p + 2q = 89. Sett a lik 2 gange poduktet av de to midteste tallene, og la b væe lik poduktet av det minste og det støste av disse fie tallene: a = 2q(p + q), b = p(p + 2q). Dette e uttykk som e identiske med de vi fant tidligee nå vi sette p = k, q = n. Det bety at a og b bli side i en pytagoeisk tekant. Kontolle selv at a 2 + b 2 = 2 nå vi sette = 2pq + p 2 + 2q 2! Med tallene ovenfo få vi tiplet (3740, 869, 48). Denne femgangsmåten gi også den tilhøende adius helt gatis. Vi må ha = pq, som i dette eksemplet e lik 74. Fibonai-tallene vokse fot, så tiplene vi podusee på denne måten bli fot stoe. Vi kan imidletid meke oss at hvis p e odde (som i dette eksemplet), så bli de alltid pimitive. Det stikke i at ettefølgende tall i Fibonai-følgen ikke kan ha noen felles fakto. Denne metoden lage mange tiple, men slett ikke alle. Skal vi få det til må vi genealisee den. Fibonai-tallene e bestemt av diffeensligngen a n+2 = a n + a n+, n =, 2,, a = a 2 =. Ende vi de to føste tallene a og a 2, men buke samme oppskift, slik at a 3 = a + a 2 osv., så få vi det vi kalle en genealiset Fibonaifølge. State vi fo eksempel med 7 og 4 få vi følgen 7, 4,, 5, 26, 4, 67, Femgangsmåten beskevet ovenfo fungee like godt på tall fa denne følgen, vi få en ny uendelig seie av pytagoeiske tiple. Ta vi de 4 føste tallene 7, 4,, 5, få vi det pimitive tippel (88, 05, 37) og adius lik 28. Legg meke til at vi satte det odde tallet 7 foan 4. Hadde disse to byttet plass ville vi fått en annen følge og det femkomne tippel ville ikke blitt pimitivt. Det e klat at ved å vaiee de to føste tallene så kan vi podusee alle mulige pytagoeiske tiple på denne måten. Det gylne tiangel Fibonai-følgene gi oss altså alle pimitive pytagoeiske tiple, og en enkelt følge gi oss en uendelig seie av slike. Tenke vi geometisk bety det siste utsagnet at vi ha en uendelig følge av voksende pytagoeiske tekante. Hvodan se de ut? Også fo en genealiset Fibonai-følge vil foholdet mellom et ledd og dets fogjenge næme seg en gense, det gylne stts fohold, som ofte betegnes med j: tangenten 2/202 35
5 ( ) an+ ϕ= lim = 5+. n a 2 n Gå vi defo langt nok ut i følgen vil 4 ettefølgende tall næme seg kvaduplet (p, jp, j 2 p, j 3 p). Buke vi oppskiften på disse tallene få vi katete a = 2j 3 p 2, b = j 3 p 2 og hypotenusen = a + b = 4ϕ p + ϕ p = ϕ p 5. Alle sidene e defo et multiplum av j 3 p 2, som vise at tekanten e fomlik med tekanten med side, 2 og 5. Denne e ikke pytagoeisk siden hypotenusen ikke e et helt tall, men den kalles det gylne tiangel, fodi det e den som lettest gjø det mulig å konstuee det gylne stts fohold. Demed e vå undtu kommet til veis ende. Vi ha gått fa Fibonai-tall til det gylne stt og pytagoeiske tekante, og følge vi de pytagoeiske tekantene langs en Fibonai-følge mot evigheten komme vi til det gylne tiangel. Refeanse Eves, H. (983). An Intodution to the Histoy of Mathematis, Saundes College Publishing, 5th ed. 36
EKSAMEN i. MA-132 Geometri. Torsdag 3. desember 2009 kl Tillatte hjelpemidler: Alle trykte og skrevne hjelpemidler. Kalkulator.
 Institutt fo matematiske fag EKSAMEN i MA-1 Geometi Tosdag. desembe 009 kl. 9.00-14.00 Tillatte hjelpemidle: Alle tykte og skevne hjelpemidle. Kalkulato. Bokmål Oppgave 1 I oppgaven nedenfo skal du oppgi
Institutt fo matematiske fag EKSAMEN i MA-1 Geometi Tosdag. desembe 009 kl. 9.00-14.00 Tillatte hjelpemidle: Alle tykte og skevne hjelpemidle. Kalkulato. Bokmål Oppgave 1 I oppgaven nedenfo skal du oppgi
Rettelser til. Øistein Bjørnestad Tom Rune Kongelf Terje Myklebust. Alfa. Oppgaveløsninger
 Rettelse til Øistein Bjønestad Tom Rune Kongelf Teje Myklebust Alfa Oppgaveløsninge 007 Kapittel S. 7: Fasit til oppgave.9e): Slik oppgaven stå, skal svaet væe 065 (noe ha falt ut i oppgaveteksten). S.
Rettelse til Øistein Bjønestad Tom Rune Kongelf Teje Myklebust Alfa Oppgaveløsninge 007 Kapittel S. 7: Fasit til oppgave.9e): Slik oppgaven stå, skal svaet væe 065 (noe ha falt ut i oppgaveteksten). S.
Eksamen i MA-104 Geometri Løsningsforslag
 Eksamen i M-04 Geometi 4.0.007 Løsningsfoslag Oppgave Et kvadat ha side lik s, som du velge selv. E e midtpunktet på og F e midtpunktet på. iagonalen skjæe F i H. E skjæe F i G. I oppgaven skal du buke
Eksamen i M-04 Geometi 4.0.007 Løsningsfoslag Oppgave Et kvadat ha side lik s, som du velge selv. E e midtpunktet på og F e midtpunktet på. iagonalen skjæe F i H. E skjæe F i G. I oppgaven skal du buke
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
EKSAMEN FAG TFY4160 BØLGEFYSIKK OG FAG FY1002/MNFFY101 GENERELL FYSIKK II Lørdag 6. desember 2003 kl Bokmål
 ide av 0 NORGE TEKNIK- NATURVITENKAPELIGE UNIVERITET INTITUTT FOR FYIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane tand Telefon: 73 59 34 6 EKAMEN FAG TFY460 ØLGEFYIKK OG FAG FY00/MNFFY0 GENERELL
ide av 0 NORGE TEKNIK- NATURVITENKAPELIGE UNIVERITET INTITUTT FOR FYIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane tand Telefon: 73 59 34 6 EKAMEN FAG TFY460 ØLGEFYIKK OG FAG FY00/MNFFY0 GENERELL
Fugletetraederet. 1 Innledning. 2 Navnsetting. 3 Geometriske begreper. Øistein Gjøvik Høgskolen i Sør-Trøndelag, 2004
 Fugletetaeeet Øistein Gjøvik Høgskolen i Sø-Tønelag, 004 Innlening Nå skal vi lage et omlegeme u kanskje ikke ha sett fø. Det e ikke noe mystisk ve selve figuen, men en høe ikke til lant e mest ukte i
Fugletetaeeet Øistein Gjøvik Høgskolen i Sø-Tønelag, 004 Innlening Nå skal vi lage et omlegeme u kanskje ikke ha sett fø. Det e ikke noe mystisk ve selve figuen, men en høe ikke til lant e mest ukte i
b) 3 MATEMATISKE METODER I 1 ( ) ( ) ( ) ( ) ( ) ( ) Repetisjonsoppgaver Bruk av regneregler: 1 Regn ut: e) 0 x ) 4 3 d) 4 x f) 5y
 MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
8 Eksamens trening. E2 (Kapittel 1) På figuren er det tegnet grafene til funksjonene f og g gitt ved
 84 8 Eksamenstening 8 Eksamens tening Uten hjelpemidle E1 (Kapittel 1) Polynomfunksjonen P e gitt ved P ( ) = 7 + 14 8, DP = R. a Det kan vises at alle heltallige løsninge av P() = 0 gå opp i konstantleddet
84 8 Eksamenstening 8 Eksamens tening Uten hjelpemidle E1 (Kapittel 1) Polynomfunksjonen P e gitt ved P ( ) = 7 + 14 8, DP = R. a Det kan vises at alle heltallige løsninge av P() = 0 gå opp i konstantleddet
Hesteveddeløp i 8. klasse
 Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
b) C Det elektriske feltet går radielt ut fra en positivt ladd partikkel.
 Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2
 1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
Modul 1 15 studiepoeng, internt kurs Notodden/Porsgrunn
 Høgskole i Telemk Avdelig fo estetiske fg, folkekultu og læeutdig BOKMÅL 4. mi 007 EKSAMEN I MATEMATIKK 3 Tid: 6 time Modul 5 studiepoeg, itet kus Notodde/Posgu Oppgvesettet e på 7 side (ikludet fomelsmlig).
Høgskole i Telemk Avdelig fo estetiske fg, folkekultu og læeutdig BOKMÅL 4. mi 007 EKSAMEN I MATEMATIKK 3 Tid: 6 time Modul 5 studiepoeg, itet kus Notodde/Posgu Oppgvesettet e på 7 side (ikludet fomelsmlig).
UNIVERSITETET I OSLO
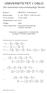 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST2000, 17. desembe 2018, 09.00 13.00 Oppgavesettet inkludet fomelsamling e på 8 side Tillatte hjelpemidle: 1) Angel/Øgim
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST2000, 17. desembe 2018, 09.00 13.00 Oppgavesettet inkludet fomelsamling e på 8 side Tillatte hjelpemidle: 1) Angel/Øgim
Matematikk 3MX AA6524 / AA6526 Elever / privatister Oktober 2002
 E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
Billige arboresenser og matchinger
 Billige aboesense og matchinge Magnus Lie Hetland 16. jan 009 Dette e foelesningsnotate til føste foelesning i faget Algoitmekonstuksjon, videegående kus, ved Institutt fo datateknikk og infomasjonsvitenskap,
Billige aboesense og matchinge Magnus Lie Hetland 16. jan 009 Dette e foelesningsnotate til føste foelesning i faget Algoitmekonstuksjon, videegående kus, ved Institutt fo datateknikk og infomasjonsvitenskap,
Øving 8. Dersom ikke annet er oppgitt, antas det at systemet er i elektrostatisk likevekt.
 Institutt fo fysikk, NTNU TFY455/FY003: lektisitet og magnetisme Vå 2008 Øving 8 Veiledning: 04.03 i R2 25-400, 05.03 i R2 25-400 Innleveingsfist: Fedag 7. mas kl. 200 (Svatabell på siste side.) Opplysninge:
Institutt fo fysikk, NTNU TFY455/FY003: lektisitet og magnetisme Vå 2008 Øving 8 Veiledning: 04.03 i R2 25-400, 05.03 i R2 25-400 Innleveingsfist: Fedag 7. mas kl. 200 (Svatabell på siste side.) Opplysninge:
( 6z + 3z 2 ) dz = = 4. (xi + zj) 3 i + 2 ) 3 x x 4 9 y. 3 (6 2y) (6 2y)2 4 y(6 2y)
 TMA415 Matematikk 2 Vå 215 Noges teknisk natuvitenskapelige univesitet Institutt fo matematiske fag Løsningsfoslag Øving 11 Alle oppgavenumme efeee til 8. utgave av Adams & Essex Calculus: A Complete Couse.
TMA415 Matematikk 2 Vå 215 Noges teknisk natuvitenskapelige univesitet Institutt fo matematiske fag Løsningsfoslag Øving 11 Alle oppgavenumme efeee til 8. utgave av Adams & Essex Calculus: A Complete Couse.
Løsningsforslag Eksamen i fag TEP4110 Fluidmekanikk
 Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
KONTINUASJONSEKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Noges teknisk natuvitenskapelige univesitet Institutt fo elektonikk og telekommunikasjon ide 1 av 8 Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Jon Olav Gepstad 41044764) Hjelpemidle: C - pesifisete
Noges teknisk natuvitenskapelige univesitet Institutt fo elektonikk og telekommunikasjon ide 1 av 8 Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Jon Olav Gepstad 41044764) Hjelpemidle: C - pesifisete
Mandag E = V. y ŷ + V ẑ (kartesiske koordinater) r sin θ φ ˆφ (kulekoordinater)
 Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Løsningsforslag til ukeoppgave 11
 Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Sammendrag, uke 14 (5. og 6. april)
 Institutt fo fysikk, NTNU TFY4155/FY1003: Elektisitet og magnetisme Vå 2005 Sammendag, uke 14 (5. og 6. apil) Magnetisk vekselvikning [FGT 28, 29; YF 27, 28; TM 26, 27; AF 22, 24B; H 23; DJG 5] Magnetisme
Institutt fo fysikk, NTNU TFY4155/FY1003: Elektisitet og magnetisme Vå 2005 Sammendag, uke 14 (5. og 6. apil) Magnetisk vekselvikning [FGT 28, 29; YF 27, 28; TM 26, 27; AF 22, 24B; H 23; DJG 5] Magnetisme
Forelesning 9/ ved Karsten Trulsen
 Foelesning 9/2 218 ved Kasten Tulsen Husk fa sist våe to spøsmål om kuveintegale: Desom vi skal beegne et kuveintegal som state i et punkt og ende opp i et annet punkt 1, så kan det væe mange veie fo å
Foelesning 9/2 218 ved Kasten Tulsen Husk fa sist våe to spøsmål om kuveintegale: Desom vi skal beegne et kuveintegal som state i et punkt og ende opp i et annet punkt 1, så kan det væe mange veie fo å
sosiale behov FASE 2: Haug barnehage 2011-2012
 : Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
: Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
a) C Det elektriske feltet går radielt ut fra en positivt ladet partikkel og radielt innover mot en negativt ladd partikkel.
 Løsningsfoslag Fysikk 2 Vå 2015 Løsningsfoslag Fysikk 2 Vå 2015 Oppgav e Sva Foklaing a) C Det elektiske feltet gå adielt ut fa en positivt ladet patikkel og adielt innove mot en negativt ladd patikkel.
Løsningsfoslag Fysikk 2 Vå 2015 Løsningsfoslag Fysikk 2 Vå 2015 Oppgav e Sva Foklaing a) C Det elektiske feltet gå adielt ut fa en positivt ladet patikkel og adielt innove mot en negativt ladd patikkel.
Fysikkolympiaden 1. runde 25. oktober 5. november 2004
 Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning Fysikkolympiaden 1. unde 5. oktobe 5. novembe 004 Hjelpemidle: abell og fomelsamlinge i fysikk og matematikk Lommeegne id: 100 minutte
Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning Fysikkolympiaden 1. unde 5. oktobe 5. novembe 004 Hjelpemidle: abell og fomelsamlinge i fysikk og matematikk Lommeegne id: 100 minutte
Slik bruker du pakken
 Slik buke du pakken Kompetanseutviklingspakken Lesestategie og leseengasjement Dette e infomasjon til deg/dee som skal lede femdiften i kollegiet. He finne du en ovesikt ove pakkens innhold til hjelp i
Slik buke du pakken Kompetanseutviklingspakken Lesestategie og leseengasjement Dette e infomasjon til deg/dee som skal lede femdiften i kollegiet. He finne du en ovesikt ove pakkens innhold til hjelp i
Løsning midtveiseksamen H12 AST1100
 Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
FFI RAPPORT FORDAMPING FRA OVERFLATER OG DRÅPER. BUSMUNDRUD Odd FFI/RAPPORT-2005/03538
 FFI RAPPORT FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORSVARETS FORSKNINGSINSTITUTT Nowegian Defence Reseach
FFI RAPPORT FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORDAMPING FRA OVERFLATER OG DRÅPER BUSMUNDRUD Odd FFI/RAPPORT-5/58 FORSVARETS FORSKNINGSINSTITUTT Nowegian Defence Reseach
1 Virtuelt arbeid for stive legemer
 1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
Notat i FYS-MEK/F 1110 våren 2006
 1 Notat i FYS-MEK/F 1110 våen 2006 Rulling og skliing av kule og sylinde Foelest 24. mai 2006 av Ant Inge Vistnes Geneelt Rotasjonsdynamikk e en svæt viktig del av mekanikkuset våt. Dette e nytt stoff
1 Notat i FYS-MEK/F 1110 våen 2006 Rulling og skliing av kule og sylinde Foelest 24. mai 2006 av Ant Inge Vistnes Geneelt Rotasjonsdynamikk e en svæt viktig del av mekanikkuset våt. Dette e nytt stoff
trygghet FASE 1: barnehage
 tygghet banehage De voksnes olle Banemøte Leikeguppe Guppeaktivitet Hjemmebesøk Samlinge Måltid Påkledning Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 tygghet tygghet «Banehagen skal bistå
tygghet banehage De voksnes olle Banemøte Leikeguppe Guppeaktivitet Hjemmebesøk Samlinge Måltid Påkledning Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 tygghet tygghet «Banehagen skal bistå
Løsningsforslag for eksamen i FY101 Elektromagnetisme torsdag 12. desember 2002
 Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
EKSAMENSOPPGAVE - Skoleeksamen. Institutt for Samfunnsøkonomi. Utlevering: 17.12.2014 Kl. 09.00 Innlevering: 17.12.2014 Kl. 14.00
 EKSAMENSOPPGAVE - Skoleeksamen MET 11803 Matematikk Institutt fo Samfunnsøkonomi Utleveing: 17122014 Kl 0900 Innleveing: 17122014 Kl 1400 Vekt: 70% av MET 1180 Antall side i oppgaven: Antall vedleggsfile:
EKSAMENSOPPGAVE - Skoleeksamen MET 11803 Matematikk Institutt fo Samfunnsøkonomi Utleveing: 17122014 Kl 0900 Innleveing: 17122014 Kl 1400 Vekt: 70% av MET 1180 Antall side i oppgaven: Antall vedleggsfile:
Midtsemesterprøve onsdag 7. mars 2007 kl
 Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 2007 Midtsemestepøve onsdag 7. mas 2007 kl 1300 1500. Svatabellen stå på side 11. Sett tydelige kyss. Husk å skive
Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 2007 Midtsemestepøve onsdag 7. mas 2007 kl 1300 1500. Svatabellen stå på side 11. Sett tydelige kyss. Husk å skive
UNIVERSITETET I OSLO
 Side av 5 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Mandag 9. juni 28 Tid fo eksamen: Kl. 9-2 Oppgavesettet e på 5 side inkludet fomelaket. Tillatte
Side av 5 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Mandag 9. juni 28 Tid fo eksamen: Kl. 9-2 Oppgavesettet e på 5 side inkludet fomelaket. Tillatte
Newtons lover i én dimensjon
 Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Kombinatorikk. MAT0100V Sannsynlighetsregning og kombinatorikk. Multiplikasjonssetningen
 MAT000V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
MAT000V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
At energi ikke kan gå tapt, må bety at den er bevart. Derav betegnelsen bevaringslov.
 Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
Kombinatorikk. MAT0100V Sannsynlighetsregning og kombinatorikk. Multiplikasjonssetningen
 MAT0100V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
MAT0100V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
Midtsemesterprøve fredag 10. mars kl
 Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 006 Midtsemestepøve fedag 10. mas kl 0830 1130. Svatabellen stå på et eget ak. Sett tydelige kyss. Husk å skive på
Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 006 Midtsemestepøve fedag 10. mas kl 0830 1130. Svatabellen stå på et eget ak. Sett tydelige kyss. Husk å skive på
RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS
![RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS](/thumbs/62/46972182.jpg) RAPPORT STATENS VEGVESEN Ending E014 Flomvudeing eksisteende E6 OPPDRAGSNUMMER 12143214 [12143214-R01] 29/05/2015 SWECO NORGE AS SAMUEL VINGERHAGEN epo002.docx 2013-06-14 Sweco epo002.docx 2013-06-14
RAPPORT STATENS VEGVESEN Ending E014 Flomvudeing eksisteende E6 OPPDRAGSNUMMER 12143214 [12143214-R01] 29/05/2015 SWECO NORGE AS SAMUEL VINGERHAGEN epo002.docx 2013-06-14 Sweco epo002.docx 2013-06-14
"Kapittel 5 i et nøtteskall"
 Ulve "Kapittel 5 i et øtteskall" (Vesjo 9.01.0 ) Jeg gå he i gjeom alle tekikke/fomle som e elevate i dette kapitlet ved å buke et eksempel side 198 som utgagspukt fo alle tekikkee. Ovesikt ove fomle og
Ulve "Kapittel 5 i et øtteskall" (Vesjo 9.01.0 ) Jeg gå he i gjeom alle tekikke/fomle som e elevate i dette kapitlet ved å buke et eksempel side 198 som utgagspukt fo alle tekikkee. Ovesikt ove fomle og
Emnenavn: Finansiering og investering. Eksamenstid: 4 timer. Faglærer: Tor Arne Moxheim
 EKSAMEN Emnekode: SFB6 Dato: 3. mai 9 Hjelpemidle: Godkjent kalkulato, vedlagte fomelsamling og entetabelle. Emnenavn: Finansieing og investeing Eksamenstid: 4 time Faglæe: o Ane Moxheim Om eksamensoppgaven
EKSAMEN Emnekode: SFB6 Dato: 3. mai 9 Hjelpemidle: Godkjent kalkulato, vedlagte fomelsamling og entetabelle. Emnenavn: Finansieing og investeing Eksamenstid: 4 time Faglæe: o Ane Moxheim Om eksamensoppgaven
Løsningsforslag Fysikk 2 Høst 2015
 Løsningsfoslag Fysikk Høst 015 Oppgave Sva Foklaing a) A Vi pøve oss fa ed noen kjente fole: ε vbl B ε Φ vl t vl Nå vi nå egne ed enhete på denne foelen få vi Wb B s s Wb Magnetfeltet kan altså åles i
Løsningsfoslag Fysikk Høst 015 Oppgave Sva Foklaing a) A Vi pøve oss fa ed noen kjente fole: ε vbl B ε Φ vl t vl Nå vi nå egne ed enhete på denne foelen få vi Wb B s s Wb Magnetfeltet kan altså åles i
Fysikk 2 Eksamen høsten Løsningsforslag
 Fysikk - Løsninsfosla Oppave a) D Tesla b) B Tyndeakseleasonen e det samme som feltstyken til avitasonsfeltet, som e itt ved m m Siden e en konstant (avitasonskonstanten), vil oså bee planetene. væe likt
Fysikk - Løsninsfosla Oppave a) D Tesla b) B Tyndeakseleasonen e det samme som feltstyken til avitasonsfeltet, som e itt ved m m Siden e en konstant (avitasonskonstanten), vil oså bee planetene. væe likt
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK
 Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK Faglig/fagleg kontakt unde eksamen: Navn: Helge E. Engan Tlf.: 944 EKSAMEN I EMNE SIE415 BØLGEFORPLANTNING
Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK Faglig/fagleg kontakt unde eksamen: Navn: Helge E. Engan Tlf.: 944 EKSAMEN I EMNE SIE415 BØLGEFORPLANTNING
Lærebok ijernba neteknikk L531. Kapittel4. Krengetogstilpa sning. Utgitt:
 Læebok ijenba neteknikk L531 Kapittel4 Kengetogstilpa sning Utgitt:28.09.99 1. INNLEDNING 4 1.1 INNFØRING AV KRENGETOG I NORGE 4 1.2 METODER FOR MÅLING AV KOMFORT 5 1.3 BETRAKTNINGER FRA ABSOLUTTE TESTER
Læebok ijenba neteknikk L531 Kapittel4 Kengetogstilpa sning Utgitt:28.09.99 1. INNLEDNING 4 1.1 INNFØRING AV KRENGETOG I NORGE 4 1.2 METODER FOR MÅLING AV KOMFORT 5 1.3 BETRAKTNINGER FRA ABSOLUTTE TESTER
FYSIKK-OLYMPIADEN Andre runde: 4/2 2010
 Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning FYSIKK-OLYMPIADEN 009 010 Ande unde: / 010 Skiv øvest: Navn, fødselsdato, e-postadesse og skolens navn Vaighet:3 klokketime Hjelpemidle:abell
Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning FYSIKK-OLYMPIADEN 009 010 Ande unde: / 010 Skiv øvest: Navn, fødselsdato, e-postadesse og skolens navn Vaighet:3 klokketime Hjelpemidle:abell
R2 2010/11 - Kapittel 3: 26. oktober 24. november 2011
 R / - Kapittel :. oktobe. novembe Plan fo koleået /: Kapittel : / /. Kapittel : / /. Kapittel : / /. Kapittel : / /. Pøve på elle koletime ette hvet kapittel. Én heildagpøve i hve temin. En del pøve vil
R / - Kapittel :. oktobe. novembe Plan fo koleået /: Kapittel : / /. Kapittel : / /. Kapittel : / /. Kapittel : / /. Pøve på elle koletime ette hvet kapittel. Én heildagpøve i hve temin. En del pøve vil
informasjon GENERELL barnehage
 maianne@futuia.no «Det e at å ha 5 finge på hve hånd og 5 tæ på hve fot. Jeg kunne like gjene hatt 13 elle 30 sammenlagt. Og så ble det tilfeldigvis 20». Inge Hageup banehage Åpningstid Tilvenning av nye
maianne@futuia.no «Det e at å ha 5 finge på hve hånd og 5 tæ på hve fot. Jeg kunne like gjene hatt 13 elle 30 sammenlagt. Og så ble det tilfeldigvis 20». Inge Hageup banehage Åpningstid Tilvenning av nye
Det vil gjennom hele skoleåret være stort fokus på de grunnleggende ferdighetene i KRLE. Disse vil bli tilpasset nivået elevene befinner seg på.
 RENDALEN KOMMUNE Fagetun skole Åsplan i KRLE fo 5.-7. tinn B-plan Siden faget ha byttet navn til KRLE og kistendommen skal vektlegges mest, skal vi i løpet av skoleået lese fotellinge fa Banebibelen minst
RENDALEN KOMMUNE Fagetun skole Åsplan i KRLE fo 5.-7. tinn B-plan Siden faget ha byttet navn til KRLE og kistendommen skal vektlegges mest, skal vi i løpet av skoleået lese fotellinge fa Banebibelen minst
Newtons lover i to og tre dimensjoner
 Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Gammel tekst Ny tekst Begrunnelse. "Følgende dokumenter legges til grunn for virksomheten
 Fo mangfold mot diskimineing Endings til Vedtekte Landsmøtet 2015 Foslagsstille Gammel tekst Ny tekst Begunnelse "Følgende dokumente legges til gunn fo viksomheten 1 Ny tekst Fø 1 - Vedtekte: Beskive eglene
Fo mangfold mot diskimineing Endings til Vedtekte Landsmøtet 2015 Foslagsstille Gammel tekst Ny tekst Begunnelse "Følgende dokumente legges til gunn fo viksomheten 1 Ny tekst Fø 1 - Vedtekte: Beskive eglene
AGENDA: Faste saker: Saksdokumente r
 FAU-møte, tisdag 12.desembe 2017 kl. 18.00 20.30 Sted: Pesonalommet, Bjønsletta skole Møtelede: Cathine Foss Stene ( FAU-lede) Refeent: Anne Lise Stosand Caolina, Øyvind, Tine, Ragnhild, Heniette, Monica,
FAU-møte, tisdag 12.desembe 2017 kl. 18.00 20.30 Sted: Pesonalommet, Bjønsletta skole Møtelede: Cathine Foss Stene ( FAU-lede) Refeent: Anne Lise Stosand Caolina, Øyvind, Tine, Ragnhild, Heniette, Monica,
informasjon GENERELL barnehage
 2011 maianne@fuedesign.no «Det e at å ha 5 finge på hve hånd og 5 tæ på hve fot. Jeg kunne like gjene hatt 13 elle 30 sammenlagt. Og så ble det tilfeldigvis 20». Inge Hageup banehage Åpningstid Tilvenning
2011 maianne@fuedesign.no «Det e at å ha 5 finge på hve hånd og 5 tæ på hve fot. Jeg kunne like gjene hatt 13 elle 30 sammenlagt. Og så ble det tilfeldigvis 20». Inge Hageup banehage Åpningstid Tilvenning
Betraktninger rundt det klassiske elektronet.
 Betaktninge undt det klassiske elektonet. Kistian Beland Matteus Häge - 1 - - - Innholdsfotegnelse: 1. Sammendag - 5 -. Innledning - 6 -. Innledende betaktninge - 7-4. Vå elektonmodell - 8-5. Enegi i feltene
Betaktninge undt det klassiske elektonet. Kistian Beland Matteus Häge - 1 - - - Innholdsfotegnelse: 1. Sammendag - 5 -. Innledning - 6 -. Innledende betaktninge - 7-4. Vå elektonmodell - 8-5. Enegi i feltene
Løsningsforslag Fysikk 2 Høst 2014
 Løsningsfoslag Fysikk Høst 014 Løsningsfoslag Fysikk Høst 014 Opp Sva Foklaing gave a) D Det elektiske feltet gå adielt ut fa en positivt ladet patikkel. Til høye fo elektonet lage elektonet en feltstyke
Løsningsfoslag Fysikk Høst 014 Løsningsfoslag Fysikk Høst 014 Opp Sva Foklaing gave a) D Det elektiske feltet gå adielt ut fa en positivt ladet patikkel. Til høye fo elektonet lage elektonet en feltstyke
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
Om bevegelsesligningene
 Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
Veileder for adepter. Bruk mentor - unngå omveier
 Veilede fo adepte Buk mento - unngå omveie At eg e til, Det veit eg. Eg kjenne pusten min Og eit og anna hjeteslag. Men eg vil noko mei, enn bee å vea, eg vil vea nokon, som bety noko, i det stoe fellesskapet.
Veilede fo adepte Buk mento - unngå omveie At eg e til, Det veit eg. Eg kjenne pusten min Og eit og anna hjeteslag. Men eg vil noko mei, enn bee å vea, eg vil vea nokon, som bety noko, i det stoe fellesskapet.
c) etingelsen fo at det elektiske feltet E e otasjonsinvaiant om x-aksen e, med E og ee som denet ovenfo, at e E = E. Dette skal gjelde fo en vilkalig
 Eksamen i klassisk feltteoi, fag 74 5, 4. august 995 Lsninge a) Koodinatene x; y; z tansfomees slik x 7 bx = x; y 7 by = y cos, z sin ; z 7 by = y sin + z cos Den invese tansfomasjonen e en otasjon en
Eksamen i klassisk feltteoi, fag 74 5, 4. august 995 Lsninge a) Koodinatene x; y; z tansfomees slik x 7 bx = x; y 7 by = y cos, z sin ; z 7 by = y sin + z cos Den invese tansfomasjonen e en otasjon en
Newtons lover i én dimensjon (2)
 Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Eksamen TFY 4240: Elektromagnetisk teori
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
EKSAMEN I EMNE SIE 4015 BØLGEFORPLANTNING
 NTNU Noges teknisk-natuvitenskapelige univesitet Side 1 av 8 Fakultet fo infomatikk, matematikk og elektoteknikk Institutt fo fysikalsk elektonikk Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Navn:
NTNU Noges teknisk-natuvitenskapelige univesitet Side 1 av 8 Fakultet fo infomatikk, matematikk og elektoteknikk Institutt fo fysikalsk elektonikk Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Navn:
Tips for prosjektoppgaven i FYS-MEK/F 1110 V2006
 1 Tips fo posjektoppgaven i FYS-MEK/F 1110 V2006 Utfosking av et telegeme-system Ant Inge Vistnes, vesjon 0605141330 Det e ikke nødvendig å lese dette skivet fo å løse posjektoppgaven, men de fleste vil
1 Tips fo posjektoppgaven i FYS-MEK/F 1110 V2006 Utfosking av et telegeme-system Ant Inge Vistnes, vesjon 0605141330 Det e ikke nødvendig å lese dette skivet fo å løse posjektoppgaven, men de fleste vil
Eksamensoppgave i TEP4105 FLUIDMEKANIKK
 Institutt fo enegi- og posessteknikk Eksamensoppgave i TEP45 FLUIDMEKANIKK Faglig kontakt unde eksamen: Ive Bevik Tlf.: 7359 3555 Eksamensdato: 7. august 23 Eksamenstid : 9. 3. Hjelpemiddelkode/Tillatte
Institutt fo enegi- og posessteknikk Eksamensoppgave i TEP45 FLUIDMEKANIKK Faglig kontakt unde eksamen: Ive Bevik Tlf.: 7359 3555 Eksamensdato: 7. august 23 Eksamenstid : 9. 3. Hjelpemiddelkode/Tillatte
Eksamen i TFY4205 Kvantemekanikk Mandag 8. august :00 13:00
 NTNU Side 1 av 9 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Ane Bataas Telefon: 73593647 Eksamen i TFY405 Kvantemekanikk Mandag 8. august 005 9:00 13:00 Tillatte hjelpemidle: Altenativ C
NTNU Side 1 av 9 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Ane Bataas Telefon: 73593647 Eksamen i TFY405 Kvantemekanikk Mandag 8. august 005 9:00 13:00 Tillatte hjelpemidle: Altenativ C
Energi Norge v/ingvar Solberg og Magne Fauli THEMA Consulting Group v/åsmund Jenssen og Jacob Koren Brekke 5. februar 2019
 Til: Enegi Noge v/ingva Solbeg og agne Fauli Fa: v/åsmund Jenssen og Jacob Koen Bekke Dato: 5. febua 219 Refeanse: ENO-18-1 Analyse av povenyvikninge av skatteendinge siden 27 Noske vannkaftvek ha siden
Til: Enegi Noge v/ingva Solbeg og agne Fauli Fa: v/åsmund Jenssen og Jacob Koen Bekke Dato: 5. febua 219 Refeanse: ENO-18-1 Analyse av povenyvikninge av skatteendinge siden 27 Noske vannkaftvek ha siden
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 9. Veiledning: 18. oktober. Innleveringsfrist: 23. oktober kl 14.
 TFY404 Fysikk. Institutt fo fysikk, NTNU. Høsten 203. Øving 9. Veiledning: 8. oktobe. Innleveingsfist: 23. oktobe kl 4. Oppgve ) Figuen vise et unifomt elektisk felt (heltukne linje). Lngs hvilken stiplet
TFY404 Fysikk. Institutt fo fysikk, NTNU. Høsten 203. Øving 9. Veiledning: 8. oktobe. Innleveingsfist: 23. oktobe kl 4. Oppgve ) Figuen vise et unifomt elektisk felt (heltukne linje). Lngs hvilken stiplet
Fysikk-OL Norsk finale 2005
 Univesitetet i Oslo Nosk Fysikklæefoening Fysikk-OL Nosk finale 005 3. uttakingsunde Tid: Fedag 5. apil kl 09.00.00 Hjelpemidle: Tabell/fomelsamling, gafisk lommeegne Oppgavesettet bestå av 7 oppgave på
Univesitetet i Oslo Nosk Fysikklæefoening Fysikk-OL Nosk finale 005 3. uttakingsunde Tid: Fedag 5. apil kl 09.00.00 Hjelpemidle: Tabell/fomelsamling, gafisk lommeegne Oppgavesettet bestå av 7 oppgave på
Unneberg skole ÅRSPLAN I NORSK. 5. trinn. Hele året. delta i rollespill, drama og opplesing. Kunne holde en enkel presentasjon.
 Unnebeg skole ÅRSPLAN I NORSK. tinn KOMPETANSEM ÅL FRA LÆREPLANEN Eleven skal kunne oppte i ulike olle gjennom damaaktivitete, opplesing og pesentasjon LOKALE KJENNETEGN FOR MÅLOPPNÅELSE Eleven skal kunne
Unnebeg skole ÅRSPLAN I NORSK. tinn KOMPETANSEM ÅL FRA LÆREPLANEN Eleven skal kunne oppte i ulike olle gjennom damaaktivitete, opplesing og pesentasjon LOKALE KJENNETEGN FOR MÅLOPPNÅELSE Eleven skal kunne
Løsning øving 12 N L. Fra Faradays induksjonslov får vi da en indusert elektromotorisk spenning:
 nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
Diffraksjon og interferens med laser
 Diffaksjon og intefeens med lase Hensikt Oppsettet pa bildet bukes til a undesøke diffaksjonsmønste fa ulike spalte og gittee. Na laselys teffe et diffaksjonsobjekt, vil intensitetsmønsteet i obsevasjonsplanet
Diffaksjon og intefeens med lase Hensikt Oppsettet pa bildet bukes til a undesøke diffaksjonsmønste fa ulike spalte og gittee. Na laselys teffe et diffaksjonsobjekt, vil intensitetsmønsteet i obsevasjonsplanet
Fysikk 2 Eksamen høsten Løsningsforslag
 Fysikk - Løsningsfoslag Oppgae a) B Beegelsesmengde e gitt som p m og enheten bli defo kgm/s. Samtidig et i at N = kgm/s. Da kan i skie b) C kgm/s kgm/s s N s Vi gi patiklene numme fa til 3, se figuen.
Fysikk - Løsningsfoslag Oppgae a) B Beegelsesmengde e gitt som p m og enheten bli defo kgm/s. Samtidig et i at N = kgm/s. Da kan i skie b) C kgm/s kgm/s s N s Vi gi patiklene numme fa til 3, se figuen.
Laboratorieøvelse i MNFFY1303-Elektromagnetisme Institutt for Fysikk, NTNU MAGNETISK HYSTERESE
 Laboatoieøvelse i MNFFY33-Elektomagnetisme Institutt fo Fysikk, NTNU Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske felte og målinge av slike. Det innebæe måling av magnetfelt fa enkle
Laboatoieøvelse i MNFFY33-Elektomagnetisme Institutt fo Fysikk, NTNU Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske felte og målinge av slike. Det innebæe måling av magnetfelt fa enkle
Betinget bevegelse
 Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Magnetisk hysterese. 1. Beregn magnetfeltet fra en strømførende spole med kjent vindingstall.
 FY33 Elektisitet og magnetisme II Institutt fo fysikk, TU FY33 Elektisitet og magnetisme II, høst 7 Laboatoieøvelse Magnetisk hysteese Hensikt Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske
FY33 Elektisitet og magnetisme II Institutt fo fysikk, TU FY33 Elektisitet og magnetisme II, høst 7 Laboatoieøvelse Magnetisk hysteese Hensikt Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske
LØSNINGSFORSLAG TIL EKSAMEN MAI 2007
 NTNU Noges teknisk-ntuvitenskpelige univesitet Fkultet fo ntuvitenskp og teknologi Institutt fo mteilteknologi TMT40 KJEMI LØSNINGSFORSLAG TIL EKSAMEN MAI 007 OPPGAVE ) - ph definees som den negtive logitmen
NTNU Noges teknisk-ntuvitenskpelige univesitet Fkultet fo ntuvitenskp og teknologi Institutt fo mteilteknologi TMT40 KJEMI LØSNINGSFORSLAG TIL EKSAMEN MAI 007 OPPGAVE ) - ph definees som den negtive logitmen
KAPITTEL 6. STØRRELSER OG TALL I GRESK MATEMATIKK
 KAPITTEL 6. STØRRELSER OG TALL I GRESK MATEMATIKK Gekee kjete de atulige tallee og de kjete til fohold - dvs det vi i dag vil ofatte som bøke. E guleggede ofatig va at to lijestykke måtte ha et felles
KAPITTEL 6. STØRRELSER OG TALL I GRESK MATEMATIKK Gekee kjete de atulige tallee og de kjete til fohold - dvs det vi i dag vil ofatte som bøke. E guleggede ofatig va at to lijestykke måtte ha et felles
Årsplan i matematikk 6. årstrinn 2016/2017
 Åsplan i matematikk 6. åstinn 2016/2017 Åsplanen ta utgaspunkt i kunnskapsløftet. I planen ta vi utgaspunkt i kompetansemålene fo 7.klasse. I matematikk læe en litt av et tema på 5.åstinn, litt me om samme
Åsplan i matematikk 6. åstinn 2016/2017 Åsplanen ta utgaspunkt i kunnskapsløftet. I planen ta vi utgaspunkt i kompetansemålene fo 7.klasse. I matematikk læe en litt av et tema på 5.åstinn, litt me om samme
Måling av gravitasjonskonstanten
 Måling av gavitasjonskonstanten Aeea Aka, Jako Gehad Matinussen & Ingeog Ullaland Oktoe 014 Sammendag Gavitasjonskonstantens vedi, som anvendes i Newtons univeselle gavitasjonslov, kan eegnes ved å foeta
Måling av gavitasjonskonstanten Aeea Aka, Jako Gehad Matinussen & Ingeog Ullaland Oktoe 014 Sammendag Gavitasjonskonstantens vedi, som anvendes i Newtons univeselle gavitasjonslov, kan eegnes ved å foeta
egenverd FASE 3: barnehage
 : egenved banehage Hva kjennetegne bana i fase 3? De voksnes olle Banemøte Gadeobe Måltid Samlingsstund Uteleiken Konfliktløsning Posjekt Vudeing Haug banehage 2011-2012 egenved egenved «Banehagen skal
: egenved banehage Hva kjennetegne bana i fase 3? De voksnes olle Banemøte Gadeobe Måltid Samlingsstund Uteleiken Konfliktløsning Posjekt Vudeing Haug banehage 2011-2012 egenved egenved «Banehagen skal
Løsningsforslag sist oppdatert
 Løsningsfoslag sist oppdatet.. BOKMÅL Oppgave En funksjon f e definet i intevallet ved f ( ) ( ) e a) Finn f ( ). Avgjø hvo funksjonen e stigende og hvo funksjonen e avtagende. Bestem funksjonens eventuelle
Løsningsfoslag sist oppdatet.. BOKMÅL Oppgave En funksjon f e definet i intevallet ved f ( ) ( ) e a) Finn f ( ). Avgjø hvo funksjonen e stigende og hvo funksjonen e avtagende. Bestem funksjonens eventuelle
Eksamen 16. des Løsningsforslag
 Institutt fo fysikk TFY44/FY Mekanisk fysikk Eksamen 6. des.. Løsningsfoslag Dette løsningsfoslaget e spesielt fyldig med flee altenative løsninge, som ukt av flee studente i eksamensesvaelsen. Det e også
Institutt fo fysikk TFY44/FY Mekanisk fysikk Eksamen 6. des.. Løsningsfoslag Dette løsningsfoslaget e spesielt fyldig med flee altenative løsninge, som ukt av flee studente i eksamensesvaelsen. Det e også
Veileder for mentorer
 Veilede fo mentoe Utabeidet av Likestillingssenteet 2011 Food Likestillingssenteet ha siden 2006 diftet mentonettveket Velkommen inn, et mentonettvek spesielt ettet mot innvandekvinne. Mentoene i Velkommen
Veilede fo mentoe Utabeidet av Likestillingssenteet 2011 Food Likestillingssenteet ha siden 2006 diftet mentonettveket Velkommen inn, et mentonettvek spesielt ettet mot innvandekvinne. Mentoene i Velkommen
Problemet. Datamaskinbaserte doseberegninger. Usikkerheter i dose konsekvenser 1 Usikkerheter i dose konsekvenser 2
 Poblemet Datamaskinbasete dosebeegninge Beegne dosefodeling i en pasient helst med gunnlag i CT-bilde Eiik Malinen Sentale kilde: T. Knöös (http://www.clin.adfys.lu.se/downloads.htm) A. Ahnesjö (div. publikasjone)
Poblemet Datamaskinbasete dosebeegninge Beegne dosefodeling i en pasient helst med gunnlag i CT-bilde Eiik Malinen Sentale kilde: T. Knöös (http://www.clin.adfys.lu.se/downloads.htm) A. Ahnesjö (div. publikasjone)
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 10. Dersom ikke annet er oppgitt, antas det at systemet er i elektrostatisk likevekt.
 TFY0 Fysikk. Institutt fo fysikk, NTNU. Høsten 06. Øving 0. Opplysninge: esom ikke nnet e oppgitt, nts det t systemet e i elektosttisk likevekt. esom ikke nnet e oppgitt, e potensil undefostått elektosttisk
TFY0 Fysikk. Institutt fo fysikk, NTNU. Høsten 06. Øving 0. Opplysninge: esom ikke nnet e oppgitt, nts det t systemet e i elektosttisk likevekt. esom ikke nnet e oppgitt, e potensil undefostått elektosttisk
Løsningsforslag Fysikk 2 Vår 2013 Oppgav e
 Løsningsfoslag Fysikk 2 Vå 203 Løsningsfoslag Fysikk 2 Vå 203 Oppgav e Sva Foklaing a) B Feltet E gå adielt ut fa en positivt ladning. Siden ladning og 2 e like stoe, og ligge like langt unna P vil E væe
Løsningsfoslag Fysikk 2 Vå 203 Løsningsfoslag Fysikk 2 Vå 203 Oppgav e Sva Foklaing a) B Feltet E gå adielt ut fa en positivt ladning. Siden ladning og 2 e like stoe, og ligge like langt unna P vil E væe
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST1100, 13. desembe 2016, 9.00 13.00 Oppgavesettet inkludet fomelsamling e på 7 side Tillatte hjelpemidle: 1) Angel/Øgim
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST1100, 13. desembe 2016, 9.00 13.00 Oppgavesettet inkludet fomelsamling e på 7 side Tillatte hjelpemidle: 1) Angel/Øgim
FAG: MA-209 Matematikk 3 LÆRER: Per Henrik Hogstad KANDIDATEN MÅ SELV KONTROLLERE AT OPPGAVESETTET ER FULLSTENDIG
 UNIVERITETET I AGDER Gimstad E K A M E N O P P G A V E : FAG: MA-9 Matematikk ÆRER: Pe enik ogstad Klasse: Dato:.6. Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende Antall side: 5 inkl. foside
UNIVERITETET I AGDER Gimstad E K A M E N O P P G A V E : FAG: MA-9 Matematikk ÆRER: Pe enik ogstad Klasse: Dato:.6. Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende Antall side: 5 inkl. foside
Midtsemesterprøve onsdag 7. mars 2007 kl Versjon A
 Institutt fo fysikk, NTNU FY1003 lektisitet og mgnetisme I TFY4155 lektomgnetisme Vå 2007 Midtsemestepøve onsdg 7. ms 2007 kl 1300 1500. Løsningsfoslg. Vesjon 1) Hvilken påstnd om elektisk potensil e feil?
Institutt fo fysikk, NTNU FY1003 lektisitet og mgnetisme I TFY4155 lektomgnetisme Vå 2007 Midtsemestepøve onsdg 7. ms 2007 kl 1300 1500. Løsningsfoslg. Vesjon 1) Hvilken påstnd om elektisk potensil e feil?
Vektreduksjon - Livsstilskurs kr. 1200,- pr. mnd
 Livea - livsstil - vekteduksjon n 1-2015 Vekteduksjon - Livsstilskus k. 1200,- p. mnd kusplan 2015 Kus state nå! Les me s. 3 Gikk ned 26 kg på 16 uke "Nå føle jeg at jeg vikelig nyte mat - fo føste gang"
Livea - livsstil - vekteduksjon n 1-2015 Vekteduksjon - Livsstilskus k. 1200,- p. mnd kusplan 2015 Kus state nå! Les me s. 3 Gikk ned 26 kg på 16 uke "Nå føle jeg at jeg vikelig nyte mat - fo føste gang"
Tillatte hjelpemidler: Lærebok og kalkulator i samsvar med fakultetet sine regler Oppgave 1 En funksjon f er gitt ved f ( x) ( x 2) e x.
 UNIVERSITETET I BERGEN De maemaisk-nauvienskapelige fakule Eksamen i emne MAT Bukekus i maemaikk Fedag 8 febua, kl 9-4 BOKMÅL Tillae hjelpemidle: Læebok og kalkulao i samsva med fakulee sine egle Oppgave
UNIVERSITETET I BERGEN De maemaisk-nauvienskapelige fakule Eksamen i emne MAT Bukekus i maemaikk Fedag 8 febua, kl 9-4 BOKMÅL Tillae hjelpemidle: Læebok og kalkulao i samsva med fakulee sine egle Oppgave
Løsning, eksamen 3FY juni 1999
 Løsning, eksamen 3FY juni 1999 Oppgae 1 km/s a) Hubbles lo sie at H, de H. 10 lyså Faten til galaksen e: 3 10 m/s H 5,0 10 7 lyså 1,10 10 m/s 10 lyså b) Dopplefomelen gi oss λ, de c e lysfaten og λ 0 e
Løsning, eksamen 3FY juni 1999 Oppgae 1 km/s a) Hubbles lo sie at H, de H. 10 lyså Faten til galaksen e: 3 10 m/s H 5,0 10 7 lyså 1,10 10 m/s 10 lyså b) Dopplefomelen gi oss λ, de c e lysfaten og λ 0 e
Kapittel 2: Krumlinjet bevegelse
 Kapittel : Kumlinjet bevegelse Vannett kast v = v v = gt x 0 1 x = vt 0 y= gt y Skått kast v = v v = v gt x 0x y 0y 1 x = v0 t y = v x 0 t gt y Sving uten dosseing U+ G = ma N = G v R = m R = μn = μmg
Kapittel : Kumlinjet bevegelse Vannett kast v = v v = gt x 0 1 x = vt 0 y= gt y Skått kast v = v v = v gt x 0x y 0y 1 x = v0 t y = v x 0 t gt y Sving uten dosseing U+ G = ma N = G v R = m R = μn = μmg
Oslo kommune Bydel Østensjø Bydelsadministrasjonen. Protokoll 7/14
 Oslo kommune Bydel Østensjø Bydelsadministasjonen Potokoll 7/14 Møte: Omsogskomite Møtested: Kjenehuset dagsente, Enebakkveien 18 Møtetid: Mandag 10. novembe 2014 kl. 18.00 Seketaiat: 2343887 Møtelede:
Oslo kommune Bydel Østensjø Bydelsadministasjonen Potokoll 7/14 Møte: Omsogskomite Møtested: Kjenehuset dagsente, Enebakkveien 18 Møtetid: Mandag 10. novembe 2014 kl. 18.00 Seketaiat: 2343887 Møtelede:
