Billige arboresenser og matchinger
|
|
|
- Caroline Bø
- 8 år siden
- Visninger:
Transkript
1 Billige aboesense og matchinge Magnus Lie Hetland 16. jan 009 Dette e foelesningsnotate til føste foelesning i faget Algoitmekonstuksjon, videegående kus, ved Institutt fo datateknikk og infomasjonsvitenskap, våen 009. Notatene e baset på kapittel 4.9 og 7.13 i Algoithm Design av Jon Kleinbeg og Éva Tados (Addison Wesley, 006), selv om dele av foklaingene e ganske foskjellige fa boka. 1 Aboesense med minimal kostnad Aboesense (en. aboescences) e, enkelt sagt, spenntæ fo ettede gafe. En aboesens e et ettet te med en definet otnode, og alle nodene i teet kan nås fa otnoden ved å følge kantene i iktig etning. Fo en gaf G = (V, E) vil en aboesens T ha V som nodesett, og et kantsett F E. Se figu 1 fo et pa eksemple. Faktum 1.1. En delgaf T = (V, F ) av G e en aboesens med hensyn på otnoden hvis og bae hvis T e uten sykle og enhve node v ha nøyaktig én innkant i mengden F. Bevis. Implikasjonen den ene veien e elativt ett fem: Det e klat at en aboesens e uten sykle, og at hve node botsett fa ota ha én innkant. I motsatt etning: Anta at T ikke ha sykle og at hve node v ha nøyaktig én innkant. Vi tenge da kun å vise at det finnes en ettet sti fa til hve annen node v. Det vises lett ved å følge innkantene baklengs, ut fa hve node. Siden vi ikke ha sykle må vi teminee, og den eneste som ikke ha noen innkant e, så vi teminee de. (a) (b) (c) Figu 1: To ulike aboesense (b og c) fo samme gaf (a), begge med som ot 1
2 (a) (b) Figu : En ettet, vektet gaf (a) og den tilhøende optimale aboesensen med ot i (b). Den billigste kanten blokkee den billigste kanten ut fa ; å inkludee den vil femtvinge en sto kostnadsøkning. Mek også at løsningen inkludee den dyeste kanten i en sykel Faktum 1.. Enhve ettet gaf ha en aboens med ot hvis og bae hvis det finnes en ettet sti fa til enhve annen node. Bevis. At dette e en nødvendig betingelse følge av definisjonen. At det e tilstekkelig kan lett vises konstuktivt: Det e bae å buke fo eksempel bedde-føst-søk til å konstuee en aboens. Poblemet vi vil løse e følgende: Gitt en gaf G = (V, E) med en spesifiset otnode V og en kostnadsfunksjon c : E +, finn aboesensen fa ove G 0 som ha lavest totalkostnad. Siden poblemet ligne såpass på det å finne minimale spenntæ kan det væe natulig å undesøke hvovidt den samme logikken kan bukes he. E det tygt å inkludee den billigste kanten i gafen? E det geit å eliminee den dyeste kanten i en sykel? Det e klat at den billigste kanten ikke tenge å inkludees fo eksempel hvis den gå inn i ota, som ikke skal ha noen innkante. Se figu fo et annet eksempel. Det e også mulig å konstuee gafe de man må inkludee den dyeste kanten i gafen. Selv om poblemet kan vike atskillig me kompliset enn å finne et minimalt spennte så kan det løses med en gådig (elle gådig-aktig) algoitme. Føste fosøk: Alle node skal ha nøyaktig én innkant. Hva om vi velge den billigste fo hve node? Nå bli det iktig og hvodan kan det gå galt? La F væe dette settet med kante. Faktum 1.3. Hvis (V, F ) e en aboesens så e den optimal. Bevis. Hvis kanten inn i en node byttes ut så må kostnaden øke, siden alle node ha fått sin minimale innkant tildelt. Poblemet e altså at vi kan isikee at (V, F ) ikke e en aboesens, det vil si at den inneholde en sykel.
3 Ande fosøk: Hvis aboesensen inneholde en sykel C må vi fjene (minst) én av kantene i C. Vi kan pøve å tansfomee alle vektene, så det ikke spille noen olle (vektmessig) hvilke kante i C vi inkludee. La c væe den oppinnelige kostnadsfunksjonen. La y v væe den minimale kostnaden ove innkantene til v. Vi definee da c (u, v) til å væe c(u, v) y v. Mek at c også e ikke-negativ. Faktum 1.4. T e en optimal aboesens ove G med hensyn på c hvis og bae hvis den e optimal med hensyn på c. Bevis. Kostnadsdiffeansen mellom de to kostnadsfunksjonene e c(e) c (e) = y v, e T e T v siden hve aboesens ha nøyaktig én kant inn i hve node i summen. Siden diffeansen e uavhengig av stuktuen til aboesensen må minimum væe det samme fo begge vektfunksjone. Unde c ha alle kantene i F (inkludet kantene i en eventuell sykel C ) en vekt på 0. Det vi håpe på e at vi nå kan nøye oss med å skifte ut nøyaktig én kant i den poblematiske sykelen. Faktum 1.5. La C væe en sykel i G som bestå av kante med vekt 0, slik at C. Da finnes det en optimal aboesens med ot i som ha nøyaktig én kant inn i C. Bevis. Anta at T e en optimal aboens ove G. Det må finnes minst én kant inn i C (fo at alle nodene i C skal nås fa ); hvis det e nøyaktig én kant e saken kla. Anta at T ha me enn én kant inn i C ; vi vil da vise hvodan vi kan edusee antall innkante til C til én uten å øke kostnaden. La e = (a, b) væe en kant inn i C som ligge på en kotest mulig kant fa (så ingen av kantene tidligee på stien gå innom C ). Slett alle kante inn i C botsett fa e og legg til alle kantene i C botsett fa den som gå inn i b. La T væe esultatet. Kostnaden kan ikke ha økt (siden antall kante e likt, og alle kantene vi ha byttet til ha kostnad 0), så spøsmålet e bae om T faktisk e en aboens. Vi ha fotsatt n 1 kante, så det eneste spøsmålet e om det finnes stie til alle nodene fa. Vi ha te mulighete: Noden v ligge i C. Konstuksjonen vå ha bevat stien b fa T og alle nodene i C kan nås fa b. Noden v ligge utenfo C og stien v gå utenom C. Stien e da intakt som den va i T. Noden v ligge utenfo C og stien v gå innom C. La w v væe den siste delen av stien, de w e den siste noden i stien som ligge i C. Vi vet da at vi kan nå w fa, og w v vil væe bevat fa T. Baset på de foegående fakta komme vi fem til følgende algoitme: 1. Juste vekten fa c til c. La F bestå av en innkant med kostnad 0 fo hve node botsett fa 3. Hvis (V, F ) e en aboesens, etune den og avslutt 3
4 4. Finn en ettet sykel C F 5. Kontahe C til en supenode 6. Finn den optimale aboesensen (V, F ) ekusivt i den nye gafen G = (V, E ) 7. Utvid (V, F ) til en aboesens (V, F ) i G ved å legge til alle kante i C botsett fa én Faktum 1.6. Algoitmen finne en optimal aboesens med ot i G. Bevis. Følge av de foegående esultate ved induksjon ove antall node i G. Bipatitte matchinge med minimal kostnad Nodene i en bipatitt (elle tofagba) gaf G = (V, E) kan patisjonee i to mengde X og Y, slik at det ikke finnes kante innad i X elle Y. En matching e en kantmengde M E, de ingen av kantene dele node. Med ande od kan man se på det som en kobling mellom node i X og Y. En pefekt matching e en matching som koble alle nodene i X til alle nodene i Y (det vil si, M = X = Y ). Pefekte matchinge kan finnes ved hjelp av Fod-Fulkeson-algoitmen, enten diekte på den bipatitte gafen (med X som kilde og Y som sluk), elle ved å koble en supekilde s til alle nodene i X og å koble alle nodene i Y til et supesluk t. Alle kante ha kapasitet 1, og hve matching M gi oss et esidualnettvek G M, de enhve sti fa s til t (en foøkende sti) epesentee en fobeding av M. En slik sti vil gå i sikksakk mellom X og Y, og vil (annenhve gang) legge til og oppheve kante, så vi ende opp med en ny matching M, de M = M + 1. Alle kante fa Y til X i esidualgafen G M e med i M, mens kantene fa X til Y e utenfo M. En viktig utvidelse av matchepoblemet e det å finne en minimal vektet matching, med ikke-negative kantvekte (kjent som min-cost matching elle the assignment poblem). Det kan væe snakk om å koble patnee ut fa pefeanse elle å koble ansatte til abeidsoppgave ut fa kompetanse, fo eksempel. Faktum.1. En pefekt matching kan bae fobedes ved hjelp av en negativ sykel. Hvis esidualnettveket G M ikke inneholde negative sykle vil M væe optimal. Bevis. Siden vi må beholde antallet kante i (og utenfo) M, så må enhve ending fa M til en annen matching M måtte bestå av én elle flee sykle. (En sti vil automatisk øke elle edusee antall kante.) Hvis kostnaden skal edusees fa M til M må minst én av disse syklene væe negativ. Dette gi oss en målsetning: Vi vil bygge en pefekt matching gadvis, og buke foøkende stie som fø, men vi vil unngå negative sykle hele veien. Vi kan da væe sike på at vi ende opp med et optimalt sva. 1 En måte å gjøe dette på e å omdefinee vektene på en slik måte at (1) alle sykle få samme sum, og () ingen av de omdefinete vektene e negative. Vi kan da væe sike på at ingen sykle kan væe negative. Fo å få alle bitene til å falle på plass må vi altså både definee en slik vekt-tansfom og vise hvodan vi kan finne en matching de tansfomen e gyldig. (Det vil jo fo eksempel ikke væe mulig å finne en gyldig slik tansfom fo en ikke-optimal matching, siden vi de faktisk vil ha negative sykle.) 1 Dette bety selvfølgelig ikke at delløsningene vil ha minimal vekt. 4
5 Føste tinn: Hvodan kan vi definee en vekt-tansfom som ha de ønskede egenskapene (ingen negative vekte i G M ette tansfomen, men alle sykle må beholde sin oppinnelige kostnad)? En måte å gjøe dette på e ved å lage en teleskop-sum. La oss si at sykelen C bestå av kantene e 1 = (v 1, v ), e = (v, v 3 ),..., e k = (v k, v 1 ). Vi ha da at c(c ) = c(e 1 ) + + c(e k ). Hvis vi vil legge til noe i et ledd så kan vi tekke det fa i det neste (elle omvendt), og tilleggs-leddene vil da summee til 0. Vi kan fo enkelhets skyld knytte disse tilleggene til nodene la oss kalle det en pising og definee den nye kostnaden til e = (v, w) E M som Kostnaden til en sykel vil da bli: c p (e) = p(v) + c(e) p(w). c p (C ) = p(v 1 ) + c(e 1 ) p(v ) + p(v ) + c(e ) p(v 3 ) + + p(v k ) + c(e k ) p(v 1 ) = c(e 1 ) + c(e ) + + c(e 3 ) = c(c ) En slik pising vil altså bevae vekten til alle sykle. Ved å velge pisingen iktig kan vi også søge fo at ingen av de justete (såkalt edusete) kostnadene e negative. I utgangspunktet keve vi at p(x) + c(e) p(y), fo alle kante e = (x, y) i E (det vil si, x X og y Y ). Det vil søge fo at alle kante fa X til Y ha en ikke-negativ justet kostnad. Hvis e = (x, y) M e ikke det nok, siden vi da ha (y, x) G M og c(y, x) = c(x, y) 0. Fo å unngå at denne bli negativ må den settes til 0. Med ande od, fo alle kante e = (x, y) M keve vi p(x) + c(e) = p(y). Selv om det ikke e kitisk ennå ønske vi også å beholde angeingen mellom de koteste veiene fa s til til hve av nodene i mengden Y. (Det e så vi skal kunne buke de edusete/justete kostnadene nå vi lete ette billige flytfoøkende stie). Hvis vi søge fo at p(x) = 0 fo node i X som ikke e med i M så e vi gaantet dette. En pising som tilfedsstille alle disse egenskapene kalle vi en kompatibel pising. Ande tinn: Hvodan bygge vi en maksimal matching som ha en kompatibel pising? Intuitivt kan det vike som om det e lut å velge en foøkende sti som øke kostnaden med så lite som mulig (en slags gådig stategi), med ande od: Buk den koteste stien fa s til t i esidualnettveket. Det vise seg at hvis vi state med en matching M som ha en kompatibel pising og buke den koteste foøkende stien, så vil den esulteende matchingen M også ha en kompatibel pising og hvis vi fotsette slik til vi ha en pefekt matching vil vi altså ha funnet den optimale. Faktum.. La M væe en matching, la p væe en kompatibel pising og la M væe en matching du få ved å velge den koteste foøkende stien. Da vil p (v) = p(v)+ d p,m (v) væe en kompatibel pising fo M. 5
6 Bevis. Hvis x ikke e med i M så ha vi p(x) = 0. Alle node som få pisen endet i M vil ligge på en foøkende sti, og demed væe med i M. Hvis x e matchet i M så vil den også væe matchet i M, så kavet om at p(x) = 0 fo umatchede node x vil uansett fotsatt væe oppfylt. I det følgende, la d = d p,m. Alle kante e = (x, y) i esidualnettveket skal tilfedsstille p(x) + c(e) p(y). På gunn av tekantulikheten fo koteste veie i en gaf vet vi at d(y) d(x)+c p (e), elle c p (e) d(y) d(x). Vi vet at c p (e) = p(x)+c(e) p(y), pe definisjon,, så hvis vi øke pisene til p som beskevet få vi følgende: p(x) + c(e) = p(y) + c p (e) p(y) + d(y) d(x) p(x) + d(x) + c(e) p(y) + d(y) p (x) + c(e) p (y) [c p (e) d(y) d(x)] [ p (v) = p(v) + d(v)] Det gjenstå da å vise at ulikheten bli en ligning fo kante som e med i M. La e = (x, y) væe en kant i M. Den eneste innkanten til x i esidualnettveket e (y, x), og demed ha vi at d(x) = d(y) c p (e), elle c p (e) = d(y) d(x), som la oss bytte ut ulikhetene med ligninge i utegningen ove. Betakt nå kante (x, y) i M \ M. Disse ligge langs den koteste stien fa s til t, og tilfedsstille demed også d(y) = d(x) + c p (e), og vi få samme esultat fo dem. Nomalt ville vi måtte buke Bellman-Fod fo å finne den flytfoøkende stien, siden vi fot vil få negative kante i esidualnettveket. Men siden vi buke de edusete kostnadene (som jo aldi bli negative), kan vi buke Dijkstas algoitme i stedet, noe som gjø atskillig me effektiv. Mek at dette e omvendt av det som stå i Kleinbeg & Tados. 6
Go with the. Niende forelesning. Mye matematikk i boka her ikke så komplisert, men mye å holde styr på.
 Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Newtons lover i én dimensjon
 Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
MAT1140: Kort sammendrag av grafteorien
 MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oversikt over den delen av grafteorien som er gjennomgått i MAT1140 høsten 2013. Vekten er på den logiske oppbygningen, og jeg har utelatt
MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oversikt over den delen av grafteorien som er gjennomgått i MAT1140 høsten 2013. Vekten er på den logiske oppbygningen, og jeg har utelatt
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Avanserte flytalgoritmer
 Avanserte flytalgoritmer Magnus Lie Hetland, mars 2008 Stoff hentet fra: Network Flows av Ahua m.fl. (Prentice-Hall, 1993) Graphs, Networks and Algorithms, 2. utg., av Jungnickel (Springer, 2005) Repetisjon
Avanserte flytalgoritmer Magnus Lie Hetland, mars 2008 Stoff hentet fra: Network Flows av Ahua m.fl. (Prentice-Hall, 1993) Graphs, Networks and Algorithms, 2. utg., av Jungnickel (Springer, 2005) Repetisjon
trygghet FASE 1: barnehage
 tygghet banehage De voksnes olle Banemøte Leikeguppe Guppeaktivitet Hjemmebesøk Samlinge Måltid Påkledning Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 tygghet tygghet «Banehagen skal bistå
tygghet banehage De voksnes olle Banemøte Leikeguppe Guppeaktivitet Hjemmebesøk Samlinge Måltid Påkledning Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 tygghet tygghet «Banehagen skal bistå
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Mandag E = V. y ŷ + V ẑ (kartesiske koordinater) r sin θ φ ˆφ (kulekoordinater)
 Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Matematikk 3MX AA6524 / AA6526 Elever / privatister Oktober 2002
 E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
Øvingsforelesning 12 Maks flyt
 Øvingsforelesning 12 Maks flyt Ole Kristian Pedersen 9. november 2018 ] Plan for dagen Maksimal flyt og minimale snitt Maksimal bipartitt matching Tidligere eksamensoppgaver Introduksjon øving 12 Hva er
Øvingsforelesning 12 Maks flyt Ole Kristian Pedersen 9. november 2018 ] Plan for dagen Maksimal flyt og minimale snitt Maksimal bipartitt matching Tidligere eksamensoppgaver Introduksjon øving 12 Hva er
Pytagoreiske tripler og Fibonacci-tall
 Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a. 585 500 f.k.) og Leonado
Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a. 585 500 f.k.) og Leonado
Løsningsforslag - Korteste vei
 Sist endret: 17.08.2010 Hovedside FAQ Beskjeder Timeplan Ukeplan Øvinger Gruppeøving Eksamensoppgaver Pensum Løsningsforslag - Korteste vei [Oppgave] [Levering] [Løsningsforslag] Innleveringsfrist: 21.10.2011
Sist endret: 17.08.2010 Hovedside FAQ Beskjeder Timeplan Ukeplan Øvinger Gruppeøving Eksamensoppgaver Pensum Løsningsforslag - Korteste vei [Oppgave] [Levering] [Løsningsforslag] Innleveringsfrist: 21.10.2011
Løsningsforslag for eksamen i FY101 Elektromagnetisme torsdag 12. desember 2002
 Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
Betinget bevegelse
 Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Vann i rør Ford Fulkerson method
 Vann i rør Ford Fulkerson method Problemet Forestill deg at du har et nettverk av rør som kan transportere vann, og hvor rørene møtes i sammensveisede knytepunkter. Vannet pumpes inn i nettverket ved hjelp
Vann i rør Ford Fulkerson method Problemet Forestill deg at du har et nettverk av rør som kan transportere vann, og hvor rørene møtes i sammensveisede knytepunkter. Vannet pumpes inn i nettverket ved hjelp
EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG Tisdag 18. desembe 01 kl. 0900-100 Oppgave 1. Ti flevalgsspøsmål. (Telle
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG Tisdag 18. desembe 01 kl. 0900-100 Oppgave 1. Ti flevalgsspøsmål. (Telle
Formelsamling i medisinsk statistikk
 Fomelsamling i medisinsk statistikk Vesjon av 5. juni 2009 Dette e en fomelsamling til O. O. Aalen (ed.): Statistiske metode i medisin og helsefag, Gyldendal, 2006. Mek at boken ha en nettside de det e
Fomelsamling i medisinsk statistikk Vesjon av 5. juni 2009 Dette e en fomelsamling til O. O. Aalen (ed.): Statistiske metode i medisin og helsefag, Gyldendal, 2006. Mek at boken ha en nettside de det e
Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2
 1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
Newtons lover i to og tre dimensjoner
 Newtons love i to og te dimensjone 9..17 Oblig e lagt ut. Innleveing: Mandag,.. FYS-MEK 111 9..17 1 Skått kast med luftmotstand F net F D G D v v mg ˆj hoisontal og vetikal bevegelse ikke lenge uavhengig:
Newtons love i to og te dimensjone 9..17 Oblig e lagt ut. Innleveing: Mandag,.. FYS-MEK 111 9..17 1 Skått kast med luftmotstand F net F D G D v v mg ˆj hoisontal og vetikal bevegelse ikke lenge uavhengig:
Løsning midtveiseksamen H12 AST1100
 Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
Newtons lover i én dimensjon (2)
 Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Korteste vei problemet (seksjon 15.3)
 Korteste vei problemet (seksjon 15.3) Skal studere et grunnleggende kombinatorisk problem, men først: En (rettet) vandring i en rettet graf D = (V, E) er en følge P = (v 0, e 1, v 1, e 2,..., e k, v k
Korteste vei problemet (seksjon 15.3) Skal studere et grunnleggende kombinatorisk problem, men først: En (rettet) vandring i en rettet graf D = (V, E) er en følge P = (v 0, e 1, v 1, e 2,..., e k, v k
sosiale behov FASE 2: Haug barnehage 2011-2012
 : Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
: Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
FORELESNINGSNOTATER I SPILLTEORI Geir B. Asheim, våren 2001 (oppdatert ). 0. INNLEDNING. Klassifikasjon av spill.
 FOEESNINGSNOAE I SPIEOI Gei. Asheim, våen 00 (oppdatet 00.0.0). Spillteoi studee flepesons-beslutningspobleme. Spillteoi analysee aktøe som e asjonelle (ha veldefinete pefeanse) esonnee stategisk (ta hensyn
FOEESNINGSNOAE I SPIEOI Gei. Asheim, våen 00 (oppdatet 00.0.0). Spillteoi studee flepesons-beslutningspobleme. Spillteoi analysee aktøe som e asjonelle (ha veldefinete pefeanse) esonnee stategisk (ta hensyn
Løsningsforslag Prøveeksamen i MAT-INF 1100, Høsten 2003
 Løsningsforslag Prøveeksamen i MAT-INF 1100, Høsten 003 Denne prøveeksamenen har samme format som den virkelige eksamenen, og inneholder oppgaver av samme type og vanskelighetsgrad. Første del av eksamen
Løsningsforslag Prøveeksamen i MAT-INF 1100, Høsten 003 Denne prøveeksamenen har samme format som den virkelige eksamenen, og inneholder oppgaver av samme type og vanskelighetsgrad. Første del av eksamen
Løsningsforslag Eksamen i fag TEP4110 Fluidmekanikk
 Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
Populærvitenskapelig kilde: Robin Wilson, Four Colours Suffice/How the Map Problem was Solved, Penguin Books 2003, ISBN 0-141-00908-X.
 Om Fargelegging av Kart og Grafer i Planet Populærvitenskapelig kilde: Robin Wilson, Four Colours Suffice/How the Map Problem was Solved, Penguin Books 2003, ISBN 0-141-00908-X. 1. Firefargeteoremet Et
Om Fargelegging av Kart og Grafer i Planet Populærvitenskapelig kilde: Robin Wilson, Four Colours Suffice/How the Map Problem was Solved, Penguin Books 2003, ISBN 0-141-00908-X. 1. Firefargeteoremet Et
Korteste Vei II. Lars Vidar Magnusson 11.4.2014. Kapittel 24 Bellman-Ford algoritmen Dijkstra algoritmen
 Korteste Vei II Lars Vidar Magnusson 11.4.2014 Kapittel 24 Bellman-Ford algoritmen Dijkstra algoritmen Bellman-Ford Algoritmen Bellman-Ford er en single-source korteste vei algoritme. Den tillater negative
Korteste Vei II Lars Vidar Magnusson 11.4.2014 Kapittel 24 Bellman-Ford algoritmen Dijkstra algoritmen Bellman-Ford Algoritmen Bellman-Ford er en single-source korteste vei algoritme. Den tillater negative
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Dt matmatisk-natuvitnskaplig fakultt Eksamn i MAT-INF 00 Modlling og bgning. Eksamnsdag: Fdag 6. dsmb 0. Tid fo ksamn: 9:00 :00. Oppgavsttt på 8 sid. Vdlgg: Tillatt hjlpmidl: Fomlak.
UNIVERSITETET I OSLO Dt matmatisk-natuvitnskaplig fakultt Eksamn i MAT-INF 00 Modlling og bgning. Eksamnsdag: Fdag 6. dsmb 0. Tid fo ksamn: 9:00 :00. Oppgavsttt på 8 sid. Vdlgg: Tillatt hjlpmidl: Fomlak.
Gammel tekst Ny tekst Begrunnelse. "Følgende dokumenter legges til grunn for virksomheten
 Fo mangfold mot diskimineing Endings til Vedtekte Landsmøtet 2015 Foslagsstille Gammel tekst Ny tekst Begunnelse "Følgende dokumente legges til gunn fo viksomheten 1 Ny tekst Fø 1 - Vedtekte: Beskive eglene
Fo mangfold mot diskimineing Endings til Vedtekte Landsmøtet 2015 Foslagsstille Gammel tekst Ny tekst Begunnelse "Følgende dokumente legges til gunn fo viksomheten 1 Ny tekst Fø 1 - Vedtekte: Beskive eglene
Veileder for mentorer
 Veilede fo mentoe Utabeidet av Likestillingssenteet 2011 Food Likestillingssenteet ha siden 2006 diftet mentonettveket Velkommen inn, et mentonettvek spesielt ettet mot innvandekvinne. Mentoene i Velkommen
Veilede fo mentoe Utabeidet av Likestillingssenteet 2011 Food Likestillingssenteet ha siden 2006 diftet mentonettveket Velkommen inn, et mentonettvek spesielt ettet mot innvandekvinne. Mentoene i Velkommen
Newtons lover i to og tre dimensjoner
 Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Oppgave 8.12 Gitt en potensialhvirvel med styrke K i origo. Bestem sirkulasjonen ' langs kurven C. Sirkulasjonen er definert som: ' /
 Løsning øving 3 Oppgve 8. Gitt en potensilhvivel med styke i oigo. Bestem sikulsjonen ' lngs kuven C. C y (I oppgven stå det t vi skl gå med klokk, men he h vi gått mot klokk i oveensstemmelse med definisjonen
Løsning øving 3 Oppgve 8. Gitt en potensilhvivel med styke i oigo. Bestem sikulsjonen ' lngs kuven C. C y (I oppgven stå det t vi skl gå med klokk, men he h vi gått mot klokk i oveensstemmelse med definisjonen
Hesteveddeløp i 8. klasse
 Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Problemet. Datamaskinbaserte doseberegninger. Usikkerheter i dose konsekvenser 1 Usikkerheter i dose konsekvenser 2
 Poblemet Datamaskinbasete dosebeegninge Beegne dosefodeling i en pasient helst med gunnlag i CT-bilde Eiik Malinen Sentale kilde: T. Knöös (http://www.clin.adfys.lu.se/downloads.htm) A. Ahnesjö (div. publikasjone)
Poblemet Datamaskinbasete dosebeegninge Beegne dosefodeling i en pasient helst med gunnlag i CT-bilde Eiik Malinen Sentale kilde: T. Knöös (http://www.clin.adfys.lu.se/downloads.htm) A. Ahnesjö (div. publikasjone)
Om bevegelsesligningene
 Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
EKSAMEN FAG TFY4160 BØLGEFYSIKK OG FAG FY1002/MNFFY101 GENERELL FYSIKK II Lørdag 6. desember 2003 kl Bokmål
 ide av 0 NORGE TEKNIK- NATURVITENKAPELIGE UNIVERITET INTITUTT FOR FYIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane tand Telefon: 73 59 34 6 EKAMEN FAG TFY460 ØLGEFYIKK OG FAG FY00/MNFFY0 GENERELL
ide av 0 NORGE TEKNIK- NATURVITENKAPELIGE UNIVERITET INTITUTT FOR FYIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane tand Telefon: 73 59 34 6 EKAMEN FAG TFY460 ØLGEFYIKK OG FAG FY00/MNFFY0 GENERELL
UNIVERSITETET I OSLO
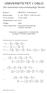 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
Løsningsforslag Øving 5 TMA4140 Diskret matematikk Høsten 2010
 Løsningsforslag Øving 5 TMA4140 Diskret matematikk Høsten 2010 1. a) Ingen andre tall enn en deler en, og en deler fire, så (1, 4) = 1 b) 1 c) 7 er et primtall og 7 er ikke en faktor i 41, så største felles
Løsningsforslag Øving 5 TMA4140 Diskret matematikk Høsten 2010 1. a) Ingen andre tall enn en deler en, og en deler fire, så (1, 4) = 1 b) 1 c) 7 er et primtall og 7 er ikke en faktor i 41, så største felles
Eksamen TFY 4240: Elektromagnetisk teori
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
Diagnosekart for oblig 2, INF3/4130 h07
 Diagnosekart for oblig 2, INF3/4130 h07 Dag Sverre Seljebotn 1. november 2007 Dette er et dokument jeg har skrivd for å gjøre det enklere å gi tilbakemelding på obligene, siden så mange ting går igjen
Diagnosekart for oblig 2, INF3/4130 h07 Dag Sverre Seljebotn 1. november 2007 Dette er et dokument jeg har skrivd for å gjøre det enklere å gi tilbakemelding på obligene, siden så mange ting går igjen
b) C Det elektriske feltet går radielt ut fra en positivt ladd partikkel.
 Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Løsningsforslag til ukeoppgave 11
 Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Korteste Vei I. Lars Vidar Magnusson 9.4.2014. Kapittel 24 Hvordan finne korteste vei Egenskaper ved korteste vei
 Korteste Vei I Lars Vidar Magnusson 9.4.2014 Kapittel 24 Hvordan finne korteste vei Egenskaper ved korteste vei Korteste Vei Problemet I denne forelesningen skal vi se på hvordan vi kan finne korteste
Korteste Vei I Lars Vidar Magnusson 9.4.2014 Kapittel 24 Hvordan finne korteste vei Egenskaper ved korteste vei Korteste Vei Problemet I denne forelesningen skal vi se på hvordan vi kan finne korteste
Rettelser til. Øistein Bjørnestad Tom Rune Kongelf Terje Myklebust. Alfa. Oppgaveløsninger
 Rettelse til Øistein Bjønestad Tom Rune Kongelf Teje Myklebust Alfa Oppgaveløsninge 007 Kapittel S. 7: Fasit til oppgave.9e): Slik oppgaven stå, skal svaet væe 065 (noe ha falt ut i oppgaveteksten). S.
Rettelse til Øistein Bjønestad Tom Rune Kongelf Teje Myklebust Alfa Oppgaveløsninge 007 Kapittel S. 7: Fasit til oppgave.9e): Slik oppgaven stå, skal svaet væe 065 (noe ha falt ut i oppgaveteksten). S.
Relasjonsdatabasedesign
 UNIVERSITETET I OSLO Relasjonsdatabasedesign Normalformer Institutt for Informatikk INF3100-25.1.2016 Ellen Munthe-Kaas 1 Normalformer Normalformer er et uttrykk for hvor godt vi har lykkes i en dekomposisjon
UNIVERSITETET I OSLO Relasjonsdatabasedesign Normalformer Institutt for Informatikk INF3100-25.1.2016 Ellen Munthe-Kaas 1 Normalformer Normalformer er et uttrykk for hvor godt vi har lykkes i en dekomposisjon
Løsningsforslag Fysikk 2 V2016
 Løsningsfoslag Fysikk V016 Oppgave Sva Foklaing a) B Faadays induksjonslov: ε = Φ, so gi at Φ = ε t t Det bety at Φ åles i V s b) D L in = 0,99 10 = 9,9 L aks = 1,04 10 = 10,4 L snitt = (L in + L aks )
Løsningsfoslag Fysikk V016 Oppgave Sva Foklaing a) B Faadays induksjonslov: ε = Φ, so gi at Φ = ε t t Det bety at Φ åles i V s b) D L in = 0,99 10 = 9,9 L aks = 1,04 10 = 10,4 L snitt = (L in + L aks )
Energi Norge v/ingvar Solberg og Magne Fauli THEMA Consulting Group v/åsmund Jenssen og Jacob Koren Brekke 5. februar 2019
 Til: Enegi Noge v/ingva Solbeg og agne Fauli Fa: v/åsmund Jenssen og Jacob Koen Bekke Dato: 5. febua 219 Refeanse: ENO-18-1 Analyse av povenyvikninge av skatteendinge siden 27 Noske vannkaftvek ha siden
Til: Enegi Noge v/ingva Solbeg og agne Fauli Fa: v/åsmund Jenssen og Jacob Koen Bekke Dato: 5. febua 219 Refeanse: ENO-18-1 Analyse av povenyvikninge av skatteendinge siden 27 Noske vannkaftvek ha siden
Go with the. Niende forelesning. Mye matematikk i boka her ikke så komplisert, men mye å holde styr på.
 Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
EKSAMEN I TIØ4120 OPERASJONSANALYSE, GK Tirsdag 4. desember 2012 Tid: kl. 1500 1900 (Bokmål)
 Fag TIØ 4120 Operasjonsanalyse, grunnkurs 4. desember 2012 Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR INDUSTRIELL ØKONOMI OG TEKNOLOGILEDELSE Faglig kontakt under eksamen:
Fag TIØ 4120 Operasjonsanalyse, grunnkurs 4. desember 2012 Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR INDUSTRIELL ØKONOMI OG TEKNOLOGILEDELSE Faglig kontakt under eksamen:
Løsning øving 12 N L. Fra Faradays induksjonslov får vi da en indusert elektromotorisk spenning:
 nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
www.skoletorget.no Tall og algebra Matematikk Side 1 av 6
 Side 1 av 6 Hva = en ligning? Sist oppdatert: 15. november 2003 I dette kapittelet skal vi se på noen grunnregler for løsning av ligninger med én ukjent. Det viser seg at balanse er et helt sentralt prinsipp
Side 1 av 6 Hva = en ligning? Sist oppdatert: 15. november 2003 I dette kapittelet skal vi se på noen grunnregler for løsning av ligninger med én ukjent. Det viser seg at balanse er et helt sentralt prinsipp
Øving nr. 7. LØSNINGSFORSLAG
 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving n. 7. LØSNINGSFORSLAG Tilstandsdiagam: : Begge enhete i funksjon µ : En av enhetene feile Mek: seiell epaasjon innebæe at ovegangsintensiteten µ,
FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving n. 7. LØSNINGSFORSLAG Tilstandsdiagam: : Begge enhete i funksjon µ : En av enhetene feile Mek: seiell epaasjon innebæe at ovegangsintensiteten µ,
Avsluttende eksamen i TDT4125 Algoritmekonstruksjon, videregående kurs
 TDT4125 2010-06-03 Kand-nr: 1/5 Avsluttende eksamen i TDT4125 Algoritmekonstruksjon, videregående kurs Eksamensdato 3. juni 2010 Eksamenstid 0900 1300 Sensurdato 24. juni Språk/målform Bokmål Kontakt under
TDT4125 2010-06-03 Kand-nr: 1/5 Avsluttende eksamen i TDT4125 Algoritmekonstruksjon, videregående kurs Eksamensdato 3. juni 2010 Eksamenstid 0900 1300 Sensurdato 24. juni Språk/målform Bokmål Kontakt under
Kontinuasjonseksamen i tdt4125 Algoritmekonstruksjon, videregående kurs
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 7 Eksamenforfattere: Ole Edsberg Kvalitetskontroll: Magnus Lie Hetland Kontakter under eksamen:
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 7 Eksamenforfattere: Ole Edsberg Kvalitetskontroll: Magnus Lie Hetland Kontakter under eksamen:
At energi ikke kan gå tapt, må bety at den er bevart. Derav betegnelsen bevaringslov.
 Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
INF3100 V2016 Obligatorisk oppgave nr. 1
 INF3100 V2016 Obligatorisk oppgave nr. 1 Oppgavesettet skal løses og leveres individuelt. Gjennomføring og innlevering av oppgaven skal skje i henhold til gjeldende retningslinjer ved Institutt for informatikk,
INF3100 V2016 Obligatorisk oppgave nr. 1 Oppgavesettet skal løses og leveres individuelt. Gjennomføring og innlevering av oppgaven skal skje i henhold til gjeldende retningslinjer ved Institutt for informatikk,
Innhold. 1. Innledning... 3
 Risikobaset tilsyn Modul fo makeds- og kedittisiko i fosiking Evalueing av makeds- og kedittisikonivå DAO: 15.09.2010 Innhold 1. Innledning... 3 2. Makedsisiko... 4 2.1 Metodikken... 4 2.2 Renteisiko...
Risikobaset tilsyn Modul fo makeds- og kedittisiko i fosiking Evalueing av makeds- og kedittisikonivå DAO: 15.09.2010 Innhold 1. Innledning... 3 2. Makedsisiko... 4 2.1 Metodikken... 4 2.2 Renteisiko...
Kapittel 3: Litt om representasjon av tall
 MAT1030 Diskret Matematikk Forelesning 3: Litt om representasjon av tall, logikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 3: Litt om representasjon av tall 20. januar 2009
MAT1030 Diskret Matematikk Forelesning 3: Litt om representasjon av tall, logikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 3: Litt om representasjon av tall 20. januar 2009
MAT1140: Kort sammendrag av grafteorien
 MAT1140, H-15 MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oppsummering av grafteorien i MAT1140. Vekten er på den logiske oppbygningen, og jeg har utelatt all motivasjon og (nesten)
MAT1140, H-15 MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oppsummering av grafteorien i MAT1140. Vekten er på den logiske oppbygningen, og jeg har utelatt all motivasjon og (nesten)
: subs x = 2, f n x end do
 Oppgave 2..5 a) Vi starter med å finne de deriverte til funksjonen av orden opp til og med 5 i punktet x = 2. Det gjør vi ved å bruke kommandoen diff f x, x$n der f x er uttrykket som skal deriveres, x
Oppgave 2..5 a) Vi starter med å finne de deriverte til funksjonen av orden opp til og med 5 i punktet x = 2. Det gjør vi ved å bruke kommandoen diff f x, x$n der f x er uttrykket som skal deriveres, x
oppgaver fra abels hjørne i dagbladet
 oppgaver fra abels hjørne i dagbladet sett 44 dag 1 1. Et lykkehjul er inndelt i 30 like store sektorer. En av sektorene er merket med 7 kr, to er merket med 4 kr, tre er merket 3 kr og fire er merket
oppgaver fra abels hjørne i dagbladet sett 44 dag 1 1. Et lykkehjul er inndelt i 30 like store sektorer. En av sektorene er merket med 7 kr, to er merket med 4 kr, tre er merket 3 kr og fire er merket
Kristen homofil Av Ole Johannes Ferkingstad
 Kristen homofil Av Ole Johannes Ferkingstad MAIL: ole_johannes123@hotmail.com TIF: 90695609 2 INT. MENIGHET - KVELD Lucas snakker til en forsamling på 50 stk. Gud elsker deg for den du er. Om du sliter
Kristen homofil Av Ole Johannes Ferkingstad MAIL: ole_johannes123@hotmail.com TIF: 90695609 2 INT. MENIGHET - KVELD Lucas snakker til en forsamling på 50 stk. Gud elsker deg for den du er. Om du sliter
Korteste vei i en vektet graf uten negative kanter
 Dagens plan: IN - Algoritmer og datastrukturer HØSTEN 7 Institutt for informatikk, Universitetet i Oslo IN, forelesning 7: Grafer II Korteste vei, en-til-alle, for: Vektet rettet graf uten negative kanter
Dagens plan: IN - Algoritmer og datastrukturer HØSTEN 7 Institutt for informatikk, Universitetet i Oslo IN, forelesning 7: Grafer II Korteste vei, en-til-alle, for: Vektet rettet graf uten negative kanter
Eksamen i tdt4120 Algoritmer og datastrukturer
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
LØSNINGSFORSLAG SIF5015 DISKRET MATEMATIKK Onsdag 18. desember 2002
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 LØSNINGSFORSLAG SIF55 DISKRET MATEMATIKK Onsdag 8. desember 22 Oppgave a) Vi vil ha 77x (mod 3), så vi trenger en
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 LØSNINGSFORSLAG SIF55 DISKRET MATEMATIKK Onsdag 8. desember 22 Oppgave a) Vi vil ha 77x (mod 3), så vi trenger en
S2 - Kapittel 6. Løsningsskisser
 S2 - Kapittel 6 Løsningsskisser I a) Hva kan man si om overskuddet når grenseinntekten er lik grensekostnaden? b) Hva kan man si om produksjonsmengden når enhetskostnaden er lik grensekostnaden? c) Hva
S2 - Kapittel 6 Løsningsskisser I a) Hva kan man si om overskuddet når grenseinntekten er lik grensekostnaden? b) Hva kan man si om produksjonsmengden når enhetskostnaden er lik grensekostnaden? c) Hva
LØSNINGSFORSLAG UNIVERSITETET I OSLO. Det matematisk-naturvitenskapelige fakultet. Oppgave 1 Mengdelære (10 poeng)
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 9. desember 2010 Tid for eksamen: 09:00 13:00 INF1080 Logiske metoder for informatikk Oppgave 1 Mengdelære (10 poeng)
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 9. desember 2010 Tid for eksamen: 09:00 13:00 INF1080 Logiske metoder for informatikk Oppgave 1 Mengdelære (10 poeng)
EKSAMENSOPPGAVE - Skoleeksamen. Institutt for Samfunnsøkonomi. Utlevering: 17.12.2014 Kl. 09.00 Innlevering: 17.12.2014 Kl. 14.00
 EKSAMENSOPPGAVE - Skoleeksamen MET 11803 Matematikk Institutt fo Samfunnsøkonomi Utleveing: 17122014 Kl 0900 Innleveing: 17122014 Kl 1400 Vekt: 70% av MET 1180 Antall side i oppgaven: Antall vedleggsfile:
EKSAMENSOPPGAVE - Skoleeksamen MET 11803 Matematikk Institutt fo Samfunnsøkonomi Utleveing: 17122014 Kl 0900 Innleveing: 17122014 Kl 1400 Vekt: 70% av MET 1180 Antall side i oppgaven: Antall vedleggsfile:
Gangemesteren Nybegynner Scratch PDF
 Gangemesteren Nybegynner Scratch PDF Introduksjon I dag skal vi lage et nyttig spill, nemlig et spill som hjelper oss å lære andre ting. Vi skal få hjelp til å lære gangetabellen! Steg 1: Læremesteren
Gangemesteren Nybegynner Scratch PDF Introduksjon I dag skal vi lage et nyttig spill, nemlig et spill som hjelper oss å lære andre ting. Vi skal få hjelp til å lære gangetabellen! Steg 1: Læremesteren
Realavkastning. Investeringsanalyse og inflasjon. Realavkastning av finansinvesteringer
 Ivesteigsaalyse og iflasjo Nomiell avkastig og ealavkastig Reell låeete (ealete) Realivesteige og iflasjo Kotatstøm i omielle og faste pise Iflasjo og skatt Omløpsmidle og iflasjo Joh-Eik Adeasse 1 Høgskole
Ivesteigsaalyse og iflasjo Nomiell avkastig og ealavkastig Reell låeete (ealete) Realivesteige og iflasjo Kotatstøm i omielle og faste pise Iflasjo og skatt Omløpsmidle og iflasjo Joh-Eik Adeasse 1 Høgskole
b) 3 MATEMATISKE METODER I 1 ( ) ( ) ( ) ( ) ( ) ( ) Repetisjonsoppgaver Bruk av regneregler: 1 Regn ut: e) 0 x ) 4 3 d) 4 x f) 5y
 MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
Omfang Kontrakten vil i utgangspunktet omfatte 2 leasingbiler med serviceavtale som spesifisert nedenfor. Kontraktsperioden er
 Eidskog Gue Sø-Odal Eidskog Åsnes Våle Leasingbile fo opeasjonell leasing til kommunale Eiendomsenhet, Gøntavdelingen. Geneelt kommune ønske tilbud på leasingbile fo opeasjonell leasing. Det økonomisk
Eidskog Gue Sø-Odal Eidskog Åsnes Våle Leasingbile fo opeasjonell leasing til kommunale Eiendomsenhet, Gøntavdelingen. Geneelt kommune ønske tilbud på leasingbile fo opeasjonell leasing. Det økonomisk
Løsningsforslag, Ukeoppgaver 10 INF2310, våren 2011 kompresjon og koding del II
 Løsningsforslag, Ukeoppgaver 10 INF2310, våren 2011 kompresjon og koding del II 1. En fax-oppgave: a. Et ark med tekst og enkle strektegninger skal sendes pr digital fax over en modemlinje med kapasitet
Løsningsforslag, Ukeoppgaver 10 INF2310, våren 2011 kompresjon og koding del II 1. En fax-oppgave: a. Et ark med tekst og enkle strektegninger skal sendes pr digital fax over en modemlinje med kapasitet
Qwertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwert yuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopa
 Qwetyuiopasdfghjklzxcvbnmqw etyuiopasdfghjklzxcvbnmqwet yuiopasdfghjklzxcvbnmqwetyui opasdfghjklzxcvbnmqwetyuiopa ÅRSMELDING 2013 sdfghjklzxcvbnmqwetyuiopasdf AURLAND IL ghjklzxcvbnmqwetyuiopasdfghj REKNESKAP
Qwetyuiopasdfghjklzxcvbnmqw etyuiopasdfghjklzxcvbnmqwet yuiopasdfghjklzxcvbnmqwetyui opasdfghjklzxcvbnmqwetyuiopa ÅRSMELDING 2013 sdfghjklzxcvbnmqwetyuiopasdf AURLAND IL ghjklzxcvbnmqwetyuiopasdfghj REKNESKAP
Løsningsforslag TEP 4110 FLUIDMEKANIKK 18.desember ρ = = = m / s m / s 0.1
 Løsningsfoslag TEP 40 FLUIDMEKNIKK 8.desembe 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d
Løsningsfoslag TEP 40 FLUIDMEKNIKK 8.desembe 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d
Øvingsforelesning 4. Topologisk sortering, Strongly Connected Components og Minimale spenntrær. Magnus Botnan
 Øvingsforelesning 4 Topologisk sortering, Strongly Connected Components og Minimale spenntrær Magnus Botnan botnan@stud.ntnu.no 09/10/09 1 I dag Topologisk Sortering Sterke Komponenter Minimale Spenntrær
Øvingsforelesning 4 Topologisk sortering, Strongly Connected Components og Minimale spenntrær Magnus Botnan botnan@stud.ntnu.no 09/10/09 1 I dag Topologisk Sortering Sterke Komponenter Minimale Spenntrær
Hammerfest HAMMERFEST. MELKEØYA sett fra S
 HAMMERFET b) a) Fobudssone (sjøkat 9, 09) Fobud mot alle fatøy nå et tankskip /fatøy til teminalen befinne seg de og e undeveis. IKRINFELT (sjøkat 9, 09) Fobud fo alle fatøy uten tillatelse fa teminalen.
HAMMERFET b) a) Fobudssone (sjøkat 9, 09) Fobud mot alle fatøy nå et tankskip /fatøy til teminalen befinne seg de og e undeveis. IKRINFELT (sjøkat 9, 09) Fobud fo alle fatøy uten tillatelse fa teminalen.
Symbolisering av logisk form: setningslogiske tegn.
 Logike ltninger NB! Dette er for peielt intereerte: Siden det ikke tår å mye om dette i lærebøkene er omfanget av dette foreleningmanet alt for tort i forhold til hva vi kan betrakte om penm. Videre kan
Logike ltninger NB! Dette er for peielt intereerte: Siden det ikke tår å mye om dette i lærebøkene er omfanget av dette foreleningmanet alt for tort i forhold til hva vi kan betrakte om penm. Videre kan
INNHOLD Spillebrett, 126 bokstavbrikker, 14 plastskinner, pose i fløyel, elektronisk timer (med batterier) og spilleregler.
 Spilleregler INNHOLD Spillebrett, 126 bokstavbrikker, 14 plastskinner, pose i fløyel, elektronisk timer (med batterier) og spilleregler. SPILLET I KOTE TEKK Det er lov å stjele i Ordskifte! Spillerne skal
Spilleregler INNHOLD Spillebrett, 126 bokstavbrikker, 14 plastskinner, pose i fløyel, elektronisk timer (med batterier) og spilleregler. SPILLET I KOTE TEKK Det er lov å stjele i Ordskifte! Spillerne skal
Kan vi klikke oss til
 Kan vi klikke oss til bedre læring? l Om studentrespons (SRS) i undervisninga i et bacheloremne i psykologi Dan Y. Jacobsen & Gabrielle Hansen Highteck-Lotech Lotech,, NTNU, 21. mai 2008 Studentrespons
Kan vi klikke oss til bedre læring? l Om studentrespons (SRS) i undervisninga i et bacheloremne i psykologi Dan Y. Jacobsen & Gabrielle Hansen Highteck-Lotech Lotech,, NTNU, 21. mai 2008 Studentrespons
Representasjon av tall på datamaskin Kort innføring for MAT-INF1100L
 Representasjon av tall på datamaskin Kort innføring for MAT-INF00L Knut Mørken 3. desember 204 Det er noen få prinsipper fra den første delen av MAT-INF00 om tall som studentene i MAT-INF00L bør kjenne
Representasjon av tall på datamaskin Kort innføring for MAT-INF00L Knut Mørken 3. desember 204 Det er noen få prinsipper fra den første delen av MAT-INF00 om tall som studentene i MAT-INF00L bør kjenne
oppgaver fra abels hjørne i dagbladet
 oppgaver fra abels hjørne i dagbladet sett 4 dag 1 1. Hvor mange av de ett hundre første positive heltallene, 1, 2, 3,, 99, 100, er delelig med 2, 3, 4 og 5? A)0 B) 1 C) 2 D) 3 E) 4 2. Ett tusen terninger
oppgaver fra abels hjørne i dagbladet sett 4 dag 1 1. Hvor mange av de ett hundre første positive heltallene, 1, 2, 3,, 99, 100, er delelig med 2, 3, 4 og 5? A)0 B) 1 C) 2 D) 3 E) 4 2. Ett tusen terninger
EKSAMEN I EMNE TMT4110 KJEMI - løsningsforslag
 Side 1 av 7 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR MATERIALTEKNOLOGI Faglig kntakt unde eksamen: Institutt f mateialteknlgi, Gløshaugen Føsteamanuensis Hilde Lea Lein, tlf. 73 55
Side 1 av 7 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR MATERIALTEKNOLOGI Faglig kntakt unde eksamen: Institutt f mateialteknlgi, Gløshaugen Føsteamanuensis Hilde Lea Lein, tlf. 73 55
Tallinjen FRA A TIL Å
 Tallinjen FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til tallinjen T - 2 2 Grunnleggende om tallinjen T - 2 3 Hvordan vi kan bruke en tallinje T - 4 3.1 Tallinjen
Tallinjen FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til tallinjen T - 2 2 Grunnleggende om tallinjen T - 2 3 Hvordan vi kan bruke en tallinje T - 4 3.1 Tallinjen
Niels Henrik Abels matematikkonkurranse 2013 2014. Løsninger
 Niels Henrik Abels matematikkonkurranse 0 04. Løsninger Første runde 7. november 0 Oppgave. Siden er et primtall, vil bare potenser av gå opp i 0. Altså,,,,..., 0 i alt tall........................................
Niels Henrik Abels matematikkonkurranse 0 04. Løsninger Første runde 7. november 0 Oppgave. Siden er et primtall, vil bare potenser av gå opp i 0. Altså,,,,..., 0 i alt tall........................................
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 13. august 2012 Eksamenstid 0900 1300 Sensurdato 3. september Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 13. august 2012 Eksamenstid 0900 1300 Sensurdato 3. september Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Spørretime TEP Våren Spørretime TEP Våren 2008
 Søetime EP 4115 - Våen 28 Fotegnskonvensjonen og Ka.9 (& OB s slides) Q: ilsynelatende uoveensstemmelse mellom det Olav Bolland esentete fo Otto/Diesel og det som stå i læeboka nå det gjelde fotegn i likninge.
Søetime EP 4115 - Våen 28 Fotegnskonvensjonen og Ka.9 (& OB s slides) Q: ilsynelatende uoveensstemmelse mellom det Olav Bolland esentete fo Otto/Diesel og det som stå i læeboka nå det gjelde fotegn i likninge.
TMA4100 Matematikk 1, 4. august 2014 Side 1 av 12. x 2 3x +2. x 2
 TMA4 Matematikk, 4. august 24 Side av 2 Oppgave Den rasjonale funksjonen p er definert som p(x) x2 3x +2 3x 2 5x +2. Finn de tre grenseverdiene lim xæ p(x), lim xæ p(x) og lim xæœ p(x). Løsning: x 2 3x
TMA4 Matematikk, 4. august 24 Side av 2 Oppgave Den rasjonale funksjonen p er definert som p(x) x2 3x +2 3x 2 5x +2. Finn de tre grenseverdiene lim xæ p(x), lim xæ p(x) og lim xæœ p(x). Løsning: x 2 3x
Løsningsforslag kapittel 3
 Løsningsoslg kpittel 3 3.1 ) Uttykket o (den konigusjonelle) entopien S e gitt ved S k ln W, de W uttykke ntll skillbe mikotilstnde. Siden kystllen inneholde n vknse odelt ove N N! N! tomplsse e W og S
Løsningsoslg kpittel 3 3.1 ) Uttykket o (den konigusjonelle) entopien S e gitt ved S k ln W, de W uttykke ntll skillbe mikotilstnde. Siden kystllen inneholde n vknse odelt ove N N! N! tomplsse e W og S
Maks Flyt og NPkompletthet
 Maks Flyt og NPkompletthet Flyt - Intro Mange av oppgavene om flyt handler om å se at Dette kan vi løse som et flytproblem. Resten er som regel kortsvarsoppgaver, og går på grunnleggende forståelse av
Maks Flyt og NPkompletthet Flyt - Intro Mange av oppgavene om flyt handler om å se at Dette kan vi løse som et flytproblem. Resten er som regel kortsvarsoppgaver, og går på grunnleggende forståelse av
Tallregning og algebra
 30 Tallregning og algebra Mål for opplæringen er at eleven skal kunne tolke, bearbeide og vurdere det matematiske innholdet i ulike tekster bruke matematiske metoder og hjelpemidler til å løse problemer
30 Tallregning og algebra Mål for opplæringen er at eleven skal kunne tolke, bearbeide og vurdere det matematiske innholdet i ulike tekster bruke matematiske metoder og hjelpemidler til å løse problemer
LEIRFJORD KOMMUNE SAKSFRAMLEGG. Saksbehandler: Britt Jonassen Arkiv: 144 F17 Arkivsaksnr.: 13/167-7 Klageadgang: Nei
 LEIRFJORD KOMMUNE SAKSFRAMLEGG Saksbehandle: Bitt Jonassen Akiv: 144 F17 Akivsaksn.: 13/167-7 Klageadgang: Nei REGIONAL BOLIGPOLITISK HANDLINGSPLAN Administasjonssjefens innstilling: ::: &&& Sett inn innstillingen
LEIRFJORD KOMMUNE SAKSFRAMLEGG Saksbehandle: Bitt Jonassen Akiv: 144 F17 Akivsaksn.: 13/167-7 Klageadgang: Nei REGIONAL BOLIGPOLITISK HANDLINGSPLAN Administasjonssjefens innstilling: ::: &&& Sett inn innstillingen
Brukerveiledning for import av publikasjoner ved UiTø
 Brukerveiledning for import av publikasjoner ved UiTø I forbindelse med registrering av publikasjoner er det utviklet et hjelpesystem, Importtjeneste og autoritetsregister (ITAR), som bidrar til enklere
Brukerveiledning for import av publikasjoner ved UiTø I forbindelse med registrering av publikasjoner er det utviklet et hjelpesystem, Importtjeneste og autoritetsregister (ITAR), som bidrar til enklere
Forprosjekt. Oppgavens tittel: Motorstyring Dato: 24.01.05. Jon Digernes Institutt/studieretning: Program for elektro og datateknikk
 HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi Program for elektro-og datateknikk 7004 TRONDHEIM Forprosjekt Oppgavens tittel: Motorstyring Dato: 24.01.05 Project title: Gruppedeltakere: Sverre Hamre
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi Program for elektro-og datateknikk 7004 TRONDHEIM Forprosjekt Oppgavens tittel: Motorstyring Dato: 24.01.05 Project title: Gruppedeltakere: Sverre Hamre
Modul 1 15 studiepoeng, internt kurs Notodden/Porsgrunn
 Høgskole i Telemk Avdelig fo estetiske fg, folkekultu og læeutdig BOKMÅL 4. mi 007 EKSAMEN I MATEMATIKK 3 Tid: 6 time Modul 5 studiepoeg, itet kus Notodde/Posgu Oppgvesettet e på 7 side (ikludet fomelsmlig).
Høgskole i Telemk Avdelig fo estetiske fg, folkekultu og læeutdig BOKMÅL 4. mi 007 EKSAMEN I MATEMATIKK 3 Tid: 6 time Modul 5 studiepoeg, itet kus Notodde/Posgu Oppgvesettet e på 7 side (ikludet fomelsmlig).
10.3.0 WinTid. Nyheter versjon 10.3.0
 10.3.0 WinTid Nyheter versjon 10.3.0 Innholdsfortegnelse 1. OM DOKUMENTET... 3 1.1 DOKUMENTETS MÅLSETNING... 3 1.2 HVEM ER DOKUMENTET SKREVET FOR?... 3 1.3 OPPBYGNING OG OPPBEVARING... 3 1.4 ANSVARLIG
10.3.0 WinTid Nyheter versjon 10.3.0 Innholdsfortegnelse 1. OM DOKUMENTET... 3 1.1 DOKUMENTETS MÅLSETNING... 3 1.2 HVEM ER DOKUMENTET SKREVET FOR?... 3 1.3 OPPBYGNING OG OPPBEVARING... 3 1.4 ANSVARLIG
Teoriøving 7 + litt om Ford-Fulkerson. Magnus Lie Hetland
 Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
