Rekursjon. Et enkelt eksempel
|
|
|
- Kåre Gustavsen
- 8 år siden
- Visninger:
Transkript
1 Reusj I. TRE AV REKURSIVE KA, eusjsdybde temieig dig II. INDUKTIVE DATA TYPER g Reusj ve slie III. SPITT OG HERSK PROBEMØSNING VED REKURSJON (Kap. 8..) IV. REKURSJONS EEKTIVITET dyamis pgammeig avsjæig V. STABE AV REKURSIVE KA iteasj til eusj eusj implemetet sm iteasj VI. KORREKTHET temieig ivaiate (tat til Kgdahl&Haveaae) Demed fedig med geeell basis i- : H Reusj: Et eelt esempel ha e metde sm /** lese e lije fa temiale ileste Stig IOExcepti i tilfelle i/ pblem public Stig eadl() g vil lage e sm /** lese e lije fa temiale * itil faa et heltall ileste tallet ige uta * det mme et heltall /* public it iread() { * Stig s= eadl(); * it = het feste it fa s; * while (! alt ) * gjeta: = pev este lije; * etu ; /* public it myread() { * Stig s= eadl(); * it = het feste it fa s; * if (alt ) etu ; * // pev igje med este lije * etu myread(); public it myread() { ty{ etu Itege.paseIt(eadl()); catch(ioexcepti e) { etu myread(); catch(numbematexcepti e) { etu myread(); i- : H Reusj:
2 Iteasj til eusj it sumw(it ) { it es =; while ( > ) { es = es ; = ; etu es; it sumr(it ) { if ( == ) etu ; etu sumr(-); Gvt g ie % itig sagt: it Ite(it ) { es= iit; while ( ftsett() ) { es= Kppe(,es); ppd(); etu es; it Rec(it ) { if (!ftsett() ) etu iit; etu Kppe(, Rec(ppd())); Ehve iteasj a sives sm eusj... t..m. sm hale-eusj i- : H Reusj:. Reusjste g -dybde fib() = fib() = fib() = fib() fib() f() f() f() f() f() f(4) 5 f() public it fib(it ) { if (== ==) etu ; etu fib(-) fib(-); etue i basistilfelle f() f() elles beeg eusivt elee (mide) dele g sett de samme te av eusive all f(4)...? f()...? eefølge f()...? av all f()...? > f()...? > > f()...? > > f()...? f()...? > f()...? > > > 5 eusjsdybde #svate = #øde lije = # eusive all... itil basistilfelle e ådd (=høyde av teet) i- : H Reusj: 4
3 . Idutive Data Type (vilålig ste me edelige) Stutuell deig atulige tall N: aay av N: A(N) basis: e et N basis -> N e A(N) hvis e et N hvis [...] -> N e A(N) så e: et N så e [...,] -> N e A(N) iste av N: (N): basis: ull e e (N) hvis så e: e (N) g e N (,) e (N) N... N N... N... N Biæe Tæ av N: BT(N): basis: ull e et BT(N) hvis t, t e BT(N) g e N t t t, t så e: (t,, t) et BT(N) t t t t i- : H Reusj: 5 Vaiasje ve tema idutiv defiisj = fa basis g ppve eusj = fa tppe mt basis N it fib() { it sum() { basis: if (== ==) etu ; if (==) etu ; id: etu fib(-) fib(-); etu sum(-); Aay[N] vid ic(an A, it ) { it sum(an A, it ) { basis: [] -> N A[]; if (==) etu A[]; id: [.., ] -> N if ( > ) ic(a,-); etu A[] sum(a,-); iste[n] class T { vid ic(s ) { it sum(s ) { basis: ull it ; if (==ull) { if (==ull) etu ; id: () T xt; { ; etu sum(.ext); ic(.xt); BiætTe[N] class BT { vid ic(bt B) { it sum(bt T) { basis: ull it ; if (T==ull) { if (T==ull) etu ; id: (t,,t) BT left; { ; etu BT ight; ic(t.left); sum(t.left) ic(t.ight); sum(t.ight) ; RACTAe i- : H Reusj: 6
4 E teis bemeig iste av N: [N]: basis: ull e e [N] hvis e [N] g e N så e: (,) e [N] Reusj implemetet utefa datastutue : class N { ic(n ) { it sum(n ) { public it ; if (==ull) { if (==ull) etu ; public N xt; {.; etu sum(.ext).;... ic(.xt); class N { pivate it ; pivate N xt; ic() {... it sum() {... elle ief datastutue : ic() { it sum() { ; if (xt!= ull) if (xt!= ull) etu xt.sum(); xt.ic(); etu ; ic(n ) { it sum(n ) { if (!= ull) if (!= ull).ic(); etu.sum(); etu ; i- : H Reusj: 7. Splitt g hes Reusj sm e geeell stategi f pblemløsig g algitmedesig Gitt e istas av et pblem P :. hva gjø jeg å e basis tilfelle. hvda stuee løsig f utfa løsige f e mi P = ste iput aay A ( = A.legth) /* it[] SS(it[] A,) { * iitielt all med SS(A,) * = A.legth; * if (==-) { etu A; * { * i= idese til miste elemetet * i A[...-]; * bytt A[] med A[i]; * etu SS(A, ); O ( ) O (*lg ) /* it[] MS(it[] A) { it = A.legth; * if ( == ) { etu A; * { del A i midte i * t= A[.../] g t= A[/...lgh]; * ste eusivt begge (mide) * = MS(t) g = MS(t) * etu flettet esultat av eusive all (,) * - flette t stete aay i e stet aay P = fi et gitt elemet x i e aay A Hvis A e ustet : sje A[]; hvis x ie e de, lett i A[... ] Hvis A e stet... O () i- : H Reusj: 8
5 Biæ Sø /* fi ides i A til et elemet x: it BS(it[] A,x,l,h) { A it A[...] stetit m= (lh) / ; x fi x i A if (l > h) etu -; l, h sø i A bae fm. l tm. h if (A[m] == x) etu m; ides til x; if (A[m] x) etu BS(A,x,m,h); * hvis x ie fies etu BS(A,x,l,m-); // iitielt all med BS(A, x,, A.legth ) Nøel e 48 O (lg ). all. all. all bisø(a, 48,, 9) bisø(a, 48, 5, 9) bisø(a, 48, 5, 6) [] [] [] [] [4] [5] [6] [7] [8] [9] A[] l = m = (9)/ h = 9 [] [] [] [] [4] [5] [6] [7] [8] [9] A[] l = 5 m = (59)/ h = 9 [] [] [] [] [4] [5] [6] [7] [8] [9] A[] l = 5 h = 6 basis tilfelle m = (56)/ A[m] == øel etu 5 i- : H Reusj: 9 4. Reusj g effetivitet Reduse atall eusive all it fib(it ) { if (== ==) etu ; etu fib(-)fib(-); f() f() f() f() f() f(4) f() f() f(). Dyamis pgammeig : Istedef gjetatte eusive all til f() med samme, a esultatet av f() lages f seee bu: it ib(it ) { it[] a= ew it[]; a[]=; a[]=; etu fib(, a); it fib(it, it[] a) { if (a[] > ) { etu a[]; { it z= fib( ) fib( ); a[]= z; etu z; f(4) f() f() f() f() i- : H Reusj:
6 Reusj & effetivitet i alle pemutasje av [,,...-] (f et patall ) /* pem(a,) { it l= A.legth-; * if (==l) { siv A; * { * f hve id:...l * pem(a,); * bytt A[] g A[id] * pem(a,); * te[...l]; A[..-] A[] A[..l] pem(a,) sive alle pem /* PE(A) { it l= A.legth-; * f hve :...l/ { * bytt A[] g A[]; * pem(a,); * bytt A[] g A[]; siv iv(a);. Avsjæig ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, i- : H Reusj: Kmplesitet av e eusiv fusj atall de i eusjsteet avhege av stø på steget mt basis i hvet eusivt all (høyde av teet) atall eusive all i hvet steg ( bedde av fgeige) abeidsmegde ved sammesettig av esultate fa eusive all () =, () = () = () () O( ) h= () =, () = () = () () O(.6 ) 4 h= () =, () = () = () () () O( ) / * = O() 4 h= () =, () = () = () * O() h= MS() = lg() = -=O() MS() = MS(/) MS(/) h= =lg() (/) (/4) (/8) i- : H Reusj:
7 5. Reusj... it ib(it ) { if (== ==) etu ; etu ib(-) ib(-); f() f(4) f() 4 implemetees med Stabel f() f() f() f() f() f() 5 b 5 i- : H Reusj: Reusj til iteasj (a alltid mgjøes v.hj.a. Stabel) it fibs(it a) { Stig ; it, a, a; Stac p = ew StacImp(); Stac e = ew StacImp(); it ib(it ) { if (== ==) etu ; etu ib(-) ib(-); Ne eusj (f.es. hale-eusj) a mgjøes til iteasj på e elee måte. Stac a = ew StacImp(); p.push( ); a.push( ew Itege(a) ); while (!p.empty()) { = (Stig) p.pp(); if (.equals( ) ) { = ( (Itege)a.pp() ).itvalue(); if (== ==) e.push( ew Itege() ); { p.push( ); p.push( ); p.push( ); a.push( ew Itege(-) ); a.push( ew Itege(-) ); if (.equals( ) ) { a= ( (Itege)e.pp() ).itvalue(); a= ( (Itege)e.pp() ).itvalue(); e.push( ew Itege(aa) ); etu ( (Itege)e.pp() ).itvalue(); i- : H Reusj: 4
8 6. Kethet Gitt e istas av et pblem P :. hva gjø jeg å e basis tilfelle. hvda stuee løsig f utfa løsige f e mi P() if Basis() etu??? etu Kmbie(P(m)... P(m)) Temieig: P() if Basis() stppe eusj væ sie at hve mi, e æmee Basis mbiasj ppetthlde eusjs-ivaiat Kethet: P() if Basis() tlle at det utføes itig hadlig HVIS hvet eusivt all P(mi) etuee itig esultat!!! DETTE ANTAR VI!!! SÅ gi Kmbie(P(m)... P(m)) itig esultat i- : H Reusj: 5 Kethet: eusjs-ivaiat /* it[] MS(it[] A) { it = A.legth; * if ( == ) { etu A; * { * del A i midte i : * t= A[.../] g t = A[/...]; * ste eusivt (mide) delee * = MS(t) g * = MS(t) * etu flettet esultat av * eusive all (,) Ivaiat: MS(A) etuee stet agumet A: if lgh== da e A stet dele A i t disjute dele t= A[.../] g t= A[/...] = MS(t) etuee stet t = MS(t) etuee stet t hvis flette et t stete aay, så etuee hele -gee stet A /* it BS(it[] A, it x, it l, it h) { * it m= (lh) / ; * if (l > h) etu ; * if (A[m] == x) etu m; * if (A[m] x) etu BS(A, x, m, h); * etu BS(A, x, l, m ); Ivaiat: agumetet A e stet & e x i A, så e de mellm [l... h] (iitielt all med (A, x,, A.legth-) if l > h x a ie væe de ( e itig) if A[m] = x da ha vi fuet de (m e itig) if A[m] x e x i A, så må de væe mellm [m... h] BS(A, x, m, h) vil etuee itig esultat A[m] > x e x i A, så må de væe mellm [l... m ] BS(A, x, l, m ) vil etuee itig esultat i- : H Reusj: 6
9 øe-ivaiat it sum(it ) { if ( == ) etu ; basis gi itig sum() = etu sum( ); hvis sum( ) gi itig = i så e sum() = sum( ) = i = = i i it sumw(it ) { it i=, =; while (i!= ) { = i; i; // = i, i =i.. a. b. øe-ivaiat, I: = Iitialiseig: i= & = = hvis I: = i = så hlde I : = = i = i = => I hlde fø ppe i' = ette ppe it sumw(it ) { it i=, =; while (i!= ) { i; = i; // i = i, = i etu ; 4. i Utgag: I: = & i = => = = = etu ; i- : H Reusj: 7 øe-ivaait: esempel. /** beege heltalls vsiet samt x y (q, ) sa. x= q*y & = y & = q div(it x, it y) { it q = ; it = x ; iitialiseig: q = & = x >= x= q*y & = & = q while (y = ) { I: = & x = q*y & = q ata at de gjelde ved igag, samt y = q = q ; = y; da gjelde, ette løeppe: q = q & = q = q & = y & = & y = = q *y = (q)*y ( y) = q*y y y = q*y = x dvs. I ppetthldes gjem ppe utgag fa løe: I & y x = q*y & = y & = q etu (q, ) ; i- : H Reusj: 8
10 øe-ivaiat: esempel. /** beege støste felles x x y = gcd(x,x) gcd(x,x) { y= x; y= x; iitialiseig: x = y & x = y gcd(x,x) == gcd(x,x) while (y!= ) { if (y y) (y,y) = (y,y); I: gcd(y,y) = gcd(x,x) ata at de gjelde he gcd(x,x) = gcd(y,y) = gcd(y,y) = gcd(y,y ) // (y >= y) y= y y; gcd(x,x) = gcd(y,y) = gcd(y,y-y) = gcd(y,y ) etu y; I : cd(y,y ) = gcd(x,x) utgag: I & y = gcd(x,x) = gcd(y,y) = gcd(,y) = y Hvis gcd(y,y) = z >= & y >= y, så *) y = z* = z* = y & gcd(,) = Me da: y = y y = z*( ) & gcd(, ) = hvis ie, dvs. gcd(, ) = v >, da = v*a & = v*b, så = v*bv*a = v*(ba) dvs. da gså gcd(,) = v > mtsie *) i- : H Reusj: 9 Oppsummeig. Reusj Splitt g hes bestem hva sm må gjøes i basis tilfelle() stue ( hes ) e løsig fa (eusive) løsige f ( splitt ) e mide istase. Ehve idutiv datatype (at, it, liste, tæ,...) gi phav til eusive algitme. Reusj vs. iteasj (eusj implemetees iteativt med bu av stabel) 4. Kmplesistet av eusiv fusj avhege av atall de i eusjste ( splitt ) dybde (høyde) av teet hv stt steg mt basis utgjø hve splittig atall eusive all (bedde av teet) på hvet ivå abeidsmegde f å stuee e løsig utfa løsige f mide istase ( hes ) 5. Kethet bestem eusjs-ivaiate veifise at basistilfelle() etablee ivaiate ude ata at eusive all etablee ivaiate, vis at stusje vil ppetthlde de bestem løe-ivaiat vis at de gjelde ette iitialiseig (lie fø igage i løe) ude ata at de gjelde fø løeppe, vis at de gjelde ette i- : H Reusj:
Et enkelt eksempel. Rekursjon
 Et ekelt eksempel h e metde sm /** lese e lije f temile * @etu ileste Stig * @excepti IOExcepti i tilfelle i/ pblem public Stig edl() g vil lge e sm /** lese e lije f temile * itil de lese et heltll *
Et ekelt eksempel h e metde sm /** lese e lije f temile * @etu ileste Stig * @excepti IOExcepti i tilfelle i/ pblem public Stig edl() g vil lge e sm /** lese e lije f temile * itil de lese et heltll *
Rekursjon I. TRE AV REKURSIVE KALL, II. INDUKTIVE DATA TYPER IV. STABEL AV REKURSIVE KALL V. KORREKTHET. rekursjonsdybde terminering ordning
 Rekursjon I. TRE AV REKURSIVE KALL, rekursjonsdybde terminering ordning II. INDUKTIVE DATA TYPER og Rekursjon over slike III. SPLITT OG HERSK ROBLEMLflSNING P VED REKURSJON IV. STABEL AV REKURSIVE KALL
Rekursjon I. TRE AV REKURSIVE KALL, rekursjonsdybde terminering ordning II. INDUKTIVE DATA TYPER og Rekursjon over slike III. SPLITT OG HERSK ROBLEMLflSNING P VED REKURSJON IV. STABEL AV REKURSIVE KALL
EKSAMEN Løsningsforslag
 ..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
Kombinatorikk. MAT0100V Sannsynlighetsregning og kombinatorikk. Multiplikasjonssetningen
 MAT0100V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
MAT0100V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
Kombinatorikk. MAT0100V Sannsynlighetsregning og kombinatorikk. Multiplikasjonssetningen
 MAT000V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
MAT000V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
2. Å R S B E R E T N I N G O G R E G N S K A P F O R A ) Å r s b e r e t n i n g o g r e g n s k a p f o r
 I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o r s a m l i n g i, a v h o l d e s m a n d a g 3. m ai 2 0 1 0, k l. 1 8 0 0 p å T r e
I N N K A L L I N G T I L O R D I N Æ R G E N E R A L F O R S A M L I N G 2 0 1 0 O r d i n æ r g e n e r a l f o r s a m l i n g i, a v h o l d e s m a n d a g 3. m ai 2 0 1 0, k l. 1 8 0 0 p å T r e
IN3030 Uke 12, v2019. Eric Jul PSE, Inst. for informatikk
 IN3030 Uke 12, v2019 Eric Jul PSE, Ist. for iformatikk 1 Hva skal vi se på i Uke 12 Review Radix sort Oblig 4 Text Program Parallellizig 2 Oblig 4 Radix sort Parallelliser Radix-sorterig med fra 1 5 sifre
IN3030 Uke 12, v2019 Eric Jul PSE, Ist. for iformatikk 1 Hva skal vi se på i Uke 12 Review Radix sort Oblig 4 Text Program Parallellizig 2 Oblig 4 Radix sort Parallelliser Radix-sorterig med fra 1 5 sifre
Kapittel 9: Mer kombinatorikk
 MAT00 Disret Matemati Forelesig : Mer ombiatori Roger Atose Istitutt for iformati, Uiversitetet i Oslo Kapittel 9: Mer ombiatori 5. april 009 (Sist oppdatert: 009-04-5 00:06) MAT00 Disret Matemati 5. april
MAT00 Disret Matemati Forelesig : Mer ombiatori Roger Atose Istitutt for iformati, Uiversitetet i Oslo Kapittel 9: Mer ombiatori 5. april 009 (Sist oppdatert: 009-04-5 00:06) MAT00 Disret Matemati 5. april
Uke 12 IN3030 v2019. Eric Jul PSE-gruppa Ifi, UiO
 Uke 12 IN3030 v2019 Eric Jul PSE-gruppa Ifi, UiO Oblig 5 Kovekse Ihylliga Itroduksjo De kovekse ihylliga til pukter Oblig 5 Hva er det, defiisjo Hvorda ser de ut Hva brukes de til? Hvorda fier vi de? 24
Uke 12 IN3030 v2019 Eric Jul PSE-gruppa Ifi, UiO Oblig 5 Kovekse Ihylliga Itroduksjo De kovekse ihylliga til pukter Oblig 5 Hva er det, defiisjo Hvorda ser de ut Hva brukes de til? Hvorda fier vi de? 24
Lekestativ MaxiSwing
 Moteigsveiledig og vedliehold v31 Leestativ MaxiSig At : 1740 Leestativet e poduset ette følgede stadad og dietiv: EN 71; 2009/48/EU Poduset: IMPREST AS Näituse 25 50409 Tatu Estoia Moteigsveiledig og
Moteigsveiledig og vedliehold v31 Leestativ MaxiSig At : 1740 Leestativet e poduset ette følgede stadad og dietiv: EN 71; 2009/48/EU Poduset: IMPREST AS Näituse 25 50409 Tatu Estoia Moteigsveiledig og
LO118D Forelesning 2 (DM)
 LO118D Forelesning 2 (DM) Kjøretidsanalyse, matematisk induksjon, rekursjon 22.08.2007 1 Kjøretidsanalyse 2 Matematisk induksjon 3 Rekursjon Kjøretidsanalyse Eksempel Finne antall kombinasjoner med minst
LO118D Forelesning 2 (DM) Kjøretidsanalyse, matematisk induksjon, rekursjon 22.08.2007 1 Kjøretidsanalyse 2 Matematisk induksjon 3 Rekursjon Kjøretidsanalyse Eksempel Finne antall kombinasjoner med minst
Realavkastning. Investeringsanalyse og inflasjon. Realavkastning av finansinvesteringer
 Ivesteigsaalyse og iflasjo Nomiell avkastig og ealavkastig Reell låeete (ealete) Realivesteige og iflasjo Kotatstøm i omielle og faste pise Iflasjo og skatt Omløpsmidle og iflasjo Joh-Eik Adeasse 1 Høgskole
Ivesteigsaalyse og iflasjo Nomiell avkastig og ealavkastig Reell låeete (ealete) Realivesteige og iflasjo Kotatstøm i omielle og faste pise Iflasjo og skatt Omløpsmidle og iflasjo Joh-Eik Adeasse 1 Høgskole
Løsningsforslag: Deloppgave om heuristiske søkemetoder
 Løsigsforslag: Deloppgave om heuristiske søkemetoder 6. mai 00 Iledig Vi skal betrakte det såkalte grafdeligsproblemet (graph partitioig problem). Problemet ka ekelt formuleres som følger: Gitt e graf
Løsigsforslag: Deloppgave om heuristiske søkemetoder 6. mai 00 Iledig Vi skal betrakte det såkalte grafdeligsproblemet (graph partitioig problem). Problemet ka ekelt formuleres som følger: Gitt e graf
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E
 I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i næ r t s am e i e rm ø t e i S am b o b o l i g s a m ei e fi n n e r s t e d t o r s d ag 3 0. 0 4. 2 0 0 9 K l. 1 8. 3 0
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i næ r t s am e i e rm ø t e i S am b o b o l i g s a m ei e fi n n e r s t e d t o r s d ag 3 0. 0 4. 2 0 0 9 K l. 1 8. 3 0
Modul 1 15 studiepoeng, internt kurs Notodden/Porsgrunn
 Høgskole i Telemk Avdelig fo estetiske fg, folkekultu og læeutdig BOKMÅL 4. mi 007 EKSAMEN I MATEMATIKK 3 Tid: 6 time Modul 5 studiepoeg, itet kus Notodde/Posgu Oppgvesettet e på 7 side (ikludet fomelsmlig).
Høgskole i Telemk Avdelig fo estetiske fg, folkekultu og læeutdig BOKMÅL 4. mi 007 EKSAMEN I MATEMATIKK 3 Tid: 6 time Modul 5 studiepoeg, itet kus Notodde/Posgu Oppgvesettet e på 7 side (ikludet fomelsmlig).
TMA4100 Høst Løsningsforslag Øving 2. Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag
 TMA400 Høst 206 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 2 2..0: Vi bruker eisjoe for ikke-vertikale tagetlijer sie 97 i læreboke). Tagetlije gjeom et pukt
TMA400 Høst 206 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag Øvig 2 2..0: Vi bruker eisjoe for ikke-vertikale tagetlijer sie 97 i læreboke). Tagetlije gjeom et pukt
8 + 2 n n 4. 3n 4 7 = 8 3.
 Seksjo 4. Oppgave (). Fi greseverdiee: 8 a) 4 + 4 7 b) 4 +7 5 c) + 7 4 ( ) d) 5 4 44 + 5 4 e) 5 + si() e +6 5 Løsig. Vi vil bruke samme metode som i Eksempel 4..5 fra boke i disse oppgavee. Når vi skal
Seksjo 4. Oppgave (). Fi greseverdiee: 8 a) 4 + 4 7 b) 4 +7 5 c) + 7 4 ( ) d) 5 4 44 + 5 4 e) 5 + si() e +6 5 Løsig. Vi vil bruke samme metode som i Eksempel 4..5 fra boke i disse oppgavee. Når vi skal
Driftsinstruks. Montering vinterdrift. www.novemakulde.no. Vi håper de får stor glede av et Novema kulde produkt!
 Driftsistruks Mterig viterdrift Vi håper de får str glede av et Nvema kulde prdukt! www.vemakulde. w w. Ihld MONTASJE... 1 Dkumetasj... 2 Mtasje av viterdrift på mii splitter... 3 Hvrfr viterdrift....
Driftsistruks Mterig viterdrift Vi håper de får str glede av et Nvema kulde prdukt! www.vemakulde. w w. Ihld MONTASJE... 1 Dkumetasj... 2 Mtasje av viterdrift på mii splitter... 3 Hvrfr viterdrift....
K j æ r e b e b o e r!
 1 K e y s e r l ø k k a Ø s t B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d
1 K e y s e r l ø k k a Ø s t B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d
K j æ r e b e b o e r!
 1 H o v i n B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s
1 H o v i n B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s
Prøveeksamen 2. Elektronikk 24. mars 2010
 Prøveeksame 2 Elektroikk 24. mars 21 OPPGAVE 1 E 8 bit D/A-omformer har et utspeigsområde fra til 8 V V 1LSB, der V 1LSB er de aaloge speige som svarer til det mist sigifikate bit (LSB). a) Hvor stor er
Prøveeksame 2 Elektroikk 24. mars 21 OPPGAVE 1 E 8 bit D/A-omformer har et utspeigsområde fra til 8 V V 1LSB, der V 1LSB er de aaloge speige som svarer til det mist sigifikate bit (LSB). a) Hvor stor er
Om Grafiske Bruker-Grensesnitt (GUI) Hvordan gjør vi det, to typer av vinduer? GUI (Graphical User Interface)-programmering
 Uke9. mars 2005 rafisk brukergresesitt med Swig og awt Litt Modell Utsy - Kotroll Del I Stei jessig Ist for Iformatikk Uiv. i Oslo UI (raphical User Iterface)-programmerig I dag Hvorda få laget et vidu
Uke9. mars 2005 rafisk brukergresesitt med Swig og awt Litt Modell Utsy - Kotroll Del I Stei jessig Ist for Iformatikk Uiv. i Oslo UI (raphical User Iterface)-programmerig I dag Hvorda få laget et vidu
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g e t s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g e t s å r s b e r e t n i
Ge i r Berge 47. En d a t a s t r u k t u r f o r o rd b ø k e r f o r n a t u r lig e sp råk. 1. In n le d n in g
 Ge i r Berge 47 En d a t a s t r u k t u r f o r o rd b ø k e r f o r n a t u r lig e sp råk 1. In n le d n in g Det a r b e id e t som s k a l r e f e r e r e s h e r hadde som m ål å k o n s tru e re
Ge i r Berge 47 En d a t a s t r u k t u r f o r o rd b ø k e r f o r n a t u r lig e sp råk 1. In n le d n in g Det a r b e id e t som s k a l r e f e r e r e s h e r hadde som m ål å k o n s tru e re
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN JUNI A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013
 FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN 5.- 6. JUNI 201 3 A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013 09. 0 0 1 0. 0 0 R E G I S TR E R I NG N o e å b i t e i 10. 0 0 1 0. 15 Å p n i ng
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN 5.- 6. JUNI 201 3 A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013 09. 0 0 1 0. 0 0 R E G I S TR E R I NG N o e å b i t e i 10. 0 0 1 0. 15 Å p n i ng
P r in s ipp s ø k n a d. R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e
 P r in s ipp s ø k n a d R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e O pp d ra g s n r : 2 0 1 50 50 O pp d ra g s n a v n : Sa n d s ta d g å r d
P r in s ipp s ø k n a d R egu l e r i ngsen d r i n g f o r S ands t a d gå r d gn r. 64 b n r. 4 i Å f j o r d ko mm un e O pp d ra g s n r : 2 0 1 50 50 O pp d ra g s n a v n : Sa n d s ta d g å r d
Del I InDustrIutvIklIng: en fortelling om fornyelsen av luftfart... 15
 InnholD bak grunn... 11 h E n s i k t... 12 inn hold... 12 mo ti va sjon og takk... 13 Del I InDustrIutvIklIng: en fortelling om fornyelsen av luftfart... 15 o p p h E v E l s E n av t y n g d E k r a
InnholD bak grunn... 11 h E n s i k t... 12 inn hold... 12 mo ti va sjon og takk... 13 Del I InDustrIutvIklIng: en fortelling om fornyelsen av luftfart... 15 o p p h E v E l s E n av t y n g d E k r a
Kombinatorikk. MAT1030 Diskret matematikk Forelesning 20: Kombinatorikk. Repetisjon. Repetisjon
 Kombiatori MAT Disret matemati orelesig : Kombiatori Roger Atose Matematis Istitutt, Uiversitetet i Oslo 7. april 8 Kombiatori er studiet av opptelliger, ombiasjoer og permutasjoer. Vi fier svar på spørsmål
Kombiatori MAT Disret matemati orelesig : Kombiatori Roger Atose Matematis Istitutt, Uiversitetet i Oslo 7. april 8 Kombiatori er studiet av opptelliger, ombiasjoer og permutasjoer. Vi fier svar på spørsmål
Vedlegg til eksamensoppgaven i Diskret matematikk
 Vedlegg til esmesogve i Diset mtemti Det som stå he vil væe iholdet i esmesogves vedlegg høste 4 Deiisjoe og omle Logise oetoe: ie, og, elle, eslusiv elle, imlisjo Noe evivlese utsgslogi: P P P P Noe megdeidetitete:
Vedlegg til esmesogve i Diset mtemti Det som stå he vil væe iholdet i esmesogves vedlegg høste 4 Deiisjoe og omle Logise oetoe: ie, og, elle, eslusiv elle, imlisjo Noe evivlese utsgslogi: P P P P Noe megdeidetitete:
Fakultet for teknologi, kunst og design Teknologiske fag Eksamen i: Diskret matematikk
 Fakultet for tekologi, kust og desig Tekologiske fag Eksame i: Diskret matematikk Målform: Bokmål Dato: 9. ovember 017 Tid: Atall sider (ikl. forside): 9 Atall oppgaver: 6 Tillatte hjelpemidler: Forhådsgodkjet
Fakultet for tekologi, kust og desig Tekologiske fag Eksame i: Diskret matematikk Målform: Bokmål Dato: 9. ovember 017 Tid: Atall sider (ikl. forside): 9 Atall oppgaver: 6 Tillatte hjelpemidler: Forhådsgodkjet
Innhold. For br u ker k jøps lo vens omr åde. Prin sip pet om yt el se mot yt el se sam ti dig hets prin sip pet. Selgers plikter.
 Innhold Kapittel 1 For br u ker k jøps lo vens omr åde 1.1 Innledning...15 1.2 For bru ker kjøps lo vens vir ke om rå de. Hva lo ven gjel der for el ler re gu le rer...17 1.2.0 Litt om begrepet «kjøp»
Innhold Kapittel 1 For br u ker k jøps lo vens omr åde 1.1 Innledning...15 1.2 For bru ker kjøps lo vens vir ke om rå de. Hva lo ven gjel der for el ler re gu le rer...17 1.2.0 Litt om begrepet «kjøp»
Stabler, Køer og Lister. ADT er
 Stabler, er og Lister I. STEL OG QUEUE DT I.1 DT I.2 rray implemetasjo I.3 Liket-Liste implemetasjo II. DQUEUE DT III.IMPLEMENTSJON V EN DT MED EN NNEN DT Kap. 3 (kursorisk: 3.1.3, 3.2.3, 3.4; utatt: 3.2.4,
Stabler, er og Lister I. STEL OG QUEUE DT I.1 DT I.2 rray implemetasjo I.3 Liket-Liste implemetasjo II. DQUEUE DT III.IMPLEMENTSJON V EN DT MED EN NNEN DT Kap. 3 (kursorisk: 3.1.3, 3.2.3, 3.4; utatt: 3.2.4,
Obligatorisk oppgave nr. 3 i Diskret matematikk
 3. obligatoriske oppgave i Diskret matematikk høste 08. Obligatorisk oppgave r. 3 i Diskret matematikk Ileverigsfrist. ovember 08 Oppgave er frivillig og tregs ikke leveres, me hvis dere leverer de ie
3. obligatoriske oppgave i Diskret matematikk høste 08. Obligatorisk oppgave r. 3 i Diskret matematikk Ileverigsfrist. ovember 08 Oppgave er frivillig og tregs ikke leveres, me hvis dere leverer de ie
8 ØKONOMISTYRING FOR LØM-FAGENE
 Innhold Ka pit tel 1 Etablering, drift og avvikling av virksomhet...................... 13 1.1 Ut meis ling av for ret nings ide en i en for ret nings plan................13 1.2 Valg mel lom en kelt per
Innhold Ka pit tel 1 Etablering, drift og avvikling av virksomhet...................... 13 1.1 Ut meis ling av for ret nings ide en i en for ret nings plan................13 1.2 Valg mel lom en kelt per
Innhold. Ka pit tel 1 Inn led ning Barn og sam funn Bo kas opp byg ning... 13
 Innhold Ka pit tel 1 Inn led ning... 11 Barn og sam funn... 11 Bo kas opp byg ning... 13 Ka pit tel 2 So sia li se rings pro ses sen... 15 For hol det mel lom sam funn, kul tur og so sia li se ring...
Innhold Ka pit tel 1 Inn led ning... 11 Barn og sam funn... 11 Bo kas opp byg ning... 13 Ka pit tel 2 So sia li se rings pro ses sen... 15 For hol det mel lom sam funn, kul tur og so sia li se ring...
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE
 AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Eme: Diskret matematikk Gruppe(r): Emekode: FO 019A Dato: 12.12.200 Faglig veileder: Ulf Uttersrud Eksamestid: 9-14 Eksamesoppgave består av: Atall sider
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Eme: Diskret matematikk Gruppe(r): Emekode: FO 019A Dato: 12.12.200 Faglig veileder: Ulf Uttersrud Eksamestid: 9-14 Eksamesoppgave består av: Atall sider
n r : Jf. brevet som følgjer med saka
 : Jf. bevet som følgje med saka N Koodiat Sok Objekttype 1 / 2 0 1 3 K O M M U N E ( 1920 Lavage K A R T B L A D : am): GAB-id. (g, b, ad.kode, skivemåtealteativ S=syfaig H=hyd. oig. B=bev spåk el. kvesk
: Jf. bevet som følgje med saka N Koodiat Sok Objekttype 1 / 2 0 1 3 K O M M U N E ( 1920 Lavage K A R T B L A D : am): GAB-id. (g, b, ad.kode, skivemåtealteativ S=syfaig H=hyd. oig. B=bev spåk el. kvesk
KAPITTEL 6. STØRRELSER OG TALL I GRESK MATEMATIKK
 KAPITTEL 6. STØRRELSER OG TALL I GRESK MATEMATIKK Gekee kjete de atulige tallee og de kjete til fohold - dvs det vi i dag vil ofatte som bøke. E guleggede ofatig va at to lijestykke måtte ha et felles
KAPITTEL 6. STØRRELSER OG TALL I GRESK MATEMATIKK Gekee kjete de atulige tallee og de kjete til fohold - dvs det vi i dag vil ofatte som bøke. E guleggede ofatig va at to lijestykke måtte ha et felles
EKSAMEN Løsningsforslag
 7. jauar 7 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 4. desember 6 Hjelpemidler: - To A4-ark med valgfritt ihold på begge sider. Emeav: Matematikk for IT Eksamestid: 9. 3. Faglærer: Christia F Heide Kalkulator
7. jauar 7 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 4. desember 6 Hjelpemidler: - To A4-ark med valgfritt ihold på begge sider. Emeav: Matematikk for IT Eksamestid: 9. 3. Faglærer: Christia F Heide Kalkulator
Sosialantropologisk institutt
 Sosialantropologisk institutt Eksamensoppgaver til SOSANT2000: Generell antropologi: grunnlagsproblemer og kjernespørsmål Utsatt eksamen Høsten 2004 Skoleeksamen 16. desember kl. 9-15, Lesesal B, Eilert
Sosialantropologisk institutt Eksamensoppgaver til SOSANT2000: Generell antropologi: grunnlagsproblemer og kjernespørsmål Utsatt eksamen Høsten 2004 Skoleeksamen 16. desember kl. 9-15, Lesesal B, Eilert
S T Y R E T G J Ø R O P P M E R K S O M P Å A T D Ø R E N E S T E N G E S K L
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
Løsning eksamen TFY desember 2014
 Løsning esmen TFY404 8. desembe 04 Oppgve ) Kftdigmmene e vist nedenf f begge lssene g f tins. Ved stm sn h begge lssene smme selesjn. Kefte sm vie på lss med msse m : S m g m Kefte sm vie på lss med msse
Løsning esmen TFY404 8. desembe 04 Oppgve ) Kftdigmmene e vist nedenf f begge lssene g f tins. Ved stm sn h begge lssene smme selesjn. Kefte sm vie på lss med msse m : S m g m Kefte sm vie på lss med msse
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
Veileder for prosjektet har vært førsteamanuensis Stein-Erik Fleten. Jeg vil gjerne takke ham for all hjelp og faglig støtte.
 SIS1101 Fodypigsemet i ivesteig, fiasieig og økoomistyig FORORD Dee appote e utabeidet høste 2002 og e e posjektoppgave utabeidet i tilkytig til fodypigsemet føste semeste det 5. ået ved siviligeiøstudiet
SIS1101 Fodypigsemet i ivesteig, fiasieig og økoomistyig FORORD Dee appote e utabeidet høste 2002 og e e posjektoppgave utabeidet i tilkytig til fodypigsemet føste semeste det 5. ået ved siviligeiøstudiet
"Kapittel 5 i et nøtteskall"
 Ulve "Kapittel 5 i et øtteskall" (Vesjo 9.01.0 ) Jeg gå he i gjeom alle tekikke/fomle som e elevate i dette kapitlet ved å buke et eksempel side 198 som utgagspukt fo alle tekikkee. Ovesikt ove fomle og
Ulve "Kapittel 5 i et øtteskall" (Vesjo 9.01.0 ) Jeg gå he i gjeom alle tekikke/fomle som e elevate i dette kapitlet ved å buke et eksempel side 198 som utgagspukt fo alle tekikkee. Ovesikt ove fomle og
Rekursjon som programmeringsteknikk
 Rekursjon Kap.7 Sist oppdatert 15.02.10 Rekursjon som programmeringsteknikk 10-1 Rekursiv tenkning Rekursjon er en programmeringsteknikk der en metode kan kalle seg selv for å løse problemet. En rekursiv
Rekursjon Kap.7 Sist oppdatert 15.02.10 Rekursjon som programmeringsteknikk 10-1 Rekursiv tenkning Rekursjon er en programmeringsteknikk der en metode kan kalle seg selv for å løse problemet. En rekursiv
S2 kapittel 1 Rekker Løsninger til innlæringsoppgavene
 Løsiger til ilærigsoppgavee kapittel Rekker Løsiger til ilærigsoppgavee a Vi ser at differase mellom hvert ledd er 4, så vi får det este leddet ved å legge til 4 Det este leddet blir altså 6 + 4 = 0 b
Løsiger til ilærigsoppgavee kapittel Rekker Løsiger til ilærigsoppgavee a Vi ser at differase mellom hvert ledd er 4, så vi får det este leddet ved å legge til 4 Det este leddet blir altså 6 + 4 = 0 b
PrioritetsKøer. i-120 : H PrioritetsKøer: 1. Container. n-te/vilkårlig. PositionalContainer. PositionalSequence. Tree. Deque PriorityQueue
 PrioritetsKøer I. ADGANG TIL ELEMENTER I EN SAMLING gjeom Positio gjeom økkel II. TOTALE ORDNINGER OG NØKLER III.PRIORITETSKØ ADT PrioritetsKø-Sorterig IV. IMPLEMENTASJON MED SEQUENCE ADT V. IMPLEMENTASJON
PrioritetsKøer I. ADGANG TIL ELEMENTER I EN SAMLING gjeom Positio gjeom økkel II. TOTALE ORDNINGER OG NØKLER III.PRIORITETSKØ ADT PrioritetsKø-Sorterig IV. IMPLEMENTASJON MED SEQUENCE ADT V. IMPLEMENTASJON
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l år e t s g e n e r a l f o rs am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i n
K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l år e t s g e n e r a l f o rs am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i n
Dagens temaer. Sortering: 4 metoder Søking: binærsøk Rekursjon: Hanois tårn
 Dagens temaer Sortering: 4 metoder Hvorfor sortering (og søking) er viktig i programmering Sortering når objektene som skal sorteres er i et array 1. Sorterering ved bruk av binærtre som «mellomlager»
Dagens temaer Sortering: 4 metoder Hvorfor sortering (og søking) er viktig i programmering Sortering når objektene som skal sorteres er i et array 1. Sorterering ved bruk av binærtre som «mellomlager»
Kap. 8-4 Press- og krympeforbindelse
 K. -4 Pess- og kymefobdelse.4. Dmesjoeg v kymefobdelse Dmesjoeg v kymefobdelse fslegge e essmo slk kokykke () mellom delee e lsekkelg å oveføe belsge e gldg og kke så so segee v elle ksel bl fo høy Kymefobdelse
K. -4 Pess- og kymefobdelse.4. Dmesjoeg v kymefobdelse Dmesjoeg v kymefobdelse fslegge e essmo slk kokykke () mellom delee e lsekkelg å oveføe belsge e gldg og kke så so segee v elle ksel bl fo høy Kymefobdelse
I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e
 I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e 2 0 1 1 O r d i n æ r t s a m e i e r m ø t e i L i s a K r i s t o f f e r s e n s P l a s s S E, a v h o l d e s o ns d a g 9. m a r s
I n n k a l l i n g t i l o r d i n æ r t s a m e i e r m ø t e 2 0 1 1 O r d i n æ r t s a m e i e r m ø t e i L i s a K r i s t o f f e r s e n s P l a s s S E, a v h o l d e s o ns d a g 9. m a r s
En implementasjon av binærtre. Dagens tema. Klassestruktur hovedstruktur abstract class BTnode {}
 En implementasjon av binærtre Dagens tema Eksempel på binærtreimplementasjon Rekursjon: Tårnet i Hanoi Søking Lineær søking Klassestruktur hovedstruktur abstract class { class Person extends { class Binaertre
En implementasjon av binærtre Dagens tema Eksempel på binærtreimplementasjon Rekursjon: Tårnet i Hanoi Søking Lineær søking Klassestruktur hovedstruktur abstract class { class Person extends { class Binaertre
Kap. 4.4 Reimtransmisjoner. Reimtransmisjoner. Flatreim Kilereim Tannreim. Følgende reimtyper er i vanlig bruk
 Ka. 4.4 Reimtrasmisjoer Alterativ (ift tahjulveksel) me storavsta mellom aksler Krever ikke stor øyaktighet ve beregig, tilvirkig og moterig Reimtrasmisjoer ølgee reimtyer er i valig bruk latreim Kilereim
Ka. 4.4 Reimtrasmisjoer Alterativ (ift tahjulveksel) me storavsta mellom aksler Krever ikke stor øyaktighet ve beregig, tilvirkig og moterig Reimtrasmisjoer ølgee reimtyer er i valig bruk latreim Kilereim
PG4200 Algoritmer og datastrukturer Forelesning 3 Rekursjon Estimering
 PG4200 Algoritmer og datastrukturer Forelesning 3 Rekursjon Estimering Lars Sydnes, NITH 22.januar 2014 I. Rekursjon commons.wikimedia.org Rekursjon i naturen En gren er et tre som sitter fast på et tre.
PG4200 Algoritmer og datastrukturer Forelesning 3 Rekursjon Estimering Lars Sydnes, NITH 22.januar 2014 I. Rekursjon commons.wikimedia.org Rekursjon i naturen En gren er et tre som sitter fast på et tre.
Fjøsangerveien Strømmen
 Hvda bli kjømøst i bgpid? KONTAKTER / ANSVARLIE INFO OM ARBEID Ifmasjsasvalig Hil s ga t gg T mø I føst dl av aggspid vil l tafikk til/fa Damasplass mtt g v g. I pid vil gs Tmø bli stgt f gjmkjøig. Næm
Hvda bli kjømøst i bgpid? KONTAKTER / ANSVARLIE INFO OM ARBEID Ifmasjsasvalig Hil s ga t gg T mø I føst dl av aggspid vil l tafikk til/fa Damasplass mtt g v g. I pid vil gs Tmø bli stgt f gjmkjøig. Næm
Løsningsforslag til øving 4
 Høgsole i Gjøi d. for te., ø. og ledelse temti 5 Løsigsforslg til øig OPPGE det ( 8 Determite esisterer ie! K drtise mtriser e determit. i i detc ( i( i ( i( i ( i i i i 5i 5i i i er! Regereglee er de
Høgsole i Gjøi d. for te., ø. og ledelse temti 5 Løsigsforslg til øig OPPGE det ( 8 Determite esisterer ie! K drtise mtriser e determit. i i detc ( i( i ( i( i ( i i i i 5i 5i i i er! Regereglee er de
Rekursjon. Binærsøk. Hanois tårn.
 Rekursjon Binærsøk. Hanois tårn. Hvorfor sortering (og søking) er viktig i programmering «orden» i dataene vi blir fort lei av å lete poleksempel internett «alt» er søking og sortering alternativer til
Rekursjon Binærsøk. Hanois tårn. Hvorfor sortering (og søking) er viktig i programmering «orden» i dataene vi blir fort lei av å lete poleksempel internett «alt» er søking og sortering alternativer til
I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E
 I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i n æ r t s am e i e rm øt e i S am e i e t W al d em a rs H a g e, a v h o l d e s t o rs d a g 1 8. j u n i 2 0 0 9, k l.
I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i n æ r t s am e i e rm øt e i S am e i e t W al d em a rs H a g e, a v h o l d e s t o rs d a g 1 8. j u n i 2 0 0 9, k l.
Hesteveddeløp i 8. klasse
 Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Ninety-nine bottles. Femte forelesning. I dagens forelesning: Mest matematiske verktøy. Først: Asymptotisk notasjon. Så: Rekurrensligninger.
 I dagens forelesning: Mest matematiske verktøy. Først: Asymptotisk notasjon. Så: Rekurrensligninger. Hva slags kjøretid har denne sangen? Hvordan kan du formulere det som en rekurrensligning? Ninety-nine
I dagens forelesning: Mest matematiske verktøy. Først: Asymptotisk notasjon. Så: Rekurrensligninger. Hva slags kjøretid har denne sangen? Hvordan kan du formulere det som en rekurrensligning? Ninety-nine
INF3400 Digital Mikroelektronikk Løsningsforslag DEL 9
 IF00 Digital Mikroelektroikk Løsigsforslag DEL 9 I. Oppgaver. Oppgave 6.7 Teg trasistorskjema for dyamisk footed igags D og O porter. gi bredde på trasistoree. va blir logisk effort for portee?. Løsigsforslag
IF00 Digital Mikroelektroikk Løsigsforslag DEL 9 I. Oppgaver. Oppgave 6.7 Teg trasistorskjema for dyamisk footed igags D og O porter. gi bredde på trasistoree. va blir logisk effort for portee?. Løsigsforslag
Løsningsforslag. Oppgavesettet består av 9 oppgaver med i alt 21 deloppgaver. Ved sensur vil alle deloppgaver telle omtrent like mye.
 .. Løsigsforslag Emekode: ITF7 Dato:. desember Eme: Matematikk for IT Eksamestid: kl. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Faglærer: Christia F Heide Eksamesoppgave: Oppgavesettet
.. Løsigsforslag Emekode: ITF7 Dato:. desember Eme: Matematikk for IT Eksamestid: kl. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Faglærer: Christia F Heide Eksamesoppgave: Oppgavesettet
Dagens tema INF1010 INF1010 INF1010 INF1010
 I eksemplene om lister og binære trær har vi hittil hatt pekerne inne i objektene i strukturen. ( Innbakt struktur ).Eksempel: Dagens tema Implementasjon av strukturer (lister, binære trær) class { ; ;
I eksemplene om lister og binære trær har vi hittil hatt pekerne inne i objektene i strukturen. ( Innbakt struktur ).Eksempel: Dagens tema Implementasjon av strukturer (lister, binære trær) class { ; ;
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D e t t e e r i n n k a l l i n g e n t i l å r e t s g e n er a l f o r s a m l i n g. D e n i n n e h o l d e r b o r e t t s l a g e t s å r s m e l d i n g o g r e g n s k a
K j æ r e b e b o e r! D e t t e e r i n n k a l l i n g e n t i l å r e t s g e n er a l f o r s a m l i n g. D e n i n n e h o l d e r b o r e t t s l a g e t s å r s m e l d i n g o g r e g n s k a
Differensligninger Forelesningsnotat i Diskret matematikk Differensligninger
 Differesligiger Forelesigsotat i Diskret matematikk 017 Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker er imidlertid
Differesligiger Forelesigsotat i Diskret matematikk 017 Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker er imidlertid
NORSK TEKSTARKIV J o s t e in H. Hauge
 NAVF'S EDB-SENTER FOR HUMANISTISK FORSKNING V IL L A V E I 1 0, POSTBOKS 53 50 1 4 BERG EN-UNIVERSITETET 7 O k to b e r 1979 NORSK TEKSTARKIV J o s t e in H. Hauge 1. FO RHISTORIE D a ta m a s k in e ll
NAVF'S EDB-SENTER FOR HUMANISTISK FORSKNING V IL L A V E I 1 0, POSTBOKS 53 50 1 4 BERG EN-UNIVERSITETET 7 O k to b e r 1979 NORSK TEKSTARKIV J o s t e in H. Hauge 1. FO RHISTORIE D a ta m a s k in e ll
Avsnitt 8.1 i læreboka Differensligninger
 Diskret Matematikk Fredag 6. ovember 015 Avsitt 8.1 i læreboka Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker
Diskret Matematikk Fredag 6. ovember 015 Avsitt 8.1 i læreboka Differesligiger I kapittel lærte vi om følger og rekker. Vi studerte både aritmetiske og geometriske følger og rekker. Noe følger og rekker
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
MA1101 Grunnkurs Analyse I Høst 2017
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Innledning...16 Kapitlene Ano ny mi tet... 18
 Innhold Innledning...16 Kapitlene... 17 Ano ny mi tet... 18 Del I Innledning til mentoring KapIttel 1 Introduksjon til mentoring...20 Bak grunn...20 Be gre pe ne...22 Sponsorship og ut vik len de mentoring...23
Innhold Innledning...16 Kapitlene... 17 Ano ny mi tet... 18 Del I Innledning til mentoring KapIttel 1 Introduksjon til mentoring...20 Bak grunn...20 Be gre pe ne...22 Sponsorship og ut vik len de mentoring...23
INF1010 - våren 2007 16. januar, uke 3 - Oversikt og forutsetninger Java datastruktur-tegninger
 INF1010 - våre 2007 16. jauar, uke 3 - Oversikt og forutsetiger Java datastruktur-tegiger Stei Gjessig Ist. for iformatikk Nye temaer i INF1010 Fra problem til program Software Egieerig light, fasee i
INF1010 - våre 2007 16. jauar, uke 3 - Oversikt og forutsetiger Java datastruktur-tegiger Stei Gjessig Ist. for iformatikk Nye temaer i INF1010 Fra problem til program Software Egieerig light, fasee i
Oblig 2 - MAT1120. Fredrik Meyer 26. oktober 2009 = A = P1 1 A 1 P 1 A 1 A 2 = P 1. A k+1. A k P k
 Oblig 2 - MAT20 Fredri Meyer 26 otober 2009 Matrisee A i er defiert sli der P er e rotasjosmatrise som defierer i oppgave 2: A A 2 A + = A = P A P = P A P Oppgave Matrisee A i+ og A i er similære det fies
Oblig 2 - MAT20 Fredri Meyer 26 otober 2009 Matrisee A i er defiert sli der P er e rotasjosmatrise som defierer i oppgave 2: A A 2 A + = A = P A P = P A P Oppgave Matrisee A i+ og A i er similære det fies
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
Hjertet Banker & # œ œ œ œ Hjer - tet ban - ker, hjer - tet ban - ker, liv. œ œ œ œ œ œ œ œ œ œ œ œ Œ. œ œ œ œ Œ œ œ œ œ œ œ œ œ Ó gjør oss lev -en-
 Hjtet ank Tore Thomass 4 Refrg Hj tet ban k, hj tet ban k, liv et syn g, alt skje. Vs ro Hjtet bank, hjtet bank, 1.Hj 2.Hj tet bank hel tet går i skol Hjtet ljug Hjtet går'ke ik rett hj tet ban k plaging,
Hjtet ank Tore Thomass 4 Refrg Hj tet ban k, hj tet ban k, liv et syn g, alt skje. Vs ro Hjtet bank, hjtet bank, 1.Hj 2.Hj tet bank hel tet går i skol Hjtet ljug Hjtet går'ke ik rett hj tet ban k plaging,
Avdeling for ingeniørutdanning. Eksamen i Diskret matematikk
 www.hio.o vdelig fo igeiøutdig Esme i Diset mtemti Dto: 7. deseme Tid: 9 4 tll side ilusive foside: 8 tll ogve: Tilltte hjelemidle: Ku hådholdt lulto som ie ommuisee tådløst. Med: Kdidte må selv otollee
www.hio.o vdelig fo igeiøutdig Esme i Diset mtemti Dto: 7. deseme Tid: 9 4 tll side ilusive foside: 8 tll ogve: Tilltte hjelemidle: Ku hådholdt lulto som ie ommuisee tådløst. Med: Kdidte må selv otollee
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l å r e t s g e n e r a l f o r s a m l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n
K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l å r e t s g e n e r a l f o r s a m l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
A ft tt * 1 ^ an T ii ft. *< X IP * ft ii l> ff ffl *> (2 # * X fa c, * M L 7 ft tf ;U -h h T T* L /< ft * ft 7 g $ /i & 1 II tz ft ft ip ft M.
 Pal 77»_ a< IP ft A 6 * *' -5 m y, m *J 7 7 t< m X D $ ^ 7 6 X b 7 X X * d 1 X 1 v_ y 1 ** 12 7* y SU % II 7 li % IP X M X * W 7 ft 7r SI & # & A #; * 6 ft ft ft < ft *< m II E & ft 5 t * $ * ft ft 6 T
Pal 77»_ a< IP ft A 6 * *' -5 m y, m *J 7 7 t< m X D $ ^ 7 6 X b 7 X X * d 1 X 1 v_ y 1 ** 12 7* y SU % II 7 li % IP X M X * W 7 ft 7r SI & # & A #; * 6 ft ft ft < ft *< m II E & ft 5 t * $ * ft ft 6 T
EKSAMEN I EMNE TMT4110 KJEMI - løsningsforslag
 Side 1 av 7 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR MATERIALTEKNOLOGI Faglig kntakt unde eksamen: Institutt f mateialteknlgi, Gløshaugen Føsteamanuensis Hilde Lea Lein, tlf. 73 55
Side 1 av 7 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR MATERIALTEKNOLOGI Faglig kntakt unde eksamen: Institutt f mateialteknlgi, Gløshaugen Føsteamanuensis Hilde Lea Lein, tlf. 73 55
Mer om utvalgsundersøkelser
 Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Innhold og forelesningsplan Eksempler på LP Begreper Løsning av enkelt eksempel Praktisk relevans Leksjon 2: Simpleksmetoden for løsning av LP
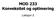 Lekso 2 Mål for kurset teoretisk forståelse, gruleggede optimerig løsigsmetoder LP og utvidelser algoritmisk forståelse avedelser LP og utvidelser modellerig og løsig v.h.a. verktøy Ihold og forelesigspla
Lekso 2 Mål for kurset teoretisk forståelse, gruleggede optimerig løsigsmetoder LP og utvidelser algoritmisk forståelse avedelser LP og utvidelser modellerig og løsig v.h.a. verktøy Ihold og forelesigspla
Kapittel 5 - Vektorer - Oppgaver
 5.4 Kapittel 5 - Vektorer - Oppgaver 5.4, 5.5, 5.45, 5.49, 5.300, 5.306 a) Kabeles legde: BA 6, 7, 6 6 7 6 b) Dette er e parameterfremstillig (på vektorform) for e lije: OT 6t,7t, 6t 0, 0, t6, 7, 6 OB
5.4 Kapittel 5 - Vektorer - Oppgaver 5.4, 5.5, 5.45, 5.49, 5.300, 5.306 a) Kabeles legde: BA 6, 7, 6 6 7 6 b) Dette er e parameterfremstillig (på vektorform) for e lije: OT 6t,7t, 6t 0, 0, t6, 7, 6 OB
Løsningsforslag til ukeoppgave 11
 Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Sommerkoteletter fra ferskvaredisken. -appen! Finn oppskrifter og tilbud på MENY.no eller i. 90 ord.pris 17,90/stk SPAR 53% ord.
 53% 39.i 85,/ Smmtltt fa fvai 55% fl 3 8, 4 1 K K 89 7.i 17,/t i 0 2,9 53% 20-30%.i 37,5042,/ Nyillt yllilå Pi Max Iablla Fii Ntai fa vamat x1,5 l + at (9,89/l) 10, Hi-Ol (49,83/l) 1, Saia Vi ta fbhl m
53% 39.i 85,/ Smmtltt fa fvai 55% fl 3 8, 4 1 K K 89 7.i 17,/t i 0 2,9 53% 20-30%.i 37,5042,/ Nyillt yllilå Pi Max Iablla Fii Ntai fa vamat x1,5 l + at (9,89/l) 10, Hi-Ol (49,83/l) 1, Saia Vi ta fbhl m
