KONGSVINGER: Postboks 510, Stasjonssida, 2201 Kongsvinger Tlf. (02) * Tlf. (066) *14 988
|
|
|
- Even Håland
- 8 år siden
- Visninger:
Transkript
1 OSLO: Postbos 8131 Dep, Oslo 1 KONGSVINGER: Postbos 510, Stasjonssida, 2201 Kongsvinger Tlf. (02) * Tlf. (066) * IO 78/26 9. otober 1978 STTISTISK SENTRLBYRÅS BEFOLKNINGSPROGNOSEMODELL: TEKNISK DOKUMENTSJON V FRMSKRIVINGSMODELLEN 1977 av Knut 0. Sørensen * INNHOLD 1. Innledning Side 1 2. Framsrivingsmodellen for de primære prognoseregionene 2.1. Generelt Symbolliste Framsrivingsrelasjoner Rateberegninger Diverse 8 3. Nedbryting av framsrivingen for de primære prognoseregionene til ommunenivå Generelt Symbolliste Formler lternativ uten flytting lternativ med flytting Rateberegninger 13i 3.5. En del egensaper ved nedbrytingsmodellen Konsistensegensaper Sammenhengen mellom framsrivingen 1977 uten flytting og en framsriving uten flytting direte på ommunenivå Tolningsproblemer for anslagene for bruttoinnflytting i nedbrytingsmodellen Nærmere om betydningen av anslagene for inn- og utflytting i nedbrytingsmodellen Tillempninger ved alternativ nedbryting i samarbeid med fylene 18 Referanser 20 Jeg vil tae rne Rideng, Per Sevaldson og Kjetil Sørlie, som har lest gjennom manusriptet og gitt nyttige ommentarer. 1 Ie for offentliggjoring. Dette notat er et arbeidsdoument og an siteres eller refereres bare etter spesiell tillatelse i bagert enelt tilfelle. Synspunter og onlusjoner an ie uten videre tas som uttry for Statistis Sentralbyrås oppfatning.
2 1. INNLEDNING Statistis Sentralbyrå utarbeidet en ny regional befolningsframsriving i Den forrige framsrivingen,i 1975,ble besrevet i en artiel (rtiej 80), som ga en forholdsvis tenis doumentasjon av framsrivingsmodellen (se Sorensen (1975)). Det er nå nødvendig å ajourføre denne doumentasjonen. Framsrivingsmodellen er siden sist blitt endret på en ree punter. Vi tar nå hensyn til inn- og utvandring. Modellens 2. trinn, nedbrytingen fra de primære prognoseregionene til ommuner, er helt ny. Dessuten er det foretatt justeringer når det gjelder dødsrater og avrundingsregler. Inndelingen i primære prognoseregioner er den samme som i forrige framsriving. Den er gjengitt som vedlegg 2 i Sorensen (1975). Det vil senere bli gitt ut en artiel med mer summaris presentasjon av framsrivingsmodellen. Den artielen vil bli mindre tenis preget enn dette notatet. Vi vil i artielen også legge vet på å presentere visse hovedtre ved framsrivingsresultatene. 2. FRMSKRIVINGSMODELLEN FOR DE PRIME PROGNOSEREGIONENE 2.1. Generelt Framsrivingen tar utgangspunt i folemengden sli den var registrert i det sentrale personregisteret ved utgangen av Folemengden framsrives ved år for år å anslå størrelsen av de demografise endringsomponentene fødsler og dødsfall, og dessuten (i alternativ med flytting) inn- og utflytting for hver primære prognoseregion (pp.-region). For personer som var i live ved inngangen til et år, anslås antall døde og utflyttere ved å anvende rater som er spesifie for hvert jønn, hver ettårig alderslasse og region. Innflyttere fordeles på regioner i samme forholdsom de observerte tall i en basisperiode. Regionfordelingen er spesifi for hvert jønn og hver ettårig alderslasse. De regionale utflyttingsratene gjelder all flytting ut av regionen, både innenlands flytting og flytting til utlandet. Bruttoutvandring anslås for Norge under ett ved hjelp av utvandringsrater. Bruttoutvandring tillagt en antatt størrelse på nettoinnvandringen gir anslaget på bruttoinnvandringen, -som fordeles på jønn og alder i samme forhold som observert i en basisperiode. Tall på innflyttere til fordeling på regionene, fås så for hver jonns- og alderslasse ved å legge bruttoinnvandringen til den innenlandse flyttingen. Fodte i løpet av framsrivingsåret blir anslått ved å anvende alders- og regionspesifie frutbarhetsrater på bestanden av vinner i fodedytig alder (15-44 år). ntallet av de nyfødte som (tor innen utløpet av fødselsåret blir anslått ved hjelp av en egen dødsrate. Framsrivingstall for fyler og landet som helhet fås ved å aggregere tallene for primære prognoseregioner. I modellens forste trinn får vi lievel bare tall for Oslo og ershus under ett, siden disse to fylene er én primær prognoseregion Symbolliste Primær prognoseregion (forortet til p.p.-region) angis med fotsriften r (r = region). Størreiser uten fotsrift gjelder hele landet. lder betegnes med indesen x. Med alder menes det her differansen i år mellom observasjons- (eller framsrivings-) år og fødselsår, dvs. alder i fylte år ved utgangen av alenderåret. Kalenderåret betegnes med indes t (t tid). For å forenle siller vi ie mellom framsrevne og observerte størrelser på annen måte enn at en indes t for t = 1977 eller senere viser at det dreier seg om en framsrevet størrelse, mens en indes t som er mindre enn 1977 viser til observerte størrelser. I formlene er det brut indesen J for å betegne jønn. Indesen J an da ta en av de to verdiene M for menn og K for vinner.
3 2 i. Symboler som betegner antall personer L r (x,t,m) er antall x år gamle menn i p.p.-region r den 31/12 i år t; x = 0,1,..,99. Den mire aldersgruppen omfatter personer som er 99 år og eldre. L r (x,t,k) B (x $ t) er det tilsvarende tall for vinner. er antall barn født i år t i p.p.-region r av modre som selv var født i år (t - x); x = 15,..,44. B r (t) er antall levendefødte i år t i p.p.-region r. B r (t,m) er antall levendefødte gutter i r t i p.p.-region r. B (t,k) er det tilsvarende antall jenter. Dr (0,t,M) er antall gutter som dot- i fødselsåret t i p.p.-region r. Dr (0,t,K) er det tilsvarende antall jenter. D r (x,t,m) er antall dødsfall i år t i p.p.-region r blant menn som var født i år t x; X = 1,2,..,99. D r (x,t,k) er det tilsvarende tall for vinner. Dr (100,t,M) er antall dødsfall i år t i p.p.-region r blant menn som var født år t eller for. D (100,t,K) er det tilsvarende tall for vinner. Ur(x,t,M) er antall menn som flytter ut fra p.p.-region r i år t $ og som var født i år t - x; x = 0,1,..,69. (Omfatter både innenlandse flyttere og utvandrere.) Det regnes ie med flytting for personer på 70 år eller eldre. U r (x,t,k) er det tilsvarende tall for vinner. Ut(x,t,M) er antall menn i alder x som utvandrer i år t; x = 0,1t..,69. U 1 (x,t,k) er det tilsvarende tall for vinner. Ii(x,t,M) er antall menn i alder x som flytter inn til p.p.-region r i *Wet av år t; X = 0,1,..,69. (Omfatter både innenlandse flyttere og utvandrere.) I r (x,t,k) er det tilsvarende tall for vinner. I(x,t,M) er summen av innenlandse flyttere og innvandrere for menn i alder x i år t; X = I(x,t,K) er tilsvarende tall for vinner. I 1 (x,t,m) er antall menn i alder x som innvandrer fra utlandet i løpet av år t; x = 0,1,..,69. Ii(x,t,K) er tilsvarende tall for vinner. Il(t) er antall innvandrere til Norge i år t. N er total årlig netto-innvandring fra utlandet. Symboler som betegner parametre q(x,m) er sannsynligheten for at en mann sal do i det alenderår da han er x år (ifølge vår aldersdefinisjon), når han lever ved begynnelsen av året; x = 1,2,..,99. q(x,k) er den tilsvarende størrelse for vinner. q(100,m) er sannsynligheten for at en mann som var 99 år eller eldre ved begynnelsen av et år, sal do i løpet av året. q(100,k) er den tilsvarende størrelsen for vinner.
4 3 q(0,m) er sannsynligheten for at et levendefødt guttebarn dor i løpet av det alenderår da han blir født. q(0,k) er den tilsvarende størrelsen for jenter. fr(x't) er forventet antall barn som fødes i år t av vinner i p.p.-region r som selv var født i år t - x; x = 15,..,44. CMer sannsynligheten for at et barn som fødes, er en gutt (guttefødselsvotienten). c K er den tilsvarende størrelsen for jenter (c m+c K=1). u r (x,m) er sannsynligheten for at en mann sal flytte ut fra p.p.-region i det alenderår da han er x år (ifølge vår aldersdefinisjon); x = 0,..,69. u r (x,k) er den tilsvarende størrelsen for vinner. i (x,m) r er den betingede sannsynligheten for at en x år gammel mann sal bo i p.p.-region r den 31/12 et år, gitt at han flyttet mellom p.p.-regioner eller inn fra utlandet det året; x = 0,1,..,69. (Ei r (x,m)=1) i (x,k) er den tilsvarende størrelsen for vinner. r ul(x,m) er sannsynligheten for at en x år gammel mann sal utvandre fra Norge; x =0,1,..,69. u 1 (x,k) er den tilsvarende størrelsen for vinner. i'(x,j) er sannsynligheten for at en innvandrer sal være x år og være av jønn J; X = 0,1,..,69, J = M (for menn), K (for vinner). (Ei'(x,M) + Eil(x,K) = 1) Xx Symbolet q(x) betegner en estimator for sannsyligheten q(x). Tilsvarende for de andre para- metrene. Spesielt tilsvarer u r (x,m) og u (x,k) det som alles utflyttingsrater, mens i r (x,m) og,r i çx,k) tilsvarer innflyttingsandelene. f r r (x,t) aller vi frutbarhetsrater, q p(x,m) og El(x,K) døds-. rater, og u 1 (x,k) og u'(x,m) alles utvandringsrater Framsrivingsrelasjoner Indesen t (for alenderår) gjennomløper her hvert år fra t = 1976 til t = i. Fødsler ntall (levende-)fodte finnes ved å multiplisere antall vinner i feidedytig alder ved begynnelsen av året med de tilsvarende frutbarhetsratene 44 (1) Br(t+1) = E f,(x,t+1).l r (x-1,t,k) x=15 Fødslene fordeles på gutter og, jenter i samme forhold som observert i perioden (2a) Br(t+1,M) = r (t+1) (2b) Br(t+1,K) = c.b r (t+1) ii. Dødsfall Dødsfallene beregnes ved å multiplisere antall personer ved begynnelsen av året med de tilhørende dødsratene. (3a) Dr(x,t+1,J) = q(x,j).l r (x-1,t,j); J = M,K X = 1,..,100 (3b) 0r(0,t+1,J) = q(0,j).b r (t+1,j); J = M,K
5 4 iii. De nye bestandene i alternativ uten flytting Når vi ser bort fra flytting, er det bare fødsler og dødsfall som påvirer utvilingen i foletallet. ntall personer i én bestemt alder ved utgangen av et framsrivingsår er li antall personer på et alderstrinn lavere ved utgangen av året for, minus de av dem som do,- i løpet av framsrivingsåret. (4a) Lr(x,t+1,J) = L r (x-1,t,j) Dr(x,t+1,J); J = M,K X = 1,..,98 For aldersgruppen 99 år og over, må vi også tree inn overlevende blant de som var 99 år og over ved begynnelsen av året. (4b) Lr(99,t+1,J) = L r (98,t,J) - D r (99,t+1,J) + L r (99,t,J) Dr(100,t+1,J); J = M,K For å finne det nye antallet null-åringer må vi ta utgangspunt i de som blir født i løpet av året og tree fra de av dem som dør i løpet av det samme året. (4c) Lr(0,t+1,J) = B r (t+1,j) Dr (0,t+1,J); J = M,K iv. Utflytting Vi regner ie med inn- eller utflytting for personer som er 70 år eller eldre. For de øvrige aldersgruppene er utflyttingen beregnet ved å multiplisere antall personer med inngangen av året med tilhørende flytterater. Utflyttingen omfatter bade innenlands flytting og utvandring. (5a) Ur(x,t+1,J) = Ûr (x,j).l r (x-1,t,j); J = M,K X = 1,..,69 (5b)' U r (0,t+1,J) = Û r (0,J).b r (t+1,j): J = M,K v. Inn- og utvandring Det er sett bort fra inn- og utvandring for personer som er 70 år eller eldre. Egne beregninger av inn- og utvandring foregår bare for landet under ett. Utvandringen finnes ved å anvende utvandringsratene på bestanden av personer ved begynnelsen av framsrivingsåret. (6a) U'(x,t+1,J) = 6 1 (x,j)*l(x-1,t,j); J = M,K X = 1,..,99 (6b) W(0,t+1,J) = lp(0,j).b(t+1,j); J = M,K Her er L(x-1,t,J) EL ( -1,t,J) B(t+1,J) = EB,(t+1,J) r Når antall utvandrere er beregnet, finnes total innvandring ved a legge netto-innvandringen til den samlede størrelsen på utvandringen. 69 (7) P(t+1) =N+z z U'(x,t+1,J) x=0 J=M,K Innvandrerne fordeles så på jønn og alder i samsvar med den tilsvarende fordelingen i basisperioden. ( ).
6 5 (8) I'(x,t+1,J) = i'(x,j).i 1 (t 1); J = M,K X = 0, vi. Innflytting Vi ser bort fra innflytting for personer i alderen 70 år og over. Innflyttingen omfatter både innenlands flytting og innvandring. Innenlands flytting an beregnes ved å summere utflyttingen beregnet i ligning 5, og tree fra utvandringen. Deretter må vi legge til innvandringen. ( 9 ) I(x,t+1,J) = EU,(x,t+1,J) - U 1 (x,t+1,j) + Ii(x,t+1,J); J = M,K r x = 0,1,..,69 Innflyttingen fordeles så på de primære prognoseregioner ved å brue innflyttingsandelene. (10) Ir(x,t+1,J) = i r(x,j).i(x,t+1,j); J = M,K X = 0,1,..,69 vii. De nye bestandene i alternativene med flytting De nye bestandene finnes som i tilfellet uten flytting, bortsett fra at vi nå må legge til innflytterne og tree fra utflytterne. For personer i alder 70 år og over, er både antall utflyttere og antall innflyttere satt li null. Gruppen "99 år og over" er behandlet som i alternativet uten flytting. (11a) (11b) Lr (x,t+1,j) = L r (x-1,t,j) - D r(x,t+1,j) - Ur(x,t+1,J) + I r(x,t+1,j); J = M,K X = 1,..,98 Lr(0,t+1,J) = B r (t+1,j) Dr(0,t+1,J) - Ur(0,t+1,J) + 0,t+1,J); J = M,K (11c) Lr(99,t+1,J) = L (98,t,J) - D r(99,t+1,j) + L r (99,t,J;,Dr(100,t+1,J); J = M,K 2.4. Rateberegninger. Frutbarhetsrater Ratene er basert på observasjoner for årene Ellers er framgangsmåten Ved beregning og glatting av ratene den samme som ved forrige framsriving. Forst har vi beregnet et sett av "rårater" ut fra de tilsvarende observerte ratene i basisperioden. X 1976 E 8,(x,t) t=1973 ' / = 1976 E 0,5-EL r (x-1,t-1,k)+l r(x,t,k): t=1973 X15,...,44 Ved beregningen av råratene har vi slått sammen endel av de minste primære prognoseregionene for å få et tilfredsstillende antall observasjoner ba hver rate. Vi har derfor 60 regioner ved rateberegningen. En liste over hvile regioner som er slått sammen an finnes i vedlegg 3 i artiel 80. (Sorensen (1975) s. 43). For å utjevne virningene av at noen årslasser i et område av tilfeldige årsaer an ha fått svært høye eller svært lave fødselsrater i observasjonsperioden, er råratene for hvert av de 60 områdene glattet ved hjelp av Hadwigerfunsjonen. Parametrene i denne funsjonen er estimert på grunnlag av råratene, sli som forlart av Hoem et.al. (1974) og av Berge og Hoem (1974). De glattede ratene er deretter beregnet ved hjelp av de estimerte Hadwigerparametrene. Hadwigerfunsjonen besriver utvilingen i frutbarhetsratene som funsjon av alderen ved hjelp av bare fire parametre. Dette, sammen med sammenslåingen av p.p.-regionene,er en måte å mote problemet med små datagrunnlag på, samtidig som en får ta hensyn til regionale forsjeller i frutbarheten.
7 6 Tilpassingen av frutbarhetsnivaet er endret litt i forhold til forrige framsriving. For å få frutbarhetsrater med samme nivå som frutbarheten i 1976, (frutbarhetsalternativet H) er alle frutbarhetsratene multiplisert med samme orresjonsfator. Denne orresjonsfatoren er li forholdet mellom samlet frutbarhetstall i 1976 og gjennomsnittlig samlet frutbarhetstall i basisperioden. Tilpasningen av frutbarheten til alternativ L sjer tilsvarende, med li prosentvis redusjon i alle regioner og for alle aldre. Kjønnsvotientene cm og c K er estimert ut fra observasjoner for perioden Dødsrater Ved forrige framsriving to vi utgangspunt i dødsrater der alderen ble beregnet som alder ved dodstidspuntet. (Se Sorensen (1975, s )). I framsrivingen er alderen definert som alenderår minus fødselsår, sli at ratene måtte regnes om. Vi har nå tatt utgangspunt i rater med vår aldersdefinisjon fra starten av. Bortsett fra aldersdefinisjonen, er beregningsmåten besrevet i vedlegg 1 i Statistis Sentralbyrå (1978). De beregnede råratene er glattet ved hjelp av glidende gjennomsnitt. Metoden er nærmere besrevet av Haldorsen (1974). Dødsratene er beregnet ut fra årene 1974 og lle dødsratene er senet med to prosent for de er brut i framsrivingen. Dødsraten for gruppen 100 år og over er satt til 0,7. Utflyttingsrater Basisperioden er Utflyttingsratene omfatter bade innenlands flytting og utvandring. Det er ie gjort forsø på glatting eller på å legge inn trender i flyttetilbøyelighetene. En person som har meldt flere flyttinger i år n, er regnet som utflytter dersom vedommende ie flyttet til utgangsreg4onen i løpet av året. En sli person blir regnet som innflytter til den primære prognoseregionen som var bostedet den 31/12 i år n. Utflyttingsratene er beregnet ved å sette antall utflyttere i hver ohort et år i forhold til ohortens størrelse ved inngangen av året. Det er sett bort fra flytting for personer som er 70 år eller eldre. u r (x,j) = 1976 E Ur(x,t,J) t=1973. J = M,K 1976 ' x = 1,..,69 L r (x-1,t-1,j) t= E Ur(0,t,J) t=1973 u r (0,J) = 1976 E B (to)) t=1973 r iv. Innflyttingsandeler ; J = M,K Basisperioden er Siden innflyttingsandelene omfatter bade innenlands flytting og innvandring, avvier formelen litt fra den forrige formelen som er gjengitt i artiel 80. Innflyttingsandelene er estimert ved: 1976 E Ir(x,t,J) t=1973 J = M,K = 1976 x = 0,1,..,69 I(x,t,J) t=1973
8 7 v. Utvandringsrater og jønns- og aldersfordeling for (brutto-) innvandringen Også her er basisperioden En vurdering av inn- og utvandringsrelasjonene er gitt i apittel 4 i Sorensen (1977). Ratene for utvandring og aldersfordelingen for innvandrere er i store tre beregnet som de tilsvarende rater og aldersfordelingen som gjaldt i basisperioden under ett. Ved beregningen av utvandringsratene er det forutsatt lie rater for begge jønn i aldrene 0-15 år. Det samme gjelder aldersgruppen år. W(0, E E U1(0,t,i) _ i=m,k t=1973 ; J = M,K 1976 E E B,(t) t=1973 r ' 1976 E U'(x,t,i) '1.;. (x,j) _ i=m,k t=1973 J = M,K 1976 ; x = 1,..,15 E E L(x-1,t-1,i) 50,..,54 i=m,k t=1973 For aldersgruppene år er utvandringsratene ie glattet E U'(x,t,J) t=1973 u'(x,v) = 1977 J = M,K ; x = 16,..,49 E L(x-1,t-1,J) t=1973 Vi har regnet med at utvandringsratene er uavhengig av alder og jønn innen hver av aldersgruppene dr, år og år. Det er sett bort fra flytting for personer i alderen 70 år og eldre E E E Ul(n,t,i) i=m,k t=1973 n=1 J = M,K ' x = 55, E E E L(n-,t-1,i) 1 = 55 for x = 55,..,59 i=m,k t=1973-n=1 1 = 60 for x = 60,..,64 1 = 65 for x = 65,..,69 ldersfordelingen for innvandrene er glattet etter de samme prinsippene 0 og 1-åringene er imidlertid holdt utenfor glattingen, siden det er en marert blant innvandrerne i disse aldrene. som utvandringsratene. overvet av jenter 1976 E P(x,t,J) 1, t=1973 il(x J = M,K '" x = 0,1 5 16,..,49 E Is(t) t=1973 Det er forutsatt at fordelingen på ettårige alderslasser innen aldersgruppen 2-15 år er li for vinner og menn. En tilsvarende forutsetning er gitt for aldersgruppen år E E I'(n,t,J) E E Ii(x,t,i) t=1973 n=2 t=1973 i=m,k J = M,K ii(x '" = ' x = 2,..,15 E I'(t)E E E P(n,t,i) t=1973 t=1973 i=m,k n=2
9 8 i'(x,j) E E Ii(n,t,J) E E Il(x,t,i) t=1973 n=50 t=1973 i=m,k J. M,K ; x = 50,..,54 E I'(t) E E E Ii(n,t,i) t=1973 t=1973 i=m,k n=50 Innen hver av aldersgruppene år, år og år, er dessuten fordelingen av innvandrerne på ettårige alderslasser forutsatt uavhengig av alder E P(n,t,J) ^t=1973 n=1 1 i'(x,j) J = M,K 1976 ; x = 55,..,69 EP(t) 1 = 55 for x = 55,..,59 t= = 60 for x = 60,.., for x = 65,..,69 Det er sett bort fra innvandring av personer i alderen 70 år og over Diverse v øvrige endringer i modellens første trinn, vil vi nevne at vi har et nytt sett avrundingsrelasjoner. lle resultater i framsrivingen blir nå avrundet til heltall for neste framsrivingsår blir beregnet. vrundingsrelasjonene er lagd sli at avrundingsfeilene ie sal hope seg opp i samme region hveren når vi ser på alle aldre for ett gitt år, eller for samme region over flere år. vrundingsrelasjonene vil bli doumentert i et eget notat (Sorlie (1979)). 3. NEDBRYTING V FRMSKRIVINGEN FOR DE PRIMÆRE PROGNOSEREGIONENE TIL KOMMUNENIV 3.1. Oversit I annet trinn av framsrivingen blir tallene for hver av de primære prognoseregionene fordelt på de ommuner regionen omfatter. Tall for de primære prognoseregionene vil foreligge som resultat av forste trinn. Fordelingsprosessene er noe forsjellig for de forsjellige aldersgrupper, men er alle avstemt sli at sum av tall fra ommunene i en region vil stemme med det gitte tall for hele regionen for såvel vinner som menn i alle alderslasser. For 0-åringer og for alderslassene 50 år og over blir framgangsmåten den samme for beregningsalternativene med og uten flytting. Tallet på nyfødte, alderslassen 0 år, beregnes for hver ommune ved å anvende et sett av aldersspesifie frutbarhetsrater på de vinner som er bosatt i ommunen i et gitt år. Disse frutbarhetsratene stemmer ie helt overens med de ratene som brues for prognoseregionen i trinn 1. Derfor må tallene for 0-åringer i ommunen avstemmes, sli at summen av 0-åringer i ommunene stemmer med tallet for prognoseregionen under ett. For aldersgruppen 50 år og over er flyttingene av liten betydning. Her forutsettes derfor at nettoflyttingene og dødsfallene ie vil endre de enelte ommuners andel ay prognoseregionens befolning i en gitt alderslasse. En ommunes andel av f.es. 58-åringene et år, settes da li samme ommunes andel av 57-åringer året for. I beregningsalternativer uten flytting går vi fram på samme måte også for alderlassene mellom 0 og 50 år. I alternativer med flytting blir tall for alderslassene mellom 0 og 50 år beregnet ved at vi tar for oss de fire gruppene: menn og vinner 1-15 år, menn år, vinner år og menn og vinner år. For hver av disse gruppene beregnes tall for utgangen av et framsrivingsår ved å anvende en netto vestrate på antallet i gruppen ved årets begynnelse. Vestratene er beregnet på grunnlag av befolningsutvilingen i den enelte ommune i perioden , men blir justert sli at forsjellene i vestrater mellom ommunene i en prognoseregion reduseres med 7 prosent hvert år fra 1978 av, og sli at endringstallene for hver prognoseregion stemmer med dem som følger av beregningene på første trinn. Fordelingen på hver enelt alderslasse i
10 9 den enelte ommune finnes deretter ved å ta hensyn til de demografise endringsfatorene dødsfall, uflytting og innflytting. Mens nedbrytingen for 0-åringer og for aldersgruppen 50 år og over, og i alternativet uten flytting også for aldrene 1-49 år sjer på samme måte som i forrige framsriving, er framgangsmåten for aldrene 1-49 år i tilfellet med flytting helt ny. I besrivelsen som følger tener vi oss at vi ser på nedbrytingen for en gitt primær prognoseregion. Formlene er de samme for alle regioner. Noen regioner består av bare en ommune. For disse primære prognoseregionene er det selvsagt ie behov for noen nedbryting. I besrivelsen forutsetter vi derfor at det er to eller flere ommuner i regionen Symbolliste Kommune betegnes med fotsrift. Størrelser uten sli fotsrift gjelder for hele p.p.-regionen under ett. For øvrig er symbolene bygget opp analogt med symbolene til modellens 1.trinn. lder er definert som alenderår (t) minus fødselsår, (dvs. alder ved utgangen av året) og betegnes med indesen x. Vi har tre aldersgrupper i modellen; 1-15 år, år og år. Vi lar indesen z betegne aldersgruppe, og z_ l aldersgruppen forsjøvet ett år, dvs år, år og år. Når "aldersgruppe" (z eller z_ 1 ) innsettes for alder (x), sal symbolet gjelde alle aldre i aldersgruppen under ett. formlene er det som for brut bostaven J som indes for jønn. J an ta verdiene M (for menn) eller K (for vinner). i. Symboler som betegner antall personer L (x,t,m) er antall x år gamle menn i ommune den 31/12 i år t; x = 0,1,..,99. Den øvre aldersgruppen omfatter 'personer som er 99 år og eldre. L (x,t,k) er det tilsvarende tall for vinner. B (t) er antall levendefødte i år t i ommune. (x,t,m) er samlet avgang ved dødsfall og utflytting for ommune av menn i alder x i år t; X = 1,..,49. (x ' t,k) er den tilsvarende størrelse for vinner. I(x,t,M) er et anslag på brutto innflytting til p.p.-regionen av menn i alder x i år t; X = I(x,t,K) Tilsvarende anslag for vinner. I (z,t,m) er et anslag på brutto-innflytting til ommune av menn i aldersgruppe z i år t; z = 1,2,3. I (z,t,k) er tilsvarende anslag for vinner. ii. Symboler som betegner parametre f (x) er en frutbarhetsrate for vinner i alder x i ommune ; x = 15,..,44. (Dette er et annet sett frutbarhetsrater enn de som ble definert i framsrivingsmodellens forste trinn.) q(x,m) er dødsraten for menn i alder x; x = 1,..,49. Dette er de samme dødsratene som er brut i framsrivingens forste trinn. er tilsvarende rate for vinner. er utflyttingsrate for flytting ut av bostedsommunen for x år gamle menn i p.p.- regionen; x = 1,..,49. Denne raten er ie li den tilsvarende raten for samme p.p.-region i framsrivingens forste trinn, siden den omfatter flytting også mellom ommuner innen regionen.
11 10 er den tilsvarende raten for vinner. er utflyttingsrate for x år gamle menn i ommune ; x = 1,..,49. Omfatter innenlands flytting, også flytting til andre ommuner i samme p.p.-region, og utvandring. u (x,k) er tilsvarende rate for vinner. r (z,m) Årlig vestprosent i basisperioden for menn i ommune i aldersgruppe z; z = s 2,3. r (z,k) er tilsvarende vestprodusent for vinner. p (z,t,m) er justert vestprosent i år t for menn i ommune som tilhørte aldersgruppe z; z = 1,2,3. p (z,t,k) er tilsvarende vestprosent for vinner. m(z,t,m) er en orresjonsfator til vestprosentene for menn i aldersgruppe z i p.p.- regionen. m(z,t,k) er tilsvarende størrelse for vinner. Y dempningsfator. Forsjellene i vestprosenter mellom ommuner dempes med 100. (l -y) prosent pr. år. v(t,m) er antall 98-årige menn i p.p.-regionen i prosent av menn i alderen 98 år og eldre i år t. a (x,t,m) er ommune 's andel av p.p.-regionens befolning av menn i alder x i år t; X = 0,1,..,99. za,(x,t,m) = 1. " a (x,t,k) er den tilsvarende andel av vinnene Formler lternativ uten flyttin9 i. Fordelingen av null-åringer Forst gis et anslag på fødsler ut fra fødselsratene. 44 B (t+1) = E f (x).l (x-1 ' t,k) x=15 Hver ommunes andel av befolningen i alder null år settes så li andelen av fødslene. 8,(t+1) (12) a(0,t+1,j) " EB,(t+1) ; J = M ' K " I ligningen (12) har vi sett bort fra jønnsvotienten ved fødselen og dødeligheten for nullåringer av hvert jønn, siden disse fatorene er forutsatt a være lie for alle ommuner i hele landet. Det samme gjelder nivået på frutbarhetsratene, siden dette er justert med samme prosent i alle ommuner. Fordelingen av de andre aldersgruppene Også her vil vi benytte oss av at dødeligheten ie påvirer andelen av et fødselsull som bor i en ommune, siden dødeligheten pr. forutsetning er den samme i alle ommuner. Siden dødeligheten i tilfellet uten flytting er den eneste fator som påvirer størrelsen av en ohort etter at den først er født, blir derfor andelene av ullet som bor i hver av ommunene onstante. x = 1,2,..,98 (13) a(x,t+1,j). a (x-1,t,j); j = m,k
12 1 1 ldersgruppen 99 år og over ved utgangen av et år består dels av personer som var 98 år ved begynnelsen av året og som overlever, dels av de overlevende fra aldersgruppen 99 år og over i begynnelsen av året. Siden de to aldersgruppene ved begynnelsen av året an ha forsjellig fordeling på ommuner, er fordelingen av gruppen 99 år og over ved slutten av året bestemt som et veid gjennomsnitt av fordelingene til de to alderslassene ved begynnelsen av året. Vetene er satt li hver av de to aldersgruppenes andel av summen av befolningen i de to aldersgruppene ved begynnelsen av året. De samme vetene brues for alle ommunene i regionen, og det er ie foretatt noen orresjon på grunn av den ulie dødeligheten i de to aldersgruppene. Slie orresjoner ville ie spille noen rolle for resultatet. Vi har da: v(t+1,j) L(98,t,J) L(98,t,J) + L(99,t,J) ; j = M ' K (14) a(99,t+1,j) = v(t+1,j).a (98,t,J) + (1- (t+1,j)). (99,t,J); J = M,K Foletallet i hver ommune finnes så ved å ta det foletallet som allerede er beregnet for p.p.-regionen, og fordele på ommuner i samsvar med andelene ovenfor. (15) L(x,t+1,J) = (x,t+1,j).l(x,t+1,j). J = M ' K x = 0,1,.., lternativ med flytting a. Fordelingen av nullåringer og av personer i alderen 50 år og eldre Fordelingen av null-åringene sjer på samme måte som i alternativene uten flytting (jmf. formel (12)). Ved nedbrytingen forutsetter vi at flyttingen for personer i alderen 50 år og over ie vil påvire andelene av regionens befolning som bor i hver ommune. ndelene finnes dermed etter formel (13) og (14) for personer i alderen 50 år og over, mens foletallet finnes ved ligning (19). b. Fordelingen av personer i alderen 1-49 år i. Vestrater I det første framsrivingsåret er de justerte vestprosentene satt li de observerte vestprosentene i basisperioden pluss et orresjonsledd som sirer onsistens med tallene for p.p.-regionen fra 1.trinn i framsrivingen. (16a) p (z,1977,j) = r (z,j) + m(z,1977,j); jzt: IL 3 For de andre årene beregnes den justerte vestprosenten ut fra den tilsvarende prosenten året for, men med en dempningsfator og et nytt orresjonsledd. (16b) p1, ( Z =,t+1,j) = y.p (z,t,j) + m(z,t+1,v ) ; j = m9k Dempningsfatoren y er satt li 0,93. Setter vi inn fra høyresiden i ligning (16b) i differansen mellom de justerte vestprosentene for ommune i og ommune j, får vi: :p i (,t+1,j) - pj(z,t+1,j)] = Y[Pi( 'ton (t,j): Forsjellene mellom vestratene for to ommuner et år er altså 100(1 - y)% mindre enn forsjellen året for. Med tiden vil dermed vestprosentene for alle ommunene i en region nærme seg den felles vestprosenten for regionen som helhet.
13 12 Korresjonsfatorene regnes ut sli: (17a) m(z,t,j) - L(z,t,J) - (z,j).l( t = 1977 L(z_1,t-1,J) L(z_1,t-1,J) ; J = M,K z = 1,2,3 E y-p (z t-1 J).L (z,t-1 J) -1't L(z,t,J) - L(z t-1,j) (17b) m(z,t,j) - = L(z_ r t-1,j) L(z_1,t-1,J) M = J,K z = 1,2,3 Uttryet for orresjonsfatoren består av to ledd. Det første leddet svarer til vestraten for p.p.-regionen under ett for ohortene som tilhørte aldersgruppe z i år t (og z...1 i år t-1). Denne vestraten beregnes ut fra resultatene i framsrivingens første trinn. I det andre leddet er uttryet (y.p (z,t-1,j) den vestprosenten ommune ville hatt (ut fra formel 16), dersom det ie foreom noen orresjon. Det andre leddet er derfor vestprosenten for regionen basert på de ommunevise vestratene uten orresjon. Korresjonsfatoren settes li differansen, sli at vestprosenten for regionen, basert på de justerte vestprosentene, blir li den vesten som an beregnes i framsrivingens første trinn. ii. Samlet avgang ved dødsfall og utflytting Summen av dødsfall og antall utflyttere finnes ved å multiplisere foletallet ved inngangen av året med de tilhørende døds- og utflyttingsrater: J = M,K (18) (x,t+1,j) = L (x-1,t,j)q(x,j) + u(x,j): x = 1,..,49 iii. nslagene på brutto-innflytting Netto-vesten i tallet på personer i hver ohort er li netto-innflyttingen minus dødsfall. Hvis vi derfor legger sammen tallet for netto tilvest og tallet for samlet avgang gjennom dødsfall og utflytting, får vi tall for brutto-innvandring. (19) I(x,t+1,J) = [L(x,t+1,J) - L(x-1,t,J): E (x,t+1,j) ' J x = M,K I formel (19), som gjelder hele regionen og hver enelt årslasse (x), unne vi bygge anslaget for netto-vesten på de tallene som er beregnet i 1.trinn av framsrivingsmodellen. I anslaget for innflytting til hver ommune bruer vi isteden de justerte vestratene for hver av de tre aldersgruppene,(z). (20) I(z,t+1,J) = L(z_i,t,J).p z,t+1,j) + (z,t+1,j); j z = M,K Det er vist i avsnitt at anslagene på brutto-innvandring etter de to formlene (19) og (20) er onsistente, dvs. EI J M,K (z,t+1,j) = E I(x,t+ 1,J); z = xcz 1 2,3 Vi må nevne at det fins regioner der anslaget på brutto-innvandringen I(x,t,J) har blitt negativt et stye ut i framsrivingsperioden. Tallverdien tilsvarer da imidlertid bare ca. 1 person. Vi har ie foretatt oss noe spesielt i disse tilfellene. Tolningen av variablen I(x,t,J) som brutto-innvandring faller naturligvis sammen i slie tilfelle. Dette tolningsproblemet er nærmere drøftet i avsnitt
14 13 iv. De nye bestandene for aldrene 1-49 år i alternativ med flytting Foletallet finnes ved å ta utgangspunt i størrelsen på samme ohort ved inngangen av året, tree fra avgangen ved dødsfall og utflytting, og til slutt legge til brutto-innflyttingen. Bruttoinnflyttingen er her beregnet som en andel av brutto-innflyttingen for hele aldersgruppen z som eneltalderen tilhører. ndelen avspeiler aldersfordelingen for den beregnede innflyttingen til samtlige ommuner i regionen som helhet. (21) L(x,t+1,J) = L (x-1,t,j) - (x,t+1,j) x,t+1,j J = M,K I (z,,j) t+1 z,t+,j x = 1,2,..,49 x_c z Z = 1,2,3 Som vist i avsnitt 3.5.4, følger det av modellen at for aldersgruppene z under ett, gjelder folgende sammenheng: (22) L(z,t+1,J) = L (z_ i,t,j) P (z,t+1,j): ; =,",, For de tre aldersgruppene under ett framsrives altså befolningen ved hjelp av de justerte vestprosentene. Beregningen av tall for ut- og innflytting vil imidlertid medføre en viss aldersomfordeling innen aldersgruppen, i forhold til hva vi ville fått ved å framsrive også hver eneltalder med den justerte vestprosenten for aldersgruppen under ett Rateberegninger i. Fødselsrater Fødselsratene er regnet ut,for samme basisperiode ( ), og etter samme metode som fødselsratene i framsrivingens 1.trinn. Regioninndelingen er forsjellig, idet ratene i modellens 1.trinn ble beregnet for de primære prognoseregionene (noen regioner ble slått sammen i beregningene). Ratene til modellens 2.trinn er beregnet for et sett frutbarhetsregioner, som ble laget spesielt for denne framsrivingen. Grupperingen er doumentert og drøftet i Rideng (1978). Grensene for frutbarhetsregionene rysser p.p.-regiongrensene, sli at vi får tatt hensyn til antatte frutbarhetsforsjeller innen p.p.-regionen. Vestrater De observerte vestratene er beregnet sli: r (z,j) E [L (z,t,j) - L (..1,t-1 01)] t=1973 J=M,K J = M,K 1976 z = 1,3 E E L (z,t-1,j) -1 t=1973 J=M,K r (z J _ E [L (z,t,j) - L (z_ r t-1,j): t=1973. J = M,K 1976 ' z = 2 E L (z,t-1,j) -1 t=1973 For aldersgruppene 1-15 år og r er det altså regnet samme vestrate for begge jønn. Beregningene av vestraten baserer seg på endringen (ved dødsfall og netto-flytting) for de samme ohortene fra et år til det neste. Disse vestratene atsiller seg derfor fra de vestratene som ble benyttet i forrige framsriving, som også ble påviret av variasjoner på størrelsen av årsullene.
15 14 Flytterater Til bru i nedbrytingsmodellen er det beregnet et nytt sett rater for p.p.-regionene under ett [u(x,t,j):i. Beregningsmåten tilsvarer beregningen av flytterater i modellens 1.trinn. Forsjellen er at de flytteratene som brues i nedbrytingsmodellen også omfatter flyttinger innen den primære prognoseregi onen. Det er dessuten beregnet et sett flytterater for ommunene. Ratene er beregnet for en ommunegruppering som er helt forsjellig fra inndelingen i primære prognoseregioner. Beregningsmåten tilsvarer beregningen av flytterater for p.p.-regionene, ved at summen av utflytterne for alle ommunene i en ommunegruppe i basisperioden ( ) settes i forhold til summen av befolningens størrelse ved inngangen til hvert av disse årene. Ratene beregnes separat for hvert jønn og (ett-årige) alderslasse, og inluderer utflytting bade til andre ommuner, inludert andre ommuner i samme primære prognoseregion, og flytting til utlandet. Den ommunegrupperingen som er anvendt tar i utgangspuntet site på å omme fram til grupper av ommuner som er mest mulig homogene med hensyn på flytting. Gruppene, 22 i alt, danner ie sammenhengende regioner. Ofte vil de primære prognoseregionene, som er tent som funsjonelle regioner, bestå av ommuner som tilhører ulie ommunegrupper. Vi får dermed på en måte tatt hensyn til for- sjeller i flytteativiteten mellom ommunene i de primære prognoseregionene. Kommunegrupperingen er utvilet som en del av prosjetet "justerte flytterelasjoner", og er doumentert og drøftet i arbeidsrapport nr. 1 fra dette prosjetet (Stordahl (1976), apittel 5 og vedlegg 1 og 2). Flytteratene er normert sli at et veid gjennomsnitt av de normerte ratene, med befolningsandelene pr. 31/ som veter, blir li raten for regionen under ett. Betegner vi de unormerte ratene med u (x,j), får vi: u (x,j) = u (x,j) + V(x,J), der V(x,J) finnes ved ligningen L,(x,1976,J) (23) E[u,(x,J) + V(x,J): L(x 1976 J) = u(x 'j) 3.5. En del egensaper ved nedbrytingsmodellen Konsistensegensaper Vi sal her vise at framsrivingstallene for ommunene virelig summerer seg opp til de tilsvarende tall for regionen under ett, som er beregnet i framsrivingens 1.trinn. a) For null-åringenes del ser vi dette uten videre av ligning (12). III/ For andre aldre i alternativ uten flytting er andelene li observerte andeler for samme ohort ved utgangen av 1976 for de som var fodt på det tidspuntet. For yngre årslasser er andelen li andelen av nullåringer for et år i framsrivingsperioden. I begge tilfelle må andelene summere seg til en. b) For flyttealternativene må det vises at framsrivingstallene er onsistente for alderen 1-49 år. For å vise dette vil vi -Forst vise onsistensen mellom de to typene beregninger ay tall for brutto-innflytting. i. Konsistens i anslagene for brutto-innflytting Vi vil nå vise formelen som ble gjengitt i pt. 3.3.iii. (24)EI,(z,t+1,J) = I(z,t+1,J), der I(z,t+1,J) = E I(x,t+1,J) J = M,K ' xez z = 1,2,3 innsetting fra (20) gir: EI (z t+1,j) = EL (z,t,j)-p (z,t+1,j) + E,(z,t+1,J) -1
16 15 setter vi inn uttryet for den justerte vestprosenten fra ligning (16b), får vi: EI,(z,t+1,J) = zl, ' K -1 (z,ton.y.p (z,t,j) + m(z,t+1 03).zL ii (z_ i,t,j) + E(z,t+1,J) Innsetting for m(z,t+1,j) fra ligning (17b) gir d Ey-p,(z,t,J).L(z_i,t,J-) L(z,t+1,J)L(z._,t,j) N EI (z,t+1,j) = EL (z 1,t,J).y-p (z,t,j) + L(z 1,t,J L z 1,t,J + (z,t+1,j) Ordning gir nå, sammen med ligning (19): EI,(z,t+1,J) = L(z,t+1,J) L( 1,t,J) + E (,t 1,J) = I(Z,t+1,J) = z I(x,t+1,J) ' XeZ Konsistens i anslagene på befolningen Vi har fra ligning (21): I(x,t+1,J EL (x,t+1,j) = EL,(x-1,t,J) - E (x,t+1,j) +,- z,t+,j ' I (z,t+1,j) I siste ledd an vi her sette inn fra ligning (24) og får: EL,(x,t+1,J) = L(,t,J) E,(x,t+1,J) + I(x,t+1,J) ' ' Innsetting for I(x,t+1,J) fra ligning (19) gir nå: EL (x,t+1,j) = L(x-1,t,J) - E (x ' t+1,j) + L(x,t+1,J) - L(x-1,t,J) + E,(x,t+1,J) ' det vil si EL (x,t+1,j) = L(x,t+1,J) som beregnet fra 1.trinn i modellen. K c) Til slutt vil vi nevne at avrundingsrelasjonene i nedbrytingsprogrammet sirer onsistens også av de avrundete tallene. vrundingen er besrevet av Sorlie (1979). Ill/ Sammenhengen mellom framsrivingen 1977 uten flytting og en framsriving uten flytting direte på ommunenivå I dette apitlet sal vi se nærmere på sammenhengen mellom framsrivingen uten flytting i 1977 og en tent alternativ framsriving. Denne alternative framsrivingen er også uten flytting og med samme dodelighetsforutsetninger. Framsriving foregår direte for hver ommune, og som frutbarhetsrater benyttes de frutbarhetsratene som brues i nedbrytingsmodellen (rater for frutbarhetsområdene), justert til samme nivå som det alternativ i 1977-framsrivingen vi sammenligner med. v resonnementet i avsnitt fremgår det at tallene i de to framsrivingene må være lie for alle ohorter som var fodt i 1976 eller for. I det forste framsrivingsåret gjelder dette alle sm er ett år ellereldre,og i det siste framsrivingsåret (2 000 for ommunetall), gjelder det alle i alderen 24 år og over. I de andre aldrene blir antallet i de to framsrivingene lit hvis (og bare hvis) antall fodte i de to alternativene er lie stort i hver ommune. I den tente framsrivingen som foretas direte på ommunenivå, lar vi "B(t) være antall fodte i ommune, i år t. Siden frutbarhetsratene som ligger ba fodselstallet-5 (t) er proporsjonale med de som er brut i nedbrytingsprogrammet, har vi fra formel (12):
17 16 B (t) B (t) a " (0 t J - EBL.(t) 14.\ "L) Kaller vi antall fødsler, beregnet i 77-framsrivingens første trinn, for BM og det tilsvarende tall for ommune, beregnet i annet trinn for B (t), har vi: B (t) = Ei(t). a (0,t,J) = Š (t).;(t);(t) - (t) ntallet fødte er altså lit bortsett fra en orresjonsfator som angir forholdet mellom totalt antall fødsler i regionen beregnet i modellens første trinn, og totalt antall fødsler i ommunene i regionen, beregnet i den tente framsrivingen direte på ommunenivå Tolnin s roblemer for ansla ene for brutto-innflytting i nedbr tin smodellen Vi sal nå drøfte muligheten for at anslaget på brutto-innflyttingen til alle ommunene i p.p.-regionen under ett an bli negativ. Brutto-innflyttingen beregnes sli: Ill/ (19) I(x,t+1,J) = [L(x,t+1,J) L(x-1,t,J) -1 + E (x t+1,j). J = M ' K - x = 1,..,49 Her er leddet i haeparentesen li netto endring i størrelsen av en ohort menn eller vinner fra ett år til det neste i regionen. Dette er det samme som netto-innflyttingen til regionen minus dødsfall. Siden dødsfallene blir lagt til igjen i 2.1edd, blir anslaget på brutto-innflyttingen ie påviret av dødsfallene. Vi ser at negativ størrelse på I(x,t+1,J) bare an foreomme i regioner med netto-utflytting. Vi betegner nå størrelser fra framsrivingens forste trinn med hatt over symbolet. I disse størrelsene er flytting mellom ommuner i den primære prognoseregionen ie medregnet. Vi har da: J M K I(x,t+1,J) = i(x,t+1,j) 6(x,t+1,J) - b(x t+1 J) + E (x t+1,j). ' x = 1,..,49 Her er altså I(...), U(...) og D(...) de tallene for henholdsvis innflyttere,utflyttere og døde som ble beregnet for regionen i framsrivingens forste trinn. Innsetting for (...) og U(...) og sammentreing gir: 411/ I(x,t+1,J) = i(x,t+1,j) - U(x,J).L,t,J) + Eu u (x,j).l (x-1,t,j Vi definerer nå i5(x,j) = u(x,j) - U(x,J). Som tidligere forlart blir da u(x,j).l(x-1,t,j) et anslag på flytting mellom ommunene innen p.p.-regionen. Innsetting gir da: (25) I(x,t+1,J) = i(x,t+1,j) + i5(x,j),. L(x-1,t,J) + E[u (x,j) u(x,j)=1.l (x-1,t,j) Her er de to første leddene i uttryet positive, eller ihvertfall ie-negative. Fortegnet avhenger dermed av det siste leddet. v ligning (23) får vi for t -= 1976 dvs. Eu 6 (x,j). L (x,1976,j) = u(x,j).l(x,1976,j) " ED I,(x,J) - u(x,j)1.l (x,1976,j) = 0 " For alle regioner må derfor anslaget for brutto-innflytting i det første framsrivingsåret bli posi-
18 17 tivt. Siden utflyttingsraten for regionen, u(x,j), er et veid gjennomsnitt av ratene for ommunene, vil det i alle regionene være minst en ommune som har lavere utflyttingsrate enn gjennomsnittet. Hvis slie ommuner etter hvert får en øende andel av befolningen i regionen, blir siste ledd i (25) negativt. (En ommune øer sin andel av regionens befolning eller lavere netto-utflytting (prosentvis) enn gjennomsnittet i regionen.) I et par tilfelle har dette blitt så framtredende at hele anslaget på brutto-innflyttingen er blitt negativt. Dette an som sagt bare hende for regioner som har netto utflytting ifølge beregningene i 1.trinn av framsrivingen. Vi får nemlig: d.v.s i(x,t+1) < 0 betyr i(x,t+1,j) - u(x,j)l(x-1,t,j) + Eu,(x,J)L (x-1,t,j) < 0 ' Eu,(x,J)L (x-1,t,j) < u(x,j)l(x-1,t,j) i(x,t+1,j) ' Her er venstre ledd positivt og høyre ledd er netto-utflytting fra p.p.-regionen iflg. trinn 1. U- liheten betyr også at utflyttingsratene for enelt-ommunene, u (x,j), ie er store no til å dee selv den netto-utflyttingen fra regionen som er beregnet i 1.trinn av framsrivingen. I beregningene betyr dette bare at vi i 2. av framsrivingene må redusere foletallet i ommunene ut over det som følger av ratene a (x,t,j) for den alderslassen det gjelder, istedet for å øe det med brutto-innflyttingsraten.. Dette unne vært unngått ved a justere flytteratene analogt med formel (23) hvert år i framsrivingsperioden. Dette har vi ie gjort, siden tilfellene med de negative anslag på brutto-innflyttingen foreom relativt sjelden, og da bare med ubetydelig tallverdi. En må også huse på at betegnelsen "brutto-innvandring" egentlig er en tolning av en størrelse som beregnes internt i data-. masinen. Det er denne tolningen som bryter sammen når anslaget på brutto-innvandringen blir negativt, og ie programmet i seg selv Nærmere om betydningen av anslagene for inn- og utflytting i nedbrytingsmodellen Vi sal først mere oss, at inn- og utflyttingstallene ie har noen betydning for størrelsen på befolningen i de aldersgruppene vi har definert (z = 1,2,3). Summerer vi befolningen i en ommune over alle aldre som inngår i aldersgruppen, får vi fra ligning (21): L (z,t+1,j) = L (z_ l,t,j) (z,t+1,j) + I (zst+1,j); j = M ' K z = 1,2,3 Her har vi benyttet oss av at I(x,t+1,J) = I(z,t+1,J) pr. definisjon. xez Setter vi inn for brutto-innflyttingen fra formel (20), får vi L (z,t+1,j) = L (z_ r t,j) - (z,t+1,j) + L (z_r t,j).p (z,t+1,j) + (z,t+1,j) Dette gir: L (z,t+1,j) = L (z_ i,i,j).: p(z,t+1,j)] Vi har dermed utledet formel (22).
19 18 Beregningene av ut- og innflyttere får følgelig etter dette bare betydning for alderssammensetningen innen aldersgruppene. Dersom alle eneltaldrene ble framsrevet med de justerte vestratene, ville forholdet mellom ohortenes størrelse vært onstant, og bare endret seg ved sifte av aldersgruppe. I forhold til dette får vi en viss aldersomfordeling av befolningen innen en aldersgruppe ved at aldersfordelingen for innflytterne an avvie fra den for utflytterne for den enelte ommune. Dette syldes i første ree at innflytternes fordeling på enelt-aldre innenfor aldersgruppen er satt li gjennomsnittet for flyttere i den primære prognoseregionen i alle ommunene. Tener vi oss at en ommune har et "ha" i aldersfordelingen, f.es. spesielt få 43-åringer i utgangsbestanden som andel av befolningen år samme år i forhold til andre aldre i samme ommune og. i forhold til tilsvarende andel i andre ommuner i regionen, vil vi få en tendens til at andelen personer i dette ullet etterhvert nærmer seg det "normale" for ommunen og regionen. Siden ullet er relativt lite, vil det bli relativt få personer i avgang ved utflytting og dødsfall. Dette vil ritigno påvire beregningen av antall innflyttere for denne alderen i regionen, og for denne aldersgruppen i ommunen. Begge disse beregningene er imidlertid summer av flere størrelser, sli at den relative betydningen av "haet" på hver av summene blir av mindre betydning. På den ene siden vil altså ommunen ha "unormalt" få personer i avgang for dette ullet, på den andresiden vil det motta et "normalt" antall personer som innflyttere. "Haet" i aldersfordelingen vil dermed etterhvert jevnes ut Tillem nin er ved alternativ nedbr ting i samarbeid med f lene Vi har her tent oss å be fylenes utbyggingsavdelinger om alternative vestrater for de ommunene der fyles-administrasjonen mener at de observerte vestratene gir et dårlig grunnlag for framsrivingen. Siden de primære prognoseregioliene i flere tilfelle gir en for snever ramme for de justeringene som ønses, vil vi tilby muligheter for justeringer innen fylet. Dette betyr at summen av foletallet for hver alder og hvert jønn for hele fylet blir liggende fast (li fyles-tallene i alt L 1 77), mens fordelingen ommunene imellom lar seg påvire. Tenis gjør vi dette ved å anvende nedbrytingsprogrammet på tall for det enelte fylet, i- stedet for på tall for den enelte p.p.-region. Utgangspuntet er tall fra første trinn i framsrivingen aggregert fra prognoseregion-nivå til fylesnivå. Vestprosentene blir behandlet på en, litt annen måte enn i den ordinære nedbrytingen for å ta hensyn til justeringene som er foreslått. Tidshorisonten blir fram til i. jberegning av alternative vestrater Til bru i nedbrytingen trenger vi vestrater for hver av de fire persongruppene 1-15 år (begge jønn), år menn, år vinner og år (begge jønn), i hvert år fram til Trolig blir det for mye å be fylene fylle ut alle vestratene i en sli tabell, med 52 celler for hver ommune. I stedet har vi bedt fylene gi alternative vestrater for aldersgruppen år under ett for hvert år i perioden. Differansen mellom den alternative raten og raten i basisperioden vil bli lagt til vestratene (for basisperioden) i hver av aldersgruppene. Justering av de alternative vestratene De alternative vestratene blir justert analogt med vestratene i den ordinære framsrivingen, sli at ommunetallene summerer seg opp til tallene for fylene. Noen dempningsfator regner vi ie med. (y = 1,0). Dette syldes at fylene oppgir alternative vestrater for hvert år i perioden. Dersom fylene ønser å bygge inn en utjamning av vesten for ommunene i fylet, an de gjøre dette selv. Formelt an den justerte vestraten defineres ved ligning (16a) og (17a), hvor r (z,j) nå står for den alternative vestraten, og formelen gjelder alle år (t) fram til og med 1990.
20 19 iii. Litt om virningen av å justere vestratene for en ommune Det er to ting vi må huse på som ansje ie er selvsagte. For det forste vil justeringsmeanismene sorge for at foletallet for fylene ie endres. Oer vi vestprosentene for en ommune isolert sett, vil denne ommunen få en ot andel av fylets befolning i de atuelle alderslassene. Dette vil sje på beostning av de andre ommunene i fylet, som da vil få senet sin andel av befolningen tilsvarende. For det andre vil justeringene omfatte også personer i en del andre aldersgrupper enn 1-49 år. I og med at en ommunes andel av 49-åringene endres, vil denne endringen også gjelde andelen 50-åringer året etter, 51-åringer året etter der, osv. I det siste året, 1990, vil alle ull som da er 62 år og yngre were berørt av omfordelingene. Det er imidlertid ie mulig å endre fordelingen av personer som er 49 år og eldre ved utgangen av 1977 (eller eldre enn 62 år ved utgangen av 1990). Fordelingen av de som blir fodt i løpet av et år vil endres som følge av en endret fordeling av vinner i fødedytig alder. Ser vi på en ommune som har fått øt sin andel av befolningen i alderen år tre år på rad, så vil antallet 1-åringer ved utgangen av det tredje året ha øt av to grunner: a: (Den ujusterte) vestraten for personer i aldersgruppen 1-15 år er øt med lie mange prosentpeng som den ujusterte vestraten for åringene (jmfr. pt.i). Dette vil medfør6 øt antall ettåringer, selv med samme antall null-åringer ved årets begynnelse. b: ntall null-åringer ved begynnelsen av det tredje året er ot. Siden ommunen ved slutten av det første av de tre årene har fått øt antall vinner i alderen år, vil dette i det andre året medføre flere fødsler, og dermed flere null-åringer ved slutten av det andre året.
Kort om forutsetninger for befolkningsprognosen
 Kort om forutsetninger for befolkningsprognosen Nettoflytting fordeles automatisk av modellen på alder og kjønn ved hjelp av en glattefunksjon (Rogers-Castro). Befolkningsutviklingen i PANDA bestemmes
Kort om forutsetninger for befolkningsprognosen Nettoflytting fordeles automatisk av modellen på alder og kjønn ved hjelp av en glattefunksjon (Rogers-Castro). Befolkningsutviklingen i PANDA bestemmes
Kort om forutsetninger for befolkningsprognosen
 Kort om forutsetninger for befolkningsprognosen Nettoflytting fordeles automatisk av modellen på alder og kjønn ved hjelp av en glattefunksjon (Rogers- Castro). Befolkningsutviklingen i PANDA bestemmes
Kort om forutsetninger for befolkningsprognosen Nettoflytting fordeles automatisk av modellen på alder og kjønn ved hjelp av en glattefunksjon (Rogers- Castro). Befolkningsutviklingen i PANDA bestemmes
Definisjon: I en BEFOLKNINGSPROGNOSE forsøker en å basere seg på realistiske og plausible forutsetninger når det gjelder vekstfaktorene "FORECAST"
 BEFOLKNINGSFRAMSKRIVINGER Definisjon: En BEFOLKNINGSFRAMSKRIVING defineres som en beregning om den fremtidige befolkningen (størrelse, alderssammensetning, utvikling osv.) basert på visse antakelser for
BEFOLKNINGSFRAMSKRIVINGER Definisjon: En BEFOLKNINGSFRAMSKRIVING defineres som en beregning om den fremtidige befolkningen (størrelse, alderssammensetning, utvikling osv.) basert på visse antakelser for
Om Fylkesprognoser.no. Definisjoner
 1 Om Fylkesprognoser.no Fylkesprognoser.no er et samarbeidsprosjekt mellom fylkeskommunene som deltar i Pandagruppen. Denne gruppen eier Plan- og analysesystem for næring, demografi og arbeidsmarked (PANDA).
1 Om Fylkesprognoser.no Fylkesprognoser.no er et samarbeidsprosjekt mellom fylkeskommunene som deltar i Pandagruppen. Denne gruppen eier Plan- og analysesystem for næring, demografi og arbeidsmarked (PANDA).
Kort om forutsetninger for befolkningsprognosen
 Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Modell for befolkningsprojeksjoner for norske regioner. av Eivind Giij e x )
 IO 68/15 Oslo, 23. juli 1968 Modell for befolningsprojesjoner for norse regioner av Eivind Giij e ) Arbeidsdoument til Nordis demografis symposium i Mattby, Finland, 14. - 16. august 1968. INNHOLD I. Innledning
IO 68/15 Oslo, 23. juli 1968 Modell for befolningsprojesjoner for norse regioner av Eivind Giij e ) Arbeidsdoument til Nordis demografis symposium i Mattby, Finland, 14. - 16. august 1968. INNHOLD I. Innledning
BEFOLKNINGSFRAMSKRIVINGER ECON 1730
 BEFOLKNINGSFRAMSKRIVINGER ECON 1730 Definisjon: En BEFOLKNINGSFRAMSKRIVING defineres som en beregning om den fremtidige befolkningen (størrelse, alderssammensetning, utvikling osv.) basert på visse antakelser
BEFOLKNINGSFRAMSKRIVINGER ECON 1730 Definisjon: En BEFOLKNINGSFRAMSKRIVING defineres som en beregning om den fremtidige befolkningen (størrelse, alderssammensetning, utvikling osv.) basert på visse antakelser
Kort om forutsetninger for befolkningsprognosen
 Kort om forutsetninger for befolkningsprognosen Nettoflytting fordeles automatisk av modellen på alder og kjønn ved hjelp av en glattefunksjon (Rogers-Castro). Befolkningsutviklingen i PANDA bestemmes
Kort om forutsetninger for befolkningsprognosen Nettoflytting fordeles automatisk av modellen på alder og kjønn ved hjelp av en glattefunksjon (Rogers-Castro). Befolkningsutviklingen i PANDA bestemmes
Slik framskriver SSB befolkningen i kommunene. Marianne Tønnessen, Statistisk sentralbyrå
 1 Slik framskriver SSB befolkningen i kommunene Marianne Tønnessen, Statistisk sentralbyrå mto@ssb.no 1 SSBs modeller for befolkningsframskriving BEFINN BEFREG Egen liten modell som framskriver innvandringen
1 Slik framskriver SSB befolkningen i kommunene Marianne Tønnessen, Statistisk sentralbyrå mto@ssb.no 1 SSBs modeller for befolkningsframskriving BEFINN BEFREG Egen liten modell som framskriver innvandringen
Homogenitet av grad 1; makro og lang sikt, rollen til frikonkurranse
 Chapter 3 Solow-modellen Forsjell mellom land i apital per arbeider Kapitalens rolle i) Er produtiv ii) Blir produsert; avveining forbru investering iii) Gir avastning iv) Bærer av tenologi v) Blir slitt
Chapter 3 Solow-modellen Forsjell mellom land i apital per arbeider Kapitalens rolle i) Er produtiv ii) Blir produsert; avveining forbru investering iii) Gir avastning iv) Bærer av tenologi v) Blir slitt
Kort om forutsetninger for befolkningsprognosen i PANDA. Kort om middelalternativet i SSBs framskrivning av folketall
 Kort om forutsetninger for befolkningsprognosen i PANDA Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Kort om forutsetninger for befolkningsprognosen i PANDA Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
d) Poenget er å regne ut terskeltrykket til kappebergarten og omgjøre dette til en tilsvarende høyde av en oljekolonne i vann.
 Sisse til løsning Esamen i Reservoarteni 3. juni, 999 Oppgave a) Kapillartry er differansen i try mellom to faser på hver side av den infinitesimale overflaten som siller fasene. Det følger av en minimalisering
Sisse til løsning Esamen i Reservoarteni 3. juni, 999 Oppgave a) Kapillartry er differansen i try mellom to faser på hver side av den infinitesimale overflaten som siller fasene. Det følger av en minimalisering
Normalfordeling. Høgskolen i Gjøvik Avdeling for teknologi, økonomi og ledelse. Statistikk Ukeoppgaver uke 7
 Ueoppgaver i BtG207 Statisti, ue 7 : Normalfordeling. 1 Høgsolen i Gjøvi Avdeling for tenologi, øonomi og ledelse. Statisti Ueoppgaver ue 7 Normalfordeling. Oppgave 1 Anta Z N(0, 1), dvs. Z er standard
Ueoppgaver i BtG207 Statisti, ue 7 : Normalfordeling. 1 Høgsolen i Gjøvi Avdeling for tenologi, øonomi og ledelse. Statisti Ueoppgaver ue 7 Normalfordeling. Oppgave 1 Anta Z N(0, 1), dvs. Z er standard
Cobb - Douglas funksjonen ( ), Kut Wicksell, 1893, doktoravhandling,
 Chapter 3 Solow-modellen Forsjell mellom land i apital per arbeider Kapitalens rolle Produtfunsjonen Y F( K, L), F F F F F K K L L K L 0, 0, 0, 0, 0 F( zk, zl) uy, u z: øende salautbytte u z:onstant salautbytte
Chapter 3 Solow-modellen Forsjell mellom land i apital per arbeider Kapitalens rolle Produtfunsjonen Y F( K, L), F F F F F K K L L K L 0, 0, 0, 0, 0 F( zk, zl) uy, u z: øende salautbytte u z:onstant salautbytte
Oppgaver i kapittel 1 - Løsningsskisser og kommentarer Lærebok:
 Oppgaver i apittel - Løsningssisser og ommentarer Lærebo:.6 Vitig oppgave, viser hvordan ree-summer an tilnærmes med integraler. Atuelt hvis vi har formelen for n te ledd, men ie har noen summeformel.
Oppgaver i apittel - Løsningssisser og ommentarer Lærebo:.6 Vitig oppgave, viser hvordan ree-summer an tilnærmes med integraler. Atuelt hvis vi har formelen for n te ledd, men ie har noen summeformel.
MODELL FOR REGIONALE BEFOLKNINGSFRAMSKRIVINGER
 RAPPORTER FRA STATISTISK SENTRALBYRA 85/7 MODELL FOR REGIONALE BEFOLKNINGSFRAMSKRIVINGER AV ARNE RIDENG, KNUT Ø. SØRENSEN OG KJETIL SØRLIE STATISTISK SENTRALBYRA OSLO - KONGSVINGER 1985 ISBN 82-537-2162-5
RAPPORTER FRA STATISTISK SENTRALBYRA 85/7 MODELL FOR REGIONALE BEFOLKNINGSFRAMSKRIVINGER AV ARNE RIDENG, KNUT Ø. SØRENSEN OG KJETIL SØRLIE STATISTISK SENTRALBYRA OSLO - KONGSVINGER 1985 ISBN 82-537-2162-5
SEPTEMBER 2016 FET KOMMUNE PLANFORUTSETNINGER FOR KOMPAS-ANALYSER
 SEPTEMBER 2016 FET KOMMUNE PLANFORUTSETNINGER FOR KOMPAS-ANALYSER ADRESSE COWI A/S Kobberslagerstædet 2 1671 Kråkerøy TLF +47 02694 WWW cowi.no SEPTEMBER 2016 FET KOMMUNE PLANFORUTSETNINGER FOR KOMPAS-ANALYSER
SEPTEMBER 2016 FET KOMMUNE PLANFORUTSETNINGER FOR KOMPAS-ANALYSER ADRESSE COWI A/S Kobberslagerstædet 2 1671 Kråkerøy TLF +47 02694 WWW cowi.no SEPTEMBER 2016 FET KOMMUNE PLANFORUTSETNINGER FOR KOMPAS-ANALYSER
Kort om forutsetninger for befolkningsprognosen
 Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Førsteordens lineære differensiallikninger
 Førsteordens lineære differensiallininger Begrepet førsteordens lineære differensiallininger er ie sielig definert i Sinus R. Denne artielen omhandler det temaet. En førsteordens lineær differensiallining
Førsteordens lineære differensiallininger Begrepet førsteordens lineære differensiallininger er ie sielig definert i Sinus R. Denne artielen omhandler det temaet. En førsteordens lineær differensiallining
Om Fylkesprognoser.no. Definisjoner
 1 Om Fylkesprognoser.no Fylkesprognoser.no er et samarbeidsprosjekt mellom fylkeskommunene som deltar i Pandagruppen. Denne gruppen eier Plan- og analysesystem for næring, demografi og arbeidsmarked (PANDA).
1 Om Fylkesprognoser.no Fylkesprognoser.no er et samarbeidsprosjekt mellom fylkeskommunene som deltar i Pandagruppen. Denne gruppen eier Plan- og analysesystem for næring, demografi og arbeidsmarked (PANDA).
Obligatorisk oppgave 4 i INF4400 for Jan Erik Ramstad
 Obligatoris oppgave i INF for Jan Eri Ramstad Jan Eri Ramstad Institutt for Informati Universitetet i Oslo janera@fys.uio.no. Mars6 6. april Bagrunn Worst case transient simulering NAND port Oppgave I
Obligatoris oppgave i INF for Jan Eri Ramstad Jan Eri Ramstad Institutt for Informati Universitetet i Oslo janera@fys.uio.no. Mars6 6. april Bagrunn Worst case transient simulering NAND port Oppgave I
R Differensialligninger
 R - 6.0.05 - Differensialligninger Løsningssisser Oppgave Løs differensialligningene y x y b) y y x c) y 8y 7y 0 Separabel: y y x y dy xdx y x C y x 4 C y C x 4 Da ligningen er ulineær, bør vi også se
R - 6.0.05 - Differensialligninger Løsningssisser Oppgave Løs differensialligningene y x y b) y y x c) y 8y 7y 0 Separabel: y y x y dy xdx y x C y x 4 C y C x 4 Da ligningen er ulineær, bør vi også se
STATISTISK SENTRALBYRÅS BEFOLKNINGSPROGNOSEMODELL VED DE REGIONALE FRAMSKRIVINGER 1975
 ARTIKLER FRA STATISTISK SENTRALBYRÅ NR. 80 STATISTISK SENTRALBYRÅS BEFOLKNINGSPROGNOSEMODELL VED DE REGIONALE FRAMSKRIVINGER 1975 Av Knut Ø. Sørensen THE POPULATION PROJECTION MODEL OF THE CENTRAL BUREAU
ARTIKLER FRA STATISTISK SENTRALBYRÅ NR. 80 STATISTISK SENTRALBYRÅS BEFOLKNINGSPROGNOSEMODELL VED DE REGIONALE FRAMSKRIVINGER 1975 Av Knut Ø. Sørensen THE POPULATION PROJECTION MODEL OF THE CENTRAL BUREAU
MA1301/MA6301 Tallteori Høst 2016
 Norges tenis naturvitensapelige universitet Institutt for ateatise fag MA/MA6 Tallteori Høst 6 a Vi starter ed å sjee at liheten steer for n. Vi har at i. Heldigvis er (, så vi ser at påstanden steer i
Norges tenis naturvitensapelige universitet Institutt for ateatise fag MA/MA6 Tallteori Høst 6 a Vi starter ed å sjee at liheten steer for n. Vi har at i. Heldigvis er (, så vi ser at påstanden steer i
Kort om forutsetninger for befolkningsprognosen
 Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Oslo vokser #1 Hva kjennetegner befolkningen i Oslo? Kjetil Sørlie (NIBR) og Inger Texmon (SSB) Norsk Form, 16. februar 2012
 Oslo vokser #1 Hva kjennetegner befolkningen i Oslo? Kjetil Sørlie (NIBR) og Inger Texmon (SSB) Norsk Form, 16. februar 2012 Oslofolk» Hvem er det? Oslofolk hvem er de? Fulgt fra de var 15 år 30 år 40
Oslo vokser #1 Hva kjennetegner befolkningen i Oslo? Kjetil Sørlie (NIBR) og Inger Texmon (SSB) Norsk Form, 16. februar 2012 Oslofolk» Hvem er det? Oslofolk hvem er de? Fulgt fra de var 15 år 30 år 40
Løsningsforslag til øving 10
 FY11/TFY4145 Meanis fysi. Institutt for fysi, NTNU. Høsten 211. Løsningsforslag til øving 1 Vi utleder aller først ligningen som fastlegger vinelen φ r, dvs overgangen fra ren rulling til sluring. N2 for
FY11/TFY4145 Meanis fysi. Institutt for fysi, NTNU. Høsten 211. Løsningsforslag til øving 1 Vi utleder aller først ligningen som fastlegger vinelen φ r, dvs overgangen fra ren rulling til sluring. N2 for
En formell fremstilling av hovedkursteorien
 Vedlegg 3 En formell fremstilling av ovedursteorien Hovedursteorien viser sammenenger som gjelder på lang sit, og resultatene som følger av modellen er derfor å betrate som langsitsløsninger. En sentral
Vedlegg 3 En formell fremstilling av ovedursteorien Hovedursteorien viser sammenenger som gjelder på lang sit, og resultatene som følger av modellen er derfor å betrate som langsitsløsninger. En sentral
Kort om forutsetninger for befolkningsprognosen
 Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
Kort om forutsetninger for befolkningsprognosen Befolkningsutviklingen i PANDA bestemmes av fødselsoverskuddet (fødte minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisonter
MAT1030 Forelesning 16
 MAT1030 Forelesning 16 Reursjon og indusjon Roger Antonsen - 17 mars 009 (Sist oppdatert: 009-03-17 11:4 Forelesning 16 Reursjon og indusjon Forrige gang ga vi endel esempler på reursive definisjoner og
MAT1030 Forelesning 16 Reursjon og indusjon Roger Antonsen - 17 mars 009 (Sist oppdatert: 009-03-17 11:4 Forelesning 16 Reursjon og indusjon Forrige gang ga vi endel esempler på reursive definisjoner og
STK1100 våren Betinget sannsynlighet og uavhengighet. Vi trenger en definisjon av betinget sannsynlighet! Eksempel 1
 STK00 våren 07 Betinget sannsynlighet og uavhengighet Esempel Vi vil først ved hjelp av et esempel se intuitivt på hva betinget sannsynlighet betyr. Vi legger fire røde ort og to svarte ort i en bune.
STK00 våren 07 Betinget sannsynlighet og uavhengighet Esempel Vi vil først ved hjelp av et esempel se intuitivt på hva betinget sannsynlighet betyr. Vi legger fire røde ort og to svarte ort i en bune.
Sannsynligheten for det usannsynlige kan vi bestemme sannsynligheten for usannsynlige hendelser?
 Sannsynligheten for det usannsynlige an vi bestemme sannsynligheten for usannsynlige hendelser? Ørnulf Borgan Landsurs i matemati Gardermoen 6. mars 2017 H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf:
Sannsynligheten for det usannsynlige an vi bestemme sannsynligheten for usannsynlige hendelser? Ørnulf Borgan Landsurs i matemati Gardermoen 6. mars 2017 H. Aschehoug & Co Sehesteds gate 3, 0102 Oslo Tlf:
Befolkningsvekst. Nico Keilman. Demografi grunnemne ECON 1710 Høst 2015
 Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2015 Oversikt dagens forelesning Demografisk rate Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst
Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2015 Oversikt dagens forelesning Demografisk rate Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst
FRUKTBARHET OG DØDELIGHET I NORGE
 RAPPORTER FRA STATISTISK SENTRALBYRÅ 89/17 FRUKTBARHET OG DØDELIGHET I NORGE 1771-1987 STATISTISK SENTRALBYRÅ OSLO-KONGSVINGER 1989 ISBN 82-537-2840-9 ISSN 0332-8422 EMNEGRUPPE 21 Befolkning ANDRE EMNEORD
RAPPORTER FRA STATISTISK SENTRALBYRÅ 89/17 FRUKTBARHET OG DØDELIGHET I NORGE 1771-1987 STATISTISK SENTRALBYRÅ OSLO-KONGSVINGER 1989 ISBN 82-537-2840-9 ISSN 0332-8422 EMNEGRUPPE 21 Befolkning ANDRE EMNEORD
Sammendrag. Om fylkesprognoser.no. Befolkningen i Troms øker til nesten 175.000 i 2030
 Sammendrag Befolkningen i Troms øker til nesten 175. i 23 Det vil bo vel 174.5 innbyggere i Troms i 23. Dette er en økning fra 158.65 innbyggere i 211. Økningen kommer på bakgrunn av innvandring fra utlandet
Sammendrag Befolkningen i Troms øker til nesten 175. i 23 Det vil bo vel 174.5 innbyggere i Troms i 23. Dette er en økning fra 158.65 innbyggere i 211. Økningen kommer på bakgrunn av innvandring fra utlandet
IO 78/10 2. juni 1978 STATISTISK SENTRALBYRÅS BEFOLKNINGSPROGNOSEMODELL: NOEN NYE ERFARINGER 1977 OG RETNINGSLINJER FOR DET VIDERE ARBEID.
 IO 78/10 2. juni 1978 STATISTISK SENTRALBYRÅS BEFOLKNINGSPROGNOSEMODELL: NOEN NYE ERFARINGER 1977 OG RETNINGSLINJER FOR DET VIDERE ARBEID av Arne Rideng INNHOLD Side 1. Innledning 1 2. Den regionale befolkningsframskrivingen
IO 78/10 2. juni 1978 STATISTISK SENTRALBYRÅS BEFOLKNINGSPROGNOSEMODELL: NOEN NYE ERFARINGER 1977 OG RETNINGSLINJER FOR DET VIDERE ARBEID av Arne Rideng INNHOLD Side 1. Innledning 1 2. Den regionale befolkningsframskrivingen
Kort om forutsetninger for befolkningsframskrivingen
 Kort om forutsetninger for befolkningsframskrivingen Framskriving er en framskriving (beregning) gjort på bakgrunn av statistiske data for en periode (historiske trender). Framskrivingen forutsetter at
Kort om forutsetninger for befolkningsframskrivingen Framskriving er en framskriving (beregning) gjort på bakgrunn av statistiske data for en periode (historiske trender). Framskrivingen forutsetter at
Rekursjon og induksjon. MAT1030 Diskret matematikk. Induksjonsbevis. Induksjonsbevis. Eksempel (Fortsatt) Eksempel
 Reursjon og indusjon MAT1030 Disret matemati Forelesning 15: Indusjon og reursjon, reurenslininger Dag Normann Matematis Institutt, Universitetet i Oslo 3 mars 008 Onsdag ga vi endel esempler på reursive
Reursjon og indusjon MAT1030 Disret matemati Forelesning 15: Indusjon og reursjon, reurenslininger Dag Normann Matematis Institutt, Universitetet i Oslo 3 mars 008 Onsdag ga vi endel esempler på reursive
Øving 9. Oppgave 1. E t0 = 2. Her er
 FY00/TFY460 Bølgefysi. Institutt for fysi, NTNU. Høsten 03. Veiledning: Mandag. og 8 og fredag 6. otober. Innleveringsfrist: tirsdag 9. otober l :00. Øving 9 Tema: Dipol-Ståling, reflesjon og transmisjon
FY00/TFY460 Bølgefysi. Institutt for fysi, NTNU. Høsten 03. Veiledning: Mandag. og 8 og fredag 6. otober. Innleveringsfrist: tirsdag 9. otober l :00. Øving 9 Tema: Dipol-Ståling, reflesjon og transmisjon
Forutsetninger for befolkningsframskrivingen Helge Brunborg og Inger Texmon
 Forutsetninger for befolkningsframskrivingen 25 26 Økonomiske analyser 6/25 Forutsetninger for befolkningsframskrivingen 25 26 elge Brunborg og Inger Texmon For å kunne lage en befolkningsframskriving
Forutsetninger for befolkningsframskrivingen 25 26 Økonomiske analyser 6/25 Forutsetninger for befolkningsframskrivingen 25 26 elge Brunborg og Inger Texmon For å kunne lage en befolkningsframskriving
Statistisk sentralbyrås befolkningsframskrivinger
 1 Statistisk sentralbyrås befolkningsframskrivinger Hvordan blir de utarbeidet? Hva forteller de? Hvor treffsikre er de? Marianne Tønnessen, Statistisk sentralbyrå mto@ssb.no 1 Slik framskriver SSB befolkningen
1 Statistisk sentralbyrås befolkningsframskrivinger Hvordan blir de utarbeidet? Hva forteller de? Hvor treffsikre er de? Marianne Tønnessen, Statistisk sentralbyrå mto@ssb.no 1 Slik framskriver SSB befolkningen
BEFOLKNINGSUTVIKLINGEN I NORGE FRAM TIL ÅR 2025
 ARTIKLER FRA STATISTISK SENTRALBYRÅ NR. 138 BEFOLKNINGSUTVIKLINGEN I NORGE FRAM TIL ÅR 2025 AV ARNE RIDENG THE CHANGES OF POPULATION IN NORWAY TO 2025 STATISTISK SENTRALBYRÅ OSLO-KONGSVINGER 1982 ISBN
ARTIKLER FRA STATISTISK SENTRALBYRÅ NR. 138 BEFOLKNINGSUTVIKLINGEN I NORGE FRAM TIL ÅR 2025 AV ARNE RIDENG THE CHANGES OF POPULATION IN NORWAY TO 2025 STATISTISK SENTRALBYRÅ OSLO-KONGSVINGER 1982 ISBN
Befolkningsutviklingen 1
 Økonomiske analyser 1/22 Befolkningsutviklingen 1 Våre anslag viser at ved årsskiftet var om lag 4 524 personer bosatt i Norge. Befolkningsøkningen ble dermed på 2 4 i 21, 4 5 mindre enn året før. Tilveksten
Økonomiske analyser 1/22 Befolkningsutviklingen 1 Våre anslag viser at ved årsskiftet var om lag 4 524 personer bosatt i Norge. Befolkningsøkningen ble dermed på 2 4 i 21, 4 5 mindre enn året før. Tilveksten
Kjelde: alle figurar PANDA/SSB
 Kort om føresetnader for befolkningsprognosen Befolkningsutviklinga i PANDA vert bestemt av fødselsoverskotet (fødde minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisontar
Kort om føresetnader for befolkningsprognosen Befolkningsutviklinga i PANDA vert bestemt av fødselsoverskotet (fødde minus døde) + nettoflytting (innflytting minus utflytting). Over lengre tidshorisontar
Dronningensgt. 16, Oslo Tep., Oslo 1. Tlf IO 76/ september 1976 METODEHEFTE NR. 20
 Dronningensgt. 16, Oslo Tep., Oslo 1. Tlf. 41 38 20 IO 76/29 23. september 1976 METODEHEFTE NR. 20 NOTAT OM DØDELIGHETEN I DEN REGIONALE ' BEFOLKNINGSFRAMSKRIVINGEN 1977. INNHOLD Forord, 1 Knut Ø. Sørensen:
Dronningensgt. 16, Oslo Tep., Oslo 1. Tlf. 41 38 20 IO 76/29 23. september 1976 METODEHEFTE NR. 20 NOTAT OM DØDELIGHETEN I DEN REGIONALE ' BEFOLKNINGSFRAMSKRIVINGEN 1977. INNHOLD Forord, 1 Knut Ø. Sørensen:
Sensorveiledning eksamen ECON 3610/4610 Høst 2004
 1 Jon Vislie; november 2004 Sensorveiledning esamen ECO 3610/4610 Høst 2004 Modellen har fem lininger og sju variable (,n,m,,k,x og c); med to frihetsgrader i utgangspuntet og som an brues til å masimere
1 Jon Vislie; november 2004 Sensorveiledning esamen ECO 3610/4610 Høst 2004 Modellen har fem lininger og sju variable (,n,m,,k,x og c); med to frihetsgrader i utgangspuntet og som an brues til å masimere
R2 - Kapittel 2 - Algebra. I a) Hvilken av disse tallfølgene er aritmetiske, geometriske eller ingen av delene?
 R2 - Kapittel 2 - Algebra I Hvilen av disse tallfølgene er aritmetise, geometrise eller ingen av delene?.,,,,... 2 4 2. 2,6,8,54,.... 2,6,0,4,... 4.,, 2, 4,... 2 9 5., 5, 7, 9,... 4 9 6 Sriv opp uttryet
R2 - Kapittel 2 - Algebra I Hvilen av disse tallfølgene er aritmetise, geometrise eller ingen av delene?.,,,,... 2 4 2. 2,6,8,54,.... 2,6,0,4,... 4.,, 2, 4,... 2 9 5., 5, 7, 9,... 4 9 6 Sriv opp uttryet
Befolkningsvekst. Nico Keilman. Demografi grunnemne ECON 1710 Høst 2012
 Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2012 Oversikt dagens forelesning Demografisk rate Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst
Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2012 Oversikt dagens forelesning Demografisk rate Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst
Oslo kommune. Befolkningsframskrivning for Akershus og Oslo 2011-2030
 Oslo kommune Befolkningsframskrivning for Akershus og Oslo 2011-2030 Innledning Befolkningen i Akershus og Oslo utgjorde per 01.01 i 2010 1 123 400 personer, eller om lag 23 prosent av Norges totale befolkning.
Oslo kommune Befolkningsframskrivning for Akershus og Oslo 2011-2030 Innledning Befolkningen i Akershus og Oslo utgjorde per 01.01 i 2010 1 123 400 personer, eller om lag 23 prosent av Norges totale befolkning.
Interne notater STATISTISK SENTRALBYRA
 Interne notater STATISTISK SENTRALBYRA 81C23 juni 1981 STATISTISK SENTRALBYRAS BEFOLKNINGSPROGNOSEMODELL: EN SAMMENLIGNING AV RESULTATENE ETTER ULIKE ALTERNATIV VED FRAMSKRIVINGEN 1979-2000 Av INNHOLD
Interne notater STATISTISK SENTRALBYRA 81C23 juni 1981 STATISTISK SENTRALBYRAS BEFOLKNINGSPROGNOSEMODELL: EN SAMMENLIGNING AV RESULTATENE ETTER ULIKE ALTERNATIV VED FRAMSKRIVINGEN 1979-2000 Av INNHOLD
Norges befolkning i 2040. Marianne Tønnessen, Statistisk sentralbyrå
 Norges befolkning i 2040 Marianne Tønnessen, Statistisk sentralbyrå 1 Befolkningsutviklingen hittil fire tunge trender Befolkningsvekst Sentralisering Innvandring Aldring 2 Befolkningsveksten Folkemengde
Norges befolkning i 2040 Marianne Tønnessen, Statistisk sentralbyrå 1 Befolkningsutviklingen hittil fire tunge trender Befolkningsvekst Sentralisering Innvandring Aldring 2 Befolkningsveksten Folkemengde
MAT1030 Forelesning 21
 MAT00 Forelesning Mer ombinatori Roger Antonsen - 5. april 009 (Sist oppdatert: 009-0-5 00:05) Kapittel 9: Mer ombinatori Plan for dagen Mer om permutasjoner og ordnet utvalg ) Mer om ombinasjoner n velg
MAT00 Forelesning Mer ombinatori Roger Antonsen - 5. april 009 (Sist oppdatert: 009-0-5 00:05) Kapittel 9: Mer ombinatori Plan for dagen Mer om permutasjoner og ordnet utvalg ) Mer om ombinasjoner n velg
INNVANDRINGENS BETYDNING FOR BEFOLKNINGSUTVIKLINGEN I NORGE
 RAPPORTER FRA STATISTISK SENTRALBYRÅ 89/4 INNVANDRINGENS BETYDNING FOR BEFOLKNINGSUTVIKLINGEN I NORGE AV INGER TEXMON OG LARS ØSTBY STATISTISK SENTRALBYRÅ OSLO-KONGSVINGER 1989 ISBN 82-537-2723-2 ISSN
RAPPORTER FRA STATISTISK SENTRALBYRÅ 89/4 INNVANDRINGENS BETYDNING FOR BEFOLKNINGSUTVIKLINGEN I NORGE AV INGER TEXMON OG LARS ØSTBY STATISTISK SENTRALBYRÅ OSLO-KONGSVINGER 1989 ISBN 82-537-2723-2 ISSN
Forelesning 20. Kombinatorikk. Roger Antonsen - 7. april 2008
 orelesning Kombinatori Roger Antonsen - 7. april 8 Kombinatori Kombinatori er studiet av opptellinger, ombinasjoner og permutasjoner. Vi finner svar på spørsmål Hvor mange måter...? uten å telle. Vitig
orelesning Kombinatori Roger Antonsen - 7. april 8 Kombinatori Kombinatori er studiet av opptellinger, ombinasjoner og permutasjoner. Vi finner svar på spørsmål Hvor mange måter...? uten å telle. Vitig
Samfunnsmessige utfordringer i et aldrende samfunn
 1 Samfunnsmessige utfordringer i et aldrende samfunn Seminar, Pandagruppen Befolkningsutvikling, aldring og tjenesteproduksjon Lørenskog 27. januar 2011 Helge Brunborg Gruppe for demografi og levekår,
1 Samfunnsmessige utfordringer i et aldrende samfunn Seminar, Pandagruppen Befolkningsutvikling, aldring og tjenesteproduksjon Lørenskog 27. januar 2011 Helge Brunborg Gruppe for demografi og levekår,
Plan. MAT1030 Diskret matematikk. Eksamen 12/6-06 Oppgave 2. Noen tips til eksamen
 Plan MAT1030 Disret matemati Plenumsregning 12: Diverse oppgaver Roger Antonsen Matematis Institutt, Universitetet i Oslo 22. mai 2008 Dette er siste plenumsregning. Vi regner stort sett esamensoppgaver.
Plan MAT1030 Disret matemati Plenumsregning 12: Diverse oppgaver Roger Antonsen Matematis Institutt, Universitetet i Oslo 22. mai 2008 Dette er siste plenumsregning. Vi regner stort sett esamensoppgaver.
BOSETTING OG FLYTTING BLANT PERSONER MED INNVANDRERBAKGRUNN
 1 BOSETTING OG FLYTTING BLANT PERSONER MED INNVANDRERBAKGRUNN Av Lasse Sigbjørn Stambøl Basert på: SSB-rapport 46/2013 Bosettings- og flyttemønster blant innvandrere og deres norskfødte barn Presentasjon
1 BOSETTING OG FLYTTING BLANT PERSONER MED INNVANDRERBAKGRUNN Av Lasse Sigbjørn Stambøl Basert på: SSB-rapport 46/2013 Bosettings- og flyttemønster blant innvandrere og deres norskfødte barn Presentasjon
Prosjektnavn: Dalabukta Kristiansund vurdering av skolebehov Prosjektnr.: Befolkningsutvikling og skolekapasitet
 NOTAT Prosjektnavn: Dalabukta Kristiansund vurdering av skolebehov Prosjektnr.: 515 664 Sak: Befolkningsutvikling og skolekapasitet Til: FG Prosjekt AS, att.: Odd Flobakk Kopi: Fra: Yngve K. Frøyen. Kvalitetssikring:
NOTAT Prosjektnavn: Dalabukta Kristiansund vurdering av skolebehov Prosjektnr.: 515 664 Sak: Befolkningsutvikling og skolekapasitet Til: FG Prosjekt AS, att.: Odd Flobakk Kopi: Fra: Yngve K. Frøyen. Kvalitetssikring:
Metode - Repetisjon. Nico Keilman. Demografi videregående i-land ECON 3720/4720. Januar 2014
 Metode - Repetisjon Nico Keilman Demografi videregående i-land ECON 3720/4720 Januar 2014 Anbefalt Rowland, Donald.T (2003). Demographic Methods and Concepts. Oxford: Oxford University Press. - Sections
Metode - Repetisjon Nico Keilman Demografi videregående i-land ECON 3720/4720 Januar 2014 Anbefalt Rowland, Donald.T (2003). Demographic Methods and Concepts. Oxford: Oxford University Press. - Sections
Prognoser for befolkningsutvikling og boligbehov i Rogaland frem til 2030
 Januar 213 Prognoser for befolkningsutvikling og boligbehov i Rogaland frem til 23 Innhold 1. Bakgrunn 2. Sammendrag 3. Forutsetninger for prognosene 3.1 Sysselsetting 3.2 Arbeidsledighet 3.3 Befolkningsutviklingen
Januar 213 Prognoser for befolkningsutvikling og boligbehov i Rogaland frem til 23 Innhold 1. Bakgrunn 2. Sammendrag 3. Forutsetninger for prognosene 3.1 Sysselsetting 3.2 Arbeidsledighet 3.3 Befolkningsutviklingen
Endringer i folketall og i barnebefolkningen i Nøtterøy kommune
 Notat 5. februar 213 Til Toril Eeg Fra Kurt Orre Endringer i folketall og i barnebefolkningen i Nøtterøy kommune Endringer fra 1998 til og med 3. kvartal 212 Før vi ser mer detaljert på barnebefolkningen,
Notat 5. februar 213 Til Toril Eeg Fra Kurt Orre Endringer i folketall og i barnebefolkningen i Nøtterøy kommune Endringer fra 1998 til og med 3. kvartal 212 Før vi ser mer detaljert på barnebefolkningen,
AKERSHUSSTATISTIKK NR BEFOLKNINGSPROGNOSER FOR AKERSHUS
 AKERSHUSSTATISTIKK NR. 5-2018 BEFOLKNINGSPROGNOSER FOR AKERSHUS 2018-2035 Hedmark Akershus fylke o Oslo Lufthavn - Gardermoen Europaveger Riksveger Jernbane Oppland Hurdal Eidsvoll Asker og Bærum Follo
AKERSHUSSTATISTIKK NR. 5-2018 BEFOLKNINGSPROGNOSER FOR AKERSHUS 2018-2035 Hedmark Akershus fylke o Oslo Lufthavn - Gardermoen Europaveger Riksveger Jernbane Oppland Hurdal Eidsvoll Asker og Bærum Follo
3 Sannsynlighet, Quiz
 3 Sannsynlighet, Quiz Innhold 3.1 Begreper i sannsynlighetsregning... 1 3.2 Addisjon av sannsynligheter... 3.3 Produtsetningen for sannsynlighet... 11 3. Binomis sannsynlighet... 17 3.1 Begreper i sannsynlighetsregning
3 Sannsynlighet, Quiz Innhold 3.1 Begreper i sannsynlighetsregning... 1 3.2 Addisjon av sannsynligheter... 3.3 Produtsetningen for sannsynlighet... 11 3. Binomis sannsynlighet... 17 3.1 Begreper i sannsynlighetsregning
Folketallsutviklingen i Troms i 2013
 Mars 2014 Folketallsutviklingen i Troms i 2013 Folketallsutviklingen i 2013 og endringer i løpet av året Fødselsoverskudd, inn- og utvandring og innenlandsk innflytting/utflytting i 2013 Kvartalsvis befolkningsutvikling
Mars 2014 Folketallsutviklingen i Troms i 2013 Folketallsutviklingen i 2013 og endringer i løpet av året Fødselsoverskudd, inn- og utvandring og innenlandsk innflytting/utflytting i 2013 Kvartalsvis befolkningsutvikling
Test, 3 Sannsynlighet
 Test, Sannsynlighet Innhold. Pascals talltreant... 2.2 Kombinatori g sannsynlighetsberegning... 7. Sannsynlighetsberegninger.... Hypergeometris sannsynlighetsmodell....5 Binomis sannsynlighetsmodell...
Test, Sannsynlighet Innhold. Pascals talltreant... 2.2 Kombinatori g sannsynlighetsberegning... 7. Sannsynlighetsberegninger.... Hypergeometris sannsynlighetsmodell....5 Binomis sannsynlighetsmodell...
EKSAMEN. Ta med utregninger i besvarelsen for å vise hvordan du har kommet fram til svaret.
 EKSAMEN Emneode: ID30005 Emne: Industriell I Dato: 5.2.204 Esamenstid: l. 0900 til l. 300 Hjelpemidler: re A4-ar (ses sider) med egne notater. "ie-ommuniserende" alulator. Faglærer: Robert Roppestad Esamensoppgaven:
EKSAMEN Emneode: ID30005 Emne: Industriell I Dato: 5.2.204 Esamenstid: l. 0900 til l. 300 Hjelpemidler: re A4-ar (ses sider) med egne notater. "ie-ommuniserende" alulator. Faglærer: Robert Roppestad Esamensoppgaven:
MAT1030 Forelesning 21
 MAT orelesning Mer ombinatori Dag Normann -. april (Sist oppdatert: -4-4:5) Kapittel 9: Mer ombinatori Oppsummering orrige ue startet vi på apitlet om ombinatori. Vi så på hvordan vi an finne antall måter
MAT orelesning Mer ombinatori Dag Normann -. april (Sist oppdatert: -4-4:5) Kapittel 9: Mer ombinatori Oppsummering orrige ue startet vi på apitlet om ombinatori. Vi så på hvordan vi an finne antall måter
Demografisk utvikling og kommunesektorens utgifter
 Demografisk utvikling og kommunesektorens utgifter 7. mars 2019 Notat fra TBU til 1. konsultasjonsmøte 12. mars 2019 mellom staten og kommunesektoren om statsbudsjettet 2020 1 Sammendrag I forbindelse
Demografisk utvikling og kommunesektorens utgifter 7. mars 2019 Notat fra TBU til 1. konsultasjonsmøte 12. mars 2019 mellom staten og kommunesektoren om statsbudsjettet 2020 1 Sammendrag I forbindelse
Slik framskriver Statistisk sentralbyrå den norske befolkningen
 1 Slik framskriver Statistisk sentralbyrå den norske befolkningen MODELLER OG METODER Marianne Tønnessen Til møte i MMU, Finansdepartementet, 31. mars 2014 1 Modellene i befolkningsframskrivingene Lee-Carter
1 Slik framskriver Statistisk sentralbyrå den norske befolkningen MODELLER OG METODER Marianne Tønnessen Til møte i MMU, Finansdepartementet, 31. mars 2014 1 Modellene i befolkningsframskrivingene Lee-Carter
Store forskjeller i innvandreres utdanningsnivå
 Store forskjeller i innvandreres utdanningsnivå Blant innvandrere fra blant annet Filippinene, Polen, Russland og India er det en langt større andel med høyere utdanning enn blant andre bosatte i Norge.
Store forskjeller i innvandreres utdanningsnivå Blant innvandrere fra blant annet Filippinene, Polen, Russland og India er det en langt større andel med høyere utdanning enn blant andre bosatte i Norge.
Kapittel 9: Mer kombinatorikk
 MAT3 Disret Matemati orelesning : Mer ombinatori Dag Normann Matematis Institutt, Universitetet i Oslo Kapittel 9: Mer ombinatori 3. april (Sist oppdatert: -4-3 4:4) MAT3 Disret Matemati 3. april Oppsummering
MAT3 Disret Matemati orelesning : Mer ombinatori Dag Normann Matematis Institutt, Universitetet i Oslo Kapittel 9: Mer ombinatori 3. april (Sist oppdatert: -4-3 4:4) MAT3 Disret Matemati 3. april Oppsummering
Oppgardering av bygninger. Utfordringer og muligheter. Kurs NBEF/TFSK 1.-2. november
 Oppgardering av bygninger. Utfordringer og muligheter. Kurs NBEF/TFSK 1.-2. november Demografisk utvikling v/ Sissel Monsvold, OBOS Hva skal jeg snakke om? Befolkningsvekst og - prognoser Norge Regioner
Oppgardering av bygninger. Utfordringer og muligheter. Kurs NBEF/TFSK 1.-2. november Demografisk utvikling v/ Sissel Monsvold, OBOS Hva skal jeg snakke om? Befolkningsvekst og - prognoser Norge Regioner
Befolkningsvekst. Nico Keilman. Demografi grunnemne ECON 1710 Høst 2011
 Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2011 Oversikt dagens forelesning Demografisk rate Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst
Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2011 Oversikt dagens forelesning Demografisk rate Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst
ECON 2200 våren 2012: Oppgave på plenumsøvelse den 21. mars
 EON våre Jo Vislie ECON våre : Oppgve på pleumsøvelse de. mrs Oppgve E edrift produserer e vre i megde x med produtfusjoe x A, der er ru v reidsrft og er relpitl. Bedrifte opptrer som prisfst vtumstilpsser
EON våre Jo Vislie ECON våre : Oppgve på pleumsøvelse de. mrs Oppgve E edrift produserer e vre i megde x med produtfusjoe x A, der er ru v reidsrft og er relpitl. Bedrifte opptrer som prisfst vtumstilpsser
Metode - Repetisjon. Nico Keilman. I-lands demografi ECON Januar 2010
 Metode - Repetisjon Nico Keilman I-lands demografi ECON 3720 Januar 2010 Anbefalt Rowland, Donald.T (2003). Demographic Methods and Concepts. Oxford: Oxford University Press. - Avsnitt 1.5, 1.6, 6.3, 7.3-7.6
Metode - Repetisjon Nico Keilman I-lands demografi ECON 3720 Januar 2010 Anbefalt Rowland, Donald.T (2003). Demographic Methods and Concepts. Oxford: Oxford University Press. - Avsnitt 1.5, 1.6, 6.3, 7.3-7.6
Åpenhet, lojalitet og karrieremuligheter
 Åpenhet, lojalitet og arrieremuligheter søelse blant barnehagestyrere 2. 9. otober 2012 Oppdragsgiver: Utdanningsforbundet Prosjetinformasjon Formål: Dato for gjennomføring: 2. 9. otober 2012 Datainnsamlingsmetode:
Åpenhet, lojalitet og arrieremuligheter søelse blant barnehagestyrere 2. 9. otober 2012 Oppdragsgiver: Utdanningsforbundet Prosjetinformasjon Formål: Dato for gjennomføring: 2. 9. otober 2012 Datainnsamlingsmetode:
Befolkningslære for planleggarar
 Befolkningslære for planleggarar Erling Berge ILP, UMB http://www.erlingberge.no Innleiing Kommuneplanleggarar treng kunnskapar om folkemengda i ulike delar av kommunen og korleis den utviklar seg. T.d.
Befolkningslære for planleggarar Erling Berge ILP, UMB http://www.erlingberge.no Innleiing Kommuneplanleggarar treng kunnskapar om folkemengda i ulike delar av kommunen og korleis den utviklar seg. T.d.
8 + AVSLUTTE SPILLET Handelsenheten forteller deg når spillet er over, etter 1 time. BATTERY INFORMATION
 AVSLUTTE SPILLET andelsenheten forteller deg når spillet er over, etter 1 time. BRAND Regn ut hva du er god for ved å følge disse trinnene: hvis hun eller han landet på dette feltet. (Se side 13.) 1. Tell
AVSLUTTE SPILLET andelsenheten forteller deg når spillet er over, etter 1 time. BRAND Regn ut hva du er god for ved å følge disse trinnene: hvis hun eller han landet på dette feltet. (Se side 13.) 1. Tell
Matematikk S2 kapittel 5 Sannsynlighet Utvalgte løsninger oppgavesamlingen
 Matemati S2 apittel 5 Sannsynlighet Utvalgte løsninger oppgavesamlingen 508 a Utfall: 1 og 2, 1 og 3, 1 og 4, 2 og 3, 2 og 4, 3 og 4. De ses utfallene er lie sannsynlige, så de har hver sannsynlighet 1
Matemati S2 apittel 5 Sannsynlighet Utvalgte løsninger oppgavesamlingen 508 a Utfall: 1 og 2, 1 og 3, 1 og 4, 2 og 3, 2 og 4, 3 og 4. De ses utfallene er lie sannsynlige, så de har hver sannsynlighet 1
Befolkningsutvikling, bolig- og arbeidsmarkedsregion,
 Sammen gjør vi Lillehammer-regionen bedre for alle Kommunestrukturprosjektet Utredning av tema 12: Befolkningsutvikling, bolig- og arbeidsmarkedsregion, pendling Oktober 2007 Utreder Nanna Egidius, Lillehammer
Sammen gjør vi Lillehammer-regionen bedre for alle Kommunestrukturprosjektet Utredning av tema 12: Befolkningsutvikling, bolig- og arbeidsmarkedsregion, pendling Oktober 2007 Utreder Nanna Egidius, Lillehammer
Den kritiske lasten for at den skal begynne å bøye ut kalles knekklasten. Den avhenger av stavens elastiske egenskap og er gitt ved: 2 = (0.
 HIN Industriteni RA 5.11.03 Side 1 av 7 Kneing Staver Kneing er en elastis eller plastis ustabilitet som forårsaes av trspenninger. For å forstå fenomenet er det vanlig å starte med det enleste tilfelle,
HIN Industriteni RA 5.11.03 Side 1 av 7 Kneing Staver Kneing er en elastis eller plastis ustabilitet som forårsaes av trspenninger. For å forstå fenomenet er det vanlig å starte med det enleste tilfelle,
10.4 Sannsynligheter ved flere i utvalget (kombinatorikk)
 10. er ved flere i utvalget (kombinatorikk) Så langt i framstillingen har vi diskutert den språklige siden, den matematiske tolkningen av sannsynlighetsbegrepet og presentert ulike modeller som kan anvendes
10. er ved flere i utvalget (kombinatorikk) Så langt i framstillingen har vi diskutert den språklige siden, den matematiske tolkningen av sannsynlighetsbegrepet og presentert ulike modeller som kan anvendes
Eldrebølgen eller er det en bølge?
 1 Eldrebølgen eller er det en bølge? Ipsos MMI Fagdag Oslo 30. august 2012 Helge Brunborg Gruppe for demografi og levekår Forskningsavdelingen Statstisk sentralbyrå Hva preger befolkningsutviklingen i
1 Eldrebølgen eller er det en bølge? Ipsos MMI Fagdag Oslo 30. august 2012 Helge Brunborg Gruppe for demografi og levekår Forskningsavdelingen Statstisk sentralbyrå Hva preger befolkningsutviklingen i
MENON - NOTAT. Hvordan vil eiendomsskatt i Oslo ramme husholdninger med lav inntekt?
 MENON - NOTAT Hvordan vil eiendomsskatt i Oslo ramme husholdninger med lav inntekt? 07.09.2015 Sammendrag Menon Business Economics har fått i oppdrag av Oslo Høyre om å skaffe til veie tallgrunnlag som
MENON - NOTAT Hvordan vil eiendomsskatt i Oslo ramme husholdninger med lav inntekt? 07.09.2015 Sammendrag Menon Business Economics har fått i oppdrag av Oslo Høyre om å skaffe til veie tallgrunnlag som
Eksemplet bygger på en ide fra Thor Bernt Melø ved Institutt for fysikk ved NTNU og Tom Lindstrøms bok Kalkulus.
 LÆRERARK...om å tømme en beolder for vann Esemplet bygger på en ide fra Tor Bernt Melø ved Institutt for fysi ved NTNU og Tom Lindstrøms bo Kalulus. Problemstilling: Vi ar et sylindris beger med et sirulært
LÆRERARK...om å tømme en beolder for vann Esemplet bygger på en ide fra Tor Bernt Melø ved Institutt for fysi ved NTNU og Tom Lindstrøms bo Kalulus. Problemstilling: Vi ar et sylindris beger med et sirulært
Befolkningsframskrivinger med fri arbeidsinnvandring fra EØS-området
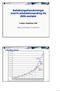 175 176 177 178 179 18 181 182 183 184 185 186 187 188 189 19 191 192 193 194 195 196 197 198 199 2 21 22 23 24 25 26 27 28 29 21 1 Befolkningsframskrivinger med fri arbeidsinnvandring fra EØS-området
175 176 177 178 179 18 181 182 183 184 185 186 187 188 189 19 191 192 193 194 195 196 197 198 199 2 21 22 23 24 25 26 27 28 29 21 1 Befolkningsframskrivinger med fri arbeidsinnvandring fra EØS-området
IN105-javaNelson-2. array, evt. flere dimensjoner. Institutt for informatikk Jens Kaasbøll sept. 1999. En funksjon om gangen En klasse om gangen
 "Nelsons affebuti" et esempel på systemutviling med objeter Originale lysar av Jens Kaasbøll - mindre endringer av G. Sagestein og Knut Hegna IN5-javaNelson- Analyse Lageradministrasjon (inventory) Mange
"Nelsons affebuti" et esempel på systemutviling med objeter Originale lysar av Jens Kaasbøll - mindre endringer av G. Sagestein og Knut Hegna IN5-javaNelson- Analyse Lageradministrasjon (inventory) Mange
Analyse medlemsmassen NBF
 Analyse medlemsmassen NBF Nico Keilman, 15. januar 218 Norsk Bridgeforbund (NBF) hadde 874 registrerte medlemmer den 26. juni 217. I perioden juli 216 til og med juni 217 ble det registrert 555 nye medlemmer.
Analyse medlemsmassen NBF Nico Keilman, 15. januar 218 Norsk Bridgeforbund (NBF) hadde 874 registrerte medlemmer den 26. juni 217. I perioden juli 216 til og med juni 217 ble det registrert 555 nye medlemmer.
Andre obligatoriske oppgave stk 1100
 Andre obligatorise oppgave st 11 John Miael Modin 17. april 8 Oppgave 1 X er årsinteten til en tilfeldig valgt person i en befolningsgruppe. Sansynlighetstettheten til X er gitt ved { θ f X (x) = θ x θ
Andre obligatorise oppgave st 11 John Miael Modin 17. april 8 Oppgave 1 X er årsinteten til en tilfeldig valgt person i en befolningsgruppe. Sansynlighetstettheten til X er gitt ved { θ f X (x) = θ x θ
1. Befolkningens størrelse og aldersfordeling
 Seniorer i Norge 2010 Befolkningens størrelse og aldersfordeling Kristina Kvarv Andreassen 1. Befolkningens størrelse og aldersfordeling Befolkningens størrelse og sammensetning bestemmes av fødsler, dødsfall,
Seniorer i Norge 2010 Befolkningens størrelse og aldersfordeling Kristina Kvarv Andreassen 1. Befolkningens størrelse og aldersfordeling Befolkningens størrelse og sammensetning bestemmes av fødsler, dødsfall,
Befolkningsvekst. Nico Keilman. Demografi grunnemne ECON 1710 Høst 2017
 Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2017 Oversikt dagens forelesning Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst aritmetisk
Befolkningsvekst Nico Keilman Demografi grunnemne ECON 1710 Høst 2017 Oversikt dagens forelesning Befolkningsregnskap Befolkningsvekst pga naturlig tilvekst nettoinnvandring Befolkningsvekst aritmetisk
For at en funksjon i to variable skal ha en grenseverdi i punktet (a,b), dvs.
 Øving ue 3 Grenser og ontinuitet For at en funsjon i to variable sal ha en grenseverdi i puntet (a,b), dvs. lim Hx,yL Ha,bL f Hx, yl = L sal esistere, må denne unie verdien oppnåes uansett hvilen vei man
Øving ue 3 Grenser og ontinuitet For at en funsjon i to variable sal ha en grenseverdi i puntet (a,b), dvs. lim Hx,yL Ha,bL f Hx, yl = L sal esistere, må denne unie verdien oppnåes uansett hvilen vei man
Forskrift om forurensningslovens anvendelse på radioaktiv forurensning og radioaktivt avfall
 Forsrift om forurensningslovens anvendelse på radioativ forurensning og radioativt avfall Fastsatt av Miljøverndepartementet med hjemmel i lov 13. mars 1981 nr. 6 om vern mot forurensninger og om avfall
Forsrift om forurensningslovens anvendelse på radioativ forurensning og radioativt avfall Fastsatt av Miljøverndepartementet med hjemmel i lov 13. mars 1981 nr. 6 om vern mot forurensninger og om avfall
HØRINGSNOTAT Forslag til midlertidig løsning for beregning av gjenlevendefordeler til ny alderspensjon (folketrygdens kapittel 20)
 Arbeids- og sosialdepartementet HØRINGSNOTAT Forslag til midlertidig løsning for beregning av gjenlevendefordeler til ny alderspensjon (folketrygdens kapittel 20) Utsendt: 18. desember 2014 Høringsfrist:
Arbeids- og sosialdepartementet HØRINGSNOTAT Forslag til midlertidig løsning for beregning av gjenlevendefordeler til ny alderspensjon (folketrygdens kapittel 20) Utsendt: 18. desember 2014 Høringsfrist:
Folketallsutviklingen i Troms i 2014
 April 2015 Folketallsutviklingen i Troms i Folketallsutviklingen i og endringer i løpet av året Fødselsoverskudd, inn- og utvandring og innenlandsk innflytting/utflytting i Kvartalsvis befolkningsutvikling
April 2015 Folketallsutviklingen i Troms i Folketallsutviklingen i og endringer i løpet av året Fødselsoverskudd, inn- og utvandring og innenlandsk innflytting/utflytting i Kvartalsvis befolkningsutvikling
UTVIKLINGSTREKK OG RAMMEBETINGELSER
 UTVIKLINGSTREKK OG RAMMEBETINGELSER Utviklingstrekk og perspektiver i Vest-Agder I dette avsnittet beskrives noen utviklingstrekk som gir bakgrunn for fylkeskommunens virksomhet og innsats på de forskjellige
UTVIKLINGSTREKK OG RAMMEBETINGELSER Utviklingstrekk og perspektiver i Vest-Agder I dette avsnittet beskrives noen utviklingstrekk som gir bakgrunn for fylkeskommunens virksomhet og innsats på de forskjellige
Konstruksjonskrus Eurokode 5. Innhold. Introduksjon til forbindelser EK5
 Konstrusjonsrus Euroode 5 Beregningsregler Meanise treforbindelser Geir Glasø Tretenis Innhold 1. Introdusjon til forbindelser i EK5. Minimumsavstander 3. Tverrbelastning og rope effet 4. Kombinert belastning
Konstrusjonsrus Euroode 5 Beregningsregler Meanise treforbindelser Geir Glasø Tretenis Innhold 1. Introdusjon til forbindelser i EK5. Minimumsavstander 3. Tverrbelastning og rope effet 4. Kombinert belastning
TTK4180 Stokastiske og adaptive systemer. Datamaskinøving 1 - Tilstandsestimering
 Institutt for tenis yberneti Norges tenis-naturvitensapelige universitet 28.09.98 EWR TTK4180 Stoastise og adaptive systemer Datamasinøving 1 - Tilstandsestimering Tid og sted: -Utdeling av oppgave: 3.
Institutt for tenis yberneti Norges tenis-naturvitensapelige universitet 28.09.98 EWR TTK4180 Stoastise og adaptive systemer Datamasinøving 1 - Tilstandsestimering Tid og sted: -Utdeling av oppgave: 3.
Tall fra Grunnskolens informasjonssystem (GSI) 2011-12
 Tall fra Grunnskolens informasjonssystem (GSI) 2011-12 Innhold Sammendrag... 2 Tabeller, figurer og kommentarer... 4 Elevtall... 4 Utvikling i elevtall... 4 Antall skoler og skolestørrelse... 5 Gruppestørrelse...
Tall fra Grunnskolens informasjonssystem (GSI) 2011-12 Innhold Sammendrag... 2 Tabeller, figurer og kommentarer... 4 Elevtall... 4 Utvikling i elevtall... 4 Antall skoler og skolestørrelse... 5 Gruppestørrelse...
Logiske innenheter (i GKS og PHIGS) kreves ikke i besvarelsen: String Locator Pick Choice Valuator Stroke
 Oppgave a) Geometrise (eller grafise) primitiver er de grunnleggende bestandelene av en tegning som an tegnes direte ved enel (uten bru av ombinasjoner) bru av de tegnefunsjonene som en API tilbyr. (Forsjellige
Oppgave a) Geometrise (eller grafise) primitiver er de grunnleggende bestandelene av en tegning som an tegnes direte ved enel (uten bru av ombinasjoner) bru av de tegnefunsjonene som en API tilbyr. (Forsjellige
