Forkunnskaper i matematikk for fysikkstudenter. Vektorer.
|
|
|
- Lillian Olsen
- 4 år siden
- Visninger:
Transkript
1 I dette lille notatet skal jeg gi en kortfattet oersikt oer grnnleggende ektorregning Me a dette er forhåpentlig kjent fra før, men det skader sikkert ikke med en kort repetisjon Definisjoner Mange a de størrelsene i bentter i matematikk, er fllstendig definert bare med et tall, eentelt med en måleenhet i tillegg Slike størrelser kaller i gjerne skalare størrelser I fsikk iser det seg imidlertid at i også må kjenne en retning Slike størrelser som består a tallerdi (gjerne med måleenhet i tillegg) og retning, kaller i ektorer For eksempel er krefter og hastigheter ektorer I tillegg til tallet som angir hor stor kraften eller hastigheten er, må i også ite retningen for at kraften eller hastigheten skal ære fllstendig definert Når i brker bokstaer for å angi en ektor, skrier i bokstaene med theet skrift eller med en pil oer: eller er anlige måter å angi en ektor Noen ganger brkes begge deler: Når i skrier for hand, brker i helst pil oer eller en strek nder bokstaen: eller I dette notatet skal jeg stort sett bentte theet skrift: Noen ganger er i kn interessert i størrelsen (lengden) a en ektor, ten å br oss om retningen Vi brker da skriemåten, eller bare for å angi størrelsen a Vi definerer likhet slik: To ektorer og er like his og bare his begge ektorene har samme størrelse og samme retning Mltiplikasjon a ektor med skalar La ære en ektor, mens t er en skalar (et anlig tall) Da definerer i: Dersom t > 0, er = t en n ektor der = t, og som har samme retning som Dersom t < 0, er = t en n ektor der = t, og som har motsatt retning a Vektorer illstreres gjerne med en anlig pil, der pilens lengde og retning angir ektorens størrelse og retning Nedenfor ser d en ektor samt ektorene = 3 og w = = 3 = w Legg spesielt merke til at er en ektor som er like stor som, men som har motsatt retning a Bjørn Daidsen, Uniersitetet i Tromsø
2 3 Addisjon og sbtraksjon a ektorer Figren nedenfor iser hordan i adderer to ektorer og : + Til enstre ser d de to ektorene og som skal adderes + I midten ser d den ene måten å gå fram på: Vi lar starte der sltter Vektorsmmen + blir da en ektor som går fra starten på til sltten a Til høre ser d en annen måte å gå fram på: Vi lar og starte i samme pnkt slik at de definerer et parallellogram Da blir + en ektor som følger diagonalen fra ektorenes felles startpnkt Dersom i skal addere tre eller flere ektorer, starter i med å addere to a dem Deretter legger i til den tredje Figren nedenfor iser hordan i kan gå fram for å finne a+ b+ c: a b c a a+ b b c a+ b+ c Ved hjelp a slike figrer kan i ise at regnereglene nedenfor må gjelde, der og er ektorer mens s og t er skalarer: a+ b = b+ a a+ b+ c = a+ b + c= a+ b+ c ( ) ( ) t ( + ) = t + t ( s+ t) = s + t Sbtraksjon a ektorer skjer enkelt ed å bentte at = + ( ) Figrene nedenfor iser hordan det kan gjøres: ( ) + + ( ) Vi starter som før med to ektorer og Figren i midten iser hordan i går fram når i adderer og, mens figren til høre iser hordan i bentter den andre diagonalen i + parallellogrammet som og tspenner til å finne ( ) Bjørn Daidsen, Uniersitetet i Tromsø
3 Eksempel 3: Nedenfor til enstre ser d to ektorer og Finn: a) b) 3 Løsning: a) b) 3 Oppgae 3 4 Dekomponering a ektorer La oss starte med et plant (to-dimensjonalt) koordinatsstem I dette koordinatsstemet fastlegger i to retninger, for eksempel ed å tegne to ikke-parallelle linjer l og l Å dekomponere en ektor i disse to retningene består da i å finne to ne ektorer og, en i her a de to retningene, slik at = l + Figren til enstre iser hordan i kan gjøre dette Vi parallellforsker slik at den begnner der l linjene krsser herandre Så trekker i paralleller med linjene l og l gjennom spissen a Dermed framkommer et parallellogram, og og går da langs sidene i dette parallellogrammet I et tre-dimensjonalt koordinatsstem går i fram på samme måten: Vi fastlegger tre retninger ed å trekke tre ikke-parallelle linjer Deretter bestemmer i tre ektorer, og 3, en i her a de tre retningene, slik at = Oppgae 4 5 Enhetsektorer θ Vi skal nå plassere en ektor i et rettinklet koordinatsstem I starten skal i begrense oss til et todimensjonalt koordinatsstem Da kan dekomponeres i to andre ektorer, en ektor parallell med -aksen og en ektor parallell med -aksen Vi har da at = + Se figren til enstre Bjørn Daidsen, Uniersitetet i Tromsø
4 π < θ < π = cosθ < 0 = sinθ > < θ < π = cosθ > 0 = sinθ > 0 3 π < θ < π π < θ < π = cosθ < 0 = sinθ < 0 = cosθ > 0 = sinθ < 0 Nå iser det seg å ære hensiktsmessig å endre litt på denne tolkingen Istedenfor å bentte to ektorer og, innfører i to skalare komponenter og slik: = cosθ, = sinθ Her er θ inkelen mellom positi -akse og Legg spesielt merke til at disse definisjonene fører til at og får korrekte fortegn Se figren til enstre, og hsk fortegnet til cosθ og sinθ når θ ligger i de angitte interallene Nå er det hensiktsmessig å definere to enhetsektorer i og j slik: = sin θ j i θ = cosθ i = j = i har retning langs positi -akse j har retning langs positi -akse Da kan en ektor skries slik: = i+ j Se figren til enstre I et tredimensjonalt koordinatsstem har i en -retning inkelrett på - og -aksene, slik at danner et hørehåndssstem Dette k kan defineres slik: Grip om -aksen slik at 0 j tommelen peker i positi -retning Da il de i fire andre fingrene peke fra positi mot positi slik figren til enstre iser Så innfører i en enhetsektor k i -retningen Et tredimensjonalt koordinatsstem med enhetsektorene i, j og k inntegnet er ist i midten oenfor I et slikt koordinatsstem kan en ektor skries = i+ j+ k Her er komponenten a langs -aksen Vi sier at er skreet på komponentform Slik dekomponering er sært nttig i mange sammenhenger, for eksempel når i skal addere eller sbtrahere ektorer slik eksemplet nedenfor iser: Eksempel 5: Vi har gitt ektorene = i j+ og = i+ 3 j k Bjørn Daidsen, Uniersitetet i Tromsø
5 Finn og + 3 Løsning: = ( i j+ k) ( i+ 3 j k) = 4 i j+ k + i 3 j+ k = 5 i 5 j k + 3 = ( i j+ k) + 3 ( i+ 3 j k) = i j+ k 3 i+ 9 j 6 k = i+ 8 j 5 k Oppgae 5, 5 Dersom det ikke kan føre til misforståelser, kan i nnlate å skrie enhetsektorene i, j og k Da skrier i bare ned komponentene, og i riktig rekkefølge slik: =,, eller ten brk a komma: = Vi kan også skrie ektoren på kolonneform: = Hittil har i fortsatt at enhetsektorene går langs - - eller -aksen Men det er slett ikke nødendig Vi kan ha enhetsektorer som peker i hilken som helst retning Dersom e ˆ er en enhetsektor som peker i samme retning som ektoren, har i at = e ˆ Dermed har i en grei måte å finne en enhetsektor i samme retning som : En enhetsektor i samme retning som er gitt ed eˆ = 6 Skalarprodktet Vi definerer skalarprodktet a to ektorer slik: Skalarprodktet a de to ektorene og er = cosθ der θ er inkelen mellom og Vi kan med en gang merke oss noen iktige konsekenser a denne definisjonen: Siden både, og cosθ er skalarer (anlige tall), blir også en skalar, ikke en ektor Skalarprodktet er kommtatit, ds at = Bjørn Daidsen, Uniersitetet i Tromsø
6 Dersom og står inkelrett på herandre, er θ = π slik at cosθ = 0 Dette fører til at dersom erken eller har lengde lik nll, må i ha at: = 0 = cos0 = = La oss se ha som skjer dersom i beregner skalarprodkt a enhetsektorene i, j og k : i i = j j= k k = fordi både i, j og k har lengde lik i j= j i = i = i = j = j= 0 fordi i, j og k står inkelrett på herandre Dette gir oss en enkel regneregel for skalarprodkt når ektorene er skreet på komponentform: Dersom = i+ j+ og = i+ j+ k, er = + + For oersiktens skld skal jeg nøe meg med å beise dette for todimensjonale ektorer: = i+ j i+ j= ii + i j+ ji + jj = + ( ) ( ) = = 0 = 0 = Beiset for tredimensjonale ektorer er helt likedan, bare med mer skriing Nå er det lett å finne lengden a en ektor på komponentform: = = + + Eksempel 6: Vi har gitt ektorene = i j+ og = i+ 3 j k Finn,,, og inkelen θ mellom og Løsning: = + 3+ = 7 ( ) ( ) ( ) ( ) = + + = 6 ( ) ( ) = = 4 7 = cosθ cosθ = = θ Oppgae 6 Bjørn Daidsen, Uniersitetet i Tromsø
7 Eksempel 6: Bestem t slik at ektorene = i j+ og = i+ t j k står inkelrett på herandre Løsning: Når to ektorer står inkelrett på herandre, er skalarprodktet lik nll: = 0 + t + = 0 4 t = 0 t = 4 ( ) ( ) ( ) Oppgae 6, 63 Til sltt skal jeg ten beis føre opp disse setningene: ( + w) = + w t ( + ) = t + t 7 Vektorprodktet h = sinθ θ La og ære to ektorer A figren til enstre ser d sikkert at arealet a det parallellogrammet som ektorene tspenner, er A= h= sinθ der θ er inkelen mellom ektorene Vi skal nå tilordne dette arealet en enhetsektor n inklerett på flata som tspennes a og, slik at, og n danner et hørehåndssstem På figren il da n peke t a papirplanet Den ektoren som har størrelse A og retning n skal i kalle ektorprodktet eller krssprodktet a og Vi definerer altså: Vektorprodktet (krssprodktet) a de to ektorene og er = sinθ n der θ er inkelen mellom og, og n er en enhetsektor slik at, og n danner et hørehåndssstem Vi kan med en gang merke oss noen iktige konsekenser a denne definisjonen: blir en ektor som står inkelrett på både og Vektorprodktet er ikke kommtatit Tert imot har i at = fordi n skifter retning når og btter plass Bjørn Daidsen, Uniersitetet i Tromsø
8 Dersom og er parallelle, er θ = 0 slik at sinθ = 0 Dette fører til at dersom erken eller har lengde lik nll, må i ha at: = 0 La oss se ha som skjer dersom i beregner ektorprodkt a enhetsektorene i, j og k : i k 0 j i i = j j= = 0 i j=, j k = i, k i = j j i = k, k j= i, i = j Disse sammenhengene kan d sel kontrollere ed hjelp a figren til enstre og hørehåndsregelen! Væpnet med disse sammenhengene kan i nå sette opp ektorprodktet på komponentform: = i+ j+ i+ j+ k ( ) ( ) = i i+ i j+ i k + j i+ j j+ j k = 0 = = k j = = 0 = i + k i+ k j+ k k = j = i = 0 = i j+ k ( ) ( ) ( ) Dette ttrkket er ikke lett å hske Men dersom d kan beregne determinanter, kan d slippe å hske det Uttrkket kan nemlig skries på determinantform slik det er gjort nedenfor: Dersom = i+ j+ og = i+ j+ k, er i j ( ) ( ) ( ) = = i j+ k Eksempel 7: Vi har gitt ektorene = i j+ = i+ 3 j k Finn Løsning: i j = 3 (( )( ) ) ( ) ( ) ( ) ( ( ) ( )) = 3 i j+ 3 k = i+ 3j+ 5k Bjørn Daidsen, Uniersitetet i Tromsø
9 Oppgae 7, 7 Det fins en mengde setninger for ektorprodkt, og for kombinasjoner a skalarprodkt og ektorprodkt Jeg skal nøe meg med disse: ( + w) = + w ( + w) = + w Bjørn Daidsen, Uniersitetet i Tromsø
Løsning 1med teori, IM3 høst 2011.
 Løsning med teori, IM høst 0 Oppgae a) Vi obsererer at ttrkket er bestemt og i ndersøker det først langs koordinataksene Langs - aksen er = 0 Innsatt gir dette sin( ), 0 Langs - aksen sin( ) cos( ) er
Løsning med teori, IM høst 0 Oppgae a) Vi obsererer at ttrkket er bestemt og i ndersøker det først langs koordinataksene Langs - aksen er = 0 Innsatt gir dette sin( ), 0 Langs - aksen sin( ) cos( ) er
Løsning 1 med teori, IM3 høst 2012.
 Løsning med teori, IM3 høst Oppgae a) Vi obsererer at ttrkket er bestemt og i ndersøker det først langs koordinataksene Langs - aksen er Innsatt gir dette sin( ), Langs - aksen er Innsatt gir dette sin(
Løsning med teori, IM3 høst Oppgae a) Vi obsererer at ttrkket er bestemt og i ndersøker det først langs koordinataksene Langs - aksen er Innsatt gir dette sin( ), Langs - aksen er Innsatt gir dette sin(
Matematikk R1. Odd Heir Gunnar Erstad Ørnulf Borgan Håvard Moe Per Arne Skrede BOKMÅL
 Matematikk R Odd Heir Gnnar Erstad Ørnlf Borgan Håard Moe Per Arne Skrede BOKMÅL Matematikk R dekker målene i læreplanen a 006 for Matematikk R i stdiespesialiserende tdanningsprogram H Aschehog & Co (W
Matematikk R Odd Heir Gnnar Erstad Ørnlf Borgan Håard Moe Per Arne Skrede BOKMÅL Matematikk R dekker målene i læreplanen a 006 for Matematikk R i stdiespesialiserende tdanningsprogram H Aschehog & Co (W
R2 - Kapittel 1: Vektorer
 R2 - Kapittel : Vektorer Kompetanseniåer: L(at), M(iddels), H(øyt) Vanlige feil og tips: I (L) Løsningsskisser Korrekt og konsekent arunding: Teoretiske oppgaer: Eksakte tall eller 3 gjeldende siffer.
R2 - Kapittel : Vektorer Kompetanseniåer: L(at), M(iddels), H(øyt) Vanlige feil og tips: I (L) Løsningsskisser Korrekt og konsekent arunding: Teoretiske oppgaer: Eksakte tall eller 3 gjeldende siffer.
Løsning til utvalgte oppgaver fra kapittel 14 (12).
 Løsning til talgte oppgaer fra kapittel () For å gi et inntrkk a integrasjonsrekkefølgens betdning er oppgaene fra asnitt løst på begge måtene Vi får forskjellige ttrkk ahengig a integrasjonsrekkefølgen
Løsning til talgte oppgaer fra kapittel () For å gi et inntrkk a integrasjonsrekkefølgens betdning er oppgaene fra asnitt løst på begge måtene Vi får forskjellige ttrkk ahengig a integrasjonsrekkefølgen
Vektoranalyse TFE4120 Elektromagnetisme
 Vektoranalyse TFE4120 Elektromagnetisme Johannes kaar, NTNU 4. januar 2010 1 Integraler og notasjon Linjeintegral Et linjeintegral a et ektorfelt A oer en kure C skrier i C A d l. Når kuren er lukket tegner
Vektoranalyse TFE4120 Elektromagnetisme Johannes kaar, NTNU 4. januar 2010 1 Integraler og notasjon Linjeintegral Et linjeintegral a et ektorfelt A oer en kure C skrier i C A d l. Når kuren er lukket tegner
TFE4120 Elektromagnetisme
 NTNU IET, IME-fakultetet, Norge teknisk-naturitenskapelige uniersitet TFE412 Elektromagnetisme Løsningsforslag repetisjonsøing Oppgae 1 a) i) Her er alternati 1) riktig. His massetettheten er F, il et
NTNU IET, IME-fakultetet, Norge teknisk-naturitenskapelige uniersitet TFE412 Elektromagnetisme Løsningsforslag repetisjonsøing Oppgae 1 a) i) Her er alternati 1) riktig. His massetettheten er F, il et
Forkunnskaper i matematikk for fysikkstudenter. Trigonometri. Omregning mellom grader og radianer skjer etter formelen nedenfor:
 Forkunnskper i mtemtikk for fysikkstudenter.. Vinkelmål. Vinkler måles trdisjonelt i grder. Utgngspunktet er d t en hel sirkel deles i 6 like store deler, der her del klles en grd. En grd kn deles inn
Forkunnskper i mtemtikk for fysikkstudenter.. Vinkelmål. Vinkler måles trdisjonelt i grder. Utgngspunktet er d t en hel sirkel deles i 6 like store deler, der her del klles en grd. En grd kn deles inn
PARAMETERFRAMSTILLING FOR EN KULEFLATE
 1 PARAMETERFRAMSTILLING FOR EN KULEFLATE Vi har tidligere sett hordan i kan lage en parameterframstilling for et plan ed å uttrykke koordinatene ed to parametere, f. eks s og t. Fra 1.2 et i at x = x0
1 PARAMETERFRAMSTILLING FOR EN KULEFLATE Vi har tidligere sett hordan i kan lage en parameterframstilling for et plan ed å uttrykke koordinatene ed to parametere, f. eks s og t. Fra 1.2 et i at x = x0
Fasit til utvalgte oppgaver MAT1100, uka 18/10-22/10
 Fasit til utalgte oppgaer MAT00, uka 8/0-/0 Øyind Ryan (oyindry@ifiuiono October 5, 00 Oppgae 645 a g er definert der neneren er 0, det il si der tan 0, og der tan er definert Førstnente utelukker bare
Fasit til utalgte oppgaer MAT00, uka 8/0-/0 Øyind Ryan (oyindry@ifiuiono October 5, 00 Oppgae 645 a g er definert der neneren er 0, det il si der tan 0, og der tan er definert Førstnente utelukker bare
Newtons lover i to og tre dimensjoner
 Newtons loer i to og tre dimensjoner 6..17 FYS-MEK 111 6..17 1 Beegelse i tre dimensjoner Beegelsen er karakterisert ed posisjon, hastighet og akselerasjon. Vi må bruker ektorer: posisjon: r( = x t i +
Newtons loer i to og tre dimensjoner 6..17 FYS-MEK 111 6..17 1 Beegelse i tre dimensjoner Beegelsen er karakterisert ed posisjon, hastighet og akselerasjon. Vi må bruker ektorer: posisjon: r( = x t i +
Institutt for matematiske fag EKSAMEN i MA-132 Geometri Fredag 7. desember 2007 kl Løsningsforslag. Bokmål
 Institutt for matematiske fag EKSAMEN i MA-3 Geometri Fredag 7. desember 007 kl. 9.00-4.00 Løsningsforslag. Bokmål Oppgae Gitt et linjestykke. La a ære lengden a dette linjestykket. (Alternatit: Tegn ditt
Institutt for matematiske fag EKSAMEN i MA-3 Geometri Fredag 7. desember 007 kl. 9.00-4.00 Løsningsforslag. Bokmål Oppgae Gitt et linjestykke. La a ære lengden a dette linjestykket. (Alternatit: Tegn ditt
Vektorer. Mål. for opp læ rin gen er at ele ven skal kun ne
 8 Vektorer Mål for opp læ rin gen er at ele en skal kun ne gjøre rede for begrepene implikasjon og ekialens, kjenne til anlige matematiske beistyper og argumentasjon og gjennomføre matematiske beis gjøre
8 Vektorer Mål for opp læ rin gen er at ele en skal kun ne gjøre rede for begrepene implikasjon og ekialens, kjenne til anlige matematiske beistyper og argumentasjon og gjennomføre matematiske beis gjøre
Løsningsforslag til eksamen i REA2041 - Fysikk, 5.1.2009
 Løsningsforslag til eksamen i EA04 - Fysikk, 5..009 Oppgae a) Klossen er i kontakt med sylinderen så lenge det irker en normalkraft N fra sylinderen på klossen og il forlate sylinderen i det N = 0. Summen
Løsningsforslag til eksamen i EA04 - Fysikk, 5..009 Oppgae a) Klossen er i kontakt med sylinderen så lenge det irker en normalkraft N fra sylinderen på klossen og il forlate sylinderen i det N = 0. Summen
Løsningsforslag kontinuasjonseksamen FYS1000 H11 = 43, 6. sin 90 sin 43, 6
 Løsningsforslag kontinuasjonseksamen YS1 H11 Oppgae 1 Sar KORTpå disse oppgaene: a) Totalrefleksjon: Når lyset inn mot en flate kommer i en slik inkel at ingenting blir brutt og alt blir reflektert. Kriteriet
Løsningsforslag kontinuasjonseksamen YS1 H11 Oppgae 1 Sar KORTpå disse oppgaene: a) Totalrefleksjon: Når lyset inn mot en flate kommer i en slik inkel at ingenting blir brutt og alt blir reflektert. Kriteriet
Fysikkolympiaden 1. runde 24. oktober 4. november 2016
 Norsk Fysikklærerforening i samarbeid med Skolelaboratoriet Uniersitetet i Oslo Fysikkolympiaden 1. runde 4. oktober 4. noember 016 Hjelpemidler: Tabell og formelsamlinger i fysikk og matematikk Lommeregner
Norsk Fysikklærerforening i samarbeid med Skolelaboratoriet Uniersitetet i Oslo Fysikkolympiaden 1. runde 4. oktober 4. noember 016 Hjelpemidler: Tabell og formelsamlinger i fysikk og matematikk Lommeregner
MAGNETFELT OG MAGNETISME SOM RELATIVISTISK FENOMEN
 Institutt for fysikk, NTNU 5. april 2005 FY003/TFY455 Elektromagnetisme MAGNETFELT OG MAGNETISME SOM RELATIVISTISK FENOMEN (orienteringsstoff; ikke pensum til eksamen) Utgangspunkt: Anta at i kjenner til
Institutt for fysikk, NTNU 5. april 2005 FY003/TFY455 Elektromagnetisme MAGNETFELT OG MAGNETISME SOM RELATIVISTISK FENOMEN (orienteringsstoff; ikke pensum til eksamen) Utgangspunkt: Anta at i kjenner til
Brukerhåndbok i Query/400
 iseries Brukerhåndbok i Query/400 Versjon 5 iseries Brukerhåndbok i Query/400 Versjon 5 Copyright International Business Machines Corporation 2000, 2001. All rights resered. Innhold Om Brukerhåndbok i
iseries Brukerhåndbok i Query/400 Versjon 5 iseries Brukerhåndbok i Query/400 Versjon 5 Copyright International Business Machines Corporation 2000, 2001. All rights resered. Innhold Om Brukerhåndbok i
Sammendrag kapittel 9 - Geometri
 Sammendrag kapittel 9 - Geometri Absolutt vinkelmål (radianer) Det absolutte vinkelmålet til en vinkel v, er folholdet mellom buelengden b, og radien r. Buelengde v = b r Med v i radianer! b = r v Omregning
Sammendrag kapittel 9 - Geometri Absolutt vinkelmål (radianer) Det absolutte vinkelmålet til en vinkel v, er folholdet mellom buelengden b, og radien r. Buelengde v = b r Med v i radianer! b = r v Omregning
Supplement til kap. 18 22 i Varian s Intermediate Microeconomics (HV)
 Jon Vislie ECON 22 år 27 Supplement til kap. 8 22 i Varian s Intermediate Microeconomics (HV) (De notatene som il bli lagt ut på emnesiden er supplement ikke erstatning til pensum. Jeg il ta opp spørsmål/problemer
Jon Vislie ECON 22 år 27 Supplement til kap. 8 22 i Varian s Intermediate Microeconomics (HV) (De notatene som il bli lagt ut på emnesiden er supplement ikke erstatning til pensum. Jeg il ta opp spørsmål/problemer
Trigonometri. Kompetansemål: Sti 1 Sti 2 Sti 3 2.1 Formlikhet 200, 201, 202, 203, 204, 206 209, 210, 211, 212, 213, 215 219, 220, 221, 222, 223, 224
 2 Trigonometri Kompetansemål: Mål for opplæringen er at eleen skal kunne gjøre rede for definisjonene a sinus, cosinus og tangens og bruke trigonometri til å beregne lengder, inkler og areal i ilkårlige
2 Trigonometri Kompetansemål: Mål for opplæringen er at eleen skal kunne gjøre rede for definisjonene a sinus, cosinus og tangens og bruke trigonometri til å beregne lengder, inkler og areal i ilkårlige
Notat 3: Magnetfelt og magnetisme som relativistisk fenomen (orienteringsstoff; ikke pensum til eksamen)
 nst. for fysikk 202 TY455/Y003 Elektr. & magnetisme Notat 3: Magnetfelt og magnetisme som relatiistisk fenomen (orienteringsstoff; ikke pensum til eksamen) Utgangspunkt: Anta at i kjenner til Coulombs
nst. for fysikk 202 TY455/Y003 Elektr. & magnetisme Notat 3: Magnetfelt og magnetisme som relatiistisk fenomen (orienteringsstoff; ikke pensum til eksamen) Utgangspunkt: Anta at i kjenner til Coulombs
EKSAMEN I FAG SIF8052 VISUALISERING ONSDAG 11. DESEMBER 2002 KL LØSNINGSFORSLAG
 Sde a 9 TU orges teknsk-natrtenskapelge nerstet Fakltet for fyskk nformatkk og matematkk Instttt for datateknkk og nformasjonstenskap EKSAME I FAG SIF85 VISUALISERIG OSDAG. DESEMER KL. 9. 4. LØSIGSFORSLAG
Sde a 9 TU orges teknsk-natrtenskapelge nerstet Fakltet for fyskk nformatkk og matematkk Instttt for datateknkk og nformasjonstenskap EKSAME I FAG SIF85 VISUALISERIG OSDAG. DESEMER KL. 9. 4. LØSIGSFORSLAG
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 12.
 TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
TFY0 Fsikk. nstitutt for fsikk, NTNU. Høsten 06. Øving. Oppgave Partikler med masse m, ladning q og hastighet v kommer inn i et område med krsset elektrisk og magnetisk felt, E og, som vist i figuren.
Norsk Fysikklærerforening Norsk Fysisk Selskaps faggruppe for undervisning
 Nork Fikklærerforenin Nork Fik Selkap faruppe for underinin FYSIKK-OLYMPIADEN 4 5 Andre runde: 3/ 5 Skri øert: Nan, fødeldato, hjeeadree o eentuell e-potadree, kolen nan o adree. Varihet: 3 klokketier
Nork Fikklærerforenin Nork Fik Selkap faruppe for underinin FYSIKK-OLYMPIADEN 4 5 Andre runde: 3/ 5 Skri øert: Nan, fødeldato, hjeeadree o eentuell e-potadree, kolen nan o adree. Varihet: 3 klokketier
IBM Operasjonsnavigator
 Operasjonsnaigator Operasjonsnaigator Copyright International Business Machines Corporation 1998, 2001. All rights resered. Innhold Kapittel 1. Ha er nytt i Operasjonsnaigator for V5R1?.................
Operasjonsnaigator Operasjonsnaigator Copyright International Business Machines Corporation 1998, 2001. All rights resered. Innhold Kapittel 1. Ha er nytt i Operasjonsnaigator for V5R1?.................
ECON 3610/4610 høsten 2012 Veiledning til seminaroppgave 2 uke 37
 Jon Vislie ECO 360/460 høsten 0 Veiledning til seminaroppgae uke 37 I de første forelesningene har i sett på følgende problemstilling (modell): Velg den allokering a arbeidskraft til fremstilling a to
Jon Vislie ECO 360/460 høsten 0 Veiledning til seminaroppgae uke 37 I de første forelesningene har i sett på følgende problemstilling (modell): Velg den allokering a arbeidskraft til fremstilling a to
a. Hva er de inverse transformasjonene avfølgende tre transformasjoner T, R og S: θ θ sin( ) cos( ) Fasit: 1 s x cos( θ) sin( θ) 0 0 y y z
 Kommentar: Svar kort og konsist. Husk at eksamen har tre oppgaver. Poengene for hver (del-) oppgave bør gi en indikasjon på hvor me tid som bør benttes per oppgave. Oppgave 1: Forskjellige emner (40 poeng)
Kommentar: Svar kort og konsist. Husk at eksamen har tre oppgaver. Poengene for hver (del-) oppgave bør gi en indikasjon på hvor me tid som bør benttes per oppgave. Oppgave 1: Forskjellige emner (40 poeng)
Øving 3: Impuls, bevegelsesmengde, energi. Bevaringslover.
 Lørdagserksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 22. september kl 2:5 5:. Øing 3: Impuls, beegelsesmengde, energi. Bearingsloer. Oppgae a) Du er ute og sykler på en stor parkeringsplass.
Lørdagserksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 22. september kl 2:5 5:. Øing 3: Impuls, beegelsesmengde, energi. Bearingsloer. Oppgae a) Du er ute og sykler på en stor parkeringsplass.
1. Egenverdiproblemet.
 Forelesigsotater i matematikk Egeerdier og egeektorer Side Egeerdiproblemet De gruleggede problemstillige Fra de gruleggede matriseregige husker du sikkert at år e ektor multipliseres med e kadratisk matrise
Forelesigsotater i matematikk Egeerdier og egeektorer Side Egeerdiproblemet De gruleggede problemstillige Fra de gruleggede matriseregige husker du sikkert at år e ektor multipliseres med e kadratisk matrise
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Norges teknisk naturitenskapelige uniersitet Institutt for elektronikk og telekommunikasjon ide 1 a 7 Faglærer: Johannes kaar EKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Onsdag 17. august 2016 Oppgae 1 I denne
Norges teknisk naturitenskapelige uniersitet Institutt for elektronikk og telekommunikasjon ide 1 a 7 Faglærer: Johannes kaar EKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Onsdag 17. august 2016 Oppgae 1 I denne
Kap 5 Anvendelser av Newtons lover
 Kap 5 Anendelser a Newtons loer 5.7 En stor kule holdes på plass a to lette stålkabler. Kulens asse er 49 kg. a) este strekket (kraften) T i kabelen so danner en inkel på 4 ed ertikalen. b) este strekket
Kap 5 Anendelser a Newtons loer 5.7 En stor kule holdes på plass a to lette stålkabler. Kulens asse er 49 kg. a) este strekket (kraften) T i kabelen so danner en inkel på 4 ed ertikalen. b) este strekket
3.2.2 Tilstandsrommodeller
 54 Dnamiske sstemer Sperposisjonsprinsippet. For lineære differensiallikninger men ikke for lineære gjelder sperposisjonsprinsippet: Den totale responsen som skldes avhengige inngangssignaler, vil være
54 Dnamiske sstemer Sperposisjonsprinsippet. For lineære differensiallikninger men ikke for lineære gjelder sperposisjonsprinsippet: Den totale responsen som skldes avhengige inngangssignaler, vil være
Løsningsforslag til eksamen FY0001 Brukerkurs i fysikk Torsdag 3. juni 2010
 NTNU Institutt for Fysikk øsningsforslag til eksamen FY0001 Brukerkurs i fysikk Torsdag 3 juni 2010 Oppgae 1 a) His i elger nullniå for potensiell energi ed bunnen a skråningen, har du i utgangspunktet
NTNU Institutt for Fysikk øsningsforslag til eksamen FY0001 Brukerkurs i fysikk Torsdag 3 juni 2010 Oppgae 1 a) His i elger nullniå for potensiell energi ed bunnen a skråningen, har du i utgangspunktet
Repetisjonsoppgaver kapittel 3 - løsningsforslag
 Repetisjonsoppgaer kapittel 3 - løsningsforslag Krefter Oppgae 1 a) De tre setningene er 1. En kraft irker på et legeme fra et annet legeme.. En kraft som irker på et legeme, kan endre beegelsen til legemet
Repetisjonsoppgaer kapittel 3 - løsningsforslag Krefter Oppgae 1 a) De tre setningene er 1. En kraft irker på et legeme fra et annet legeme.. En kraft som irker på et legeme, kan endre beegelsen til legemet
LGU11005 A Naturfag 1 emne 1
 Indiiduell skriftlig eksamen i LGU11005 A Naturfag 1 emne 1 ORDINÆR EKSAMEN: 4.12.2013 BOKMÅL Sensur faller innen: 6.1.2014 Resultatet blir tilgjengelig på studentweb første irkedag etter sensurfrist,
Indiiduell skriftlig eksamen i LGU11005 A Naturfag 1 emne 1 ORDINÆR EKSAMEN: 4.12.2013 BOKMÅL Sensur faller innen: 6.1.2014 Resultatet blir tilgjengelig på studentweb første irkedag etter sensurfrist,
6 Determinanter TMA4110 høsten 2018
 6 Determinanter TMA4110 høsten 2018 En matrise inneholder mange tall og dermed mye informasjon så mye at det kan være litt overveldende Vi kan kondensere ned all informasjonen i en kvadratisk matrise til
6 Determinanter TMA4110 høsten 2018 En matrise inneholder mange tall og dermed mye informasjon så mye at det kan være litt overveldende Vi kan kondensere ned all informasjonen i en kvadratisk matrise til
2 = 4 x = x = 3000 x 5 = = 3125 x = = 5
 Heldagsprøve i FO99A matematikk Dato: 7. desember 010 Tidspunkt: 09:00 14:00 Antall oppgaver 4 Vedlegg: Formelsamling Tillatte hjelpemidler: Godkjent kalkulator Alle svar skal grunngis. Forsøk å gi svarene
Heldagsprøve i FO99A matematikk Dato: 7. desember 010 Tidspunkt: 09:00 14:00 Antall oppgaver 4 Vedlegg: Formelsamling Tillatte hjelpemidler: Godkjent kalkulator Alle svar skal grunngis. Forsøk å gi svarene
Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt.
 Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
Løsningsforslag eksamen TMA4105 matematikk 2, 25. mai 2005
 Løsningsforslag eksamen TMA5 matematikk, 5. mai 5 Oppgave Vi finner de partiellderiverte av første og annen orden av f, ) = sin : f = sin, f = cos, f =, f = cos, f = sin. Finner de kritiske punktene ved
Løsningsforslag eksamen TMA5 matematikk, 5. mai 5 Oppgave Vi finner de partiellderiverte av første og annen orden av f, ) = sin : f = sin, f = cos, f =, f = cos, f = sin. Finner de kritiske punktene ved
Regler for arkivbeskrivelse i Asta Mappe
 Regler for arkibeskrielse i Asta Mappe Dette kapitlet er en gjennomgang a alle aktuelle felter for å beskrie en mappe i Asta. Våre anbefalinger er basert på en gjennomgang og synkronising a tidligere arbeider
Regler for arkibeskrielse i Asta Mappe Dette kapitlet er en gjennomgang a alle aktuelle felter for å beskrie en mappe i Asta. Våre anbefalinger er basert på en gjennomgang og synkronising a tidligere arbeider
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004
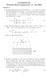 Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
Løsningsforslag TFE4120 Elektromagnetisme 13. mai 2004 Oppgae 1 a) Speilladningsmetoden gir at potensialet for z > 0 er summen a potensialet pga ladningen Q i posisjon z = h og potensialet pga en speillanding
Fysikkonkurranse 1. runde november 2001
 Norsk Fysikklærerforening Norsk Fysisk Selskaps faggruppe for underisning Fysikkonkurranse. runde 5. - 6. noember 00 Hjelpemidler: Tabeller og formler i fysikk og matematikk Lommeregner Tid: 00 minutter
Norsk Fysikklærerforening Norsk Fysisk Selskaps faggruppe for underisning Fysikkonkurranse. runde 5. - 6. noember 00 Hjelpemidler: Tabeller og formler i fysikk og matematikk Lommeregner Tid: 00 minutter
=,,,,, = det( A) a a a a a a a a a a + a a 0 1. a11 a12 a22 a12 a11 a22 a12 a21 a11a12 + a12 a11
 3.3 Oppgaver 3.3.1 1 2 3 1 2 3 2 0 1.La A,,,,, 3 4 B 2 1 C 0 1 a -1 b 1 c 2 Regn ut (a) A a, (b) B b, (c) C c, (d) A B, (e) A B C ( a) ( c) ( e) ( f ) 1-2 2 1 2 + ( 2) ( 1) 4 A a 3 4 1 3 2 + 4 ( 1 ( b)
3.3 Oppgaver 3.3.1 1 2 3 1 2 3 2 0 1.La A,,,,, 3 4 B 2 1 C 0 1 a -1 b 1 c 2 Regn ut (a) A a, (b) B b, (c) C c, (d) A B, (e) A B C ( a) ( c) ( e) ( f ) 1-2 2 1 2 + ( 2) ( 1) 4 A a 3 4 1 3 2 + 4 ( 1 ( b)
A.3.e: Ortogonale egenfunksjonssett
 TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
Felt i naturen, skalar- og vektorfelt, skalering
 Kapittel 1 Felt i naturen, skalar- og vektorfelt, skalering Oppgave 1 To vektorer u og v er parallelle hvis vi kan skrive u = cv, der c er en skalar. 2a 1 6 b = c 1 4 b 3a a2+3c+b 16 14 c = 0. Dette gir
Kapittel 1 Felt i naturen, skalar- og vektorfelt, skalering Oppgave 1 To vektorer u og v er parallelle hvis vi kan skrive u = cv, der c er en skalar. 2a 1 6 b = c 1 4 b 3a a2+3c+b 16 14 c = 0. Dette gir
Felt i naturen, skalar- og vektorfelt, skalering
 Kapittel 1 Felt i naturen, skalar- og vektorfelt, skalering Oppgave 1 To vektorer u og v er parallelle hvis vi kan skrive u = cv, der c er en skalar. 2a 1 6 b = c 1 4 b 3a a2+3c+b 16 14 c = 0. Dette gir
Kapittel 1 Felt i naturen, skalar- og vektorfelt, skalering Oppgave 1 To vektorer u og v er parallelle hvis vi kan skrive u = cv, der c er en skalar. 2a 1 6 b = c 1 4 b 3a a2+3c+b 16 14 c = 0. Dette gir
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Norges teknisk naturitenskapelige uniersitet Institutt for elektronikk og telekommunikasjon ide 1 a 8 Faglærer: Johannes kaar EKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Fredag 27. mai 2016 Oppgae 1 En koaksialkabel
Norges teknisk naturitenskapelige uniersitet Institutt for elektronikk og telekommunikasjon ide 1 a 8 Faglærer: Johannes kaar EKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Fredag 27. mai 2016 Oppgae 1 En koaksialkabel
, og dropper benevninger for enkelhets skyld: ( ) ( ) L = 432L L = L = 1750 m. = 0m/s, og a = 4.00 m/s.
 eegelse øsninger på blandede oppgaer Side - Oppgae Vi kaller lengden a en runde for Faren il joggerne er da: A = m/s = m/s 6 6 + 48 48 = m/s = m/s 7 6 + 4 Når de møes, ar de løp like lenge Da er + 5 m
eegelse øsninger på blandede oppgaer Side - Oppgae Vi kaller lengden a en runde for Faren il joggerne er da: A = m/s = m/s 6 6 + 48 48 = m/s = m/s 7 6 + 4 Når de møes, ar de løp like lenge Da er + 5 m
Lineærtransformasjoner
 Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK
 TFY445/FY00 6. des. 20 Side a 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støneng, telefon: 45 45 55 33 EKSAMEN I FY00 og TFY445 MEKANISK FYSIKK
TFY445/FY00 6. des. 20 Side a 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støneng, telefon: 45 45 55 33 EKSAMEN I FY00 og TFY445 MEKANISK FYSIKK
TMA4105 Matematikk2 Vår 2008
 TMA4105 Matematikk2 Vår 2008 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 5 11.4.1 Vi ser på kurven i xy-planet gitt ved r(t) ti + (ln(cos t))j π/2
TMA4105 Matematikk2 Vår 2008 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 5 11.4.1 Vi ser på kurven i xy-planet gitt ved r(t) ti + (ln(cos t))j π/2
MA1201 Lineær algebra og geometri Høst 2017
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA1201 Lineær algebra og geometri Høst 2017 Løsningsforslag Øving 1 Med forbehold om feil. Kontakt gjerne mads.sandoy@ntnu.no
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA1201 Lineær algebra og geometri Høst 2017 Løsningsforslag Øving 1 Med forbehold om feil. Kontakt gjerne mads.sandoy@ntnu.no
Viktige Fourier-transform par. Konvolusjons-teoremet. 2-D Diskret Fourier-Transform (DFT) INF 2310 Digital bildebehandling
 - iskret Forier-Transform FT INF 3 igital bildebehandling FILTRERING I FREKVENS-OMÈNET II Konolsjons-teoremet Lapass- øypass- og Båndpass-filter esign a filtre i frekens-doménet Rask implementasjon a konolsjons-filtre
- iskret Forier-Transform FT INF 3 igital bildebehandling FILTRERING I FREKVENS-OMÈNET II Konolsjons-teoremet Lapass- øypass- og Båndpass-filter esign a filtre i frekens-doménet Rask implementasjon a konolsjons-filtre
Tegn en skisse som tydelig viser integrasjonsområdet og grensene: = 1 3. dy = 1 3
 Integral y x Vi har integralet e x dxdy yx y Tegn en skisse som tydelig iser integrasjonsområdet og grensene: Integrassjonsområdet bestemmes a øre og nedre grenser i integralene Integranten har ingen betydning
Integral y x Vi har integralet e x dxdy yx y Tegn en skisse som tydelig iser integrasjonsområdet og grensene: Integrassjonsområdet bestemmes a øre og nedre grenser i integralene Integranten har ingen betydning
Fysikkolympiaden 1. runde 26. oktober 6. november 2009
 Norsk Fysikklærerforening i samarbeid med Skolelaboratoriet Uniersitetet i Oslo Fysikkolympiaden. runde 6. oktober 6. noember 009 Hjelpemidler: Tabell og formelsamlinger i fysikk og matematikk Lommeregner
Norsk Fysikklærerforening i samarbeid med Skolelaboratoriet Uniersitetet i Oslo Fysikkolympiaden. runde 6. oktober 6. noember 009 Hjelpemidler: Tabell og formelsamlinger i fysikk og matematikk Lommeregner
R2 2010/11 - Kapittel 4: 30. november 2011 16. januar 2012
 R 00/ - Kpittel 4: 0. noemer 0 6. jnr 0 Pln for skoleåret 0/0: Kpittel 5: 6/ 6/. Kpittel 6: 6/ /. Kpittel 7: / /4. Prøer på eller skoletime etter hert kpittel. Én heildgsprøe i her termin. En del prøer
R 00/ - Kpittel 4: 0. noemer 0 6. jnr 0 Pln for skoleåret 0/0: Kpittel 5: 6/ 6/. Kpittel 6: 6/ /. Kpittel 7: / /4. Prøer på eller skoletime etter hert kpittel. Én heildgsprøe i her termin. En del prøer
Innlevering i matematikk Obligatorisk innlevering nr. 5 Innleveringsfrist: 18. februar 2011 kl Antall oppgåver: 5 Ein skal grunngi alle svar.
 Innleering i matematikk Obligatorisk innleering nr. Innleeringsfrist: 18. februar 2011 kl. 14.00 Antall oppgåer: Ein skal grunngi alle sar. Oppgåe 1 f(x) = x2 +3 x+1. Skjæring med aksane Nullpunkt: f(x)
Innleering i matematikk Obligatorisk innleering nr. Innleeringsfrist: 18. februar 2011 kl. 14.00 Antall oppgåer: Ein skal grunngi alle sar. Oppgåe 1 f(x) = x2 +3 x+1. Skjæring med aksane Nullpunkt: f(x)
Forelesning Elkraftteknikk 1, 17.08.2004 Oppdatert 23.08.2004 Skrevet av Ole-Morten Midtgård. HØGSKOLEN I AGDER Fakultet for teknologi
 Forelesig Elkrafttekikk, 7.08.004 Oppdatert 3.08.004 Skreet a Ole-Morte Midtgård HØGSKOEN I AGDER Fakultet for tekologi Komplekse tall og isere Komplekse tall er sært yttige i aalyse a elkraftsystemer.
Forelesig Elkrafttekikk, 7.08.004 Oppdatert 3.08.004 Skreet a Ole-Morte Midtgård HØGSKOEN I AGDER Fakultet for tekologi Komplekse tall og isere Komplekse tall er sært yttige i aalyse a elkraftsystemer.
FASIT OG TIPS til Rinvold: Visuelle perspektiv. Lineær algebra. Caspar forlag, 1.utgave 2003 og 2.opplag 2004.
 FAIT OG TIP til Rinvold: Visuelle perspektiv. Lineær algebra. Caspar forlag,.utgave og.opplag. Versjon..9. Det er ikke tatt med svar på alle oppgaver. Denne fasiten vil bli oppdatert etter hvert. Oppdager
FAIT OG TIP til Rinvold: Visuelle perspektiv. Lineær algebra. Caspar forlag,.utgave og.opplag. Versjon..9. Det er ikke tatt med svar på alle oppgaver. Denne fasiten vil bli oppdatert etter hvert. Oppdager
Relativitet og matematikk
 Reatiitet og matematikk Eementær agebra og igninger Beregning dersom rommet er absoutt og dersom det er reatit Horfor måingen i 887 ga det resutat man fant. At yset bruker ike ang tid ti å gå i ae retninger
Reatiitet og matematikk Eementær agebra og igninger Beregning dersom rommet er absoutt og dersom det er reatit Horfor måingen i 887 ga det resutat man fant. At yset bruker ike ang tid ti å gå i ae retninger
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
Avdeling for ingeniørutdanning
 Adeling for ingeniørutdanning Emne: Elektro & Reguleringsteknikk Gruppe(r): 2M Emnekode: LO521 M Dato: 16.12.2003 Faglig eiledere: Bjørn Engebretsen Eksamenstid: 09.00-12.00 Eksamensoppgaen består a: Tillatte
Adeling for ingeniørutdanning Emne: Elektro & Reguleringsteknikk Gruppe(r): 2M Emnekode: LO521 M Dato: 16.12.2003 Faglig eiledere: Bjørn Engebretsen Eksamenstid: 09.00-12.00 Eksamensoppgaen består a: Tillatte
Egenverdier for 2 2 matriser
 Egenverdier for matriser (Bearbeidet versjon av tidligere notat på nett-sidene til MA101 - Lineær algebra og geometri Versjon oppdatert med referanser til 10utg av læreboken) Egenvektorer og egenverdier
Egenverdier for matriser (Bearbeidet versjon av tidligere notat på nett-sidene til MA101 - Lineær algebra og geometri Versjon oppdatert med referanser til 10utg av læreboken) Egenvektorer og egenverdier
9 Spenninger og likevekt
 9 Spenninger og likevekt Innhold: Volumkrefter og flatekrefter Traksjonsvektoren Spenningsmatrisen Retningscosinuser Cauchs ligning Hovedspenninger og hovedspenningsretninger Spenningsinvarianter Hdrostatisk
9 Spenninger og likevekt Innhold: Volumkrefter og flatekrefter Traksjonsvektoren Spenningsmatrisen Retningscosinuser Cauchs ligning Hovedspenninger og hovedspenningsretninger Spenningsinvarianter Hdrostatisk
Forelesning nr.5 INF 1410
 Forelesning nr.5 INF 40 Operasjonsforsterker Oersikt dagens temaer Kort historikk til operasjonsforsterkeren (OpAmp) Enkel Karakteristikker modell for OpAmp til ideell OpAmp Konfigurasjoner Mer med OpAmp
Forelesning nr.5 INF 40 Operasjonsforsterker Oersikt dagens temaer Kort historikk til operasjonsforsterkeren (OpAmp) Enkel Karakteristikker modell for OpAmp til ideell OpAmp Konfigurasjoner Mer med OpAmp
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
Geometri. Kapittel 3. 3.1 Vektorproduktet
 Kapittel 3 Geometri I dette kapitlet skal vi benytte den teorien vi utviklet i kapittel 1 og 2 til å studere geometriske problemstillinger. Vi skal se på kurver og flater, og vi skal også studere hvordan
Kapittel 3 Geometri I dette kapitlet skal vi benytte den teorien vi utviklet i kapittel 1 og 2 til å studere geometriske problemstillinger. Vi skal se på kurver og flater, og vi skal også studere hvordan
Seksjonene : Vektorer
 Seksjonene 10.2-3: Vektorer Andreas Leopold Knutsen 22. mars 2010 Vektorer i R 3 Vektor = objekt med både størrelse (lengde) og retning. Lengden til en vektor v betegnes med v Nullvektoren 0 er vektoren
Seksjonene 10.2-3: Vektorer Andreas Leopold Knutsen 22. mars 2010 Vektorer i R 3 Vektor = objekt med både størrelse (lengde) og retning. Lengden til en vektor v betegnes med v Nullvektoren 0 er vektoren
9 Lineærtransformasjoner TMA4110 høsten 2018
 9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Repetisjon
 Repetisjon 1.5.13 FYS-MEK 111 1.5.13 1 Lorentz transformasjon x ( x t) y z y z t t 1 1 x transformasjon tilbake: omven fortegn for og bytte S og S x ( x t) y z y z t t x små hastighet : 1 og x t t x t
Repetisjon 1.5.13 FYS-MEK 111 1.5.13 1 Lorentz transformasjon x ( x t) y z y z t t 1 1 x transformasjon tilbake: omven fortegn for og bytte S og S x ( x t) y z y z t t x små hastighet : 1 og x t t x t
TDT4195 Bildeteknikk
 TDT495 Bildeteknikk Grafikk Vår 29 Forelesning 5 Jo Skjermo Jo.skjermo@idi.ntnu.no Department of Computer And Information Science Jo Skjermo, TDT423 Visualisering 2 TDT495 Forrige gang Attributter til
TDT495 Bildeteknikk Grafikk Vår 29 Forelesning 5 Jo Skjermo Jo.skjermo@idi.ntnu.no Department of Computer And Information Science Jo Skjermo, TDT423 Visualisering 2 TDT495 Forrige gang Attributter til
Mer om kvadratiske matriser
 Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
Seksjonene : Vektorer
 Seksjonene 10.2-3: Vektorer Andreas Leopold Knutsen 22. mars 2010 Vektorer i R 3 Vektor = objekt med både størrelse (lengde) og retning. Lengden til en vektor v betegnes med v Nullvektoren 0 er vektoren
Seksjonene 10.2-3: Vektorer Andreas Leopold Knutsen 22. mars 2010 Vektorer i R 3 Vektor = objekt med både størrelse (lengde) og retning. Lengden til en vektor v betegnes med v Nullvektoren 0 er vektoren
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. Kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. Kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
TMA4105 Matematikk 2 vår 2013
 TMA4105 Matematikk vår 013 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavene er fra læreboka Merk: I løsningene til alle oppgavene fra seksjon
TMA4105 Matematikk vår 013 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavene er fra læreboka Merk: I løsningene til alle oppgavene fra seksjon
Oppfriskningskurs i matematikk 2008
 Oppfriskningskurs i matematikk 2008 Marte Pernille Hatlo Institutt for matematiske fag, NTNU 4.-9. august 2008 Velkommen! 2 Temaer Algebra Trigonometri Funksjoner og derivasjon Integrasjon Eksponensial-
Oppfriskningskurs i matematikk 2008 Marte Pernille Hatlo Institutt for matematiske fag, NTNU 4.-9. august 2008 Velkommen! 2 Temaer Algebra Trigonometri Funksjoner og derivasjon Integrasjon Eksponensial-
Oppgaver og fasit til seksjon
 1 Oppgaver og fasit til seksjon 3.1-3.3 Oppgaver til seksjon 3.1 1. Regn ut a b når a) a = ( 1, 3, 2) b = ( 2, 1, 7) b) a = (4, 3, 1) b = ( 6, 1, 0) 2. Finn arealet til parallellogrammet utspent av a =
1 Oppgaver og fasit til seksjon 3.1-3.3 Oppgaver til seksjon 3.1 1. Regn ut a b når a) a = ( 1, 3, 2) b = ( 2, 1, 7) b) a = (4, 3, 1) b = ( 6, 1, 0) 2. Finn arealet til parallellogrammet utspent av a =
Løsning, Stokes setning
 Ukeoppgaver, uke 4 Matematikk, tokes setning 1 Løsning, tokes setning Oppgave 1 a) b) c) F x y z x y z F x x + y y + z z 1+1+1 iden F er feltet konservativt. ( z y y ) ( x i z z z ) ( y x x x ) k i +k
Ukeoppgaver, uke 4 Matematikk, tokes setning 1 Løsning, tokes setning Oppgave 1 a) b) c) F x y z x y z F x x + y y + z z 1+1+1 iden F er feltet konservativt. ( z y y ) ( x i z z z ) ( y x x x ) k i +k
Forelesningsnotater SIF8039/ Grafisk databehandling
 Forelesningsnotater SIF839/ Grafisk databehandling Notater til forelesninger over: Kapittel 4: Geometric Objects and ransformations i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 orbjørn
Forelesningsnotater SIF839/ Grafisk databehandling Notater til forelesninger over: Kapittel 4: Geometric Objects and ransformations i: Edward Angel: Interactive Computer Graphics Vårsemesteret 22 orbjørn
Kompetansemål Geometri, R Vektorer Regning med vektorer... 5 Addisjon av vektorer... 5 Vektordifferanse... 5
 1 Geometri Innhold Kompetansemål Geometri, R2... 3 1.1 Vektorer... 4 1.2 Regning med vektorer... 5 Addisjon av vektorer... 5 Vektordifferanse... 5 Multiplikasjon av vektor med tall... 6 Parallelle vektorer...
1 Geometri Innhold Kompetansemål Geometri, R2... 3 1.1 Vektorer... 4 1.2 Regning med vektorer... 5 Addisjon av vektorer... 5 Vektordifferanse... 5 Multiplikasjon av vektor med tall... 6 Parallelle vektorer...
Determinanter. Kapittel 6. Determinanter for 2 2-matriser. La oss beregne arealet av dette parallellogrammet. Vi tegner på noen hjelpelinjer:
 Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
I C Q R. Øving 11. Institutt for fysikk, NTNU TFY4155/FY1003: Elektromagnetisme
 nstitutt for fsikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Øving 11 Veiledning: Mandag 23. mars og fredag 27. mars nnleveringsfrist: Fredag 27. mars Oppgave 1 nnledning (dvs vi rekapitulerer fra
nstitutt for fsikk, NTNU TFY4155/FY1003: Elektromagnetisme Vår 2009 Øving 11 Veiledning: Mandag 23. mars og fredag 27. mars nnleveringsfrist: Fredag 27. mars Oppgave 1 nnledning (dvs vi rekapitulerer fra
Leksjon G2: Transformasjoner
 Programmering grunnkurs TDAT: Grafikkdel Leksjon G: Transformasjoner Fra modell til tegning på skjerm side Modell Plantransformasjoner/translasjon side 3 Modell Plantransformasjoner/skalering side 4 Modell
Programmering grunnkurs TDAT: Grafikkdel Leksjon G: Transformasjoner Fra modell til tegning på skjerm side Modell Plantransformasjoner/translasjon side 3 Modell Plantransformasjoner/skalering side 4 Modell
8 Vektorrom TMA4110 høsten 2018
 8 Vektorrom TMA4 høsten 8 I de foregående kapitlene har vi tatt en lang vandring gjennom den lineære algebraens jungel. Nå skal vi gå opp på en fjelltopp og skue ut over landskapet vi har vandret gjennom.
8 Vektorrom TMA4 høsten 8 I de foregående kapitlene har vi tatt en lang vandring gjennom den lineære algebraens jungel. Nå skal vi gå opp på en fjelltopp og skue ut over landskapet vi har vandret gjennom.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNVERTETET OLO Det matematisk-naturitenskapelige fakultet Eksamen i: Fys1120 Eksamensdag: Onsdag 12. desember 2018 Tid for eksamen: 0900 1300 Oppgaesettet er på: 5 sider Vedlegg: Formelark Tilatte hjelpemidler
UNVERTETET OLO Det matematisk-naturitenskapelige fakultet Eksamen i: Fys1120 Eksamensdag: Onsdag 12. desember 2018 Tid for eksamen: 0900 1300 Oppgaesettet er på: 5 sider Vedlegg: Formelark Tilatte hjelpemidler
Arbeidsoppgaver i vektorregning
 Arbeidsoppgaver i vektorregning Fagdag 17.03.2016 Løsningsskisser! God arbeidsinnsats på disse oppgavene vil som vanlig gi stor gevinst på prøven 18.03.16! Hva man bør kunne etter å ha gjort disse arbeidsoppgavene:
Arbeidsoppgaver i vektorregning Fagdag 17.03.2016 Løsningsskisser! God arbeidsinnsats på disse oppgavene vil som vanlig gi stor gevinst på prøven 18.03.16! Hva man bør kunne etter å ha gjort disse arbeidsoppgavene:
LotusLive. LotusLive Administrasjonsveiledning
 LotusLie LotusLie Administrasjonseiledning LotusLie LotusLie Administrasjonseiledning Merknad Før du bruker denne informasjonen og produktet den støtter, må du lese informasjonen i Merknader på side 83.
LotusLie LotusLie Administrasjonseiledning LotusLie LotusLie Administrasjonseiledning Merknad Før du bruker denne informasjonen og produktet den støtter, må du lese informasjonen i Merknader på side 83.
Mer om kvadratiske matriser
 Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
Kapittel 2 Mer om kvadratiske matriser Vi lader opp til anvendelser, og skal bli enda bedre kjent med matriser. I mange anvendelser er det ofte de kvadratiske matrisene som dukker opp, så fra nå skal vi
MAT Onsdag 7. april Lineær uavhengighet (forts. 1.8 Underrom av R n, nullrom, basis MAT Våren UiO. 7.
 MAT 2 april 2.7 Lineær.8 Underrom MAT 2 Våren 2 UiO 7. april 2 / 23 MAT 2 april 2.7 Lineær.8 Underrom Minner om:.7 Lineær (fortsettelse) Definisjon. To vektorer u og v i R n kalles lineært avhengige dersom
MAT 2 april 2.7 Lineær.8 Underrom MAT 2 Våren 2 UiO 7. april 2 / 23 MAT 2 april 2.7 Lineær.8 Underrom Minner om:.7 Lineær (fortsettelse) Definisjon. To vektorer u og v i R n kalles lineært avhengige dersom
OPPGAVER FOR FORUM
 OPPGAVER FOR FORUM 2007-2008 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
OPPGAVER FOR FORUM 2007-2008 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Norges teknisk naturitenskapelige uniersitet Institutt for elektroniske systemer ide 1 a 8 Faglærer: Johannes kaar EKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Mandag 29. mai 2017 Alle anlige deloppgaer teller
Norges teknisk naturitenskapelige uniersitet Institutt for elektroniske systemer ide 1 a 8 Faglærer: Johannes kaar EKAMEN I EMNE TFE 4120 ELEKTROMAGNETIME Mandag 29. mai 2017 Alle anlige deloppgaer teller
Forelesning 5/ ved Karsten Trulsen
 Forelesning 5/4 2018 ved Karsten Trulsen Litt regning med del-operatoren Rottmann s.64, M s.82 Eksempel: Se på uttrkket a b hvor pila som peker ned på krøllparentesen indikerer at del-operatoren sin derivasjonsoperasjon
Forelesning 5/4 2018 ved Karsten Trulsen Litt regning med del-operatoren Rottmann s.64, M s.82 Eksempel: Se på uttrkket a b hvor pila som peker ned på krøllparentesen indikerer at del-operatoren sin derivasjonsoperasjon
Fysikkolympiaden Norsk finale 2010
 Uniesitetet i Oslo Nosk Fysikklæefoening Fysikkolympiaden Nosk finale. ttakingsnde Fedag 6. mas kl 9. til. Hjelpemidle: abell/fomelsamling, lommeegne og tdelt fomelak Oppgaesettet bestå a 6 oppgae på side
Uniesitetet i Oslo Nosk Fysikklæefoening Fysikkolympiaden Nosk finale. ttakingsnde Fedag 6. mas kl 9. til. Hjelpemidle: abell/fomelsamling, lommeegne og tdelt fomelak Oppgaesettet bestå a 6 oppgae på side
Newtons lover i to og tre dimensjoner
 Newons loer i o og re dimensjoner 8..16 Innleeringsfris oblig 1: Tirsdag, 9.Feb. kl.18 Innleering kun ia: hps://deilry.ifi.uio.no/ Fellesinnleeringer (N 3): Alle må bidra il besarelsen i sin helhe. Definer
Newons loer i o og re dimensjoner 8..16 Innleeringsfris oblig 1: Tirsdag, 9.Feb. kl.18 Innleering kun ia: hps://deilry.ifi.uio.no/ Fellesinnleeringer (N 3): Alle må bidra il besarelsen i sin helhe. Definer
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer.
 Kapittel 2 Matriser I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer. 2.1 Definisjoner og regneoperasjoner
Kapittel 2 Matriser I dette kapittelet skal vi studerer noen matematiske objekter som kalles matriser. Disse kan blant annet brukes for å løse lineære likningssystemer. 2.1 Definisjoner og regneoperasjoner
Løsningsforslag til utvalgte oppgaver i kapittel 3
 Løsningsforslag til utvalgte oppgaver i kapittel 3 I dette kapittelet har mange av oppgavene et mindre teoretisk preg enn i de foregående kapitlene, og jeg regner derfor med at lærebokas eksempler og fasit
Løsningsforslag til utvalgte oppgaver i kapittel 3 I dette kapittelet har mange av oppgavene et mindre teoretisk preg enn i de foregående kapitlene, og jeg regner derfor med at lærebokas eksempler og fasit
Fiktive krefter
 Fiktie krefter 5.04.013 FYS-MEK 1110 5.04.013 1 Fiktie krefter problem: Newtons loer gjelder bare i inertialsystemer hordan analyserer i en beegelse i et akselerert system? z z x y transformasjon transformasjon
Fiktie krefter 5.04.013 FYS-MEK 1110 5.04.013 1 Fiktie krefter problem: Newtons loer gjelder bare i inertialsystemer hordan analyserer i en beegelse i et akselerert system? z z x y transformasjon transformasjon
