Fakultet for realfag Ho/gskolen i Agder - Va ren 2007
|
|
|
- Odd Olsen
- 8 år siden
- Visninger:
Transkript
1 Msteroppgve i mtemtikkdidktikk Fkultet for relfg Ho/gskolen i Agder - V ren 2007 Integrl og integrsjon Roger Mrkussen
2 Roger Mrkussen Integrl og integrsjon Msteroppgve i mtemtikkdidktikk Høgskolen i Agder Fkultet for relfg 2007
3 Smmendrg Integrsjon og derivsjon er to viktige begreper som blir behndlet i den videregående skolen. Nesten uten unntk blir derivsjon introdusert før integrsjon. Snnsynligvis fordi mn tenker seg t derivsjon er lettest. Jeg mener integrsjon hr en enklere geometrisk tolkning enn derivsjon. Det er lettere å se for seg et rel, enn stigningen til en grf i et punkt. I den videregående skolen ligger ikke fokuset på den geometriske tolkningen v integrlet, men heller på den mer tekniske biten som blir klt ntiderivsjon. I Kpittel 1 diskuterer vi fordeler og ulemper med denne fremgngsmåten. Resten v oppgven skl prøve å gi en begrepsmessig innføring i forskjellige integrsjonsteorier. Oppbygningen følger en gnske kronologisk tnkegng. Vi strter med de teoriene mnge kjenner fr før. I Kpittel 2 gjennomgår vi integrsjonsteorier som ikke trenger en etblert målteori. Dette er Newtonsog Riemnns teorier, smt litt om Stieltjes integrl. Vi smmenlikner disse, og ser på oppbygning og bruksområder. Fokuset ligger i å prøve å gi en forståelse v begrepene som nturlig dukker opp. Kpittel 3 tr for seg utviklingen v mål- og integrsjonsteorien fr Riemnn til Lebesgue. Jeg bruker historien ktivt for å motivere begrepene som trengs for å etblere målteorien. I Kpittel 4 ser vi på oppbygningen v Lebesgues teori. Her blir relevnt målteori forklrt, og Lebesgue-integrlet blir definert. Jeg prøver å gi et bilde v den nye teorien ved å smmenlikne den med Riemnns teori. I det siste kpitlet går jeg litt videre mot mer generell målteori. Ser på hvordn et generelt målrom er bygd opp, og hvordn vi kn konstruere slike ved hjelp v Crtheodory-utvidelse. Vi får se et eksempel på hvordn målteorien kn bli brukt for å beskrive snnsynlighetsteori. Til slutt hr jeg med en liten introduksjon til et generlisert Riemnn integrl som første gng ble introdusert i 1912 v Arnud Denjoy. En v fordelene med dette integrlet er t det kn invertere lle deriverte funksjoner. Høgskolen i Agder Institutt for mtemtiske fg, Roger Mrkussen
4 Summry Integrtion nd differentition re two importnt concepts which is treted in upper secondry school. Almost without exeption is the derivtive introduced before the integrl. Probbly becuse textbookuthors think tht differentition is esier thn integrtion. In my opinion integrtion hs n esier geometric interprettion thn the one of differentition. It is esier to hve mentl picture of re thn mentl picture of the rte of chnge of function t point. In upper secondry school the focus is not on the geometric interprettion, but rther on the more technicl prt which is clled ntidifferentition. In Chpter 1 we discuss the dvntges or disdvntges of this procedure. The remining prt of this thesis focuses minly on giving conceptul introduction to different theories of integrtion. The concepts is presented in n llmost chronologicl order. We strt with the theories for which mny of the reders re fmilir. In Chpter 2 we discuss the theories which don t build on mesure theory. This is Newton s nd Riemnn s theories, together with the Stieltjes integrl. We compre these nd look closer t construction nd ppliction of the theories. The min issue is to give n understnding of the concepts s they pper. Chpter 3 focuses on the development of mesure- nd integrtion theory. The relevnt theory is being explined, nd the Lebesgue-integrl is defined. I hve tried to give mentl picture of the new theory by compring it with Riemnn s theory. In the lst chpter we tke step towrds more generl mesure theory. We define generl mesure spce, nd we see how mesures cn be constructed by the Crtheodory-extension theorem. We shll see n exmple where mesure theory is used to describe probbility. I end this thesis with smll introduction to the generlized Riemnn integrl, which ws first introduced in 1912 by Arnud Denjoy. One of the dvntges with this integrl is tht it cn invert ll derivtives. Agder University College Deprtment of Mthemtics, Roger Mrkussen
5 Forord Det å finne relet til figurer og etterhvert relet mellom grfer og kser, hr vært v stor interesse for mnge mtemtikere opp gjennom tiden. Integrsjon ble gjennom tiden det viktigste verktøyet vi hr for å regne ut reler og volumer. Mtemtikken og integrsjonsteorien hr utviklet seg. Den blir nå brukt i mnge flere smmenhenger enn bre klkulering v reler og volumer. Det er helt klrt t integrsjonsteori spiller en uhyre sentrl rolle i moderne nlyse. Det å vgjøre størrelsen til forskjellige mengder er ikke lltid like lett. For eksempel: Hvor stor er mengden v rsjonle tll? Hvor stor er mengden v irrsjonle tll? Kn vi finne en målemetode som virker på slike mengder? Kn vi knskje måle lle tenkelige mengder med en slik metode? Disse spørsmålene blir besvrt innenfor et mtemtisk felt som blir klt målteori. I moderne integrsjonsteori får vi bruk for mye målteori. Fktisk er integrsjonsteorien og målteorien nå blitt så vhengige v hverndre t lt er smeltet smmen til mål- og integrsjonsteori. Fokuset i oppgven er å gi et begrepsmessig overblikk innenfor integrsjonsteori. Jeg prøver å følge begrepsutviklingen kronologisk frem til og med Lebesgues teori. Ved å følge en historisk tidslinje tror jeg det blir lettere å gi fornuftige motivsjonsfktorer for begrepenes betydning. Jeg skl prøve å bygge opp, finne bruksområder og smmenlikne flere forskjellige integrsjonsteorier. Elever i den vidergående skolen trener mye på ntiderivsjon. Jeg tror elever vil h mer igjen for et sterkere fokus på intuitiv forståelse v integrsjon. En mtemtikklærer med dypere forståelse v integrsjon vil h bedre forutsetninger for å velge kjernestoff og undervisningsmetoder som stimulerer til forståelse v begrepet. Jeg hr skrevet denne oppgven for t jeg selv skulle få en dypere innsikt i integrsjonsbegrepet, og for t ndre mtemtikklærere skl kunne få et overblikk over denne teorien på en reltivt tilgjengelig måte. Jeg ønsker å rette en stor tkk til min veileder, førstemnuensis Olv Nygrd, for kjempegode råd og kommentrer som uten tvil forbedret oppgven min krftig. Du hdde lltid tid til en prt/diskusjon når jeg kom innom kontoret ditt. Roger Mrkussen iii
6 Innhold Kpittel 1. Innledning 1 1. Integrlets historie i korte trekk 1 2. Integrsjon i skolen 4 3. Anlysens fundmentlteorem 6 Kpittel 2. God gmmeldgs integrsjon 8 1. Newtons integrl 8 2. Riemnns integrl Smmenlikning v N- & R-integrlet Uekte integrler Riemnn-Stieltjes integrl 20 Kpittel 3. Perioden fr Riemnn til Lebesgue Riemnns «Hbilitsjon» Topologiske små mengder og målteoretiske små mengder Ingensteds tette mengder med positivt mål Ytre innhold Målbre mengder og Fubini s teorem Borel s målteori Klssifisering v mengder og funksjoner Henry Lebesgue 38 Kpittel 4. Lebesgues mål og integrsjonsteori Mål og nullmengder Lebesgue-målbre mengder Målbre funksjoner Definisjonen v L-integrlet Integrerbre funksjoner Det normerte rommet L 1 v L-integrerbre funksjoner Smmenlikning v R- og L-integrlet 52 Kpittel 5. Mer generell mål og integrsjonsteori Generell mål- og integrsjonsteori Hhn-Crtheodory-utvidelse Integrl i snnsynlighetsteori Det generliserte Riemnn integrlet 63 Littertur 67 iv
7 KAPITTEL 1 Innledning 1. Integrlets historie i korte trekk Mtemtikere hr strevd med å bestemme rel og volum v geometriske figurer i mer enn 2000 år. Arkimedes vr knskje den første som brukte integrsjonsliknende metoder for å bestemme relet v blnt nnet en sirkel. Hn gjorde dette ved å beregne relet v innskrevne regulære polygoner. Når hn økte ntll knter i polygonene ble tilnærmingen til sirkelen bedre. Den beste tilnærmingen gjorde Arkimedes med en 96 knt, som medfører t tilnærmingen til π hr en reltiv feil på 0,04 % (godt gjort å klre dette med utregninger skrevet i snd) [12]. Arkimedes klrte også å vise t relet under grfen til f(x) = x 2 fr 0 til x vr gitt ved formelen 1 3 x3 (ltså viste hn x 0 t2 dt = 1 3 x3 ). Hn tenkte seg et rektngel med høyde x 2 og lengde x, og fnt ut t relet under kurven ble nøyktig 1 3 v relet til rektngelet. Se Figur 1. Metoden hn brukte vr å tilnærme relet med mnge rektngler. Hn viste t hvis rektnglene lltid lå under kurven, så ble summen v relene til rektnglene mindre enn 1 3 x3 og hvis rektnglene lltid lå over kurven, ble relet til summen v rektnglene større enn 1 3 x3. Senere skl vi se t dette blir klt nedre- og øvre Drboux-summer. Er det noen forskjell på Arkimedes metode og vår integrsjonsmetode? Selve metoden er helt lik Riemnns integrsjon. Forskjellen ligger i rgumentsjonen for t dette virker. Arkimedes rgumentsjon bygger på et intuitivt bilde; Arkimedes kunne h sgt: «dette må stemme bre vi fortsetter å øke ntllet rektngler i det uendelige». Denne måten å rgumentere på ble klt «Method of exhustion». Vår rgumentsjon bygger på konvergensteorien Figur 1. Arkimedes klrte denne integrsjonen 1
8 Figur 2. Leibniz integrsjon Cuchy gjorde skikkelig rede for på 1820-tllet. Det er verdt å merke t fundmentet for integrlet vr ekvivlent med «Method of exhustion» frem til Cuchy. Strten på den integrsjonsteorien vi kjenner begynte midt på 1600-tllet. Vitenskpsmennene som vr i hovedrollen vr Isc Newton ( ) og Gottfried Leibniz ( ). Teoriene til disse to hr gnske forskjellig oppbygning, men det viser seg t de er ekvivlente. Selv om det er Newton som hr fått mesteprten v æren, så er notsjonen vi bruker i dg den smme som Leibniz brukte. Leibniz tenkte på å finne relet under en grf ved å summere relet v mnge små rektngler som lå tett oppunder grfen (se Figur 2). For å finne det riktige relet tenkte hn seg t bredden til disse rektnglene vr uendelig liten. Denne bredden klte hn dx. Notsjonen hn brukte for å illustrere t disse uendelig små rektnglene skulle summeres vr en lngstrkt S ( ). Fr dette følger notsjonen f(x) dx, som vi kjenner godt [7]. Når det ikke er viktig å presisere hvilken «dummy» vribel som gjelder, tr jeg meg friheten til å bruke notsjonen f. Disse uendelig små størrelsene ble klt for infinitesimler. Det t en regnet med uendelig små størrelser som om de vr endelige gjorde t mnge vr skeptiske til teorien. Mtemtikerne ble ofte stt i en vnskelig situsjon når de skulle redegjøre for dette. De fnt likevel ut t denne måten å regne på vr veldig nyttig. Etter å h feilet i å lge en solid teori rundt infinitesimlene, uttlte Leibniz i 1673 t senere genersjoner fikk rydde opp [7]. Litt senere oppdget Newton, Leibniz og Joh. Bernoulli ( ) uvhengig v hverndre t integrsjon vr motstt opersjon v det å derivere [10]. Som følge v dette kom den første vrinten v fundmentlteoremet. Teorem 1.1 (Fundmentlteoremet i Klkulus). Ant F er en primitiv til f på intervllet [, b]; dvs. F (x) = f(x) for lle x [, b]. D hr vi t b f(x) dx = F (b) F (). I de neste 140 årene, frem til c 1820, tenkte mtemtikere på integrsjon som det motstte v å derivere. Måten det ble gjort på vr å finne (når de klrte 2
9 dette) en ntiderivert (primitiv), og deretter bruke fundmentlteoremet. Denne måten å integrere på klles Newton-integrsjon, og integrlet klles Newton-integrlet (N-integrlet). Når begreper som grense, kontinuitet og konvergens ble skikkelig definert på begynnelsen v 1800-tllet vr tiden moden for å forndre på synet v integrsjon. I 1823 publiserte Augustin-Louis Cuchy ( ) en tekst om det å regne med infinitesimler, her vr integrsjonsteorien bnebrytende. Cuchy gikk bort fr bildet der integrsjon vr definert som det motstte v å derivere. Hn definerte nå integrsjon på en helt nnen måte. Noen v grunnene til dette kn være [12]. Det vr klrt t relet under en kurve kunne være fornuftig å snkke om selv om integrlet ikke kunne evlueres med bruk v ntiderivert og endepunktene til et intervll. Et eksempel er de stykkevise kontinuerlige funksjonene som dukket opp i Fouriers rbeid med rekker med trigonometriske funksjoner (Fourier-rekker). En nnen grunn kn være t hn fnt ut t det ikke nødvendigvis fntes en ntiderivert til lle funksjoner. Cuchys egen forklring på hvorfor hn ville definere integrlet som en sum, vr t det fungerte. Måten Cuchy kom frem til sin definisjon v integrlet vr snnsynligvis ved t hn så på rbeid som vr gjort v Euler og Lcroix i forbindelse med å pproksimere bestemte integrl [12]. Det Cuchy gjorde vr å nt t f(x) er kontinuerlig på [, b], hn prtisjonerte intervllet inn i n deler = x 0 < x 1 < x 2 < < x n 1 < x n = b og lget summen S = (x 1 x 0 )f(x 0 ) + (x 2 x 1 )f(x 1 ) + + (x n x n 1 )f(x n 1 ). Hn vr selvfølgelig veldig klr over t S vhenger v både n og verdiene x i som er vlgt. Hn gjorde et greit resonnement for t bre n ble stor nok, så ville ikke vlget v x i er være viktige. Det vr Cuchys nye definisjoner v kontinuitet og grenser som gjorde t dette nå ble en skikkelig definisjon. Cuchy jobbet ikke så mye med hvilke krv som måtte til for t en funksjon skulle være integrerbr. Hn jobbet hovedskelig med kontinuerlige funksjoner, eller evt. funksjoner med et endelig ntll diskontinuiteter på et intervll. Det vr Georg Friedrich Bernhrd Riemnn ( ) som i vhndlingen til sin hbilitsjon i 1854 tok tk i disse tingene. Hn forndret litt på definisjonen, fnt et kriterium for når en funksjon vr (Riemnn) integrerbr og kom med et flott eksempel på en integrerbr funksjon som hr uendelig mnge diskontinuiteter i hvert intervll. Fktisk vr det slik t mengden v diskontinuiteter til denne funksjonen ligger tett i de reelle tll. Når dette først ble publisert i 1867 (nesten to år etter hns død), ble denne definisjonen sett på som den mest mulig generelle. Det viste seg likevel t Riemnn-integrlet (R-integrlet) hdde noen svkheter. Disse svkhetene kommer vi tilbke til i Kpittel 2. Etter Riemnn vr det mnge som jobbet med integrsjon i årene fremover mot Det vr i løpet v denne tiden t målteorien begynte å t form. 3
10 I 1902 kom Lebesgue med sin doktorvhndling Intègrle, Longueur, Aire (Integrl, Lengde, Arel), denne vhndlingen vr bnebrytende. Lebesgues intensjon vr å hnskes med ulempene ved R-integrlet. Dette klrte hn på fremrgende måte, og teorien viste seg å være mer fruktbr enn Lebesgue selv kunne tenke seg. Mål- og integrsjonsteorien utviklet seg rskt utover på 1900-tllet. Det vr Lebesgues teori som ble grunnlget for mye v mtemtikken som oppsto på denne tiden. Snnsynlighetsteorien vr en v de grenene som virkelig fikk nytte v mål- og integrsjonsteorien til Lebesgue. Den store hjernen bk ksiomtiseringen v snnsynlighetsteorien vr den russiske mtemtikereren Andrey Nikolevich Kolmogorov. Dette ble gjort rundt 1933 og vr et gjennombrudd i måten å se på snnsynlighet (vi kn godt si t fundmentet for moderne snnsynlighetsteori ble lgt her). Lebesgues integrl (L-integrl) hr også noen svkheter, blnt nnet fordi det er et bsolutt integrl. Senere i oppgven skl vi se hv et bsolutt integrl er. Lebesgues teori gjorde ikke så mye for å forenkle fundmentlteoremet. Med motivsjon i å finne et integrl der den deriverte lltid er integrerbr, vr det Arnud Denjoy og Oskr Perron klrte å utvikle slike integrler. Dette ble gjort på to veldig forskjellige måter. Det viste seg overskende nok t integrlene vr ekvivlente [2]. Rundt 1960 lget Jroslv Kurzweil og Rlph Henstock en nnen definisjon som vr ekvivlent med Denjoy-Perron integrlet. Denne definisjonen er bre en modifiksjon v Riemnns definisjon, og ble derfor klt det generliserte Riemnn integrlet. Det viste seg nemlig t lle R-integrerbre funksjoner, lle N-integrerbre funksjoner og lle L- integrerbre funksjoner vr integrerbre med denne metoden, og integrlene vr de smme. Det smme gjldt fktisk også for uekte integrler. Denne teorien er fktisk gnske ukjent, selv for mtemtikere som hr rbeidet sitt bsert på Lebesgue teori. 2. Integrsjon i skolen Allerede tidlig i brneskolen skl elevene prøve å bestemme reler. Ved hjelp v enkle geometriske smmenhenger finner de frem til relet v rektngler, prllellogrmmer, romber, sirkler, osv. Det er først i grunnkurset på videregående skole t de kommer borti integrsjon for å beregne relet under grfer, og d bre som numeriske løsninger ved hjelp v klkultoren. I ndre klsse er det vnlig t elevene blir formelt introdusert for integrsjonsbegrepet. D følger som regel integrsjon som en nturlig fortsettelse på derivsjon. I oppleggene jeg hr sett for denne introduksjonen blir integrsjon sgt å være det motstte v å derivere. Elevene trener i begynnelsen på oppgver v typen: Ant f (x) = x 2, hv er f(x)? Elevene blir nå fortlt t de integrerer x 2. Er dette en fornuftig introduksjon v integrsjonsbegrepet? Etter min mening skper denne fremgngsmåten forvirring, og den bidrr til å demotivere elever for videre rbeid med integrsjon. Elevene hr så godt som ingen idé om hvorfor de trenger dette, og dermed ingen forståelse v integrsjon som et verktøy for å finne et rel. 4
11 Jeg tror det er mnge måter å gjøre en god introduksjon til integrsjon på, men jeg er gnske sikker på t felles for disse er en øyeblikkelig motivsjon for «hvorfor gjør vi dette?». Det å gjøre tidlig klrt t dette brukes i mnge smmenhenger, blnt nnet for å bestemme reler, vil være en nturlig motivsjonsfktor for elever i den videregående skolen. Senere skl en selvfølgelig trekke linjene til derivsjon og fundmentlteoremet. Bressoud [3] mener integrsjon bør h en prktisk tilnærming, der en tr utgngspunkt i å finne reler. Hn tror på det genetiske prinsipp innenfor didktikken, som betyr t progresjonen i undervisningen skl til en hvis grd følge historien. Grunnen til t integrsjon ble «funnet opp» vr for å bestemme reler, deretter ble det utviklet metoder for å tilnærme relet, og på grunnlg v dette kom mn frem til solide teorier. Hn mener denne rekkefølgen også bør brukes i forbindelse med å introdusere integrlbegrepet. Det betyr t ntiderivsjon og fundmentlteoremet skl introduseres før Riemnn integrlet. Stein [21] mener det er veldig viktig å tenke over hvilke begreper og metoder det er fornuftig å undervise. Hn mener det skl være en smmenheng mellom pensum, vektleggingen v begrepene og spørsmålet om hv elevene kommer borti i prktiske smmenhenger senere. Vi må ikke tenke «Jeg må kltre opp fjellet siden det står her». Blnt nnet så mener hn t å bruke msse tid på ntiderivsjon v elementære funksjoner, kn bli litt kunstig ttt i betrktning t svært mnge elementære funksjoner ikke hr en elementær ntiderivert. Noe v dette bør likevel gjøres siden veldig mnge funksjoner i forbindelse med fysikk og ndre nturvitenskper hr elementære ubestemte integrler (ntideriverte). I denne forbindelse bør elevene få tilgng til store integrsjonstbeller delvis istedenfor å lære mnge «lure» triks for å finne ubestemte integrl. Hn ønsker mer vekt på numerisk integrsjon og det konseptuelle bilde v integrl som rel. Thurston [24] mener den vnlige måten å undervise derivsjon og integrsjon på er ulogisk. Hn ønsker en forndring v notsjon for å gjøre klkulus mer intuitivt. Hn mener blnt nnet t den deriverte som skrives både som f (x) og dy dx ikke er smstemte. Mn skriver ofte f (3) (f derivert i punktet 3), men mn skriver ldri dy d3. Hn viser til flere prdokser både innenfor derivsjon og integrsjon på grunn v dette. Hn legger frem et forslg som ifølge hn skl være mye bedre. Hn mener også t bruken v konstnten c i forbindelse med ubestemte integrl blir upresist brukt. Hn mener det bør tenkes over om en ønsker å finne en ntiderivert (det er nok i forbindelse med fundmentlteoremet), eller om en vil h et utrykk med lle ntideriverte. Som regel blir bre c en ubetenksomt hengt på den ntideriverte, noen gnger unødvendig, ndre gnger skulle det h vært flere konstnter. På dette grunnlget mener hn t vi ikke trenger ubestemte integrl i det hele ttt. Jeg hr vlgt å vise til en eldre rtikkel d denne hr noen viktige poeng ngående å få frem meningen med mtemtikken. Drgoo [6] mener det er meningen og den prktiske nytten som er det viktigste å få frem i mtemtikken. Det finnes de som mener t mtemtikk består v å bygge opp kunnskp fr bunnen v. Mn kn derfor ikke få en god forståelse for f.eks. 5
12 funksjoner, hvis mn ikke hr bygget opp de reelle tll fr bunnen. Forftteren her mener dette er «gmmeldgs» og psser bre for de brillinte elevene. Hn viser til følgende utsgn hentet fr S. P. Thomson: Du forbyr ikke en person å bruke klokke hvis hn ikke vet hvordn mn lger den. Hvordn skl mn få elevene til selv å utforske og se smmenhengen mellom integrsjon og derivsjon? Dette synes jeg Strng [22] hr et veldig interessnt synspunkt på. Hn mener vi skl «glemme» det meste vi llerede vet om klkulus. Hn tr utgngspunkt i t det bre finnes to funksjoner i verden, v = frt og f = strekning. Med utgngspunkt i dette lger hn på en flott måte en diskret modell, som oppfyller lt en elev trenger å vite om smmenhengen mellom derivsjon og integrsjon. Etter hvert som elevene blir mer vnserte kn en gå til grenseverdier for å ende opp med fundmentlteoremet under litt sterke forutsetninger. I Norge er det mest vnlig å introdusere derivsjon før integrsjon (Jeg tror dette stemmer for de fleste lnd). Schumn [20] mener integrsjon som en metode for å finne et rel er lettere å skjønne intuitivt enn stigningstllet i et punkt. Dette bygger på de fleste hr et godt etblert bilder v hv rel er, men det er mindre ssosisjoner knyttet til stigning. Forslget til forftteren er ltså å introdusere integrsjon før derivsjon. En bok som følger forslget til Schumn er Tom Apostols Clculus [1]. Apostol skriver følgende i forordet: «The pproch in this book hs been suggested by the historicl nd philosophicl development of clculus nd nlytic geometry. For exmple, integrtion is treted before differentition. Although to some this my seem unusul, it is historiclly correct nd pedgogiclly sound. Moreover, it is the best wy to mke meningful the true connection between the integrl nd the derivtive». Det er gnske tydelig t også Apostol er tilhenger v det genetiske prinsipp, smmen med blnt nnet Bressoud. Integrsjonsdelen i denne boken skiller seg litt fr hvordn ndre clulusbøker introduserer integrsjon. Apostol bygger opp teorien på en måte som etter min mening gjør det mye lettere og vnsere videre til ndre integrler som for eksempel Lebesgues integrl. Det er nok snnsynligvis mnge som mener boken er litt vnskelig som grunnlget for et første klkulus kurs. 3. Anlysens fundmentlteorem Fundmentlteoremet er setningen som knytter integrsjon til derivsjon. Det vr først på Newtons tid t begrepene integrsjon og derivsjon ble etblert. Det vr på denne tiden vi fikk det første fundmentlteoremet. Etter hvert som vi hr fått nye måter å integrere på, hr også fundmentlteoremet blitt noe endret. Vi ønsker ller helst å h et teorem som gjør t vi kn integrere lle deriverte funksjoner. Vi sier t vi ønsker å «tilbkestille» lle deriverte funksjoner. Dessverre er det slik t de fleste metodene må legge tilleggskrv på den deriverte for å oppnå dette. 6
13 Det første fundmentlteoremet vi skl se på er det eldste. Integrsjonsmetoden vi bruker er Newton-integrsjon. Teorem 3.1 (Fundmentlteoremet med N-integrlet). Ant F er en primitiv til f på intervllet [, b]; dvs. F (x) = f(x) for lle x [, b]. D hr vi t b f(x) dx = F (b) F (). Legg merke til t her må den deriverte h en ntiderivert for å kunne «tilbkestilles». I det neste fundmentlteoremet skl vi bruke Riemnnintegrsjon. Selv om dette er et integrl som ble utviklet mye senere enn N-integrlet, kn det likevel ikke krkteriseres som en generlisering siden det finnes N-integrerbre funksjoner som ikke er R-integrerbre. Dette medfører t det finnes funksjoner med begrenset derivert i et intervll, som ikke er integrerbre i intervllet. En konsekvens v dette blir omtlt i Kpittel 3.1. Teorem 3.2 (Fundmentlteoremet med R-integrlet). Ant F er deriverbr på intervllet [, b]. Hvis F = f er R-integrerbr på [, b] så hr vi t b f(x) dx = F (b) F (). I fundmentlteoremet med R-integrlet, ser vi t vi trenger et litt «kjedelig» tilleggskrv t den deriverte må være integrerbr. Ved å bruke Lebesgueintegrsjon får vi en forbedring v fundmentlteoremet. Teorem 3.3 (Fundmentlteoremet med L-integrlet). Ant F er deriverbr på intervllet [, b]. Hvis F = f er begrenset på [, b], så er f L-integrerbr på [, b], og b f(x) dx = F (b) F (). Vi kn merke oss t L-integrlet er en generlisering v R-integrlet men ikke v N-integrlet, og fortstt trenger vi et tilleggskrv om begrensning v den deriverte. Det finnes også et integrl som er en generlisering v både L-integrlet og N-integrlet, og som klrer å tilbkestille lle deriverte. Dette integrlet klles «det generliserte Riemnn-integrlet». Teorem 3.4 (Fundmentlteoremet med det generliserte R-integrlet). Ant F er deriverbr på intervllet [, b]. D er F = f integrerbr på [, b], og b f(x) dx = F (b) F (). Det generliserte Riemnn-integrlet er en gnske ny teori (c 1960). I denne oppgven skl jeg konsentrere meg om N, R og L-integrlet, d det blir for mye teori hvis en skl prøve å gi et godt bilde v det generliserte R- integrlet. Jeg hr likevel vlgt å h med en kort innføring på slutten v Kpittel 5. 7
14 KAPITTEL 2 God gmmeldgs integrsjon I dette kpitlet skl jeg prøve å bygge opp teorien for Newtons- og Riemnns integrler. Dette er to typer integrl som hr veldig forskjellig oppbygging. Det ene kommer fr en tid før begreper som grense, kontinuitet og konvergens vr skikkelig definert, mens det ndre integrlet bserer seg på integrsjon som en grenseprosess. Disse to integrlene, i tillegg til Stieltjes integrl, er de som kn evlueres på en god måte uten bruk v målteori. Jeg skl smmenlikne disse, se på fordeler og ulemper, og prøve å få frem begrensningene til hvert v disse. Jeg strter med å definere N-integrlet, forklre litt om oppbyggingen og få frem noen egenskper. Deretter blir det smme gjort med R-integrlet, for så å smmenlikne. En liten del om Riemnn-Stieltjes integrl (R-S-integrlet) blir vslutningen v dette kpitlet. En del v egenskpene ved R-integrlet blir uteltt i dette kpitlet, fordi disse hr mer relevns når jeg senere skl smmenlikne R-integrlet med L-integrlet. 1. Newtons integrl Som jeg forklrte i innledningen, er oppbyggingen v Newtons integrl bsert på t integrsjon er det motstte v å derivere. Det å derivere vr noe mtemtikere på 1600-tllet visste en del om. I den følgende rgumentsjonen til Newton hr jeg vlgt å bruke moderne (Leibniz) notsjon. Newton brukte en nnen notsjon, men siden denne er mindre kjent, vil det snnsynligvis bre komplisere rgumentsjonen å bruke dette. Newton ønsket, for et gitt funksjonsutrykk y = f(x), å finne relet mellom x-ksen og grfen til denne funksjonen. Fiksér et punkt og l z = F (x) være grfen til f mellom og x. D viste Newton t funksjonen f er den deriverte til F. Vi kller F (x) en ntiderivert eller primitiv til f(x). Dette ble redegjort for på følgende måte: Hvis x øker med x så vil relet øke med z = F (x + x) F (x) = f(x) x. I grensen x 0 får vi dz = f(x) dx og dz dx = f(x). Merknd 1.1. Husk t d dette ble utledet hdde ikke begreper som grense, kontinuitet, konvergens og funksjon blitt skikkelig definert. Nå i moderne tid er det blitt utrbeidet en skikkelig definisjon på N-integrlet, og N-integrerbre funksjoner. Følgende definisjon er hentet fr [13]. 8
15 Definisjon 1.2. L b +. En funksjon f : (, b) R blir sgt å være N-integrerbr på (, b) hvis f hr en ntiderivert F på (, b), og hvis de ensidige grensene F (+) og F (b ) eksisterer og er endelige. Det reelle tllet b f(x) dx = F (b ) F (+) er N-integrlet til f over intervllet (, b). Måten N-integrlet blir brukt på for å finne et rel under en kurve er å finne en ntiderivert og deretter bruke fundmentlteoremet. Eksempel 1.3. L f(x) = 1 x. Finn relet begrenset v x-ksen og f når x [1, 5]. Løsning: Vet t en ntiderivert til f er F (x) = ln x. Arelet blir 5 1 f(x) dx = [ln x]5 1 = ln 5 ln 1 = ln 5. Merknd 1.4. For t vi skl klre å uttrykke en ntiderivert, så må den være en elementær funksjon. Selv om den ntideriverte eksisterer, så er det ltså ikke sikkert t vi klrer å uttrykke den. Svært mnge elementære funksjoner hr fktisk ikke en elementær ntiderivert [21]. Integrsjonsprosessen hr en veldig viktig egenskp den er lineær. Dette betyr t hvis α, β R, f og g er to integrerbre funksjoner så er αf + βg = α f + β g. Dette brukes mye når en regner med integrler, og vi skl bruke dette flere gnger senere i oppgven. Vi sier t N ([, b]) er mengden v Newton integrerbre funksjoner på intervllet [, b]. Vi skriver som regel bre N når det ikke er nødvendig å spesifisere intervllet. Hvilke funksjoner ligger i N? Her ligger lle funksjoner der vi kn finne en ntiderivert på det gitte intervllet. Problemet er t det egentlig er gnske få funksjoner vi kn finne en ntiderivert til. Vi kjenner heller ikke til noen spesiell egenskp som krkteriserer disse funksjonene (f.eks. lle monotone funksjoner eller lle kontinuerlige funksjoner). Eksempler på kontinuerlige funksjoner som ikke ligger i N er f 1 (x) = e x2 og f 2 (x) = sin x x. Nå skl det også nevnes t i forbindelse med enkle mtemtiske modeller, så dukker det som regel opp funksjoner som ligger i N. Dette kommer v t ntgelsene for modellen gjøres på en slik måte t beregningene blir greie å jobbe med. Newton-integrlet gir oss d muligheten for å løse disse (som regel differensillikninger) problemene nlytisk. Det er gnske ofte t en nlytisk løsning gir mer innblikk i løsningen enn f.eks en numerisk løsning. Den viktigste klssen v funksjoner som ligger i N er snnsynligvis polynomene. Disse hr egenskpen t de ligger tett i de kontinuerlige funksjonene [19]. Det betyr t en kontinuerlig funksjon kn tilnærmes vilkårlig br med et polynom, der tilnærmingen kn gjøres uniformt. Dette gir oss en mulighet for 9
16 å jobbe med de «snille» polynomene istedenfor mer kompliserte funksjoner (som knskje ikke hr noen ntiderivert). Nå skl jeg prøve å gi en forklring på hv det vil si t tilnærmingen kn gjøres uniformt. Dette betyr t en kn finne en følge v polynomer som konvergerer uniformt mot en kontinuerlig funksjon. Uniform konvergens er noe vi kommer borti flere gnger senere i oppgven, derfor ønsker jeg å gi en forståelse for dette begrepet. Det finnes flere måter en funksjonsfølge kn konvergere på, de to mest vnlige er punktvis og uniform konvergens. Først kommer den formelle definisjonen på disse to begrepene, deretter prøver jeg å forklre. Definisjon 1.5. Vi sier t en funksjonsfølge (f n ) konvergerer punktvis mot en grensefunksjon f hvis det for lle ɛ > 0 eksisterer N N, slik t bre n > N(ɛ, x), så er f n (x) f(x) < ɛ for lle x. Det kn være greit å tenke på dette som t tllfølgen (f n (x)) konvergerer for hver x. Her kommer den tilsyneltende nesten like definisjonen på uniform konvergens. Definisjon 1.6. Vi sier t en funksjonsfølge (f n ) konvergerer uniformt mot en grensefunksjon f hvis det for lle ɛ > 0 eksisterer en N(ɛ) N, som er uvhengig v x, slik t f n (x) f(x) < ɛ bre n > N(ɛ). Hvis en følge konvergerer punktvis kn vi tenke oss t det er en N som virker for hver x. Hvis konvergensen er uniform finnes det én N som virker for lle x ene på en gng. Nå følger to eksempler som skl prøve å illustrere bedre (se Figur 1). Eksempel 1.7. L f n (x) = x n, x [0, 1). Dette er en funksjon som konvergerer punktvis mot f(x) = 0. Konvergensen er ikke uniform siden vi for ethvert vlg v N lltid kn velge en x-verdi så nær 1 t f N (x) er så nær 1 som vi bre ønsker. Det neste eksemplet bruker den smme funksjonen, bre med et nnet definisjonsområde. Figur 1. Punktvis og uniform konvergens 10
17 Eksempel 1.8. L f n (x) = x n, x [0, 1 2 ]. Dette er en funksjon som konvergerer uniformt mot f(x) = 0. Denne funksjonen konvergerer ldri «tregere» enn f n ( 1 2 ). Det betyr t vi kn velge N slik t f N( 1 2 ) f(1 2 ) < ɛ. Siden funksjonen konvergerer rskere for lle ndre verdier v x, vet vi t denne N en virker for lle x [0, 1 2 ]. Ved første øyekst kn det se ut som det ikke er så stor forskjell mellom punktvis og uniform konvergens, men hvis mn jobber litt innenfor nlyse finner en fort ut hvor mye strengere uniform konvergens er. Her følger en rsk oppsummering v de viktigste ulempene ved N-integrlet. Vi blir nødt til å finne en ntiderivert for å kunne integrere. I forbindelse med funksjonsfølger kn det være vnskelig å vite om lle leddene er integrerbre. En funksjon må være gitt ved et funksjonsuttrykk for å gi mening til dette integrsjonsbegrepet. Nå beveger vi oss videre i integrsjonens verden til Riemnns integrl. 2. Riemnns integrl Det er to hovedmetoder å bygge opp R-integrlet etter, den ene er Riemnns metode, den ndre er Drboux s metode. Jeg velger å bruke Drboux s metode, som jeg mener er noe klrere i forhold til hv integrl egentlig er. Det kn også nevnes t Drboux s metode hr visse svkheter hvis en skl utvide definisjonen til funksjoner med mer generelle verdier enn bre reelle tll f.eks komplekse tll. Dette kommer v vhengigheten v t de reelle tllene er en velordnet kropp. Når vi jobber med komplekse tll finnes det ingen slik velordning. Vi kn ikke si t et komplekst tll er større enn et nnet. Brtle [2] mener t det er gnske tungt å bevise t Drboux s metoder er ekvivlent med Riemnns. Drbuox viste t for lle begrensede funksjoner og lle intervller [, b] så eksisterer tre tll m, M og R definert på følgende måte: m R er største nedre begrensning og M R er den minste øvre begrensningen til f på [, b]. = M m blir klt «vrisjonen» til f på [, b]. Drbuox presiserte t disse verdiene trengte ikke å bli truffet v f på intervllet. Hn vr en v de første som skilte mellom supremum og mksimum, og infimum og minimum [11]. Det er likevel slik t på de lukkede intervllene der f er kontinuerlig, så vil supremum være lik mksimum og infimum være lik minimum. Dette kommer som en følge v kompletthetsksiomet (Det er fktisk en lterntiv måte å definere kompletthet på). L nå f være en vilkårlig begrenset funksjon på [, b] R. For en vilkårlig prtisjon = x o < x 1 < < x n = b kn vi se på følgende uttrykk: M(n) = M 1 δ M n δ n, m(n) = m 1 δ m n δ n, (n) = 1 δ n δ n. 11
18 Figur 2. Nedre og øvre Drboux-sum Her er δ i = x i x i 1 lengden v det i te intervllet, M i = sup{f(t) : t [x i 1, x i ]}, m i = inf{f(t) : t [x i 1, x i ]} og i = M i m i. Drboux viste t grenseverdiene til M(n), m(n) og Δ(n) (når n og δ i 0) er entydige, endelige og vhenger bre v, b og f. Vi kller M(n) for den øvre Drbouxsum, og m(n) for den nedre Drboux-sum (se Figur 2). Grenseverdiene for M(n) og m(n) klles henholdsvis øvre og nedre Drboux-integrl, og skrives henholdsvis f(x) dx og f(x) dx[14]. Vi er nå klre for følgende definisjon: Definisjon 2.1. En funksjon f er R-integrerbr hvis og bre hvis f(x) dx = f(x) dx og vi definerer Riemnn integrlet ved f(x) dx = f(x) dx = f(x) dx. Jeg presiserer t de øvre og nedre Drboux-integrlene lltid eksisterer! Her kommer et eksempel på hvordn vi kn bruke definisjonen på R-integrsjon til å finne et rel. Eksempel 2.2. L f(x) = x 2. Bruk definisjonen v R-integrlet til å vise t 2 0 f(x) dx eksisterer, og finn relet begrenset v grfen til f og x-ksen når x [0, 2] (se Figur 3). Løsning: Vi lger en prtisjon som består v n like store deler, dvs. lengden på delintervllene blir b n = 2 n. Legg merke til t f er monoton på intervllet [0, 2], Figur 3. Hjelpefigur for eksempel
19 som betyr t m i lltid er venstre, og M i lltid er høyre endepunkt i delintervll i. m(n) = n (2(i 1)) 2 i=1 2 n 2 n = n 8(i 1) 2 i=1 og M(n) = n 2 n 3 i=1 n 2 2 n = n i=1 8i2 som viser t M(n) = m(n) + 8n2, og d er det opplgt t n 3 n 3 lim n M(n) = f(x) dx = f(x) dx = lim n m(n) som gir t f(x) = x 2 er integrerbr. Velger nå å regne ut lim n M(n) = lim n n i=1 8i2 = n 3 8 lim n n n 3 i=1 i2 8 = lim n n(n+1)(2n+1) 8n n 3 6 = lim 3 +12n 2 +4n n = 8 3n 3 3. Altså er 2 0 f(x) dx = 8 3. I eksemplet over hr jeg vlgt en måte å prtisjonere intervllet [0, 2] på, nemlig å bre l lle delene være like store. Kunne det tenkes t jeg kunne fått et nnet svr hvis jeg hdde prtisjonert på en nnen måte? Nei, R- integrlet er uvhengig v hvilken måte du prtisjonerer intervllet på, bre lengden v det største intervllet går mot null. Dette kn vi rgumentere for på følgende måte: Unsett hvilken prtisjon vi hr vlgt, kn vi lge en ny prtisjon P der lle intervllene er like lnge og mindre enn det minste v intervllene i den ndre prtisjonen. Det er lltid slik t sup x I f(x) sup f(x) x J og inf f(x) inf f(x) x I x J dersom I J er intervller. Dette medfører t P lltid vil gi en Drboux-sum som er en bedre tilnærming til relet. Vi sier t R er mengden v de Riemnn integrerbre funksjonene. Det er nturlig å spørre seg hvilke funksjoner som ligger i R? Det fullstendige svret får vi i neste Kpittel, men vi skl se på noen funksjoner her også. Riemnn viste t lle monotone funksjoner ligger i R (husk t vi snkker om begrensede funksjoner). Dette betyr t lle funksjoner med begrenset vrisjon ligger i R. Dette stemmer fordi lle funksjoner med begrenset vrisjon er differnsen mellom to monotone funksjoner [5]. Drboux vr den første som viste t lle kontinuerlige funksjoner ligger i R. Er det flere funksjoner i R? J, mnge flere. Riemnn kom med et eksempel på en funksjon i R som hdde uendelig mnge diskontinuiteter på ethvert delintervll. Det er lett å vise t lle funksjoner med et endelig ntll diskontinuiteter ligger i R. Hvilke «rre» begrensede funksjoner ligger ikke i R? Funksjonene trenger egentlig ikke å være så veldig rre, men de må være «veldig diskontinuerlige». Et eksempel, er en funksjon som blir klt Dirichlets monster. Den er definert slik: { 1 x er rsjonl f(x) =. 0 x er irrsjonl Heretter skriver vi denne funksjonen som f = 1 Q, dette kller vi en krkteristisk funksjon over Q 1. Det er ikke vnskelig å vise t denne ikke ligger i R. Vi observerer t unsett hvor lite intervll vi velger så vil mksimumsverdien være 1 og minimumsverdien være 0. Fr definisjonen hr vi t forskjellen mellom supremum og infimum på ethvert delintervll må kunne bli så liten 0 ellers. 1 Generelt hr vi t en krkteristisk funksjon f(x) = 1A hr verdien 1 når x A og 13
20 vi ønsker bre ved å gjøre prtisjonen fin nok. Det t en prtisjon er fin nok, betyr rett og slett t lengden på det største intervllet er lite nok. Mye v rbeidet i forbindelse med mtemtisk nlyse er å lge grense- og konvergensteorier. Derfor blir den følgende ulempen med R-integrlet krkterisert som lvorlig i moderne nlyse. Det er nemlig mulig å finne (punktvis) konvergente funksjonsfølger f n som er R-integrerbre for lle n, men der grensefunksjonen ikke er integrerbr. Nå følger et eksempel som viser dette. Eksempel 2.3. L f n (x) = 1 Qn, der Q n = {q 1, q 2,..., q n }, q i er en opprmsing v n forskjellige rsjonle tll. Det er nå klrt t f n R siden det bre er endelig mnge steder f n 0. Vi ser t lim n f n = 1 Q / R. Det er fktisk også mulig t grensen til en funksjonsfølge kn ligge i R, men t lim f n f. Her kommer et eksempel som viser dette også. Eksempel 2.4. L f n (x) = n1 [0, 1 n ]. D er lim f n = 1 f = 0, fordi lim f n = 0. Problemene kn omgås ved å kreve uniform konvergens, men det er et veldig strengt krv. Det finnes mnge punktvise grenser der lt går greit, derfor hdde det vært ønskelig med et svkere krv enn uniform konvergens. Det finnes et konvergensteorem for R-integrlet som hr litt svkere krv. Dette klles Riemnns begrensede konvergensteorem (noen steder klles det Arzel s begrensede konvergensteorem [17]). Dette teoremet ble vist v den itlienske mtemtikeren Cesre Arzel i 1885 [9]. Teorem 2.5. [Riemnns begrensede konvergensteorem]l (f n ) være en følge v R-integrerbre funksjoner på intervllet [, b]. Ant t f n f punktvis og t f er R-integrerbr på [, b]. Ant videre t f n K, der K er en reell konstnt, d hr vi t lim n b f n = Beviset for dette resulttet er gnske tungt når vi ikke skl involvere målteori [16]. Senere i oppgven skl vi se t resulttet bre er et spesiltilfelle v Lebesgues dominerte konvergensteorem. Vi så i Kpittel 1.3 t vi ikke kunne være sikre på t en begrenset funksjon sin deriverte vr Riemnn integrerbr. Her kommer et eksempel som viser dette. b Eksempel 2.6. En funksjon som er deriverbr på [ 1, 1] er { x f(x) = 2 sin( 1 ) når x 0 x 2 0 når x = 0. Den deriverte til denne funksjonen er ubegrenset på intervllet [ 1, 1], som medfører t den ikke er R-integrerbr her. Det finnes også eksempler på t den deriverte er begrenset, men likevel ikke R-integrerbr. 14 f.
21 2.1. Det normerte vektorrommet R 1. For å kunne lge mye god teori rundt en mengde med visse egenskper, er det ofte veldig nyttig hvis denne mengden er et vektorrom. Det viser seg t R er et vektorrom (vi lr sklrkroppen være R). Teorem 2.7. L f, g R og α, β R. D hr vi t Dette betyr t R er et vektorrom. (αf + βg) R. Det t R er et vektorrom betyr t enhver lineærkombinsjon v R-integrerbre funksjoner igjen er R-integrerbre. Det er også nturlig å gi vektorrommet et vstndsmål slik t vi kn snkke om konvergens v følger v funksjoner i R. For å kunne gjøre dette på en fornuftig måte bør vi se på vektorrommet over et intervll. Vi sier nå t R(I) er mengden v R-integrerbre funksjoner på intervllet I. R(I) er et vektorrom for lle intervller I R. En måte å definere et vstndsmål på R(I) er å si t vstnden mellom to funksjoner f og g er gitt ved: f g = sup x I f(x) g(x). Vi hr nå definert en norm på R(I) 2. Det betyr t hver funksjon i R(I) hr blitt tildelt en lengde som er gitt ved: f = sup x I f(x). Vi sier nå t en funksjonsfølge {f n } konvergerer til en funksjon f hvis sup x I f n (x) f(x) 0 når n. Problemet med dette normerte vektorrommet er t det bre er en nnen måte å si t vi trenger uniform konvergens for å få frem våre ønskede egenskper. Vi husker fr tidligere t dette vr et uønsket strengt krv. D vi definerte normen over tok vi ikke hensyn til t vi jobbet med integrsjon. Kn det hende t vi kn definere en nnen norm, som er reltert til integrsjon, og som gir oss flere konvergente følger v funksjoner? En god kndidt må være: f = I f(x) dx for f R(I)3. Vi kller denne normen for R 1 -norm, og vektorrommet R(I) med denne normen for R 1 (I). Dette er en norm som hr mnge v egenskpene vi ønsker, men dessverre hr R-integrsjon en svkhet som gjør t vi kommer opp i noen problemer med dette normerte vektorrommet. Problemet er mngel på kompletthet. Jeg skl nå prøve å forklre hv det betyr t et normert vektorrom er komplett. Vi husker fr reell nlyse t lle Cuchy-følger v reelle tll er konvergente. Dette er en nnen måte å si t R er komplett på. Det er dessverre ikke lltid slik t Cuchy-følger er konvergente i normerte vektorrom. L oss først få fullstendig klrhet i hv en Cuchy-følge i vektorrommet R 1 (I) er: Definisjon 2.8. En følge (f n ) R 1 (I) er Cuchy hvis det for lle ɛ > 0 finnes en N N slik t I f n f m < ɛ når bre n, m > N. En følge er ltså Cuchy hvis vstnden mellom to funksjoner i følg kn gjøres så liten vi bre ønsker, når den minste v indeksene til funksjonene er lngt nok ute i følg. Vi kn finne følger som er Cuchy, men som likevel hopper ut v R 1 (I) når vi går til grensen. For å finne eksempel på dette 2 Senere i oppgven skl vi se på den presise definisjonen v norm-begrepet. 3 Legg merke til t f er et endelig tll, siden f er en begrenset funksjon på I. 15
22 trenger vi bre å se på Eksempel 2.3. Denne følg er opplgt Cuchy siden vstnden mellom to punkter lltid er 0. Altså er ikke R 1 (I) komplett. Hvorfor er det så viktig t et vektorrom skl være komplett? Fr reell nlyse husker vi t det ksiomet som skiller de rsjonle tllene fr de reelle vr kompletthetsksiomet. Altså kn vi si t å jobbe med et vektorrom som ikke er komplett, blir som å jobbe med rsjonle tll istedenfor reelle tll. Det er ltså mulig å konstruere mye mer mtemtisk struktur hvis vi jobber under kompletthet. I Kpittel 4 skl vi se t geniet Henry Lebesgue løser dette problemet ved å definere en generlisering v R-integrlet (L-integrlet). Her følger en rsk oppsummering v de viktigste ulempene ved R-integrlet. Det oppstår problemer når vi skl integrere over mer kompliserte mengder enn intervller. Et enkelt eksempel på dette er funksjonen f = 1 Q. Vi kn risikere t grensefunksjonen f til en Cuchy følge v R- integrerbre funksjoner (f n ) ikke er R-integrerbr. Det kn også hende t lim f n f når f er R-integrerbr. Vi kn finne funksjoner f som er deriverbre på et begrenset intervll [, b], men integrlet til den deriverte eksisterer ikke. Fktisk kn også den deriverte være begrenset, og integrlet eksisterer fortstt ikke. Igjen hr vi t når integrlet eksisterer, kn det likevel hende t f f. Vektorrommet R 1 (I) er ikke komplett. 3. Smmenlikning v N- & R-integrlet Newton og Riemnns integrsjonsteori er veldig forskjellig. N-integrlet bygger på en observsjon om t derivsjon og integrsjon er motstte opersjoner. Fundmentet til dette integrlet bygger på litt vge teorier om bruken v uendelig små størrelser (infinitesimler). R-integrlet bygger på et ønske om å lge en geometrisk metode for å vgjøre relet under en grf. Denne teorien er solid begrunnet ved hjelp v grense og konvergensteorien til Cuchy og komplettheten til de reelle tll 4. Hvordn skl vi gå frem for å smmenlikne en ren nlytisk teori som N- integrlet er, og R-integrlets geometriske teori? Jeg tror vi må finne ut hv hver v dem kn brukes til. Jeg begynner med å diskutere litt rundt de sterke sidene til N-integrlet. Det første som må nevnes er brukervennligheten. Hvis du først hr plukket frem en N-integrerbr funksjon og funnet en ntiderivert, så er det bre å sette inn grensene og fundmentlteoremet produserer integrlet. Hvis du husker tilbke til Eksempel 2.2, minnes du sikkert t ting vr litt mer tungvinte med R-integrlet. I forbindelse med å lge mtemtiske modeller v virkeligheten, dukker det ofte opp reltivt enkle differensillikninger. Disse kn gjerne løses ved å bruke N-integrlet som verktøy. Den store fordelen med denne fremgngsmåten er t løsningen(e) produseres nlytisk. Anlytiske løsninger gir ofte større 4 Denne teorien hr selvfølgelig utviklet seg siden Cuchy, men jeg velger likevel å klle teorien hns. 16
23 innblikk i modellens struktur og dynmikk. Dette fører igjen til t modellen kn utvikles lengre og dypere enn hvis løsningene blir produsert numerisk. Av denne grunn blir N-integrlet veldig mye brukt i forbindelse med å søke grunnleggende forklringer på nturfenomener. Riemnn-integrlet hr en stor fordel fremfor Newton-integrlet, det er t vi ikke trenger noe funksjonsutrykk. Hvis vi f.eks bre hr grfen til en funksjon, gir R-integrlets geometriske oppbygning oss en fremgngsmåte for å bestemme relet. Dette gjør t fundmentet til R-integrlet brukes for å definere numeriske integrsjonsmetoder. Spesielt kn vi trekke frem t R-integrlets oppbygning gjør det mulig å bestemme reler under funksjonsgrfer der funksjonen er gitt som en rekke. N-integrlet kn også klre dette, men bre hvis mn kn finne en ntiderivert til hvert ledd, og ledd for ledd integrsjon er mulig. Vi hr kontinuerlige funksjoner som ikke er N-integrerbre, f.eks f(x) = e x2 som blir brukt mye i snnsynlighetsteori. Her fungerer R-integrlet ypperlig selv om utregningen som regel må gjøres numerisk. Det er fktisk verdt å nevne t de R-integrerbre funksjonene som vi fktisk regner ut for hånd, nesten lltid er N-integrerbre og derfor blir behndlet som sådn. 4. Uekte integrler Vi skl nå se integrler på formen: ( ) f, f og f, eller 1 dx 0 x. Alterntivet f hr jeg stt i prntes siden rgumentsjonen er helt nlog med f. Vi snkker ltså om bestemte integrler der enten integrsjonsintervllet eller funksjonen er ubegrenset. Disse klles uekte integrler. Det er verdt å påpeke t uekte integrler ikke regnes som en del v de R-integrerbre funksjonene. L oss først gå gjennom hvordn uekte integrler er definert. Vi lr først intervllet være ubegrenset. Det finnes to muligheter: enten ( f ) f eller f. Vi ser på disse mulighetene hver for seg. Definisjon 4.1. L f : [, ) R være en funksjon som er integrerbr på lle intervller [, b], der b >. Dersom integrlet b f L < når b, sier vi t integrlet f konvergerer og vi skriver f = L. Dersom integrlet ikke konvergerer, sier vi t det divergerer. En metode for å regne ut verdien til et uekte integrl på denne formen er å først finne en ntiderivert og deretter t grenseverdien. Her kommer et eksempel som viser dette (eksemplet er hentet fr [18]). Eksempel 4.2. Avgjør om 0 e x dx konvergerer, og finn eventuelt verdien. Vi ser t b 0 e x dx = [ e x] b 0 = e b
24 Figur 4. f(x) = e x som går mot 1 når b. Altså konvergerer integrlet, og 0 e x dx = 1. Den geometriske tolkningen er t det skrverte område i Figur 4 hr rel 1 selv om vi hdde sett uendelig lngt ut på x-ksen. Det kn sikkert være greit med et eksempel der integrlet er divergent også. Eksempel lim b ln b =. dx x divergerer fordi lim b b 1 dx x = lim b [ln x] b 1 = Dersom vi skl integrere over en mengde som er ubegrenset i begge retninger, må vi trø litt vrsomt. Vi begynner med definisjonen. Definisjon 4.4. Dersom f : R R er integrerbr på lle intervller [, b], sier vi t integrlet f konvergerer hvis begge de to integrlene 0 f og f konvergerer. D definerer vi 0 f = 0 f + Noen synes knskje denne definisjonen virket unødvendig komplisert. Hvorfor kn vi ikke bre si t hvis integrlet b b f L < når b, så er f = L? Grunnen til dette er t det finnes funksjoner f slik t 0 f. f med denne definisjonen er et endelig tll, men 0 f og 0 f divergerer. Et eksempel på dette er funksjonen f(x) = x. Det som gjør t dette kn skje er t uendelighetene oppveier hverndre, vi får ltså. Dette gjør t de vnlige regnereglene for integrler ikke lenger gjelder. Hr vi noen gng bruk for integrler over ubegrensede mengder? J, dette blir brukt mye innenfor både mtemtikk og fysikk. Det mest kjente eksempelet er knskje i forbindelse med stndrd normlfordeling i sttistikken. Her integrerer mn funksjonen f(x) = 1 2π e x2 2 fr til (integrlet blir 1, se Figur 5). Vi vet jo lle hvor mye denne teorien blir brukt innenfor utllige områder. 18
25 Figur 5. Stndrd normlfordeling Nå går vi videre og ser på integrsjon over intervller der funksjonen hr en eller flere vertikle symptoter. Igjen finnes det flere måter dette kn skje på. Vi ser først på når et v endepunktene til integrsjonsintervllet er en vertikl symptote. I definisjonen ntr vi dette skjer i høyre endepunkt (b), men det er klrt t det blir tilsvrende for venstre endepunkt. Definisjon 4.5. Dersom f : [, b) R er integrerbr på lle intervller [, y], der y < b sier vi t integrlet b f konvergerer hvis grenseverdien f eksisterer. I så fll skriver vi y lim y b b f = lim y b Vi ser t det er smme fremgngsmåte som blir brukt her, først finner vi uttrykket for et begrenset intervll, for så å t grenseverdien. Vi skl se t den smme metoden også blir brukt hvis vi hr vertikl symptote i begge endepunktene. Definisjon 4.6. L f : (, b) R være integrerbr på lle intervller [c, d], der < c < d < b og l y (, b). Vi sier t integrlet b f konvergerer dersom begge integrlene y f og b y f konvergerer for lle y [, b]. I så fll er b f = y Hvis det nå er flere vertikle symptoter inne i integrsjonsintervllet kn vi bre dele inn intervllet i flere delintervller med uendelighetene i hvert v endepunktene, for deretter å summere integrlene. Jeg ønsker å vise et eksempel på hvor glt ting kn gå hvis mn ikke er forsiktig. Eksempel 4.7. Det finnes et teorem som sier t integrlet 1 dx 0 x konvergerer p for p < 1 og divergerer ellers. Det betyr t 1 dx 1 divergerer. Men l oss nå x 2 lte som vi «glemte» t funksjonen vår hr noen uendelighet. Vi regner ut på vnlig måte; 1 [ dx 1 x 2 = 1 ] 1 = 1 x 1 1 ( 1 1 ) = f + y b y f. f.
Integrasjon Skoleprosjekt MAT4010
 Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
Matematikk 1000. Øvingsoppgaver i numerikk leksjon 8 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
M2, vår 2008 Funksjonslære Integrasjon
 M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
2 Symboler i matematikken
 2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
1 k 2 + 1, k= 5. i=1. i = k + 6 eller k = i 6. m+6. (i 6) i=1
 TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
Kapittel 4 Tall og algebra Mer øving
 Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Integralregning. Mål. for opplæringen er at eleven skal kunne
 8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
Brøkregning og likninger med teskje
 Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Matematikk Øvingsoppgaver i numerikk leksjon 9 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER:
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
5: Algebra. Oppgaver Innhold Dato
 5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
Numerisk derivasjon og integrasjon utledning av feilestimater
 Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
1 Mandag 25. januar 2010
 Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
R2 - Heldagsprøve våren 2013
 Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Integrasjon av trigonometriske funksjoner
 Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: a n x n. R > 0, med summen s(x). Da gjelder: a n n + 1 xn+1 for hver x < R.
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
1 Tallregning og algebra
 Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
Faktorisering. 1 Hva er faktorisering? 2 Hvorfor skal vi faktorisere? Per G. Østerlie Senter for IKT i utdanningen 11.
 Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
1 Mandag 18. januar 2010
 Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
x 1, x 2,..., x n. En lineær funksjon i n variable er en funksjon f(x 1, x 2,..., x n ) = a 1 x 1 + a 2 x a n x n,
 Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
MAT 100A: Mappeeksamen 4
 . november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
. november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
1 Mandag 1. mars 2010
 Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
E K S A M E N. Matematikk 3MX. Elevar/Elever Privatistar/Privatister. AA6524/AA6526 8. desember 2004 UTDANNINGSDIREKTORATET
 E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
MAT 100a - LAB 4. Før vi gjør dette, skal vi for ordens skyld gjennomgå Maple-kommandoene for integrasjon (cf. GswM kap. 12).
 MAT 00 - LAB 4 Denne øvelsen er i hovedsk viet til integrsjon. For mnge er integrsjon i prksis det smme som ntiderivsjon, og noe som kn rukes til å eregne relet v enkelte områder i plnet som lr seg egrense
MAT 00 - LAB 4 Denne øvelsen er i hovedsk viet til integrsjon. For mnge er integrsjon i prksis det smme som ntiderivsjon, og noe som kn rukes til å eregne relet v enkelte områder i plnet som lr seg egrense
Eneboerspillet. Håvard Johnsbråten
 Håvrd Johnsråten Eneoerspillet Når vi tenker på nvendelser i mtemtikken, ser vi gjerne for oss Pytgors læresetning eller ndre formler som vi kn ruke til å eregne lengder, reler, kostnder osv. Men mer strkte
Håvrd Johnsråten Eneoerspillet Når vi tenker på nvendelser i mtemtikken, ser vi gjerne for oss Pytgors læresetning eller ndre formler som vi kn ruke til å eregne lengder, reler, kostnder osv. Men mer strkte
Temahefte nr. 1. Hvordan du regner med hele tall
 1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
Løsningsforslag Kollokvium 1
 Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Terminprøve Matematikk for 1P 1NA høsten 2014
 Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
Fasit. Grunnbok. Kapittel 2. Bokmål
 Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
Fasit til utvalgte oppgaver MAT1100, uka 20-24/9
 Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
S1 kapittel 6 Derivasjon Løsninger til oppgavene i boka
 S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
Kvadratur. I(f) = f(x)dx.
 Kvdrtur Når mn snkker om numerisk kvdrtur er mn interessert i pproksimere integrler v funksjoner (som representerer reler, volumer, densiteter, o.s.v.) I(f) = f(x)dx. Det klles for kvdrtur fordi i gmle
Kvdrtur Når mn snkker om numerisk kvdrtur er mn interessert i pproksimere integrler v funksjoner (som representerer reler, volumer, densiteter, o.s.v.) I(f) = f(x)dx. Det klles for kvdrtur fordi i gmle
Løsningsforslag Kollokvium 6
 Løsningsforslg Kollokvium 6 25. februr 25 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 6. Oppgve Diskusjonsoppgve Diskuter følgende spørsmål med hverndre og prøv å bli
Løsningsforslg Kollokvium 6 25. februr 25 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 6. Oppgve Diskusjonsoppgve Diskuter følgende spørsmål med hverndre og prøv å bli
Kapittel 5 Verb. 5.4 For å få tak i en engelsk avis. For å finne utenlandske varer. For å treffe venninna si. For å invitere henne med til lunsj.
 Kpittel 5 Ver 5.1 For eksempel: Hver dg pleier jeg å sove middg Liker du ikke å dnse? I dg kn jeg ikke hndle mt. Jeg orker ikke å lge slt. Nå må jeg lese norsk. Jeg hr ikke tid til å t ferie. Kn du synge?
Kpittel 5 Ver 5.1 For eksempel: Hver dg pleier jeg å sove middg Liker du ikke å dnse? I dg kn jeg ikke hndle mt. Jeg orker ikke å lge slt. Nå må jeg lese norsk. Jeg hr ikke tid til å t ferie. Kn du synge?
Projeksjon. Kapittel 11. Ortogonal projeksjon i R 2. Skalarproduktet i R n. w på v. Fra figuren ovenfor ser vi at komponenten til w ortogonalt på v er
 Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
1 Mandag 8. mars 2010
 1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
EKSAMEN. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
Sensorveiledning Oppgaveverksted 4, høst 2013 (basert på eksamen vår 2011)
 Sensorveiledning Oppgveverksted 4, høst 203 (bsert på eksmen vår 20) Ved sensuren tillegges oppgve vekt 0,2, oppgve 2 vekt 0,4, og oppgve 3 vekt 0,4. For å bestå eksmen, må besvrelsen i hvert fll: gi minst
Sensorveiledning Oppgveverksted 4, høst 203 (bsert på eksmen vår 20) Ved sensuren tillegges oppgve vekt 0,2, oppgve 2 vekt 0,4, og oppgve 3 vekt 0,4. For å bestå eksmen, må besvrelsen i hvert fll: gi minst
Numerisk matematikk. Fra Matematikk 3MX (2002) Side
 Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Sammendrag kapittel 1 - Aritmetikk og algebra
 Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
MED SVARFORSLAG UNIVERSITETET I OSLO
 Eksmen i : MED SVARFORSLAG UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet INF5110 - Kompiltorteknikk Eksmensdg : Onsdg 6. juni 2012 Tid for eksmen : 14.30-18.30 Oppgvesettet er på : Vedlegg
Eksmen i : MED SVARFORSLAG UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet INF5110 - Kompiltorteknikk Eksmensdg : Onsdg 6. juni 2012 Tid for eksmen : 14.30-18.30 Oppgvesettet er på : Vedlegg
1 Geometri KATEGORI 1. 1.1 Vinkelsummen i mangekanter. 1.2 Vinkler i formlike figurer
 Oppgver 1 Geometri KTGORI 1 1.1 Vinkelsummen i mngeknter Oppgve 1.110 ) I en treknt er to v vinklene 65 og 5. Finn den tredje vinkelen. b) I en firknt er tre v vinklene 0, 50 og 150. Finn den fjerde vinkelen.
Oppgver 1 Geometri KTGORI 1 1.1 Vinkelsummen i mngeknter Oppgve 1.110 ) I en treknt er to v vinklene 65 og 5. Finn den tredje vinkelen. b) I en firknt er tre v vinklene 0, 50 og 150. Finn den fjerde vinkelen.
TMA4100 Matematikk1 Høst 2008
 TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
Nøtterøy videregående skole
 Til elever og forestte Borgheim, 1. ugust 2018 Viktig info om vlg v mtemtikkfg for elever på vg1 studiespesilisering I vg1 får elevene vlget mellom to ulike mtemtikkfg. Mtemtikk 1T (teoretisk) og Mtemtikk
Til elever og forestte Borgheim, 1. ugust 2018 Viktig info om vlg v mtemtikkfg for elever på vg1 studiespesilisering I vg1 får elevene vlget mellom to ulike mtemtikkfg. Mtemtikk 1T (teoretisk) og Mtemtikk
Kapittel 3. Potensregning
 Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
Integrasjon. et supplement til Kalkulus. Harald Hanche-Olsen 14. november 2016
 Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
... JULEPRØVE 9. trinn...
 .... JULEPRØVE 9. trinn.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres rett på rket. I noen oppgver
.... JULEPRØVE 9. trinn.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres rett på rket. I noen oppgver
9.6 Tilnærminger til deriverte og integraler
 96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
Løsningsforslag til Eksamen i fag MA1103 Flerdimensjonal analyse
 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Fag: Matematikk 1T-Y for elever og privatister. Antall sider i oppgaven: 8 inklusiv forside og opplysningsside
 Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x 2 ) + sin(x 2 ) dx = 2π. x s 1 e x 1 dx = Γ(s)
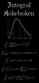 Integrl Kokeboken 4 3 4 6 8 log sinπ sinh π 4 + loglog loglog + C cos + sin π s e Γs n n s Γsζs π + sin +cos log + cos i Del I. Brøk................................... Trigonometriske funksjoner.....................
Integrl Kokeboken 4 3 4 6 8 log sinπ sinh π 4 + loglog loglog + C cos + sin π s e Γs n n s Γsζs π + sin +cos log + cos i Del I. Brøk................................... Trigonometriske funksjoner.....................
Del 2. Alle oppgaver føres inn på eget ark. Vis tydelig hvordan du har kommet frem til svaret. Oppgave 2
 Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
Integrasjon Fundamentalteoremet Substitusjon Forelesning i Matematikk 1 TMA4100
 Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
Numerisk Integrasjon
 Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
2 Tallregning og algebra
 Tllregning og lger KATEGORI. Regnerekkefølge Oppgve.0 Regn uten digitlt hjelpemiddel. + ( + ) ( ) Oppgve. Regn uten digitlt hjelpemiddel. Oppgve. Regn ut med og uten digitlt hjelpemiddel. + (7 + ) ( 9)
Tllregning og lger KATEGORI. Regnerekkefølge Oppgve.0 Regn uten digitlt hjelpemiddel. + ( + ) ( ) Oppgve. Regn uten digitlt hjelpemiddel. Oppgve. Regn ut med og uten digitlt hjelpemiddel. + (7 + ) ( 9)
Oppfriskningskurs i matematikk 2007
 Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Løsningsforslag til avsluttende eksamen i HUMIT1750 høsten 2003.
 Løsningsforslg til vsluttende eksmen i HUMIT1750 høsten 2003. Teksten under hr litt litt prtsom fordi jeg hr villet forklre hvordn jeg gikk frm. Fr en studentesvrelse le det ikke forventet nnet enn sluttresulttene.
Løsningsforslg til vsluttende eksmen i HUMIT1750 høsten 2003. Teksten under hr litt litt prtsom fordi jeg hr villet forklre hvordn jeg gikk frm. Fr en studentesvrelse le det ikke forventet nnet enn sluttresulttene.
Årsprøve 2014 10. trinn Del 2
 2 Årsprøve 2014 10. trinn Del 2 Informsjon for del 2 Prøvetid: Hjelpemidler på del 2: Vedlegg: Andre opplysninger: Fremgngsmåte og forklring: Veiledning om vurderingen: 5 timer totlt Del 2 skl du levere
2 Årsprøve 2014 10. trinn Del 2 Informsjon for del 2 Prøvetid: Hjelpemidler på del 2: Vedlegg: Andre opplysninger: Fremgngsmåte og forklring: Veiledning om vurderingen: 5 timer totlt Del 2 skl du levere
a 2πf(x) 1 + (f (x)) 2 dx.
 MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
Bioberegninger - notat 3: Anvendelser av Newton s metode
 Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
1T kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
Løsningsforslag til Obligatorisk oppgave 2
 Løsningsforslg til Oligtorisk oppgve INF1800 Logikk og eregnrhet Høsten 008 Alfred Brtterud Oppgve 1 Vi hr lfetet A = {} og språkene L 1 = {s s } L = {s s inneholder minst tre forekomster v } L 3 = {s
Løsningsforslg til Oligtorisk oppgve INF1800 Logikk og eregnrhet Høsten 008 Alfred Brtterud Oppgve 1 Vi hr lfetet A = {} og språkene L 1 = {s s } L = {s s inneholder minst tre forekomster v } L 3 = {s
Eksamen R2, Va ren 2014, løsning
 Eksmen R, V ren 04, løsning Tid: timer Hjelpemidler: Vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler er tilltt. Oppgve ( poeng) Deriver funksjonene ) f sin Vi bruker kjerneregelen på sin,
Eksmen R, V ren 04, løsning Tid: timer Hjelpemidler: Vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler er tilltt. Oppgve ( poeng) Deriver funksjonene ) f sin Vi bruker kjerneregelen på sin,
3.7 Pythagoras på mange måter
 Oppgve 3.18 Vis t det er mulig å multiplisere og dividere linjestykker som vist i figur 3.. Bruk formlikhet. 3.7 Pythgors på mnge måter Grekeren Pythgors le født på Smos 569 og døde. år 500 f. Kr. Setningen
Oppgve 3.18 Vis t det er mulig å multiplisere og dividere linjestykker som vist i figur 3.. Bruk formlikhet. 3.7 Pythgors på mnge måter Grekeren Pythgors le født på Smos 569 og døde. år 500 f. Kr. Setningen
R2 2010/11 - Kapittel 4: 30. november 2011 16. januar 2012
 R 00/ - Kpittel 4: 0. noemer 0 6. jnr 0 Pln for skoleåret 0/0: Kpittel 5: 6/ 6/. Kpittel 6: 6/ /. Kpittel 7: / /4. Prøer på eller skoletime etter hert kpittel. Én heildgsprøe i her termin. En del prøer
R 00/ - Kpittel 4: 0. noemer 0 6. jnr 0 Pln for skoleåret 0/0: Kpittel 5: 6/ 6/. Kpittel 6: 6/ /. Kpittel 7: / /4. Prøer på eller skoletime etter hert kpittel. Én heildgsprøe i her termin. En del prøer
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i analyse II Vår 219 8.4.1 Vi skal finne lengden til kurven x = 3t 2, y = 2t 3 der t 1. Som boka beskriver på
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i analyse II Vår 219 8.4.1 Vi skal finne lengden til kurven x = 3t 2, y = 2t 3 der t 1. Som boka beskriver på
Mer øving til kapittel 3
 Mer øving til kpittel 3 KAPITTEL 3 FUNKSJONER Oppgve 1 Tegn et koordintsystem og merk v punktene (1, 5) d (3, 2) ( 2, 3) e ( 3, 5) (4, 0) f (0, 4) Oppgve 2 Hvilke koordintpr hr de ulike punktene i koordintsystemet?
Mer øving til kpittel 3 KAPITTEL 3 FUNKSJONER Oppgve 1 Tegn et koordintsystem og merk v punktene (1, 5) d (3, 2) ( 2, 3) e ( 3, 5) (4, 0) f (0, 4) Oppgve 2 Hvilke koordintpr hr de ulike punktene i koordintsystemet?
Problemløsning eller matematiske idéer i undervisningen?
 Prolemløsning eller mtemtiske idéer i undervisningen? n Lksov Något som oft förekommer i diskussionen om skolns mtemtikundervisning är vvägningen melln prolemlösning och teori. I denn rtikel poängterr
Prolemløsning eller mtemtiske idéer i undervisningen? n Lksov Något som oft förekommer i diskussionen om skolns mtemtikundervisning är vvägningen melln prolemlösning och teori. I denn rtikel poängterr
YF kapittel 10 Eksamenstrening Løsninger til oppgavene i læreboka
 YF kpittel 10 Eksmenstrening Løsninger til oppgvene i læreok Uten hjelpemidler Oppgve E1 5 + 5 + 6 11 5 + 4 (5 + ) 5 + 4 7 10 6 + 8 d + ( + 1) 5 + 4 5 + 16 5 + 10 5 4 + 4 4 + 8 1 + + + + + + + + 49 49
YF kpittel 10 Eksmenstrening Løsninger til oppgvene i læreok Uten hjelpemidler Oppgve E1 5 + 5 + 6 11 5 + 4 (5 + ) 5 + 4 7 10 6 + 8 d + ( + 1) 5 + 4 5 + 16 5 + 10 5 4 + 4 4 + 8 1 + + + + + + + + 49 49
Kalkulus 2. Volum av et omdreiningslegeme. Rotasjon rundt x-aksen
 Klkulus Klkulus Volum v et omdreiningslegeme Rotsjon rundt x-ksen På figuren nedenfor hr vi skrvert området vgrenset v grfen til den kontinuerlige funksjonen y = f( x) og x-ksen fr x= til x=. Når vi roterer
Klkulus Klkulus Volum v et omdreiningslegeme Rotsjon rundt x-ksen På figuren nedenfor hr vi skrvert området vgrenset v grfen til den kontinuerlige funksjonen y = f( x) og x-ksen fr x= til x=. Når vi roterer
Numerisk kvadratur. PROBLEM STILLING: Approksimér. f(x)dx. I(f) = hvor f : R R. Numerisk sett, integralet I(f) = b. f(x)dx approksimeres med en summe
 Numerisk kvdrtur PROBLEM STILLING: Approksimér 1/18 I(f) = f(x)dx. hvor f : R R. Numerisk sett, integrlet I(f) = f(x)dx pproksimeres med en summe Q n (f) = w i f(x i ), n-punkter regel hvor x 1 < x 2
Numerisk kvdrtur PROBLEM STILLING: Approksimér 1/18 I(f) = f(x)dx. hvor f : R R. Numerisk sett, integrlet I(f) = f(x)dx pproksimeres med en summe Q n (f) = w i f(x i ), n-punkter regel hvor x 1 < x 2
Løsningsforslag til obligatorisk oppgave i ECON 2130
 Andres Mhre April 13 Løsningsforslg til obligtorisk oppgve i ECON 13 Oppgve 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) X og Z er uvhengige v hverndre, så Cov(X, Z) =.
Andres Mhre April 13 Løsningsforslg til obligtorisk oppgve i ECON 13 Oppgve 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) X og Z er uvhengige v hverndre, så Cov(X, Z) =.
6 Brøk. Matematisk innhold Brøk i praktiske situasjoner Brøk som del av en mengde. Utstyr Eventuelt ulike konkreter, som brikker og knapper
 Brøk I dette kpitlet lærer elevene om røk som del v en helhet, der helheten kn være en mengde, en lengde eller en figur, og de skl lære om røk som del v en mengde. De skl lære å finne delen når det hele
Brøk I dette kpitlet lærer elevene om røk som del v en helhet, der helheten kn være en mengde, en lengde eller en figur, og de skl lære om røk som del v en mengde. De skl lære å finne delen når det hele
Derivasjon. Oversikt over Matematikk 1. Derivasjon anvendelser. Sekantsetningen
 3 Oversikt over Mtemtikk Induksjon Grenser og kontinuitet Skjæringssetningen Eksistens v ekstrempunkt Elementære funksjoner Derivsjon Sekntsetningen Integrsjon Differensilligninger Kurver i plnet Rekker
3 Oversikt over Mtemtikk Induksjon Grenser og kontinuitet Skjæringssetningen Eksistens v ekstrempunkt Elementære funksjoner Derivsjon Sekntsetningen Integrsjon Differensilligninger Kurver i plnet Rekker
Nytt skoleår, nye bøker, nye muligheter!
 Nytt skoleår, nye øker, nye muligheter! Utstyret dere trenger, er som i fjor: Læreok lånes v skolen vinkelmåler, --9 og - -9-treknter, psser, lynt, viskelær, penn, A-rk til innføring og A klddeok. Og en
Nytt skoleår, nye øker, nye muligheter! Utstyret dere trenger, er som i fjor: Læreok lånes v skolen vinkelmåler, --9 og - -9-treknter, psser, lynt, viskelær, penn, A-rk til innføring og A klddeok. Og en
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 8. a =
 TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
Feilestimeringer. i MAT-INF1100
 Feilestimeringer i MAT-INF11 Ett v de viktigste punktene i MAT-INF11, og smtidig det som nsees som det vnskeligste i pensum, er feilestimter. Vi bruker mye tid på å beregne tilnærmede verdier for funksjoner,
Feilestimeringer i MAT-INF11 Ett v de viktigste punktene i MAT-INF11, og smtidig det som nsees som det vnskeligste i pensum, er feilestimter. Vi bruker mye tid på å beregne tilnærmede verdier for funksjoner,
1T kapittel 3 Funksjoner Løsninger til oppgavene i læreboka
 1T kpittel 3 Funksjoner Løsninger til oppgvene i læreok Oppgve 3.1 Origo er skjæringspunktet mellom førsteksen og ndreksen. Koordintene til origo er ltså (0, 0). Førstekoordinten til punktet A er 15, og
1T kpittel 3 Funksjoner Løsninger til oppgvene i læreok Oppgve 3.1 Origo er skjæringspunktet mellom førsteksen og ndreksen. Koordintene til origo er ltså (0, 0). Førstekoordinten til punktet A er 15, og
2x 3 4/x dx. 2 5 x 3 + LF: Vi utfører polynomdivisjon. 2x + 1 dx = + C = 5x8/ ln 2x C 4. πx 2 e 3x3 dx = π
 Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: MAT1140 Strukturer og rgumenter Eksmensdg: Fredg 8. desemer 2017 Tid for eksmen: 14:30 18:30 Oppgvesettet er på 5 sider. Vedlegg: Ingen
UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: MAT1140 Strukturer og rgumenter Eksmensdg: Fredg 8. desemer 2017 Tid for eksmen: 14:30 18:30 Oppgvesettet er på 5 sider. Vedlegg: Ingen
Fag: Matematikk 1T-Y for yrkesfag for elever og privatisterr. Eksamensdato: 16. januar 2012
 Loklt gittt eksmen Eksmen Fg: Mtemtikk 1T-Y for yrkesfg for elever og privtisterr Fgkode: MAT1006 Eksmensdto: 16. jnur 2012 Antll sider i oppgven: 7 inklusiv forside og opplysningsside Del 1: oppgve 1-5
Loklt gittt eksmen Eksmen Fg: Mtemtikk 1T-Y for yrkesfg for elever og privtisterr Fgkode: MAT1006 Eksmensdto: 16. jnur 2012 Antll sider i oppgven: 7 inklusiv forside og opplysningsside Del 1: oppgve 1-5
... JULEPRØVE
 Ashehoug JULEPRØVE 2014 9. trinn.... JULEPRØVE 2014.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres
Ashehoug JULEPRØVE 2014 9. trinn.... JULEPRØVE 2014.... Nvn: Gruppe: DELPRØVE 1 uten hjelpemidler ( 37 poeng) På denne delprøven kn du re ruke skrivesker, psser og linjl. Alle oppgvene i del 1 skl føres
Løsningsforslag til øving 4
 1 Oppgve 1 FY1005/TFY4165 Termisk fysikk Institutt for fysikk, NTNU åren 2015 Løsningsforslg til øving 4 For entomig gss hr vi c pm = 5R/2 og c m = 3R/2, slik t γ = C p /C = 5/3 Lngs dibten er det (pr
1 Oppgve 1 FY1005/TFY4165 Termisk fysikk Institutt for fysikk, NTNU åren 2015 Løsningsforslg til øving 4 For entomig gss hr vi c pm = 5R/2 og c m = 3R/2, slik t γ = C p /C = 5/3 Lngs dibten er det (pr
9 Potenser. Logaritmer
 9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
dx = 1 2y dy = dx/ x 3 y3/2 = 2x 1/2 + C 1
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
R1 kapittel 1 Algebra
 Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Kvalitetssikring av elektronisk pasientjournal - Skjema 1
 70778 EPJ Kvlitetssikring Skjem v. Hllvrd Lærum (tlf. 79886) Kvlitetssikring v elektronisk psientjournl - Skjem I dette spørreskjemet ønsker vi å få vite noe om din prktiske ruk v og ditt syn på elektronisk
70778 EPJ Kvlitetssikring Skjem v. Hllvrd Lærum (tlf. 79886) Kvlitetssikring v elektronisk psientjournl - Skjem I dette spørreskjemet ønsker vi å få vite noe om din prktiske ruk v og ditt syn på elektronisk
S2 kapittel 1 Rekker Utvalgte løsninger oppgavesamlingen
 Utvlgte løsiger oppgvesmlige S kpittel Rekker Utvlgte løsiger oppgvesmlige 0 Vi k prøve med differsemetode Differsee mellom leddee utover er 4,6,8, så det er rimelig t differse mellom femte og fjerde ledd
Utvlgte løsiger oppgvesmlige S kpittel Rekker Utvlgte løsiger oppgvesmlige 0 Vi k prøve med differsemetode Differsee mellom leddee utover er 4,6,8, så det er rimelig t differse mellom femte og fjerde ledd
2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5.
![2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5. 2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5.](/thumbs/88/116391567.jpg) NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 6 Avsnitt 6. 7 Ved å bruke disk-metoden får mn t volumet er π[r(x)] 2 dx 3 Ved å bruke disk-metoden får mn t volumet er L u
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 6 Avsnitt 6. 7 Ved å bruke disk-metoden får mn t volumet er π[r(x)] 2 dx 3 Ved å bruke disk-metoden får mn t volumet er L u
KAPITTEL 9 Approksimasjon av funksjoner
 KAPITTEL 9 Approksimsjon v funksjoner En grunnleggende teknikk som ofte brukes i ulike deler v mtemtikk og nvendelser er å tilnærme eller pproksimere et objekt med et nnet. Som regel er objektet som skl
KAPITTEL 9 Approksimsjon v funksjoner En grunnleggende teknikk som ofte brukes i ulike deler v mtemtikk og nvendelser er å tilnærme eller pproksimere et objekt med et nnet. Som regel er objektet som skl
6. Beregning av treghetsmoment.
 Forelesningsnotter i mtemtikk Bruk v integrsjon Beregning v treghetsmoment Side 1 6 Beregning v treghetsmoment 61 Definisjoner Først de grunnleggende definisjonene: Momentkse r m en liten punktformet prtikkel
Forelesningsnotter i mtemtikk Bruk v integrsjon Beregning v treghetsmoment Side 1 6 Beregning v treghetsmoment 61 Definisjoner Først de grunnleggende definisjonene: Momentkse r m en liten punktformet prtikkel
a 5 (2 + 8) d 5 (2 + 8) 4 g b 3 5 (2 + 8) e h 3 ( ) j Begrunn hvorfor du ikke får samme svar på oppgave b og g.
 Mtemtikk for ungomstrinnet KAPITTEL 4 TALL OG ALGEBRA MER ØVING Oppgve 1 Oppgve 2 Se på uttrykket A = g h. Hv forteller e ulike okstvene? Se på uttrykket O = 2π. Hv står e ulike symolene for? Forklr hv
Mtemtikk for ungomstrinnet KAPITTEL 4 TALL OG ALGEBRA MER ØVING Oppgve 1 Oppgve 2 Se på uttrykket A = g h. Hv forteller e ulike okstvene? Se på uttrykket O = 2π. Hv står e ulike symolene for? Forklr hv
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: MAT1140 Strukturer og rgumenter Eksmensdg: Mndg 22. jnur 2018 Tid for eksmen: 09:00 13:00 Oppgvesettet er på 7 sider. Vedlegg: Ingen
UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: MAT1140 Strukturer og rgumenter Eksmensdg: Mndg 22. jnur 2018 Tid for eksmen: 09:00 13:00 Oppgvesettet er på 7 sider. Vedlegg: Ingen
LØSNINGSFORSLAG(Sensor) I TMA4140 og MA0302
 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Sie 1 v 6 LØSNINGSFORSLAG(Sensor) I TMA4140 og MA0302 12. esemer 2006 Oppgve 1 ) Skriv ne efinisjonen på en tutologi. Svr: En tutologi
Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Sie 1 v 6 LØSNINGSFORSLAG(Sensor) I TMA4140 og MA0302 12. esemer 2006 Oppgve 1 ) Skriv ne efinisjonen på en tutologi. Svr: En tutologi
OPPLÆRINGSREGION NORD. Skriftlig eksamen. MAT1001 Matematikk 1P-Y HØSTEN 2011. Privatister. Yrkesfag. Alle yrkesfaglige utdanningsprogrammer
 OPPLÆRINGSREGION NORD LK06 Finnmrk fylkeskommune Troms fylkeskommune Nordlnd fylkeskommune Nord-Trøndelg fylkeskommune Sør-Trøndelg fylkeskommune Møre og Romsdl fylke Skriftlig eksmen MAT1001 Mtemtikk
OPPLÆRINGSREGION NORD LK06 Finnmrk fylkeskommune Troms fylkeskommune Nordlnd fylkeskommune Nord-Trøndelg fylkeskommune Sør-Trøndelg fylkeskommune Møre og Romsdl fylke Skriftlig eksmen MAT1001 Mtemtikk
Integrasjon del 2. October 15, Department of Mathematical Sciences, NTNU, Norway. Integrasjon
 Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
Kapittel 4.7. Newtons metode. Kapittel 4.8.
 Ekskt løsning Newtons metode - Integrsjon Forelesning i Mtemtikk TMA00 Hns Jko Rivertz Institutt for mtemtiske fg 0. septemer 0 Kpittel.7. Newtons metode Den ekskte løsningen v x x = 0er ikke særlig rukelig
Ekskt løsning Newtons metode - Integrsjon Forelesning i Mtemtikk TMA00 Hns Jko Rivertz Institutt for mtemtiske fg 0. septemer 0 Kpittel.7. Newtons metode Den ekskte løsningen v x x = 0er ikke særlig rukelig
ALTERNATIV GRUNNBOK BOKMÅL
 Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
Rekker, Konvergenstester og Feilestimat
 NTNU December 8, 2012 Oversikt 1 2 3 4 5 6 For å forstå, må vi først forstå potensrekker For å forstå potensrekker, må vi først forstå rekker. For å forstå rekker, må vi først forstå følger. Definisjon
NTNU December 8, 2012 Oversikt 1 2 3 4 5 6 For å forstå, må vi først forstå potensrekker For å forstå potensrekker, må vi først forstå rekker. For å forstå rekker, må vi først forstå følger. Definisjon
1 dx cos 1 x =, 1 x 2 sammen med kjerneregelen for derivasjon. For å forenkle utregningen lar vi u = Vi regner først ut den deriverte til u,
 TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
