Dette er en FORELØBIG versjon fra 13. juni 2001, for korrektur og kommentarer!
|
|
|
- Gunnar Bakke
- 8 år siden
- Visninger:
Transkript
1 MATEMATIKK Dette er en FORELØBIG versjon fra 3. juni 00, for korrektur og kommentarer! Det har tatt adskillig mer tid å skrive dette enn antatt. Noen konsekvenser av dette: Kapittel 8, lineær algebra, er ikke skrevet enda, og vil ikke bli det til studiestart. Det vil bli delt ut til studentene utpå høsten en gang. Fasit og stikkordregister rekker jeg ikke før i neste utgave. Kvaliteten er et godt stykke unna målet. Jeg har ikke rukket å bruke dere så mye som jeg burde. Spesielt gjelder dette DMM-lærerne. Blant annet er noen av de datarelaterte eksemplene jeg har skrevet med svak bakgrunnskunnskap, og burde sikkert forbedres. De inneholder kanskje direkte feil. Og så burde det vært flere av dem, kanskje jeg rekker åfå med rotasjon av bilder i kapittel 6. Jeg planlegger en større revisjon før neste års utgave, og da vil jeg mer aktivt spørre dere om råd, eksempler, valg av emner, innnfallsvinkler til temaer osv. Tilbakemeldinger fra studenter vil da også kunne bidra til dette. Det er ikke så mye tid igjen, der er jo ferie og en del andre forsømte oppgaver som også skalgjøres. Resten av tiden vil i hovedsak brukes til korrektur av kapittel 6 (trigonometri) og 7 (eksponentialog logaritmefunksjonen), som er skrevet intensivt i det siste, uten at jeg en gang har rukket ålese igjennom dem selv, og ikke fått luket bort de mest opplagte svakhetene. Forord og forside må også skrives. Jeg tar gjerne i mot kommentarer og feilmeldinger til alle deler, og vil selvfølgelig også følge opp dette hvis endringene ikke krever mer tid enn jeg har i denne omgang. i
2 ii
3 Innhold Repetisjon av algebra 3. Polynomer Brøkregning Potensregning Likninger Litt bakgrunn og utdy ping Mengder og funksjoner 9. Mengder Mengdeoperasjoner og Venndiagram Funksjoner Sammensatte og inverse funksjoner Oppgaver Logikk og tallsystemer Utsagnslogikk Tallsy stemer Oppgaver Algebraiske funksjoner Poly nomfunksjoner Rasjonale funksjoner Rotfunksjoner Oppgaver Derivasjon Grenserogkontinuitet Definisjon av den deriverte Anvendelser av derivasjon Andrederiverte Flere derivasjonsregler iii
4 5.6 Integrasjon Oppgaver Trigonometri 5 6. Absolutt vinkelmål (radianer) Definisjon av sinus, cosinus og tangens Trekantberegninger Trigonometriske omregningsformler Sinus og cosinus som funksjoner De deriverte av sinus og cosinus Plot av noen funksjoner med sinus og cosinus Oppgaver Eksponential- og logaritmefunksjoner 3 7. Eksponentialfunksjonen med vilkårliggrunntall Derivasjon av eksponentialfunksjonen Den naturlige logaritmen Logaritmer med vilkårlig grunntall Oppgaver Lineær algebra Matriser og vektorer Matriseoperasjoner og determinanter Affine transformasjoner
5
6 Kapittel Repetisjon av algebra En viktig grunn til at mange studenter sliter med matematikk er problemer med grunnleggende regneteknikk. Dette er selvsagt et problem i seg selv. Det fører også til at for mye av konsentrasjonen brukes opp pååforstå vanlige omforminger, framfor det nye stoffet som er hovedhensikten der og da. Dette repetisjonskapitlet er lagt opp med tanke på repetisjon og trening på multiplikasjon av polynomer, brøkregning, potensregning og likninger før oppstart med det egentlige pensum. Dette kan gjøres i form av et repetisjonskurs, for eksempel på en uke før oppstart. Det er antagelig ikke tid til åtakapitletså nøye som ønskelig innenfor den ordinære framdriftsplanen. Kapitlet er oppgavebasert. Oppgavene som er innbakt i teksten er det man bør bruke mest tid på. Disse studeres best ved å regne samtidig som kapitlet leses. Du bør likevel prøve åforståde forholdsvis få og enkle utledningene som finnes i disse avsnittene. I praktisk matematikk er det både enklere og sikrere å kunne utlede regler fra et forholdsvis beskjedent antall grunnregler, som du er sikker på stemmer, enn åprøveå huske alle mulige formler du støter på. Hovedavsnitt.5 er litt mer teoretisk og gir noe av grunnlaget for og utdyping av regnereglene i oppgaveavsnittene. Strever du med oppgavene er det kanskje riktig å nedprioritere dette, ihvertfall i første omgang. Kapitlet bruker leilighetsvis begrepene mengde, naturlige tall N, heltall Z, rasjonale tall Q og reelle tall R som først behandles i kapittel.. Dette avsnittet kan eventuelt leses først, men det byr nok ikke på storeproblemerå utsette det.. Polynomer Hensikten med dette avsnittet er å trene i manipulasjon med polynomer. Dette inkluderer regning med vanlige tall, som er spesialtilfeller av polynomer. Avsnitt.5. danner bakgrunn for regnereglene i.. og..3. Den noe unaturlige rekkefølgen med teorien etter anvendelsene skyldes at fokus er på regneteknikken i dette kapitlet... Parentesbruk Parentesen i regnestykket 0 (5 + ) betyr at (5 + ) skal behandles som et enkelt tall. Det betyr at parentesen skal regnes ut først, slik at 0 (5 + ) = 0 7 = 3. En annen parentessetting gir et annet resultat: (0 5) + = 5+ = 7. Med flere parenteser utenpå hverandre brukes ofte andre parentestyper (f.eks hakeparenteser) for å tydeliggjøre hvilke parentespar som hører sammen, men det vil i liten grad bli brukt her. Som input i dataprogrammer brukes hakeparenteser nesten aldri 3
7 4 KAPITTEL. REPETISJON AV ALGEBRA til dette formålet, de får gjerne tildelt andre betydninger. I uttrykk med flere parenteser regner vi først ut de innerste parentesene: ( (5 + (4 ))) = ( (5 + 3)) = ( 8) = 3=6 Regneoperasjonene i de fire regningsartene addisjon, subtraksjon, multiplikasjon og divisjon er i utgangspunktet definert for to og to tall. Lange uttrykk med slike utregninger skal da i prinsippet ha parenteser som gjør at alle utregninger skal gjøres for to og to ledd. For eksempel kan summen skrives ((( + ) + 3) + 4) + 5 for å angi rekkefølgen vi regner ut dette: = ((( + ) + 3) + 4) + 5 = ((3 + 3) + 4) + 5 = (6 + 4) + 5 = = 5 Dette er antagelig rekkefølgen du ville regnet ut denne summen på ved hoderegning ( en pluss to er tre pluss tre er seks pluss fire er... ). Om parentesene plasseres på en annen måte i regnestykket over, for eksempel + ((( + 3) + 4) + 5), blir resultatet det samme. Vi sløyfer derfor gjerne parentesene i dette tilfellet, og skriver summen uten parentes. Det er imidlertid aldri farlig å skrive parentes selv om det ikke er helt nødvendig. Rådet er: Vær raus med parentesene,og bruk alltid parentes hvis du er i tvil om det er nødvendig. Dette gjelder kanskje i enda sterkere grad i programmering enn i matematikk. I uttrykk uten parentes er det allment akseptert (konvensjonelt) at tolkningen skal være: I lange uttrykk bygd opp av de fire regningsartene er regelen at vi utfører multiplikasjoner og divisjoner før addisjoner og subtraksjoner. Bortsett fra dette regner vi fra venstre. Endringer i denne rekkefølgen kan oppnås ved parentesbruk. Skal vi regne ut /4 + begynner vi med multiplikasjonen og divisjonen og forenkler til Deretter regner vi sammmen fra venstre:...= 3 + = 9 + = 0. Ønsker vi utføre addisjonen først, og divisjonen helt til slutt skriver vi (( + 5) 4 )/4 =(7 4 )/4 =(8 )/4 =6/4 =4 For bokstavuttrykk (f.eks polynomer eller funksjonsuttrykk) gjelder de samme reglene. Vi kan da tenke oss at parentesen angir rekkefølgen vi skulle regnet ut uttrykket på omvisattinntall for bokstavene. En litt annen nyans er at om vi i bokstavuttrykk erstatter en bokstav med et sammensatt uttrykk vil vi i første omgang ha en parentes rundt dette. Hovedregelen over gjelder fortsatt, men i fortsettelsen får vi noen flere omformingsregler for parentesuttrykk med bokstaver. Oppgave. Regn ut: a) /6 b) (7 + 4 ) + 4 9/6 c) (7 + 4) +4 9/6 d) (7 + 4) ( + 4) 9/6.. Manipulasjon av polynomer Polynomer er utrykk som er bygd opp av tall og bokstaver sammen med operasjonene addisjon, subtraksjon og multiplikasjon. Bokstavene som inngår (eller som det er naturlig å tillate) kaller polynomets variable. For eksempel er x 3x + et polynom i variablen x. Leddet x er også framkommet ved multiplikasjon da det er en skrivemåte for x x. Eksempler på polynomer i variablene a og b er 0, 7ab 0, b +, 4og(a b)(a +3b). Det finnes også andre måter å bruke parentes på i denne boken. I avsnitt.4 skal vi representere ordnede par på formen (x,y), for eksempel (5, 3). Seinere skal vi også se på funksjonsuttrykk som for eksempel f(x) eller sin(x), der parentesen også har en annen rolle enn her.
8 .. POLYNOMER 5 Tall kan oppfattes som spesialtilfeller av polynomer. Tallet 3 kan for eksempel betraktes som et polynom i variablen x ved åskrive3=3+0 x. Ipolynomet7x 3 x + 5 kalles addendene 7x, 3x og 5 polynomets ledd. Potensen variablen i et ledd opphøyes i er leddets grad, slik at 7x har grad, 3x har grad og 5 har grad 0. Den høyeste potensen som finnes på leddene i polynomet kalles polynomets grad. Polynomet i dette eksemplet er således av grad, et andregradspolynom. Tallene 7, og 5 som variablene multipliseres med kalles koeffisientene. Koeffisienten i leddet av høyeste grad, her 7, kalles ledekoeffisienten, og tallet 5 er konstantleddet. Multiplikasjon av polynomer De viktigste prinsippene for multiplikasjon mellom polynomer (eller parenteser), formuleres her verbalt. I avsnitt.5. finnes bakgrunnen for disse. Det som alltid er bakgrunnen for at noen omforminger er lovlige er at uansett hvilken verdi vi setter inn for variablene får det opprinnelige og omformede polynomet samme verdi. Produktet av to polynomer er summen av alle produktene med et ledd (en addend) fra første og et ledd fra andre faktor. Eksempel (a + b)(a b +3)=a a + a ( b)+a 3+b a + b ( b)+b 3 Parentesen rundt b presiserer at dette betraktes som et enkelt tall, men hovedgrunnen til åhadenmed er å unngå å forveksle produktet a( b) med subtraksjonen a b. De tre første leddene er kombinasjonene med første ledd a fra første polynom og hvert av de tre leddene i andre polynom. De tre siste leddene er andre ledd b multiplisert med hvert av leddene i andre polynom. Dette uttrykket kan så pyntes videre med andre regler: Hvis antallet faktorer med minus foran i et produkt er et oddetall kan alle minustegnene erstattes av en felles minus foran produktet. Hvis antallet faktorer med minus foran i et produkt er et partall kan minusene sløyfes. Dette betyr for eksempel at ( ) a ( b) c ( d) = abcd I hovedeksemplet over kan vi sette minusen foran andre ledd, a ( b), og nestsiste ledd b ( b) ved denne regelen, siden de inneholder en (et oddetall) minus: a a + a ( b)+a 3+b a + b ( b)+b 3=a a a b + a 3+b a b b + b 3 Rekkefølgen på faktorene i et produkt kan omorganiseres som du ønsker. Rekkefølgen på addendene i en sum kan omorganiseres som du ønsker. Vi kan ikke bytte om rekkefølgen i en differens, a b b a. Hvis vi betrakter minustegnet som en del av leddet b kan vi omorganisere ved å la minusen følge med som en del av leddet: a b = a +( b) =( b)+a = b + a. Eksempel (forts.) Vi skriver a a kortere som a og b b som b. Multiplikasjonstegn i produkter sløyfes hvis dette ikke kan føre til misforståelser. Ledd med samme bokstavkombinasjon samles i en naturlig rekkefølge (gjerne dalende eller økende potens). I eksemplet kan vi da få omformingen: a a a b + a 3+b a b b + b 3=a ab +ab b +3a +3b Hvis det er flere variable er summen av eksponentene til variablene i leddet leddets grad, og graden på det eller de leddene med høyest grad er polynomets grad. For eksempel er 0.7ab 0.b +.4 et 3. grads polynom i variablene a og b.
9 6 KAPITTEL. REPETISJON AV ALGEBRA Hvis flere ledd i en addisjon har en faktor felles, kan denne settes utenfor en parentes som omfatter leddene uten denne faktoren. Eksempel (forts.) I delen ab + ab i eksemplet er ab felles faktor (hvis ab fjernes fra ab står vi igjen med ). Dette kan da skrives som ab( +) = ab =ab. Vedå gjøre denne sammenslåingen kan utregningen i eksemplet oppsummeres til (a + b)(a b +3)=a + ab b +3a +3b (.) Omforminga i formel (.) skal forstås slik at uansett hvilke tall som settes inn for a og b vil likheten gjelde. Hvis vi for eksempel velger a =3ogb = 4 blir venstresiden (3 + 4)( 3 4+3)= 7 5 = 35. Høyresiden blir det samme: = = 35. I praksis gjøres ofte flere av skrittene i eksemplet over i en og samme operasjon, så utregningen blir noe kortere. Det er imidlertid en fare at fristelsen er stor til å ta for mange skritt om gangen og pådra seg slurvefeil. Ikke minst er den neste omformingsregelen en hyppig feilkilde: Hvis det står en minus foran en parentes kan parentesen fjernes samtidig som alle leddene i parentesen bytter fortegn. Eksempel: a (a 3b +4)=a a +3b 4= a +3b 4. Oppgave. Regn sammen polynomene : a) (x +)(x +) b) (x 5)(x ) c) (y + )(3y ) d) (x +)(x +) e) (x )(x x +) f) (5x +)(x +x 3) g) (a + b 3)(a b +) h) (t )(t )(t 3) i) (x )(x 4 + x 3 + x + x +) j) (x +)(x ) (x +)(x +) Oppgave.3 Sett inn a = x og b =x i uttrykkene nedenfor, og regn sammen: a) (a + b)(a b +3) b) a + ab b +3a +3b Hvis du har regnet riktig vil du se at begge svarene i forrige oppgave er like. Uttrykkene er høyre og venstresiden i uttrykket i (.), svaret på eksempelet i starten av dette avsnittet. Dette er et eksempel på at ikke bare tall kan settes inn for bokstavene i disse utregningene, men også polynomer. Funksjonsuttrykk, som for eksempel x eller /x, kan også settes inn. Å omforme funksjonsuttrykk vil være en viktig anvendelse av regneteknikken fra dette kapitlet seinere i boken...3kvadratsetningene Oppgave.4 Begynn dette kapitlet med å regne sammen følgende polynomer (med metodene fra forrige underavsnitt):
10 .. POLYNOMER 7 a) (a + b)(a + b) b) (a b)(a b) c) (a + b)(a b) Produktet (a + b)(a + b) skrives vanligvis som (a + b),og(a b)(a b) som(a b).hvisdu har regnet oppgaven over riktig vil resultatet kunne oppsummeres i følgende setninger, som kalles kvadratsetningene: Første kvadratsetning (a + b) = a +ab + b Andre kvadratsetning (a b) = a ab + b (.) Tredje kvadratsetning (a + b)(a b) = a b Tredje kvadratsetning kalles også konjugatsetningen. Setningene kan forståes slik at ved å sette inn vilkårlige tall for a og b vil høyre- og venstresiden av likningene bli det samme tallet. Polynomer (eller funksjonsuttrykk) kan også settes inn for a og b, ogdagirformlenemåter å omforme et polynom (eller funksjonsuttrykk) på. Oppgave.5 Bruk kvadratsetningene til å regne sammen uttrykkene: a) (x +) b) (t ) c) (y +3)(y 3) d) (x + y) (x y) e) (s +3t) f) ( x )( x +) g) (a +( b)) (bruk første kvadratsetning! ) Kvadratsetningene bør læres. Ikke hovedsaklig fordi det går litt raskere å sette inn i formelen enn å regne det ut etter metoden i oppgaven over, men fordi du ofte trenger å bruke dem baklengs. Det vil si å skrive om polynomer fra utregnet form til produktform. Faktorisering Vi ønsker ofte å omforme polynomer den omvendte vegen av det som er gjort tidligere. For eksempel kan vi ønske åskrivex +4x +4 som (x +),noesomvisermå være riktig fra a oppgaven over. Dette kalles å faktorisere polynomet. Teknikken er ikke så automatisk som å regne sammen kvadratet. Først må du finne et kvadrat som skal erstatte a,ogdermeda, ienavformlenei(.) (dette vil ofte være leddet x, som i dette eksemplet). Deretter finner du ut hva som skal tilsvare ab (dette vil ofte være leddet som inneholder x i første potens, dvs. 4x i eksemplet). Siden vi nåharbestemta kan a settes utenfor ab leddet, og b bestemmes (med fortegn). I eksemplet er 4x =x, så b = (og det passer heldigvis med at b =4). Oppgave.6 Polynomene nedenfor tilsvarer høyresiden i en av kvadratsetningen ved passende valg av a og b. Faktoriser polynomene. a) x +x + b) x 4x +4 c) x 6 d) 4t +4t +36 e) y +6xy +9x f) 8 x + x +6 I disse oppgaven gikk faktoriseringen greit da uttrykkene passet akkurat inn i mønsteret til kvadratsetningene. En metode som kalles utfylling av kvadratet utvider denne framgangsmåten til å kunne faktorisere generelle andregradspolynomer (komplekse tall må tillates for at alle andregradspolynomer skal kunne faktoriseres). Utledningen av løsningsformelen for andregradslikningen på side7er et eksempel på bruk av denne teknikken.
11 8 KAPITTEL. REPETISJON AV ALGEBRA. Brøkregning Dette hovedavsnittet handler om brøkregning. Siden det er regneteknikken som skal oppøves skal kalkulator ikke brukes på oppgavene. Svarene skal normal gies på brøkform, ikke som desimaltall. Avsnitt.5. gir noe mer bakgrunn for regnereglene i dette avsnittet. Med brøk menes et uttrykk på formen a b (som også kanskrivesa/b). Størrelsene a og b kan være tall, polynomer eller funksjonsuttrykk. a kalles brøkens teller og b kalles brøkens nevner. Nevneren kan ikke være 0. Brøker på formen a kan settes lik a, ogbrøken a a = for alle a 0. Hvis a og b er heltall kalles brøken et rasjonalt tall... Addisjon, multiplikasjon og forkorting av brøker Regnereglene for brøk bygger på hovedregelen (.4) for multiplikasjon og (.5) for addisjon. Multiplikasjon av brøker Et heltall multipliseres med en brøk ved å multiplisere tallet inn i telleren: Multiplikasjon mellom heltall og brøk : c a b = ac b To brøker multipliseres ved å multiplisere teller med teller og nevner med nevner: Multiplikasjon av brøker: a b c d = ac bd Ved å skrive heltallet c som c er regel (.3) et spesialtilfelle av regel (.4) En konsekvens av denne regelen er forkortningsregelen for brøker. Hvis teller og nevner inneholder en felles faktor, kan denne forkortes bort. Det vil si: ac bc = a b Utregningen under følger fra multiplikasjonsregelen, og det at c c =. a b = a b = a b c c = ac bc Siden likhetstegn er symmetrisk (a = b betyr det samme som b = a) er det gyldig å gjøre denne utregningen fra høyre mot venstre, og da har vi forkortningsregelen. (.3) (.4) Oppgave.7 Skriv brøkene så enkelt som mulig. Det vil si med (maksimum) en brøkstrek, og uten felles faktor i teller og nevner. a) 3 d) g) 5xy 0xz b) e) h) (x ) (x )(x +) c) f) i) p q q p 55x x x +x + x
12 .. BRøKREGNING 9 Addisjon av brøker Hvis nevneren er lik i to brøker som skal adderes, adderes tellerne mens fellesnevneren beholdes: Addisjon av brøker med samme nevner: a b + c b = a + c b (.5) Hvis nevneren er forskjellig kan det ordnes slik at nevnerne blir like før det adderes. Siden d d = b b = kan brøkene multipliseres med disse uten å endres. Derfor gjelder følgende omforming: a b + c d = a b d d + c d b b = ad bd + cb db Nå er nevnerene like (siden bd = db), og addisjonsregel (.5) kan brukes. Resultatet kan oppsummeres i den generelle addisjonsregelen a b + c ad + bc = d bd Hvis nevnerne har en felles faktor greier det seg å multiplisere teller og nevner med et mindre tall for å oppnå samme nevner i brøkene (fellesnevner): = = = = = Det vil ikke bli feil om du ordner fellesnevneren til 0 5 = 50, du kan i så fall forkorte med 5 til slutt. Det er likevel vanligvis enklere å regne med lavere tall underveis. (.6) Subtraksjon av brøker. Vi har at a b = a b, og subtraksjon kan fåes fra addisjonsformelen ved å flytte minusen opp i telleren: = ( 5) = = Oppgave.8 Skriv brøkene så enkelt som mulig. Det vil si med (maksimum) en brøkstrek, og uten felles faktor i teller og nevner. a) d) g) x + 3 x + 4 b) + 3 e) h) x x c) f) i) 3 9xy 6yz ( p p q q + q ) p Oppsplitting av brøker Ofte er vi interessert i å omforme den motsatte vegen av å sette på felles brøkstrek. Det vil si at vi ønsker å splitte opp en brøk som en sum eller et produkt av to eller flere brøker. Som eksempel vises oppsplitting av brøken ( x 3 6x +8x )/ (4x): x 3 6x +8x 4x = x3 4x + 6x 4x + 8x 4x
13 0 KAPITTEL. REPETISJON AV ALGEBRA Her er summeregelen brukt motsatt, adderes leddene på høyresiden sammen fåes brøken på venstresiden. Noen forkortinger kan nå gjøres i hvert ledd: x 3 4x + 6x 4x + 8x 4x = x + 3x + Dette er et polynom, og en standardmåte å skrive polynomer på er med koeffisientene på brøkform, med monomene utenfor brøkstreken. I brøker foretrekkes også ofteatbådetellerognevnerer positive, så minusen settes foran i andre ledd: x 3 6x +8x 4x = x + 3x + = x 3 x + De siste omformingene er egentlig multiplikasjonsregelen brukt omvendt. For det første leddet kan dette presiseres slik: x = x = x = x... Kommentar:... Advarsel: Fra reglene over kan du greit omforme x+y x til + y. Hvis summen derimot finnes i nevneren, som i finnes ingen omformingsregel. En vanlig og alvorlig feil er å omforme dette til x+y +. Du ser at dette er helt feil ved åprøveå sette inn noen tall. Hvis omformingen var riktig ville x y svarene da blitt like. Hvis du setter inn x =ogy =erførstebrøk =, mens andre brøk er + + =4. Denne innsettingsmåten er ofte nyttig for å sjekke om en omforming er gal. Hvis utrykkene blir forskjellige, er den det. Hvis utrykkene blir like kan du likevel ikke være sikker på om omformingen er riktig. Likhet kan tilfeldigvis gjelde for de tallene du har valgt uten å gjelde generelt. Studenter som gjør omformingsfeil av denne typen spør av og til: Hvorfor har jeg ikke lov til ågjøre dette?. Ågietmoteksempel som det over er et svar. Generelt bør likevel svaret være: Spørsmålet er galt stilt. I matematikk må du spørre deg selv om hvorfor du har lov til å gjøre ting. Dette må du besvare ved å tilbakeføre omformingen til regler du vet er riktige (som for eksempel multiplikasjonsog addisjonsreglene (.4) og (.5)). Noen ganger ser du dette lett, andre ganger trengs en utledning. Klarer du ikke dette kan den nye regelen heller ikke brukes.... Oppgave.9 Gjør, om mulig, en naturlig oppspalting av følgende brøker som en sum av enklere brøker. Skriv resultatet så enkelt som mulig. a) c) x + x 3x +5x +x 3 + x 4 b) d) x x + (a + b)(a b) ab.. Brudden brøk Vi kan ha brøker der teller og nevner selv er brøker. Det er da viktig å holde orden på hvasom er hovedbrøkstreken. Det er ikke likegyldig om 8/4/ tolkes som 8/4 = =(somerriktig,i 8 følge konvensjonen om åregnefravenstre)eller 4/ = 8 = 4. Uttrykkene over og under hovedbrøkstreken kalles fortsatt brøkens teller og nevner, mens tellerne og nevnerne i brøkene som inngår over og under hovedbrøkstreken kalles smånevnere og småtellere. Brudne brøker kan omformes til utrykk med bare en (hoved)brøkstrek. Metoden baserer seg på at teller og nevner multipliseres med smånevnerne, og dermed kan disse forkortes bort. Dette illustreres i følgende eksempel: = = = = 0
14 .3. POTENSREGNING Metoden oppsummeres gjerne i følgende form: En brudden brøk forenkles ved å flytte smånevneren i telleren ned i nevneren, og smånevneren i nevneren opp i telleren: a/b c/d = a d (.7) c b Oppgave.0 Skriv som ubrudne brøker: a) /3 4 b) / c) /5 /5 d) 5/4 5/6 e) /x f) s/ t/3 g) h) x + x + i) x 6 x j) x + y k) /3 /4 6 l) a/ b/5 /a /b.3potensregning.3. Potenser med fast grunntall Med heltall mener vi tallene {...,,, 0,,,...}, menspositive heltall er tallene {,, 3, 4,...}. Rasjonale tall er alle tall som kan skrives som brøker m/n mellom heltall. Reelle tall er alle tall som kan skrives som desimaltall, eventuelt med uendelig mange desimaler. Dette skal presiseres litt mer i neste kapittel, men denne definisjonen klarer seg foreløbig. Heltallspotenser For n>0, et positivt heltall, og a et reelt tall er a n definert som a n def = a a a } {{ } n faktorer Foreksempeler9 3 =9 9 9 = 79. Spesialtilfellet a = a regnes som en del av denne definisjonen. Ipotensena n, kalles a grunntallet, ogn kalles eksponenten. For to positive heltall n og m følger da: a n a m =(a a a) (a a a a) = a } {{ } } {{ } } a a {{ a a a a } = a n+m n faktorer m faktorer n + m faktorer Ved å droppe prikkene fåes spesialtilfellet n =3,m =4. (.8) Dette gir en hovedregel for potensregning: a m a n = a m+n (.9)
15 KAPITTEL. REPETISJON AV ALGEBRA Vi skal nå utvide definisjonen av potenser til n = 0 og n negativt heltall. En viktig motivasjon for måten å gjøre dette på er at vi ønsker at multiplikasjonsregelen (.9) fortsatt skal gjelde. Da tvinger følgende omforminger fram definisjonene av a 0 og a n : a = a +0 = a a 0 = a a 0. Derfor må vi sette a 0 = =a 0 = a n n = a n+( n) = a n a n. Derfor må vi sette a n = a n a) a 0 = (a 0) b) a n = a n (a 0) (.0) Det er ikke så vanskelig å sjekke at regel.9 gjelder alle heltall m og n med disse definisjonene. Det gjennomføres ikke her. Oppgave. Fyll ut (uten kalkulator) verdiene av n i tabellen nedenfor. n n Toerpotensene er ofte viktige i datasammenheng. De er blant annet sentrale i kapittel 3.. Ordet kilo betyr egentlig tusen, men i datasammenheng betyr det gjerne 0.Enkilobyte er ikke nøyaktig 000 bytes, men derimot 04 bytes. En megabyte betyr en million bytes, men er egentlig 0 = bytes. Oppgave. Fyll ut (uten kalkulator) verdiene av 0 n i tabellen nedenfor. Bruk desimaltall. n n Oppgave.3 Regn ut ( ) 0,( ),( ),( ) 3 og ( ) 4. Multiplikasjon med ( ) n brukes som et triks for åfå til ledd med alternerende fortegn i matematiske formler og dataprogrambiter. Brøkpotenser For vilkårlige heltall m og positive heltall n kan vi bruke regel (.9) n ganger og får (a m ) n = a } m a m {{ a m regel (.9) } = a m+m+ +m = a m n n faktorer Vi kan på liknenede måte sjekke at denne regelen også gjelder for n =0ogn<0. Dette er også en grunnlegende potensregneregel: ( a m ) n = a m n (.) Vi skal nå utvide definisjonen av potenser til brøker x = m/n, og denne utvidelsen er motivert av at vi ønsker at regel. fortsatt skal gjelde. Vi begynner med x =/n, som vi setter inn for m i denne regelen. Da tvinger følgende definisjon seg fram: ( a /n) n = a n n = a = a. Derfor må vi sette a /n = n a
16 .3. POTENSREGNING 3 Vi definerer n a som det positive tallet som oppfyller ( n a) n = a. Viforutsetterata er positiv, og da eksisterer det et entydig positivt reellt tall som oppfyller dette. Ved isteden å erstatte m med m/n i regel. får vi følgende definisjon: ( a m/n) n m = a n n = a m Derfor må vi sette a m/n = n a m En alternativ måte å bruke regel., sammne med at vi nå har definert a /n = n a tvinger fram et annet uttrykk for a m/n : ( a m/n) n ( ) m = a n m = a n Derfor må vi sette a m/n = ( n a ) m Skal det derfor i det hele tatt være mulig å gjøre denne utvidelsen med disse reglene intakt må de to uttrykkene for a m/n være like, dvs. at n a m =( n a) m for alle positive tall a, og alle heltall m og n. Dette er tilfellet, selv om vi ikke viser det her. Det er også slik at reglene.9 og. fortsatt gjelder om vi erstatter m og n med vilkårlige brøker. Dette trenger en egen sjekk, som ikke taes med her. Vi oppsummerer til følgende definisjoner: a) a /n = n a b) a m/n = n a m (.) c) a m/n = ( n a) m Ved å bruke de to definisjonene for a m/n kan for eksempel 7 /3 regnes ut regnes ut på tomåter. Enten ved åskrive7 /3 = 3 79 = 9 (siden 9 3 = 79), eller (noe enklere hoderegning) ved åskrive 7 /3 = ( 3 7 ) =3 = 9. At svarene er like er en konsekvens at det er en gyldig regneregel at de to definisjonene av a m/n er like.... Kommentar:... For at vi skal være sikre på at alle reglene over gjelder må viantaatgrunntalleta er positivt, og at a x er positiv for alle rasjonale tall x. Vi kan tillate negative verdier av a om eksponenten er et heltall (også negative), men vi kan ikke ha a = 0 for negativ eksponent siden 0 n =/0 n =/0 ikkegår an. 0 0 er er et ubestemt uttrykk:0 n = 0 skulle tilsi at 0 0 =0,mensa 0 = skulle tilsi at 0 0 =. Det er tryggest åla0 0 forbli udefinert. For brøker i eksponenten kan ikke negative verdier av a tillates. For det første er ikke noe reelt tall. Selv om det finnes negative tredjerøtter av negative tall, fører det til selvmotsigelser åbruke disse i potensregningen, som følgende eksempel viser: ( ) /3 = 3 = (siden( ) 3 = ). Samtidig er ( ) /3 =( ) /6 = 6 ( ) = 6 =.Det er selvmotsigende åhaat( ) /3 er både og,så( ) /3 bør forbli udefinert. For positive tall a har vi ( ) ( ) a = a / = a. Dette gjelder ikke negative tall: ( ) = 4=.Det som alltid gjelder er x = x, der x er absoluttverdien til x. Absoluttverdien er det ikke negative tallet vi får om vi stryker en eventuell minus foran tallet.... Oppgave.4 Regn ut følgende potenser, uten kalkulator: a) 3 b) 3 3 c) 3 4 d) 6 e) 6 3 f) 6 4 g) 6 / h) 6 /4 i) 6 3/4
17 4 KAPITTEL. REPETISJON AV ALGEBRA j) 6 / k) 6 3/ l) 6 3/ m) a a 4 n) 0 r+ 0 r o) 7 r+3/ 7 r+ p) q) ( 5 ) r) ( /) 4 s) ( 8 ) 4 t) 8 4 u) (5 ) v) 7 4 w) x) Tierpotensene, som det ble regnet ut noen av i oppgave., er grunnelementene i desimaltallsystemet. For eksempel kan 35.6 skrivessom Enbrukavdisseerå skrive store eller små tallpå en mer oversiktlig måte: = = 7 0. En alternativ standard for å skrive desimaltalltall er med et siffer 0 foran komma, og med en tierpotens som sier hvor langt desimalpunkumet 3 skal flyttes mot høyre eller venstre: = og = Dette skrives ofte med bokstaven E (for eksponent): =.345 E5, og kalles teknisk notasjon. Representasjonen av desimaltall internt i datamaskiner følger et liknende prinsipp (bortsett fra at da er grunntallet (en potens av) istedenfor 0). Oppgave.5 Regn sammen tallene under, uten bruk av kalkulator. ( a) 0 ) (5 0 3) ( b) c) 0 ) 3 d) ( ) ( ) e) f) g) 8.45 E.00 E-9.3. Potenser med fast eksponent I reglene over, for eksempel multiplikasjonsregelen (.9), var grunntallet (a) det samme på begge sider av likhetstegnet. Vi har også en viktig og grunnleggende multiplikasjonsregel med forskjellige grunntall, men samme eksponent. Her begrunnes den først for positive heltall, før vi (uten bevis) setter den opp som en generell regel: (a b) n =(ab) (ab) (ab) } {{ } n faktorer = } a a {{ a } b } b {{ b } = a n b n n faktorer n faktorer a x b x =(a b) x (.3) Følgende er et eksempel der eksponenten x =/ ikke er et heltall, men hvor du likevel kan se at resultatet stemmer: 6= 36 = 4 9=(4 9) / =4 / 9 / = 4 9= 3 Her følger en liste på noen flere regler du bør kjenne. De er kanskje lettest å huske som spesialtilfeller av reglene tidligere i dette avsnittet: 3 Jeg har valgt å bruke amerikansk notasjon med desimalpunktum herfra og i resten av boken, framfor norsk notasjon med desimalkomma. Dette skyldes dels at det er mest vanlig i dataprogrammer, og dels at det er enklere når vi skal skrive par av desimaltall, som f.eks. (7.3, 4.9).
18 .3. POTENSREGNING 5 a) b) n c) a d) a x a y = a x y a x ( a ) x b x = b n n b = ab n a n b = n a b (.4) En bruk av (.4c) er åskrive på formen = 4 3= 4 3= 3... Kommentar:... Advarsel: Det er ingen enkel omformingsregel om vi bytter ut multiplikasjon med addisjon på enav sidene i formel (.3). Spesielt finnes ingen forenkling av uttrykket x + y. Dumå unngå den vanlige feilen å omforme dette til x + y.hvisvisetterinnx =9ogy =6er x + y = 9+6=5,mens x + y = 9+ 6=3+4=7. Dette er sterkt beslektet med tilfellet i kommentaren på side 0. Det finnes heller ingen enkel omformingsregel for a x b y,når både grunntall og eksponent er forskjellige.... Gjør, om mulig, naturlige omforminger av potensuttrykkene (uten kalku- Oppgave.6 lator): a) a 3 b 3 b) n 3 n c) 6 3 d) (x) 3 e) 8 6 f) 9x 4 ( ) 3 3 g) 8 h) x /5 i) 4 /3 /3 j) 3 x8 / 3 8x k) 4 x/8 l) 3 9 x + 3 m) a +4b n) x +x + o) x +9 x 4 Oppgave.7 Regel (.4c) får vi slik: n a n b = a /n b /n regel (.3) = (ab) /n = n ab Utled reglene (.4a), (.4b) og (.4d) på tilsvarende måte. I brøker anses det gjerne for ryddigere å unngå rotuttrykk i nevneren. Her er et eksempel på en omforming for åfå til dette: = = ( ) = 3 3 Oppgave.8 Omform til brøker uten rottegn i nevner: x a) b) c) x + 3 d) + Hint:Multipliser med itellerognevner.
19 6 KAPITTEL. REPETISJON AV ALGEBRA.4 Likninger Dette hovedavsnittet tar for seg lineære likninger i en og to variable, og andregradslikninger. Det inneholder også litt om likninger for rette linjer og parabler, og tegning av disse i et kartesisk koordinatsystem (xy planet). Noe mer teori om likninger finnes i avsnitt.5.3 Samlingen av alle løsninger av en likning 4 (eller et likningssystem) skal vi kalle løsningsmengden. To likninger (eller likningssystemer) som har samme løsningsmengde kalles ekvivalente, ogkan bindes sammen med tegnet. Når likninger skal løses er metoden vanligvis å omforme likningene til en form der vi direkte kan se hva løsningsmengden må være. Et viktig prinsipp for omforming av likninger er at om samme operasjon utføres på begge sider av likhetstegnet vil alle løsninger i den opprinnelige likningen også være løsninger i den omformede likningen. Hvis det også finnes en operasjon som kan utføres på begge sider i den nye likningen slik at den blir omformet til den opprinnnelige likningen har de samme løsningsmengde..4. Førstegradslikninger En likning (med x som ukjent) som kan ordnes til formen ax + b =0(dera 0) kalles en lineær likning med en ukjent, eller kort bare en førstegradslikning. Eteksempelerx 8 = 0. En løsning er et tall som når det settes inn for den ukjente x, gjør at venstresiden (her x 8) og høyresiden (her 0) er samme tall. I dette tilfellet er dette x =4siden 4 8=0.Når dette tallet er funnet sier vi at likningen er løst med hensyn på x. Eksempel Løsning av likningen x 3 = 5 kan starte med å addere tallet 3 til begge sider av likhetstegnet: x 3=5 x 3+3=5+3 x =8 Denne operasjonen kan reverseres (ved å subtrahere 3 fra begge sider av likningen x =8),sådet omformede likningssystemet har samme løsningsmengde. Denne operasjonen beskrives vanligvis som Et ledd i en likning kan flyttes over på motsatt side av likhetstegnet ved å bytte fortegn på leddet. Løsningsmengden endres ikke ved denne operasjonen. Vi kan fortsette med å dividere begge sider av likhetstegnet med tallet : x =8 x =8 x =4 Siden denne operasjonen kan reverseres (ved å multiplisere begge sider av likningen x = 4 med ) er likningene ekvivalente. Denne operasjonen kan vi generelt beskrive slik: Et tall forskjellig fra 0 kan multipliseres eller divideres på begge sider av likningen. Løsningsmengden endres ikke ved denne operasjonen. Det har nå framkommet en likning der x står alene på den ene siden av likhetstegnet. I denne likningen ser vi direkte at det er 4 vi må sette inn for x for at begge sider av likhetstegnet skal få samme verdi. Ved innsetting i den opprinnelige likningen er venstresiden 4 3=5,somerdet samme som tallet på høyresiden. 4 Utgangspunktet her er at leseren vet hva likninger og løsninger er, ihvertfall i tilstrekkelig grad til å følge framstillingen videre. Jeg tar derfor ikke med noen detaljert og formell forklaring på dette. Tilsvarende utgangspunkt taes også flere ganger seinere, blant annet i dette hovedavsnittet når vi tar i bruk kartesisk koordinatsystem (xyplanet)
20 .4. LIKNINGER 7 Oppgave.9 Løs likningene under med hensyn på x: a) 3x =3 b) 6x 5=3 c) x +=x d) 4x +5=3( x) e) x 0.5 =0.7 f) x =0.75x g) 5x = 3 i) k) h) 3 x +4= x += x 3 j) x = x x = l) x +3 = 3 x + Likninger med parametre I mange situasjoner kan det være naturlig eller hensiktsmessig å kalle den ukjente noe annet enn x. Hvis likningen i eksemplet over dreide seg om en problemstilling der tiden skulle finnes for et eller annet ville vi kallt den ukjente t, og skrevet likningen t 3 = 5 med løsning t =4. I mange problemstillinger inngår andre bokstaver enn den ukjente. Disse bokstavene behandles på samme måte som de kjente tallene, og kalles parametre. Løsningen(e) vil da også (vanligvis) inneholde parametrene. Likningen x 4t = har løsning x =t + om x er den ukjente og t en parameter. Dette kan tolkes som at uansett hvilket tall vi setter inn for t i likningen så får vi løsningen ved å sette dette tallet inn for t iformelenx =t +. Det er viktig å vite hvilken bokstav som er den ukjente, t kan også være ukjent i likningen x 4t =. Den kan da løses med hensyn på t og ha løsningen t = x 4. Oppgave.0 Løs likningene under med hensyn på variabelen som står til slutt. Angi også eventuelle begrensninger på hva parameteren kan være for at løsningen skal gjelde. a) x t =, x b) x t =, t c) µ σ =, σ d) x +y =8, x e) kx + l =0, x f) ax + by = c, y g) p(p + q) =, q h) xy =, x.4. Lineære likninger med to ukjente Likning for en rett linje En likning på formenx +y = 8, eller mer generelt ax + by = c, kalles en lineær likning med to ukjente (dvs. de ukjente er x og y). Løsninger av denne vil bestå avbåde en x verdi og en y verdi. Vi skriver derfor en løsning som et ordnet tallpar (x, y). Samtlige av slike løsninger kalles løsningsmengden. For eksempel er (, 3) og (6, ) begge i løsningsmengden til x +y =8,siden innsetting av x =ogy = 3 gir venstresiden + 3 = 8, og x =6,y =gir6+ =8.Det finnes uendelig mange slike tallpar som oppfyller denne likningen, så alle kan ikke listes opp. Det som kan gjøres er å tegne dem inn i et koordinatsystem, og de vil da sammen danne en rett linje. Den er selvfølgelig uendelig lang, og har tykkelse 0, men vi må nøyeossmedå tegne et passende utsnitt, som i figur.. Løsningene (, 3) og (, 6) er markert som store prikker.
21 8 KAPITTEL. REPETISJON AV ALGEBRA y x Figur.: Løsningsmengden til x +y =8 Hvis b 0 kan likningen ax + by = c omformes til y = a b x + c b a b med k og c b med l blir da likningen på formen (jfr. oppgave.0f). Ved å erstatte y = kx + l. For eksempel kan likningen x +y =8omformestily = x + 8 y = x +4. Velges en verdi for x er det bare ett par (x, y) med denne x verdien som er løsning. Velges f.eks. x = 4 i eksemplet over må y være y = 4+4=6. Ved åsepåfigur.får vi bektreftet at (4, ) ligger i løsningsmengden. Om x velges lik 0 fåes et punkt på y aksen. Generelt har vi da at y = k 0+l = l. Dermedkan konstantleddet l tolkes geometrisk som skjæring med y aksen. Differensen mellom y verdien i et punkt med x koordinat x 0 og punktet som har x koordinat x 0, det vil si punktet til venstre for det første, er [kx 0 + l] [k(x 0 ) + l] =kx 0 + l kx 0 + k l = k Konstanten k kan dermed tolkes som hvor mye y verdien øker om x økes med. Dette betyr at k er et mål for hvor bratt kurven er, og kalles stigningskoeffisienten. Mer generelt har vi at om x verdien endres med et tall x, og den tilsvarende økning i y verdien kalles y er stigningskoeffisienten k = y x. Oppgave. Skissér løsningsmengden, og finn likningene på formeny = kx + l for linjene med følgende egenskaper: a ) Stigningskoeffisienten er, og skjæring med y aksen er y = 3. b ) Stigningskoeffisenten er, og skjæring med x aksen er x = 3. c ) Stigningskoeffisienten er 3, og linja går gjennom punktet (4, ). d) Linja skjærer y aksen i y =,oggår dessuten gjennom punktet (3, 7). e ) Linja er parallell med x aksen, og skjærer y aksen i y =5. f ) Linja er løsningsmengden av likningen x 3y =.
22 .4. LIKNINGER y x 3y = x +y = x Figur.: Løsningsmengden til likningsystemet x +y =8,x 3y = Vertikale linjer kan ikke skrives på formeny = kx + l. De kan derimot skrives som for eksempel x = 3. Dette kan oppfattes som spesialtilfelle av formen ax + by = c, meda =,b =0ogc =3. Et likningssystem av to lineære likninger med to ukjente et for eksempel x + y = 8 x 3y = Det eller de parene (x, y) som tilfredstiller begge likningene kalles likningssystemets løsningsmengde. Det er som oftest bare ett tallpar som oppfyller dette, og i så fall sier man at likningssystemet har entydig løsning. Vedå tegne begge løsningsmengdene som linjer i et koordinatsystem vil denne løsningen være skjæringspunktet mellom disse linjene. I figur. er dette gjort for likningene i eksemplet, og det kan leses av firguren at (4, 6) er den entydige løsningen. Dette kalles grafisk løsning av likningssystemet. En regnemessig (analytisk) måte å løse slike likninger på ervedinnsettingsmetoden, somher illustreres ved eksemplet: Først løser vi den ene likningen med hensyn på den ene ukjente. Likning og ukjent er fritt valgt, her velges x i den første likningen: x +y =8 x = y +8 Dette settes så inn i den andre likningen ved at x erstattes med y uttrykket for x, slik at dette blir en likning med en ukjent (y) ( y +8) 3y = 4y +6 3y = 7y = 4 y = y verdien i løsningen er nå funet, og denne settes inn i en av likningene for å finne x, for eksempel idenførste: x + =8 x =4 Dermed er løsningen x =4,y =, som også kanskrives(4, ). Dette er den samme løsningen som ble funnet grafisk. Oppgave. Løs likningssystemene både grafisk og ved innsettingsmetoden:
23 0 KAPITTEL. REPETISJON AV ALGEBRA a) x + y = 5 x y =. b) 3x + y = 3 7x 3y = 7. c) y = x 5 y = 3x 9. d) y = 3 x 3 x = 7. e) x y = 0 x + 4y = 0. f) x y = 0 x + 4y = 4. I de to siste deloppgavene brøt innsettingsmetoden sammen. Grafisk løsning viser hva som skjedde: I det ene likningssystemet falt linjene oppå hverandre. Det vil si at alle de uendelig mange løsningene i den ene likningen også er løsninger i den andre, så det er uendelig mange løsninger. Egentlig er det samme likning, multipliseres x y = 0 med på begge sider av likhetstegnet blir resultatet x +4y =0. I det andre systemet er linjene parallelle, og har ingen skjæring. Likningssystemet har ingen løsninger. Dette kalles også et selvmotsigende likningssystem. I kapittel 8 skal vi se på en alternativ løsningsmetode, kallt Gausseliminasjon. Gausseliminasjon er bedre hvis det er flere ukjente, og til å hanskes med varianter som ingen eller uendelig mange løsninger, og forskjellig antall ukjente og likninger. Gausseliminasjon er også enklere å programmere i dataspråk. Eksempel De ukjente behøver selvfølgelig ikke kalles x og y. Her er et eksempel der x og y inngår, men de er ikke de ukjente i likningene som skal løses: Koeffisientene k og l i likningen y = kx+ l for linja gjennom punktene (, 3) og (4, 4) skal bestemmes. For at punktet (, 3) skal ligge på linja må disse passe inn i y = kx+ l: 3=k +l. Tilsvarende gir punktet (4, 4) likningen 4 = k 4+l. Dermed er det to likninger med k og l som ukjente: k + l = 3 4k + l = 4 Første likning gir l =3 k, som settes inn i andre likning: 4k +3 k =4 k = 3. Dette settes så inn i første likning: 3 + l =3 l = 8 3. Det vil si at likningen for linja er y = 3 x som også kanskrives 3y x =8. Oppgave.3 a ) Finn en likning for linja gjennom punktene (, 5) og (4, 3). b ) Finn en likning for linja gjennom punktene (0, 4) og (, 0). c ) Finn en formel for k og l (uttrykt ved hjelp av x 0, y 0, x og y ) for linja gjennom punktene (x 0,y 0 )og(x,y ). d ) Vis at likningen for linja gjennom punktene (x 0,y 0 )og(x,y )kanskrives y y 0 = y y 0 x x 0 (x x 0 ) Her er x og y kalt de ukjente, siden vi har et likningsperpektiv på linjene. Seinere vil dette sees fra et funksjonsperspektiv, og da er det naturlig å kalle x og y variablene. Her er koordinataksene kalt x aksen og y aksen. Vi kan selvfølgelig ha andre navn på variablene, og må skifte navn på aksene deretter. Et navn på x aksen som ikke referer til variabelnavnet er abscisseaksen, og. aksen brukes av noen. Tilsvarende navn på y aksen er ordinataksen, eller. aksen.
24 .4. LIKNINGER.4.3Andregradslikninger En likning som kan ordnes til formen ax +bx+c =0,medx som ukjent, kalles en andregradslikning. Hvis likningen er på faktorisert form, for eksempel (x )(x 3) = 0, kan løsningen sees direkte. Et produkt er 0 når en av faktorene er 0, ikke ellers. Det vil si (x )(x 3) = 0 når x = 0 eller x 3 = 0. Løsningen er dermed x = eller x =3. Dette formuleres også som at løsningsmengden er {, 3 }. Løsningene av andregradslikninger (og generelt likninger på formenp(x) = 0derp(x) eretpoly- nom) kalles røtter. En annengradslikning kan ha ingen, en eller to røtter blant de reelle tallene. Oppgave.4 Løs andre- og tredjegradslikningene a) (x )(x +3)=0 b) (x +7) =0 c) (x )(x 3)(x 4) = 0 d) x 5 =0 e) x(x 4) = 0 f) x +x +=0 Hvis polynomet ikke er faktorisert er i prinsippet framgangsmåten å begynne med å faktorisere det. Dette er imidlertid gjort en gang for alle for andregradsfunksjonen. Det er utledet en formel for røttene (se side 7 i avsnitt.5.3): Andregradslikningen ax + bx + c = 0 har røttene b + b 4ac a og b b 4ac a (.5) Eksempel: I likningen x 5x +6=0era =,b = 5 ogc =6,så den ene roten er ( 5) + ( 5) 4 6 Litt mindre omstendelig regnet er den andre roten = = 5+ = 5+ =3. ( 5) ( 5) 4 6 = 5 Løsningsmengden er altså {, 3 }, den samme som i eksemplet i starten av avsnittet. Dette skyldes at om vi regner sammen har vi (x )(x 3) = x 5x +6. Siden det bare er et fortegnsskille et sted i formelen for de to røttene skrives dette gjerne på en mer kompakt form som b ± b 4ac a der tegnet ± leses pluss eller minus. Hvis det b 4ac < 0 er det under rottegnet negativt, og vi har ingen reelle røtter 5.Hvisb 4ac =0 smelter de to røttene sammen til en rot. I mange sammenhenger kalles denne da en dobbel rot, eller en rot av multiplisitet. 5 Men tillater vi komplekse tall har vi to komplekse røtter. Derfor brukes helst formuleringen ingen reelle røtter, og ikke bare ingen røtter. =.
25 KAPITTEL. REPETISJON AV ALGEBRA y x Figur.3: Parabelen med likning y = x 5x +6 Hvis b 4ac ikke er et kvadrattall, som i likningen x x = 0 med røtter ( ± +4 ) /, kan røttene ikke skrives som brøker mellom heltall. Vi har da to muligheter: Eksakt form, der rottegnet bevares, eller ved hjelp av kalkulator å regne ut røttene tilnærmet som desimaltall, med så mange desimaler som situasjonen krever: { Løsning av x + x =0på eksakt form: 5, } 5 Løsning av x x =0pådesimalform: {.680, } Behold røttene på eksakt form hvis det ikke er noen spesiell grunn til åhadempå desimalform. Alle oppgavene i dette avsnittet skal løses uten kalkulator, og da er det nesten nødvendig åbrukeeksakt form. Oppgave.5 Løs likningene med hensyn på x a) x 4x 5=0 b) x 3x +=0 c) x x =0 d) x 9=0 e) x x =0 f) x x +=0 g) x x +=0 h) x +rx + s =0 i) x =8x 5 j) (x +)(x 3) = 5 k) x = x x l) x +rx + s =0 En likning på formeny = ax +bx+c, for eksempel y = x 5x+6, har en uendelig løsningsmengde av par (x, y).foreksempeler(0, 6), (, ), (, 0) og (3, 0) alle løsninger i eksemplet. Ved åtegne løsningsmengden inn i xy planet vil enhver slik likning gi en kurvetype som kalles parabel. I figur.3 er parabelen for y = x 5x + 6 tegnet inn. Parabelens skjæringspunkt med y aksen har x koordinat 0. y koordinaten finnes da ved å sette inn x = 0, og konstantleddet c = 6 blir stående igjen.
26 .5. LITT BAKGRUNN OG UTDYPING 3 Skjæringspunktene med x aksen betyr at y-koordinaten er 0, så disse finnes ved å løse andregradslikningen x 5x + 6 = 0 (som ovenfor ble regnet ut til 3 og 4). At annengradslikningen ikke har noen løsninger svarer til at parabelen i sin helhet ligger over eller under x aksen. En (dobbel) rot tilsvarer at den akkurat tangerer x aksen. Alle parabler har samme form, bortsett fra at de kan være forstørret eller forminsket, dreid eller parallellforskjøvet. Hvis ledekoeffisienten a>0åpner parabelen seg oppover, hvis a<0åpner den seg nedover. Med utgangspunkt i dette kan man tegne en brukbar parabel ved bare å kjenne noen få punkter på den (3 punkter er i prinsippet nok). Dette er en teknikk man bør lære seg. Oppgave.6 Finn skjæringspunktene med koordinataksene og skissér parablene gitt ved likningene under. Tegn tre og tre i samme koordinatsystem. a) y = x b) y = x c) y =x d) y = x e) y = x f) y =4 x g) y =(x +) h) y =(x ) i) y = x 4x +4 j) y = x 4x 5 k) y =x 5x + l) y = x x +.5 Litt bakgrunn og utdyping I dette hovedavsnittet behandles noe av teorien for de foregående avsnittene grundigere. Det er ikke strengt nøødvendig å gå gjennom dette for å lære seg regneteknikken i de avsnittene..5. Aksiomer for addisjon, subtraksjon og multiplikasjon I dette avsnittet behandles noe av teorien som ligger til grunn for de algebraiske omformingene i hovedavsnitt. De grunnleggende regnereglene for +, og kan oppsummeres i følgende liste, som vi tar som utgangspunkt: Grunnregler for addisjon og multiplikasjon: a) Kommutativitet a + b = b + a b) Kommutativitet a b = b a c) Assosiativitet (a + b)+c = a +(b + c) d) Assosiativitet (a b) c = a (b c) e) Distributivitet a (b + c) = a b + a c f)eksistens av 0 a +0 = a g) Eksistens av a = a h) Eksistens av For hver a finnes en b slik at a + b =0 (.6) Andre vanlige regneregler som kun omhandler addisjon, subtraksjon og multiplikasjon (som i avsnittene foran) kan finnes ved gjentatt bruk av disse reglene. For eksempel kan tre gangers bruk av distributiviteten (.6e) lede til følgende omforming: (a + b)(c + d) =(a + b)c +(a + b)d =(ac + bc)+(ad + bd) =ac + ad + bc + bd (Kommutativitet og assosiativitet er også brukt i denne omformingen.) Reglene kan oppfattes som regler for bruk av +, og for tall. De leses slik at uansett hvilke tall du setter inn for a, b og c skal likhetene gjelde. Hvis du for eksempel setter inn a =5,b =og
27 4 KAPITTEL. REPETISJON AV ALGEBRA c = 7 i distributiviteten (.6e) vil utregning av venstre side være 5 ( + 7) = 5 9 = 45, mens utregning av høyre side er = = 45. Polynomer i seg selv vil også oppfylle disse grunnreglene. Dermed er det også lovå erstatte bokstavene a, b og c med polynomer. Både grunnreglene, og regler utledet fra disse (for eksempel kvadratsetningene) vil dermed gjelde også for polynomer. Det samme gjelder funksjoner. Reglene (.6a og b), som kalles kommutativitet sier i praksis at rekkefølgen er likegyldig i addisjon og multiplikasjon. Det er ikke noen komplisert utledning som trengs for å generalisere til lengre summerogprodukter(somat3 7 =3 7 3eller++3+4=3++4+). Subtraksjon og divisjon er derimot ikke kommutative. For eksempel er Reglene (.6c og d) som kalles assosiativitet medfører at parenteser er unødvendige i lange summer eller produkt. Det kan entydig skrives , da resultatet blir det samme om det tolkes som (3+7)+ (= 0+ = ), eller som 3+(7+) (= 3+9 = ). Det tilsvarende med multiplikasjon, 3 7 = 4 uansett om det tolkes som (3 7) eller 3 (7 ). Subtraksjon og divisjon er ikke assosiative. Du bør for eksempel unngå åskrive4//. Dette tolkes vanligvis som (4/)/ =/ =, men kan lett feiltolkes som 4/(/) = 4/6 =4. Regelen (.6e), som kalles distributivitet forteller hvordan et tall eller uttrykk multipliseres inn i en parentes. Dette er dermed den viktigste regelen for å utvikle teknikken for å multiplisere sammen polynomer. Reglene (.6f og g) definerer tallene 0 og som enheter for addisjon og multiplikasjon. Regelen ( (.6h) definerer minus. Tallet b som oppfyller a + b = 0, og som denne regelen sier finnes, er det som vanligvis kalles a. Subtraksjonen c a kan da defineres som addisjonen c+( a). Her listes opp noen flere regneregler som forholdsvis enkelt utledes fra de grunnleggende reglene (.6): a) (a + b)c = ac + bc b) a (b + b + + b n ) = ab + ab + ab n c) a(b c) = ab ac d) a 0 = 0 e) ( a)b = ab f) ( a)( b) = ab (.7) Til slutt i dette avsnittet kommer noen kommentarer som utdyper temaet ytterligere 6 :... Kommentar:... En fellesbetegnelse på alle mengder som oppfyller grunnreglene (.6) er en (kommutativ) ring, og disse reglene kalles aksiomene for ringer. Alle utregningene i de forrige avsnittene, og reglene i (.7) vil dermed være riktig om elementer fra en ring settes inn for bokstavene. Heltallene Z, de rasjonale tallene Q og de reelle tallene R er eksempler på ringer. De naturlige tallene N oppfyller ikke (.6h), så regler basert på minus vil ofte gi resultater der svaret ikke er i N. Mengden av alle polynomer i x (eller i en annen bestemt mengde variable) er også eksempler på en ring. Funksjoner 7 oppfyller også disse reglene. Fuksjonsuttrykk kan dermed settes inn for a, b og c i (.6), og i alle omformingene fra de foregående avsnittene. I kapitlet om lineær algebra støter du på (kvadratiske) matriser, der +, og er definert, men kommutativiteten for multiplikasjon (regel.6c) gjelder ikke generelt for disse. For matriser kan 6 For en fullstendig redegjørelse trenger man selvfølgelig en bok med høyere ambisjonsnivå enn denne. På biblioteket kan dere starte med åsøkepå algebra, eventuelt med søkeordet ring i tillegg. Aktuelle bøker har ofte tittel som likner elementary algebra eller algebraic structures 7 Mer presist: Mengden av alle funksjoner fra en mengde A inn i en ring R, danner en ring. Addisjon og multiplikasjon mellom to funksjoner f og g er da definert ut fra hva funksjonsverdien blir for en vilkårlig x A: (f + g)(x) =f(x)+g(x) og(f g)(x) =f(x)g(x)
Matematikk 01 - Matematikk for data- og grafiske fag.
 Høgskolen i Gjøvik Avdeling for teknologi Versjon per. juni 004 Matematikk 0 - Matematikk for data- og grafiske fag. y x Hans Petter Hornæs hans.hornaes@hig.no Forord Dette kompendiet er skrevet for faget
Høgskolen i Gjøvik Avdeling for teknologi Versjon per. juni 004 Matematikk 0 - Matematikk for data- og grafiske fag. y x Hans Petter Hornæs hans.hornaes@hig.no Forord Dette kompendiet er skrevet for faget
Tallregning og algebra
 30 Tallregning og algebra Mål for opplæringen er at eleven skal kunne tolke, bearbeide og vurdere det matematiske innholdet i ulike tekster bruke matematiske metoder og hjelpemidler til å løse problemer
30 Tallregning og algebra Mål for opplæringen er at eleven skal kunne tolke, bearbeide og vurdere det matematiske innholdet i ulike tekster bruke matematiske metoder og hjelpemidler til å løse problemer
1.1 Tall- og bokstavregning, parenteser
 MATEMATIKK: 1 Algebra 1 Algebra 1.1 Tall- og bokstavregning, parenteser Matematikk er et morsomt fag hvis vi får det til. Som på de fleste områder er det er morsomt og givende når vi lykkes. Skal en f.eks.
MATEMATIKK: 1 Algebra 1 Algebra 1.1 Tall- og bokstavregning, parenteser Matematikk er et morsomt fag hvis vi får det til. Som på de fleste områder er det er morsomt og givende når vi lykkes. Skal en f.eks.
KAPITTEL 1 - ALGEBRA. 1. Regnerekkefølger og regneregler. Legg først merke til at: Legg spesielt merke til at :
 KAPITTEL - ALGEBRA. Regnerekkefølger og regneregler Legg først merke til at: 2( ) = 2 ( ) = 6, ab = a b = b a = ba og a a = a 2 Legg spesielt merke til at : a 2 = a a, ( a) 2 = ( a) ( a) = a 2 og ( a)
KAPITTEL - ALGEBRA. Regnerekkefølger og regneregler Legg først merke til at: 2( ) = 2 ( ) = 6, ab = a b = b a = ba og a a = a 2 Legg spesielt merke til at : a 2 = a a, ( a) 2 = ( a) ( a) = a 2 og ( a)
INNHOLD SAMMENDRAG ALGEBRA OG FUNKSJONER
 INNHOLD ALGEBRA OG FUNKSJONER... PARENTESER... USYNLIGE PARENTESER... USYNLIGE MULTIPLIKASJONSTEGN... DE TI GRUNNLEGGENDE ALGEBRAISKE LOVENE... REGNEUTTRYKK INNSATT FOR VARIABLER... 3 SETTE OPP FORMLER...
INNHOLD ALGEBRA OG FUNKSJONER... PARENTESER... USYNLIGE PARENTESER... USYNLIGE MULTIPLIKASJONSTEGN... DE TI GRUNNLEGGENDE ALGEBRAISKE LOVENE... REGNEUTTRYKK INNSATT FOR VARIABLER... 3 SETTE OPP FORMLER...
Prosent- og renteregning
 FORKURSSTART Prosent- og renteregning p prosent av K beregnes som p K 100 Eksempel 1: 5 prosent av 64000 blir 5 64000 =5 640=3200 100 p 64000 Eksempel 2: Hvor mange prosent er 9600 av 64000? Løs p fra
FORKURSSTART Prosent- og renteregning p prosent av K beregnes som p K 100 Eksempel 1: 5 prosent av 64000 blir 5 64000 =5 640=3200 100 p 64000 Eksempel 2: Hvor mange prosent er 9600 av 64000? Løs p fra
4 Matriser TMA4110 høsten 2018
 Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
Matriser TMA høsten 8 Nå har vi fått erfaring med å bruke matriser i et par forskjellige sammenhenger Vi har lært å løse et lineært likningssystem ved å sette opp totalmatrisen til systemet og gausseliminere
Matriser. Kapittel 4. Definisjoner og notasjon
 Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
SAMMENDRAG OG FORMLER
 SAMMENDRAG OG FORMLER SAMMENDRAG OG FORMLER Nye Mega 8A Kapittel A GEOMETRI LINJE, LINJESTYKKE OG STRÅLE linje stråle linjestykke VINKLER VINKELBEIN OG TOPPUNKT En vinkel har et toppunkt. Denne vinkelen
SAMMENDRAG OG FORMLER SAMMENDRAG OG FORMLER Nye Mega 8A Kapittel A GEOMETRI LINJE, LINJESTYKKE OG STRÅLE linje stråle linjestykke VINKLER VINKELBEIN OG TOPPUNKT En vinkel har et toppunkt. Denne vinkelen
SAMMENDRAG OG FORMLER. Nye Mega 9A og 9B
 SAMMENDRAG OG FORMLER Nye Mega 9A og 9B 1 Sammendrag og formler Nye Mega 9A Kapittel A GEOMETRI Regulære mangekanter Når alle sidene er like lange og alle vinklene er like store i en mangekant, sier vi
SAMMENDRAG OG FORMLER Nye Mega 9A og 9B 1 Sammendrag og formler Nye Mega 9A Kapittel A GEOMETRI Regulære mangekanter Når alle sidene er like lange og alle vinklene er like store i en mangekant, sier vi
Heldagsprøve i matematikk. Svar og løsningsforslag
 Heldagsprøve i matematikk Svar og løsningsforslag Mandag 19. desember 005 Forkurset, Høgskolen i Oslo Tillatte hjelpemidler: Lommeregner. Formelsamling i matematikk. Tid: 5 klokketimer Alle svar må være
Heldagsprøve i matematikk Svar og løsningsforslag Mandag 19. desember 005 Forkurset, Høgskolen i Oslo Tillatte hjelpemidler: Lommeregner. Formelsamling i matematikk. Tid: 5 klokketimer Alle svar må være
Forberedelseskurs i matematikk
 Forberedelseskurs i matematikk Formålet med kurset er å friske opp matematikkunnskapene før et år med realfag. Temaene for kurset er grunnleggende algebra med regneregler, regnerekkefølgen, brøk, ligninger
Forberedelseskurs i matematikk Formålet med kurset er å friske opp matematikkunnskapene før et år med realfag. Temaene for kurset er grunnleggende algebra med regneregler, regnerekkefølgen, brøk, ligninger
Tempoplan: Kapittel 5: 2/1 1/2. Kapittel 6: 1/2 1/3. Kapittel 7: 1/3 1/4. Resten av tida repetisjon og prøver. 4: Algebra
 Tempoplan: Kapittel 5: /1 1/. Kapittel 6: 1/ 1/. Kapittel 7: 1/ 1/4. Resten av tida repetisjon og prøver. 4: Algebra Algebra omfatter tall- og bokstavregninga i matematikken. Et viktig grunnlag for dette
Tempoplan: Kapittel 5: /1 1/. Kapittel 6: 1/ 1/. Kapittel 7: 1/ 1/4. Resten av tida repetisjon og prøver. 4: Algebra Algebra omfatter tall- og bokstavregninga i matematikken. Et viktig grunnlag for dette
NAVN: INNHOLD. IVAR RICHARD LARSEN/algebra - oppsummering, Side 1 av 18
 NAVN: INNHOLD FORORD... 2 LÆREPLAN... 3 ALGEBRA.... 3 REGNING MED VARIABLER... 3 MONOM... 3 POLYNOM... 3 TREKKE SAMMEN UTTRYKK (addisjon/subtraksjon)... 4 MULTIPLIKASJON... 4 DIVISJON... 4 ADDISJON AV
NAVN: INNHOLD FORORD... 2 LÆREPLAN... 3 ALGEBRA.... 3 REGNING MED VARIABLER... 3 MONOM... 3 POLYNOM... 3 TREKKE SAMMEN UTTRYKK (addisjon/subtraksjon)... 4 MULTIPLIKASJON... 4 DIVISJON... 4 ADDISJON AV
Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den?
 side 1 Detaljert eksempel om Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den? Dette er et forslag til undervisningsopplegg der utgangspunktet er sentrale problemstillinger
side 1 Detaljert eksempel om Likninger - en introduksjon på 8. trinn Hva er en likning og hva betyr å løse den? Dette er et forslag til undervisningsopplegg der utgangspunktet er sentrale problemstillinger
Enkel matematikk for økonomer. Del 1 nødvendig bakgrunn. Parenteser og brøker
 Vedlegg Enkel matematikk for økonomer I dette vedlegget går vi gjennom noen grunnleggende regneregler som brukes i boka. Del går gjennom de helt nødvendige matematikk-kunnskapene. Dette må du jobbe med
Vedlegg Enkel matematikk for økonomer I dette vedlegget går vi gjennom noen grunnleggende regneregler som brukes i boka. Del går gjennom de helt nødvendige matematikk-kunnskapene. Dette må du jobbe med
Studentene skal kunne. gjøre rede for begrepene naturlige, hele, rasjonale og irrasjonale tall. skrive mengder på listeform
 1 10 Tall og tallregning Studentene skal kunne gjøre rede for begrepene naturlige, hele, rasjonale og irrasjonale tall definere og benytte de anerkjente skrivemåtene for åpne, halvåpne og lukkede intervaller
1 10 Tall og tallregning Studentene skal kunne gjøre rede for begrepene naturlige, hele, rasjonale og irrasjonale tall definere og benytte de anerkjente skrivemåtene for åpne, halvåpne og lukkede intervaller
De hele tall har addisjon, multiplikasjon, subtraksjon og lineær ordning, men ikke divisjon.
 Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Kapittel 1. Tallregning
 Kapittel 1. Tallregning Regning med tall er grunnlaget for mer avansert matematikk. I dette kapitlet repeteres følgende fra grunnskolen: Brøkregning Desimaltall Regning med positive og negative tall Potenser
Kapittel 1. Tallregning Regning med tall er grunnlaget for mer avansert matematikk. I dette kapitlet repeteres følgende fra grunnskolen: Brøkregning Desimaltall Regning med positive og negative tall Potenser
CAS GeoGebra. Innhold. Matematikk for ungdomstrinnet
 CAS GeoGebra Innhold CAS GeoGebra... 1 REGNING MED CAS-VERKTØYET... 2 Rette opp feil, slette linjer... 3 Regneuttrykk... 4 FAKTORISERE TALL... 4 BRØK... 4 Blandet tall... 5 Regneuttrykk med brøk... 5 POTENSER...
CAS GeoGebra Innhold CAS GeoGebra... 1 REGNING MED CAS-VERKTØYET... 2 Rette opp feil, slette linjer... 3 Regneuttrykk... 4 FAKTORISERE TALL... 4 BRØK... 4 Blandet tall... 5 Regneuttrykk med brøk... 5 POTENSER...
Kapittel 1. Tallregning
 Kapittel 1. Tallregning Regning med tall er grunnlaget for mer avansert matematikk. I dette kapitlet repeteres følgende fra grunnskolen: Brøkregning Desimaltall Regning med positive og negative tall Potenser
Kapittel 1. Tallregning Regning med tall er grunnlaget for mer avansert matematikk. I dette kapitlet repeteres følgende fra grunnskolen: Brøkregning Desimaltall Regning med positive og negative tall Potenser
Enkel matematikk for økonomer 1. Innhold. Parenteser, brøk og potenser. Ekstranotat, februar 2015
 Ekstranotat, februar 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser, brøk og potenser... Funksjoner...4 Tilvekstform (differensialregning)...5 Nyttige tilnærminger...8
Ekstranotat, februar 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser, brøk og potenser... Funksjoner...4 Tilvekstform (differensialregning)...5 Nyttige tilnærminger...8
Funksjoner og andregradsuttrykk
 88 4 Funksjoner og andregradsuttrykk Mål for opplæringen er at eleven skal kunne bruke matematiske metoder og hjelpemidler til å løse problemer fra ulike fag og samfunnsområder løse likninger, ulikheter
88 4 Funksjoner og andregradsuttrykk Mål for opplæringen er at eleven skal kunne bruke matematiske metoder og hjelpemidler til å løse problemer fra ulike fag og samfunnsområder løse likninger, ulikheter
Innhold Innhold... 1 Kompetansemål Algebra, S Innledning Potenser og kvadratrøtter... 4
 1 Algebra Innhold Innhold... 1 Kompetansemål Algebra, S1... 3 Innledning... 3 1.1 Potenser og kvadratrøtter... 4 Regneregler for potenser... 5 Definisjoner og regnereglene for potenser Oppsummering...
1 Algebra Innhold Innhold... 1 Kompetansemål Algebra, S1... 3 Innledning... 3 1.1 Potenser og kvadratrøtter... 4 Regneregler for potenser... 5 Definisjoner og regnereglene for potenser Oppsummering...
REGEL 1: Addisjon av identitetselementer
 REGEL 1: Addisjon av identitetselementer Addisjon av identitetselementer a + 0 = a x + 0 = x Et identitetselement (nøytralt element) er et element som ikke medfører noen endring når det kombineres med
REGEL 1: Addisjon av identitetselementer Addisjon av identitetselementer a + 0 = a x + 0 = x Et identitetselement (nøytralt element) er et element som ikke medfører noen endring når det kombineres med
Regning med tall og bokstaver
 Regning med tall og bokstaver M L N r du har lest dette kapitlet, skal du kunne ^ bruke reglene for br kregning ^ trekke sammen, faktorisere og forenkle bokstavuttrykk ^ regne med potenser ^ l se likninger
Regning med tall og bokstaver M L N r du har lest dette kapitlet, skal du kunne ^ bruke reglene for br kregning ^ trekke sammen, faktorisere og forenkle bokstavuttrykk ^ regne med potenser ^ l se likninger
Hans Petter Hornæs,
 Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Funksjoner, repetisjonsoppgaver.
 Repetisjonsoppgaver, uke og, i Matematikk 0, Funksjoner, repetisjonsoppgaver. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke og Funksjoner, repetisjonsoppgaver. Oppgave Funksjoner
Repetisjonsoppgaver, uke og, i Matematikk 0, Funksjoner, repetisjonsoppgaver. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke og Funksjoner, repetisjonsoppgaver. Oppgave Funksjoner
TALL. 1 De naturlige tallene. H. Fausk
 TALL H. Fausk 1 De naturlige tallene De naturlige tallene er 1, 2, 3, 4, 5,... (og så videre). Disse tallene brukes til å telle med, og de kalles også telletallene. Listen med naturlige tall stopper ikke
TALL H. Fausk 1 De naturlige tallene De naturlige tallene er 1, 2, 3, 4, 5,... (og så videre). Disse tallene brukes til å telle med, og de kalles også telletallene. Listen med naturlige tall stopper ikke
Kompendium til MATH001 - Forkurs i matematikk
 Kompendium til MATH001 - Forkurs i matematikk Høst 017, NMBU Kine Josefine Aurland-Bredesen, e-post: kine.josefine.aurland-bredesen@nmbu.no f (x) = 1 x Kompendiumet gir en rask gjennomgang av grunnleggende
Kompendium til MATH001 - Forkurs i matematikk Høst 017, NMBU Kine Josefine Aurland-Bredesen, e-post: kine.josefine.aurland-bredesen@nmbu.no f (x) = 1 x Kompendiumet gir en rask gjennomgang av grunnleggende
Kapittel 8. Potensregning og tall på standardform
 Kapittel 8. Potensregning og tall på standardform I potensregning skriver vi tall som potenser og forenkler uttrykk som inneholder potenser. Standardform er en metode som er nyttig for raskt å kunne skrive
Kapittel 8. Potensregning og tall på standardform I potensregning skriver vi tall som potenser og forenkler uttrykk som inneholder potenser. Standardform er en metode som er nyttig for raskt å kunne skrive
Lineære likningssystemer og matriser
 Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Faktorisering og multiplisering med konjugatsetningen
 Faktorisering og multiplisering med konjugatsetningen De følgende oppgavene er øvinger i faktorisering og multiplisering ved hjelp av konjugatsetningen /3. kvadratsetning. Gjennom oppgavene gir vi elevene
Faktorisering og multiplisering med konjugatsetningen De følgende oppgavene er øvinger i faktorisering og multiplisering ved hjelp av konjugatsetningen /3. kvadratsetning. Gjennom oppgavene gir vi elevene
wxmaxima Brukermanual for Matematikk 1T Bjørn Ove Thue
 wxmaxima Brukermanual for Matematikk 1T Bjørn Ove Thue Om wxmaxima wxmaxima er en utvidet kalkulator som i tillegg til å regne ut alt en vanlig kalkulator kan regne ut, også regner symbolsk. Det vil si
wxmaxima Brukermanual for Matematikk 1T Bjørn Ove Thue Om wxmaxima wxmaxima er en utvidet kalkulator som i tillegg til å regne ut alt en vanlig kalkulator kan regne ut, også regner symbolsk. Det vil si
Kapittel 1. Tallregning
 Kapittel 1. Tallregning Mål for Kapittel 1, Tallregning. Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere
Kapittel 1. Tallregning Mål for Kapittel 1, Tallregning. Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere
Tall SKOLEPROSJEKT MAT VÅR 2014 AUTHORS: ASTRI STRAND LINDBÆCK CAMILLA HELVIG PIA LINDSTRØM. Date: March 31,
 Tall SKOLEPROSJEKT MAT400 - VÅR 204 AUTHORS: ASTRI STRAND LINDBÆCK CAMILLA HELVIG PIA LINDSTRØM Date: March 3, 204. 2. Innledning Vårt skoleprosjekt omhandler ulike konsepter innenfor det matematiske området
Tall SKOLEPROSJEKT MAT400 - VÅR 204 AUTHORS: ASTRI STRAND LINDBÆCK CAMILLA HELVIG PIA LINDSTRØM Date: March 3, 204. 2. Innledning Vårt skoleprosjekt omhandler ulike konsepter innenfor det matematiske området
Komplekse tall og trigonometri
 Kapittel Komplekse tall og trigonometri Grunnen til at vi har dette kapittelet midt i temaet Differenslikninger er for å kunne løse andre ordens differenslikninger. Da vil vi trenge å løse andregradslikninger.
Kapittel Komplekse tall og trigonometri Grunnen til at vi har dette kapittelet midt i temaet Differenslikninger er for å kunne løse andre ordens differenslikninger. Da vil vi trenge å løse andregradslikninger.
Forkurshefte i matematikk variant 1
 Forkurshefte i matematikk variant 1 2014 Inger Christin Borge Matematisk institutt, UiO (Plan for kurset: se side 3) Forord Velkommen til Universitetet i Oslo (UiO), og til forkurs i matematikk! Dette
Forkurshefte i matematikk variant 1 2014 Inger Christin Borge Matematisk institutt, UiO (Plan for kurset: se side 3) Forord Velkommen til Universitetet i Oslo (UiO), og til forkurs i matematikk! Dette
Verktøyopplæring i kalkulator
 Verktøyopplæring i kalkulator Enkel kalkulator... 3 Regneuttrykk uten parenteser... 3 Bruker kalkulatoren riktig regnerekkefølge?... 3 Negative tall... 4 Regneuttrykk med parenteser... 5 Brøk... 5 Blandet
Verktøyopplæring i kalkulator Enkel kalkulator... 3 Regneuttrykk uten parenteser... 3 Bruker kalkulatoren riktig regnerekkefølge?... 3 Negative tall... 4 Regneuttrykk med parenteser... 5 Brøk... 5 Blandet
Analyse og metodikk i Calculus 1
 Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
En konstant er et symbol med en fast verdi. 2 og er eksempler pô konstanter.
 Algebra Variabel Konstant trekke sammen Algebra er bokstavregning. Det er et verktöy som forenkler regneoperasjonene i forskjellige omrôder av matematikken. Bokstavene er symboler for tall og skal behandles
Algebra Variabel Konstant trekke sammen Algebra er bokstavregning. Det er et verktöy som forenkler regneoperasjonene i forskjellige omrôder av matematikken. Bokstavene er symboler for tall og skal behandles
Regelbok i matematikk 1MX og 1MY
 Regelbok i matematikk 1MX og 1MY Utgave 1.4 Skrevet av Bjørnar Tollaksen. Hele regelboka er et sammendrag av læreboka. Dette er ment som et supplement til formelheftet, ikke en erstatning. Skrivefeil kan
Regelbok i matematikk 1MX og 1MY Utgave 1.4 Skrevet av Bjørnar Tollaksen. Hele regelboka er et sammendrag av læreboka. Dette er ment som et supplement til formelheftet, ikke en erstatning. Skrivefeil kan
Komplekse tall og komplekse funksjoner
 KAPITTEL Komplekse tall og komplekse funksjoner. Komplekse tall.. Definisjon av komplekse tall. De komplekse tallene er en utvidelse av de reelle tallene. Dvs at de komplekse tallene er en tallmengde som
KAPITTEL Komplekse tall og komplekse funksjoner. Komplekse tall.. Definisjon av komplekse tall. De komplekse tallene er en utvidelse av de reelle tallene. Dvs at de komplekse tallene er en tallmengde som
Lær å bruke Microsoft Mathematics, Matematikk-tillegget i Word og WordMat. Av Sigbjørn Hals
 Lær å bruke Microsoft Mathematics, Matematikk-tillegget i Word og WordMat Av Sigbjørn Hals 1 Innhold Hva er matematikktillegget for Word?... 2 Nedlasting og installasjon av matematikktillegget for Word...
Lær å bruke Microsoft Mathematics, Matematikk-tillegget i Word og WordMat Av Sigbjørn Hals 1 Innhold Hva er matematikktillegget for Word?... 2 Nedlasting og installasjon av matematikktillegget for Word...
Funksjoner (kapittel 1)
 Ukeoppgaver, uke 34 og 35, i Matematikk 0, Funksjoner og grenser. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke 34 og 35 Funksjoner (kapittel ) Oppgave Figuren til øyre viser
Ukeoppgaver, uke 34 og 35, i Matematikk 0, Funksjoner og grenser. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke 34 og 35 Funksjoner (kapittel ) Oppgave Figuren til øyre viser
Forord. Molde, august 2011. Per Kristian Rekdal. Copyright c Høyskolen i Molde, 2011.
 1 13. august 011 Forord Høgskolen i Molde gjennomfører forkurs i matematikk for studenter som har svakt grunnlag i dette faget, eller som ønsker å friske opp gamle kunnskaper. Formål: Målet med forkurset
1 13. august 011 Forord Høgskolen i Molde gjennomfører forkurs i matematikk for studenter som har svakt grunnlag i dette faget, eller som ønsker å friske opp gamle kunnskaper. Formål: Målet med forkurset
Oppfriskningskurs i matematikk 2008
 Oppfriskningskurs i matematikk 2008 Marte Pernille Hatlo Institutt for matematiske fag, NTNU 4.-9. august 2008 Velkommen! 2 Temaer Algebra Trigonometri Funksjoner og derivasjon Integrasjon Eksponensial-
Oppfriskningskurs i matematikk 2008 Marte Pernille Hatlo Institutt for matematiske fag, NTNU 4.-9. august 2008 Velkommen! 2 Temaer Algebra Trigonometri Funksjoner og derivasjon Integrasjon Eksponensial-
Kapittel 2. Algebra. Kapittel 2. Algebra Side 29
 Kapittel. Algebra Algebra kalles populært for bokstavregning. Det er ikke mye algebra i Matematikk P-Y. Det viktigste er å kunne løse enkle likninger og regne med formler. Kapittel. Algebra Side 9 1. Forenkling
Kapittel. Algebra Algebra kalles populært for bokstavregning. Det er ikke mye algebra i Matematikk P-Y. Det viktigste er å kunne løse enkle likninger og regne med formler. Kapittel. Algebra Side 9 1. Forenkling
1 C z I G + + = + + 2) Multiplikasjon av et tall med en parentes foregår ved å multiplisere tallet med alle leddene i parentesen, slik at
 Ekstranotat, 7 august 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser og brøker... Funksjoner...3 Tilvekstform (differensialregning)...4 Telleregelen...7 70-regelen...8
Ekstranotat, 7 august 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser og brøker... Funksjoner...3 Tilvekstform (differensialregning)...4 Telleregelen...7 70-regelen...8
Hva man må kunne i kapittel 2 - Algebra
 Hva man må kunne i kapittel 2 - Algebra Teknikker og type-eksempler Faktorisering Se også eget notat om faktorisering på nettsidene mine. Faktorisering brukes til å: Finne fellesnevner i rasjonale uttrykk.
Hva man må kunne i kapittel 2 - Algebra Teknikker og type-eksempler Faktorisering Se også eget notat om faktorisering på nettsidene mine. Faktorisering brukes til å: Finne fellesnevner i rasjonale uttrykk.
9 Potenser. Logaritmer
 9 Potenser. Logaritmer 9.1 Potenser Regneregler 2 3 ¼ 2 2 2 Vi kaller 2 3 for en potens. 2 kaller vi for potensens grunntall og 3 for eksponenten. En potens er per definisjon produktet av like store tall.
9 Potenser. Logaritmer 9.1 Potenser Regneregler 2 3 ¼ 2 2 2 Vi kaller 2 3 for en potens. 2 kaller vi for potensens grunntall og 3 for eksponenten. En potens er per definisjon produktet av like store tall.
Eneboerspillet del 2. Håvard Johnsbråten, januar 2014
 Eneboerspillet del 2 Håvard Johnsbråten, januar 2014 I Johnsbråten (2013) løste jeg noen problemer omkring eneboerspillet vha partall/oddetall. I denne parallellversjonen av artikkelen i vil jeg i stedet
Eneboerspillet del 2 Håvard Johnsbråten, januar 2014 I Johnsbråten (2013) løste jeg noen problemer omkring eneboerspillet vha partall/oddetall. I denne parallellversjonen av artikkelen i vil jeg i stedet
Ronny Kjelsberg. Noen grunnleggende elementer innen manipulasjon av brøk og enkle algebraiske uttrykk
 Ronny Kjelsberg Noen grunnleggende elementer innen manipulasjon av brøk og enkle algebraiske uttrykk Contents Hvordan bli en BRØKREGNER på en, to, tre:. EN: Basics................................ Hva er
Ronny Kjelsberg Noen grunnleggende elementer innen manipulasjon av brøk og enkle algebraiske uttrykk Contents Hvordan bli en BRØKREGNER på en, to, tre:. EN: Basics................................ Hva er
Brøk Vi på vindusrekka
 Brøk Vi på vindusrekka Brøken... 2 Teller og nevner... 3 Uekte brøk... 5 Blanda tall... 6 Desimalbrøk... 8 Pluss/minus... 9 Multiplikasjon... 11 Likeverdige brøker... 12 Utviding... 13 Forkorting... 14
Brøk Vi på vindusrekka Brøken... 2 Teller og nevner... 3 Uekte brøk... 5 Blanda tall... 6 Desimalbrøk... 8 Pluss/minus... 9 Multiplikasjon... 11 Likeverdige brøker... 12 Utviding... 13 Forkorting... 14
Regning med variabler
 Regning med variabler???? (x y) (x y) Hvordan kan Herman regne ut uttrykket på tavla? Når vi skal regne ut bokstavuttrykk med parenteser, må vi løse opp parentesene først. Hvis det står et tall eller et
Regning med variabler???? (x y) (x y) Hvordan kan Herman regne ut uttrykket på tavla? Når vi skal regne ut bokstavuttrykk med parenteser, må vi løse opp parentesene først. Hvis det står et tall eller et
Sammendrag R1. Sandnes VGS 19. august 2009
 Sammendrag R1 Sandnes VGS 19. august 2009 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A
Sammendrag R1 Sandnes VGS 19. august 2009 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A
Komplekse tall. Kapittel 2. Den imaginære enheten. Operasjoner på komplekse tall
 Kapittel Komplekse tall Oppfinnelsen av nye tallsystemer henger gjerne sammen med polynomligninger x + 4 0 har ingen positiv løsning, selv om koeffisientene er positive tall Vi må altså inn med negative
Kapittel Komplekse tall Oppfinnelsen av nye tallsystemer henger gjerne sammen med polynomligninger x + 4 0 har ingen positiv løsning, selv om koeffisientene er positive tall Vi må altså inn med negative
Oppfriskningskurs i matematikk Dag 3
 Oppfriskningskurs i matematikk Dag 3 Petter Nyland Institutt for matematiske fag Onsdag 8. august 2018 Dagen i dag Tema 4 Polynomer: Faktorisering, røtter, polynomdivisjon, kvadratiske ligninger og rasjonale
Oppfriskningskurs i matematikk Dag 3 Petter Nyland Institutt for matematiske fag Onsdag 8. august 2018 Dagen i dag Tema 4 Polynomer: Faktorisering, røtter, polynomdivisjon, kvadratiske ligninger og rasjonale
Sammendrag R1. 26. januar 2011
 Sammendrag R1 26. januar 2011 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A B hvis to påstander
Sammendrag R1 26. januar 2011 1 1 Notasjon Implikasjon Vi skriver A B hvis påstanden A impliserer B. Det vil si at hvis påstand A er riktig, så er påstand B riktig. Ekvivalens Vi skriver A B hvis to påstander
Egenverdier og egenvektorer
 Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Brukerveiledning for webapplikasjonen. Mathemateria 01.02.2015. Terje Kolderup
 Brukerveiledning for webapplikasjonen Mathemateria 01.02.2015 Terje Kolderup Innhold Brukerveiledning for webapplikasjonen...1 Mathemateria...1 Introduksjon...3 Typisk eksempel og bryterstyring...3 Innlogging...4
Brukerveiledning for webapplikasjonen Mathemateria 01.02.2015 Terje Kolderup Innhold Brukerveiledning for webapplikasjonen...1 Mathemateria...1 Introduksjon...3 Typisk eksempel og bryterstyring...3 Innlogging...4
Vektorligninger. Kapittel 3. Vektorregning
 Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Løsningsforslag. 7(x + 1/2) 5 = 5/6. 7x = 5/ /2 = 5/6 + 3/2 = 14/6 = 7/3. Løsningen er x = 1/3. b) Finn alle x slik at 6x + 1 x = 5.
 Prøve i FO99A - Matematikk Dato: 3. desember 01 Målform: Bokmål Antall oppgaver: 5 (0 deloppgaver) Antall sider: Vedlegg: Formelsamling Hjelpemiddel: Kalkulator Alle svar skal grunngis. Alle deloppgaver
Prøve i FO99A - Matematikk Dato: 3. desember 01 Målform: Bokmål Antall oppgaver: 5 (0 deloppgaver) Antall sider: Vedlegg: Formelsamling Hjelpemiddel: Kalkulator Alle svar skal grunngis. Alle deloppgaver
Oppgavesett med fasit
 TIL ENT3R ELEVENE Oppgavesett med fasit Tommy Odland Sist oppdatert: 1. november 2013 http://is.gd/ent3rknarvik http://tommyodland.com/ent3r 1 INNHOLD 1 Om dette dokumentet 3 1.1 Formål og oppbygging..................................
TIL ENT3R ELEVENE Oppgavesett med fasit Tommy Odland Sist oppdatert: 1. november 2013 http://is.gd/ent3rknarvik http://tommyodland.com/ent3r 1 INNHOLD 1 Om dette dokumentet 3 1.1 Formål og oppbygging..................................
Emnekode: LGU 51014 Emnenavn: Matematikk 1 (5 10), emne 1. Semester: VÅR År: 2016 Eksamenstype: Skriftlig
 Sensurveiledning Emnekode: LGU 51014 Emnenavn: Matematikk 1 (5 10), emne 1 Semester: VÅR År: 2016 Eksamenstype: Skriftlig Oppgave 1 Figuren viser hvordan en nettside forklarer en metode for addisjon og
Sensurveiledning Emnekode: LGU 51014 Emnenavn: Matematikk 1 (5 10), emne 1 Semester: VÅR År: 2016 Eksamenstype: Skriftlig Oppgave 1 Figuren viser hvordan en nettside forklarer en metode for addisjon og
Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra
 Anne-Mari Jensen Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra Innledning I ungdomsskolen kommer funksjoner inn som et av hovedområdene i læreplanen i matematikk. Arbeidet
Anne-Mari Jensen Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra Innledning I ungdomsskolen kommer funksjoner inn som et av hovedområdene i læreplanen i matematikk. Arbeidet
Husk at minustegn foran et tall eller en variabel er å tenke på som tallet multiplisert med det som kommer etter:
 Økonomisk Institutt, november 2006 Robert G. Hansen, rom 1207 ECON 1210: Noen regneregler og løsningsprosedyrer som brukes i kurset (A) Faktorisering og brøkregning (1) Vi kan sette en felles faktor utenfor
Økonomisk Institutt, november 2006 Robert G. Hansen, rom 1207 ECON 1210: Noen regneregler og løsningsprosedyrer som brukes i kurset (A) Faktorisering og brøkregning (1) Vi kan sette en felles faktor utenfor
Gauss-Jordan eliminasjon; redusert echelonform. Forelesning, TMA4110 Fredag 18/9. Reduserte echelonmatriser. Reduserte echelonmatriser (forts.
 Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
2 Likninger. 2.1 Førstegradslikninger med én ukjent
 MATEMATIKK: 2 Likninger 2 Likninger 2.1 Førstegradslikninger med én ukjent Ulike problemer kan løses på ulike måter. I den gamle folkeskolen brukte man delingsregning ved løsning av enkelte oppgaver. Eksempel
MATEMATIKK: 2 Likninger 2 Likninger 2.1 Førstegradslikninger med én ukjent Ulike problemer kan løses på ulike måter. I den gamle folkeskolen brukte man delingsregning ved løsning av enkelte oppgaver. Eksempel
Repetisjon i Matematikk 1: Derivasjon 2,
 Repetisjon i Matematikk 1: Derivasjon 2, 201. 1 Høgskolen i Gjøvik Avdeling TØL Repetisjonsoppgaver MATEMATIKK 1 REA1141 og REA1141F Derivasjon 2, 201. Oppgave 1 Denne oppgaven har forholdsvis enkle derivasjoner,
Repetisjon i Matematikk 1: Derivasjon 2, 201. 1 Høgskolen i Gjøvik Avdeling TØL Repetisjonsoppgaver MATEMATIKK 1 REA1141 og REA1141F Derivasjon 2, 201. Oppgave 1 Denne oppgaven har forholdsvis enkle derivasjoner,
DAFE BYFE Matematikk 1000 HIOA Obligatorisk innlevering 1 Innleveringsfrist Fredag 22. januar :00 Antall oppgaver: 5.
 Innlevering DAFE BYFE Matematikk 000 HIOA Obligatorisk innlevering Innleveringsfrist Fredag. januar 06 4:00 Antall oppgaver: 5 Vi anbefaler at dere regner oppgaver fra boken først. Det er en liste med
Innlevering DAFE BYFE Matematikk 000 HIOA Obligatorisk innlevering Innleveringsfrist Fredag. januar 06 4:00 Antall oppgaver: 5 Vi anbefaler at dere regner oppgaver fra boken først. Det er en liste med
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen. Digitalt verktøy for Sigma 1T. Casio fx 9860
 Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Casio fx 9860 Innhold 1 Innstillinger 4 2 Regning 5 2.1 Regnerekkefølge................................ 5 2.2 Tallet π.....................................
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Casio fx 9860 Innhold 1 Innstillinger 4 2 Regning 5 2.1 Regnerekkefølge................................ 5 2.2 Tallet π.....................................
Oppfriskningskurs i matematikk Dag 1
 Oppfriskningskurs i matematikk Dag 1 Petter Nyland Institutt for matematiske fag Mandag 6. august 2018 Om meg Bachelor- og mastergrad i matematiske fag (2014, 2016) Doktorgradsstipendiat i matematikk (2016
Oppfriskningskurs i matematikk Dag 1 Petter Nyland Institutt for matematiske fag Mandag 6. august 2018 Om meg Bachelor- og mastergrad i matematiske fag (2014, 2016) Doktorgradsstipendiat i matematikk (2016
Brøkregning og likninger med teskje
 Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Oppgave 1. Del A. (i) Skriv de to desimaltallene 0, 7 og 3, 12 som vanlig brøk og forkort hvis mulig. som desimaltall. 3x 6
 Oppgave 1 (i) Skriv de to desimaltallene 0, 7 og 3, 12 som vanlig brøk og forkort hvis mulig. (ii) Skriv 314 100 og 4 5 (iii) Forkort brøkene som desimaltall. 12 15 og 3x 6 9x. (iv) Sorter disse seks tallene
Oppgave 1 (i) Skriv de to desimaltallene 0, 7 og 3, 12 som vanlig brøk og forkort hvis mulig. (ii) Skriv 314 100 og 4 5 (iii) Forkort brøkene som desimaltall. 12 15 og 3x 6 9x. (iv) Sorter disse seks tallene
Noen regneregler som brukes i Keynes-modeller
 Forelesningsnotat nr 5, august 2009, Steinar Holden Noen regneregler som brukes i Keynes-modeller Først litt repetisjon ) Vi kan sette en felles faktor utenfor en parentes: Y ty = Y(-t) der det siste uttrykket
Forelesningsnotat nr 5, august 2009, Steinar Holden Noen regneregler som brukes i Keynes-modeller Først litt repetisjon ) Vi kan sette en felles faktor utenfor en parentes: Y ty = Y(-t) der det siste uttrykket
Oppfriskningskurs i Matematikk
 Oppfriskningskurs i Matematikk Dag 3 Stine M. Berge 07.08.19 Stine M. Berge (NTNU) Oppfriskningskurs i Matematikk 07.08.19 1 / 19 Polynomer Polynomer er de enkleste funksjonene Definert og kontinuerlig
Oppfriskningskurs i Matematikk Dag 3 Stine M. Berge 07.08.19 Stine M. Berge (NTNU) Oppfriskningskurs i Matematikk 07.08.19 1 / 19 Polynomer Polynomer er de enkleste funksjonene Definert og kontinuerlig
Vi bruker desimaltall for Ô oppgi verdiene mellom de hele tallene. Tall med komma kaller vi desimaltall, og sifrene bak komma kaller vi desimaler.
 196 FAKTA De naturlige tallene bestôr av ett eller ere sifre: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,...Alle de hele positive tallene kaller vi naturlige tall, og tallmengden kaller vi N. NÔr vi tar med 0 og
196 FAKTA De naturlige tallene bestôr av ett eller ere sifre: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,...Alle de hele positive tallene kaller vi naturlige tall, og tallmengden kaller vi N. NÔr vi tar med 0 og
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Teknostart Forelesning 3 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart Forelesning 3 Tema Logikk Definisjoner og Teoremer Mengder og Egenskaper ved de Reelle Tall
TMA4100 Matematikk 1, høst 2013 Teknostart Forelesning 3 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart Forelesning 3 Tema Logikk Definisjoner og Teoremer Mengder og Egenskaper ved de Reelle Tall
Matematikk for økonomi og samfunnsfag
 Harald Bjørnestad Ulf Henning Olsson Svein Søyland Frank Tolcsiner Matematikk for økonomi og samfunnsfag 9. utgave Innhold Forord... 11 Kapittel 1 Grunnleggende emner 1.1 Tall og tallsystemer... 13 1.2
Harald Bjørnestad Ulf Henning Olsson Svein Søyland Frank Tolcsiner Matematikk for økonomi og samfunnsfag 9. utgave Innhold Forord... 11 Kapittel 1 Grunnleggende emner 1.1 Tall og tallsystemer... 13 1.2
1T eksamen høsten 2017 løsning
 1T eksamen høsten 017 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform. 105000 0,15
1T eksamen høsten 017 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform. 105000 0,15
Mer om likninger og ulikheter
 Mer om likninger og ulikheter Studentene skal kunne utføre polynomdivisjon anvende nullpunktsetningen og polynomdivisjon til faktorisering av polynomer benytte polynomdivisjon til å løse likninger av høyere
Mer om likninger og ulikheter Studentene skal kunne utføre polynomdivisjon anvende nullpunktsetningen og polynomdivisjon til faktorisering av polynomer benytte polynomdivisjon til å løse likninger av høyere
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen. Digitalt verktøy for Sigma 1P. Geogebra
 Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Geogebra Innhold 1 Om Geogebra 4 1.1 Innstillinger................................... 5 2 Regning 5 2.1 Tallregning...................................
Øgrim Bakken Pettersen Skrindo Thorstensen Thorstensen Digitalt verktøy for Geogebra Innhold 1 Om Geogebra 4 1.1 Innstillinger................................... 5 2 Regning 5 2.1 Tallregning...................................
Verktøyopplæring i kalkulator for elever
 Verktøyopplæring i kalkulator for elever Innholdsfortegnelse Enkel kalkulator... 2 Kalkulator med brøk og parenteser... 7 GeoGebra som kalkulator... 11 H. Aschehoug & Co. www.lokus.no Side 1 Enkel kalkulator
Verktøyopplæring i kalkulator for elever Innholdsfortegnelse Enkel kalkulator... 2 Kalkulator med brøk og parenteser... 7 GeoGebra som kalkulator... 11 H. Aschehoug & Co. www.lokus.no Side 1 Enkel kalkulator
Desimaltall FRA A TIL Å
 Desimaltall FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side Innledning til desimaltall D - 2 2 Grunnleggende om desimaltall D - 2 2. Tideler, hundredeler og tusendeler D - 6 3 Å regne
Desimaltall FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side Innledning til desimaltall D - 2 2 Grunnleggende om desimaltall D - 2 2. Tideler, hundredeler og tusendeler D - 6 3 Å regne
Løsningsforslag Matematikk for ungdomstrinnet Del 1, Modul 1, 4MX130UM1-K
 Løsningsforslag Matematikk for ungdomstrinnet Del 1, Modul 1, 4MX130UM1-K ORDINÆR EKSAMEN 11.1.009 Oppgave 1 a) En følge av parallellaksiomet er at samsvarende vinkler ved parallelle linjer er like store.
Løsningsforslag Matematikk for ungdomstrinnet Del 1, Modul 1, 4MX130UM1-K ORDINÆR EKSAMEN 11.1.009 Oppgave 1 a) En følge av parallellaksiomet er at samsvarende vinkler ved parallelle linjer er like store.
Krasjkurs MAT101 og MAT111
 Krasjkurs MAT101 og MAT111 Forord Disse notatene ble skrevet under et åtte timer (to firetimers forelesninger) i løpet av 10. og 11. desember 2012. Det er mulig at noen av utregningene ikke stemmer, enten
Krasjkurs MAT101 og MAT111 Forord Disse notatene ble skrevet under et åtte timer (to firetimers forelesninger) i løpet av 10. og 11. desember 2012. Det er mulig at noen av utregningene ikke stemmer, enten
Separable differensiallikninger.
 Ukeoppgaver, uke 46, i Matematikk 0, Separable differensiallikninger. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke 46 I løpet av uken blir løsningsforslag lagt ut på emnesiden
Ukeoppgaver, uke 46, i Matematikk 0, Separable differensiallikninger. Høgskolen i Gjøvik Avdeling for ingeniørfag Matematikk 0 Ukeoppgaver uke 46 I løpet av uken blir løsningsforslag lagt ut på emnesiden
Eksempel på løsning. Sentralt gitt skriftlig eksamen MAT1008 Matematikk 2T Eksamen 30.11.2009. Bokmål
 Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1008 Matematikk T Eksamen 30.11.009 Bokmål MAT1008 Matematikk T HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Eksempel på løsning 010 Sentralt gitt skriftlig eksamen MAT1008 Matematikk T Eksamen 30.11.009 Bokmål MAT1008 Matematikk T HØSTEN 009 Eksempel på løsning med vekt på bruk av digitale verktøy Hva er en
Matematikk for økonomer Del 2
 Matematikk for økonomer Del 2 Formelark Dokument type: Formelark Antall kapitler: 10 kapitler Antall sider: 17 Sider Forfatter: Studiekvartalets kursholdere rett til bruk av materialet. Det innebærer at
Matematikk for økonomer Del 2 Formelark Dokument type: Formelark Antall kapitler: 10 kapitler Antall sider: 17 Sider Forfatter: Studiekvartalets kursholdere rett til bruk av materialet. Det innebærer at
Tema. Beskrivelse. Husk!
 Dette er ment som en hjelpeoversikt når du bruker boka til å repetisjon. Bruk Sammendrag etter hvert kapittel som hjelp. Verktøykassen fra side 272 i boka er og til stor hjelp for repetisjon til terminprøve.
Dette er ment som en hjelpeoversikt når du bruker boka til å repetisjon. Bruk Sammendrag etter hvert kapittel som hjelp. Verktøykassen fra side 272 i boka er og til stor hjelp for repetisjon til terminprøve.
Regning med tall og algebra
 Regning med tall og algebra Dette er en variert samling av oppgaver. De kan alle løses ved algebraisk, men det fins også andre måter å løse dem på. Man kan bruke kvadratsetningene, potensregning, prosentregning
Regning med tall og algebra Dette er en variert samling av oppgaver. De kan alle løses ved algebraisk, men det fins også andre måter å løse dem på. Man kan bruke kvadratsetningene, potensregning, prosentregning
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
7 Egenverdier og egenvektorer TMA4110 høsten 2018
 7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
Lineære likningssystemer
 Kapittel 1 Lineære likningssystemer Jeg tenker på et tall slik at π ganger tallet er 12. 1.1 Lineære likninger Matematikk dreier seg om å løse problemer. Problemene gjøres ofte om til likninger som så
Kapittel 1 Lineære likningssystemer Jeg tenker på et tall slik at π ganger tallet er 12. 1.1 Lineære likninger Matematikk dreier seg om å løse problemer. Problemene gjøres ofte om til likninger som så
KURSHEFTE TIL FORKURS I MATEMATIKK
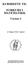 KURSHEFTE TIL FORKURS I MATEMATIKK Variant av Magnus Dehli Vigeland UNIVERSITETET I OSLO MATEMATISK INSTITUTT Innhold Oppvarming 3. Noen viktige tallmengder. Notasjon.................... 3. Mer om mengder.............................
KURSHEFTE TIL FORKURS I MATEMATIKK Variant av Magnus Dehli Vigeland UNIVERSITETET I OSLO MATEMATISK INSTITUTT Innhold Oppvarming 3. Noen viktige tallmengder. Notasjon.................... 3. Mer om mengder.............................
Innhold Kompetansemål Tall og algebra, 1T Tallregning... 4
 1 Tall og algebra Innhold Kompetansemål Tall og algebra, 1T... 3 1.1 Tallregning... 4 Tallene våre... 4 Tall og tallmengder... 5 Regningsarter... 11 Å regne med negative tall... 1 Addisjon og subtraksjon
1 Tall og algebra Innhold Kompetansemål Tall og algebra, 1T... 3 1.1 Tallregning... 4 Tallene våre... 4 Tall og tallmengder... 5 Regningsarter... 11 Å regne med negative tall... 1 Addisjon og subtraksjon
