Estimering og hypotesetesting. Estimering og hypotesetesting. Estimering og hypotesetesting. Kapittel 10. Ett- og toutvalgs hypotesetesting
|
|
|
- Ellinor Christoffersen
- 8 år siden
- Visninger:
Transkript
1 3 Estimerig og hypotesetestig Kapittel 10 Ett- og toutvalgs hypotesetestig TMA445 V007: Eirik Mo Feome Bilkjørig Høyde til studeter Estimator ˆp = X, X atall ˆµ = X gjeomsittlig høyde. som syes de er flikere e gjeomsittet av spurte. Størrelse med kjet fordelig For store, og p ikke for ært 0 eller 1, så er Z = ormal- tilærmet fordelt ˆp p ˆp(1 ˆp)/ T = X µ S/ t-fordelt med 1 frihetsgrader. Estimerig og hypotesetestig Feome Bilkjørig Høyde til studeter Spørsmål Hvor stor adel av studetee syes de er flikere e gjeomsittet til å kjøre bil? Hvor høye er studetee? Populasjo Alle studeter, eller evt. me og kvier som to populasjoer. Parameter Utvalg Data, u.i.f og represetative? Adele p som syes de er flikere e gjeomsittet. Alle studeter som svarte på spørreudersøkelse. Flikere eller ikke e gjeomsittet. Alle studeter, eller evt. me og kvier som to populasjoer. Forvetet høyde, µ. Alle studeter som svarte på spørreudersøkelse. Høyde. 4 Estimerig og hypotesetestig Feome Bilkjørig Høyde til studeter Kvatiler i fordelig z α/ og z α/ t α/,( 1) og t α/,( 1) Itervall Hypotesetestig: [ˆp z α/ ˆp(1 ˆp), [ X t α/,( 1)) s, ˆp(1 ˆp) ˆp + z α/ ] X + s tα/,( 1)) ] Er adele av studeter som syes de er malige stude- Er dette årets flikere e gjeomsittet til å kjøre bil ter høyerer e gjeomsittet større e 0.5? Tror flere me e kvier at de er gode sjåfører? for værepliktige, 179.8cm? Er byggstudeter høyere e studeter fra mari?
2 5 7 Hypotese Hypotesetestig og rettsak DEF 10.1: E statistisk hypotese er e atakelse eller påstad om egeskaper ved e eller fl ere populasjoer. Nullhypotese: Hypotese vi vil udersøke om vi har grulag fra data for å forkaste. E bestemt verdi for e parameter. Alterativ hypotese: Hvis vi forkaster ullhypotese så aksepterer vi de alterative hypotese. Ofte mer e e verdi for e parameter (større e, midre e og ulik). Spørsmål: Er gru til å tro at skruee som produseres ikke er 15 mm lage? Statistisk hypotesetestig: Udersøke om det er ok bevis som uderbygger at skruee ikke er 15 mm lage. Som i rettssak: tiltalte er atatt uskyldig til ha er bevist skyldig. Nullhypotese: skruee som produseres er 15 mm. Alterativ hypotese: skuee som produseres er ikke 15 mm. H 0 : µ = 15mm vs. H 1 : µ 15mm 6 8 Kvalitetskotroll av skruer Hypoteser og tester Hypoteser: Nullhypotese (H 0 ): Hypotese vi vil udersøke om vi har grulag fra data for å forkaste. Ieholder e bestemt verdi for e parameter. Alterativ hypotese (H 1 ): Hypotese vi aksepterer dersom vi forkastar ullhypotese. Ofte mer e e verdi for e parameter. Produksjo av skruer. Legde på produsert skrue skal være 15 mm. Tar jevlig stikkprøve fra prosesse, for å sjekke om skruee som produseres er 15 mm lage. Hvis stikkprøve tyder på at de produserte skruee ikke er 15 mm, må maskie som lager skruee kalibreres på ytt. Hvilke ullhypotese og alterativ hypotese vil vi udersøke? Statistisk hypotesetestig: Udersøke om dataee gir tilstrekkelig bevis for at de alterative hypotese er sa. To typer tester: To-sidig test: H 0 : θ = θ 0 mot H 1 : θ θ 0 E-sidig test: H 0 : θ θ 0 ( evt. θ = θ 0 ) mot H 1 : θ < θ 0, eller H 0 : θ θ 0 ( evt. θ = θ 0 ) mot H 1 : θ > θ 0
3 9 To typer feil 11 Ett utvalg: test for µ med σ kjet DEF 10.: Forkastig av ullhypotese år dee er sa, kalles e type-i-feil. Vi vil være sikre på at skruee ikke er 15 mm før vi bestemmer oss for å stoppe produksjoe for å kalibrere. Produksjosstopp for kalibrerig av maski gjør at produsete taper peger pga. forsiket produksjo. DEF 10.3: Å ikke forkaste ullhypotese år de er gal, kalles e type-ii-feil. Vi vil gjere kalibrere maskie på ytt hvis skruee som produseres ikke er 15 mm. For lage og for korte skruer påfører kjøper problemer. Geerell fremgagsmåte 0 X 1, X,..., X u.i.f. ormal(µ, σ) der σ er kjet. Kvalitetskotroll av skruer Stikkprøve (utvalg) av = 10 skruer, atar ormalfordelig og kjeer σ =0.1mm. 1 To-sidig test Er gru til å tro at skruee som produseres ikke er 15 mm lage? H 0 : µ = µ 0 vs. H 1 : µ µ 0 H 0 : µ = 15 vs. H 1 : µ 15 Sigifikasivå α bestemmes. Velger α = Testobservator Z 0 = X µ 0 σ/ er uder H 0 stadard ormalfordelt Forkast H 0 hvis z 0 > z α eller z 0 < z α. 10 To typer feil 1 Ett utvalg: test for µ med σ kjet Type-I: forkaste H 0 gitt at H 0 er sa. Justismord. Type-II-feil: ikke forkaste H 0 gitt at H 0 er falsk. La skyldig tiltalt gå fri. H 0 sa H 0 falsk Aksepter H 0 Korrekt Type-II feil Forkast H 0 Type-I feil Korrekt Geerell fremgagsmåte Kvalitetskotroll av skruer 4 z α z 0.05 = 1.96 Observerer x fra utvalget x = mm. (stikkprøve) Bereger z = x µ 0 σ/ z 0 = / = Sammeliger z α, z 0 og z α -1.96<1.58<1.96 Forkast H 0 og kokluder med Beholder H 0. Har ikke sterke H 1, eller behold H 0. ok bevis for at µ 15mm.
4 13 Ett utvalg: tosidig test for µ med σ kjet X 1, X,..., X u.i.f. ormal(µ,σ) der σ er kjet. To-sidig test: 1. H 0 : µ = µ 0 vs. H 1 : µ µ 0. Sigifikasivå α bestemmes. 3. Testobservator uder H 0 er Z 0. Z 0 = X µ 0 σ/ er uder H 0 stadard ormalfordelt. Forkast H 0 hvis Z 0 > z α. 4. Bereg x fra utvalget, og videre z 0 = x µ 0 σ/. Sammelig z 0 og z α, og forkast H 0 hvis z 0 > z α. 15 P-verdi [10.4] DEF 10.5: E P-verdi er det laveste ivået hvor de observerte verdie til testobservatore er sigifikat. Utregig: P-verdi = P(for det vi har observert eller oe verre H 0 er sa) Steg: Bestem ull- og alterativ hypotese. Velg testobservator. Bereg P-verdie basert på testobservatore. Bestem om vi vil forkaste eller beholde ullhypotese basert på P-verdie og kuskap om systemet. Tilleggsiformasjo: Ka også gjøre hypotesetestig basert på sigifikasivå og forkastigsregio og oppgi P-verdi som tilleggsiformasjo. 14 Ett utvalg: tosidig test for µ med σ kjet [10.5] 16 Kvalitetskotroll: legde av skruer X 1, X,..., X u.i.f. N(µ,σ ) der σ er kjet. To-sidig test: 1. H 0 : µ = µ 0 vs. H 1 : µ µ 0. Sigifikasivå α bestemmes. 3. Testobservator uder H 0 er Z 0. Z 0 = X µ 0 σ/ er uder H 0 stadard ormalfordelt. Regel: Forkast H 0 hvis Z 0 > z α. 4. Bereg x fra utvalget, og videre z 0 = x µ 0 σ/. Sammelig z 0 og z α, og forkast H 0 hvis z 0 > z α. X 1, X,...,X er legde på skruer. Ata at X 1, X,...,X er u.i.f N(µ, σ = 0.1 ). Estimerig Gi et aslag (puktestimat) og itervall (kofidesitervall) der vi har 95% tillit til at sa legde for produserte skruer ligger. Hypotesetest Udersøk om det er gru til å tro at de produserte skruee ikke er 15 mm lage (test hypotese). Bruk sigifikasivå 5%. H 0 : µ = 15 vs. H 1 : µ 15 Z = X µ σ/ er stadard ormalfordelt, Z 0 = X µ 0 σ/
5 17 Kvalitetskotroll: legde av skruer Estimerig 95% kofidesitervall for µ. x z α σ < µ < x + z α σ 95 % kofidesitervall: [14.99, 15.11] Hypotesetest Forkast H 0 hvis z 0 > z α eller z 0 < z α. Behold H 0 hvis z α < z 0 < z α σ < dvs. behold hvis x z α µ 0 < x + z α σ z 0 = 1.58, z 0.05 = 1.96, dermed ikke forkast H 0. p-verdi Hvis et (1 α)100% kofidesitervall ieholder µ 0 vil vi med e tosidig hypotesetest med sigifikasivå α ikke forkaste H 0 på ivå α. Hvis et (1 α)100% kofidesitervall ikke ieholder µ 0 vil vi med e tosidig hypotesetest med sigifikasivå α forkaste H 0 på ivå α. 19 Ett utvalg: esidig test for µ med σ ukjet [10.7] X 1, X,..., X u.i.f. N(µ, σ ) der σ er ukjet. S = 1 1 i=1 (X i X). E-sidig test (større): 1. H 0 : µ = µ 0 vs. H 1 : µ > µ 0. Sigifikasivå α bestemmes. 3. Testobservator T 0 = X µ 0 s/ er uder H 0 t-fordelt med 1 frihetsgrader. Forkast H 0 hvis T 0 > t α,( 1). 4. Bereg x og s fra utvalget, og videre t 0 = x µ 0 s/. Sammelig t 0 og t α,( 1), og forkast H 0 hvis t > t α,( 1). E-sidig test (midre): H 0 : µ = µ 0 H 1 : µ < µ 0... Forkast H 0 hvis t 0 < t α,( 1). 18 Ett utvalg: esidig test for µ med σ kjet [10.5] X 1, X,..., X u.i.f. N(µ, σ ) der σ er kjet. E-sidig test (større): 1. H 0 : µ = µ 0 vs. H 1 : µ > µ 0. Sigifikasivå α bestemmes. 3. Testobservator Z 0 = X µ 0 σ/ er uder H 0 stadard ormalfordelt. Forkast H 0 hvis Z 0 > z α. 4. Observerer x fra utvalget, bereg z 0 = x µ 0 σ/. Sammelig z 0 og z α, og forkast H 0 hvis z 0 > z α. E-sidig test (midre): H 0 : µ = µ 0 H 1 : µ < µ 0... Forkast H 0 hvis z < z α. 0 Ett utvalg: tosidig test for µ med σ ukjet [10.7] X 1, X,..., X u.i.f. N(µ, σ ) der σ er ukjet. S = 1 1 i=1 (X i X). To-sidig test: 1. H 0 : µ = µ 0 vs. H 1 : µ µ 0. Sigifikasivå α bestemmes. 3. Testobservator T 0 = X µ 0 s/ er uder H 0 t-fordelt med 1 frihetsgrader. Forkast H 0 hvis T 0 > t α,( 1). 4. Bereg x og s fra utvalget, og videre t 0 = x µ 0 s/. Sammelig t 0 og t α,( 1), og forkast H 0 hvis t 0 > t α,( 1).
6 1 Sigifikasivå og teststyrke Defierer α β = P(Type I-feil) = P(Type II-feil) Sigifikasivået for e test = P(Type I-feil) = α. Styrke for e test er sasylighete for å forkaste H 0 år et bestemt alterativ er sat (DEF 10.4), dvs. Styrke = 1 P(Type II-feil, bestemt alterativ) = 1 β. Har at Reduserer α β øker og 1 β (styrke) miker. Øker α miker, β miker og 1 β (styrke) øker. 3 Fartskotroll med laser Ved fartskotroll beytter ofte politiet laser til å måle farte til bilee. Hvis Y er målt fart (km/t) til e tilfeldig valgt bil, atar vi at Y er ormalfordelt med forvetig µ og stadardavvik σ = 1.5 km/t. Politiet gjeomfører e fartskotroll i e 50-soe der farte til hver bil måles med e lasermålig. Politiet vil fastsette e verdi k slik at sasylighete for at e bilist feilaktig beskyldes for fartsovertredelse blir høyst a) Formuler hypotesetest og fi miste verdi k ka være. b) Hva er sasylighete for at e bilist som kjører i 55 km/t ikke blir beskyldt for fartsovertredelse? c) Hvor mage måliger må vi har for å oppdager at biliste kjører for fort med styrke 0.95 år biliste kjører i 55 km/t? Fasit: k=53.5, ikke beskyldt=0.16, mist observasjoer. Teststyrke, illustrasjo Tester hypotese H 1 : µ = µ 0 mot H 1 : µ < µ 0. Forkastar H 0 dersom z 0 < z α, eller ekvivalet x < k, der k = µ 0 z α σ/. Ata sa verdi µ = µ 1, hva er teststyrke 1 β? Areal:α Areal:β Forkast H[0] µ 1 k µ 0 σ Aksepter H[0] 4 Hypotesetest: geerell fremgagsmåte Geerell fremgagsmåte Kvalitetskotroll av skruer 0 Observasjoer X 1, X,..., X Stikkprøve (utvalg) av = 10 u.i.f. fra fordelig med kjete og ukjete parametere. skruer, atar ormalfordelig og kjeer σ =0.1mm. 1 Esidig eller to-sidig test Er gru til å tro at skruee som produseres ikke er 15 mm lage? H 0 vs. H 1 H 0 : µ = 15 vs. H 1 : µ 15 Sigifikasivå α bestemmes. Velger α = Testobservator: størrelse med kjet fordelig uder ullhypotese. Forkasigsområde fra P(forkaste H 0 H 0 sa) α. Z 0 = X µ 0 σ/ er uder H 0 stadard ormalfordelt Forkast H 0 hvis z 0 z 0 < z α. > z α eller
7 5 Hypotesetest: geerell fremgagsmåte 7 To utvalg: eksempler Geerell fremgagsmåte 4 Koklusjo basert på observasjoer Forkast H 0 og kokluder med H 1, eller behold H 0. 5 Tilleggsiformasjo: p- verdi=p(det vi har observert eller oe verre H 0 er sa), teststyrke ved bestemt alterativ Kvalitetskotroll av skruer = 1.96, x = mm. z 0.05 z 0 = / = <1.58<1.96 Beholder H 0. Har ikke sterke ok bevis for at µ 15mm. p-verdi Betog: to ulike oppskrifter, A og B, skal sammeliges. Er det forskjell i styrke ( crushig stregth ) for betog fra oppskrift A og fra oppskrift B? Sykdom: tester ut y blodtrykksmedisi. Er de ye medisie bedre e de åværede markedsledede blodtrykksmedisi? Kosthold: får jeg e vektreduksjo på mer e 10 kg hvis jeg følger Dr Fedo Lidbergs kostråd i et halvt år? (balase i blodsukker, lav glykemisk ideks) Bildekk: to typer dekk, A og B, skal sammeliges mhp slitasje. Slites A og B dekk forskjellig? 6 Utvalgsstørrelse [10.9] 8 To utvalg: statistisk situasjo Esidig test, σ kjet. H 0 : µ = µ 0 vs. H 1 : µ > µ 0 Hvis vi øsker å ha sasylighet (1 β) for å oppdage µ = µ 0 + δ (for gitt δ) og øsker sigifikasivå α, må vi mist ha utvalgsstørrelse Tosidig test, σ kjet. = (z α + z β ) σ δ H 0 : µ = µ 0 vs. H 1 : µ µ 0 Som over, da blir mist utvalgsstørrelse (tilærmet) Øsker å sammelige to populasjoer basert på et u.i.f. utvalg fra hver populasjo. Nå: Studerer e egeskap som ka sies å være ormalfordelt i hver populasjo, og øsker å utføre e hypotesetest om forholdet medllom forveigsverdiee i de to populasjoee Sammeligigee ka være parvise eller ikke parvise. I 10.1 ser vi på egeskaper som er biomisk fordelt. = (z α + z β) σ δ
8 9 10.8: To utvalg, ormalfordelig Situasjo: X A 1, X A,..., X A 1 er u.i.f., X A i N(µ A, σ A ). X B 1, X B,..., X B er u.i.f., X B j N(µ B, σ B ). Problemstillig: Vil teste hypotese H 0 : µ A µ B = d 0 mot H 1 : µ A µ B d 0 (Alterativt: H 1 : µ A µ B < d 0 eller H 1 : µ A µ B > d 0 ) Hypotesetest, tre tilfelle: 1. σ A og σ B kjete.. σ A = σ B = σ, der σ er ukjet 3. σ A σ B, σ A og σ B ukjete. 31 To utvalg, ormalfordelig (forts.) 1. σa og σ B kjete: Normalfordelig.. σ A = σ B = σ, der σ er ukjet: Estimator for σ : S p = Bruker at A 1 A + B [ (Xi A X A ) + i=1 T 0 = (X A X B ) d 0 1 S p A + 1 B B j=1 (X B j X B ) ] er t-fordelt med A + B frihetsgrader uder H 0. Forkast H 0 dersom t 0 > t α,( A+ B ), der t 0 er observert verdi for T σa σ B, σ A og σ B ukjete: Se læreboka. 30 To utvalg, ormalfordelig (forts.) 3 Parvist eksempel: Dekkslitasje 1. σa og σ B kjete: Bruker at σ A 1 Z 0 = ( X A X B ) d 0 + σ B N(0, 1) uder H 0. Forkast H 0 dersom z 0 > z α, der z 0 er observert verdi for Z 0.. σ A = σ B = σ, der σ er ukjet: T-fordelig med A + B frihetsgrader. 3. σa σ B, σ A og σ B ukjete: Se læreboka. Spørsmål: Er slitasje for A-dekka større e for B-dekka? Forsøk: Utstyr tilfeldig valgte biler med to dekk av type A og to av type B. La X i, i = 1,..., være slitasje til type A-dekka på de bilee (gj.sitt over to dekk). La Y i, i = 1,..., være slitasje til de tilsv. paree av type B-dekk (gj.sitt over to dekk). Da er D i = X i Y i, i = 1,..., uavhegige, og D i N(µ D, σ D ). Observasjoer: = 15 forsøk med observerte verdier d = 0.7 og s d = 0.97.
9 33 Parvist eksempel: Dekkslitasje Hypotesetest: H 0 : µ D = µ 0 mot H 1 : µ D > µ 0, der µ 0 = [10.13] Hypotesetest av varias La X 1, X,..., X være et tilfeldig utvalg fra e populasjo som beskrives av e ormalfordelig med forvetig µ og varias σ. S = 1 1 i=1 (X i X) er e estimator for σ (forvetigsrett, me ikke SME). Størrelse V = ( 1)S σ er kjikvadrat-fordelt med 1 frihetsgrader. T 0 = D µ 0 S D / = D 0 S D / er t-fordelt med 1 frihetsgrader uder H 0. Gjeomfør teste som for ett utvalg. 1 α α α 0 χ (1 α ) ν χ α 34 Hypotesetest av varias (10.13) Ispirert av eksame, august 003, oppgave 1. E laborat skal udersøke måleusikkerhete til et istrumet som beyttes til å bestemme kosetrasjoe av et stoff i e oppløsig. Det gjeomføres måliger med istrumetet på e oppløsig. Observasjoee X 1, X,..., X ka atas å være uavhegige og ormalfordelte med forvetig µ og varias σ. I oppgave arbeider ma med kjet kosetrasjo av stoffet, me vi skal her ata at kosetrasjoe er ukjet. Vi ka teke oss at produsete av måleistrumetet reklamerer med at måleusikkerhete i istrumetet ikke er høyere e σ0 = Vi øsker å teste om dette er tilfellet. Data fra oppgave: = 10, 10 i=1 (x i x) = 0.43 og α = Laba strakk seg ikke leger, me smaker de bedre? Vi øsker å fie ut om studeter syes at Nidar Laba smaker bedre e COOP Seigme. Formuler spørsmålet som e hypotesetest. Etter seigma-strekkige på forelesige, svarte de studetee som hadde strukket (og spist) både Laba og Seigme på hvilket av merkee som smakte best. Data: = 51 studeter svarte, av disse likte x = 30 studeter Laba bedre e COOP Seigma. Gjeomfør teste. Hva blir koklusjoe? Hva ville koklusjoe blitt hvis vi hadde observert samme adel, ˆp = = 0.59, me = 10 og x = 6, = 100 og x = 59.
10 37 [10.11] Hypotesetest av e adel X er atall suksesser i et biomisk forsøk med parametere atallet og adele p. Vi vil teste e hypotese om p, dvs. relatere p til bestemte verdier (esidig eller tosidig test). Estimator ˆp = X p(1 p), der E(ˆp) = p og Var(ˆp) =. Forkastigsområdet ka ete fies fra biomisk fordelig: relatert til verdie av X, treger å fie forkastigsområde fra tabell over kumulativ biomisk fordelig, fra ormaltilærmig av ˆp år er stor, og p > 5, (1 p) > 5 og p ikke er ær 0 eller 1. ˆp p 0 Z 0 = 1 p 0(1 p 0 ) er tilærmet stadard ormalfordelt uder H Studeter og bilkjørig x x Me Kvier Alle b) La p være sasylighete for at e tilfeldig valgt studet syes ha/hu er bedre e gjeomsittet til å kjøre bil. Ville hypotese H 0 : p = 0.5 vs. H 0 : p 0.5 blitt forkastet? Hvilke sigifikasivå ville ført til forkastig? Baser resoemetet på fasit fra a), dvs. ute regig. Hvilke hypoteser (valg av p 0 ) ville ikke blitt forkastet på ivå 0.01? 38 Studeter og bilkjørig Her agir atall studeter i utvalget som hadde sertifikat, og x atall studeter som svarte at de er bedre e gjeomsittet av Norges befolkig til å kjøre bil. x x Me Kvier Alle a) Fi puktestimat og 99% kofidesitervall for adele av studeter som syes sie kjøreegeskaper er bedre e gjeomsittet. Fasit: 0.4 ± (1 0.4) 139 =[0.3, 0.53]. 40 Studeter og bilkjørig, forts. x x Me Kvier Alle c) Fi puktestimat og 99% kofidesitervall for differese mellom adele av malige studeter og kvilige studeter som syes sie kjøreegeskaper er bedre e gjeomsittet. Fasit: [0.03, 0.47]. d) La p 1 være sasylighete for at e tilfeldig valgt malig studet syes ha er bedre e gjeomsittet til å kjøre bil, og tilsvarede p for kvier. Ville hypotese H 0 : p 1 p = 0 vs. H 0 : p 1 p 0 blitt forkastet? Hvilke sigifikasivå ville ført til forkastig? Baser resoemetet på fasit fra c), dvs. ute regig. Hvilke hypoteser ville ikke blitt forkastet på ivå 0.01?
11 41 Lovlydige bilførere? BOT: Kjørig med motorvog på eller over sperrelije og/eller i sperreområde begreset av heltrukke lije, på fortau, gagveg/gagbae, sykkelveg/sykkelbae og gag- og sykkelveg/gag- og sykkelbae. Kr. 500,- sub. 5 dgs fegsel. Måliger av kryssig av hvit heltrukket sperrelije ved fartsdempere ved bussholdeplass Gløshauge Nord ( , fra 08:0 til 08:35). =atall observasjoer X =atall bilister som kjører rudt fartsdempere (over hvit heltrukket sperrelije). x x Me Kvier Alle Lovlydige bilførere? x x Me Kvier Alle a) Er det gru til å tro at det er flere e 5% av bilistee som sviger rudt fartsdempere? (Fasit: forkast esidig test på ivå 0.01, p-verdi= 0.004) b) Er det gru til å tro at kvier og me er like lovlydige i dee situasjoe? (Fasit: ikke forkast tosidig hypotese, p-verdi 0.1)
Estimering og hypotesetesting. Estimering og hypotesetesting. Estimering og hypotesetesting. Kapittel 10. Ett- og toutvalgs hypotesetesting
 3 Estimerig og hypotesetestig Kapittel 10 Ett- og toutvalgs hypotesetestig TMA4240 H2006: Eirik Mo Feome Bilkjørig Høyde til studeter Estimator ˆp = X, X atall ˆµ = X gjeomsittlig høyde. som syes de er
3 Estimerig og hypotesetestig Kapittel 10 Ett- og toutvalgs hypotesetestig TMA4240 H2006: Eirik Mo Feome Bilkjørig Høyde til studeter Estimator ˆp = X, X atall ˆµ = X gjeomsittlig høyde. som syes de er
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2010 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 12. april Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 59
ÅMA110 Sasylighetsregig med statistikk, våre 2010 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 12. april Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 59
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Kp. 6, del 4. Hypotesetesting, del 4
 ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 19. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 27 Bjør
ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 19. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 27 Bjør
TMA4240 Statistikk H2010 (20)
 TMA4240 Statistikk H2010 (20) 10.5: Ett normalfordelt utvalg, kjent varians (repetisjon) 10.4: P-verdi 10.6: Konfidensintervall vs. hypotesetest 10.7: Ett normalfordelt utvalg, ukjent varians Mette Langaas
TMA4240 Statistikk H2010 (20) 10.5: Ett normalfordelt utvalg, kjent varians (repetisjon) 10.4: P-verdi 10.6: Konfidensintervall vs. hypotesetest 10.7: Ett normalfordelt utvalg, ukjent varians Mette Langaas
Estimering og hypotesetesting
 Kapittel 10 Ett- og toutvalgs hypotesetesting TMA4245 V2007: Eirik Mo 2 Estimering og hypotesetesting Fenomen Bilkjøring Høyden til studenter Spørsmål Hvor stor andel av studentene synes de er flinkere
Kapittel 10 Ett- og toutvalgs hypotesetesting TMA4245 V2007: Eirik Mo 2 Estimering og hypotesetesting Fenomen Bilkjøring Høyden til studenter Spørsmål Hvor stor andel av studentene synes de er flinkere
Estimering og hypotesetesting
 Kapittel 10 Ett- og toutvalgs hypotesetesting TMA4240 H2006: Eirik Mo 2 Estimering og hypotesetesting Fenomen Bilkjøring Høyden til studenter Spørsmål Hvor stor andel av studentene synes de er flinkere
Kapittel 10 Ett- og toutvalgs hypotesetesting TMA4240 H2006: Eirik Mo 2 Estimering og hypotesetesting Fenomen Bilkjøring Høyden til studenter Spørsmål Hvor stor andel av studentene synes de er flinkere
Mer om utvalgsundersøkelser
 Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Kap. 9: Inferens om én populasjon. Egenskaper ved t-fordelingen. ST0202 Statistikk for samfunnsvitere. I Kapittel 8 brukte vi observatoren
 2 Kap. 9: Iferes om é populasjo I Kapittel 8 brukte vi observatore z = x μ σ/ for å trekke koklusjoer om μ. Dette krever kjet σ (urealistisk). ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for
2 Kap. 9: Iferes om é populasjo I Kapittel 8 brukte vi observatore z = x μ σ/ for å trekke koklusjoer om μ. Dette krever kjet σ (urealistisk). ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for
Hypotesetest: generell fremgangsmåte
 TMA4240 Statistikk H2010 (21) 10.8, 10.10: To normalfordelte utvalg 10.9: Teststyrke og antall observasjoner Mette Langaas Foreleses mandag 1.november, 2010 2 Hypotesetest: generell fremgangsmåte Generell
TMA4240 Statistikk H2010 (21) 10.8, 10.10: To normalfordelte utvalg 10.9: Teststyrke og antall observasjoner Mette Langaas Foreleses mandag 1.november, 2010 2 Hypotesetest: generell fremgangsmåte Generell
X = 1 5. X i, i=1. som vil være normalfordelt med forventningsverdi E( X) = µ og varians Var( X) = σ 2 /5. En rimelig estimator for variansen er
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 11, blokk II Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 11, blokk II Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Kp. 6, del 5. Hypotesetesting, del 5
 ÅMA11 Sasylighetsregig med statistikk, våre 7 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 59 Bjør
ÅMA11 Sasylighetsregig med statistikk, våre 7 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 59 Bjør
Høgskolen i Telemark Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 12. desember 2008
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. desember 8 EKSAMEN I MATEMATIKK, Utsatt røve Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig).
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. desember 8 EKSAMEN I MATEMATIKK, Utsatt røve Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig).
Introduksjon. Hypotesetesting / inferens (kap 3) Populasjon og utvalg. Populasjon og utvalg. Populasjonsvarians
 Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
Hypotesetesting, del 5
 Oversikt, del 5 Kofidesitervall p-verdi Kofidesitervall E (tosidig test ka gjeomføres vha. av et kofidesitervall. For eksempel, dersom vi i målemodell 1 vil teste: H 0 : μ = μ 0 mot H 1 : μ μ 0, ka vi
Oversikt, del 5 Kofidesitervall p-verdi Kofidesitervall E (tosidig test ka gjeomføres vha. av et kofidesitervall. For eksempel, dersom vi i målemodell 1 vil teste: H 0 : μ = μ 0 mot H 1 : μ μ 0, ka vi
Statistikk og økonomi, våren 2017
 Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
ÅMA110 Sannsynlighetsregning med statistikk, våren 2008 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 56
ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 56
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1 / 56
ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 3. april Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1 / 56
Kapittel 8: Estimering
 Kaittel 8: Estimerig Estimerig hadler kort sagt om hvorda å aslå verdie å arametre som,, og dersom disse er ukjete. like arametre sier oss oe om oulasjoe vi studerer (dvs om alle måliger av feomeet som
Kaittel 8: Estimerig Estimerig hadler kort sagt om hvorda å aslå verdie å arametre som,, og dersom disse er ukjete. like arametre sier oss oe om oulasjoe vi studerer (dvs om alle måliger av feomeet som
Hypotesetesting, del 4
 Oversikt, del 4 t-fordelig t-test t-itervall Del 5 Kofidesitervall vs. test p-verdi t-fordelig Rett på defiisjo: Utgagspuktet er målemodelle med ormalatakelse: X 1,...,X,u.i.f.tilf.var.derX i Nμ, σ 2 ).La
Oversikt, del 4 t-fordelig t-test t-itervall Del 5 Kofidesitervall vs. test p-verdi t-fordelig Rett på defiisjo: Utgagspuktet er målemodelle med ormalatakelse: X 1,...,X,u.i.f.tilf.var.derX i Nμ, σ 2 ).La
ECON240 Statistikk og økonometri
 ECON240 Statistikk og økoometri Arild Aakvik, Istitutt for økoomi 1 Mellomregig MKM Model: Y i = a i + bx i + e i MKM-estimator for b: b = = Xi Y i 1 Xi Yi Xi 1 ( X i ) 2 (Xi X)(Y i Ȳi) (Xi X) 2 hvor vi
ECON240 Statistikk og økoometri Arild Aakvik, Istitutt for økoomi 1 Mellomregig MKM Model: Y i = a i + bx i + e i MKM-estimator for b: b = = Xi Y i 1 Xi Yi Xi 1 ( X i ) 2 (Xi X)(Y i Ȳi) (Xi X) 2 hvor vi
KLMED8004 Medisinsk statistikk. Del I, høst Estimering. Tidligere sett på. Eksempel hypertensjon
 Tidligere sett på KLMED8004 Medisisk statistikk Del I, høst 008 Estimerig Hvorda kjete sasylighetsfordeliger (biomialfordelig, ormalfordelig) med kjete populasjosparametrer (forvetig, varias osv.) ka gi
Tidligere sett på KLMED8004 Medisisk statistikk Del I, høst 008 Estimerig Hvorda kjete sasylighetsfordeliger (biomialfordelig, ormalfordelig) med kjete populasjosparametrer (forvetig, varias osv.) ka gi
ÅMA110 Sannsynlighetsregning med statistikk, våren 2008 Kp. 6, del 5
 ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 53
ÅMA110 Sasylighetsregig med statistikk, våre 2008 Kp. 6, del 5 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 26. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 5 1/ 53
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Kp. 6, del 4
 ÅMA11 Sasylighetsregig med statistikk, våre 21 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 22. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 29 Bjør
ÅMA11 Sasylighetsregig med statistikk, våre 21 Kp. 6, del 4 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 22. mars Bjør H. Auestad Kp. 6: Hypotesetestig del 4 1/ 29 Bjør
H 1 : µ 1 µ 2 > 0. t = ( x 1 x 2 ) (µ 1 µ 2 ) s p. s 2 p = s2 1 (n 1 1) + s 2 2 (n 2 1) n 1 + n 2 2
 TMA4245 Statistikk Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave 1 Vi øsker å fie ut om et ytt serum ka stase leukemi. 5 mus får serumet, 4
TMA4245 Statistikk Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave 1 Vi øsker å fie ut om et ytt serum ka stase leukemi. 5 mus får serumet, 4
TMA4240 Statistikk H2010 (19)
 TMA4240 Statistikk H2010 (19) Hypotesetesting 10.1-10.3: Generelt om statistiske hypoteser 10.5: Ett normalfordelt utvalg Mette Langaas Foreleses mandag 25.oktober, 2010 2 Estimering og hypotesetesting
TMA4240 Statistikk H2010 (19) Hypotesetesting 10.1-10.3: Generelt om statistiske hypoteser 10.5: Ett normalfordelt utvalg Mette Langaas Foreleses mandag 25.oktober, 2010 2 Estimering og hypotesetesting
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007
 ÅMA Sasylighetsregig med statistikk, våre 27 Kp. 6 (kp. 6) Tre deler av faget/kurset:. Beskrivede statistikk 2. Sasylighetsteori, sasylighetsregig 3. Statistisk iferes estimerig kofidesitervall hypotesetestig
ÅMA Sasylighetsregig med statistikk, våre 27 Kp. 6 (kp. 6) Tre deler av faget/kurset:. Beskrivede statistikk 2. Sasylighetsteori, sasylighetsregig 3. Statistisk iferes estimerig kofidesitervall hypotesetestig
Econ 2130 uke 15 (HG) Poissonfordelingen og innføring i estimering
 Eco 130 uke 15 (HG) Poissofordelige og iførig i estimerig 1 Poissofordelige (i) Tilærmig til biomialfordelige. Regel. ( Poissotilærmelse ) Ata Y ~ bi(, p) E( Y ) = p og var( Y ) = p(1 p). Hvis er stor
Eco 130 uke 15 (HG) Poissofordelige og iførig i estimerig 1 Poissofordelige (i) Tilærmig til biomialfordelige. Regel. ( Poissotilærmelse ) Ata Y ~ bi(, p) E( Y ) = p og var( Y ) = p(1 p). Hvis er stor
TMA4240 Statistikk Høst 2015
 Høst 205 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Løsigsskisse Oppgave a) X bi(, p) fordi: Udersøker uavhegige delar av DNA-strukture. Fi for kvar del
Høst 205 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Løsigsskisse Oppgave a) X bi(, p) fordi: Udersøker uavhegige delar av DNA-strukture. Fi for kvar del
LØSNINGSFORSLAG TILEKSAMEN I FAG TMA4240/TMA4245 STATISTIKK 10. august 2005
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 8 LØSNINGSFORSLAG TILEKSAMEN I FAG TMA440/TMA445 STATISTIKK 0. august 005 Oppgave Smeltepuktsbestemmelse a) Vi jobber i dette
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 8 LØSNINGSFORSLAG TILEKSAMEN I FAG TMA440/TMA445 STATISTIKK 0. august 005 Oppgave Smeltepuktsbestemmelse a) Vi jobber i dette
8 (inkludert forsiden og formelsamling) Tegne- og skrivesaker, kalkulator, formelsamling (se vedlagt).
 Eksamesoppgave våre 011 Ordiær eksame Bokmål Fag: Matematikk Eksamesdato: 10.06.011 Studium/klasse: GLU 5-10 Emekode: MGK00 Eksamesform: Skriftlig Atall sider: 8 (ikludert forside og formelsamlig) Eksamestid:
Eksamesoppgave våre 011 Ordiær eksame Bokmål Fag: Matematikk Eksamesdato: 10.06.011 Studium/klasse: GLU 5-10 Emekode: MGK00 Eksamesform: Skriftlig Atall sider: 8 (ikludert forside og formelsamlig) Eksamestid:
TMA4240 Statistikk H2010
 TMA440 Statistikk H00 9.8: To uvalg (siste del) 9.9: Parvise observasjoer 9.0-9.: Adelser 9.: Varias Mette Lagaas Foreleses oag 0.oktober, 00 Norske hoppdommere og Jae Ahoe Jae Ahoe er e fisk skihopper,
TMA440 Statistikk H00 9.8: To uvalg (siste del) 9.9: Parvise observasjoer 9.0-9.: Adelser 9.: Varias Mette Lagaas Foreleses oag 0.oktober, 00 Norske hoppdommere og Jae Ahoe Jae Ahoe er e fisk skihopper,
) = P(Z > 0.555) = > ) = P(Z > 2.22) = 0.013
 TMA4240 Statistikk Vår 2008 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b5 Løsigsskisse Oppgave 1 a) X 1,...,X 16 er u.i.f. N(80,18 2 ). Setter Y = X. i) P(X 1 >
TMA4240 Statistikk Vår 2008 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b5 Løsigsskisse Oppgave 1 a) X 1,...,X 16 er u.i.f. N(80,18 2 ). Setter Y = X. i) P(X 1 >
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006
 ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 2 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 1/ 38 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 2/ 38 Oversikt 1. Hva er hypotesetestig? 2. Hypotesetestig
ÅMA110 Sasylighetsregig med statistikk, våre 2006 Kp. 6, del 2 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 1/ 38 Bjør H. Auestad Kp. 6: Hypotesetesig del 2 2/ 38 Oversikt 1. Hva er hypotesetestig? 2. Hypotesetestig
Kapittel 10: Hypotesetesting
 Kapittel 10: Hypotesetesting TMA445 Statistikk 10.1, 10., 10.3: Introduksjon, 10.5, 10.6, 10.7: Test for µ i normalfordeling, 10.4: p-verdi Turid.Follestad@math.ntnu.no p.1/19 Estimering og hypotesetesting
Kapittel 10: Hypotesetesting TMA445 Statistikk 10.1, 10., 10.3: Introduksjon, 10.5, 10.6, 10.7: Test for µ i normalfordeling, 10.4: p-verdi Turid.Follestad@math.ntnu.no p.1/19 Estimering og hypotesetesting
Eksempler fra slutten av forrige uke. Eksempler (styrke, dimensjonering,...) Eksempler fra slutten av forrige uke
 Oversikt, del 5 Hypotesetestig, del 4 (oppsummerig fra Hypotesetestig, del 5 Kofidesitervall dimesjoerig Eksempler fra slutte av forrige uke Kofidesitervall p-verdi Eksempler Eksempler (styrke, dimesjoerig,...
Oversikt, del 5 Hypotesetestig, del 4 (oppsummerig fra Hypotesetestig, del 5 Kofidesitervall dimesjoerig Eksempler fra slutte av forrige uke Kofidesitervall p-verdi Eksempler Eksempler (styrke, dimesjoerig,...
LØSNING, EKSAMEN I STATISTIKK, TMA4240, DESEMBER Anta at sann porøsitet er r. Måling med utstyret gir da X n(x; r, 0,03).
 LØSNING, EKSAMEN I STATISTIKK, TMA440, DESEMBER 006 OPPGAVE 1 Ata at sa porøsitet er r. Målig med utstyret gir da X (x; r, 0,03). a) ( ) X r P(X > r) P 0,03 > 0 P(Z > 0) 0,5. ( X r P(X r > 0,05) P 0,03
LØSNING, EKSAMEN I STATISTIKK, TMA440, DESEMBER 006 OPPGAVE 1 Ata at sa porøsitet er r. Målig med utstyret gir da X (x; r, 0,03). a) ( ) X r P(X > r) P 0,03 > 0 P(Z > 0) 0,5. ( X r P(X r > 0,05) P 0,03
Høgskolen i Telemark Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 20. mai 2008
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. mai 8 EKSAMEN I MATEMATIKK Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig). Hjelemidler:
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. mai 8 EKSAMEN I MATEMATIKK Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig). Hjelemidler:
Rep.: generelle begrep og definisjoner Kp. 10.1, 10.2 og 10.3
 Kp. 1, oversikt ; oversikt, t- ; oversikt ; stor ; Hypoteseig; ett- og to-utvalg Rep.: geerelle begrep og defiisjoer Kp. 1.1, 1.2 og 1.3 Rep.: ett-utvalgser for μ (...), p Kp. 1 og 1.8 Nytt: ett-utvalgs
Kp. 1, oversikt ; oversikt, t- ; oversikt ; stor ; Hypoteseig; ett- og to-utvalg Rep.: geerelle begrep og defiisjoer Kp. 1.1, 1.2 og 1.3 Rep.: ett-utvalgser for μ (...), p Kp. 1 og 1.8 Nytt: ett-utvalgs
TMA4240 Statistikk Høst 2016
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 11 Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som vil være ormalfordelt
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 11 Løsigsskisse Oppgave 1 a) E rimelig estimator for forvetigsverdie µ er gjeomsittet X = 1 X i, som vil være ormalfordelt
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK 5.august 2004
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK 5.august 2004 Oppgave Foruresig X er e stokastisk variabel som agir
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK 5.august 2004 Oppgave Foruresig X er e stokastisk variabel som agir
TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i << >>.
 1 ECON130: EKSAMEN 013 VÅR - UTSATT PRØVE TALLSVAR. Det abefales at de 9 deloppgavee merket med A, B, teller likt uasett variasjo i vaskelighetsgrad. Svaree er gitt i
1 ECON130: EKSAMEN 013 VÅR - UTSATT PRØVE TALLSVAR. Det abefales at de 9 deloppgavee merket med A, B, teller likt uasett variasjo i vaskelighetsgrad. Svaree er gitt i
Kap. 9: Inferens om én populasjon
 2 ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for matematiske fag Ka. 9: Iferes om é oulasjo Hvis σ er ukjet bytter vi ut σ med s i Ny observator blir t = x μ s/ z = x μ σ/ der s = Σx 2 (Σx)
2 ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for matematiske fag Ka. 9: Iferes om é oulasjo Hvis σ er ukjet bytter vi ut σ med s i Ny observator blir t = x μ s/ z = x μ σ/ der s = Σx 2 (Σx)
Oppgaver fra boka: X 2 X n 1
 MOT30 Statistiske metoder, høste 00 Løsiger til regeøvig r 3 (s ) Oppgaver fra boka: 94 (99:7) X,, X uif N(µ, σ ) og X,, X uif N(µ, σ ) og alle variable er uavhegige Atar videre at σ = σ = σ og ukjet Kodesitervall
MOT30 Statistiske metoder, høste 00 Løsiger til regeøvig r 3 (s ) Oppgaver fra boka: 94 (99:7) X,, X uif N(µ, σ ) og X,, X uif N(µ, σ ) og alle variable er uavhegige Atar videre at σ = σ = σ og ukjet Kodesitervall
TMA4245 Statistikk Eksamen mai 2017
 TMA445 Statistikk Eksame mai 07 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsskisse Oppgave a Når vi reger ut disse tre sasylighetee må ma huske på at de mulige verdiee
TMA445 Statistikk Eksame mai 07 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Løsigsskisse Oppgave a Når vi reger ut disse tre sasylighetee må ma huske på at de mulige verdiee
Kap. 9: Inferens om én populasjon
 2 ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for matematiske fag Ka. 9: Iferes om é oulasjo Hvis σ er ukjet bytter vi ut σ med s i Ny observator blir t = x μ s/ z = x μ σ/ der s = Σx 2 (Σx)
2 ST0202 Statistikk for samfusvitere Bo Lidqvist Istitutt for matematiske fag Ka. 9: Iferes om é oulasjo Hvis σ er ukjet bytter vi ut σ med s i Ny observator blir t = x μ s/ z = x μ σ/ der s = Σx 2 (Σx)
Estimering 1 -Punktestimering
 Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Oppgaver fra boka: Med lik men ukjent varians antatt har vi fra pensum at. t n1 +n 2 2 under H 0 (12 1) (12 1)
 MOT30 Statistiske metoder, høste00 Løsiger til regeøvig r. 5 (s. ) Oppgaver fra boka: Oppgave 0.36 (0.0:8) Dekkslitasje X,..., X u.i.f. N(µ, σ ) og X,..., X u.i.f. N(µ, σ ) og alle variable er uavhegige.
MOT30 Statistiske metoder, høste00 Løsiger til regeøvig r. 5 (s. ) Oppgaver fra boka: Oppgave 0.36 (0.0:8) Dekkslitasje X,..., X u.i.f. N(µ, σ ) og X,..., X u.i.f. N(µ, σ ) og alle variable er uavhegige.
Oppgave 1. (i) Hva er sannsynligheten for at det øverste kortet i bunken er et JA-kort?
 ECON EKSAMEN 8 VÅR TALLSVAR Oppgave Vi har e kortstokk beståede av 6 kort. På av disse står det skrevet JA på forside mes det står NEI på forside av de adre kortee. Hvis ma får se kortet med bakside vedt
ECON EKSAMEN 8 VÅR TALLSVAR Oppgave Vi har e kortstokk beståede av 6 kort. På av disse står det skrevet JA på forside mes det står NEI på forside av de adre kortee. Hvis ma får se kortet med bakside vedt
2. Hypotesetesting i ulike sitausjoner: i. for forventingen, μ, i målemodellen med normalantakelse og kjent varians, σ 2.
 Oversikt 1. Hva er hypotesetestig? 2. i ulike sitausjoer: i. for forvetige, μ, med ormalatakelse og kjet varias, σ 2. ii. for forvetige, μ, med stor og ormaltilærmig (variase, σ 2, ukjet). iii. for suksessasylighete,
Oversikt 1. Hva er hypotesetestig? 2. i ulike sitausjoer: i. for forvetige, μ, med ormalatakelse og kjet varias, σ 2. ii. for forvetige, μ, med stor og ormaltilærmig (variase, σ 2, ukjet). iii. for suksessasylighete,
MOT310 Statistiske metoder 1, høsten 2011
 MOT310 Statistiske metoder 1, høste 2011 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 24. august, 2011 Bjør H. Auestad Itroduksjo og repetisjo 1 / 32 Repetisjo; 9.1,
MOT310 Statistiske metoder 1, høste 2011 Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 24. august, 2011 Bjør H. Auestad Itroduksjo og repetisjo 1 / 32 Repetisjo; 9.1,
Estimering 1 -Punktestimering
 Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Estimerig 1 -Puktestimerig Dekkes av kap. 8, 9.1-9.3 og 9.15/9.14. Vi har til å settpå e rekke forskjellige sasylighetsfordeliger og sett hvorda disse ka brukes til å modellere mage forskjellige typer
Repetisjon; 9.1, 9.2, 9.3, 9.4, 9.5, og Repetisjon; 9.1, 9.2, 9.3, 9.4, 9.5, og 9.10
 Repetisjo; 9.1, 9.2, 9.3, 9.4, 9.5, og 9.10 og Geerell defiisjo av : Situasjo: Data x 1,...,x ;utfallav:x 1,...,X ; u.i.f. tilfeldige variable Ukjet parameter i fordelige til X i ee: θ Dersom L og U L
Repetisjo; 9.1, 9.2, 9.3, 9.4, 9.5, og 9.10 og Geerell defiisjo av : Situasjo: Data x 1,...,x ;utfallav:x 1,...,X ; u.i.f. tilfeldige variable Ukjet parameter i fordelige til X i ee: θ Dersom L og U L
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Kp. 6, del 2
 ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 2 Bjør H. Auestad Istitutt for matematikk og aturviteskap 5. mars 21 Bjør H. Auestad Kp. 6: del 1/2 1/ 42 Bjør H. Auestad Kp. 6: del 1/2 2/ 42
ÅMA11 Sasylighetsregig med statistikk, våre 27 Kp. 6, del 2 Bjør H. Auestad Istitutt for matematikk og aturviteskap 5. mars 21 Bjør H. Auestad Kp. 6: del 1/2 1/ 42 Bjør H. Auestad Kp. 6: del 1/2 2/ 42
211.7% 2.2% 53.0% 160.5% 30.8% 46.8% 17.2% 11.3% 38.7% 0.8%
 Prøve-eksame II MET 1190 Statistikk Dato 31. mai 2019 kl 1100-1400 Alle svar skal begrues. Når besvarelse evalueres, blir det lagt vekt på at framgagsmåte og resultat preseteres så klart, presist og kortfattet
Prøve-eksame II MET 1190 Statistikk Dato 31. mai 2019 kl 1100-1400 Alle svar skal begrues. Når besvarelse evalueres, blir det lagt vekt på at framgagsmåte og resultat preseteres så klart, presist og kortfattet
ÅMA110 Sannsynlighetsregning med statistikk, våren Estimering. Målemodellen. Sannsynlighetsregning med statistikk. Kp. 5 Estimering.
 ÅMA asylighetsregig med statistikk våre 008 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp. 5.3)
ÅMA asylighetsregig med statistikk våre 008 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp. 5.3)
Forelesning 4 og 5 Transformasjon, Weibull-, lognormal, beta-, kji-kvadrat -, t-, F- fordeling
 STAT (V6) Statistikk Metoder Yushu.Li@uib.o Forelesig 4 og 5 Trasformasjo, Weibull-, logormal, beta-, kji-kvadrat -, t-, F- fordelig. Oppsummerig til Forelesig og..) Momet (momet about 0) og setral momet
STAT (V6) Statistikk Metoder Yushu.Li@uib.o Forelesig 4 og 5 Trasformasjo, Weibull-, logormal, beta-, kji-kvadrat -, t-, F- fordelig. Oppsummerig til Forelesig og..) Momet (momet about 0) og setral momet
Konfidensintervall. Notat til STK1110. Ørnulf Borgan, Ingrid K. Glad og Anders Rygh Swensen Matematisk institutt, Universitetet i Oslo.
 Kofidesitervall Notat til STK1110 Ørulf Borga, Igrid K. Glad og Aders Rygh Swese Matematisk istitutt, Uiversitetet i Oslo August 2007 Formål E valig metode for å agi usikkerhete til et estimat er å berege
Kofidesitervall Notat til STK1110 Ørulf Borga, Igrid K. Glad og Aders Rygh Swese Matematisk istitutt, Uiversitetet i Oslo August 2007 Formål E valig metode for å agi usikkerhete til et estimat er å berege
Løsningsforslag ST2301 øving 3
 Løsigsforslag ST2301 øvig 3 Kapittel 1 Exercise 11 Et utvalg på 100 idivider trekkes fra e populasjo med tilfeldig parrig. Det ble observert AA 63 idivider av geotype AA, Aa 27, og aa 10. Lag et 95 % kofidesitervall
Løsigsforslag ST2301 øvig 3 Kapittel 1 Exercise 11 Et utvalg på 100 idivider trekkes fra e populasjo med tilfeldig parrig. Det ble observert AA 63 idivider av geotype AA, Aa 27, og aa 10. Lag et 95 % kofidesitervall
Løsningsforsalg til første sett med obligatoriske oppgaver i STK1110 høsten 2018
 Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2018 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2018 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
ÅMA110 Sannsynlighetsregning med statistikk, våren Kp. 5 Estimering. Målemodellen.
 ÅMA0 Sasylighetsregig med statistikk, våre 0 Kp. 5 Estimerig. Målemodelle. Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.). (Pukt)Estimerig i målemodelle
ÅMA0 Sasylighetsregig med statistikk, våre 0 Kp. 5 Estimerig. Målemodelle. Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.). (Pukt)Estimerig i målemodelle
TMA4240 Statistikk Høst 2009
 TMA440 Statistikk Høst 009 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave Øsker å fie 99% kofidesitervall for µ µ år vi atar ormalfordeliger
TMA440 Statistikk Høst 009 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b4 Løsigsskisse Oppgave Øsker å fie 99% kofidesitervall for µ µ år vi atar ormalfordeliger
Estimering 2. -Konfidensintervall
 Estimerig 2 -Kofidesitervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesigsotatee. Dersom forsøket gjetas mage gager vil (1 α)100% av itervallee [ ˆΘ L, ˆΘ U ] ieholde de ukjete parametere θ (som er
Estimerig 2 -Kofidesitervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesigsotatee. Dersom forsøket gjetas mage gager vil (1 α)100% av itervallee [ ˆΘ L, ˆΘ U ] ieholde de ukjete parametere θ (som er
Oppgaven består av 9 delspørsmål, A,B,C,., som anbefales å veie like mye, Kommentarer og tallsvar er skrevet inn mellom <<.. >>.
 ECON 130 EKSAMEN 008 VÅR - UTSATT PRØVE SENSORVEILEDNING Oppgave består av 9 delspørsmål, A,B,C,., som abefales å veie like mye, Kommetarer og tallsvar er skrevet i mellom . Oppgave 1 Ved e spørreudersøkelse
ECON 130 EKSAMEN 008 VÅR - UTSATT PRØVE SENSORVEILEDNING Oppgave består av 9 delspørsmål, A,B,C,., som abefales å veie like mye, Kommetarer og tallsvar er skrevet i mellom . Oppgave 1 Ved e spørreudersøkelse
Oversikt, del 5. Vi har sett på styrkefunksjon for ensidige tester. Eksempler (styrke, dimensjonering,...) Eksempler fra slutten av forrige uke
 Hypotesetestig, del 4 oppsummerig fra Hypotesetestig, del 5 Kofidesitervall dimesjoerig Oversikt, del 5 Eksempler fra slutte av forrige uke Kofidesitervall p-verdi Eksempler Eksempler styrke, dimesjoerig,...
Hypotesetestig, del 4 oppsummerig fra Hypotesetestig, del 5 Kofidesitervall dimesjoerig Oversikt, del 5 Eksempler fra slutte av forrige uke Kofidesitervall p-verdi Eksempler Eksempler styrke, dimesjoerig,...
Eksamen REA3028 S2, Våren 2011
 Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (8 poeg) a) Deriver fuksjoee ) f 5 f 6 5 ) g g ) h l 9 9 6 4 h l
Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (8 poeg) a) Deriver fuksjoee ) f 5 f 6 5 ) g g ) h l 9 9 6 4 h l
Emnenavn: Eksamenstid: 4 timer. Faglærer: Hans Kristian Bekkevard
 EKSAMEN Emekode: SFB107111 Emeav: Metode 1, statistikk deleksame Dato: 7. mai 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Has Kristia Bekkevard
EKSAMEN Emekode: SFB107111 Emeav: Metode 1, statistikk deleksame Dato: 7. mai 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Has Kristia Bekkevard
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007 Oppsummering
 ÅMA110 Sasylighetsregig med statistikk, våre 2007 Oppsummerig Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 19. april Bjør H. Auestad Oppsummerig våre 2006 1 / 37 Oversikt
ÅMA110 Sasylighetsregig med statistikk, våre 2007 Oppsummerig Bjør H. Auestad Istitutt for matematikk og aturviteskap Uiversitetet i Stavager 19. april Bjør H. Auestad Oppsummerig våre 2006 1 / 37 Oversikt
TMA4245 Statistikk. Øving nummer b5. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4245 Statistikk Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b5 Oppgave 1 Eksame mai 2001, oppgave 1 av 4 Vi ser på kosetrasjoe av et giftstoff i havbue like utefor
TMA4245 Statistikk Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b5 Oppgave 1 Eksame mai 2001, oppgave 1 av 4 Vi ser på kosetrasjoe av et giftstoff i havbue like utefor
TMA4240 Statistikk H2010 (22)
 TMA4240 Statistikk H2010 (22) 10.11-10.12: Testing av andelser 10.13: Testing av varians i ett N utvalg Mette Langaas Foreleses onsdag 3.november, 2010 2 Laban strakk seg ikke lenger, men smaker den bedre?
TMA4240 Statistikk H2010 (22) 10.11-10.12: Testing av andelser 10.13: Testing av varians i ett N utvalg Mette Langaas Foreleses onsdag 3.november, 2010 2 Laban strakk seg ikke lenger, men smaker den bedre?
TMA4240/4245 Statistikk 11. august 2012
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA424/4245 Statistikk. august 22 Eksame - løsigsforslag Oppgave Vi har N Nµ,σ 2, µ 85 og X > 88. a X µ X > 88 σ > 88 µ Z > 88 85
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA424/4245 Statistikk. august 22 Eksame - løsigsforslag Oppgave Vi har N Nµ,σ 2, µ 85 og X > 88. a X µ X > 88 σ > 88 µ Z > 88 85
Introduksjon. Hypotesetesting / inferens (kap 3) Populasjon og utvalg. Populasjon og utvalg. Populasjonsvarians
 Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet «The hardest thig to teach i ay itroductory statistics
Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet «The hardest thig to teach i ay itroductory statistics
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 19 des. 2014 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 19 des. 2014 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 5 jui 2015 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 5 jui 2015 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
ÅMA110 Sannsynlighetsregning med statistikk, våren Estimering. Målemodellen. Konfidensintervall, innledning. Kp. 5 Estimering.
 ÅMA0 Sasylighetsregig med statistikk våre 006 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (Pukt)Estimerig i målemodelle (kp. 5.3)
ÅMA0 Sasylighetsregig med statistikk våre 006 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (Pukt)Estimerig i målemodelle (kp. 5.3)
STK1100 våren 2017 Estimering
 STK1100 våre 017 Estimerig Svarer til sidee 331-339 i læreboka Ørulf Borga Matematisk istitutt Uiversitetet i Oslo 1 Politisk meigsmålig Spør et tilfeldig utvalg på 1000 persoer hva de ville ha stemt hvis
STK1100 våre 017 Estimerig Svarer til sidee 331-339 i læreboka Ørulf Borga Matematisk istitutt Uiversitetet i Oslo 1 Politisk meigsmålig Spør et tilfeldig utvalg på 1000 persoer hva de ville ha stemt hvis
TMA4240 Statistikk Eksamen desember 2015
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA20 Statistikk Eksame desember 205 Løsigsskisse Oppgave a) De kumulative fordeligsfuksjoe til X, F (x) P (X x): F (x) P (X x) x
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA20 Statistikk Eksame desember 205 Løsigsskisse Oppgave a) De kumulative fordeligsfuksjoe til X, F (x) P (X x): F (x) P (X x) x
Løsningsforslag til eksamen i STK desember 2010
 Løsigsforslag til eksame i STK0 0. desember 200 Løsigsforslaget har med flere detaljer e det vil bli krevd til eksame. Oppgave a Det er tilpasset e multippel lieær regresjosmodell av forme β 0 + β x i
Løsigsforslag til eksame i STK0 0. desember 200 Løsigsforslaget har med flere detaljer e det vil bli krevd til eksame. Oppgave a Det er tilpasset e multippel lieær regresjosmodell av forme β 0 + β x i
Løsningsforslag Oppgave 1
 Løsigsforslag Oppgave 1 a X i µ 0 σ X i µ 0 2 σ 2, i 1,..., er uavhegige og stadard N0, 1 fordelte. Da er, i 1,..., uavhegige og χ 2 -fordelte med e frihetsgrad. Da er summe χ 2 -fordelt med atall frihetsgrader
Løsigsforslag Oppgave 1 a X i µ 0 σ X i µ 0 2 σ 2, i 1,..., er uavhegige og stadard N0, 1 fordelte. Da er, i 1,..., uavhegige og χ 2 -fordelte med e frihetsgrad. Da er summe χ 2 -fordelt med atall frihetsgrader
ÅMA110 Sannsynlighetsregning med statistikk, våren 2011
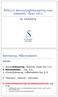 ÅMA110 asylighetsregig med statistikk våre 011 Kp. 5 Estimerig 1 Estimerig. Målemodelle. Ihold: 1. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp.
ÅMA110 asylighetsregig med statistikk våre 011 Kp. 5 Estimerig 1 Estimerig. Målemodelle. Ihold: 1. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp.
Oppgave 1 Hardheten til en bestemt legering er undersøkt med åtte målinger og resultatene ble (i kg/mm 2 ) som i tabellen til høyre.
 EKSAMEN I: ÅMA110 SANNSYNLIGHETSREGNING MED STATISTIKK VARIGHET: 4 TIMER DATO: 28. AUGUST 2010 BOKMÅL TILLATTE HJELPEMIDLER: KALKULATOR: HP30S, Casio FX82 eller TI-30 OPPGAVESETTET BESTÅR AV 3 OPPGAVER
EKSAMEN I: ÅMA110 SANNSYNLIGHETSREGNING MED STATISTIKK VARIGHET: 4 TIMER DATO: 28. AUGUST 2010 BOKMÅL TILLATTE HJELPEMIDLER: KALKULATOR: HP30S, Casio FX82 eller TI-30 OPPGAVESETTET BESTÅR AV 3 OPPGAVER
Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte
 Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 29. mai 2007
 Høgskole Telemark Avdelg for estetske fag, folkekultur og lærerutdag BOKMÅL 9. ma 7 EKSAMEN I MATEMATIKK, Modul 5 studepoeg Td: 5 tmer Hjelpemdler: Kalkulator og vedlagt formelsamlg (bakerst oppgavesettet).
Høgskole Telemark Avdelg for estetske fag, folkekultur og lærerutdag BOKMÅL 9. ma 7 EKSAMEN I MATEMATIKK, Modul 5 studepoeg Td: 5 tmer Hjelpemdler: Kalkulator og vedlagt formelsamlg (bakerst oppgavesettet).
TMA4245 Statistikk Vår 2015
 TMA4245 Statistikk Vår 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II Oppgave 1 Kari har ylig kjøpt seg e y bil. Nå øsker hu å udersøke biles besiforbruk
TMA4245 Statistikk Vår 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II Oppgave 1 Kari har ylig kjøpt seg e y bil. Nå øsker hu å udersøke biles besiforbruk
TMA4240 Statistikk Høst 2015
 TMA4240 Statistikk Høst 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II I dee siste øvige fokuserer vi på lieær regresjo, der vi har kjete kovariater
TMA4240 Statistikk Høst 2015 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer 12, blokk II I dee siste øvige fokuserer vi på lieær regresjo, der vi har kjete kovariater
11,7 12,4 12,8 12,9 13,3.
 TMA4240 Statistikk Vår 2008 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b6 Oppgave 1 Eksame mai 2001, oppgave 1 av 4 Vi ser på kosetrasjoe av et giftstoff i havbue
TMA4240 Statistikk Vår 2008 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer b6 Oppgave 1 Eksame mai 2001, oppgave 1 av 4 Vi ser på kosetrasjoe av et giftstoff i havbue
Econ 2130 Forelesning uke 11 (HG)
 Eco 130 Forelesig uke 11 (HG) Mer om ormalfordelige og setralgreseteoremet Uke 1 1 Fra forrige gag ~ betyr er fordelt som. ~ N( µσ, ) E( ) = µ, og var( ) = σ Normalfordelige er symmetrisk om μ og kotiuerlig
Eco 130 Forelesig uke 11 (HG) Mer om ormalfordelige og setralgreseteoremet Uke 1 1 Fra forrige gag ~ betyr er fordelt som. ~ N( µσ, ) E( ) = µ, og var( ) = σ Normalfordelige er symmetrisk om μ og kotiuerlig
TMA4245 Statistikk Eksamen 9. desember 2013
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA4245 Statistikk Eksame 9. desember 2013 Oppgave 1 I kortspillet Blackjack får ma de høyeste geviste hvis de to første kortee ma
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag TMA4245 Statistikk Eksame 9. desember 2013 Oppgave 1 I kortspillet Blackjack får ma de høyeste geviste hvis de to første kortee ma
Løsningsforsalg til første sett med obligatoriske oppgaver i STK1110 høsten 2015
 Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2015 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
Løsigsforsalg til første sett med obligatoriske oppgaver i STK1110 høste 2015 Oppgave 1 (a Et 100(1 α% kofidesitervall for forvetigsverdie µ er gitt ved formel (8.15 på side 403 i læreboka. For situasjoe
n 2 +1) hvis n er et partall.
 TMA445 Statistikk Vår 04 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Oppgave Mediae til et datasett, X, er de midterste verdie. Hvis vi har stokastiske
TMA445 Statistikk Vår 04 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Øvig ummer, blokk II Oppgave Mediae til et datasett, X, er de midterste verdie. Hvis vi har stokastiske
TMA4240 Statistikk Høst 2016
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 8 Løsigsskisse Oppgave 1 a) Simuler 1000 datasett i MATLAB. Hvert datasett skal bestå av 100 utfall fra e ormalfordelig
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalt øvig 8 Løsigsskisse Oppgave 1 a) Simuler 1000 datasett i MATLAB. Hvert datasett skal bestå av 100 utfall fra e ormalfordelig
ST0202 Statistikk for samfunnsvitere Kapittel 9: Inferens om én populasjon
 ST0202 Statistikk for samfunnsvitere Kapittel 9: Inferens om én populasjon Bo Lindqvist Institutt for matematiske fag 2 Kap. 9: Inferens om én populasjon Statistisk inferens har som mål å tolke/analysere
ST0202 Statistikk for samfunnsvitere Kapittel 9: Inferens om én populasjon Bo Lindqvist Institutt for matematiske fag 2 Kap. 9: Inferens om én populasjon Statistisk inferens har som mål å tolke/analysere
Kort repetisjon fra kapittel 4. Oppsummering kapittel ST0202 Statistikk for samfunnsvitere. Betinget sannsynlighet og trediagram
 2 Kort reetisjo fra kaittel 4 Betiget sasylighet og trediagram Eksemel: Fra e oulasjo av idrettsfolk trekkes e erso tilfeldig og testes for doig. De iteressate hedelsee er D=ersoe er doet, A=teste er ositiv.
2 Kort reetisjo fra kaittel 4 Betiget sasylighet og trediagram Eksemel: Fra e oulasjo av idrettsfolk trekkes e erso tilfeldig og testes for doig. De iteressate hedelsee er D=ersoe er doet, A=teste er ositiv.
Emnenavn: Metode 1, statistikk deleksamen. Eksamenstid: 4 timer. Faglærer: Bjørnar Karlsen Kivedal
 EKSAMEN Emekode: SFB10711 Emeav: Metode 1, statistikk deleksame Dato: 10. oktober 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Bjørar Karlse Kivedal
EKSAMEN Emekode: SFB10711 Emeav: Metode 1, statistikk deleksame Dato: 10. oktober 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Bjørar Karlse Kivedal
Oppgave 1 a) Minste kvadraters metode tilpasser en linje til punktene ved å velge den linja som minimerer kvadratsummen. x i (y i α βx i ) = 0, SSE =
 Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 2, blokk II Løsigsskisse Oppgave a Miste kvadraters metode tilpasser e lije til puktee ved å velge de lija som
Norges tekisk-aturviteskapelige uiversitet Istitutt for matematiske fag Abefalte oppgaver 2, blokk II Løsigsskisse Oppgave a Miste kvadraters metode tilpasser e lije til puktee ved å velge de lija som
Oversikt over konfidensintervall i Econ 2130
 HG April 00 Oversikt over kofidesitervall i Eco 30 Merk at dee oversikte ikke er met å leses istedefor framstillige i Løvås, me som et supplemet. Løvås ieholder mage verdifulle kommetarer og eksempler.
HG April 00 Oversikt over kofidesitervall i Eco 30 Merk at dee oversikte ikke er met å leses istedefor framstillige i Løvås, me som et supplemet. Løvås ieholder mage verdifulle kommetarer og eksempler.
Løsning TALM1005 (statistikkdel) juni 2017
 Løsig TALM1005 statistikkdel jui 2017 Oppgave 1 a Har oppgitt at sasyligte for at é harddisk svikter er p = 0, 037. Ifører hedelsee A : harddisk 1 svikter B : harddisk 2 svikter C : harddisk 3 svikter
Løsig TALM1005 statistikkdel jui 2017 Oppgave 1 a Har oppgitt at sasyligte for at é harddisk svikter er p = 0, 037. Ifører hedelsee A : harddisk 1 svikter B : harddisk 2 svikter C : harddisk 3 svikter
Løsningsforslag ST1101/ST6101 kontinuasjonseksamen 2018
 Løsigsforslag ST/ST6 kotiuasjoseksame Oppgave a Defier hedelsee R, B, B rød kule i første trekig, blå kule i adre trekig, blå kule i tredje trekig. Vi skal fie PR B B for to ulike situasjoer. Geerelt vet
Løsigsforslag ST/ST6 kotiuasjoseksame Oppgave a Defier hedelsee R, B, B rød kule i første trekig, blå kule i adre trekig, blå kule i tredje trekig. Vi skal fie PR B B for to ulike situasjoer. Geerelt vet
ÅMA110 Sannsynlighetsregning med statistikk, våren 2007
 ÅMA0 Sasylighetsregig med statistikk, våre 007 Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett
ÅMA0 Sasylighetsregig med statistikk, våre 007 Kp. 4 Kotiuerlige tilfeldige variable; Normalfordelig Kotiuerlige tilfeldige variable, itro. (eller: Kotiuerlige sasylighetsfordeliger) Vi har til å sett
Kapittel 7: Noen viktige sannsynlighetsfordelinger
 Kapittel 7: Noe viktige sasylighetsfordeliger I mage situasjoer ka feomeet vi ser på beskrives med e bestemt type sasylighetsfordelig e sasylighetsfordelig gitt ved e bestemt formel. Vi skal se på oe av
Kapittel 7: Noe viktige sasylighetsfordeliger I mage situasjoer ka feomeet vi ser på beskrives med e bestemt type sasylighetsfordelig e sasylighetsfordelig gitt ved e bestemt formel. Vi skal se på oe av
