FFI RAPPORT INTEGRERING AV TREGHETSNAVIGASJON I EN AUTONOM UNDERVANNSFARKOST. Gade Kenneth FFI/RAPPORT-97/03179
|
|
|
- Sverre Ask
- 5 år siden
- Visninger:
Transkript
1 FFI RAPPORT INTEGRERING AV TREGHETSNAVIGASJON I EN AUTONOM UNDERVANNSFARKOST Gade Kenneth FFI/RAPPORT-97/3179
2
3 INTEGRERING AV TREGHETSNAVIGASJON I EN AUTONOM UNDERVANNSFARKOST Gade Kenneth FFI/RAPPORT-97/3179 FORSVARETS FORSKNINGSINSTITUTT Norwegian Defence Research Establishment Postbos 25, 227 Kjeller, Norge
4
5 2a FORSVARETS FORSKNINGSINSTITUTT (FFI) Norwegian Defence Research Establishment UNCASSIFIED P O OX 25 NO-227 KJEER, NORWAY REPORT DOCUMENTATION PAGE SECURITY CASSIFICATION OF THIS PAGE (when data entered) 1) PU/REPORT NUMER 2) SECURITY CASSIFICATION 3) NUMER OF FFI/RAPPORT-97/3179 UNCASSIFIED PAGES 1a) PROJECT REFERENCE 2a) DECASSIFICATION/DOWNGRADING SCHEDUE 157 FFIE/71/ ) TITE INTEGRERING AV TREGHETSNAVIGASJON I EN AUTONOM UNDERVANNSFARKOST DESIGN OF AN INTEGRATED STRAPDOWN INS FOR AN AUTONOMOUS UNDERWATER VEHICE 5) NAMES OF AUTHOR(S) IN FU (surname first) GADE Kenneth 6) DISTRIUTION STATEMENT Approved for public release. Distribution unlimited. (Offentlig tilgjengelig) 7) INDEXING TERMS IN ENGISH: IN NORWEGIAN: a) Inertial navigation a) Treghetsnavigasjon b) Integrated navigation system b) Integrert navigasjonssystem c) Sensor error modelling c) Modellering av sensorfeil d) Kalman filter d) Kalmanfilter e) Autonomous underwater vehicle (AUV) e) Autonom undervannsfarost THESAURUS REFERENCE: 8) ASTRACT The purpose of this wor has been to design an integrated strapdown inertial navigation system for FFI's autonomous underwater vehicle HUGIN. The integrated navigation system is implemented as a Kalman filter estimating the velocity, attitude and position based on measurements from the following sensors/systems: Inertial navigation system based on a strapdown inertial measurement unit (IMU) located in the AUV. This IMU has three gyros and three accelerometers. HPR (Hydro-acoustic Position Reference) and GPS. A surface-vessel following HUGIN measures the AUVposition by means of GPS and HPR. Doppler velocity log mounted on the AUV. This sensor measures the velocity relative to the sea floor. The Kalman filter was implemented and tested in simulations. The simulations showed that the accuracy in the roll and pitch estimates were between.2 and.6. The estimated yaw angle accuracy was approximately.25 at a depth of 1 meters and a velocity of 2.1 m/s. At this depth and velocity the uncertainty in the position estimate was approximately.5 m in the speed direction and 5 m in the crosswise direction 9) DATE AUTHORIZED Y POSITION This page only 28 July 1997 Paul Narum Director of Research UNCASSIFIED ISN SECURITY CASSIFICATION OF THIS PAGE (when data entered) FFI
6 2b
7 3 INNHOD Side 1 INNEDNING 7 2 MATEMATISK AKGRUNN Definisjoner og notasjon Nyttige sammenhenger Rotasjonsmatrise Rotasjonsmatrise og vinelhastighet Similaritetstransformasjonen Enel tidsderivasjon i ulie oordinatsystemer Dobbel tidsderivasjon i ulie oordinatsystemer Rotasjonsmatrisen ved små rotasjoner Tilnærmet rotasjonsmatrise 17 3 TREGHETSNAVIGASJON Terrestris navigasjon Gravitasjonsraft Andre effeter Gyroompensasjon pga rotasjonen oalt oordinatsystem Navigasjonsligningene i ved srogfast sensormontering Initialisering Oppsummering av de oordinatsystemer som er brut Treghetssensorer Generelle sensorfeil Aselerometre Gyroer Feilutviling ved srogfast sensormontering 39 4 SYSTEMESKRIVESE AUV Treghetssensorenhet Feilmodell for gyromåling Feilmodell for aselerometermåling Disretisering av måleligningene Hydro-austis posisjonering Feilmodell Dopplerlogg Feilmodell Dybdemåler Feilmodell 71
8 4 5 DESIGN AV KAMANFITER Kalmanfilter Design Forenlinger av feilutvilingen Systeminformasjon på tilstandsromform Disretisering av prosessligning Endelig filter Vurdering av tilstander 88 6 SIMUERINGER Simulator Simulering AUVens bevegelse Resultater Simulering AUVens bevegelse Resultater Simulering 3 til Alternativ treghetssensorenhet AUVens bevegelse Resultater 19 7 DISKUSJON OG KONKUSJON Simulering Orienteringsfeil Hastighetsfeil Posisjonsfeil Gyrofeil Aselerometerfeil HPR-feil Simulering Orienteringsfeil Hastighetsfeil Posisjonsfeil Gyrofeil Aselerometerfeil HPR-feil Simulering 3 til Konlusjon Videre arbeid 123 itteratur 123
9 5 APPENDIKS 125 A DIVERSE 125 A.1 Notasjon 125 A.2 Variansen til en første ordens Marovprosess 126 A.3 Forlaring av forløp på figur 6.8 (graf 1 og 2) 127 PROGRAMISTINGER Hovedprogram Funsjoner 135 Fordelingsliste 157
10 6
11 7 INTEGRERING AV TREGHETSNAVIGASJON I EN AUTONOM UNDER- VANNSFARKOST 1 INNEDNING HUGIN er et prosjet der FFI i samarbeid med Simrad utviler en autonom undervannsfarost (eng: Autonomous Underwater Vehicle, AUV) til artleggingsformål. Kartleggingen foregår ved at AUVen tar bilder av havbunnen ved hjelp av en multistrålesonar. I denne oppgaven sal det undersøes hvordan en treghetssensorenhet 1 bør ombineres med AUVens øvrige sensorutrustning for å få et best mulig løpende estimat av posisjon, hastighet og orientering. Rapportens disposisjon I apittel 2 presenteres den vitigste notasjonen og relevant matematis teori. Kapittel 3 gir en generell innføring i det teoretise grunnlaget for treghetsnavigasjon og en utledning av navigasjonsligningene. Videre blir de ulie prinsipper som brues i treghetssensorer presentert. Til slutt utledes formler for feilutvilingen i navigasjonsligningene. En besrivelse av sensorene og en modellering av feil i disse er å finne i apittel 4. I apittel 5 designes et filter for integrasjon av treghetsnavigasjon med de øvrige sensorer. Det er også laget en simulator for å teste filteret, og denne blir presentert i apittel 6 sammen med de vitigste simuleringsresultatene. Kapittel 7 gir en disusjon basert på simuleringsresultatene og munner ut i en onlusjon. Hva er nytt i apitlet om treghetsnavigasjon? Det finnes mye litteratur som omhandler treghetsnavigasjon (f es ritting (1971), Fossen (1996) og Savage (1991)), og det an derfor være på sin plass å nevne noe av det som er annerledes her. For det første er det innført en entydig notasjon for bl a posisjon, hastighet og aselerasjon, hvor et subsript angir størrelsens relasjoner 2 til de atuelle oordinatsystemer. Dessuten har en utvidet bru og tolning av feilvetorer 3 gitt enlere utledninger av feilutvilingen og vært avgjørende for design av Kalmanfilteret og forståelse av feildynamien. 1. Enhet som inneholder flere gyroer og aselerometre. 2. For esempel vil en aselerasjons subsript fortelle hva som aselererer og i forhold til hvilet oordinatsystem. 3. Det vil si vetorer som uttryer en feil/sjevhet i en rotasjonsmatrise.
12 8 2 MATEMATISK AKGRUNN 2.1 Definisjoner og notasjon Først defineres noen fundamentale begrep som notasjonen sal nyttes til: Punt: Definerer en posisjon i rommet. Vetor: Definerer lengde og retning i rommet. Symboliseres med pil over vetornavnet. Ved i tillegg å innføre tid, har en det begrepsgrunnlaget som er nødvendig, og som det senere an nyttes tallverdier til. Et oordinatsystem an nå defineres som en mengde vetorer med en definert reefølge og et punt. Puntet definerer posisjonen til origo, mens vetorene definerer retningen til og saleringen langs asene. Ved hjelp av et oordinatsystem an man uttrye alle vetorer som ligger i det rommet asene utspenner som en lineærombinasjon av asene. Hvis vi f es har oordinatsystemet A, med tre lineært uavhengige aser x A, y A og z A, an en vilårlig vetor som ligger i det tredimensjonale rom uttryes som: = a 1 x A + a 2 y A + a 3 z A (2.1) hvor a i, i { 123,, } er salare tallverdier. Vetoren an også uttryes som: a 1 A = (2.2) a 2 a 3 hvor omponentenes reefølge samsvarer med asenes reefølge, og supersriptet sier hvilet oordinatsystems aser lineærombinasjonen er bygget opp av. En vetor som representeres på denne måten sies å være deomponert eller projisert ned i det atuelle oordinatsystemet, og alles da oordinatvetor. Venstre supersript brues på derivasjonsoperatoren ved tidsderivasjon av en generell (oordinatfri) vetor for å vise hvilet system det er derivert i forhold til. Ved tidsderivasjon av en oordinatvetor er det underforstått at hvert enelt element deriveres for seg, noe som følgelig tilsvarer tidsderivasjon i forhold til oordinatsystemet vetoren er deomponert i. (Dette fatum resulterer i (2.3).) Hvis ie annet er sagt, betrates de størrelser som innføres som deterministise, tidsvariante størrelser. Der det er nødvendig, vises tidsavhengigheten esplisitt.
13 9 Symbolene som betegner ulie relasjoner mellom to oordinatsystemer, er definert i tabell 2.1 for to vilårlige oordinatsystemer, A og. Symbol Definisjon esrivelse p A v A a A (Defineres ved sin besrivelse) A d ---- ( p A ) dt A d ---- ( v A ) dt En vetor som har lengde og retning sli at den går fra origo i oordinatsystem A til origo i oordinatsystem. Hastigheten til origo i oordinatsystem i forhold til oordinatsystem A. Aselerasjonen til origo i oordinatsystem i forhold til oordinatsystem A. ω A Se ligning (2.22) Vinelhastigheten til oordinatsystem i forhold til oordinatsystem A. r A pa Avstanden mellom origo i oordinatsystem A og. R A (Defineres ved sin besrivelse) Denne matrisen betegnes rotasjonsmatrise, og an brues og besrives på to forsjellige måter: Koordinattransformasjon: Ved å premultiplisere en vetor deomponert i oordinatsystem med denne matrisen, får vi den samme vetoren deomponert i A. A Rˆ Se ligning (2.46) Rotasjon: Ved å premultiplisere en vetor deomponert A med denne matrisen, får vi en ny vetor deomponert i A, som er rotert på en sli måte at den får samme oordinatrepresentasjon i som den hadde i A før rotasjonen ( rotasjon fra A til ). Denne matrisen besriver dermed entydig orienteringen til oordinatsystem i forhold til A. En rotasjonsmatrise som roterer/transformerer omtrent som R A. (Vanligvis er dette en beregnet versjon av den virelige R A.) e A Se ligning (2.52) A Vetor som besriver forsjellen mellom Rˆ og R A, (som vanligvis an toles som feilen i Rˆ A ). Deomponert består den av tre små feilvinler. Tabell 2.1 Notasjon som brues for å betegne relasjoner mellom to vilårlige oordinatsystemer A og.
14 1 Det an med en gang være verdt å mere seg at C v A C p A (2.3) Grunnen til dette er altså at til høyre i (2.3) står vetoren C d ---- ( p A ) (deomponert i dt C) som jo generelt ie er li vetoren v A. Tilsvarende vil selvsagt gjelde for aselerasjon. Alle oordinatsystemer som innføres er bygget opp av tre ortogonale vetorer med lengde én og med en reefølge x, y, z som følger høyrehåndsregelen. De ulie oordinatsystemer blir definert etter hvert som det blir bru for dem, en oppsummering finnes i tabell 3.1, side Nyttige sammenhenger I dette underapitlet blir det utledet noen matematise sammenhenger som det vil bli bru for senere Rotasjonsmatrise Utgangspuntet er to vilårlige oordinatsystemer med uli orientering. Det vil da alltid være mulig å besrive deres relative orientering som en rotasjon om en ase λ. Vinelen det roteres alles β og fortegnet er gitt av høyrehåndsregelen. Da det un er retningen til λ som er av interesse, defineres denne vetoren til å ha lengde en: λ = Δ 1 (2.4) En rotasjon i det tredimensjonale rom an derfor defineres entydig med tre parametre. Det sal nå utledes et uttry for rotasjonsmatrisen, og det tas da utgangspunt i to oordinatsystemer, A og, som begge har sin z-ase parallell med λ, men ellers er vilårlige. En vetor 1 roteres fra A til og heter 2 etter rotasjonen (dvs 1 A Dette gir: = 2 ). 1 = a 1 x A + a 2 y A + a 3 λ 2 = a 1 x + a 2 y + a 3 λ (2.5)
15 11 og: x = x A cosβ + y A sinβ y = x A sinβ + y A cosβ (2.6) Vi får dermed at: 2 = a 1 x A cosβ + a 1 y A sinβ a 2 x A sinβ + a 2 y A cosβ + a 3 λ = cosβ( a 1 x A + a 2 y A + a 3 λ) + sinβ( a 1 y A a 2 x A ) + a 3 λ( 1 cosβ) (2.7) Da vi har at 1 srive (2.7) som: λ = a 3 ( betegner salarprodut) og λ 1 = a 1 y A a 2 x A, an vi 2 = cosβ( 1 ) + sinβ( λ 1 ) + ( 1 cosβ)λ( λ 1 ) (2.8) Ved å fatorisere ut 1 på høyre side vil uttryet som 1 er multiplisert med være en dyade. Denne dyaden roterer da oordinatfrie vetorer en vinel β om λ. En dyade an deomponeres i et vilårlig oordinatsystem, f es C, og vi får da en rotasjonsmatrise som roterer vetorer deomponert i C på den besrevne måte. Dyader sal ie behandles i dette arbeidet, vi sal un finne rotasjonsmatrisen. Dette gjøres ved å deomponere (2.8) i oordinatsystem C. Vi får altså: 2 C C cosβ( 1 ) sinβ λ C C ( 1 ) ( 1 cosβ)λ C ( λ C ) T C = (2.9) Dette blir videre: 2 C ( cosβ I + sinβ S( λ C ) + ( 1 cosβ)λ C ( λ C ) T C = ) 1 (2.1) hvor S( ) er ryssprodutoperatoren (gitt i (2.22) på omponentform). Vi an nå definere: A ( R ) C cosβ I + sinβ S( λ C ) + ( 1 cosβ)λ C ( λ C ) T = Δ (2.11) A ( R ) C er altså rotasjonsmatrisen som roterer vetorer deomponert i C en vinel β om λ. Da det i dette arbeidet vanligvis vil bli rotert vetorer gitt i A eller, definerer vi: R A Δ = = A ( R ) A A R ( ) (2.12) Grunnen til at de to siste er lie er jo at λ er rotasjonsasen, og derfor har vi at: λ A = λ (2.13)
16 12 Det an nevnes at R A også an brues på en vetor deomponert i det vilårlige oordinatsystemet C. Da vil den imidlertid generelt ie rotere om λ, men derimot om en ase bestemt av oordinatsystem C. For esempel vil cosβ sinβ sinβ cosβ 1 rotere en vinel β om z-asen til C. En rotasjonsmatrise har dermed, i motsetning til en rotasjonsdyade, ingen informasjon om retninger i rommet når den brues på denne måten. Denne måten å brue en rotasjonsmatrise på, gir opphav til alternative formuleringer av en generell rotasjonsmatrise som en sevens av enle rotasjoner. Alternativ formulering 1 En generell rotasjonsmatrise R A, an besrives på følgende måte: Først roteres oordinatsystem A en vinel α A, x rundt sin egen x-ase, deretter en vinel α A, y rundt sin nye y-ase og til slutt en vinel α A, z rundt sin nyeste z-ase. Koordinatsystemet vi har fått etter alle rotasjonene er altså, og vi an dermed uttrye rotasjonsmatrisen som: R A = 1 cα x sα x sα x cα x cα y sα y 1 sα y cα y cα z sα z sα z cα z 1 (2.14) = cα y cα z cα y sα z sα y sα x sα y cα z + cα x sα z sα x sα y sα z + cα x cα z sα x cα y cα x sα y cα z + sα x sα z cα x sα y sα z + sα x cα z cα x cα y hvor α i = α A, i og c( )=cos( ) og s( )=sin( ). De tre parameterne gir altså en entydig representasjon av R A (når det er underforstått at vi roterer som besrevet), og disse an samles til en orienterings vetor som an srives: θ A = Δ α A, x α A, y α A, z (2.15) Det er imidlertid vitig å mere seg at dette ie er noen fysis vetor som er deomponert, men un en gruppe tall som det matematis er hensitsmessig å håndtere samlet.
17 13 Alternativ formulering 2 Vi an lage en ny alternativ formulering ved å rotere i reefølgen z, y, x i stedet for x, y, z. esrivelsen av R A blir da: Først roteres oordinatsystem A en vinel α A, z rundt sin egen z-ase, deretter en vinel α A, y rundt sin nye y-ase og til slutt en vinel α A, x rundt sin nyeste x-ase. Vi får dermed: R A = = cα z sα z sα z cα z 1 cα y sα y 1 sα y cα y 1 cα x sα x sα x cα x cα z cα y sα z cα x + cα z sα y sα x sα z sα x + cα z sα y cα x sα z cα y cα z cα x + sα z sα y sα x cαzsα x + sα z sα y cα x sα y cα y sα x cα y cα x (2.16) hvor α i = α A, i og c( )=cos( ) og s( )=sin( ). Vetoren som besriver R A som rotasjon om nye aser i reefølgen z, y, x betegnes: * θ A = Δ α A, x α A, y α A, z (2.17) Rotasjonsmatrise og vinelhastighet Orienteringen til oordinatsystem i forhold til A an altså representeres med R A, mens vinelhastigheten til i forhold til A er ω A. Det er dermed lart at endringen i R A må være funsjon av ω A. Denne sammenhengen vil det ofte bli bru for og sal nå utledes, noe som gjøres ved hjelp av selve definisjonen på vinelhastighet:
18 14 Fordi alle rotasjonsmatriser mellom våre oordinatsystemer er ortogonale vil følgende gjelde for R A : A ( R ) T A R = I (2.18) Da vi er interessert i endring av rotasjonsmatrisen med hensyn på tiden, tidsderiverer vi og får: A ( R ) T A R A A A + R R ( ) T R Hvis vi nå definerer: A A (( ) T R ) T A = + ( R ) T R = (2.19) S Δ = A ( R ) T A R (2.2) ser vi at S har følgende egensap: S T + S = (2.21) og dermed er sjevsymmetris. Fordi S er sjevsymmetris finnes det en oordinat- vetor ω A = [ ω 1, ω 2, ω 3 ] T som oppfyller følgende: S( ω A ) ω 3 ω 2 = ω 3 ω (2.22) 1 ω 2 ω 1 Denne vetoren er per definisjon vinelhastigheten til vetorer som dreies av rotasjonsmatrisen. Ved å premultiplisere (2.2) med R A får vi: A R = R A S( ω A ) (2.23) Vi har dermed fått sammenhengen vi var ute etter (med ω A deomponert i ) Similaritetstransformasjonen Det sal her vises hvordan en vetor som er argument i ryssprodutoperatoren an transformeres mellom ulie oordinatsystemer. Vi tar utgangspunt i den generelle vetoren: 1 = 2 (2.24) Denne an deomponeres i de vilårlige oordinatsystemene A og, altså: 1 A = = (2.25) A A 2 eller 1 2
19 15 Ved å oordinattransformere 1 til A får vi: A A 2 R A 2 eller evivalent: S ( A A ) 2 = ( ) (2.26) R A S ( = ) 2 (2.27) Hvis vi erstatter 2 med 2 A transformert til, får vi: S ( A A ) 2 R A S ( )R A = A 2 (2.28) Dette gjelder altså for alle 2 A og vi har dermed: S ( A ) R A S ( = )R A (2.29) Denne sammenhengen blir ofte alt similaritetstransformasjonen Enel tidsderivasjon i ulie oordinatsystemer En annen nyttig formel er sammenhengen mellom den tidsderiverte av en vilårlig vetor i to ulie oordinatsystemer: Vi tar utgangspunt i: A = R A (2.3) Tidsderivasjon av dette gir: A R A R A = + (2.31) Ved å brue (2.23), fås: A R A S( ω A ) R A = + (2.32) som gir: A R A S( ω A ) ( + ) R A = = ( + ω A ) (2.33) På oordinatfri form blir dette: A d ---- ( ) dt d = ---- ( ) + ω A (2.34) dt
20 16 Dette resultatet illustrerer det fatum at vetorer ie har posisjon. Den tidsderiverte av er jo identis i to systemer som un har lineær hastighet og aselerasjon i forhold til hverandre. Hvis systemene derimot endrer sin relative orientering ( ω A ) vil dette fanges opp av en vetor, og den deriverte blir ie li i de to systemene. (Vi ville også fått et tilleggsledd om systemene endret sin relative salering.) Dobbel tidsderivasjon i ulie oordinatsystemer Det an også være nyttig å se på sammenhengen mellom den dobbeltderiverte i to vilårlige oordinatsystemer: Derivasjon av (2.33) med hensyn på tiden gir: A A R S( ω A ) ( + ) R A S( ω A) = + ( + S( ω A ) + ) (2.35) ru av (2.23) gir: A R A S( ω A ) S( ω A ) ( + ) S( ω A) = + + S( ω A ) + (2.36) Dette an forenles til: A R A S( ω A )S( ω A ) S( ω A) + + 2S( ω A ) + = (2.37) eller eventuelt: A R A ω A ( ω A ) ω A = ( ω A ) (2.38) På oordinatfri form blir dette: A d ( ) = dt 2 d 2 d ( ) ω dt 2 A ( ω A ) ---- ( ω A ) d + + dt + 2ω A ---- ( ) dt (2.39) Dette er altså sammenhengen mellom den dobbelt tidsderiverte av en generell vetor i to vilårlige oordinatsystemer Rotasjonsmatrisen ved små rotasjoner Det sal her gjøres en første ordens tilnærmelse av rotasjonsmatrisen ved små rotasjoner. Dette an finnes ved å ta utgangspunt i (2.11). Vi har også at: β 5 β 7 sinβ = β ---- β ! 5! 7! β 4 β 6 β cosβ = ! 4! 6! (2.4)
21 17 En første ordens tilnærmelse vil altså være å sette sinβ = β og cosβ = 1. Ved å brue (2.11) og (2.12) får vi da følgende tilnærmede uttry for R A : R A I + βs( λ A ) = I + βs( λ ) (2.41) For å forstå dette uttryet an vi gjøre tilsvarende tilnærmelse av en av de alternative formuleringene av rotasjonsmatrisen 1, ligning (2.14) eller (2.16), som gir: R A 1 α A, z α A, y α A, z 1 α A, x α A, y α A, x 1 (2.42) Vi har dermed at: α A, x βλ A = βλ = (2.43) α A, y α A, z Vi definerer nå: α A = Δ βλ (2.44) α A vil altså generelt betegne vetoren som deomponert i A eller er bestående av små vinler som tilsvarer rotasjonsmatrisen R A. Vetoren vil ligge langs rotasjonsasen, og ha en lengde li vinelen det roteres. Sammenhengen mellom matrisen og vetoren (som un gjelder ved små vinler) er gitt av: R A A I + S( α A ) = I + S( α A ) (2.45) A En an til slutt mere seg at α A = α A un gjelder fordi α A ligger langs rotasjonsasen. Tilnærmelsen A = for en generell vetor, vil være av nullte orden (dvs ha en feil proporsjonal med β.) Tilnærmet rotasjonsmatrise En rotasjonsmatrise som er omtrent li R A A, an betegnes Rˆ. Vi an uttrye denne som: A Rˆ R A' A R ' = = (2.46) 1. Det er liegyldig hvilen av dem som brues fordi rotasjonsreefølgen med små vinler er vilårlig ved første ordens tilnærming.
22 18 hvor A' ligger litt sjevt i forhold til A, og ' ligger tilsvarende sjevt i forhold til. Vi an videre uttrye disse som: R A' A R ' = = R A A' R A R A R ' (2.47) Ved å brue (2.45) an vi dermed sette opp følgende første ordens tilnærmelser: R A A' R ' A' I + S( α A'A ) = I + S( α A'A ) I + S( α ' ) = I + S( α ' ) A ' (2.48) A åde α A'A og α ' A uttryer altså feilen i Rˆ, men de er referert til hvert sitt oordinatsystem. Det er nå nærliggende å tro at dette må være den samme vetoren, bare deomponert i hvert sitt oordinatsystem. At det fatis er sli an vises ved å ombinere (2.46) og (2.47), som gir: R A A' R A R A = R ' (2.49) ru av (2.48) gir: A A ( I + S( α A'A ))R = R A ( I + S( α ' )) (2.5) Ved å benytte similaritetstransformasjonen er det dermed lart at: α A'A = α ' (2.51) A Denne vetoren gir altså en besrivelse av sjevheten/feilen til Rˆ og betegnes heretter e A, altså: (i forhold til R A ), Δ e A = α A'A = α ' (2.52) Til slutt an resultatene i dette underapitlet oppsummeres som: A Rˆ A A ( I + Se ( A ))R R A = ( I + Se ( A )) (2.53) 3 TREGHETSNAVIGASJON Treghet er tradisjonelt betegnelsen på det fenomenet at masse motsetter seg endring i sin hastighetsvetor, det være seg retning eller lengde. Det reves altså en raft for å endre denne vetoren, og denne an uttryes ved Newtons 2. lov (antar onstant masse): F = ma IP (3.1)
23 19 hvor m er størrelsen på massen og a IP er den resulterende aselerasjon. P er her et oordinatsystem som er festet til massen og I er et inertielt 1 oordinatsystem uten gravitasjon. Navigasjon besriver bl a det at man ønser å finne sin posisjon i forhold til et hensitsmessig oordinatsystem. Vi antar i første omgang at dette systemet er I. I treghetsnavigasjon sal man altså finne sin posisjon ved å benytte treghetsprinsippet. Dette an gjøres ved å måle raften en jent (onstant) masse utsettes for, og dermed an aselerasjonen til massen regnes ut. En sli masse an monteres i referansepuntet 2 til farosten som sal navigeres, og farosten vil da (ideelt) ha samme aselerasjon som massen. Aselerasjonen an integreres opp en gang, og vil da (sammen med en initialverdi) gi hastighet. Denne an igjen integreres opp til å gi posisjon i forhold til I. For detaljer om initialisering, se underapittel I prasis vil et instrument som måler aselerasjon, et aselerometer, un måle aselerasjon i én retning i rommet, denne retningen alles aselerometrets monteringsase. Det er dermed a IP sin omponent langs monteringsasen som måles. For å måle hele a IP trengs derfor minst tre aselerometre montert i tre lineært uavhengige retninger i rommet. Det antas nå at det brues tre aselerometre montert perfet ortogonalt, rett ved referansepuntet. Koordinatsystem P defineres herved til å ha origo i referansepuntet og asene parallelt med monteringsasene til aselerometrene. Dermed er det lart at aselerometrene i tallverdi vil måle a P I IP. Det vi trenger er imidlertid a IP I an integreres opp til å gi p IP. Vi må derfor ha informasjon om orienteringen til P i forhold til I. Denne an finnes på litt ulie måter avhengig av hvordan P er realisert i farosten: Srogfast aselerometermontering (strapdown system) Det defineres et oordinatsystem, som er festet til fartøyet (eng. body-fixed), med origo i fartøyets referansepunt. x-asen peer framover i fartøyet, y-asen mot styrbord og z-asen nedover. Hvis aselerometrene er montert direte på farosten, settes = P. (Vi unne vært mer generelle og sagt at aselerometrene var montert rotert men fast i forhold til P, og at var rotert, men fast i forhold til P. Dette ville øe omplesiteten uten å belyse noen nye effeter, og utelates derfor.) Hvis nå farosten endrer sin orientering i forhold til I, vil P være et lite hensitsmessig (ie-inertielt) oordinatsystem å oppgi posisjonen i. For å få posisjonen gitt i I må vi vite fartøyets orientering (i forhold til I). For å finne orienteringen an man brue gyroer montert direte på fartøyet. Disse finner vinel/vinelhastighet ved hjelp av treghetsegensaper til masse eller lys (se underapittel for en oversit over mulige prinsipper). De 1. Et inertielt eller Newtons system er et ie-aselerert system. (Newtons 2. lov gjelder un i et slit system.) 2. Referansepuntet er fartøyets origo, og dette definerer fartøyets posisjon. som
24 2 måler derfor vinelhastighet/vinel i forhold til I, altså ω I (hvis de måler vinelhastighet), som er nettopp det vi ønser. Målingen an gjøres ved hjelp av flere prinsipp, men uansett vil en enelt gyro som oftest måle vinelhastighetens projesjon langs én ase i rommet, monteringsasen. Det trengs derfor minst tre gyroer montert i tre lineært uavhengige retninger i rommet for å måle den totale vinelhastighet. Hvis monteringsasene sammenfaller med asene til, måles ω I. Denne an deretter integreres opp til R I ved å brue (2.23), og dermed har man fartøyets orientering. Kardans opphengt plattform (gimbal basert system) Man unne også tene seg en løsning der aselerometrene var montert på en ardans opphengt ( gimbalisert ) plattform som holdt sin orientering onstant i forhold til I. Man unne da holde orienteringen til P li I s orientering, og aselerometrene ville P måle a IP I = a IP. I så fall an man integrere opp direte to ganger for å få den ønsede posisjon gitt i I. Man må imidlertid også her ha gyroer, disse sal nemlig sørge for at plattformen virelig ie endrer sin orientering i forhold til I. Gyroene an også monteres på plattformen (sammenfallende med P), og måler dermed ω P IP. Hvis de da måler noe annet enn null vinelhastighet, tyder det på at plattformen har rotert i forhold til I, og den må da roteres på plass igjen. Plattformen an også tvinges til å ha en (lav) vinelhastighet, i de tilfeller der det er hensitsmessig. 3.1 Terrestris navigasjon Ved navigasjon i nærheten av jordas overflate er det ofte hensitsmessig å oppgi posisjonen i forhold til jorda (dvs i et jordfast oordinatsystem). Som et esempel an vi tene oss et oordinatsystem med origo i jordas geometrise sentrum, yz-planet sammenfallende med evatorplanet, y-asen peende mot 9 østlig lengdegrad og x- asen mot nord. Dette oordinatsystemet, som altså er festet til jorda, betegnes heretter som E. Oppgaven blir dermed å finne p EP ved hjelp av aselerometre og gyroer. Det sal nå gis en oversit over de hensyn som da må tas Gravitasjonsraft Ved terrestris navigasjon vil det alltid være et betydelig gravitasjonsfelt tilstede. Dette gir opphav til en raft på aselerometermassen, aurat som om massen hadde en aselerasjon i motsatt retning av raften. I følge Einsteins evivalensprinsipp er det ie teoretis mulig å sille dette fra en virelig aselerasjon (om man un har ett målepunt). Det an derfor hevdes at gravitasjon er aselerasjon. I dette arbeidet blir imidlertid gravitasjon og aselerasjon behandlet som to forsjellige fenomen. Vi
25 21 an derfor si at aselerometrene måler differansen mellom virelig aselerasjon og gravitasjon, og denne målingen an alles spesifi raft (raft på aselerometermassen dividert på massen): f IP = a IP g P (3.2) hvor gravitasjonsvetoren som gjelder ved origo i P, er definert som: g P = Δ F gravitasjon m (3.3) hvor F gravitasjon er den raften gravitasjonsfeltet gir opphav til på massen, m. For å finne a IP må vi derfor legge g P til målingen og det trengs følgelig en modell av gravitasjonen (som ie behøver å være bedre enn det aselerometernøyatigheten tilsier). Gravitasjonen varierer i sted (i forhold til jorda) pga jordas (tilnærmet) elliptise form og pga inhomogen massefordeling i jorda. Gravitasjonen varierer også i tid, først og fremst pga tidevannet, men også fordi gravitasjon fra sol og måne an være målbar. Andre himmellegemer gir ie målbar gravitasjon fordi de er så langt borte 1. Hvis vi jenner tiden og vår omtrentlige posisjon i forhold til jordoverflaten, er det i dag mulig å finne gravitasjonsvetoren med god nøyatighet, enten ved hjelp av tabelloppslag eller matematise funsjoner Andre effeter Siden jorda roterer vil ethvert punt på jordoverflaten (bortsett fra nord- og sydpolen) være aselerert (i forhold til I). Vi har altså at a EP forlaring på årsaene til dette, deretter bevises det matematis. a IP. Det blir først gitt en fysis Den fysise forlaringen tar utgangspunt i et forsø på å sette opp Newtons 2. lov i forhold til jorda (altså med a EP i stedet for a IP ): F ma EP Men da E ie er noe inertielt oordinatsystem må vi innføre noen tilleggsrefter som ser ut til å vire i E, såalte fitive refter: F (3.4) + ΣF fitiv = ma EP (3.5) Disse tilleggsreftene sal nå studeres litt nærmere: (Det er antatt at jorda og dermed E har onstant vinelhastighet i forhold til I.) 1. Gravitasjonsraften avtar jo omvendt-proporsjonalt med vadratet av avstanden.
26 22 Sentrifugalraft Fordi jorda roterer og vi dermed beveger oss i en sirelbevegelse, er vi hele tiden aselerert (av gravitasjonsraften) inn mot rotasjonsasen (sentripetal- eller sentersøende aselerasjon). Sett fra E har vi derimot ingen sli aselerasjon og det vil derfor se ut som om det virer en raft i motsatt 1 retning av sentripetalaselerasjonen. For å unne brue Newtons 2. lov i E må vi derfor innføre en fitiv raft som står normalt på jordas rotasjonsase og har absoluttverdi li massen ganger sentripetalaselerasjonen. Denne raften alles ofte sentrifugalraft (lat. centrum, midtpunt, og fugere, flyte) og er dermed gitt ved: 2 F sentrifugal = m ω IE rrot = ω IE ( ω IE p EP )m (3.6) hvor m er aselerometermassen og ω IE er jordas vinelhastighet. r rot er rotasjonsradien (normalt på jordas rotasjonsase, retning ut fra asen) og p EP er posisjonsvetor fra jordas sentrum. På samme måte burde vi innføre en sentrifugalraft fordi jorda går i bane rundt sola (som gjør oss tyngre om dagen enn om natten), sola går igjen i bane i meleveien som gir en ny sentrifugalraft osv. Disse sentrifugalreftene blir imidlertid ytterst små til tross for stor r rot, fordi ω 2 -fatoren blir uhyre liten. Kreftene er så små at med dagens aselerometerusierhet er de neglisjerbare. Coriolisraft Når vi beveger oss i et roterende system må vi innføre enda en fitiv raft for å unne brue Newtons 2. lov, denne alles Coriolisraften 2. Coriolisraften består av to omponenter. Den ene ommer fra øst-vest bevegelse fordi dette gjør at vår vinelhastighet om jordasen ie lenger er ω IE som i forrige underapittel. Sentrifugalraften er jo uavhengig av fartøyets hastighet, så den første delen av Coriolisraften an ses på som en justering av sentrifugalraften pga fartøyets hastighet. Denne delen er derfor parallell med sentrifugalraften. d Den andre delen oppstår når ---- r rot, altså typis for nord-sør bevegelse og dt høyde-endring. Denne raften ser ut til å vire i E fordi vår rotasjonsradius endres når d ---- r rot dt. Hvis vi endrer vår rotasjonsradius, men ellers står stille i forhold til jorda, må vi aselereres normalt på r rot og ω IE (dvs tangentielt). Retningen fås ved å 1. Tilsvarende situasjon har en f es idet en bil rasjer, dvs aselererer baover (retarderer). Da vil passasjerene føle at det virer en raft framover i forhold til bilen. 2. Postulert av den Franse ingeniøren og matematieren Gustave Gaspard Coriolis i 1835.
27 23 d innse at vi må aselereres med jordrotasjonen om vi øer vår radius ( ---- r rot > ), dt fordi punter med større radius har større lineær hastighet (ved samme vinelhastighet). egge de to delene av Coriolisraften an sammenfattes i følgende matematise uttry: F Coriolis = ( 2ω IE v EP )m (3.7) hvor v EP er fartøyets hastighet i forhold til E. I teorien vil vi tilsvarende som for sentrifugalraft få et bidrag pga vår bane rundt sola osv, men den lave vinelhastigheten vil også her sørge for at bidraget blir ubetydelig. Det er nå drøftet de hensyn som må tas fordi E roterer. En an dermed mere seg at det un er jordas egen rotasjon som gir merbart bidrag. Matematis an denne tilnærmelsen uttryes: I d ( p dt 2 IE ) = a IE =, for alle t (3.8) hvor p IE altså er vetoren fra origo i I til jordas (geometrise) sentrum. Dette er grunnen til at I ofte blir definert til å ha sammenfallende origo med E, men da uten å rotere med jorda. Matematis bevis Vi har nå sett at ΣF fitiv = F sentrifugal + F Coriolis (3.9) som ved divisjon med m gir følgende sammenheng mellom a EP og a IP : a EP = a IP ω IE ( ω IE p EP ) 2ω IE v EP (3.1) Matematis an denne sammenhengen finnes ved å ta utgangspunt i tabell 2.1 som sier at: I d a 2 IP = ( p dt 2 IP ) (3.11)
28 24 Ved å substituere p IP = p IE + p EP inn i (3.11) og i tillegg brue tilnærmelsen (3.8) får vi: I d a 2 IP = ( p dt 2 EP ) (3.12) E d Fra tabell 2.1 har vi også at a 2 EP = ( p dt 2 EP ). Det er derfor sammenhengen mellom dobbel tidsderivasjon av vetoren p EP i systemene I og E som sal finnes. Vi an dermed brue (2.39) som gir: I d ( p dt 2 EP ) E d 2 E d = ( p dt 2 EP ) + ω IE ( ω IE p EP ) ( ω IE ) p dt EP (3.13) E d + 2ω IE ---- ( p EP ) dt Spinnet til jorda an regnes som tidsonstant i forhold til I, og dermed vil tilsvarende også gjelde ω IE. I ligningen inngår imidlertid den tidsderiverte av ω IE i forhold til E. Fordi ω IE per definisjon er parallell med rotasjonsasen til E, vil den da også være tidsonstant i forhold til E. Ved i tillegg å brue notasjonen fra tabell 2.1 får vi: I d ( p dt 2 EP ) = a EP + ω IE ( ω IE p EP ) + 2ω IE v EP (3.14) Ved hjelp av (3.12) får vi til slutt: a IP = a EP + ω IE ( ω IE p EP ) + 2ω IE v EP (3.15) og (3.1) er dermed vist Gyroompensasjon pga rotasjonen Det er til nå besrevet hvile hensyn som må tas på jorda i forhold til aselerometermålingene. For gyroene er det ie så omplisert, de måler alltid ω IP. Fordi jorda roterer vil E hele tiden endre sin orientering i forhold til I. Dette vil gyroene dermed måle og siden vi er interessert i orientering relativt til E må rotasjonen trees fra. Jordas vinelhastighet, ω IE er meget godt jent både i retning og amplitude, og usierheten er neglisjerbar for vårt formål oalt oordinatsystem Med de hensyn som nå er tatt, an vi finne vår posisjon i E, p EP ved å integrere opp a EP gitt som a EP = f IP + g P ω IE ( ω IE p EP ) 2ω IE v EP (3.16)
29 25 Uttryet er en ombinasjon av (3.1) og (3.2). Det er imidlertid svært vanlig å innføre enda ett oordinatsystem og relatere en del størrelser til dette. Det såalte loale oordinatsystemet,, har ofte x- og y-asene peende henholdsvis nordover og østover, mens z-asen peer nedover, normalt på jordoverflaten (sli den er modellert). Koordinatsystemet følger altså med fartøyet, og origo er vanligvis 1 definert sli at fartøyets referansepunt har null x- og y-oordinat, og den modellerte jordoverflaten har null z-oordinat i. Denne versjonen av betegnes NED (eng. North East Down), og i tillegg til å rotere med E vil det jo også endre orientering med jordrumningen ettersom fartøyet beveger seg. En ulempe med NED-systemet er at det vil endre sin orientering svært hurtig hvis fartøyet beveger seg i polområdene (uendelig hurtig ved passering av en pol). For srogfaste systemer vil dette bl a reve estra høy tastetid i en datamasin som sal beregne orienteringen til NED. For gimbal baserte systemer som holder plattformens orientering onstant i forhold til, reves mye bru av pådrag for å sifte plattformens orientering hurtig. For å omgå slie problemer an vi la nord- og øst-asene rotere fritt om z-asen. F es an vinelhastigheten til de horisontale asene i forhold til jorda ha null omponent langs z-asen. Denne versjonen av alles vandrende azimuth (eng. Wander Azimuth), og blir betegnet AZI. Azimuth-vinelen, som betegnes a, er definert som vinelen NED må dreies om sin z- ase for å sammenfalle med AZI. (Fortegnet er gitt av høyrehåndsregelen). Figur 3.1 viser oordinatsystemene I, E og (versjon AZI) med asene tegnet ut fra origo (saleringen er ie vist). reddegrad (μ) og lengdegrad (l) er også vist på figuren. 1. Ved navigasjon i un et begrenset område, vil ie nord, øst og ned retningene endre seg mye i forhold til jorda. Dette oordinatsystemet an dermed tilnærmes som jordfast, og man an bestemme seg for en hensitsmessig (jordfast) plassering av origo.
30 26 I x N x a z z y E μ y l Nullmeridianen S Figur 3.1 Koordinatsystemene I, E og (versjon AZI). Vi an mere oss at definisjonen på azimuth, lengde- og breddegrad gjør at R E uttryes som en rotasjonssevens om nye aser i reefølgen x, y, z. Ved å brue notasjonen definert i (2.15) får vi dermed: an θ E = lμ (3.17) a Orienteringen til fartøyet oppgis vanligvis i forhold til det loale oordinatsystemet, og an dermed uttryes som R. Rull- (φ), stamp- (θ) og girvinel (ψ) an nå (i tråd med (2.16) og (2.17)) defineres som: φ θ ψ = Δ * θ (3.18)
31 Navigasjonsligningene i ved srogfast sensormontering I dette underapitlet sal navigasjonsligningene i, versjon AZI utledes. Det antas at aselerometrene og gyroene er montert srogfast, og vi har dermed P =. Utledningen an gjøres på flere måter og med uli grad av forenling, avhengig av anvendelsen. I dette arbeidet sal ligningene brues til å se på hvordan feil i aselerometre og gyroer gir feil posisjonsestimat, det er imidlertid un to dimensjoner av posisjonen som sal undersøes. Hvis vi tener oss posisjonen gitt i uleoordinater i forhold til E, er det un de to vinlene som sal studeres, ie radien. Grunnen til dette er at radien enelt an måles med en trymåler og feilutvilingen vil begrenses betratelig. igningene som utledes sal altså brues til feilanalyse, og ie navigasjon. Det er derfor et begrenset rav til nøyatighet, og jorda an trygt tilnærmes som en ule. For fullstendige ligninger som modellerer jorda som en ellipsoide, henvises det til Fossen (1996). En annen forenling som er gjort er at gravitasjonen er onstant med hensyn på tiden. Hvis vi antar at gyroene måler vinelhastighet, er utgangspuntet vårt altså målingene f I og ω I (og initialisering, se underapittel 3.1.6). Det vi sal fram til, er posisjon gitt som R E. Orienteringen til i forhold til E vil jo definere en entydig todimensjonal posisjon (i tillegg til azimuth-vinelen). Fartøyets orientering sal gis som R, og hastigheten som v E. Det an være greit å begynne med hastigheten, og vi trenger da sammenhengen mel- lom v E og aselerometermålingen. I (3.16) er denne sammenhengen gitt, bortsett fra E d at v E her er derivert i forhold til E i stedet for (vi har jo at a EP = a E = ---- ( v E )). dt d For å finne ---- ( v E ) bruer vi sammenhengen mellom eneltderivert i ulie systemer, altså (2.34) som i dette tilfellet dt gir: d ---- ( v E ) dt E d = ---- ( v E ) ω E v E (3.19) dt Vi ser dermed at i får vi tillegget ω E v E i forhold til derivasjon i E, altså: d ---- ( v E ) = f I + g ω IE ( ω IE p E ) 2ω IE v E ω E v E (3.2) dt
32 28 Dette an forenles til: d ---- ( v E ) = f I + g ω IE ( ω IE p E ) ( 2ω IE + ω E ) v E (3.21) dt Deomponert i blir (3.21): v E = R f I + ωie ( ω IE p E ) ( 2ω IE + ω E ) v E (3.22) g Sentripetalaselerasjonen og gravitasjonen er begge un avhengig av posisjon og an til sammen alles tyngdeaselerasjon (eng. plumb bob gravity), som an betegnes: g g ωie ω IE p E = ( ) (3.23) Summen av disse leddene vil altså gi retningen til en loddlinje, og vil ha en neglisjerbar horisontalomponent 1. Det antas at g blir funnet med tilstreelig nøyatighet når posisjonen er gitt tilnærmet. For detaljer i utregningen av gravitasjon henvises det til Fossen (1996) eller ritting (1971). Den endelige ligningen for v E blir altså: v E = R f I + ( 2ω IE + ω E ) v E (3.24) g Ved å integrere opp (3.24) får vi v E, men for å gjøre det trenger vi R, ω IE og ω E. For vandrende azimuth sal un rotere om sine x- og y-aser i forhold til jorda, altså sal den vertiale delen av ω E alltid være li null. Da jorda modelleres som en ule, vil vinelhastigheten til i forhold til jorda rett og slett bli: 1 ω E r E = ( u E v E ) (3.25) hvor r E = p E, altså jordradien pluss fartøyets høyde over jordoverflaten. u E er enhetsvetoren p E , deomponert i, altså [,, 1] T. p E 1. Et godt estimat av jordas elliptise form an fatis finnes ved å resonnere at g hele tiden må stå normalt på overflaten (det er jo sentripetalleddet som er årsaen til ellipsiteten).
33 29 ω IE E finnes ved å deomponere den jente vetoren ω IE ned i, altså: = [ 7,29 1 5,, ] T rad/s ω IE R E = E ω IE (3.26) For å finne R trenger vi gyromålingen, og vi an ved hjelp av (2.23) sette opp: R = R S( ω ) (3.27) Vi trenger altså ω som er gitt av sammenhengen: ω I = ω IE + ω E + ω (3.28) Vi får altså: R = R S( ω I ω IE ω E ) (3.29) Da vi allerede har ω IE og ω E, an disse transformeres til og så brues i (3.29), det er imidlertid enlere å omforme (3.29) til å brue ω IE og ω E direte: R R = S( ω I ) R S( ω IE + ω E ) (3.3) Similaritetstransformasjonen gitt i (2.29) gir oss: S( ω IE + ω E ) R = S( ω IE + ω E )R (3.31) Vi an derfor srive (3.3) som: R R = S( ω I ) S( ω IE + ω E )R (3.32) som an integreres opp til R. Den eneste størrelsen som ie er funnet nå er R E, som enelt finnes fra ω E brue sammenhengen mellom disse gitt av (2.23), og vi får: ved å E R = R E S( ω E ) (3.33) som integreres til å gi R E. I figur 3.2 er det gitt en grafis oversit over datastrømmen og ligningene som er utledet i dette underapitlet.
34 3 Gyroer ω I R = (3.32) R S( ω I ) S( ω IE + ω E )R ω IE (3.26) = R E E ω IE Init ( ) dt Aselerometre f I (3.24) R R v E = R f I + ( 2ω IE + ω E ) v E g ( ) dt Init g Tyngdeberegning v E (3.25) 1 ω E r E (3.33) = ( u E v E ) R = E R E S( ω E ) ( ) dt R E r E Trymåler Init v E Figur 3.2 Dataflyt for de horisontale navigasjonsligningene i (versjon AZI), ved antatt uleformet jord Initialisering Alle integralene i figur 3.2 må initialiseres. Vi må altså ha verdier for hastighet, posisjon og orientering før vi starter å navigere. Her følger un en ort prinsipiell oversit over hvordan dette gjøres, for en mer detaljert besrivelse henvises det til Savage (1991). Hastighet Hastigheten ved start må være jent sli at vi får initialisert dette integralet. For et fly vil denne typis være null, idet flyet står på flyplassen. For et fartøy i bevegelse (f es en båt i bølger) trengs en estern hastighetsmåling.
35 31 Posisjon Posisjonen initialiseres gjerne av en operatør. Dette er vanligvis ie noe problem, da posisjonen som regel er jent ved start. (I vårt tilfelle er utgangspuntet et moderfartøy med GPS, og i andre tilfeller an det f es være en havn eller flyplass.) Den initielle lengde- og breddegrad bestemmer sammen med azimuth-vinelen R E entydig. Azimuth-vinelen an initialiseres til en vilårlig verdi. (For gimbal-baserte systemer sal ha samme orientering som plattformen, og det reves derfor informasjon om plattformens girvinel.) Orientering Hvis farosten ie aselererer i forhold til jorda, an den vertiale retningen finnes ved hjelp av aselerometermålingene, som da måler g. For marine fartøy som har varierende aselerasjon pga bølger og vind bør det brues en middelverdi over et passende tidsintervall (lavpassfiltrering). Kursen til fartøyet (evt. plattformen) finnes ved å benytte seg av at gyroene un vil måle jordrotasjonen når fartøyet ie har vinelhastighet i forhold til jorda. Man benytter seg da av at horisontalomponenten av vinelhastigheten alltid vil pee nordover. Dette gjøres altså etter at horisontalplanet er funnet Oppsummering av de oordinatsystemer som er brut Her gis en oversit i tabellform over alle oordinatsystemene som er brut i oppgaven. Andre olonne angir navnet brut i Fossen (1996):
36 32 Navn Tilsvarer Definisjon I (Inertielt) E (Jordfast) (oalt) Omtrent som SFR (Space fixed) ECEF (Earth- Centered Earth-fixed) NED (North- East-Down) Inertielt system uten gravitasjon. Vilårlig plassering av origo. Origo er plassert i jordas geometrise sentrum, yzplanet sammenfaller med evatorplanet, y-asen peer mot 9 østlig lengdegrad og x-asen mot nord. z-asen peer nedover, normalt på overflaten til den jordmodellen som brues. x- og y-asene peer henholdsvis nordover og østover. Origo er plassert sli at fartøyets referansepunt får null x- og y-oordinat, og sli at overflaten i jordmodellen har null z- oordinat. P (Plattformfast) (Srogfast) AZI (Azimuth) Ie brut AC (ody fixed) Origo og z-ase som NED, men x- og y-asen roterer på en sli måte at deres vinelhastighet i forhold til jorda har null omponent langs z-asen. ( Roterer med jorda. ) Origo i fartøyets referansepunt, asene sammenfallende med aselerometrenes monteringsaser. Srogfast oordinatsystem med origo i fartøyets referansepunt. x-asen peer framover, y-asen mot styrbord og z-asen nedover. Ved srogfast aselerometermontering settes dette li P. Tabell 3.1 Oversit over de oordinatsystemer som brues. 3.2 Treghetssensorer Treghetssensorer er som nevnt sensorer som benytter seg av tregheten til masse eller lys for å måle aselerasjon eller vinel (-hastighet). En stor fordel med slie sensorer er at de ie setter rav til omgivelsene. De er selvstendige og an ie jammes eller forstyrres. En treghetssensorenhet (TSE) er betegnelsen på en enhet som inneholder flere gyroer og aselerometre, ofte tre av hver, montert ortogonalt i forhold til hverandre. En sli enhet, sammen med en datamasin som regner ut navigasjonsligningene, alles ofte et treghetsnavigasjonssystem (TNS).
37 Generelle sensorfeil Målingen en sensor gir, er generelt en funsjon av den størrelsen som sal måles. Hvis vi hadde jent denne funsjonen perfet, ville vi hatt en feilfri måling av den atuelle størrelsen. I prasis er ofte funsjonen også avhengig av andre størrelser enn den som måles, f es tid, temperatur, ytre refter og futighet. Den atuelle målingen an også være funsjon av verdiens forhistorie, og i såfall har vi hysterese. Uansett ønser vi å finne et estimat av funsjonen, f es vha polynomtilpasninger, flere rette linjestyer eller lignende, avhengig av ønset nøyatighet. I mange sensorer vil funsjonen unne tilnærmes som en rett linje i det atuelle måleområdet. Det er da un to parametre som sal bestemmes og disse betegnes salafator (stigningstall) og offset (vertial forsyvning av grafen). I figur 3.3 er en sli lineær tilnærming vist ved tiden t. Vi ser at det hadde vært mulig å gjøre en bedre lineær tilpasning ved dette tidspuntet, og har dermed både salafatorfeil og offsetfeil. Målt verdi Sann verdi Figur 3.3 Sammenheng mellom sann verdi og målt verdi ved tiden t (antatt null hysterese). Heltruen linje viser den virelige sammenheng, mens stiplet viser vår lineære tilpasning. Hvis vi nå antar at (den salare) størrelsen som sal måles heter x, så har vi følgende sammenheng: x = x + δx (3.34) hvor x betegner den målte verdi. δx representerer dermed feilen. Hvis vi tilnærmer den virelige funsjonen som en rett linje, vil vi unne srive feilen som: δx = Δx salafator x + Δx bias + ξ x salafatorfeil offsetfeil (3.35)
38 34 Δx salafator betegnes altså salafatorfeil og vil i treghetssensorer være tilnærmet onstant (mhp tiden). Grunnen til at offsetfeilen er delt opp i to ledd, er at den ofte modelleres som en langsomtvarierende bias ( Δx bias ) pluss hvitstøy (ξ x ). For en nærmere redegjørelse for hvordan den ontinuerlige hvitstøyen sal toles, se underapittel Aselerometre Prinsipp Følgende forlaring er basert på awrence (1993): Aselerometre måler som nevnt den raft en jent masse utsettes for pga aselerasjon og gravitasjon. En enel løsning på dette er å henge opp en masse i en fjær med demping og måle utslaget massen får. En relativt stiv fjær reves for å gi aselerometret et aseptabelt dynamis område, dette vil også gi god linearitet pga lite utslag. En stiv fjær gir imidlertid hysterese og temperaturavhengighet, og i tillegg reves en svært nøyatig avlesningsmeanisme. En god løsning på disse problemene er å brue en reguleringssløyfe med et pådragsorgan som holder massen tilnærmet rundt sitt nullpunt. Pådraget er da et mål på den spesifie raft og aselerometret får god linearitet og stort dynamis område. En annen løsning er å spenne opp massen i en streng parallell med monteringsasen. Strengen an settes i svingninger, og svingefrevensen vil da være et mål på den spesifie raft. Feilbesrivelse Ideelt sal en gruppe på tre lineært uavhengige og ortogonalt monterte aselerometre måle f P IP, men pga ulie feil får vi sammenhengen: P f IP P f IP P δf IP = + (3.36) P hvor f IP P er den målte verdi og δf IP tråd med (3.35) gi målingen: er målefeilen. Hvert enelt aselerometer vil i P f IP, i P f IP, i P Δf IP, salafator, i P f IP, i P Δf IP, bias, i = (3.37) ξ f, i hvor i { x', y', z' } er monteringsasen. Grunnen til at disse størrelsene er meret, er at vi i prasis aldri vil lare å montere aselerometrene helt sammenfallende med x, y og z-asen til P (eventuelt ved srogfast sensormontering.) Det som egentlig er
39 35 omponenten langs x', blir dermed tolet som omponenten langs x osv 1. Dette gir et P feilledd i δf IP P som betegnes Δf IP, sjev fra den enelte aselerometermåling, og vi har: P. Forøvrig vil δf IP bestå av feil som ommer hvor P δf IP = P Δf IP, sjev P Δf IP, salafator, x + P Δf IP, salafator, y f IP + Δf IP, bias +ξ f Δf IP s P, alafator, z P P (3.38) P Δf IP, bias P Δf IP, bias, x ξ f, x = og ξ f = (3.39) P Δf IP, bias, y P Δf IP, bias, z ξ f, y ξ f, z For en gitt type treghetssensorenheter, vil det være av interesse å vite hvilen størrelsesorden de ulie feilene har. Det er da hensitsmessig å besrive feil, som f es salafatorfeil i x-aselerometret, som en tilfeldig (stoastis) variabel som varierer fra enhet til enhet (vi antar at denne er onstant for hver enhet). Denne an da besrives med statistise størrelser. Hvis vi antar at forventningsverdien er null, vil variansen til salafatorfeilen være et godt mål på valiteten. For å besrive en variabel som endrer seg med tiden, f es en langsomtvarierende bias, betrater vi den som en stoastis prosess. Vi betrater altså amplituden ved et bestemt tidspunt som en tilfeldig variabel. Hvis vi antar at prosessen er stasjonær og ergodis, med forventningsverdi li null, vil variansen til amplituden ved et vilårlig tidspunt være et godt mål på valiteten. Det sal nå redegjøres for hvordan størrelsen på de ulie feilbidrag an besrives statistis, i lys av disusjonen over. Størrelsen på sjevstillingen (som antas onstant) vil unne oppgis som standardavviet til monteringssjevheten til de ulie aselerometre. For å besrive størrelsene til de øvrige feil, vil det være hensitsmessig først å definere ryssovariansmatrisen til to stoastise vetorer 2, η 1 og η 2, som: cov( η 1, η 2 ) E[ ( η 1 η 1 )( η 2 η 2 ) T ] = Δ (3.4) 1. Det vil imidlertid ofte være mulig å fjerne en del av denne feilen ved hjelp av alibrering, men selv da vil det være en viss usierhet i vår viten om monteringsasen. Dessuten an vi få langsom meanis drift pga temperatur- og tryendringer og refter utenfra. 2. Dette er generelt un matematise vetorer, altså un en mengde tall som behandles samlet, og ie noen deomponert fysis vetor.
Løsningsforslag til øving 10
 FY11/TFY4145 Meanis fysi. Institutt for fysi, NTNU. Høsten 211. Løsningsforslag til øving 1 Vi utleder aller først ligningen som fastlegger vinelen φ r, dvs overgangen fra ren rulling til sluring. N2 for
FY11/TFY4145 Meanis fysi. Institutt for fysi, NTNU. Høsten 211. Løsningsforslag til øving 1 Vi utleder aller først ligningen som fastlegger vinelen φ r, dvs overgangen fra ren rulling til sluring. N2 for
Overflatebølger på stasjonær strøm
 Overflatebølger på stasjonær strøm Stasjonær strøm La den stasjonære strømmen være gitt ved hastighetsfelt = (,V,W) = Φ og overflatehevning ζ. De horisontale omponentene an vi srive som en 2D vetor H =
Overflatebølger på stasjonær strøm Stasjonær strøm La den stasjonære strømmen være gitt ved hastighetsfelt = (,V,W) = Φ og overflatehevning ζ. De horisontale omponentene an vi srive som en 2D vetor H =
MAT1030 Forelesning 16
 MAT1030 Forelesning 16 Reursjon og indusjon Roger Antonsen - 17 mars 009 (Sist oppdatert: 009-03-17 11:4 Forelesning 16 Reursjon og indusjon Forrige gang ga vi endel esempler på reursive definisjoner og
MAT1030 Forelesning 16 Reursjon og indusjon Roger Antonsen - 17 mars 009 (Sist oppdatert: 009-03-17 11:4 Forelesning 16 Reursjon og indusjon Forrige gang ga vi endel esempler på reursive definisjoner og
Rekursjon og induksjon. MAT1030 Diskret matematikk. Induksjonsbevis. Induksjonsbevis. Eksempel (Fortsatt) Eksempel
 Reursjon og indusjon MAT1030 Disret matemati Forelesning 15: Indusjon og reursjon, reurenslininger Dag Normann Matematis Institutt, Universitetet i Oslo 3 mars 008 Onsdag ga vi endel esempler på reursive
Reursjon og indusjon MAT1030 Disret matemati Forelesning 15: Indusjon og reursjon, reurenslininger Dag Normann Matematis Institutt, Universitetet i Oslo 3 mars 008 Onsdag ga vi endel esempler på reursive
Førsteordens lineære differensiallikninger
 Førsteordens lineære differensiallininger Begrepet førsteordens lineære differensiallininger er ie sielig definert i Sinus R. Denne artielen omhandler det temaet. En førsteordens lineær differensiallining
Førsteordens lineære differensiallininger Begrepet førsteordens lineære differensiallininger er ie sielig definert i Sinus R. Denne artielen omhandler det temaet. En førsteordens lineær differensiallining
Logiske innenheter (i GKS og PHIGS) kreves ikke i besvarelsen: String Locator Pick Choice Valuator Stroke
 Oppgave a) Geometrise (eller grafise) primitiver er de grunnleggende bestandelene av en tegning som an tegnes direte ved enel (uten bru av ombinasjoner) bru av de tegnefunsjonene som en API tilbyr. (Forsjellige
Oppgave a) Geometrise (eller grafise) primitiver er de grunnleggende bestandelene av en tegning som an tegnes direte ved enel (uten bru av ombinasjoner) bru av de tegnefunsjonene som en API tilbyr. (Forsjellige
Øving 11. Oppgave 1. E t0 = 2. Her er
 FY00/TFY460 Bølgefysi. Institutt for fysi, NTNU. Høsten 0. Veiledning: Mandag 5. og tirsdag 6. november. Innleveringsfrist: Mandag. november l :00. Øving Tema: Dipol-Ståling, reflesjon og transmisjon av
FY00/TFY460 Bølgefysi. Institutt for fysi, NTNU. Høsten 0. Veiledning: Mandag 5. og tirsdag 6. november. Innleveringsfrist: Mandag. november l :00. Øving Tema: Dipol-Ståling, reflesjon og transmisjon av
R Differensialligninger
 R - 6.0.05 - Differensialligninger Løsningssisser Oppgave Løs differensialligningene y x y b) y y x c) y 8y 7y 0 Separabel: y y x y dy xdx y x C y x 4 C y C x 4 Da ligningen er ulineær, bør vi også se
R - 6.0.05 - Differensialligninger Løsningssisser Oppgave Løs differensialligningene y x y b) y y x c) y 8y 7y 0 Separabel: y y x y dy xdx y x C y x 4 C y C x 4 Da ligningen er ulineær, bør vi også se
Oppgaver i kapittel 1 - Løsningsskisser og kommentarer Lærebok:
 Oppgaver i apittel - Løsningssisser og ommentarer Lærebo:.6 Vitig oppgave, viser hvordan ree-summer an tilnærmes med integraler. Atuelt hvis vi har formelen for n te ledd, men ie har noen summeformel.
Oppgaver i apittel - Løsningssisser og ommentarer Lærebo:.6 Vitig oppgave, viser hvordan ree-summer an tilnærmes med integraler. Atuelt hvis vi har formelen for n te ledd, men ie har noen summeformel.
Normalfordeling. Høgskolen i Gjøvik Avdeling for teknologi, økonomi og ledelse. Statistikk Ukeoppgaver uke 7
 Ueoppgaver i BtG207 Statisti, ue 7 : Normalfordeling. 1 Høgsolen i Gjøvi Avdeling for tenologi, øonomi og ledelse. Statisti Ueoppgaver ue 7 Normalfordeling. Oppgave 1 Anta Z N(0, 1), dvs. Z er standard
Ueoppgaver i BtG207 Statisti, ue 7 : Normalfordeling. 1 Høgsolen i Gjøvi Avdeling for tenologi, øonomi og ledelse. Statisti Ueoppgaver ue 7 Normalfordeling. Oppgave 1 Anta Z N(0, 1), dvs. Z er standard
MAT1030 Forelesning 21
 MAT00 Forelesning Mer ombinatori Roger Antonsen - 5. april 009 (Sist oppdatert: 009-0-5 00:05) Kapittel 9: Mer ombinatori Plan for dagen Mer om permutasjoner og ordnet utvalg ) Mer om ombinasjoner n velg
MAT00 Forelesning Mer ombinatori Roger Antonsen - 5. april 009 (Sist oppdatert: 009-0-5 00:05) Kapittel 9: Mer ombinatori Plan for dagen Mer om permutasjoner og ordnet utvalg ) Mer om ombinasjoner n velg
Forelesning 20. Kombinatorikk. Roger Antonsen - 7. april 2008
 orelesning Kombinatori Roger Antonsen - 7. april 8 Kombinatori Kombinatori er studiet av opptellinger, ombinasjoner og permutasjoner. Vi finner svar på spørsmål Hvor mange måter...? uten å telle. Vitig
orelesning Kombinatori Roger Antonsen - 7. april 8 Kombinatori Kombinatori er studiet av opptellinger, ombinasjoner og permutasjoner. Vi finner svar på spørsmål Hvor mange måter...? uten å telle. Vitig
FY1006/TFY Øving 4 1 ØVING 4
 FY1006/TFY4215 - Øving 4 1 Oppgave 13 ØVING 4 Vibrerende to-partiel-system Som disutert side 110 i boa, er det et vitig poeng både i lassis meani og i vantemeani at et to-partiel-problem essensielt an
FY1006/TFY4215 - Øving 4 1 Oppgave 13 ØVING 4 Vibrerende to-partiel-system Som disutert side 110 i boa, er det et vitig poeng både i lassis meani og i vantemeani at et to-partiel-problem essensielt an
Plan. MAT1030 Diskret matematikk. Eksamen 12/6-06 Oppgave 2. Noen tips til eksamen
 Plan MAT1030 Disret matemati Plenumsregning 12: Diverse oppgaver Roger Antonsen Matematis Institutt, Universitetet i Oslo 22. mai 2008 Dette er siste plenumsregning. Vi regner stort sett esamensoppgaver.
Plan MAT1030 Disret matemati Plenumsregning 12: Diverse oppgaver Roger Antonsen Matematis Institutt, Universitetet i Oslo 22. mai 2008 Dette er siste plenumsregning. Vi regner stort sett esamensoppgaver.
Øving 9. Oppgave 1. E t0 = 2. Her er
 FY00/TFY460 Bølgefysi. Institutt for fysi, NTNU. Høsten 03. Veiledning: Mandag. og 8 og fredag 6. otober. Innleveringsfrist: tirsdag 9. otober l :00. Øving 9 Tema: Dipol-Ståling, reflesjon og transmisjon
FY00/TFY460 Bølgefysi. Institutt for fysi, NTNU. Høsten 03. Veiledning: Mandag. og 8 og fredag 6. otober. Innleveringsfrist: tirsdag 9. otober l :00. Øving 9 Tema: Dipol-Ståling, reflesjon og transmisjon
Fysikkolympiaden Norsk finale 2012
 Nors Fysilærerforening Fysiolympiaden Nors finale 3. uttaingsrunde Fredag 3. mars l. 9. til. Hjelpemidler: Tabell/formelsamling, lommeregner og utdelt formelar Oppgavesettet består av 7 oppgaver på 3 sider
Nors Fysilærerforening Fysiolympiaden Nors finale 3. uttaingsrunde Fredag 3. mars l. 9. til. Hjelpemidler: Tabell/formelsamling, lommeregner og utdelt formelar Oppgavesettet består av 7 oppgaver på 3 sider
EKSAMEN Styring av romfartøy Fagkode: STE 6122
 Avdeling for teknologi Sivilingeniørstudiet RT Side 1 av 5 EKSAMEN Styring av romfartøy Fagkode: STE 6122 Tid: Fredag 16.02.2001, kl: 09:00-14:00 Tillatte hjelpemidler: Godkjent programmerbar kalkulator,
Avdeling for teknologi Sivilingeniørstudiet RT Side 1 av 5 EKSAMEN Styring av romfartøy Fagkode: STE 6122 Tid: Fredag 16.02.2001, kl: 09:00-14:00 Tillatte hjelpemidler: Godkjent programmerbar kalkulator,
EKSAMEN. Ta med utregninger i besvarelsen for å vise hvordan du har kommet fram til svaret.
 EKSAMEN Emneode: ID30005 Emne: Industriell I Dato: 5.2.204 Esamenstid: l. 0900 til l. 300 Hjelpemidler: re A4-ar (ses sider) med egne notater. "ie-ommuniserende" alulator. Faglærer: Robert Roppestad Esamensoppgaven:
EKSAMEN Emneode: ID30005 Emne: Industriell I Dato: 5.2.204 Esamenstid: l. 0900 til l. 300 Hjelpemidler: re A4-ar (ses sider) med egne notater. "ie-ommuniserende" alulator. Faglærer: Robert Roppestad Esamensoppgaven:
Eksemplet bygger på en ide fra Thor Bernt Melø ved Institutt for fysikk ved NTNU og Tom Lindstrøms bok Kalkulus.
 LÆRERARK...om å tømme en beolder for vann Esemplet bygger på en ide fra Tor Bernt Melø ved Institutt for fysi ved NTNU og Tom Lindstrøms bo Kalulus. Problemstilling: Vi ar et sylindris beger med et sirulært
LÆRERARK...om å tømme en beolder for vann Esemplet bygger på en ide fra Tor Bernt Melø ved Institutt for fysi ved NTNU og Tom Lindstrøms bo Kalulus. Problemstilling: Vi ar et sylindris beger med et sirulært
1. Åpen sløyfefunksjon når den langsomme digitale regulatoren er en P-regulator.
 D:\Per\Fag\Styresys\SANNOV\11LØSØV5.wd Fag SO507E Styresystemer Løsning heimeøving 5 Sanntid HIST-AFT Mars2011 PHv Utleveres: Ogave 1 A) Analogisering og frevensanalyse. 1. Åen sløyfefunsjon når den langsomme
D:\Per\Fag\Styresys\SANNOV\11LØSØV5.wd Fag SO507E Styresystemer Løsning heimeøving 5 Sanntid HIST-AFT Mars2011 PHv Utleveres: Ogave 1 A) Analogisering og frevensanalyse. 1. Åen sløyfefunsjon når den langsomme
R2 - Kapittel 2 - Algebra. I a) Hvilken av disse tallfølgene er aritmetiske, geometriske eller ingen av delene?
 R2 - Kapittel 2 - Algebra I Hvilen av disse tallfølgene er aritmetise, geometrise eller ingen av delene?.,,,,... 2 4 2. 2,6,8,54,.... 2,6,0,4,... 4.,, 2, 4,... 2 9 5., 5, 7, 9,... 4 9 6 Sriv opp uttryet
R2 - Kapittel 2 - Algebra I Hvilen av disse tallfølgene er aritmetise, geometrise eller ingen av delene?.,,,,... 2 4 2. 2,6,8,54,.... 2,6,0,4,... 4.,, 2, 4,... 2 9 5., 5, 7, 9,... 4 9 6 Sriv opp uttryet
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11)
 Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Forkunnskaper i matematikk for fysikkstudenter. Integrasjon.
 De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
TTK4180 Stokastiske og adaptive systemer. Datamaskinøving 1 - Tilstandsestimering
 Institutt for tenis yberneti Norges tenis-naturvitensapelige universitet 28.09.98 EWR TTK4180 Stoastise og adaptive systemer Datamasinøving 1 - Tilstandsestimering Tid og sted: -Utdeling av oppgave: 3.
Institutt for tenis yberneti Norges tenis-naturvitensapelige universitet 28.09.98 EWR TTK4180 Stoastise og adaptive systemer Datamasinøving 1 - Tilstandsestimering Tid og sted: -Utdeling av oppgave: 3.
Kapittel 9: Mer kombinatorikk
 MAT3 Disret Matemati orelesning : Mer ombinatori Dag Normann Matematis Institutt, Universitetet i Oslo Kapittel 9: Mer ombinatori 3. april (Sist oppdatert: -4-3 4:4) MAT3 Disret Matemati 3. april Oppsummering
MAT3 Disret Matemati orelesning : Mer ombinatori Dag Normann Matematis Institutt, Universitetet i Oslo Kapittel 9: Mer ombinatori 3. april (Sist oppdatert: -4-3 4:4) MAT3 Disret Matemati 3. april Oppsummering
d) Poenget er å regne ut terskeltrykket til kappebergarten og omgjøre dette til en tilsvarende høyde av en oljekolonne i vann.
 Sisse til løsning Esamen i Reservoarteni 3. juni, 999 Oppgave a) Kapillartry er differansen i try mellom to faser på hver side av den infinitesimale overflaten som siller fasene. Det følger av en minimalisering
Sisse til løsning Esamen i Reservoarteni 3. juni, 999 Oppgave a) Kapillartry er differansen i try mellom to faser på hver side av den infinitesimale overflaten som siller fasene. Det følger av en minimalisering
For at en funksjon i to variable skal ha en grenseverdi i punktet (a,b), dvs.
 Øving ue 3 Grenser og ontinuitet For at en funsjon i to variable sal ha en grenseverdi i puntet (a,b), dvs. lim Hx,yL Ha,bL f Hx, yl = L sal esistere, må denne unie verdien oppnåes uansett hvilen vei man
Øving ue 3 Grenser og ontinuitet For at en funsjon i to variable sal ha en grenseverdi i puntet (a,b), dvs. lim Hx,yL Ha,bL f Hx, yl = L sal esistere, må denne unie verdien oppnåes uansett hvilen vei man
Oppgave 1. Oppgave 2. 3MX eksamen Privatister Løsningsskisse Ikke kontrollert og dobbeltsjekket! Kan være feil her...
 MX esamen.5.5 - Privatister Løsningssisse Ie ontrollert og dobbeltsjeet! Kan være feil her... Oppgave a) sin cos,, sin cos sin,tan sin.588.588.588 L.588 b) f lncos f fu lnu,u cos, i vadrant f f u u u sin
MX esamen.5.5 - Privatister Løsningssisse Ie ontrollert og dobbeltsjeet! Kan være feil her... Oppgave a) sin cos,, sin cos sin,tan sin.588.588.588 L.588 b) f lncos f fu lnu,u cos, i vadrant f f u u u sin
MAT1030 Forelesning 21
 MAT orelesning Mer ombinatori Dag Normann -. april (Sist oppdatert: -4-4:5) Kapittel 9: Mer ombinatori Oppsummering orrige ue startet vi på apitlet om ombinatori. Vi så på hvordan vi an finne antall måter
MAT orelesning Mer ombinatori Dag Normann -. april (Sist oppdatert: -4-4:5) Kapittel 9: Mer ombinatori Oppsummering orrige ue startet vi på apitlet om ombinatori. Vi så på hvordan vi an finne antall måter
Solow-modellen - et tilleggsnotat i ECON2915
 Solow-modellen - et tilleggsnotat i Herman ruse 27. september 2013 Innhold 1 Solow-modellen en innføring 2 1.1 Forklaring av likningene............................ 2 1.2 Å sette modellen på intensivform.......................
Solow-modellen - et tilleggsnotat i Herman ruse 27. september 2013 Innhold 1 Solow-modellen en innføring 2 1.1 Forklaring av likningene............................ 2 1.2 Å sette modellen på intensivform.......................
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
Løsningsforslag til øving 3
 Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Konstruksjonskrus Eurokode 5. Innhold. Introduksjon til forbindelser EK5
 Konstrusjonsrus Euroode 5 Beregningsregler Meanise treforbindelser Geir Glasø Tretenis Innhold 1. Introdusjon til forbindelser i EK5. Minimumsavstander 3. Tverrbelastning og rope effet 4. Kombinert belastning
Konstrusjonsrus Euroode 5 Beregningsregler Meanise treforbindelser Geir Glasø Tretenis Innhold 1. Introdusjon til forbindelser i EK5. Minimumsavstander 3. Tverrbelastning og rope effet 4. Kombinert belastning
Theory Norwegian (Norway) Vær vennlig å lese de generelle instruksjonene i den separate konvolutten før du begynner på dette problemet.
 Q1-1 To problemer i mekanikk (10 poeng) Vær vennlig å lese de generelle instruksjonene i den separate konvolutten før du begynner på dette problemet. Del A. Den gjemte disken (3,5 poeng) Vi ser på en massiv
Q1-1 To problemer i mekanikk (10 poeng) Vær vennlig å lese de generelle instruksjonene i den separate konvolutten før du begynner på dette problemet. Del A. Den gjemte disken (3,5 poeng) Vi ser på en massiv
Brukerkurs i Gauss feilforplantning
 Brukerkurs i Gauss feilforplantning Knut S. Gjerden 9. august 2011 evt. gaussisk feilforplantning eller bruk av Gauss lov for feilforplantning. Samt litt generelt om fysikkting.
Brukerkurs i Gauss feilforplantning Knut S. Gjerden 9. august 2011 evt. gaussisk feilforplantning eller bruk av Gauss lov for feilforplantning. Samt litt generelt om fysikkting.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateni og informasjonsvitensap Esamensoppgave i TDT40 Algoritmer og datastruturer Faglig ontat under esamen Magnus Lie Hetland Telefon 98 5 949 Esamensdato 5 august, 08 Esamenstid (fra
Institutt for datateni og informasjonsvitensap Esamensoppgave i TDT40 Algoritmer og datastruturer Faglig ontat under esamen Magnus Lie Hetland Telefon 98 5 949 Esamensdato 5 august, 08 Esamenstid (fra
STK1100 våren Betinget sannsynlighet og uavhengighet. Vi trenger en definisjon av betinget sannsynlighet! Eksempel 1
 STK00 våren 07 Betinget sannsynlighet og uavhengighet Esempel Vi vil først ved hjelp av et esempel se intuitivt på hva betinget sannsynlighet betyr. Vi legger fire røde ort og to svarte ort i en bune.
STK00 våren 07 Betinget sannsynlighet og uavhengighet Esempel Vi vil først ved hjelp av et esempel se intuitivt på hva betinget sannsynlighet betyr. Vi legger fire røde ort og to svarte ort i en bune.
Dataøving 2. TTK5 Kalmanfiltrering og navigasjon Løsningsforslag
 Dataøving TTK5 Kalmanfiltrering og navigasjon Løsningsforslag Oppgave 1 a) Sammenhengen mellom pseudorange ρ og posisjon x i ECEF rammen når man har n satellitter er: q ρ i = (x si x) T (x si x)+cτ (1)
Dataøving TTK5 Kalmanfiltrering og navigasjon Løsningsforslag Oppgave 1 a) Sammenhengen mellom pseudorange ρ og posisjon x i ECEF rammen når man har n satellitter er: q ρ i = (x si x) T (x si x)+cτ (1)
Løsningsforslag til eksamen i TFY4205 Kvantemekanikk 12. august 2004
 NTNU Side 1 av 6 Institutt for fysi Faultet for naturvitensap og tenologi Løsningsforslag til esaen i TFY405 Kvanteeani 1. august 004 Dette løsningsforslaget er på 6 sider. Oppgave 1. To-diensjonal eletron-gass
NTNU Side 1 av 6 Institutt for fysi Faultet for naturvitensap og tenologi Løsningsforslag til esaen i TFY405 Kvanteeani 1. august 004 Dette løsningsforslaget er på 6 sider. Oppgave 1. To-diensjonal eletron-gass
Dato: fredag 14 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen. 1 Diskret tilstandsrommodell 2. 2 Stående pendel 4
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Regneoppgaver i GEOF110 Innføring i atmosfærens og havets dynamikk
 Regneoppgaver i GEOF110 Innføring i atmosfærens og havets dynamikk Dato 17. januar 2014 Oppgavegjennomgang, i hovedsak, fredager kl. 1015-1200 i Auditorium 105 helge.drange@gfi.uib.no 1. Polare koordinater
Regneoppgaver i GEOF110 Innføring i atmosfærens og havets dynamikk Dato 17. januar 2014 Oppgavegjennomgang, i hovedsak, fredager kl. 1015-1200 i Auditorium 105 helge.drange@gfi.uib.no 1. Polare koordinater
KONTINUASJONSEKSAMEN I EMNE TDT4230 VISUALISERING TIRSDAG 7. AUGUST 2007 KL LØSNINGSFORSLAG
 Side av 7 NTNU Norges tenis-naturvitensapelige universitet Faultet for fysi, inforati og ateati Institutt for datateni og inforasjonsvitensap KONTINUASJONSEKSAMEN I EMNE TT23 VISUALISERING TIRSAG 7. AUGUST
Side av 7 NTNU Norges tenis-naturvitensapelige universitet Faultet for fysi, inforati og ateati Institutt for datateni og inforasjonsvitensap KONTINUASJONSEKSAMEN I EMNE TT23 VISUALISERING TIRSAG 7. AUGUST
Andre obligatoriske oppgave stk 1100
 Andre obligatorise oppgave st 11 John Miael Modin 17. april 8 Oppgave 1 X er årsinteten til en tilfeldig valgt person i en befolningsgruppe. Sansynlighetstettheten til X er gitt ved { θ f X (x) = θ x θ
Andre obligatorise oppgave st 11 John Miael Modin 17. april 8 Oppgave 1 X er årsinteten til en tilfeldig valgt person i en befolningsgruppe. Sansynlighetstettheten til X er gitt ved { θ f X (x) = θ x θ
Enkel matematikk for økonomer. Del 1 nødvendig bakgrunn. Parenteser og brøker
 Vedlegg Enkel matematikk for økonomer I dette vedlegget går vi gjennom noen grunnleggende regneregler som brukes i boka. Del går gjennom de helt nødvendige matematikk-kunnskapene. Dette må du jobbe med
Vedlegg Enkel matematikk for økonomer I dette vedlegget går vi gjennom noen grunnleggende regneregler som brukes i boka. Del går gjennom de helt nødvendige matematikk-kunnskapene. Dette må du jobbe med
Anvendt Robotteknikk Konte Sommer 2019 EKSAMEN HARIS JASAREVIC
 2019 Anvendt Robotteknikk Konte Sommer 2019 EKSAMEN HARIS JASAREVIC Innhold Oppgaver... 2 Oppgave 1... 2 Oppgave 2... 2 Oppgave 3... 2 Oppgave 4... 2 Oppgave 5... 3 Oppgave 6... 4 Oppgave 7... 5 Oppgave
2019 Anvendt Robotteknikk Konte Sommer 2019 EKSAMEN HARIS JASAREVIC Innhold Oppgaver... 2 Oppgave 1... 2 Oppgave 2... 2 Oppgave 3... 2 Oppgave 4... 2 Oppgave 5... 3 Oppgave 6... 4 Oppgave 7... 5 Oppgave
Sensorveiledning eksamen ECON 3610/4610 Høst 2004
 1 Jon Vislie; november 2004 Sensorveiledning esamen ECO 3610/4610 Høst 2004 Modellen har fem lininger og sju variable (,n,m,,k,x og c); med to frihetsgrader i utgangspuntet og som an brues til å masimere
1 Jon Vislie; november 2004 Sensorveiledning esamen ECO 3610/4610 Høst 2004 Modellen har fem lininger og sju variable (,n,m,,k,x og c); med to frihetsgrader i utgangspuntet og som an brues til å masimere
Obligatorisk oppgave 4 i INF4400 for Jan Erik Ramstad
 Obligatoris oppgave i INF for Jan Eri Ramstad Jan Eri Ramstad Institutt for Informati Universitetet i Oslo janera@fys.uio.no. Mars6 6. april Bagrunn Worst case transient simulering NAND port Oppgave I
Obligatoris oppgave i INF for Jan Eri Ramstad Jan Eri Ramstad Institutt for Informati Universitetet i Oslo janera@fys.uio.no. Mars6 6. april Bagrunn Worst case transient simulering NAND port Oppgave I
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Løsningsforslag Eksamen i Fys-mek1110 våren 2010
 Side av Løsningsforslag Eksamen i Fys-mek våren Oppgave (Denne oppgaven teller dobbelt) Ole og Mari vil prøve om lengdekontraksjon virkelig finner sted. Mari setter seg i sitt romskip og kjører forbi Ole,
Side av Løsningsforslag Eksamen i Fys-mek våren Oppgave (Denne oppgaven teller dobbelt) Ole og Mari vil prøve om lengdekontraksjon virkelig finner sted. Mari setter seg i sitt romskip og kjører forbi Ole,
MAT 1001, høsten 2015 Oblig 2
 MAT 1001, høsten 2015 Oblig 2 Innleveringsfrist: Torsdag 5. november kl. 14:30 Det er lov til å samarbeide om løsning av oppgavene, men alle skal levere inn sin egen versjon. Husk å skrive på navn og kurskode
MAT 1001, høsten 2015 Oblig 2 Innleveringsfrist: Torsdag 5. november kl. 14:30 Det er lov til å samarbeide om løsning av oppgavene, men alle skal levere inn sin egen versjon. Husk å skrive på navn og kurskode
9 + 4 (kan bli endringer)
 Innlevering DAFE ELFE Matematikk HIOA Obligatorisk innlevering 4 Innleveringsfrist Onsdag 29. april 25 Antall oppgaver: 9 + 4 (kan bli endringer) Finn de ubestemte integralene a) 2x 3 4/x dx b) c) 2 5
Innlevering DAFE ELFE Matematikk HIOA Obligatorisk innlevering 4 Innleveringsfrist Onsdag 29. april 25 Antall oppgaver: 9 + 4 (kan bli endringer) Finn de ubestemte integralene a) 2x 3 4/x dx b) c) 2 5
Den kritiske lasten for at den skal begynne å bøye ut kalles knekklasten. Den avhenger av stavens elastiske egenskap og er gitt ved: 2 = (0.
 HIN Industriteni RA 5.11.03 Side 1 av 7 Kneing Staver Kneing er en elastis eller plastis ustabilitet som forårsaes av trspenninger. For å forstå fenomenet er det vanlig å starte med det enleste tilfelle,
HIN Industriteni RA 5.11.03 Side 1 av 7 Kneing Staver Kneing er en elastis eller plastis ustabilitet som forårsaes av trspenninger. For å forstå fenomenet er det vanlig å starte med det enleste tilfelle,
Om flo og fjære og kunsten å veie Månen
 Om flo og fjære og kunsten å veie Månen Jan Myrheim Institutt for fysikk NTNU 28. mars 2012 Innhold Målt flo og fjære i Trondheimsfjorden Teori for tidevannskrefter Hvordan veie Sola og Månen Friksjon
Om flo og fjære og kunsten å veie Månen Jan Myrheim Institutt for fysikk NTNU 28. mars 2012 Innhold Målt flo og fjære i Trondheimsfjorden Teori for tidevannskrefter Hvordan veie Sola og Månen Friksjon
TFY4115: Løsningsforslag til oppgaver gitt
 Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
Løsningsforslag Eksamen 1. desember 2008 TFY4250 Atom- og molekylfysikk/fy2045 Kvantefysikk
 Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
A.3.e: Ortogonale egenfunksjonssett
 TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
TFY4250/FY2045 Tillegg 2 1 Tillegg 2: A.3.e: Ortogonale egenfunksjonssett Ikke-degenererte egenverdier La oss først anta at en operator ˆF har et diskret og ikke-degeneret spektrum. Det siste betyr at
,QQOHGQLQJ 3-1/ )DJ 67( 6W\ULQJ DY URPIDUW \ / VQLQJVIRUVODJ WLO YLQJ
 3-1/ )DJ 67( 6W\LQJ DY RPIDW \ / VQLQJVIRVODJ WLO YLQJ,QQOHGQLQJ Der det er angitt referanser, er det underforstått at dette er til sider, figurer, ligninger, tabeller etc., i læreboken, dersom andre referanser
3-1/ )DJ 67( 6W\LQJ DY RPIDW \ / VQLQJVIRVODJ WLO YLQJ,QQOHGQLQJ Der det er angitt referanser, er det underforstått at dette er til sider, figurer, ligninger, tabeller etc., i læreboken, dersom andre referanser
SENSORS. HAIN An Integrated Acoustic Positioning and Inertial Navigation System
 SENSORS HAIN An Integrated Acoustic Positioning and Inertial Navigation System Hans Petter Jacobsen and Jan Erik Faugstadmo Session Chair Steve Browne, Thales Geo Solutions September 16-17, 2003 Houston,
SENSORS HAIN An Integrated Acoustic Positioning and Inertial Navigation System Hans Petter Jacobsen and Jan Erik Faugstadmo Session Chair Steve Browne, Thales Geo Solutions September 16-17, 2003 Houston,
Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].
![Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm]. Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].](/thumbs/58/41840831.jpg) Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Emne 10 Litt mer om matriser, noen anvendelser
 Emne 10 Litt mer om matriser, noen anvendelser (Reelle) ortogonale matriser La A være en reell, kvadratisk matrise, dvs. en (n n)-matrise hvor hvert element Da vil A være ortogonal dersom: og Med menes
Emne 10 Litt mer om matriser, noen anvendelser (Reelle) ortogonale matriser La A være en reell, kvadratisk matrise, dvs. en (n n)-matrise hvor hvert element Da vil A være ortogonal dersom: og Med menes
Fiktive krefter
 Fiktive krefter Materiale for: Fiktive krefter Spesiell relativitetsteori 02.05.2016 http://www.uio.no/studier/emner/matnat/fys/fys-mek1110/v16/materiale/ch17_18.pdf Ingen forelesning på torsdag (Himmelfart)
Fiktive krefter Materiale for: Fiktive krefter Spesiell relativitetsteori 02.05.2016 http://www.uio.no/studier/emner/matnat/fys/fys-mek1110/v16/materiale/ch17_18.pdf Ingen forelesning på torsdag (Himmelfart)
Prosjektoppgave i FYS-MEK 1110
 Prosjektoppgave i FYS-MEK 1110 03.05.2005 Kari Alterskjær Gruppe 1 Prosjektoppgave i FYS-MEK 1110 våren 2005 Hensikten med prosjektoppgaven er å studere Jordas bevegelse rundt sola og beregne bevegelsen
Prosjektoppgave i FYS-MEK 1110 03.05.2005 Kari Alterskjær Gruppe 1 Prosjektoppgave i FYS-MEK 1110 våren 2005 Hensikten med prosjektoppgaven er å studere Jordas bevegelse rundt sola og beregne bevegelsen
KORT INTRODUKSJON TIL TENSORER
 KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
Flervalgsoppgaver. Gruppeøving 8 Elektrisitet og magnetisme. 1. SI-enheten til magnetisk flukstetthet er tesla, som er ekvivalent med A. E.
 Flervalgsoppgaver 1. SI-enheten til magnetisk flukstetthet er tesla, som er ekvivalent med A. N s C m B. N C s m C. N m s 2 D. C A s E. Wb m 2 Løsning: F = q v B gir [B] = N Cm/s = N s C m. 2. Et elektron
Flervalgsoppgaver 1. SI-enheten til magnetisk flukstetthet er tesla, som er ekvivalent med A. N s C m B. N C s m C. N m s 2 D. C A s E. Wb m 2 Løsning: F = q v B gir [B] = N Cm/s = N s C m. 2. Et elektron
EKSAMEN I EMNE TDT4195 BILDETEKNIKK LØRDAG 26. MAI 2007 KL LØSNINGSFORSLAG - GRAFIKK
 Side av 7 NTNU Norges tenis-naturvitensapelige universitet Faultet for informasjonstenologi, matemati og eletroteni Institutt for datateni og informasjonsvitensap EKSAMEN I EMNE TDT495 BILDETEKNIKK LØRDAG
Side av 7 NTNU Norges tenis-naturvitensapelige universitet Faultet for informasjonstenologi, matemati og eletroteni Institutt for datateni og informasjonsvitensap EKSAMEN I EMNE TDT495 BILDETEKNIKK LØRDAG
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 10.2.27 a) Vi skal vise at u + v 2 = u 2 + 2u v + v 2. (1) Som boka nevner på side 581,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 10.2.27 a) Vi skal vise at u + v 2 = u 2 + 2u v + v 2. (1) Som boka nevner på side 581,
Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt.
 Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
Øving 4. a) Verifiser at en transversal bølge som forplanter seg langs x-aksen med utsving D med komponentene
 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 010. Veiledning: Tirsdag 1. og onsdag. september. Innleveringsfrist: Mandag 7. september kl 1:00. Øving 4 Oppgave 1 a) Verifiser at en transversal
FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 010. Veiledning: Tirsdag 1. og onsdag. september. Innleveringsfrist: Mandag 7. september kl 1:00. Øving 4 Oppgave 1 a) Verifiser at en transversal
Løsningsforslag til øving
 1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
1 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2012. Løsningsforslag til øving 11-2012 Oppgave 1 a) Forplantning i z-retning betyr at E og B begge ligger i xy-planet. La oss for eksempel
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
5.8 Iterative estimater på egenverdier
 5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
SG: Spinn og fiktive krefter. Oppgaver
 FYS-MEK1110 SG: Spinn og fiktive krefter 04.05.017 Oppgaver 1 GYROSKOP Du studerer bevegelsen til et gyroskop i auditoriet på Blindern og du måler at presesjonsbevegelsen har en vinkelhastighet på ω =
FYS-MEK1110 SG: Spinn og fiktive krefter 04.05.017 Oppgaver 1 GYROSKOP Du studerer bevegelsen til et gyroskop i auditoriet på Blindern og du måler at presesjonsbevegelsen har en vinkelhastighet på ω =
Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun standard enkel kalkulator, HP 30S
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Krefter, Newtons lover, dreiemoment
 Krefter, Newtons lover, dreiemoment Tor Nordam 13. september 2007 Krefter er vektorer En ting som beveger seg har en hastighet. Hastighet er en vektor, som vi vanligvis skriver v. Hastighetsvektoren har
Krefter, Newtons lover, dreiemoment Tor Nordam 13. september 2007 Krefter er vektorer En ting som beveger seg har en hastighet. Hastighet er en vektor, som vi vanligvis skriver v. Hastighetsvektoren har
Eksamen R2 høst 2011, løsning
 Eksamen R høst 0, løsning Oppgave (4 poeng) a) Deriver funksjonene f e ) Bruker produktregelen for derivasjon, uv uv uv f e e e e ) g sin Bruker kjerneregelen på uttrykket cos der u og g u sinu Vi har
Eksamen R høst 0, løsning Oppgave (4 poeng) a) Deriver funksjonene f e ) Bruker produktregelen for derivasjon, uv uv uv f e e e e ) g sin Bruker kjerneregelen på uttrykket cos der u og g u sinu Vi har
Test, 3 Sannsynlighet
 Test, Sannsynlighet Innhold. Pascals talltreant... 2.2 Kombinatori g sannsynlighetsberegning... 7. Sannsynlighetsberegninger.... Hypergeometris sannsynlighetsmodell....5 Binomis sannsynlighetsmodell...
Test, Sannsynlighet Innhold. Pascals talltreant... 2.2 Kombinatori g sannsynlighetsberegning... 7. Sannsynlighetsberegninger.... Hypergeometris sannsynlighetsmodell....5 Binomis sannsynlighetsmodell...
Egenverdier for 2 2 matriser
 Egenverdier for matriser (Bearbeidet versjon av tidligere notat på nett-sidene til MA101 - Lineær algebra og geometri Versjon oppdatert med referanser til 10utg av læreboken) Egenvektorer og egenverdier
Egenverdier for matriser (Bearbeidet versjon av tidligere notat på nett-sidene til MA101 - Lineær algebra og geometri Versjon oppdatert med referanser til 10utg av læreboken) Egenvektorer og egenverdier
UNIVERSITETET I OSLO
 Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014
 FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
TTK4100 Kybernetikk introduksjon Øving 1 - Løsningsforslag
 TTK4100 Kybernetikk introduksjon Øving 1 - Løsningsforslag Oppgave 1: UAV En AUV (Autonoous Underwater Vehicle) er et ubeannet undervannsfartøy so kan utføre selvstendige oppdrag under vann. I denne oppgaven
TTK4100 Kybernetikk introduksjon Øving 1 - Løsningsforslag Oppgave 1: UAV En AUV (Autonoous Underwater Vehicle) er et ubeannet undervannsfartøy so kan utføre selvstendige oppdrag under vann. I denne oppgaven
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Corioliskraften. Forsøk på å forstå et eksotisk fenomen Arnt Inge Vistnes, 27. mars 2006
 1 Corioliskraften Forsøk på å forstå et eksotisk fenomen Arnt Inge Vistnes, 27. mars 2006 Fiktive krefter I FYS-MEK/F1110 lærer vi om hvorfor det kan være praktisk å innføre fiktive krefter i visse sammenhenger.
1 Corioliskraften Forsøk på å forstå et eksotisk fenomen Arnt Inge Vistnes, 27. mars 2006 Fiktive krefter I FYS-MEK/F1110 lærer vi om hvorfor det kan være praktisk å innføre fiktive krefter i visse sammenhenger.
Eksamen i fag FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Kalmanfilter på svingende pendel
 Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
Dokking av AUV ved bruk av feiltilstandskalmanfilter
 Dokking av AUV ved bruk av feiltilstandskalmanfilter Kristine Elisabeth Aas Herje Master i kybernetikk og robotikk Innlevert: juni 217 Hovedveileder: Edmund Førland Brekke, ITK Medveileder: Are B. Willumsen,
Dokking av AUV ved bruk av feiltilstandskalmanfilter Kristine Elisabeth Aas Herje Master i kybernetikk og robotikk Innlevert: juni 217 Hovedveileder: Edmund Førland Brekke, ITK Medveileder: Are B. Willumsen,
LØSNINGSFORSLAG TIL EKSAMEN STE 6251 Styring av romfartøy
 HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi MSc-studiet Studieretning for romteknologi Side 1 av 4 LØSNINGSFORSLAG TIL EKSAMEN STE 6251 Styring av romfartøy Tid: Tirsdag 18.01.2005,
HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi MSc-studiet Studieretning for romteknologi Side 1 av 4 LØSNINGSFORSLAG TIL EKSAMEN STE 6251 Styring av romfartøy Tid: Tirsdag 18.01.2005,
LØSNINGSFORSLAG EKSAMEN FYS119 VÅR 2017
 LØSNINGSFORSLAG EKSAMEN FYS119 VÅR 2017 Oppgave 1 a) Bruker bevaring av bevegelsesmengde i - og y-retning og velger positiv -akse mot høyre og positiv y-akse oppover, og lar vinkelen være = 24. Dekomponerer
LØSNINGSFORSLAG EKSAMEN FYS119 VÅR 2017 Oppgave 1 a) Bruker bevaring av bevegelsesmengde i - og y-retning og velger positiv -akse mot høyre og positiv y-akse oppover, og lar vinkelen være = 24. Dekomponerer
UNIVERSITETET I OSLO
 vx [m/s] vy [m/s] Side UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: 3 mars 8 Tid for eksamen: 9: : (3 timer) Oppgavesettet er på 3 sider Vedlegg: Formelark
vx [m/s] vy [m/s] Side UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: 3 mars 8 Tid for eksamen: 9: : (3 timer) Oppgavesettet er på 3 sider Vedlegg: Formelark
7 Egenverdier og egenvektorer TMA4110 høsten 2018
 7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
Poissonprosesser og levetidsfordelinger
 Poissonprosesser og levetidsfordelinger Poissonfordeling som grensetilfelle for binomisk fordeling La X være binomisk fordelt med fordeling P (X = x) = ( ) n p x (1 p) n x, for x = 0, 1,... n. (1) x Forventningsverdien
Poissonprosesser og levetidsfordelinger Poissonfordeling som grensetilfelle for binomisk fordeling La X være binomisk fordelt med fordeling P (X = x) = ( ) n p x (1 p) n x, for x = 0, 1,... n. (1) x Forventningsverdien
Anvendt Robotteknikk Konte Sommer FASIT EKSAMEN HARIS JASAREVIC
 2019 Anvendt Robotteknikk Konte Sommer 2019 - FASIT EKSAMEN HARIS JASAREVIC Innhold Oppgaver... 2 Oppgave 1... 2 Oppgave 2... 3 Oppgave 3... 3 Oppgave 4... 3 Oppgave 5... 3 Oppgave 6... 4 Oppgave 7...
2019 Anvendt Robotteknikk Konte Sommer 2019 - FASIT EKSAMEN HARIS JASAREVIC Innhold Oppgaver... 2 Oppgave 1... 2 Oppgave 2... 3 Oppgave 3... 3 Oppgave 4... 3 Oppgave 5... 3 Oppgave 6... 4 Oppgave 7...
EKSAMENSOPPGAVE I FYS-1001
 side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
LØSNINGSFORSLAG TIL EKSAMEN STE 6251 Styring av romfartøy
 HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi MSc-studiet Studieretning for romteknologi Side 1 av 5 LØSNINGSFORSLAG TIL EKSAMEN STE 6251 Styring av romfartøy Tid: Torsdag 14.1.24,
HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi MSc-studiet Studieretning for romteknologi Side 1 av 5 LØSNINGSFORSLAG TIL EKSAMEN STE 6251 Styring av romfartøy Tid: Torsdag 14.1.24,
Generell informasjon om faget er tilgjengelig fra It s learning. 1 En kort oppsummering Adaptiv filtrering 2. 3 Prediksjon 4
 Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Newtons (og hele universets...) lover
 Newtons (og hele universets...) lover Kommentarer og referanseoppgaver (2.25, 2.126, 2.136, 2.140, 2.141, B2.7) Newtons 4 lover: (Gravitasjonsloven og Newtons første, andre og tredje lov.) GL: N I: N III:
Newtons (og hele universets...) lover Kommentarer og referanseoppgaver (2.25, 2.126, 2.136, 2.140, 2.141, B2.7) Newtons 4 lover: (Gravitasjonsloven og Newtons første, andre og tredje lov.) GL: N I: N III:
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
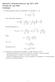 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
