Optimalregulering av lineært-kvadratisk-gaussisk system (LQG-regulering/H 2 -regulering) Oddvar Hallingstad
|
|
|
- Hilde Simensen
- 6 år siden
- Visninger:
Transkript
1 Optimalregulering av lineært-kvadratisk-gaussisk system (LQG-regulering/H 2 -regulering) Oddvar Hallingstad 22. april 2001
2 Kapittel 4 Kapittel 4: Kommentar: 4.1 : Dette notatet bygger på : Ching-Fang Lin : Advanced Control Systems Design, Printice Hall 1994 og er en del av faget SIE 38KB Robust multivariabel regulering ved UniK. Jeg har brukt samme kapittel-, tabell-, Þgur- og likningsnummerering som i boka. De referansene det er henvist til Þnnes i referanselista til Lin. Lin bruker en litt annen notasjon enn Rolf Henriksen så vær oppmerksom ved bruk av formlene i dette notatet! I dette notatet sies det hvor det blir tatt tavlebevis, men det gjelder SIE 38KB kurset og ikke SIE Lineære, kvadratiske, gaussiske (LQG) optimaliseringsproblem er en fundamental del av det generelle optimalreguleringsproblemet. Vi får for dette problemet en elegant løsning på slutta form. I dette kapittelet ser vi på basisproblema ved optimalisering av LQG-system. Figur 4-1 viser sammenhengen mellom H 2 - optimaliseringsproblema som blir behandlet i boka. LQ optimalreguleringsproblem (4.1) Singulære LQ optimaliseringsproblem (5) Null-sum LQ spill (6) Variasjoner på LQ problemet: : LQ regulator (4.2.1) Banefølging (4.2.2) Optimal støyundertrykking (4.2.3) Eksplisitt modellfølging (4.2.4) Implisitt modellfølging (4.2.5) LQ regulatordesign (4.3) LQG problem (4.4) Gjenoppretting av sløyfetransferfunksjonen for LQG regulatorer (4.5) Anvendelser : Missile autopilot (4.6) Store romstrukturer (4.7) Våpen styring (4.8) Integrert fly/flymotor reguleringssystem (4.9) Figur 4-1 Lineære kvadratiske optimalreguleringsproblem På neste side vises de nødvendige betingelsene som må oppfylles for et generelt ulineært optimalreguleringsproblem. Tabellen er hentet fra boka til O. A. Solheim : Optimalregulering. Legg merke til at tabellen viser de nødvendige betingelsene og gir en åpen-sløyve løsning. 2
3 Ole Andreas Solheim : Optimalregulering PROBLEM NØDVENDIGE BETINGELSER Avs Prosess Kriterium t2 Grenseb. Hamilton Kanonisk Minimums H o (t) Grenseb. x(t2) funksjon system prinsipp p o (t2) 3.2 úx = f(x,u) J = R t2 H = L(x,u) t1 +p T f (x,u) úx o = H p úp o = H x o o H o = H x o,u o,p o =min H x o,u,p o H o (t) =H o (t2) fri u U 3.3 fri H o (t) =H o (t o 2 )=0 3.4 gitt G(x 2 ) H o (t) =H o (t2) G(x o (t2)) fri úx = f(x,u,t) J = R t2 H = L(x,u,t) t1 +p T f (x,u,t) 3.6 J = S (x(t2)) + R t2 t1 L (x,u,t) dt gitt fri H o = H x o,u o,p o,t =min H x o,u,p o,t R t Ho 2 H (t) = t t dt o u U H o (t o 2 )=0 fri H o (t) =H o (t2) R t2 dt o t H t S x xo (t 2) G (x) = {x gi(x) =0,i=1, 2...n k} p G (x) p = n k X i=1 αi gi x k : dimensjonen på mangfoldigheten
4 Kapittel 4 Oppgave: 4.1 Finn det optimale pådraget for systemet úx 1 = u úx 2 = x 1 med grensebetingelser x(0) = 0,x(T )= og kriterium J = Z T 0 0 a u(t) dt hvor u U 4.1 Basis LQ-regulator problemet Problem: 4.1 LQ optimaliseringsproblem Bestem et tillatt pådrag u(t) U som minimaliserer kriteriet Z tf J = 1 2 xt (t f )S f x(t f )+ 1 2 t 0 x T Qx +2u T Cx + u T Ru dt (4-1) x og u tilfredsstiller prosesslikninga (bibetingelsen) úx = Ax + B 0 u, (A, B 0 ) antas styrbar (4-2) med grensebetingelser t 0 og t f er gitte, x (t 0 )=x 0, Dx(t f )=0 (4-3) Vi antar i dette kapittelet at S f = Sf T 0, Q = QT 0, R = R T > 0 U betegner mengden av tillatte pådrag (her antas mengden av stykkevis kontinuerlige funksjoner). Siden R er ikke-singulær kan vi alltid få systemet over på en form hvor C =0. Vi sløyfer derfor leddet med C senere. Tilfellet med R singulær (singulært LQ optimaliserings problem) behandles i kapittel Sluttstyringsregulator Problem: 4.2 Sluttstyringsproblemet Finn pådraget u(t) U som minimaliserer kriteriet J = 1 2 xt (t f )S f x(t f )+ 1 2 t 0 x T Qx + u T Ru dt (4-4) x og u tilfredsstiller prosesslikninga (bibetingelsen) úx = Ax + B 0 u, (A, B 0 ) antas styrbar med grensebetingelser t 0 og t f er gitte, x (t 0 )=x 0 Z tf Teorem: 4.1 Det optimale pådrag som løser sluttstyringsproblemet (åpen-sløyfe løsning) ovenfor er gitt ved u(t) = R 1 B0 T λ(t) (4-10) hvor λ(t) Þnnes ved å løse følgende to-punkts grenseverdiproblem (det kanoniske system) : úx(t) A B0 R = 1 B T ¾ 0 x(t) x(t úλ(t) Q A T, 0 ) = x 0 (4-12) λ(t) λ(t f ) = S f x(t f ) 4
5 4.2 Variasjoner av LQ-problemet Legg merke til at vi her får en åpen-sløyfe løsning. Vi skal nedenfor se at u kan uttrykkes ved x, dvs. en lukka-sløyfe løsning. Proof. Beviset tas på tavla. Teorem: 4.2 Det optimale pådrag som løser sluttstyringsproblemet (lukka-sløyfe løsning) ovenfor er gitt ved (transisjonsmatrise metoden) u(t) = R 1 B0 T S(t)x(t) (4-20) hvor S(t) =[Φ λx (t, t f )+Φ λλ (t, t f )S f ][Φ xx (t, t f )+Φ xλ (t, t f )S f ] 1 (4-21) Her er Φ(t, τ); t, τ [t 0,t f ] transisjonsmatrisa tilhørende likning (4-12),dvs. : A B0 R úφ(t, t f )= 1 B0 T Q A T Φ(t, t f ), Φ(t f,t f )=I Φxx (t, t Φ(t, t f )= f ) Φ xλ (t, t f ) Φ λx (t, t f ) Φ λλ (t, t f ) Proof. Beviset tas på tavla. Teorem: 4.3 Matrisa S(t) deþnert i likning (4-20) er løsning av følgende Riccatilikning : ús(t)+s(t)a + A T S(t)+Q S(t)B 0 R 1 B T 0 S(t) =0, S(t f )=S f (4-19) Riccatimatrisa kan enten Þnnes fra transisjonsmatrisa Φ(t, t f ) i (4-21) eller vi kan integrere (4-19) bakover itid.dersomq =0og systemet er tidsinvariant er løsningen av Riccatilikninga spesielt enkel. Proof. Beviset tas på tavla. 4.2 Variasjoner av LQ-problemet Vi skal i dette avsnittet se på noen spesialtilfeller av LQ-problemet Uendelig-horisont, tidsinvariant LQ-problem Dette er kanskje det viktigste optimalreguleringsproblemet. Problem: 4.3 Det lineære kvadratiske regulatorproblem (LQR) : Finn det pådraget u(t), t (0, ) idet tidsinvariante system úx = Ax + B 0 u, (A, B 0 ) antas styrbar (4-2) som minimaliserer kriteriet J = 1 Z (z T 1 z u T Ru)dt = 1 Z (x T Qx + u T Ru)dt Q = C1 T C 1 Hovedformålet med pådraget er her å regulere utgangen z 1 til 0 og samtidig stabilisere lukka-sløyfe systemet. Vektmatrisa R må balansere de motstridende krava om god regulering med lite forbruk av energi. Løsningen på problemet fås i grensetilfellet t forsystemetiavsnitt Teorem: 4.4 Løsningen på LQR problemet er u(t) = R 1 B T 0 Sx(t) 5
6 Kapittel 4 hvor den symmetriske matrisa S er konstant, positiv semideþnit og tilfredsstiller den algebraiske Riccatilikninga SA + A T S + Q SB 0 R 1 B T 0 S =0 Dersom (A, B 0 ) er styrbar og (C 1,A) er observerbar har denne likninga en entydig løsning. Og lukkasløyfe systemet úx =(A B 0 R 1 B T o S)x, x(0) = x 0 er asymptotisk stabilt. Proof. Beviset tas på tavla Trajektorfølging I et optimalt trajektorfølgingssystem skal utgangen z 1 (t) følge en ønska tidsvarierende trajektor z r (t) så nøyaktig som mulig under hensyntagen til hva det koster å bruke pådraget. I tillegg designer vi her systemet slik at det undertrykker en deterministisk forstyrrelse r(t). Teorem: 4.5 Det optimale pådrag u(t) som minimaliserer kriteriet J = 1 Z tf h i (z 2 1 z r ) T Q (z 1 z r )+u T Ru dt (4-23) t 0 med bibetingelse úx = Ax + B 0 u + B r r ; z 1 = C 1 x (4-24) hvor z r (t) og r(t) er kjente tidsfunksjoner, er gitt ved : u(t) = R 1 B0 T [S(t)x(t)+g(t)] = F (t)x(t) R 1 B0 T g(t) (4-30) hvor Riccatimatrisa S(t) og vektoren g(t) tilfredsstiller likningene : ús(t)+s(t)a + A T S(t)+C1 T QC 1 S(t)B 0 R 1 B0 T S(t) =0, S(t f )=0 (4-28) úg(t) = (A + B 0 F ) T T g(t) SB {z } r r(t)+c1 Qz r (t), g(t f )=0 (4-29) ÃT úx(t) =(A + B 0 F ) x(t) B {z } 0 R 1 B0 T g(t)+b r r (t) Ã Kommentar : Den optimale regulatoren består av en optimal tilbakekobling (samme som vi har uten kommando/forstyrrelse) og en foroverkobling fra ønska trajektor z r (t) og forstyrrelse r(t). Legg merke til at systemmatrisa for det tilbakekobla system og for g(t) er adjungerte. Vi ser at dersom lukka-sløyfe systemet er stabilt vil differensiallikninga for g(t) være ustabil. Både Riccatilikninga og differensiallikninga for g(t) løses bakover i tid. Proof. Bevises på tavla. Lineær kvadratisk regulator med konstant forstyrrelse. Dersomvårtsystemertidsinvariant,z r (t) =0 (dvs. vi ønsker å drive utgangen z 1 til 0) og forstyrrelsen er konstant, r(t) =r 0, vil (4-28) og (4-29) ha stasjonære løsninger, S og r, når t f.vifår: g = A T SB r r 0 = [A T + F T B0 T ] 1 SB r r 0 u(t) =Fx(t)+K FF r 0 F = R 1 B T 0 S K FF = R 1 B T 0 [A T + F T B T 0 ] 1 SB r (4-34a) (4-34b) (4-34c) Tips: 4.1 Tegn blokkskjema her 6
7 4.2.3 Optimal støyundertrykking 4.2 Variasjoner av LQ-problemet Effektspekteret for turbulens og andre stokastiske forstyrrelser som vi ønsker å ta hensyn til ved regulatordesign, er ofte ikke konstant i det aktuelle frekvensområdet. Vi må da modellere disse forstyrrelsene som farga støyprosesser. F.eks. modellerer vi ofte vindkast som en førsteordens prosess drevet av hvit støy, og vibrasjoner som et sett av oscillatoriske 2. ordens system. Ved å estimere tilstandene i støymodellene kan vi lage en tilbakekobling som motvirker disse forstyrrelsene. I utledninga som følger tilbakekobler vi direkte fra tilstandene i støyprosessene. Disse tilstandene er normalt ikke tilgjengelige slik at vi i praksis må tilbakekoble fra en estimator. Problem: 4.4 Vi antar at forstyrrelsen kan beskrives av følgende lineære tilstandsrommodell úx D = A D x D + B D w 1,y D = C D x D + D D w 1 (4-35) hvor x D er tilstanden til forstyrrelsen og y D selve forstyrrelsen, w 1 er en hvit støyprosess. Forstyrrelsen påvirker systemet på følgende måte : úx = Ax + B 0 u + A y y D = Ax + B 0 u + A 12 x D + B 12 w 1 (4-36) Matrisene A 12 og B 12 bestemmes av hvor forstyrrelsen påvirker systemet (dersom forstyrrelsen påvirker pådraget er A 12 = B 0 C D og B 12 = B 0 D D ). Bestem det optimale pådrag for å drive utgangen z 1 = C 1 x til 0. Dette problemet kan løses ved å lage en optimal regulator for den deterministiske delen av det utvidete system nedenfor. Ved å inkludere modellen av forstyrrelsen i systemlikningen (internal model prinsiple) får vi : úx A A12 x B0 B12 = + u + w úx D 0 A D x D 0 B 1 (4-37) D {z } {z } {z } {z } {z } x à x B 0 B 1 her er w 1 hvit støy. Vi ønsker så å bestemme den tilbakekoblinga u som minimaliserer J = 1 Z (z T 1 z u T Ru)dt hvor z 1 = C 1 x.systemet ernå 0. x = A x + B 0 u Dette optimal reguleringsproblemet ble løst i avsnitt : u = R 1 B 0 T S x = F x = x F 1 F 2 x D hvor S er løsningen av den algebraiske Riccatilikning for det utvidete system. Innsatt i (4-37) får vi nå følgende tilbakekobla system : úx A + B0 F = 1 A 12 + B 0 F 2 x B12 + w úx D 0 A D x D B 1 (4-39) D Egenverdiene til det lukka-system består av egenverdiene for A + B 0 F 1 og A D. Ved å sette opp Riccatilikninga vil vi se at F 1 er uavhengig av forstyrrelsesmodellen. Leddet F 2 x D virker som en foroverkobling og påvirker ikke stabiliteten til systemet, men reduserer system responsen på forstyrrelsen y D. F 2 x D blir en del av tilbakekoblingssløyfa dersom x D estimeres fra system responsen Design av et system for eksplisitt modellfølging (EMF) Problem: 4.5 Gitt systemet úx = Ax + B 0 u, z 1 = C 1 x Finn pådraget u som gjør at utgangen z 1 (t) fra systemet følger utgangen z d (t) fra et ideelt system úx d = A d x d + B d r, z d = C d x d (4-40a) (4-40b) 7
8 Kapittel 4 på en optimal måte. Her er r kommandoen vi påtrykker det ideelle systemet. I designen lar vi r være et sprang av ukjent størrelse. Likningene (4-40a) og (4-40b) kan slås sammen i ei utvidet systemlikning : úx A 0 x B0 0 = + u + r (4-41a) úxd 0 Ad x d 0 B d {z } {z } {z } {z } {z } x à x B 0 B r z 1 z d = x C 1 C d (4-41b) x d Problemet ovenfor kan nå formuleres som et optimaliseringsproblem hvor vi ønsker å bestemme den u som minimaliserer J = 1 Z tf ( z T 1 Q z u T Ru)dt (4-43) 0 og samtidig tilfredsstiller bibetingelsen (4-41a). Vi søker løsningen for tilfellet t f og r er en konstant. Dette problemet ble løst i avsnitt Dersom vi setter inn de matrisene vi har her får vi : u = F x + K FF r = F 1 x + F 2 x d + K FF r F = R 1 B 0 T S, K FF = R 1 B 0 T ( A T S B 0 R 1 B 0 T ) 1 S B r S er løsningen av Riccatilikninga S A + A T S + C T 1 Q C 1 S B 0 R 1 B T 0 S =0 Kommentarer : Formålet med eksplisitt modellfølging er å gi systemet samme responsen som et ideelt system. Metoden kan gi høye forsterkninger dersom vi ikke tuner forsterkningene skikkelig. Noen problemer som kan formuleres som eksplisitt modellfølging følging av longitudinal akselerasjonskommando følging av normal akselerasjonskommando følging av lateral akselerasjonskommando sideslipp kommandofølging rull kommandofølging rullhastighet kommandofølging Tilstrekkelige betingelser for perfekt modell matching (eksistens av forsterkningsmatrisene F 1,F 2 og K FF )er: rang B 0 =rang B 0 B d =rang B0 A d A Tilbakekoblinga F 1 gir stabilitetsforbedring, mens foroverkoblinga F 2 x d + K FF r gir følgeegenskapene Design av et system for implisitt modellfølging (IMF) Modellen som beskriver den ønska responsen kan også legges inn i kriteriet uten å utvide tilstandsvektoren. Den implisitte modellfølginga (IMF) gir lavere forsterkninger og er mer praktisk enn EMF. Metoden kalles også modell-i-kriteriet-teknikken. Problem: 4.6 Gitt systemet úx = Ax + B 0 u (4-46a) Finn et optimalt pådrag u slik at responsen til dette systemet ligger nærmest mulig repsonsen fra det ideelle systemet úx d = A d x d (4-46b) Feilen deþneres ved e =úx úx d (A A d )x + B 0 u (4-47) 8
9 4.3 Egenskaper til LQ-optimalregulering Vi ønsker her å lage en tilbakekobling bare fra x : u = Fx (4-48) Vi kan nå sette opp følgende tilnærma uttrykk for feilen : e =(A + B 0 F A d )x (4-49) En prosedyre som reduserer feilen e må derfor endre F slik at A + B 0 F nærmer seg A d. Dette oppnås ved å Þnne den optimale u som minimaliserer Z tf J = 1 (e T Qe + u T Ru)dt (4-50) 2 t 0 med bibetingelse (4-46a) og hvor e er gitt i (4-47). Vi setter så (4-47) inn i (4-50), fjerner kryssleddet mellom x og u (innfører u = M 1 N T x + u 1 )og bruker løsningen på standard problemet. Etter en del mellomregning får vi : u = M 1 (N T + B0 T S)x = Fx (4-53a) M = B0 T QB 0 + R N =(A A d ) T QB 0 L =(A A d ) T Q(A A d ) T ús + SA + A T S + L (SB 0 + N)M 1 (SB 0 + N) T =0, S(t f )=0 (4-53b) (4-53c) (4-53d) (4-53e) 4.3 Egenskaper til LQ-optimalregulering Kalmans identitet Vi skal her bevise Kalmans identitet som kan brukes til å vise viktige egenskaper for optimalt tilbakekoblede systemer. Siden stabiliteten og robustheten for et system bare påvirkes av tilbakekoblinga, ser vi her bort fra foroverkoblinga. Vi har tidligere vist at løsningen av LQR problemet for et lineært, tidsinvariant system úx = Ax + B 0 u, z 1 = C 1 x (4-54a) medkvadratiskkriterium J = 1 Z (z T 1 Qz u T Ru)dt (4-54b) 0 er u = Fx, F = R 1 B0 T S ¾ SA + A T S + C1 T QC 1 SB 0 R 1 B0 T S =0 (4-54c) Teorem: 4.6 Kalmans identitet Matrisene i den lineære kvadratiske regulatoren gitt i (4-54) tilfredsstiller følgende likhet i T i i T i hi F ( si A) 1 B 0 R hi F (si A) 1 B 0 = R+ hc 1 ( si A) 1 B 0 Q hc 1 (si A) 1 B 0 (4-59) Proof. Kalmans identitet Den algebraiske Riccatilikning i (4-54c) kan også skrives S( si + A)+(sI + A T )S + C1 T QC 1 SB 0 R 1 B0 T S =0 (4-57) Multiplikasjon av (4-57) med B0 T ( si AT ) 1 fra venstre, (si A) 1 B 0 fra høgre og innsetting av F = R 1 B0 T S gir (4-59) 9
10 Kapittel 4 Dersom vi har et SISO system og velger R =1iKalmanslikhet,fårvisidenQ 0 : i T i h1 F ( si A) 1 B 0 h1 F (si A) 1 B 0 1 (4-60) Dette betyr at Nyquist kurven ikke skjærer enhetssirkelen om ( 1, 0) i det komplekse plan, se Þgur 4-3. Dette betyr at den lineære kvadratiske regulatoren har følgende robusthetsegenskaper : Fasemarginen er minst ±60 og forsterkningsmarginen er. Im -1 Figur 4-3 Nyquist kurven for LQR Valg av Q-ogR-matrisene At et system er optimalt betyr bare at pådraget minimaliserer et gitt kriterium. Systemets oppførsel avhenger av vektmatrisene Q og R. Det kan være vanskelig å velge disse matrisene slik at systemet får de ønska egenskaper. Den generelle form på kriteriet er gitt i likning (4-54b) hvor z 1 representerer utgangen som skal styres eller feilen som skal minimaliseres. For ßy vilz 1 typisk uttrykke sideslipp, avvik fra banen, høydefeil, stillingsfeil, osv. Vanligvis vil både Q og R være forskjellige fra 0. For gitte vekter vil kriteriet J få en verdi som kan brukes som et mål for effektiviteten av regulatoren. Tuning av Q og R. Ved design av LQR må en gjøre en avveining av pådragets aktivitet og ytelsen til utgangen z 1. Dette gjøres ved en iterativ prosess hvor en systematisk endrer vektene i kriteriet. Følgende to metoderkanværenyttigevedvalgavdeførstevektmatrisene: 1. Den midlere kvadratiske verdi til hvert ledd i kriteriet bør i utgangspunktet gi omtrent samme bidrag til kriteriet. Dette kan oppnås på følgende måte : Q =diag(q 1,...,q n ), R =diag(r 1,...,r p1 ) > 0 (4-61) hvor en som første gjetning setter q i =[(z i ) max ] 2 og r i =[(u i ) max ] 2 (4-62) hvor subskriptet max angir den maksimale tillatte verdi. 2. Siden den veiede integrerte kost av utgangen z 1 blir tilnærmet lik den veiede integrerte kost for pådraget u, kan en starte med diagonalelementer i matrisene ovenfor som hhv. den inverse integrerte kvadratiske feil for de ønska tilstandene og pådragene. 3. Dersom systemet er stokastisk kan en bruke variansene som startverdier i vektmatrisene. Kommentarer : Når R eller Q 0 vil S 0 og F 0 i stabile åpen-sløyfe systemer. I ustabile åpen-sløyfe systemer vil F 6= 0og egenverdiene for det lukka system går mot de stabile 10
11 4.4 Lineært-kvadratisk-gaussisk (LQG) problem egenverdiene som er vhp. reßeksjonene av de ustabile hhp. polene. Dette kalles for minimum energi reguleringslova. Når R 0 eller Q vil tilbakekoblingsforsterkninga F og båndbredden øke. Valg av Q og R kan gjøres på basis av : ønska lukka-sløyfe egenverdier, egenvektorer og båndbredde R diagonal for å sikre robusthet størrelsen på nøkkelvariable inngangsdekobling innsikt vha. rotlokus integrert kvadratisk feil LQR med forming av frekvensgangen Det er ßere måter å oppnå forming av frekvensgangen for en LQR : Vi kan utvide systemet med et frekvensformet Þlter. Utgangen fra Þlteret kan så tas med i kriteriet sammen med de andre kostledda. F.eks. kan vi, dersom spekteret til ytelsesvektoren viser for mye energi i et visst frekvensområde for pådraget, utvide systemet med et Þlter (drevet av pådraget) som bare har respons i dette frekvensområdet. Vi tar så med utgangen fra Þlteret i kriteriet. I boka er det vist hvordan en kan oppnå frekvensforming av det lukka system ved å bruke Kalmans identitet. 4.4 Lineært-kvadratisk-gaussisk (LQG) problem LQR design antar at alle tilstandene er tilgjengelige for tilbakekobling. Det er ikke alltid tilfelle i praksis. Et mer realistisk problem enn LQR problemet i avsnitt er derfor det følgende. Problem: 4.7 Det lineære kvadratiske gaussiske (LQG) reguleringsproblem. Anta følgende system er gitt úx = Ax + B 0 u + B 1 w 1 prosesslikning (4-66a) y = C 0 x + v målelikning (4-66b) x(t 0 ) N(öx 0,P 0 ) w 1 (t) hvit med 0 middelverdi og spektraltetthhet lik W 0 v(t) hvit med 0 middelverdi og spektraltetthet lik V>0 x(t 0 ),w 1 (t) og v(t) er ukorrelerte støybeskrivelse Gitt målinga y(σ), σ [t 0,t], Þnn det pådraget u(τ), τ [t, t f ] som minimaliserer J = 1 Z tf ½x 2 E T (t f ) S f x(t f )+ x T Qx + u T Ru ¾ dt y(σ), σ [t 0,t] t (4-66c) (4-66d) Dette problemet kan løses ved å bruke separasjonsprinsippet. Teorem: 4.7Løsningen av LQG problemet Þnnes ved først å lage den optimale regulator for den deterministiske del av (4-66a) til (4-66d), deretter lages en optimal estimator (KalmanÞlter) for det stokastiske system (4-66a) til (4-66c). Siden tilstanden x ikke er tilgjengelig brukes öx istedet for x som inngang til regulatoren designet i trinn en. 11
12 Kapittel KalmanÞlter KalmanÞlteret for systemet gitt i likningene (4-66a) til (4-66c) er :. öx = Aöx + B 0 u + K KF (y C 0 öx), öx(t 0 )=öx 0 (4-67a) ú P = AP + PA T + B 1 WB T 1 PC T 0 V 1 C 0 P, P(t 0 )=P 0 (4-67b) K KF = PC0 T V 1 (4-67c) KalmanÞlteret vil avveie estimeringshastighet og støydempning. Filteret vil være stabilt når systemet er observerbart. Spektraltetthets matrisene W ogv kanses på somdesignmatriserfor ågiønskabåndbredde og respons til KalmanÞlteret. Den resulterende optimale LQG regulator vil bestå av KalmanÞlteret og den deterministiske regulatoren som vist i Þgur 4-4. LQG regulatoren gir generelt u = u FB + u FF hvor u FF er foroverkoblinga (i vårt LQG problem får vi bare en tilbakekobling). Tilbakekoblinga er her gitt ved u FB (t) =K FB öx(t), K FB = R 1 B0 T S (4-68) Optimal LQG regulator Prosess støy Optimal estimator (Kalman filter) Optimal regulator (som for deterministisk system) Prosess som skal reguleres Målestøy Sensor Figur 4-4 LQG regulator struktur Stasjonærløsningene av de to Riccatilikningene for LQG regulatoren Þnnes fra A T S + SA + C1 T QC 1 SB 0 R 1 B0 T S =0 ¾ AP + PA T + B 1 WB1 T PCT 0 V 1 (4-69) C 0 P =0 Design av KalmanÞlteret er det duale problem tillqrdesign.nårvibrukeretkalmanþlter for å estimere tilstandene, er forsterkningsmarginene til regulatoren ikke lenger sikret. En har sett at bruk av KalmanÞlteret kan redusere stabilitetsmarginene drastisk (se avsnitt 4.5) Egenskaper til en LQG basert regulator VeddesignavKalmanÞlteret har vi to matriser vi kan spille på. For å beholde robustheten og egenskapene til en LQR bør KalmanÞlteret lages slik at sløyfeforsterkninga blir tilnærmet lik den vi har ved full tilstandstilbakekobling. Figur 4-5 viser LQG regulatorstrukturen i detalj. 12
13 4.4 Lineært-kvadratisk-gaussisk (LQG) problem System G(s) w 1 B 1 r B r C 1 z 1 z r B 0 1 s 3 x y 0 C 0 v K FF Nominelt system A u FF 1 w 2 z 2 B 2 2 C 2 y u 2 - u FB - B r K KF K FB B 0 1 s ^x C 0 A Kalmanfilter Figur 4-5 Detaljert LQG regulatorstruktur 13
14 Kapittel 4 Kommentarer til Þgur 4-5 : 1. Transferfunksjonen fra kommandoen r til tilstanden x (pil 3) er den samme for den KF baserte regulatoren i Þgur 4-5 som for full tilstandstilbakekobling i Þgur Dersom vi bryter sløyfa ved pil 2 i Þgur 4-5 blir sløyfeforsterkningene omtrent de samme som for full tilstandstilbakekobling. 3. Dersom vi derimot bryter sløyfa ved pil 1 i Þgur 4-5 blir sløyfeforsterkningene forskjellige. Dette indikerer forskjeller i robustheten til de to systemene. Det viser seg at LQG-regulatoren kan ha vesentlig dårligere robusthet enn LQR. 4. Transientresponsen til LQG-regulatoren er forskjellig fra den til LQR. Som en måtte vente innfører KalmanÞlteret med sine n differensiallikninger en forsinkelse. 5. For å gi LQG-regulatoren tilsvarende sløyfeforsterkninger som LQR (for å sikre den samme robusthet og transientrespons) må en bruke LQG sløyfetransfergjenvinningsmetoden i avsnitt 4.5. Generelle kommentarer til regulatorer for stokastiske systemer En regulator for et stokastisk system vil ha to oppgaver (duale funksjoner) : a. estimere tilstandene basert på målingene b. realisere reguleringslova basert på informasjon fra estimatoren Generelt kan en få en interaksjon mellom de duale funksjonene til regulatoren a. usikkerhet om tilstanden kan føre til at regulatoren regulerer forsiktig (cautious control) sålenge det er stor usikkerhet om tilstanden b. regulatoren kan innføre ekstra eksitasjoner (probing action) som vil bedre estimerbarheten og dermed redusere framtidig tilstandsusikkerhet. Interaksjonen mellom de duale funksjonene til regulatoren kan karakteriseres ved følgende tre begrep : a. Separabilitet : Et stokastisk reguleringsproblem har separabilitetsegenskapen dersom den eneste informasjon reguleringslova trenger er estimatet av nåværende tilstand u = u(öx) b. Nøytralitet : Et stokastisk reguleringsproblem sies å være nøytralt dersom usikkerheten om tilstanden ikke avhenger av pådraget. c. Certainty equivalence : Et separabelt stokastisk reguleringsproblem sies å være certainty equivalent dersom formen på reguleringslova er den samme som for det ekvivalente deterministiske system. Et LQG problem tilfredsstiller kravet om certainty equivalence. Dette er det strengeste kravet og LQG problemet er derfor også både separabelt og nøytralt. Eksempel: 4.1 Cautious control Forskjellen mellom det optimale pådrag u o og certainty equivalence pådraget u c kalles ofte tilsiktet feil (intentional error). I dette eksempelet får vi en slik forskjell som skyldes at regulatoren blir forsiktig pga. støy. Vi har derimot ikke ekstra eksitasjoner (probing action) fordi det ikke er noen usikkerhet om tilstandene. Problemet er ikke separabelt, nøytralt og ikke certainty equivalent. Gitt x k+1 = ax k +(b + w k ) u k y k = x k hvor a og b er ukjente konstanter, w k er en sekvens av uavhengige, stokastiske variable med null middelverdi og varians lik σ 2. Dersom kriteriet som skal minimaliseres er ( X ) J = E 14 k=1 x 2 i
15 4.4 Lineært-kvadratisk-gaussisk (LQG) problem kan en vise at det optimale pådrag er gitt ved u o k = ab b 2 + σ 2 x k mens certainty equivalence pådraget er gitt ved u c k = a b x k Frekvenstolkning av en LQG-basert regulator Et forenkla blokkdiagram for Þgur 2-2, med B r og B 2 lik 0, y = C 0 x er utgangen for systemet og v og w = B 1 w 1 hvit støy med null middelverdi og spektraltetthets matriser V og W, ervistiþgur 4-6 w r=0 - K u G y v Figur 4-6 Blokkskjema for et tilbakekoblet system Vi kan sette opp følgende transferfunksjoner y(s) =(I + GK) 1 Gw(s) (I + GK) 1 GKv(s) (4-72) u(s) = (I + KG) 1 KGw(s) (I + KG) 1 Kv(s) (4-73) Vi deþnerer så sensitivitetsfunksjonen på inngangen og utgangen S i og S o, og de tilsvarende komplementære sensitivitets funksjonene T i og T 0 (merk : S i + T i = I, S o + T o = I): S o =(I + GK) 1, S i =(I + KG) 1 (4-74) T o = GK (I + GK) 1, T i =(I + KG) 1 KG (4-75) Ved å bruke Parsevals teorem får vi : J = 1 2 E R 0 z T Qz + u T Ru dt ª ¾ [z (jω)qz(jω)+u (4-76) (jω)ru(jω)] dω = 1 2π R 0 vedåsetteinnforz og u fra (4-72) til (4-76) Þnner en at LQG regulatoren minimaliserer en veiet sum som inneholder sensitivitets- og den komplementære sensitivitets funksjon. Kost- og støymatrisene (Q, R, V, W ) gir oss mulighet for å avveie sensitivitet og stabilitetsmarginer Reduksjon av dimensjonen på LQG-regulatoren Design av regulatorer for stokastiske MIMO systemer foregår vanligvis ved at en først lager et KalmanÞlter med full orden, for deretter å foreta en modellreduksjon uten vanligvis å tape noe særlig i ytelse og robusthet. Figur 4-7 illustrerer design prosessen fra en lineær regulator av høy orden til et mer praktisk design. 15
16 Kapittel 4 Forsterkningsmargin 60 grader fase margin 1. Design en deterministisk regulator med full tilstandstilbakekobling og forover-kobling (avsn ) Garantert Ikke garantert Tilfreds? 2. Design et Kalman filter av full orden (avsn. 4.4) Tilfreds? 3. Kombiner den deterministiske regulatoren av full orden med Kalman filteret av full orden Tilfreds? 4. Lag en lav-ordens og reoptimalisert regulator (avsn. 4.4) Tilfreds? Kandidat NGC system Figur 4-7 LQG designprosess Det Þns mange prinsipp for eliminering av tilstander i et KalmanÞlter. I boka er det omtalt 5 metoder hvorav bare to blir omtalt i noen detalj. 1. Modal metoden Her diagonaliseres først systemet. De modene som ikke blir eksitert blir eliminert. Raske moder med vesentlige eksitasjoner antar en svinger så raskt inn at de når stasjonærverdiene før resten av systemet. Stasjonærverdiene Þnnes ved å løse en algebraisk likning (setter úx raske =0) og løsningene settes så inn i det gjenværende system. Det reduserte KalmanÞlter må så tunes for å få den beste egenverdiplassering og dermed robusthet. 2. Modell reduksjon ved bruk av balansert realisering Dette er ifølge Lin en av de beste metodene. Denne metoden skiller subsystemer med dårlig observerbarhet/styrbarhet (disse tilstandene elimineres) fra de med god observerbarhet/styrbarhet. Metoden sikrer stabilitet dersom det opprinnelige system er stabilt. I Matlabs Control System Toolboks Þnns det funksjoner for balansert modellreduksjon. 16
17 4.5 LQG-loop transfer recovery methodology 4.5 LQG-loop transfer recovery methodology Hver for seg er den optimale tilstandsregulator og KalmanÞlteret svært robuste. Men det viser seg at satt sammen kan den totale regulatoren få vilkårlig liten stabilitetsmargin. Det vanlige råd en gir ved tilstandstilbakekobling - KalmanÞlterdesign er å gjøre KF mye raskere enn dynamikken til det tilbakekoblede systemet. En skulle derfor kanskje forvente at ved å ßytte egenverdiene til estimatoren, A K KF C 0, tilstrekkelig til venstre i det komplekse plan ville en få beholde robustheten på systeminngangen (pil 1 i Þgur 4-5). Dette viser seg ikke å være tilfellet. I visse tilfeller blir stabilitetsmarginene tvertimot dårligere. Eksempel: 4.2 Stabiliteten av en LQG-regulator (systemet er åpent-ustabilt). Gitt følgende system úx1 1 1 x1 0 1 = + u + w úx x 2 m 1 {z } {z } {z } {z } A x B 0 B 1 y = 1 0 x + v {z } C 0 ρ ρ Q =,R=1,W= σ, V=1 ρ ρ Under design av deterministisk regulator og KF setter vi m =1, B0 0 =. Riccati likninga for deterministisk 1 regulator : A T S + SA + Q S B 0 R 1 B 0 T S =0 Vi plukker ut den løsningen som gir S>0 : p p 4+2 (4 + ρ) 2+ (4 + ρ) S = 2+ p (4 + ρ) 2+ p (4 + ρ) p K FB = R 1 B0 T 2+ (4 + ρ) S = 2+ p (4 + ρ) {z } {z } = α 1 1 α α Vi kan så gjøre tilsvarende for KalmanÞlteret. AP + PA T + B 1 WB1 T PC0 T V 1 C 0 P =0 1 K KF = β, β =2+ 4+σ 1 Systemmatrisa for det tilbakekoblede system med estimator blir : A B A = 0 K FB K KF C 0 A K KF C 0 + B 0 K FB A = 0 1 mα mα β 0 1 β 1 β 0 β α 1 α det s s s s A Det karakteristiske polynom blir : s 4 + s 3 ( 4+α + β)+s 2 (6 + βα 2α 2β)+s (α + β 4+2(m 1)αβ)+1+(1 m)βα =0 Ifølge Rouths teorem er en tilstrekkelig betingelse for ustabilitet at en av koefþsientene i det karakteristiske polynom er negativ. Vi ser at for tilstrekkelig store α og β (ρ og σ) vil vi få ustabilitet dersom inngangsforsterkninga m får en vilkårlig liten endring fra designverdien 1. Dvs. LQG -regulatoren har vilkårlig liten forsterkningsmargin. Det Þns ßere metoder for å gjenvinne robustheten som en optimal deterministisk regulator har (loop transfer recovery - LTR). For et minimumfase system kan en argumentere som følger : Vi starter med en basis LQG regulator som ikke har den ønska robusthet på inngangen til prosessen. Ved å øke prosesstøyen på Þltermodellen (dvs. vi øker W) vil KalmanÞlteret tro at vi har mer prosessstøy enn vi i virkeligheten har. 17
18 Kapittel 4 KalmanÞlteret vil derfor behandle det som kommer inn på prosessen på en mer forsiktig måte. Og det kan vises av vi får en gjenvinning av robustheten når W [Anderson and Moore, 1989]. Systemet blir mer ufølsom overfor fase- og forsterkningsendringer på inngangen til systemet. Ettersom den prosesstøyen vi nå bruker ikke er den riktige vil naturlig nok systemet ikke lenger behandle prosesstøy og målestøy optimalt. Så vi må avveie robusthet og støyundertrykking. DetÞns en dual teknikk som gjenvinner utgangs robustheten. Metoden som blir presentert i Lin er mer en frekvensformingsmetode. LTR teknikker kan også anvendes på ikke-minimumfase systemer, men med forsiktighet. For fra syntese av regulatorer for SISO systemer vet vi at det kan være vanskelig eller umulig å lage en robust regulator for ikke-minimumfase systemer. 18
DESIGN AV KALMANFILTER. Oddvar Hallingstad UniK
 DESIGN AV KALMANFILTER Oddvar Hallingstad UniK Hva er et Kalmanfilter? Kalmanfilteret er en rekursiv algoritme som ved å prosessere målinger av inngangen og utgangen av et system og ved å utnytte en matematisk
DESIGN AV KALMANFILTER Oddvar Hallingstad UniK Hva er et Kalmanfilter? Kalmanfilteret er en rekursiv algoritme som ved å prosessere målinger av inngangen og utgangen av et system og ved å utnytte en matematisk
Tilstandsestimering Oppgaver
 University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
Tilstandsestimering Oppgaver
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks 203,
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks 203,
TTK4180 Stokastiske og adaptive systemer. Datamaskinøving 2 - Parameterestimering
 Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
Løsning til eksamen i IA3112 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge
 Løsning til eksamen i IA3112 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge Eksamensdato: 30.11 2016. Varighet 5 timer. Vekt i sluttkarakteren: 100%. Emneansvarlig: Finn Aakre Haugen (finn.haugen@hit.no).
Løsning til eksamen i IA3112 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge Eksamensdato: 30.11 2016. Varighet 5 timer. Vekt i sluttkarakteren: 100%. Emneansvarlig: Finn Aakre Haugen (finn.haugen@hit.no).
A 2 = PDP 1 PDP 1 = PD 2 P 1. og ved induksjon får vi. A k = PD k P 1. Kommentarer:
 5.3 Diagonalisering Det ville være fint om en matrise A var similær med en diagonalmatrise D: da har vi funnet egenverdiene, og kan f.eks. lett beregne A k. Når er dette tilfelle? Det er tema i denne seksjonen.
5.3 Diagonalisering Det ville være fint om en matrise A var similær med en diagonalmatrise D: da har vi funnet egenverdiene, og kan f.eks. lett beregne A k. Når er dette tilfelle? Det er tema i denne seksjonen.
NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER
 NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER SIE 3080 STOKASTISKE OG ADAPTIVE SYSTEMER Oddvar Hallingstad 0. februar 00 Vi skal her utlede noen nyttige formler for arbeidet med kovariansmatriser
NORMALFORDELINGER, KOVARIANSMATRISER OG ELLIPSOIDER SIE 3080 STOKASTISKE OG ADAPTIVE SYSTEMER Oddvar Hallingstad 0. februar 00 Vi skal her utlede noen nyttige formler for arbeidet med kovariansmatriser
Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun standard enkel kalkulator, HP 30S
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Løsningsforslag Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: Mandag 8 desember 28 Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: Mandag 8 desember 28 Lengde på eksamen: 4 timer Tillatte
Dato: fredag 14 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen. 1 Diskret tilstandsrommodell 2. 2 Stående pendel 4
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
5.8 Iterative estimater på egenverdier
 5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
Kapittel 6 Stabilitetsanalyse Oppgave 6.1 Stabilitetsegenskap for transferfunksjoner
 Figur 30: Oppgave 5.2: Frekvensresponsen fra T i til T for regulert system Kapittel 6 Stabilitetsanalyse Oppgave 6. Stabilitetsegenskap for transferfunksjoner Bestem stabilitetsegenskapen for følgende
Figur 30: Oppgave 5.2: Frekvensresponsen fra T i til T for regulert system Kapittel 6 Stabilitetsanalyse Oppgave 6. Stabilitetsegenskap for transferfunksjoner Bestem stabilitetsegenskapen for følgende
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: 21 februar 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen Bokmål
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: 21 februar 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen Bokmål
Løsningsforslag MAT 120B, høsten 2001
 Løsningsforslag MAT B, høsten Sett A = ( ) (a) Finn egenverdiene og egenvektorene til A ( ) λ =, e = ( λ =, e = ) (b) Finn matrisen e ta og den generelle løsningen på initialverdiproblemet Ẋ = AX, X()
Løsningsforslag MAT B, høsten Sett A = ( ) (a) Finn egenverdiene og egenvektorene til A ( ) λ =, e = ( λ =, e = ) (b) Finn matrisen e ta og den generelle løsningen på initialverdiproblemet Ẋ = AX, X()
Contents. Oppgavesamling tilbakekobling og stabilitet. 01 Innledende oppgave om ABC tilbakekobling. 02 Innledende oppgave om Nyquist diagram
 Contents Oppgavesamling tilbakekobling og stabilitet... Innledende oppgave om ABC tilbakekobling... Innledende oppgave om Nyquist diagram... 3 Bodeplott og stabilitet (H94 5)... 4 Bodediagram og stabilitet
Contents Oppgavesamling tilbakekobling og stabilitet... Innledende oppgave om ABC tilbakekobling... Innledende oppgave om Nyquist diagram... 3 Bodeplott og stabilitet (H94 5)... 4 Bodediagram og stabilitet
Løsning til eksamen i IA3112 Automatiseringsteknikk
 Løsning til eksamen i IA3112 Automatiseringsteknikk Eksamensdato: 03.12 2018. Varighet 5 timer. Emneansvarlig: Finn Aakre Haugen (finn.haugen@usn.no). Løsning til oppgave 1 (35%) a (5%) Massebalanse: ρ*a*dh/dt
Løsning til eksamen i IA3112 Automatiseringsteknikk Eksamensdato: 03.12 2018. Varighet 5 timer. Emneansvarlig: Finn Aakre Haugen (finn.haugen@usn.no). Løsning til oppgave 1 (35%) a (5%) Massebalanse: ρ*a*dh/dt
13 Oppsummering til Ch. 5.1, 5.2 og 8.5
 3 Oppsummering til Ch. 5. 5. og 8.5 3. Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A. I kalkulus (teori av differensiallikninger) er det viktig å beregne
3 Oppsummering til Ch. 5. 5. og 8.5 3. Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A. I kalkulus (teori av differensiallikninger) er det viktig å beregne
0 M. Z w Z q w M w M q q. M D G b 1 s
 US Navy s Deep Submergence Rescue Vehicle Oppgave 1 - DSRV DSRV kinematisk bevegelseslikninger x ucos wsin ż usin wcos q Dynamiske likninger for heave og pitch # m Z w Z q w M w I y M q q Z w Z q w M w
US Navy s Deep Submergence Rescue Vehicle Oppgave 1 - DSRV DSRV kinematisk bevegelseslikninger x ucos wsin ż usin wcos q Dynamiske likninger for heave og pitch # m Z w Z q w M w I y M q q Z w Z q w M w
Løsningsforslag øving 6
 TTK5 Reguleringsteknikk, Vår Løsningsforslag øving Oppgave Vi setter inntil videre at τ = e τs. a) Finn først h s) gitt ved h s) = T i s T s) + T i s) ) ) ) ) + ζ s ω + s ω Vi starter med amplitudeforløpet.
TTK5 Reguleringsteknikk, Vår Løsningsforslag øving Oppgave Vi setter inntil videre at τ = e τs. a) Finn først h s) gitt ved h s) = T i s T s) + T i s) ) ) ) ) + ζ s ω + s ω Vi starter med amplitudeforløpet.
Slik skal du tune dine PID-regulatorer
 Slik skal du tune dine PID-regulatorer Ivar J. Halvorsen SINTEF, Reguleringsteknikk PROST temadag Tirsdag 22. januar 2002 Granfos Konferansesenter, Oslo 1 Innhold Hva er regulering og tuning Enkle regler
Slik skal du tune dine PID-regulatorer Ivar J. Halvorsen SINTEF, Reguleringsteknikk PROST temadag Tirsdag 22. januar 2002 Granfos Konferansesenter, Oslo 1 Innhold Hva er regulering og tuning Enkle regler
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: Mandag 8 desember 2008 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: Mandag 8 desember 2008 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE
 AVDELING FOR INGENIØRUTDANNING ESAMENSOPPGAVE Emne: Gruppe(r): Eksamensoppgaven består av: ybernetikk I 2E Antall sider (inkl. forsiden): Emnekode: SO 318E Dato: Antall oppgaver: 6 Faglig veileder: Veslemøy
AVDELING FOR INGENIØRUTDANNING ESAMENSOPPGAVE Emne: Gruppe(r): Eksamensoppgaven består av: ybernetikk I 2E Antall sider (inkl. forsiden): Emnekode: SO 318E Dato: Antall oppgaver: 6 Faglig veileder: Veslemøy
NB! Vedlegg 2 skal benyttes i forbindelse med oppgave 3a), og vedlegges besvarelsen.
 SLUTTPRØVE EMNE: EE407 Kybernetikk videregående LÆRER Kjell Erik Wolden KLASSE(R): IA, EL DATO: 0..0 PRØVETID, fra - til (kl.): 9.00.00 Oppgavesettet består av følgende: Antall sider (inkl. vedlegg): 0
SLUTTPRØVE EMNE: EE407 Kybernetikk videregående LÆRER Kjell Erik Wolden KLASSE(R): IA, EL DATO: 0..0 PRØVETID, fra - til (kl.): 9.00.00 Oppgavesettet består av følgende: Antall sider (inkl. vedlegg): 0
Lineær analyse i SIMULINK
 Lineær analyse i SIMULINK Av Finn Haugen (finn@techteach.no) TechTeach (http://techteach.no) 20.12 2002 1 2 Lineær analyse i SIMULINK Innhold 1 Innledning 7 2 Kommandobasert linearisering av modeller 9
Lineær analyse i SIMULINK Av Finn Haugen (finn@techteach.no) TechTeach (http://techteach.no) 20.12 2002 1 2 Lineær analyse i SIMULINK Innhold 1 Innledning 7 2 Kommandobasert linearisering av modeller 9
Til enhver m n matrise A kan vi knytte et tall, rangen til A, som gir viktig informasjon.
 4.6 Rang Til enhver m n matrise A kan vi knytte et tall, rangen til A, som gir viktig informasjon. Definisjon: Rangen til en m n matrise A betegnes med rank A og er definert som dimensjonen til kolonnerommet
4.6 Rang Til enhver m n matrise A kan vi knytte et tall, rangen til A, som gir viktig informasjon. Definisjon: Rangen til en m n matrise A betegnes med rank A og er definert som dimensjonen til kolonnerommet
MAT UiO mai Våren 2010 MAT 1012
 200 MAT 02 Våren 200 UiO 0-2. 200 / 48 200 Betrakt et system x = A x der A M n (R) er diagonaliserbar. Vi har sett at systemet kan løses ved frakoblingsmetoden: Vi finner da P = [v v n ] (inverterbar)
200 MAT 02 Våren 200 UiO 0-2. 200 / 48 200 Betrakt et system x = A x der A M n (R) er diagonaliserbar. Vi har sett at systemet kan løses ved frakoblingsmetoden: Vi finner da P = [v v n ] (inverterbar)
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Lørdag 25. Mai 29. Tid for eksamen: :5 4:5. Oppgavesettet er på 7 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Lørdag 25. Mai 29. Tid for eksamen: :5 4:5. Oppgavesettet er på 7 sider. Vedlegg:
Kalmanfilter på svingende pendel
 Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk. Løsningsforslag Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: torsdag 6 desember Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: torsdag 6 desember Lengde på eksamen: 4 timer Tillatte
Kap. 5 Egenverdier og egenvektorer
 Kap. 5 Egenverdier og egenvektorer Egenverdier, egenvektorer og diagonaliserbarhet er sentrale begreper for kvadratiske matriser. Mye er kjent fra tidligere, skal repetere dette og gå videre. Sammenhengen
Kap. 5 Egenverdier og egenvektorer Egenverdier, egenvektorer og diagonaliserbarhet er sentrale begreper for kvadratiske matriser. Mye er kjent fra tidligere, skal repetere dette og gå videre. Sammenhengen
Computer Problem 1 TTK 4190 NavFart
 Computer Problem 1 TTK 419 NavFart Frode Efteland efteland@stud.ntnu.no 3 mars 24 Innhold 1 Oppgave 1 - DSRV 4 1.1 a)forwardspeedmodell... 5 1.1.1 Simulinkmodell... 6 1.1.2 Matlabplott... 7 1.1.3 Resultat...
Computer Problem 1 TTK 419 NavFart Frode Efteland efteland@stud.ntnu.no 3 mars 24 Innhold 1 Oppgave 1 - DSRV 4 1.1 a)forwardspeedmodell... 5 1.1.1 Simulinkmodell... 6 1.1.2 Matlabplott... 7 1.1.3 Resultat...
Løsning Eksamensrelevante oppgaver i ELE 3719 Matematikk Vektorer, matriser og lineær algebra Dato Februar Oppgave 1. (A) Vi leser av at
 Løsning Eksamensrelevante oppgaver i ELE 379 Matematikk Vektorer, matriser og lineær algebra Dato Februar 05 Oppgave. (A) Vi leser av at A = 3 5, B = ( 0 5 ), C = 0 5 9 og har dermed at π x = Ax + BT =
Løsning Eksamensrelevante oppgaver i ELE 379 Matematikk Vektorer, matriser og lineær algebra Dato Februar 05 Oppgave. (A) Vi leser av at A = 3 5, B = ( 0 5 ), C = 0 5 9 og har dermed at π x = Ax + BT =
12 Diagonalisering av matriser og operatorer (Ch. 5.1, 5.2 og 8.5)
 Diagonalisering av matriser og operatorer (Ch 5, 5 og 85) Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A I kalkulus (teori av differensiallikninger) er
Diagonalisering av matriser og operatorer (Ch 5, 5 og 85) Motivasjon Det er veldig viktig å kunne beregne funksjonsverdier f (A) for kvadratiske matriser A I kalkulus (teori av differensiallikninger) er
SLUTTPRØVE (Teller 60% av sluttkarakteren)
 Høgskolen i Telemark Avdeling for teknologiske fag SLUTTPRØVE (Teller 60% av sluttkarakteren) EMNE: EE4209 Modellbasert regulering LÆRERE Kjell - Erik Wolden og Hans - Petter Halvorsen KLASSE(R): 2IA DATO:
Høgskolen i Telemark Avdeling for teknologiske fag SLUTTPRØVE (Teller 60% av sluttkarakteren) EMNE: EE4209 Modellbasert regulering LÆRERE Kjell - Erik Wolden og Hans - Petter Halvorsen KLASSE(R): 2IA DATO:
Eksamensoppgave i TELE2001 Reguleringsteknikk
 Fakultet for teknologi Eksamensoppgave i TELE2001 Reguleringsteknikk Faglig kontakt under eksamen: Fredrik Dessen Tlf.: 48159443 Eksamensdato: 7. juni 2016 Eksamenstid (fra-til): 09:00 til 14:00 Hjelpemiddelkode/Tillatte
Fakultet for teknologi Eksamensoppgave i TELE2001 Reguleringsteknikk Faglig kontakt under eksamen: Fredrik Dessen Tlf.: 48159443 Eksamensdato: 7. juni 2016 Eksamenstid (fra-til): 09:00 til 14:00 Hjelpemiddelkode/Tillatte
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
LO510D Lin.Alg. m/graf. anv. Våren 2005
 TF Høgskolen i Sør Trøndelag Avdeling for informatikk og e læring LO5D Lin.Alg. m/graf. anv. Våren 5 Løsningsforslag Eksamen a) Setter α = og β = i ligningssystemet og gausseliminerer totalmatrisen til
TF Høgskolen i Sør Trøndelag Avdeling for informatikk og e læring LO5D Lin.Alg. m/graf. anv. Våren 5 Løsningsforslag Eksamen a) Setter α = og β = i ligningssystemet og gausseliminerer totalmatrisen til
MAT1120 Oppgaver til plenumsregningen torsdag 25/9
 MAT1120 Oppgaver til plenumsregningen torsdag 25/9 Øyvind Ryan (oyvindry@i.uio.no) September 2008 Oppgaver fra 5.1 Denisjon av egenverdier, egenvektorer, egenrom. Teorem 1 s. 306: Egenverdiene til en triangulær
MAT1120 Oppgaver til plenumsregningen torsdag 25/9 Øyvind Ryan (oyvindry@i.uio.no) September 2008 Oppgaver fra 5.1 Denisjon av egenverdier, egenvektorer, egenrom. Teorem 1 s. 306: Egenverdiene til en triangulær
MA1201/MA6201 Høsten 2016
 MA/MA6 Høsten 6 Norges teknisk naturvitenskapelige universitet Institutt for matematikk Løsningsforslag Øving Med forebehold om feil. Hvis du finner en, ta kontakt med Karin. Kapittel 6. a) Stemmer. Anta
MA/MA6 Høsten 6 Norges teknisk naturvitenskapelige universitet Institutt for matematikk Løsningsforslag Øving Med forebehold om feil. Hvis du finner en, ta kontakt med Karin. Kapittel 6. a) Stemmer. Anta
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE
 AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Emne: Gruppe(r): Eksamensoppgaven består av: Kybernetikk I E Antall sider (inkl. forsiden): 7 Emnekode: SO 8E Dato: 7. juni Antall oppgaver: Faglig veileder:
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Emne: Gruppe(r): Eksamensoppgaven består av: Kybernetikk I E Antall sider (inkl. forsiden): 7 Emnekode: SO 8E Dato: 7. juni Antall oppgaver: Faglig veileder:
5.5 Komplekse egenverdier
 5.5 Komplekse egenverdier Mange reelle n n matriser har komplekse egenverdier. Vi skal tolke slike matriser når n = 2. Ved å bytte ut R med C kan man snakke om komplekse vektorrom, komplekse matriser,
5.5 Komplekse egenverdier Mange reelle n n matriser har komplekse egenverdier. Vi skal tolke slike matriser når n = 2. Ved å bytte ut R med C kan man snakke om komplekse vektorrom, komplekse matriser,
LP. Kap. 17: indrepunktsmetoder
 LP. Kap. 17: indrepunktsmetoder simpleksalgoritmen går langs randen av polyedret P av tillatte løsninger et alternativ er indrepunktsmetoder de finner en vei i det indre av P fram til en optimal løsning
LP. Kap. 17: indrepunktsmetoder simpleksalgoritmen går langs randen av polyedret P av tillatte løsninger et alternativ er indrepunktsmetoder de finner en vei i det indre av P fram til en optimal løsning
c;'1 høgskolen i oslo
 c;'1 høgskolen i oslo Emne \ Emnekode Faglig veileder sa 318E Vesle møy Tyssø Bjørn EnqebretseQ ruppe(r) Dato' O, (jk.o{reksamenstid O.J 2E - 2004 -- 1ST ()~ -Ll..- j,elcsamensoppgav.ien består av Tillatte
c;'1 høgskolen i oslo Emne \ Emnekode Faglig veileder sa 318E Vesle møy Tyssø Bjørn EnqebretseQ ruppe(r) Dato' O, (jk.o{reksamenstid O.J 2E - 2004 -- 1ST ()~ -Ll..- j,elcsamensoppgav.ien består av Tillatte
Control Engineering. State-space Models. Hans-Petter Halvorsen
 Control Engineering State-space Models Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie,
Control Engineering State-space Models Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie,
= 3 11 = = 6 4 = 1.
 MAT3000/4000 Eksamen V3 Løsningsforslag Oppgave [0 poeng] Sjekk at 3 er en kvadratisk rest i Z/(3) og finn løsningene av likningen x = 3 i Z/(3) (uten å lage en tabell for x ) Du får lov til å bruke at
MAT3000/4000 Eksamen V3 Løsningsforslag Oppgave [0 poeng] Sjekk at 3 er en kvadratisk rest i Z/(3) og finn løsningene av likningen x = 3 i Z/(3) (uten å lage en tabell for x ) Du får lov til å bruke at
Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl Løysingsforslag:
 Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl. 09-15 Løysingsforslag: 1a Her er r 2 løysing av det karakteristiske polynomet med multiplisitet 2 pga. t-faktor. Det karakteristiske
Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl. 09-15 Løysingsforslag: 1a Her er r 2 løysing av det karakteristiske polynomet med multiplisitet 2 pga. t-faktor. Det karakteristiske
Tilstandsestimering Løsninger
 University College of Southeast Norway Tilstandsestimering Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
University College of Southeast Norway Tilstandsestimering Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
Quo vadis prosessregulering?
 Quo vadis prosessregulering? Morten Hovd PROST industrimøte Granfos, 24. Januar 2001 PROST Industrimøte, Granfos, 24. januar 2001 Hvor står vi? Et subjektivt bilde PROST Industrimøte, Granfos, 24. januar
Quo vadis prosessregulering? Morten Hovd PROST industrimøte Granfos, 24. Januar 2001 PROST Industrimøte, Granfos, 24. januar 2001 Hvor står vi? Et subjektivt bilde PROST Industrimøte, Granfos, 24. januar
7.4 Singulærverdi dekomposisjonen
 7.4 Singulærverdi dekomposisjonen Singulærverdi dekomposisjon til en matrise A er en av de viktigste faktoriseringene av A (dvs. A skrives som et produkt av matriser). Den inneholder nyttig informasjon
7.4 Singulærverdi dekomposisjonen Singulærverdi dekomposisjon til en matrise A er en av de viktigste faktoriseringene av A (dvs. A skrives som et produkt av matriser). Den inneholder nyttig informasjon
MAT Prøveeksamen 29. mai - Løsningsforslag
 MAT0 - Prøveeksamen 9 mai - Løsningsforslag Oppgave Sett A = 4 4 0 x 0, x = x, b =, x 0 og la v, v, v betegne kolonnevektorene til A a) Skriv A x = y som en vektorlikning x Svar : Siden A x = [v v v ]
MAT0 - Prøveeksamen 9 mai - Løsningsforslag Oppgave Sett A = 4 4 0 x 0, x = x, b =, x 0 og la v, v, v betegne kolonnevektorene til A a) Skriv A x = y som en vektorlikning x Svar : Siden A x = [v v v ]
Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: onsdag 24 november 2010 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: onsdag 24 november 2010 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Egenverdier og egenvektorer
 Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Kapittel 9 Egenverdier og egenvektorer Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer Hvis A er en m n-matrise, så gir A en transformasjon
Lineær algebra. 0.1 Vektorrom
 Lineær algebra Siden dette temaet er alt for stort til å kunne gjennomgås på en halvtime, med alle de teoremene og denisjonene som skal til, har jeg laget dette notatet. Det bygger hovedsakelig på notatene
Lineær algebra Siden dette temaet er alt for stort til å kunne gjennomgås på en halvtime, med alle de teoremene og denisjonene som skal til, har jeg laget dette notatet. Det bygger hovedsakelig på notatene
6 Modellering av smelteovn Modellering Tilstandsromform Diskretisering Observerbarthet Tidssteg...
 Stavanger, 28. mai 2019 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2019. Innhold 6 Modellering av smelteovn. 1 6.1 Modellering............................. 1 6.2 Tilstandsromform..........................
Stavanger, 28. mai 2019 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2019. Innhold 6 Modellering av smelteovn. 1 6.1 Modellering............................. 1 6.2 Tilstandsromform..........................
Gauss-Jordan eliminasjon; redusert echelonform. Forelesning, TMA4110 Fredag 18/9. Reduserte echelonmatriser. Reduserte echelonmatriser (forts.
 Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Løsningsforslag Eksamen i MIK130, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte
Utledning av Skogestads PID-regler
 Utledning av Skogestads PID-regler + +?!?!! (This version: August 0, 1998) 1 Approksimasjon av dynamikk (Skogestads halveringsregel) Vi ønsker å approksimere høyre ordens dynamikk som dødtid. Merk at rene
Utledning av Skogestads PID-regler + +?!?!! (This version: August 0, 1998) 1 Approksimasjon av dynamikk (Skogestads halveringsregel) Vi ønsker å approksimere høyre ordens dynamikk som dødtid. Merk at rene
Løsninger for eksamen i MAT Lineær algebra og M102 - Lineær algebra, fredag 28. mai 2004, Oppgave 1. M s = = 1 2 (cofm 2) T.
 Løsninger for eksamen i MAT - Lineær algebra og M - Lineær algebra, fredag 8. mai 4, (a) Finn determinanten til matrisen M s = Oppgave s uttrykt ved s, og bruk dette til å avgjøre for hvilke s matrisen
Løsninger for eksamen i MAT - Lineær algebra og M - Lineær algebra, fredag 8. mai 4, (a) Finn determinanten til matrisen M s = Oppgave s uttrykt ved s, og bruk dette til å avgjøre for hvilke s matrisen
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas.
 Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. Kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. Kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
Løsningsforslag Dataøving 2
 TTK45 Reguleringsteknikk, Vår 6 Løsningsforslag Dataøving Oppgave a) Modellen er gitt ved: Setter de deriverte lik : ẋ = a x c x x () ẋ = a x + c x x x (a c x ) = () x ( a + c x ) = Det gir oss likevektspunktene
TTK45 Reguleringsteknikk, Vår 6 Løsningsforslag Dataøving Oppgave a) Modellen er gitt ved: Setter de deriverte lik : ẋ = a x c x x () ẋ = a x + c x x x (a c x ) = () x ( a + c x ) = Det gir oss likevektspunktene
Stabilitetsanalyse. Kapittel Innledning
 Kapittel 6 Stabilitetsanalyse 6.1 Innledning I noen sammenhenger er det ønskelig å undersøke om, eller betingelsene for at, et system er stabilt eller ustabilt. Spesielt innen reguleringsteknikken er stabilitetsanalyse
Kapittel 6 Stabilitetsanalyse 6.1 Innledning I noen sammenhenger er det ønskelig å undersøke om, eller betingelsene for at, et system er stabilt eller ustabilt. Spesielt innen reguleringsteknikken er stabilitetsanalyse
Emnekode: Faglig veileder: Veslemøy Tyssø Bjørn Ena~bretsen. Gruppe(r): I Dato: Alle skrevne og trykte hjelpemidler, skrivesaker og kalkulator
 G høgskolen i oslo Emne: Kybemetikk Emnekode: to 358E Faglig veileder: Veslemøy Tyssø Bjørn Enabretsen. Gruppe(r): Dato: Eksamenstid: ST - 2E i 7. juni 2005 ' Eksamensoppgaven består av: forsiden): 7 5
G høgskolen i oslo Emne: Kybemetikk Emnekode: to 358E Faglig veileder: Veslemøy Tyssø Bjørn Enabretsen. Gruppe(r): Dato: Eksamenstid: ST - 2E i 7. juni 2005 ' Eksamensoppgaven består av: forsiden): 7 5
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning. 1 Stokastiske system og prosesser 2
 Stavanger, 4. august 016 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 4. august 016 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Observer HANS-PETTER HALVORSEN, 2012.02.24. Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Observer HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56,
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Observer HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56,
TMA4110 Matematikk 3 Eksamen høsten 2018 Løsning Side 1 av 9. Løsningsforslag. Vi setter opp totalmatrisen og gausseliminerer:
 TMA4 Matematikk 3 Eksamen høsten 8 Løsning Side av 9 Løsningsforslag Oppgave Vi setter opp totalmatrisen og gausseliminerer: 8 5 4 8 3 36 8 4 8 8 8 Den siste matrisen her er på redusert trappeform, og
TMA4 Matematikk 3 Eksamen høsten 8 Løsning Side av 9 Løsningsforslag Oppgave Vi setter opp totalmatrisen og gausseliminerer: 8 5 4 8 3 36 8 4 8 8 8 Den siste matrisen her er på redusert trappeform, og
Tilstandsestimering Løsninger
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Løsninger HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Løsninger HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks
Kap. 6 Ortogonalitet og minste kvadraters problemer
 Kap. 6 Ortogonalitet og minste kvadraters problemer vanlig indreprodukt (prikkprod.) i IR n, egenskaper. ortogonalitet i IR n Pythagoras teorem: u og v i IR n er ortogonale hvis og bare hvis u + v 2 =
Kap. 6 Ortogonalitet og minste kvadraters problemer vanlig indreprodukt (prikkprod.) i IR n, egenskaper. ortogonalitet i IR n Pythagoras teorem: u og v i IR n er ortogonale hvis og bare hvis u + v 2 =
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
Løsningsforslag øving 4
 TTK405 Reguleringsteknikk, Vår 206 Oppgave Løsningsforslag øving 4 Når k 50, m 0, f 20, blir tilstandsromformen (fra innsetting i likning (3.8) i boka) Og (si A) blir: (si A) [ ] [ ] 0 0 ẋ x + u 5 2 0.
TTK405 Reguleringsteknikk, Vår 206 Oppgave Løsningsforslag øving 4 Når k 50, m 0, f 20, blir tilstandsromformen (fra innsetting i likning (3.8) i boka) Og (si A) blir: (si A) [ ] [ ] 0 0 ẋ x + u 5 2 0.
MAT 1110: Bruk av redusert trappeform
 Tom Lindstrøm 10/5, 2006: MAT 1110: Bruk av redusert trappeform I Lays bok brukes den reduserte trappeformen til matriser til å løse en rekke problemer knyttet til ligningssystemer, lineærkombinasjoner,
Tom Lindstrøm 10/5, 2006: MAT 1110: Bruk av redusert trappeform I Lays bok brukes den reduserte trappeformen til matriser til å løse en rekke problemer knyttet til ligningssystemer, lineærkombinasjoner,
7 Egenverdier og egenvektorer TMA4110 høsten 2018
 7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
Egenverdier for 2 2 matriser
 Egenverdier for matriser (Bearbeidet versjon av tidligere notat på nett-sidene til MA101 - Lineær algebra og geometri Versjon oppdatert med referanser til 10utg av læreboken) Egenvektorer og egenverdier
Egenverdier for matriser (Bearbeidet versjon av tidligere notat på nett-sidene til MA101 - Lineær algebra og geometri Versjon oppdatert med referanser til 10utg av læreboken) Egenvektorer og egenverdier
Kap. 5 Egenverdier og egenvektorer
 Kap. 5 Egenverdier og egenvektorer Egenverdier, egenvektorer og diagonaliserbarhet er sentrale begreper for kvadratiske matriser. Mye er kjent fra tidligere, skal repetere dette og gå videre. Sammenhengen
Kap. 5 Egenverdier og egenvektorer Egenverdier, egenvektorer og diagonaliserbarhet er sentrale begreper for kvadratiske matriser. Mye er kjent fra tidligere, skal repetere dette og gå videre. Sammenhengen
MAT UiO. 10. mai Våren 2010 MAT 1012
 MAT Våren UiO. / 7 Betrakt et system x = A x der A M n (R) er diagonaliserbar. Vi har sett at systemet kan løses ved frakoblingsmetoden: Vi finner da P = [v v n ] (inverterbar) og D (diagonal) som diagonaliserer
MAT Våren UiO. / 7 Betrakt et system x = A x der A M n (R) er diagonaliserbar. Vi har sett at systemet kan løses ved frakoblingsmetoden: Vi finner da P = [v v n ] (inverterbar) og D (diagonal) som diagonaliserer
6.4 Gram-Schmidt prosessen
 6.4 Gram-Schmidt prosessen La W {0} være et endeligdimensjonalt underrom av R n. (Senere skal vi mer generelt betrakte indreprodukt rom; se seksjon 6.7). Vi skal se hvordan vi kan starte med en vanlig
6.4 Gram-Schmidt prosessen La W {0} være et endeligdimensjonalt underrom av R n. (Senere skal vi mer generelt betrakte indreprodukt rom; se seksjon 6.7). Vi skal se hvordan vi kan starte med en vanlig
Løsningsforslag øving 8
 K405 Reguleringsteknikk, Vår 206 Oppgave Løsningsforslag øving 8 a Vi begynner med å finne M 2 s fra figur 2 i oppgaveteksten. M 2 s ω r 2 ω h m sh a sh R2 sr 2 ω K v ω 2 h m sh a sh R2 sr 2 h m sh a sh
K405 Reguleringsteknikk, Vår 206 Oppgave Løsningsforslag øving 8 a Vi begynner med å finne M 2 s fra figur 2 i oppgaveteksten. M 2 s ω r 2 ω h m sh a sh R2 sr 2 ω K v ω 2 h m sh a sh R2 sr 2 h m sh a sh
Eksamen i ELE Matematikk valgfag Torsdag 18. mai Oppgave 1
 Eksamen i ELE79 - Matematikk valgfag Torsdag 8. mai 07 LØSNINGFORSLAG Oppgave (a) Den utvidede matrisen til likningssystemet er 6 Gausseliminasjon: ganger rad I legges til rad II: 0 0 Rad I trekkes fra
Eksamen i ELE79 - Matematikk valgfag Torsdag 8. mai 07 LØSNINGFORSLAG Oppgave (a) Den utvidede matrisen til likningssystemet er 6 Gausseliminasjon: ganger rad I legges til rad II: 0 0 Rad I trekkes fra
4.4 Koordinatsystemer
 4.4 Koordinatsystemer Minner om at B = { b 1, b 2,..., b n } V kalles en basis for et vektorrom V dersom B er lineært uavhengig og B utspenner V. I samme vektorrom kan vi innføre ulike koordinatsystemer
4.4 Koordinatsystemer Minner om at B = { b 1, b 2,..., b n } V kalles en basis for et vektorrom V dersom B er lineært uavhengig og B utspenner V. I samme vektorrom kan vi innføre ulike koordinatsystemer
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
Vektorligninger. Kapittel 3. Vektorregning
 Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
Kapittel Vektorligninger I denne uken skal vi bruke enkel vektorregning til å analysere lineære ligningssystemer. Vi skal ha et spesielt fokus på R, for det går an å visualisere; klarer man det, går det
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Lineær algebra Eksamensdag: Mandag,. desember 7. Tid for eksamen: 4. 8.. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Lineær algebra Eksamensdag: Mandag,. desember 7. Tid for eksamen: 4. 8.. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler:
Kalmanfilter HANS-PETTER HALVORSEN, 2012.02.24
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56, N-3901 Porsgrunn,
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56, N-3901 Porsgrunn,
Generell informasjon om faget er tilgjengelig fra It s learning. 1 En kort oppsummering Adaptiv filtrering 2. 3 Prediksjon 4
 Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Emne 10 Litt mer om matriser, noen anvendelser
 Emne 10 Litt mer om matriser, noen anvendelser (Reelle) ortogonale matriser La A være en reell, kvadratisk matrise, dvs. en (n n)-matrise hvor hvert element Da vil A være ortogonal dersom: og Med menes
Emne 10 Litt mer om matriser, noen anvendelser (Reelle) ortogonale matriser La A være en reell, kvadratisk matrise, dvs. en (n n)-matrise hvor hvert element Da vil A være ortogonal dersom: og Med menes
Løsning til eksamen i EE4107 Kybernetikk- videregående
 Høgskolen i elemark. Finn Haugen(finn.haugen@hit.no). Løsning til eksamen i EE4107 Kybernetikk- videregående Eksamensdato: 11.6 2009. Varighet 3 timer. Vekt i sluttkarakteren: 70%. Hjelpemidler: Ingen
Høgskolen i elemark. Finn Haugen(finn.haugen@hit.no). Løsning til eksamen i EE4107 Kybernetikk- videregående Eksamensdato: 11.6 2009. Varighet 3 timer. Vekt i sluttkarakteren: 70%. Hjelpemidler: Ingen
Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:
![Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene: Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:](/thumbs/64/52216522.jpg) HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
LP. Leksjon 7. Kapittel 13: Nettverk strøm problemer
 LP. Leksjon 7. Kapittel 13: Nettverk strøm problemer Skal studere matematiske modeller for strøm i nettverk. Dette har anvendelser av typen fysiske nettverk: internet, vei, jernbane, fly, telekommunikasjon,
LP. Leksjon 7. Kapittel 13: Nettverk strøm problemer Skal studere matematiske modeller for strøm i nettverk. Dette har anvendelser av typen fysiske nettverk: internet, vei, jernbane, fly, telekommunikasjon,
,QQOHGQLQJ 3-1/ )DJ 67( 6W\ULQJ DY URPIDUW \ / VQLQJVIRUVODJ WLO YLQJ
 3-1/ )DJ 67( 6W\ULQJ DY URPIDUW \ / VQLQJVIRUVODJ WLO YLQJ,QQOHGQLQJ Der det er angitt referanser, er det underforstått at dette er til sider, figurer, ligninger, tabeller etc., i læreboken, dersom andre
3-1/ )DJ 67( 6W\ULQJ DY URPIDUW \ / VQLQJVIRUVODJ WLO YLQJ,QQOHGQLQJ Der det er angitt referanser, er det underforstått at dette er til sider, figurer, ligninger, tabeller etc., i læreboken, dersom andre
Gammafordelingen og χ 2 -fordelingen
 Gammafordelingen og χ 2 -fordelingen Gammafunksjonen Gammafunksjonen er en funksjon som brukes ofte i sannsynlighetsregning. I mange fordelinger dukker den opp i konstantleddet. Hvis man plotter n-fakultet
Gammafordelingen og χ 2 -fordelingen Gammafunksjonen Gammafunksjonen er en funksjon som brukes ofte i sannsynlighetsregning. I mange fordelinger dukker den opp i konstantleddet. Hvis man plotter n-fakultet
Control Engineering. MathScript. Hans-Petter Halvorsen
 Control Engineering MathScript Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie, Parallel,
Control Engineering MathScript Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie, Parallel,
University College of Southeast Norway. Observer HANS-PETTER HALVORSEN.
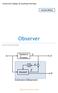 University College of Southeast Norway HANS-PETTER HALVORSEN http://home.hit.no/~hansha Forord Dette dokumentet tar for seg modellbasert regulering over temaet s og tilstandsestimering. Noen forenklinger
University College of Southeast Norway HANS-PETTER HALVORSEN http://home.hit.no/~hansha Forord Dette dokumentet tar for seg modellbasert regulering over temaet s og tilstandsestimering. Noen forenklinger
Opp til nå har problemstilling vart: Gitt en funksjon f, finn for hvilket verdier av de variabler f tar en bestemt verdi. Ax = b, f(x) = 0.
 Interpolasjon Opp til nå har problemstilling vart: Gitt en funksjon f, finn for hvilket verdier av de variabler f tar en bestemt verdi. 1/9 Ax = b, f(x) = 0. Ved interpolasjon, er problemet det motsatte:
Interpolasjon Opp til nå har problemstilling vart: Gitt en funksjon f, finn for hvilket verdier av de variabler f tar en bestemt verdi. 1/9 Ax = b, f(x) = 0. Ved interpolasjon, er problemet det motsatte:
Løsningsforslag til utvalgte oppgaver i kapittel 10
 Løsningsforslag til utvalgte oppgaver i kapittel 0 I kapittel 0 får du trening i å løse ulike typer differensialligninger, og her får du bruk for integrasjonsteknikkene du lærte i forrige kapittel. Men
Løsningsforslag til utvalgte oppgaver i kapittel 0 I kapittel 0 får du trening i å løse ulike typer differensialligninger, og her får du bruk for integrasjonsteknikkene du lærte i forrige kapittel. Men
Generell informasjon om faget er tilgjengelig fra It s learning. 7.1 Stokastisk prosess Lineær prediktor AR-3 prosess...
 Stavanger, 1. september 013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 7.1 Stokastisk prosess..........................
Stavanger, 1. september 013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 7.1 Stokastisk prosess..........................
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
Løsning til eksamen i IA3112 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge
 Løsning til eksamen i IA32 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge Eksamensdato: 24. 207. Varighet 5 timer. Emneansvarlig: Finn Aakre Haugen (finn.haugen@usn.no). Løsning til oppgave a (5%).
Løsning til eksamen i IA32 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge Eksamensdato: 24. 207. Varighet 5 timer. Emneansvarlig: Finn Aakre Haugen (finn.haugen@usn.no). Løsning til oppgave a (5%).
