Tilstandsestimering Oppgaver
|
|
|
- Are Ellefsen
- 8 år siden
- Visninger:
Transkript
1 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN, Faculty of Technology, Postboks 203, Kjølnes ring 56, N-3901 Porsgrunn, Norway. Tel: Fax:
2 Innholdsfortegnelse 1 Grunnlag Statistikk og Stokastiske systemer Foroverkobling Matriser Observerbarhet Tilstandsrommodeller Modellbasert PID tuning Kalmanfilter Innledning Kalmanfilter algoritmer Observer
3 1 Grunnlag Her er noen utvalgte oppgaver ifm den teoretiske bakgrunnen til tilstandsestimatorer som Kalmanfilter og Observer. 1.1 Statistikk og Stokastiske systemer Task 1: Middelverdi/Gjennomsnitt: Forklar begrepet middelverdi og sett opp uttrykket for middelverdien Finn middelverdien for følgende: Gitt følgende datasett: Sjekk svaret vha MathScript og LabVIEW Task 2: Forventningsverdi Forklar begrepet forventingsverdi Task 3: Varians Forklar begrepet varians Finn variansen for følgende: 3
4 4 Grunnlag Gitt følgende datasett: Sjekk svaret vha MathScript og LabVIEW Task 4: Standardavvik Forklar begrepet standardavvik Finn standardavviket for følgende: Gitt følgende datasett: Sjekk svaret vha MathScript og LabVIEW Task 5: Farget og Hvit støy Forklar hva vi mener med farget og hvit støy 1.2 Foroverkobling Task 6: Foroverkobling Vi ønsker å forbedre reguleringen av en vanntank, dvs. regulere nivået i en vanntanken. Vi måler nivået i tanken og bruker en vanlig PID regulator til å regulere nivået (bildet til venstre). Det renner vann ut fra tanken i bunnen som kan betraktes som en forstyrrelse og som gjør det vanskeligere å regulere nivået.
5 5 Grunnlag Matematisk modell for systemet: der er arealet i tanken, er pumpeforsterkning, er pådraget, er nivået i tanken, er utstømningen fra tanken. Vi ønsker å forbedre reguleringen av nivået ved å innføre en foroverkobling fra forstyrrelsen figur til høyre. Problemet er at vi med dagens prosess ikke måler utstrømningen, dermed ønsker vi å estimere denne, slik at dette estimatet kan inngå i reguleringen., se Tegn en skisse av reguleringssystemet med tilbakekobling og foroverkobling Design regulatoren som skal brukes i foroverkoblingen. 1.3 Matriser Task 7: Determinant Finn determinanten til følgende matrise (penn og papir): [ ]
6 6 Grunnlag Vis hvordan dette gjøres i MathScript Finn determinanten til følgende matrise: [ ] Vis hvordan dette gjøres i MathScript Task 8: Egenverdier Gitt en matrise. Sett opp formelen for å finne egenverdiene til A Sett opp den karakteristiske likning Sett opp det karakteristiske polynom Task 9: Egenverdier 2.ordens system Finn egenverdiene til følgende matrise: [ ] Bruk MathScript for å verifisere svaret ditt
7 7 Grunnlag Finn egenverdiene til følgende matrise: [ ] Bruk MathScript for å verifisere svaret ditt. Task 10: Egenverdier 3.ordens system Finn egenverdiene til følgende matrise: [ ] Bruk MathScript for å verifisere svaret ditt. 1.4 Observerbarhet Task 11: Utledning av Observerbarhetsmatrisen Utled uttrykket for Observerbarhetsmatrisen Task 12: Finn Observerbarhetsmatrisen Finn Observerbarhetsmatrisen for følgende system: [ ] [ ] [ ] [ ]
8 8 Grunnlag Vis hvordan dette gjøres i MathScript Task 13: Observerbarhet Gitt følgende blokkdiagram: u 6-1 s x1 2 1 s x2 2 Sjekk om systemet er Observerbart. Sett Bruk MathScript for å gjøre det samme 1.5 Tilstandsrommodeller Task 14: Tilstandsrommodell Gitt følgende system: eller [ ] der er arealet i tanken, er pumpeforsterkning, er pådraget, er nivået i tanken, er utstømningen fra tanken.
9 9 Grunnlag For det virkelige systemet blir kun nivået ( ) målt, så vi ønsker å benytte et Kalman Filter for estimering av utstømningen ( ). En generell tilstandsrommodell kan skrives: Vi setter og Vi antar at er konstant, dvs., Finn tilstandsrommodellen for systemet Finn matrisene tilstandsrommodellen. i Sjekk om systemet er Observerbart. Implementer modellen i MathScript/LabVIEW. Sjekk om systemet er Observerbart. Bruk og
10 10 Grunnlag Task 15: Diskretisering I forrige oppgave fant vi en kontinuerlig tilstandsrommodell av en vanntank. Finn den diskrete lineære tilstandsrommodellen på følgende form: Bruk Euler Forover hvor er samplingstiden. Finn matrisene. Bruk MathScript/LabVIEW for å verifisere svaret ditt. Sett. Sjekk om det diskrete systemet er Observerbart 1.6 Modellbasert PID tuning Task 16: Skogestad s metode Forklar Skogestad s metode for å finne PID parametrene i en PID regulator. Ta utgangspunkt i at prosessen er gitt ved følgende modell:
11 2 Kalmanfilter Her er noen utvalgte oppgaver ifm bruk av Kalmanfilter som tilstandsestimator. 2.1 Innledning Task 17: Hva er et Kalmanfilter? Hva er et Kalmanfilter? Gi en overordnet beskrivelse. Tegn og forklar. Task 18: Estimator - Kalmanfilter Sett opp de matematiske likningene for prosessen (systemet) og estimatoren. På bakgrunn av disse likningene sett opp et blokkdiagram. Forklar blokkdiagrammet. Task 19: Optimal Estimator Tegn og forklar hvorfor Kalmanfilteret betegnes som en optimal estimator? Task 20: Testing av Kalmanfilter Det lønner seg å teste ut Kalmanfilteret på en simulert prosess før du tar det i bruk på den virkelige prosessen. Du kan bruke f.eks. bruke LabVIEW, MATLAB eller andre simulerings- og programmeringsspråk. Forklar hvordan du vil teste dette 11
12 12 Kalmanfilter Task 21: Observerbarhet En nødvendig betingelse for at Kalmanfilteret skal virke ordentlig er at systemet er observerbart. Forklar dette begrepet og sett opp Observerbarhetsmatrisen. Task 22: Kovariansmatrisene Q og R Forklar disse kovariansmatrisene og. Task 23: Tuning av Kalmanfilteret Forklar hvordan du kan bruke og til å tune Kalmanfilteret. Task 24: Stasjonær Kalmanfilter forsterkning Hva menes med den stasjonære Kamanfilter forsterkningen? Hva slags informasjon er nødvendig for å finne/beregne den stasjonære Kalmanfilter forsterkningen? 2.2 Kalmanfilter algoritmer Task 25: Den generelle Kalmanfilter algoritmen
13 13 Kalmanfilter Sett opp de forskjellige stegene i Kalmanfilter-algoritmen og tegn et blokkdigram. Forklar blokkdiagrammet. Task 26: Ulike typer algoritmer Nevn 2 forskjellige Kalmanfilter-algoritmer og hva som er forskjellen på disse? Tegn blokkdiagram for disse. Task 27: Kalmanfilter-algoritmen for gitt system Gitt følgende system: hvor er pumpeforsterkningen Sett systemet opp på formen: Lag en diskret versjon av systemet vha Euler forover. ( ) ( ) Du kan også sette det diskrete systemet opp på formen: Sjekk svaret vha LabVIEW.
14 14 Kalmanfilter Sjekk om systemet er observerbart (penn og papir). Sett opp likningene i Kalmanfilter-algoritmen for dette systemet. Den generelle algoritmen er som følger: Steg 1: Finn måleestimatet ( ) Steg 2: Finn estimator-avviket Steg 3: Finn det korrigerte tilstandsestimatet Steg 4: Finn det predikerte (fremtidige) tilstandsestimatet ( ) Finn den statiske Kalman forsterkningen ( observerbart (i LabVIEW). ) vha LabVIEW. Sjekk også om systemet er Du kan bruke følgende kovariansmatriser: [ ] Tips! Følgende funksjoner i LabVIEW er kjekke å bruke: CD Contruct State-Space Model.vi CD Convert Continuous to Discrete.vi CD Observability Matrix.vi CD Kalman Gain.vi Du kan også bruke følgende: [ ]
15 15 Kalmanfilter Task 28: Kalmanfilter-algoritmen for vanntanken Sett opp likningene i Kalmanfilter-algoritmen for vanntanken basert på det diskrete systemet funnet i en tidligere oppgave. Systemet er gitt ved: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) Den generelle algoritmen er som følger: Steg 1: Finn måleestimatet ( ) Steg 2: Finn estimator-avviket Steg 3: Finn det korrigerte tilstandsestimatet Steg 4: Finn det predikerte (fremtidige) tilstandsestimatet ( )
16 16 Kalmanfilter Task 29: Dynamisk system Gitt følgende system: Tegn et blokkdiagram for systemet Finn Observerbarhetsmatrisen for systemet. Sjekk om systemet er Observerbart. Sett Kontroller svaret vha MathScript Lag en diskret versjon av systemet vha Euler forover. ( ) ( ) Bruk MathScript/LabVIEW for å verifisere svaret ditt. Sett. Sett opp likningene i Kalmanfilter-algoritmen for dette systemet. Den generelle algoritmen er som følger: Steg 1: Finn måleestimatet ( ) Steg 2: Finn estimator-avviket Steg 3: Finn det korrigerte tilstandsestimatet
17 17 Kalmanfilter Steg 4: Finn det predikerte (fremtidige) tilstandsestimatet ( )
18 3 Observer Her er noen utvalgte oppgaver ifm bruka av Observer som tilstandsestimator. Task 30: Observer Forklar prinsippene for en Observer. Task 31: Alternativer - Observers Fordeler/ulemper Kalmanfilter/ Observers? Task 32: Butterworth polynom 2. orden En enkel måte å finne egenverdiene på er å bruke Butterworth egenverdiene fra Butterworth polynomet. Gitt: [ ] [ ] Finn Observerforsterkningsmatrisen K (penn og papir). Bruk MathScript og Ackerman (funksjonen heter acker()) og finn Observerforsterkningsmatrisen K vha denne. Sammenlign resultatet med dine utregninger. Task 33: Butterworth polynom 3. orden En enkel måte å finne egenverdiene på er å bruke Butterworth egenverdiene fra Butterworth polynomet. 18
19 19 Observer Gitt: [ ] [ ] Bruk et 3.ordens Butterworth filter og finn (penn og papir). Bruk MathScript og Ackerman (funksjonen heter acker()) og finn Observerforsterkningsmatrisen K vha denne. Sammenlign resultatet med dine utregninger. Task 34: Blokkdiagram Gitt følgende system: u 3 x ,5s s x2 Finn tilstandsrommodellen til systemet Tips! Konverter systemet til en tilstandsrommodell på formen: Tip! Bruk Inverse Laplace. Sett Sjekk om systemet er Observerbart (penn og papir). Kontroller svaret vha MathScript. Lag en diskret versjon av systemet vha Euler forover. ( ) ( )
20 20 Observer Sett opp likningene som inngår i Observeren basert på dette systemet.
21 Telemark University College Faculty of Technology Kjølnes Ring 56 N-3914 Porsgrunn, Norway Hans-Petter Halvorsen, M.Sc. Telemark University College Faculty of Technology Department of Electrical Engineering, Information Technology and Cybernetics Blog:
Tilstandsestimering Oppgaver
 University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
Tilstandsestimering Løsninger
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Løsninger HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Løsninger HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks
Observer HANS-PETTER HALVORSEN, 2012.02.24. Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Observer HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56,
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Observer HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56,
Kalmanfilter HANS-PETTER HALVORSEN, 2012.02.24
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56, N-3901 Porsgrunn,
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics HANS-PETTER HALVORSEN, 2012.02.24 Faculty of Technology, Postboks 203, Kjølnes ring 56, N-3901 Porsgrunn,
Systemidentifikasjon Oppgaver
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Systemidentifikasjon Oppgaver HANS-PETTER HALVORSEN, 2012.03.16 Faculty of Technology, Postboks
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Systemidentifikasjon Oppgaver HANS-PETTER HALVORSEN, 2012.03.16 Faculty of Technology, Postboks
Tilstandsestimering Løsninger
 University College of Southeast Norway Tilstandsestimering Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
University College of Southeast Norway Tilstandsestimering Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
SLUTTPRØVE (Teller 60% av sluttkarakteren)
 Høgskolen i Telemark Avdeling for teknologiske fag SLUTTPRØVE (Teller 60% av sluttkarakteren) EMNE: EE4209 Modellbasert regulering LÆRERE Kjell - Erik Wolden og Hans - Petter Halvorsen KLASSE(R): 2IA DATO:
Høgskolen i Telemark Avdeling for teknologiske fag SLUTTPRØVE (Teller 60% av sluttkarakteren) EMNE: EE4209 Modellbasert regulering LÆRERE Kjell - Erik Wolden og Hans - Petter Halvorsen KLASSE(R): 2IA DATO:
University College of Southeast Norway. Observer HANS-PETTER HALVORSEN.
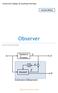 University College of Southeast Norway HANS-PETTER HALVORSEN http://home.hit.no/~hansha Forord Dette dokumentet tar for seg modellbasert regulering over temaet s og tilstandsestimering. Noen forenklinger
University College of Southeast Norway HANS-PETTER HALVORSEN http://home.hit.no/~hansha Forord Dette dokumentet tar for seg modellbasert regulering over temaet s og tilstandsestimering. Noen forenklinger
Systemidentifikasjon Oppgaver
 University College of Southeast Norway Systemidentifikasjon Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Innledning... 3 2 Minste kvadraters metode... 4 3 Validering...
University College of Southeast Norway Systemidentifikasjon Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Innledning... 3 2 Minste kvadraters metode... 4 3 Validering...
Control Engineering. State-space Models. Hans-Petter Halvorsen
 Control Engineering State-space Models Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie,
Control Engineering State-space Models Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie,
Tilstandsrommodeller. Hans- Pe1er Halvorsen, M.Sc.
 Tilstandsrommodeller Hans- Pe1er Halvorsen, M.Sc. Tilstandsrom- modeller Dataverktøy Spesial>lfelle MathScript LabVIEW Differensial - likninger Tidsplanet Laplace Blokk- diagrammer Transfer- funksjoner
Tilstandsrommodeller Hans- Pe1er Halvorsen, M.Sc. Tilstandsrom- modeller Dataverktøy Spesial>lfelle MathScript LabVIEW Differensial - likninger Tidsplanet Laplace Blokk- diagrammer Transfer- funksjoner
Systemidentifikasjon Løsninger
 University College of Southeast Norway Systemidentifikasjon Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Innledning... 3 2 Minste kvadraters metode... 7 3 Validering...
University College of Southeast Norway Systemidentifikasjon Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Innledning... 3 2 Minste kvadraters metode... 7 3 Validering...
University College of Southeast Norway. Kalmanfilter HANS-PETTER HALVORSEN,
 University College of Southeast Norway HANS-PETTER HALVORSEN, 2016.11.01 http://home.hit.no/~hansha Forord Dette dokumentet tar for seg grunnleggende modellbasert regulering over temaet. Noen forenklinger
University College of Southeast Norway HANS-PETTER HALVORSEN, 2016.11.01 http://home.hit.no/~hansha Forord Dette dokumentet tar for seg grunnleggende modellbasert regulering over temaet. Noen forenklinger
Control Engineering. Stability Analysis. Hans-Petter Halvorsen
 Control Engineering Stability Analysis Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie,
Control Engineering Stability Analysis Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie,
Control Engineering. MathScript. Hans-Petter Halvorsen
 Control Engineering MathScript Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie, Parallel,
Control Engineering MathScript Hans-Petter Halvorsen Dataverktøy MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/ Implementering Reguleringsteknikk Serie, Parallel,
Stabilitetsanalyse. Hans- Pe/er Halvorsen, M.Sc.
 Stabilitetsanalyse Hans- Pe/er Halvorsen, M.Sc. Tilstandsrom- modeller Dataverktøy Spesial@lfelle MathScript LabVIEW Differensial - likninger Tidsplanet Laplace Blokk- diagrammer Transfer- funksjoner 2.orden
Stabilitetsanalyse Hans- Pe/er Halvorsen, M.Sc. Tilstandsrom- modeller Dataverktøy Spesial@lfelle MathScript LabVIEW Differensial - likninger Tidsplanet Laplace Blokk- diagrammer Transfer- funksjoner 2.orden
Kalmanfilter på svingende pendel
 Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
Systemidentifikasjon
 University College of Southeast Norway HANS-PETTER HALVORSEN http://home.hit.no/~hansha Forord Dette dokumentet brukes som forelesningsnotater i modellbasert regulering over temaet systemidentifikasjon.
University College of Southeast Norway HANS-PETTER HALVORSEN http://home.hit.no/~hansha Forord Dette dokumentet brukes som forelesningsnotater i modellbasert regulering over temaet systemidentifikasjon.
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: 21 februar 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen Bokmål
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: 21 februar 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen Bokmål
MathScript. Hans- Pe1er Halvorsen, M.Sc.
 MathScript Hans- Pe1er Halvorsen, M.Sc. Ja! De1e er et IA fag dvs. både AutomaFsering og InformaFkk! Arbeidslivet krever anvendt kunnskap! Tilstandsrom- modeller Dataverktøy SpesialFlfelle MathScript LabVIEW
MathScript Hans- Pe1er Halvorsen, M.Sc. Ja! De1e er et IA fag dvs. både AutomaFsering og InformaFkk! Arbeidslivet krever anvendt kunnskap! Tilstandsrom- modeller Dataverktøy SpesialFlfelle MathScript LabVIEW
2-Tank System. Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics 2-Tank System Hans- Petter Halvorsen, 2013.06.20 Faculty of Technology, Postboks 203, Kjølnes ring
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics 2-Tank System Hans- Petter Halvorsen, 2013.06.20 Faculty of Technology, Postboks 203, Kjølnes ring
Dato: fredag 14 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen. 1 Diskret tilstandsrommodell 2. 2 Stående pendel 4
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for elektroteknikk og databehandling Eksamen i MIK130, Systemidentifikasjon Dato: Mandag 28. november 2005 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for elektroteknikk og databehandling Eksamen i MIK130, Systemidentifikasjon Dato: Mandag 28. november 2005 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun standard enkel kalkulator, HP 30S
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Stabilitetsanalyse i MATLAB og LabVIEW
 Stabilitetsanalyse i MATLAB og LabVIEW Av Finn Haugen (finn@techteach.no) TechTeach (http://techteach.no) 21.12 2002 1 2 TechTeach Innhold 1 Stabilitetsanalyse i MATLAB og LabVIEW 7 1.1 MATLAB... 7 1.1.1
Stabilitetsanalyse i MATLAB og LabVIEW Av Finn Haugen (finn@techteach.no) TechTeach (http://techteach.no) 21.12 2002 1 2 TechTeach Innhold 1 Stabilitetsanalyse i MATLAB og LabVIEW 7 1.1 MATLAB... 7 1.1.1
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk. Løsningsforslag Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: torsdag 6 desember Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: torsdag 6 desember Lengde på eksamen: 4 timer Tillatte
DESIGN AV KALMANFILTER. Oddvar Hallingstad UniK
 DESIGN AV KALMANFILTER Oddvar Hallingstad UniK Hva er et Kalmanfilter? Kalmanfilteret er en rekursiv algoritme som ved å prosessere målinger av inngangen og utgangen av et system og ved å utnytte en matematisk
DESIGN AV KALMANFILTER Oddvar Hallingstad UniK Hva er et Kalmanfilter? Kalmanfilteret er en rekursiv algoritme som ved å prosessere målinger av inngangen og utgangen av et system og ved å utnytte en matematisk
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning. med Kalman-filter og RLS.
 Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Artikkelserien Reguleringsteknikk
 Finn Haugen (finn@techteach.no) 18. november, 2008 Artikkelserien Reguleringsteknikk Dette er artikkel nr. 7 i artikkelserien Reguleringsteknikk: Artikkel 1: Reguleringsteknikkens betydning og grunnprinsipp.
Finn Haugen (finn@techteach.no) 18. november, 2008 Artikkelserien Reguleringsteknikk Dette er artikkel nr. 7 i artikkelserien Reguleringsteknikk: Artikkel 1: Reguleringsteknikkens betydning og grunnprinsipp.
TTK4180 Stokastiske og adaptive systemer. Datamaskinøving 2 - Parameterestimering
 Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
Kapittel 6 Stabilitetsanalyse Oppgave 6.1 Stabilitetsegenskap for transferfunksjoner
 Figur 30: Oppgave 5.2: Frekvensresponsen fra T i til T for regulert system Kapittel 6 Stabilitetsanalyse Oppgave 6. Stabilitetsegenskap for transferfunksjoner Bestem stabilitetsegenskapen for følgende
Figur 30: Oppgave 5.2: Frekvensresponsen fra T i til T for regulert system Kapittel 6 Stabilitetsanalyse Oppgave 6. Stabilitetsegenskap for transferfunksjoner Bestem stabilitetsegenskapen for følgende
KYBERNETIKKLABORATORIET. FAG: Kybernetikk DATO: 01.13 OPPG. NR.: R134 TEMPERATURREGULERING
 KYBERNETIKKLABORATORIET FAG: Kybernetikk DATO: 01.13 OPPG. NR.: R134 TEMPERATURREGULERING Denne øvelsen inneholder følgende momenter: a) En prosess, styring av luft - temperatur, skal undersøkes, og en
KYBERNETIKKLABORATORIET FAG: Kybernetikk DATO: 01.13 OPPG. NR.: R134 TEMPERATURREGULERING Denne øvelsen inneholder følgende momenter: a) En prosess, styring av luft - temperatur, skal undersøkes, og en
Eksamen i MIK130, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun
Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: Mandag 8 desember 2008 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: Mandag 8 desember 2008 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: onsdag 24 november 2010 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: onsdag 24 november 2010 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
KYBERNETIKKLABORATORIET. FAG: Dynamiske systemer DATO: 09.13 OPPG.NR.: DS3 MOTOR GENERATOROPPGAVE I
 KYBERNETIKKLABORATORIET FAG: Dynamiske systemer DATO: 09.13 OPPG.NR.: DS3 MOTOR GENERATOROPPGAVE I Et reguleringssystem består av en svitsjstyrt (PWM) motor-generatorenhet og en mikrokontroller (MCU) som
KYBERNETIKKLABORATORIET FAG: Dynamiske systemer DATO: 09.13 OPPG.NR.: DS3 MOTOR GENERATOROPPGAVE I Et reguleringssystem består av en svitsjstyrt (PWM) motor-generatorenhet og en mikrokontroller (MCU) som
Løsningsforslag Eksamen i MIK130, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte
Simuleringsalgoritmer
 Simuleringsalgoritmer Finn Aakre Haugen, dosent Høgskolen i Telemark 14. september 2015 1 Innledning 1.1 Hva er simulering? Simulering av et system er beregning av tidsresponser vha. en matematisk modell
Simuleringsalgoritmer Finn Aakre Haugen, dosent Høgskolen i Telemark 14. september 2015 1 Innledning 1.1 Hva er simulering? Simulering av et system er beregning av tidsresponser vha. en matematisk modell
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas.
 Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
TMA4240 Statistikk 2014
 TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
Eksamensoppgave i ST0103 Brukerkurs i statistikk
 Institutt for matematiske fag Eksamensoppgave i ST0103 Brukerkurs i statistikk Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: August 2018 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i ST0103 Brukerkurs i statistikk Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: August 2018 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Løsningsforslag MAT102 Vår 2018
 Løsningsforslag MAT102 Vår 2018 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT102 Tirsdag 12 juni 2018, kl 0900-1400 Oppgavesettet har fem oppgaver Hver deloppgave
Løsningsforslag MAT102 Vår 2018 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT102 Tirsdag 12 juni 2018, kl 0900-1400 Oppgavesettet har fem oppgaver Hver deloppgave
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
Eksamensoppgave i ST1201/ST6201 Statistiske metoder
 Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 20. desember 2016 Eksamenstid (fra til): 09:00
Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 20. desember 2016 Eksamenstid (fra til): 09:00
Båtsimulering med diskret Kalmanfilter TTK4115 Lineær systemteori
 NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for teknisk kybernetikk Båtsimulering med diskret Kalmanfilter TTK4115 Lineær
NTNU Norges teknisk-naturvitenskapelige universitet Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for teknisk kybernetikk Båtsimulering med diskret Kalmanfilter TTK4115 Lineær
år i 1 2 3 4 5 6 7 8 9 alder x i 37 38 39 40 41 42 43 44 45 tid y i 45.54 41.38 42.50 38.80 41.26 37.20 38.19 38.05 37.45 i=1 (x i x) 2 = 60, 9
 TMA424 Statistikk Vår 214 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 11, blokk II Oppgave 1 Matlabkoden linearreg.m, tilgjengelig fra emnets hjemmeside, utfører
TMA424 Statistikk Vår 214 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 11, blokk II Oppgave 1 Matlabkoden linearreg.m, tilgjengelig fra emnets hjemmeside, utfører
Løsningsforslag Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: Mandag 8 desember 28 Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: Mandag 8 desember 28 Lengde på eksamen: 4 timer Tillatte
Eksamensoppgave i TELE2001 Reguleringsteknikk
 Fakultet for teknologi Eksamensoppgave i TELE2001 Reguleringsteknikk Faglig kontakt under eksamen: Fredrik Dessen Tlf.: 48159443 Eksamensdato: 7. juni 2016 Eksamenstid (fra-til): 09:00 til 14:00 Hjelpemiddelkode/Tillatte
Fakultet for teknologi Eksamensoppgave i TELE2001 Reguleringsteknikk Faglig kontakt under eksamen: Fredrik Dessen Tlf.: 48159443 Eksamensdato: 7. juni 2016 Eksamenstid (fra-til): 09:00 til 14:00 Hjelpemiddelkode/Tillatte
Slik skal du tune dine PID-regulatorer
 Slik skal du tune dine PID-regulatorer Ivar J. Halvorsen SINTEF, Reguleringsteknikk PROST temadag Tirsdag 22. januar 2002 Granfos Konferansesenter, Oslo 1 Innhold Hva er regulering og tuning Enkle regler
Slik skal du tune dine PID-regulatorer Ivar J. Halvorsen SINTEF, Reguleringsteknikk PROST temadag Tirsdag 22. januar 2002 Granfos Konferansesenter, Oslo 1 Innhold Hva er regulering og tuning Enkle regler
Høgskoleni østfold EKSAMEN. Emnekode: Emne: ITD30005 Industriell IT. Dato: Eksamenstid: kl til kl. 1300
 Høgskoleni østfold EKSAMEN Emnekode: Emne: ITD30005 Industriell IT Dato: 15.12.2014 Eksamenstid: kl. 0900 til kl. 1300 Hjelpemidler: Faglærer: Tre A4-ark (seks sider) med egne notater. Robert Roppestad
Høgskoleni østfold EKSAMEN Emnekode: Emne: ITD30005 Industriell IT Dato: 15.12.2014 Eksamenstid: kl. 0900 til kl. 1300 Hjelpemidler: Faglærer: Tre A4-ark (seks sider) med egne notater. Robert Roppestad
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE. Forfatter: Bjørnar Langeland
 DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Kybernetikk/signalbehandling Vårsemesteret, 21 Åpen / Konfidensiell Forfatter: Bjørnar Langeland Fagansvarlig: Morten
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Kybernetikk/signalbehandling Vårsemesteret, 21 Åpen / Konfidensiell Forfatter: Bjørnar Langeland Fagansvarlig: Morten
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Kapittel 4.4: Forventning og varians til stokastiske variable
 Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
MIK-130 Systemidentifikasjon Løsningsforslag eksamen 28 mai 2004
 MIK-130 Systemidentifikasjon Løsningsforslag eksamen 28 mai 2004 Oppgave 1 a Energibalanse: Endring i energi = sum av tilført energi - sum av avgitt energi. Her får en da for vannet E t = (m vc pv T v
MIK-130 Systemidentifikasjon Løsningsforslag eksamen 28 mai 2004 Oppgave 1 a Energibalanse: Endring i energi = sum av tilført energi - sum av avgitt energi. Her får en da for vannet E t = (m vc pv T v
6 Modellering av smelteovn Modellering Tilstandsromform Diskretisering Observerbarthet Tidssteg...
 Stavanger, 28. mai 2019 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2019. Innhold 6 Modellering av smelteovn. 1 6.1 Modellering............................. 1 6.2 Tilstandsromform..........................
Stavanger, 28. mai 2019 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2019. Innhold 6 Modellering av smelteovn. 1 6.1 Modellering............................. 1 6.2 Tilstandsromform..........................
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas.
 Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
TMA4240 Statistikk Eksamen desember 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Simuleringseksempel. Vi ønsker å simulere følgende system (vanntank) i MathScript: Matematisk modell:
 Simuleringseksempel Vi ønsker å simulere følge system (vanntank) i MathScript: Matematisk modell: Vi har funnet følge matematiske modell for systemet: [ ] der: er nivået i tanken er pådragssignalet til
Simuleringseksempel Vi ønsker å simulere følge system (vanntank) i MathScript: Matematisk modell: Vi har funnet følge matematiske modell for systemet: [ ] der: er nivået i tanken er pådragssignalet til
TMA4240 Statistikk Høst 2009
 TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b6 Oppgave 1 Oppgave 11.5 fra læreboka. Oppgave 2 Oppgave 11.21 fra læreboka. Oppgave
TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b6 Oppgave 1 Oppgave 11.5 fra læreboka. Oppgave 2 Oppgave 11.21 fra læreboka. Oppgave
Side av 5 fra matriseteori har vi at en symmetrisk matrise alltid er ortogonalt diagonaliserbar. Det vil si at X kan skrives på formen X = M M (6) der
 Side av 5 Norges teknisk- naturvitenskapelige universitet Institutt for teknisk kybernetikk SIE38 Stokastiske og adaptive systemer Fasit til ving Oppgave Gitt at den stokastiske vektoren v er normalfordelt
Side av 5 Norges teknisk- naturvitenskapelige universitet Institutt for teknisk kybernetikk SIE38 Stokastiske og adaptive systemer Fasit til ving Oppgave Gitt at den stokastiske vektoren v er normalfordelt
Løsning til eksamen i IA3112 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge
 Løsning til eksamen i IA3112 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge Eksamensdato: 30.11 2016. Varighet 5 timer. Vekt i sluttkarakteren: 100%. Emneansvarlig: Finn Aakre Haugen (finn.haugen@hit.no).
Løsning til eksamen i IA3112 Automatiseringsteknikk ved Høgskolen i Sørøst- Norge Eksamensdato: 30.11 2016. Varighet 5 timer. Vekt i sluttkarakteren: 100%. Emneansvarlig: Finn Aakre Haugen (finn.haugen@hit.no).
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag 7. desember 2012 Tid: 09:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Jo Eidsvik og Arild Brandrud Næss Tlf: 90 12 74 72 og 99 53 82 94 Eksamensdato: 9. desember 2013 Eksamenstid
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Jo Eidsvik og Arild Brandrud Næss Tlf: 90 12 74 72 og 99 53 82 94 Eksamensdato: 9. desember 2013 Eksamenstid
Til: Aktuelle studenter for Cyberneticas studentprogram Antall sider: 5 Dato: 2015-11-01
 Address: Cybernetica AS Leirfossveien 27 N-7038 Trondheim Norway Phone.: +47 73 82 28 70 Fax: +47 73 82 28 71 STUDENTOPPGAVER 2016 Til: Aktuelle studenter for Cyberneticas studentprogram Antall sider:
Address: Cybernetica AS Leirfossveien 27 N-7038 Trondheim Norway Phone.: +47 73 82 28 70 Fax: +47 73 82 28 71 STUDENTOPPGAVER 2016 Til: Aktuelle studenter for Cyberneticas studentprogram Antall sider:
TMA4240 Statistikk Høst 2016
 TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 11 Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale begreper
TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 11 Oppgavene i denne øvingen dreier seg om hypotesetesting og sentrale begreper
MAT4010 PROSJEKTOPPGAVE: Statistikk i S2. Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem
 MAT400 PROSJEKTOPPGAVE: Statistikk i S2 Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem 20. mai 205 Innhold. Stokastisk Variabel.. Stokastiske variable som funksjoner 3 2. Forventningsverdi
MAT400 PROSJEKTOPPGAVE: Statistikk i S2 Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem 20. mai 205 Innhold. Stokastisk Variabel.. Stokastiske variable som funksjoner 3 2. Forventningsverdi
7 Tilstandsestimering for smelteovn.
 Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
HØGSKOLEN I STAVANGER
 EKSAMEN I: MOT310 STATISTISKE METODER VARIGHET: 4 TIMER DATO: 27. FEBRUAR 2004 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV 3 OPPGAVER PÅ 5
EKSAMEN I: MOT310 STATISTISKE METODER VARIGHET: 4 TIMER DATO: 27. FEBRUAR 2004 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV 3 OPPGAVER PÅ 5
TMA4240 Statistikk Høst 2018
 TMA4240 Statistikk Høst 2018 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 5 Dette er andre av tre innleveringer i blokk 2. Denne øvingen skal oppsummere pensum
TMA4240 Statistikk Høst 2018 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 5 Dette er andre av tre innleveringer i blokk 2. Denne øvingen skal oppsummere pensum
1 Tidsdiskret PID-regulering
 Finn Haugen (finn@techteach.no), TechTeach (techteach.no) 16.2.02 1 Tidsdiskret PID-regulering 1.1 Innledning Dette notatet gir en kortfattet beskrivelse av analyse av tidsdiskrete PID-reguleringssystemer.
Finn Haugen (finn@techteach.no), TechTeach (techteach.no) 16.2.02 1 Tidsdiskret PID-regulering 1.1 Innledning Dette notatet gir en kortfattet beskrivelse av analyse av tidsdiskrete PID-reguleringssystemer.
TMA4240 Statistikk Høst 2016
 TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 12 Denne øvingen består av oppgaver om enkel lineær regresjon. De handler blant
TMA4240 Statistikk Høst 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 12 Denne øvingen består av oppgaver om enkel lineær regresjon. De handler blant
TMA4240 Statistikk Eksamen desember 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlege stokastiske variabelen X ha fordelingsfunksjon (sannsynstettleik
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlege stokastiske variabelen X ha fordelingsfunksjon (sannsynstettleik
EKSAMEN I FAG 75510/75515 STATISTIKK 1 Tirsdag 20. mai 1997 Tid: 09:00 14:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Siden vi her har brukt første momentet i fordelingen (EX = EX 1 ) til å konstruere estimatoren kalles denne metoden for momentmetoden.
 Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
4.1 Diskretisering av masse-fjær-demper-system. K f m. x m u m y = x 1. x m 1 K d. Dette kan skrives på matriseform som i oppgaven med 0 1 A =
 Stavanger, 5. september 08 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 08. Innhold 4 Løsningsforslag og kommentarer, noen regneoppgaver. 4. Diskretisering av masse-fjær-demper-system...........
Stavanger, 5. september 08 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 08. Innhold 4 Løsningsforslag og kommentarer, noen regneoppgaver. 4. Diskretisering av masse-fjær-demper-system...........
Forelening 1, kapittel 4 Stokastiske variable
 Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
Eksamensoppgave i TMA4110/TMA4115 Calculus 3
 Institutt for matematiske fag Eksamensoppgave i TMA4110/TMA4115 Calculus 3 Faglig kontakt under eksamen: Markus Szymik Tlf: 411 16 793 Eksamensdato: August 2018 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4110/TMA4115 Calculus 3 Faglig kontakt under eksamen: Markus Szymik Tlf: 411 16 793 Eksamensdato: August 2018 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Frequency Response and Stability Analysis. Hans- Pe9er Halvorsen, M.Sc.
 Frequency Response and Stability Analysis Hans- Pe9er Halvorsen, M.Sc. Tilstandsrom- modeller Dataverktøy SpesialElfelle MathScript LabVIEW Differensial - likninger Tidsplanet Laplace Blokk- diagrammer
Frequency Response and Stability Analysis Hans- Pe9er Halvorsen, M.Sc. Tilstandsrom- modeller Dataverktøy SpesialElfelle MathScript LabVIEW Differensial - likninger Tidsplanet Laplace Blokk- diagrammer
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
48 Praktisk reguleringsteknikk
 48 Praktisk reguleringsteknikk Figur 2.18: Simulering av nivåreguleringssystemet for flistanken. Regulatoren er en PI-regulator. (Resten av frontpanelet for simulatoren er som vist i figur 2.14.) Kompenseringsegenskaper:
48 Praktisk reguleringsteknikk Figur 2.18: Simulering av nivåreguleringssystemet for flistanken. Regulatoren er en PI-regulator. (Resten av frontpanelet for simulatoren er som vist i figur 2.14.) Kompenseringsegenskaper:
n n i=1 x2 i n x2 n i=1 Y i og x = 1 n i=1 (x i x)y i = 5942 og n T = i=1 (x i x) 2 t n 2
 TMA4245 Statistikk Vår 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 12, blokk II Denne øvingen består av oppgaver om enkel lineær regresjon. De handler
TMA4245 Statistikk Vår 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 12, blokk II Denne øvingen består av oppgaver om enkel lineær regresjon. De handler
TMA4245 Statistikk. Innlevering 3. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
Eksamensoppgave i TMA4245 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4245 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland Tlf: 48 22 18 96 Eksamensdato:??. august 2014 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4245 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland Tlf: 48 22 18 96 Eksamensdato:??. august 2014 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
a) The loop transfer function with the process model with a P controller is given by h 0 (s) = h c (s)h p (s) = K p (1 + s)(2 + s) K p
 Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, November 9, 006 SCE1106 Control Theory Solution Exercise 8 Task 1 a) The loop transfer function with
Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, November 9, 006 SCE1106 Control Theory Solution Exercise 8 Task 1 a) The loop transfer function with
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1. Oppgave 1. Oppgave 2. Oppgave 3
 Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1 Oppgave 1 For AR(2)-modellen: X t = 0.4X t 1 + 0.45X t 2 + Z t (der {Z t } er hvit søy med varians 1), finn γ(3), γ(4)
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1 Oppgave 1 For AR(2)-modellen: X t = 0.4X t 1 + 0.45X t 2 + Z t (der {Z t } er hvit søy med varians 1), finn γ(3), γ(4)
Frequency Response and Stability Analysis
 Control Engineering Frequency Response and Stability Analysis Hans-Petter Halvorsen Dataverktøy Spesialtilfelle MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/
Control Engineering Frequency Response and Stability Analysis Hans-Petter Halvorsen Dataverktøy Spesialtilfelle MathScript LabVIEW Differensial -likninger Tidsplanet Laplace 2.orden 1.orden Realisering/
Eksamen i ELE620, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentifikasjon (10 sp) Dato: tirsdag 17 desember 2013 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentifikasjon (10 sp) Dato: tirsdag 17 desember 2013 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DEL 1 GRUNNLEGGENDE STATISTIKK
 INNHOLD 1 INNLEDNING 15 1.1 Parallelle verdener........................... 18 1.2 Telle gunstige.............................. 20 1.3 Regneverktøy og webstøtte....................... 22 1.4 Oppgaver................................
INNHOLD 1 INNLEDNING 15 1.1 Parallelle verdener........................... 18 1.2 Telle gunstige.............................. 20 1.3 Regneverktøy og webstøtte....................... 22 1.4 Oppgaver................................
Fasit for tilleggsoppgaver
 Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Fasit for tilleggsoppgaver Uke 5 Oppgave: Gitt en rekke med observasjoner x i (i = 1,, 3,, n), definerer vi variansen til x i som gjennomsnittlig kvadratavvik fra gjennomsnittet, m.a.o. Var(x i ) = (x
Forelesning 27. mars, 2017
 Forelesning 27. mars, 2017 AVSNITT 5.5 Ordningsobservatorene AVSNITT 6.1 Observatorer og deres fordelinger Ordningsobservatorene La X 1,..., X n være n uavhengige stokastiske variable som alle har samme
Forelesning 27. mars, 2017 AVSNITT 5.5 Ordningsobservatorene AVSNITT 6.1 Observatorer og deres fordelinger Ordningsobservatorene La X 1,..., X n være n uavhengige stokastiske variable som alle har samme
TMA4240 Statistikk Høst 2012
 TMA424 Statistikk Høst 212 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving blokk II Oppgave 1 Oppgave 11.3 fra læreboka. Oppgave 2 Oppgave 11.19 fra læreboka. Oppgave
TMA424 Statistikk Høst 212 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving blokk II Oppgave 1 Oppgave 11.3 fra læreboka. Oppgave 2 Oppgave 11.19 fra læreboka. Oppgave
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT-INF 11 Modellering og beregninger Eksamensdag: Mandag 1 Desember 218 Tid for eksamen: 9: 13: Oppgavesettet er på 5 sider
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT-INF 11 Modellering og beregninger Eksamensdag: Mandag 1 Desember 218 Tid for eksamen: 9: 13: Oppgavesettet er på 5 sider
TMA4240 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Eksamensoppgåve i ST0103 Brukarkurs i statistikk
 Institutt for matematiske fag Eksamensoppgåve i ST0103 Brukarkurs i statistikk Fagleg kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: August 2018 Eksamenstid (frå til): 09:00 13:00 Hjelpemiddelkode/Tillatne
Institutt for matematiske fag Eksamensoppgåve i ST0103 Brukarkurs i statistikk Fagleg kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: August 2018 Eksamenstid (frå til): 09:00 13:00 Hjelpemiddelkode/Tillatne
Bølgekompensering under boring med RamRig
 Bølgekompensering under boring med RamRig Modellering og regulering Yngvild Aurlien Master i teknisk kybernetikk Oppgaven levert: Juli 2007 Hovedveileder: Thor Inge Fossen, ITK Norges teknisk-naturvitenskapelige
Bølgekompensering under boring med RamRig Modellering og regulering Yngvild Aurlien Master i teknisk kybernetikk Oppgaven levert: Juli 2007 Hovedveileder: Thor Inge Fossen, ITK Norges teknisk-naturvitenskapelige

 I c;'1 høgskolen i oslo lemne: I I Gruppe(r) Kvbem~ti!
I c;'1 høgskolen i oslo lemne: I I Gruppe(r) Kvbem~ti!