TERMINPRØVE SINUS 1MXY
|
|
|
- Flemming Finstad
- 7 år siden
- Visninger:
Transkript
1 TERMINPRØVE SINUS MXY Høsten 005 I noen av oppgavene i dette settet er det gitt to alternativer. Du skal velge enten alternativ I med lavest vanskelighetsgrad eller alternativ II med størst vanskelighetsgrad. Ved rettingen vil du få mest uttelling for alternativ II hvis det er løst riktig. Oppgave a) Regn ut. ( 5 ) ( 8 7) ( 5 8) + ( 9) : b) Regn ut. Sondre bruker daglig h og 0 min på lekser. Han gjør lekser fem dager i uken. Hvor lang tid bruker Sondre til sammen på lekser i en uke? c) Regn ut. 5 d) Regn ut. 5 0 ( ) Randi løper orientering. En helg løp hun to løp. Lørdag startet hun kl. 0. og brukte h min. Søndag var hun i mål kl..8 etter å ha brukt h 7 min. Når var hun i mål lørdag, og når startet hun søndag? ( a b) ( ab ) ( a b) e) Løs likningen. 5 ( + ) = + = ( 6 ) CAPPELEN TERMINPRØVE MXY
2 Oppgave En hundrekroneseddel har lengden 6 mm, bredden 65 mm og tykkelsen 8 0 mm. a) Vi legger noen slike sedler etter hverandre i lengderetning. Hvor mange må vi bruke for at lengden skal bli minst m? b) Vi tenker oss at vi vil dekke et kvadrat med sider m med slike sedler. Hvor mange sedler må vi bruke? c) Hvor mange kroner er det i en bunke med slike sedler som har høyden 8 cm? d) Tenk deg at du har en million kroner i hundrekronesedler. ) Du legger sedlene opp på hverandre. Hvor høy blir bunken? ) Du vil kontrolltelle pengene. Tenk deg at du bruker ett sekund per seddel. Hvor lang tid tar tellingen? Oppgave En kjøreskole har disse prisene: Kjøretime Teorikurs inklusiv tentamen Glattkjøring Landeveiskjøring Mørkekjøring Kjøretest Førerprøve 50 kr per time 600 kr 800 kr 00 kr 00 kr 700 kr 00 kr Mona er elev ved skolen og tar alt som er nevnt ovenfor. a) Forklar at dersom Mona bruker kjøretimer, så er de totale utgiftene U i kroner til bilsertifikat U = b) Hva er de totale utgiftene til Mona dersom hun bruker 0 kjøretimer? c) Tegn grafen til U på ruteark. Velg mellom 0 timer og 0 timer. d) Mona ønsker ikke å bruke mer enn kr til bilsertifikat. Finn både grafisk og ved regning hvor mange kjøretimer hun høyst kan ha. e) Bruk formelen fra oppgave a og finn uttrykt ved U. f) Bruk formelen i oppgave e og kontroller svaret i oppgave d. g) En annen kjøreskole tilbyr de samme kursene og kjøringene for 7800 kr og en kjøretime for 90 kr. Finn ved regning det antallet kjøretimer som gjør at utgiftene til sertifikat blir like store ved de to kjøreskolene. CAPPELEN TERMINPRØVE MXY
3 Oppgave a) Størrelsene y og er proporsjonale. ) Fyll ut tabellen til høyre. 0,5,5 5,0 y 0,6, ) Avsett punktene i et koordinatsystem og lag en graf som viser sammenhengen mellom y og. ) Finn y uttrykt ved. b) Størrelsene s og t er omvendt proporsjonale. ) Fyll ut tabellen til høyre. t 5 0 s ) Avsett punktene i et koordinatsystem og lag en graf som viser sammenhengen mellom s og t. ) Finn s uttrykt ved t. Oppgave 5 I klassen til Solveig og Marius er det jenter og 6 gutter. a) En dag trekker læreren tilfeldig ut en elev til leksehøring. ) Hva er sannsynligheten for at Solveig eller Marius blir hørt? ) Hva er sannsynligheten for at en gutt blir hørt? b) En dag fikk elevene i klassen et spørreskjema med to spørsmål. På det første spørsmålet var det fire svaralternativer, og på det andre var det fem svaralternativer. Hvor mange svarkombinasjoner gir dette? c) Solveig regner med at sannsynligheten for at hun får eller bedre på en matematikkprøve, er 0,9. Det er to matematikkprøver igjen i. termin. Hva er sannsynligheten for at Solveig får eller bedre på begge disse prøvene? d) Marius har fått en prøve med to oppgaver. Han regner med at sannsynligheten er 0,8 for at han klarer oppgave, og 0,6 for at han klarer oppgave. ) Hva er sannsynligheten for at han ikke klarer oppgave? ) Hva er sannsynligheten for at han ikke klarer noen av oppgavene? ) Hva er sannsynligheten for at han klarer minst én av oppgavene? e) Dersom en elev har fått eller bedre på en matematikkprøve, sier vi at eleven har fått en god matematikkarakter. På en matematikkprøve der alle elevene i klassen var til stede, fikk åtte av jentene og åtte av guttene god matematikkarakter. Vi innfører disse hendingene: G: Eleven er en gutt J: Eleven er ei jente M: Eleven har fått god matematikkarakter CAPPELEN TERMINPRØVE MXY
4 Finn disse sannsynlighetene: ( ) ( ) ( ) og ( ) ) P M og P M J ) P G M P J M ) P( G og M ) ) Undersøk om G og M er uavhengige hendinger. Oppgave 6 Hans og Grete er naboer og eier sammen det flate, trekantede området ABC som vist på figuren. Hans bor ved hjørnet A og Grete ved hjørnet C. På figuren er AB = 8 m, DC = 9,5 m og A = 0. Naboforholdet blir etter hvert litt anstrengt, så de blir enige om å dele området med et gjerde BD som skal stå normalt på linja AC. På den måten får de hvert sitt område. C 9,5 m D 0 A 8 m B a) Vis at lengden av gjerdet BD må være 5 m. b) Finn C. c) Finn lengden av AC. d) Finn lengden av BC. e) Hans er ikke fornøyd med plasseringen av gjerdet. Han vil finne et punkt E på linja mellom A og C, slik at arealene av områdene ABE og BCE blir like store. Finn avstanden AE i dette tilfellet. CAPPELEN TERMINPRØVE MXY
5 Oppgave 7 a) En spesiell fyrstikkeske har lengden 5 mm, bredden 6 mm og høyden 9,6 mm. ) Finn volumet av esken uttrykt i både mm og cm. ) En fyrstikk til denne esken har et kvadratisk tverrsnitt med sider, mm. Lengden av fyrstikken er 5 mm. Hvor mange fyrstikker er det teoretisk plass til i denne esken? b) Arild har en glasskule til såpe på badet. Den indre radien i glasskula er 5, cm. Hvor mange liter rommer glasskula? c) En lampeskjerm er formet som en rett avkortet kjegle slik figuren viser. Radien i grunnflaten er R og i toppflaten r. Lampeskjermen har høyden h =,0 cm, og vinkelen mellom sideflaten og grunnflaten er v = 80. r ) Finn radien R når omkretsen av grunnflaten er 75, cm. ) Vis at r = 6,0 cm. ) Hvis vi forlenger sideflaten oppover, får vi en hel kjegle med høyden H. Vis at H h =. h R v ) Finn volumet av lampeskjermen. CAPPELEN TERMINPRØVE MXY
6 TERMINPRØVE SINUS MX Høsten 005 I noen av oppgavene i dette settet er det gitt to alternativer. Du skal velge enten alternativ I med lavest vanskelighetsgrad eller alternativ II med størst vanskelighetsgrad. Ved rettingen vil du få mest uttelling for alternativ II hvis det er løst riktig. Oppgave a) Løs likningen. = + = b) Løs ulikheten. + > 0 + > c) Løs likningen. cos v = 0, 7, v [ 0, 60 sin v ( cos v + ) = 0, v [ 0, 60 d) To vektorer a og b Løs en av oppgavene. Tegn a, b, a + b og a b. har begge lengden 5 cm. Vinkelen mellom a og b er 60. Tegn figur og finn a b og a + b. e) Løs en av oppgavene. ph-verdien i en oppløsning med konsentrasjon K av H O + målt i M (molar), er gitt ved ph = lg K Finn konsentrasjonen av H O + i en oppløsning der ph = 9,7. Hvis lydintensiteten er I målt i W/m, er lydstyrken L målt i db (desibel) gitt ved L = 0 lg I + 0 På et diskotek var lydstyrken db. Finn lydintensiteten. CAPPELEN TERMINPRØVE MX
7 Oppgave I en trekantet park ABC er lengden av sidene 90 m, 50 m og 00 m slik figuren viser. Fra hjørnet B går det to rette stier BD og BE gjennom parken slik at trekanten BDE blir likesidet. A E 00 m D C 90 m 50 m B a) Finn B. b) Finn arealet av parken. c) Finn A. d) Hvor lange er stiene gjennom parken? Oppgave Punktene A(, ), B(, ) og C(8, ) er gitt. a) Bruk vektorregning og vis at trekanten ABC er rettvinklet. b) Bruk vektorregning og vis at trekanten ABC er likebeint. c) Bruk vektorregning og finn koordinatene til et punkt D slik at firkanten ABCD blir et kvadrat. d) Finn lengden av diagonalene i kvadratet ABCD. e) Diagonalene i kvadratet skjærer hverandre i et punkt E. Finn ved regning koordinatene til dette punktet. Oppgave Vi har noen ulike kuler. Tabellen viser sammenhengen mellom volumet V av kulene, målt i kubikkcentimeter, og arealet O av overflaten til kulene, målt i kvadratcentimeter. V (cm ) O (cm ), 6,66 65,6 86,0 0, ln V ln O a) Bruk de to første radene i tabellen og finn den potensfunksjonen O(V) som passer best med tallene. b) Finn arealet av overflaten til ei kule som har volumet 60 cm. c) Fyll ut tabellen. CAPPELEN TERMINPRØVE MX
8 d) Legg tallene fra de to siste radene i tabellen inn i listene på lommeregneren. Gjør en lineær regresjon og finn den linja som passer best. e) Tegn linja fra oppgave d i et koordinatsystem med logaritmisk skala på begge aksene. f) Bruk likningen for den rette linja i oppgave d og finn O uttrykt ved V. Sammenlikn med svaret i oppgave a. g) Ei kule med radius r har overflatearealet O = π r og volumet V = π r. Vis ved regning at vi kan skrive O = 6π V Hvordan stemmer dette med det uttrykket du fant i oppgave a? Oppgave 5 En kurve K har parameterframstillingen = t K : y = t t a) Finn ved regning skjæringspunktene med y-aksen. b) Finn ved regning skjæringspunktene med -aksen. c) Fyll ut tabellen. t 0 y d) Tegn kurven K. Oppgave 6 Når radioaktiv stråling treffer ei blyplate, vil mengden av stråling som slipper gjennom, avhenge av tykkelsen på blyplata. Vi setter aktiviteten i strålingen fra en bestemt isotop til 00 %. Etter at strålen har passert ei blyplate med tykkelsen mm, er aktiviteten A() målt i prosent redusert til 0, 65 A( ) = 00 e, [ 0, 0] a) Hvor mange prosent er aktiviteten redusert med når tykkelsen på blyplata er mm? b) Tegn grafen til A. c) Finn grafisk og ved regning hvor tykk blyplata må være hvis aktiviteten i strålingen skal bli halvert. d) Finn ved regning hvor tykk blyplata må være hvis en ønsker å redusere aktiviteten i strålingen til %. e) Aktiviteten i strålingen fra en annen isotop, blir redusert med % når tykkelsen på blyplata er 5 mm. Finn aktiviteten B() målt i prosent når tykkelsen på blyplata er mm. CAPPELEN TERMINPRØVE MX
9 TERMINPRØVE SINUS MZ Høsten 005 I noen av oppgavene i dette settet er det gitt to alternativer. Du skal velge enten alternativ I med lavest vanskelighetsgrad eller alternativ II med størst vanskelighetsgrad. Ved rettingen vil du få mest uttelling for alternativ II hvis det er løst riktig. Oppgave a) Løs likningen. 5 = 6 0, 75 0 =, 5 b) Løs likningen. lg + 6 = 0 lg + lg lg ( ) = c) I en aritmetisk rekke er det første leddet a =, og differansen d =. Finn summen av rekken når det siste leddet er a = 5. det siste leddet er a n =. d) Du får utbetalt kr om 5 år. Regn med,5 % rente og finn nåverdien av beløpet. Nåverdien av beløpet er 57 kr. Finn ved regning hvilken rente som er brukt. e) Løs en av oppgavene. Ei rett linje går gjennom punktene (, ) og (, 5). Finn ved regning stigningstallet til linja. En funksjon f er gitt ved f ( ) = + Finn ved regning den gjennomsnittlige vekstfarten til f i intervallet [, 5]. CAPPELEN TERMINPRØVE MZ
10 Oppgave a) ph-verdien i en oppløsning er gitt ved ph = lg K der K er konsentrasjonen av H O + målt i M (molar). ) Konsentrasjonen av H O + i tomater er,6 0 M. Finn ph-verdien i tomater. ) I et glass melk er ph-verdien 6,5. Finn konsentrasjonen av H O + i melken. ) Vi hundredobler konsentrasjonen av H O + i en væske. Hvor mye øker eller minker ph-verdien i væsken? b) Når lydintensiteten er I målt i W/m, er lydstyrken L målt i desibel (db) L = 0 lg I + 0 ) På en rockekonsert er lydintensiteten målt til 0, W/m. Finn lydstyrken. ) På fortauet i en sterkt trafikkert gate er lydstyrken målt til 78 db. Finn lydintensiteten. ) I et rom hundredobler vi lydintensiteten I. Hvor mye øker eller minker lydstyrken i rommet? Oppgave Vi har gitt rekken a) Forklar hvorfor rekken er geometrisk. b) Forklar hvorfor rekken konvergerer. c) Hva er summen av den uendelige rekken? d) Til høyre ser du et kvadrat med sider. I kvadratet er det tegnet inn en rekke rettvinklede trekanter med arealene A, B, C, D, E, F og G. Finn arealene av trekantene og sett svarene opp som en rekke i denne ordningen: A + (B + C) + D + (E + F) + G. B D E G F e) Forklar hvordan vi kan finne summen av rekken A C ved hjelp av trekanter i kvadratet. CAPPELEN TERMINPRØVE MZ
11 Oppgave På en byggeplass skal en slå ned med fallodd noen støttebjelker i grunnen. Bjelkene stikker,50 m over bakken. Det første støtet fra loddet får bjelken 0 cm ned i bakken. For hvert nytt støt reduseres denne lengden med 5 %. a) Hvor langt ned i bakken går en bjelke på det. støtet? b) Hvor langt har en bjelke gått ned i bakken etter støt? c) Bjelkene skal stikke 67,5 cm over bakken. Hvor mange støt må til fra falloddet for å nå denne høyden? d) Hvor langt kan en teoretisk få en bjelke ned i bakken på denne måten? Oppgave 5 En bonde har et jordstykke ABCD der han vil dyrke jordbær. Han har jordbærrekker fra CD og nedover. Den første rekka er 0 m lang, den andre, m, og den tredje,8 m. For hver ny rekke er den nye rekka, m lengre enn den forrige. Se figuren nedenfor. a) Hvor lang er den 6. rekka? b) Hvor mange meter jordbærrekker er det til og med den 6. rekka? D C c) Den lengste rekka er 8, m lang. Hvor mange rekker med jordbær er det? A B d) Vi tenker oss at vi legger alle jordbærrekkene etter hverandre. Hvor lang blir rekka? Oppgave 6 En høst kom det mye nedbør i Storevik, og i løpet av noen få døgn var det flom i Storelva. Vannstanden kom høyt over det normale nivået. Grafen viser denne utviklingen over en periode på døgn. m y a) Hvor mange meter over det normale nivået var elva etter ) døgn ) døgn døgn b) Finn den gjennomsnittlige vekstfarten i vannstanden i perioden ) [0, ] ) [, ] c) Bruk en grafisk metode til å anslå den momentane vekstfarten etter døgn. d) Når vil du si at vannet trekker seg fortest tilbake? Begrunn svaret. CAPPELEN TERMINPRØVE MZ
12 TERMINPRØVE SINUS MX Høsten 005 Oppgave a) Finn de eksakte løsningene. ) cos = π, [0, π> ) sin, [, ] ( 0 ) = b) Finn integralene. ) 6sin d ) ( + ) e d ) e + d Oppgave a) Figuren til venstre nedenfor viser en sirkel med radius som er delt i fire deler (tre ringer og en sirkelflate). Hver ring har bredden. Finn arealet av hver av ringene og bruk det til å vise at = n b) Figuren i midten ovenfor viser en sirkel med radius n. Inne i sirkelen er det tegnet en ring med bredde. Finn et uttrykk for arealet av ringen. c) Forklar hvordan du kan bruke sirkelen i midten ovenfor til å vise at summen av de n første oddetallene er lik n. d) Vis ved regning at summen av de n første oddetallene er lik n. e) Figuren til høyre ovenfor er sammensatt av mange sirkler med samme sentrum. Den største sirkelen har radius, den andre, den tredje osv. Bruk denne figuren til å finne summen av den uendelige rekken f) Finn summen av rekken i oppgave e ved regning. CAPPELEN TERMINPRØVE MX
13 Oppgave Harry Davidsen ønsker å kjøpe en tung motorsykkel. Den koster kr. Han har kr på ei bankbok som gir 0, % rente per måned. a) Hvor mye penger har han i banken om to år? b) Harry sparer 500 kr per måned. Det første beløpet sparer han om én måned. Han får 0, % rente per måned på disse pengene også. Hvor mye penger har Harry da i banken om to år? c) Hvor mye må han spare per måned for at han skal kunne kjøpe sykkelen om to år? Harry Davidsen vil gjerne kjøpe sykkelen med en gang. Han må da låne penger i banken til 0, % rente per måned. Han vil betale 500 kr per måned i renter og avdrag på lånet. Det første beløpet vil han betale om én måned. Banken regner ut lånesummen slik at den blir lik summen av nåverdiene til alle innbetalingene. Kalkulasjonsrenten er lik renten på lånet. d) Hva mener vi med nåverdien til et beløp? Hva er nåverdien til det første beløpet som Harry skal betale? e) Hvor mye får Harry låne hvis han vil betale 500 kr per måned i år framover? f) Hvor lenge må Harry betale på lånet hvis han låner kr? Oppgave Kåre Krovert driver en uteplass for ungdom. På et tidspunkt var besøket heller dårlig. Kåre bestemte seg da for at alle jenter skulle få kjøpe mat og drikke for halv pris de neste åtte ukene. Grafen viser hvor mange jenter som kom per uke t uker etter at han satte i gang tiltaket. 500 y j t uker a) Finn perioden, likevektslinja og amplituden til denne cosinusfunksjonen. Forklar at antall jenter per uke er gitt ved j( t) = cos π t, t [0, 6] 8 CAPPELEN TERMINPRØVE MX
14 b) Finn ved regning når det var 00 jenter per uke på uteplassen. c) Finn ved regning hvor mange jenter det var til sammen i de 6 første ukene etter at Kåre Krovert satte i gang tiltaket. Det viste seg at guttene ikke likte at det bare var jentene som fikk billig mat og drikke. Tallet på gutter per uke etter t uker var gitt ved g( t) = sin π t, t [0, 6] 8 d) Tegn grafen til g sammen med grafen til j i et koordinatsystem. e) Finn ved regning når tallet på gutter var på det høyeste. Hvor mange gutter var det på uteplassen da? f) La s(t) være tallet på gjester per uke etter t uker der s er en sinusfunksjon. Finn funksjonsuttrykket til s. g) Finn ved regning når det var 700 gjester på uteplassen. Oppgave 5 Oljeselskapet Noroil skal bygge en oljetank på Utøya. Tanken har sirkulær grunnflate. Hvis vi tenker oss at vi lager et snitt gjennom tanken meter over bakken, får vi en sirkel med radius r( ) = 5 0, [ 0,, 5] Radien er målt i meter. a) Lag en tegning av tanken. b) Finn volumet av tanken. Noroil skal legge en rørledning inn til fastlandet. Det er 00 km inn til land målt langs havoverflaten. Havet er veldig dypt hele veien. Noroil legger ledningen i rett linje gjennom havet. c) Hvor langt under havoverflaten ligger rørledningen på midten når jordradien er 657 km? d) Hvor mye kortere blir rørledningen når den blir lagt i rett linje og ikke langs havoverflaten? CAPPELEN TERMINPRØVE MX
15 TERMINPRØVE SINUS MZ Høsten 005 Oppgave a) Faktoriser andregradsuttrykkene mest mulig. ) ) + 6 ) + b) Løs ulikhetene ved regning. ) + 7 > 5 5 ) c) Løs likningene ved regning. ) = ) + = ) e = ) 5ln + = ln + 7 d) Deriver uttrykkene. ) e + ) ( + ) ) + Oppgave a) Finn største felles divisor for tallene 95 og 65 ved hjelp av Euklidalgoritmen. b) Finn minste felles multiplum for tallene 95 og 65. c) Finn summen uten å bruke lommeregneren. Forkort svaret mest mulig ved regning. d) Forklar hvorfor den diofantiske likningen y = har heltallige løsninger. e) Musikkforretningen Empetre har to typer MP-spillere, en som koster 95 kr, og en som koster 65 kr. En dag solgte de MP-spillere for kr. Hvor mange spillere av hver type solgte de denne dagen? Bruk blant annet Euklidalgoritmen når du løser oppgaven. CAPPELEN TERMINPRØVE MZ
16 Oppgave Godlyden AS produserer MP-spillere. Hvis bedriften produserer spillere per dag, er kostnaden i kroner per dag gitt ved K( ) = , 6 Inntekten per dag hvis bedriften selger spillere per dag, er gitt ved I( ) = 00 0, a) Finn uttrykk for grensekostnaden og grenseinntekten. b) Vil du anbefale bedriften å øke produksjonen hvis den produserer og selger 00 spillere per dag? Hvordan begrunner du anbefalingen? c) Godlyden AS produserer og selger spillere per dag. Vis at overskuddet per dag er gitt ved O( ) = d) Finn ved regning når overskuddet er størst. Hvor stort er overskuddet da? e) Løs ulikheten O( ) > 0 ved regning. Hva forteller løsningen deg? Oppgave Godlyden AS selger 50 MP-spillere per dag. Firmaet syns det er for lite og lager en kortvarig reklamekampanje. Etter måneder er da salget per dag gitt ved f ( ) = e a) Tegn en graf som viser salget per dag det første halvåret. b) Omtrent hvor lenge varer effekten av reklamekampanjen? c) Vis at f '( ) = 000 ( ) e og at f ''( ) = 000 ( + ) e d) Finn med støtte i grafen nøyaktig når salget er høyest. Hvor mange spillere selger bedriften per dag da? e) Finn med støtte i grafen nøyaktig når salget avtar fortest. Hvor mye avtar salget da? CAPPELEN TERMINPRØVE MZ
17 FASIT Fasit til oppgaver til Sinus MXY Oppgave a) Alternativ I: 5 Alternativ II: b) Alternativ I: 6 h 0 min Alternativ II: lørdag: kl..5, søndag kl.. c) Alternativ I: Alternativ II: 5 d) Alternativ I: 6 Alternativ II: a 6 e) Alternativ I: = Alternativ II: = 5 Oppgave a) 8 sedler b) 8 sedler c) kr d) ) 80 cm ) h 6 min 0 s Oppgave b) 500 kr d) kjøretimer U e) = g) 0 kjøretimer 9000 U ( eller 0) Oppgave a) ) 0,5,5,0 5,0 y 0,6,8, 6,0 b) ) t s,6 0,8 ) y =, ) s = 8 t Oppgave 5 a) ) 5 ) 8 5 b) 0 c) 0,8 d) ) 0, ) 0,08 ) 0,9 CAPPELEN FASIT
18 e) ) P( M ) = 8 5, P( M J ) = 7 ) P G M, P J M ) 5 ( ) = ( ) = ) P( G) P( G M ) G og M er derfor ikke uavhengige hendinger. Oppgave 6 b) C = 0 c) 57,8 m d) 08 m e) 78,9 m Oppgave 7 a) ) 8 7 mm = 8, cm ) 60 fyrstikker b) 0,59 liter c) ) cm ) 9,0 dm Fasit til oppgaver til Sinus MX Oppgave a) Alternativ I: = Alternativ II: = b) Alternativ I: <, > Alternativ II: <, > c) Alternativ I: v = 68, eller v = 9,7 Alternativ II: v = 0, v = 0, v = 80 eller v = 0 d) Alternativ II: a b = 5cm, a + b = 8, 7cm (5 cm) e) Alternativ I: K =,0 0 0 M Alternativ II: I = 0, W/m Oppgave a) B = 0, b) 68 m c) A =, 7 d) 7, m Oppgave c) D(, 8) d) 0, ( = 6 ) e) E(, ) CAPPELEN FASIT
19 Oppgave a) O(V) =,8 V 0,67 b) 7, cm c) V (cm ) O (cm ), 6,66 65,6 86,0 0, ln V,0,0,9,,6 ln O,,8,8,5,65 d) ln O = 0,667 ln V +,57 f) O =,8 V 0,67 Oppgave 5 a) (0, ) og (0, ) b) (, 0) og (, 0) c) t y Oppgave 6 a) 5 % c), mm d) 8, mm e) B( ) = 00 e 0, 08 Fasit til oppgaver til Sinus MZ Oppgave a) Alternativ I: = 0, Alternativ II: = 0, b) Alternativ I: = 00 Alternativ II: = 0 c) Alternativ I: 9 Alternativ II: 5 d) Alternativ I: 09, kr Alternativ II:, % e) Alternativ I: Alternativ II: Oppgave a) ),9 ),6 0 7 M ) ph-verdien minker med. b) ) 0 db ) 6, 0 5 W/m ) Lydstyrken øker med 0 db. CAPPELEN FASIT
20 Oppgave a) Fordi a a n n b) Fordi k = = for alle n og dermed < k < c) d) + ( ) ( + + ) 6 = e) Summen av alle trekantene vil nærme seg å dekke hele kvadratet. Da må vi ha at = Oppgave a) 5,9 cm b) 66,5 cm c) 5 støt d),00 m Oppgave 5 a) 6 m b) 8 m c) rekker d) 50, m Oppgave 6 a) ),5 m ),5 m b) ) 0,65 m per døgn ) 0,5 m per døgn c) ca. 0,6 m per døgn d) Etter ca. 7 døgn. Kurven er der mest avtakende. Fasit til oppgaver til Sinus MX Oppgave π 5π 8 0 a) ) = eller = ) = eller = b) ) cos + C ) ( ) e + C ) + e + C Oppgave b) π(n ) e) f) Oppgave a) 5 89 kr b) 6 5 kr c) 66 kr d) 8 kr e) 0 78 kr f) 9 måneder. Det siste beløpet blir mindre enn 500 kr. CAPPELEN FASIT
21 Oppgave a) Perioden er 6 uker, likevektslinja er y = 00 og amplituden 00. b) Etter ca. 5 uker og etter ca. uker. c) 800 d) y g j t uker e) Guttetallet var høyest etter uker. Det var da 500 gutter per uke. f) s( t) = sin π t +, g) Etter ca. 6 uker og etter ca. uker. Oppgave 5 b) 795 m c) 787 m d) 8,5 m Fasit til oppgaver til Sinus MZ Oppgave a) ) ( )( + ) ) ( )( + ) ) ( ) b) ) < 6 ) < c) ) = ) = ) = ln ) = e d) ) e + ) 6 ( + ) ) 7 ( ) Oppgave a) 5 b) c) d) Største felles divisor for 95 og 65 går opp i e) spillere til 95 kr og 7 spillere til 65 kr. CAPPELEN FASIT
22 Oppgave a) K '( ) = 600 +, I '( ) = 00 0, 8 b) Når bedriften produserer og selger 00 spillere per dag, er grensekostnaden 80 kr og grenseinntekten 90 kr. Det vil da lønne seg å øke produksjonen og salget. d) Overskuddet er størst når bedriften produserer 50 spillere per dag. Overskuddet er da 500 kr per dag. e) 00 < < 00 Bedriften går med overskudd når produksjonen er mellom 00 og 00 spillere per dag. Oppgave a) y f 5 6 måneder b) ca. måneder d) Salget er høyest etter måned. Bedriften selger da 5 spillere per dag. e) Salget avtar fortest etter måned og dager. Salget er da i ferd med å avta med 9 spillere per måned. OFF ISBN-0: ISBN-:
DEL 1. Uten hjelpemidler. Oppgave 1 (2 poeng) Oppgave 2 (4 poeng) Oppgave 3 (4 poeng) I er en konstant. Deriver funksjonene
 DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Deriver funksjonene 3 a) f( x) 5x x 5 b) g( x) x e x Oppgave (4 poeng) Polynomfunksjonen P er gitt ved 3 P( x) x x 10x 8, DP a) Faktoriser P( x ) i førstegradsfaktorer.
DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Deriver funksjonene 3 a) f( x) 5x x 5 b) g( x) x e x Oppgave (4 poeng) Polynomfunksjonen P er gitt ved 3 P( x) x x 10x 8, DP a) Faktoriser P( x ) i førstegradsfaktorer.
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 7, 5 10 4 7,5 4,0 10 0 10, 1 4 1 ( 4) 8 9,0 10 0 10 Oppgave (4 poeng) Siv har fire blå og seks svarte bukser i skapet.
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 7, 5 10 4 7,5 4,0 10 0 10, 1 4 1 ( 4) 8 9,0 10 0 10 Oppgave (4 poeng) Siv har fire blå og seks svarte bukser i skapet.
Eksamen R1 høsten 2014
 Eksamen R1 høsten 014 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Deriver funksjonene 3 a) f x x x x b) gxx e 5 5 Oppgave
Eksamen R1 høsten 014 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Deriver funksjonene 3 a) f x x x x b) gxx e 5 5 Oppgave
DEL 1. Uten hjelpemidler. Oppgave 1 (5 poeng) Oppgave 2 (5 poeng) Deriver funksjonene gitt ved. Polynomet P er gitt ved
 DEL Uten hjelpemidler Oppgave (5 poeng) Deriver funksjonene gitt ved a) b) f x x x ( ) 3 6 4 g x x x 3 ( ) 5ln( ) c) h( x) x x Oppgave (5 poeng) Polynomet P er gitt ved 3 P( x) x 7x 4x k a) Vis at P er
DEL Uten hjelpemidler Oppgave (5 poeng) Deriver funksjonene gitt ved a) b) f x x x ( ) 3 6 4 g x x x 3 ( ) 5ln( ) c) h( x) x x Oppgave (5 poeng) Polynomet P er gitt ved 3 P( x) x 7x 4x k a) Vis at P er
Eksamen R1 høsten 2014 løsning
 Eksamen R1 høsten 014 løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Deriver funksjonene 3 a) f x x x 5 5 f x 15x 4x
Eksamen R1 høsten 014 løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Deriver funksjonene 3 a) f x x x 5 5 f x 15x 4x
1P eksamen høsten Løsningsforslag
 1P eksamen høsten 2017 - Løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (2 poeng) En vare koster 640 kroner. Butikkeieren
1P eksamen høsten 2017 - Løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (2 poeng) En vare koster 640 kroner. Butikkeieren
Eksamen R2 høst 2011, løsning
 Eksamen R høst 0, løsning Oppgave (4 poeng) a) Deriver funksjonene f e ) Bruker produktregelen for derivasjon, uv uv uv f e e e e ) g sin Bruker kjerneregelen på uttrykket cos der u og g u sinu Vi har
Eksamen R høst 0, løsning Oppgave (4 poeng) a) Deriver funksjonene f e ) Bruker produktregelen for derivasjon, uv uv uv f e e e e ) g sin Bruker kjerneregelen på uttrykket cos der u og g u sinu Vi har
Løsning eksamen R1 våren 2008
 Løsning eksamen R våren 008 Oppgave a) f ( ) ln f ( ) ( ) ln (ln ) ln ln b) c) d) e) ( 4 6) : ( ) 4 6 6 0 64 ( 8) ( 8) 8 8 8 6 lim lim lim 8 8 6 8 ( 8) 8 lg( y ) lg y lg lg lg y lg y lg lg y lg lg y y
Løsning eksamen R våren 008 Oppgave a) f ( ) ln f ( ) ( ) ln (ln ) ln ln b) c) d) e) ( 4 6) : ( ) 4 6 6 0 64 ( 8) ( 8) 8 8 8 6 lim lim lim 8 8 6 8 ( 8) 8 lg( y ) lg y lg lg lg y lg y lg lg y lg lg y y
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Tenk deg at du har et spann med 8 L maling. Du vil helle malingen over i mindre bokser. I hver boks er det plass til 2 3 L. Hvor mange bokser trenger du? Oppgave
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Tenk deg at du har et spann med 8 L maling. Du vil helle malingen over i mindre bokser. I hver boks er det plass til 2 3 L. Hvor mange bokser trenger du? Oppgave
Eksamen MAT1013 Matematikk 1T Høsten 2014
 Eksamen MAT1013 Matematikk 1T Høsten 01 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 50000000000,0005 10 10 ( ) 6 7,510 5,010,55,010 1,510 1,510 Oppgave (1 poeng) Løs likningen 16 lg lg16
Eksamen MAT1013 Matematikk 1T Høsten 01 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 50000000000,0005 10 10 ( ) 6 7,510 5,010,55,010 1,510 1,510 Oppgave (1 poeng) Løs likningen 16 lg lg16
DEL 1 Uten hjelpemidler
 Eksamen MAT1013 Matematikk 1T Høsten 2013 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 7,5 10 4,0 10 12 4 Oppgave 2 (4 poeng) Siv har fire blå og seks svarte bukser
Eksamen MAT1013 Matematikk 1T Høsten 2013 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 7,5 10 4,0 10 12 4 Oppgave 2 (4 poeng) Siv har fire blå og seks svarte bukser
Del 2: Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamen 1T våren 2016
 Eksamen 1T våren 016 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005 Oppgave (3 poeng) A B C D E F G H I J K L På tallinjen ovenfor er det merket av 1 punkter. Hvert av tallene
Eksamen 1T våren 016 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005 Oppgave (3 poeng) A B C D E F G H I J K L På tallinjen ovenfor er det merket av 1 punkter. Hvert av tallene
Eksamen 1T, Høsten 2012
 Eksamen 1T, Høsten 01 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) En rett linje har stigningstall. Linjen skjærer
Eksamen 1T, Høsten 01 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) En rett linje har stigningstall. Linjen skjærer
Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. x x x x
 Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (5 poeng) Deriver funksjonene gitt ved f 3 6 4 a) f 3 6 6 6 b) g 5ln 3 3 Vi bruker kjerneregelen
Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (5 poeng) Deriver funksjonene gitt ved f 3 6 4 a) f 3 6 6 6 b) g 5ln 3 3 Vi bruker kjerneregelen
Eksamen. Fag: AA6516 Matematikk 2MX. Eksamensdato: 7. desember 2005. Vidaregåande kurs I / Videregående kurs I
 Eksamen Fag: AA6516 Matematikk 2MX Eksamensdato: 7. desember 2005 Vidaregåande kurs I / Videregående kurs I Studieretning: Allmenne, økonomiske og administrative fag Privatistar/Privatister Oppgåva ligg
Eksamen Fag: AA6516 Matematikk 2MX Eksamensdato: 7. desember 2005 Vidaregåande kurs I / Videregående kurs I Studieretning: Allmenne, økonomiske og administrative fag Privatistar/Privatister Oppgåva ligg
Eksamen MAT1013 Matematikk 1T Høsten 2014
 Eksamen MAT03 Matematikk T Høsten 04 Oppgave ( poeng) Regn ut og skriv svaret på standardform 50000000000,0005 Oppgave ( poeng) Løs likningen 6 Oppgave 3 ( poeng) Løs likningen lg( 3) 0 Oppgave 4 ( poeng)
Eksamen MAT03 Matematikk T Høsten 04 Oppgave ( poeng) Regn ut og skriv svaret på standardform 50000000000,0005 Oppgave ( poeng) Løs likningen 6 Oppgave 3 ( poeng) Løs likningen lg( 3) 0 Oppgave 4 ( poeng)
Løsningsforslag heldagsprøve våren 2010 1T
 Løsningsforslag heldagsprøve våren 00 T DEL OPPGAVE a) Regn ut x x x x x x x x x x 9x x x x x 6x x x x 6x x 6x b) Løs likninga x x 6 x x 6 x x 6 x x 6 x x x x c) Løs likningssettet ved regning x y x y
Løsningsforslag heldagsprøve våren 00 T DEL OPPGAVE a) Regn ut x x x x x x x x x x 9x x x x x 6x x x x 6x x 6x b) Løs likninga x x 6 x x 6 x x 6 x x 6 x x x x c) Løs likningssettet ved regning x y x y
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005 Oppgave (3 poeng) A B C D E F G H I J K L På tallinjen ovenfor er det merket av 1 punkter. Hvert av tallene
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005 Oppgave (3 poeng) A B C D E F G H I J K L På tallinjen ovenfor er det merket av 1 punkter. Hvert av tallene
1 Geometri R2 Oppgaver
 1 Geometri R2 Oppgaver Innhold 1.1 Vektorer... 2 1.2 Regning med vektorer... 15 1.3 Vektorer på koordinatform... 19 1.4 Vektorprodukt... 22 1.5 Linjer i rommet... 27 1.6 Plan i rommet... 30 1.7 Kuleflater...
1 Geometri R2 Oppgaver Innhold 1.1 Vektorer... 2 1.2 Regning med vektorer... 15 1.3 Vektorer på koordinatform... 19 1.4 Vektorprodukt... 22 1.5 Linjer i rommet... 27 1.6 Plan i rommet... 30 1.7 Kuleflater...
Eksamen MAT1013 Matematikk 1T Våren 2013
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 750 000 0,005 5 7,510 7,5 5 3 8 3 10 1,5 10 510 5 Oppgave (1 poeng) Løs likningssystemet x3y7 5xy8 Velger å løse likningen
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 750 000 0,005 5 7,510 7,5 5 3 8 3 10 1,5 10 510 5 Oppgave (1 poeng) Løs likningssystemet x3y7 5xy8 Velger å løse likningen
Eksamen MAT1013 Matematikk 1T Va ren 2014
 Eksamen MAT1013 Matematikk 1T Va ren 014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform,5 10 3,0 10 15 5 15 ( 5) 10,5 3,0 10 7,5 10 Oppgave ( poeng) Regn ut og skriv svaret så enkelt som mulig
Eksamen MAT1013 Matematikk 1T Va ren 014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform,5 10 3,0 10 15 5 15 ( 5) 10,5 3,0 10 7,5 10 Oppgave ( poeng) Regn ut og skriv svaret så enkelt som mulig
Lærerveiledning. Oppgave 1. Tallene på figuren viser omkretsen av hver av de fire små trekantene. Hva er omkretsen av den store trekanten?
 Oppgave 1 Tallene på figuren viser omkretsen av hver av de fire små trekantene. Hva er omkretsen av den store trekanten? A 43 B 59 C 55 D 67 E 91 Hvilke linjestykker er en del av omkretsen til den store
Oppgave 1 Tallene på figuren viser omkretsen av hver av de fire små trekantene. Hva er omkretsen av den store trekanten? A 43 B 59 C 55 D 67 E 91 Hvilke linjestykker er en del av omkretsen til den store
Eksamen 1P våren 2011
 Eksamen 1P våren 011 Del 1: Uten hjelpemidler Oppgave 1 a) Når kursen på islandske kroner er 5,5, svarer 500 ISK til 5, 5 kr 500 = 6, 5 kr 100 b) Hvis vi setter kursen på islandske kroner til 5, blir omregningen
Eksamen 1P våren 011 Del 1: Uten hjelpemidler Oppgave 1 a) Når kursen på islandske kroner er 5,5, svarer 500 ISK til 5, 5 kr 500 = 6, 5 kr 100 b) Hvis vi setter kursen på islandske kroner til 5, blir omregningen
Eksamen 1T, Høsten 2012
 Eksamen 1T, Høsten 01 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) En rett linje har stigningstall. Linjen skjærer
Eksamen 1T, Høsten 01 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) En rett linje har stigningstall. Linjen skjærer
Oppgave 1. Del A. (i) Skriv de to desimaltallene 0, 7 og 3, 12 som vanlig brøk og forkort hvis mulig. som desimaltall. 3x 6
 Oppgave 1 (i) Skriv de to desimaltallene 0, 7 og 3, 12 som vanlig brøk og forkort hvis mulig. (ii) Skriv 314 100 og 4 5 (iii) Forkort brøkene som desimaltall. 12 15 og 3x 6 9x. (iv) Sorter disse seks tallene
Oppgave 1 (i) Skriv de to desimaltallene 0, 7 og 3, 12 som vanlig brøk og forkort hvis mulig. (ii) Skriv 314 100 og 4 5 (iii) Forkort brøkene som desimaltall. 12 15 og 3x 6 9x. (iv) Sorter disse seks tallene
Del 2: Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamen R2, Våren 2011 Løsning
 R Eksamen, Våren 0 Løsning Eksamen R, Våren 0 Løsning Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (8 poeng) a) Deriver funksjonene
R Eksamen, Våren 0 Løsning Eksamen R, Våren 0 Løsning Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (8 poeng) a) Deriver funksjonene
DEL 1 Uten hjelpemidler
 DEL Uten hjelpemidler Oppgave ( poeng) Regn ut og skriv svaret på standardform 5000000000 0,0005 Oppgave ( poeng) Løs likningen 6 Oppgave 3 ( poeng) Løs likningen lg( 3) 0 Oppgave 4 ( poeng) Løs ulikheten
DEL Uten hjelpemidler Oppgave ( poeng) Regn ut og skriv svaret på standardform 5000000000 0,0005 Oppgave ( poeng) Løs likningen 6 Oppgave 3 ( poeng) Løs likningen lg( 3) 0 Oppgave 4 ( poeng) Løs ulikheten
Eksamen MAT 1011 Matematikk 1P Va ren 2015
 Eksamen MAT 1011 Matematikk 1P Va ren 015 Oppgave 1 (1 poeng) Skriv som prosent a) 0,451 45,1 % 5 0 b) 0 % 5 100 Oppgave ( poeng) a) Forklar at de to trekantene ovenfor er formlike. Vinkelsummen i en trekant
Eksamen MAT 1011 Matematikk 1P Va ren 015 Oppgave 1 (1 poeng) Skriv som prosent a) 0,451 45,1 % 5 0 b) 0 % 5 100 Oppgave ( poeng) a) Forklar at de to trekantene ovenfor er formlike. Vinkelsummen i en trekant
Eksamen R2 høsten 2014 løsning
 Eksamen R høsten 04 løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (3 poeng) Deriver funksjonene a) f x cos3x Vi bruker kjerneregelen
Eksamen R høsten 04 løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (3 poeng) Deriver funksjonene a) f x cos3x Vi bruker kjerneregelen
Eksamen REA3022 R1, Våren 2009
 Eksamen REA0 R, Våren 009 Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave a) Deriver funksjonene ) f x x 4 4 8 f x x x x x ) g x x
Eksamen REA0 R, Våren 009 Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave a) Deriver funksjonene ) f x x 4 4 8 f x x x x x ) g x x
Løsningsforslag Matematikk 2MX - AA mai 2006
 Løsningsforslag Matematikk 2MX - AA6516-3. mai 2006 eksamensoppgaver.org September 21, 2008 2 Om løsningsforslaget Løsningsforslaget for matematikk eksamen i 2MX er gratis, og det er lastet ned på eksamensoppgaver.org.
Løsningsforslag Matematikk 2MX - AA6516-3. mai 2006 eksamensoppgaver.org September 21, 2008 2 Om løsningsforslaget Løsningsforslaget for matematikk eksamen i 2MX er gratis, og det er lastet ned på eksamensoppgaver.org.
Eksamen 1T våren 2015 løsning
 Eksamen T våren 05 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave ( poeng) Regn ut og skriv svaret på standardform 5 7,5 0 0,003
Eksamen T våren 05 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave ( poeng) Regn ut og skriv svaret på standardform 5 7,5 0 0,003
DEL 1. Uten hjelpemidler. Oppgave 1 (3 poeng) Oppgave 2 (5 poeng) Oppgave 3 (4 poeng) S( x) 1 e e e. Deriver funksjonene. Bestem integralene
 DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Deriver funksjonene a) f( x) 6cos(x 1) b) g( x) cos x sin x Oppgave (5 poeng) Bestem integralene a) (x 3 x) dx b) x cos( x ) dx c) x d x Oppgave 3 ( poeng) En
DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Deriver funksjonene a) f( x) 6cos(x 1) b) g( x) cos x sin x Oppgave (5 poeng) Bestem integralene a) (x 3 x) dx b) x cos( x ) dx c) x d x Oppgave 3 ( poeng) En
2P, Modellering Quiz fasit. Test, 3 Modellering
 Test, 3 Modellering Innhold 3.1 Lineære modeller og lineær regresjon... 3. Modell for svingetiden til en pendel... 8 3.3 Potensfunksjon som modell... 8 3.4 Eksponentialfunksjon som modell... 18 3.5 Polynomfunksjoner
Test, 3 Modellering Innhold 3.1 Lineære modeller og lineær regresjon... 3. Modell for svingetiden til en pendel... 8 3.3 Potensfunksjon som modell... 8 3.4 Eksponentialfunksjon som modell... 18 3.5 Polynomfunksjoner
R1 eksamen høsten 2015
 R1 eksamen høsten 2015 Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (5 poeng) Deriver funksjonene a) f x x x 2 ( ) 3 5 2 b) g( x)
R1 eksamen høsten 2015 Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (5 poeng) Deriver funksjonene a) f x x x 2 ( ) 3 5 2 b) g( x)
Funksjoner S2 Oppgaver
 Funksjoner S Funksjoner S Oppgaver. Derivasjon... Den deriverte til en konstant funksjon... Den deriverte til en potensfunksjon... Den deriverte til et produkt av to funksjoner... 4 Den deriverte til en
Funksjoner S Funksjoner S Oppgaver. Derivasjon... Den deriverte til en konstant funksjon... Den deriverte til en potensfunksjon... Den deriverte til et produkt av to funksjoner... 4 Den deriverte til en
Eksamen 1T våren 2016 løsning
 Eksamen T våren 06 løsning Oppgave ( poeng) Regn ut og skriv svaret på standardform,8 0 0,0005,8 0,8 0 3,6 0 0,5 0 0,5 3 3 5 Oppgave (3 poeng) A B C D E F G H I J K L På tallinjen ovenfor er det merket
Eksamen T våren 06 løsning Oppgave ( poeng) Regn ut og skriv svaret på standardform,8 0 0,0005,8 0,8 0 3,6 0 0,5 0 0,5 3 3 5 Oppgave (3 poeng) A B C D E F G H I J K L På tallinjen ovenfor er det merket
Eksamen MAT1015 Matematikk 2P Va ren 2015
 Eksamen MAT1015 Matematikk P Va ren 015 Oppgave 1 ( poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 1 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet
Eksamen MAT1015 Matematikk P Va ren 015 Oppgave 1 ( poeng) Dag Temperatur Mandag 4 C Tirsdag 10 C Onsdag 1 C Torsdag 5 C Fredag 6 C Lørdag Tabellen ovenfor viser hvordan temperaturen har variert i løpet
Eksamen S2 høsten 2010 Løsning
 Eksamen S høsten 010 Løsning Del 1 Oppgave 1 (4 poeng) a) Deriver funksjonene f x x 3x 4 1) 3 3 3 4 3 3 3 1 1 f x x x f x x f x x x g x 6x e ) x x 6x e x x 6 6 x 6 1 g x g x e x e g x e x P x x 6x 8x 4
Eksamen S høsten 010 Løsning Del 1 Oppgave 1 (4 poeng) a) Deriver funksjonene f x x 3x 4 1) 3 3 3 4 3 3 3 1 1 f x x x f x x f x x x g x 6x e ) x x 6x e x x 6 6 x 6 1 g x g x e x e g x e x P x x 6x 8x 4
Årsprøve i matematikk for 9. trinn Kannik skole
 Årsprøve i matematikk for 9. trinn Kannik skole Våren 2013 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir delt ut samtidig, men
Årsprøve i matematikk for 9. trinn Kannik skole Våren 2013 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir delt ut samtidig, men
Eksamen REA3022 R1, Våren 2011
 Eksamen REA30 R1, Våren 011 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (18 poeng) 500 8 er a) Vis at den deriverte til funksjonen
Eksamen REA30 R1, Våren 011 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (18 poeng) 500 8 er a) Vis at den deriverte til funksjonen
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform 10 5 000 0,15 Oppgave ( poeng) Løs likningen grafisk 1 1 9 x x Oppgave 3 ( poeng) Løs ulikheten x x 1 0 Oppgave 4 ( poeng)
DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform 10 5 000 0,15 Oppgave ( poeng) Løs likningen grafisk 1 1 9 x x Oppgave 3 ( poeng) Løs ulikheten x x 1 0 Oppgave 4 ( poeng)
M1_01. Funksjonene f og g er definert ved f( x)= x 1. g( f( x)) er da lik. b ( x + 3) d ( x + 2) e x MA M1 Side 1
 Funksjonene f og g er efinert ve f( )= 1 og g ( ) = ( +3). M1_01 g( f( )) er a lik a ( 1)( + 3) b ( + 3) 1 c ( ) ( + ) e + 8 MA13001 M1 Sie 1 En funksjon f er efinert ve: M1_0 f( )= 1 hvis < 1 f( )= +1
Funksjonene f og g er efinert ve f( )= 1 og g ( ) = ( +3). M1_01 g( f( )) er a lik a ( 1)( + 3) b ( + 3) 1 c ( ) ( + ) e + 8 MA13001 M1 Sie 1 En funksjon f er efinert ve: M1_0 f( )= 1 hvis < 1 f( )= +1
R2 eksamen våren 2018 løsningsforslag
 R eksamen våren 08 løsningsforslag DEL Uten hjelpemidler Oppgave ( poeng) Deriver funksjonene a) f ( x) = cos ( x ) f ( x) = sin( x ) = sin( x ) b) g ( x) = x sin x g ( x) = sin x + x cos x = sin x + x
R eksamen våren 08 løsningsforslag DEL Uten hjelpemidler Oppgave ( poeng) Deriver funksjonene a) f ( x) = cos ( x ) f ( x) = sin( x ) = sin( x ) b) g ( x) = x sin x g ( x) = sin x + x cos x = sin x + x
Eksamen MAT1013 Matematikk 1T Va ren 2014
 Eksamen MAT1013 Matematikk 1T Va ren 2014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 2,510 3,010 15 5 Oppgave 2 (2 poeng) Regn ut og skriv svaret så enkelt som mulig 1 2 0 1 3 2 9 6 4
Eksamen MAT1013 Matematikk 1T Va ren 2014 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 2,510 3,010 15 5 Oppgave 2 (2 poeng) Regn ut og skriv svaret så enkelt som mulig 1 2 0 1 3 2 9 6 4
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 15 5,5 10 3,0 10 Oppgave ( poeng) Regn ut og skriv svaret så enkelt som mulig 1 0 1 3 9 6 4 8 Oppgave 3 (1 poeng) Løs
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 15 5,5 10 3,0 10 Oppgave ( poeng) Regn ut og skriv svaret så enkelt som mulig 1 0 1 3 9 6 4 8 Oppgave 3 (1 poeng) Løs
Eksamen AA6524 Matematikk 3MX Elevar/Elever AA6526 Matematikk 3MX Privatistar/Privatister. Nynorsk/Bokmål
 Eksamen 05.12.2007 AA6524 Matematikk 3MX Elevar/Elever AA6526 Matematikk 3MX Privatistar/Privatister Nynorsk/Bokmål Oppgave 1 a) Deriver funksjonen: f x 2 ( ) = cos( x + 1) b) Løs likningen og oppgi svaret
Eksamen 05.12.2007 AA6524 Matematikk 3MX Elevar/Elever AA6526 Matematikk 3MX Privatistar/Privatister Nynorsk/Bokmål Oppgave 1 a) Deriver funksjonen: f x 2 ( ) = cos( x + 1) b) Løs likningen og oppgi svaret
Eksamen R1, Va ren 2014, løsning
 Eksamen R1, Va ren 014, løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (4 poeng) Deriver funksjonene a) f x lnx x Vi bruker
Eksamen R1, Va ren 014, løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (4 poeng) Deriver funksjonene a) f x lnx x Vi bruker
Tall i arbeid Påbygging kapittel 3 Funksjoner Løsninger til innlæringsoppgavene
 Tall i arbeid Påbygging kapittel 3 Funksjoner Løsninger til innlæringsoppgavene 3.1 a Origo er skjæringspunktet mellom x-aksen og y-aksen. Koordinatene til origo er altså. (0, 0) b Førstekoordinaten til
Tall i arbeid Påbygging kapittel 3 Funksjoner Løsninger til innlæringsoppgavene 3.1 a Origo er skjæringspunktet mellom x-aksen og y-aksen. Koordinatene til origo er altså. (0, 0) b Førstekoordinaten til
Faktor terminprøve i matematikk for 10. trinn
 Faktor terminprøve i matematikk for 10. trinn Våren 2011 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir utdelt samtidig, men del
Faktor terminprøve i matematikk for 10. trinn Våren 2011 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir utdelt samtidig, men del
Eksamen våren 2008 Løsninger
 Eksamen våren 008 Løsninger Eksamen våren 008 Løsninger Del Hjelpemidler: Vanlige skrivesaker, passer, linjal med cm-mål og vinkelmåler Oppgave a f x ( ) x ln = x f ( x) = x lnx+ x = xlnx+x x b c ( ) (
Eksamen våren 008 Løsninger Eksamen våren 008 Løsninger Del Hjelpemidler: Vanlige skrivesaker, passer, linjal med cm-mål og vinkelmåler Oppgave a f x ( ) x ln = x f ( x) = x lnx+ x = xlnx+x x b c ( ) (
INNHOLD SAMMENDRAG GEOMETRI
 INNHOLD GEOMETRI... 3 LINJE, STRÅLE OG LINJESTYKKE... 3 VINKEL... 3 STUMP, SPISS OG RETT VINKEL... 3 TOPPVINKLER... 4 NABOVINKLER... 4 SAMSVARENDE VINKLER... 4 OPPREISE EN NORMAL FRA ET PUNKT PÅ EN LINJE...
INNHOLD GEOMETRI... 3 LINJE, STRÅLE OG LINJESTYKKE... 3 VINKEL... 3 STUMP, SPISS OG RETT VINKEL... 3 TOPPVINKLER... 4 NABOVINKLER... 4 SAMSVARENDE VINKLER... 4 OPPREISE EN NORMAL FRA ET PUNKT PÅ EN LINJE...
Del 1. Oppgave 1 (5 poeng) Oppgave 2 (4 poeng) Oppgave 3 (5 poeng) ( ) 2 e x. f x x x. Deriver funksjonene. Løs likningene
 Del 1 Oppgave 1 (5 poeng) Deriver funksjonene a) b) f ( ) e g( ) ln e 1 c) h( ) 1 Oppgave (4 poeng) Løs likningene a) b) e 7e 8 0 ln( 5 1) ln(3 ) 0 Oppgave 3 (5 poeng) Gitt vektorene a, 3 og b 5, 3 a)
Del 1 Oppgave 1 (5 poeng) Deriver funksjonene a) b) f ( ) e g( ) ln e 1 c) h( ) 1 Oppgave (4 poeng) Løs likningene a) b) e 7e 8 0 ln( 5 1) ln(3 ) 0 Oppgave 3 (5 poeng) Gitt vektorene a, 3 og b 5, 3 a)
11 Nye geometriske figurer
 11 Nye geometriske figurer Det gylne snitt 1 a) Mål lengden og bredden på et bank- eller kredittkort. Regn ut forholdet mellom lengden og bredden. Hvilket tall er forholdet nesten likt, og hva kaller vi
11 Nye geometriske figurer Det gylne snitt 1 a) Mål lengden og bredden på et bank- eller kredittkort. Regn ut forholdet mellom lengden og bredden. Hvilket tall er forholdet nesten likt, og hva kaller vi
4 Funksjoner og andregradsuttrykk
 4 Funksjoner og andregradsuttrkk KATEGORI 1 4.1 Funksjonsbegrepet Oppgave 4.110 Regn ut f (0), f () og f (4) når a) f () = + b) f () = 4 c) f () = + 5 d) f () = 3 3 Oppgave 4.111 f() = + + 1 4 3 1 0 1
4 Funksjoner og andregradsuttrkk KATEGORI 1 4.1 Funksjonsbegrepet Oppgave 4.110 Regn ut f (0), f () og f (4) når a) f () = + b) f () = 4 c) f () = + 5 d) f () = 3 3 Oppgave 4.111 f() = + + 1 4 3 1 0 1
Funksjoner oppgaver. Innhold. Funksjoner R1
 Funksjoner oppgaver Innhold 3.1 Funksjoner... 3. Kontinuitet, grenseverdier og asymptoter til funksjoner... 3 Grenseverdier... 3 Rasjonale funksjoner og asymptoter... 6 Kontinuitet... 8 Funksjoner med
Funksjoner oppgaver Innhold 3.1 Funksjoner... 3. Kontinuitet, grenseverdier og asymptoter til funksjoner... 3 Grenseverdier... 3 Rasjonale funksjoner og asymptoter... 6 Kontinuitet... 8 Funksjoner med
Eksamen REA 3022 Høsten 2012
 Eksamen REA 0 Høsten 01 Del 1 Uten hjelpemidler Oppgave 1 (5 poeng) Deriver funksjonene a) f x x 1 f '( x) x 1 f ' x 8x b) g x x x 1 g( x) x x 1 1 1 g( x) x x x x 1 g x x x x c) hx x e h x x e x e x x
Eksamen REA 0 Høsten 01 Del 1 Uten hjelpemidler Oppgave 1 (5 poeng) Deriver funksjonene a) f x x 1 f '( x) x 1 f ' x 8x b) g x x x 1 g( x) x x 1 1 1 g( x) x x x x 1 g x x x x c) hx x e h x x e x e x x
Eksamen MAT 1011 Matematikk 1P Høsten 2014
 Eksamen MAT 1011 Matematikk 1P Høsten 2014 Oppgave 1 (2 poeng) Diagrammet ovenfor viser hvor mange bøker en forfatter har solgt hvert år de fire siste årene. Når var den prosentvise økningen i salget fra
Eksamen MAT 1011 Matematikk 1P Høsten 2014 Oppgave 1 (2 poeng) Diagrammet ovenfor viser hvor mange bøker en forfatter har solgt hvert år de fire siste årene. Når var den prosentvise økningen i salget fra
Innlevering FO929A - Matematikk forkurs HIOA Obligatorisk innlevering 2 Innleveringsfrist Torsdag 25. oktober 2012 kl. 14:30 Antall oppgaver: 16
 Innlevering FO929A - Matematikk forkurs HIOA Obligatorisk innlevering 2 Innleveringsfrist Torsdag 25. oktober 2012 kl. 14:30 Antall oppgaver: 16 1 Finn volum og overateareal til følgende gurer. Tegn gjerne
Innlevering FO929A - Matematikk forkurs HIOA Obligatorisk innlevering 2 Innleveringsfrist Torsdag 25. oktober 2012 kl. 14:30 Antall oppgaver: 16 1 Finn volum og overateareal til følgende gurer. Tegn gjerne
Geometri R1, Prøve 2 løsning
 Geometri R, Prøve løsning Del Tid: 90 min Hjelpemidler: Skrivesaker Oppgave Gitt punktene A,, B 0, og D,6 a) Bestem koordinatene til AB og lengden til AB AB 0, 8, AB 8 68 7 A, B og D er hjørner i parallellogrammet
Geometri R, Prøve løsning Del Tid: 90 min Hjelpemidler: Skrivesaker Oppgave Gitt punktene A,, B 0, og D,6 a) Bestem koordinatene til AB og lengden til AB AB 0, 8, AB 8 68 7 A, B og D er hjørner i parallellogrammet
SAMMENDRAG OG FORMLER. Nye Mega 9A og 9B
 SAMMENDRAG OG FORMLER Nye Mega 9A og 9B 1 Sammendrag og formler Nye Mega 9A Kapittel A GEOMETRI Regulære mangekanter Når alle sidene er like lange og alle vinklene er like store i en mangekant, sier vi
SAMMENDRAG OG FORMLER Nye Mega 9A og 9B 1 Sammendrag og formler Nye Mega 9A Kapittel A GEOMETRI Regulære mangekanter Når alle sidene er like lange og alle vinklene er like store i en mangekant, sier vi
Eksamen våren Fag: MAT1006 Matematikk 1T-Y. Eksamensdato: 7. mai Kunnskapsløftet. Videregående trinn 1. Yrkesfag.
 Eksamensoppgave for følgende fylker: Akershus, Oslo, Buskerud, Vestfold, Østfold, Oppland, Hedmark, Telemark, Aust-Agder, Vest-Agder, Rogaland, Hordaland, Sogn og Fjordane Eksamen våren 013 Fag: MAT1006
Eksamensoppgave for følgende fylker: Akershus, Oslo, Buskerud, Vestfold, Østfold, Oppland, Hedmark, Telemark, Aust-Agder, Vest-Agder, Rogaland, Hordaland, Sogn og Fjordane Eksamen våren 013 Fag: MAT1006
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (2 poeng) Regn ut og skriv svaret på standardform 0,72 10 60 10 8 8 Oppgave 2 (1 poeng) Regn ut 4 2 (2 ) 0 3 3 2 Oppgave 3 (2 poeng) Regn ut og skriv svaret så enkelt
DEL 1 Uten hjelpemidler Oppgave 1 (2 poeng) Regn ut og skriv svaret på standardform 0,72 10 60 10 8 8 Oppgave 2 (1 poeng) Regn ut 4 2 (2 ) 0 3 3 2 Oppgave 3 (2 poeng) Regn ut og skriv svaret så enkelt
1P eksamen våren 2017 løsningsforslag
 1P eksamen våren 017 løsningsforslag Tid: timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) Du har 15 L saft. Du skal helle saften over i
1P eksamen våren 017 løsningsforslag Tid: timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) Du har 15 L saft. Du skal helle saften over i
DEL 1. Uten hjelpemidler. Oppgave 1 (3 poeng) Oppgave 2 (3 poeng) Oppgave 3 (4 poeng) Oppgave 4 (4 poeng) Deriver funksjonene. b) g( x) 5e sin(2 x)
 DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Deriver funksjonene a) f( x) cos(3 x) x b) g( x) 5e sin( x) Oppgave (3 poeng) Bestem integralene a) b) 3 ( )d e 1 x x x x ln x dx Oppgave 3 (4 poeng) a) Løs
DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) Deriver funksjonene a) f( x) cos(3 x) x b) g( x) 5e sin( x) Oppgave (3 poeng) Bestem integralene a) b) 3 ( )d e 1 x x x x ln x dx Oppgave 3 (4 poeng) a) Løs
Eksamen MAT 1011 Matematikk 1P Våren 2013
 Eksamen MAT 1011 Matematikk 1P Våren 01 Oppgave 1 ( poeng) Hilde skal kjøpe L melk,5 kg poteter 0,5 kg ost 00 g kokt skinke Gjør et overslag og finn ut omtrent hvor mye hun må betale. L melk:14,95 kr 15
Eksamen MAT 1011 Matematikk 1P Våren 01 Oppgave 1 ( poeng) Hilde skal kjøpe L melk,5 kg poteter 0,5 kg ost 00 g kokt skinke Gjør et overslag og finn ut omtrent hvor mye hun må betale. L melk:14,95 kr 15
Eksamen REA3022 R1, Høsten 2010
 Eksamen REA30 R1, Høsten 010 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (0 poeng) a) Deriver funksjonene 1) f x x e x e x
Eksamen REA30 R1, Høsten 010 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (0 poeng) a) Deriver funksjonene 1) f x x e x e x
Eksamen R2 vår 2012, løsning
 Eksamen R vår 0, løsning Oppgave ( poeng) a) Deriver funksjonene ) f sin Bruker kjerneregelen på uttrykket sin der Vi har da guu sinu u cosu cos f cos 6cos ) g sin Vi bruker produktregelen for derivasjon.
Eksamen R vår 0, løsning Oppgave ( poeng) a) Deriver funksjonene ) f sin Bruker kjerneregelen på uttrykket sin der Vi har da guu sinu u cosu cos f cos 6cos ) g sin Vi bruker produktregelen for derivasjon.
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (0 poeng) a) Deriver funksjonene f = e 1) ( ) ) g( ) = 3 1 b) Vis at = 1 er en løsning av likningen 3 6 + 6= 0 Bruk polynomdivisjon til å finne de andre løsningene. c)
DEL 1 Uten hjelpemidler Oppgave 1 (0 poeng) a) Deriver funksjonene f = e 1) ( ) ) g( ) = 3 1 b) Vis at = 1 er en løsning av likningen 3 6 + 6= 0 Bruk polynomdivisjon til å finne de andre løsningene. c)
R1 eksamen høsten 2015 løsning
 R1 eksamen høsten 15 løsning Løsninger laget av Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (5 poeng) Deriver funksjonene a) f
R1 eksamen høsten 15 løsning Løsninger laget av Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (5 poeng) Deriver funksjonene a) f
TERMINPRØVE SINUS 1M
 TERMINPRØVE SINUS 1M Høsten 2005 Fellesoppgaver Oppgave 1 a) Regn ut. 1) 5 3 2 2) 3 2 4( 3 1) 3) 2 3( 2) + 2( 6 4) b) Skriv desimaltallene som brøker og forkort mest mulig. 1) 0,25 2) 1,325 c) Regn ut
TERMINPRØVE SINUS 1M Høsten 2005 Fellesoppgaver Oppgave 1 a) Regn ut. 1) 5 3 2 2) 3 2 4( 3 1) 3) 2 3( 2) + 2( 6 4) b) Skriv desimaltallene som brøker og forkort mest mulig. 1) 0,25 2) 1,325 c) Regn ut
Del 2: Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
eksamensoppgaver.org 4 oppgave1 a.i) Viharulikheten 2x 4 x + 5 > 0 2(x 2) x + 5 > 0 Sådaserviatløsningenpådenneulikhetenblir
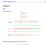 eksamensoppgaver.org 4 oppgave1 a.i) Viharulikheten 2x 4 x + 5 > 0 2(x 2) x + 5 > 0 Sådaserviatløsningenpådenneulikhetenblir x, 5 2, eksamensoppgaver.org 5 a.ii) Vi har ulikheten og ordner den. 10 x 2
eksamensoppgaver.org 4 oppgave1 a.i) Viharulikheten 2x 4 x + 5 > 0 2(x 2) x + 5 > 0 Sådaserviatløsningenpådenneulikhetenblir x, 5 2, eksamensoppgaver.org 5 a.ii) Vi har ulikheten og ordner den. 10 x 2
Eksamen REA3022 Matematikk R1. Nynorsk/Bokmål
 Eksamen 31.05.011 REA30 Matematikk R1 Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del : 5 timer: Del 1 skal leveres inn etter timer. Del skal leveres inn
Eksamen 31.05.011 REA30 Matematikk R1 Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del : 5 timer: Del 1 skal leveres inn etter timer. Del skal leveres inn
Eksamen R2, Høsten 2015, løsning
 Eksamen R, Høsten 05, løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (4 poeng) Deriver funksjonene a) f( ) 5cos( ) f 5 sin 0sin
Eksamen R, Høsten 05, løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (4 poeng) Deriver funksjonene a) f( ) 5cos( ) f 5 sin 0sin
Eksamen REA3024 Matematikk R2. Nynorsk/Bokmål
 Eksamen 3.05.0 REA304 Matematikk R Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del : Hjelpemiddel på Del : 5 timar: Del skal leverast inn etter timar. Del skal leverast inn
Eksamen 3.05.0 REA304 Matematikk R Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del : Hjelpemiddel på Del : 5 timar: Del skal leverast inn etter timar. Del skal leverast inn
Faktor terminprøve i matematikk for 9. trinn
 Faktor terminprøve i matematikk for 9. trinn Våren 2013 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir delt ut samtidig, men del
Faktor terminprøve i matematikk for 9. trinn Våren 2013 bokmål Navn: Gruppe: Informasjon Oppgavesettet består av to deler hvor alle oppgaver skal besvares. Del 1 og del 2 blir delt ut samtidig, men del
Punktene A, B, C og D ligger på linje med innbyrdes avstander AB = 3, BC = 6, CD = 8 og DE = 4.
 Oppgave Punktene A, B, C og D ligger på linje med innbyrdes avstander AB =, BC = 6, CD = 8 og DE =. Hva er minste mulige verdi for AE? A 0 B C D E 5 Tegn! Start med å tegne ei lang rett linje, plasser
Oppgave Punktene A, B, C og D ligger på linje med innbyrdes avstander AB =, BC = 6, CD = 8 og DE =. Hva er minste mulige verdi for AE? A 0 B C D E 5 Tegn! Start med å tegne ei lang rett linje, plasser
Eksamen MAT1013 Matematikk 1T Våren 2013
 Eksamen MAT1013 Matematikk 1T Våren 2013 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform DEL 1 Uten hjelpemidler 750 000 0,005 Oppgave 2 (1 poeng) Løs likningssystemet 2x3y7 5x2y8 Oppgave 3
Eksamen MAT1013 Matematikk 1T Våren 2013 Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform DEL 1 Uten hjelpemidler 750 000 0,005 Oppgave 2 (1 poeng) Løs likningssystemet 2x3y7 5x2y8 Oppgave 3
Eksamen REA3024 Matematikk R2
 Eksamen 03.1.009 REA304 Matematikk R Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del : Bruk av kilder: Vedlegg: Framgangsmåte: Veiledning om vurderingen:
Eksamen 03.1.009 REA304 Matematikk R Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del : Bruk av kilder: Vedlegg: Framgangsmåte: Veiledning om vurderingen:
DEL1 Uten hjelpemidler
 DEL1 Uten hjelpemidler Oppgave 1 a) Brukopplysningenenedenfortilåfinneuthvaénballkoster,oghvaén hockeykølle koster. 500 kroner 100kroner b) Figuren viser grafene til tre andregradsfunksjoner f, g og h.
DEL1 Uten hjelpemidler Oppgave 1 a) Brukopplysningenenedenfortilåfinneuthvaénballkoster,oghvaén hockeykølle koster. 500 kroner 100kroner b) Figuren viser grafene til tre andregradsfunksjoner f, g og h.
Løsningsforslag R2 Eksamen Nebuchadnezzar Matematikk.net Øistein Søvik
 Løsningsforslag R2 Eksamen 6 Vår 3.05.20 Nebuchadnezzar Matematikk.net Øistein Søvik Sammendrag De fleste forlagene som gir ut lærebøker til den videregående skolen, gir ut løsningsforslag til tidligere
Løsningsforslag R2 Eksamen 6 Vår 3.05.20 Nebuchadnezzar Matematikk.net Øistein Søvik Sammendrag De fleste forlagene som gir ut lærebøker til den videregående skolen, gir ut løsningsforslag til tidligere
Faktor terminprøve i matematikk for 10. trinn
 Faktor terminprøve i matematikk for 10. trinn Høsten 201 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt
Faktor terminprøve i matematikk for 10. trinn Høsten 201 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt
Del 2: Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
1T eksamen høsten 2017 løsning
 1T eksamen høsten 017 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform. 105000 0,15
1T eksamen høsten 017 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform. 105000 0,15
Løsning eksamen R1 våren 2009
 Løsning eksamen R1 våren 009 Oppgave 1 a) 1) f( ) ( 1) 4 f ( ) 4( 1) ( 1) 4( 1) 8 ( 1) ) g ( ) e 3 3 3 g( ) e ( e ) 1 e e ( ) 1e e (1) e b) ( ) lim lim lim ( ) 4 4 4 ( ) ( ) ( ) ( ) c) ( ) ( ) ( ) ( )
Løsning eksamen R1 våren 009 Oppgave 1 a) 1) f( ) ( 1) 4 f ( ) 4( 1) ( 1) 4( 1) 8 ( 1) ) g ( ) e 3 3 3 g( ) e ( e ) 1 e e ( ) 1e e (1) e b) ( ) lim lim lim ( ) 4 4 4 ( ) ( ) ( ) ( ) c) ( ) ( ) ( ) ( )
Fasit. Funksjoner Vg1T. Innhold
 Fasit Innhold 4.1 Funksjonsbegrepet... 4. Lineære funksjoner... 6 4.3 Andre funksjoner... 15 Andregradsfunksjoner... 15 Polynomfunksjoner... 18 Rasjonale funksjoner... 19 Potensfunksjoner og eksponentialfunksjoner...
Fasit Innhold 4.1 Funksjonsbegrepet... 4. Lineære funksjoner... 6 4.3 Andre funksjoner... 15 Andregradsfunksjoner... 15 Polynomfunksjoner... 18 Rasjonale funksjoner... 19 Potensfunksjoner og eksponentialfunksjoner...
Eksamen REA3022 Matematikk R1. Nynorsk/Bokmål
 Eksamen 30.05.014 REA30 Matematikk R1 Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del 1: Hjelpemiddel på Del : 5 timar: Del 1 skal leverast inn etter timar. Del skal leverast
Eksamen 30.05.014 REA30 Matematikk R1 Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del 1: Hjelpemiddel på Del : 5 timar: Del 1 skal leverast inn etter timar. Del skal leverast
R2 kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 R kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka E Bruker formelen cos 36 cos( 8 ) E sin 8 v og sin8 5 cos v sin sin8 5 5 6 5 5 8 5 5 8 6 5 8 6 5 8 8 3 5 5 5 a f ( ) sin 5 cos f ( ) 5cos
R kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka E Bruker formelen cos 36 cos( 8 ) E sin 8 v og sin8 5 cos v sin sin8 5 5 6 5 5 8 5 5 8 6 5 8 6 5 8 8 3 5 5 5 a f ( ) sin 5 cos f ( ) 5cos
JULETENTAMEN, 9. KLASSE, 2015. FASIT
 JULETENTAMEN, 9. KLASSE, 2015. FASIT DELPRØVE 1. OPPGAVE 1.1: 367 + 254 = 621 c: 67. 88 536 536 = 5896 e: 18,4-9,06 = 9,34 24,8 + 7,53 = 32,33 d: 3,2 : 0,8 = 32 : 8 = 4 32 f: 12 2. 5 2 = 12 2. 25 = 12
JULETENTAMEN, 9. KLASSE, 2015. FASIT DELPRØVE 1. OPPGAVE 1.1: 367 + 254 = 621 c: 67. 88 536 536 = 5896 e: 18,4-9,06 = 9,34 24,8 + 7,53 = 32,33 d: 3,2 : 0,8 = 32 : 8 = 4 32 f: 12 2. 5 2 = 12 2. 25 = 12
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (2 poeng) En vare koster 640 kroner. Butikkeieren vurderer å sette opp prisen med 10 % eller 15 %. a) Hvor mye vil varen koste dersom prisen settes opp med 10 %? b) Hvor
DEL 1 Uten hjelpemidler Oppgave 1 (2 poeng) En vare koster 640 kroner. Butikkeieren vurderer å sette opp prisen med 10 % eller 15 %. a) Hvor mye vil varen koste dersom prisen settes opp med 10 %? b) Hvor
Eksempel på løsning 2011 MAT1013 Matematikk 1T Sentralt gitt skriftlig eksamen Høsten 2010 Bokmål
 Eksempel på løsning 011 MAT1013 Matematikk 1T Sentralt gitt skriftlig eksamen Høsten 010 Bokmål MAT1013 Matematikk 1T, Høst 010 Del 1 Uten hjelpemidler Kun vanlige skrivesaker, passer, linjal med centimetermål
Eksempel på løsning 011 MAT1013 Matematikk 1T Sentralt gitt skriftlig eksamen Høsten 010 Bokmål MAT1013 Matematikk 1T, Høst 010 Del 1 Uten hjelpemidler Kun vanlige skrivesaker, passer, linjal med centimetermål
Del 2: Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Hjelpemidler på Del 1: Ingen hjelpemidler er tillatt, bortsett fra vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamen R2, Høst 2012, løsning
 Eksamen R, Høst 0, løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave ( poeng) Deriver funksjonene a) cos f e Vi bruker produktregelen
Eksamen R, Høst 0, løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave ( poeng) Deriver funksjonene a) cos f e Vi bruker produktregelen
1T eksamen våren 2017
 1T eksamen våren 2017 Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (2 poeng) Regn ut og skriv svaret på standardform 0,72 10 60 10 8 8 Oppgave
1T eksamen våren 2017 Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (2 poeng) Regn ut og skriv svaret på standardform 0,72 10 60 10 8 8 Oppgave
Løsningsforslag eksamen 1T våren 2010 DEL 1. Oppgave 1. a) Funksjonen f er gitt ved f x 2x 3. Tegn grafen og finn nullpunktene for f f x 2x 3 Grafen
 Løsningsforslag eksamen T våren 00 DEL Oppgave a) Funksjonen f er gitt ved f 3. Tegn grafen og finn nullpunktene for f f 3 Grafen y 0 8 6 4-4 -3 - - 3 4 - -4 Nullpunkt 3 0 3 Nullpunkt når 3 b) Løs likningen
Løsningsforslag eksamen T våren 00 DEL Oppgave a) Funksjonen f er gitt ved f 3. Tegn grafen og finn nullpunktene for f f 3 Grafen y 0 8 6 4-4 -3 - - 3 4 - -4 Nullpunkt 3 0 3 Nullpunkt når 3 b) Løs likningen
