1. Intégrales définies et indéfinies I. (a) Soit b > 0. Montrer que pour tout x > 0 la fonction. 2 b. F (x) = arctan bx. 1 (1 + bx) x. f(x) = x t dt.
|
|
|
- Krister Løken
- 6 år siden
- Visninger:
Transkript
1 Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R clculer t. +π sin d, +π cos d, (d) Clculer (e) Clculer +π +π sin d, sin cos d, +π +π ( ) 9 d. sin π cos π d cos d, sin cos d. 78
2 CHAPITRE 6. CALCUL INTÉGRAL 79 (f) * Soit f : R R une fonction continue de période T >. Soit F définie pr F () = f(t). Montrer que F est périodique vec période T si et seulement si. Intégrles indéfinies. T f(t) =. () (b) + cos t e t+ (c) (d) (e) (f) sinh t e t + cosh t e t cosh t rctn t (g) rctn( t) (h) rcsin t (i) t (j) t cos t (k) t cos t
3 CHAPITRE 6. CALCUL INTÉGRAL 8 (l) (m). Intégrles indéfinies. () + cos t + tn t cos t + e t (b) sin(ln t) (c) t ln t (d) ( + t) ln t (e) t ln t (f) ln t (g) t ln( + t) (h) (i) (j) ln t ( + t) + sin 7 t cos t (k) (l) + + cos t
4 CHAPITRE 6. CALCUL INTÉGRAL 8 (m) (n) (o) sin t cos t + sin t t t( + t) ( + t ) t (p) t 5 t (q) (r) (s) (t) t + t + t t t(4 t) t t 4. Integrles définies pour l règle du trpèze. Soient < b et µ = +b. Donner les intégrles suivntes : µ b ( ) ( )(b ) d b (b ) d + d µ 5. Fonction primitive de l fonction réciproque. Soient f une fonction inversible, f s fonction reciproque et F une primitive de f. Montrer que l fonction G() = f () F (f ()) est une primitive de f. En déduire les primitives de ln, rcsin, rctn.
5 CHAPITRE 6. CALCUL INTÉGRAL 8 6. Intégrles définies et indéfinies II. Formules utiles. b Clculer les intégrles : () (b) (c) (d) (e) 7. Intégrles générlisées I. () (b) (c) (d) (e) (f) d = rctn b rctn + t + t + t 5 + t + t 4 t + t 5 + t + t t 4 + t 4 + t t ln t + t t + 6t + t t(4t + ) t t
6 CHAPITRE 6. CALCUL INTÉGRAL 8 (g) (h) (i) 8. Intégrles générlisées II. () (b) (c) (d) (e) (f) (g) t t t t t( + t) e t ln t ln t t t e t cosh t rctn t + t rctn t t 9. Intégrles générlisées III - Étude de convergence. Discuter, en fonction du nombre réel α >, l convergence des intégrles générlisées suivntes () (b) t α t α
7 CHAPITRE 6. CALCUL INTÉGRAL 84 (c) (d) (e) (f) t α + t t α ln t ln t t α ln t t α
8 CHAPITRE 6. CALCUL INTÉGRAL 85. Intégrles générlisées et l fonction Gmm. L fonction Gmm - Formules utiles. Soit > et n N : Γ() = t e t Γ() = Γ( + ), Γ(n + ) = n!, Γ( ) = π Formule de Stirling. n! π n n+ e n i.e. lim n n! π n n+ e = n Intégrle de Guss. π e d = () Soient µ, σ deu nombres réels et σ >. Clculer les intégrles générlisées i. ii. iii. ( µ) e σ d πσ ( µ) e σ d πσ ( µ) e σ d πσ (b) Soient y > et n N. Clculer les intégrles (en terme de l fonction Gmm) i. (t n + )(t n )e yt ii. ( ln t) y iii. t e t (c) Soient > et k, n N. Clculer ( ) n ( ) k ( ) n k lim n k n n ( ) n n! où = k (n k)!k!. Idée : Utiliser l formule de Stirling pour n! et (n k)! et le fit que pour tout R lim n ( + n )n = e.
9 CHAPITRE 6. CALCUL INTÉGRAL Corrigés. Intégrles définies et indéfinies I. Clculer les dérivées des fonctions suivntes uniqument à l ide de l définition de l dérivée : () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Corrigé. (c) Pour R (d) (e) Vérifier que F () = f(). +π +π +π +π +π t = { si si sin d = cos cos( + π) =, cos d = sin( + π) sin =, sin d = cos cos( + π) = cos, cos d = sin( + π) sin = sin +π sin cos d = sin sin cos d = sin +π +π ( ) 9 d = ( ) 4 sin π cos π d = ln( cos π) =, =, = = ln π. (f) * Soit f : R R une fonction continue de période T >. Soit F définie pr F () = f(t). Montrer que F est périodique vec période T si et seulement si T f(t) =.
10 CHAPITRE 6. CALCUL INTÉGRAL 87 Corrigé. Si F est périodique vec période T, lors Si T = F (T ) F () = f(t) =, on note que d (F ( + T ) F ()) d T i.e. F ( + T ) F () est constnte. Donc F ( + T ) F () = F (T ) F () = f(t). = f( + T ) f() =, T pour tout, i.e. F est périodique vec période T.. Intégrles indéfinies. f(t) = () (b) = ln( + cos ) + cos t e t+ = + s e s ds = ( + )e + (c) Noter que (d) donc sinh t e t + = e t et e t + = e t sinh t + e e t = + e cosh t = + s ds = rctn(e ). (e) Noter que e = cosh + sinh donc (f) rctn t = e t cosh t = + sinh = + ln(cosh ) cosh t (t) t rctn t = rctn + t = rctn ln( + )
11 CHAPITRE 6. CALCUL INTÉGRAL 88 (g) (h) rctn( t) = s rctn s ds rcsin t = (t) rcsin t = (s ) rctn s ds = rctn( ) s + s ds = rctn( ) + s ds = rctn( ) + rctn( ) = rcsin t rc t (i) On voit que = rcsin ( t ) rc = rcsin + t rcsin t = rcsin + rcsin t cos = ou bien pr un chngement de vrible s = t : t = sin s ds = cos. (j) Pr une intégrtion pr prtie et l eercice précedent t cos t = t ( ) = sin t = sin + cos ou pr un chngement de vrible et une intégrtion pr prtie t cos t = = s cos s = sin ds s(sin s) ds = sin + cos sin s ds
12 CHAPITRE 6. CALCUL INTÉGRAL 89 (k) Pr deu intégrtions pr prtie successives : I := t cos t = t cos t() = cos sin t cos t + t sin t = cos sin t(sin t) + t ( cos t) = cos sin sin + sin t + t I = cos sin sin + sin cos vec le résultt du cours pour sin t. Pr conséquent, t cos t = cos sin sin sin cos + (l) Noter que + tn t = cos, donc (m) + cos t + tn t = cos t + cos t et pr conséquent + cos t + tn t = ln( + cos ) cos t + + I +. Les intégrnds contennts des fonctions trigonométriques R(, cos t, tn t, cot t) peuvent être trnsformê dns des intégrnds lgébriques pr le chngement de vrible En effet, nous vons z = tn t = cos t = tn t cos t = z + z, cos t = cos t t sin = z + z tn t = z z et d t d z = + z. Donc tn ( z R(, cos t, tn t, cot t) = R + z, z + z, z z, z ) z + z dz
13 CHAPITRE 6. CALCUL INTÉGRAL 9 En prticulier, tn cos t + = + z ( z) + z dz. Intégrles indéfinies. tn = z dz = ln tn () Pr deu intégrtions pr prtie (voir cours) on trouve que e t = e (sin cos ). (b) Avec le chngement de vrible s = ln t i.e. t = e s et l eercice precedent ln sin(ln t) = e s (sin(ln ) cos(ln )) sin s ds =. (c) t ln t = t ln t (t ) ln t = 4 (d) (e) = ln 4 4 = ln 8 t t ( + t) ln t = (( + t) ) ln t = ( + t) ln t ( + t) t = ( + t) ln t ln t t t t t ln t = (t ) ln t = ln = ln = ln = ln t ln t (t ) ln t 9 ln + t 9 9 ln 9 + 7
14 CHAPITRE 6. CALCUL INTÉGRAL 9 (f) ln t = (t) ln t (g) (h) = ln ln t =... = ln ln + 6 ln 6 t ln( + t) = (t ) ln( + t) = ln( + ) = ln( + ) = ln( + ) ln( + ) t + t t + + t ln t ( + t) = (( + t) ) ln t = ln + + = ln + + = ln ln( + ) t( + t) t + t (i) Soit pr le chngement de vrible de l eercice donné pr z = tn t, i.e. = z donc + z tn + = 4z ( + z) ( + z ) dz tn = + z ( + z) dz = tn + z + rctn z = + tn +
15 CHAPITRE 6. CALCUL INTÉGRAL 9 ou bien pr une intégrtion pr prtie + = ( cos t) + d ou on déduit que = cos + sin cos t ( + ) = cos + sin + = cos + sin + + cos = + + sin + et pr conséquent que + = cos = sin. (j) (k) sin 7 t cos t = sin8 8 + = cos t + = cos t 4 cos t + = sin 4 ln( + sin ) (l) En utilisnt le chngement de vrible s = cos t on trouve cos + cos t = + s ds Un deuième chngement de vrible s = z (idélment on fit les deu chngements de vrible en un temps) nous donne cos + cos t = ( + z ) dz = rctn( cos ) (m) Pr le chngement de vrible s = : sin t cos t sin + sin t = s ds = sin rctn(sin ) + s (n) Pr le chngement de vrible t = s : t t( + t) = + s ds = rctn
16 CHAPITRE 6. CALCUL INTÉGRAL 9 (o) ( + t ) t = (p) Pr le chngement de vrible t = s : t 5 t = s s ds = = ( ) / 9 (q) Pr le chngement de vrible t = s : t + = t (r) Pr une intégrtion pr prtie ( s) / ( s) / ds t + + = + + ( ) 5/ 5 t t + + s ds = + rctnh + + t t = ( t ) + t = + = t + rcsinh (s) (t) = = rcsin ( ) t(4 t) 4 (t ) t t = ln + 4. Integrles définies pour l règle du trpèze. Soient < b et µ = +b. Donner les intégrles suivntes : µ ( ) b ( )(b ) d = (b ). b (b ) (b ) (b ) (b ) d + d = + = µ
17 CHAPITRE 6. CALCUL INTÉGRAL Fonction primitive de l fonction réciproque. Soient f une fonction inversible, f s fonction reciproque et F une primitive de f. Montrer que l fonction G() = f () F (f ()) est une primitive de f. En déduire les primitives de ln, rcsin, rctn. G () = f () + d f () d f () f(f ()) = f (). d d () ln : G() = ln e ln = ln. (b) rcsin : (c) rctn : G() = rcsin + cos(rcsin ) = rcsin +. G() = rctn + ln(cos(rctn )) = rctn + ln(cos (rctn )) = rctn ln( + tn (rctn )) = rctn ln( + ). 6. Intégrles définies et indéfinies II. () (b) (c) t + t + = t + t + t + = ln( + ) + rctn t 5 + t + = t + t + t + = t t t t + = t t t t + + t t + = ln( + ) + rctn ( ) t 4 t + = (t 4 + t) (t + ) + t + = t t t + + t + t t t + = t t t + + t + t t t + = rctn ( ) + ln( + ) 6 ln( + )
18 CHAPITRE 6. CALCUL INTÉGRAL 95 (d) (e) t 5 + t + t t 4 + = t + t t 4 + = + 4 ln(4 + ) t 4 + t = t t t + = ln() ln( + ) 7. Intégrles générlisées I. () (b) (c) t ln t = (t ) ln t = = lim + t rctn + t = 4 lim rctn = π + t + 6t + = + (t + ) + = + t = π (d) t + t(4t + ) = 4t + t + 4t 4t + = rctn(t) + ( ln t + ln(4t + )) = rctn(t) + ln ( 4t + ) t = π 4 rctn() + ln() ln(5) (e) (f) (g) t t = t = π = t t = t + t = 8
19 CHAPITRE 6. CALCUL INTÉGRAL 96 (h) Pr le chngement de vrible s = t, i.e. t = s + : + t t = + s ds = π (i) Pr le chngement de vrible s = t, i.e. t = s : 8. Intégrles générlisées II. + = t( + t) + s ds = π () Pr le chngement de vrible s = t, i.e. t = s : (b) (c) e t = ln t = ln t t = (d) Pr deu intégrtions pr prtie se s ds = Γ() = (t) ln t = ln t( t ) = = t = t e t = 5 e (e) Pr le chngement de vrible s = e t, i.e. t = ln s : + cosh t = e t = + et + s = (π π 4 ) = π (f) (g) rctn t t rctn t + t = rctn t = rctn t t = π 8 + t( + t ) = π 4 + ln 9. Intégrles générlisées III - Étude de convergence. Discuter, en fonction du nombre réel α >, l convergence des intégrles générlisées suivntes () converge si α < est diverge sinon. t α
20 CHAPITRE 6. CALCUL INTÉGRAL 97 (b) (c) (d) (e) (f) converge si α > est diverge sinon. t α t α + t converge si < α < est diverge sinon. t α ln t converge si < α est diverge sinon. ln t t α converge si α < est diverge sinon. ln t t α converge si α > est diverge sinon.. Intégrles générlisées et l fonction Gmm. L fonction Gmm - Formules utiles. Soit > et n N : Formule de Stirling. Γ() = t e t Γ() = Γ( + ), Γ(n + ) = n!, Γ( ) = π n! π n n+ e n i.e. lim n n! π n n+ e = n Intégrle de Guss. π e d = () Soient µ, σ deu nombres réels et σ >. Clculer les intégrles générlisées i. ii. ( µ) e σ d πσ ( µ) e σ d πσ
21 CHAPITRE 6. CALCUL INTÉGRAL 98 iii. ( µ) e σ d πσ Corrigé. On utilise l intégrle de Guss π e d =. Pr le chngement de vrible y = µ σ, i.e. = σy + µ : ( µ) e σ d = πσ = ( µ) e σ d = πσ = cr l fonction intégrble σy e y R est zéro. πσ e ( µ) σ d = = πσ e y d dy dy π e y dy = πσ (σy + µ) e y π µ e y dy = µ d dy dy est impir, donc son intégrle sur πσ (σy + µ) e y π (σ y + µ ) e y d dy dy cr l fonction intégrble σy e y est impir, donc son intégrle sur R est zéro. Pr une intégrtion pr prtie dy π y e y dy = y d π dy = y e y + ( ) e y dy π e y dy =, donc (b) Soient y > et n N. πσ e ( µ) σ d = σ + µ i. Pr le chngement de vrible s = yt on (t n + )(t n )e yt = (t n )e yt = y n s n e s ds y e s ds = y n Γ(n + ) y
22 CHAPITRE 6. CALCUL INTÉGRAL 99 ii. Pr le chngement de vrible s = ln t, i.e. t = e s on ( ln t) y = = = y s ds ds s y e s ds s y e s ds = Γ(y) iii. Pr le chngement de vrible s = t, i.e. t = s +, on t e t = s e s = Γ( )e = Γ( )e = (c) Soient > et k, n N. Clculer ( ) n ( ) k ( ) n k lim n k n n ( ) n n! où = k (n k)!k!. Idée : Utiliser l formule de Stirling pour n! et (n k)! et le fit que pour tout R Corrigé. fie et Donc ( n k Avec ) ( n lim ( + n n )n = e. π e Pr l formule de Stirling nous vons pour n et k n! π n n+ e n (n k)! π (n k) n k+ e n+k ) k ( ) n k n n+ k n (n k) n k+ n k e k k! k ( = ( k n )n k+ e k k! n ( ) n k n ) n k lim ( k n n )n k+ = lim ( k n n )n = e k et lim ( n n )n k = lim ( n n )n = e nous obtenons ( ) n ( ) k ( ) n k k e lim = n k n n e k e k k! = k e. k!
23 Annee A Dérivées et primitives de fonctions usuelles
24 Annee B Intégrles générlisées
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 2008
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
Energie et corrélation. Systèmes de Traitement du Signal Polytech Marseille INFO 2016
Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Integrale cu parametru
1 Definiti integrlei cu prmetru Derivre integrlelor cu prmetru Integrre unei integrle cu prmetru 2 3 Definiti integrlei cu prmetru Definiti integrlei cu prmetru Derivre integrlelor cu prmetru Integrre
Roulements à rouleaux cylindriques
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Roulements à rouleaux cylindriques
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
Laser vert : moins de plus de 300. Acheter Laser PRODUITS CHAUDS. Pointeur Laser étanche
Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
MAT 100A: Mappeeksamen 4
. november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
AB a donc OM = = 2 2
ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t
Løsningsforslag Eksamen M100 Høsten 1998
Løsningsforslag Eksamen M00 Høsten 998 Oppgave { x y = f(x) = + x + a hvis x ln( + x ) x hvis < x lim f(x) = f( ) = + a = a x lim f(x) = ln( + x ( ) ) ( ) = ln + For at f(x) skal være kont. i x = må lim
MeijerG1. Notations. Primary definition. Traditional name. Traditional notation. Mathematica StandardForm notation. Generalized Meijer G-function
MeijerG Nottions Trditionl nme Generlied Meijer G-function Trditionl nottion Mthemtic StndrdForm nottion MeijerG,, n, n,,, b,, b m, b m,, b,, r Primry definition 07.5.0.000.0 m k n r r 0 m n m n n b k
Figur 2: Fortegnsskjema for g (x)
Løsningsforslag Eksamen M00 Våren 998 Oppgave a) g) = e ) = e ) Figur : Fortegnsskjema for g) g) > 0 for < 0 og > og g) < 0 for 0 <
a 2πf(x) 1 + (f (x)) 2 dx.
MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
Bobine à noyau de fer
1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
Derivasjon. Oversikt over Matematikk 1. Derivasjon anvendelser. Sekantsetningen
3 Oversikt over Mtemtikk Induksjon Grenser og kontinuitet Skjæringssetningen Eksistens v ekstrempunkt Elementære funksjoner Derivsjon Sekntsetningen Integrsjon Differensilligninger Kurver i plnet Rekker
Corrigés des exercices du chapitre 25
MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
Repetisjon i Matematikk 1, 4. desember 2013: Komplekse tall og Derivasjon 1
Repetisjon i Mtemtikk, 4. desember 0: Komplekse tll og Derivsjon Komplekse tll. Regn ut og skriv på normlform i 5 + i b 8 i 7 + 5i c 5 + i 6 i. Regn ut og skriv på normlform d 4 i + i e i 5 + 4i eiπ 6
Høgskolen i Bergen. Formelsamling. for. ingeniørutdanningen. FOA150 høsten 2006 fellespensum. 3.utgave
Høgskolen i Bergen Formelsmling for ingeniørutdnningen FOA5 høsten 6 fellespensum. 3.utgve Funksjoner. Elementære regneregler og funksjoner: y = y, ( ) =, y y =,, =, = ) = ) = = log = ln ln c) ln y = y
Eksamen FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. Nynorsk/Bokmål
Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
SIF5003 Matematikk 1, 5. desember 2001 Løsningsforslag
SIF5003 Matematikk, 5. desember 200 Oppgave For den første grensen får vi et /-uttrykk, og bruker L Hôpitals regel markert ved =) : lim 0 + ln ln sin 0 + cos sin 0 + cos sin ) =. For den andre får vi et
Oppgaver og fasit til seksjon
1 Oppgaver og fasit til seksjon 3.4-3.6 Oppgaver til seksjon 3.4 1. Anta at f(x, y) = x 2 y 3 og r(t) = t 2 i + 3t j. Regn ut g (t) når g(t) = f(r(t)). 2. Anta at f(x, y) = x 2 e xy2 og r(t) = sin t i+cos
Brosses intérieures avec manche
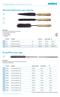18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
dx = 1 2y dy = dx/ x 3 y3/2 = 2x 1/2 + C 1
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
REQUÊTE APPLICATION KLAGESKJEMA
Voir Note explicative See Explanatory Note Se klageveiledningen NOR Numéro de dossier File-number Klage nr. COUR EUROPÉENNE DES DROITS DE L HOMME EUROPEAN COURT OF HUMAN RIGHTS DEN EUROPEISKE MENNESKERETTIGHETSDOMSTOL
FYS2140 Kvantefysikk, Løsningsforslag for Oblig 1
FYS4 Kvantefysikk, Løsningsforslag for Oblig. januar 8 Her er løsningsforslag for Oblig som dreide seg om å friske opp en del grunnleggende matematikk. I tillegg finner dere til slutt et løsningsforslag
Lsningsforslag ved Klara Hveberg Lsningsforslag til utvalgte oppgaver i kapittel 8 I kapittel 8 er integrasjon og integrasjonsteknikker det store tema
Lsningsforslag til utvalgte ogaver i kaittel 8 I kaittel 8 er integrasjon og integrasjonsteknikker det store temaet, og her er det mange regneogaver som gir deg anledning til a trene inn disse teknikkene.
DYNAMIQUE. Etude des mouvements de tangage d une transmission de puissance d hélicoptère. x r 2. y r 2. x 1. y r y r
e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
2 n+2 er konvergent eller divergent. Observer først at; 2n+2 2 n+2 = n=1. n=1. 2 n > for alle n N. Denne summen er.
MA2 Vår 28 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag 9.2.9 Ønsker å finne ut om 3+ 2 n+2 er konvergent eller divergent. Observer først at; 3 + 2 n 2 n+2 = ( 3 ) + +2
Clôture Métallique. Portails / Portillons / Accessoires
Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
On remet la machine en route
Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
y = x y, y 2 x 2 = c,
TMA415 Matematikk Vår 17 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 9 Alle oppgavenummer referer til 8. utgave av Adams & Essex alculus: A omplete
Repitisjon av Diverse Emner
NTNU December 15, 2012 Oversikt 1 2 3 4 5 Å substituere x med en trigonometrisk funksjon, gjør det mulig å evaluere integral av typen I = dx a 2 +x 2 I = dx a 2 +x 2 I = dx a 2 x 2 der a er en positiv
Eksamen i emnet M117 - Matematiske metodar Onsdag 6. november 2002, kl Løysingsforslag:
Eksamen i emnet M117 - Matematiske metodar Onsdag 6 noember 2002, kl 09-15 Løysingsforslag: 1a Her er r 0 løysing a det karakteristiske polynomet med mltiplisitet 2 pga t 3 -faktor i den partiklære løysinga
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2
![Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2](/thumbs/77/75859899.jpg "Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2")
Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Formelsamling i matematikk
Formelsmling i mtemtikk Algebr Aritmetiske opersjoner (b + c) b + c + c b Potensregler Polynom b + c b b + c d + bc d bc b c d b d c d bc x y x+y x x / x y x y n x x /n 0 x n x n ( x ) y xy (b) x x y (
Funksjoner av stokastiske variable.
Funksjoner av stokastiske variable. Dekkes av pensumsidene i kap. 7 I ulike sammenhenger, blant annet for å finne fordelingen til estimatorer, er vi interesserte i fordelingen til funksjoner av stokastiske
Oppsummering av vekstdel ECON 2915
Oppsummering av vekstdel ECON 2915 Kjell Arne Brekke UiO November 17, 2008 KAB (Økonomisk Insitutt) Oppsummering November 17, 2008 1 / 9 Solow-modellen Y = F (K, L) Vi antar konstant skalautbytte samt
Derivasjon Forelesning i Matematikk 1 TMA4100. Hans Jakob Rivertz Institutt for matematiske fag 2. september 2011
Derivasjon Forelesning i Matematikk TMA400 Hans Jakob Rivertz Institutt for matematiske fag 2. september 20 Kapittel 3.7. Derivasjon av inverse funksjoner 3 Derivasjon av inverse til deriverbare funksjoner
Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
1 MAT100 Obligatorisk innlevering 1. 1 Regn ut i) iii) ii) Regn ut i) ii)
1 MAT1 Obligatorisk innlevering 1 1 Regn ut 3 7 + 1 2. i) 13 14 ii) 11 14 iii) 9 14 2 Regn ut 8 9 + 3 4. i) 57 36 ii) 59 36 iii) 61 36 3 Regn ut 1 4 + 1 8. i) 3 16 ii) 3 8 iii) 5 8 4 Regn ut 1 8 + 1 16.
EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
EKSAMEN. 1. klassene, ingenørutdanning og flexing. ANTALL SIDER UTLEVERT: 5(innkl. forside og 2 sider formelark)
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
Funksjoner av stokastiske variable.
Funksjoner av stokastiske variable. Dekkes av pensumsidene i kap. 7 I ulike sammenhenger, blant annet for å finne fordelingen til estimatorer, er vi interesserte i fordelingen til funksjoner av stokastiske
1 k 2 + 1, k= 5. i=1. i = k + 6 eller k = i 6. m+6. (i 6) i=1
TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
I. Évolution du commerce mondial
I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
Kommunikasjonsperm. Overvåking og undersøkelser side 1. Smerter side 2. Naturlige funksjoner, eliminasjon side 3. Sengeleie og stell side 4
Kommunikasjonsperm Fransk Overvåking og undersøkelser side 1 Smerter side 2 Naturlige funksjoner, eliminasjon side 3 Sengeleie og stell side 4 Mat, drikke kvalme side 5 Bevegelse, syn, temperatur side
TMA4120 Matematikk 4K Høst 2015
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA41 Matematikk 4K Høst 15 Chapter 6.7 Systemer av ODE. Vi bruker L t} 1 s, L e at f(t } F (s a 6.7:9 Løs IVP. y 1 y 1 + y,
MA1102 Grunnkurs i analyse II Vår 2019
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 10.2.27 a) Vi skal vise at u + v 2 = u 2 + 2u v + v 2. (1) Som boka nevner på side 581,
EKSAMEN. Om eksamen. EMNE: MA2610 FAGLÆRER: Svein Olav Nyberg, Morten Brekke. Klasser: (div) Dato: 18. feb Eksamenstid:
. EKSAMEN EMNE: MA61 FAGLÆRER: Svein Olav Nyberg, Morten Brekke Klasser: (div) Dato: 18. feb. 4 Eksamenstid: 9 1 Eksamensoppgaven består av følgende: Antall sider (ink. forside): 8 Antall oppgaver: 5 Antall
Oppgaver og fasit til seksjon
1 Oppgaver og fasit til seksjon 3.1-3.3 Oppgaver til seksjon 3.1 1. Regn ut a b når a) a = ( 1, 3, 2) b = ( 2, 1, 7) b) a = (4, 3, 1) b = ( 6, 1, 0) 2. Finn arealet til parallellogrammet utspent av a =
Tillegg om strømfunksjon og potensialstrøm
Kapittel 9 Tillegg om strømfunksjon og potensialstrøm 9.1 Divergensfri strøm 9.1.1 Strømfunksjonen I kompendiet, kap. 4.6 og kap. 9, er det påstått at dersom et todimensjonalt strømfelt v(x y) = v x (x
TMA4120 Matematikk 4K Høst 2015
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA41 Matematikk 4K Høst 15 Løsningsforslag Øving 9 hapter 13.7 La z. Logaritmen til z, ln z, er definert som tallene ln z ln
dy ycos 2 y = dx. Ved å integrere på begge sider av likhetstegnet får man ved å substituere u = y,du = dy dy ycos 2 y = 2du cos 2 u = x.
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
Vi regner først ut de nødvendige partiellderiverte for å se om vektorfeltet er konservativt. z = 2z, F 2 F 2 z = 2y, F 3. x = 2x, F 3.
TMA415 Matematikk Vår 15 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 7 Alle oppgavenummer refererer til 8. utgave av Adams & Essex alculus: A omplete
MAT Vår Oblig 2. Innleveringsfrist: Fredag 23.april kl. 1430
MAT 00 Vår 00 Oblig Innleveringsfrist: Fredag 3.april kl. 430 Oppgaven leveres stiftet med forsideark på ekspedisjonskontoret til Matematisk institutt i 7. etg. i Niels Henrik Abels hus innen fristen.
1 Mandag 1. mars 2010
Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Abstract. i x + a x +. a = (a x, a y ) z γ + 1 γ + z )
Abstract R, Aharonov-Bohm Schrödinger Landau level Aharonov-Bohm Schrödinger 1 Aharonov-Bohm R Schrödinger ( ) ( ) 1 1 L a = i + a = i x + a x + ( ) 1 i y + a y (1). a = (a x, a y ) rot a = ( x a y y a
1 OA i = f. OA o. 1 < 1 OA o. f 1. O 2 A i O 2 A 1 = = f 2 O 2 A i. f 2O 2 A i 5 `c mffl `a vfle c O 2 A i = 20 `c mffl `eˇt f 2 = 20 `c mffl
. B L`affl r`e l åtˇi`o nffl `d`e `c o n jˇu`g åi sfi`o nffl `d`o n n`e OA i = + f P`o u rffl u n`e l e n tˇi l l e m i n`c e `c o n vfleˇr`g e n t e, < f `d`o n`c L i m`àg e `eṡfi t r`é e l l e. f > 0.
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. HansPetterHornæsogLarsNilsBakken. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 4 sider formelark)
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO: 9. desember 0 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: HnsPetterHornæsogLrsNilsBkken
Eksamen FSP5020 Fransk I PSP5013 Fransk nivå I. Nynorsk/Bokmål
Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
Løsningsforslag Eksamen M100 Våren 2002
Løsningsforslag Eksamen M00 Våren 00 Oppgave Evaluerer grensen cos( ) 0 ( sin( ) ) 0 6 0 6 5 0 sin( ) 0 sin( ) = Har brukt l Hôpitals regel (derivert teller og nevner hver for seg) i første og tredje overgang.
FORMELSAMLING TIL STK1100 OG STK1110
FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 16. november 2009) 1. Sannsynlighet La A, B, A 1, A 2,...,B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
EKSAMEN. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 2 sider formelark)
KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
Equations fondamentales de la mécanique linéaire de la rupture
//5 Aee A Equatios fodaetales de la écaique liéaie de la uptue A. Zeghloul MMAE appels d élasticité plae octio d Ai e vaiables coplees epésetatio des déplaceets et des cotaites Epessio du toseu des effots
Løsningsforslag, eksamen FY desember 2017
1 Løsninsforsla, eksamen FY1001 14. desember 017 1 3 områder av t = 4 s, a konstant i hvert omrde. 1 : a 1 = 0; v 0 = 5m/s = x 1 = v 0 t; v 1 = v 0 : a = v/ t = 1.5 m/s = x = x 1 + v 1 t + a t = v 0 t
Eksamen i MAT1100 H14: Løsningsforslag
Eksamen i MAT H4: Løsningsforslag Oppgave. ( poeng) Dersom f(x, y) x sin(xy ), er f y lik: A) sin(xy ) + xy cos(xy ) B) x cos(xy ) C) x y cos(xy ) D) sin(xy ) + x y cos(xy ) E) cos(xy ) Riktig svar: C):
Forkunnskaper i matematikk for fysikkstudenter. Integrasjon.
De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
Løsningsforslag AA6524 Matematikk 3MX Elever 7. juni eksamensoppgaver.org
Løsningsforslag AA654 Matematikk MX Elever 7. juni 004 eksamensoppgaver.org eksamensoppgaver.org Om løsningsforslaget Løsningsforslaget for matematikk eksamen i MX er gratis, og det er lastet ned på eksamensoppgaver.org.
NTNU. TMA4100 Matematikk 1 høsten Løsningsforslag - Øving 5. Avsnitt Vi vil finne dx ( cos t dt).
NTNU Instittt for matematiske fag TMA4 Matematikk høsten Løsningsforslag - Øving 5 Avsnitt 5.4 ( + cos x)dx = dx + cos xdx = π + [sin x] π = π + (sin π sin) = π. 44 Vi vil finne d x dx ( cos t dt). Merk
GAMME DETENTE DIRECTE SOMMAIRE. X32 monosplit Inverter Page 88. X3 multisplit Inverter Page 90. Monosplits/Multisplits
SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
Løsningsforslag, Ma-2610, 18. februar 2004
Løsningsforslag, Ma-60, 8. februar 004 For sensor og kandidater.. Lineær uavhengighet Avgjør hvorvidt de følgende funksjonene er lineært uavhengige på den reelle tallinja: f(x) x g(x) 3x h(x) 5x 8x Svaralternativ
m15/1/aynor/hp2/nor/tz0/xx Monday 11 May 2015 (morning) Lundi 11 mai 2015 (matin) Lunes 11 de mayo de 2015 (mañana) 2 hours / 2 heures / 2 horas
m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
Nicolai Kristen Solheim
Oppgave 1. 1a) 1, 0, 2, sin 5 4cos sin 54cos sin 8 sin cos cos 54cos 8 sin cos 5cos 4cos 8sin cos 5cos 4cos Dersom vi plotter grafen for vil vi se hvor vokser og avtar. 1 Fra grafen for ser vi følgende
Høgskolen i Oslo og Akershus. ln x sin x 2 (ln x) (ln x) 2 = cos ( x2. (ln x) 2 = cos x 2 2x ln x x sin x 2 (ln x) 2 x + 2 = 1, P = (2, 2 4 y4 = 0
Løysingsforslag. Oppgåve a f cos f cos + cos cos + sin cos sin g g sin ln sin ln sin ln ln cos ln sin ln cos ln sin ln cos ln sin ln b 4 4 + y 4, P, 4 5 Implisitt derivasjon: d 4 y 4 + d d 4 d d d 4 4
EKSAMEN I FY2045 KVANTEFYSIKK Mandag 2. juni 2008 kl
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
Eksamen i TMA4123/TMA4125 Matematikk 4M/N
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Anne Kværnø: mobil 92663824 Eksamen i TMA423/TMA425 Matematikk 4M/N Bokmål Mandag 2.
UNIVERSITETET I OSLO
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk og stil variere noe fra oppgave til oppgave.
NTNU Institutt for matematiske fag TMA4105 Matematikk, øving 7, vår 011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Disjoncteurs sélectifs
233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
dx = 1 1 )dx = 3 y= x . Tangentplanet til hyperboloiden i (2, 1, 3) er derfor gitt ved x 2, y 1, z 3 = 0 x 2 + 2(y 1) 2 (z 3) = 0 x + 2y 2z 3 = 2
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA415 Matematikk vår 9 øsningsforslag til eksamen 15. august 9 1 Treghetsmoment med hensyn på x-aksen er gitt ved x [ ] y I
Une version feuilletée du théorème de translation de Brouwer
Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
Korreksjoner til fasit, 2. utgave
Korreksjoner til fasit,. utgave Kapittel. Oppgave.. a): / Oppgave.. e):.887, 0.58 Oppgave..9: sin00πt). + ) x Oppgave.7.5 c): ln for 0 < x. x Oppgave.8.0: Uttrykket for a + b) 7 skal være a + b) 7 = a
Matematik, LTH Kontinuerliga system vt Formelsamling. q t. + j = k. u t. (Allmännare ρ 2 u. t2 Svängningar i gaser (ljud) t 2 c2 2 u
Matematik, LH Kontinuerliga system vt 7 Formelsamling Formelsamligen utgör bara ett stöd för minnet. Beteckningar förklaras sålunda ej. Ej heller anges förutsättningar för formlernas giltighet. Fysikaliska
MA1101 Grunnkurs Analyse I Høst 2017
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA Grunnkurs Analyse I Høst 7 9.5. a) Har at + x b arctan b = π + x [arctan x]b (arctan b arctan ) f) La oss først finne en
1 Mandag 8. mars 2010
1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
MA0002 Brukerkurs i matematikk B Vår 2017
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA Brukerkurs i matematikk B Vår 7 Kapittel 7.3: Rasjonale funksjoner og delbrøkoppspaltning 7.3:3 Bruk polynomdivisjon for
Løysingsforslag for TMA4120, Øving 6
Løysingsforslg for TMA42, Øving 6 October, 26 2..3 Set inn i likning: 2 u t 2 = c2 2 u x 2 2 (cos 4t sin 2x t 2 = c 2 2 (cos 4t sin 2x x 2 6 cos 4t sin 2x = 4c 2 cos 4t sin 2x. u er med ndre ord ei løysing
LIBER BVEL MAGI SVB FIGVRÂ I $ Cliquer sur la version désirée klikk på ønsket versjon. Règlement financier - Année scolaire Betalingsreglement for skoleåret
Cliquer sur la version désirée klikk på ønsket versjon Règlement financier - Année scolaire 2010-2011 Betalingsreglement for skoleåret 2010-2011 LYCÉE FRANÇAIS RENÉ CASSIN D OSLO Règlement financier -
MAT 1110: Obligatorisk oppgave 1, V-07: Løsningsforslag
1 MAT 111: Obligatorisk oppgave 1, V-7: Løsningsforslag Oppgave 1. a) Vi deriverer på vanlig måte: ( e (sinh x) x e x ) = = ex + e x = cosh x, ( e (cosh x) x + e x ) = = ex e x = sinh x Enkel algebra gir
Løsningsforslag til prøveeksamen i MAT1100, H-14 DEL 1
Løsningsforslag til prøveeksamen i MT, H- DEL. ( poeng Hva er den partiellderiverte f y sin(xy cos(xy y sin(xy x sin(xy cos(xy xy sin(xy cos(xy y sin(xy + xy sin(xy når f(x, y = y cos(xy? Riktig svar:
Anbefalte oppgaver - Løsningsforslag
Anbefalte oppgaver - Løsningsforslag Uke 6 12.6.4: Vi finner først lineariseringen i punktet (2, 2). Vi har at Lineariseringen er derfor 2x + y f x (x, y) = 24 (x 2 + xy + y 2 ) 2 2y + x f y (x, y) = 24
Eksamensoppgave i TMA4123/TMA4125 Matematikk 4M/4N
Institutt for matematiske fag Eksamensoppgave i TMA4123/TMA4125 Matematikk 4M/4N Faglig kontakt under eksamen: Dag Wessel-Berg Tlf: 924 48 828 Eksamensdato: 1. juni 216 Eksamenstid (fra til): 9: 13: Hjelpemiddelkode/Tillatte
Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x2 ) + sin(x 2 ) dx = 2π. 1 k t.
Integral Kokeboken 4 3 4 6 8 sinπ sinh π 4 log + loglog loglog + C cos + sin π t e Γt k k t Γtζt arcsin + arccos π + C Integral fra R til Z π 6 sec y dy ln 3 i 64 The integral sec y dy From zero to one-sith
Løsningsforslag til eksamen i TFY4230 STATISTISK FYSIKK Tirsdag 9. aug 2011
NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 5 sider. Løsningsforslag til eksamen i TFY430 STATISTISK FYSIKK Tirsdag 9. aug 011 Oppgave 1.