Bobine à noyau de fer
|
|
|
- Thoralf Eriksen
- 6 år siden
- Visninger:
Transkript
1 1 Bobne à noyau de fer
2 Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2
3 Bobne à noyau de fer Conventons v Φ f Φ c On fxe un sens de la tenson. Conventon récepteur Flux sut la règle d ampère Une f.e.m. est ndute dans l enroulement qu s oppose à la varaton de flux 3
4 Bobne à noyau de fer Conventons v e Φ f Φ c On fxe un sens de la tenson. Conventon récepteur Flux sut la règle d ampère e = + dφ dt 4
5 Bobne à noyau de fer Flux Flux Commun Total: Φ c = N. c Φ f Φ c Flux de Futes moyen: f = 1 N fk Pour 1 spre k k 5
6 Bobne à noyau de fer Flux Flux Commun Total: Φ c = N. c Φ f Φ c Flux de Futes Total: f = 1 N k fk Φ f = N. f Pour 1 spre en moyenne 6
7 Bobne à noyau de fer Flux Φ c Flux Total: Φ f Φ = N. c + l f. Qques % 7
8 Equatons générales v r e v = r. + e or e = dφ dt Φ = N. c + l f. 8
9 Equatons générales v r e v = r. + e or e = dφ dt Φ = N. c + l f. v = r. + l f. d dt + N d c dt 9
10 Equatons générales v = r. + l f. d N. = R c. c dt + N d c dt 10
11 Hypothèses de KAPP v = r. + l f. d dt + N d c dt Chute ohmque néglgeable devant la f.e.m ndute 11
12 Hypothèses de KAPP v = r. + l f. d dt + N d c dt Flux de fute néglgeable devant le flux commun 12
13 Hypothèses de KAPP v = r. + l f. d dt + N d c dt v = N d c dt r fable futes fables 13
14 Hypothèses de KAPP Expresson du flux v = N d c dt devent c = 1 N v.dt Tenson mpose le flux 14
15 Hypothèses de KAPP Expresson du flux c = 1 N v.dt = V 2 Nω sn( ω.t)+ 0 Flux rémanent. Néglgé par la sute 15
16 Hypothèses de KAPP Expresson du flux c = 1 N v.dt = V 2 Nω sn( ω.t) c = V 2 Nω Ampltude ( ) Pulsaton sn ω.t ω Retard π/2 sur v Tenson mpose le flux Machne à Flux Forcé M = V 2 Nω
17 Hypothèses de KAPP Expresson du flux M = V 2 Nω V = 4,44.N.f.S.B M Relaton de Boucherot 17
18 Hypothèses de KAPP Courant appelé Relaton de Hopknson N. = R c. c R c = 1 µ. l S Dépend du flux 18
19 Hypothèses de KAPP Courant appelé: constructon 19
20 Hypothèses de KAPP Courant appelé: constructon t 20 t
21 Hypothèses de KAPP Courant appelé: constructon t 21 t
22 Hypothèses de KAPP Courant appelé: constructon t 22 t
23 Hypothèses de KAPP Courant appelé: constructon t 23 t
24 Hypothèses de KAPP Courant appelé: constructon t 24 t
25 Hypothèses de KAPP Courant appelé: constructon t 25 t
26 Hypothèses de KAPP Courant appelé: constructon t 26 t
27 Hypothèses de KAPP Courant appelé: constructon t 27 t
28 Hypothèses de KAPP Courant appelé: constructon t 28 t
29 Hypothèses de KAPP Courant appelé: constructon t 29 t
30 Hypothèses de KAPP Courant appelé: constructon t 30 t
31 Hypothèses de KAPP Courant appelé: expresson t ( t)= I 2 cos 2k +1 2k k= 0 [ ] ( )ω.t ϕ 2k +1
32 Hypothèses de KAPP Pussance absorbée Courant non snusoïdal. ->Défnton de la pussance. p t ( )= v t ( ). t ( ) v( t)= V 2 cos( ω.t) ( t)= I 2k +1 2 cos ( 2k +1)ω.t ϕ 2k +1 k= 0 [ ] 32
33 Hypothèses de KAPP Pussance absorbée Courant non snusoïdal. ->Défnton de la pussance. p t ( )= v t ( ). t ( ) p t ( )= V 2 cos ω.t k= 0 ( ) I 2k +1 2 cos 2k +1 [ ] ( )ω.t ϕ 2k+1 33
34 Hypothèses de KAPP Pussance absorbée Valeur effcace du courant: I 2 = I I I 2k Pussance apparente: S 2 = V 2 I 2 = V 2 I V 2 I V 2 2 I 2k V 2 I 2 1 cos( ϕ 1 )+ V 2 I 2 1 sn( ϕ ) 1 P 2 Q 2 V 2 2 I k=1 2k +1 D 2
35 Hypothèses de KAPP Pussance absorbée Valeur effcace du courant: I 2 = I I I 2k Pussance apparente: S 2 = P 2 + Q 2 + D 2 Bobnage = pertes Joules Matérau = pertes Ferromagnétques 35
36 Pertes fer Hystéréss du matérau dw mag =.dφ 36
37 Pertes fer Hystéréss du matérau dw mag =.dφ > 0 37
38 Pertes fer Hystéréss du matérau dw mag =.dφ < 0 38
39 Pertes fer Hystéréss du matérau Compensaton des ares dw mag =.dφ < 0 39
40 Pertes fer Hystéréss du matérau dw mag =.dφ > 0 40
41 Pertes fer Hystéréss du matérau dw mag =.dφ < 0 41
42 Pertes fer Hystéréss du matérau Compensaton des ares dw mag =.dφ < 0 42
43 Pertes fer Hystéréss du matérau dw mag =.dφ > 0 43
44 Pertes fer Hystéréss du matérau Energe perdue en 1 parcours Perte lors d un parcours à fréquence f P H = f Are 44
45 Pertes fer Hystéréss du matérau On admet une forme emprque De l are P H = k H.f.B M 2 45
46 Pertes fer Courants de Foucault Inducton magnétque B = B M sn ω.t ( ) Lgne de courants de Foucault f.e.m. e F = d ndute par B: dt = S FB M.ω.cos( ω.t) Surface de la boucle de courant 46
47 Pertes fer Courants de Foucault p F Inducton magnétque B = B M sn ω.t ( ) Lgne de courants de Foucault f.e.m. e F = d ndute par B: dt = S FB M.ω.cos( ω.t) ( t)= e F Sot en pertes joules 2 r F Résstance de la lgne de courant 47
48 Pertes fer Courants de Foucault Inducton magnétque B = B M sn ω.t ( ) 48 p F Lgne de courants de Foucault f.e.m. e F = d ndute par B: dt = S FB M.ω.cos( ω.t) ( t)= e F Sot en pertes joules 2 2 r F = S F r F B 2 M.ω 2 cos 2 ( ω.t)
49 Pertes fer Courants de Foucault p F 2 ( t)= e F r F = S 2 F r F B 2 M.ω 2 cos 2 ( ω.t) 49
50 Pertes fer Courants de Foucault p F 2 ( t)= e F r F = S 2 F r F B 2 M.ω 2 cos 2 ( ω.t) P F = k F.B M 2.f 2 50
51 Pertes fer Pertes totales P Fer = k H.f.B M 2 + k F.f 2.B M 2 51
52 Bobne fctve équvalente Beson d un modèle lnéare 52
53 Bobne fctve équvalente Beson d un modèle lnéare Courant absorbé snusoïdal ( t)= I 2 cos( ω.t ϕ) Valeur effcace I = I = I I I n 53
54 Bobne fctve équvalente Beson d un modèle lnéare Courant absorbé snusoïdal ( t)= I 2 cos( ω.t ϕ) Pussance actve conservée Bobne réelle Valeur effcace I = I = I I I n Bobne fctve P = V.I 1 cos( ϕ ) 1 P = V.I cos( ϕ) 54
55 Bobne fctve équvalente Schéma équvalent R f L µ P Fer = V 2 55 R f Dsspent les pertes fer = k H.f.B 2 M + k F.f 2 2.B M V = 4,44.N. f.s.b M P Fer K 1+ 1 f
56 Bobne fctve équvalente Schéma équvalent R f L µ L µ.ω = V 2 56 Q = V 2 S 2 P 2 = V V I Absorbe la pussance réactve 2 ( ) 2 P 2 Q = V 2 L µ.ω
57 Bobne fctve équvalente Représentaton de Fresnel I a V R f L µ ϕ α I r I Angle d écart hystérétque 57
58 Bobne fctve équvalente Grandeurs magnétques Flux et nducton c = 1 N v.dt avec v( t)= V 2 cos( ω.t) B ( t)= B( t)= B M sn( ω.t) Inchangé 58
59 Bobne fctve équvalente Grandeurs magnétques Champ magnétque H l = N. avec ( t)= V 2 cos( ω.t ϕ) H ( t)= N I 2 l sn ω.t + π 2 ϕ 59
60 Bobne fctve équvalente Grandeurs magnétques Champ magnétque H l = N. avec ( t)= V 2 cos( ω.t ϕ) H ( t)= N I 2 l sn ω.t + π 2 ϕ = H M sn( ω.t + α) Snusoïdal Angle d écart hystérétque 60
61 Bobne fctve équvalente Cycle d hystéréss B ( t)= B( t)= B M sn ω.t H t ( ) ( ) ( )= H M sn ω.t + α B M snα Are = Energe volumque totale perdue par cycle. Perméablté magnétque devent alors complexe: µ = B H = B M e jα H M H M snα 61
62 Bobne fctve équvalente Lmtes du modèle Eléments du schéma valable à (V,f) donné Pussances actves non conservées. Bobne réelle Bobne fctve Q = V.I 1 sn( ϕ ) 1 Q = V.Isn( ϕ) 62
63 Bobne fctve équvalente Modèle fctf complet r l f R f L µ 63
64 Mesure des pertes Mesure drecte W On mesure P = r.i 2 + P Fer 64
65 Mesure des pertes Méthode d Epsten W N 1 N 2 Nécessté de 2 enroulements On mesure P = v et d v 2 = N 2 dt = N 2 ( v 1 r 1. 1 ) N 1 P = N 2.v 1 1 N 2 2.r 1 1 N 1 N 1 P = N 2 N 1 P tot N 2 N 1 P joule
Energie et corrélation. Systèmes de Traitement du Signal Polytech Marseille INFO 2016
 Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 2008
 Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
1. Intégrales définies et indéfinies I. (a) Soit b > 0. Montrer que pour tout x > 0 la fonction. 2 b. F (x) = arctan bx. 1 (1 + bx) x. f(x) = x t dt.
 Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
1 OA i = f. OA o. 1 < 1 OA o. f 1. O 2 A i O 2 A 1 = = f 2 O 2 A i. f 2O 2 A i 5 `c mffl `a vfle c O 2 A i = 20 `c mffl `eˇt f 2 = 20 `c mffl
 . B L`affl r`e l åtˇi`o nffl `d`e `c o n jˇu`g åi sfi`o nffl `d`o n n`e OA i = + f P`o u rffl u n`e l e n tˇi l l e m i n`c e `c o n vfleˇr`g e n t e, < f `d`o n`c L i m`àg e `eṡfi t r`é e l l e. f > 0.
. B L`affl r`e l åtˇi`o nffl `d`e `c o n jˇu`g åi sfi`o nffl `d`o n n`e OA i = + f P`o u rffl u n`e l e n tˇi l l e m i n`c e `c o n vfleˇr`g e n t e, < f `d`o n`c L i m`àg e `eṡfi t r`é e l l e. f > 0.
Brosses intérieures avec manche
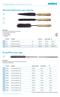 18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
LØSNINGSFORSLAG EKSAMEN, MAT 1001, HØSTEN (x + 1) 2 dx = u 2 du = u 1 = (x + 1) 1 = 1 x + 1. ln x
 LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
UNIVERSITETET I OSLO
 UNIVERITETET I OO Det matematsk-naturvtenskapelge fakultet Eksamen : FY110 Elektromagnetsme Eksamensdag: 6. desember 01 Td for eksamen: 14:30 18:30 Oppgavesettet er på: sder Vedlegg: Formelark (3 sder)
UNIVERITETET I OO Det matematsk-naturvtenskapelge fakultet Eksamen : FY110 Elektromagnetsme Eksamensdag: 6. desember 01 Td for eksamen: 14:30 18:30 Oppgavesettet er på: sder Vedlegg: Formelark (3 sder)
Clôture Métallique. Portails / Portillons / Accessoires
 Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
GAMME DETENTE DIRECTE SOMMAIRE. X32 monosplit Inverter Page 88. X3 multisplit Inverter Page 90. Monosplits/Multisplits
 SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
TFY4160 Bølgefysikk/FY1002 Generell Fysikk II 1. Løsning Øving 2. m d2 x. k = mω0 2 = m. k = dt 2 + bdx + kx = 0 (7)
 TFY4160 Bølgefysikk/FY100 Generell Fysikk II 1 Løsning Øving Løsning oppgave 1 Ligning 1) i oppgaveteksten er i dette tilfellet: Vi setter inn: i lign. 1) og får: m d x + kx = 0 1) dt x = A cosω 0 t +
TFY4160 Bølgefysikk/FY100 Generell Fysikk II 1 Løsning Øving Løsning oppgave 1 Ligning 1) i oppgaveteksten er i dette tilfellet: Vi setter inn: i lign. 1) og får: m d x + kx = 0 1) dt x = A cosω 0 t +
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
41307 Kraftelektroniske motordrifter Løsningsforslag Kapittel 4 Roterende elektriske maskiner
 47 Kraftelektroniske motordrifter Løsningsforslag Kapittel 4 Roterende elektriske maskiner OPPGAVE. Den magnetiske ekvivalenten for den roterande maskina i figur. på oppgåve arket, er vist på figuren under.
47 Kraftelektroniske motordrifter Løsningsforslag Kapittel 4 Roterende elektriske maskiner OPPGAVE. Den magnetiske ekvivalenten for den roterande maskina i figur. på oppgåve arket, er vist på figuren under.
Laser vert : moins de plus de 300. Acheter Laser PRODUITS CHAUDS. Pointeur Laser étanche
 Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Chapter 4 Reflection and Transmission of Waves
 4- Chapter 4 Reflecton and Transmsson of Waves Dr. Stuart Long 4- Boundary Condtons ^ n H H 3 H 4 w H l y (fg. 4.) 4-3 Boundary Condtons n ^ H H 3 H4 w H l y Tae ˆ component of H J+ jω D (fg. 4.) H y H
4- Chapter 4 Reflecton and Transmsson of Waves Dr. Stuart Long 4- Boundary Condtons ^ n H H 3 H 4 w H l y (fg. 4.) 4-3 Boundary Condtons n ^ H H 3 H4 w H l y Tae ˆ component of H J+ jω D (fg. 4.) H y H
Key objectives in lighting design
 Key objectives in lighting design Qualifications no strong "contrasts" good "color rendering" adequate "light levels" no "disturbing reflections" no direct "glare" Radiometry vs. Photometry absolute (energy)
Key objectives in lighting design Qualifications no strong "contrasts" good "color rendering" adequate "light levels" no "disturbing reflections" no direct "glare" Radiometry vs. Photometry absolute (energy)
Corrigés des exercices du chapitre 25
 MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
Eksamen FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. Nynorsk/Bokmål
 Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Arbeid og energi. Energibevaring.
 Arbeid og energi. Energibevaring. Arbeid = dw = F ds Kinetisk energi E k = ½ m v 2 Effekt = arbeid/tid = P = dw /dt Arbeid på legeme øker E k : Potensiell energi E p (x,y,z) dw = de k (Tyngdefelt: E p
Arbeid og energi. Energibevaring. Arbeid = dw = F ds Kinetisk energi E k = ½ m v 2 Effekt = arbeid/tid = P = dw /dt Arbeid på legeme øker E k : Potensiell energi E p (x,y,z) dw = de k (Tyngdefelt: E p
Eksamensoppgave i TFY4115 FYSIKK
 Side 1 av 6. Institutt for fysikk Eksamensoppgave i TFY4115 FYSIKK for MTNANO, MTTK og MTEL Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen Tlf.: 486 05 392 Eksamensdato: Torsdag 11.
Side 1 av 6. Institutt for fysikk Eksamensoppgave i TFY4115 FYSIKK for MTNANO, MTTK og MTEL Faglig kontakt under eksamen: Institutt for fysikk v/arne Mikkelsen Tlf.: 486 05 392 Eksamensdato: Torsdag 11.
Løysingsforslag Kontinuasjonseksamen TFE4120 Elektromagnetisme 13. august 2004
 Løysinsforsla Kontinuasjonseksamen TFE4120 Elektromanetisme 13. auust 2004 Oppåve 1 a) Fiure 1: Ei telefonlinje som år parallelt med ei straumlinje. Det skraverte området er definert av kurva C 2. Innbyrdes
Løysinsforsla Kontinuasjonseksamen TFE4120 Elektromanetisme 13. auust 2004 Oppåve 1 a) Fiure 1: Ei telefonlinje som år parallelt med ei straumlinje. Det skraverte området er definert av kurva C 2. Innbyrdes
PremiCron. Tresse synthétique non résorbable de polyester enduit. PremiCron
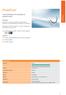 Tresse synthétique non résorbable de polyester enduit Description PremiCron est une tresse synthétique non résorbable de Polyester. Les sutures PremiCron sont enduites avec du silicone. PremiCron Disponible
Tresse synthétique non résorbable de polyester enduit Description PremiCron est une tresse synthétique non résorbable de Polyester. Les sutures PremiCron sont enduites avec du silicone. PremiCron Disponible
I. Évolution du commerce mondial
 I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
Løsningsforslag til eksamen i SIF4022 Fysikk 2 Tirsdag 3. desember 2002
 NTNU Side 1 av 6 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF40 Fysikk Tirsdag 3. desember 00 Dette løsningsforslaget er på 6 sider. Oppgave 1. a) Amplituden
NTNU Side 1 av 6 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF40 Fysikk Tirsdag 3. desember 00 Dette løsningsforslaget er på 6 sider. Oppgave 1. a) Amplituden
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
 FILTERDESIGN Ukeoppgavene skal leveres som selvstendige arbeider. Det forventes at alle har satt seg inn i instituttets krav til innleverte oppgaver: Norsk versjon: http://www.ifi.uio.no/studinf/skjemaer/erklaring.pdf
FILTERDESIGN Ukeoppgavene skal leveres som selvstendige arbeider. Det forventes at alle har satt seg inn i instituttets krav til innleverte oppgaver: Norsk versjon: http://www.ifi.uio.no/studinf/skjemaer/erklaring.pdf
Løysingsforslag Kontinuasjonseksamen TFE4120 Elektromagnetisme 13. august 2004
 Løysinsforsla Kontinuasjonseksamen TFE4120 Elektromanetisme 13. auust 2004 Oppåve 1 a) Fiure 1: Ei telefonlinje som år parallelt med ei straumlinje. Det skraverte området er definert av kurva C 2. Innbyrdes
Løysinsforsla Kontinuasjonseksamen TFE4120 Elektromanetisme 13. auust 2004 Oppåve 1 a) Fiure 1: Ei telefonlinje som år parallelt med ei straumlinje. Det skraverte området er definert av kurva C 2. Innbyrdes
Qi-Wu-Zhang model. 2D Chern insulator. León Martin. 19. November 2015
 Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Eksamen i TMA4123/TMA4125 Matematikk 4M/N
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Anne Kværnø: mobil 92663824 Eksamen i TMA423/TMA425 Matematikk 4M/N Bokmål Mandag 2.
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Anne Kværnø: mobil 92663824 Eksamen i TMA423/TMA425 Matematikk 4M/N Bokmål Mandag 2.
Løsningsforslag Eksamen 27. mai 2011 FY1006/TFY4215 Innføring i kvantefysikk
 Eksamen FY1006/TFY4215 27. mai 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2011 FY1006/TFY4215 Innføring i kvantefysikk a. For en energiegenfunksjon med energi E V 1 følger det fra
Eksamen FY1006/TFY4215 27. mai 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2011 FY1006/TFY4215 Innføring i kvantefysikk a. For en energiegenfunksjon med energi E V 1 følger det fra
TECHNOLOGIE POUR CHAUDIERES DE BRUNNER. Kamin-Kessel Eck 57/67/44 Porte relevable (easy-lift) État: made in germany
 TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
Disjoncteurs sélectifs
 233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
NOGES TEKNISK- NATUVITENSKAPEIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 EEKTISITET OG MAGNETISME TFY4155
Eksamensoppgave i TFY4108 Fysikk
 Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf.: 97 94 00 36 Eksamensdato: 13. august 2014 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf.: 97 94 00 36 Eksamensdato: 13. august 2014 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
TECHNIQUE DE CHAUDIERE PAR BRUNNER. Kamin-Kessel 62/76. État: made in germany
 TCHNIQU D CHAUDIR PAR BRUNNR KaminKessel 62/76 État: 30.04.2013 made in germany KaminKessel 62/76 S S securité départ 1/2" fil.ext. securité retour 1/2" fil.ext. porte battante avec isolation et lisiére
TCHNIQU D CHAUDIR PAR BRUNNR KaminKessel 62/76 État: 30.04.2013 made in germany KaminKessel 62/76 S S securité départ 1/2" fil.ext. securité retour 1/2" fil.ext. porte battante avec isolation et lisiére
S S. Eksamen i SIF4022 Fysikk 2 7. desember 1999 LØYSINGAR. Oppgave 1. t Kraft opp: y x. Newtons 2. lov. gir. som er bølgjelikninga, av form
 Esamn i SIF4 Fsi 7. smb 999 LØYSINGAR Oppgav a S [ÃÃÃÃÃÃÃ[Ã [ S DVVHÃ ÃÂÃ [ÃÃ$NVHOHUDVMRQÃ t Kaft opp: S sinα -Ssinα S α S S Nwtons. lov gi som bølgjlininga, av fom S µ t µ S t v t m v bølgjfat som v v
Esamn i SIF4 Fsi 7. smb 999 LØYSINGAR Oppgav a S [ÃÃÃÃÃÃÃ[Ã [ S DVVHÃ ÃÂÃ [ÃÃ$NVHOHUDVMRQÃ t Kaft opp: S sinα -Ssinα S α S S Nwtons. lov gi som bølgjlininga, av fom S µ t µ S t v t m v bølgjfat som v v
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN TFY4155 ELEKTROMAGNETISME FY1003
Skinndybde. FYS 2130
 Skinndybde. FYS 130 Vi skal se hvordan en elektromagnetisk bølge oppfører seg i et ledende medium. ølgeligningen for E-feltet i vakuum ble utledet i notatet om elektromagnetiske bølger: E E =εµ 0 0 Denne
Skinndybde. FYS 130 Vi skal se hvordan en elektromagnetisk bølge oppfører seg i et ledende medium. ølgeligningen for E-feltet i vakuum ble utledet i notatet om elektromagnetiske bølger: E E =εµ 0 0 Denne
Eksamen i fag FY1004 Innføring i kvantemekanikk Fredag 30. mai 2008 Tid: a 0 = 4πǫ 0 h 2 /(e 2 m e ) = 5, m
 Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Løsningsforslag til eksamen i TFY4170 Fysikk 2 Fysikk 2 Lørdag 8. august 2005
 NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
Løsningsforslag, eksamen FY desember 2017
 1 Løsninsforsla, eksamen FY1001 14. desember 017 1 3 områder av t = 4 s, a konstant i hvert omrde. 1 : a 1 = 0; v 0 = 5m/s = x 1 = v 0 t; v 1 = v 0 : a = v/ t = 1.5 m/s = x = x 1 + v 1 t + a t = v 0 t
1 Løsninsforsla, eksamen FY1001 14. desember 017 1 3 områder av t = 4 s, a konstant i hvert omrde. 1 : a 1 = 0; v 0 = 5m/s = x 1 = v 0 t; v 1 = v 0 : a = v/ t = 1.5 m/s = x = x 1 + v 1 t + a t = v 0 t
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3440/4440 Signalbehandling Eksamensdag: 11. desember 006 Tid for eksamen: 15.30 18.30 Oppgavesettet er på 7 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3440/4440 Signalbehandling Eksamensdag: 11. desember 006 Tid for eksamen: 15.30 18.30 Oppgavesettet er på 7 sider. Vedlegg:
Eksamensoppgave i TFY4108 Fysikk
 Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf.: 97 94 00 36 Eksamensdato: 7. august 2015 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf.: 97 94 00 36 Eksamensdato: 7. august 2015 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
Compress Bosch Compress LW-Tx C 35 C A ++ A + A B C D E F G. db kw kw /2013
 Bosch 5000 7 LW-Tx 55 C 35 C + A B C D E F G 47 8 9 7 8 7 7 db kw kw db 2015 811/2013 Bosch 5000 7 LW-Tx ++ + + + + + A B C D E F G 2015 811/2013 Bosch 5000 7 LW-Tx Opplysningene er i samsvar med kravene
Bosch 5000 7 LW-Tx 55 C 35 C + A B C D E F G 47 8 9 7 8 7 7 db kw kw db 2015 811/2013 Bosch 5000 7 LW-Tx ++ + + + + + A B C D E F G 2015 811/2013 Bosch 5000 7 LW-Tx Opplysningene er i samsvar med kravene
 Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I TFY4155 ELEKTROMAGNETISME Fredag 8. juni 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTISITET OG MAGNETISME I TFY4155
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
TFY4104 Fysikk Eksamen 28. november 2016 Side 13 av 22
 TFY4104 Fysikk Eksamen 28. november 2016 Side 13 av 22 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas
TFY4104 Fysikk Eksamen 28. november 2016 Side 13 av 22 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas
Formelsamling Bølgefysikk Desember 2006
 Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Kap. 14 Mekaniske svingninger. 14. Mekaniske svingninger. Vi skal se på: Udempet harmonisk svingning. kap
 kap14 1.11.1 Kap. 14 Mekaniske svingninger Mye svingning i dagliglivet: Pendler Musikkinstrument Elektriske og magnetiske svingninger Klokker Termiske vibrasjoner (= temperatur) Måner og planeter Historien
kap14 1.11.1 Kap. 14 Mekaniske svingninger Mye svingning i dagliglivet: Pendler Musikkinstrument Elektriske og magnetiske svingninger Klokker Termiske vibrasjoner (= temperatur) Måner og planeter Historien
TFY4104 Fysikk Eksamen 28. november 2016 Side 13 av 22
 TFY4104 Fysikk Eksamen 28. november 2016 Side 13 av 22 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas
TFY4104 Fysikk Eksamen 28. november 2016 Side 13 av 22 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas
DYNAMIQUE. Etude des mouvements de tangage d une transmission de puissance d hélicoptère. x r 2. y r 2. x 1. y r y r
 e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
UNIVERSITETET I OSLO
 Side UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS0 Svingninger og bølger. Eksamensdag: 7. juni 0. Tid for eksamen: kl. 4:0-8:0. Oppgavesettet er på: + sider. Vedlegg:
Side UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS0 Svingninger og bølger. Eksamensdag: 7. juni 0. Tid for eksamen: kl. 4:0-8:0. Oppgavesettet er på: + sider. Vedlegg:
r r t t r t s r r st str t r P s r s t t t r ss rt s r t ss rt tt rs t tt rs s r ü r ss r r q 3 t tt ss s t r ä t ss s ss r tt ä
 tt rs r ö 1 ü r r ts r3 s r r t t r t s r r st str t r P s r s t t t r ss rt s r t ss rt tt rs t tt 3 t tt rs s r ü r ss r r q 3 t tt 3 t tt ss s t r ä t ss s ss r tt ä s rt s rs sr t ω(k) s t r t tt ss
tt rs r ö 1 ü r r ts r3 s r r t t r t s r r st str t r P s r s t t t r ss rt s r t ss rt tt rs t tt 3 t tt rs s r ü r ss r r q 3 t tt 3 t tt ss s t r ä t ss s ss r tt ä s rt s rs sr t ω(k) s t r t tt ss
Second Order ODE's (2P) Young Won Lim 7/1/14
 Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
EKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon ide 1 av 7 Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen: Guro vendsen (73592773) Hjelpemidler: C - pesifiserte
Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon ide 1 av 7 Bokmål/Nynorsk Faglig/fagleg kontakt under eksamen: Guro vendsen (73592773) Hjelpemidler: C - pesifiserte
EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK
 TFY4145/FY1001 18. des. 2012 Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 EKSAMEN I FY1001
TFY4145/FY1001 18. des. 2012 Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 EKSAMEN I FY1001
EKSAMEN FY1013 ELEKTRISITET OG MAGNETISME II Fredag 9. desember 2005 kl
 NORGES TEKNSK- NATURTENSKAPELGE UNERSTET NSTTUTT FOR FYSKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 EKSAMEN FY1013 ELEKTRSTET OG MAGNETSME Fredag 9. desember 2005 kl.
NORGES TEKNSK- NATURTENSKAPELGE UNERSTET NSTTUTT FOR FYSKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 EKSAMEN FY1013 ELEKTRSTET OG MAGNETSME Fredag 9. desember 2005 kl.
 FILTERDESIGN Ukeoppgavene skal leveres som selvstendige arbeider. Det forventes at alle har satt seg inn i instituttets krav til innleverte oppgaver: Norsk versjon: http://www.ifi.uio.no/studinf/skjemaer/erklaring.pdf
FILTERDESIGN Ukeoppgavene skal leveres som selvstendige arbeider. Det forventes at alle har satt seg inn i instituttets krav til innleverte oppgaver: Norsk versjon: http://www.ifi.uio.no/studinf/skjemaer/erklaring.pdf
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCouseWae http://ocw.mt.edu 6.641 Electomagnetc Felds, Foces, and Moton, Spng 5 Please use the followng ctaton fomat: Maus Zahn, 6.641 Electomagnetc Felds, Foces, and Moton, Spng 5. (Massachusetts
MIT OpenCouseWae http://ocw.mt.edu 6.641 Electomagnetc Felds, Foces, and Moton, Spng 5 Please use the followng ctaton fomat: Maus Zahn, 6.641 Electomagnetc Felds, Foces, and Moton, Spng 5. (Massachusetts
Faradays lov: Flere muligheter for induksjon: Magnetisme. Kap29
 Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl K. Rottmann: Matematisk formelsamling (eller tilsvarende).
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 17. desember
A. forbli konstant B. øke med tida C. avta med tida D. øke først for så å avta E. ikke nok informasjon til å avgjøre
 Flervlgsoppgver 1. En induktor L og en motstnd R er forbundet til en spenningskilde E som vist i figuren. Bryteren S 1 lukkes og forblir lukket slik t konstnt strøm går gjennom L og R. Så åpnes bryter
Flervlgsoppgver 1. En induktor L og en motstnd R er forbundet til en spenningskilde E som vist i figuren. Bryteren S 1 lukkes og forblir lukket slik t konstnt strøm går gjennom L og R. Så åpnes bryter
Rotasjon: Translasjon: F = m dv/dt = m a. τ = I dω/dt = I α. τ = 0 => L = konstant (N1-rot) stivt legeme om sym.akse: ω = konst
 Translasjon: Rotasjon: Bevegelsesmengde (linear momentum): p = m v Spinn (angular momentum): L = r m v L = I ω Stivt legeme om sym.akse N2-trans: F = dp/dt Stivt legeme (konst. m): F = m dv/dt = m a N2-rot
Translasjon: Rotasjon: Bevegelsesmengde (linear momentum): p = m v Spinn (angular momentum): L = r m v L = I ω Stivt legeme om sym.akse N2-trans: F = dp/dt Stivt legeme (konst. m): F = m dv/dt = m a N2-rot
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Fredag 11. august 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTNUASJONSEKSAMEN TFY4155 ELEKTOMAGNETSME Fredag 11.
KONTINUASJONSEKSAMEN TFY4160 BØLGEFYSIKK Torsdag 9. august 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 15 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTINUASJONSEKSAMEN TFY4160 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 15 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 KONTINUASJONSEKSAMEN TFY4160 BØLGEFYSIKK
Positive dispersion: 2 n. λ 2 > 0. ω 2 > 0, Negative dispersion: ω < 0, 2 n
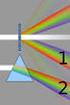 Positive dispersion: 2 n ω 2 > 0, 2 n λ 2 > 0 Negative dispersion: 2 n ω < 0, 2 n 2 λ < 0 2 φ(z,ω) = k ( n ω )z E( z,t)= 1 2π E ( z = 0,ω )e iωt iφ z,ω e ( ) dω φ(z,ω) = k ( n ω )z φ( ω )= φ 0 + ω ω 0
Positive dispersion: 2 n ω 2 > 0, 2 n λ 2 > 0 Negative dispersion: 2 n ω < 0, 2 n 2 λ < 0 2 φ(z,ω) = k ( n ω )z E( z,t)= 1 2π E ( z = 0,ω )e iωt iφ z,ω e ( ) dω φ(z,ω) = k ( n ω )z φ( ω )= φ 0 + ω ω 0
Obligatorisk oppgave nr 1 FYS Lars Kristian Henriksen UiO
 Obligatorisk oppgave nr 1 FYS-2130 Lars Kristian Henriksen UiO 28. januar 2015 2 For at en kraft skal danne grunnlaget for svingninger, må det virke en kraft som til en hver tid virker inn mot likevektspunktet.
Obligatorisk oppgave nr 1 FYS-2130 Lars Kristian Henriksen UiO 28. januar 2015 2 For at en kraft skal danne grunnlaget for svingninger, må det virke en kraft som til en hver tid virker inn mot likevektspunktet.
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].
![Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm]. Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].](/thumbs/58/41840831.jpg) Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 30. mai 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME
Advanced Quantum Field Theory (Version of November 2015) Jorge Crispim Romão
 Advanced Quantum Feld Teory (Verson of November 015) Jorge Crsm Romão Pyscs Deartment 015 Aendx D Feynman Rules for te Standard Model D.1 Introducton To do actual calculatons t s very mortant to ave all
Advanced Quantum Feld Teory (Verson of November 015) Jorge Crsm Romão Pyscs Deartment 015 Aendx D Feynman Rules for te Standard Model D.1 Introducton To do actual calculatons t s very mortant to ave all
TMA 4110 Matematikk 3 Høsten 2004 Svingeligningen med kompleks regnemåte
 TMA 4 Matematikk Høsten 4 Svingeligningen med kompleks regnemåte H.E.K., Inst. for matematiske fag, NTNU Svingeligningen forekommer i mange sammenhenger, og ofte vil vi møte regning og utledninger der
TMA 4 Matematikk Høsten 4 Svingeligningen med kompleks regnemåte H.E.K., Inst. for matematiske fag, NTNU Svingeligningen forekommer i mange sammenhenger, og ofte vil vi møte regning og utledninger der
Faradays lov: Flere muligheter for induksjon: Magnetisme. Kap29
 Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
Kap. 8 Bevegelsesmengde. Flerpartikkelsystem. Kap. 8 Bevegelsesmengde. Flerpartikkelsystem. Sentralt elastisk støt. Generell løsning: kap8.
 Kap. 8 evegelsesmengde. Flepatkkelsystem. V skal se på: ewtons 2. lov på ny. Defnsjon evegelsesmengde. Kaftstøt, mpuls. Impulsloven. Flepatkkelsysteme: Kollsjone: Elastsk, uelastsk, fullstendg uelastsk
Kap. 8 evegelsesmengde. Flepatkkelsystem. V skal se på: ewtons 2. lov på ny. Defnsjon evegelsesmengde. Kaftstøt, mpuls. Impulsloven. Flepatkkelsysteme: Kollsjone: Elastsk, uelastsk, fullstendg uelastsk
Mandag 7. mai. Elektromagnetisk induksjon (fortsatt) [FGT ; YF ; TM ; AF ; LHL 24.1; DJG 7.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke19 Mandag 7. mai Elektromagnetisk induksjon (fortsatt) [FGT 30.1-30.6; YF 29.1-29.5; TM 28.2-28.3; AF 27.1-27.3; LHL 24.1;
Institutt for fysikk, NTNU TFY4155/FY1003: Elektrisitet og magnetisme Vår 2007, uke19 Mandag 7. mai Elektromagnetisk induksjon (fortsatt) [FGT 30.1-30.6; YF 29.1-29.5; TM 28.2-28.3; AF 27.1-27.3; LHL 24.1;
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3440/4440 Signalbehandling Eksamensdag: xx. desember 007 Tid for eksamen: Oppgavesettet er på 6 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3440/4440 Signalbehandling Eksamensdag: xx. desember 007 Tid for eksamen: Oppgavesettet er på 6 sider. Vedlegg: Tillatte hjelpemidler:
Eksamen i fag FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011
 Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011
 Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011 Oppgave 1. a) Vi velger her, og i resten av oppgaven, positiv retning oppover. Dermed gir energibevaring m 1 gh = 1 2 m 1v 2 0 v 0 = 2gh. Rett
Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011 Oppgave 1. a) Vi velger her, og i resten av oppgaven, positiv retning oppover. Dermed gir energibevaring m 1 gh = 1 2 m 1v 2 0 v 0 = 2gh. Rett
Eksamensoppgave i TFY4108 Fysikk
 Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf: 97 94 00 36 Eksamensdato: 16 august 2013 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf: 97 94 00 36 Eksamensdato: 16 august 2013 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
Faradays lov: Flere muligheter for induksjon: Magnetisme. Kap29
 Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
BOKMÅL Side 1 av 6. En partikkel med masse m beveger seg i det endimensjonale brønnpotensialet V 1 = h 2 /(2ma 2 0) for x < 0,
 BOKMÅL Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Jon Andreas Støvneng, tel. 73 59 36 63, eller 45 45 55 33 EKSAMEN I FY1006 INNFØRING
BOKMÅL Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Jon Andreas Støvneng, tel. 73 59 36 63, eller 45 45 55 33 EKSAMEN I FY1006 INNFØRING
Eksamen i TFY4205 Kvantemekanikk Mandag 8. august :00 13:00
 NTNU Side 1 av 9 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Ane Bataas Telefon: 73593647 Eksamen i TFY405 Kvantemekanikk Mandag 8. august 005 9:00 13:00 Tillatte hjelpemidle: Altenativ C
NTNU Side 1 av 9 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Ane Bataas Telefon: 73593647 Eksamen i TFY405 Kvantemekanikk Mandag 8. august 005 9:00 13:00 Tillatte hjelpemidle: Altenativ C
TMA4115 Matematikk 3 Vår 2012
 Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag TMA4115 Matematikk 3 Vår 01 Oppgaver fra læreboka, s lxxxiv 9 a) Likninga for systemet vert y + 4y = 4 cos ωt Me løyser først den
Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag TMA4115 Matematikk 3 Vår 01 Oppgaver fra læreboka, s lxxxiv 9 a) Likninga for systemet vert y + 4y = 4 cos ωt Me løyser først den
EKSAMEN i TFY4108 FYSIKK
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4108 FYSIKK Eksamensdato: Fredag 14 desember 01 Eksamenstid: 09:00-13:00 Faglig kontakt under eksamen:
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk BOKMÅL EKSAMEN i TFY4108 FYSIKK Eksamensdato: Fredag 14 desember 01 Eksamenstid: 09:00-13:00 Faglig kontakt under eksamen:
EKSAMEN I FAG SIF 4012 ELEKTROMAGNETISME (SIF 4012 FYSIKK 2) Onsdag 11. desember kl Bokmål
 Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
Side av 6 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 4 43 39 3 EKSAMEN I FAG SIF 42 ELEKTROMAGNETISME
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 17. desember 2007 kl
 NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
NOGES TEKNISK- NATUVITENSKAPELIGE UNIVESITET INSTITUTT FO FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFOSLAG TIL EKSAMEN I FY1003 ELEKTISITET OG
Faradays lov: Flere muligheter for induksjon: Magnetisme. Kap
 Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
Magnetisme Magnetostatikk (ingen tidsvariasjon): Kap 27. Magnetiske krefter Kap 28: Magnetiske kilder B/ t = 0 Hvilke er rett, a,b,c eller d? Elektrodynamikk: Kap 29: Elektromagnetisk induksjon Kap 30:
Stationary Phase Monte Carlo Methods
 Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK
 TFY4145/FY1001 18. des. 2012 Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 EKSAMEN I FY1001
TFY4145/FY1001 18. des. 2012 Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støvneng, telefon: 45 45 55 33 / 73 59 36 63 EKSAMEN I FY1001
Øving 13. Induksjon. Forskyvningsstrøm. Vekselstrømskretser.
 Inst for fysikk 2017 FY1003 Elektr & magnetisme Øving 13 Induksjon Forskyvningsstrøm Vekselstrømskretser Denne siste øvingen innholder ganske mye, for å få dekket opp siste del av pensum Den godkjennes
Inst for fysikk 2017 FY1003 Elektr & magnetisme Øving 13 Induksjon Forskyvningsstrøm Vekselstrømskretser Denne siste øvingen innholder ganske mye, for å få dekket opp siste del av pensum Den godkjennes
Eksamensoppgave i TFY4108 Fysikk
 Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf.: 97 94 00 36 Eksamensdato: 11. desember 2014 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
Institutt for fysikk Eksamensoppgave i TFY4108 Fysikk Faglig kontakt under eksamen: Førsteamanuensis John Ove Fjærestad Tlf.: 97 94 00 36 Eksamensdato: 11. desember 2014 Eksamenstid (fra-til): 9-13 Hjelpemiddelkode/Tillatte
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
