1 k 2 + 1, k= 5. i=1. i = k + 6 eller k = i 6. m+6. (i 6) i=1
|
|
|
- Klaus Erlandsen
- 6 år siden
- Visninger:
Transkript
1 TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis k = 5 og i =. Vi ser derfor t vi hr smmenhengen i = k + 6 eller k = i 6. Det siste leddet i summen er når k = m, det vil si i = m + 6. Hvis vi setter inn for k i den opprinnelig summen får vi t m k=5 m+6 k + = (i 6) +. i= For å sjekke svret kn mn skrive ut de første og det siste leddene i begge summene og se om de er like, m+6 i= m k=5 k + = (5) + + (4) m +, (i 6) + = ( 6) + + ( 6) + + (m + 6 6) + = (5) + + (4) m Gitt en funksjon f(), vet vi t vi kn pproksimere relet, A, begrenset v y =, kurven y = f(), = og = b som en sum v n rektngler med bredde = b n og høyde f( i), der i = + i og i =,..., n, A f( i ). i= Se figurene side 97 i bok for en illustrsjon. Vi ønsker derfor å skrive om vår sum på en slik form, n + i ( S n = n = + i ). n n i= i= 9. september 6 Side v 6
2 Løsningsforslg Øving 5 Med = og b = hr vi = n og i = i n, slik t S n = ( + i ). i= Ved smmenligning med summen øverst i denne oppgven, ser vi t vår sum er en pproksimsjon til relet begrenset v y =, y = +, = og =. Siden y = + er en rett linje, er dette området et trpes med høyde og sideknter og 5, og med rel, A = + 5 = 7. Ved å l n vil summen S n gå mot dette relet. Altså er lim S n = 7 n Vi er gitt funksjonen f() =. Vi deler intervllet [, ] inn i n like store underintervll [ i, i ], i =,,..., n, med størrelse = n, og der i = i = i n. Mengden v punkter {,,..., n } er nå en prtisjon, P n, v intervllet [, ]. Siden f() er en synkende funksjon for lle, hr vi t minimum v f på intervllet [ i, i ] er l i = i, og tilsvrende t mksimum på intervllet [ i, i ] er u i = i. Den nedre Riemnn-summen for f og P n er nå gitt ved (se Definisjon side i bok) L(f, P n ) = f(l i ) = f( i ) n = ( i ) n i= i= i= = i n n n = 4 n i i= i= i= = 4 n(n + ) = n + n n n = n. Her hr vi blnt nnet brukt summeringsreglene () og (b) i Teorem, side 9 i bok. På tilsvrende måte kn vi finne et uttrykk for den øvre Riemnn-summen, Vi ser t Dette betyr t U(f, P n ) = f(u i ) = i= f( i ) n = n i= ( i ) i= = (i ) = 4 n n n n (i ) i= i= i= = 4 n i + 4 n = 4 n(n + ) + 4 n n i= i= = n + n n + 4 n = n + 4 n = n. lim L(f, P n) = lim U(f, P n) =. n n ( )d =. 9. september 6 Side v 6
3 Løsningsforslg Øving 5 Kommentr: Hvorfor impliserer lim n L(f, P n ) = lim n U(f, P n ) = L t integrlet eksisterer? Fr definisjonen på et bestemt integrl (Definisjon, side i bok) hr vi t f er integrerbr på [, b] dersom det bre finnes et tll I slik t for lle prtisjoner P v [, b], så hr vi t L(f, P ) I U(f, P ). () Vi må ltså vise t denne betingelsen gjelder. L P være en vilkårlig prtisjon v [, b]. Vi kn d finne en uniform prtisjon P n som er like fin eller finere enn P ved å velge n stor nok. D vet i t L(f, P n ) L(f, P ). Dette gjelder også i grensen n, slik t lim L(f, P n) L(f, P ). n Siden P er vilkårlig, vil denne ulikheten gjelde for lle P. Tilsvrende kn vi vise t lim U(f, P n) U(f, P ), n for lle P. Ved å sette smmen disse ulikhetene hr vi t L(f, P ) lim n L(f, P n) = L = lim n U(f, P n) U(f, P ), for lle P. Siden betingelsen () skl gjelde for lle prtisjoner P, også P n for lle n, må vi kreve t I = L for t den skl være tilfredsstilt. Ingen ndre vlg v I vil oppfylle (). Vi hr ltså vist t f er integrerbr på [, b] med b f()d = L når lim n L(f, P n ) = lim n U(f, P n ) = L I denne oppgven bruker vi spesielt lineritet i det bestemte integrlet og dditivitet v integrsjonsintervller (se punktene (c) og (d) i Teorem side 6 i bok), henholdsvis og b A A b b f() d + f() d, for lle konstnter A, c b c Vi strter med å dele opp hvert ledd i integrler over intervllene [, ], [, ] og [, ], f() d + f() d + f() d f() d, f() d, f() d f() d, 9. september 6 Side v 6
4 Løsningsforslg Øving 5 Hvis vi summerer lle bidrgene til intervllene over [, ] står vi igjen med f() d For intervllet [, ] står vi igjen med f() d + f() d Til slutt, for intervllet [, ] står vi igjen med f() d f() d Dersom vi nå summerer lle disse leddene står vi igjen med f() d + f() d + Uttrykket i oppgven kn ltså forenkles til integrlet v f() over intervllet [, ] Vi skl finne gjennomsnittsverdien til f over [, ]. Den er gitt som (se Definisjon 4 side 9 i bok) f = e d. () 4 Vi vet t F () = e er den ntideriverte til f() siden F () = e = f(). Fr nlysens fundmentlteorem (The Fundmentl Theorem of Clculus, side i bok) følger det t f = 4 e d = (F () F ()) 4 = ( 4 e6 ) e6 = ( e 6 e 6) = sinh(6), Vi bruker substitusjon, og lr u =. D hr vi t du = d. Innstt i integrlet får vi nå t I = + 6 d = ( + 6 ) d = du + u. Vi ser nå t u = vr et godt vlg fordi vi står igjen med en enklere integrnd som kun er vhengig v u. Vi gjenkjenner integrnden,, som den ntideriverte til ( ) +u tn u (se punkt 6 øverst side 8 i bok). Altså hr vi t du + u = ( ) u tn + C. 9. september 6 Side 4 v 6
5 Løsningsforslg Øving 5 Vi setter så inn igjen for u, og får t I = ( ) tn + C = 6 tn ( ) + C. Husk t vi enkelt kn undersøke om vi hr regnet riktig ved å derivere svret og se om vi d ender opp med integrnden L u() = sin. D er og sin cos d = u () = cos, u() u () d = +u du = ln +u = ln +sin. D får vi sin cos d = ln (+sin π +sin π 4 ) = ln ( + ) Me ser t funksjonen y = er ikkje-negtiv for [, ]. Dermed kn me +6 finn relet A til området vgrens v y =, y =, = og = ved å +6 integrer den første vgrensing med omsyn på frå til, A = + 6 d. Dette integrlet kn løysst ved hjelp v substitusjonen u = + 6, som gjev du = d. Dermed får me svret A = = + 6 d 6 u du = [ln u] u=6 = ln Vi skisserer først kurvene og finner området vi skl finne relet v: y y = y = sin π/ π/ 9. september 6 Side 5 v 6
6 Løsningsforslg Øving 5 Vi er ltså ute etter relet, A, mellom kurvene y = og y = sin, se det skrverte feltet i figuren over. Disse kurvene skjærer hverndre i = ± π. D er A = π/ π/ ( sin ) d = π/ ( sin ) d = π/ d π/ sin d. Vi [ hr her brukt t sin er en like funksjon slik t integrlet over intervllet π, π ] [ ] er lik to gnger intergrlet over intervllet, π. Videre gjenkjenner vi det første integrlet som relet v rektngelet gitt v linjene y =, y =, = π og = π, mens det ndre integrlet er relet under kurven y = sin mellom = π og = π. Det første integrlet kn vi enkelt evluere, mens for det ndre bruker vi t sin = ( cos ) og t cos = sin + C. A = π/ π/ ( π ) = ( π ) = π = π. ( cos ) d ( sin ) π/ 9. september 6 Side 6 v 6
TMA4100 Matematikk1 Høst 2008
 TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
1 Mandag 18. januar 2010
 Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
1 dx cos 1 x =, 1 x 2 sammen med kjerneregelen for derivasjon. For å forenkle utregningen lar vi u = Vi regner først ut den deriverte til u,
 TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
Integrasjon Skoleprosjekt MAT4010
 Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
dx = 1 2y dy = dx/ x 3 y3/2 = 2x 1/2 + C 1
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
dy ycos 2 y = dx. Ved å integrere på begge sider av likhetstegnet får man ved å substituere u = y,du = dy dy ycos 2 y = 2du cos 2 u = x.
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
Integrasjon Fundamentalteoremet Substitusjon Forelesning i Matematikk 1 TMA4100
 Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
1 Mandag 25. januar 2010
 Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
MAT 100A: Mappeeksamen 4
 . november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
. november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
Matematikk Øvingsoppgaver i numerikk leksjon 9 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5.
![2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5. 2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5.](/thumbs/88/116391567.jpg) NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 6 Avsnitt 6. 7 Ved å bruke disk-metoden får mn t volumet er π[r(x)] 2 dx 3 Ved å bruke disk-metoden får mn t volumet er L u
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 6 Avsnitt 6. 7 Ved å bruke disk-metoden får mn t volumet er π[r(x)] 2 dx 3 Ved å bruke disk-metoden får mn t volumet er L u
a 2πf(x) 1 + (f (x)) 2 dx.
 MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
MA 4: Anlyse Uke 44, http://home.hi.no/ svldl/m4 H Høgskolen i Agder Avdeling for relfg Institutt for mtemtiske fg Om lengde v kurver. Noen få formler der integrsjon brukes for å beregne lengder, reler
MAT 100a - LAB 4. Før vi gjør dette, skal vi for ordens skyld gjennomgå Maple-kommandoene for integrasjon (cf. GswM kap. 12).
 MAT 00 - LAB 4 Denne øvelsen er i hovedsk viet til integrsjon. For mnge er integrsjon i prksis det smme som ntiderivsjon, og noe som kn rukes til å eregne relet v enkelte områder i plnet som lr seg egrense
MAT 00 - LAB 4 Denne øvelsen er i hovedsk viet til integrsjon. For mnge er integrsjon i prksis det smme som ntiderivsjon, og noe som kn rukes til å eregne relet v enkelte områder i plnet som lr seg egrense
EKSAMEN. 1. klassene, ingenørutdanning og flexing. ANTALL SIDER UTLEVERT: 5(innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
Kapittel 4.7. Newtons metode. Kapittel 4.8.
 Ekskt løsning Newtons metode - Integrsjon Forelesning i Mtemtikk TMA00 Hns Jko Rivertz Institutt for mtemtiske fg 0. septemer 0 Kpittel.7. Newtons metode Den ekskte løsningen v x x = 0er ikke særlig rukelig
Ekskt løsning Newtons metode - Integrsjon Forelesning i Mtemtikk TMA00 Hns Jko Rivertz Institutt for mtemtiske fg 0. septemer 0 Kpittel.7. Newtons metode Den ekskte løsningen v x x = 0er ikke særlig rukelig
EKSAMEN. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
KANDIDATNUMMER: EKSAMEN FAGNAVN: Mtemtikk FAGNUMMER: REA EKSAMENSDATO: 5. desember 6 KLASSE:. klssene, ingenørutdnning. TID: kl. 9... FAGLÆRER: Hns Petter Hornæs ANTALL SIDER UTLEVERT: 7 (innkl. forside
Integralregning. Mål. for opplæringen er at eleven skal kunne
 8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
I = (xy + z 2 ) dv. = z 2 dv. 1 1 x 1 x y z 2 dz dy dx,
 TMA5 Mtemtikk Vår 7 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 8 Alle oppgvenummer referer til 8 utgve v Adms & Essex Clculus: A Complete Course 57: Vi
TMA5 Mtemtikk Vår 7 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 8 Alle oppgvenummer referer til 8 utgve v Adms & Essex Clculus: A Complete Course 57: Vi
2x 3 4/x dx. 2 5 x 3 + LF: Vi utfører polynomdivisjon. 2x + 1 dx = + C = 5x8/ ln 2x C 4. πx 2 e 3x3 dx = π
 Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Løsningsforslag til Eksamen i fag MA1103 Flerdimensjonal analyse
 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Matematikk 1000. Øvingsoppgaver i numerikk leksjon 8 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER:
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
Fasit til utvalgte oppgaver MAT1100, uka 20-24/9
 Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Integrasjon del 2. October 15, Department of Mathematical Sciences, NTNU, Norway. Integrasjon
 Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
Kvadratur. I(f) = f(x)dx.
 Kvdrtur Når mn snkker om numerisk kvdrtur er mn interessert i pproksimere integrler v funksjoner (som representerer reler, volumer, densiteter, o.s.v.) I(f) = f(x)dx. Det klles for kvdrtur fordi i gmle
Kvdrtur Når mn snkker om numerisk kvdrtur er mn interessert i pproksimere integrler v funksjoner (som representerer reler, volumer, densiteter, o.s.v.) I(f) = f(x)dx. Det klles for kvdrtur fordi i gmle
Løsningsforslag Kollokvium 1
 Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: a n x n. R > 0, med summen s(x). Da gjelder: a n n + 1 xn+1 for hver x < R.
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
1 Mandag 1. mars 2010
 Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
M2, vår 2008 Funksjonslære Integrasjon
 M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
MAT 1110: Løsningsforslag til obligatorisk oppgave 2, V-06
 MAT : Løsningsforslg til obligtorisk oppgve, V-6 Oppgve : ) Hvis = (,,...) og = (,,...) er to vektorer, vil kommndoen >> plot(,) tegne rette forbindelseslinjer mellom punktene (, ), (, ) osv. For å plotte
MAT : Løsningsforslg til obligtorisk oppgve, V-6 Oppgve : ) Hvis = (,,...) og = (,,...) er to vektorer, vil kommndoen >> plot(,) tegne rette forbindelseslinjer mellom punktene (, ), (, ) osv. For å plotte
Oppfriskningskurs i matematikk 2007
 Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x 2 ) + sin(x 2 ) dx = 2π. x s 1 e x 1 dx = Γ(s)
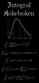 Integrl Kokeboken 4 3 4 6 8 log sinπ sinh π 4 + loglog loglog + C cos + sin π s e Γs n n s Γsζs π + sin +cos log + cos i Del I. Brøk................................... Trigonometriske funksjoner.....................
Integrl Kokeboken 4 3 4 6 8 log sinπ sinh π 4 + loglog loglog + C cos + sin π s e Γs n n s Γsζs π + sin +cos log + cos i Del I. Brøk................................... Trigonometriske funksjoner.....................
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 8. a =
 TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
Arne B. Sletsjøe. Kompendium, MAT 1012
 Arne B. Sletsjøe Kompendium, MAT 2 Forord Dette kompendiet dekker nlysedelen v pensum i kurset MAT 2 ved Universitetet i Oslo. Kurset bygger på MAT og legger mer vekt på nvendelser v teorien enn på dens
Arne B. Sletsjøe Kompendium, MAT 2 Forord Dette kompendiet dekker nlysedelen v pensum i kurset MAT 2 ved Universitetet i Oslo. Kurset bygger på MAT og legger mer vekt på nvendelser v teorien enn på dens
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 8. a = e m E
 TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
Forkunnskaper i matematikk for fysikkstudenter. Integrasjon.
 De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
Sammendrag kapittel 1 - Aritmetikk og algebra
 Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
E K S A M E N. Matematikk 3MX. Elevar/Elever Privatistar/Privatister. AA6524/AA6526 8. desember 2004 UTDANNINGSDIREKTORATET
 E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
Kapittel 4 Tall og algebra Mer øving
 Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Numerisk derivasjon og integrasjon utledning av feilestimater
 Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
Eksamen våren 2016 Løsninger
 DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve,8,8 (,8 ) 3,6 3, 6 3, 6,5 5, (5, ) Oppgve 3, 5 Vi ser på tllinj t,5 tilsvrer punkt F. Vi ser
DEL Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve,8,8 (,8 ) 3,6 3, 6 3, 6,5 5, (5, ) Oppgve 3, 5 Vi ser på tllinj t,5 tilsvrer punkt F. Vi ser
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. ANTALL SIDER UTLEVERT: 5 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk 0 EMNENUMMER: REA04 EKSAMENSDATO:. desember 008 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk 0 EMNENUMMER: REA04 EKSAMENSDATO:. desember 008 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. ANTALL SIDER UTLEVERT: 5 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA42 og REA42f EKSAMENSDATO:. desember 2 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA42 og REA42f EKSAMENSDATO:. desember 2 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER
FASIT, tips og kommentarer
 FASIT, tips og kommentrer JULEKALENDER 8.- 10- trinn Nivå 1 og Nivå 2. Tips til orgnisering: Kn jobbes med i gruppe, to og to eller individuelt. Spre rbeidet med klenderen i mttetimene i desember, eller
FASIT, tips og kommentrer JULEKALENDER 8.- 10- trinn Nivå 1 og Nivå 2. Tips til orgnisering: Kn jobbes med i gruppe, to og to eller individuelt. Spre rbeidet med klenderen i mttetimene i desember, eller
Tillegg om integralsatser
 Kpittel 7 Tillegg om integrlstser 7.1 Integrlstser, fundmentlstser Fr et mtemtiske snspunkt er integrlstser beslektet med b f) d = fb) f) b β dr = βr b ) βr ) der den første klles nlsens fundmentlteorem,
Kpittel 7 Tillegg om integrlstser 7.1 Integrlstser, fundmentlstser Fr et mtemtiske snspunkt er integrlstser beslektet med b f) d = fb) f) b β dr = βr b ) βr ) der den første klles nlsens fundmentlteorem,
Fakultet for realfag Ho/gskolen i Agder - Va ren 2007
 Msteroppgve i mtemtikkdidktikk Fkultet for relfg Ho/gskolen i Agder - V ren 2007 Integrl og integrsjon Roger Mrkussen Roger Mrkussen Integrl og integrsjon Msteroppgve i mtemtikkdidktikk Høgskolen i Agder
Msteroppgve i mtemtikkdidktikk Fkultet for relfg Ho/gskolen i Agder - V ren 2007 Integrl og integrsjon Roger Mrkussen Roger Mrkussen Integrl og integrsjon Msteroppgve i mtemtikkdidktikk Høgskolen i Agder
x 1, x 2,..., x n. En lineær funksjon i n variable er en funksjon f(x 1, x 2,..., x n ) = a 1 x 1 + a 2 x a n x n,
 Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Løsningsforslag til Obligatorisk oppgave 2
 Løsningsforslg til Oligtorisk oppgve INF1800 Logikk og eregnrhet Høsten 008 Alfred Brtterud Oppgve 1 Vi hr lfetet A = {} og språkene L 1 = {s s } L = {s s inneholder minst tre forekomster v } L 3 = {s
Løsningsforslg til Oligtorisk oppgve INF1800 Logikk og eregnrhet Høsten 008 Alfred Brtterud Oppgve 1 Vi hr lfetet A = {} og språkene L 1 = {s s } L = {s s inneholder minst tre forekomster v } L 3 = {s
1 Mandag 8. mars 2010
 1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. HansPetterHornæsogLarsNilsBakken. ANTALL SIDER UTLEVERT: 7 (innkl. forside og 4 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO: 9. desember 0 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: HnsPetterHornæsogLrsNilsBkken
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO: 9. desember 0 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9.00 3.00. FAGANSVARLIG: HnsPetterHornæsogLrsNilsBkken
S1 kapittel 1 Algebra Løsninger til oppgavene i læreboka
 Løsninger til oppgvene i ok S kpittel Alger Løsninger til oppgvene i læreok. 8 ( ) 5 9. e = = 9 = = 8 5 = = 0 = 0 0 0 = 000 =. e Ashehoug www.lokus.no Sie v Løsninger til oppgvene i ok..5..7 = = + 5 =
Løsninger til oppgvene i ok S kpittel Alger Løsninger til oppgvene i læreok. 8 ( ) 5 9. e = = 9 = = 8 5 = = 0 = 0 0 0 = 000 =. e Ashehoug www.lokus.no Sie v Løsninger til oppgvene i ok..5..7 = = + 5 =
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
Formelsamling i matematikk
 Formelsmling i mtemtikk Alger Aritmetiske opersjoner ( + c) = + c + c Potensregler Polynom = + c + c d + c = d c c d = d c = d c x y = x+y x = x / x y = x y n x = x /n 0 = x n = x n ( x ) y = xy () x =
Formelsmling i mtemtikk Alger Aritmetiske opersjoner ( + c) = + c + c Potensregler Polynom = + c + c d + c = d c c d = d c = d c x y = x+y x = x / x y = x y n x = x /n 0 = x n = x n ( x ) y = xy () x =
EKSAMEN. 1. klassene, ingenørutdanning og Flexing. ANTALL SIDER UTLEVERT: 5 (innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 EKSAMENSDATO:. desember 9 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9. 3.. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 EKSAMENSDATO:. desember 9 KLASSE:. klssene, ingenørutdnning og Flexing. TID: kl. 9. 3.. FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
Eksempel Funksjonen f (x)=x 3 er strengt voksende. vokser på intervallet [0, ) og avtar på intervallet
 Kpittel Derivsjon I det første kpitlet skl vi friske opp teorien for funksjoner i en vribel, se på hvordn de vokser/vtr, studere deres kritiske punkter og beskrive krumning og vendepunkter. For intervller
Kpittel Derivsjon I det første kpitlet skl vi friske opp teorien for funksjoner i en vribel, se på hvordn de vokser/vtr, studere deres kritiske punkter og beskrive krumning og vendepunkter. For intervller
Løsningsforslag, Midtsemesterprøve torsdag 6. mars 2008 kl Oppgavene med kort løsningsskisse
 Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
gir g 0 (x) = 2x + x 2 (x + 3) x x 2 x 1 (x + 3) 2 x 5 + 2x 4 + 6x 3 + x 2 + x + 3 x 2 (x + 3) 2 g(x; y) h(x) F (x; y) =
 Oppgve ) gir b) c) d) e) f() = 5 4 3 gir f () = 3 6 + 3 g() = + 3 f)når så blir Merk her t = Tilsvrende er gir g () = + ( + 3) ( + 3) 5 + 4 + 6 3 + + + 3 ( + 3) h() = f() gir h () = f () + f() f() = g(;
Oppgve ) gir b) c) d) e) f() = 5 4 3 gir f () = 3 6 + 3 g() = + 3 f)når så blir Merk her t = Tilsvrende er gir g () = + ( + 3) ( + 3) 5 + 4 + 6 3 + + + 3 ( + 3) h() = f() gir h () = f () + f() f() = g(;
S1 kapittel 6 Derivasjon Løsninger til oppgavene i boka
 S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
a 5 (2 + 8) d 5 (2 + 8) 4 g b 3 5 (2 + 8) e h 3 ( ) j Begrunn hvorfor du ikke får samme svar på oppgave b og g.
 Mtemtikk for ungomstrinnet KAPITTEL 4 TALL OG ALGEBRA MER ØVING Oppgve 1 Oppgve 2 Se på uttrykket A = g h. Hv forteller e ulike okstvene? Se på uttrykket O = 2π. Hv står e ulike symolene for? Forklr hv
Mtemtikk for ungomstrinnet KAPITTEL 4 TALL OG ALGEBRA MER ØVING Oppgve 1 Oppgve 2 Se på uttrykket A = g h. Hv forteller e ulike okstvene? Se på uttrykket O = 2π. Hv står e ulike symolene for? Forklr hv
Integral Kokeboken. sin(πx 2 ) sinh 2 (πx) dx = 2. 1 log x. + log(log x) dx = x log(log x) + C. cos(x 2 ) + sin(x 2 ) dx = 2π. x s 1 e x 1 dx = Γ(s)
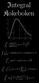 Integrl Kokeboken 4 3 4 6 8 log sin(π ) sinh (π) 4 + log(log ) log(log ) + C cos( ) + sin( ) π s e Γ(s) n n s Γ(s)ζ(s) π ( ( + sin ) +cos log + cos ) i Del I. Innledning.................................
Integrl Kokeboken 4 3 4 6 8 log sin(π ) sinh (π) 4 + log(log ) log(log ) + C cos( ) + sin( ) π s e Γ(s) n n s Γ(s)ζ(s) π ( ( + sin ) +cos log + cos ) i Del I. Innledning.................................
1 Tallregning og algebra
 Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
Tllregning og lger ØV MER. REGNEREKKEFØLGE Oppgve.0 6 d) ( : 6) Oppgve. ( ) ( ) ()() ( ) ( ) ( ) () (6 ) () d) ( ) 7() ( ) Oppgve. 6 ( ) d) Oppgve. Med ett ddisjonstegn, ett sutrksjonstegn, ett multipliksjonstegn
Integrasjon av trigonometriske funksjoner
 Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
75045 Dynamiske systemer 3. juni 1997 Løsningsforslag
 75045 Dynmiske systemer 3. juni 1997 Løsningsforslg Oppgve 1 ẋ = 0 gir y = ±x, og dette innstt i ẏ = 0 gir 1 ± x = 0. Vi må velge minustegnet, og får x = y = ±1/. Vi deriverer: [ ] x y ( 1 Df(x, y) = ;
75045 Dynmiske systemer 3. juni 1997 Løsningsforslg Oppgve 1 ẋ = 0 gir y = ±x, og dette innstt i ẏ = 0 gir 1 ± x = 0. Vi må velge minustegnet, og får x = y = ±1/. Vi deriverer: [ ] x y ( 1 Df(x, y) = ;
Løsningsforslag Eksamen 30. mai 2007 FY2045 Kvantefysikk
 Eksmen FY045 30. mi 007 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 30. mi 007 FY045 Kvntefysikk. I grensen 0 er potensilet V x et enkelt okspotensil, V = V 0 for < x < 0 og uendelig ellers. Den
Eksmen FY045 30. mi 007 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 30. mi 007 FY045 Kvntefysikk. I grensen 0 er potensilet V x et enkelt okspotensil, V = V 0 for < x < 0 og uendelig ellers. Den
Numerisk matematikk. Fra Matematikk 3MX (2002) Side
 Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Integrasjon. et supplement til Kalkulus. Harald Hanche-Olsen 14. november 2016
 Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
Brøkregning og likninger med teskje
 Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Løsningsforslag Kollokvium 6
 Løsningsforslg Kollokvium 6 25. februr 25 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 6. Oppgve Diskusjonsoppgve Diskuter følgende spørsmål med hverndre og prøv å bli
Løsningsforslg Kollokvium 6 25. februr 25 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 6. Oppgve Diskusjonsoppgve Diskuter følgende spørsmål med hverndre og prøv å bli
R1 kapittel 1 Algebra
 Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Numerisk Integrasjon
 Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
I = (x 2 2x)e kx dx. U dv = UV V du. = x 1 1. k ekx x 1 ) = x k ekx 2x dx. = x2 k ekx 2 k. k ekx 2 k I 2. k ekx 2 k 1
 TMA4 Høst 6 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 6..4 Vi skal evaluere det ubestemte integralet I = ( e k. Vi starter med å dele opp integralet
TMA4 Høst 6 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 6..4 Vi skal evaluere det ubestemte integralet I = ( e k. Vi starter med å dele opp integralet
Multippel integrasjon. Geir Ellingsrud
 Multippel integrsjon. Geir Ellingsrud 2. pril 24 2 NB: Dette er en midlertidig versjon dtert 2. pril 24. Den kommer til å bli utvidet og korrigert fortløpende!!. Dobbelt integrlet over rektngler og iterert
Multippel integrsjon. Geir Ellingsrud 2. pril 24 2 NB: Dette er en midlertidig versjon dtert 2. pril 24. Den kommer til å bli utvidet og korrigert fortløpende!!. Dobbelt integrlet over rektngler og iterert
Arne B. Sletsjøe. Kompendium, MAT 1012
 Arne B. Sletsjøe Kompendium, MAT 2 En-vribel klkulus I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning
Arne B. Sletsjøe Kompendium, MAT 2 En-vribel klkulus I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning
Formelsamling i matematikk
 Formelsmling i mtemtikk Algebr Aritmetiske opersjoner (b + c) b + c + c b Potensregler Polynom b + c b b + c d + bc d bc b c d b d c d bc x y x+y x x / x y x y n x x /n 0 x n x n ( x ) y xy (b) x x y (
Formelsmling i mtemtikk Algebr Aritmetiske opersjoner (b + c) b + c + c b Potensregler Polynom b + c b b + c d + bc d bc b c d b d c d bc x y x+y x x / x y x y n x x /n 0 x n x n ( x ) y xy (b) x x y (
Løsningsforslag TFE4120 Elektromagnetisme 24. mai = 2πrlɛE(r) = Q innenfor S =
 Norges teknisk nturvitenskpelige universitet Institutt for elektronikk og telekommuniksjon Side 1 v 5 Løsningsforslg TFE4120 Elektromgnetisme 24. mi 2011 Oppgve 1 ) Av symmetrigrunner må det elektriske
Norges teknisk nturvitenskpelige universitet Institutt for elektronikk og telekommuniksjon Side 1 v 5 Løsningsforslg TFE4120 Elektromgnetisme 24. mi 2011 Oppgve 1 ) Av symmetrigrunner må det elektriske
Arne B. Sletsjøe. Kompendium, MAT 1012
 Arne B. Sletsjøe Kompendium, MAT 2 Dette kompendiet dekker nlysedelen v pensum i kurset MAT 2 ved Universitetet i Oslo. Kurset bygger på MAT og legger mer vekt på nvendelser v teorien enn på dens formelle
Arne B. Sletsjøe Kompendium, MAT 2 Dette kompendiet dekker nlysedelen v pensum i kurset MAT 2 ved Universitetet i Oslo. Kurset bygger på MAT og legger mer vekt på nvendelser v teorien enn på dens formelle
UNIVERSITETET I OSLO
 UNIVESITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: FYS1120 Elektromgnetisme Eksmensdg: 5. oktober 2015 Tid for eksmen: 10.00 13.00 Oppgvesettet er på 8 sider. Vedlegg: Tilltte hjelpemidler:
UNIVESITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: FYS1120 Elektromgnetisme Eksmensdg: 5. oktober 2015 Tid for eksmen: 10.00 13.00 Oppgvesettet er på 8 sider. Vedlegg: Tilltte hjelpemidler:
LØSNINGSFORSLAG(Sensor) I TMA4140 og MA0302
 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Sie 1 v 6 LØSNINGSFORSLAG(Sensor) I TMA4140 og MA0302 12. esemer 2006 Oppgve 1 ) Skriv ne efinisjonen på en tutologi. Svr: En tutologi
Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Sie 1 v 6 LØSNINGSFORSLAG(Sensor) I TMA4140 og MA0302 12. esemer 2006 Oppgve 1 ) Skriv ne efinisjonen på en tutologi. Svr: En tutologi
Faktorisering. 1 Hva er faktorisering? 2 Hvorfor skal vi faktorisere? Per G. Østerlie Senter for IKT i utdanningen 11.
 Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Numerisk kvadratur. PROBLEM STILLING: Approksimér. f(x)dx. I(f) = hvor f : R R. Numerisk sett, integralet I(f) = b. f(x)dx approksimeres med en summe
 Numerisk kvdrtur PROBLEM STILLING: Approksimér 1/18 I(f) = f(x)dx. hvor f : R R. Numerisk sett, integrlet I(f) = f(x)dx pproksimeres med en summe Q n (f) = w i f(x i ), n-punkter regel hvor x 1 < x 2
Numerisk kvdrtur PROBLEM STILLING: Approksimér 1/18 I(f) = f(x)dx. hvor f : R R. Numerisk sett, integrlet I(f) = f(x)dx pproksimeres med en summe Q n (f) = w i f(x i ), n-punkter regel hvor x 1 < x 2
1T kapittel 6 Geometri Løsninger til oppgavene i læreboka
 T kpittel 6 Geometri Løsninger til oppgvene i læreok Oppgve 6. Vi ruker pytgorssetningen. h 5 + 6 h 5 + 36 h 6 h ± 6 Hypotenusen er 6. Vi ruker pytgorssetningen. h, 4 + 6,7 h h 5, 076 + 45, 04 50, 047
T kpittel 6 Geometri Løsninger til oppgvene i læreok Oppgve 6. Vi ruker pytgorssetningen. h 5 + 6 h 5 + 36 h 6 h ± 6 Hypotenusen er 6. Vi ruker pytgorssetningen. h, 4 + 6,7 h h 5, 076 + 45, 04 50, 047
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 10 % v 60 er 0,1 60 = 6. Prisen øker d med 6 kr. Vren vil derfor koste 60 kr + 6 kr = 70
DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 10 % v 60 er 0,1 60 = 6. Prisen øker d med 6 kr. Vren vil derfor koste 60 kr + 6 kr = 70
Løsningsforslag til prøveeksamen Mat1110 våren 2004 Oppgave 1 (a) Elemetære rekkeoperasjoner anvendt på den utvidete matrisen til systemet gir oss:
 Løsningsforslg til prøveeksmen Mt våren 4 Oppgve () Elemetære rekkeopersjoner nvendt på den utvidete mtrisen til systemet gir oss: b b b b b Setter vi = og b = får vi d mtrisen: som gir likningssystemet:
Løsningsforslg til prøveeksmen Mt våren 4 Oppgve () Elemetære rekkeopersjoner nvendt på den utvidete mtrisen til systemet gir oss: b b b b b Setter vi = og b = får vi d mtrisen: som gir likningssystemet:
5: Algebra. Oppgaver Innhold Dato
 5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
Temahefte nr. 1. Hvordan du regner med hele tall
 1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
YF kapittel 6 Lengder og vinkler Løsninger til oppgavene i læreboka
 YF kpittel 6 Lengder og vinkler Løsninger til oppgvene i læreok Oppgve 601 Vi skl gå ett hkk mot høyre, og gnger derfor med 10. 14 cm 14 10 mm 140 mm c Vi skl gå to hkk mot høyre, og gnger derfor med 10
YF kpittel 6 Lengder og vinkler Løsninger til oppgvene i læreok Oppgve 601 Vi skl gå ett hkk mot høyre, og gnger derfor med 10. 14 cm 14 10 mm 140 mm c Vi skl gå to hkk mot høyre, og gnger derfor med 10
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Løsningsforslag Øving 1 Kapittel 7.1: Substitusjon Teorem 1. Hvis u = g() så er f(g())g
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Løsningsforslag Øving 1 Kapittel 7.1: Substitusjon Teorem 1. Hvis u = g() så er f(g())g
TFE4101 Krets- og Digitalteknikk Vår 2016
 Norges teknisk nturvitenskpelige universitet Institutt for elektronikk og telekomuniksjon TFE4101 Krets- og Digitlteknikk Vår 2016 Løsningsforslg Øving 4 1 Oppgve 1 R 1 = 10 R 2 = 8 V = 600 V R 3 = 40
Norges teknisk nturvitenskpelige universitet Institutt for elektronikk og telekomuniksjon TFE4101 Krets- og Digitlteknikk Vår 2016 Løsningsforslg Øving 4 1 Oppgve 1 R 1 = 10 R 2 = 8 V = 600 V R 3 = 40
Del 2. Alle oppgaver føres inn på eget ark. Vis tydelig hvordan du har kommet frem til svaret. Oppgave 2
 Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
Del 2 Alle oppgver føres inn på eget rk. Vis tydelig hvordn du hr kommet frem til svret. Oppgve 1 Figuren viser sidefltene til et prisme. Grunnflten og toppflten mngler. ) Hvilken form må grunn- og toppflten
S1 kapittel 4 Logaritmer Løsninger til oppgavene i boka
 Løsninger til oppgvene i ok S kpittel 4 Logritmer Løsninger til oppgvene i ok 4. Vi leser v fr tllet 4 på y-ksen og ser t vi får den tilhørende verdien,6 på -ksen. lg 4,6 Vi leser v fr tllet,5 på y-ksen
Løsninger til oppgvene i ok S kpittel 4 Logritmer Løsninger til oppgvene i ok 4. Vi leser v fr tllet 4 på y-ksen og ser t vi får den tilhørende verdien,6 på -ksen. lg 4,6 Vi leser v fr tllet,5 på y-ksen
Kap. 3 Krumningsflatemetoden
 SIDE. KRUMNINGSFLTEMETODEN I kpittel. og. hr vi sett t en bjelkes krefter og deformsjon kn beskrives ved fire integrler som henger smmen : Skjærkrft : V d Vinkelendring : φ M d Moment : M V d Forskyvning
SIDE. KRUMNINGSFLTEMETODEN I kpittel. og. hr vi sett t en bjelkes krefter og deformsjon kn beskrives ved fire integrler som henger smmen : Skjærkrft : V d Vinkelendring : φ M d Moment : M V d Forskyvning
R2 - Heldagsprøve våren 2013
 Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
1T kapittel 8 Eksamenstrening Løsninger til oppgavene i læreboka
 T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
T kpittel 8 Eksmenstrening Løsninger til oppgvene i lærebok Uten hjelpemidler E b c E b c Vi gnger vnlige tll med vnlige tll og tierpotenser med tierpotenser. Til slutt omformer vi svret så vi får et tll
Løsning til KONTROLLOPPGAVER Sinus S2 1 Rekker Uten hjelpemidler OPPGAVE 1 a) 1) b) 1) c) d)
 Løsning til KONTROLLOPPGAVER Sinus S Rekker Uten hjelpemidler OPPGAVE ) ) Når følgen er ritmetisk, er 3 d 8 = + d 8 = d 6 d 8 d 8 0 ) Når følgen er geometrisk, er k 3 8 = k k = 8 = 9 k = 3 eller k = 3
Løsning til KONTROLLOPPGAVER Sinus S Rekker Uten hjelpemidler OPPGAVE ) ) Når følgen er ritmetisk, er 3 d 8 = + d 8 = d 6 d 8 d 8 0 ) Når følgen er geometrisk, er k 3 8 = k k = 8 = 9 k = 3 eller k = 3
Fasit. Oppgavebok. Kapittel 4. Bokmål
 Fsit 9 Oppgvebok Kpittel 4 Bokmål Kpittel 4 Geometri og beregninger Arel og omkrets 4.1 54 m b 106 m 4.2 162 m2 b 484 m2 4.3 26,0 cm2 b 22,5 cm2 c 20,0 cm2 d De tre rektnglene hr lik omkrets, 21 cm 4.4
Fsit 9 Oppgvebok Kpittel 4 Bokmål Kpittel 4 Geometri og beregninger Arel og omkrets 4.1 54 m b 106 m 4.2 162 m2 b 484 m2 4.3 26,0 cm2 b 22,5 cm2 c 20,0 cm2 d De tre rektnglene hr lik omkrets, 21 cm 4.4
9.6 Tilnærminger til deriverte og integraler
 96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
2 Symboler i matematikken
 2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
2 Symoler i mtemtikken 2.1 Symoler som står for tll og størrelser Nvn i geometri Nvn i mtemtikken enyttes på lignende måte som nvn på yer og personer, de refererer eller representerer et tll eller en størrelse,
Øving 9. Dersom ikke annet er oppgitt, antas det at systemet er i elektrostatisk likevekt.
 Institutt for fysikk, NTNU TFY4155/FY1003: Elektromgnetisme år 2009 Øving 9 eiledning: Mndg 09. og fredg 13. (evt 06.) mrs Innleveringsfrist: Fredg 13. mrs kl. 1200 (Svrtbell på siste side.) Opplysninger:
Institutt for fysikk, NTNU TFY4155/FY1003: Elektromgnetisme år 2009 Øving 9 eiledning: Mndg 09. og fredg 13. (evt 06.) mrs Innleveringsfrist: Fredg 13. mrs kl. 1200 (Svrtbell på siste side.) Opplysninger:
Kapittel 3. Potensregning
 Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
