AB a donc OM = = 2 2
|
|
|
- Hallvard Berger
- 6 år siden
- Visninger:
Transkript
1 ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t ) = + = + + = + 3 x = y + 3 y = t t = y + 0 y Equation de la trajectoire : y = ± x - 3 (Parabole d axe Ox, avec x 3 et y - ) dom / v = = (t 4)i + j γ dv d = ( (t 4) i j ) i = + = γ : constante en norme ( γ = ) et en direction (direction du vecteur i ). v γ = 0 (t 4)i + j i = (t 4) = 0 t = s t = s x = 3, y = 0 v(t = ) = j = 1j 3/ [ ] Exercice : 1/ rajectoire de M : OM = x i + yj OAB triangle rectangle et M milieu de l'hypoténuse, AB a donc OM = = a OM = x + y = 4 La trajectoire de M est un cercle de centre O et de rayon a de cercle. ; c est un quart 1
2 ) Composantes de OM, v et γ : OB vot x = = OM 1 y = a - vot dx vo vx = = v dy 1 1 v y = = ( vot) = a vot vot - a - v t o dvx γ x = = 0 γ = dvy vo 1/ 1 3 / a vo γ y = = (a vot ) + t ( vot) (a vot ) = - (a - v t ) Pour ces expressions, il faut que a > v t. Représentation de v et γ : v est tangent à la trajectoire en M. γ est parallèle à j et de sens contraire. 3/ v(m) en fonction de : M M o y y a v t sin = = = a / a a v o (vot) vo a vo 1 vo v = + = = v = 4 4(a vot ) 4 (a vot ) 4 sin sin v v(m) = o π car 0 < < sin o 3 o
3 Exercice 3: - 1/ ρ = ae, =ωt L équation de la trajectoire en coordonnées polaires est ici : - ρ = ae. C est une «spirale». π π 3π 5π 3π 7π 0 π π ρ a 0,456a 0,08a 0,095a 0,043a 0,019a 0,009a 0,004a 0,00a / v et γ en coordonnées polaires : * OM =ρu ρ = ae uρ dom * v = v = aωe (-u ρ + u ) v = v = aω e dv * γ = γ = -aω e u γ =γ=aω e v et γ en coordonnées cartésiennes : OM = x i + yj En utilisant les relations de transfert entre ( ρ, ) et (x, y), on trouve : *OM = xi + yj =ρcosi +ρsinj = ae (cosωti +sinωtj) dom dx dy * v = = i + j v = aωe (-(cosωt + sinωt)i + (cosωt - sinωt)j) v = v = aω e dv dv dv x y * γ = = i + j γ = aω e (sinωti - cosωtj) γ =γ= aω e 3/ v et γ et R (t) en coordonnées intrinsèques : * v = vu = aω e u dv d * γ = = (aω e ) γ = -aω e * γ =γu +γnu N, γ =γ +γ N, γ N = γ -γ 4 γ N =γ -γ = (aω e ) - (-aω e ) = a ω e γ N = aω e 3
4 * γ = aω e (-u + u N ) *Expression du rayon de courbure : v v (aω e ) aω e γ = R(t) = = = N R(t) γn aω e aω e R (t) = Donc le rayon de courbure R varie avec la position du point M au cours du mouvement. ae 4/ Le point O est-il centre des accélérations? Pour cela, il faut que O soit fixe (c est le cas) et que OM γ = 0, t. OM γ = (ae u ) (-aω e u ) = -aω e k 0 ρ Le mouvement n est pas à accélération centrale. Le point O n est pas centre des accélérations. 5/ * u en fonction de (u ρ,u ) : On connait les expressions de v en coordonnées intrinsèques et en coordonnées polaires, donc : 1 aω e u = aωe (-u ρ + u ) u = (-u ρ + u ) * u en fonction de (i, j) : A partir des expressions de v en coordonnées intrinsèques et en coordonnées cartésiennes, on a : 1 u = -(cosωt + sinωt)i + (cosωt - sinωt)j aω e u = aωe -(cosωt + sinωt)i + (cosωt - sinωt)j 6/ Abscisse curviligne s( ) et longueur totale de la trajectoire : ds ds d ds ds - ds v = = = ɺ = ω = aω e = a e s() = a e d + C = -a e + C d d d d - = 0 s = 0 C = a s() = a (1 - e ) Longueur totale de la trajectoire : L = a. Exercice 4 : 1/ Le pas est MM ' = h M(t) z = at z' z = h = a M'(t + ) z' = a(t + ) π = ωt π = ω = ω h = πa ω /OM = Ruρ + atk v = R ɺ u + ak v = Rωu + ak ste v = R ω + a = C dv ste γ = = Rɺɺ u Rɺ u ρ, ω = C ɺɺ = 0 γ = -Rω u ρ u k, γ // u γ Oz ρ ρ 4
5 v = Rω u + ak α = (v,k) v.k = vcosα = a cosα = 3/ a R ω + a = C x = R cos x = R cosωt ω x(z) = Rcos z a M y = R sin M y = R sin ωt M ω z = at z = at y(z) = Rsin z a Mouvements projetés sur Ox : x = R cos ωt : Mouvement sinusoïdal de période. Mouvements projetés sur Oy : y = R sin ωt : Mouvements projetés sur Oz : z = at : Mouvement uniforme. Mouvement projeté de M sur xoy : ste Mouvement sinusoïdal de période. x + y = R. C est un cercle de centre O et de rayon R. dv 4/ γ =, v = cste γ = 0 N γ = γ γ = γ γ = Rω v Rω + a R = = γ Rω N N ds 5/ = v = R ω + a s = v = R ω + a t + C s(t = 0) = 0 C = 0 s(t) = R ω + a t 5
6 Exercice 5 : 1/ A l instant t, la roue est en contact avec Ox au point I d abscisse vot ; la position de M est définie par l angle = (CI, CM). Le roulement sans glissement impose que IM = OI, soit : R = vot et vot =. R vot x(m) = vot R sin x(m) = R( sin ) R y(m) = R(1 cos ) y(m) = R(1 cos ) x = R( - sin) Soit finalement : y = R(1- cos) Ces équations représentent une trajectoire appelée «cycloïde». Attention! ce sont les équations paramétriques du mouvement du point M dans lesquelles est en radians. En attribuant des valeurs au paramètre, on trouve les couples (x,y). Par exemple : Pour = π : x = R( π 0) = Rπ et y = R(1 ( 1)) = R. / Calcul du module de v(t) du point M : v(t) = v(t) = vx + vy, v(t) est noté v(t), donc v(t) 0, t. dx vot vo vx = = R ɺ (1 cos ) = v o(1 cos ), (t) =, ɺ = = Cste R R dy vy = = Rɺ sin = vo sin 6
7 [ ] [ ] vot v(t) = vx + vy = v o(1 cos ) + vosin = v o(1 cos ) = 4vosin = 4vosin R vot v(t) = vo sin R 3/ Etude de la fonction v( ) pour 0 π. Cela correspond à 1 tour de la roue pendant lequel la valve M aura effectuée une arche (1 période). vot vot v(t) = vo sin et = v() = vo sin R R v() 0 pour 0 π, soit : 0 π et on a dans ce domaine : v() = +vosin * = 0 : v(0) = 0 * = π : v( π ) = vmax = vo * = π : v( π ) = 0 4/ Représentation de v( ) entre 0 4π. π π sin 0, soit pour π 4π et alors, puisque v( ) est toujours positif ou nul, v() = -v sin. Il suffit d inverser la branche du sinus dans ce domaine vers les valeurs postives. o 4/ Calcul de γ(m) et orientation : dv γ = = vxi + vyj = voɺ sin i + voɺ v ɺ ɺ cosj, soit : γ = o (sini + cosj) R MC π π = R cos( )i R sin( ) j = R(sin i + cos j) v o γ = MC γ (M) est orientée vers le point C. R Pour que C soit centre des accélérations, il faut que γ MC = 0 et C fixe. C n étant pas fixe, donc il n est pas centre des accélérations. 7
8 5/ Calcul de γ, γ N et R. dv * γ =, v = vo sin dv dv d 1 vo 0 π : v( ) = + vo sin γ = = = vo cos d R vo π 4 π : v( ) = vo sin γ = - cos R, soit : γ = o v cos R vo vo vo N cos sin γ = γ γ = = R R R vo γ N = sin R : on prend la valeur absolue car γn est toujours positif. v * R = = 4R sin : le rayon de courbure est toujours positif! γ N 6/ v et MK parallèle? v// MK v MK = 0 MK = MO + OI + IK = (x i + yj) + vo t i + Rj = (vo t x)i + (R y) j MK = (R x)i + (R y) j i j k v MK = v v 0 = v (R y) v (R x) k [ ] x y x y R x R y 0 v MK = [ v o (1 cos )(R R(1 cos )) vo sin (R R( sin )) ] k v MK = vor(1 cos )(1 + cos ) vor sin k v MK = vor (1 cos ) sin k = 0 Ou bien : v MI v.mi = 0 MI = MO + OI = (x i + yj) + vo t i = (vo t x) i yj = (R x) i yj v.mi = v x (R x) vyy = v o (1 cos )(R R( sin )) (vo sin )R(1 cos ) v.mi = Rv o (1 cos ) sin Rvo sin )(1 cos ) = 0 Conclusion : v étant tangent à la cycloïde en M, il en est de même de MK. 7/ Représentation : * v tangent à la cycloïde, porté par MK. * u : v = vu donc, u porté par MK. * u N est perpendiculaire à u, dirigé vers le centre de courbure. * γ est porté par CM et dirigé vers le point C (voir question 4). * γ et γ N sont respectivement les projections orthogonales sur les vecteurs du repère intrinsèque (u,u N). *Position du centre de courbure de la cycloïde à un instant t : A un instant, le centre de courbure C est situé sur le support de u N, donc également sur le support de MI à une distance de M égale à R. Exprimons le rayon de courbure en fonction de MI : MI = (R x) i yj = R sin i R(1 cos ) j MI = R (1 cos ) = 4R sin 8
9 MI = Rsin R = MI On en déduit que le centre de courbure C est tel que I est le milieu du segment MC. Exercice 6 : 1/ vb = v a(b) = vbi Loi de composition des vitesses (cas général) : v a (M) = v(m) ( R) = v(m) ( R') + v e( R'/ R ) = v r (M) + v(o') ( R) + ωr '/ R O'M Mobile M B O' A ( R) fixe d'origine O. ( R') Repère lié à A. ω = 0 : ( R') est en translation rectiligne / ( R). R'/ R v a (B) = v(b) ( R) = vb = v(b) ( R') + v(a) ( R) = v(b/ A) + v v(b/a) = vb - v = (vb - v)i A.N. : v(b / A) = 0,5m / s 9
10 / Mobile M C O' A ( R) fixe d'origine O. ( R') Repère lié à A. v(m) ( R) = v(m) ( R') + v(o') ( R) v(c) ( R) = v(c) ( R') + v(a) ( R) v = v(c/ A) + v v(c/a) = -v = -vi A.N.: v(c/ A) = 1m / s 3/ Mobile M B O' C ( R) fixe d'origine O. ( R') Repère lié à C. v(m) ( R) = v(m) ( R') + v(o') ( R) v(b) ( R) = v(b) ( R') + v(c) ( R) vb = v(b/ C) v v(b/c) = v + v = (v + v)i B A.N.: v(b/ C) = 1,5m /s B Exercice 7 : 1/ Vitesse angulaire des aiguilles. π La grande aiguille décrit un angle (t) = ω t avec une vitesse angulaire ω = 1tr / h = = 3600(s) Lorsque la petite auguille fait un tour complet, la grande aiguille fait 1 tours. Donc : ω1 π La petite aiguille décrit un angle 1(t) = ω 1t avec une vitesse angulaire ω 1 = = rd/s π rd/s
11 Concernant les vecteurs vitesses angulaires des deux aiguilles, la règle du tournevis montre qu ils sont dirigés suivant ( k) ou ( k '), k étant parallèle à k ' au cours du mouvement de celles-ci, donc : ω 1 = -ω1k' et ω = -ω k'. / Equation de la trajectoire de M dans ( R '). O'M = x ' i ' + y' j' = O'O + OM = lj' + L(sin i ' + cos j'), = ( ω ω1)t O'M = Lsin i ' + (Lcos l) j' x' = Lsin x' + (y' + l ) = L y' = Lcos l rajectoire de M dans ( R ') : cercle (C) de rayon L et de centre O(0,- l ). 3/ Vitesse absolue de M. Loi de composition des vitesses (cas général) : v a(m) = v r(m) + v e( R'/ R) do'm d * v r (M) = = Lsin i ' + (Lcos l ) j' = L ɺ (cos i ' sin j') = L( ω ω 1 )(cos i ' sin j') ( R') ( R') car = ( ω ω1 )t ɺ = ( ω ω1). * v e = v(o') ( R ) + ωr '/ R O'M doo' d( lj') dj' v(o') ( R) = = = l = lωr '/ R j' = l( ω1k ') j' = l ω1 i ' ( R) ( R) ( R) ωr '/ R O'M = ( ω 1 k ') (Lsin i ' + (Lcos l) j') = ω 1 Lsin j' + ω 1 (Lcos l )i ') v e = lω 1 i ' ω 1 Lsin j' + ω 1 (Lcos l )i ') = ω 1 L(cos i ' sin j') Après remplacement, on trouve : v a(m) = L ω(cos i ' sin j') 11
12 Soit : v (M) = Lω (cos(ω -ω )ti' - sin(ω -ω )tj') a 1 1 4/ Accélération absolue de M. Loi de composition des accélérations (cas général) : γ a(m) = γ r(m) + γe( R'/ R ) + γc(m) dv r(m) d * γ r(m) = = L( ω ω1 )(cos i ' sin j') = L( ω ω1) ɺ (sin i ' + cosj') ( R') ( R') γ r(m) = L( ω ω1 ) (sin i ' + cosj') * γ c (M) = ωr '/ R vr = ( ω1k') ( L( ω ω1 )(cos i ' sin j') ) = L ω1 ( ω ω1 )(sin i ' + cos j') * γ e = γ (O') ( R ) + ωɺ R '/ R O'M + ωr '/ R ( ωr '/ R O'M) dv(o') ( R) d( lω1 i ') di ' γ (O')( R) = = = lω 1 = lω1 ( ωr '/ R i ') = lω1 ( ω1k ' i ') = l ω1 j' ( R) ( R) ( R) ωɺ R '/ R O'M = 0, ω R '/ R = ω 1 k' = cste ωr '/ R ( ω ɺ R'/ R O'M) = ( ω1k') ω1lsin j' + ω1 (Lcos l)i ') = ω1 Lsin i ' + (Lcos l ) j' γ e = lω 1 j' + ω1 ( Lsin i ' + (Lcos l ) j' ) = L ω1 (sin i ' + cos j') Après remplacement, on trouve : γ a (M) = L ω(sin i ' + cosj') Soit : γ (M) = -Lω (sin(ω -ω )ti' + cos(ω -ω )tj') ( ) a 1 1 5/ Facultatif : v a(m) et γa(m) par la méthode directe : dom( R) d v a (M) = = L( sin ω ti + cosωtj) ( R) ( R) v a (M) = Lω ( cos ωti sinωtj ) et dv a (M) d γ a (M) = = Lω ( cosω ti sin ω tj) = Lω ( sin ω t i + cosω tj) ( R) ( R) Exprimons ces vecteurs en fonction des vecteurs i ' et j' de la base de ( R ') : i = cosω 1ti ' + sinω1 tj' j = sin ω 1ti ' + cos ω 1tj' *Remplaçons dans l expression de v a : v a (M) = L ω(cos ω t cosω 1t + sin ω t sin ω 1t)i ' + (sin ω1 t cosω t cosω1 t sin ω t) j' v a (M) = L ω(cos ω t cosω 1t + sin ω t sin ω1 t)i ' (sin ω t cosω1 t cos ω t sinω1 t) j' Sachant que : cos(a b) = cosa cosb + sin asin b et sin(a b) = sin a cosb cosa sin b, on obtient bien : v (M) = Lω cos(ω -ω )ti' - (sin(ω -ω )tj' ( ) a 1 1 *Remplaçons dans l expression de γa : ( γ ) a(m) = Lω sin ω t(cos ω 1ti ' + sin ω 1tj') + cos ω t( sin ω 1ti ' + cos ω1 tj') γ a(m) = L ω (sin ω t cos ω1 t cos ω t sin ω 1t)i ' + (cos ω t cos ω 1t + sin ω t sin ω1 t) j' γ (M) = -Lω sin(ω -ω )ti' + cos(ω -ω )tj' ( ) ( ) a 1 1 1
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 2008
 Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
1. Intégrales définies et indéfinies I. (a) Soit b > 0. Montrer que pour tout x > 0 la fonction. 2 b. F (x) = arctan bx. 1 (1 + bx) x. f(x) = x t dt.
 Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Energie et corrélation. Systèmes de Traitement du Signal Polytech Marseille INFO 2016
 Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
 http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
Laser vert : moins de plus de 300. Acheter Laser PRODUITS CHAUDS. Pointeur Laser étanche
 Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Bobine à noyau de fer
 1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
Brosses intérieures avec manche
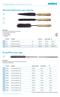 18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
DYNAMIQUE. Etude des mouvements de tangage d une transmission de puissance d hélicoptère. x r 2. y r 2. x 1. y r y r
 e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
 Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
I. Évolution du commerce mondial
 I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
PremiCron. Tresse synthétique non résorbable de polyester enduit. PremiCron
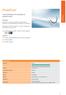 Tresse synthétique non résorbable de polyester enduit Description PremiCron est une tresse synthétique non résorbable de Polyester. Les sutures PremiCron sont enduites avec du silicone. PremiCron Disponible
Tresse synthétique non résorbable de polyester enduit Description PremiCron est une tresse synthétique non résorbable de Polyester. Les sutures PremiCron sont enduites avec du silicone. PremiCron Disponible
Eksamen FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. Nynorsk/Bokmål
 Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Design d'un champ de vecteurs tangents
 Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
Ma Flerdimensjonal Analyse Øving 2
 Ma1 - Flerdimensjonal Analyse Øving Øistein Søvik Brukernavn: Oistes.1.1 Oppgaver 11. In Exercises 1 4, find the required parametrization of the first quadrant part of the circular arc x + y 1 1. In terms
Ma1 - Flerdimensjonal Analyse Øving Øistein Søvik Brukernavn: Oistes.1.1 Oppgaver 11. In Exercises 1 4, find the required parametrization of the first quadrant part of the circular arc x + y 1 1. In terms
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide
 Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Corrigés des exercices du chapitre 25
 MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
On remet la machine en route
 Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
Clôture Métallique. Portails / Portillons / Accessoires
 Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN. Langue vivante 2
 Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
β = r 2 cosθsinθ. β = β β i+ j = yi+xj. (8.1) = 2rcosθsinθi r +r( sinθsinθ+cosθcosθ)i θ
 Kapittel 8 Polarkoordinater Oppgave 1 Vi har gitt skalarfeltet β(x, y) = xy i kartesiske koordinater. a) For polarkoordinater (r,θ) og kartesiske koordinater (x,y) har vi sammenhengen x = rcosθ og y =
Kapittel 8 Polarkoordinater Oppgave 1 Vi har gitt skalarfeltet β(x, y) = xy i kartesiske koordinater. a) For polarkoordinater (r,θ) og kartesiske koordinater (x,y) har vi sammenhengen x = rcosθ og y =
EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012
 Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
Eksamen FSP5020 Fransk I PSP5013 Fransk nivå I. Nynorsk/Bokmål
 Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
β = r 2 cosθsinθ. β = β β i+ j = yi+xj. (8.1)
 Kapittel 8 Polarkoordinater Oppgave 1 Vi har gitt skalarfeltet β(x, y) = xy i kartesiske koordinater. a) For polarkoordinater (r, θ) og kartesiske koordinater (x, y) har vi sammenhengen x = rcosθ og y
Kapittel 8 Polarkoordinater Oppgave 1 Vi har gitt skalarfeltet β(x, y) = xy i kartesiske koordinater. a) For polarkoordinater (r, θ) og kartesiske koordinater (x, y) har vi sammenhengen x = rcosθ og y
LØSNINGSFORSLAG TIL ØVING 11, TMA4105, V2008. x = r cos θ, y = r sin θ, z = 2r for 0 θ 2π, 2 2r 6. i j k. 5 r dr dθ = 8
 LØNINGFORLAG TIL ØVING, TMA45, V8 Oppgave 4.5.9. Parametrisering: x = r cos θ, y = r sin θ, z = r for θ π, r 6. r(r, θ) = r cos θ, r sin θ, r. N = r r r θ = cos θ sin θ = r cos θ, r sin θ, r. r sin θ r
LØNINGFORLAG TIL ØVING, TMA45, V8 Oppgave 4.5.9. Parametrisering: x = r cos θ, y = r sin θ, z = r for θ π, r 6. r(r, θ) = r cos θ, r sin θ, r. N = r r r θ = cos θ sin θ = r cos θ, r sin θ, r. r sin θ r
[0005] den indre ende av sylinderen passer inn i nevnte fordypning i låst inngrep med denne for å danne et skjøte, og også forme et sete på basen.
![[0005] den indre ende av sylinderen passer inn i nevnte fordypning i låst inngrep med denne for å danne et skjøte, og også forme et sete på basen. [0005] den indre ende av sylinderen passer inn i nevnte fordypning i låst inngrep med denne for å danne et skjøte, og også forme et sete på basen.](/thumbs/66/56311936.jpg) 2 552 619 1 Beskrivelse [0001] Oppfinnelsen er en fremgangsmåte for fremstilling av tomhylse ved kaldforming av sømløse eller skjøtede rør. Oppfinnelsen kommer under klasse F24B5/02 i den internasjonale
2 552 619 1 Beskrivelse [0001] Oppfinnelsen er en fremgangsmåte for fremstilling av tomhylse ved kaldforming av sømløse eller skjøtede rør. Oppfinnelsen kommer under klasse F24B5/02 i den internasjonale
Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo. Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo
 Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo L HISTOIRE DU LYCEE SKOLENS HISTORIE Recherches / Etterforskning : Paul Monceyron
Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo L HISTOIRE DU LYCEE SKOLENS HISTORIE Recherches / Etterforskning : Paul Monceyron
Une version feuilletée du théorème de translation de Brouwer
 Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
Anbefalte oppgaver - Løsningsforslag
 TMA45 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 5.5.: Kulen er grafen til rφ, θ) asinφ) cosθ)i + sin φ sinθ)j + cosφ)k), φ π, θ < π. Vi har slik at φ θ acosφ) cosθ)i + sinφ) sinθ)j + cosφ)k)
TMA45 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 5.5.: Kulen er grafen til rφ, θ) asinφ) cosθ)i + sin φ sinθ)j + cosφ)k), φ π, θ < π. Vi har slik at φ θ acosφ) cosθ)i + sinφ) sinθ)j + cosφ)k)
GAMME DETENTE DIRECTE SOMMAIRE. X32 monosplit Inverter Page 88. X3 multisplit Inverter Page 90. Monosplits/Multisplits
 SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
K j æ r e b e b o e r!
 1 K e y s e r l ø k k a Ø s t B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d
1 K e y s e r l ø k k a Ø s t B o r e t t s l a g K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d
TFY4160 Bølgefysikk/FY1002 Generell Fysikk II 1. Løsning Øving 2. m d2 x. k = mω0 2 = m. k = dt 2 + bdx + kx = 0 (7)
 TFY4160 Bølgefysikk/FY100 Generell Fysikk II 1 Løsning Øving Løsning oppgave 1 Ligning 1) i oppgaveteksten er i dette tilfellet: Vi setter inn: i lign. 1) og får: m d x + kx = 0 1) dt x = A cosω 0 t +
TFY4160 Bølgefysikk/FY100 Generell Fysikk II 1 Løsning Øving Løsning oppgave 1 Ligning 1) i oppgaveteksten er i dette tilfellet: Vi setter inn: i lign. 1) og får: m d x + kx = 0 1) dt x = A cosω 0 t +
Qi-Wu-Zhang model. 2D Chern insulator. León Martin. 19. November 2015
 Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
NTNU. MA1103 Flerdimensjonal Analyse våren Maple-øving 2. Viktig informasjon. Institutt for matematiske fag. maple02 28.
 NTNU Institutt for matematiske fag MA1103 Flerdimensjonal Analyse våren 2011 Maple-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
NTNU Institutt for matematiske fag MA1103 Flerdimensjonal Analyse våren 2011 Maple-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
PREPARATION BREVET BLANC 1 CALCUL FRACTIONNAIRE : AIDE : d'abord transformer l'écriture du nombre entier 1. Tout nombre a peut s'écrire 1
 THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160 BØLGEFYSIKK Onsdag 20. desember 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l år e t s g e n e r a l f o rs am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i n
K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l år e t s g e n e r a l f o rs am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i n
Part 8. Acoustic Radiators
 Pat 8 Acoustic Radiatos Sphical Wavs Oscillating sphical cavity, a va adius of th oscillating sphical cavity vlocity amplitud of th cavity oscillation a) oscillating cavity b) point souc ( a > λ
Pat 8 Acoustic Radiatos Sphical Wavs Oscillating sphical cavity, a va adius of th oscillating sphical cavity vlocity amplitud of th cavity oscillation a) oscillating cavity b) point souc ( a > λ
EGENSKAPER ANVENDELSE. Technical data sheet SBE - BJELKESKO
 SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
TMA4110 Matematikk 3 Haust 2011
 Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag TMA4110 Matematikk 3 Haust 2011 Løysingsforslag Øving 2 Oppgåver frå læreboka, s. xliv-xlv 9 Me finn først fjørkonstanten k. Når
Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag TMA4110 Matematikk 3 Haust 2011 Løysingsforslag Øving 2 Oppgåver frå læreboka, s. xliv-xlv 9 Me finn først fjørkonstanten k. Når
Second Order ODE's (2P) Young Won Lim 7/1/14
 Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Ma Flerdimensjonal Analyse Øving 1
 Ma1203 - Flerdimensjonal Analyse Øving 1 Øistein Søvik Brukernavn: Oistes 23.01.2012 Oppgaver 10.1 6. Show that the triangle with verticies (1, 2, 3), (4, 0, 5) and (3, 6, 4) has a right angle. z y x Utifra
Ma1203 - Flerdimensjonal Analyse Øving 1 Øistein Søvik Brukernavn: Oistes 23.01.2012 Oppgaver 10.1 6. Show that the triangle with verticies (1, 2, 3), (4, 0, 5) and (3, 6, 4) has a right angle. z y x Utifra
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E
 I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i næ r t s am e i e rm ø t e i S am b o b o l i g s a m ei e fi n n e r s t e d t o r s d ag 3 0. 0 4. 2 0 0 9 K l. 1 8. 3 0
I N N K AL L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i næ r t s am e i e rm ø t e i S am b o b o l i g s a m ei e fi n n e r s t e d t o r s d ag 3 0. 0 4. 2 0 0 9 K l. 1 8. 3 0
I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E
 I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i n æ r t s am e i e rm øt e i S am e i e t W al d em a rs H a g e, a v h o l d e s t o rs d a g 1 8. j u n i 2 0 0 9, k l.
I N N K A L L I N G T I L O R D I N Æ R T S A M E I E R M Ø T E 2 0 0 9 O r d i n æ r t s am e i e rm øt e i S am e i e t W al d em a rs H a g e, a v h o l d e s t o rs d a g 1 8. j u n i 2 0 0 9, k l.
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Forelesning nr.13 INF 1410
 Forelesning nr.3 INF 4 Komplekse frekvenser og Laplace-transform Oversikt dagens temaer Me Mer om sinusformede signaler om komplekse frekvenser Introduksjon til Laplace-transform Løsning av kretsligninger
Forelesning nr.3 INF 4 Komplekse frekvenser og Laplace-transform Oversikt dagens temaer Me Mer om sinusformede signaler om komplekse frekvenser Introduksjon til Laplace-transform Løsning av kretsligninger
Equations fondamentales de la mécanique linéaire de la rupture
 //5 Aee A Equatios fodaetales de la écaique liéaie de la uptue A. Zeghloul MMAE appels d élasticité plae octio d Ai e vaiables coplees epésetatio des déplaceets et des cotaites Epessio du toseu des effots
//5 Aee A Equatios fodaetales de la écaique liéaie de la uptue A. Zeghloul MMAE appels d élasticité plae octio d Ai e vaiables coplees epésetatio des déplaceets et des cotaites Epessio du toseu des effots
Anbefalte oppgaver - Løsningsforslag
 Anbefalte oppgaver - Løsningsforslag Uke 6 12.6.4: Vi finner først lineariseringen i punktet (2, 2). Vi har at Lineariseringen er derfor 2x + y f x (x, y) = 24 (x 2 + xy + y 2 ) 2 2y + x f y (x, y) = 24
Anbefalte oppgaver - Løsningsforslag Uke 6 12.6.4: Vi finner først lineariseringen i punktet (2, 2). Vi har at Lineariseringen er derfor 2x + y f x (x, y) = 24 (x 2 + xy + y 2 ) 2 2y + x f y (x, y) = 24
Formelsamling Bølgefysikk Desember 2006
 Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Kommunikasjonsperm. Overvåking og undersøkelser side 1. Smerter side 2. Naturlige funksjoner, eliminasjon side 3. Sengeleie og stell side 4
 Kommunikasjonsperm Fransk Overvåking og undersøkelser side 1 Smerter side 2 Naturlige funksjoner, eliminasjon side 3 Sengeleie og stell side 4 Mat, drikke kvalme side 5 Bevegelse, syn, temperatur side
Kommunikasjonsperm Fransk Overvåking og undersøkelser side 1 Smerter side 2 Naturlige funksjoner, eliminasjon side 3 Sengeleie og stell side 4 Mat, drikke kvalme side 5 Bevegelse, syn, temperatur side
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
m15/1/aynor/hp2/nor/tz0/xx Monday 11 May 2015 (morning) Lundi 11 mai 2015 (matin) Lunes 11 de mayo de 2015 (mañana) 2 hours / 2 heures / 2 horas
 m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
TFY4108 Fysikk: Løysing kontinuasjonseksamen 13. aug. 2014
 TFY48 Fysikk: Løysing kontinuasjonseksamen 3. aug. 4 Oppgåve (a) Reknar først ut venstresida av TUSL. Sidan bølgjefunksjonen i dette tilfellet er uavhengig av θ og φ, forsvinn ledda som involverer deriverte
TFY48 Fysikk: Løysing kontinuasjonseksamen 3. aug. 4 Oppgåve (a) Reknar først ut venstresida av TUSL. Sidan bølgjefunksjonen i dette tilfellet er uavhengig av θ og φ, forsvinn ledda som involverer deriverte
1 OA i = f. OA o. 1 < 1 OA o. f 1. O 2 A i O 2 A 1 = = f 2 O 2 A i. f 2O 2 A i 5 `c mffl `a vfle c O 2 A i = 20 `c mffl `eˇt f 2 = 20 `c mffl
 . B L`affl r`e l åtˇi`o nffl `d`e `c o n jˇu`g åi sfi`o nffl `d`o n n`e OA i = + f P`o u rffl u n`e l e n tˇi l l e m i n`c e `c o n vfleˇr`g e n t e, < f `d`o n`c L i m`àg e `eṡfi t r`é e l l e. f > 0.
. B L`affl r`e l åtˇi`o nffl `d`e `c o n jˇu`g åi sfi`o nffl `d`o n n`e OA i = + f P`o u rffl u n`e l e n tˇi l l e m i n`c e `c o n vfleˇr`g e n t e, < f `d`o n`c L i m`àg e `eṡfi t r`é e l l e. f > 0.
EKSAMEN BOKMÅL STEMMER. DATO: TID: OPPG. SIDER: VEDLEGG: 3 desember :00-13: FAGKODE: IR Matematikk 1
 EKSAMEN BOKMÅL DATO: TID: OPPG. SIDER: VEDLEGG: 3 desember 15 9:-13: FAGKODE: FAGNAVN: IR151 Matematikk 1 HJELPEMIDLER: Del 1: kl 9.-11. Ingen Del : kl 11.-13. Lommeregner Lærebok etter fritt valg Matematisk
EKSAMEN BOKMÅL DATO: TID: OPPG. SIDER: VEDLEGG: 3 desember 15 9:-13: FAGKODE: FAGNAVN: IR151 Matematikk 1 HJELPEMIDLER: Del 1: kl 9.-11. Ingen Del : kl 11.-13. Lommeregner Lærebok etter fritt valg Matematisk
Integralsatser: Green, Stokes og Gauss
 Kapittel 7 Integralsatser: Green, tokes og Gauss Oppgave 1 Vi har gitt strømfeltet v = ωyi+ωxj der ω er en konstant. a) trømfarten: v = ω 2 y 2 +ω 2 x 2 = ωr, r = x 2 +y 2. Langs sirkelen r 2 = x 2 +y
Kapittel 7 Integralsatser: Green, tokes og Gauss Oppgave 1 Vi har gitt strømfeltet v = ωyi+ωxj der ω er en konstant. a) trømfarten: v = ω 2 y 2 +ω 2 x 2 = ωr, r = x 2 +y 2. Langs sirkelen r 2 = x 2 +y
Løsning av utvalgte øvingsoppgaver til Sigma R2 kapittel 5
 Løsning av utvalgte øvingsoppgaver til Sigma R kapittel 5 5.5 Ce kx y = kce kx Vi setter inn i y + ky og ser om vi får 0: 5.5 ax + a y = ax Vi setter inn i y 5.54 kce kx + k Ce kx = 0 x x + y: ax x(ax
Løsning av utvalgte øvingsoppgaver til Sigma R kapittel 5 5.5 Ce kx y = kce kx Vi setter inn i y + ky og ser om vi får 0: 5.5 ax + a y = ax Vi setter inn i y 5.54 kce kx + k Ce kx = 0 x x + y: ax x(ax
Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with.
![Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with. Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with.](/thumbs/80/81672304.jpg) Solutions #1 1. a Show that the path γ : [, π] R 3 defined by γt : cost ı sint j sint k lies on the surface z xy. b valuate y 3 cosx dx siny z dy xdz where is the closed curve parametrized by γ. Solution.
Solutions #1 1. a Show that the path γ : [, π] R 3 defined by γt : cost ı sint j sint k lies on the surface z xy. b valuate y 3 cosx dx siny z dy xdz where is the closed curve parametrized by γ. Solution.
Matematik, LTH Kontinuerliga system vt Formelsamling. q t. + j = k. u t. (Allmännare ρ 2 u. t2 Svängningar i gaser (ljud) t 2 c2 2 u
 Matematik, LH Kontinuerliga system vt 7 Formelsamling Formelsamligen utgör bara ett stöd för minnet. Beteckningar förklaras sålunda ej. Ej heller anges förutsättningar för formlernas giltighet. Fysikaliska
Matematik, LH Kontinuerliga system vt 7 Formelsamling Formelsamligen utgör bara ett stöd för minnet. Beteckningar förklaras sålunda ej. Ej heller anges förutsättningar för formlernas giltighet. Fysikaliska
v(t) = r (t) = (2, 2t) v(t) = t 2 T(t) = 1 v(t) v(t) = (1 + t 2 ), t 2 (1 + t 2 ) t = 2(1 + t 2 ) 3/2.
 NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
S T Y R E T G J Ø R O P P M E R K S O M P Å A T D Ø R E N E S T E N G E S K L
 K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r! D u h o l d e r n å i n nk a l l i n g e n t i l å r e t s g e n e r a l f o r s am l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n i
K j æ r e b e b o e r!
 K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l å r e t s g e n e r a l f o r s a m l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n
K j æ r e b e b o e r! D u h o l d e r n å i n n k a l l i n g e n t i l å r e t s g e n e r a l f o r s a m l i n g i h å n d e n. D e n i n n e h o l d e r b o r e t t s l a g et s å r s b e r e t n
EKSAMENSOPPGAVE. Vil det bli gått oppklaringsrunde i eksamenslokalet? Svar: JA Hvis JA: ca. kl.10:00 og 12:00
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: MAT-1003 Kalkulus 3 Dato: Tirsdag 1.1.017 Klokkeslett: 09:00-13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Pedersen et al.: Teknisk
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: MAT-1003 Kalkulus 3 Dato: Tirsdag 1.1.017 Klokkeslett: 09:00-13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Pedersen et al.: Teknisk
31-VF1210WH-127. Vanity Meuble-lavabo. Porcelain top VT-SQ mm. 1194mm. 845mm. Tools You Will Need - Outils Requis. 465mm. 1215mm.
 Porcelain top VT-SQ207 3-VF20WH-27 25mm Vanity Meuble-lavabo 465mm 20mm 456mm 94mm 845mm Tools You Will Need - Outils Requis Screwdriver Tournevis Pencil Crayon Silicone Silicone Rev. Dec, 208 Replacement
Porcelain top VT-SQ207 3-VF20WH-27 25mm Vanity Meuble-lavabo 465mm 20mm 456mm 94mm 845mm Tools You Will Need - Outils Requis Screwdriver Tournevis Pencil Crayon Silicone Silicone Rev. Dec, 208 Replacement
BACCALAURÉAT GÉNÉRAL
 Session 2018 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU MERCREDI 20 JUIN 2018 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire
Session 2018 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU MERCREDI 20 JUIN 2018 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET, INSTITUTT FOR FYSIKK. Utarbeidet av: Jon Andreas Støvneng
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET, INSTITUTT FOR FYSIKK Utarbeidet av: Jon Andreas Støvneng (jon.stovneng@ntnu.no) LØSNINGSFORSLAG (8 SIDER) TIL EKSAMEN I FY100 og TFY4160 BØLGEFYSIKK Fredag
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET, INSTITUTT FOR FYSIKK Utarbeidet av: Jon Andreas Støvneng (jon.stovneng@ntnu.no) LØSNINGSFORSLAG (8 SIDER) TIL EKSAMEN I FY100 og TFY4160 BØLGEFYSIKK Fredag
Tích Vô Hướng Và Ứng Dụng
 Trần Thành Minh Phan Lưu iên - Trần Quang Nghĩa H ÌNH H Ọ 10 h ư ơng. Tích Vô Hướng Và Ứng Dụng http://www.sasangsng.cm.vn/ Save Yur Time and Mney Sharpen Yur Self-Study Skill Suit Yur Pace hương. Tích
Trần Thành Minh Phan Lưu iên - Trần Quang Nghĩa H ÌNH H Ọ 10 h ư ơng. Tích Vô Hướng Và Ứng Dụng http://www.sasangsng.cm.vn/ Save Yur Time and Mney Sharpen Yur Self-Study Skill Suit Yur Pace hương. Tích
Asymptotique des nombres de Betti, invariants l 2 et laminations
 Comment. Math. Helv. 79 (2004) 362 395 0010-2571/04/020362-34 DOI 10.1007/s00014-003-0798-1 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Asymptotique des nombres de Betti, invariants
Comment. Math. Helv. 79 (2004) 362 395 0010-2571/04/020362-34 DOI 10.1007/s00014-003-0798-1 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Asymptotique des nombres de Betti, invariants
BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN. Mardi 23 juin 2015. Langue vivante 2
 Session 2015 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Mardi 23 juin 2015 Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L Langue vivante obligatoire (LVO) Durée
Session 2015 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Mardi 23 juin 2015 Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L Langue vivante obligatoire (LVO) Durée
Anbefalte oppgaver - Løsningsforslag
 TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
TFY4104 Fysikk Eksamen 4. desember Løsningsforslag. 1) m = ρv = ρ 4πr 2 t = π g 24g. C
 TFY4104 Fysikk ksamen 4. desember 2015 Løsningsforslag 1) m = ρv = ρ 4πr 2 t = 19.32 4π 100 2 10 5 g 24g. 2) a = v 2 /r = (130 1000/3600) 2 /(300/2π)m/s 2 27m/s 2. 3) ω(4) = 0.25 (1 e 0.25 4 ) = 0.25 (1
TFY4104 Fysikk ksamen 4. desember 2015 Løsningsforslag 1) m = ρv = ρ 4πr 2 t = 19.32 4π 100 2 10 5 g 24g. 2) a = v 2 /r = (130 1000/3600) 2 /(300/2π)m/s 2 27m/s 2. 3) ω(4) = 0.25 (1 e 0.25 4 ) = 0.25 (1
Finite Elements Methods. Formulary for Prof. Estor's exam
 Finite Elements Methods Formulary for Prof. Estor's exam Finite Element Method in General One wants to obtain the equilibrium eqautions for the body, discretized by nite elements in the form M Ü + C U
Finite Elements Methods Formulary for Prof. Estor's exam Finite Element Method in General One wants to obtain the equilibrium eqautions for the body, discretized by nite elements in the form M Ü + C U
St.prp. nr. 3 ( )
 St.prp. nr. 3 (1999-200) Om samtykke til å setje i kraft ein tilleggsavtale til skatteavtalen mellom Noreg og Frankrike av 19. desember 1980 med tilleggsavtalar av 14. november 1984 og 7. april 1995, underskriven
St.prp. nr. 3 (1999-200) Om samtykke til å setje i kraft ein tilleggsavtale til skatteavtalen mellom Noreg og Frankrike av 19. desember 1980 med tilleggsavtalar av 14. november 1984 og 7. april 1995, underskriven
Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk og stil variere noe fra oppgave til oppgave.
 NTNU Institutt for matematiske fag TMA4105 Matematikk, øving 7, vår 011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk, øving 7, vår 011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Mise à jour des marges requises
 Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
Tillegg om flateintegraler
 Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
TFY4109 Fysikk Eksamen 14. desember 2015 Side 13 av 22
 TFY4109 Fysikk Eksamen 14. desember 2015 Side 13 av 22 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas
TFY4109 Fysikk Eksamen 14. desember 2015 Side 13 av 22 FORMLER: Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighetsområde og de ulike symbolenes betydning antas
REQUÊTE APPLICATION KLAGESKJEMA
 Voir Note explicative See Explanatory Note Se klageveiledningen NOR Numéro de dossier File-number Klage nr. COUR EUROPÉENNE DES DROITS DE L HOMME EUROPEAN COURT OF HUMAN RIGHTS DEN EUROPEISKE MENNESKERETTIGHETSDOMSTOL
Voir Note explicative See Explanatory Note Se klageveiledningen NOR Numéro de dossier File-number Klage nr. COUR EUROPÉENNE DES DROITS DE L HOMME EUROPEAN COURT OF HUMAN RIGHTS DEN EUROPEISKE MENNESKERETTIGHETSDOMSTOL
EKSAMEN FRA0502 Fransk II HØSTEN 2012
 Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk - EKSAMEN FRA0502 Fransk II HØSTEN 2012 Faglig kontakt under eksamen: Sophie Vauclin Tlf.: 73596873/ 93063953 Eksamensdato:
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk - EKSAMEN FRA0502 Fransk II HØSTEN 2012 Faglig kontakt under eksamen: Sophie Vauclin Tlf.: 73596873/ 93063953 Eksamensdato:
x..i» \. . ikl.r.. .v». .t I .41.
 , å _:,_.a x..i» \..v».. ikl.r...a A, f. a..4 h 4. m.41..t I A AA AVFALISROI m 15-3"- Icaatoumon I2,7m= AA o m 'n G 4.. 195.3!!! o f 8_ E I BBS E m H arrexksnvsnxs sum! 9,3,": i (783 i. ij I i- -.to F
, å _:,_.a x..i» \..v».. ikl.r...a A, f. a..4 h 4. m.41..t I A AA AVFALISROI m 15-3"- Icaatoumon I2,7m= AA o m 'n G 4.. 195.3!!! o f 8_ E I BBS E m H arrexksnvsnxs sum! 9,3,": i (783 i. ij I i- -.to F
BACCALAURÉAT GÉNÉRAL
 Session 2017 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU LUNDI 19 JUIN 2017 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire (LVO)
Session 2017 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU LUNDI 19 JUIN 2017 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire (LVO)
UDIRs eksempeloppgave høsten 2008
 UDIRs eksempeloppgave høsten 008 Løsningsskisser Del Oppgave f x cos3x x sin3x 3 cos3x 6x sin3x fx 3u, u e 4x (Produktregel og kjerneregel på cos3x.) u e 4x 4 (Kjerneregel enda en gang...) d) f x 6uu 6u4e
UDIRs eksempeloppgave høsten 008 Løsningsskisser Del Oppgave f x cos3x x sin3x 3 cos3x 6x sin3x fx 3u, u e 4x (Produktregel og kjerneregel på cos3x.) u e 4x 4 (Kjerneregel enda en gang...) d) f x 6uu 6u4e
Sommaire. Montre MOVETIME Family Aperçu de la montre... 1 Touche Marche-Arrêt Retrait des bracelets Résistance à l eau...
 Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
a 2 x 2 dy dx = e r r dr dθ =
 NTNU Institutt for matematiske fag TMA4 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk
NTNU Institutt for matematiske fag TMA4 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Korreksjoner til fasit, 2. utgave
 Korreksjoner til fasit,. utgave Kapittel. Oppgave.. a): / Oppgave.. e):.887, 0.58 Oppgave..9: sin00πt). + ) x Oppgave.7.5 c): ln for 0 < x. x Oppgave.8.0: Uttrykket for a + b) 7 skal være a + b) 7 = a
Korreksjoner til fasit,. utgave Kapittel. Oppgave.. a): / Oppgave.. e):.887, 0.58 Oppgave..9: sin00πt). + ) x Oppgave.7.5 c): ln for 0 < x. x Oppgave.8.0: Uttrykket for a + b) 7 skal være a + b) 7 = a
Løsninger til forkursstartoppgaver
 Løsninger til forkursstartoppgaver Prosent: Oppgave 1. Prisforskjell er 20. 20 100 Kylling er da =66 2 prosent dyrere. 30 3 Vi beregner hvor mange prosent 20 er av 30. Kylling er også 20 100 =40 prosent
Løsninger til forkursstartoppgaver Prosent: Oppgave 1. Prisforskjell er 20. 20 100 Kylling er da =66 2 prosent dyrere. 30 3 Vi beregner hvor mange prosent 20 er av 30. Kylling er også 20 100 =40 prosent
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK Mandag 10. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
EKSAMEN I FAG SIF4002 FYSIKK. Mandag 5. mai 2003 Tid: Sensur uke 23.
 side 1 av 5 (bokmål) NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET, INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Institutt for fysikk, Gløshaugen Professor Arnljot Elgsæter, 73940078 EKSAMEN I
side 1 av 5 (bokmål) NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET, INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Institutt for fysikk, Gløshaugen Professor Arnljot Elgsæter, 73940078 EKSAMEN I
Integralsatser: Green, Stokes og Gauss
 Kapittel 7 Integralsatser: Green, tokes og Gauss Oppgave 1 Vi har gitt strømfeltet v ωyi+ωxj der ω er en konstant. a) trømfarten: v ω 2 y 2 +ω 2 x 2 ωr, r x 2 +y 2. Langs sirkelen r 2 x 2 +y 2 er r konstant
Kapittel 7 Integralsatser: Green, tokes og Gauss Oppgave 1 Vi har gitt strømfeltet v ωyi+ωxj der ω er en konstant. a) trømfarten: v ω 2 y 2 +ω 2 x 2 ωr, r x 2 +y 2. Langs sirkelen r 2 x 2 +y 2 er r konstant
Eksamensoppgave i TMA4135 Matematikk 4D
 Institutt for matematiske fag Eksamensoppgave i TMA4135 Matematikk 4D Faglig kontakt under eksamen: Gunnar Taraldsen Tlf: 46432506 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4135 Matematikk 4D Faglig kontakt under eksamen: Gunnar Taraldsen Tlf: 46432506 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
(ii) x = 0or 4. (ix) x = or 3. (xii) x = or. (vi) x = 4. (xiv) x = Exercise (i) ( x 3) 8. (iii) ( 3q. (iii) 3( x + 2) 16.
 Cambridge International A and AS Level Mathematics Pure Mathematics Practice Book Universit of Cambridge International Eaminations bears no responsibilit for the eample answers to questions taken from
Cambridge International A and AS Level Mathematics Pure Mathematics Practice Book Universit of Cambridge International Eaminations bears no responsibilit for the eample answers to questions taken from
LØSNINGSFORSLAG TIL EKSAMEN I FAGET 5005/7 MATEMATIKK 2 1. august der k er et vilkårlig heltall. Det gir
 LØNINGFOLAG IL EKAMEN I FAGE 55/7 MAEMAIKK. august Oppgave. (i Ja. (ii Ja. (iii Nei. Alternativt: (i Ja. (ii Ja. (iii Ja. Oppgave. curlf (x, y F i j k (x, y / x / y / z e y + ye x +x xe y + e x + Altså
LØNINGFOLAG IL EKAMEN I FAGE 55/7 MAEMAIKK. august Oppgave. (i Ja. (ii Ja. (iii Nei. Alternativt: (i Ja. (ii Ja. (iii Ja. Oppgave. curlf (x, y F i j k (x, y / x / y / z e y + ye x +x xe y + e x + Altså
Gradient. Masahiro Yamamoto. last update on February 29, 2012 (1) (2) (3) (4) (5)
 Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill
Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill

 LIBER BVEL MAGI SVB FIGVRÂ I $
LIBER BVEL MAGI SVB FIGVRÂ I $