Skalarfelt og kvantefluktuasjoner
|
|
|
- Erna Clausen
- 4 år siden
- Visninger:
Transkript
1 Sklrfelt og kvntefluktusjoner I forrige sett v notter regnet vi ut kvntefluktusjonene i tensorperturbsjonen h. Sklrfeltet φ spilte d bre en pssiv rolle ved å drive universets ekspnsjon. Nå skl vi regne på kvntefluktusjonene i sklrfeltet. D oppstår en kompliksjon ved t disse fluktusjonene fungerer som kilde til de sklre perturbsjonene i metrikken, Ψ og Φ. Vi må finne ut hvordn vi skl håndtere denne situsjonen. Strtegien vår vil være: Sette opp ligningen som beskriver tidsutviklingen v en Fouriermode v sklrfeltperturbsjon δφ. Vi tr hensyn til t Φ og Ψ kn være forskjellige fr null. Vise t Ψ og Φ er neglisjerbre for de tidsrommene vi er interesserte i. Finne en bevrt størrelse som inneholder både δφ og Ψ. Vise t i inflsjonsfsen er denne proporsjonl med δφ, mens den etter inflsjon er proporsjonl med Ψ. Regne ut fluktusjonene δφ, oversette disse til fluktusjoner i Ψ etter inflsjon. Bevegelsesligning for sklrfeltperturbsjoner Bevegelsesligningen for det uperturberte sklrfeltet fnt vi fr ν = -komponenten v T µ ν:µ =. Nå bruker vi denne betingelsen igjen, men med den perturberte energi-impulstensoren. Husk t vi bre skl regne til første orden i perturbsjonene. Ligningen vi tr utgngspunkt i er T µ,µ + Γα αµ T α Γα µ T µ α =. Vi vil i det følgende også benytte oss v t Φ Ψ, som vi fnt i diskusjonen v initilbetingelsene. Tidligere regnet vi ut Christoffelsymbolene, og for klrhetens skyld gjengir jeg resulttene her (i Fourierrommet): Γ = Ψ, Γ i = Γ i = ik i Ψ Γ ij = δ ij 2 (H + 4HΨ Ψ, ) Γ i = iki 2 Ψ Γ i j = Γ i j = δ ij (H Ψ, ) Vi skriver ut ligningen i litt mer detlj: Γ i jk = iψ(δ ij k k + δ ik k j δ jk k i ). δt, + ik i δt i + Γ µ µ T + Γ µ iµ T i Γ µt µ Γi µt µ i =.
2 Ledd for ledd finner vi: Γ µ µ T = (Γ + Γ i i)t = [Ψ, + i δ ii (H Ψ, )]T = (Ψ, + 3H 3Ψ, = 2Ψ, + 3H. Γ µ iµ T i = (Γ i + j Γ j ij )T i = [ik i Ψ + j ( iψ)(δ ji k j + δ jj k i δ ij k j )]T i = (ik i Ψ 3ik i Ψ)T i = 2ik iψt i. Γ µ T µ = Γ T Γ i T i = Ψ, T ik i ΨT i. Γ i µ T µ i = Γ i T i Γi j T j i = iki 2 ΨT i ij δ ij (H Ψ, )T j i = iki 2 ΨT i (H Ψ, )T i i. Siden vi bre skl regne til første orden, må vi sette inn nullteordensutrykket for energi-impulstensoren i lle ledd der det forekommer en fktor Ψ. Det gir oss Nå er = δt + ik i δt i + 3HδT 2Ψ, T () 2ik i ΨT ()i Ψ, T () ik i ΨT ()i iki () ΨT 2 i HδTi i + Ψ ()i i. T () i = g ν Ψ (),ν Ψ(),i =, siden ψ () bre er en funksjon v tiden, og T ()i = g i g (ψ (), )2 + g i siden g i =. Dermed forenkler ligningen seg til [ 2 (φ(), )2 V (φ () ) ] =, δt + ik i δt i + 3HδT HδT i i = 3Ψ, T () Ψ, T ()i i. Siden T ()µ ν er energi-impulstensoren for en perfekt væske hr vi t T () og T ()i i = i T ()i i = i p = 3p. Dermed: δt + ik i δt i + 3HδT HδT i i = 3(ρ + p) Ψ. 2 = ρ
3 Nå ville det være veldig prktisk om vi kunne se bort i fr Ψ. Hvis vi skl kunne gjøre det, så må høyresiden være mindre enn hvert enkelt ledd på venstresiden. Og slik er det fktisk. Vi kn vise det for det første leddet på høyresiden. Altså: min påstnd er t Ψ δt p + ρ. L oss t utgngspunkt i en ligning vi utledet tidligere: ( ) k 2 Φ + 3ȧ Φ Ψȧ = 4πG 2 δt. Vi setter inn ȧ/ = H og Φ = Ψ. Det gir k 2 Ψ + 3H( Ψ + HΨ) = 4πG 2 δt. Moder som er i ferd med å krysse horisonten er spesielt interessnte, fordi etter t de hr gjort det kn ikke kusle prosesser påvirke dem. For slike moder gjelder k H, og d er k 2 Ψ 2 H 2 Ψ. For t ligningen over skl være oppfylt må vi d h t 2 H 2 Ψ G 2 δt, dvs. Ψ GδT H 2. Men fr Friedmnnligningene hr vi t H 2 Gρ, så Ψ δt ρ = p + ρ ( ) δt. ρ p + ρ Dodelson innfører slow-roll-prmeteren ǫ ved ǫ = d dt H = Ḣ H 2, og denne er liten mens inflsjon pågår. Nå hr vi t [ d dt H = dh H 2 dt = H 2 ( d 2 dt = 3 8πGρ [ 8πGρ 3 ) 2 + ] 4πG (ρ + 3p) 3 = + 3(ρ + p) (ρ + 3p) =, 2ρ 2ρ der jeg hr brukt Friedmnnligningene flittig. Dette gir oss t ρ + p ρ = 2 3 ǫ, ] d 2 dt 2 3
4 og dermed ( ) δt Ψ ǫ δt p + ρ p + ρ, fordi ǫ, ihvertfll så lenge inflsjon pågår. Tilsvrende kn mn vise t høyresiden er neglisjerbr i forhold til de øvrige leddene på venstresiden (merk t dette ikke ligger noen politiske føringer på denne fremgngsmåten. Du kn godt skrive opp ligningen speilvendt og vise t leddene på høyresiden dominerer venstresiden, dersom du føler deg mer komfortbel med det.) Det som gjenstår nå er å regne ut førsteordensperturbsjonen i energiimpulstensoren når vi hr φ( x, t) = φ () (t) + δφ( x, t). Vi finner t [ ] T i = g iν φ,ν φ, g i 2 gµν φ,µ φ,ν + V (φ) = 2 δ iνφ,ν φ, = 2 φ,iφ, = 3 δφ,iφ () iki φ () δφ, der jeg i siste overgng hr gått over i Fourierrommet. Videre: [ ] T = g ν φ,ν φ, g 2 gµν φ,µ φ,ν + V (φ) slik t Til slutt: 3 = (φ, ) 2 2 gµν φ,µ φ,ν V (φ) = (φ, ) (φ,) φ,iφ,i V (φ) = 2 (φ(), + δφ,) δφ,iδφ,i V (φ () + δφ) = 2 (φ(), )2 φ (), δφ, V (φ () ) V (φ () )δφ = 2 (φ(), )2 V (φ () ) φ (), δφ, V δφ, δt = φ(), δφ, V φ δφ = () δφ V δφ. T i j 2 [ ] = g iν φ,ν φ,j gj i 2 gµν φ,µ φ,ν + V (φ) [ ] = g ii φ,i φ,j gj i 2 gµν φ,µ φ,ν + V (φ). Det første leddet ser vi vil være v ndre orden i perturbsjonene. Dessuten er gj i = δ ij, så [ Tj i = δ ij 2 φ,φ, + ] 2 2 φ,iφ,i + V (φ) 4
5 slik t [ = δ ij ] 2 (φ(), )2 φ (), δφ(), + V (φ() ) + V δφ = δ ij [ 2 (φ(), )2 V ] + δ ij (φ (), δφ, V δφ), ( δtj i = δ ij [φ (), δφ, V φ δφ] = δ () ) δφ ij V δφ. D blir ligningen vår ( ) ( η + 3H φ () δφ ) 2 V δφ +ik iiki 3 φ () δφ H i Vi skriver ut lle leddene: = φ δφ 3 φ δφ ȧ φ 4 δφ V φδφ V δφ 3H φ δφ 2 3HV δφ k2 φδφ 3 3H φ δφ 2 + 3HV, δφ og etter multipliksjon med 3 gir dette eller (bruker ȧ/ = H = φ δφ φ δφ + 2ȧ φ δφ 2 V φδφ 2 V δφ 3H φ δφ k 2 φδφ 3H φ δφ, φ δφ + δφ( φ 4H φ 2 V ) + δφ( 2 V φ k 2 φ) =. 2 ( φ δ () ) δφ ij V δφ =. Mn kn vise t dersom slow-roll-betingelsene er oppfylt, så er 2 V k 2, så dette leddet kn neglisjeres. Videre hr vi fr nullteordensligningen t som gir og dermed får vi t og endelig φ + 2H φ + 2 V =, φ 4H φ 2 V = 2H φ, φδ φ 2H φδ φ k 2 φδφ =, δ φ + 2Hδ φ + k 2 δφ =. Som en test på din helse kn du smmenligne denne ligningen med ligningen for tensorperturbsjonene: ḧ + 2Hḣ + k2 h =. 2 5
6 Dersom du ikke ser t disse ligningene er identiske, bør du oppsøke lege. At de er identiske betyr t kvntiseringen og beregningen v styrkespekteret blir nøyktig mken. Den eneste forskjellen er normliseringen v h, som gir en fktor 6πG i forskjell. Dermed får vi P δ φ = H2 2k 3. Nå hr vi vist t grvitsjonspotensilet Ψ = Φ er neglisjerbrt i inflsjonsfsen. Dette hr vi så brukt til å beregne spekteret v kvntefluktusjoner i sklrfeltet φ. Men vi er ennå ikke helt i mål, for vi må finne ut hv som skjer med disse fluktusjonene når inflsjonsfsen er over. Dersom fluktusjonene også blir borte er vi ikke kommet noe lenger i vårt forsøk på å generere initilbetingelsene for tetthetsfluktusjoner og temperturnisotropier. Heldigvis er ikke verden så slem. Helt umotivert innfører vi nå størrelsen ζ = ik iδt i H k 2 (ρ + p) Ψ. For moder som er innenfor horisonten eller kkurt hr forltt den er Ψ neglisjerbr. Videre er ρ + p = ( φ (),) 2 () φ = 2, og D får vi t T i [ ] = g ν φ,ν φ,i gi 2 gµν φ,µ φ,ν + V (φ) = g φ (), ik φ iδφ = () ik i δφ. φ () ik iδφ ( ik i ζ = ( k 2 φ() = k2 φ() δφh (k φ () ) 2 = Hδφ φ (). ) 2 ) H Med ndre ord: rundt tiden d en mode med bølgetll k krysser horisonten er ζ bestemt v sklrfeltet φ. To spørsmål gjenstår: hv skjer med ζ etter inflsjon, og hvorfor skylle vi bry oss om det? For å få til den riktige drmtiske stigningen begynner jeg med det første spørsmålet. Vi befinner oss i epoken d 6
7 inflsjon nettopp vr unngjort. Universet vr d strålingsdominert, og energiimpulstensoren vr d dominert v fotonene. Vi hr d t T ν µ d 3 p P µ P ν = 2 (2π) 3 f( x, p, t), P der jeg tidligere hr vist t vi kn bruke de uperturberte uttrykkene for lle de kinemtiske størrelsene som inngår. D hr vi t Ti d 3 p P P i = 2 (2π) 3 P f d 3 p = 2 (2π) 3 pˆp if. Vi husker t den perturberte fordelingsfunksjonen for fotonene er f = f () p f() p Θ. Førsteordensperturbsjonen til energi-impulstensoren blir d δti d 3 p = 2 (2π) 3 pˆp ip f() p Θ, og d får vi t ik i δti = 2ki(2π) = 4πk ( i) 2 = 8πkΘ ( 4) = 4kΘ 2 4π = 4kΘ 2 = 4kρ r Θ. Smtidig er ρ + p = 4ρ r /3, så dµˆk iˆp i Θ dp f () (2π) 3 p p4 dµ {[p 2 µθ 4 f () ] 4 d 3 p (2π) 3 pf() dpp 2 (2π) 3 pf() dpp 2 (2π) 3 pf() ζ = 4kρ rθ H 4 3 ρ Ψ = 3HΘ Ψ. rk 2 k } dp (2π) 3 p3 f () For å komme helt i mål, må vi reltere dipolen til Ψ. L oss se på ligningene for hstighetene v og v b : v + ȧ v = ikψ v b + ȧ v b = ikψ + τ R [v b + 3iΘ ]. 7
8 Under diskusjonen v initilbetingelser fnt vi t Φ og Ψ til å begynne med er konstnte. Videre er vi i den strålingsdominerte fsen der η og ȧ/ = /η = H. D får vi t v + v = ikψ = konstnt, η dvs. η v + v = d (ηv) = ikψ. dη For η = bør vi h v =, og siden Ψ er konstnt kn vi lett integrere opp denne ligningen: ηv == ikψ 2 η2, slik t v = ikψ 2 η = ikψ 2H. I de tidligste fsene spres fotonene hyppig på bryonene, og d er τ stor. Til å begynne med vil derfor leddet proporsjonlt med τ dominere i ligningen for v b. Det vil føre til t v b øker rskt til å begynne med, men bre inntil uttrykket i prentesen etter τ/r blir lik null. D er v b = 3iΘ, og når dette hr skjedd vil v b følge smme ligning som v. Vi hr derfor t v = v b = 3iΘ, og følgelig Det gir endelig ζ = 3H k Θ = kψ 6H. k 6H Ψ Ψ = 3 2 Ψ. Dermed hr vi vist t ζ = Hδφ/ φ () for en mode som er i ferd med å krysse horisonten i inflsjonsfsen, og t ζ = 3Ψ/2 etter inflsjon. Dersom vi nå kn vise t ζ er en bevrt størrelse, dvs. t den hr smme verdi før og etter inflsjon, så kn vi reltere Ψ = Φ til sklrfeltfluktusjonene δφ. Å vise t ζ er bevrt innebærer litt rbeid, men det er vi jo vnt til. Vi strter med ligningen vi utledet tidligere: δt + ik iδt i + 3HδT HδT i i = 3(p + ρ) Ψ. Det er først og fremst store moder (dvs moder der k/h ) vi er interesserte i. Ser vi først på δt i = iki 3 φδφ, så hr vi t ik i δt i = k2 3 φδφ k 2, og d kn dette leddet neglisjeres. Dermed blir ligningen δt + 3HδT HδT i i = 3(p + ρ) Ψ. 8
9 Vi må få inn ζ på en eller nnen måte, og det kn vi gjøre ved å reltere den til Ψ. Vi fnt tidligere t ζ = 3Ψ/2 etter inflsjon, men nå trenger vi imidlertid et uttrykk som er gyldig for lle tider siden vi skl vise t ζ er bevrt. Vi får imidlertid lov til å nt t vi ser på store skler. Grvitsjonspotensilet Ψ inngår som et v leddene i ζ, så vi er godt i gng. Jeg skl nå vise t det ndre leddet kn forenkles til ik i δti H k 2 = 3 δt. For å vise dette trenger vi et pr ligninger. Den ene hr vi sett før, k 2 Φ + 3ȧ ( ) φ Ψȧ = 4πG 2 δt, som kommer fr -komponenten v den perturberte Einsteinligningen. Vi vil trenge en ligning til som kommer fr i-komponenten. Den hr vi ikke regnet ut før, så det betyr en ny runde med indeksgymnstikk. Vi merker oss først t G i = g ν R νi = g G i [ = ( + 2Ψ) R i ] 2 g ir = ( + 2Ψ)R i, og nå vil jubelen ingen ende t, for lt vi trenger å gjøre er å regne ut R i. Vi blir knskje litt deprimerte når vi innser t R i = Γ α i,α Γ α α,i + Γ α βαγ β i Γα βiγ β α, men så blir vi veldig glde når vi kommer på t vi llerede hr regnet ut lle Christoffelsymbolene vi tregner og t det egentlig er veldig gøy med både derivsjon og summsjon. Vi regner ut de enkelte leddene: Γ α i,α = Γ i, + Γj i,j = ik i Ψ, + x j Γj i j = ik i Ψ, + x j δ ji(h + Φ, ) j = ik i Ψ, + ik i Φ,. Γ α α,i = Γ,i + Γj j,i = ik i Ψ, + x i δ jj(h + Φ, ) j = ik i Ψ, + 3ik i Φ,. 9
10 Γ α βα Γβ i = Γ β Γβ i + Γj βj Γβ i = Γ Γ i + Γ kγ k i + Γ j j Γ i + Γ j kj Γk i = ik k Ψδ ki H + ik i Ψδ jj H + iφ[δ jj k k + δ jk k j δ kj k j ]δ ki H k j k j = ik i HΨ + 3ik i HΨ + iφδ jj k k δ ki H k j = 4ik i HΨ + 3ik i HΦ. Γ α βi Γβ α = Γ βi Γβ + Γj βi Γβ j D får vi Men d blir = Γ i Γ + Γ ki Γk + Γj i Γ j + Γj ki Γk j = ik k 2 Ψδ ki 2 H + ik j Ψδ ij + iφ(δ ij k k + δ jk k i δ ik k j )δ kj H k j k j = ik i HΨ + ik i HΨ + ihφ (δ ij δ kj k k + δ jk δ kj k i δ ik δ kj k j ) k j = 2ik i HΨ + ihφ(k i + 3k i k i ) = 2ik i HΨ 3ik i HΦ. R i = ik i Ψ, + ik i Φ, ik i Ψ, 3ik i Φ, + 4ik i HΨ + 3ik i HΦ 2ik i HΨ 3ik i HΨ = 2ik i Φ, + 2ik i HΨ = 2ik i (Φ, HΨ) ( ) Φ = 2ik i HΨ. G i = ( + 2Ψ)R i = ( + 2Ψ)( 2ik i ) ( ) Φ = 2ik i HΨ = δg i, ( ) Φ HΨ fordi det ikke er noe nullteordens bidrg. Dermed gir δg i = 8πGδT i ( ) Φ 2ik i HΨ = 8πGδTi. Ved å sette inn Φ = Ψ får vi d de to ligningene ( ) k 2 Ψ + 3ȧ Ψ Ψȧ = 4πG 2 δt ( 2ik i / Ψ ) HΨ = 8πGδTi.
11 Vi multipliserer den ndre ligningen med ik i og summerer over i: ( 2ik i ik i Ψ ) HΨ = 8πGik i δti, som gir ( ) Ψ k 2 + HΨ = 4πGik i δti. Setter vi inn ȧ/ = H i den første ligningen får vi Men den ndre ligningen gir k 2 Ψ 3H( Ψ + HΨ) = 4πG 2 δt. k 2 ( Ψ + HΨ) = 4πGik i δt i, så k 2 Ψ 3H 4πG k 2 ik i δti = 4πG 2 δt. Fordi vi ser på store skler er det første leddet på venstresiden neglisjerbrt. Dermed får vi ik i δti H k 2 ( 3 2 4πG) = 4πG 2 δt, som gir ik i δti H k 2 = 3 δt. På store skler hr vi derfor t som gjør t vi kn skrive Ψ som δt ζ = 3 ρ + p Ψ, δt Ψ = ζ 3 ρ + p. Vi setter dette inn i ligningen vi strtet med: δt + 3HδT HδTi i = 3(ρ + p) [ ζ δt ] 3 ρ + p Dermed = 3(p + ρ) ζ + (p + ρ) = 3(p + ρ) ζ + δt 3HδT HδT i i = 3(p + ρ) ζ + (p + ρ)δt ( δt p + ρ + (p ρ )δt ) p + ρ, (ρ + p).
12 slik t 3(p + ρ) ζ [ = δt 3H (p + ρ) p + ρ [ = δt 3H + ( ρ ρ + p + p ] HδT i i )] HδT i i. Siden ρ og p er uperturbert trykk og uperturbert energitetthet oppfyller de dvs. Dette setter vi inn: 3(ρ + p) ζ ρ = δt = δt = 3H(ρ + p), ρ ρ + p = 3H. ( 3H 3H + ρ + p p ρ + p HδT i i. ) p HδTi i Og endelig får vi et uttrykk for ζ/ på stor skl: [ ζ = 3(ρ + p) 2 = 3(ρ + p) 2 H(ρ + p)δt i i δt ( ρ 3 δt i i p δt Høyresiden v denne ligningen er proporsjonl med δt i i 3 + p ρ δt. ] p ). I det uperturberte tilfellet er T i i /3 = p og T = ρ, så δρ = δt og δp = δt i i /3. Dermed kn vi skrive uttrykket over som δp δρ p ρ =, for dibtiske perturbsjoner (pr. def.) Det er denne type perturbsjoner som er mest interessnte kosmologisk sett. Dermed hr vi vist t på store skler og for dibtiske perturbsjoner er ζ =, og dermed er ζ en bevrt størrelse. L oss håpe t det vr verdt bryet å vise dette. 2
13 Og det vr det! Nå er det nemlig plnkekjøring å finne styrkespekteret v fluktusjoner i Ψ. Siden ζ er bevrt må vi h ( ) 3 2 Ψ Hδφ etter =. φ () slik t D må vi også h Ψ etter = 2 3 H ( δφ φ () ) k=h k=h ( ) 2 P Ψ (k) = 4 H P 9 φ () δφ(k = H) ( ) 2 ( = 4 ) H H 2 9 φ () 2k 3 k=h ( ) 2 2 H 2 = 9k 3. φ () k=h Fr definisjonen v slow-rollprmeteren ǫ hr vi ǫ = d ( ) = Ḣ dt H H 2.. Vi hr også ρ ( ) 2 φ = 3H(ρ + p) = 3H (), som er ekvivlent med ( ) ρ 2 η = 3H φ (), og med H ρ η = 3H2 ( φ () ) 2 ( ) 2 φ = 8πGρ (), der vi hr brukt Friedmnnligningen H 2 = 8πGρ/3. Dette kn vi skrive som Men vi kn også skrive 8πG( φ () ) 2 = 2 H ρ ρ η = H ρ ρ η. ρ ρ η = 8πG 3H 2 3H 2 η 8πG = H 2 H2 = 2HḢ H 2 3 = 2Ḣ H.
14 I tillegg hr vi Det kn vi sette inn over og få slik t Ḣ H = ǫh. 8πG( φ () ) 2 = 2ǫ 2 H 2, 4πG( φ () ) 2 = ǫ 2 H 2. Dette kn vi sette inn i uttrykket for P Ψ : P Ψ (k) = P Φ (k) = 8πG 9k 3 Brødrene Dl og spektrlindeksene ( ) H 2 ǫ. H=k Vi hr nå vist t dersom en inflsjonsfse drevet v et sklrfelt virkelig fnt sted i det tidlige univers, så vil en nødvendig konsekvens v dette være t det lges grvitsjonsbølger (dvs. tensorperturbsjoner, h) og fluktusjoner i grvitsjonspotensilet Φ. De siste fluktusjonene fungerer, hr vi sett, som en kilde til tetthetsperturbsjoner og temperturnisotropier. Med ndre ord: dersom inflsjon fnt sted, så hr vi nå i grove trekk forklrt hvordn vi ble til. Muligens en omstendelig forklring, men jeg vil tro t mnge foreldre fktisk ville foretrekke å fortelle denne historien når deres brn spør om hvordn de ble til. Dette kurset hr, slik jeg ser det, et stort potensile til å bli en hit blnt blyge småbrnsforeldre. Det store spørsmålet er selvfølgelig om inflsjon virkelig fnt sted. Vi så i AST422 t inflsjon løser noen vnskelige problemer i Big Bng-modeller, og nå hr vi sett t vi som en bonus kn få lget tetthetsfluktusjoner. Men t inflsjon er fint betyr ikke t det er snt. I troskp mot de vitenskpelige ideler vi er stt til å forvlte må vi finne en empirisk test for dette scenriet. Den eneste måten å gjøre det på er å måle egenskpene til perturbsjonene som inflsjon genererer, med ndre ord bestemme (illefll delvis) P Φ (k) og P h (k) ved hjelp v observsjoner. Som dere vil få se senere i kurset er ikke det så helt enkelt, siden de fleste fluktusjonene vi kn se hr gjennomgått en utvikling siden de kom nyfødt ut v inflsjonsfsen. En nnen kompliksjon er t inflsjon er mer en ide enn en modell: veldig mnge ulike modeller med ett eller flere sklrfelter kn brukes til å lge en inflsjonsfse i det veldig tidlige univers. En vnlig strtegi for å knytte forbindelsen til observsjoner er å prmetrisere fluktusjonsspektrene ved hjelp v to mplituder mplitude A T og δ H, og to såklte spektrlindekser n T og n: ( ) 8πGH 2 nt 3 P h (k) = A T k P Φ (k) = k 3 ( 8πG H 2 ) 9k 3 ǫ k=h k=h 5π ( ) n ( ) 2 k 9k 3 δh 2 Ω m. H D ( = ) 4
15 Disse definisjonene, spesielt den siste, ser litt tåpelige ut, og inneholder en funksjon som dere først vil lære om i kpittel 7, vekstfunksjonen D. Hv verre er, så finnes det ndre konvensjoner for hvordn mplitudene til de to spektrene skl defineres. Men lt dette blåser vi i nå. Hvis n T = og n = sies spektrene å være sklinvrinte. Det kommer v t d er de dimensjonsløse størrelsene k 3 P h (k) og k 3 P Φ (k) uvhengige v k. Det vi skl gjøre nå er å reltere n T og n til potensilet som infltonet beveger seg i. Vi strter med tensorfluktusjonene. Vi ser t slik t lnp h (k) = lna T + (n T 3)lnk, n T 3 = d lnp h d lnk. Men vi kn også bruke uttrykket for P h som vi beregnet, lnp h (k) = ln(8πg) 3 lnk + 2 lnh, der det her og fr nå v er underforstått t uttrykkene skl regnes ut ved k = H. Deriverer vi, få r vi d lnp h d lnk = 3 + 2d lnh d lnk. D ser vi t vi må h n T = 2 d lnh d lnk. Vi skl nå se t dersom vi ntr slow-rollinflsjon, så kn n T uttrykkes ved slowrollprmetrene. Dodelson bruker en litt uvnlig (for ikke å si veldig idiotisk) definisjon v disse. Jeg vil gå tilbke til definisjonene jeg brukte i AST422: ( V ǫ = 6πG V V η = 8πG V, der V er potensilet til sklrfeltet. Et problem her er t vi llerede hr brukt η til å betegne konform tid. Men jeg orker ikke å tenke ut et nytt nvn (δ-en til Dodelson er fullstendig tullete), og jeg hr ikke tenkt til å bruke konform tid i dette vsnittet unsett, så det burde være mulig å unngå misforståelser. En nnen ting jeg kommer til å gjøre er å betegne den homogene biten v sklrfeltet for φ, ikke φ () som tidligere. L oss først sjekke t vår gode, gmle ǫ stemmer overens med Dodelsons nye, teite ǫ så lenge vi hr slow-roll-inflsjon. Den dumme definisjonen v ǫ vr ǫ = d dt H. Under slow-roll-inflsjon gjelder ligningene ) 2 H 2 8πG 3 V 3H dφ V, dt 5
16 der V = dv/dφ. Dette kn vi sette inn i det teite uttrykket for ǫ og gjøre det finere: ǫ = dh H 2 dt = 38πG d ( 8πG dt 3 ( ) /2 3 = 8πG V ( 3 = 8πG Men fr den ndre slow-roll-ligningen hr vi t og d får vi ) /2 dv 2V /2 dt ) /2 dφ 2V 3/2 dt V. dφ dt = V 3H, ( ) /2 3 V ǫ = 8πG ( ) /2 3 (V ) 2 = 8πG 6V 3/2 ( V = 6πG V ) 2, 2V 3/2 ( V ) ( 3 8πG 3H ) /2 V /2 og utrykket er blitt slik vi ville h det. Så Dodelsons ǫ er også vår ǫ. Den ndre slow-roll-prmeteren hn bruker, δ, er imidlertid ikke helt den smme som vår η, så den vil jeg ikke snkke mere om. Vi ønsker å derivere med hensyn på lnk, og vi ønsker å gjøre det ved epoken der k = H, dvs. lnk = ln + lnh. Under slow-roll vrierer H lngsomt, og illefll mye lngsommere enn. Derfor tilnærmer vi H med en konstnt og får Slow-roll-ligningen kn skrives som d(ln k) = d(ln) = d ln dt = d dt = Hdt. dt dt 3H dφ dt = V dt = 3 H V dφ, og dermed hr vi t d d(ln k) = d H dt = V d 3H 2 dφ, 6
17 og ved å bruke t får vi H 2 = 8πG 3 V d d lnk = V d 8πG V dφ, som ltså gjelder ved epoken der k = H. Siden lnh = 2 lnv +konstnt, finner vi d t På tilsvrende vis finner vi nå n T = d lnv d lnk = V d 8πG V dφ lnv = V V 8πG V V = ( ) V 2 = 2ǫ. 8πG V n 3 = d lnp Φ d lnk = d lnh d lnk d lnǫ d lnk = 3 2ǫ 2 d d lnk ln V V, der vi i det ndre leddet hr brukt resulttet fr utregningen v n T, og i det tredje leddet hr vi brukt uttrykket for ǫ. Vi kn regne videre på dette leddet: d d lnk ln V V = d 8πG V dφ (lnv lnv ) = V ( V 8πG V V V ) V = V 8πG V + ( ) V 2 8πG V = η + 2ǫ, V der vi i den siste overgngen igjen hr brukt uttrykkene for ǫ og η. Dermed får vi n 4 = 3 2ǫ + 2η 4ǫ = 3 + 2η 6ǫ, eller, om du vil n = + 2η 6ǫ. Siden ǫ og ǫ må være små hvis vi skl h slow-roll-inflsjon, betyr det t vi forventer t spektrene for både sklr-og tensorperturbsjoner skl være nær 7
18 sklinvrinte. Men dersom sklrfeltet gjør noe interessnt i det hele ttt, vil ǫ og η være forskjellige fr null, så det burde være små vvik fr sklinvrins dersom inflsjon hr noe for seg. Vi hr ltså lært t spektrlindeksene er bestemt v ǫ og η. Disse vhenger v potensilet til sklrfeltet og dets deriverte. Ved å måle både sklr- og tensorperturbsjoner kn vi i prinsippet bestemme A T, δ H, n T og n. Fr n T og n kn vi bestemme ǫ og η. Men går vi tilbke til uttrykkene for P h og P Φ, ser vi t P h P Φ = 9ǫ. Dette forteller oss to ting: for det første t siden vi forventer t ǫ skl være liten, så vil tensormodene h en betydelige lvere mplitude enn sklrmodene. For det ndre ser vi t dersom vi kn måle begge typer moder, så hr vi også en konsistensjekk: spektrlindeksene gir ǫ og η, og d sier teorien t forholdet mellom mplitudene skl være lik 9ǫ. Dette kn vi sjekke mot det målte forholdet A T /δ H. Dersom dette ikke er lik 9ǫ er det noe glt med inflsjon. Dette høres lovende ut, men for å helle litt mlurt i begeret med en gng må jeg si t denne konsistensbetingelsen bre gjelder dersom bre ett sklrfelt hr hovednsvret for inflsjonsfsen. Det kn godt tenkes t mer enn ett felt er involvert (det er fktisk gnske populært for tiden å regne på inflsjonsmodeller med mer enn ett felt), og d går denne konsistensbetingelsen i dss. En nnen og mer prktisk utfordring er t tensormodene er små, og ingen hr sett klre tegn til t de finnes ennå. Det klreste tegnet på t de virkelig finnes får vi om vi ser såklte B-moder i polrissjonen v bkgrunnstrålingen. Dette får dere knskje vite mere om senere. Så er våre lidelser over Melodi: My wy. Synges med stor innlevelse. Og nå er enden her, vi hr beregnet lle spektr. Min venn, det vr vel gøy, personlig er jeg blitt helt hekt. Vi hr slitt og strevet trutt, men så til slutt, hr vi nådd målet. Og d, j d ser vi t lt vr verdt å tåle. For hv er en µ og en derivsjon? En Riccisklr og en kontrksjon? Når pennen er tom og hjernen blør, hever vi hodet og hr godt humør! For til slutt så koker lt ned til slow-roll-prmeeeeeeeetrene! 8
Kosmologisk perturbasjonsteori: Einsteintensoren vender tilbake
 Kosmologisk perturbsjonsteori: Einsteintensoren vender tilbke Vi hr funnet Boltzmnnligninger for fotoner, bryoner og mørk mterie. Om vi hdde ønsket det, kunne vi også stt opp ligningene for msseløse nøytrinoer.
Kosmologisk perturbsjonsteori: Einsteintensoren vender tilbke Vi hr funnet Boltzmnnligninger for fotoner, bryoner og mørk mterie. Om vi hdde ønsket det, kunne vi også stt opp ligningene for msseløse nøytrinoer.
Numerisk derivasjon og integrasjon utledning av feilestimater
 Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
Numerisk derivsjon og integrsjon utledning v feilestimter Knut Mørken 6 oktober 007 1 Innledning På forelesningen /10 brukte vi litt tid på å repetere inhomogene differensligninger og rkk dermed ikke gjennomgå
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
Bioberegninger - notat 3: Anvendelser av Newton s metode
 Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
Bioberegninger - nott 3: Anvendelser v Newton s metode 20. februr 2004 1 Euler-Lotk ligningen L oss tenke oss en populsjon bestående v individer v ulik lder. L n være mksiml lder. L m i være ntll vkom
M2, vår 2008 Funksjonslære Integrasjon
 M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
Løsningsforslag Kollokvium 1
 Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Brøkregning og likninger med teskje
 Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
Brøkregning og likninger med teskje Dette heftet gir en uformell trinn for trinn gjennomgng v grunnleggende regler for brøkregning og likninger. Dette er sto som vi i FYS 000 egentlig forventer t dere
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER:
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken n x n n= konvergerer i ( R, R), R >, med summen s(x). D gjelder: og s (x) = n n x n for hver x med x < R, s(t) dt = n= (Dette er
9.6 Tilnærminger til deriverte og integraler
 96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
96 TILNÆRMINGER TIL DERIVERTE OG INTEGRALER 169 Figur 915 Bezier-kurve med kontrollpolygon som representerer bokstven S i Postscript-fonten Times-Romn De ulike Bezier-segmentene ser du mellom kontrollpunktene
Eneboerspillet. Håvard Johnsbråten
 Håvrd Johnsråten Eneoerspillet Når vi tenker på nvendelser i mtemtikken, ser vi gjerne for oss Pytgors læresetning eller ndre formler som vi kn ruke til å eregne lengder, reler, kostnder osv. Men mer strkte
Håvrd Johnsråten Eneoerspillet Når vi tenker på nvendelser i mtemtikken, ser vi gjerne for oss Pytgors læresetning eller ndre formler som vi kn ruke til å eregne lengder, reler, kostnder osv. Men mer strkte
FY2045/TFY4250 Kvantemekanikk I, øving 10 1 ØVING 10
 FY45/TFY45 Kvntemeknikk I, - øving ØVING Mesteprten v denne øvingen går ut på å gjøre seg kjent med spinn, men øvingen inneholder også en oppgve om koherente tilstnder. Denne er en fortsettelse v oppgve
FY45/TFY45 Kvntemeknikk I, - øving ØVING Mesteprten v denne øvingen går ut på å gjøre seg kjent med spinn, men øvingen inneholder også en oppgve om koherente tilstnder. Denne er en fortsettelse v oppgve
Løsningsforslag til øving 4
 1 Oppgve 1 FY1005/TFY4165 Termisk fysikk Institutt for fysikk, NTNU åren 2015 Løsningsforslg til øving 4 For entomig gss hr vi c pm = 5R/2 og c m = 3R/2, slik t γ = C p /C = 5/3 Lngs dibten er det (pr
1 Oppgve 1 FY1005/TFY4165 Termisk fysikk Institutt for fysikk, NTNU åren 2015 Løsningsforslg til øving 4 For entomig gss hr vi c pm = 5R/2 og c m = 3R/2, slik t γ = C p /C = 5/3 Lngs dibten er det (pr
TKP4100 Strømning og varmetransport Løsningsforslag til øving 10
 TKP4 Strømning og vrmetrnsport Løsningsforslg til øving Oppgve ) Entlpi ved utløpet (5 br, ), kj/kg Entlpi ved innløpet (5 br, x,95), 7 kj/kg overført: kj/kg Dvs. 4*/6,7 kw b) I området med overhetet dmp
TKP4 Strømning og vrmetrnsport Løsningsforslg til øving Oppgve ) Entlpi ved utløpet (5 br, ), kj/kg Entlpi ved innløpet (5 br, x,95), 7 kj/kg overført: kj/kg Dvs. 4*/6,7 kw b) I området med overhetet dmp
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
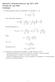 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
x 1, x 2,..., x n. En lineær funksjon i n variable er en funksjon f(x 1, x 2,..., x n ) = a 1 x 1 + a 2 x a n x n,
 Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Introduksjon Velkommen til emnet TMA45 Mtemtikk 3, våren 9 Disse nottene inneholder det vi gjennomgår i forelesningene, og utgjør, smmen med lle øvingene, pensum for emnet Læreoken nefles som støttelittertur
Initialbetingelser: I begynnelsen var φ
 Initialbetingelser: I begynnelsen var φ I fysikken er diffligninger og initialbetingelser som wienerpølser og rekesalat: de trenger hverandre. Vi har etter mye slit satt opp diffligningene som styrer tidsutviklingen
Initialbetingelser: I begynnelsen var φ I fysikken er diffligninger og initialbetingelser som wienerpølser og rekesalat: de trenger hverandre. Vi har etter mye slit satt opp diffligningene som styrer tidsutviklingen
dx = 1 2y dy = dx/ x 3 y3/2 = 2x 1/2 + C 1
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så y + 3y = e + 3e = e. b) En hr t y = e 3 e (3/), så y + 3y = e 3e (3/) + 3e + 3e (3/) = e. c)
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: a n x n. R > 0, med summen s(x). Da gjelder: a n n + 1 xn+1 for hver x < R.
 LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
LEDDVIS INTEGRASJON OG DERIVASJON AV POTENSREKKER: Vi ntr t potensrekken konvergerer i ] R, R[, n x n R >, med summen s(x). D gjelder: s (x) = n n x n 1 for hver x < R, og s(t)dt = n n + 1 xn+1 for hver
Integrasjon Skoleprosjekt MAT4010
 Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
En kort introduksjon til generell relativitetsteori
 En kort introduksjon til generell relativitetsteori Generell relativitetsteori (GR) representerer vår mest fundamentale forståelse av tid, rom og gravitasjon, og er helt nødvendig for å formulere konsistente
En kort introduksjon til generell relativitetsteori Generell relativitetsteori (GR) representerer vår mest fundamentale forståelse av tid, rom og gravitasjon, og er helt nødvendig for å formulere konsistente
Fasit til utvalgte oppgaver MAT1100, uka 20-24/9
 Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
MAT 1110: Løsningsforslag til obligatorisk oppgave 2, V-06
 MAT : Løsningsforslg til obligtorisk oppgve, V-6 Oppgve : ) Hvis = (,,...) og = (,,...) er to vektorer, vil kommndoen >> plot(,) tegne rette forbindelseslinjer mellom punktene (, ), (, ) osv. For å plotte
MAT : Løsningsforslg til obligtorisk oppgve, V-6 Oppgve : ) Hvis = (,,...) og = (,,...) er to vektorer, vil kommndoen >> plot(,) tegne rette forbindelseslinjer mellom punktene (, ), (, ) osv. For å plotte
A. forbli konstant B. øke med tida C. avta med tida D. øke først for så å avta E. ikke nok informasjon til å avgjøre
 Flervlgsoppgver 1. En induktor L og en motstnd R er forbundet til en spenningskilde E som vist i figuren. Bryteren S 1 lukkes og forblir lukket slik t konstnt strøm går gjennom L og R. Så åpnes bryter
Flervlgsoppgver 1. En induktor L og en motstnd R er forbundet til en spenningskilde E som vist i figuren. Bryteren S 1 lukkes og forblir lukket slik t konstnt strøm går gjennom L og R. Så åpnes bryter
1 dx cos 1 x =, 1 x 2 sammen med kjerneregelen for derivasjon. For å forenkle utregningen lar vi u = Vi regner først ut den deriverte til u,
 TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
TMA0 Høst 205 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg 3.5.30: Vi bruker erivsjonsregelen for cos x, x cos x =, x 2 smmen me kjerneregelen for erivsjon. For å forenkle utregningen
Feilestimeringer. i MAT-INF1100
 Feilestimeringer i MAT-INF11 Ett v de viktigste punktene i MAT-INF11, og smtidig det som nsees som det vnskeligste i pensum, er feilestimter. Vi bruker mye tid på å beregne tilnærmede verdier for funksjoner,
Feilestimeringer i MAT-INF11 Ett v de viktigste punktene i MAT-INF11, og smtidig det som nsees som det vnskeligste i pensum, er feilestimter. Vi bruker mye tid på å beregne tilnærmede verdier for funksjoner,
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Matematikk 1000. Øvingsoppgaver i numerikk leksjon 8 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
75045 Dynamiske systemer 3. juni 1997 Løsningsforslag
 75045 Dynmiske systemer 3. juni 1997 Løsningsforslg Oppgve 1 ẋ = 0 gir y = ±x, og dette innstt i ẏ = 0 gir 1 ± x = 0. Vi må velge minustegnet, og får x = y = ±1/. Vi deriverer: [ ] x y ( 1 Df(x, y) = ;
75045 Dynmiske systemer 3. juni 1997 Løsningsforslg Oppgve 1 ẋ = 0 gir y = ±x, og dette innstt i ẏ = 0 gir 1 ± x = 0. Vi må velge minustegnet, og får x = y = ±1/. Vi deriverer: [ ] x y ( 1 Df(x, y) = ;
Løsningsforslag til avsluttende eksamen i HUMIT1750 høsten 2003.
 Løsningsforslg til vsluttende eksmen i HUMIT1750 høsten 2003. Teksten under hr litt litt prtsom fordi jeg hr villet forklre hvordn jeg gikk frm. Fr en studentesvrelse le det ikke forventet nnet enn sluttresulttene.
Løsningsforslg til vsluttende eksmen i HUMIT1750 høsten 2003. Teksten under hr litt litt prtsom fordi jeg hr villet forklre hvordn jeg gikk frm. Fr en studentesvrelse le det ikke forventet nnet enn sluttresulttene.
Løsningsforslag TFE4120 Elektromagnetisme 24. mai = 2πrlɛE(r) = Q innenfor S =
 Norges teknisk nturvitenskpelige universitet Institutt for elektronikk og telekommuniksjon Side 1 v 5 Løsningsforslg TFE4120 Elektromgnetisme 24. mi 2011 Oppgve 1 ) Av symmetrigrunner må det elektriske
Norges teknisk nturvitenskpelige universitet Institutt for elektronikk og telekommuniksjon Side 1 v 5 Løsningsforslg TFE4120 Elektromgnetisme 24. mi 2011 Oppgve 1 ) Av symmetrigrunner må det elektriske
Løsningsforslag til Eksamen i fag MA1103 Flerdimensjonal analyse
 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Side 1 v 5 Løsningsforslg til Eksmen i fg MA113 Flerdimensjonl nlyse 2.5.6 Oppgve 1 Vi hr f(x, y) = (4 x 2 y 2 )e x+y. ) Kritiske
Løsningsforslag Kollokvium 6
 Løsningsforslg Kollokvium 6 25. februr 25 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 6. Oppgve Diskusjonsoppgve Diskuter følgende spørsmål med hverndre og prøv å bli
Løsningsforslg Kollokvium 6 25. februr 25 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 6. Oppgve Diskusjonsoppgve Diskuter følgende spørsmål med hverndre og prøv å bli
TKP4100 og TMT4206 Løsningsforslag til øving 9
 TKP4 og TMT46 Løsningsforslg til øving 9 Oppgve ) Entlpi ved utløpet (5 br, C), kj/kg Entlpi ved innløpet (5 br, x =,95), 7 kj/kg overført: kj/kg Dvs. 4*/6 =,7 kw b) I området med overhetet dmp (T >4C
TKP4 og TMT46 Løsningsforslg til øving 9 Oppgve ) Entlpi ved utløpet (5 br, C), kj/kg Entlpi ved innløpet (5 br, x =,95), 7 kj/kg overført: kj/kg Dvs. 4*/6 =,7 kw b) I området med overhetet dmp (T >4C
Løsningsforslag SIE4010 Elektromagnetisme 5. mai 2003
 Oppgve 1 Løsningsforslg SIE4010 Elektromgnetisme 5. mi 2003 ) Av symmetrigrunner må det elektriske feltet være rdielt rettet og uvhengig v φ, E = E(r)u r.vilrs være overflten til en sylinder med rdius
Oppgve 1 Løsningsforslg SIE4010 Elektromgnetisme 5. mi 2003 ) Av symmetrigrunner må det elektriske feltet være rdielt rettet og uvhengig v φ, E = E(r)u r.vilrs være overflten til en sylinder med rdius
MED SVARFORSLAG UNIVERSITETET I OSLO
 Eksmen i : MED SVARFORSLAG UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet INF5110 - Kompiltorteknikk Eksmensdg : Onsdg 6. juni 2012 Tid for eksmen : 14.30-18.30 Oppgvesettet er på : Vedlegg
Eksmen i : MED SVARFORSLAG UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet INF5110 - Kompiltorteknikk Eksmensdg : Onsdg 6. juni 2012 Tid for eksmen : 14.30-18.30 Oppgvesettet er på : Vedlegg
1 k 2 + 1, k= 5. i=1. i = k + 6 eller k = i 6. m+6. (i 6) i=1
 TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
Faktorisering. 1 Hva er faktorisering? 2 Hvorfor skal vi faktorisere? Per G. Østerlie Senter for IKT i utdanningen 11.
 Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
LØSNINGSFORSLAG EKSAMEN TEP 4115/4120 TERMODYNAMIKK 1 (KONT) Fredag 19. august 2005 Tid: kl. 09:00-13:00
 Side v 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK LØSNINGSFORSLAG EKSAMEN TEP 45/40 TERMODYNAMIKK (KONT) Fredg 9. ugust 005 Tid: kl. 09:00
Side v 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK LØSNINGSFORSLAG EKSAMEN TEP 45/40 TERMODYNAMIKK (KONT) Fredg 9. ugust 005 Tid: kl. 09:00
FY2045/TFY4250 Kvantemekanikk I, løsning øving 10 1 LØSNING ØVING 10
 FY45/TFY45 Kvntemeknikk I, løsning øving LØSNING ØVING Løsning oppgve Spinn. D åde χ + og χ i likhet med lle ndre spinorer er egentilstnder til enhetsmtrisen med egenverdi lik, hr vi Videre finner vi t
FY45/TFY45 Kvntemeknikk I, løsning øving LØSNING ØVING Løsning oppgve Spinn. D åde χ + og χ i likhet med lle ndre spinorer er egentilstnder til enhetsmtrisen med egenverdi lik, hr vi Videre finner vi t
Løsningsforslag Eksamen 19. august 2005 TFY4250 Atom- og molekylfysikk
 Eksmen TFY450 19. ugust 005 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 19. ugust 005 TFY450 Atom- og molekylfysikk. For det oppgitte, symmetriske brønnpotensilet er bundne energiegentilstnder enten
Eksmen TFY450 19. ugust 005 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 19. ugust 005 TFY450 Atom- og molekylfysikk. For det oppgitte, symmetriske brønnpotensilet er bundne energiegentilstnder enten
Kap. 3 Krumningsflatemetoden
 SIDE. KRUMNINGSFLTEMETODEN I kpittel. og. hr vi sett t en bjelkes krefter og deformsjon kn beskrives ved fire integrler som henger smmen : Skjærkrft : V d Vinkelendring : φ M d Moment : M V d Forskyvning
SIDE. KRUMNINGSFLTEMETODEN I kpittel. og. hr vi sett t en bjelkes krefter og deformsjon kn beskrives ved fire integrler som henger smmen : Skjærkrft : V d Vinkelendring : φ M d Moment : M V d Forskyvning
gir g 0 (x) = 2x + x 2 (x + 3) x x 2 x 1 (x + 3) 2 x 5 + 2x 4 + 6x 3 + x 2 + x + 3 x 2 (x + 3) 2 g(x; y) h(x) F (x; y) =
 Oppgve ) gir b) c) d) e) f() = 5 4 3 gir f () = 3 6 + 3 g() = + 3 f)når så blir Merk her t = Tilsvrende er gir g () = + ( + 3) ( + 3) 5 + 4 + 6 3 + + + 3 ( + 3) h() = f() gir h () = f () + f() f() = g(;
Oppgve ) gir b) c) d) e) f() = 5 4 3 gir f () = 3 6 + 3 g() = + 3 f)når så blir Merk her t = Tilsvrende er gir g () = + ( + 3) ( + 3) 5 + 4 + 6 3 + + + 3 ( + 3) h() = f() gir h () = f () + f() f() = g(;
1 Mandag 8. mars 2010
 1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
A.5 Stasjonære og ikke-stasjonære tilstander
 TFY4250/FY2045 Tillegg 4 - Stasjonære og ikke-stasjonære tilstander 1 Tillegg 4: A.5 Stasjonære og ikke-stasjonære tilstander a. Stasjonære tilstander (Hemmer p 26, Griffiths p 21) Vi har i TFY4215 (se
TFY4250/FY2045 Tillegg 4 - Stasjonære og ikke-stasjonære tilstander 1 Tillegg 4: A.5 Stasjonære og ikke-stasjonære tilstander a. Stasjonære tilstander (Hemmer p 26, Griffiths p 21) Vi har i TFY4215 (se
TFY4104 Fysikk. Institutt for fysikk, NTNU. Lsningsforslag til ving 8. a =
 TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
TFY414 Fysikk. Institutt for fysikk, NTNU. Lsningsforslg til ving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, s elektronets kselersjon blir = e m E lts mot venstre. b) C Totlt elektrisk felt i
Integrasjon av trigonometriske funksjoner
 Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
9 Potenser. Logaritmer
 9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
9 Potenser. Logritmer Foret utregingene nedenfor: 5 5 c 6 7 d e 5 f g h i Regn ut og gjør svrene så enkle som mulige: c y y d e f g h i j y y + y + y + + y Prisen på en motorsg vr kr 56 i 99. Vi regner
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Løsningsforslag til øving 8. a = e m E
 TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
TFY414 Fysikk. Institutt for fysikk, NTNU. Høsten 16. Løsningsforslg til øving 8. Oppgve 1. ) C F = E = m Newtons. lov. Her er = e, så elektronets kselersjon blir = e m E ltså mot venstre. b) C Totlt elektrisk
MAT 100A: Mappeeksamen 4
 . november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
. november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
Numerisk Integrasjon
 Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
Numerisk Integrsjon Anne Kværnø Mrch 1, 018 1 Problemstilling Vi skl ltså finne en numerisk tilnærmelse til integrlet for en gitt funksjon f (x). I(, b) = f (x)dx Teknikken vi skl diskutere klles numeriske
Matematikk Øvingsoppgaver i numerikk leksjon 9 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 9 Numerisk integrsjon Forståelsen v integrlet som et rel ligger til grunn når vi skl beregne integrler numerisk. Litt mer presist: Når f(x) 0 for lle x i
Løsningsforslag til eksamensoppgaver i ECON 2200 våren 2015
 Løsningsforslg til eksmensogver i ECON 00 våren 05 Ogve (7 oeng) Deriver følgende funskjoner 3 ) f ( ) gir f ( ) 3 ) f ( ) e e( ) gir f ( ) e c) f ( ) ln gir f ( ) 3 3 (3 ) 3 lterntivt f ( ) ln ln 3 gir
Løsningsforslg til eksmensogver i ECON 00 våren 05 Ogve (7 oeng) Deriver følgende funskjoner 3 ) f ( ) gir f ( ) 3 ) f ( ) e e( ) gir f ( ) e c) f ( ) ln gir f ( ) 3 3 (3 ) 3 lterntivt f ( ) ln ln 3 gir
R1 kapittel 1 Algebra
 Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Tema 2: Stokastiske variabler og sannsynlighetsfordelinger Kapittel 3 ST :44 (Gunnar Taraldsen)
 Tem 2: Stokstiske vribler og snnsynlighetsfordelinger Kpittel 3 ST1101 2019-01-13 12:44 (Gunnr Trldsen) Det nts i nottet t S er et utfllsrom utstyrt med en snnsynlighet P (A) for enhver hendelse A F. F
Tem 2: Stokstiske vribler og snnsynlighetsfordelinger Kpittel 3 ST1101 2019-01-13 12:44 (Gunnr Trldsen) Det nts i nottet t S er et utfllsrom utstyrt med en snnsynlighet P (A) for enhver hendelse A F. F
R1 kapittel 7 Sannsynlighet. Kapitteltest. Oppgave 1. Oppgave 2. Oppgave 3. Del 1 Uten hjelpemidler. Løsninger til oppgavene i boka
 Løsninger til oppgvene i ok R1 kpittel 7 Snnsynlighet Løsninger til oppgvene i ok Kpitteltest Del 1 Uten hjelpemidler Oppgve 1 De fem lppene kn ordnes i rekkefølge på 5! = 15 = forskjellige måter. Vi kn
Løsninger til oppgvene i ok R1 kpittel 7 Snnsynlighet Løsninger til oppgvene i ok Kpitteltest Del 1 Uten hjelpemidler Oppgve 1 De fem lppene kn ordnes i rekkefølge på 5! = 15 = forskjellige måter. Vi kn
Løsningsforslag til Obligatorisk oppgave 2
 Løsningsforslg til Oligtorisk oppgve INF1800 Logikk og eregnrhet Høsten 008 Alfred Brtterud Oppgve 1 Vi hr lfetet A = {} og språkene L 1 = {s s } L = {s s inneholder minst tre forekomster v } L 3 = {s
Løsningsforslg til Oligtorisk oppgve INF1800 Logikk og eregnrhet Høsten 008 Alfred Brtterud Oppgve 1 Vi hr lfetet A = {} og språkene L 1 = {s s } L = {s s inneholder minst tre forekomster v } L 3 = {s
Terminprøve Matematikk for 1P 1NA høsten 2014
 Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
Terminprøve Mtemtikk for 1P 1NA høsten 2014 DEL 1 Vrer 1,5 time Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med entimetermål og vinkelmåler. Forsøk på lle oppgvene selv om du er usikker
Løsningsforslag Eksamen 30. mai 2007 FY2045 Kvantefysikk
 Eksmen FY045 30. mi 007 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 30. mi 007 FY045 Kvntefysikk. I grensen 0 er potensilet V x et enkelt okspotensil, V = V 0 for < x < 0 og uendelig ellers. Den
Eksmen FY045 30. mi 007 - løsningsforslg 1 Oppgve 1 Løsningsforslg Eksmen 30. mi 007 FY045 Kvntefysikk. I grensen 0 er potensilet V x et enkelt okspotensil, V = V 0 for < x < 0 og uendelig ellers. Den
Sem 1 ECON 1410 Halvor Teslo
 Løsningsforslg til seminr i ECON : Internsjonl økonomi.seminruke V ) Den økonomien vi her står ovenfor produserer re to goder, tø og vin. Altså vil lterntivkostnden for den ene vren nødvendigvis måles
Løsningsforslg til seminr i ECON : Internsjonl økonomi.seminruke V ) Den økonomien vi her står ovenfor produserer re to goder, tø og vin. Altså vil lterntivkostnden for den ene vren nødvendigvis måles
Løsningsforslag, Midtsemesterprøve torsdag 6. mars 2008 kl Oppgavene med kort løsningsskisse
 Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
Institutt for fysikk, NTNU FY1003 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2008 Løsningsforslg, Midtsemesterprøve torsdg 6. mrs 2008 kl 1000 1200. Fsit side 12. Oppgvene med kort løsningsskisse
1 Mandag 18. januar 2010
 Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
1 Mandag 25. januar 2010
 Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Løsningsforslag, Midtsemesterprøve fredag 13. mars 2009 kl Oppgavene med kort løsningsforslag (Versjon A)
 Institutt for fysikk, NTNU FY100 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2009 Løsningsforslg, Midtsemesterprøve fredg 1. mrs 2009 kl 1415 1615. Fsit side 10. Oppgvene med kort løsningsforslg
Institutt for fysikk, NTNU FY100 Elektrisitet og mgnetisme TFY4155 Elektromgnetisme Vår 2009 Løsningsforslg, Midtsemesterprøve fredg 1. mrs 2009 kl 1415 1615. Fsit side 10. Oppgvene med kort løsningsforslg
Nøtterøy videregående skole
 Til elever og forestte Borgheim, 1. ugust 2018 Viktig info om vlg v mtemtikkfg for elever på vg1 studiespesilisering I vg1 får elevene vlget mellom to ulike mtemtikkfg. Mtemtikk 1T (teoretisk) og Mtemtikk
Til elever og forestte Borgheim, 1. ugust 2018 Viktig info om vlg v mtemtikkfg for elever på vg1 studiespesilisering I vg1 får elevene vlget mellom to ulike mtemtikkfg. Mtemtikk 1T (teoretisk) og Mtemtikk
Kinematikk i to og tre dimensjoner
 Kinemtikk i to og tre dimensjoner 3.1.218 Innleveringsfrist oblig 1: Mndg, 5.eb. kl.18 Innlevering kun vi: https://devilry.ifi.uio.no/ Mulig å levere som gruppe (i Devilry, N 3) Bruk gjerne Pizz ved spørsmål
Kinemtikk i to og tre dimensjoner 3.1.218 Innleveringsfrist oblig 1: Mndg, 5.eb. kl.18 Innlevering kun vi: https://devilry.ifi.uio.no/ Mulig å levere som gruppe (i Devilry, N 3) Bruk gjerne Pizz ved spørsmål
Kapittel 3. Potensregning
 Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
Kpittel. Potensregning I potensregning skriver vi tll som potenser og forenkler uttrykk som inneholder potenser. Dette kpitlet hndler blnt nnet om: Betydningen v potenser som hr negtiv eksponent eller
R2 - Heldagsprøve våren 2013
 Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsforslag til eksamen i TFY4170 Fysikk 2 Fysikk 2 Torsdag 2. desember 2004
 NTNU Side 1 v 7 Institutt for fysikk Fkultet for nturvitenskp og teknologi Dette løsningsforslget er på 7 sider. Løsningsforslg til eksmen i TFY417 Fysikk Fysikk Torsdg. desember 4 Oppgve 1. Kvntemeknikk
NTNU Side 1 v 7 Institutt for fysikk Fkultet for nturvitenskp og teknologi Dette løsningsforslget er på 7 sider. Løsningsforslg til eksmen i TFY417 Fysikk Fysikk Torsdg. desember 4 Oppgve 1. Kvntemeknikk
Projeksjon. Kapittel 11. Ortogonal projeksjon i R 2. Skalarproduktet i R n. w på v. Fra figuren ovenfor ser vi at komponenten til w ortogonalt på v er
 Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
Kpittel Projeksjon En projeksjon er en lineærtrnsformsjon P som tilfredsstiller P x P x. for lle x. Denne ligningen sier t intet nytt skjer om du benytter lineærtrnsformsjonen for ndre gng, og mn kn tenke
EKSAMEN. 1. klassene, ingenørutdanning og flexing. ANTALL SIDER UTLEVERT: 5(innkl. forside og 2 sider formelark)
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
KANDIDATNUMMER: EKSAMEN EMNENAVN: Mtemtikk EMNENUMMER: REA4 og REA4f EKSAMENSDATO:. ugust 9 KLASSE:. klssene, ingenørutdnning og fleing. TID: kl. 9... FAGANSVARLIG: Hns Petter Hornæs ANTALL SIDER UTLEVERT:
1 Mandag 1. mars 2010
 Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Sensorveiledning Oppgaveverksted 4, høst 2013 (basert på eksamen vår 2011)
 Sensorveiledning Oppgveverksted 4, høst 203 (bsert på eksmen vår 20) Ved sensuren tillegges oppgve vekt 0,2, oppgve 2 vekt 0,4, og oppgve 3 vekt 0,4. For å bestå eksmen, må besvrelsen i hvert fll: gi minst
Sensorveiledning Oppgveverksted 4, høst 203 (bsert på eksmen vår 20) Ved sensuren tillegges oppgve vekt 0,2, oppgve 2 vekt 0,4, og oppgve 3 vekt 0,4. For å bestå eksmen, må besvrelsen i hvert fll: gi minst
Institutt for elektroteknikk og databehandling
 Institutt for elektroteknikk og dtbehndling Stvnger, 7. mi 997 Løsningsforslg til eksmen i TE 9 Signler og Systemer, 6. mi 997 Oppgve ) Et system er lineært dersom superposisjonsprinsippet gjelder, d.v.s.
Institutt for elektroteknikk og dtbehndling Stvnger, 7. mi 997 Løsningsforslg til eksmen i TE 9 Signler og Systemer, 6. mi 997 Oppgve ) Et system er lineært dersom superposisjonsprinsippet gjelder, d.v.s.
S1 kapittel 4 Logaritmer Løsninger til oppgavene i boka
 Løsninger til oppgvene i ok S kpittel 4 Logritmer Løsninger til oppgvene i ok 4. Vi leser v fr tllet 4 på y-ksen og ser t vi får den tilhørende verdien,6 på -ksen. lg 4,6 Vi leser v fr tllet,5 på y-ksen
Løsninger til oppgvene i ok S kpittel 4 Logritmer Løsninger til oppgvene i ok 4. Vi leser v fr tllet 4 på y-ksen og ser t vi får den tilhørende verdien,6 på -ksen. lg 4,6 Vi leser v fr tllet,5 på y-ksen
INF1800 Forelesning 19
 INF1800 Forelesning 19 Førsteordens logikk Roger Antonsen - 21. oktober 2008 (Sist oppdtert: 2008-10-21 20:12) Repetisjon Semntikk Hvis M er en modell og ϕ er en lukket formel, så definerte vi M = ϕ. Vi
INF1800 Forelesning 19 Førsteordens logikk Roger Antonsen - 21. oktober 2008 (Sist oppdtert: 2008-10-21 20:12) Repetisjon Semntikk Hvis M er en modell og ϕ er en lukket formel, så definerte vi M = ϕ. Vi
NORSK TEKST Side 1 av 4. Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245/TFY425 KVANTEMEKANIKK
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 972355 EKSAMEN I FY245/TFY425 KVANTEMEKANIKK
1b) Beregn den elektriske ladningstettheten inni kjernen og finn hvor stor den totale ladningen er.
 FYS112 H-211: Løsningsforslg for vsluttende eksmen Oppgve 1 I en modell for en kuleformet tomkjerne med rdius R vrierer det elektriske feltet inne i kjernen som E(r) = Cr(xe x + ye y + ze z ). Her er C
FYS112 H-211: Løsningsforslg for vsluttende eksmen Oppgve 1 I en modell for en kuleformet tomkjerne med rdius R vrierer det elektriske feltet inne i kjernen som E(r) = Cr(xe x + ye y + ze z ). Her er C
Løsningsforslag til obligatorisk oppgave i ECON 2130
 Andres Mhre April 13 Løsningsforslg til obligtorisk oppgve i ECON 13 Oppgve 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) X og Z er uvhengige v hverndre, så Cov(X, Z) =.
Andres Mhre April 13 Løsningsforslg til obligtorisk oppgve i ECON 13 Oppgve 1: E(XY) = E(X(Z X)) Setter inn Y = Z - X E(XY) = E(XZ X ) E(XY) = E(XZ) E(X ) X og Z er uvhengige v hverndre, så Cov(X, Z) =.
Numerisk kvadratur. Newton-Cotes kvadratur. PROBLEM STILLING: Approksimér. I(f) = f(x)dx. hvor f : R R kan Riemann-integreres.
 Numerisk kvdrtur PROBLEM STILLING: Approksimér 1/15 I(f) = hvor f : R R kn Riemnn-integreres. b f(x)dx. Newton-Cotes kvdrtur Newton-Cotes kvdrtur erbsert på ekvidistnte noder i [, b]: For en n-noder åpen
Numerisk kvdrtur PROBLEM STILLING: Approksimér 1/15 I(f) = hvor f : R R kn Riemnn-integreres. b f(x)dx. Newton-Cotes kvdrtur Newton-Cotes kvdrtur erbsert på ekvidistnte noder i [, b]: For en n-noder åpen
Integrasjon. et supplement til Kalkulus. Harald Hanche-Olsen 14. november 2016
 Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
Integrsjon et supplement til Klkulus Hrl Hnhe-Olsen 14. novemer 2016 Dette nottet er ment som et supplement og elvis lterntiv til eler v kpittel 8 i Tom Linstrøm: Klkulus (åe 3. og 4. utgve). Foruten et
Fakultet for realfag Ho/gskolen i Agder - Va ren 2007
 Msteroppgve i mtemtikkdidktikk Fkultet for relfg Ho/gskolen i Agder - V ren 2007 Integrl og integrsjon Roger Mrkussen Roger Mrkussen Integrl og integrsjon Msteroppgve i mtemtikkdidktikk Høgskolen i Agder
Msteroppgve i mtemtikkdidktikk Fkultet for relfg Ho/gskolen i Agder - V ren 2007 Integrl og integrsjon Roger Mrkussen Roger Mrkussen Integrl og integrsjon Msteroppgve i mtemtikkdidktikk Høgskolen i Agder
KAPITTEL 9 Approksimasjon av funksjoner
 KAPITTEL 9 Approksimsjon v funksjoner En grunnleggende teknikk som ofte brukes i ulike deler v mtemtikk og nvendelser er å tilnærme eller pproksimere et objekt med et nnet. Som regel er objektet som skl
KAPITTEL 9 Approksimsjon v funksjoner En grunnleggende teknikk som ofte brukes i ulike deler v mtemtikk og nvendelser er å tilnærme eller pproksimere et objekt med et nnet. Som regel er objektet som skl
Fasit. Grunnbok. Kapittel 2. Bokmål
 Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
Fsit 9 Grunnbok Kpittel Bokmål Kpittel Lineære funksjoner rette linjer. ƒ(x) = 4x + 5 ƒ() = 3 ƒ(4) = ƒ(6) = 9.6 ƒ(x) = -x b ƒ(x) = x b ƒ(x) = (x + ) 3 ƒ() = ƒ(4) = 8 ƒ(6) = 4 ƒ(x) = x 4 ƒ() = - ƒ(4) =
5: Algebra. Oppgaver Innhold Dato
 5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
5: Alger Pln resten v året: - Kpittel 6: Ferur - Kpittel 7: Ferur/mrs - Kpittel 8: Mrs - Repetisjon: April/mi - Eventuell offentlig eksmen: Mi - Økter, prøver, prosjekter: Mi - juni For mnge er egrepet
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ÿ Œ œ ˆ ˆ Š Œ. .. ³μ. μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö Œ Œ ˆˆ 79 ˆ Š ˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
Temahefte nr. 1. Hvordan du regner med hele tall
 1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
1 ARBEIDSHEFTE I MATEMATIKK SNART MATTE EKSAMEN Hvordn du effektivt kn forberede deg til eksmen Temhefte nr. 1 Hvordn du regner med hele tll Av Mtthis Lorentzen mttegrisenforlg.com Opplysning: De nturlige
LØSNINGSFORSLAG TIL EKSAMEN I TEP4145 KLASSISK MEKANIKK Mandag 21. mai 2007 kl Løsningsforslaget er på i alt 9 sider.
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
dy ycos 2 y = dx. Ved å integrere på begge sider av likhetstegnet får man ved å substituere u = y,du = dy dy ycos 2 y = 2du cos 2 u = x.
 NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 7 Avsnitt 6.5 ) En hr t y = e, så 2y +y = 2e +e = e. b) En hr t y = e 2 e (/2), så 2y +y = 2e e (/2) +e +e (/2) = e. c) En hr
Numerisk matematikk. Fra Matematikk 3MX (2002) Side
 Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Numerisk mtemtikk Fr Mtemtikk 3MX (2002) Side 142 147 142 Kpittel 4: Integrlregning 47 NUMERISK MATEMATIKK pffiffiffiffiffi På lommeregneren finner du rskt t 71 er lik 8,426150, og t lg 5 er lik 0,698970
Derivasjon. Oversikt over Matematikk 1. Derivasjon anvendelser. Sekantsetningen
 3 Oversikt over Mtemtikk Induksjon Grenser og kontinuitet Skjæringssetningen Eksistens v ekstrempunkt Elementære funksjoner Derivsjon Sekntsetningen Integrsjon Differensilligninger Kurver i plnet Rekker
3 Oversikt over Mtemtikk Induksjon Grenser og kontinuitet Skjæringssetningen Eksistens v ekstrempunkt Elementære funksjoner Derivsjon Sekntsetningen Integrsjon Differensilligninger Kurver i plnet Rekker
Regn i hodet. a) 15 : 3 = b) 24 : 6 = c) 36 : 4 = d) 48 : 8 = Regn i hodet. a) 21 : 3 = b) 28 : 7 = c) 49 : 7 = d) 64 : 8 =
 10 Divisjon 2 1 Regn i hodet. ) 15 : 3 = b) 24 : 6 = c) 36 : 4 = d) 48 : 8 = 2 Regn i hodet. ) 21 : 3 = b) 28 : 7 = c) 49 : 7 = d) 64 : 8 = 3 ) 39 : 3 = b) 56 : 4 = c) 96 : 8 = d) 98 : 7 = 4 Gi svret med
10 Divisjon 2 1 Regn i hodet. ) 15 : 3 = b) 24 : 6 = c) 36 : 4 = d) 48 : 8 = 2 Regn i hodet. ) 21 : 3 = b) 28 : 7 = c) 49 : 7 = d) 64 : 8 = 3 ) 39 : 3 = b) 56 : 4 = c) 96 : 8 = d) 98 : 7 = 4 Gi svret med
Fra fotball til business. Historien om Newbody
 Fr fotbll til business Historien om Newbody Vi hjelper skoler og foreninger med å tjene penger til cuper, treningsleirer og skoleturer. Ved å selge populære sokker og undertøy v høy kvlitet kn de enkelt
Fr fotbll til business Historien om Newbody Vi hjelper skoler og foreninger med å tjene penger til cuper, treningsleirer og skoleturer. Ved å selge populære sokker og undertøy v høy kvlitet kn de enkelt
NORSK TEKST Side 1 av 4. Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I FY2045/TFY4250 KVANTEMEKANIKK
NORSK TEKST Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 97012355 EKSAMEN I FY2045/TFY4250 KVANTEMEKANIKK
Mer øving til kapittel 3
 Mer øving til kpittel 3 KAPITTEL 3 FUNKSJONER Oppgve 1 Tegn et koordintsystem og merk v punktene (1, 5) d (3, 2) ( 2, 3) e ( 3, 5) (4, 0) f (0, 4) Oppgve 2 Hvilke koordintpr hr de ulike punktene i koordintsystemet?
Mer øving til kpittel 3 KAPITTEL 3 FUNKSJONER Oppgve 1 Tegn et koordintsystem og merk v punktene (1, 5) d (3, 2) ( 2, 3) e ( 3, 5) (4, 0) f (0, 4) Oppgve 2 Hvilke koordintpr hr de ulike punktene i koordintsystemet?
UNIVERSITETET I OSLO
 UNIVESITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: FYS1120 Elektromgnetisme Eksmensdg: 5. oktober 2015 Tid for eksmen: 10.00 13.00 Oppgvesettet er på 8 sider. Vedlegg: Tilltte hjelpemidler:
UNIVESITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: FYS1120 Elektromgnetisme Eksmensdg: 5. oktober 2015 Tid for eksmen: 10.00 13.00 Oppgvesettet er på 8 sider. Vedlegg: Tilltte hjelpemidler:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: STK1110 Sttistiske metoder og dtnlyse 1 Eksmensdg: Tirsdg 18. desemer 2018 Tid for eksmen: 09.00 13.00 Oppgvesettet er på 5 sider.
UNIVERSITETET I OSLO Det mtemtisk-nturvitenskpelige fkultet Eksmen i: STK1110 Sttistiske metoder og dtnlyse 1 Eksmensdg: Tirsdg 18. desemer 2018 Tid for eksmen: 09.00 13.00 Oppgvesettet er på 5 sider.
Forkunnskaper i matematikk for fysikkstudenter. Integrasjon.
 De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
6. Beregning av treghetsmoment.
 Forelesningsnotter i mtemtikk Bruk v integrsjon Beregning v treghetsmoment Side 1 6 Beregning v treghetsmoment 61 Definisjoner Først de grunnleggende definisjonene: Momentkse r m en liten punktformet prtikkel
Forelesningsnotter i mtemtikk Bruk v integrsjon Beregning v treghetsmoment Side 1 6 Beregning v treghetsmoment 61 Definisjoner Først de grunnleggende definisjonene: Momentkse r m en liten punktformet prtikkel
ALTERNATIV GRUNNBOK BOKMÅL
 Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
Anne Rsch-Hlvorsen Oddvr Asen Illustrtør: Bjørn Eidsvik 7B NY UTGAVE ALTERNATIV GRUNNBOK BOKMÅL CAPPELEN DAMM AS, 2011 Mterilet i denne publiksjonen er omfttet v åndsverklovens bestemmelser. Uten særskilt
