En kort introduksjon til generell relativitetsteori
|
|
|
- Unni Helgesen
- 7 år siden
- Visninger:
Transkript
1 En kort introduksjon til generell relativitetsteori Generell relativitetsteori (GR) representerer vår mest fundamentale forståelse av tid, rom og gravitasjon, og er helt nødvendig for å formulere konsistente kosmologiske modeller. Den er en geometrisk teori, og kan formuleres på en koordinatfri måte. Det vil føre for langt å gjøre dette her, og i praktiske beregninger må man allikevel velge et koordinatsystem å gjøre beregningene i. Vi vil derfor bruke den mer gammeldagse formuleringen av teorien i disse forelesningene. Først av alt trenger vi å vite hva tensorer er for noe. Tensorer Gitt to punkter P og Q med koordinater henholdsvis x µ og x µ + dx µ, der µ = 0, 1,...n 1 (slik at rommet har n dimensjoner). Disse to punktene definerer en infinitesimal vektor PQ, som vi betrakter som festet til begynnelsespunktet P. Komponentene av vektoren i x µ -koordinatsystemet er dx µ. I et annet koordinatsystem x µ forbundet med x µ -systemet ved transformasjonene x µ = x µ (x ν ), har den samme vektoren koordinater som vi finner ved å bruke kjerneregelen for derivasjon, dx µ = x µ x ν dxν, der vi bruker konvensjonen om at en indeks som forekommer to ganger skal summeres over, dvs. vi summerer over ν. Den partiellderiverte skal regnes ut i punktet P. En kontravariant vektor (kan også kalles en kontravariant tensor av rang 1) er et sett av størrelser A µ i x µ -systemet som transformerer på samme måte som dx µ : A µ = x µ x ν Aν, der de partiellderiverte igjen skal regnes ut i punktet P. En kontravariant tensor av rang 2 er et sett av n 2 størrelser assosiert med punktet P, T µν i x µ -systemet som transformerer slik: T µν = x µ x α x ν x β T αβ. Et enkelt eksempel på en slik størrelse er produktet av to kontravariante vektorer A µ B ν. Vi kan definere kontravariante tensorer av vilkårlig høy rang ved å ta med flere x µ / x α -faktorer. Et viktig spesialtilfelle er en kontravariant tensor av rang null, en såkalt skalar φ som transformerer som φ = φ La φ = φ(x µ ) være en skalar funksjon som er kontinuerlig og deriverbar, slik at den deriverte φ/ x µ eksisterer i alle punkter i rommet. Vi kan betrakte koordinatene x µ som funksjoner av x ν og skrive φ = φ(x µ (x ν )). 1
2 Bruker vi kjerneregelen til å derivere med hensyn til x ν, får vi φ x ν = xµ φ x ν x µ. Dette er prototypen på hvordan en kovariant vektor (også kalt en kovariant tensor av rang 1) transformerer. Dette er generelt et sett av størrelser A µ assosiert med punktet x µ som transformerer som A µ = xν x µ A ν. Merk at x og x har byttet plass i den partiellderiverte som inngår. På samme måte som med kontravariante tensorer kan vi gå videre og definere kovariante tensorer av høyere rang. For eksempel: en kovariant tensor av rang 2 transformerer som T µν = xα x β x µ x ν T αβ. Vi kan også ha blandede tensorer. En blandet tensor av rang 3 kan for eksempel ha én kontravariant og to kovariante indekser, og vil da transformere som T µ νσ = x µ x β x γ x α x ν x σ T βγ. α Hvorfor er tensorer viktige? En viktig grunn til at de er viktige i relativitetsteori ser vi dersom vi ser på tensorligningen X µν = Y µν. Dette er en ligning som sier at komponentene til de kovariante tensorene X og Y er like i et koordinatsystem x. Men da har vi også at x µ x ν x α x β X µν = xµ x ν x α x β Y µν og siden vi vet at X og Y transformerer som kovariante tensorer av rang 2, har vi at X αβ = Y αβ. Med andre ord er alle komponentene til X og Y like også i det nye koordinatsystemet. En tensorligning er med andre ord gyldig i alle koordinatsystemer, og tensorer spiller derfor en avgjørende rolle når vi skal formulere naturlover som er gyldige uavhengig av valg av referansesystem. Tensorer kan adderes og subtraheres på opplagt vis. En tensor av rang 2 er symmetrisk dersom (vist her for kovariante tensorer) X µν = X νµ, og antisymmetrisk dersom X µν = X νµ. Enhver tensor av rang 2 kan skrives som en sum av en symmetrisk del X (µν) og en antisymmetrisk del X [µν], der X (µν) = 1 2 (X µν + X νµ ) X [µν] = 1 2 (X µν X νµ ) 2
3 noe du lett kan sjekke. En annen viktig operasjon er kontraksjon: fra en tensor av kontravariant rang p 1 og kovariant rang q 1 kan vi danne en tensor av rang (p 1, q 1) ved å sette to indekser lik hverandre og summere over dem. For eksempel kan vi fra tensoren X µ νγσ danne tensoren Y γσ ved å sette Y γσ = X µ µγσ. Merk at dersom vi kontraherer en tensor av rang (1, 1) får vi en skalar. Den metriske tensor En spesielt viktig tensor g µν av rang 2 er den metriske tensoren eller metrikken. Den er en symmetrisk tensor som kan brukes til å definere avstanden mellom to nabopunkter x µ, x µ + dx µ : ds 2 = g µν (x)dx µ dx ν. Den definerer også lengden til en vektor A i punktet x ved A 2 = g µν (x)a µ A ν, og skalarproduktet mellom to vektorer A og B, AB = g µν (x)a µ B ν. To vektorer sies å være ortogonale dersom skalarproduktet deres er lik null. I relativitetsteori er det mulig at lengden av en vektor (som ikke er lik nullvektoren) kan være lik null, A 2 = 0. Vi kan oppfatte metrikken som en n n-matrise, og determinanten dens betegnes med g, g = det(g µν ). Dersom determinanten er forskjellig fra null, har metrikken en invers, og denne er en kontravariant tensor av rang 2, g µν som oppfyller g µα g αν = δ ν µ, der δ ν µ = 1 for µ = ν og lik null ellers. Tensoren g µν kan brukes til å senke indekser, og g µν hever indekser. For eksempel: Ekvivalensprinsippet T ν µ = g µα T αν T µ ν = g µα T αν. Generell relativitetsteori starter med ekvivalensprinsippet. En observatør i fritt fall observerer ikke noe tyngdefelt. Om han slipper en gjenstand som han til å begynne med holder i ro ved siden av seg, vil gjenstanden forbli i ro etter at han har sluppet den, Han har derfor rett til å regne seg selv for å være i ro. Mer presist kan vi si: I et vilkårlig punkt i et tyngdefelt kan vi velge et referansesystem, det såkalte fritt-fallsystemet, definert ved at det beveger seg med akselerasjonen 3
4 et legeme i fritt fall ville hatt i det samme punktet. I dette systemet vil alle fysikkens lover ha samme form som i den spesielle relativitetsteorien. Unntaket er tyngdekraften, som forsvinner lokalt i dette systemet. To kommentarer er på sin plass: 1. Denne formuleringen av ekvivalensprinsippet omfatter at treg masse, m I (som inngår i Newtons 2. lov) er lik graviterende masse m G (som inngår i tyngdeloven). Hvis ikke dette var tilfellet, ville f.eks. observatøren og gjenstanden han slipper kunne ha forskjellige akselerasjoner, og da ville de ikke være i ro relativt til hverandre. 2. Merk at formuleringen sier i et punkt. Det vil si: det er generelt ikke mulig å finne et referansesystem som dekker hele tidrommet og der tyngdekraften er transformert bort. Ekvivalensprinsippet er viktig fordi vi kan bruke det til å lage relativistisk korrekte ligninger: start med å analysere situasjonen i fritt-fallsystemet der fysikken er forholdsvis enkel, Dersom vi kan formulere resultatet som en tensorligning, vet vi at den vil være gyldig i alle referansesystemer. Geodetligningen La oss bruke ekvivalensprinsippet til å finne bevegelsesligningen for en partikkel i et tyngdefelt. Vi starter i fritt-fallsystemet der vi kan bruke spesiell relativitetsteori. La punktet vi ser på ha koordinater ξ µ = (t, x, y, z), der vi har valgt enheter der c = 1. Jeg følger Dodelson og skriver linjelementet som ds 2 = dt 2 + dx 2 + dy 2 + dz 2 = η µν dξ µ dξ ν, der Minkowskimetrikken altså er η µν = diag( 1, 1, 1, 1). Siden partikkelen ikke er påvirket av noen krefter i fritt-fallsystemet er bevegelsesligningen i følge spesiell relativitetsteori ganske enkelt d 2 ξ µ dτ 2 = 0, der dτ 2 = ds 2 er egentid, dvs. tid målt på en klokke i systemet der partikkelen er i ro. Denne ligningen er en tensorligning i spesiell relativitetsteori: under Lorentztransformasjoner oppfører ξ seg som en firervektor, og τ er en skalar. Men Lorentztransformasjoner gjelder bare mellom systemer som er beveger seg med konstant hastighet i forhold til hverandre. Vi må ha en ligning som er invariant under mer generelle transformasjoner enn dette. La oss se på hva som skjer med ligingen over under en generell transformasjon til nye koordinater x µ. Under en slik generell transformasjon vil slik at dξ µ = ξµ x ν dxν, dξ µ dτ = ξµ x ν dx ν dτ. 4
5 Da har vi at 0 = d2 ξ µ dτ 2 = d ( ξ µ dx ν dτ x ν dτ = ξµ d 2 x ν x ν dτ 2 + dxν d dτ dτ ) ( ) ξ µ x ν = ξµ d 2 x ν x ν dτ ξ µ dx ν dx ρ x ν x ρ dτ dτ Nå ganger vi ligningen med x σ / ξ µ og summerer over µ. I det første leddet får vi da faktoren Dermed får vi Vi skriver denne ligningen som der x σ ξ µ d 2 x ν ξ µ x ν dτ 2 = xσ d 2 x ν x ν dτ 2 = d 2 x ν δσ ν dτ 2 = d2 x σ dτ 2 d 2 x σ dτ 2 + xσ 2 ξ µ dx ν dx ρ ξ µ x ν x ρ dτ dτ = 0. d 2 x σ dτ 2 + dx ν dx ρ Γσ νρ dτ dτ = 0, Γ σ νρ = xσ ξ µ 2 ξ µ x ν x ρ kalles Christoffelsymbolet eller konneksjonen. I de nye koordinatene er uttrykket for egentiden gitt ved dτ 2 = η µν dξ µ dξ ν = η µν ξ µ x α ξ ν der metrikken i de nye koordinatene er g αβ = η µν ξ µ x α ξ ν x β. x β dxα dx β g αβ dx α dx β, Du kan nå overbevise deg selv om at den nye bevegelsesligningen, som kalles geodetligningen, beholder formen dersom vi gjennomfører en generell koordinattransformasjon. Det du trenger å vite er at Christoffelsymbolet ikke er en tensor, men transformer som Γ α βγ = x α x δ x η x β Hvis vi innfører den kovariant deriverte x φ x γ Γδ ηφ + x α x δ γ A α = Aα x γ + Γα βγ Aβ, 2 x δ x β x γ. 5
6 (skriver ofte denne som A α ;γ ) kan vi vise at γa α transformerer som en blandet tensor av rang 2. Partikkelens bane er gitt ved x µ (τ). Tangentvektoren til banen i et gitt punkt er gitt ved X µ = dx µ /dτ, som transformerer som en kontravariant vektor. Det er da ikke så vanskelig å vise (gjør det!) at geodetligningen kan skrives som X γ γ X α = 0. Ofte bruker vi notasjonen γ X α = X;γ α Xα, og x γ geodetligningen enkelt som X γ X;γ α = 0. = X,γ α. Da kan vi skrive Skrevet på denne formen er det helt klart at geodetligningen er en tensorligning, som dermed er gyldig i alle referansesystemer. Merk at ligningen er invariant under generelle transformasjoner, også rene koordinattransformasjoner som for eksempel et bytte fra kartesiske til sfæriske koordinater. Dette gjør at det i generell relativitetsteori av og til kan være vanskelig å skille fysiske effekter fra effekter som skyldes valg av koordinater. Dette er et problem som dukker opp i forbindelse med kosmologisk perturbasjonsteori, det såkalte gaugeproblemet. Vi kommer tilbake til dette senere. I etterpåklokskap kan vi også utlede geodetligningen på en veldig enkel måte. I fritt-fallsystemet er tangentvektoren til partikkelens bane gitt ved Ξ µ = dξ µ /dτ, og bevegelsesligingen kan skrives d dτ ( ) dξ µ dτ = d dτ Ξµ = 0. Ved å bruke kjerneregelen kan vi skrive dette om til dξ ν dτ Ξ µ ξ ν = Ξν Ξ µ,ν = 0. Partiellderivasjon er ingen tensoroperasjon, men kovariant derivasjon er, og i fritt-fallsystemet er disse to operasjonene de samme (siden alle Christoffelsymbolene er lik null i dette systemet), så vi kan bytte ut kommaet med et semikolon: Ξ ν Ξ µ ;ν = 0. Nå har vi ført bevegelsesligningen over på en form som er en tensorligning, og følgelig er den gyldig i alle referansesystemer. Legg merke til at Γ og g µν er geometriske størrelser. Tyngdekraften er bakt inn i geometrien til tidrommet, og er dermed blitt til en geometrisk effekt. Siden både Γ og g er geometriske størrelser, er det kanskje ikke noen overraskelse at det er en sammenheng mellom dem. Jeg setter opp sammenhengen uten bevis: Γ σ µν = 1 ( gνρ 2 gρσ x µ + g µρ x ν g µν x ρ Metrikken er dermed et meget viktig objekt i GR: kjenner vi denne, så kjenner vi geometrien til tidrommet, og geometrien til tidrommet bestemmer hvordan partikler beveger seg. ). 6
7 Litt mer om den kovariant deriverte til slutt. Generelt for en blandet tensor har vi at den kovariant deriverte er gitt ved γ T α β = x γ T α β + Γ α δγt δ β + Γ δ βγt α δ, slik at hver kontravariant indeks gir opphav til et Christoffelsymbol med positivt fortegn, mens hver kovariant indeks gir opphav til et Christoffelsymbol med negativt fortegn. For en kontravariant tensor av rang 2 blir uttrykket Newtonsk grense γ T µν = x γ T µν + Γ µ βγ T βν + Γ ν βγt µβ. Vi ser på en partikkel som beveger sakte i et svakt, statisk gravitasjonsfelt. Husk at vi har satt lyshastigheten lik 1, så sakte bevegelse betyr dx i dt 1. I geodetligningen betyr dette at alle ledd som inneholder dx i /dτ (i = 1, 2, 3) kan neglisjeres sammenlignet med (dt/dτ) 2 -leddet, slik at vi får d 2 x σ dτ 2 + Γσ 00 ( ) 2 dt = 0. dτ At gravitasjonsfeltet er svakt betyr at metrikken er ikke kan avvike mye fra Minkowskimetrikken for flatt tidrom. Vi skriver den derfor som g µν = η µν + h µν, der h µν 1. Vi kan derfor neglisjere alle ledd som innholder mer enn én faktor h µν. At gravitasjonsfeltet er statisk betyr at g µν t Christoffelsymbolet vi trenger blir da Γ σ 00 = gρσ 2 = h µν t = 0. ( g0ρ x 0 + g 0ρ x 0 g ) 00 x ρ For σ = i = 1, 2, 3 blir geodetligningen d 2 x i ( dτ 2 = ηiρ h 00 dt 2 x ρ dτ ) 2 = 1 2 = 1 2 ηρσ h 00 x ρ. ( ) 2 dt h 00 dτ x i. Videre, for σ = 0 ser vi at Γ 0 00 h00 t = 0, så denne komponenten av geodetligningen blir rett og slett d 2 t dτ 2 = 0, 7
8 slik at dt/dτ = konstant. Da kan vi dele ligningene for σ = i med (dt/dτ) 2 og få d 2 x i dt 2 = 1 h 00 2 x i. For en partikkel i et statisk gravitasjonspotensial Ψ i Newtonsk mekanikk ville bevegelsesligningen være d 2 x i dt 2 = Ψ x i, så vi ser at dersom vi identifiserer h 00 = 2Ψ, så gir geodetligningen oss den Newtonske grensen. Med andre ord må 00-komponenten av metrikken være g 00 = 1 2Ψ. Viktige tensorer i GR Som sagt er Christoffelsymbolet ingen tensor. Men det kan brukes til å konstruere tensorer som er relatert til rommets krumning. De vi trenger å kjenne til er Riemanntensoren der jeg har innført notasjonen R µ σβα = Γµ σα,β Γµ σβ,α + Γµ ρβ Γρ σα Γ µ ραγ ρ σβ,,α = x α. Riccitensoren får vi ved å kontrahere to indekser i Riemanntensoren: Ricciskalaren er gitt ved R µν = Γ α µν,α Γα µα,ν + Γα βα Γβ µν Γα βν Γβ µα. Endelig er Einsteintensoren gitt ved R = g µν R µν. G µν = R µν 1 2 g µνr. Einsteintensoren har den viktige egenskapen at dens kovariante divergens er lik null: G µν ;ν = 0. Energi-impulstensoren La oss vende tilbake til spesiell relativitetsteori et øyeblikk. Vi ser på et system av ikke-vekselvirkende partikler med tetthet beskrevet av funksjonen ρ(x). Denne funksjonen lar vi representere tettheten målt av en observatør som beveger seg med partikkelstrømmen, karakterisert ved firerhastighetsfeltet u µ = dxµ dτ. 8
9 Fra disse størrelsene kan vi danne en kontravariant tensor av rang 2: I spesiell relativitetsteori har vi der u = d x/dt, T µν = ρu µ u ν. u µ = γ(1, u), dτ 2 = ds 2 = dt 2 d x 2 = dt 2 (1 u 2 ) = dt2 γ 2, og γ = (1 u 2 ) 1/2. Hvis vi skriver ut T som en matrise, ser den slik ut: 1 u x u y u z (T µν ) = ρ u x u 2 x u x u y u x u z u y u x u y u 2 y u y u z u z u x u z u y u z u 2 z Fra fluidmekanikk kjenner vi kontinuitetsligningen ρ + (ρ u) = 0, t som uttrykker bevaring av masse. Med vår definisjon av T kan vi uttrykke denne ligningen på en veldig kompakt måte. For hvis vi regner ut T,ν 0ν, får vi T,ν 0ν 0ν T = x ν = ρ t + ρu x x + ρu y y + ρu z z Dermed kan kontinuitetsligningen skrives som T 0ν,ν = 0. = ρ t + (ρ u). En annen viktig ligning i hydrodynamikk, Navier-Stokesligningen sier at for en væske uten indre trykk og ytre krefter gjelder [ ] u ρ + ( u ) u = 0. t Fysisk sier denne ligningen at bevegelsesmengden er bevart. Man kan vise at denne ligningen på komponentform med vårt valg av T kan skrives som T iν,ν = 0, for i = 1, 2, 3. Vi kan dermed sammenfatte bevaring av masse og bevegelsesmengde for systemet vårt på en svært elegant måte i ligningen T µν,ν = 0. 9
10 Skrevet på denne formen ser vi også straks at generaliseringen av denne ligningen til GR bør være T ;ν µν = 0. Fordi den oppsummerer bevaring av masse (energi) og bevegelsesmengde (impuls), kalles denne tensoren for energi-impulstensoren. Det tilfellet vi vil ha mest med å gjøere, er en perfekt væske. Denne er karakterisert ved (energi)tettheten, ρ = ρ(x), trykket p = p(x) og firerhastighetsfeltet u µ = dx µ /dτ. Dersom trykket p = 0, bør vi ende opp med samme energi-impulstensor som i forrige avsnitt. Det antyder at vi bør velge T µν = ρu µ u ν + ps µν, der S µν er en symmetrisk tensor. De eneste symmetriske tensorene av rang 2 som er forbundet med væsken er u µ u ν og den metriske tensoren g µν, så det enkleste valget er S µν = Au µ u ν + Bg µν, der A og B er konstanter. Vi benytter oss av det faktum at tensoren bør ha en spesiell-relativistisk grense vi kan leve med. I denne grensen er g µν = η µν, Minkowskimetrikken. Det vi ønsker oss aller mest i hele verden er at T,ν µν igjen skal uttrykke bevaring av energi og bevegelsesmengde. Krever vi at T,ν 0ν = 0 skal gi oss kontinuitetsligningen, og at T,ν iν = 0 skal gi oss Navier-Stokes (denne gangen med trykkledd, men uten ytre krefter), finner vi at dette bare er tilfellet dersom A = B = 1. Vi velger derfor T µν = (ρ + p)u µ u ν + pg µν, og den oppfyller betingelsen T µν ;ν = 0: vi sier at den har kovariant divergens lik 0. Einsteins feltligninger Vi har nå to tensorer, G µν og T µν, som begge har kovariant divergens lik null. Den ene, Einsteintensoren, har med geometri å gjøre. Den andre, energiimpulstensoren, har med masse, energi, og trykk å gjøre. Einstein postulerte at disse to tensorene er proporsjonale, G µν = 8πGT µν, der proporsjonalitetskonstanten 8πG er med for å få riktig newtonsk grense. Dette er Einsteins feltligninger, et av høydepunktene i menneskets intellektuelle historie (og dette sier jeg uten det minste snev av ironi). Merk at Einsteins feltligninger ikke kan utledes matematisk fra postulatene i relativitetsteorien, men valget over er det enkleste som er konsistent med dem. Om man ønsker det, så kan man skrive ned mer kompliserte feltligninger. Den riktige formen må til syvende og sist avgjøres av naturen. Så langt har den ikke gitt oss noen vektige grunner til å tro at Einsteins valg var galt. 10
11 Friedmannligningene For en gitt energi-impulstensor kan det å løse Einsteinligningene være en svært komplisert oppgave. Men i noen tilfeller har T µν symmetrier som forenkler problemet nok til at vi kan klare brasene. Ett slikt tilfelle er for et homogent, isotropt univers fylt med en eller flere perfekte væsker. Et slikt univers husker vi er beskrevet av Robertson-Walkerlinjeelementet. I dette kurset skal vi begrense oss til å se på flate universmodeller. I dette tilfellet er linjeelementet gitt ved ds 2 = dt 2 + a 2 (t)(dr 2 + r 2 dθ 2 + r 2 sin 2 θdφ 2 ), i sfæriske koordinater. For oss er det enklere å jobbe med kartesiske koordinater, og i disse er linjeelementet ganske enkelt ds 2 = dt 2 + a 2 (t)((dx 1 ) 2 + (dx 2 ) 2 + (dx 3 ) 2 ) = dt 2 + a 2 (t)d x 2. Jeg minner om at x i er medfølgende koordinater, dvs. de sitter fast i legemer som følger ekspansjonen og er konstante i tiden. Fysiske avstander finnes ved å multiplisere med skalafaktoren a(t) x. Vi kan nå sette opp Einsteinligningene for universet. Da trenger vi først Christoffelsymbolene. Disse er gitt ved Γ µ αβ = gµν 2 (g αν,β + g βν,α g αβ,ν ). Fra Robertson-Walkerlinjeelementet leser vi ut at metrikken er gitt ved og følgelig er For µ = 0 finner vi da g µν = diag( 1, a 2, a 2, a 2 ), g µν = diag( 1, 1/a 2, 1/a 2, 1/a 2 ). Γ 0 αβ = g0ν 2 (g αν,β + g βν,α g αβ,ν ) = 1 2 (g α0,β + g β0,α g αβ,0 ) = g αβ,0, som gir Γ 0 00 = 0, Γ0 0i = Γ0 i0 = 0, og For µ = i finner vi videre Γ 0 ij = 1 2 δ ij t a2 = aȧδ ij. Γ i αβ = 1 2 giν (g αν,β + g βν,α g αβ,ν ) = = 1 2a 2(g αi,β + g βi,α g αβ,i ) 1 2a 2(g αi,β + g βi,α ), 11
12 slik at og Γ i 00 = 1 2a 2 (g 0i,0 + g 0i,0 ) = 0, Γ i 0j = 1 2a 2 (g 0i,j + g ji,0 ) = 1 2a 2 δ ij t a2 = ȧ a δ ij = Γ i j0, Γ i jk = 1 2a 2(g ji,k + g ki,j ) = 0. De eneste Christoffelsymbolene som er forskjellige fra 0 er altså Γ 0 ij = δ ij aȧ Γ i 0j = Γ i j0 = δ ȧ ij a. Nå er vi klare til å gå løs på Riccitensoren: Vi finner at R µν = Γ α µν,α Γα µα,ν + Γα βα Γβ µν Γα βν Γβ µα. R 00 = Γ α 00,α Γα 0α,0 + Γα βα Γβ 00 Γα β0 Γβ 0α = Γ i 0i,0 Γ i j0γ j 0i = ȧ δ ii t a ȧ δ ij a δ ȧ ij a i i,j (ȧ ) 2 ȧ2 = 3äa a 2 δ ij δ ij a i j (ȧ ) 2 (ȧ ) 2 = 3ä a a a = 3ä a. I noen av mellomregningene har jeg satt inn summasjonstegnene eksplisitt i et desperat håp om å gjøre utregningen litt klarere. Vi må regne mere: Og nå en skikkelig versting: R 0i = Γ α 0i,α Γ α 0α,i + Γ α βαγ β 0i Γα βiγ β 0α = Γ 0 β0γ β 0i + Γj βj Γβ 0i Γ0 βiγ β 0i Γj βi Γβ 0j = 0. R ij = Γ α ij,α Γα iα,j + Γα βα Γβ ij Γα βj Γβ iα = Γ 0 ij,0 0 + Γα 0α Γ0 ij Γ0 βj Γβ i0 Γk βj Γβ ik = t (δ ijaȧ) + δ ij aȧ k δ kk ȧ a Γ0 kjγ k i0 Γ k 0jΓ 0 ik 12
13 = δ ij (ȧ 2 + aä) + 3δ ij ȧ 2 ȧ δ kj aȧδ ki a k k = δ ij (ȧ 2 + aä) + 3δ ij ȧ 2 δ ij ȧ 2 δ ij ȧ 2 = δ ij (2ȧ 2 + aä). Sammenlignet med dette er Ricciskalaren den rene barnemat: R = g µν R µν = R a 2 = 3ä a + 1 a 2 δ ii (2ȧ 2 + aä) = 3ä a + 3 a 2 (2ȧ2 + aä) [ (ȧ ) ] 2 ä = 6 a +. a Vi kan endelig finne f.eks. 00-komponenten av Einsteintensoren: G 00 i i R ii = R g 00R [ = 3ä a + 1 (ȧ ) ] ä a + a (ȧ ) 2 = 3. a δ kj ȧ a δ ikaȧ For å finne 00-komponenten av Einsteinligningen, trenger vi også den tilsvarende komponenten av energi-impulstensoren. For en perfekt væske var denne gitt ved T µν = (ρ + p)u µ u ν + pg µν. I medfølgende koordinater har væsken treerhastighet lik 0, slik at u µ = (1, 0), og ρ + p p T µν = p/a p/a 2 0 = p/a 2 Da blir T 00 = g 0α g 0β T αβ = ( 1)( 1)T 00 = T 00 = ρ, og 00-komponenten av Einsteinligningene, gir dermed G 00 = 8πGT 00, (ȧ ) 2 3 = 8πGρ, a 13 ρ p/a p/a p/a 2.
14 eller (ȧ ) 2 = 8πG a 3 ρ. Den oppmerksomme leser vil kjenne igjen denne ligningen som Friedmannligningen for ȧ i tilfellet k = 0 (romlig flatt univers). Vi husker at den kovariante divergensen til energi-impulstensoren er lik null: T µν ;ν = 0. Ser vi på µ = 0-komponenten av denne ligningen, får vi et resultat som du kanskje kjenner igjen: T 0ν ;ν = T 0ν,ν + Γ0 βν T βν + Γ ν βν T 0β = T 00,0 + Γ 0 βνt βν + Γ ν 0νT 00 = ρ t + Γ0 ijt ij + Γ i 0iρ = ρ t + p δ ij aȧδ ij a 2 + i j i = ρ t + 3ȧ (ρ + p), a der jeg har brukt de tidligere resultatene for Christoffelsymobelene for RWmetrikken, og uttrykket for energi-impulstensoren. Dermed gir µ = 0-komponenten av T ;ν µµ = 0 at ρ + 3ȧ (ρ + p) = 0, a som mange sikkert kjenner igjen fra AT4220, der vi utledet denne ligningen på en mye enklere, men mer tvilsom måte. ȧ a ρ 14
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
KORT INTRODUKSJON TIL TENSORER
 KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
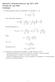 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Lørdag 26. mai 2001
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 8 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF407 KLASSISK FELTTEORI Lørdag 6. mai
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 8 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF407 KLASSISK FELTTEORI Lørdag 6. mai
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007
 Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsdag 8. august 2002
 NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
Relativistiske effekter i GNSS
 Olav Mathisen Olav Mathisen: Relativisti effets in GNSS KART OG PLAN, Vol. 73, pp. 64 68, POB 5003, NO-43 Ås, ISSN 0047-378 This short artile provides an overview of relativisti effets in GPS. First I
Olav Mathisen Olav Mathisen: Relativisti effets in GNSS KART OG PLAN, Vol. 73, pp. 64 68, POB 5003, NO-43 Ås, ISSN 0047-378 This short artile provides an overview of relativisti effets in GPS. First I
FYS307 - V03 OPPGAVEARK A. Oppgave A1: Tidekraftpendel
 FYS307 - V03 OPPGAVEARK A Oppgave A1: Tidekraftpendel a) Utled uttrykket for perioden til en matematisk pendel med lengde l i et område der tyngdens akselerasjon er g. Hva er perioden til en matematisk
FYS307 - V03 OPPGAVEARK A Oppgave A1: Tidekraftpendel a) Utled uttrykket for perioden til en matematisk pendel med lengde l i et område der tyngdens akselerasjon er g. Hva er perioden til en matematisk
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
z2 u(z, 0) = 0, u(0, t) = U. (8) Hvilken standardlikning er dette? b) Vi antar (håper) at u kan uttrykkes som en similaritetsløsning δδ ν ηf + F = 0,
 Oppg. 13 Det enkleste grensesjiktsproblemet?. Vi har en uendelig lang plate som faller sammen med xy-planet (I Blasiusproblemet har vi en halvuendelig plate). Over denne er det en Newtonsk væske. For t
Oppg. 13 Det enkleste grensesjiktsproblemet?. Vi har en uendelig lang plate som faller sammen med xy-planet (I Blasiusproblemet har vi en halvuendelig plate). Over denne er det en Newtonsk væske. For t
Løsningsforslag til eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006
 NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
LØSNINGSFORSLAG TIL EKSAMEN I TEP4145 KLASSISK MEKANIKK Mandag 21. mai 2007 kl Løsningsforslaget er på i alt 9 sider.
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
1 I mengdeteori er kontinuumshypotesen en antakelse om at det ikke eksisterer en mengde som
 Forelesning 12/3 2019 ved Karsten Trulsen Fluid- og kontinuumsmekanikk Som eksempel på anvendelse av vektor feltteori og flervariabel kalkulus, og som illustrasjon av begrepene vi har gått igjennom så
Forelesning 12/3 2019 ved Karsten Trulsen Fluid- og kontinuumsmekanikk Som eksempel på anvendelse av vektor feltteori og flervariabel kalkulus, og som illustrasjon av begrepene vi har gått igjennom så
Spesiell relativitetsteori
 Spesiell relativitetsteori 8.05.05 FYS-MEK 0 8.05.05 Einsteins postulatene. Fysikkens lover er de samme i alle inertialsystemer.. Lyshastigheten er den samme i alle inertialsystemer, og er uavhengig av
Spesiell relativitetsteori 8.05.05 FYS-MEK 0 8.05.05 Einsteins postulatene. Fysikkens lover er de samme i alle inertialsystemer.. Lyshastigheten er den samme i alle inertialsystemer, og er uavhengig av
UNIVERSITETET I OSLO
 Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
Repetisjon
 Repetisjon 18.05.017 Eksamensverksted: Mandag, 9.5., kl. 1 16, Origo Onsdag, 31.5., kl. 1 16, Origo FYS-MEK 1110 18.05.017 1 Lorentz transformasjon ( ut) y z y z u t c t 1 u 1 c transformasjon tilbake:
Repetisjon 18.05.017 Eksamensverksted: Mandag, 9.5., kl. 1 16, Origo Onsdag, 31.5., kl. 1 16, Origo FYS-MEK 1110 18.05.017 1 Lorentz transformasjon ( ut) y z y z u t c t 1 u 1 c transformasjon tilbake:
Kinematikk i to og tre dimensjoner
 Kinematikk i to og tre dimensjoner 2.2.217 Innleveringsfrist oblig 1: Mandag, 6.eb. kl.14 Innlevering kun via: https://devilry.ifi.uio.no/ Mulig å levere som gruppe (i Devilry, N 3) Bruk gjerne Piazza
Kinematikk i to og tre dimensjoner 2.2.217 Innleveringsfrist oblig 1: Mandag, 6.eb. kl.14 Innlevering kun via: https://devilry.ifi.uio.no/ Mulig å levere som gruppe (i Devilry, N 3) Bruk gjerne Piazza
VELKOMMEN TIL INTERNATIONAL MASTERCLASSES 2017 FYSISK INSTITUTT, UNIVERSITETET I OSLO
 VELKOMMEN TIL INTERNATIONAL MASTERCLASSES 2017 FYSISK INSTITUTT, UNIVERSITETET I OSLO SOSIALE MEDIA facebook/fysikk fysikkunioslo @fysikkunioslo Fysikk_UniOslo INTRODUKSJON TIL PARTIKKELFYSIKK INTERNATIONAL
VELKOMMEN TIL INTERNATIONAL MASTERCLASSES 2017 FYSISK INSTITUTT, UNIVERSITETET I OSLO SOSIALE MEDIA facebook/fysikk fysikkunioslo @fysikkunioslo Fysikk_UniOslo INTRODUKSJON TIL PARTIKKELFYSIKK INTERNATIONAL
MAT Grublegruppen Notat 11
 MAT1100 - Grublegruppen Notat 11 Jørgen O. Lye Matrisegrupper Den store gruppen vi skal se på er GL(n, K) = {inverterbare n n matriser med koesienter i K} Forkortelsen står for den generelle lineære gruppen
MAT1100 - Grublegruppen Notat 11 Jørgen O. Lye Matrisegrupper Den store gruppen vi skal se på er GL(n, K) = {inverterbare n n matriser med koesienter i K} Forkortelsen står for den generelle lineære gruppen
UNIVERSITETET I OSLO
 Side 1 UNIVERSITETET I OSO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: mars 017 Tid for eksamen: 14:30 17:30 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Side 1 UNIVERSITETET I OSO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: mars 017 Tid for eksamen: 14:30 17:30 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Enkel introduksjon til kvantemekanikken
 Kapittel Enkel introduksjon til kvantemekanikken. Kort oppsummering. Elektromagnetiske bølger med bølgelengde og frekvens f opptrer også som partikler eller fotoner med energi E = hf, der h er Plancks
Kapittel Enkel introduksjon til kvantemekanikken. Kort oppsummering. Elektromagnetiske bølger med bølgelengde og frekvens f opptrer også som partikler eller fotoner med energi E = hf, der h er Plancks
Impuls, bevegelsesmengde, energi. Bevaringslover.
 Impuls, bevegelsesmengde, energi. Bevaringslover. Kathrin Flisnes 19. september 2007 Bevegelsesmengde ( massefart ) Når et legeme har masse og hastighet, viser det seg fornuftig å definere legemets bevegelsesmengde
Impuls, bevegelsesmengde, energi. Bevaringslover. Kathrin Flisnes 19. september 2007 Bevegelsesmengde ( massefart ) Når et legeme har masse og hastighet, viser det seg fornuftig å definere legemets bevegelsesmengde
AST1010 En kosmisk reise. Forelesning 19: Kosmologi, del I
 AST1010 En kosmisk reise Forelesning 19: Kosmologi, del I Astronomiske avstander Hvordan vet vi at nærmeste stjerne er 4 lysår unna? Parallakse (kun nære stjerner) Hvordan vet vi at galaksen vår er 100
AST1010 En kosmisk reise Forelesning 19: Kosmologi, del I Astronomiske avstander Hvordan vet vi at nærmeste stjerne er 4 lysår unna? Parallakse (kun nære stjerner) Hvordan vet vi at galaksen vår er 100
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
AST1010 En kosmisk reise. Astronomiske avstander https://www.youtube.com/watch? v=vsl-jncjak0. Forelesning 20: Kosmologi, del I
 AST1010 En kosmisk reise Forelesning 20: Kosmologi, del I Astronomiske avstander Hvordan vet vi at nærmeste stjerne er 4 lysår unna? Parallakse (kun nære stjerner) Hvordan vet vi at galaksen vår er 100
AST1010 En kosmisk reise Forelesning 20: Kosmologi, del I Astronomiske avstander Hvordan vet vi at nærmeste stjerne er 4 lysår unna? Parallakse (kun nære stjerner) Hvordan vet vi at galaksen vår er 100
EKSAMENSOPPGAVE I FYS-1001
 side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august :00 13:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006
 NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
Spesiell relativitetsteori
 Spesiell relativitetsteori 4.05.04 FYS-MEK 0 4.05.04 Einsteins postlatene. Fysikkens lover er de samme i alle inertialsystemer.. Lyshastigheten er den samme i alle inertialsystemer, og er avhengig av observatørens
Spesiell relativitetsteori 4.05.04 FYS-MEK 0 4.05.04 Einsteins postlatene. Fysikkens lover er de samme i alle inertialsystemer.. Lyshastigheten er den samme i alle inertialsystemer, og er avhengig av observatørens
Kinematikk i to og tre dimensjoner
 Kinematikk i to og tre dimensjoner 4.2.216 Innleveringsfrist oblig 1: Tirsdag, 9.eb. kl.18 Innlevering kun via: https://devilry.ifi.uio.no/ Devilry åpnes snart. YS-MEK 111 4.2.216 1 v [m/s] [m] Eksempel:
Kinematikk i to og tre dimensjoner 4.2.216 Innleveringsfrist oblig 1: Tirsdag, 9.eb. kl.18 Innlevering kun via: https://devilry.ifi.uio.no/ Devilry åpnes snart. YS-MEK 111 4.2.216 1 v [m/s] [m] Eksempel:
Forelesning 13. mars, 2017
 Forelesning 13. mars, 217 AVSNITT 5.2 Kovariansen mellom to variable Korrelasjon mellom to variable AVSNITT 5.3 Betingede fordelinger Kovariansen mellom to stokastiske variable Kovariansen mellom to stokastiske
Forelesning 13. mars, 217 AVSNITT 5.2 Kovariansen mellom to variable Korrelasjon mellom to variable AVSNITT 5.3 Betingede fordelinger Kovariansen mellom to stokastiske variable Kovariansen mellom to stokastiske
Lineære likningssystemer og matriser
 Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Kapittel 3 Lineære likningssystemer og matriser I dette kapittelet skal vi sette sammen Kapittel 1 og 2. 3.1 Den utvidede matrisen til et likningssystem Vi starter med et lineært likningssystem med m likninger
Brukerkurs i Gauss feilforplantning
 Brukerkurs i Gauss feilforplantning Knut S. Gjerden 9. august 2011 evt. gaussisk feilforplantning eller bruk av Gauss lov for feilforplantning. Samt litt generelt om fysikkting.
Brukerkurs i Gauss feilforplantning Knut S. Gjerden 9. august 2011 evt. gaussisk feilforplantning eller bruk av Gauss lov for feilforplantning. Samt litt generelt om fysikkting.
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11)
 Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
EKSAMENSOPPGAVE Njål Gulbrandsen / Ole Meyer /
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: FYS-1001 Mekanikk Dato: 21.2.2017 Klokkeslett: 09:00 13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Fire A4-sider (to dobbeltsidige
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAVE Eksamen i: FYS-1001 Mekanikk Dato: 21.2.2017 Klokkeslett: 09:00 13:00 Sted: Åsgårdvegen 9 Tillatte hjelpemidler: Fire A4-sider (to dobbeltsidige
Obligatorisk oppgave nr 4 FYS Lars Kristian Henriksen UiO
 Obligatorisk oppgave nr 4 FYS-13 Lars Kristian Henriksen UiO. februar 15 Oppgave 1 Vi betrakter bølgefunksjonen Ψ(x, t) Ae λ x e iωt hvor A, λ og ω er positive reelle konstanter. a) Finn normaliseringen
Obligatorisk oppgave nr 4 FYS-13 Lars Kristian Henriksen UiO. februar 15 Oppgave 1 Vi betrakter bølgefunksjonen Ψ(x, t) Ae λ x e iωt hvor A, λ og ω er positive reelle konstanter. a) Finn normaliseringen
UNIVERSITETET I OSLO
 Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Oskar Klein og den femte dimensjon
 Oskar Klein og den femte dimensjon Finn Ravndal Fysisk Institutt, Universitetet i Oslo. Abstract Etter en kort oppsummering av det vitenskapelige liv til Oskar Klein, blir en mer detaljert utledning av
Oskar Klein og den femte dimensjon Finn Ravndal Fysisk Institutt, Universitetet i Oslo. Abstract Etter en kort oppsummering av det vitenskapelige liv til Oskar Klein, blir en mer detaljert utledning av
Kosmologisk perturbasjonsteori: forpostfektninger
 Kosmologisk perturbasjonsteori: forpostfektninger I kapittel 4 i Dodelson starter han arbeidet med å sette opp ligningene som beskriver hvordan små inhomogeniteter i fordelingen av fotoner og materie utvikler
Kosmologisk perturbasjonsteori: forpostfektninger I kapittel 4 i Dodelson starter han arbeidet med å sette opp ligningene som beskriver hvordan små inhomogeniteter i fordelingen av fotoner og materie utvikler
Spesiell relativitetsteori
 Spesiell relativitetsteori 13.05.015 FYS-MEK 1110 13.05.015 1 Spesiell relativitetsteori Einsteins mirakelår 1905 6 år gammel patentbehandler ved det sveitsiske patentbyrået i Bern i 1905 publiserte han
Spesiell relativitetsteori 13.05.015 FYS-MEK 1110 13.05.015 1 Spesiell relativitetsteori Einsteins mirakelår 1905 6 år gammel patentbehandler ved det sveitsiske patentbyrået i Bern i 1905 publiserte han
Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober :15 16:00
 NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
Newtons lover i én dimensjon
 Newtons lover i én dimensjon 3.01.018 snuble-gruppe i dag, kl.16:15-18:00, Origo FYS-MEK 1110 3.01.018 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon
Newtons lover i én dimensjon 3.01.018 snuble-gruppe i dag, kl.16:15-18:00, Origo FYS-MEK 1110 3.01.018 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon
Repetisjon
 Repetisjon 1.5.13 FYS-MEK 111 1.5.13 1 Lorentz transformasjon x ( x t) y z y z t t 1 1 x transformasjon tilbake: omven fortegn for og bytte S og S x ( x t) y z y z t t x små hastighet : 1 og x t t x t
Repetisjon 1.5.13 FYS-MEK 111 1.5.13 1 Lorentz transformasjon x ( x t) y z y z t t 1 1 x transformasjon tilbake: omven fortegn for og bytte S og S x ( x t) y z y z t t x små hastighet : 1 og x t t x t
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
Eksamen i fag FY1004 Innføring i kvantemekanikk Fredag 30. mai 2008 Tid: a 0 = 4πǫ 0 h 2 /(e 2 m e ) = 5, m
 Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
HAVBØLGER. Her skal vi gjennomgå den enkleste teorien for bølger på vannoverflaten:
 HAVBØLGER Her skal vi gjennomgå den enkleste teorien for bølger på vannoverflaten: Airy teori, også kalt lineær bølgeteori eller bølger av første orden Fremstillingen her vil temmelig nøyaktig følge kompendiet
HAVBØLGER Her skal vi gjennomgå den enkleste teorien for bølger på vannoverflaten: Airy teori, også kalt lineær bølgeteori eller bølger av første orden Fremstillingen her vil temmelig nøyaktig følge kompendiet
Litt GRUPPETEORI for Fys4170
 Litt GRUPPETEORI for Fys4170 GRUPPER: Ei gruppe G = {g i } er ei samling element med disse egenskapene: * multiplikasjon slik at g i g j G ; * et enhetselement g 0 = 1 slik at g i g 0 = g 0 g i = g i ;
Litt GRUPPETEORI for Fys4170 GRUPPER: Ei gruppe G = {g i } er ei samling element med disse egenskapene: * multiplikasjon slik at g i g j G ; * et enhetselement g 0 = 1 slik at g i g 0 = g 0 g i = g i ;
Oppsummert: Kap 1: Størrelser og enheter
 Oppsummert: Kap 1: Størrelser og enheter s = 3,0 m s = fysisk størrelse 3,0 = måltall = {s} m = enhet = dimensjon = [s] OBS: Fysisk størrelse i kursiv (italic), enhet opprettet (roman) (I skikkelig teknisk
Oppsummert: Kap 1: Størrelser og enheter s = 3,0 m s = fysisk størrelse 3,0 = måltall = {s} m = enhet = dimensjon = [s] OBS: Fysisk størrelse i kursiv (italic), enhet opprettet (roman) (I skikkelig teknisk
Spesiell relativitetsteori
 Spesiell relativitetsteori 6.05.03 FYS-MEK 0 6.05.03 Einsteins postlatene. Fysikkens lover er de samme i alle inertialsystemer.. Lyshastigheten er den samme i alle inertialsystemer, og er avhengig av observatørens
Spesiell relativitetsteori 6.05.03 FYS-MEK 0 6.05.03 Einsteins postlatene. Fysikkens lover er de samme i alle inertialsystemer.. Lyshastigheten er den samme i alle inertialsystemer, og er avhengig av observatørens
Løsningsforslag til eksamen i FY3404 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 2004
 NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
Spesiell relativitetsteori
 Spesiell relativitetsteori 23.05.2016 FYS-MEK 1110 23.05.2016 1 man tir uke 21 uke 22 uke 23 23 30 6 forelesning: spes. relativitet gruppe 5: gravitasjon+likevekt Ingen datalab forelesning: repetisjon
Spesiell relativitetsteori 23.05.2016 FYS-MEK 1110 23.05.2016 1 man tir uke 21 uke 22 uke 23 23 30 6 forelesning: spes. relativitet gruppe 5: gravitasjon+likevekt Ingen datalab forelesning: repetisjon
Siden vi her har brukt første momentet i fordelingen (EX = EX 1 ) til å konstruere estimatoren kalles denne metoden for momentmetoden.
 Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Kap. 6+7 Arbeid og energi. Energibevaring.
 TFY4145/FY11 Mekanisk fysikk Størrelser og enheter (Kap 1) Kinematikk i en, to og tre dimensjoner (Kap. +3) Posisjon, hastighet, akselerasjon. Sirkelbevegelse. Dynamikk (krefter): Newtons lover (Kap. 4)
TFY4145/FY11 Mekanisk fysikk Størrelser og enheter (Kap 1) Kinematikk i en, to og tre dimensjoner (Kap. +3) Posisjon, hastighet, akselerasjon. Sirkelbevegelse. Dynamikk (krefter): Newtons lover (Kap. 4)
(1 + x 2 + y 2 ) 2 = 1 x2 + y 2. (1 + x 2 + y 2 ) 2, x 2y
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
AST1010 En kosmisk reise. Forelesning 19: Kosmologi
 AST1010 En kosmisk reise Forelesning 19: Kosmologi Hubble og Big Bang Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman og bakgrunnsstrålingen Oppdagelsen av bakgrunnsstrålingen Universets historie
AST1010 En kosmisk reise Forelesning 19: Kosmologi Hubble og Big Bang Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman og bakgrunnsstrålingen Oppdagelsen av bakgrunnsstrålingen Universets historie
Løsningsforslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag 26. mai 2005
 NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
MAT Grublegruppen Notat 6
 MAT00 - Grublegruppen Notat 6 Jørgen O. Lye Vektorrom og indreprodukt Vektorrom Vi trenger å si litt om vektorrom og indreprodukt for å formulere Fourierrekker. Denisjonen av vektorrom kan man tenke på
MAT00 - Grublegruppen Notat 6 Jørgen O. Lye Vektorrom og indreprodukt Vektorrom Vi trenger å si litt om vektorrom og indreprodukt for å formulere Fourierrekker. Denisjonen av vektorrom kan man tenke på
Hvorfor mørk materie er bare tull
 Hvorfor mørk materie er bare tull En sammenligning av MOND og CDM Karsten Kvalsund 1 2 1 Institutt for fysikk NTNU 2 Trondheim Astronomiske Forening 28 oktober 2008 Kepler Kepler beskriver planetbanene
Hvorfor mørk materie er bare tull En sammenligning av MOND og CDM Karsten Kvalsund 1 2 1 Institutt for fysikk NTNU 2 Trondheim Astronomiske Forening 28 oktober 2008 Kepler Kepler beskriver planetbanene
Øving 4. a) Verifiser at en transversal bølge som forplanter seg langs x-aksen med utsving D med komponentene
 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 010. Veiledning: Tirsdag 1. og onsdag. september. Innleveringsfrist: Mandag 7. september kl 1:00. Øving 4 Oppgave 1 a) Verifiser at en transversal
FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 010. Veiledning: Tirsdag 1. og onsdag. september. Innleveringsfrist: Mandag 7. september kl 1:00. Øving 4 Oppgave 1 a) Verifiser at en transversal
Analysedrypp IV: Metriske rom
 Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Forelesningsnotater i FYS4520
 Forelesningsnotater i FYS4520 1 Det kvantemekaniske mange-partikkel problem 1.1 Definisjon av mange-partikkel problemet Vi skal begrense oss til systemer av fermioner, som kan behandles ikkerelativistisk.
Forelesningsnotater i FYS4520 1 Det kvantemekaniske mange-partikkel problem 1.1 Definisjon av mange-partikkel problemet Vi skal begrense oss til systemer av fermioner, som kan behandles ikkerelativistisk.
Geometri på ikke-kommutative algebraer
 Geometri på ikke-kommutative algebraer Ski og matematikk 2011 Rondablikk Arne B. Sletsjøe Universitetet i Oslo January 4, 2012 Algebraiske varieteter k = k (f.eks. C), S = k[x 1,..., x n ] Affint algebraisk
Geometri på ikke-kommutative algebraer Ski og matematikk 2011 Rondablikk Arne B. Sletsjøe Universitetet i Oslo January 4, 2012 Algebraiske varieteter k = k (f.eks. C), S = k[x 1,..., x n ] Affint algebraisk
Keplers lover. Statikk og likevekt
 Keplers lover Statikk og likevekt 30.04.018 FYS-MEK 1110 30.04.018 1 Ekvivalensprinsippet gravitasjonskraft: gravitasjonell masse m m F G G r m G 1 F g G FG R Gm J J Newtons andre lov: inertialmasse m
Keplers lover Statikk og likevekt 30.04.018 FYS-MEK 1110 30.04.018 1 Ekvivalensprinsippet gravitasjonskraft: gravitasjonell masse m m F G G r m G 1 F g G FG R Gm J J Newtons andre lov: inertialmasse m
Foreta omskrivninger av den stedsderiverte av et produkt som forekommer i den vanlige formen:
 . 2 65 Løsning E.1 Foreta omskrivninger av den stedsderiverte av et produkt som forekommer i den vanlige formen: Dette er den søkte formen. " Løsning E.2 %'& Legg en -akse i # s retning, dvs. # () -,&
. 2 65 Løsning E.1 Foreta omskrivninger av den stedsderiverte av et produkt som forekommer i den vanlige formen: Dette er den søkte formen. " Løsning E.2 %'& Legg en -akse i # s retning, dvs. # () -,&
Skalarfelt og kvantefluktuasjoner
 Sklrfelt og kvntefluktusjoner I forrige sett v notter regnet vi ut kvntefluktusjonene i tensorperturbsjonen h. Sklrfeltet φ spilte d bre en pssiv rolle ved å drive universets ekspnsjon. Nå skl vi regne
Sklrfelt og kvntefluktusjoner I forrige sett v notter regnet vi ut kvntefluktusjonene i tensorperturbsjonen h. Sklrfeltet φ spilte d bre en pssiv rolle ved å drive universets ekspnsjon. Nå skl vi regne
Eksamen i fag FY8104 Symmetri i fysikken Fredag 7. desember 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Lørdag 22. desember
Oskar Klein The Dirac Theory of the Electron in General Relativity Theory DKNVS Forhandlinger
 Det Kongelige Norske Videnskabers Selskabs Skrifter (Kgl. Norske Vidensk. Selsk. Skr. 2011 (4), 173-181) Oskar Klein The Dirac Theory of the Electron in General Relativity Theory DKNVS Forhandlinger 1958
Det Kongelige Norske Videnskabers Selskabs Skrifter (Kgl. Norske Vidensk. Selsk. Skr. 2011 (4), 173-181) Oskar Klein The Dirac Theory of the Electron in General Relativity Theory DKNVS Forhandlinger 1958
Oppgaver og fasit til seksjon
 1 Oppgaver og fasit til seksjon 3.1-3.3 Oppgaver til seksjon 3.1 1. Regn ut a b når a) a = ( 1, 3, 2) b = ( 2, 1, 7) b) a = (4, 3, 1) b = ( 6, 1, 0) 2. Finn arealet til parallellogrammet utspent av a =
1 Oppgaver og fasit til seksjon 3.1-3.3 Oppgaver til seksjon 3.1 1. Regn ut a b når a) a = ( 1, 3, 2) b = ( 2, 1, 7) b) a = (4, 3, 1) b = ( 6, 1, 0) 2. Finn arealet til parallellogrammet utspent av a =
Oppgaver MAT2500 høst 2011
 Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
Eksamen i SIF5036 Matematisk modellering Onsdag 12. desember 2001 Kl
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Løsning til øving 23 for FY1004, våren 2008
 Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
5.3. LAPLACE OG POISSON LIKNINGANE 95. f = f, (5.45) = e i x i
 5.3. LAPLACE OG POISSON LIKNINGANE 95 Oppgåver: 1. Lat f(x 1,x 2,x 3 )=f(r), der r = {(x 1 x 1) 2 +(x 2 x 2) 2 +(x 3 x 3) 2 } 1 2. Syn at f = f, (5.45) når = e i, = e i x i x i. (5.46) 2. Syn v.h.a. resultatet
5.3. LAPLACE OG POISSON LIKNINGANE 95 Oppgåver: 1. Lat f(x 1,x 2,x 3 )=f(r), der r = {(x 1 x 1) 2 +(x 2 x 2) 2 +(x 3 x 3) 2 } 1 2. Syn at f = f, (5.45) når = e i, = e i x i x i. (5.46) 2. Syn v.h.a. resultatet
Newtons lover i én dimensjon
 Newtons lover i én dimensjon 6.01.017 YS-MEK 1110 6.01.017 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon av en fjær. YS-MEK 1110 6.01.017 Bok på bordet
Newtons lover i én dimensjon 6.01.017 YS-MEK 1110 6.01.017 1 Hva er kraft? Vi har en intuitivt idé om hva kraft er. Vi kan kvantifisere en kraft med elongasjon av en fjær. YS-MEK 1110 6.01.017 Bok på bordet
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014
 FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
FYS-MEK 1110 Løsningsforslag Eksamen Vår 2014 Oppgave 1 (4 poeng) Forklar hvorfor Charles Blondin tok med seg en lang og fleksibel stang når han balanserte på stram line over Niagara fossen i 1859. Han
Vi viser denne ekvivalensen ved å vise begge implikasjoner. " "Anta at G virker trofast på X og anta at g, h G er slik at gx = hx for alle
 TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
SIGNERT DOMINASJON OG RETTEDE MATROIDESYSTEMER
 SIGNERT DOMINASJON OG RETTEDE MATROIDESYSTEMER Matematisk institutt Binære monotone systemer Grunnelementer i modell: X i = I(ite komponent virker), i = 1, 2, 3 φ(x) = I(Systemet virker) = X 1 X 2 + X
SIGNERT DOMINASJON OG RETTEDE MATROIDESYSTEMER Matematisk institutt Binære monotone systemer Grunnelementer i modell: X i = I(ite komponent virker), i = 1, 2, 3 φ(x) = I(Systemet virker) = X 1 X 2 + X
Løsningsforslag til Øving 6 Høst 2016
 TEP4105: Fluidmekanikk Løsningsforslag til Øving 6 Høst 016 Oppgave 3.13 Skal finne utløpshastigheten fra røret i eksempel 3. når vi tar hensyn til friksjon Hvis vi antar at røret er m langt er friksjonen
TEP4105: Fluidmekanikk Løsningsforslag til Øving 6 Høst 016 Oppgave 3.13 Skal finne utløpshastigheten fra røret i eksempel 3. når vi tar hensyn til friksjon Hvis vi antar at røret er m langt er friksjonen
Matematikk og fysikk RF3100
 DUMMY Matematikk og fysikk RF3100 Løsningsforslag, Øving 11 8mai 201 Tidsfrist: 18mai 201 klokken 1400 Oppgave 1 Obs: I denne oppgaven reperesenterer vi vektorer med 1 n-matriser, altså radvektorer I hele
DUMMY Matematikk og fysikk RF3100 Løsningsforslag, Øving 11 8mai 201 Tidsfrist: 18mai 201 klokken 1400 Oppgave 1 Obs: I denne oppgaven reperesenterer vi vektorer med 1 n-matriser, altså radvektorer I hele
Aristoteles (300 f.kr): Kraft påkrevd for å opprettholde bevegelse. Dvs. selv UTEN friksjon må oksen må trekke med kraft S k
 TFY4115 Fysikk Mekanikk: (kap.ref Young & Freedman) SI-systemet (kap. 1); Kinematikk (kap. 2+3). (Rekapitulasjon) Newtons lover (kap. 4+5) Energi, bevegelsesmengde, kollisjoner (kap. 6+7+8) Rotasjon, spinn
TFY4115 Fysikk Mekanikk: (kap.ref Young & Freedman) SI-systemet (kap. 1); Kinematikk (kap. 2+3). (Rekapitulasjon) Newtons lover (kap. 4+5) Energi, bevegelsesmengde, kollisjoner (kap. 6+7+8) Rotasjon, spinn
A) 1 B) 2 C) 3 D) 4 E) 5
 Side 2 av 5 Oppgave 1 Hvilket av de følgende fritt-legeme diagrammene representerer bilen som kjører nedover uten å akselerere? Oppgave 2 A) 1 B) 2 C) 3 D) 4 E) 5 En lampe med masse m er hengt opp fra
Side 2 av 5 Oppgave 1 Hvilket av de følgende fritt-legeme diagrammene representerer bilen som kjører nedover uten å akselerere? Oppgave 2 A) 1 B) 2 C) 3 D) 4 E) 5 En lampe med masse m er hengt opp fra
Institutt for fysikk Fakultet for fysikk, informatikk og matematikk. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 31.
 NTNU Side av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 3. mai 007 Oppgave.
NTNU Side av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 3. mai 007 Oppgave.
Auditorieøving 6, Fluidmekanikk
 Auditorieøving 6, Fluidmekanikk Utført av (alle i gruppen): Oppgave 1 En beholder er åpen i ene enden og har et hull i bunnen, påsatt et innadrettet rør av lengde l og med sirkulært tverrsnitt A 0. Beholderen,
Auditorieøving 6, Fluidmekanikk Utført av (alle i gruppen): Oppgave 1 En beholder er åpen i ene enden og har et hull i bunnen, påsatt et innadrettet rør av lengde l og med sirkulært tverrsnitt A 0. Beholderen,
Løsningsforslag Øving 12
 Løsningsforslag Øving 1 TEP4100 Fluidmekanikk, Vår 013 Oppgave 9-89 Løsning Vi skal finne et uttrykk for trykket som funksjon av x og y i et gitt hastighetsfelt. Antagelser 1 Strømningen er stasjonær.
Løsningsforslag Øving 1 TEP4100 Fluidmekanikk, Vår 013 Oppgave 9-89 Løsning Vi skal finne et uttrykk for trykket som funksjon av x og y i et gitt hastighetsfelt. Antagelser 1 Strømningen er stasjonær.
Diagonalisering. Kapittel 10
 Kapittel Diagonalisering I te kapitlet skal vi anvende vår kunnskap om egenverdier og egenvektorer til å analysere matriser og deres tilsvarende lineærtransformasjoner Eksempel Vi begynner med et eksempel
Kapittel Diagonalisering I te kapitlet skal vi anvende vår kunnskap om egenverdier og egenvektorer til å analysere matriser og deres tilsvarende lineærtransformasjoner Eksempel Vi begynner med et eksempel
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Avsluttende eksamen i AST2000, 13. desember 2017, 14.30 18.30 Oppgavesettet inkludert formelsamling er på 8 sider Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Avsluttende eksamen i AST2000, 13. desember 2017, 14.30 18.30 Oppgavesettet inkludert formelsamling er på 8 sider Tillatte hjelpemidler:
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Løsningsforslag til ukeoppgave 4
 Oppgaver FYS1001 Vår 2018 1 Løsningsforslag til ukeoppgave 4 Oppgave 4.03 W = F s cos(α) gir W = 1, 2 kj b) Det er ingen bevegelse i retning nedover, derfor gjør ikke tyngdekraften noe arbeid. Oppgave
Oppgaver FYS1001 Vår 2018 1 Løsningsforslag til ukeoppgave 4 Oppgave 4.03 W = F s cos(α) gir W = 1, 2 kj b) Det er ingen bevegelse i retning nedover, derfor gjør ikke tyngdekraften noe arbeid. Oppgave
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 6 juni 2017 Tid for eksamen: 14:30 18:30 (4 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 6 juni 2017 Tid for eksamen: 14:30 18:30 (4 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark Tillatte
MAT1110. Obligatorisk oppgave 1 av 2
 30. mai 2017 Innleveringsfrist MAT1110 Obligatorisk oppgave 1 av 2 Torsdag 23. FEBRUAR 2017, klokken 14:30 i obligkassen, som står i gangen utenfor ekspedisjonen i 7. etasje i Niels Henrik Abels hus. Instruksjoner
30. mai 2017 Innleveringsfrist MAT1110 Obligatorisk oppgave 1 av 2 Torsdag 23. FEBRUAR 2017, klokken 14:30 i obligkassen, som står i gangen utenfor ekspedisjonen i 7. etasje i Niels Henrik Abels hus. Instruksjoner
Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: Løsningsforslag. Oppgave 1
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: 09.00 12.00 Løsningsforslag Oppgave 1 Robertson-Walker metrikken
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: 09.00 12.00 Løsningsforslag Oppgave 1 Robertson-Walker metrikken
Løsningsforslag Eksamen i Fys-mek1110 våren 2010
 Side av Løsningsforslag Eksamen i Fys-mek våren Oppgave (Denne oppgaven teller dobbelt) Ole og Mari vil prøve om lengdekontraksjon virkelig finner sted. Mari setter seg i sitt romskip og kjører forbi Ole,
Side av Løsningsforslag Eksamen i Fys-mek våren Oppgave (Denne oppgaven teller dobbelt) Ole og Mari vil prøve om lengdekontraksjon virkelig finner sted. Mari setter seg i sitt romskip og kjører forbi Ole,
