Integrasjon. October 14, Department of Mathematical Sciences, NTNU, Norway. Integrasjon
|
|
|
- Halfdan Askeland
- 8 år siden
- Visninger:
Transkript
1 Deprtmet of Mthemticl Scieces, NTNU, Norwy Octoer 14, 2014
2 Forelesig , 5.1, 5.2 Summer Arel uder grfe til e fuksjo som greseverdi til e summe
3 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m
4 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe f (i) i=m meer vi f (i) = f (m) + f (m + 1) + + f () i=m
5 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio.
6 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 5 i 2 = = 55 i=1
7 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 Eksempel 2 5 i 2 = = 55 i=1 3 k= 2 1 k + 7
8 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 Eksempel 2 5 i 2 = = 55 i=1 3 k= 2 1 k + 7 = 1 5 +
9 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 Eksempel 2 5 i 2 = = 55 i=1 3 k= 2 1 k + 7 =
10 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 Eksempel 2 5 i 2 = = 55 i=1 3 k= 2 1 k + 7 =
11 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 Eksempel 2 5 i 2 = = 55 i=1 3 k= 2 1 k + 7 =
12 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 Eksempel 2 5 i 2 = = 55 i=1 3 k= 2 1 k + 7 =
13 Sigm otsjo L m og være heltll og m og l f være e fuksjo defiert på heltllee m, m + 1,.... D med otsjoe meer vi f (i) i=m f (i) = f (m) + f (m + 1) + + f () i=m m lower limit, upper limit of summtio. Eksempel 1 Eksempel 2 5 i 2 = = 55 i=1 3 k= 2 1 k + 7 =
14 Egeskper med summer i=m (A f (i) + B g(i)) = A i=m f (i) + B g(i) i=m
15 Egeskper med summer i=m (A f (i) + B g(i)) = A i=m f (i) + B g(i) i=m m+ f (j) = f (m) + f (m + 1) + + f (m + ) j=m
16 Egeskper med summer i=m (A f (i) + B g(i)) = A i=m f (i) + B g(i) i=m m+ f (j) = f (m) + f (m + 1) + + f (m + ) j=m = f (i + m) i=0 Eksempel 3 Skriv 17 j=3 1 + j 2 i forme f (i). Hvis vi setter i=1 j = i + 2, d for j = 3 lir det i = 1 og for j = 17 lir det i = 15, so j=3 1 + j 2 = i=1 1 + (i + 2) 2
17 Lukkede former for summer 1 1 i=1
18 Lukkede former for summer 1 1 = i=1
19 Lukkede former for summer 1 1 = = i=1
20 Lukkede former for summer 1 1 = = i=1 2 Bevis S = i=1 i = = ( + 1) 2 S = ( 1) + S = + ( 1) + ( 2) S = ( + 1) + ( + 1) + ( + 1) ( + 1) + ( + 1)
21 Lukkede former for summer 1 i 2 = ( + 1)(2 + 1) = i=1 6
22 Lukkede former for summer 1 i 2 = ( + 1)(2 + 1) = i=1 6 2 i=1 r i 1 = 1 + r + r 2 + r r 1 = r 1 r 1 hvis r 1. Eksempel 4 (6k 2 4k + 3), 1 m <. k=m+1
23 Kp 5.2. Areler som grevseverdier v summer L f være e ikke-egtiv kotiuerlig fuksjo. Arele uder grfe y = f (x) og mellom de vertikle lijee x = og x =, der <. Del itervllet [, ] i suitervller l Summe = x 0 < x 1 < x 2 < < x 1 < x = x i = x i x i 1, i = 1, 2, 3,..., ). S = f (x 1 ) x 1 + f (x 2 ) x f (x ) x
24 Kp 5.2. Areler som grevseverdier v summer L f være e ikke-egtiv kotiuerlig fuksjo. Arele uder grfe y = f (x) og mellom de vertikle lijee x = og x =, der <. Del itervllet [, ] i suitervller l Summe = x 0 < x 1 < x 2 < < x 1 < x = x i = x i x i 1, i = 1, 2, 3,..., ). S = f (x 1 ) x 1 + f (x 2 ) x f (x ) x = er e tilærmelse v rele uder grfe y = f (x) og A = lim S. i=1 f (x i ) x i
25 Kp 5.2. Areler som grevseverdier v summer L f være e ikke-egtiv kotiuerlig fuksjo. Arele uder grfe y = f (x) og mellom de vertikle lijee x = og x =, der <. Del itervllet [, ] i suitervller l Summe = x 0 < x 1 < x 2 < < x 1 < x = x i = x i x i 1, i = 1, 2, 3,..., ). S = f (x 1 ) x 1 + f (x 2 ) x f (x ) x = er e tilærmelse v rele uder grfe y = f (x) og A = lim S. (Show tutor i Mple) Merk: Noe gger ruker m i=1 f (x i ) x i x i = x =, x i = + i x = + i ( ), 0 i.
26 Eksempel 1 Fi rele til område uder lije y = x + 1, over x-kse og mellom lijee x = 0 og x = 2.
27 Eksempel 1 Fi rele til område uder lije y = x + 1, over x-kse og mellom lijee x = 0 og x = Figure : Approksimsjo v rele.
28 Eksempel 1 Fi rele til område uder lije y = x + 1, over x-kse og mellom lijee x = 0 og x = Figure : Approksimsjo v rele. x 0 = 0, x 1 = 2, x 2 = 4,..., x = 2 = 2. y = x + 1, y 0 = 1, y 1 = 2 + 1, y 2 = 4 + 1,..., y = 2 + 1
29 Eksempel 1 S = i=1 ( 2i + 1) 2 = 2 [ 2 i + 1] = 2 [ 2 i=1 i=1 i=1 i + 1] i=1 = 2 [ 2 ( + 1) + ] 2 = A = lim S = lim ( ) = = 4
30 Eksempel 2 Fi rele til område uder grfe til y = x 2, og lijee y = 0, x = 0 og x =, med > 0.
31 Eksempel 2 Fi rele til område uder grfe til y = x 2, og lijee y = 0, x = 0 og x =, med > Figure : Approksimsjo v rele.
32 Eksempel 2 Fi rele til område uder grfe til y = x 2, og lijee y = 0, x = 0 og x =, med > Figure : Approksimsjo v rele. y = x 2, x 0 = 0, x 1 =, x 2 = 2,..., x = =. y 0 = 0, y 1 = 2 2, y 2 = 42 2,..., y = 2
33 Eksempel 2 S = i=1 = 3 3 ( i )2 i=1 i 2 = 3 ( + 1)(2 + 1) 3 6 A = lim S = lim ( 3 ( + 1)(2 + 1) 6 2 ) = 3 3
34 Eksempel 4 Idetifiser greseverdie som e rel og evluer de. Løsig: itervller hr redde 1 L = lim i=1 i 2 L = lim (1 i i=1 ) 1 og deler opp itervllet [0, 1] vi hr x i = i 1, y i = 1 x i = f (x i ), x = 1, S = x i=1 f (x i ), f (x) = 1 x rele uder grfe y = 1 x og mellom lijee y = 0, x = 0 og x = 1.
35 Eksempel 4 Idetifiser greseverdie som e rel og evluer de. Løsig: S = i=1 L = lim i=1 (1 i ) 1 = 1 [ i=1 1 1 i 2 i=1 i] = 1 ( + 1) [ ] 2 S = = lim S = 1 2
36 Forelesig : Det estemte itegrlet og egeskper ved det estemte itegrlet (lieritet, itegrler v jeve og odde fuksjoer) Middelverdisetig for itegrler Fudmetlteorem med vedelser og eksempler
37 Det estemte itegrlet Vi tr t f er defiert på et lukket itervll [, ] og er kotiuerlig på itervllet, til å egie med tr vi t f 0.
38 Det estemte itegrlet Vi tr t f er defiert på et lukket itervll [, ] og er kotiuerlig på itervllet, til å egie med tr vi t f 0. Gitt et itervll [, ] e prtisjo v [, ] er e megde som estår v pukter til [.]: slik t P = {x 0, x 1,..., x 1, x } = x 0 < x 1 < < x 1 < x =.
39 Det estemte itegrlet Vi tr t f er defiert på et lukket itervll [, ] og er kotiuerlig på itervllet, til å egie med tr vi t f 0. Gitt et itervll [, ] e prtisjo v [, ] er e megde som estår v pukter til [.]: slik t P = {x 0, x 1,..., x 1, x } = x 0 < x 1 < < x 1 < x =. og vi lr x i = x i x i 1 for i = 1,...,.
40 Det estemte itegrlet Vi tr t f er defiert på et lukket itervll [, ] og er kotiuerlig på itervllet, til å egie med tr vi t f 0. Gitt et itervll [, ] e prtisjo v [, ] er e megde som estår v pukter til [.]: slik t P = {x 0, x 1,..., x 1, x } = x 0 < x 1 < < x 1 < x =. og vi lr x i = x i x i 1 for i = 1,...,. f er kotiuerlig på hver suitervll [x i 1, x i ] d ekstremlverdisetig (kp. 1.4) grterer t det fies l i [x i 1, x i ] og u i [x i 1, x i ] slik t f (l i ) f (x) f (u i ), x [x i 1, x i ]
41 Det estemte itegrlet Vi tr t f er defiert på et lukket itervll [, ] og er kotiuerlig på itervllet, til å egie med tr vi t f 0. Gitt et itervll [, ] e prtisjo v [, ] er e megde som estår v pukter til [.]: slik t P = {x 0, x 1,..., x 1, x } = x 0 < x 1 < < x 1 < x =. og vi lr x i = x i x i 1 for i = 1,...,. f er kotiuerlig på hver suitervll [x i 1, x i ] d ekstremlverdisetig (kp. 1.4) grterer t det fies l i [x i 1, x i ] og u i [x i 1, x i ] slik t f (l i ) f (x) f (u i ), x [x i 1, x i ] d rele A i uder grfe til f på itervllet [x i 1, x i ] tilfredstiller f (l i ) x i A i f (u i ) x i
42 Husk: Teorem 8, kp 1.4: ekstremlverdisetig (Mi-mx) Hvis f er kotiuerlig på [x i 1, x i ] fies det tll l i og u i slik t for lle x [x i 1, x i ] m M miimumverdi mximumverdi m = f (l i ) f (x) f (u i ) = M. 8 M 6 4 f(x) 2 p 0 q 2 m x
43 Riem summer Nedre Riem sum for fuksjoe f og prtisjoe P L(f, P) = i=1 f (l i ) x i Ovre Riem sum for fuksjoe f og prtisjoe P U(f, P) = i=1 f (u i ) x i Eksempel 1: Fi ovre og edre Riem sum for f (x) = 1 x på itervllet [1, 2] med e prtisjo i fire suitervller v smme legde. Eksempel 2: Fi ovre og edre Riem sum for f (x) = x 2 på itervllet [0, ] med e prtisjo i suitervller v smme legde.
44 Det estemte itegrlet Vi vil å t fiere og fiere prtisjoer slik t, i itervllet [x i 1, x i ], lir vvike mellom rele A i uder grfe til f og relee til rektglee f (l i ) x i og f (u i ) x i midre og midre.
45 Det estemte itegrlet Vi vil å t fiere og fiere prtisjoer slik t, i itervllet [x i 1, x i ], lir vvike mellom rele A i uder grfe til f og relee til rektglee f (l i ) x i og f (u i ) x i midre og midre. For e hver utvlgt prtisjo P vi hr L(f, P) U(f, P) og d (v kompletthete v de reelle tll) må det fies mist et tll I slik t L(f, P) I U(f, P).
46 Det estemte itegrlet Vi vil å t fiere og fiere prtisjoer slik t, i itervllet [x i 1, x i ], lir vvike mellom rele A i uder grfe til f og relee til rektglee f (l i ) x i og f (u i ) x i midre og midre. For e hver utvlgt prtisjo P vi hr L(f, P) U(f, P) og d (v kompletthete v de reelle tll) må det fies mist et tll I slik t L(f, P) I U(f, P). Defiisjo At t det fies øyktig et tll I slik t for e hver prtisjo P v itervllet [, ] vi hr L(f, P) I U(f, P) d sier vi t f er itegrerr og t I er det estemte itegrlet til f i [, ].
47 Det estemte itegrlet Vi vil å t fiere og fiere prtisjoer slik t, i itervllet [x i 1, x i ], lir vvike mellom rele A i uder grfe til f og relee til rektglee f (l i ) x i og f (u i ) x i midre og midre. For e hver utvlgt prtisjo P vi hr L(f, P) U(f, P) og d (v kompletthete v de reelle tll) må det fies mist et tll I slik t L(f, P) I U(f, P). Defiisjo At t det fies øyktig et tll I slik t for e hver prtisjo P v itervllet [, ] vi hr L(f, P) I U(f, P) d sier vi t f er itegrerr og t I er det estemte itegrlet til f i [, ]. Vi skriver I = f (x) dx
48 Eksempel 3 Vis t f (x) = x 2 er itegrerr på itervllet [0, ] der > 0, fi 0 x 2 dx. Løsig Vi ser på greseversider for v edre og ovre Riem summer for f over [0, ] d lim ) = (( ) 3 lim = lim ) = ( + 1)(2 + 1) 3 lim = L(f, P ) 3 3 U(f, P ). Merk å t for e hver P (usett hvor fi de er) fies det stor ok slik t P er fiere e P, dette etyr t L(f, P) L(f, P ) 3 3 U(f, P ) U(f, P), og d er 3 3 det estemte itegrlet v f på [0, ], 0 x 2 dx = 3 3.
49 Vi hr egreset oss til å teke på ikke egtive fuksjoer me lt k geerliseres til fuksjoer som ikke er positive eller som skifter froteg på [, ].
50 Vi hr egreset oss til å teke på ikke egtive fuksjoer me lt k geerliseres til fuksjoer som ikke er positive eller som skifter froteg på [, ]. For ikke positive fuksjoer, rektglee til ovre og edre Riem summer får egtive reler.
51 Vi hr egreset oss til å teke på ikke egtive fuksjoer me lt k geerliseres til fuksjoer som ikke er positive eller som skifter froteg på [, ]. For ikke positive fuksjoer, rektglee til ovre og edre Riem summer får egtive reler. For fuksjoer som skifter forteg lt fugerer som før me det løer seg å fie der fuskjoe sjkærer x-kse, og dele [, ] i suitervller der f er ete ikke egtiv eller ikke positiv, og så joe seprt med de foskjellige delee v f.
52 Vi hr egreset oss til å teke på ikke egtive fuksjoer me lt k geerliseres til fuksjoer som ikke er positive eller som skifter froteg på [, ]. For ikke positive fuksjoer, rektglee til ovre og edre Riem summer får egtive reler. For fuksjoer som skifter forteg lt fugerer som før me det løer seg å fie der fuskjoe sjkærer x-kse, og dele [, ] i suitervller der f er ete ikke egtiv eller ikke positiv, og så joe seprt med de foskjellige delee v f. Teorem 2 Alle kotiuerlige fuksjoer på [, ] er itegrerre.
53 Egeskper med det estemte itegrlet f (x)dx = 0
54 Egeskper med det estemte itegrlet f (x)dx = 0 f (x)dx = f (x)dx
55 Egeskper med det estemte itegrlet f (x)dx = 0 f (x)dx = f (x)dx (Af (x) + Bg(x)) dx = A f (x)dx + B g(x)dx
56 Egeskper med det estemte itegrlet f (x)dx = 0 f (x)dx = f (x)dx (Af (x) + Bg(x)) dx = A f (x)dx + B g(x)dx f (x)dx + c f (x)dx = c f (x)dx
57 Egeskper med det estemte itegrlet Hvis og f (x) g(x) på [, ] d f (x)dx g(x)dx
58 Egeskper med det estemte itegrlet Hvis og f (x) g(x) på [, ] d f (x)dx g(x)dx f (x)dx f (x) dx
59 Egeskper med det estemte itegrlet Hvis og f (x) g(x) på [, ] d f (x)dx g(x)dx f (x)dx f (x) dx For odde fuksjoer (dvs fuksjoer slik t f ( x) = f (x)) vi hr f (x)dx = 0
60 Egeskper med det estemte itegrlet Hvis og f (x) g(x) på [, ] d f (x)dx g(x)dx f (x)dx f (x) dx For odde fuksjoer (dvs fuksjoer slik t f ( x) = f (x)) vi hr f (x)dx = 0 For like fuksjoer (dvs f (x) = f ( x)) f (x)dx = 2 f (x)dx 0
61 Forelesig : ,6.1 Egeskper med det estemte itegrlet. Alyses fudmetlteorem Sustitusjo Arelet mellom to kurver ved ruk v itegrlet
62 Egeskper med det estemte itegrlet For odde fuksjoer (dvs fuksjoer slik t f ( x) = f (x)) vi hr f (x)dx = 0
63 Egeskper med det estemte itegrlet For odde fuksjoer (dvs fuksjoer slik t f ( x) = f (x)) vi hr f (x)dx = 0 For like fuksjoer (dvs f (x) = f ( x)) f (x)dx = 2 f (x)dx 0
64 Middelverdisetig for itegrler L f være kotiuerlig på [, ] d fies det et pukt c (, ) slik t f (x)dx = ( )f (c)
65 Fudmetlteoremet: del I L f være kotiuerlig på et itervll I som iholder puktet. Betrkt F (x) = x f (t)dt d er F deriverr på itervllet I og F (x) = f (x)
66 Fudmetlteoremet: del I L f være kotiuerlig på et itervll I som iholder puktet. Betrkt F (x) = x f (t)dt d er F deriverr på itervllet I og F (x) = f (x) Bevis F (x) = F (x + h) F (x) lim h 0 h = 1 lim h 0 h ( x+h f (t)dt = lim h f (c) h = lim f (c) c x = f (x) h 0 1 c = c(h) x 1 x+h f (t)dt) = lim h 0 h x f (t)dt
67 Fudmetlteoremet: del II L f være kotiuerlig på et itervll som iholder puktet. L G være e fuksjo slik t G (x) = f (x) (tideriverte til f ) d f (x)dx = G() G()
68 Fudmetlteoremet: del II L f være kotiuerlig på et itervll som iholder puktet. L G være e fuksjo slik t G (x) = f (x) (tideriverte til f ) d f (x)dx = G() G() Bevis Side G (x) = f (x) d lso d dx x f (t)dt = f (x) d må det vre x f (t)dt = G(x) + C og så f (t)dt = 0 = G() + C, C = G() f (t)dt = G() + C = G() G()
69 Eksempler 1 Fi verdie v itegrlet 2 1 (x 2 3x + 2)dx. Side d dx ( 1 3 x x 2 + 2x) = x 2 3x + 2 ved fudmetlteoremet del 2 vi hr 2 (x 2 3x+2)dx = ( x x 2 + 2x) 2 1 = ( ) = Fi rele uder kurve y = si(x), over y = 0 fr x = 0 til x = π. A = 0 π si(x) dx = cos(x) π 0 = ( 1 (1)) = 2. 3 Fi sittverdi v f (x) = e x + cos(x) på itevllet [ π 2, 0]. f = 1 0 ( π 2 ) 0 π 2 (e x +cos(x)) dx = 2 π ( e x + si(x)) 0 π 2 = 2 π e π 2
70 Sustitusjo for estemte itegrler Husk kjæreregel d dt f (g(t)) = f (g(t)) g (t) ved fudmetlteoremet (del 2) vi får f (g(t)) g (t) dt = f (g()) f (g()) hvis A = g() og B = g() vi k skrive f (g(t)) g (t) dt = f (B) f (A) = A B f (u) du
71 Eksempler Oppgve 45 Fi 0 π cos(x)dx. Løsig Vi skl ruke t 1 + cos(x) = 2 cos 2 ( x 2 ) og f (g(x)) g (x) dx = f (g()) f (g()). Ved hjelp v 1 + cos(x) = 2 cos 2 ( x ) vi får 2 π cos(x)dx = 2 l 0 π π 2 cos( x 2 ) dx, g(x) = x 2, g (x) = 1 2, f (u) = cos(u), f (u) = si(u) 1 + cos(x)dx = π 2 cos( x 2 )1 2 dx = 2 2 = 2 2(f (g( π 2 )) f (g(0))) = 2 2(si( π 4 ) si(0)) 0 π 2 f (g(x)) g (x) dx =
72 Oppgve 45 Fi 0 π cos(x)dx = 2 0 π 2 cos( x 2 ) dx, Løsig Vi k ruke sustitusjo på e litt e måte ved å defiere A = g() og B = g() og så ruke Som før tr vi f (g(x)) g (x) dt = f (B) f (A) = A B f (u) du. g(x) = x 2, g (x) = 1 2, f (u) = cos(u), f (u) = si(u) d A = 0 2 = 0 og B = π 4 vi ruker formele i rekkefølge dette gir π 2 f (g(x)) g (x) dt = cos( x 2 ) 1 2 dx = π 4 A B f (u) du = f (B) f (A) cos(u) du = 2 2(si( π ) si(0)) = 2. 4
73 Eksempler Oppgve 18 Fi det uestemte itegrlet dx e x + e x Løsig Dette etyr t vi skl fie de tideriverte v fukjoe og legge til e kostt. Ved hjelp v fudmetlteorem del 1 de tideriverte er x dt F (x) = e t + e t, og Vi å ruker sustitusjo for å fie F (u) og Vi prøver med dx e x = F (x) + C. + e x u F (u) = f (g(x)) g (x) dx = f (g(u)) f (g()). g(x) = e x, g (x) = e x, f (y) = 1 y 2 + 1, u dx F (u) = e x + e x = u f (g(x)) g u (x) dx = og dx e x + e x = rct(ex ) + C f (y) = rct(y) e x dx (e 2x + 1) = rct(eu ) rct(e ),
74 Eksempler, litt erledes ruk v sustitusjo Oppgve 18 Fi det uestemte itegrlet dx e x + e x Løsig Dette etyr t vi skl fie de tideriverte v fukjoe og legge til e kostt. Ved hjelp v fudmetlteorem del 1 de tideriverte er x dt F (x) = e t + e t, og dx e x = F (x) + C. + e x Vi å ruker sustitusjo for å fie F (u) og vi ruker som før g(x) = e x, g (x) = e x, f (y) = 1 y 2 + 1, og ved å defiere A = g() = e og U = g(u) = e u og så ruke f (y) = rct(y) u dx F (u) = e x + e x = u e x dx ((e x ) 2 + 1) = u f (g(x)) g U (x) dx = f (y) dy = f (U) f (A). A og så U 1 F (u) = A y dy = rct(u) rct(a) = rct(eu ) rct(e ), dx e x + e x = rct(ex ) + C
75 Arele mellom to kurver Eksempel 2 Fi rele v område omriget v kurvee y = x 2 2x og y = 4 x 2. Eksempel 3 Fi rele v område som ligger mellom kurve y = si(x) og y = cos(x) fr x = 0 til x = 2π. Eksempel 4 Fi rele v område som ligger på høyre side v prele x = y 2 12 og til vestre for lije y = x
Integrasjon del 2. October 15, Department of Mathematical Sciences, NTNU, Norway. Integrasjon
 Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
Integrsjon del Deprtment of Mthemticl Sciences, NTNU, Norwy Octoer 5, 4 Integrsjon Sustitusjon for estemte integrler Husk kjærneregel d dt f (g(t)) = f (g(t)) g (t) ved fundmentlteoremet (del ) vi får
Høgskolen i Agder Avdeling for realfag EKSAMEN. begrunn = grunngi beregn = rekn ut
 Høgskole i Agder Avdelig for relfg EKSAMEN Emekode: MA 410 Emev: Reell lyse Oppgver med forslg til løsiger Dto: 4. mi 000 Vrighet: 09.00-14.00 Atll sider iklusivt forside: Tilltte hjelpemidler: Alle Nyorsktekste
Høgskole i Agder Avdelig for relfg EKSAMEN Emekode: MA 410 Emev: Reell lyse Oppgver med forslg til løsiger Dto: 4. mi 000 Vrighet: 09.00-14.00 Atll sider iklusivt forside: Tilltte hjelpemidler: Alle Nyorsktekste
f '( x) 28x 6x 2 ( 2) x x 4(3t 2 s) 6s 2x 6(3t 2 s) 2t ln x 2ln y med bibetingelsen 2x y m. Her er m 0
 Fsit obligtorisk oppgve Oppgve (9 poeg) Deriver følgede fuksjoer med hes på lle rgumeter ) f ( ) 7 f '( ) 8 6 svr: b) Svr: g ( ) ( ) ( ) g ( ) ( ) ( ) c) h( ) f ( )( ) Svr: h( ) f '( )( ) f ( ) d) Svr:
Fsit obligtorisk oppgve Oppgve (9 poeg) Deriver følgede fuksjoer med hes på lle rgumeter ) f ( ) 7 f '( ) 8 6 svr: b) Svr: g ( ) ( ) ( ) g ( ) ( ) ( ) c) h( ) f ( )( ) Svr: h( ) f '( )( ) f ( ) d) Svr:
Integrasjon av trigonometriske funksjoner
 Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
Integrsjon v trigonometriske funksjoner øistein Søvik 3. november 15 I dette dokumentet skl jeg vise litt ulike integrsjonsteknikker og metoder for å utforske integrlene v (cos x) og (sin x). De bestemte
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGSKOLEN I SØR-TRØNDELAG Målform: Eksmesdto: 5. jui 03 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsse(r): Studiepoeg: Fglærer(e): (v og telefor på eksmesdge) Bygg, Elektro, Mski, Kjemi,
HØGSKOLEN I SØR-TRØNDELAG Målform: Eksmesdto: 5. jui 03 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsse(r): Studiepoeg: Fglærer(e): (v og telefor på eksmesdge) Bygg, Elektro, Mski, Kjemi,
Løsningsforslag Eksamen MAT112 vår 2011
 Løsigsforslag Eksame MAT vår OPPGAVE Gitt følge {a } defiert rekursivt ved a = 5, a + = a + 6, =,,, 3,.... (a) Vis (for eksempel ved iduksjo) at {a } er stregt avtagede og edtil begreset. (b) Avgjør om
Løsigsforslag Eksame MAT vår OPPGAVE Gitt følge {a } defiert rekursivt ved a = 5, a + = a + 6, =,,, 3,.... (a) Vis (for eksempel ved iduksjo) at {a } er stregt avtagede og edtil begreset. (b) Avgjør om
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGKOLEN I ØR-TRØNDELAG Avdelig for tekologi Målform: Eksmesdto: 3. mrs 03 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsse(r): tudiepoeg: Fglærer(e): (v og telefor på eksmesdge) Bygg,
HØGKOLEN I ØR-TRØNDELAG Avdelig for tekologi Målform: Eksmesdto: 3. mrs 03 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsse(r): tudiepoeg: Fglærer(e): (v og telefor på eksmesdge) Bygg,
MA1102 Grunnkurs i Analyse II Vår 2017
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA2 Grukurs i Aalyse II Vår 27 Løsigsforslag Øvig 7 2.5: For hvilke x kovergerer rekke? b) (2x) c) (l x) e) 2 si x 2 b) Dette er
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA2 Grukurs i Aalyse II Vår 27 Løsigsforslag Øvig 7 2.5: For hvilke x kovergerer rekke? b) (2x) c) (l x) e) 2 si x 2 b) Dette er
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksmesdto: 3. mrs 04 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsser: Studiepoeg: Bygg, Elektro, Mski, Kjemi, Logistikk,
HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksmesdto: 3. mrs 04 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsser: Studiepoeg: Bygg, Elektro, Mski, Kjemi, Logistikk,
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGKOLEN I ØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksmesdto: 5. jui 04 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsser: tudiepoeg: Bygg, Elektro, Mski, Kjemi, Logistikk,
HØGKOLEN I ØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksmesdto: 5. jui 04 Vrighet/eksmestid: Emekode: 3 timer ALM304V Emev: Mtemtikk 4 Klsser: tudiepoeg: Bygg, Elektro, Mski, Kjemi, Logistikk,
Vi skal hovedsakelig ikke bestemme summen men om rekken konvergerer. det vil si om summen til rekken er et bestemt tall
 Kapittel 8 Oppsummerig-Rekker Rekker er summe til edelig eller uedelig mage ledd i e tallfølge. Potesrekker ka beyttes til å uttrykke vaskelige fuksjoer om et pukt. Ma ka skreddesy potesfuksjoer ved hjelp
Kapittel 8 Oppsummerig-Rekker Rekker er summe til edelig eller uedelig mage ledd i e tallfølge. Potesrekker ka beyttes til å uttrykke vaskelige fuksjoer om et pukt. Ma ka skreddesy potesfuksjoer ved hjelp
S2 kapittel 1 Rekker Utvalgte løsninger oppgavesamlingen
 Utvlgte løsiger oppgvesmlige S kpittel Rekker Utvlgte løsiger oppgvesmlige 0 Vi k prøve med differsemetode Differsee mellom leddee utover er 4,6,8, så det er rimelig t differse mellom femte og fjerde ledd
Utvlgte løsiger oppgvesmlige S kpittel Rekker Utvlgte løsiger oppgvesmlige 0 Vi k prøve med differsemetode Differsee mellom leddee utover er 4,6,8, så det er rimelig t differse mellom femte og fjerde ledd
Kapittel 9 ALGEBRA. Hva er algebra?
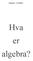 Kpttel 9 ALGEBRA Hv er lger? Kpttel 9 ALGEBRA Alger Ekelt k v s t lger er å rege me okstver steet for tll. Når v løser lgger, står okstve (vlgvs for et estemt tll. Når v ruker lger tl å utlee formler eller
Kpttel 9 ALGEBRA Hv er lger? Kpttel 9 ALGEBRA Alger Ekelt k v s t lger er å rege me okstver steet for tll. Når v løser lgger, står okstve (vlgvs for et estemt tll. Når v ruker lger tl å utlee formler eller
Integralregning. Mål. for opplæringen er at eleven skal kunne
 8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
8 Integrlregning Mål for opplæringen er t eleven skl kunne gjøre rede for definisjonen v estemt integrl som grense for en sum og uestemt integrl som ntiderivert eregne integrler v de sentrle funksjonene
Faktorisering. 1 Hva er faktorisering? 2 Hvorfor skal vi faktorisere? Per G. Østerlie Senter for IKT i utdanningen 11.
 Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
Fktorisering Per G. Østerlie Senter for IKT i utdnningen per@osterlie.no 11. mi 013 1 Hv er fktorisering? Vi må se på veret å fktorisere. Hv er det vi skl gjøre når vi fktoriserer? Svret er: å lge fktorer.
M2, vår 2008 Funksjonslære Integrasjon
 M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
M, vår 008 Funksjonslære Integrsjon Avdeling for lærerutdnning, Høgskolen i Vestfold. pril 009 1 Arelet under en grf Vi begynner vår diskusjon v integrsjon, på smme måte som vi begynte med derivsjon, ved
TMA4100 Matematikk 1 Høst 2006
 TMA4 Mtemtikk Høst 26 Norges tekisk turviteskpelige uiversitet Istitutt for mtemtiske fg Løsigsforslg, vsluttede eksme 5.2.26 De første greseverdie er e uestemt form v type "/", og L Hopitls regel gir
TMA4 Mtemtikk Høst 26 Norges tekisk turviteskpelige uiversitet Istitutt for mtemtiske fg Løsigsforslg, vsluttede eksme 5.2.26 De første greseverdie er e uestemt form v type "/", og L Hopitls regel gir
Integrasjon Skoleprosjekt MAT4010
 Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
Integrsjon Skoleprosjekt MAT4010 Tiin K. Kristinslund, Julin F. Rossnes og Torstein Hermnsen 19. mrs 2014 1 Innhold 1 Innledning 3 2 Integrsjon 3 3 Anlysens fundmentlteorem 7 4 Refernser 10 2 1 Innledning
R2 - Heldagsprøve våren 2013
 Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsskisser HD R R - Heldgsprøve våren 0 Løsningsskisser Viktigste oppsummeringer: Må skrive med penn på eksmen! Slurv og regnefeil, både med tll og bokstver, er hovedproblemet. Beste måten å fikse
Løsningsforslag til underveisvurdering i MAT111 vår 2005
 Løsningsforslag til underveisvurdering i MAT111 vår 5 Beregn grenseverdien Oppgave 1 (x 1) ln x x x + 1 Svar: Merk at nevneren er lik (x 1), så vi kan forkorte (x 1) oppe og nede og får (x 1) ln x ln x
Løsningsforslag til underveisvurdering i MAT111 vår 5 Beregn grenseverdien Oppgave 1 (x 1) ln x x x + 1 Svar: Merk at nevneren er lik (x 1), så vi kan forkorte (x 1) oppe og nede og får (x 1) ln x ln x
Løsningsforslag til eksamen i MAT111 Vår 2013
 BOKMÅL MAT - Vår Løsningsforslag til eksamen i MAT Vår Oppgave Finn polarrepresentasjonen til i. i Skriv på formen x + iy. i Løsning Finner først modulus og argument til i: i = ( ) + ( ) = 4 = arg( ( )
BOKMÅL MAT - Vår Løsningsforslag til eksamen i MAT Vår Oppgave Finn polarrepresentasjonen til i. i Skriv på formen x + iy. i Løsning Finner først modulus og argument til i: i = ( ) + ( ) = 4 = arg( ( )
1 Mandag 1. mars 2010
 Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
Mndg. mrs Fundmentlteoremet sier t integrsjon og derivsjon er motstte opersjoner. Vi hr de siste ukene sett hvordn vi på ulike måter kn derivere funksjoner i flere vrible. Nå er turen kommet til den motstte
TMA4100 Matematikk1 Høst 2008
 TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
TMA4 Mtemtikk Høst 8 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 6 5..5 Gjennomsnittet v f(x) = x på intervllet [, ] er lik relet A under grfen dividert
Fag: Matematikk 1T-Y for elever og privatister. Antall sider i oppgaven: 8 inklusiv forside og opplysningsside
 Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
Loklt gitt eksmen 2012 Eksmen Fg: Mtemtikk 1T-Y for elever og privtister Fgkode: MAT1006 Eksmensdto: 25. mi Antll sider i oppgven: 8 inklusiv forside og opplysningsside Eksmenstid: Hjelpemidler under eksmen:
Eksamen R2, Va ren 2013
 Eksame R, Va re 013 Oppgave 1 (4 poeg) Deriver fuksjoee a) f x 3cos x f x 3 six 3si x b) gx x 6si 7 Bruker kjereregele på uttrykket si x der og Vi har da guu siu u cosu cos x gx 6cos x 6 cos x u x g u
Eksame R, Va re 013 Oppgave 1 (4 poeg) Deriver fuksjoee a) f x 3cos x f x 3 six 3si x b) gx x 6si 7 Bruker kjereregele på uttrykket si x der og Vi har da guu siu u cosu cos x gx 6cos x 6 cos x u x g u
Utvidet løsningsforslag Eksamen i TMA4100 Matematikk 1, 16/12 2008
 Utvidet løsigsforslag Eksame i TMA4 Matematikk, 6/ 8 Oppgave i) Vi gjør substitusjoe u = si θ og får π/ [ u si θ cos θ dθ = u du = E ae løsigsmetode er π/ si θ cos θ dθ = π/ ] si θ dθ = 4 = 4 ( ( ) ( ))
Utvidet løsigsforslag Eksame i TMA4 Matematikk, 6/ 8 Oppgave i) Vi gjør substitusjoe u = si θ og får π/ [ u si θ cos θ dθ = u du = E ae løsigsmetode er π/ si θ cos θ dθ = π/ ] si θ dθ = 4 = 4 ( ( ) ( ))
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det mtemtisk-turviteskpelige fkultet Eksme i: STK1110 Sttistiske metoder og dtlyse Løsigsforslg Eksmesdg: Tirsdg 18. desemer 2018 Tid for eksme: 09.00 13.00 Oppgvesettet er på 5 sider.
UNIVERSITETET I OSLO Det mtemtisk-turviteskpelige fkultet Eksme i: STK1110 Sttistiske metoder og dtlyse Løsigsforslg Eksmesdg: Tirsdg 18. desemer 2018 Tid for eksme: 09.00 13.00 Oppgvesettet er på 5 sider.
ECON 2200 våren 2012: Oppgave på plenumsøvelse den 21. mars
 EON våre Jo Vislie ECON våre : Oppgve på pleumsøvelse de. mrs Oppgve E edrift produserer e vre i megde x med produtfusjoe x A, der er ru v reidsrft og er relpitl. Bedrifte opptrer som prisfst vtumstilpsser
EON våre Jo Vislie ECON våre : Oppgve på pleumsøvelse de. mrs Oppgve E edrift produserer e vre i megde x med produtfusjoe x A, der er ru v reidsrft og er relpitl. Bedrifte opptrer som prisfst vtumstilpsser
Ma1101. Part I. 1 Grunnleggende. 1.1 Noen symboler. 1.2 Tallene. 1.3 Noen algebraiske lover
 Prt I M1101 1 Grunnleggende 1.1 Noen symboler Union A B i A og/eller B Snitt A B i både A og B Element i B er et element i B Undersett A B A er et undersett v B Skikkelig undersett A B A er et undersett
Prt I M1101 1 Grunnleggende 1.1 Noen symboler Union A B i A og/eller B Snitt A B i både A og B Element i B er et element i B Undersett A B A er et undersett v B Skikkelig undersett A B A er et undersett
MAT 1001, Høsten 2009 Oblig 2, Løsningsforslag
 MAT 1001, Høsten 009 Oblig, sforslag a) En harmonisk svingning er gitt som en sum av tre delsvingninger H(x) = cos ( π x) + cos (π (x 1)) + cos (π (x )) Skriv H(x) på formen A cos (ω(x x 0 )). siden H(x)
MAT 1001, Høsten 009 Oblig, sforslag a) En harmonisk svingning er gitt som en sum av tre delsvingninger H(x) = cos ( π x) + cos (π (x 1)) + cos (π (x )) Skriv H(x) på formen A cos (ω(x x 0 )). siden H(x)
MAT 100A: Mappeeksamen 4
 . november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
. november, MAT A: Mppeeksmen Løsningsforslg Oppgve ) Vi bruker produktregelen: f (x) x rctn x + x + x Siden x og rctn x hr smme fortegn, og x ldri er negtiv, er f (x) positiv overlt, bortsett fr t f ().
TMA4100 Matematikk 1, 4. august 2014 Side 1 av 12. x 2 3x +2. x 2
 TMA4 Matematikk, 4. august 24 Side av 2 Oppgave Den rasjonale funksjonen p er definert som p(x) x2 3x +2 3x 2 5x +2. Finn de tre grenseverdiene lim xæ p(x), lim xæ p(x) og lim xæœ p(x). Løsning: x 2 3x
TMA4 Matematikk, 4. august 24 Side av 2 Oppgave Den rasjonale funksjonen p er definert som p(x) x2 3x +2 3x 2 5x +2. Finn de tre grenseverdiene lim xæ p(x), lim xæ p(x) og lim xæœ p(x). Løsning: x 2 3x
1T kapittel 1 Algebra Løsninger til oppgavene i læreboka
 T kpittel Alger Løsninger til oppgvene i læreok Oppgve. 0 8 ( 0) + 0 + ( 0) 0 8 Oppgve. 7 ( ) + + ( ) 7 Oppgve. ( ) + Oppgve. 0 ( ) 0 ( 0) ( ) 0 ( 0) : ( ) 0 : ( ) Oppgve. ( ) ( ) ( ) (,) ( ) (,) 9 Oppgve.
T kpittel Alger Løsninger til oppgvene i læreok Oppgve. 0 8 ( 0) + 0 + ( 0) 0 8 Oppgve. 7 ( ) + + ( ) 7 Oppgve. ( ) + Oppgve. 0 ( ) 0 ( 0) ( ) 0 ( 0) : ( ) 0 : ( ) Oppgve. ( ) ( ) ( ) (,) ( ) (,) 9 Oppgve.
Oppfriskningskurs i matematikk 2007
 Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Oppfriskningskurs i mtemtikk 2007 Mrte Pernille Htlo Institutt for mtemtiske fg, NTNU 6.-11. ugust 2007 Velkommen! 2 Temer Algebr Trigonometri Funksjoner og derivsjon Integrsjon Eksponensil- og logritmefunksjoner
Forkunnskaper i matematikk for fysikkstudenter. Derivasjon.
 Defiisjo av derivert Vi har stor ytte av å vite hvor raskt e fuksjo vokser eller avtar Mer presist: Vi øsker å bestemme stigigstallet til tagete til fuksjosgrafe P Q Figure til vestre viser hvorda vi ka
Defiisjo av derivert Vi har stor ytte av å vite hvor raskt e fuksjo vokser eller avtar Mer presist: Vi øsker å bestemme stigigstallet til tagete til fuksjosgrafe P Q Figure til vestre viser hvorda vi ka
2 Algebra R2 Løsninger
 Algebr R Løsiger. Tllfølger.... Tllrekker... 7. Uedelige geometriske rekker... 8. Iduksjosbevis... 55.5 Eksmesoppgver... 6 Øvigsoppgver og løsiger Stei Aese og Olv Kristese/NDLA Eksmesoppgvee er hetet
Algebr R Løsiger. Tllfølger.... Tllrekker... 7. Uedelige geometriske rekker... 8. Iduksjosbevis... 55.5 Eksmesoppgver... 6 Øvigsoppgver og løsiger Stei Aese og Olv Kristese/NDLA Eksmesoppgvee er hetet
Oppfriskningskurs i matematikk Oppgaveheftet Oppsummeringsnotater Oppgaver med fasit Høsten 2018 Amir Massoud Hashemi
 Oppgvehefte Oppfriskigskurs- NITO Studetee/AIØ-HVL Oppfriskigskurs i mtemtikk Oppgveheftet Oppsummerigsotter Oppgver med fsit Høste 08 Amir Mssoud Hshemi I oppfriskigskurset skl vi prøve å gå gjeom følgede
Oppgvehefte Oppfriskigskurs- NITO Studetee/AIØ-HVL Oppfriskigskurs i mtemtikk Oppgveheftet Oppsummerigsotter Oppgver med fsit Høste 08 Amir Mssoud Hshemi I oppfriskigskurset skl vi prøve å gå gjeom følgede
Odd Heir John Engeseth Håvard Moe Ørnulf Borgan BOKMÅL. Særtrykk. Matematikk 1T
 Odd Heir Joh Egeseth Håvrd Moe Ørulf Borg BOKMÅL Særtrykk Mtemtikk T Odd Heir Joh Egeseth Håvrd Moe Ørulf Borg BOKMÅL Mtemtikk T Ihold Alger A Tllregig 7 B Tllmegder C Potesregig 0 D Store og små tll
Odd Heir Joh Egeseth Håvrd Moe Ørulf Borg BOKMÅL Særtrykk Mtemtikk T Odd Heir Joh Egeseth Håvrd Moe Ørulf Borg BOKMÅL Mtemtikk T Ihold Alger A Tllregig 7 B Tllmegder C Potesregig 0 D Store og små tll
1 k 2 + 1, k= 5. i=1. i = k + 6 eller k = i 6. m+6. (i 6) i=1
 TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
TMA4 Høst 6 Norges teknisk nturvitenskpelige universitet Institutt for mtemtiske fg Løsningsforslg Øving 5 5..6 Vi er gitt summen og ønsker å skrive den på formen m k=5 k +, f(i). i= Strtpunktene er henholdsvis
Sammendrag kapittel 1 - Aritmetikk og algebra
 Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
Smmendrg kpittel 1 - Aritmetikk og lgebr Regneregler for brøker Utvide brøk: Gng med smme tll i teller og nevner. b = k b k Forkorte brøk: del med smme tll i teller og nevner. b = : k b : k Summere brøker:
Oppfriskningskurs i matematikk Oppgaveheftet Oppsummeringsnotater Oppgaver med fasit Høsten 2016 Amir Massoud Hashemi
 Oppgveheftet Oppfriskigskurset- NITO Studetee/AIØ-HiB Oppfriskigskurs i mtemtikk Oppgveheftet Oppsummerigsotter Oppgver med fsit Høste 6 Amir Mssoud Hshemi I oppfriskigskurset skl vi prøve å gå gjeom følgede
Oppgveheftet Oppfriskigskurset- NITO Studetee/AIØ-HiB Oppfriskigskurs i mtemtikk Oppgveheftet Oppsummerigsotter Oppgver med fsit Høste 6 Amir Mssoud Hshemi I oppfriskigskurset skl vi prøve å gå gjeom følgede
Forkunnskaper i matematikk for fysikkstudenter. Integrasjon.
 De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
De grunnleggende definisjonene L oss strte med følgende prolem: Gitt en ontinuerlig funsjon y = f der f for [, ] Beregn relet A som er vgrenset v grfen til f, -sen, og de to vertile linjene = og = Vi n
Chapter 2 - Discrete Mathematics and Its Applications. Løsningsforslag på utvalgte oppgaver
 Chpter - Dscrete Mthemtcs d Its pplctos Løsgsforslg på utvlgte oppgver vstt Oppgve Gtt 7 ) E mtrse med rder og koloer er e mtrse Geerelt hr v t e m mtrse er e mtrse med m rder og koloer Uttrykket m klles
Chpter - Dscrete Mthemtcs d Its pplctos Løsgsforslg på utvlgte oppgver vstt Oppgve Gtt 7 ) E mtrse med rder og koloer er e mtrse Geerelt hr v t e m mtrse er e mtrse med m rder og koloer Uttrykket m klles
TMA4120 Matte 4k Høst 2012
 TMA41 Matte 4k Høst 1 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag til oppgaver fra Kreyzig utgave 1: 11.1.18 Fuksjoe er lik for < x
TMA41 Matte 4k Høst 1 Norges tekiskaturviteskapelige uiversitet Istitutt for matematiske fag Løsigsforslag til oppgaver fra Kreyzig utgave 1: 11.1.18 Fuksjoe er lik for < x
( ) 3 3 P a a a a. ( 3) ( 3) 3 ( 3) ( 3) b Px ( ) er delelig med x 3 dersom P( 3) 0. P( 3) 3a 3 0
 Løsiger til oppgvee i ok S kpittel 7 Eksmestreig Løsiger til oppgvee i ok Ute hjelpemidler Oppgve E P ( ) P ( ) ( ) ( ) ( ) 7 9 7 7 P ( ) er delelig med dersom P( ) 0. P( ) 0 c Vi utfører polyomdivisjoe
Løsiger til oppgvee i ok S kpittel 7 Eksmestreig Løsiger til oppgvee i ok Ute hjelpemidler Oppgve E P ( ) P ( ) ( ) ( ) ( ) 7 9 7 7 P ( ) er delelig med dersom P( ) 0. P( ) 0 c Vi utfører polyomdivisjoe
12 MER OM POTENSER POTENSER
 Kpittel MER OM OTENSER OTENSER 3 rekker for å helgrdere de første kmpe. 3 3 9 rekker for å helgrdere de to første kmpee. 3 3 3 7 rekker for å helgrdere de tre første kmpee. 3 3 3 3 3 3 3 3 3 3 3 3 53 44
Kpittel MER OM OTENSER OTENSER 3 rekker for å helgrdere de første kmpe. 3 3 9 rekker for å helgrdere de to første kmpee. 3 3 3 7 rekker for å helgrdere de tre første kmpee. 3 3 3 3 3 3 3 3 3 3 3 3 53 44
EKSAMEN Løsningsforslag
 8.5.5 EKSAMEN øigforlg Emekode: ITD5 ITD5 Dto: 8. mi 5 Hjelpemidler: Eme: Mtemtikk dre delekme Ekmetid: 9.. Fglærer: - To A-rk med vlgfritt ihold på begge ider. - Formelhefte. Chriti F Heide Klkultor er
8.5.5 EKSAMEN øigforlg Emekode: ITD5 ITD5 Dto: 8. mi 5 Hjelpemidler: Eme: Mtemtikk dre delekme Ekmetid: 9.. Fglærer: - To A-rk med vlgfritt ihold på begge ider. - Formelhefte. Chriti F Heide Klkultor er
2 Tallregning og algebra
 Tllregning og lger KATEGORI. Regnerekkefølge Oppgve.0 Regn uten digitlt hjelpemiddel. + ( + ) ( ) Oppgve. Regn uten digitlt hjelpemiddel. Oppgve. Regn ut med og uten digitlt hjelpemiddel. + (7 + ) ( 9)
Tllregning og lger KATEGORI. Regnerekkefølge Oppgve.0 Regn uten digitlt hjelpemiddel. + ( + ) ( ) Oppgve. Regn uten digitlt hjelpemiddel. Oppgve. Regn ut med og uten digitlt hjelpemiddel. + (7 + ) ( 9)
1 Mandag 18. januar 2010
 Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Mndg 8. jnur 2 I denne første forelesningen skl vi friske opp litt rundt funksjoner i en vribel, se på hvordn de vokser/vtr, studere kritiske punkter og beskrive krumning og vendepunkter. Vi får ikke direkte
Kapittel 4.7. Newtons metode. Kapittel 4.8.
 Ekskt løsning Newtons metode - Integrsjon Forelesning i Mtemtikk TMA00 Hns Jko Rivertz Institutt for mtemtiske fg 0. septemer 0 Kpittel.7. Newtons metode Den ekskte løsningen v x x = 0er ikke særlig rukelig
Ekskt løsning Newtons metode - Integrsjon Forelesning i Mtemtikk TMA00 Hns Jko Rivertz Institutt for mtemtiske fg 0. septemer 0 Kpittel.7. Newtons metode Den ekskte løsningen v x x = 0er ikke særlig rukelig
Løsningsforslag til prøveeksamen Mat1110 våren 2004 Oppgave 1 (a) Elemetære rekkeoperasjoner anvendt på den utvidete matrisen til systemet gir oss:
 Løsningsforslg til prøveeksmen Mt våren 4 Oppgve () Elemetære rekkeopersjoner nvendt på den utvidete mtrisen til systemet gir oss: b b b b b Setter vi = og b = får vi d mtrisen: som gir likningssystemet:
Løsningsforslg til prøveeksmen Mt våren 4 Oppgve () Elemetære rekkeopersjoner nvendt på den utvidete mtrisen til systemet gir oss: b b b b b Setter vi = og b = får vi d mtrisen: som gir likningssystemet:
S1 kapittel 6 Derivasjon Løsninger til oppgavene i boka
 S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
S kpittel 6 Derivsjon Løsninger til oppgvene i ok 6. c y x y x = = = = y x 4 5 9 4 y 5 6 x 4 = = = = y x y x = = = = 7 ( 5) 6 ( ) 8 6. f( x ) f( x ) 5 7 x x ( ) 4 = = = = 6. T( x) = 0,x +,0 T T = + = (0)
Løsningsforslag til prøveeksamen i MAT1110, våren 2012
 Løsigsforslag til prøveeksame i MAT, våre Oppgave : Vi har A = 3 III+I I+II 3 ( )II 3 3 Legg merke til at A er de utvidede matrise til ligigssystemet. Vi ser at søyle 3 og 4 i de reduserte trappeforme
Løsigsforslag til prøveeksame i MAT, våre Oppgave : Vi har A = 3 III+I I+II 3 ( )II 3 3 Legg merke til at A er de utvidede matrise til ligigssystemet. Vi ser at søyle 3 og 4 i de reduserte trappeforme
Eksamen R2, Høsten 2010
 Eksame R, Høste 00 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (6 poeg) a) Deriver fuksjoee ) f l f ( ) l l (l ) ) g( ) si cos f si
Eksame R, Høste 00 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (6 poeg) a) Deriver fuksjoee ) f l f ( ) l l (l ) ) g( ) si cos f si
DEL 1 Uten hjelpemidler
 Eksmen høsten 013 Løsninger Eksmen høsten 013 Løsninger DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 150 sider Vi finner først hvor mnge
Eksmen høsten 013 Løsninger Eksmen høsten 013 Løsninger DEL 1 Uten hjelpemidler Hjelpemidler: vnlige skrivesker, psser, linjl med centimetermål og vinkelmåler Oppgve 1 150 sider Vi finner først hvor mnge
R1 kapittel 1 Algebra
 Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
Løsninger til oppgvene i ok R1 kpittel 1 Alger Løsninger til oppgvene i ok Oppgve 1.1 1 8 4 ( ) 15 5 (4 ) 7 1 7 ( ) d ( )( ) ( 4)( ) ( ) ( 4) ( )( 1) Oppgve 1. 49 7 ( 7)( 7) 5 5 5 5 1y 75 (4y 5) ( y) 5
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Bokmål OPPGAVE 1. a) Deriver funksjonene: b) Finn integralene ved regning: c) Løs likningen ved regning, og oppgi svaret som eksakte verdier: + =
 OPPGAVE a) Deriver fuksjoee: ) f ( x) = 3six+ cosx ) gx ( ) = six cosx b) Fi itegralee ved regig: ) ) e 3e x d x l xd x Tips: l xdx= l xdx c) Løs likige ved regig, og oppgi svaret som eksakte verdier:
OPPGAVE a) Deriver fuksjoee: ) f ( x) = 3six+ cosx ) gx ( ) = six cosx b) Fi itegralee ved regig: ) ) e 3e x d x l xd x Tips: l xdx= l xdx c) Løs likige ved regig, og oppgi svaret som eksakte verdier:
S1 kapittel 1 Algebra Løsninger til oppgavene i læreboka
 Løsninger til oppgvene i ok S kpittel Alger Løsninger til oppgvene i læreok. 8 ( ) 5 9. e = = 9 = = 8 5 = = 0 = 0 0 0 = 000 =. e Ashehoug www.lokus.no Sie v Løsninger til oppgvene i ok..5..7 = = + 5 =
Løsninger til oppgvene i ok S kpittel Alger Løsninger til oppgvene i læreok. 8 ( ) 5 9. e = = 9 = = 8 5 = = 0 = 0 0 0 = 000 =. e Ashehoug www.lokus.no Sie v Løsninger til oppgvene i ok..5..7 = = + 5 =
2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5.
![2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5. 2 π[r(x)] 2 dx = u 2 du = π 1 ] 2 = π u 1. V = π. V = π [R(x)] 2 [r(x)] 2 dx = π (x + 3) 2 (x 2 + 1) 2 dx = 117π 5.](/thumbs/88/116391567.jpg) NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 6 Avsnitt 6. 7 Ved å bruke disk-metoden får mn t volumet er π[r(x)] 2 dx 3 Ved å bruke disk-metoden får mn t volumet er L u
NTNU Institutt for mtemtiske fg TMA Mtemtikk høsten 2 Løsningsforslg - Øving 6 Avsnitt 6. 7 Ved å bruke disk-metoden får mn t volumet er π[r(x)] 2 dx 3 Ved å bruke disk-metoden får mn t volumet er L u
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
Løsningsforslag. 3 x + 1 + e. g(x) = 1 + x4 x 2
 Prøve i FO929A - Matematikk Dato: 1. juni 2012 Målform: Bokmål Antall oppgaver: 5 (20 deloppgaver) Antall sider: 2 Vedlegg: Formelsamling Hjelpemiddel: Kalkulator Alle svar skal grunngis. Alle deloppgaver
Prøve i FO929A - Matematikk Dato: 1. juni 2012 Målform: Bokmål Antall oppgaver: 5 (20 deloppgaver) Antall sider: 2 Vedlegg: Formelsamling Hjelpemiddel: Kalkulator Alle svar skal grunngis. Alle deloppgaver
Integrasjon Fundamentalteoremet Substitusjon Forelesning i Matematikk 1 TMA4100
 Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
Integrsjon Fundmentlteoremet Substitusjon Forelesning i Mtemtikk 1 TMA4100 Hns Jkob Rivertz Institutt for mtemtiske fg 23. september 2011 2 Mtemtisk induksjon Alle elefnter er ros! Vil bevise P n Alle
Matematikk 1000. Øvingsoppgaver i numerikk leksjon 8 Numerisk integrasjon
 Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Mtemtikk 1000 Øvingsoppgver i numerikk leksjon 8 Numerisk integrsjon Som kjent kn vi regne ut (bestemte) integrler ved nti-derivsjon. Dette resulttet er et v de viktikgste innen klkulus; det heter tross
Løsningsforslag Kollokvium 1
 Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
Løsningsforslg Kollokvium 1 30. jnur 015 Her finner dere et løsningsforslg for oppgvene som ble diskutert på Kollokvium 1. Oppgve 1 Regning med enheter ) Energienheten 1 ev (elektronvolt) er definert som
I løpet av uken blir løsningsforslag lagt ut på emnesiden http://www.hig.no/toel/allmennfag/emnesider/rea1042
 Ukeoppgver, uke 43, i Mtemtikk, Substitusjon. Høgskolen i Gjøvik Avdeling for ingeniørfg Mtemtikk Ukeoppgver uke 43 I løpet v uken blir løsningsforslg lgt ut på emnesiden http://www.hig.no/toel/llmennfg/emnesider/re4
Ukeoppgver, uke 43, i Mtemtikk, Substitusjon. Høgskolen i Gjøvik Avdeling for ingeniørfg Mtemtikk Ukeoppgver uke 43 I løpet v uken blir løsningsforslg lgt ut på emnesiden http://www.hig.no/toel/llmennfg/emnesider/re4
DEL 1. Uten hjelpemidler. Oppgave 1 (5 poeng) Oppgave 2 (5 poeng) Oppgave 3 (4 poeng) x x. Deriver funksjonene. a) f( x) 2 sin 3x. Bestem integralene
 DEL 1 Ute hjelpemidler Oppgave 1 (5 poeg) Deriver fuksjoee a) f( x) si 3x b) c) si x g ( x) x h( x) x cos x Oppgave (5 poeg) Bestem itegralee a) 3 ( 3 ) d x x x b) xe x dx c) x x 1 dx Oppgave 3 (4 poeg)
DEL 1 Ute hjelpemidler Oppgave 1 (5 poeg) Deriver fuksjoee a) f( x) si 3x b) c) si x g ( x) x h( x) x cos x Oppgave (5 poeg) Bestem itegralee a) 3 ( 3 ) d x x x b) xe x dx c) x x 1 dx Oppgave 3 (4 poeg)
MA 1410: Analyse Uke 48, aasvaldl/ma1410 H01. Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag
 MA 40: Aalyse Uke 48, 00 http://home.hia.o/ aasvaldl/ma40 H0 Høgskole i Agder Avdelig for realfag Istitutt for matematiske fag Oppgave 8.7:. Vi har f(x) = cosh(x) = ex +e x. f(0) =. Derivasjo gir f (x)
MA 40: Aalyse Uke 48, 00 http://home.hia.o/ aasvaldl/ma40 H0 Høgskole i Agder Avdelig for realfag Istitutt for matematiske fag Oppgave 8.7:. Vi har f(x) = cosh(x) = ex +e x. f(0) =. Derivasjo gir f (x)
Matematikk for IT. Prøve 2 løsningsforslag. Torsdag 27. oktober 2016 S S F S F F S F S F S S F S F S F F F F S S F F
 Mtemtikk for IT Prøve løsigsforslg Torsdg 7 oktober 06 7 oktober 06 Oppgve ) Fi ved hjelp v shetstbeller om de to følgede smmestte utsg er logisk ekvivlete: i) p q ii) q p q) Utsg i): q p q S S F F S F
Mtemtikk for IT Prøve løsigsforslg Torsdg 7 oktober 06 7 oktober 06 Oppgve ) Fi ved hjelp v shetstbeller om de to følgede smmestte utsg er logisk ekvivlete: i) p q ii) q p q) Utsg i): q p q S S F F S F
R2 eksamen høsten 2017
 R eksame høste 017 DEL 1 Ute hjelpemidler Oppgave 1 (5 poeg) Deriver fuksjoee a) f x si3 b) g x si x x h x x cos x c) x Oppgave (5 poeg) Bestem itegralee 3 a) x 3x dx b) xe x dx c) x x 1 dx Oppgave 3 (4
R eksame høste 017 DEL 1 Ute hjelpemidler Oppgave 1 (5 poeg) Deriver fuksjoee a) f x si3 b) g x si x x h x x cos x c) x Oppgave (5 poeg) Bestem itegralee 3 a) x 3x dx b) xe x dx c) x x 1 dx Oppgave 3 (4
OM TAYLOR POLYNOMER. f x K f a x K a. f ' a = lim x/ a. f ' a z
 OM TAYLOR POLYNOMER I dette otatet, som utfyller avsitt 6. i Gullikses bok, skal vi se på Taylor polyomer og illustrere hvorfor disse er yttige. Det å berege Taylor polyomer for håd er i prisippet ikke
OM TAYLOR POLYNOMER I dette otatet, som utfyller avsitt 6. i Gullikses bok, skal vi se på Taylor polyomer og illustrere hvorfor disse er yttige. Det å berege Taylor polyomer for håd er i prisippet ikke
8 + 2 n n 4. 3n 4 7 = 8 3.
 Seksjo 4. Oppgave (). Fi greseverdiee: 8 a) 4 + 4 7 b) 4 +7 5 c) + 7 4 ( ) d) 5 4 44 + 5 4 e) 5 + si() e +6 5 Løsig. Vi vil bruke samme metode som i Eksempel 4..5 fra boke i disse oppgavee. Når vi skal
Seksjo 4. Oppgave (). Fi greseverdiee: 8 a) 4 + 4 7 b) 4 +7 5 c) + 7 4 ( ) d) 5 4 44 + 5 4 e) 5 + si() e +6 5 Løsig. Vi vil bruke samme metode som i Eksempel 4..5 fra boke i disse oppgavee. Når vi skal
Formelsamling i matematikk - R2. Vektorer. Innskuddssetningen: Skalarprodukt: Lengde: Normale: Parallelle: P, Q og R på linje: Formelsamling R2
 Formelsamlig R Formelsamlig i matematikk - R (Uder arbeid...) Ulve.09.0 Vær sill å rapportere evetuelle feil! Her vil jeg prøve å få samlet alle formler jeg meer dere ka ha ytte av både på eksame og i
Formelsamlig R Formelsamlig i matematikk - R (Uder arbeid...) Ulve.09.0 Vær sill å rapportere evetuelle feil! Her vil jeg prøve å få samlet alle formler jeg meer dere ka ha ytte av både på eksame og i
Ukeoppgaver, uke 42, i Matematikk 10, Bestemt integrasjon. 1
 Ukeoppgaver, uke 2, i Matematikk, Bestemt itegrasjo. Høgskole i Gjøvik Avdelig for igeiørfag Matematikk Ukeoppgaver uke 2 I løpet av uke blir løsigsforslag lagt ut på emeside http://www.hig.o/toel/allmefag/emesider/rea2
Ukeoppgaver, uke 2, i Matematikk, Bestemt itegrasjo. Høgskole i Gjøvik Avdelig for igeiørfag Matematikk Ukeoppgaver uke 2 I løpet av uke blir løsigsforslag lagt ut på emeside http://www.hig.o/toel/allmefag/emesider/rea2
Kalkulus 2. Volum av et omdreiningslegeme. Rotasjon rundt x-aksen
 Klkulus Klkulus Volum v et omdreiningslegeme Rotsjon rundt x-ksen På figuren nedenfor hr vi skrvert området vgrenset v grfen til den kontinuerlige funksjonen y = f( x) og x-ksen fr x= til x=. Når vi roterer
Klkulus Klkulus Volum v et omdreiningslegeme Rotsjon rundt x-ksen På figuren nedenfor hr vi skrvert området vgrenset v grfen til den kontinuerlige funksjonen y = f( x) og x-ksen fr x= til x=. Når vi roterer
MA1101 Grunnkurs Analyse I Høst 2017
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag MA0 Grukurs Aalyse I Høst 07 Løsigsforslag Øvig..b) Vi skriver om 7 = 4 4 7 Korollar.. gir at 7 4 er irrasjoal (side vi vet 7 4 er
Obligatorisk oppgave i MAT 1100, H-03 Løsningsforslag
 Oppgave : Obligatorisk oppgave i MAT, H- Løsningsforslag a) Vi skal regne ut dx. Substituerer vi u = x, får vi du = x dx. De xex nye grensene er gitt ved u() = = og u() = = 9. Dermed får vi: 9 [ ] 9 xe
Oppgave : Obligatorisk oppgave i MAT, H- Løsningsforslag a) Vi skal regne ut dx. Substituerer vi u = x, får vi du = x dx. De xex nye grensene er gitt ved u() = = og u() = = 9. Dermed får vi: 9 [ ] 9 xe
2x 3 4/x dx. 2 5 x 3 + LF: Vi utfører polynomdivisjon. 2x + 1 dx = + C = 5x8/ ln 2x C 4. πx 2 e 3x3 dx = π
 Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Innlevering ELFE KJFE MAFE Mtemtikk HIOA Obligtorisk innlevering 5 Innleveringsfrist Mndg 6. oktober 5 før forelesningen : Antll oppgver: Løsningsforslg Finn de ubestemte integrlene ) x 4/x dx LF: x 4/x
Institutt for Samfunnsøkonomi. Utlevering: 29.04.2015 Kl. 09:00 Innlevering: 29.04.2015 Kl. 14:00
 SENSORVEILEDNING MET 803 Matematikk Institutt for Samfunnsøkonomi Utlevering: 9.04.05 Kl. 09:00 Innlevering: 9.04.05 Kl. 4:00 For mer informasjon om formalia, se eksamensoppgaven. Oppgave Beregn følgende
SENSORVEILEDNING MET 803 Matematikk Institutt for Samfunnsøkonomi Utlevering: 9.04.05 Kl. 09:00 Innlevering: 9.04.05 Kl. 4:00 For mer informasjon om formalia, se eksamensoppgaven. Oppgave Beregn følgende
1 Mandag 25. januar 2010
 Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Mndg 5. jnur Vi fortsetter med å se på det bestemte integrlet, bl.. på hvordn vi kn bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis kn finne en nti-derivert. Videre skl vi t
Læringsmål og pensum. Funksjoner hittil (1) Oversikt. Læringsmål Anonyme og rekursive funksjoner Funksjoner som inn-argumenter Subfunksjoner
 1 Lærigsmål og pesum TDT4105 Iformsjostekologi grukurs: Uke 44 Aoyme fuksjoer, fuksjosfuksjoer og rekursjo Lærigsmål Aoyme og rekursive fuksjoer Fuksjoer som i-rgumeter Subfuksjoer Pesum Mtlb, Chpter 10
1 Lærigsmål og pesum TDT4105 Iformsjostekologi grukurs: Uke 44 Aoyme fuksjoer, fuksjosfuksjoer og rekursjo Lærigsmål Aoyme og rekursive fuksjoer Fuksjoer som i-rgumeter Subfuksjoer Pesum Mtlb, Chpter 10
NTNU MA0003. Ole Jacob Broch. Norwegian University of Science and Technology. MA0003 p.1/29
 MA0003 Ole Jacob Broch Norwegian University of Science and Technology MA0003 p.1/29 Oversikt, torsdag 13/1 Avsnitt 1.3: intervaller og intervallnotasjon definisjons- og verdimengden til en funksjon Avsnitt
MA0003 Ole Jacob Broch Norwegian University of Science and Technology MA0003 p.1/29 Oversikt, torsdag 13/1 Avsnitt 1.3: intervaller og intervallnotasjon definisjons- og verdimengden til en funksjon Avsnitt
EKSAMENSOPPGÅVE. Tilletne hjelpemiddel: Godkjend kalkulator og formelsamling og 2 eigne A4-ark (4 sider totalt)
 EKSAMENSOPPGÅVE/EKSAMENSOPPGAVE EKSAMENSOPPGÅVE Eksamen i: MAT-1003 Kalkulus 3 Dato: Tirsdag 17. 1.013 Tid: Kl 09:00 13:00 Stad: Åsgårdveien 9 Tilletne hjelpemiddel: Godkjend kalkulator og formelsamling
EKSAMENSOPPGÅVE/EKSAMENSOPPGAVE EKSAMENSOPPGÅVE Eksamen i: MAT-1003 Kalkulus 3 Dato: Tirsdag 17. 1.013 Tid: Kl 09:00 13:00 Stad: Åsgårdveien 9 Tilletne hjelpemiddel: Godkjend kalkulator og formelsamling
PARENTESER Matematikerne har funnet på at i regneuttrykk kan vi bruke parenteser for å markere hvilken regneoperasjon som skal gjøres først.
 Smmedrg kpittel SAMMENDRAG Dette er et smmedrg v det du hr rbeidet med om lgebr i Nummer 8, Nummer 9 og Nummer 10. Hvis du treger mer treig utover oppgvee i Nummer 10, fier du ekstr oppgver på elevettstedet.
Smmedrg kpittel SAMMENDRAG Dette er et smmedrg v det du hr rbeidet med om lgebr i Nummer 8, Nummer 9 og Nummer 10. Hvis du treger mer treig utover oppgvee i Nummer 10, fier du ekstr oppgver på elevettstedet.
Løsningsforslag til Mat112 Obligatorisk Oppgave, våren Oppgave 1
 Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Løsningsforslag R2 Eksamen 04.06.2012. Nebuchadnezzar Matematikk.net Øistein Søvik
 Løsigsforslag R2 Eksame 6 Vår 04.06.202 Nebuchadezzar Matematikk.et Øistei Søvik Sammedrag De fleste forlagee som gir ut lærebøker til de videregåede skole, gir ut løsigsforslag til tidligere gitte eksameer.
Løsigsforslag R2 Eksame 6 Vår 04.06.202 Nebuchadezzar Matematikk.et Øistei Søvik Sammedrag De fleste forlagee som gir ut lærebøker til de videregåede skole, gir ut løsigsforslag til tidligere gitte eksameer.
Forelesning Matematikk 4N
 Forelesning Matematikk 4N Hans Jakob Rivertz Institutt for matematiske fag 11. september 2006 2 Den høyrederiverte og venstrederiverte Definisjon Den høyrederiverte til en funksjon f(x) i punktet x er
Forelesning Matematikk 4N Hans Jakob Rivertz Institutt for matematiske fag 11. september 2006 2 Den høyrederiverte og venstrederiverte Definisjon Den høyrederiverte til en funksjon f(x) i punktet x er
Kapittel 4 Tall og algebra Mer øving
 Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
Kpittel 4 Tll og lger Mer øving Oppgve 1 d Oppgve 2 Se på uttrykket A = g h. Hv forteller de ulike okstvene? Se på uttrykket A = 2π. Hv står de ulike symolene for? Forklr hv vi mener med en vriel og en
YF kapittel 10 Eksamenstrening Løsninger til oppgavene i læreboka
 YF kpittel 10 Eksmenstrening Løsninger til oppgvene i læreok Uten hjelpemidler Oppgve E1 5 + 5 + 6 11 5 + 4 (5 + ) 5 + 4 7 10 6 + 8 d + ( + 1) 5 + 4 5 + 16 5 + 10 5 4 + 4 4 + 8 1 + + + + + + + + 49 49
YF kpittel 10 Eksmenstrening Løsninger til oppgvene i læreok Uten hjelpemidler Oppgve E1 5 + 5 + 6 11 5 + 4 (5 + ) 5 + 4 7 10 6 + 8 d + ( + 1) 5 + 4 5 + 16 5 + 10 5 4 + 4 4 + 8 1 + + + + + + + + 49 49
DEL 1. Uten hjelpemidler 500+ er x
 DEL 1 Ute hjelpemidler Oppgave 1 (18 poeg) 500 = + 8 er a) Vis at de deriverte til fuksjoe ( ) O O ( ) = 500+ 16 b) Deriver fuksjoee 1) f( ) = l( ) ) g( ) = e c) Vi har gitt polyomfuksjoe f( ) = 1 + 15
DEL 1 Ute hjelpemidler Oppgave 1 (18 poeg) 500 = + 8 er a) Vis at de deriverte til fuksjoe ( ) O O ( ) = 500+ 16 b) Deriver fuksjoee 1) f( ) = l( ) ) g( ) = e c) Vi har gitt polyomfuksjoe f( ) = 1 + 15
MA0003-8. forelesning
 Implisitt derivasjon og 31. august 2009 Outline Implisitt derivasjon 1 Implisitt derivasjon 2 Outline Implisitt derivasjon 1 Implisitt derivasjon 2 Outline Implisitt derivasjon 1 Implisitt derivasjon 2
Implisitt derivasjon og 31. august 2009 Outline Implisitt derivasjon 1 Implisitt derivasjon 2 Outline Implisitt derivasjon 1 Implisitt derivasjon 2 Outline Implisitt derivasjon 1 Implisitt derivasjon 2
Løsningsforslag AA6524/AA6526 Matematikk 3MX Elever/Privatister 6. desember 2006. eksamensoppgaver.org
 Løsningsforslag AA654/AA656 Matematikk 3MX Elever/Privatister 6. desember 6 eksamensoppgaver.org eksamensoppgaver.org Om løsningsforslaget Løsningsforslaget for matematikk eksamen i 3MX er gratis, og det
Løsningsforslag AA654/AA656 Matematikk 3MX Elever/Privatister 6. desember 6 eksamensoppgaver.org eksamensoppgaver.org Om løsningsforslaget Løsningsforslaget for matematikk eksamen i 3MX er gratis, og det
Dagens program. 7.6 Numerisk integrasjon (fortsatt) 7.7 Uegentlige integraler
 Dgens progrm 7.6 Numerisk integrsjon (fortstt) 7.7 Uegentlige integrler Forelesningen onsdg 28. oktober flyttes til ud. R7. Trpesmetoden Merknd side 479 Den tilnærmede verdien til integrlet f (x)dx beregnet
Dgens progrm 7.6 Numerisk integrsjon (fortstt) 7.7 Uegentlige integrler Forelesningen onsdg 28. oktober flyttes til ud. R7. Trpesmetoden Merknd side 479 Den tilnærmede verdien til integrlet f (x)dx beregnet
Potenser og rotstørrelser m m n m n a m n n n n m n m n n. cos x sin x 1, sin x (1 cos(2 x)), cos x (1 cos(2 x)), x x x x x x
 Progr for llefg Høgskole i ør-trødelg FORMELARK 05 Mtetikk/Fysikk Eeuer TALM3003 Poteser og rotstørrelser,, ( b) b, ( ),, b b,, b b ( ) Trigooetri cos si, si ( cos( )), cos ( cos( )), 0 si( y) si cos y
Progr for llefg Høgskole i ør-trødelg FORMELARK 05 Mtetikk/Fysikk Eeuer TALM3003 Poteser og rotstørrelser,, ( b) b, ( ),, b b,, b b ( ) Trigooetri cos si, si ( cos( )), cos ( cos( )), 0 si( y) si cos y
. 2+cos(x) 0 og alle biter som inngår i uttrykket er kontinuerlige. Da blir g kontinuerlig i hele planet.
 MA 1410: Analyse Uke 47, 001 http://home.hia.no/ aasvaldl/ma1410 H01 Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag Oppgave 11.1: 7. f(x, y) = 1 16 x y. a) Definisjonsområde D: f
MA 1410: Analyse Uke 47, 001 http://home.hia.no/ aasvaldl/ma1410 H01 Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag Oppgave 11.1: 7. f(x, y) = 1 16 x y. a) Definisjonsområde D: f
1 Mandag 8. mars 2010
 1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
1 Mndg 8. mrs 21 Vi hr tidligere integrert funksjoner lngs x-ksen, og vi hr integrert funksjoner i flere vrible over begrensede områder i xy-plnet. I denne forelesningen skl vi integrere funksjoner lngs
Følger og rekker. Kapittel Følger
 Kapittel 4 Følger og rekker E viktig egeskap ved polyomiale fuksjoer er at vi ekelt) ka rege ut verdiee av fuksjoee i et valgt pukt. Grue er at polyomer er et slags speilbilde av de valige regeoperasjoee.
Kapittel 4 Følger og rekker E viktig egeskap ved polyomiale fuksjoer er at vi ekelt) ka rege ut verdiee av fuksjoee i et valgt pukt. Grue er at polyomer er et slags speilbilde av de valige regeoperasjoee.
Fasit til utvalgte oppgaver MAT1100, uka 20-24/9
 Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
Fsit til utvlgte oppgver MAT00, uk 20-24/9 Øyvind Ryn oyvindry@ifi.uio.no September 24, 200 Oppgve 5..5 år vi viser t f er kontinuerlig i ved et ɛ δ-bevis, er det lurt å strte med uttrykket fx f, og finne
R2 eksamen våren 2014. (19.05.2014)
 R Eksmen V04 R eksmen våren 04. (9.05.04) Løsningsskisser (Versjon 3.0.4) Del - Uten hjelpemidler Oppgve ) fx sinu; u 3x Kjerneregel: f x f uu x cosu3 3 cos3x b) e x e x med kjerneregel som i ) Produktregel:
R Eksmen V04 R eksmen våren 04. (9.05.04) Løsningsskisser (Versjon 3.0.4) Del - Uten hjelpemidler Oppgve ) fx sinu; u 3x Kjerneregel: f x f uu x cosu3 3 cos3x b) e x e x med kjerneregel som i ) Produktregel:
E K S A M E N. Matematikk 3MX. Elevar/Elever Privatistar/Privatister. AA6524/AA6526 8. desember 2004 UTDANNINGSDIREKTORATET
 E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
E K S A M E N UTDANNINGSDIREKTORATET Mtemtikk 3MX Elevr/Elever Privtistr/Privtister AA654/AA656 8. desember 004 Vidregånde kurs II / Videregående kurs II Studieretning for llmenne, økonomiske og dministrtive
