Lattice Boltzmann Method for ow in porous media. Samuel Corre
|
|
|
- Merete Carlsson
- 5 år siden
- Visninger:
Transkript
1 Lattice Boltzmann Method for ow in porous media. avec Aziz Belmiloudi IRMAR-INSA, Rennes. 4 ieme école EGRIN, 25 Mai 2016.
2 Contexte général Écoulements incompressibles en milieu poreux. Eets gravitationnels négligés. Application : rhéologie. Système diérentiel : loi de Darcy et équation diérentielle de type convection-diusion. (existence & unicité : Feng X. 1995) Question : Peut-on construire une méthode de Boltzmann sur réseau générale pour de telles équations?
3 1 Système 2 3 Choix des fonctions f eq j, F j et τ Algorithme 4 Résultats Conclusion
4 1 Système 2 3 Choix des fonctions f eq j, F j et τ Algorithme 4 Résultats Conclusion
5 1 Système 2 3 Choix des fonctions f eq j, F j et τ Algorithme 4 Résultats Conclusion
6 1 Système 2 3 Choix des fonctions f eq j, F j et τ Algorithme 4 Résultats Conclusion
7 Système ρ : densité de uide. U : vitesse de Darcy. p : pression. K : tenseur de conductivité hydraulique. D : tenseur de dispersion. φ : porosité. µ : viscosité. q +, q, H : termes sources. Domaine Ω R 2 : tranche du sous-sol de bord Γ.
8 Système Pour (x, t) Ω (0, T ) : div(u(x, t)) = q + (x) q (x), U(x, t) = K(x) p(x, t), µ(ρ) φ(x) ρ(x, t) div(d(x, t; U) ρ(x, t)) + div(ρ(x, t)u(x, t)) = H(ρ), t où H(ρ) = q (x)ρ(x, t) + q + ˆρ, et où les conditions initiales et aux bords sont : ρ(x, 0) = ρ 0 (x), U(x, 0) = U 0 (x). Pour x Γ : U(x, t) n = 0, D(x, t; U) ρ(x, t) n = 0. Et on respecte les conditions de compatibilité : p(x)dx = 0, q + (x)dx = q + (x)dx Ω Ω Ω
9 Modélisation du tenseur D Système Modèle statistique (Bear, 1961) pour modéliser les phénomènes de dispersion-diusion : D(x, U) = (φ(x)d m +φ(x)d t U(x) )I+ φ(x) U(x) (D l D t )(U i (x)u j (x)) 1 i,j d, où D m est le coecient de dispersion moléculaire, D l le coecient de dispersion longitudinal, et D t le coecient de dispersion transversal, tels que D l D t > 0 et D m > 0.
10 1 Système 2 3 Choix des fonctions f eq j, F j et τ Algorithme 4 Résultats Conclusion
11 Théorie : Échelle mésoscopique : distributions particulaires. Deux étapes : Collisions particulaires. (locales en espace) Transport. (selon chaque direction) Lien entre la LBM et un écoulement en milieu poreux par le développement de Chapman-Enskog. Histoire : Equation de Boltzmann, Automates de gaz sur réseau (LGA), Mécanique des uides, Généralisation, 2000 à maintenant.
12 Équation de Boltzmann Soient (x, t) Ω (0, T ) avec Ω R d, d = 2, 3 : f (x, t; e) fonction de répartition selon la vélocité e. Q(f ) Opérateur de collision. F (x, t) Terme source. f (x, t; e) + e f (x, t; e) } t {{} Transport = Q(f ) +F (x, t). }{{} Collision
13 Propriétés de la fonction de répartition Recomposition de la densité ρ : ρ(x, t) = f (x, t; e)de. Ω Recomposition de la quantité de mouvement u : ρ(x, t)u(x, t) = ef (x, t; e)de. Ω
14 Fonction d'équilibre On note f eq (x, t; e) la fonction de répartition d'équilibre dénie par : L'invariance par collision : Q(f eq (x, t; e)) = 0, (x, t; e). Les moments conservés : 1 f eq (x, t; e)de conservation de la masse. Ω 2 ef eq (x, t; e)de conservation de la quantité de mouvement. Ω 3 e 2 2 f eq (x, t; e)de conservation de l'énergie. Ω En particulier, pour tout t : f eq (x, t; e)de = Ω Ω f (x, t; e)de.
15 Opérateur de collision Conservation des moments : cet opérateur modie les répartitions, pas la quantité de matière. Opérateur de collision de Bathmagar-Gross-Krook (BGK, 1954) : Q(f ) = 1 τ (f (x, t; e) f eq (x, t; e)), où τ est un taux de relaxation adimensionnel.
16 Discrétisation : généralités x, t pas de temps et d'espace, et : c = x/ t vitesse de grille. DdQj : Modèle à j vélocités dans un domaine à d dimensions. f j (x, t) fonction de répartition le long de la vélocité e j.
17 Discrétisation : modèle D2Q9 Les poids w j et les vélocités e j respectent : 8 w j = 1 ; j=0 8 e j = j=0 ( ) 0. 0 On choisit e j les vélocités : e 0 = ( ) 0 0 (( ±1 ; e 1,...,4 = c 0 ), ( )) 0 ±1 Et w j les poids associés à chaque vélocité e j : ; e 5,...,8 = 2c ( ) ±1. ±1 w 0 = 4 9 ; w 1,...,4 = 1 9 ; w 5,...,8 = 1 36.
18 De l'équation de Boltzmann à la LBM : résumé. Équation de Boltzmann : f + e f = Q(f ) + F. t 1 Approximation de Q(f ) par l'opérateur BGK. 2 Discrétisation en temps, espace, et selon chaque vélocité e j. 3 Intégration selon la méthode des caractéristiques. Équation de Boltzmann sur réseau : f j (x + e j t, t + t) = f j (x, t) 1 τ + tf j (x, t) + t2 2 ( ) f j (x, t) f eq j (x, t) t F j(x, t) + O( t 3 ).
19 Equation de Boltzmann sur réseau : deux étapes distinctes Phase de collision pour chaque point x : fj col (x, t + t) = f j (x, t) 1 τ + tf j (x, t) + t2 2 Phase de transport selon chaque vélocité e j : ( f j (x, t) f eq j (x, t) t F j(x, t). f j (x + e j t, t + t) = fj col (x, t + t). )
20 But : Équivalence entre la résolution de l'équation de Boltzmann sur réseau et la résolution de l'edp non-linéaire à résoudre Déterminer f eq j, F j et τ. Principe de l'ansatz : Séparation des fonctions de répartition et des opérateurs selon des échelles de perturbation dénies par le nombre de Knudsen ε t. Mise en oeuvre : Faire coïncider l'équation de Boltzmann sur réseau avec le développement de Taylor des fonctions de répartition.
21 Equation de Boltzmann sur réseau et développement de Taylor Développement de Taylor : f j (x + e j t, t + t) = f j (x, t) + k=1 t k k! ( ) k t + e j f j (x, t). D'où l'égalité : k=1 t k k! ( ) k t + e j f j (x, t) = 1 τ (f j(x, t) f eq j ) + tf j (x, t) + t2 2 t F j(x, t).
22 Développement Trois étapes : Séparation selon ε des fonctions et opérateurs diérentiels : φ = φ eq + εφ (1) + ε 2 φ (2) +... x = ε x 1 + ε 2 x Sommation selon j. Choix des fonctions f eq j, F j et du taux de relaxation τ pour coïncider avec l'edp non-linéaire à résoudre.
23 Développement En pratique, on associe à chaque vélocité e j les fonctions : ( ) P 0 j = 1 f (0) j f eq j, ( τ ) P 1 j = t + e j f eq j + 1 τ f (1) j tf (1) j, où D l,n j = n k=0 P n>1 j = 1 τ f (n) j tf (n) j + k+l=n ( t l 2l! k+l=n ( ) n! n k + k!(n k)! t n k (e j l ) k. l D l,n j fj k ( t l + e j l On détermine enn f eq j, F j et τ en résolvant : N n=0 ε n ) ) F (k) j ; 8 Pj n + O(ε N+1 ) = 0. (1) j=0
24 1 Système 2 3 Choix des fonctions f eq j, F j et τ Algorithme 4 Résultats Conclusion
25 Choix des fonctions f eq, F j j et τ Algorithme But : construire une LBM pour résoudre (x, t) Ω (0, T ) : ρ (αd(ρ) ρ)) + B(ρ) = F (ρ), t où α est le coecient de diusion et D et B sont des tenseurs nonlinéaires et diérentiables par rapport à ρ. Dans notre cas : αd(ρ) = D φ. B(ρ) = ρu φ. F (ρ) = H(ρ) φ.
26 Choix des fonctions d'équilibre. Choix des fonctions f eq, F j j et τ Algorithme A l'aide du développement de Chapman-Enskog nous dénissons pour j = ( : f eq j (x, t) = w j ρ(x, t) + e j B(ρ(x,t)) + (C(ρ) 3c2 ρ(x,t)i):(ej e j 3c 2 I) 3c 2 Avec : C(ρ) = C 0 (ρ) + 3c 2 D(ρ), 6c 4 ). et C 0 (ρ) un tenseur déni par : (C 0 ) αβ = B α(ρ)b β (ρ)dρ
27 Choix des fonctions F j et de τ Choix des fonctions f eq, F j j et τ Algorithme A l'aide du développement de Chapman-Enskog nous dénissons pour j = : ( F j (x, t) = w j F (x, t) 1 + λ e j B ) (ρ(x, t)). 3c 2 Avec : et λ = 1 1 2τ, τ = α 3 tc
28 Choix des fonctions f eq, F j j et τ Algorithme Initialisation x, à t = 0 de : ρ, U, F. Boucle sur le temps t : 1 Calcul de f eq j (x, t) et F j (x, t). 2 Collision : fj col (x, t) = τ 1 f j (x, t) 1 τ τ f eq j (x, t)+ tf j (x, t)+ t 2 /2F j (x, t). 3 Transport : f j (x + e i t, t + t) = fj col (x, t). 4 Calcul des répartitions aux bords et de ρ(x, t + t). 5 Recomposition des grandeurs macroscopiques. 6 t = t + t, revenir à 1 jusqu'à t = T.
29 1 Système 2 3 Choix des fonctions f eq j, F j et τ Algorithme 4 Résultats Conclusion
30 Résultats Conclusion Considérons : Ω = [ 500, 500] [ 500, 500], T = 0.2, t = O( x 2 ), avec une porosité et une viscosité constantes : φ(x) = 1, µ(ρ) = L'opérateur D dépend des constantes : D m = 1 D t = 0.5 D l = 5. Choix de la pression p et du tenseur de conductivité hydraulique K : { 5 si x < 0, p(x) = cos(xπ/500) cos( yπ/500), K(x) = 1 sinon. On en déduit la vélocité U : U(x) = πk(x) 5 ( ) sin(xπ/500) cos( yπ/500) cos(xπ/500) sin( y π/500).
31 LBM pour EDPs non-linéaires de type convection-di usion Dé nition du problème Résultats Conclusion U2 (x) U1 (x) y y x 500 x 500 On choisit le terme source F (ρ) tel que la solution de notre système soit : ρsol (x, t) = tk (x) Remarque : x3 x Cette solution n'est pas réaliste ( x Ω tq : 1 + y3 y ρ(x) 0), 1 mais l'existence et l'unicité de la ρ(x, 0.2) solution sont préservées y x LBM for ow in porous media
32 Résultats Conclusion Err ρ = 1 N iter T t=0 ρ(t) ρ sol (t) 2 L 2 Ω ρ sol (t) 2 L 2 Ω Log2(Err) Log2( x) x Err ρ 1/ / / / / /
33 Résultats Conclusion A l'aide du développement de Chapman-Enskog, nous pouvons construire des méthodes de Boltzmann sur réseau adaptées à des équations diérentielles non-linéaires de type convection-diusion, et en particulier simuler des écoulements en milieux poreux. Trois points peuvent facilement améliorer les performances : 1 Adapter le maillage eux discontinuités connues. 2 Paralléliser les phases de collision et de transport. 3 Adapter le traitement des bords à chaque type de problème.
34 Références [1 ] S. Corre, A. Belmiloudi. Coupled Lattice Boltzmann Modeling of Bidomain type models in Cardiac Electrophysiology. In Edited Book : Mathematical and Computational Approaches in Advancing Modern Science and Engineering, (eds. J. Bélair, I. Frigaard, H. Kunze, R., Melnik, J. Spiteri), Springer-Verlag, 13 pages, [2 ] S. Corre, A. Belmiloudi. Mathematical modeling and lattice Boltzmann simulation method for Bidomain type models in cardiac electrophysiology with time-varying delays. Article en préparation. [3 ] Belmiloudi A., Stabilization, regulation and robust control of uncertain processes and parameters in porous medium systems with applications, In Edited Book : Focus on Porous Media Research, Mechanical Engineering Theory and Applications Series (ed. C. Zhao), Chapter 6, Nova Science Publishers, New York, , [4 ] Feng X. On existence and uniqueness results for a coupled system modeling miscible displacement in porous media., J. Math. Anal. Appl. 194 (1995) 3, pp [5 ] Shi B., Guo Z. Lattice Boltzmann model for nonlinear convection-diusion equations, Phys. Rev. E 79, , 2009.
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 2008
 Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
1. Intégrales définies et indéfinies I. (a) Soit b > 0. Montrer que pour tout x > 0 la fonction. 2 b. F (x) = arctan bx. 1 (1 + bx) x. f(x) = x t dt.
 Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Energie et corrélation. Systèmes de Traitement du Signal Polytech Marseille INFO 2016
 Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Brosses intérieures avec manche
 18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
Clôture Métallique. Portails / Portillons / Accessoires
 Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
Laser vert : moins de plus de 300. Acheter Laser PRODUITS CHAUDS. Pointeur Laser étanche
 Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
 http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
GAMME DETENTE DIRECTE SOMMAIRE. X32 monosplit Inverter Page 88. X3 multisplit Inverter Page 90. Monosplits/Multisplits
 SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
melting ECMI Modelling week 2008 Modelling and simulation of ice/snow melting Sabrina Wandl - University of Linz Tuomo Mäki-Marttunen - Tampere UT
 and and ECMI week 2008 Outline and Problem Description find model for processes consideration of effects caused by presence of salt point and numerical solution and and heat equations liquid phase: T L
and and ECMI week 2008 Outline and Problem Description find model for processes consideration of effects caused by presence of salt point and numerical solution and and heat equations liquid phase: T L
Analysis of ordinal data via heteroscedastic threshold models
 Analysis of ordinal data via heteroscedastic threshold models JL Foulley/Applibugs 1 Example Koch s 1990 data on a clinical trial for respiratory illness Treatment (A) vs Placebo (P) 111 patients (54 in
Analysis of ordinal data via heteroscedastic threshold models JL Foulley/Applibugs 1 Example Koch s 1990 data on a clinical trial for respiratory illness Treatment (A) vs Placebo (P) 111 patients (54 in
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Eksamen FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. Nynorsk/Bokmål
 Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Bobine à noyau de fer
 1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
Corrigés des exercices du chapitre 25
 MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
Disjoncteurs sélectifs
 233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
Splitting the differential Riccati equation
 Splitting the differential Riccati equation Tony Stillfjord Numerical Analysis, Lund University Joint work with Eskil Hansen Innsbruck Okt 15, 2014 Outline Splitting methods for evolution equations The
Splitting the differential Riccati equation Tony Stillfjord Numerical Analysis, Lund University Joint work with Eskil Hansen Innsbruck Okt 15, 2014 Outline Splitting methods for evolution equations The
TECHNOLOGIE POUR CHAUDIERES DE BRUNNER. Kamin-Kessel Eck 57/67/44 Porte relevable (easy-lift) État: made in germany
 TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
Lattice Simulations of Preheating. Gary Felder KITP February 2008
 Lattice Simulations of Preheating Gary Felder KITP February 008 Outline Reheating and Preheating Lattice Simulations Gravity Waves from Preheating Conclusion Reheating and Preheating Reheating is the decay
Lattice Simulations of Preheating Gary Felder KITP February 008 Outline Reheating and Preheating Lattice Simulations Gravity Waves from Preheating Conclusion Reheating and Preheating Reheating is the decay
Qi-Wu-Zhang model. 2D Chern insulator. León Martin. 19. November 2015
 Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Abstract. i x + a x +. a = (a x, a y ) z γ + 1 γ + z )
 Abstract R, Aharonov-Bohm Schrödinger Landau level Aharonov-Bohm Schrödinger 1 Aharonov-Bohm R Schrödinger ( ) ( ) 1 1 L a = i + a = i x + a x + ( ) 1 i y + a y (1). a = (a x, a y ) rot a = ( x a y y a
Abstract R, Aharonov-Bohm Schrödinger Landau level Aharonov-Bohm Schrödinger 1 Aharonov-Bohm R Schrödinger ( ) ( ) 1 1 L a = i + a = i x + a x + ( ) 1 i y + a y (1). a = (a x, a y ) rot a = ( x a y y a
Numerical Simulation of Shock Waves and Nonlinear PDE
 Numerical Simulation of Shock Waves and Nonlinear PDE Kenneth H. Karlsen (CMA) Partial differential equations A partial differential equation (PDE for short) is an equation involving functions and their
Numerical Simulation of Shock Waves and Nonlinear PDE Kenneth H. Karlsen (CMA) Partial differential equations A partial differential equation (PDE for short) is an equation involving functions and their
EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012
 Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
Eksamensoppgave i TMA4135 Matematikk 4D
 Institutt for matematiske fag Eksamensoppgave i TMA435 Matematikk 4D Faglig kontakt under eksamen: Helge Holden a, Gard Spreemann b Tlf: a 92038625, b 93838503 Eksamensdato: 0. desember 205 Eksamenstid
Institutt for matematiske fag Eksamensoppgave i TMA435 Matematikk 4D Faglig kontakt under eksamen: Helge Holden a, Gard Spreemann b Tlf: a 92038625, b 93838503 Eksamensdato: 0. desember 205 Eksamenstid
a) Z =ˆν/ˆp b) Z =ˆp/ˆν c) Z =ˆν ˆp ν = 1 p
 Noregs teknisk naturvitskaplege universitet Institutt for elektronikk og telekommunikasjon Side 1 av 9 Faglig kontakt under eksamen: Name: Ulf Österberg Tel: 46836143 Eksamen i emne TFE4130 B lgeforplantning
Noregs teknisk naturvitskaplege universitet Institutt for elektronikk og telekommunikasjon Side 1 av 9 Faglig kontakt under eksamen: Name: Ulf Österberg Tel: 46836143 Eksamen i emne TFE4130 B lgeforplantning
Equations fondamentales de la mécanique linéaire de la rupture
 //5 Aee A Equatios fodaetales de la écaique liéaie de la uptue A. Zeghloul MMAE appels d élasticité plae octio d Ai e vaiables coplees epésetatio des déplaceets et des cotaites Epessio du toseu des effots
//5 Aee A Equatios fodaetales de la écaique liéaie de la uptue A. Zeghloul MMAE appels d élasticité plae octio d Ai e vaiables coplees epésetatio des déplaceets et des cotaites Epessio du toseu des effots
SCE1106 Control Theory
 Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, October 26, 2006 SCE1106 Control Theory Exercise 6 Task 1 a) The poles of the open loop system is
Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, October 26, 2006 SCE1106 Control Theory Exercise 6 Task 1 a) The poles of the open loop system is
Optical Properties of Plasmas Based on an Average-Atom Model
 Optical Properties of Plasmas Based on an Average-Atom Model Walter Johnson, Notre Dame University Claude Guet, CEA/DAM Ile de France George Bertsch, University of Washington Motivation for this work:
Optical Properties of Plasmas Based on an Average-Atom Model Walter Johnson, Notre Dame University Claude Guet, CEA/DAM Ile de France George Bertsch, University of Washington Motivation for this work:
Invariants de Seiberg-Witten et Varietes. Denis AUROUX. Ecole Normale Superieure, 45 rue d'ulm, Paris, France.
 Invariants de Seiberg-Witten et Varietes Symplectiques Denis AUROUX Ecole Normale Superieure, 45 rue d'ulm, 75005 Paris, France e-mail : auroux@clipper.ens.fr Directeur : Jean Pierre BOURGUIGNON 7 novembre
Invariants de Seiberg-Witten et Varietes Symplectiques Denis AUROUX Ecole Normale Superieure, 45 rue d'ulm, 75005 Paris, France e-mail : auroux@clipper.ens.fr Directeur : Jean Pierre BOURGUIGNON 7 novembre
Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl.
 1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
Design d'un champ de vecteurs tangents
 Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN. Langue vivante 2
 Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
EGENSKAPER ANVENDELSE. Technical data sheet SBE - BJELKESKO
 SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
TFY4170 Fysikk 2 Justin Wells
 TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide
 Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
m15/1/aynor/hp2/nor/tz0/xx Monday 11 May 2015 (morning) Lundi 11 mai 2015 (matin) Lunes 11 de mayo de 2015 (mañana) 2 hours / 2 heures / 2 horas
 m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
AB a donc OM = = 2 2
 ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t
ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t
Eksamen i TFE4130 Bølgeforplantning
 Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon Side 1 av 5 Faglig kontakt under eksamen Navn: Ulf Österberg Tlf: 46 83 61 43 Eksamen i TFE4130 Bølgeforplantning
Norges teknisk naturvitenskapelige universitet Institutt for elektronikk og telekommunikasjon Side 1 av 5 Faglig kontakt under eksamen Navn: Ulf Österberg Tlf: 46 83 61 43 Eksamen i TFE4130 Bølgeforplantning
Mise à jour des marges requises
 Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
On multigrid methods for the CahnHilliard equation with obstacle potential
 On multigrid methods for the CahnHilliard equation with obstacle potential ubomír Ba as Department of Mathematics Imperial College London Joint work with Robert Nürnberg http://www.ma.ic.ac.uk/~lubo lubo@imperial.ac.uk
On multigrid methods for the CahnHilliard equation with obstacle potential ubomír Ba as Department of Mathematics Imperial College London Joint work with Robert Nürnberg http://www.ma.ic.ac.uk/~lubo lubo@imperial.ac.uk
Eksamen FSP5020 Fransk I PSP5013 Fransk nivå I. Nynorsk/Bokmål
 Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
Velocity Averaging Lemmas in Hyperbolic Sobolev Spaces for the Kinetic Transport Equation with Velocity Field on the Sphere
 Nonlinear differ. equ. appl. 6 (29), 3 42 c 29 Birkhäuser Verlag Basel/Switzerland 2-9722/3-2 published online 29 January 29 DOI.7/s3-8-84-9 Nonlinear Differential Equations and Applications NoDEA Velocity
Nonlinear differ. equ. appl. 6 (29), 3 42 c 29 Birkhäuser Verlag Basel/Switzerland 2-9722/3-2 published online 29 January 29 DOI.7/s3-8-84-9 Nonlinear Differential Equations and Applications NoDEA Velocity
Level Set methods. Sandra Allaart-Bruin. Level Set methods p.1/24
 Level Set methods Sandra Allaart-Bruin sbruin@win.tue.nl Level Set methods p.1/24 Overview Introduction Level Set methods p.2/24 Overview Introduction Boundary Value Formulation Level Set methods p.2/24
Level Set methods Sandra Allaart-Bruin sbruin@win.tue.nl Level Set methods p.1/24 Overview Introduction Level Set methods p.2/24 Overview Introduction Boundary Value Formulation Level Set methods p.2/24
Existence of resistance forms in some (non self-similar) fractal spaces
 Existence of resistance forms in some (non self-similar) fractal spaces Patricia Alonso Ruiz D. Kelleher, A. Teplyaev University of Ulm Cornell, 12 June 2014 Motivation X Fractal Motivation X Fractal Laplacian
Existence of resistance forms in some (non self-similar) fractal spaces Patricia Alonso Ruiz D. Kelleher, A. Teplyaev University of Ulm Cornell, 12 June 2014 Motivation X Fractal Motivation X Fractal Laplacian
Stationary Phase Monte Carlo Methods
 Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august :00 13:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
THE NORWEGIAN UNIVERSITY OF SCIENCE AND TECHNOLOGY DEPARTMENT OF HYDRAULIC AND ENVIRONMENTAL ENGINEERING
 Page of 4 THE NORWEGIAN UNIVERSITY OF SCIENCE AND TECHNOLOGY DEPARTMENT OF HYDRAULIC AND ENVIRONMENTAL ENGINEERING Scientific contact during the exam: Department of Hydraulic and Environmental Engineering
Page of 4 THE NORWEGIAN UNIVERSITY OF SCIENCE AND TECHNOLOGY DEPARTMENT OF HYDRAULIC AND ENVIRONMENTAL ENGINEERING Scientific contact during the exam: Department of Hydraulic and Environmental Engineering
Sommaire. Montre MOVETIME Family Aperçu de la montre... 1 Touche Marche-Arrêt Retrait des bracelets Résistance à l eau...
 Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
PREPARATION BREVET BLANC 1 CALCUL FRACTIONNAIRE : AIDE : d'abord transformer l'écriture du nombre entier 1. Tout nombre a peut s'écrire 1
 THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
 Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
BACCALAURÉAT GÉNÉRAL
 Session 2018 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU MERCREDI 20 JUIN 2018 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire
Session 2018 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU MERCREDI 20 JUIN 2018 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire
Konstanter og formelsamling finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side en selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
Second Order ODE's (2P) Young Won Lim 7/1/14
 Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Formelsamling Bølgefysikk Desember 2006
 Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Vedlegg 1 av 9 Formelsamling Bølgefysikk Desember 2006 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk
Generalization of age-structured models in theory and practice
 Generalization of age-structured models in theory and practice Stein Ivar Steinshamn, stein.steinshamn@snf.no 25.10.11 www.snf.no Outline How age-structured models can be generalized. What this generalization
Generalization of age-structured models in theory and practice Stein Ivar Steinshamn, stein.steinshamn@snf.no 25.10.11 www.snf.no Outline How age-structured models can be generalized. What this generalization
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Avsluttende eksamen i AST2000, 13. desember 2017, 14.30 18.30 Oppgavesettet inkludert formelsamling er på 8 sider Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Avsluttende eksamen i AST2000, 13. desember 2017, 14.30 18.30 Oppgavesettet inkludert formelsamling er på 8 sider Tillatte hjelpemidler:
Physical origin of the Gouy phase shift by Simin Feng, Herbert G. Winful Opt. Lett. 26, (2001)
 by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
BACCALAURÉAT GÉNÉRAL
 Session 2017 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU LUNDI 19 JUIN 2017 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire (LVO)
Session 2017 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 ÉPREUVE DU LUNDI 19 JUIN 2017 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire (LVO)
Asymptotique des nombres de Betti, invariants l 2 et laminations
 Comment. Math. Helv. 79 (2004) 362 395 0010-2571/04/020362-34 DOI 10.1007/s00014-003-0798-1 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Asymptotique des nombres de Betti, invariants
Comment. Math. Helv. 79 (2004) 362 395 0010-2571/04/020362-34 DOI 10.1007/s00014-003-0798-1 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Asymptotique des nombres de Betti, invariants
On time splitting for NLS in the semiclassical regime
 On time splitting for NLS in the semiclassical regime Rémi Carles CNRS & Univ. Montpellier Rémi Carles (Montpellier) Splitting for semiclassical NLS 1 / 21 Splitting for NLS i t u + 1 2 u = f ( u 2) u,
On time splitting for NLS in the semiclassical regime Rémi Carles CNRS & Univ. Montpellier Rémi Carles (Montpellier) Splitting for semiclassical NLS 1 / 21 Splitting for NLS i t u + 1 2 u = f ( u 2) u,
Periodic solutions for a class of non-autonomous differential delay equations
 Nonlinear Differ. Equ. Appl. 16 (2009), 793 809 c 2009 Birkhäuser Verlag Basel/Switzerland 1021-9722/09/060793-17 published online July 4, 2009 DOI 10.1007/s00030-009-0035-8 Nonlinear Differential Equations
Nonlinear Differ. Equ. Appl. 16 (2009), 793 809 c 2009 Birkhäuser Verlag Basel/Switzerland 1021-9722/09/060793-17 published online July 4, 2009 DOI 10.1007/s00030-009-0035-8 Nonlinear Differential Equations
TECHNIQUE DE CHAUDIERE PAR BRUNNER. Kamin-Kessel 62/76. État: made in germany
 TCHNIQU D CHAUDIR PAR BRUNNR KaminKessel 62/76 État: 30.04.2013 made in germany KaminKessel 62/76 S S securité départ 1/2" fil.ext. securité retour 1/2" fil.ext. porte battante avec isolation et lisiére
TCHNIQU D CHAUDIR PAR BRUNNR KaminKessel 62/76 État: 30.04.2013 made in germany KaminKessel 62/76 S S securité départ 1/2" fil.ext. securité retour 1/2" fil.ext. porte battante avec isolation et lisiére
Lipschitz Metrics for Non-smooth evolutions
 Lipschitz Metrics for Non-smooth evolutions Alberto Bressan Department of Mathematics, Penn State University bressan@math.psu.edu Alberto Bressan (Penn State) Nonsmooth evolutions 1 / 36 Well-posedness
Lipschitz Metrics for Non-smooth evolutions Alberto Bressan Department of Mathematics, Penn State University bressan@math.psu.edu Alberto Bressan (Penn State) Nonsmooth evolutions 1 / 36 Well-posedness
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK Mandag 10. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
BACCALAURÉAT GÉNÉRAL
 Session 2019 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire (LVO) coefficient : 4 Série L LVO
Session 2019 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 Séries L, ES, S Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire (LVO) coefficient : 4 Série L LVO
1 OA i = f. OA o. 1 < 1 OA o. f 1. O 2 A i O 2 A 1 = = f 2 O 2 A i. f 2O 2 A i 5 `c mffl `a vfle c O 2 A i = 20 `c mffl `eˇt f 2 = 20 `c mffl
 . B L`affl r`e l åtˇi`o nffl `d`e `c o n jˇu`g åi sfi`o nffl `d`o n n`e OA i = + f P`o u rffl u n`e l e n tˇi l l e m i n`c e `c o n vfleˇr`g e n t e, < f `d`o n`c L i m`àg e `eṡfi t r`é e l l e. f > 0.
. B L`affl r`e l åtˇi`o nffl `d`e `c o n jˇu`g åi sfi`o nffl `d`o n n`e OA i = + f P`o u rffl u n`e l e n tˇi l l e m i n`c e `c o n vfleˇr`g e n t e, < f `d`o n`c L i m`àg e `eṡfi t r`é e l l e. f > 0.
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai :00 13:00
 NTNU Side 1 av 2 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 2 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai 2012 09:00 13:00 Tillatte hjelpemidler:
Verifiable Secret-Sharing Schemes
 Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
NO X -chemistry modeling for coal/biomass CFD
 NO X -chemistry modeling for coal/biomass CFD Jesper Møller Pedersen 1, Larry Baxter 2, Søren Knudsen Kær 3, Peter Glarborg 4, Søren Lovmand Hvid 1 1 DONG Energy, Denmark 2 BYU, USA 3 AAU, Denmark 4 DTU,
NO X -chemistry modeling for coal/biomass CFD Jesper Møller Pedersen 1, Larry Baxter 2, Søren Knudsen Kær 3, Peter Glarborg 4, Søren Lovmand Hvid 1 1 DONG Energy, Denmark 2 BYU, USA 3 AAU, Denmark 4 DTU,
Une version feuilletée du théorème de translation de Brouwer
 Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
DYNAMIQUE. Etude des mouvements de tangage d une transmission de puissance d hélicoptère. x r 2. y r 2. x 1. y r y r
 e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
Trust region methods: global/local convergence, approximate January methods 24, / 15
 Trust region methods: global/local convergence, approximate methods January 24, 2014 Trust region methods: global/local convergence, approximate January methods 24, 2014 1 / 15 Trust-region idea Model
Trust region methods: global/local convergence, approximate methods January 24, 2014 Trust region methods: global/local convergence, approximate January methods 24, 2014 1 / 15 Trust-region idea Model
A Benchmark of Selected Algorithmic. Machine Learning and Computer Vision
 A Benchmark of Selected Algorithmic Differentiation Tools on Some Problems in Machine Learning and Computer Vision FILIP SRAJER ZUZANA KUKELOVA ANDREW FITZGIBBON AD2016 11.9.2016 Version for public release
A Benchmark of Selected Algorithmic Differentiation Tools on Some Problems in Machine Learning and Computer Vision FILIP SRAJER ZUZANA KUKELOVA ANDREW FITZGIBBON AD2016 11.9.2016 Version for public release
FRAISES SCIES SLITTING SAWS END-MILLS FRAISES R8010
 SCIES SLITTING SAWS NORME : ISO 2296 - NF E 66.233 - IN 1838 STANAR : ISO 2296 - NF E 66.233 - IN 1838 R8010 ENTURE FINE FINE TEETH 0 R8010 e - js16 e - js11 - H7 Z Coe Prix - 20 0,2 5 80 R8010.020.020.05
SCIES SLITTING SAWS NORME : ISO 2296 - NF E 66.233 - IN 1838 STANAR : ISO 2296 - NF E 66.233 - IN 1838 R8010 ENTURE FINE FINE TEETH 0 R8010 e - js16 e - js11 - H7 Z Coe Prix - 20 0,2 5 80 R8010.020.020.05
BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN. Mardi 23 juin 2015. Langue vivante 2
 Session 2015 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Mardi 23 juin 2015 Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L Langue vivante obligatoire (LVO) Durée
Session 2015 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Mardi 23 juin 2015 Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L Langue vivante obligatoire (LVO) Durée
BACCALAURÉAT GÉNÉRAL
 Session 2016 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 Séries L, ES, S ÉPREUVE DU VENDREDI 17 JUIN 2016 Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire
Session 2016 BACCALAURÉAT GÉNÉRAL NORVÉGIEN Langue vivante 1 Séries L, ES, S ÉPREUVE DU VENDREDI 17 JUIN 2016 Durée de l épreuve : 3 heures Séries ES/S coefficient : 3 Série L langue vivante obligatoire
Positive dispersion: 2 n. λ 2 > 0. ω 2 > 0, Negative dispersion: ω < 0, 2 n
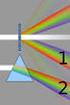 Positive dispersion: 2 n ω 2 > 0, 2 n λ 2 > 0 Negative dispersion: 2 n ω < 0, 2 n 2 λ < 0 2 φ(z,ω) = k ( n ω )z E( z,t)= 1 2π E ( z = 0,ω )e iωt iφ z,ω e ( ) dω φ(z,ω) = k ( n ω )z φ( ω )= φ 0 + ω ω 0
Positive dispersion: 2 n ω 2 > 0, 2 n λ 2 > 0 Negative dispersion: 2 n ω < 0, 2 n 2 λ < 0 2 φ(z,ω) = k ( n ω )z E( z,t)= 1 2π E ( z = 0,ω )e iωt iφ z,ω e ( ) dω φ(z,ω) = k ( n ω )z φ( ω )= φ 0 + ω ω 0
Graphs similar to strongly regular graphs
 Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Kap. 16: Kontinuerlige systemer
 Kap. 16: Kontinuerlige systemer Har betraktet systemer med én frihetsgrad (avhengig av tiden) Partikler (med føringer) Stive legemer (med føringer) Ordinære differensiallikninger (ODE) Deformerbare legemer
Kap. 16: Kontinuerlige systemer Har betraktet systemer med én frihetsgrad (avhengig av tiden) Partikler (med føringer) Stive legemer (med føringer) Ordinære differensiallikninger (ODE) Deformerbare legemer
Trianguleringer og anvendelser
 INF-MAT5370 Trianguleringer og anvendelser Fra seilflysimulatoren Silent Wings Bakgrunn for kurset: Kurset ble til til mens vi vi (foreleserne) arbeidet med oppdrag for industrien på SINTEF. Samtlige deler
INF-MAT5370 Trianguleringer og anvendelser Fra seilflysimulatoren Silent Wings Bakgrunn for kurset: Kurset ble til til mens vi vi (foreleserne) arbeidet med oppdrag for industrien på SINTEF. Samtlige deler
Des accouplements raisonnés, un élément essentiel à l amélioration génétique
 Innover aujourd hui, prospérer demain Centre Caztel, Sainte Marie Des accouplements raisonnés, un élément essentiel à l amélioration génétique Robie Morel, B.Sc., coordonnateur du secteur génétique et
Innover aujourd hui, prospérer demain Centre Caztel, Sainte Marie Des accouplements raisonnés, un élément essentiel à l amélioration génétique Robie Morel, B.Sc., coordonnateur du secteur génétique et
EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING. Mandag 14. desember 2005 Tid: 09:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for telematikk Side 1 av 12 Faglig kontakt under eksamen: Poul Heegaard (73 594321) EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING
Norges teknisk naturvitenskapelige universitet Institutt for telematikk Side 1 av 12 Faglig kontakt under eksamen: Poul Heegaard (73 594321) EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING
Rotation-driven Magnetohydrodynamic Flow Using Local Ensemble Transform Kalman Filtering
 Rotation-driven Magnetohydrodynamic Flow Using Local Ensemble Transform Kalman Filtering Kayo Ide 2 ide@umd.edu Sarah Burnett 1 burnetts@math.umd.edu Nathanaël Schaeffer 4 nathanael.schaeffer@ univ-grenoble-alpes.fr
Rotation-driven Magnetohydrodynamic Flow Using Local Ensemble Transform Kalman Filtering Kayo Ide 2 ide@umd.edu Sarah Burnett 1 burnetts@math.umd.edu Nathanaël Schaeffer 4 nathanael.schaeffer@ univ-grenoble-alpes.fr
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 15 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Tri sélectif de déchets. Kildesortering
 Tri sélectif de déchets Dans notre commune, on est légalement obligé de trier les déchets. Le but est de les recycler et ainsi contribuer à un meilleur environnement pour nous tous. Voici une description
Tri sélectif de déchets Dans notre commune, on est légalement obligé de trier les déchets. Le but est de les recycler et ainsi contribuer à un meilleur environnement pour nous tous. Voici une description
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Matematik, LTH Kontinuerliga system vt Formelsamling. q t. + j = k. u t. (Allmännare ρ 2 u. t2 Svängningar i gaser (ljud) t 2 c2 2 u
 Matematik, LH Kontinuerliga system vt 7 Formelsamling Formelsamligen utgör bara ett stöd för minnet. Beteckningar förklaras sålunda ej. Ej heller anges förutsättningar för formlernas giltighet. Fysikaliska
Matematik, LH Kontinuerliga system vt 7 Formelsamling Formelsamligen utgör bara ett stöd för minnet. Beteckningar förklaras sålunda ej. Ej heller anges förutsättningar för formlernas giltighet. Fysikaliska
P ±Ê. Š - ˆ Œˆ œ Ÿ Š ˆŒ ˆŸ ƒ Ÿ Š Œ ˆ ŠˆŒ. ² μ Ê ² Œ É ³ É Î ±μ ³μ ² μ.
 P-22-86.. ±Ê Š - ˆŒˆ œÿ Š ˆŒ ˆŸ ƒ Ÿ Š Œ ˆ ŠˆŒ ˆ Œ ² μ Ê ² Œ É ³ É Î ±μ ³μ ² μ E-mail: dnd@jinr.ru ±Ê.. P-22-86 ŠÊ μî μ- μ² μ³ ²Ó Ö μ± ³ Í Ö Ï Éμ μ μ Ö ± Éμ³ É Î ± ³ μ Ê ³ Ê ²μ ŠμÔËË Í ÉÒ ³μ ² ²μ± ²Ó μ
P-22-86.. ±Ê Š - ˆŒˆ œÿ Š ˆŒ ˆŸ ƒ Ÿ Š Œ ˆ ŠˆŒ ˆ Œ ² μ Ê ² Œ É ³ É Î ±μ ³μ ² μ E-mail: dnd@jinr.ru ±Ê.. P-22-86 ŠÊ μî μ- μ² μ³ ²Ó Ö μ± ³ Í Ö Ï Éμ μ μ Ö ± Éμ³ É Î ± ³ μ Ê ³ Ê ²μ ŠμÔËË Í ÉÒ ³μ ² ²μ± ²Ó μ
On remet la machine en route
 Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ÿ Œ œ ˆ ˆ Š Œ. .. ³μ. μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö Œ Œ ˆˆ 79 ˆ Š ˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
FYSMEK1110 Eksamensverksted 23. Mai :15-18:00 Oppgave 1 (maks. 45 minutt)
 FYSMEK1110 Eksamensverksted 23. Mai 2018 14:15-18:00 Oppgave 1 (maks. 45 minutt) Page 1 of 9 Svar, eksempler, diskusjon og gode råd fra studenter (30 min) Hva får dere poeng for? Gode råd fra forelesere
FYSMEK1110 Eksamensverksted 23. Mai 2018 14:15-18:00 Oppgave 1 (maks. 45 minutt) Page 1 of 9 Svar, eksempler, diskusjon og gode råd fra studenter (30 min) Hva får dere poeng for? Gode råd fra forelesere
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsdag 8. august 2002
 NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:
![Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene: Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:](/thumbs/64/52216522.jpg) HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
Finite Elements Methods. Formulary for Prof. Estor's exam
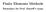 Finite Elements Methods Formulary for Prof. Estor's exam Finite Element Method in General One wants to obtain the equilibrium eqautions for the body, discretized by nite elements in the form M Ü + C U
Finite Elements Methods Formulary for Prof. Estor's exam Finite Element Method in General One wants to obtain the equilibrium eqautions for the body, discretized by nite elements in the form M Ü + C U
Løsningsforslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag 26. mai 2005
 NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
Optimale pådriv for endringer i hyppigheten av atmosfæriske strømningsmønstre, spesielt COWL
 Optimale pådriv for endringer i hyppigheten av atmosfæriske strømningsmønstre, spesielt COWL Trond Iversen, Jørn Kristiansen, Thomas Jung* and Jan Barkmeijer** * ECMWF ** KNMI Innhold Litt teori (med noen
Optimale pådriv for endringer i hyppigheten av atmosfæriske strømningsmønstre, spesielt COWL Trond Iversen, Jørn Kristiansen, Thomas Jung* and Jan Barkmeijer** * ECMWF ** KNMI Innhold Litt teori (med noen

 LIBER BVEL MAGI SVB FIGVRÂ I $
LIBER BVEL MAGI SVB FIGVRÂ I $