Invariants de Seiberg-Witten et Varietes. Denis AUROUX. Ecole Normale Superieure, 45 rue d'ulm, Paris, France.
|
|
|
- Astrid Birgit Christoffersen
- 4 år siden
- Visninger:
Transkript
1 Invariants de Seiberg-Witten et Varietes Symplectiques Denis AUROUX Ecole Normale Superieure, 45 rue d'ulm, Paris, France auroux@clipper.ens.fr Directeur : Jean Pierre BOURGUIGNON 7 novembre Introduction Une question essentielle de latopologie est la classication des varietes, qu'elles soient topologiques ou dierentiables. La classication en dimension 2 est connue depuis longtemps. A l'oppose, en dimension superieure ou egale a 5,letheoreme du h-cobordisme desmale arme que deux varietes h-cobordantes sont dieomorphes. En revanche, dans les dimensions intermediaires 3 et 4, la situation est moins claire. En dimension 4, la classication des varietes dierentiables simplement connexes compactes (orientables) a homeomorphisme pres se ramene a celle des formes quadratiques entieres : deux varietes sont homeomorphes si et seulement si leurs formes d'intersection sont isomorphes. En revanche, bien que toute forme quadratique soit la forme d'intersection d'une variete topologique, il existe des formes qui ne peuvent ^etre realisees par une variete dierentiable. On sait depuis les travaux de Donaldson [DK] que certaines varietes topologiques n'admettent pas de structure dierentiable, et qu'inversement deux varietes homeomorphes ne sont pas necessairement dieomorphes. Les polyn^omes de Donaldson, introduits audebut des annees 80, fournissent des invariantsdes varietes de dimension 4 qui vontau-delade la seule information topologique, puisqu'ils permettent de dierencier des varietes qui ont m^eme forme d'intersection. Ces invariants, qui decoulent del'etude des connexions antiautoduales, font intervenir le groupe de jauge non abelien SU(2), ce qui les rend parfois delicats a manipuler. Recemment (1994), Seiberg et Witten ont introduit de nouveaux invariants [W] dont l'utilisation est plus aisee. Ces invariants, et leurs proprietes dans le cadre des varietes symplectiques, sont l'objet du present memoire, qui s'inspire essentiellement des travaux de Taubes ([T3], [T4]) et d'un texte redige par Friedrich ([F]). 1
2 2 Structures Spin c et spineurs 2.1 Structures Spin c Denition On appelle algebre de Cliord der n euclidien, notee Cl n,le quotient de l'algebre tensorielle T R n par l'ideal engendre par les x x + kxk 2 :1 pour x 2 R n. L'espace vectoriel R n se plonge dans Cl n,etcettederniere est alors l'algebre a unite engendree par R n avec les relations x:x =,kxk 2.Par polarisation, on a egalement pour x et y elements der n Cl n, x:y + y:x =,2hx; yi. L'algebre Cl n est 2 -graduee et se subdivise en elements de longueur paire (Cl 0 n) et impaire (Cl 1 n). En outre, l'application de l'algebre exterieure R n dans Cl n qui a e i1 ^ :::^e ip associe e i1 :::::e ip est un isomorphisme d'espaces vectoriels. Enn, on a le theoremede classication des algebres complexiees Cl n C : Theoreme Cl 2k C = End(C 2k ) et Cl 2k+1 C = End(C 2k ) End(C 2k ). On denit alors le groupe Spin(n) Cl 0 n de lafacon suivante. Denition Spin(n) =fx 1 :::::x 2r ;x i 2R n ;kx i k=1g. Proposition Pour tout element q 2 Spin(n) et v 2 R n, q:v:q,1 2 R n. Ceci fournit une representation : Spin(n)! End(R n ) denie par (q):v = q:v:q,1. L'image de est exactement SO(n), et son noyau est 1. Via, Spin(n) est donc un rev^etement double de SO(n). En particulier si n 3, c'est le rev^etement universel de SO(n). On denit alors dans l'algebre complexiee le groupe Spin c (n). Denition Spin c (n) = (Spin(n) S 1 )=f1gcl n C On dispose d'une suite exacte 1! 2! Spin c (n)! c SO(n) S 1! 1 donnee par c ([g; z]) = ((g);z 2 )oudesigne le rev^etement adeux feuillets de SO(n) par Spin(n). Cette suite exacte permet de denir une spin c structure comme un relevement d'une SO(n)-structure. Denition Une spin c -structure sur une variete riemannienne orientee X dotee du SO(n)-bre principal P des reperes orthonormes directs est la donnee de : (1) un S 1 -bre principal P U (1) sur X, oudefacon equivalente via la representation canonique de U(1), un bre en droites complexes L. (2) un Spin c (n)-bre principal Q sur X qui est, bre par bre, un rev^etement double de P X P U (1) via c. 2
3 On peut alors caracteriser de la facon suivante les bres en droites L qui conviennent: Proposition Un bre endroites L correspond a une structure spin c X si et seulement si c 1 (L) w 2 (P ) mod 2 dans H (X; 2 2 ). sur Cette condition est beaucoup plus faible que l'existence d'une structure spin. On peut montrer a l'aide du theoreme des coecients universels que sur une variete compacte orientable de dimension 4, w 2 (P ) est toujours la reduction modulo 2 d'une classe entiere, ce qui implique l'existence d'une structure spin c. 2.2 Fibre des spineurs Soit X une variete de dimension paire n = 2k munie d'une structure spin c. Spin c (n) Cl n C = End(n ) par le theoreme 2.2. Spin c (n) possede donc une representation : Spin c (n)! U( n ), ou n est un C -espace vectoriel de dimension 2 k. La representation est la restriction de la representation irreductible Cl n C! End( n ) (on appelle cette action sur n la multiplication de Cliord). Il est important de noter qu'a cause de l'isomorphisme d'espaces vectoriels exhibe plus haut, l'algebre exterieure agit aussi par multiplication de Cliord. La representation permet d'associer au bre principal Q un bre vectoriel complexe S de rang 2 k appele bre des spineurs. Les elements de l'algebre de Cliord, ainsi que les formes dierentielles, agissent sur S par multiplication de Cliord. Soit maintenantl'element v = i k :e 1 :e 2 :::::e n decl n C.Ona v 2 = 1, donc la multiplication de Cliord par v admet les deux valeurs propres 1. L'element v commute avec tous les elements pairs de l'algebre de Cliord, et anticommute avec les elements impairs, et donc les deux sous-espaces propres, qui sontchacun de dimension 2 k,1, sont stables par les elements pairs et sont echanges par les elements impairs. En particulier, comme Spin c (n) Cl 0 n C, la representation de Spin c se scinde endeux sous-representations dontonpeut montrer qu'elles sont irreductibles. Le bre des spineurs se decompose en S = S + S,, S correspondant ala representation de Spin c (n), c'est-a-dire que v agit par +1 sur S + et,1 sur S,.Leselements pairs de l'algebre de Cliord preservent cette decomposition, tandis que les elements impairs permutent les deux facteurs. Dans le cas de ladimension 4, S + et S, sontdes bres complexes de rang 2. Une propriete remarquable de l'action de Spin c sur S + est que la multiplication de Cliord par g:e i ou g 2 Spin a pour determinant e 2i, ce qui correspond precisementau second facteur de la projection de Q sur P P U (1). On a donc L =det(s + ). On a d'autre part une decomposition 2 R 4 = +, en formes autoduales et anti-autoduales donnee par l'operateur de Hodge qui est l'involution de 2 denie par (e i ^ e j )=e k^e l lorsque (e i ;e j ;e k ;e l ) est une base orthonormee directe der 4. Pour 2 R +, ^ R R = ^ = jj 2. Pour R R R R 2,, ^ =, ^ =, jj2. Et alors ^ R = h; i =, R h; i = 3
4 , R h;i =, R ^, donc cette integrale est nulle. Enn on peut remarquer qu'une forme autoduale (ou antiautoduale) fermee verie d! =0,etestautomatiquement harmonique. De plus la projection sur d'une forme harmonique est harmonique, donc toute 2-forme harmonique se decompose en une partie autoduale et une partie antiautoduale. Acause de la correspondance entre classes de cohomologie et formes harmoniques, la m^eme decomposition s'applique a l'espace de cohomologie H 2 qui s'ecrit H 2 = H 2;+ H 2;,. On note b 2 la dimension de H 2;. La decomposition S = S + S, est compatible avec la decomposition de Hodge, en ce sens qu'une formeanti-autoduale agit sur S + comme 0. En eet, si on considere par exemple e 1 :e 2, e 3 :e 4, par multiplication a gauche par l'element inversible e 2 :e 1 on obtient 1,vdont lenoyau est precisement S +. On a donc, :S + = 0 et de m^eme + :S, =0. 3 Operateur de Dirac Soit une spin c -structure Q sur une variete X de dimension n, correspondant a une projection : Q! P P U (1). Sionsexeune connexion A sur P U (1) (ce qu'on notera A 2C(P U(1) )), A et la connexion de Levi-Civita sur X induisent une connexion sur Q, et donc une derivation covariante r A sur les sections de S. Denition On appelle operateur de Dirac sur le bre des spineurs S, associe alaconnexion A, l'operateur D A :,(S)!,(S) deni par D A = nx e i :r A ei i=1 ou (e i ) designe une base orthonormee quelconque. Proposition L'operateur D A est un operateur dierentiel elliptique d'ordre 1, formellement autoadjoint. (On rappelle qu'un operateur est dit formellement autoadjoint lorsqu'il verie R hd; i = R h; D i). De plus l'operateur D A envoie S + sur S, et reciproquement. On notera D + A sa restriction a,(s + )!,(S, ) (resp. D, :,(S, )!,(S + )). A Soit A une formede connexion sur P U (1),etF A =da sa courbure, qui est une 2-forme sur X a valeurs imaginaires pures. On a notamment c 1 (L) = i F 2 A (on prend cette denition de la classe de Chern au lieu de ladenition plus usuelle c 1 (L) = 1 F 2i A an d'avoir egalite entre classe de Chern et classe d'euler et de pouvoir la calculer a partir des zeros d'une section. Voir [LB]). Proposition 3.3 (formule de Weitzenbock) - Pour toute section de S, ona l'egalite D 2 A =(ra ) r A + R F A: ou R designe la courbure scalaire dex,etf A F A : = P F i<j A(e i ;e j )e i :e j :. agit par multiplication de Cliord 4
5 L'indice de l'operateur D + A :,(S+ )!,(S, )peut alors ^etre calcule gr^ace au theoreme de l'indice d'atiyah-singer. Theoreme Si on note c la classe de Chern c 1 (L) du bre L, l'indice sur C de D + A, Ind(D+ A ) = dim Ker(D+ A ), dim Coker(D+ A ),verie Ind(D + A )=(ec=2 : ^A(X)):[X]: En dimension 4 on a ^A(X) =1, 1 p 24 1(X), d'ou ondeduit Ind(D + ) = A 1, 8 c2 1 p De plus le theoreme de la signature d'hirzebruch arme que la signature de X, soit = b + 2, b,,verie = 1 p 2 3 1(X):[X], et donc Ind(D + A )= 1 8 (c2,): 4 Les invariants de Seiberg-Witten 4.1 Les equations de Seiberg-Witten Soit X une variete orientee de dimension 4 (compacte), munie d'une structure spin c caracterisee par le bre en droites L =det(s + ). Denition Pour section de S +,onpose! (x; y)=hx:y:; i + hx; yijj 2 ou h:; :i est le produit scalaire hermitien (antilineaire en le premier facteur) sur S +. Un simple calcul donne alors la proposition suivante. Proposition La 2-forme! est alternee, a valeurs imaginaires pures, et autoduale. De plus on a h! :; i = j! j 2 =2jj 4. Denition L'equation de Seiberg-Witten est l'equation suivante qui relie une connexion A sur L et une section de S + : ( DA =0 (4.1) F + = 1 A 4! ou F + A designe la projection sur + de la courbure F A de la connexion A. On a le resultat suivant, qui implique l'absence de solutions non triviales sur les varietes a courbure scalaire positive: Proposition Soit (A; ) une solution de (4.1), et soit R la courbure scalaire dex,etr min son minimum sur X, alors en tout point on a j(x)j 2 max(,r min ; 0) 5
6 Demonstration : En un point oujj 2 est maximal, on a 0 jj 2 = 2h(r A ) r A ; i,2jr A j 2 2h(r A ) r A ; i =2(h, R 4 ; i, 1 2 hf A;i)=, R 2 jj2,hf + A ; i =, R 2 jj2, 1 4 h! :; i =, R 2 jj2, 1 2 jj4 et donc si jj 2 6 0, jj 2 + R 0, d'ou leresultat. 2 On considere maintenant l'action du groupe de jauge G = Map(X; S 1 )= Aut(P U (1) ). Soit une transformation de jauge f 2G. La forme de connexion est transformee par f selon la formule classique f A = A + df f. Proposition Si (A; ) est solution de (4.1), alors (f (A);f,1 ) aussi. Le groupe de jauge agit donc sur l'espace des solutions. Demonstration : On a r f A t,r A t= df:t d'ou pour l'operateur de f Dirac D f A, D A = 1grad(f):. On a donc D f f A( 1 ) = D f A( 1 ) + f 1 grad(f):( 1 f f )=(1D f A, 1 grad(f):) + 1 grad(f): = 1 D f 2 f 2 f A. L'un est nul si et seulement si l'autre l'est. La courbure est un tenseur, donc F f A = F A,or! 1 f = jfj 1! =!, donc 2 la deuxieme equation reste veriee. 2 Denition Soit X une variete riemannienne compacte orientee de dimension 4, et L un bre endroites complexes muni d'un produit scalaire hermitien. On appelle espace des modules M L = f(;a)2,(s + ) C(P U(1) ): D A =0;F + A =1 4! g=g: Il est a noter que G agit librement sur l'espace des solutions, sauf lorsque 0 (solutions dites "triviales"). En eet si f 2Gagit trivialement, f A = A implique que df = 0, donc f estlamultiplication par une constante, et f,1 = implique f 1. Il est donc interessantde perturber l'equation (4.1) an d'eviter les solutions triviales. Denition L'equation de Seiberg-Witten perturbee est (4.2) ( DA =0 F + A = 1 4! + ou est une 2-forme autoduale a valeurs imaginaires pures. La theorie pour l'equation perturbee est preferable en ce sens qu'un choix generique de permet souvent d'eliminer les problemes qui peuvent appara^tre dans le cas = 0. Pour l'equation (4.2) on denit bien evidemment dem^eme l'espace des modules M L;. On omettra souvent par la suite depreciser la dependance en L et en. On utilisera par la suite la formule suivante. 6
7 Lemme La linearisation des equations (4.1) ou (4.2) en une solution est P 1 (;A) ( ;)=(:+D A ; (d) +, 1 4!; ) ou! ; est la variation de! avec. Demonstration : En eet le seul terme a expliquer est :, qui vient de D At,D A = P i e i:r At ei,p i e i:r A ei =P i e i:t(e i ) = t: Independance vis-a-vis des parametres Etudions maintenant ladependance en et en la metrique g sur X des solutions des equations (4.1) et (4.2), et tout particulierement l'existence de solutions triviales ( 0). La condition d'existence de solutions triviales pour (4.1) s'ecrit F A 2,. Lorsque L est trivial, il peut exister des solutions triviales. Lorsque L n'est pas trivial, la condition d'existence de solution triviales est l'appartenance de la classe de cohomologie non nulle c 1 (L) ah 2;,.Or H 2;,, lorsque la metrique varie, decrit les sous-espaces negatifs maximaux pour la forme d'intersection. Donc si c 1 (L):c 1 (L) 0, il n'y a jamais de solutions triviales, et dans le cas contraire la condition d'existence de solutions triviales est de codimension b +. 2 Pour (4.2) la situation est similaire. En ce qui concerne ladependance en dans (4.2), les solutions triviales correspondent aux connexions A 0 + telles que (d) + =, F +. La condition A0 d'existence de solutions triviales est donc,f + 2 A0 Im(d+ ), qui est de codimension b + dans 2 + (voir lemme 4.11). Les solutions triviales de (4.2) n'existent donc que si est dans un sous-espace de codimension b +. 2 On en deduit le theoreme suivant. Theoreme On suppose que b Pour un choix generique de, l'equation (4.2) n'a pas de solutions avec 0. Le terme "generique" signie ici en dehors d'un espace decodimension b + 2. Si on suppose de plus que L n'est pas trivial, alors pour un choix generique de metrique, (4.1) et (4.2) n'ont pas de solutions avec 0. Dans le cas ou b + 2 = 1, l'espace des metriques (ou des ) qui conviennent n'est pas connexe, ce qui fait que les constructions ne dependent pas que de la structure dierentiable sur X mais aussi de lametrique choisie. Pour simplier, on supposera donc en pratique que b + 2 2, l'espace des parametres g et convenables etant alors connexe, on pourra denir a partir de M des invariants qui ne dependent que de la structure dierentielle de X. L'espace M est naturellement muni d'une structure de variete analytique reelle. Le probleme est que cette variete n'est pas toujours lisse ; pour prouver qu'elle l'est generiquement, on introduit un espace parametre deni de lafacon suivante. Soit U l'ouvert des tels que (4.2) n'a pas de solutions triviales. D'apres ce qui precede, U est dense et connexe pour b On considere alors 7
8 l'espace parametre M = f(;a;)2,(s + ) C(P U(1) ) U : (;A;)=0g=G ou (;A;)=(D A ;F + A, 1 4!,). L'application est une submersion. En eet soit x un element quelconque de,(s, ),( + ). La projection de ladierentielle D de sur le premier facteur, qui est (; ; ) 7! D A + : (lemme 4.8), est surjective acause du terme :. Donc il existe x 0 dans l'image de D tel que y = x, x 0 puisse s'ecrire sous la forme y =(0;). Comme D(0; 0;)=(0;)onendeduit que y 2 Im(D) et donc x 2 Im(D) ce qui donne leresultat. On en deduit que M est une variete lisse puisque G agit librement pour 2U. En appliquant le theoreme de Sard a la projection de M sur le troisieme facteur :[ ;A;] 7! (ou [ ;A;]designe la classe de ( ;A;)modulo G), on obtient que pour presque tout, M L; est un niveau non critique et donc une variete lisse. Montrons que si M L;1 et M L;2 sont lisses, ils sont cobordants. Pour cela, on remarque que l'operateur linearise P 1 correspondant a (4.1) a une image de codimension nie, car P 1 d qui est elliptique (il a le m^eme symbole principal que (D A ;d + d ))auneimage de codimension nie, d'ou par projection le resultat pour P 1.Onpeut alors choisir un supplementaire de dimension nie de l'image de P 1, et donc se limiter a des parametres dans un ouvert connexe d'un espace vectoriel de dimension nie, V inclus dans U, contenant 1 et 2,tout en conservant la proprietedesubmersion (M\,1 (V) est donc toujours lisse). Par connexite dev,onaunchemin joignant 1 a 2. On peut construire une fonction f sur V dont la ligne de niveau correspondant a lavaleur proche de0estauvoisinage de un chemin qu'on note, passant en 1; et 2; (ces deux pointsetant proches de 1 et 2 respectivement). Par le theoremede Sard applique a f,on peut trouver aussi proche de 0 que voulu tel que,1 ( ) soit lisse, ce qui prouve que M L;1; et M L;2; sont cobordants. Or en dimension nie les pointscritiques constituentun ferme, donc auvoisinage de M L;1 et M L;2, n'a pas de points critiques, d'ou ondeduit en utilisant la compacitedem(qui sera l'objet du theoreme 4.13) que pour assez petit M L;i est dieomorphe am L;i; ce qui acheve la preuve. 2 Les M obtenus pour dierents convenables sont donc cobordants, et on peut donc denir des invariants a partir de M qui ne dependent que de la structure dierentielle sur X. 4.3 Dimension de M On va maintenant calculer la dimension virtuelle de M (c'est a dire sa dimension si M 6= ;). Pour cela on remarque que l'espace tangent a Mest deni a partir du complexe elliptique obtenu en linearisant l'equation (4.1). La linearisation de l'action de G en une solution de (4.1) est P 0 (;A)(h) =(,h;dh) En eet, si (f t ) est une famille de transformations de jauge veriant f 0 =1et d f dt tjt=0 = h, ona,ent=0, d(f A, A) = d( dft )=dh, et d( 1 ) =,h. dt t dt ft dt ft L'operateur associealalinearisation des equations (4.1) est P 1 donne par (;A) le lemme
9 Denition On appelle indice d'un complexe elliptique 0! A f! B g! C! 0 la somme alternee des dimensions des espaces de cohomologie de ce complexe, Ind = dim(h 0 ),dim(h 1 )+dim(h 2 ),oudefacon equivalente l'indice de l'operateur f g : A C! B. L'indice d'un operateur ne depend que de sa partie principale, donc le complexe elliptique a le m^eme indice que,( 0 ) P 0 (;A) 1 (;A)!,(S + ),( 1 ) P!,(S, ),( + ),( 0 ) (0;d)!,(S + ),( 1 ) (D A ;d+ )!,(S, ),( + ) qui se decompose comme la somme directe des complexes,( 0 ) d!,( 1 ) d+!,( + )et0!,(s + ) D A!,(S, ). L'indice de cedernier complexe est l'oppose de l'indice sur R de l'operateur de Dirac, qui est le double de l'indice sur C, lequel vaut par le theoreme de l'indice 1 8 (c 1(L) 2, ). L'indice du deuxieme complexe est donc 1 4 (, c 1(L) 2 ). Reste a calculer l'indice du premier complexe. Lemme L'indicede,( 0 ) d!,( 1 ) d+!,( + ) est 1 2 (+) =b 0,b 1 +b + 2. Demonstration : On a clairement H 0 = H 0 (X;R). Si on note enindice de chaque operateur le rang des formes sur lesquelles il opere, on calcule H 2 = Coker(d 1 + d 1 ) + =Ker((d 1 + d 1 ) ) \ +,ord 1 =d 2et (d 1 ) = d 1 = d 2 qui concident sur +, donc H 2 =Ker(d 2 ) \ + =Ker(d 2 ) \ + = H 2 \ +, dont la dimension est par denition b + 2. Enn H 1 =Ker(d 1) \ Ker(d 1 + d 1 );orsi x2ker(d 1 + d 1 ), alors d 1 x 2, et d 1 x 2 Ker(d 2 ), et donc d 1 x 2 Ker(d 2 ) = Im(d 1)? ce qui entra^ne d 1 x =0. Donc H 1 =Ker(d 1) \ Ker(d 1 )=H 1 est de dimension b 1. 2 Si on choisit pour une valeur reguliere de la projection denie plus haut, l'espace des modules M est lisse et son espace tangent est donne par TM =Ker(P 1 )=Im(P 0 ), c'est-a-dire le (;A) (;A) H1 du complexe linearise. Pour calculer la dimension virtuelle de M (c'est-a-dire sa dimension dans le cas ou M 6= ;), on remarque tout d'abord que l'absence de solution reductible implique l'injectivite dep 0, d'ou ondeduit (;A) H0 =0. De plus on va montrer que P 1 est surjectif dans notre cas. En eet, on (;A) a vu plus haut que l'operateur :(;A;) 7! (D A ;F + A, 1 4!,) est une submersion. Si on se donne (; ) 2,(S, ),( + ), il existe donc ( ;;)2,(S + ),( 1 ),( + )tel que D( ;;)=P 1 ( ;), (0;)=(; ). (;A) D'autre part, comme on a suppose que le parametre est une valeur reguliere de, l'image de D contient. Donc il existe 2,(S + )et2,( 1 )tels que la classe de (; ; ) modulo G soit tangente a l'espace des modules parametre M. On a donc D(; ; ) = 0, d'ou l'on deduit que D(, ;, ; 0) = P 1 (, ;, ) =(; ). L'operateur P 1 est donc surjectif, et donc le (;A) (;A) 9
10 complexe associe aux equations de Seiberg-Witten verie, lorsque l'espace des modules est lisse, H 2 =0. Il en decoule que la dimension virtuelle de l'espace des modules, qui est egale a la dimension de H 1, est egale a l'oppose de l'indice du complexe linearise. On deduit de tout ce qui precede le resultat suivant. Theoreme La dimension virtuelle d de l'espace des modules M est (4.3) d =, 1 4 (2 +3)+ 1 4 c 1(L) 2 : 4.4 Invariants de Seiberg-Witten Comme les invariants de varietes non orientees sont peu precis (il n'existe que deux varietes de dimension 0 distinctes!), il est necessaire d'orienter M. Ceci peut ^etre eectue en orientant les droites determinants des divers complexes elliptiques. La partie correspondanta l'operateur de Dirac D A est canoniquement orientee puisque cet operateur est C -lineaire. Une orientation de M est donc xee par un choix d'orientation de la droite reelle (4.4) det(h 0 (X;R)) det(h 1 (X;R)) det(h 2;+ (X;R)): Ceci ane considerablement les invariants (en dimension 0, on peut desormais compter les points en leur attribuant des signes 1). On a d'autre part le theoreme suivant: Theoreme M est compact. Demonstration : La proposition 4.4 fournit une borne sur, donc sur!, dont decoule directement une borne sur F +.L'egalite R R c A 1(L) 2 = ifa ^ if A fournit alors une borne sur F,. En eet on calcule i(f R + +F, )^i(f + +F, )= A A A A A if + ^ if + +2RR if + ^ R if, + if, ^ if,,oronavualasection 2.2 que le A A A A A A premier terme est jf + A j2, le second est nul, et le troisiemeest, R jf, A j2.ona R donc jf, j R 2 =,4 2 c A 1 (L) 2 + jf + j 2, ce qui fournit une borne L 2 pour F, et A A F +, et donc par somme pour F A A. Considerons alors l'ensemble des connexions qui ont m^eme forme de courbure, quotiente par G. Deux connexions unitaires sur L dierent d'une 1-forme imaginaire pure. A cause de F A = da,deux connexions ontm^eme formede courbure si et seulement si elles dierent d'une forme fermee. Cependantune transformation de jauge de la composante connexe de l'identite, f = e i, modie la connexion par f A = A + f,1 df = A + i:d. Ceci signie que, si on se xe une connexion A 0 dereference, on peut imposer que la connexion A diere de A 0 par une 1- forme harmonique. On se ramene ainsi a H 1 (X;R). Mais le groupe G n'est pas connexe : en eet on a 0 (G) = 0 (Map(X; S 1 )) = [X; S 1 ]=H 1 (X;). Donc [A] 7! F A (ou [A]designe la classe de A modulo G) est une bration de bre H 1 (X;R)=H 1 (X;) compacte, et la borne sur F A en fournit une sur un representant de la classe de A. La projection de M sur le facteur A est donc bornee au sens L 2. 10
11 En outre l'operateur d d + est elliptique d'ordre 1, et en choisissant = A,A 0 harmonique on dispose d'une borne L 2 sur par ce qui precede, mais aussi sur (d d + ) = F +, F + par ce qui a ete vu plus haut. Un theoreme classique A A0 sur les operateurs elliptiques permet alors d'obtenir l'existence de bornes sur A dans l'espace de Sobolev L 2 1. Or le lemme de Rellich arme que l'inclusion L 2 1! L 2 est compacte, et donc on obtient que la projection de M sur le facteur A est compacte pour la topologie L 2. De plus pour A xe, est dans la boule sup jj,r min de l'espace de dimension nie Ker(D A ), qui est compacte, et donc la projection de M sur le facteur A est une bration a bres compactes.onendeduit que M est compact. 2 Denissons enn l'espace M 0 delafacon suivante. Denition Soit un point base x 0 2 X. On denit G 0 comme le sousgroupe degconstitue des applications dont la restriction a labreenx 0 est l'identite. On denit alors M 0 comme le quotient de l'espace des solutions de L (4.1) par G 0. Lorsque M L est une variete lisse, M 0 L est un S1 -bre principal sur M L. On peut maintenant denir les invariants de Seiberg-Witten. Denition Soit X une variete compacte orientee de dimension 4 telle que b et soit L une structure spin c sur X. Une orientation de (4.4) etant xee, on denit l'invariant de Seiberg-Witten SW(L) ainsi : a) lorsque d<0dans (4.3), on pose SW(L)=0; b) lorsque d =0dans (4.3), on choisit dans (4.2) tel que M L soit une variete lisse. L'espace des modules M L est alors une reunion nie de points signes ; on denit SW(L) comme le nombre de ces points comptes avec les signes correspondants ; c) lorsque d>0dans (4.3), on choisit dans (4.2) tel que M L soit une variete lisse. L'espace des modules M L est compact et oriente, donc admet une classe fondamentale. L'invariant de Seiberg-Witten est obtenu en evaluant sur cette classe fondamentale le cup-produit maximal de la premiere classe de Chern du bre endroites M 0 L S 1 C sur M L. On a vu que la formule (4.3) s'ecrit aussi d = 2Ind C (D)+(,b 0 +b 1,b + ). 2 Comme b 0 = 1, ceci implique que d et b + + b 2 1 sont de parites opposees. Lorsque b + + b 2 1 est pair, d est donc impair, et les invariants qu'on vient dedenir sont systematiquements triviaux. Le terme d'\invariants" est justie par la proposition suivante, qui est une consequence directe des resultats precedents. Proposition Soit X une variete compacte connexe orientee de dimension 4 avec b Alors SW denit une application de l'ensemble des structures spin c sur X a valeurs dans, qui depend uniquement de la structure dierentielle de X. Autrement dit SW(L) est independant du choix de la metrique sur X et de la perturbation. L'invariant SW(L) ne depend de L 11
12 qu'a isomorphisme pres. De plus SW est invariant par les dieomorphismes de X :si est un dieomorphisme de X, alors SW( L) est egal, au signe pres, a SW(L). 5 Varietes symplectiques Denition Une 2-forme! sur une variete orientee X de dimension 4 est dite symplectique si elle verie d! =0et! ^! 6= 0, et si la 4-forme! ^! oriente X. On appelle alors variete symplectique une variete X munie d'une forme symplectique!. Denition Une structure presque complexe (c'est-a-dire un homomorphisme J : TX! TX veriant en tout point J 2 =,1) est dite compatible avec! si pour tous champs de vecteurs v et w on a!(w; Jv)=,!(Jw;v) et si pour tout champ v on a!(v; Jv) 0 avec egalite si et seulement si v =0. De facon equivalente, on peut dire que J est compatible avec! si et seulement si la forme bilineaire denie par g(x; y) =!(x; Jy) est une metrique riemannienne sur X. Une variete symplectique admet toujours une structure presque complexe compatible. En eet, on part d'une base (f 1 ;f 2 ;f 3 ;f 4 )de l'espace cotangent a Xauvoisinage d'un pointxe, dans laquelle on ecrit! sous la forme f 1^g 1 +g,ou g 1 et g ne font pas intervenir f 1. La 2-forme g est portee par un espace vectoriel de dimension 3. Par ailleurs on sait que le produit vectoriel est surjectif, et donc g peut s'ecrire h 1 ^ h 2. Si on pose 1 = f 1, 2 = g 1, 3 = h 1 et 4 = h 2,ona l'expression (5.1)! = 1 ^ ^ 4 : La construction peut clairement ^etre eectuee de telle facon que les i soient de classe C 1 dans le voisinage considere. On a ainsi construit des coordonnees locales appelees coordonnees de Darboux. Par suite,!^! =2: 1^ 2^ 3^ 4.Par denition, il est non nul et compatible avec l'orientation, et la base duale (e i )des ( i ) est une base directe. Il sut alors de denir J par Je 1 = e 2, Je 2 =,e 1, Je 3 = e 4 et Je 4 =,e 3 pour obtenir une structure presque complexe compatible avec! dans le voisinage considere. Pour transformer ce resultat d'existence locale en un resultat global, il suf- t de remarquer qu'en chaque point x 2 X l'espace des endomorphismes de T x X compatibles avec! (c'est-a-dire tels que J 2 =,1 et que!(:; J:) soit une forme symetrique denie positive) est contractible. En eet si on xe un endomorphisme J 0 compatible avec!, pour tout endomorphisme compatible J, on peut construire le chemin J t =(tj +(1,t)J 0 )Q,1,ouQ t t designe la racine carree positive delamatrice symetrique denie positive,(tj +(1,t)J 0 ) 2 = 1,t(1, t)(2 + JJ 0 + J 0 J), et ceci fournit une retraction par deformation de l'espace des endomorphismes compatibles avec! en x sur fj 0 g. Le bre sur X des endomorphismes compatibles avec! est donc un bre dont les bres sont 12
13 contractibles, et donc il admet une section, c'est-a-dire qu'il existe une structure presque complexe compatible avec! denie sur X tout entier. En pratique on travaillera avec la metrique pour laquelle la base (e i )est orthonormee. Une base orthonormee qui verie (5.1) sera dite \base standard". Notons que! est alors une forme autoduale. On peut alors denir le bre canonique K de la facon suivante, en utilisant le fait que la structure presque complexe J permet d'associer aux formes un type (p; q) comme c'est le cas avec une vraie structure complexe. Denition On appelle bre canonique, que l'on note K, le determinant du bre cotangent holomorphe 1;0 X, c'est-a-dire le bre endroites complexes des formes holomorphes de degre maximal, ou encore K = 2;0 X. Sur unevariete presque complexe, on construit une structure spin c canonique. La raison fondamentale de ceci est l'existence d'un morphisme naturel U(k)! Spin c (2k) qu'on construit de lafacon suivante. En considerant un C-espace vectoriel de dimension k comme R-espace vectoriel de dimension n = 2k,on a une inclusion j :U(k)!SO(n). En combinant cette inclusion avec le determinant, on dispose d'un homomorphisme j det : U(k)! SO(n) S 1, qui se releve dans le rev^etement double de SO(n) S 1 par Spin c (n) enun morphisme l :U(k)!Spin c (n). On peut alors considerer le Spin c -bre principal Q obtenu via l a partir du U(k)-bre principal associe a la structure presque complexe et a la metrique. Une consequence directe de la construction de l par relevement est que Q se projette bien sur le SO(n)-bre principal des reperes orthonormes directs, et on a donc bien construit une structure spin c canonique sur X. La construction de l implique egalement que le bre en droites L associe a cette structure spin c correspond a la representation det : U(k)! S 1, c'est donc le determinant du bre tangent holomorphe, soit le dual K,1 du bre canonique. Calculons maintenant la dimension virtuelle d de M. Pour cela on remarque que l'egalite L = 2 TX implique c 1 (L) =c 1 (X). De plus sur unevariete presque complexe, les classes de Pontrjagin et d'euler s'expriment en fonction des classes de Chern : p 1 = c 2 1,2c 2,ete=c 2. Onendeduit immediatement par le theoreme de lasignature que = 1 3 (c2 1, 2c 2 )et=c 2. En reportantdans (4.3), il vient 2 +3 d =, + c = 1 4 (,2c 2,(c 2 1,2c 2 )+c 2 1)=0: Placons-nous desormais dans le cas d'une metrique et d'une base orthonormee (e i )de base duale ( i )ou!= 1^ 2 + 3^ 4. Les 2-formes 1^ 2 et 3^ 4 agissent de facon identique sur S + car leur dierence est anti-autoduale, et ( 1 : 2 ) 2 =,1. Donc les deux valeurs propres de lamultiplication par! sont 2i, correspondant a des espaces propres S + de dimension complexe 1. Pour 2i S+ il est pratique de choisir une base orthonormee dont le premier vecteur v 0 est dans S +, c'est,2i a dire!:v 0 =,2i:v 0, et le second v 1 est dans S +, c'est a dire!:v +2i 1 =+2i:v 1. Les multiplications de Cliord par 1 : 2, 3 : 4 et!=2 ont alors la m^eme matrice 1 : 2 3 : 4!=2,i 0 0 i 13! :
14 Soit un element e i1! 0 0 e i 2 du tore maximal de U(2), et appliquons-lui l. On obtientdans Spin c (4) l'element [(cos : 2 sin 1 ):(cos : 4 sin 2 ); e i 2 ( 1+2) ] dont l'action sur S + est 2 donnee par le produit de cos 1, i:sin cos 1 + i:sin par e i 2 ( 1+2) soit 1 0! : 0 e i 1 e i 2 cos 2,! i:sin cos 2 + i:sin Sur le premier facteur, U(2) agit trivialement sur S + qui est donc isomorphe,2i au bre trivial I. Sur le second facteur, U(2) agit sur S + par la representation +2i determinant, donc S + est isomorphe audeterminant du bre tangent holomorphe, c'est-a-dire K,1.Pour resumer, on a donc +2i obtenu:! : Proposition Une variete symplectique admet une structure spin c canonique, pour laquelle le bre des spineurs positifs se decompose en S + = I K,1, et! agit par multiplication de Cliord sur I avec la valeur propre,2i, etsur K,1 avec la valeur propre +2i. Passons maintenant aux autres structures spin c sur X. La proposition 2.7 implique que les L qui conviennent sont exactement ceux qui sont de la forme K,1 E 2,ouEest un bre en droites sur X. La structure spin c qui correspond a un bre E est obtenue a partir de la structure canonique en \tordant" les spineurs par E, c'est-a-dire qu'on a (5.2) S + = E (K,1 E): La multiplication de Cliord par! preserve a nouveau cette decomposition, avec les m^emes valeurs propres que dans le cas precedent. La dimension virtuelle de M pour la structure associee a E s'exprime de facon simple en utilisant le fait que pour L = K,1 la dimension est d 0 =0. En eet on a d = d, d 0 qui vaut 1 4 (c 1(L) 2, c 1 (K,1 ) 2 ) d'apres la formule (4.3). On utilise c 1 (L) =c 1 (K,1 E 2 )=c 1 (K,1 )+2c 1 (E) pour developper c 1 (L) 2 et obtenir d = c 1 (K,1 ):c 1 (E)+c 1 (E):c 1 (E) soit (5.3) d =,c 1 (K):c 1 (E)+c 1 (E):c 1 (E): On vamaintenant calculer l'expression de la forme! pour la decomposition (5.2). Pour cela on se donne localement s 0 une section de E de norme1,ets 1 une section de K,1 de norme 1, et on se place dans la base orthonormee (s 0 ;s 0 s 1 ) de S +. 14
15 On ecrit! = + = s :s 0 + s :s 0 s 1, c'est-a-dire que dans notre base = s. On a vu plus haut que 1 : 2 et 3 : 4 correspondent alors a lamatrice s,i 0 0 i!.les autres 2-formes sont donnees par les matrices d'heisenberg!! 1 : 4 2 : ;,1 0 1 : 3 4 : 2 0 i i 0 (on verie qu'on a bien ( 1 : 2 ):( 1 : 4 )=, 4 : 2 ). On calcule alors! sur les vecteurs de la base. on obtient!! (e 1 ;e 2 )=! (e 3 ;e 4 )=he 1 :e 2 :; i = h,i s ; i s! s i = i(j s j 2,j s j 2 ); s ou le signe dans la derniere egalite vient du fait que le produit scalaire est antilineaire en la premiere variable. On calcule de m^eme! (e 1 ;e 4 )=! (e 2 ;e 3 )=he 1 :e 4 :; i = h! s ;, s!! (e 1 ;e 3 )=! (e 4 ;e 2 )=he 1 :e 3 :; i = h i s ; i s! s i =( s s, s s); s! s i =,i( s s + s ): s s On a donc la formule! = i(j s j 2,j s j 2 )( 1 ^ ^ 4 )+(, s s+ s s)( 1 ^ ^ 3 ), i( s s + s s )( 1 ^ 3, 2 ^ 4 ) En substituant les expressions matricielles de i : j il vient (en identiant et a leurs parties scalaires) l'expression suivante pour la multiplication de Cliord par!. (5.4)! j,jj! =2 j jj 2,jj 2 : Enn une propriete remarquable des invariants de Seiberg-Witten est leur symetrie. Pour cela on demontrera d'abord le lemme suivant. Lemme Pour 2,(S + ) et A 2C(P U(1) ),ona (jf +,1 j A 4! 2 +jd A j 2 )= (jf + +jr A j2 A j 2 + R 4 jj jj4 ): X X Demonstration : On developpe en prenant garde au fait que F + A et! sontdes formes avaleurs imaginaires pures : jf +, 1 j A 4! 2 =, P i<j(f + (e A i;e j ), P 1 4! (e i ;e j )) 2 = jf + A j2 + 1 j 16 j! F + (e 2 i<j A i;e j )he i :e j :; i = jf + A j jj2 + P i<jhf + (e A i;e j )e i :e j :; i = jf + A j2 + 1, 8 jj2 1hF + :; i. 2 A 1 2 D'autre part la formule de Weitzenbock entra^ne, en utilisant le fait que l'operateur de Dirac est formellement autoadjoint, R jd A j 2 = R (jr A j 2 + R 4 jj hf + A :; i). Le resultat est alors immediat. 2 En utilisant le fait que les solutions de (4.1) sont exactement les(;a) qui annulent l'expression ci-dessus, on obtient la symetrie suivante. 15
16 Proposition L'invariant de Seiberg-Witten associe a la structure spin c donnee par le bre E est egal en valeur absolue a celui qui correspond au bre ~E = K E,1. Demonstration : En eet, ~ E =(K,1 E),1 et ~ E K,1 = E,1,et donc par somme directe, S ~ + =(S + ). Soit (;A)une solution de (4.1) pour E, c'est-a-dire un couple qui annule l'expression du lemme 5.5. Le champ est alors une section des spineurs associes a E ~ de m^eme norme que. D'autre part la connexion r A sur S + induit une connexion r A sur ~ S+, qui verie par construction r A(f )=(r A ei ei f). La norme der A ( ) est alors bien s^ur egale a celle de r A. De plus, par passage au determinant, les connexions A et A sur L et L,1 verient lam^eme relation que r A et r A.Enutilisant ladenition de la courbure il vient F (e A i;e j ):(f )=(F A (e i ;e j ):f), soit comme la courbure est une 2-forme avaleurs imaginaires pures, F (e A i;e j )=F A (e i ;e j ) =,F A (e i ;e j ) d'ou F =,F A A. Donc (F A )+ =,F + est de m^eme norme que F +, ce qui implique A A que ( ;A ) annule aussi l'expression du lemme 5.5, c'est-a-dire que ( ;A ) est solution de (4.1). La construction eectuee induit donc une bijection entre M L et M L,etla proposition en decoule. 2 6 Invariants de Gromov Soit X une variete symplectique, et J une structure presque complexe compatible. Denition Une sous-variete compacte de dimension 2 de X (non necessairement connexe) est dite pseudo-holomorphe si son espace tangent est stable par J. Le champ d'endomorphismes J denit alors une structure complexe sur. La restriction de la forme symplectique! a est alors symplectique, et donc oriente, ce qui permet de denir sa classe fondamentale [] 2 H 2 (X;) qui est non triviale parce que!:[] = R!>0. On notera e = e() 2 H 2 (X;)le dual de Poincare de []. Un resultat important sur les sous-varietes pseudo-holomorphes connexes est la formule d'adjonction. Lemme Soit une sous-variete pseudo-holomorphe connexe de X, de genre g. Alors on a (6.1) 2, 2g + e():e() =,c 1 (K):e(): D'une part, e:e = c 1 (N) car e:e = #( \ ) est le Demonstration : nombre de zeros d'une deformation de, c'est-a-dire d'une section de N. D'autre part 2,2g = () = c 1 (T ). On a alors c 1 (T )+c 1 (N) = c 1 (TX j )= 16
17 c 1 (TX):[] =,c 1 (T X):[] =,c 1 (K):[] (car K =det T X). On obtient donc la formule voulue. 2 Denition Soit e 2 H 2 (X;) une classe de cohomologie non triviale. On note H = H(e) l'espace des sous-varietes pseudo-holomorphes plongees de X dont la classe fondamentale est le dual de Poincare dee. Remarquons que dans cette denition on souhaiterait que toutes les composantes connexes de la courbe pseudo-holomorphe soient realisees avec une multiplicite 1 (courbe simple). Cependant il est necessaire pour prouver le theoreme de compacite d'admettre eventuellement, dans le cas des tores de nombre d'autointersection nul, des multiplicites superieures (rev^etements ramies). On dispose du resultat suivant sur la structure de H (le terme "generique" designe ici un sous-ensemble G -dense au sens de Baire de l'espace des structures presque complexes lisses compatibles). Lemme Pour un choix generique de J, H est une variete lisse de dimension (6.2) d =,c 1 (K):e + e:e: De plus H est canoniquement oriente. Demonstration : Decrivons l'espace tangent a H en un de ses points. On suppose dans un premier temps que est connexe. Une deformation de peut ^etre vue, en identiant le bre normal N avec un voisinage tubulaire de, comme une section de N. Pour 2,(N ) on notera alors + la surface image de la section par cette identication (c'est-a-dire la surface obtenue en deplacant chaque point de selon le vecteur normal ). Associons a une deformation 2,(N) et a unchamp 2,(T ) (; ) = lim,1 P N (+) :J:P T (+) ():!0 La deformation est tangente a H si et seulement si (; ) = 0 pour tout (c'est-a-dire que J preserve T ( + )). Or P T (+) () =,r donc J:P T (+) () =J, J:r, dont la projection sur T ( + ) est, au premier ordre en, J,r J (). En utilisant que P N (+) = Id,P T(+), on obtient (; ) =r J,J:r qui representeledefaut d'holomorphie de. L'operateur dierentiel est donc a des termes d'ordre 0 pres egal a r :,(N)!,( 1 N) ( r couple an, c'est a dire la partie antiholomorphe der). La regularite de H en decoule, et l'orientation de H est fournie par la structure presque complexe. La dimension de H se calcule alors a l'aide du complexe de Dolbeault associe an. En eet dim C (H) =Ind( r N ) est egal a dim H 0 (; 0 (N)), dim H 1 (; 0 (N)), c'est-a-dire la caracteristique d'euler-poincaredu bre N. En appliquant le theoreme de Riemann-Roch (cf. [LB]), ceci s'exprime en fonction du degre du bre normal (;N) = deg(n) + (1, g) =e:e +1,g. 17
18 On en deduit la dimension de H sur R, d =2(;N) = 2e:e +(2,2g). Or par la formule d'adjonction (6.1), 2, 2g =,c 1 (K):e, e:e, donc on obtient d = e:e, c 1 (K):e. Si n'est pas connexe, pour chaque composante i, dont la classe fondamentale est duale de e i, l'espace H i associe est de dimension d i = e i :e i,c 1 (K):e i d'apres ce qu'on vient de prouver. Or localement, H = H i, parce que deformer revient adeformer ses composantes. Donc d = P d i = P e i :e i, c 1 (K): P e i. Or e = P e i clairement, et pour i 6= j, e i :e j = 0 car les dierentes composantes sont disjointes, d'ou e:e = P e i :e i.onendeduit que d = e:e, c 1 (K):e, et donc le lemme est prouve. 2 Il est a noter que d est toujours pair. En eet on a vu que pour chaque composante i,d i =2e i :e i +(2,2g i ) est pair, et donc d = P d i est pair. Lorsque d>0, on peut donc choisir un ensemble de d=2 points distincts de X,etdenir H comme l'ensemble des 2 H qui contiennent tous les points de. On a alors le lemme suivant. Lemme Pour un choix generique de J et, H H est une sous-variete canoniquement orientee de H, de dimension 0. Demonstration : Si 2 H, considerons une deformation de, soit 2,(N) (en identiant N avec un voisinage tubulaire de ), et un point x 0 2. La condition d'appartenance de x 0 a la surface deformee + (obtenue a partir de en deplacant chaque point selon le vecteur normal ) s'ecrit (x 0 )=0. Comme N est un bre de rang 2 sur R, pour un choix generique de x 0 la condition (x 0 ) = 0 est realisee sur un sous-espace de codimension 2. Pour un choix generique de ilfaut donc enlever 2 a ladimension pour chaque point de. Comme comporte exactement d=2 points, le resultat est vrai. 2 On a de plus le resultat de compacite suivant (voir [McS]). Theoreme Dans le cas ou d =0, l'espace H est compact pour un choix generique de J. Dans le cas d>0,h est compact pour un choix generique de J et. Idee de Demonstration : Ce theoreme est un resultat ardu, pour lequel on se contentera de donner les grandes lignes. Essentiellement, il s'agit de remarquer qu'il est possible de compactier H, les points deh,hcor- respondant a des courbes pseudo-holomorphes presentant des singularites. Le resultat s'obtient alors en constatant que ces courbes singulieres sont organisees en strates dont la dimension est strictement inferieure a celle de H. Comme on etudie ici uniquement des espaces de dimension nulle (quitte a ne considerer que des courbes passant par tous les points de ), il y a generiquement absence de courbes singulieres, et donc H (resp. H ) est compact. On traitera d'abord le cas d =0. Acause de la compacitedex, il n'y a pas de problemes de points partant a l'inni. La seule facon dont une suite deh peut ne pas converger correspond a une suite tendant vers une surface immergee 18
19 (et non plongee) dans X,eventuellement non connexe, et pouvant comporter des points singuliers. L'idee est alors de montrer que de telles limites correspondent a des equations faisant intervenir des operateurs dont l'indice est strictement inferieur a celui qui correspond a H. Placons-nous par exemple dans le cas ou la limite est une courbe pseudoholomorphe connexe immergee comportant un nombre n de points doubles, qui correspondenttous a un nombre d'intersectionpositif (car on est sur C ). L'image dans H 2 (X;)de la classe fondamentale de cette courbe est bien s^ur toujours le dual de e. Cette courbe immergee possede un bre normal, dont le degre n'est plus e:e commeavant. En eet, auvoisinage d'un point double, l'image de la courbe dans X possede deux "brins" A et B. Si on decale la courbe, il est clair que A rencontre la copie decalee de B, et B rencontre la copie decalee de A,cesdeux intersections ayantun signe positif a cause de l'holomorphie. Ces deux intersections comptent dans le nombre d'intersection e:e, cependant si on considere le bre normal a la courbe, elles n'apparaissent pas. En consequence, le degre du bre normal s'obtient en enlevant 2 pour chaque point double, c'est-a-dire = e:e, 2n: La formule d'adjonction (6.1) s'ecrit ici 2, 2g + =,c 1 (K):e: De plus la courbe immergee appartient a un espace de modules deni de facon analogue a H, mais constitue d'images d'immersions au lieu de sous-varietes. La preuve du lemme 6.4 indique que pour J generique, cet espace de modules est lisse de dimension d 0 =2,2g+2. Les formules precedentes donnent alors d 0 =,c 1 (K):e + e:e, 2n, soit strictement moins que d. Comme d =0,onen deduit que generiquement il n'existe pas de telles courbes. Le cas ou la courbe n'est pas connexe s'obtient en remarquant que par somme sur les composantes on a encore d 0 = d, 2n strictement inferieur a d. Dans le cas d>0, on procede de m^eme en remarquant que la contrainte de passage par d=2 points diminue la dimension de d, ce qui donne d 0, d =,2n <0. Le m^emetype d'argument permet de montrer que de facon generique il n'y a pas apparition de pointssinguliers ou de points d'intersection entre les dierentes composantes de la surface. 2 On peut alors denir les invariants de Gromov d'une variete symplectique. Denition Soit X une variete compacte symplectique de dimension 4. On denit pour chaque classe e 2 H 2 (X;) l'element Gr(e) 2 deni comme suit : a) Lorsque d<0dans (6.2), on pose Gr(e)=0. b) Lorsque d =0, alors pour J generique, H est un ensemble ni de points signes, et on denit Gr(e) comme le nombre de ces points comptes avec les signes correspondants. 19
20 c) Lorsque d>0, alors pour J et generiques, H est un ensemble ni de points signes, et on denit Gr(e) comme le nombre de ces points comptes avec les signes correspondants. Le terme d'\invariant" est justie par la proposition suivante. Proposition L'invariant Gr : H 2 (X;)! ne depend que du couple (X;!). Autrement dit, la valeur de Gr est independante du choix de la structure presque complexe J, et dans le cas d>0, de l'ensemble. De plus si (! t ) est une famille continue de formes symplectiques sur X, les invariants Gr associes a! 0 et! 1 concident. Enn, Gr est invariant par les dieomorphismes de X en ce sens que si : X! X est un dieomorphisme, l'invariant Gr(e) pour la forme symplectique! est egal a l'invariant Gr( e) pour la forme symplectique!. 7 Le theoreme principal 7.1 Enonce Les similarites des denitions des invariants de Seiberg-Witten et des invariants de Gromov (y compris dans les formules (5.3) et (6.2)), ainsi que le cas des varietes kahleriennes, ont conduit Taubes a conjecturer puis formuler l'enonce suivant ([T3]) : Theoreme Soit X une variete compacte orientee symplectique de dimension 4 avec b Soit E un bre endroites complexes non trivial sur X, et soit L = K,1 E 2.Alors SW(L)=Gr(c 1 (E)). On se contentera ici du resultat suivant, plus faible, qui comporte deja de nombreuses consequences interessantes. Theoreme Soit X une variete compacte orientee symplectique de dimension 4 avec b Soit E un bre endroites complexes non trivial sur X et soit L = K,1 E 2. Si SW(L) 6= 0, alors il existe une courbe symplectique plongee dont la classe fondamentale est le dual de Poincare dec 1 (E). Pour cela on considerera une famille a un parametre de perturbations des equations de Seiberg-Witten, et a partir d'une suite de solutions correspondant a des valeurs du parametretendantvers l'inni, on exhibera une courbe pseudoholomorphe comme limite du lieu des zeros de la projection des solutions sur le facteur E. L'hypothese de non-trivialite de Etient au fait que si E est egal au bre trivial I, la courbe symplectique construite a une classe fondamentale nulle, et est donc potentiellement vide. Cependant ce qui suit s'applique quand m^eme a ce cas. 20
21 7.2 Notations On munit tout d'abord X d'une metrique ou il existe une base orthonormee veriant (5.1). On a vu a lasection 5 que pour la structure spin c canonique, S + se decompose en I K,1. D'apres ce qu'on a vu a la section 3, la donnee d'une connexion sur K,1 (et de la connexion de Levi-Civita sur TX) xe une connexion sur S +, donc par projection une connexion sur le facteur I. La condition que l'on souhaite imposer est l'existence d'une section globale parallele u 0 ne s'annulant pas de I, c'est a dire que la connexion sur I doit ^etre la connexion triviale d dans la trivialisation xee par u 0.Onpeutenoutre imposer que u 0 soit partout de norme 1. Cette condition xe une unique connexion (modulo jauge), A 0, sur K,1. De plus la projection sur le second facteur de la connexion sur S + correspondante est en fait exactement A 0, car la connexion induite sur I est triviale. Si X est kahlerienne, c'est-a-dire si la structure presque complexe J est integrable, la connexion sur S + preserveladecomposition en I K,1. Cependant dans le cas general, ce n'est pas le cas. Posons r A0 u 0 = b, oubest une 1- forme avaleurs dans K,1 (dans le cas ou X est kahlerienne on a donc b = 0). La connexion r A0 diere de d A 0 d'une 1-forme antihermitienne, donc la connexion r A0 s'ecrit sous forme matricielle Lemme D A0 u 0 =0.! r A0 = d,b : b A 0 Demonstration : On applique D A0 al'equation!:u 0 =,2i:u 0. Il vient, en sous-entendant les sommations sur les indices libres, D(!):u 0 + e :!:b =,2i:e :b.ord(!)=(d+d )!=d! +d! (car! est autoduale). De plus on a d! = 0 car! est symplectique. Comme! agit sur b 2 K,1 par multiplication par +2i, il vient donc que 2i:e :b =,2i:e :b, d'ou D A0 u 0 = e :b =0. 2 On se xe desormais un bre en droites E, et donc une structure spin c.on va etudier la famille d'equations de Seiberg-Witten perturbees suivante, indexee par un reel r>0, dont les inconnues sont une connexion A sur L = K,1 E 2 et une section de S + = E (K,1 E): (7.1) ( DA =0 F + A = 1 4! +F + A0, i:r 4!: Cela revienta xer = F +, i:r! dans (4.2), donc les resultatsdelasection 4 A0 4 impliquent que cette perturbation n'aecte pas les proprietes de l'espace des solutions. Fixons les notations suivantes : tout d'abord, A induit une connexion r A sur S +.Par projection sur le premier facteur, cela fournit une connexion r a sur E, et sur le second facteur, r 0 sur A K,1 E. Cesdeux connexions s'obtiennent en fait a partir de d et A 0 qui correspondaienta la structure spin c canonique en ajoutantunem^eme connexion sur le facteur E, qui est donc necessairement r a. 21
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 2008
 Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
 http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
Une version feuilletée du théorème de translation de Brouwer
 Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
Laser vert : moins de plus de 300. Acheter Laser PRODUITS CHAUDS. Pointeur Laser étanche
 Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
I. Évolution du commerce mondial
 I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
Eksamen FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. Nynorsk/Bokmål
 Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
1. Intégrales définies et indéfinies I. (a) Soit b > 0. Montrer que pour tout x > 0 la fonction. 2 b. F (x) = arctan bx. 1 (1 + bx) x. f(x) = x t dt.
 Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Asymptotique des nombres de Betti, invariants l 2 et laminations
 Comment. Math. Helv. 79 (2004) 362 395 0010-2571/04/020362-34 DOI 10.1007/s00014-003-0798-1 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Asymptotique des nombres de Betti, invariants
Comment. Math. Helv. 79 (2004) 362 395 0010-2571/04/020362-34 DOI 10.1007/s00014-003-0798-1 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Asymptotique des nombres de Betti, invariants
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
Design d'un champ de vecteurs tangents
 Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
On remet la machine en route
 Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
Energie et corrélation. Systèmes de Traitement du Signal Polytech Marseille INFO 2016
 Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
PREPARATION BREVET BLANC 1 CALCUL FRACTIONNAIRE : AIDE : d'abord transformer l'écriture du nombre entier 1. Tout nombre a peut s'écrire 1
 THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
Avertissement Mode d'emploi
 Avertissement Mode d'emploi Ce polycopié ne constitue pas un cours au sens classique de ce terme, mais plutôt un support à celui qui sera dispensé en classe. En particulier, toutes les démonstrations ne
Avertissement Mode d'emploi Ce polycopié ne constitue pas un cours au sens classique de ce terme, mais plutôt un support à celui qui sera dispensé en classe. En particulier, toutes les démonstrations ne
EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012
 Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
BEFOLKNINGSFORHOLDENE
 TILLEGGSHEFTE TIL «MEDDELELSER FRA DET STATISTISKE CENTRALBYRÄ» 1920 Journal du Bureau Central de Statistique du Royaume de Norvège 1920. Appendice. BEFOLKNINGSFORHOLDENE NORD-NORGE MED SÆRLIG HENSYN TIL
TILLEGGSHEFTE TIL «MEDDELELSER FRA DET STATISTISKE CENTRALBYRÄ» 1920 Journal du Bureau Central de Statistique du Royaume de Norvège 1920. Appendice. BEFOLKNINGSFORHOLDENE NORD-NORGE MED SÆRLIG HENSYN TIL
Sommaire. Montre MOVETIME Family Aperçu de la montre... 1 Touche Marche-Arrêt Retrait des bracelets Résistance à l eau...
 Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
Corrigés des exercices du chapitre 25
 MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide
 Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Brosses intérieures avec manche
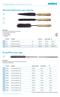 18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
AB a donc OM = = 2 2
 ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t
ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t
EKSAMEN FRA0502 Fransk II HØSTEN 2012
 Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk - EKSAMEN FRA0502 Fransk II HØSTEN 2012 Faglig kontakt under eksamen: Sophie Vauclin Tlf.: 73596873/ 93063953 Eksamensdato:
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk - EKSAMEN FRA0502 Fransk II HØSTEN 2012 Faglig kontakt under eksamen: Sophie Vauclin Tlf.: 73596873/ 93063953 Eksamensdato:
 Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
Lattice Boltzmann Method for ow in porous media. Samuel Corre
 Lattice Boltzmann Method for ow in porous media. avec Aziz Belmiloudi IRMAR-INSA, Rennes. Samuel.Corre@insa-rennes.fr 4 ieme école EGRIN, 25 Mai 2016. Contexte général Écoulements incompressibles en milieu
Lattice Boltzmann Method for ow in porous media. avec Aziz Belmiloudi IRMAR-INSA, Rennes. Samuel.Corre@insa-rennes.fr 4 ieme école EGRIN, 25 Mai 2016. Contexte général Écoulements incompressibles en milieu
Clôture Métallique. Portails / Portillons / Accessoires
 Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
Eksamen FSP5020 Fransk I PSP5013 Fransk nivå I. Nynorsk/Bokmål
 Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
GAMME DETENTE DIRECTE SOMMAIRE. X32 monosplit Inverter Page 88. X3 multisplit Inverter Page 90. Monosplits/Multisplits
 SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
Disjoncteurs sélectifs
 233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
REQUÊTE APPLICATION KLAGESKJEMA
 Voir Note explicative See Explanatory Note Se klageveiledningen NOR Numéro de dossier File-number Klage nr. COUR EUROPÉENNE DES DROITS DE L HOMME EUROPEAN COURT OF HUMAN RIGHTS DEN EUROPEISKE MENNESKERETTIGHETSDOMSTOL
Voir Note explicative See Explanatory Note Se klageveiledningen NOR Numéro de dossier File-number Klage nr. COUR EUROPÉENNE DES DROITS DE L HOMME EUROPEAN COURT OF HUMAN RIGHTS DEN EUROPEISKE MENNESKERETTIGHETSDOMSTOL
St.prp. nr. 3 ( )
 St.prp. nr. 3 (1999-200) Om samtykke til å setje i kraft ein tilleggsavtale til skatteavtalen mellom Noreg og Frankrike av 19. desember 1980 med tilleggsavtalar av 14. november 1984 og 7. april 1995, underskriven
St.prp. nr. 3 (1999-200) Om samtykke til å setje i kraft ein tilleggsavtale til skatteavtalen mellom Noreg og Frankrike av 19. desember 1980 med tilleggsavtalar av 14. november 1984 og 7. april 1995, underskriven
Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo. Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo
 Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo L HISTOIRE DU LYCEE SKOLENS HISTORIE Recherches / Etterforskning : Paul Monceyron
Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo L HISTOIRE DU LYCEE SKOLENS HISTORIE Recherches / Etterforskning : Paul Monceyron
TECHNOLOGIE POUR CHAUDIERES DE BRUNNER. Kamin-Kessel Eck 57/67/44 Porte relevable (easy-lift) État: made in germany
 TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
PremiCron. Tresse synthétique non résorbable de polyester enduit. PremiCron
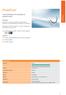 Tresse synthétique non résorbable de polyester enduit Description PremiCron est une tresse synthétique non résorbable de Polyester. Les sutures PremiCron sont enduites avec du silicone. PremiCron Disponible
Tresse synthétique non résorbable de polyester enduit Description PremiCron est une tresse synthétique non résorbable de Polyester. Les sutures PremiCron sont enduites avec du silicone. PremiCron Disponible
FRANSKLÆRERFORENINGENS STYRE
 NR. 2-2007 2 Adresses/bureau 3 Infos 4 Le mot du président 5 Grete Kleppen, traduite 7 La littérature norvégienne, en français 8 Article : Enseigner à des débutants 17 Adresses internet 18 Marte i Paris!
NR. 2-2007 2 Adresses/bureau 3 Infos 4 Le mot du président 5 Grete Kleppen, traduite 7 La littérature norvégienne, en français 8 Article : Enseigner à des débutants 17 Adresses internet 18 Marte i Paris!
6092-DV Document 5
 DOCUMENT 5 Document 5 27 Cned Document 5 28 Cned Document 5 29 Cned Document 5 30 Cned Document 5 31 Cned Document 5 32 Cned Document 5 33 Cned Document 5 34 Cned Document 5 35 Cned Document 5 36 Cned
DOCUMENT 5 Document 5 27 Cned Document 5 28 Cned Document 5 29 Cned Document 5 30 Cned Document 5 31 Cned Document 5 32 Cned Document 5 33 Cned Document 5 34 Cned Document 5 35 Cned Document 5 36 Cned
Des accouplements raisonnés, un élément essentiel à l amélioration génétique
 Innover aujourd hui, prospérer demain Centre Caztel, Sainte Marie Des accouplements raisonnés, un élément essentiel à l amélioration génétique Robie Morel, B.Sc., coordonnateur du secteur génétique et
Innover aujourd hui, prospérer demain Centre Caztel, Sainte Marie Des accouplements raisonnés, un élément essentiel à l amélioration génétique Robie Morel, B.Sc., coordonnateur du secteur génétique et
Kommunikasjonsperm. Overvåking og undersøkelser side 1. Smerter side 2. Naturlige funksjoner, eliminasjon side 3. Sengeleie og stell side 4
 Kommunikasjonsperm Fransk Overvåking og undersøkelser side 1 Smerter side 2 Naturlige funksjoner, eliminasjon side 3 Sengeleie og stell side 4 Mat, drikke kvalme side 5 Bevegelse, syn, temperatur side
Kommunikasjonsperm Fransk Overvåking og undersøkelser side 1 Smerter side 2 Naturlige funksjoner, eliminasjon side 3 Sengeleie og stell side 4 Mat, drikke kvalme side 5 Bevegelse, syn, temperatur side
DYNAMIQUE. Etude des mouvements de tangage d une transmission de puissance d hélicoptère. x r 2. y r 2. x 1. y r y r
 e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
Mise à jour des marges requises
 Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
www.philips.com/avent
 Register your product and get support at www.philips.com/avent SCD505 EN User manual 3 DA Brugervejledning 13 DE Benutzerhandbuch 23 ES Manual del usuario 47 SV Användarhandbok 121 AR 141 Innholdsfortegnelse
Register your product and get support at www.philips.com/avent SCD505 EN User manual 3 DA Brugervejledning 13 DE Benutzerhandbuch 23 ES Manual del usuario 47 SV Användarhandbok 121 AR 141 Innholdsfortegnelse
Eksamen 21.05.2013. FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. http://eksamensarkiv.net/
 Eksamen 21.05.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Oppgåve 1 Vous aimez voyager? Liker du å reise? Kvifor / kvifor ikkje? Skriv ein liten tekst på to til fire
Eksamen 21.05.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Oppgåve 1 Vous aimez voyager? Liker du å reise? Kvifor / kvifor ikkje? Skriv ein liten tekst på to til fire
Second Order ODE's (2P) Young Won Lim 7/1/14
 Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN. Langue vivante 2
 Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
La gestion de la classe Le premier contact avec sa classe La première heure de classe
 JOURNEE DU 03 FEVRIER 2010 1 Les droits et les devoirs du professeur. Les missions du professeur Les missions générales Les missions spécifiques La gestion de la classe Le premier contact avec sa classe
JOURNEE DU 03 FEVRIER 2010 1 Les droits et les devoirs du professeur. Les missions du professeur Les missions générales Les missions spécifiques La gestion de la classe Le premier contact avec sa classe
Rapport annuel 2012. p. 4 Reise til Frankrike?... p. 8 Felles språkdag... p. 12 Examens du BI. p. 16 Travailler du vocabulaire. p. 20 Et plus...
 Rapport annuel 2012. p. 4 Reise til Frankrike?... p. 8 Felles språkdag... p. 12 Examens du BI. p. 16 Travailler du vocabulaire. p. 20 Et plus... Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE SOMMAIRE/INNHOLD:
Rapport annuel 2012. p. 4 Reise til Frankrike?... p. 8 Felles språkdag... p. 12 Examens du BI. p. 16 Travailler du vocabulaire. p. 20 Et plus... Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE SOMMAIRE/INNHOLD:
Årsplan for 9. klasse i Fransk (2008 2009)
 Årsplan for 9. klasse i Fransk (2008 2009) Lærer: Serge Licius Tekstbok: Chouette Nouvelle Mål for faget dem til og fransk språkbruk og egen kultur A fremme elevenes innsikt i det s evne til å ta hånd
Årsplan for 9. klasse i Fransk (2008 2009) Lærer: Serge Licius Tekstbok: Chouette Nouvelle Mål for faget dem til og fransk språkbruk og egen kultur A fremme elevenes innsikt i det s evne til å ta hånd
LE GENRE DU LOCUTEUR ET DE L ALLOCUTAIRE DANS LES SYSTÈMES PRONOMINAUX : GENRE GRAMMATICAL ET INDEXICALITÉ DU GENRE
 Françoise Rose Bulletin de la Société de linguistique de Paris, t. CVIII (2013), fasc. 1, p. 381-417 doi:10.2143/bsl.108.1.3019222 LE GENRE DU LOCUTEUR ET DE L ALLOCUTAIRE DANS LES SYSTÈMES PRONOMINAUX
Françoise Rose Bulletin de la Société de linguistique de Paris, t. CVIII (2013), fasc. 1, p. 381-417 doi:10.2143/bsl.108.1.3019222 LE GENRE DU LOCUTEUR ET DE L ALLOCUTAIRE DANS LES SYSTÈMES PRONOMINAUX
Gustave Juvet ( ) Un Pionnier Oublié desétudes Cliffordiennes
 Adv. appl. Clifford alg. 19 (2009), 547 584 c 2009 Birkhäuser Verlag Basel/Switzerland 0188-7009/030547-38, published online October 22, 2009 DOI 10.1007/s00006-009-0183-2 Advances in Applied Clifford
Adv. appl. Clifford alg. 19 (2009), 547 584 c 2009 Birkhäuser Verlag Basel/Switzerland 0188-7009/030547-38, published online October 22, 2009 DOI 10.1007/s00006-009-0183-2 Advances in Applied Clifford
No. 1 2009. Siden 1986
 Siden 1986 No. 1 2009 3. Redaksjonelt 4. Intervju med Gahr Støre 7. Infos culturelles, Jean-Louis 8. Skoleutveksling i Larvik 11. La réforme de l orthographe. Pierre 14. Enseigner avec TV5Monde, André
Siden 1986 No. 1 2009 3. Redaksjonelt 4. Intervju med Gahr Støre 7. Infos culturelles, Jean-Louis 8. Skoleutveksling i Larvik 11. La réforme de l orthographe. Pierre 14. Enseigner avec TV5Monde, André
RAPPORT DE SYNTHESE DES ACTIVITES DE LA COMMUNAUTE EUROPENNE DANS LE CHAMP DES DROITS DE L HOMME, DE LA BONNE GOUVERNANCE ET DE LA DEMOCRATIE
 RAPPORT DE SYNTHESE DES ACTIVITES DE LA COMMUNAUTE EUROPENNE DANS LE CHAMP DES DROITS DE L HOMME, DE LA BONNE GOUVERNANCE ET DE LA DEMOCRATIE Consultants pour le développement et l'environnement c:\temp\iecache\rapport
RAPPORT DE SYNTHESE DES ACTIVITES DE LA COMMUNAUTE EUROPENNE DANS LE CHAMP DES DROITS DE L HOMME, DE LA BONNE GOUVERNANCE ET DE LA DEMOCRATIE Consultants pour le développement et l'environnement c:\temp\iecache\rapport
m15/1/aynor/hp2/nor/tz0/xx Monday 11 May 2015 (morning) Lundi 11 mai 2015 (matin) Lunes 11 de mayo de 2015 (mañana) 2 hours / 2 heures / 2 horas
 m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
Tri sélectif de déchets. Kildesortering
 Tri sélectif de déchets Dans notre commune, on est légalement obligé de trier les déchets. Le but est de les recycler et ainsi contribuer à un meilleur environnement pour nous tous. Voici une description
Tri sélectif de déchets Dans notre commune, on est légalement obligé de trier les déchets. Le but est de les recycler et ainsi contribuer à un meilleur environnement pour nous tous. Voici une description
IUFM DE BOURGOGNE DIJON
 IUFM DE BOURGOGNE DIJON!" # # $ % & " " ' 0362024 E Introduction 1 1. Les langues étrangères à l école : 2 1.1. L historique des instructions officielles.2 1.2. Les programmes de février 2002...3 1.3.
IUFM DE BOURGOGNE DIJON!" # # $ % & " " ' 0362024 E Introduction 1 1. Les langues étrangères à l école : 2 1.1. L historique des instructions officielles.2 1.2. Les programmes de février 2002...3 1.3.
Mes architectes ont 10 ans!
 D O S S I E R U N A R C H I T E C T E À L A M É D I AT H È Q U E 153 Mes architectes ont 10 ans! PAR MIRANDA CORBIERE En 2012, à l occasion de la journée d étude consacrée aux regards européens sur «Enfants
D O S S I E R U N A R C H I T E C T E À L A M É D I AT H È Q U E 153 Mes architectes ont 10 ans! PAR MIRANDA CORBIERE En 2012, à l occasion de la journée d étude consacrée aux regards européens sur «Enfants
Câble de mesure en PVC CF211
 CF211 igupur PUR TPE Câble de mesure en CF211 Pour les sollicitations moyennes Gaine extérieure en Version blindée Résistance aux huiles Non propagateur de flamme Données dynamiques Rayon de courbure chaîne
CF211 igupur PUR TPE Câble de mesure en CF211 Pour les sollicitations moyennes Gaine extérieure en Version blindée Résistance aux huiles Non propagateur de flamme Données dynamiques Rayon de courbure chaîne
LIBER VEL MANVS ET SAGITTÆ SVB FIGVRÂ
 LIBER O VEL MANVS ET SAGITTÆ SVB FIGVRÂ VI A!A! Publication en Classe B Emis par Ordre de: D.D.S. 7 = 4 Præmonstrator O.S.V. 6 = 5 Imperator N.S.F. 5 = 6 Cancellarius I 1. Ce livre est très facile à mésinterpréter;
LIBER O VEL MANVS ET SAGITTÆ SVB FIGVRÂ VI A!A! Publication en Classe B Emis par Ordre de: D.D.S. 7 = 4 Præmonstrator O.S.V. 6 = 5 Imperator N.S.F. 5 = 6 Cancellarius I 1. Ce livre est très facile à mésinterpréter;
Representasjoner om språkundervisning og språklæring
 Representasjoner om språkundervisning og språklæring & Innledning til det virtuelt rollespillet v/ førstelektor Myriam Coco Fredag 18. september 2009 3-delers kurs 1. Representasjoner/forforestillinger
Representasjoner om språkundervisning og språklæring & Innledning til det virtuelt rollespillet v/ førstelektor Myriam Coco Fredag 18. september 2009 3-delers kurs 1. Representasjoner/forforestillinger
5HVVRXUFHVKXPDLQHV HWILQDQFLqUHVGX',3
 5HVVRXUFHVKXPDLQHV HWILQDQFLqUHVGX',3 EDITION 2004 DEPARTEMENT DE L INSTRUCTION PUBLIQUE (DIP) SERVICE DE LA RECHERCHE EN EDUCATION (SRED) & SERVICES ADMINISTRATIFS ET FINANCIERS (SAFS) GENEVE Juillet
5HVVRXUFHVKXPDLQHV HWILQDQFLqUHVGX',3 EDITION 2004 DEPARTEMENT DE L INSTRUCTION PUBLIQUE (DIP) SERVICE DE LA RECHERCHE EN EDUCATION (SRED) & SERVICES ADMINISTRATIFS ET FINANCIERS (SAFS) GENEVE Juillet
Compress Bosch Compress LW-Tx C 35 C A ++ A + A B C D E F G. db kw kw /2013
 Bosch 5000 7 LW-Tx 55 C 35 C + A B C D E F G 47 8 9 7 8 7 7 db kw kw db 2015 811/2013 Bosch 5000 7 LW-Tx ++ + + + + + A B C D E F G 2015 811/2013 Bosch 5000 7 LW-Tx Opplysningene er i samsvar med kravene
Bosch 5000 7 LW-Tx 55 C 35 C + A B C D E F G 47 8 9 7 8 7 7 db kw kw db 2015 811/2013 Bosch 5000 7 LW-Tx ++ + + + + + A B C D E F G 2015 811/2013 Bosch 5000 7 LW-Tx Opplysningene er i samsvar med kravene
Hvordan lærer du best? Ulike tilnærmingsmåter
 Hvordan lærer du best? Ulike tilnærmingsmåter Lytting lytte til lærer (opplesning, fortelling, spørsmål) lytte til medelever (når de forteller, stiller spørsmål, deltar i rollespill, dramatisering, intervju,
Hvordan lærer du best? Ulike tilnærmingsmåter Lytting lytte til lærer (opplesning, fortelling, spørsmål) lytte til medelever (når de forteller, stiller spørsmål, deltar i rollespill, dramatisering, intervju,
5.1 Peuvent adhérer au Syndicat toutes personnes qui en reconnaissent les principes.
 Statuts Art. 1 Nom et siège Il est fondé, sous le nom de Syna, une association au sens des articles 60 et ss du Code civil suisse (CCS), dont le siège est à Olten (ci-après dénommée «Syndicat»). Elle
Statuts Art. 1 Nom et siège Il est fondé, sous le nom de Syna, une association au sens des articles 60 et ss du Code civil suisse (CCS), dont le siège est à Olten (ci-après dénommée «Syndicat»). Elle
EGENSKAPER ANVENDELSE. Technical data sheet SBE - BJELKESKO
 SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
MARQUE: BABYLISS REFERENCE: E 842 FCE KIT CODIC:
 MARQUE: BABYLISS REFERENCE: E 842 FCE KIT CODIC: 3285510 E842FCE BARBE DE 3 JOURS 3-DAY BEARD Fig. 1 Fig. 2 Fig. 3 Fig. 4 Fig. 5 Fig. 6 Fig. 7 Fig. 8 Fig. 9 Fig. 10 Fig. 11 FRANÇAIS LA TONDEUSE BARBE ET
MARQUE: BABYLISS REFERENCE: E 842 FCE KIT CODIC: 3285510 E842FCE BARBE DE 3 JOURS 3-DAY BEARD Fig. 1 Fig. 2 Fig. 3 Fig. 4 Fig. 5 Fig. 6 Fig. 7 Fig. 8 Fig. 9 Fig. 10 Fig. 11 FRANÇAIS LA TONDEUSE BARBE ET
Europa-Universität Viadrina
 !"#!$% & #' #! ( ))% * +%, -.!!! / 0 1!/ %0 2!!/ 0.!!!/ /! 0 / '3 %0 #$ '! 0 4!""2 " '5 + -#! & %%! ( 6+ * $ '. % & 7 7 8 (8 *& *& *( ** *8, 8 87 - - -! )- % 4!!# &! -! ( - / 9:0 ; ; & * 7 4! + /! ) %
!"#!$% & #' #! ( ))% * +%, -.!!! / 0 1!/ %0 2!!/ 0.!!!/ /! 0 / '3 %0 #$ '! 0 4!""2 " '5 + -#! & %%! ( 6+ * $ '. % & 7 7 8 (8 *& *& *( ** *8, 8 87 - - -! )- % 4!!# &! -! ( - / 9:0 ; ; & * 7 4! + /! ) %
Ça déménage! Françoise Sagan VISITE GUIDÉE EN COMPAGNIE DE VIVIANE EZRATTY, ANTOINE MORTEMARD ET NELLY GASIOREK 1
 120 Ça déménage! La nouvelle médiathèque Françoise Sagan VISITE GUIDÉE EN COMPAGNIE DE VIVIANE EZRATTY, ANTOINE MORTEMARD ET NELLY GASIOREK 1 De la rue des Prêtres-Saint-Séverin 2 aux abords de la gare
120 Ça déménage! La nouvelle médiathèque Françoise Sagan VISITE GUIDÉE EN COMPAGNIE DE VIVIANE EZRATTY, ANTOINE MORTEMARD ET NELLY GASIOREK 1 De la rue des Prêtres-Saint-Séverin 2 aux abords de la gare
Comportement du discordantiel «ne» dans six points d enquêtes du corpus PFC
 Comportement du discordantiel «ne» dans six points d enquêtes du corpus PFC Marie Therese Barkved Sous la direction de Chantal Lyche Masteroppgave i fransk språk, avlagt våren 2011 ved Det Humanistiske
Comportement du discordantiel «ne» dans six points d enquêtes du corpus PFC Marie Therese Barkved Sous la direction de Chantal Lyche Masteroppgave i fransk språk, avlagt våren 2011 ved Det Humanistiske
TECHNIQUE DE CHAUDIERE PAR BRUNNER. Kamin-Kessel 62/76. État: made in germany
 TCHNIQU D CHAUDIR PAR BRUNNR KaminKessel 62/76 État: 30.04.2013 made in germany KaminKessel 62/76 S S securité départ 1/2" fil.ext. securité retour 1/2" fil.ext. porte battante avec isolation et lisiére
TCHNIQU D CHAUDIR PAR BRUNNR KaminKessel 62/76 État: 30.04.2013 made in germany KaminKessel 62/76 S S securité départ 1/2" fil.ext. securité retour 1/2" fil.ext. porte battante avec isolation et lisiére
Sur un théorème de Mertens
 manuscripta math. 08, 495 53 (00 c Springer-Verag 00 Oivier Ramaré Sur un théorème de Mertens Received: 0 March 00 Résumé. We investigate and improve on a proof of Mertens concerning the distribution of
manuscripta math. 08, 495 53 (00 c Springer-Verag 00 Oivier Ramaré Sur un théorème de Mertens Received: 0 March 00 Résumé. We investigate and improve on a proof of Mertens concerning the distribution of
Bobine à noyau de fer
 1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
slrrd s/ t-l Fi ia Fi fl:r ged <^'(n fi Ft'H s ks F;A= HX3 I(: 2 * d;gb ri EF g 3 = t?$ lh 3[ X +i ?$i Es xe 0i i,r s E O X > t-
 #l l :ll.ll! i = l = :9X {n\j d,s.w{ 4. ld / l i i i fl: D LCJ Wi] fi ' ;= X h
#l l :ll.ll! i = l = :9X {n\j d,s.w{ 4. ld / l i i i fl: D LCJ Wi] fi ' ;= X h
BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN. Langue vivante 2 ÉPREUVE DU MARDI 21 JUIN 2016
 Session 2016 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 ÉPREUVE DU MARDI 21 JUIN 2016 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L Langue vivante obligatoire
Session 2016 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 ÉPREUVE DU MARDI 21 JUIN 2016 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L Langue vivante obligatoire
Romansk Forum Nr
 Romansk Forum Nr. 13-2001 Forord 1 Henriksen, Turid: La mise en scène de l'article partitif 3-18 Rydning, Antin Fougner: La SYNECDOQUE - concept clé en traduction 19-41 Trandem, Beate: Å skrive det sagte
Romansk Forum Nr. 13-2001 Forord 1 Henriksen, Turid: La mise en scène de l'article partitif 3-18 Rydning, Antin Fougner: La SYNECDOQUE - concept clé en traduction 19-41 Trandem, Beate: Å skrive det sagte
Yves Jamait. 6 Regning i fremmedspråk. 8 Didactique.. 14 Jeux de vocabulaire 18 Statistiques. 30
 Yves Jamait. 6 Regning i fremmedspråk. 8 Didactique.. 14 Jeux de vocabulaire 18 Statistiques. 30 Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE SOMMAIRE/INNHOLD: André Avias epost: andre.avias@hiof.no
Yves Jamait. 6 Regning i fremmedspråk. 8 Didactique.. 14 Jeux de vocabulaire 18 Statistiques. 30 Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE SOMMAIRE/INNHOLD: André Avias epost: andre.avias@hiof.no
LES VERBES. Forme de base. C'est celle trouvée dans le dictionnaire. Exemple : parler : snakke
 LES VERBES I- Forme de base : C'est celle trouvée dans le dictionnaire. parler : snakke II Infinitif : L'infinitif se forme en plaçant "å" devant la forme de base Forme de base Infinitif Payer Betale å
LES VERBES I- Forme de base : C'est celle trouvée dans le dictionnaire. parler : snakke II Infinitif : L'infinitif se forme en plaçant "å" devant la forme de base Forme de base Infinitif Payer Betale å
Mars 2014. Assemblée générale 2013 La Norvège pays exotique? La oss skravle.. Kurs i Frankrike.. Frankrig og den koloniale arv
 Mars 2014 Assemblée générale 2013 La Norvège pays exotique? La oss skravle.. Kurs i Frankrike.. Frankrig og den koloniale arv p. 4 p. 8 p. 12 p. 15 p. 22 Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE
Mars 2014 Assemblée générale 2013 La Norvège pays exotique? La oss skravle.. Kurs i Frankrike.. Frankrig og den koloniale arv p. 4 p. 8 p. 12 p. 15 p. 22 Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE
Netbook mouse SPM NO Brukerhåndbok. Register your product and get support at
 Register your product and get support at www.philips.com/welcome Netbook mouse SPM6800 NO Brukerhåndbok Philips Consumer Lifestyle AQ95-56F-1240KR 2010...... (Report No. / Numéro du Rapport) (Year in which
Register your product and get support at www.philips.com/welcome Netbook mouse SPM6800 NO Brukerhåndbok Philips Consumer Lifestyle AQ95-56F-1240KR 2010...... (Report No. / Numéro du Rapport) (Year in which
Graphs similar to strongly regular graphs
 Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
M03/108/S(2) NORWEGIAN A1 STANDARD LEVEL PAPER 2 NORVEGIEN A1 NIVEAU MOYEN ÉPREUVE 2 NORUEGO A1 NIVEL MEDIO PRUEBA 2
 c PROGRAMA IB DIPLOMA PROGRAMME PROGRAMME DU DIPLÔME DU BI DEL DIPLOMA DEL BI M03/108/S(2) NORWEGIAN A1 STANDARD LEVEL PAPER 2 NORVEGIEN A1 NIVEAU MOYEN ÉPREUVE 2 NORUEGO A1 NIVEL MEDIO PRUEBA 2 Friday
c PROGRAMA IB DIPLOMA PROGRAMME PROGRAMME DU DIPLÔME DU BI DEL DIPLOMA DEL BI M03/108/S(2) NORWEGIAN A1 STANDARD LEVEL PAPER 2 NORVEGIEN A1 NIVEAU MOYEN ÉPREUVE 2 NORUEGO A1 NIVEL MEDIO PRUEBA 2 Friday
Last ned La luxure et la purete - Per Buvik. Last ned. Last ned e-bok ny norsk La luxure et la purete Gratis boken Pdf, ibook, Kindle, Txt, Doc, Mobi
 Last ned La luxure et la purete - Per Buvik Last ned Forfatter: Per Buvik ISBN: 9788256005550 Antall sider: 327 Format: PDF Filstørrelse:23.82 Mb Dans l'ensemble, la critique huysmansienne est d'orientation
Last ned La luxure et la purete - Per Buvik Last ned Forfatter: Per Buvik ISBN: 9788256005550 Antall sider: 327 Format: PDF Filstørrelse:23.82 Mb Dans l'ensemble, la critique huysmansienne est d'orientation
StreamLine TV. Guide d'utilisation. Hearing Systems
 StreamLine TV Guide d'utilisation Hearing Systems Sommaire Avant de commencer 4 Inclus dans la livraison 6 Composants 8 Prise en main 10 Positionnement 10 Connexion à l'alimentation secteur 11 Connexion
StreamLine TV Guide d'utilisation Hearing Systems Sommaire Avant de commencer 4 Inclus dans la livraison 6 Composants 8 Prise en main 10 Positionnement 10 Connexion à l'alimentation secteur 11 Connexion
Smart Transmitter 2,4
 Smart Transmitter 2,4 Guide d'utilisation CxxAcc Smart Transmitter 2komma4 FR.indd 1 22.09.2017 07:52:03 Sommaire Avant de commencer 4 Inclus dans la livraison 6 Composants 8 Prise en main 10 Positionnement
Smart Transmitter 2,4 Guide d'utilisation CxxAcc Smart Transmitter 2komma4 FR.indd 1 22.09.2017 07:52:03 Sommaire Avant de commencer 4 Inclus dans la livraison 6 Composants 8 Prise en main 10 Positionnement
Informations sur l'hépatite A, B et C et comment éviter la contamination
 Informations sur l'hépatite A, B et C et comment éviter la contamination Fransk/norsk Fakta om hepatitt A, B og C og om hvordan du unngår smitte Hva er hepatitt? Hepatitt betyr betennelse i leveren. Mange
Informations sur l'hépatite A, B et C et comment éviter la contamination Fransk/norsk Fakta om hepatitt A, B og C og om hvordan du unngår smitte Hva er hepatitt? Hepatitt betyr betennelse i leveren. Mange
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN JUNI A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013
 FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN 5.- 6. JUNI 201 3 A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013 09. 0 0 1 0. 0 0 R E G I S TR E R I NG N o e å b i t e i 10. 0 0 1 0. 15 Å p n i ng
FAGKONFERANSE KONTROL L OG TILSYN GARDERMOEN 5.- 6. JUNI 201 3 A RSMØTE I FORU M FO R KONTROLL OG TILSYN 5. JUN I 2013 09. 0 0 1 0. 0 0 R E G I S TR E R I NG N o e å b i t e i 10. 0 0 1 0. 15 Å p n i ng
Innledende riter. Rite d'entrée. Préparation pénitentielle. Syndsbekjennelse. I Faderens og Sønnens og Den Hellige Ånds navn.
 Norsk Den hellige Messe Innledende riter I Faderens og Sønnens og Den Hellige Ånds navn. Vår Herres Jesu Kristi nåde, Guds kjærlighet og Den Hellige Ånds samfunn være med dere alle. Og med din ånd. Français
Norsk Den hellige Messe Innledende riter I Faderens og Sønnens og Den Hellige Ånds navn. Vår Herres Jesu Kristi nåde, Guds kjærlighet og Den Hellige Ånds samfunn være med dere alle. Og med din ånd. Français
bulletin sek feps
 b 3 bulletin sek feps 3 2008 Une publication de la Fédération des Églises protestantes de Suisse Gros Plan L Église dans l Europe interculturelle 16 Églises en relation Appellations des Églises de la FEPS
b 3 bulletin sek feps 3 2008 Une publication de la Fédération des Églises protestantes de Suisse Gros Plan L Église dans l Europe interculturelle 16 Églises en relation Appellations des Églises de la FEPS
Girnghuber GmbH Ludwig-Girnghuber-Straße Marklkofen T: F:
 Girnghuber GmbH Ludwig-Girnghuber-Straße 1 84163 Marklkofen T: 0 87 32-24 0 F: 0 87 32-24 200 info@gima-ziegel.de www.gima-ziegel.de www.cerpiano.de . INSPIRE PAR LA NATURE. Une innovation pour l extérieur
Girnghuber GmbH Ludwig-Girnghuber-Straße 1 84163 Marklkofen T: 0 87 32-24 0 F: 0 87 32-24 200 info@gima-ziegel.de www.gima-ziegel.de www.cerpiano.de . INSPIRE PAR LA NATURE. Une innovation pour l extérieur
MARKSCHEME BARÈME DE NOTATION ESQUEMA DE CALFICACIÓN
 IB DIPLOMA PROGRAMME PROGRAMME DU DIPLÔME DU BI PROGRAMA DEL DIPLOMA DEL BI M04/208/H(1)M MARKSCHEME BARÈME DE NOTATION ESQUEMA DE CALFICACIÓN May / mai / mayo 2004 NORWEGIAN / NORVÉGIEN / NORUEGO B Higher
IB DIPLOMA PROGRAMME PROGRAMME DU DIPLÔME DU BI PROGRAMA DEL DIPLOMA DEL BI M04/208/H(1)M MARKSCHEME BARÈME DE NOTATION ESQUEMA DE CALFICACIÓN May / mai / mayo 2004 NORWEGIAN / NORVÉGIEN / NORUEGO B Higher
MARKSCHEME BARÈME DE NOTATION ESQUEMA DE CALIFICACIÓN
 IB DIPLOMA PROGRAMME c PROGRAMME DU DIPLÔME DU BI PROGRAMA DEL DIPLOMA DEL BI M07/2/ABNOR/SP1/NOR/TZ0/XX/M MARKSCHEME BARÈME DE NOTATION ESQUEMA DE CALIFICACIÓN May / mai / mayo 2007 NORWEGIAN / NORVÉGIEN
IB DIPLOMA PROGRAMME c PROGRAMME DU DIPLÔME DU BI PROGRAMA DEL DIPLOMA DEL BI M07/2/ABNOR/SP1/NOR/TZ0/XX/M MARKSCHEME BARÈME DE NOTATION ESQUEMA DE CALIFICACIÓN May / mai / mayo 2007 NORWEGIAN / NORVÉGIEN
Daniel K. Schneider - David Ott - Vivian Synteta Version: 0.4 (modifié le 15/8/01 par DKS)
 &DVFDGLQJ6W\OH6KHHWV &DVFDGLQJ6W\OH6KHHWV &RGH 2ULJLQDX[ XUOhttp://tecfa.unige.ch/guides/tie/html/css-into/css-intro.html XUOhttp://tecfa.unige.ch/guides/tie/pdf/files/css-intro.pdf $XWHXUVHWYHUVLRQ Daniel
&DVFDGLQJ6W\OH6KHHWV &DVFDGLQJ6W\OH6KHHWV &RGH 2ULJLQDX[ XUOhttp://tecfa.unige.ch/guides/tie/html/css-into/css-intro.html XUOhttp://tecfa.unige.ch/guides/tie/pdf/files/css-intro.pdf $XWHXUVHWYHUVLRQ Daniel
SOMMAIRE EDITO. Anne-Lise Leblic Jean Sydow. Seine- Maritime. Eure. Orne. Le quotidien et la maladie
 Juin 2019 - N 41 SOMMAIRE Un nouveau directeur à la tête du service régional de Normandie...2 Un quotidien avec son handicap... 3 HANDICONSULT...5 Organiser et améliorer son handicap.4-5 Mes rendez vous
Juin 2019 - N 41 SOMMAIRE Un nouveau directeur à la tête du service régional de Normandie...2 Un quotidien avec son handicap... 3 HANDICONSULT...5 Organiser et améliorer son handicap.4-5 Mes rendez vous
Cliquer sur la version désirée klikk på ønsket versjon. Règlement financier - Année scolaire Betalingsreglement for skoleåret
 Cliquer sur la version désirée klikk på ønsket versjon Règlement financier - Année scolaire 2010-2011 Betalingsreglement for skoleåret 2010-2011 LYCÉE FRANÇAIS RENÉ CASSIN D OSLO Règlement financier -
Cliquer sur la version désirée klikk på ønsket versjon Règlement financier - Année scolaire 2010-2011 Betalingsreglement for skoleåret 2010-2011 LYCÉE FRANÇAIS RENÉ CASSIN D OSLO Règlement financier -

 LIBER BVEL MAGI SVB FIGVRÂ I $
LIBER BVEL MAGI SVB FIGVRÂ I $