Asymptotique des nombres de Betti, invariants l 2 et laminations
|
|
|
- Johanne Dahle
- 4 år siden
- Visninger:
Transkript
1 Comment. Math. Helv. 79 (2004) /04/ DOI /s c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Asymptotique des nombres de Betti, invariants l 2 et laminations N. Bergeron et D. Gaboriau Abstract. Let K be a finite simplicial complex. We are interested in the asymptotic behavior of the Betti numbers of a sequence of finite sheeted covers of K, when normalized by the index of the covers. W. Lück, has proved that for regular coverings, these sequences of numbers converge to the l 2 Betti numbers of the associated (in general infinite) limit regular cover of K. In this article we investigate the non regular case. We show that the sequences of normalized Betti numbers still converge. But this time the good limit object is no longer the associated limit cover of K, but a lamination by simplicial complexes. We prove that the limits of sequences of normalized Betti numbers are equal to the l 2 Betti numbers of this lamination. Even if the associated limit cover of K is contractible, its l 2 Betti numbers are in general different from those of the lamination. We construct such examples. We also give a dynamical condition for these numbers to be equal. It turns out that this condition is equivalent to a former criterion due to M. Farber. We hope that our results clarify its meaning and show to which extent it is optimal. In a second part of this paper we study non free measure-preserving ergodic actions of a countable group Γ on a standard Borel probability space. Extending group-theoretic similar results of the second author, we obtain relations between the l 2 Betti numbers of Γ and those of the generic stabilizers. For example, if b (2) 1 (Γ) 0, then either almost each stabilizer is finite or almost each stabilizer has an infinite first l 2 Betti number. Mathematics Subject Classification (2000). 55NXX (58J22), 37A15 (57R30) Mots clés. Betti numbers, finite covers, laminations, l 2 -Betti numbers, measure preserving actions. Introduction 0.1. Asymptotique des nombres de Betti Un complexe simplicial compact K possède des invariants topologiques numériques : ses nombres de Betti (usuels) b n (K), qui sont les dimensions des espaces vectoriels H n (K, R) d homologie en dimension n. On considère dans tout cet article une action libre cocompacte (L, Γ) d un groupe dénombrable discret Γ sur un complexe simplicial L.
2 Vol. 79 (2004) Asymptotique des nombres de Betti 363 Ses nombres de Betti l 2 notés b (2) n (L, Γ) sont les dimensions généralisées (au sens de von Neumann) des espaces hilbertiens H (2) n (L, Γ) d homologie l 2 réduite en dimension n. Les nombres de Betti l 2, introduits par M. Atiyah dans un contexte analytique [Ati76], ont connu un vaste développement, notamment dans le cadre des feuilletages mesurés (par A. Connes [Co79]), dans le cadre général des actions topologiques quelconques de groupes dénombrables (J. Cheeger et M. Gromov [CG86]), ou suivant l approche de W. Lück qui fait rentrer cette théorie dans un cadre homologique classique par une extension de la notion de dimension généralisée [Lüc98a, Lüc98b]. L article de B. Eckmann 1 [Eck00] constitue une excellente introduction aux nombres de Betti l 2. Une question récurrente dans le domaine consiste àétablir leurs liens avec les nombres de Betti usuels. Lorsque Γ est un groupe fini, la dimension généralisée au sens de von Neumann n est autre que la dimension usuelle divisée par le cardinal Γ de Γ. Dès lors, si le complexe simplicial L ci-dessus est lui-même compact (et donc Γ fini), alors b (2) n (L, Γ) = b n(l). Γ D où ilrésulte, si Λ est un sous-groupe normal d indice fini de Γ, que les nombres de Betti l 2 de l action du groupe fini Λ\Γ sur le complexe compact Λ\L coïncident avec les nombres de Betti usuels normalisés de Λ\L : b (2) n (Λ\L, Λ\Γ) = b n(λ\l). (1) [Γ : Λ] On appellera tour de sous-groupes d indices finis de Γ toute suite décroissante (Γ i ) i N de sous-groupes d indices finis de Γ telle que Γ 0 = Γ. Il lui correspond latourderevêtements L Γ i+1 \L Γ i \L Γ i 1 \L Γ 0 \L en chaque dimension n, la suite des nombres de Betti usuels (b n (Γ i \L)) i N. Si les sous-groupes Γ i sont de plus d intersection triviale ( i 0 Γ i = {e}), alors la tour de revêtements (Γ i \L) i semble converger vers le revêtement L, eton cherche à comprendre le comportement asymptotique de la suite des nombres de Betti usuels, ou plus précisément au vu de la formule (1), de ces nombres normalisés : ( bn(γi\l) [Γ:Γ i] ) i N. Un argument fort en faveur de cette normalisation est que la caractéristique d Euler, ainsi normalisée est constante dans une tour de revêtements. D. Kazhdan, dans une étude sur les variétés arithmétiques [Kaz75] a essentiellement obtenu la comparaison suivante, lorsque les sous-groupes d indices finis Γ i sont de plus normaux et d intersection triviale : 1 C est d ailleurs B. Eckmann qui le premier a introduit une structure euclidienne sur l espace des chaînes d un complexe, pour obtenir une décomposition de Hodge (voir [Eck45]). Il est également remarquable que l une des premières applications (voir [Eck49]) de cette décomposition de Hodge simpliciale concerne la théorie des revêtements, application dont la preuve contient en germes les idées de M. Atiyah conduisant aux nombres de Betti l 2 dans le cas d un revêtement galoisien fini.
3 364 N. Bergeron et D. Gaboriau CMH Inégalité de Kazhdan. lim sup i b n (Γ i \L) [Γ : Γ i ] b (2) n (L, Γ). (2) M. Gromov [Gro91, p. 13, p. 153] est ensuite amené à poser la question : l inégalité ci-dessus est-elle une égalité? En 1994, W. Lück, dans un article remarqué démontre ce résultat. Théorème (Lück [Lüc94]). Soit (Γ i ) i N une tour de sous-groupes d indices finis de Γ. Si les sous-groupes Γ i sont de plus normaux dans Γ et d intersection triviale, alors b n (Γ i \L) lim = b (2) n (L, Γ). (3) i [Γ : Γ i ] Observons que dans l énoncé original de l article [Lüc94], le complexe simplicial L est supposé simplement connexe, mais que cette hypothèse est superflue. Du coup, on peut aussi supprimer l hypothèse de trivialité de l intersection des Γ i,à condition de remplacer alors dans la conclusion, et seulement dans le terme de droite, le groupe Γ par le quotient Γ:=Γ/ i N Γ i et L par L := i N Γ i \L. Alors que le membre de gauche de (1) repose sur l existence d une action de Λ\Γ et donc sur le fait que Λ est distingué dans Γ, le membre de droite a un sens même lorsque Λ n est pas distingué dans Γ. Cette question est discutée dans la section introductive 2.1. Une généralisation du théorème de W. Lück à des revêtements non galoisiens a néanmoins été proposée par M. Farber, qui est amené à introduire une hypothèse d apparence technique. Critère de Farber. Soit n i le nombre de sous-groupes distincts de Γ qui sont conjugués à Γ i et, pour chaque g Γ, soitn i (g) le nombre de ceux-là qui contiennent g. n i (g) g Γ \{e}, lim =0. (4) i n i Théorème (Farber [Far98]). Soit (Γ i ) i N une tour de sous-groupes d indices finis de Γ d intersection triviale. Si le critère (4) est vérifié, alors b n (Γ i \L) lim i [Γ : Γ i ] = b (2) n (L, Γ). Observons que ce critère entraîne que Γ est résiduellement fini.
4 Vol. 79 (2004) Asymptotique des nombres de Betti 365 Dans la partie 4, on présente des exemples où cecritère n est pas satisfait et où la conclusion est mise en défaut, et où même l inégalité de Kazhdan (2) se trouve violée. Voici par exemple une spécialisation du théorème 4.1. Soit A un complexe simplicial compact de groupe fondamental infini et résiduellement fini. Soient K un complexe obtenu en lui attachant un cercle par un point, Γ π 1 (A) Z le groupe fondamental et L = K le revêtement universel de K. Théorème 0.1. Pour tout µ 0 [0, 1[, il existe une tour (Γ i ) i N de sous-groupes d indices finis de Γ, d intersection triviale, telle que, Γ i+1 est normal dans Γ i b et pour n 2, lim n(γ i\l) i [Γ:Γ i] = µ 0 b n (Γ\L)+(1 µ 0 )b (2) n (L, Γ), b et pour n =1, lim 1(Γ i\l) i [Γ:Γ i] = µ 0 b 1 (Γ\L)+(1 µ 0 )b (2) 1 (L, Γ) µ 0. Rappelons que b 1 (Γ\L) =1+b 1 (A) etb (2) 1 (L, Γ) = 1 + b(2) 1 (Ã, π 1(A)), et que b n (Γ\L) =b n (A) etb (2) n (L, Γ) = b (2) n (Ã, π 1(A)), pour n 2. Du coup, tout complexe A pour lequel b n (A) b (2) n (Ã, π 1(A)) (n 2) conduit à un contre-exemple. Par exemple, pour construire des exemples qui ne vérifient pas l inégalité de Kazhdan, on prend pour A le tore T p de dimension p, alors L est contractile, Γ Z p Z, b 1 (Γ\L) =p +1,b (2) 1 (L, Γ) = 1 et, pour n 2, b n(γ\l) =Cp n tandis que tous les b (2) n (L, Γ) sont nuls. Cet énoncé permetégalement de produire des exemples où cette fois l inégalité de Kazhdan se trouve fortement vérifiée (avec une inégalité stricte). Prenons A homéomorphe à une variété M de dimension 4 compacte acyclique à b 1 (M) = 0 et groupe fondamental résiduellement fini (on peut penser àunfaux CP 2 ou CP 2 d homologie [Mum79] ; π 1 (M) est alors un réseau de SU(2, 1)). On a alors : b (2) 2 (L, Γ) >b 2(Γ\L). En effet, par dualité de Poincaré, b 4 = b 0 =1,b 1 = b 3 = 0 = b (2) 4 = b (2) 0 et b (2) 1 = b (2) 3 et donc b 2 (A) +2 = χ(a) = χ (2) (Ã, π 1(A)) = b (2) 2 (Ã, π 1(A)) 2b (2) 1 (Ã, π 1(A)). Si l on se contente d un exemple avec n = 1, une égalité b 1 (A) =b (2) 1 (Ã, π 1(A)) suffit, qu on peut obtenir avec une sphère d homologie A (b 1 = 0) de dimension 3 et hyperbolique (b (2) 1 = 0). C est encore plus simple si l on se satisfait d exemples non acycliques ou avec de la torsion. Après ces préliminaires, voici le premier résultat général que nous obtenons avec des sous-groupes non nécessairement normaux. On ne connait pas d autre preuve de cet énoncé. La suite considérée n est, en général, ni monotone, ni sous-additive. Théorème 0.2. Soit (Γ i ) i N une tour de sous-groupes d indices finis de Γ. Pour tout entier n, la suite des nombres de Betti usuels normalisés ( b n(γ i\l) ) [Γ:Γ est i] i N convergente. Plus précisément, nous donnons une interprétation dynamico-géométrique de cette limite et nous montrons en quel sens le critère Farber (4) est optimal, ce qui, on l espère, clarifie sa signification. Pour cela, nous considérons une construction
5 366 N. Bergeron et D. Gaboriau CMH associée àladonnée de la tour de sous-groupes d indices finis (Γ i ) i N de Γ et de l action (L, Γ) : Pour tout entier positif i, on introduit l espace de probabilité (X i,µ i )égal à l ensemble (fini) des classes (à droite) Γ/Γ i de Γ modulo Γ i, que l on munit de la mesure de comptage normalisée. Les applications de réductions successives X i+1 =Γ/Γ i+1 X i =Γ/Γ i permettent de considérer l espace de probabilité limite projective (X, µ) :=limproj i 0 (X i,µ i ). C est un espace borélien standard. On peut le voir comme le bord (à l infini) d un arbre enraciné. C est aussi un espace topologique homéomorphe àunespacede Cantor (si la suite des indices [Γ : Γ i ] tend vers l infini). L action naturelle de Γ sur les X i fournit une action de Γ sur (X, µ), préservant la mesure µ. Cela ne dépend quedelatour. L action diagonale de Γ sur X L donne par passage au quotient une lamination transversalement mesurée qu on appellera une (L, Γ)-lamination : L(X, L, Γ) := Γ\(X L). Ses feuilles en sont les composantes connexes par arcs (lorsque L est connexe). Chacune est isomorphe au quotient de L par le stabilisateur d un point de l action (X, Γ). Les nombres de Betti l 2 d une telle lamination (pour la mesure transverse provenant de µ) ontété considérés par le second auteur [Gab01]. Nous les noterons β n (X, L, Γ). Les définitions seront rappelées en section 2. On peut les voir comme une version simpliciale des nombres de Betti des feuilletages de A. Connes. On est alors capable de donner un sens, en termes de laminations, au membre de gauche b (2) n (Λ\L, Λ\Γ) de l égalité (1) même lorsque Λ n est pas normal : β n (Γ/Λ,L,Γ). Et cette égalité reste valide (voir section 2.1). Plus généralement, nous obtenons le résultat suivant, qui est central dans cet article : Théorème 3.1. Soit (Γ i ) i N une tour de sous-groupes d indices finis de Γ. Pour tout entier n, b n (Γ i \L) lim = β n (X, L, Γ). i [Γ : Γ i ] où β n (X, L, Γ) est comme ci-dessus. On dit que l action (X, µ, Γ) est libre si l élément neutre est le seul élément de Γà avoir un ensemble de points fixes de mesure non nulle. On a alors : Théorème [Gab01, Th. 3.11]. Si l action (X, µ, Γ) est libre, alors β n (X, L, Γ) = b (2) n (L, Γ).
6 Vol. 79 (2004) Asymptotique des nombres de Betti 367 Si les Γ i sont normaux dans Γ et d intersection triviale, alors X hérite d une structure de groupe (profini), Γ est un sous-groupe et son action est par multiplication à gauche dans X. Elle est alors libre et le théorème 3.1 se spécialise en le théorème de W. Lück. Quant au critère de Farber (4), il signifie précisément que l action est libre. En effet, Proposition 2.6. Dans (X, µ, Γ), l ensemble des points fixes de g Γ est de mesure exactement lim i n i(g) n i. On doit observer que ni le théorème de Farber, ni notre théorème 3.1 ne fournissent une nouvelle preuve du théorème de Lück, puisque dans un cas comme dans l autre, il s agit d adapter les arguments de [Lüc94] Actions boréliennes non libres Le théorème 3.1 décrit les limites possibles des nombres de Betti normalisés dans les tours des revêtements finis. Un contrôle sur la combinatoire des tours de revêtements finis est donc imposé par l action (X, Γ) et la (L, Γ)-lamination associée. Il est naturel de chercher à comprendre ces actions et plus précisément à trouver des restrictions sur les stabilisateurs des points pour des actions non libres (X, µ, Γ), préservant la mesure, d un groupe dénombrable Γ sur un borélien standard de probabilité. Les nombres de Betti l 2 de (L, Γ) sont des invariants homotopiques, si bien que lorsque L est p-connexe, les nombres de Betti l 2 de l action b (2) n (L, Γ), pour n p deviennent des invariants du groupe Γ lui-même. On les appelle alors les nombres de Betti l 2 deγetonlesnoteb (2) n (Γ). Plus généralement, J. Cheeger et M. Gromov [CG86] ont introduit les nombres de Betti l 2 pour tous les groupes dénombrables discrets, même ceux ne possédant pas de K(Γ, 1) à p-squelette fini. Dans la section 5, nous démontrons : Théorème 5.4. Soit (X, µ, Γ) une action ergodique, préservant la mesure, d un groupe dénombrable Γ sur un borélien standard de probabilité sans atome. Si b (2) 1 (Γ) est non nul, alors ou bien Γ(x), le stabilisateur de x dans Γ, est un groupe fini pour µ-presque tout x X ; ou bien le premier nombre de Betti l 2, b (2) 1 (Γ(x)), estinfinipourµ-presque tout x X. Si de plus, la relation induite par l action de Γ sur X est moyennable, seul le deuxième cas est possible. Tandis que dans le premier cas, pour µ-presque tout x, les sous-groupes Γ(x) sont conjugués deux à deux et il sont presque normaux, au sens où chacun n a qu un nombre fini de conjugués distincts dans Γ.
7 368 N. Bergeron et D. Gaboriau CMH Il est intéressant de rappeler deux énoncés en lesquels ce théorème se spécialise, chacun d eux étant une généralisation dans une direction différente d un théorème de O. Schreier : Théorème (O. Schreier [Sch27, p. 162]). Un sous-groupe normal non trivial et de type fini d un groupe libre est d indice fini. D un côté, les stabilisateurs des points dans l action (X, µ, Γ) peuvent être considérés d une certaine façon comme des généralisations de sous-groupes normaux (penser par exemple à une action où tous les points ont le même stabilisateur : c est alors un sous-groupe normal). La remarque de D. Sullivan selon laquelle there is no measurable way to pick a point in a leaf impose des conditions fortes sur certaines (L, Γ)-laminations. Rappelons que dans [Ghy95], É. Ghys a montré comment déduire de cette remarque une classification topologique des feuilles génériques des laminations usuelles de dimension 2. Sous-jacent à ses idées, on peut trouver l énoncé suivant : Théorème 5.2. Soit Γ un groupe libre et (X, µ, Γ) une action libre ergodique préservant la mesure de probabilité µ sans atome sur le borélien standard X. Alors, pour µ-presque tout point x X, le stabilisateur de x est soit trivial soit de type infini. D un autre côté, un groupe libre non cyclique est un exemple de groupe à premier nombre de Betti l 2 non nul, et le second auteur a étendu le théorème de O. Schreier à tous les groupes du même genre (consulter [Gab01] pour références à des résultats antérieurs notamment de J. Cheeger, M. Gromov et W. Lück) : Théorème [Gab01, Th. 6.8]. Soit Γ un groupe dont le premier nombre de Betti l 2, b (2) 1 (Γ), estnonnul.sin est un sous-groupe normal de Γ qui a un premier nombre de Betti l 2 fini (par exemple si N estdetypefini)alorsn est ou bien fini ou bien d indice fini. La preuve dans cette généralité fait d ailleurs appel à une action libre du groupe Γ sur (X, µ) età la notion de nombres de Betti l 2 des laminations. Pour démontrer le théorème 5.4 (ainsi que 5.6 ci-dessous), nous serons conduits à prouver le résultat suivant, intéressant en lui-même, bien que pas franchement surprenant puisque les nombres de Betti l 2 des stabilisateurs sont définis explicitement sans recours à l axiome du choix. Théorème 5.7. Soit (X, µ, Γ) une action préservant la mesure d un groupe dénombrable Γ sur un borélien standard de probabilité sans atome. Alors, la fonction X R + { }, x b (2) n (Γ(x)), qui associe à x le n-ème nombre de Betti l 2 de son stabilisateur, est mesurable. En particulier, si l action de Γ est ergodique,
8 Vol. 79 (2004) Asymptotique des nombres de Betti 369 alors cette fonction est presque sûrement constante. Concernant les nombres de Betti l 2 de dimension supérieure, nous obtenons une généralisation du théorème 6.6 de [Gab01]. Rappelons qu une action mesurable est hyperfinie si la relation d équivalence engendrée est réunion croissante de relation d équivalence mesurables à classes finies. Par le théorème de Connes Feldman Weiss [CFW81], cela équivaut à la moyennabilité de la relation au sens de R. Zimmer. Théorème 5.6. Soit (X, µ, Γ) une action ergodique hyperfinie, préservant la mesure, d un groupe dénombrable Γ sur un borélien standard de probabilité sans atome. Si pour un certain n N, len-ème nombre de Betti l 2 de presque tout stabilisateur est fini (b (2) n (Γ(x)) < µ-p.s), alors b (2) n (Γ) = 0. Pour l ensemble de cette section, on se permettra de supposer une certaine familiarité avec le contexte de l article [Gab01]. Bruno Sévennec a lu attentivement une version préliminaire de cet article et nous a signalé quelques corrections. Nous l en remercions. 1. Rappels sur les nombres de Betti l 2 d une action de groupe Soit (L, Γ) une action simpliciale libre et cocompacte et q : L K := Γ\L le revêtement associé. Quitte à prendre des subdivisions barycentriques, on peut supposer que l espace K a une structure de complexe simplicial. On confondra un complexe simplicial et sa réalisation géométrique. On se donne une orientation sur les simplexes de K (et donc aussi sur ceux de L) et on appelle K n (resp. L n ) l ensemble des simplexes de dimension n de K (resp. de L). L ensemble L n est muni d une action libre de Γ qui est simplement transitive sur l image inverse q 1 (σ) de chaque simplexe σ de K n. On note C n (2) (L) l espace des n-chaînes l 2 de L : c est l espace de Hilbert dont une base hilbertienne est L n. Il vient avec une représentation π n de Γ. Les applications bord s étendent par continuité en des opérateurs bornés n : C n (2) (L) C (2) n 1 (L). Ils vérifient n n+1 =0et γ Γ, π n 1 (γ) n = n π n (γ). Soit Θ n un domaine fondamental (partie qui rencontre une fois et une seule chaque orbite) pour l action de Γ sur L n.laliberté de l action permet alors d identifier L n avec θ n := Θ n copies de Γ : L n = s Θn Γs. Cette identification induit un isomorphisme C n (2) (L) = l 2 (Γs) l 2 (Γ) (5) s Θ n s Θ n qui donne à C (2) n (L) une structure de N(Γ)-module de Hilbert, où N(Γ) est l algèbre de von Neumann de Γ.
9 370 N. Bergeron et D. Gaboriau CMH On dispose alors d un complexe de N(Γ)-modules hilbertiens : 0 C (2) 1 0 (L) C (2) 2 1 (L)... C (2) n (L) n+1... On appelle homologie l 2 réduite de L la suite d espaces H (2) n (L) := Ker n /Im n+1, où H est l adhérence de H. Ces espaces ont une structure de N(Γ)-module de Hilbert et se plongent naturellement dans C n (2) (L) comme supplémentaire orthogonal de Im n+1 dans Ker ( n ). L image de ce plongement est par définition l espace, noté H n (L), des n-chaînes harmoniques l 2 de L. Un calcul immédiat montre qu il est par ailleurs égal au noyau de l opérateur laplacien n := n n + n+1 n+1. On cherche à estimer la taille de cet espace de Hilbert H n (L). En dimension finie, la dimension d un sous-espace est donnée par la trace d un projecteur sur ce sous-espace. Ici, la trace 2 (de von Neumann) d un opérateur a de l 2 (Γ) qui commute avec N(Γ) est donnée par le produit scalaire Tr N(Γ) (a) := aδ e δ e, où δ e est la fonction caractéristique de l identité deγ.demême, grâce à l isomorphisme ci-dessus (5), la trace d un opérateur a de C n (2) (L) commutant avec N(Γ) est donnée par Tr N(Γ) (a) = a(s) s. s Θ n La N(Γ)-dimension dim N(Γ) (H) d un sous-espace fermé N(Γ)-invariant H de C n (2) (L) est alors donnée par la trace du projecteur orthogonal sur ce sous-espace. Définition 1.1. Les nombres de Betti l 2 de l action (L, Γ) sont les N(Γ)-dimensions des N(Γ)-modules H n (L) : b (2) n (L, Γ) := dim Γ (H n (L)) = Tr N(Γ) (p n )= p n (s) s. (6) s Θ n où p n est le projecteur orthogonal de C n (2) (L) surh n (L). Si L est le revêtement universel de K, on appelle aussi parfois ces nombres les nombres de Betti l 2 de K. Ces nombres sont des invariants d équivalence homotopique, si bien que lorsque L est p-connexe, les p premiers nombres de Betti l 2 de (L, Γ) deviennent des invariants du groupe : les nombres de Betti l 2 de Γ, notés b (2) n (Γ), pour n = 0, 1,,p. 2 Il peut être éclairant de penser à a comme une matrice (infinie) par rapport àlabaseprivilégiée (δ g) g Γ : a =(a g,h )=( a(δ g) δ h ) pour remarquer que les termes diagonaux a(δ g) δ g sont constants, vu la commutation de a avec N(Γ). La trace est alors l un quelconque de ces termes diagonaux. n
10 Vol. 79 (2004) Asymptotique des nombres de Betti Nombres de Betti l 2 d une (L, Γ)-lamination On rappelle dans cette section la notion de nombres de Betti l 2 d une lamination dans l esprit de [Gab01, sect. 3]. Soit (X, µ, Γ) une action mesurable du groupe Γ sur le borélien standard X, préservant la mesure de probabilité µ. On note Γ(x) le stabilisateur du point x X. Soit d autre part (L, Γ) une action libre cocompacte de Γ sur le complexe simplicial connexe L. On regarde l espace X L, avec la lamination par feuilles {x} L. L action diagonale de Γ préserve cette lamination et définit par passage au quotient ce qu on appelle une (L, Γ)-lamination transversalement mesurée L(X, L, Γ) := Γ\(X L). Nous allons rappeler la définition des nombres de Betti de la lamination sous l hypothèse que Γ\L est un complexe simplicial fini, dans ce cas chaque Θ n est fini. L image de la feuille {x} L est isomorphe àγ(x)\l. Sur X, ondisposedu champ mesurable de sous-groupes x Γ(x). Cela permet de définir le champ mesurable L de complexes simpliciaux x L x =Γ(x)\L sur lequel le groupe Γ agit encore : γ.(x, Γ(x)τ) =(γx,γγ(x)τ) =(γx,γ(γx)γτ) puisque Γ(γx) =γγ(x)γ 1. C est un complexe simplicial (hautement non connexe) équipé d une application ( fibration ) sur X, dont les fibres sont les feuilles (audessus de x X, la feuille L x ). Ses simplexes seront notés (x, Γ(x)s), où x X et s L. Pour chaque dimension n, l espace de ses n-simplexes forme un espace borélien standard L n. On dispose aussi d une application mesurable Q : X L L (7) qui est un revêtement fibre à fibre q x : {x} L L x =Γ(x)\L. À l action de Γ sur X est associée la relation d équivalence R := {(x, y) :Γx =Γy}, (8) où les points x et y de X sont dans la même classe s il existe un élément γ dans Γ tel que y = γx. La relation R possède une action sur le champ de complexes simpliciaux L : (x, y) Rdéfinit un isomorphisme L y L x donné par l isomorphisme naturel ( ) Γ(y)\L Γ(x)\L (9) Γ(y)s (x, y) Γ(y)s =Γ(x)γs où s L et γ Γvérifie x = γy, i.e. Γ(x) =γγ(y)γ 1. Bien entendu, si γ Γ est un autre tel élément, alors Γ(x)γ =Γ(x)γ. Deplus,(x, x) induit l identité.
11 372 N. Bergeron et D. Gaboriau CMH Remarque 2.1. Si L est muni d un point base, alors les espaces L x héritent d un pointage x = q x ( ) qui n est pas préservé par l isomorphisme ci-dessus. De plus, l image dans la lamination L(X, L, Γ) de ce champ de pointages permet de retrouver l espace X comme transversale et fixe donc un choix de mesure transverse invariante (et non à un multiple près). Cette action possède un domaine fondamental mesurable en chaque dimension n, Q(X {s}) = {(x, Γ(x)s) :x X} (10) s Θ n s Θ n où Θ n est toujours un domaine fondamental pour l action de Γ sur L n. Soit en effet (x, Γ(x)s )=Q((x, s )) un simplexe de L. Ilexistes Θ n et γ Γ tels que que s = γs. Alors (x, Γ(x)s )=(x, Γ(x)γs) =(x, γγ(γ 1 x)s) =(x, γ 1 x) (γ 1 x, Γ(γ 1 x)s). Ainsi, l ensemble L n des simplexes de dimension n de L peut s identifier avec θ n := Θ n copies de R. On considère le champ d espaces de Hilbert x C n (2) (L x )=C n (2) (Γ(x)\L). Chaque simplexe s L n y fournit un champ de vecteurs, que nous noterons s : x s x, (donné par le champ de simplexes x (x, Γ(x)s)). Le champ de familles génératrices (s) s L n lui donne sa structure mesurable. On dispose aussi du champ mesurable d opérateurs bord n x : C n (2) (L x ) C (2) n 1 (L x). On définit C n (2) (L) etd n comme intégrales : C (2) n (L) := X C (2) n (L x )dµ(x) etd n := X x ndµ(x). Rappelons simplement qu un vecteur u de C n (2) (L) est un champ de vecteurs x u x mesurable et de carré intégrable, au sens où les fonctions x u x s x sont mesurables pour chacun des champs s donnés par les simplexes s L, et X u x 2 dµ(x) <. On dispose alors du complexe : 0 C (2) D1 0 (L) C (2) 1 D2 (L)... Dn C (2) n (L) Dn+1... (11) Le n-ème groupe d homologie l 2 réduite H (2) n (L) = Ker D n /Im D n+1.ilest isomorphe à l espace des n-chaînes harmoniques l 2 de L : le supplémentaire orthogonal H n (2) (L) = Ker D n Im D n+1. Définition 2.2. Les nombres de Betti l 2 du R-complexe simplicial L ou de la (L, Γ)-lamination L(X, L, Γ) sont définis par : β n (L) =β n (X, L, Γ) := s Θ n P n s s, (12)
12 Vol. 79 (2004) Asymptotique des nombres de Betti 373 où P n est le projecteur orthogonal de C n (2) (L) surh n (2) (L), qu on évalue sur les champs de représentants s pour s Θ n. L identification R-équivariante de L n avec θ n copies de R construite à l aide du domaine fondamental (10) induit un isomorphisme qui donne à C n (2) (L) une structure de M-modules de Hilbert : C n (2) (L) = C n (2) (R Q(X {s}) L 2 (R,ν), (13) s Θ n s Θ n où M est l algèbre de von Neumann de la relation R. On rappelle [FM77, Gab01] que l espace R X X est un borélien standard pour la tribu induite (B B) R, où B est la tribu de X, et pour tout C (B B) R, la mesure ν est définie par ν(c) = π1 1 (x) C dµ(x) X avec π 1 : R X projection sur la première coordonnée. Si on désigne par R γ et R φ les opérateurs de L 2 (R,ν) donnés pour γ Γ et φ L (X, µ) par R γ f(x, y) = f(x, γ 1 y)etr φ f(x, y) = φ(y)f(x, y), alors M est l algèbre des opérateurs de L 2 (R,ν) qui commutent avec tous les R γ et R φ. Le complexe (11) est alors un complexe de M-modules hilbertiens et l isomorphisme entre le n-ème groupe d homologie l 2 réduite et l espace des chaînes harmoniques l 2 de L est un isomorphisme de M-modules. La trace d un opérateur A de L 2 (R,ν) qui commute avec M est donnée par la formule Tr M (A) := Pϕ 0 ϕ 0, où ϕ 0 est la fonction caractéristique de la diagonale de X X. Demême, grâce à l isomorphisme (13), la trace d un opérateur A de C n (2) (L) qui commute avec M est donnée par Tr M (A) := P n s s. (14) s Θ n La M-dimension d un sous-espace fermé M-invariant H de C n (2) (L) est alors donnée par la trace du projecteur orthogonal sur ce sous-espace. Les nombres de Betti l 2 du R-complexe simplicial L ou de la (L, Γ)-lamination L(X, L, Γ) sont donc les M-dimensions des M-modules H n (2) (L) : β n (L) =β n (X, L, Γ) = dim M H n (2) (L) =Tr M (P n ) où P n est le projecteur orthogonal de C n (2) (L) surh n (2) (L). Comme rappelé dans l introduction, lorsque l action de Γ sur X est libre (au sens de la mesure), on peut montrer, [Gab01, th. 3.11], que pour tout entier n, β n (L) =b (2) n (L, Γ). Rappelons qu inspiré par l approche de Cheeger et Gromov [CG86], on peut définir (voir [Gab01]) la notion générale de nombres de Betti l 2 d un R-complexe
13 374 N. Bergeron et D. Gaboriau CMH simplicial général sur une relation d équivalence donnée R. Dans [Gab01], une invariance homotopique de ces nombres de Betti l 2 est démontrée. Cela permet de définir les nombres de Betti l 2 de la relation R Exemple : revêtements finis Dans l introduction on a rappelé la remarque (1) selon laquelle si Λ est un sous-groupe distingué d indice fini dans un groupe Γ agissant librement et cocompactement sur un complexe simplicial L, alors (le groupe Λ\Γ agit librement sur Λ\L et) pour tout entier n, b (2) n (Λ\L, Λ\Γ) = b n(λ\l). (15) [Γ : Λ] Dans cette égalité (15), le membre de droite conserve un sens même lorsque le revêtement n est pas galoisien autrement dit même lorsque le sous-groupe Λ n est pas distingué dans Γ. Le membre de gauche quant à lui n a plus de sens, néanmoins considérons sa définition concrète, donnée par la formule (6) b (2) n (Λ\L, Λ\Γ) := p n (s) s, s Ω n où Ω n est l image d un domaine fondamental Θ n pour l action de Γ sur L n (et donc un domaine fondamental pour l action (Λ\L n, Λ\Γ)). Elle conserve toujours un sens mais sa valeur dépend du choix du domaine fondamental Θ n i.e. du choix d un point de vue. Une solution consiste à faire la moyenne de tous ces points de vue. On va détailler cela avec comme double but d illustrer la construction de la section 2 et de préparer à la section 2.2. Soit Γ un groupe agissant librement et cocompactement sur un complexe simplicial L. Soit Λ un sous-groupe d indice fini de Γ, κ := [Γ : Λ] et q : L Λ\L le revêtement correspondant. Soit X l ensemble fini Γ/Λ muni de la mesure de comptage normalisée : µ({x}) = 1 κ. L action de Γ sur X est transitive, donc la relation d équivalence R est celle où tous les points sont équivalents. La mesure ν est la mesure qui donne à chaque point de R = X X le poids 1 κ. L espace de Hilbert L2 (R,ν) est l espace vectoriel dont les points de X X forment une base, sont de norme 1 κ et deux à deux orthogonaux. La (L, Γ)-lamination L(X, L, Γ) := Γ\(X L) n est constituée que d une seule feuille isomorphe àλ\l. Le champ de complexes simpliciaux L est formé deκ complexes simpliciaux L x := Γ(x)\L, indexés par x Γ/Λ, où Γ(γΛ) = γλγ 1, isomorphes deux à deux par la formule (9). Les espaces de chaînes l 2 sont alors C (2) n (L) := X C n (2) (L x )dµ(x) = x X C n (2) (Γ(x)\L),
14 Vol. 79 (2004) Asymptotique des nombres de Betti 375 avec comme produit scalaire u v = x X 1 κ u x v x. Les nombres de Betti l 2 de cette lamination sont alors obtenus à l aide de la formule (12) : β n (L) = s Θ n P n s s, où P n est le projecteur orthogonal de C n (2) (L) surh n (2) (L), qu on évalue sur les champs de représentants s pour s Θ n. Remarquons que l algèbre de von Neumann M de R est isomorphe à l algèbre M κ des matrices κ κ. Son action sur L 2 (R,ν) identifié avec les matrices A = (A x,y ) x,y X se fait alors par multiplication à gauche. La trace Tr Mκ est alors la trace usuelle des applications linéaires, divisée par κ. Par définition de l opérateur bord D n,pourc n C n (2) (L), on a c n 1 = D n c n si et seulement si c n 1 (x) = nc x n (x) pourµ presque tout x dans X. On en déduit que P n est un opérateur décomposable P n = x X px n,oùx p x n est le champ (mesurable) d opérateurs projections orthogonales p x n : C n (2) (Γ(x)\L) (Γ(x)\L). H (2) n β n (L) = = 1 κ s Θ n x X s Θ n x X 1 κ px ns x s x p x nγ(x)s Γ(x)s où Γ(x)s est vu comme une n-chaîne dans C n (2) (Γ(x)\L). Mais l isomorphisme de la formule (9) entre Γ(y)\L et Γ(x)\L induit une isométrie entre les espaces C n (2) (Γ(y)\L) etc n (2) (Γ(x)\L) qui entrelace les projections p y n et p x n.ainsi,p x0 n (Γ(x 0 )γs) =p γ 1 x 0 n (Γ(γ 1 x 0 )s) etavecx 0 =Λ Γ/Λ et γ 1,γ 2,,γ κ des représentants des classes à gauche de Λ\Γ, β n (L) = 1 κ p n (Λγ i s) Λγ i s. κ i=1 s Θ n Par ailleurs, i=κ i=1 γ iθ n constitue un domaine fondamental pour l action de Λ sur L n. C est-à-dire, i=κ i=1 Λγ iθ n =Λ\L n, dont les élément constituent une base de l espace vectoriel de dimension finie C n (2) (Λ\L). Si bien que, avec tr(p n )latrace usuelle de l opérateur p n, β n (X, L, Γ) := 1 κ p n (Λγ i s) Λγ i s κ i=1 s Θ n = 1 κ tr(p n)= 1 κ dim C(H n (2) (Γ(x)\L)) = 1 [Γ : Λ] b n(λ\l).
15 376 N. Bergeron et D. Gaboriau CMH Les changements de point de vue évoqués plus haut consistent donc à remplacer le domaine fondamental Θ n par ses divers translatés γ i Θ n. Une autre manière de dire consiste à oublier le groupe Λ : considérons un revêtement fini d indice κ, non nécessairement galoisien, L K. Choisissons un point base dans L, son image dans K puis ses κ relevés 1, 2,, κ dans L. Chacun des revêtements pointés (L, ) (L, i ) nous fournit un sous-groupe Λ i de Γ. Ils sont deux à deux conjugués. Passer de l un à l autre constitue un changement de point de vue. Nous avons donc démontré : Proposition 2.3. Si (L, Γ) est une action libre cocompacte sur un complexe simplicial, si Λ est un sous-groupe d indice fini, et X =Γ/Λ est muni de la mesure de comptage normalisée, alors les nombres de Betti l 2 de la lamination L(X, L, Γ) = Γ\(X L) coïncident avec les nombres de Betti normalisés : β n (X, L, Γ) = b n(λ\l). [Γ : Λ] La (L, Γ)-lamination L(X, L, Γ) n est constituée que d une seule feuille isomorphe à Λ\L qui est recouverte par les projections des γθ n où Θ n est un domaine fondamental pour la Γ-action dans L n et γ décrit un système de représentants quelconque des classes àgauchedeγmodulo Λ. De plus, ces nombres de Betti l 2 peuvent se voir comme une moyenne selon les points de vue : β n (X, L, Γ) = 1 [Γ : Λ] γ Λ\Γ s Θ n p n (Λγs) Λγs. Remarque 2.4. À ce stade, une petite précision s impose. Si l on considère un sous-groupe strict Γ tel que Λ < Γ < Γ et l action restreinte (L, Γ ), alors les nombres de Betti usuels normalisés bn(λ\l) [Γ :Λ] ne sont plus les mêmes, tandis que la lamination L(X, L, Γ ) Λ\L est la même en tant qu espace laminé! L explication tient au fait que la suite des nombres de Betti l 2 d une lamination transversalement mesurée n est bien définie qu à une constante multiplicative près qui dépend du choix d une normalisation de la mesure transverse invariante. Dans notre situation, ce choix est précisé lorsqu on décide que l espace (X, µ) est un espace de probabilité (voir remarque 2.1) (L, Γ)-lamination associée à une tour de revêtements finis On appelle tour de sous-groupes d indices finis de Γ toute suite décroissanteγ=γ 0 Γ 1... Γ m... de sous-groupes d indices finis de Γ. Il lui correspond la tour de revêtements finis au-dessus de Γ\L : L Γ i+1 \L Γ i \L Γ i 1 \L Γ 0 \L. Pour tout entier positif i, on introduit l espace de probabilité (X i,µ i )égal à l ensemble (fini) des classes (à droite) Γ/Γ i de Γ modulo Γ i, que l on munit
16 Vol. 79 (2004) Asymptotique des nombres de Betti 377 de la mesure de comptage normalisée. Les applications de réductions successives ρ i : X i =Γ/Γ i X i 1 =Γ/Γ i 1 permettent de considérer l espace de probabilité limite projective (X, µ) :=limproj i 0 (X i,µ i ). C est un espace borélien standard. On peut le voir comme le bord (à l infini) d un arbre enraciné, où les sommets sont les éléments des X i et les arêtes données par les applications X i+1 X i ). C est aussi un espace topologique (homéomorphe à un espace de Cantor, si la suite des indices [Γ : Γ i ] tend vers l infini). L action naturelle de Γ sur les X i fournit une action de Γ sur (X, µ), préservant la mesure µ. Celanedépend que de la tour. Définition 2.5. L action diagonale de Γ sur X L donne par passage au quotient la (L, Γ)-lamination associée à la tour (Γ i ) i N : L(X, L, Γ) := Γ\(X L). Au vu du théorème 3.1, il est important, pour comprendre l asymptotique des nombres de Betti normalisés d une tour de revêtements finis, de comprendre l action de Γ sur l espace de probabilité X. On en isole quelques propriétés élémentaires dans la proposition suivante : Proposition Un point x X est une suite (x i ) i N de classes x i Γ/Γ i telles que ρ i (x i )=x i 1.Siγ i est un représentant de x i dans Γ, alors on obtient pour stabilisateurs Γ(x i )=γ i Γ i γ 1 i et Γ(x) = i N γ i Γ i γ 1 i. 2. Pour tout point x X et pour tout sous-complexe compact C de L, ilexiste un entier i 0 0 tel que pour tout i i 0, et tout représentant γ i de x i dans Γ le projeté deγ 1 i.c dans Γ i \L soit simplicialement équivalent aux projetés de C dans Γ(x)\L et γ i Γ i γ 1 i \L. 3. L action de Γ étant transitive sur chaque X i,onendéduit que l action de Γ sur X est ergodique : tout ensemble borélien invariant est de mesure 0 ou 1. En particulier, l ensemble des points de X à stabilisateur trivial est de mesure 0 ou Pour tout élément g dans Γ, la mesure dans X de l ensemble des points fixes de g dans X vaut : n i (g) µ(fix X (g)) = lim, i + n i où n i désigne le nombre de sous-groupes de Γ conjugués à Γ i et n i (g) le nombre de sous-groupes de Γ conjugués à Γ i et contenant g. Démonstration. Seuls les points 2 et 4 demandent une explication. Preuve du point 2 : Il n existe qu un nombre fini g 1,g 2,,g k d éléments de Γ qui envoient un simplexe de C dans C. Pouri 0 assez grand et pour tout j = 1,,k,onag j Γ(x) si et seulement si g j Γ(x i ). Pour tout i i 0, les projetés de C dans Γ(x)\L et Γ(x i )\L sont simplicialement équivalents. L isomorphisme (9) entre Γ i \L et Γ(x i )\L qui envoie Γ i γ 1 i C sur Γ(x i )C permet de conclure.
17 378 N. Bergeron et D. Gaboriau CMH Preuvedupoint4:Soitf i (g) le nombre de points fixes de l action de g sur X i. Alors : f i (g) [Γ : Γ i ] = n i(g). (16) n i En effet, le groupe Γ agit sur X i et par conjugaison sur l ensemble des conjugués de Γ i dans Γ. L application { Xi {conjugués de Γ p : i dans Γ} x Fix Γ (x) est Γ-équivariante pour ces deux actions. Chaque fibre de p est donc de cardinal a i = {x X i : Fix Γ (x) =Γ i }, égal à l indice de Γ i dans son normalisateur N Γ (Γ i ). Ainsi, avec les notations de la proposition, [Γ : Γ i ]=n i a i et le nombre de points fixes de l action d un élément quelconque g ΓsurX i est égal à n i (g) a i.d où l on conclut àl égalité (16). En passant alors à la limite (la suite fi(g) [Γ:Γ i] est décroissante, puisque f i+1 (g) [Γ i :Γ i+1 ]f i (g)), on obtient par définition de µ, l égalité annoncée du point Asymptotique des nombres de Betti On peut maintenant énoncer et démontrer le théorème principal de cet article. Soient L un complexe simplicial et Γ un groupe agissant librement et cocompactement sur L. Soit (Γ i ) i 0 une tour de sous-groupes d indices finis dans Γ. Soit L = L(X, L, Γ) := Γ\(X L) la(l, Γ)-lamination associée (déf. 2.5). Théorème ( 3.1. Pour chaque entier n, la suite des nombres de Betti normalisés bn(γ i\l) ) [Γ:Γ converge et sa limite est égale au n-ème nombre de Betti i] i N l2 de la (L, Γ)-lamination associée : β n (X, L, Γ). Démonstration. Fixons un entier n positif. Soit C n (L) l espace des n-chaînes entières de L. C est un Z[Γ]-module finiment engendré, dont la famille Θ n introduite section 1 fournit une base. Soit ũ une application positive autoadjointe des n-chaînes de L dans elles-mêmes (on peut penser au laplacien) donnée par une matrice à coefficients dans Z[Γ] (dont l action se fait par multiplication à droite). Autrement dit, avec θ n = Θ n : ũ : C n (L) C n (L), ũ Z[Γ] Mat(θ n θ n, Z). Pour que ũ commute avec N(Γ), il faut y penser comme une matrice agissant par multiplication à droite sur θ n i=1 l2 (Γ). Observons que si Λ est un sous-groupe de Γ, alors ũ induit par passage au quotient un opérateur sur les n-chaînes entières de Λ\L qui s étend en un opérateur borné sur les chaînes l 2.
18 Vol. 79 (2004) Asymptotique des nombres de Betti 379 Pour chaque i 0, considérons X i =Γ/Γ i muni de sa mesure de comptage normalisée µ i. Pour chaque i 0 et pour chaque point x i X i, l application ũ induit une application C-linéaire u xi i sur C n (L i x i ) = C n (2) (L i x i ), l espace des n-chaînes de la feuille simpliciale L i x i =Γ(x i )\L au-dessus de x i dans la (L, Γ)- lamination L i =Γ\(X i L) (dans ce cas la lamination L i n a en fait qu une feuille). Par intégration contre la mesure µ i on obtient un opérateur u i de C n (2) (L i )dans lui-même. De même, pour chaque point x X, l application ũ induit une application C-linéaire u x sur C n (L x ) qui s étend en un opérateur borné, encore noté u x,sur C n (2) (L x ), l espace des n-chaînes l 2 de la feuille simpliciale L x =Γ(x)\L au-dessus de x dans la (L, Γ)-lamination L. Par intégration contre la mesure µ on obtient un opérateur u de C n (2) (L) dans lui-même. Soit Q(z) un polynôme à coefficients réels. Pour tout x X, x i X i,ona Q(u) x = Q(u x )etq(u i ) xi = Q(u xi i ). Rappelons que si s est un simplexe dans Θ n il induit un champ de vecteurs s (resp. s i )dansla(resp.les)(l, Γ)-lamination(s) L (resp. L i )donnépar:(x (x, s)). Fait 1. Soit x =(x i ) i un point de X. Pouri suffisamment grand et s Θ n, Q(u) x (s(x)) s(x) = Q(u i ) xi (s i (x i )) s i (x i ). Les champs mesurables d opérateurs x Q(u) x sur L (resp. x i Q(u i ) xi sur L i )nesontautresquex Q(u x )(resp.x i Q(u xi i )). Le fait 1 découle alors simplement des définitions et de la proposition 2.6 (point 2). La norme d opérateur de u i est bornée uniformément par rapport à i par une constante N (on peut prendre comme valeur pour N le produit de θ n par la somme des coefficients des éléments de Γ dans la matrice ũ, cf.[lüc94] Lemma 2.5). Du théorème de convergence dominée de Lebesgue, on déduit donc : Tr M (Q(u)) = Q(u)(s) s s Θ n = Q(u) x (s(x)) s(x) dµ(x) s Θ n X = lim Q(u i) xi (s i (x i )) s i (x i ) dµ(x) s Θ X i + n = lim Q(u i ) xi (s i (x i )) s i (x i ) dµ(x) i + s Θ n = lim i + s Θ n X X i Q(u i ) xi (s i (x i )) s i (x i ) dµ i (x i )
19 380 N. Bergeron et D. Gaboriau CMH Autrement dit : = lim i + s Θ n Q(u i )(s i ) s i. Tr M (Q(u)) = lim Tr M i (Q(u i )), (17) i + où M i est l algèbre de von Neumann de la relation d équivalence sur X i engendrée par l action transitive de Γ, i.e. M i est l algèbre des matrices X i X i, munie de la trace normalisée Tr Mi, qui est la trace usuelle divisée par X i. Soit maintenant {P (λ)/λ [0,N]} la famille spectrale continue à droite de u. Notons F :[0, + [ R + ; λ Tr M (P (λ)). Fait 2. Soit Q k une suite de polynômes réels qui, sur l intervalle [0,N], converge simplement vers la fonction caractéristique χ [0,λ] de [0,λ] et reste uniformément bornée sur [0,N]. Alors lim Tr M(Q k (u)) = F (λ). k + En effet, toujours à l aide du théorème de convergence dominée de Lebesgue et des propriétés standard des traces (de von Neumann) on a : ( ) N lim Tr M(Q k (u)) = lim Tr M Q k (λ)dp (λ) k + k + N = lim Q k (λ)df (λ) k + 0 N ( ) = lim Q k(λ) df (λ) k + = 0 N 0 0 χ [0,λ] df (λ) = F (λ). Fixons un réel λ>0. Pour tout k 1, soit R R 1+ 1 f k : k si η λ η 1+ 1 k k(η λ) siλ η λ + 1 k 1 k si λ + 1 k η. On a χ [0,λ] (η) <f k+1 (η) <f k (η) etf k converge simplement vers χ [0,λ] sur [0, + [. Pour chaque k, choisissons un polynôme Q k tel que χ [0,λ] (η) < Q k (η) <f k (η) pour tout η [0,N]. Soit E i (λ) l ensemble ordonné des valeurs propres η de u i inférieures à λ et comptées avec multiplicités.
20 Vol. 79 (2004) Asymptotique des nombres de Betti k f k 1 k λ λ+ 1 k Figure 1. La fonction f k Fait 3. E i (λ) [Γ : Γ i ] Tr M i (Q k (u i )) E i(λ + 1 k ) + θ n [Γ : Γ i ] k. En effet : 1 Tr Mi (Q k (u i )) = [Γ : Γ i ] Tr C(Q k (u i )) 1 = Q k (η). [Γ : Γ i ] η E i(n) Et on conclut alors grâce à un petit calcul, cf. [Lüc94] pp Comme dans la démonstration du théorème de Lück, le lemme clef de la preuve du théorème est : Lemme de Lück [Lüc94]. Soit g : V W une application linéaire entre deux espaces de Hilbert de dimensions finies. Soit p(t) =det(tid gg ) le polynôme caractéristique de gg.onécrit p(t) =t k q(t) où q est un polynôme ne s annulant pas en zéro. Soit A un réel supérieur à 1 tel que A g 2 et soit C un nombre
21 382 N. Bergeron et D. Gaboriau CMH réel positif tel que C q(0). SoitE(λ) l ensemble des valeurs propres η de gg vérifiant η λ et comptées avec multiplicités. Alors pour 0 <λ<1 : E(λ) E(0) dim C (V ) log(c) dim C (V )( log(λ)) + log(a) log(λ). Soit ε un réel strictement positif. Dorénavant ũ est le laplacien = n+1 n+1 + n n. On a alors : b n (Γ i \L) [Γ : Γ i ] β n (L) =β n (L i ) β n (L) = E i(0) [Γ : Γ i ] β n(l) ( Ei (0) = [Γ : Γ i ] E ) ( ) i(λ) Ei (λ) + [Γ : Γ i ] [Γ : Γ i ] Tr M i (Q k ( i )) +(Tr Mi (Q k ( i )) Tr M (Q k ( ))) +(Tr M (Q k ( )) F (λ)) + ( F (λ) β n (L)) ). Pour alléger les notations on notera ces cinq parenthèses : Π 1, Π 2,...,Π 5. Puisque la famille spectrale {P (λ)/λ [0,N]} est continue à droite, la fonction F l est aussi. Or, puisque ũ désigne dorénavant le laplacien, F (0) = β n (L). On peut donc supposer que λ est suffisamment petit pour que Π 5 ε 5. On peut appliquer le lemme de Lück en prenant g = n. Puisque n est défini sur Z, la constante C peut-être prise égale à 1 (un entier strictement positif est toujours supérieur ou égal à 1). La conclusion du lemme de Lück s écrit alors (avec dim C (C (2) n (L i )) = θ n [Γ : Γ i ]) : E i (λ) E i (0) [Γ : Γ i ] 2θ n log(n) log(λ), si λ<1. Donc quitte à diminuer λ, on peut supposer que Π 1 ε 5. D après le fait 2, on peut alors choisir k de manière àceque Π 4 ε 5. En passant à la limite en i et pour k fixé dans l inégalité du fait 3, à l aide de (17), on obtient : E i (λ) lim i + [Γ : Γ i ] Tr(Q E i (λ + 1 k k( )) lim ) i + + θ n [Γ : Γ i ] k, pour tout entier k strictement positif. En particulier, en passant cette fois àla limite en k à l aide du fait 2, pour tout η>0: F (λ) lim i + E i (λ + η) [Γ : Γ i ] lim i + E i (λ + η) [Γ : Γ i ] F (λ + η). Ainsi la continuité à droite de F permet de conclure que quitte à augmenter k, il existe un entier i 0 positif tel que pour tout i i 0, Π 2 ε 5.
22 Vol. 79 (2004) Asymptotique des nombres de Betti 383 Enfin d après (17), quitte à augmenter i 0, on peut supposer que pour tout i i 0, Π 3 ε 5. Finalement on obtient que pour tout réel ε>0, il existe un entier positif i 0 tel que pour tout i i 0, β n (L) b n(γ i \L) ε. [Γ : Γ i ] Ce qui achève la démonstration du théorème Une famille d exemples Soient A et B deux complexes simpliciaux compacts, de points base respectifs des sommets A et B. Soit K le complexe simplicial compact obtenu en ajoutant àlaréunion disjointe de A et B un simplexe a de dimension 1 en attachant ses extrémités à A et B. On prend comme point base de K le point milieu de a. Soient Γ A := π 1 (A, A )etγ B := π 1 (B, B ) les groupes fondamentaux de A et B, soit Γ := π 1 (K, ) =Γ A Γ B celui de K et soit L le revêtement universel de K, avec un point base qui relève. Théorème 4.1. Supposons que les groupes fondamentaux Γ A et Γ B sont infinis et résiduellement finis. Alors pour tout µ 0 [0, 1[, il existe une tour décroissante de sous-groupes (Γ i ) i N d indices finis dans Γ, telle que 1. Γ i+1 est normal dans Γ i 2. i N Γ i = {e} b 3. lim n(γ i\l) i [Γ:Γ i] = µ 0 b n (A)+(1 µ 0 )b (2) n (Ã, ΓA )+b (2) n ( B,Γ B ),pourn 2 b 4. lim 1(Γ i\l) i [Γ:Γ i] = µ 0 b 1 (A)+(1 µ 0 )b (2) 1 (Ã, ΓA )+b (2) 1 ( B,Γ B )+(1 µ 0 ). De plus, dans l action limite (projective) (X, µ, Γ), 5. il existe un borélien X 0 de mesure µ 0 tel que l ensemble des points fixes de tout g Γ A \{e} soit exactement X 0, 6. le fixateur de µ-presque tout point de X est un produit libre de conjugués de Γ A. L énoncé duthéorème 0.1 est une spécialisation de celui-ci, avec B T 1.Dans ce cas on pourra noter que la preuve se simplifie à plusieurs endroits. On se donne une tour de sous-groupes normaux d indices finis et d intersection triviale (Γ A i ) i N (resp. (Γ B i ) i N )deγ A (resp. Γ B ). On va construire par récurrence une suite (Γ A i ) i N (resp. (Γ B i ) i N) telle que Condition C i 1. chaque Γ A i (resp. Γ B i ) est l un des sous-groupes ΓA j (resp. Γ B j )et Γ A i (resp. Γ B i ) est un sous-groupe strict de ΓA i 4 (resp. ΓB i 4 ). On appellera A i A (resp. B i B) lesrevêtements galoisiens correspondants
23 384 N. Bergeron et D. Gaboriau CMH et a i := [Γ A :Γ A i ](resp.b i := [Γ B :Γ B i ]) leurs indices. On aura encore i NΓ A i = {e}, i N Γ B i = {e} et lim i a i = lim i b i =. On va construire par récurrence des revêtements finis p i : K i K d indices κ i. Chaque K i sera un graphe d espaces, constitué deκ i arêtes :lesrelevés de a, et d un certain nombre de sommets : les composantes connexes de p 1 i (A B) auxquels on imposera les types suivants : Condition C i 2. p 1 i (A) est constitué de r i sommets isomorphes à A et de s i sommets isomorphes à A i ; p 1 i (B) est constitué det i sommets isomorphes à B i. L indice du revêtement vérifie alors κ i = r i + s i a i = t i b i. Notons qu alors le graphe G i obtenu en écrasant en un point chaque composante connexe (=sommet) de p 1 i (A B) est connexe et possède r i + s i + t i sommets et κ i arêtes. Une application de la suite longue exacte de Mayer-Vietoris permet alors de calculer : b n (K i )=r i b n (A)+s i b n (A i )+t i b n (B i )(n 2) b 1 (K i )=r i b 1 (A)+s i b 1 (A i )+t i b 1 (B i )+(1 (r i + s i + t i )+κ i ) b 0 (K i )=1. On va faire en sorte que ri µ 0 en décroissant lorsque i, alors sibn(ai) κ i ) bn(ai) κ i = (κ i r i)b n(a i) a iκ i =( κi ri κ i a i (1 µ 0 )b (2) n (Ã, ΓA ), par application du théorème de Lück. De même, tibn(bi) κ i = tibn(bi) t ib i b (2) n ( B,Γ B ). Et enfin, (1 (ri+si+ti)+κi) κ i ( µ 0 + 1). Cela permettra d assurer les points 3. et 4. de l énoncé duthéorème. Fait 1. On choisit dans chaque revêtement A i un point base A i qui relève A i 1 et pour les autres relevés de A i 1, on choisit un chemin le reliant à A i. On fait de même pour les revêtements B i. On choisit aussi un arbre maximal dans G i. Le groupe Γ i = π 1 (K i, i )s écrit alors naturellement comme produit libre des groupes fondamentaux des composantes connexes de p 1 i (A B) et du groupe fondamental π 1 (G i, i ) du graphe G i. Il est donc formé comme produit libre d un certain nombre de groupes qu on range en 4 types : (1) t i fois π 1 (B i, B i ) ΓB i (2) un groupe libre π 1 (G i, i )=F i de rang (1 (r i + s i + t i )+κ i ) (3) r i fois π 1 (A, A ) Γ A (0) s i fois π 1 (A i, A i ) ΓA i. Construction basique. Le complexe K i+1 sera alors construit à partir de K i par le procédé suivant : On va choisir un certain nombre u i de facteurs de type m (m =1, 2, 3ou0) dans la décomposition en produit libre de π 1 (K i, i ). L isomorphisme qu ils entretiennent chacun avec G i := Γ B i, F i, Γ A ou Γ A i (selon que m = 1, 2, 3ou0)
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable
 Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Exo7 Séries de Fourier Exercices de Jean-Louis Rouget Retrouver aussi cette fiche sur wwwmaths-francefr Exercice ** * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I
Une version feuilletée du théorème de translation de Brouwer
 Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
Comment. Math. Helv. 79 (2004) 229 259 0010-2571/04/020229-31 DOI 10.1007/s00014-003-0745-9 c 2004 Birkhäuser Verlag, Basel Commentarii Mathematici Helvetici Une version feuilletée du théorème de translation
 http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
http://papeteriecharlemagne.fr/ Pour être autorisé à entrer sur le site, vous devez avoir un identifiant et un mot de passe. Saisir votre code client dans la case et le mot de passe dans la case (respecter
On remet la machine en route
 Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
Psi 945 04/05 http://blog.psi945.fr DM - corrigé On remet la machine en route Quelques calculs Exercice. Il semble raisonnable (pour enlever la racine, et sachant que ça se passera bien avec le logarithme)
1. Intégrales définies et indéfinies I. (a) Soit b > 0. Montrer que pour tout x > 0 la fonction. 2 b. F (x) = arctan bx. 1 (1 + bx) x. f(x) = x t dt.
 Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Chpitre 6 Clcul intégrl 6. Eercices. Intégrles définies et indéfinies I. () Soit b >. Montrer que pour tout > l fonction F () = b rctn b est une primitive de f() = ( + b). (b) Pour R clculer (c) Pour R
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 Eléments de calcul 296 Eléments de montage 297 Suffixes
Energie et corrélation. Systèmes de Traitement du Signal Polytech Marseille INFO 2016
 Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Energie et corrélation Systèmes de raitement du Signal Polytech Marseille INFO 016 Densité spectrale d énergie Signau à énergie finie E E (t) X y dν Densité spectrale d énergie : Densité spectrale d énergie
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 2008
 Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
Corrigé du BTS, groupement A, Nouvelle-Calédonie, novembre 8 EXERCICE 1 séries de FOURIER 1 si t α f t)= si α
Laser vert : moins de plus de 300. Acheter Laser PRODUITS CHAUDS. Pointeur Laser étanche
 Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Notre entreprise Livraison et Garantie Politique de retour Avis des clients Blog E-mail Search BIENVENUE LASER VERT LASER ROUGE LASER BLEU VIOLET POINTEUR LASER POWERPOINT Accueil CHARGEUR >> Laser Vert
Roulements à rouleaux cylindriques
 Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Roulements à rouleaux cylindriques Roulements à rouleaux cylindriques 292 Définition et aptitudes 292 Séries 292 Variantes 293 Tolérances et jeux 294 léments de calcul 296 léments de montage 297 Suffixes
Eksamen FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. Nynorsk/Bokmål
 Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Eksamen 19.11.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Nynorsk/Bokmål Oppgåve 1 Comment tu dépenses ton argent? Skriv ein liten tekst på to til fire setningar om
Corrigés des exercices du chapitre 25
 MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
MPSI Corrigés des exercices du chapitre 5 Exercice I- () () Si deg P =, alors ;, P = Doc, (P,P ',P",,P ) est ue famille écheloée e degrés doc libre Comme elle cotiet + élémets et dim K [X] = + : () (P,P
Design d'un champ de vecteurs tangents
 Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
Grenoble INP ENSIMAG École Nationale Supérieure dinformatique et de Mathématiques Appliquées Rapport de Travaux d'études et de Recherche Eectué au Laboratoire Jean Kuntzmann Design d'un champ de vecteurs
PREPARATION BREVET BLANC 1 CALCUL FRACTIONNAIRE : AIDE : d'abord transformer l'écriture du nombre entier 1. Tout nombre a peut s'écrire 1
 THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
THEME : Calcul de A : CALCUL FRACTIONNAIRE : A = ( + PREPARATION BREVET BLANC Faites ce genre de calcul en colonnes ( afin d'éviter tout oubli C'est l'exercice classique du Brevet. L'élève connaitil les
Existence of resistance forms in some (non self-similar) fractal spaces
 Existence of resistance forms in some (non self-similar) fractal spaces Patricia Alonso Ruiz D. Kelleher, A. Teplyaev University of Ulm Cornell, 12 June 2014 Motivation X Fractal Motivation X Fractal Laplacian
Existence of resistance forms in some (non self-similar) fractal spaces Patricia Alonso Ruiz D. Kelleher, A. Teplyaev University of Ulm Cornell, 12 June 2014 Motivation X Fractal Motivation X Fractal Laplacian
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
I. Évolution du commerce mondial
 I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
I. Évolution du commerce mondial En 2, la valeur des exportations mondiales de marchandises a augmenté de 2 pour cent et celle des exportations de services commerciaux de pour cent. Faits saillants de
Brosses intérieures avec manche
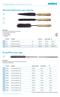 18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
18 Brosses standard Écouvillons / Brosses pour tuyaux Brosses intérieures avec manche 10 1 10 2 10 4 Pour dérouiller et nettoyer les trous ronds et ovales, ainsi que les fers ronds. ronde conique ronde
Invariants de Seiberg-Witten et Varietes. Denis AUROUX. Ecole Normale Superieure, 45 rue d'ulm, Paris, France.
 Invariants de Seiberg-Witten et Varietes Symplectiques Denis AUROUX Ecole Normale Superieure, 45 rue d'ulm, 75005 Paris, France e-mail : auroux@clipper.ens.fr Directeur : Jean Pierre BOURGUIGNON 7 novembre
Invariants de Seiberg-Witten et Varietes Symplectiques Denis AUROUX Ecole Normale Superieure, 45 rue d'ulm, 75005 Paris, France e-mail : auroux@clipper.ens.fr Directeur : Jean Pierre BOURGUIGNON 7 novembre
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide
 Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Alt for ofte blir problemer med avløpsrør i bygninger løst ved å bytte ut gamle defekte rør med nye. Dette innebærer tapphull- og utgravingsarbeide med betydelig uleilighet fra bruddstykker, støv og støyforurensing,
Clôture Métallique. Portails / Portillons / Accessoires
 Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
Clôture Métallique Portails / Portillons / Accessoires Vous trouverez dans notre gamme de clôtures métalliques tous les s nécessaires à la réalisation d une clôture de qualité grâce à aux différents s
 Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
Oppgåve 4 Vel éi av oppgåvene under, og skriv ein samanhengande tekst. a) «Il y a trop de sport dans les médias.» Synest du det er for mykje sport på TV og i avisene? Liker du best å sjå på sport på TV,
Sommaire. Montre MOVETIME Family Aperçu de la montre... 1 Touche Marche-Arrêt Retrait des bracelets Résistance à l eau...
 Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
Mode d'emploi MT40X Sommaire Montre MOVETIME Family... 1... 1 Aperçu de la montre... 1 Touche Marche-Arrêt... 1... 2... 2 Retrait des bracelets... 2... 3 Résistance à l eau... 3... 3 Obtenir une carte
Slope-Intercept Formula
 LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
DYNAMIQUE. Etude des mouvements de tangage d une transmission de puissance d hélicoptère. x r 2. y r 2. x 1. y r y r
 e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
e Cycle - ème année 8 Juin 5 DYNAIQUE Devoi de synhèse Elémens de coecions y y Eude des mouvemens de angage d une ansmission de puissance d hélicopèe. x y y x y y x, x,, x,, x cinémaique : Equaion de liaison
EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012
 Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk EKSAMENSOPPGAVE FRA1300 Fransk basisemne Vår 2012 Faglig kontakt under eksamen: Svein Eirik Fauskevåg / George Chabert
Graphs similar to strongly regular graphs
 Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Verifiable Secret-Sharing Schemes
 Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Avertissement Mode d'emploi
 Avertissement Mode d'emploi Ce polycopié ne constitue pas un cours au sens classique de ce terme, mais plutôt un support à celui qui sera dispensé en classe. En particulier, toutes les démonstrations ne
Avertissement Mode d'emploi Ce polycopié ne constitue pas un cours au sens classique de ce terme, mais plutôt un support à celui qui sera dispensé en classe. En particulier, toutes les démonstrations ne
REQUÊTE APPLICATION KLAGESKJEMA
 Voir Note explicative See Explanatory Note Se klageveiledningen NOR Numéro de dossier File-number Klage nr. COUR EUROPÉENNE DES DROITS DE L HOMME EUROPEAN COURT OF HUMAN RIGHTS DEN EUROPEISKE MENNESKERETTIGHETSDOMSTOL
Voir Note explicative See Explanatory Note Se klageveiledningen NOR Numéro de dossier File-number Klage nr. COUR EUROPÉENNE DES DROITS DE L HOMME EUROPEAN COURT OF HUMAN RIGHTS DEN EUROPEISKE MENNESKERETTIGHETSDOMSTOL
Physical origin of the Gouy phase shift by Simin Feng, Herbert G. Winful Opt. Lett. 26, (2001)
 by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
Disjoncteurs sélectifs
 233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
233 Accessoires de SLS 235 Technique 236 231 de ligne principale Meilleure sécurité, installation rapide - avec les disjoncteurs SLS Hager Hager vous propose la solution optimale pour la protection des
Second Order ODE's (2P) Young Won Lim 7/1/14
 Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
AB a donc OM = = 2 2
 ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t
ENP de CONSANINE CLASSE PREPARAOIRE/1 ère ANNEE/ PHYSIQUE 1/ UEF11 016/017 D SERIE : CINEMAIQUE DU POIN MAERIEL & MOUVEMEN RELAIF Exercice 1 : 1/ OM = xi + yj = (t 4t + 7)i + (t ) j x t 4t 7 t 4t 4 3 (t
Kneser hypergraphs. May 21th, CERMICS, Optimisation et Systèmes
 Kneser hypergraphs Frédéric Meunier May 21th, 2015 CERMICS, Optimisation et Systèmes Kneser hypergraphs m, l, r three integers s.t. m rl. Kneser hypergraph KG r (m, l): V (KG r (m, l)) = ( [m]) l { E(KG
Kneser hypergraphs Frédéric Meunier May 21th, 2015 CERMICS, Optimisation et Systèmes Kneser hypergraphs m, l, r three integers s.t. m rl. Kneser hypergraph KG r (m, l): V (KG r (m, l)) = ( [m]) l { E(KG
BEFOLKNINGSFORHOLDENE
 TILLEGGSHEFTE TIL «MEDDELELSER FRA DET STATISTISKE CENTRALBYRÄ» 1920 Journal du Bureau Central de Statistique du Royaume de Norvège 1920. Appendice. BEFOLKNINGSFORHOLDENE NORD-NORGE MED SÆRLIG HENSYN TIL
TILLEGGSHEFTE TIL «MEDDELELSER FRA DET STATISTISKE CENTRALBYRÄ» 1920 Journal du Bureau Central de Statistique du Royaume de Norvège 1920. Appendice. BEFOLKNINGSFORHOLDENE NORD-NORGE MED SÆRLIG HENSYN TIL
Oppgave 1. ( xφ) φ x t, hvis t er substituerbar for x i φ.
 Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
Des accouplements raisonnés, un élément essentiel à l amélioration génétique
 Innover aujourd hui, prospérer demain Centre Caztel, Sainte Marie Des accouplements raisonnés, un élément essentiel à l amélioration génétique Robie Morel, B.Sc., coordonnateur du secteur génétique et
Innover aujourd hui, prospérer demain Centre Caztel, Sainte Marie Des accouplements raisonnés, un élément essentiel à l amélioration génétique Robie Morel, B.Sc., coordonnateur du secteur génétique et
Moving Objects. We need to move our objects in 3D space.
 Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
Trigonometric Substitution
 Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Sur un théorème de Mertens
 manuscripta math. 08, 495 53 (00 c Springer-Verag 00 Oivier Ramaré Sur un théorème de Mertens Received: 0 March 00 Résumé. We investigate and improve on a proof of Mertens concerning the distribution of
manuscripta math. 08, 495 53 (00 c Springer-Verag 00 Oivier Ramaré Sur un théorème de Mertens Received: 0 March 00 Résumé. We investigate and improve on a proof of Mertens concerning the distribution of
Eksamen FSP5020 Fransk I PSP5013 Fransk nivå I. Nynorsk/Bokmål
 Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
Eksamen 19.05.2017 FSP5020 Fransk I PSP5013 Fransk nivå I Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid Hjelpemiddel Eksamen varer i 5 timar. Alle hjelpemiddel er tillatne, bortsett frå Internett
FRANSKLÆRERFORENINGENS STYRE
 NR. 2-2007 2 Adresses/bureau 3 Infos 4 Le mot du président 5 Grete Kleppen, traduite 7 La littérature norvégienne, en français 8 Article : Enseigner à des débutants 17 Adresses internet 18 Marte i Paris!
NR. 2-2007 2 Adresses/bureau 3 Infos 4 Le mot du président 5 Grete Kleppen, traduite 7 La littérature norvégienne, en français 8 Article : Enseigner à des débutants 17 Adresses internet 18 Marte i Paris!
6092-DV Document 5
 DOCUMENT 5 Document 5 27 Cned Document 5 28 Cned Document 5 29 Cned Document 5 30 Cned Document 5 31 Cned Document 5 32 Cned Document 5 33 Cned Document 5 34 Cned Document 5 35 Cned Document 5 36 Cned
DOCUMENT 5 Document 5 27 Cned Document 5 28 Cned Document 5 29 Cned Document 5 30 Cned Document 5 31 Cned Document 5 32 Cned Document 5 33 Cned Document 5 34 Cned Document 5 35 Cned Document 5 36 Cned
EKSAMEN FRA0502 Fransk II HØSTEN 2012
 Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk - EKSAMEN FRA0502 Fransk II HØSTEN 2012 Faglig kontakt under eksamen: Sophie Vauclin Tlf.: 73596873/ 93063953 Eksamensdato:
Norges teknisk-naturvitenskapelige universitet Institutt for moderne fremmedspråk - EKSAMEN FRA0502 Fransk II HØSTEN 2012 Faglig kontakt under eksamen: Sophie Vauclin Tlf.: 73596873/ 93063953 Eksamensdato:
Splitting the differential Riccati equation
 Splitting the differential Riccati equation Tony Stillfjord Numerical Analysis, Lund University Joint work with Eskil Hansen Innsbruck Okt 15, 2014 Outline Splitting methods for evolution equations The
Splitting the differential Riccati equation Tony Stillfjord Numerical Analysis, Lund University Joint work with Eskil Hansen Innsbruck Okt 15, 2014 Outline Splitting methods for evolution equations The
Unit Relational Algebra 1 1. Relational Algebra 1. Unit 3.3
 Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
EGENSKAPER ANVENDELSE. Technical data sheet SBE - BJELKESKO
 SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
SBE bjelkesko brukes til skjøting av trebjelker i samme plan. Bjelkeskoen kan oppta krefter i sekundærbjelkens retning. ETA-060270, UK-DoP-e060270, SE-DoP-e060270 EGENSKAPER Materiale Stålkvalitet: Galvanisert
Mes architectes ont 10 ans!
 D O S S I E R U N A R C H I T E C T E À L A M É D I AT H È Q U E 153 Mes architectes ont 10 ans! PAR MIRANDA CORBIERE En 2012, à l occasion de la journée d étude consacrée aux regards européens sur «Enfants
D O S S I E R U N A R C H I T E C T E À L A M É D I AT H È Q U E 153 Mes architectes ont 10 ans! PAR MIRANDA CORBIERE En 2012, à l occasion de la journée d étude consacrée aux regards européens sur «Enfants
Databases 1. Extended Relational Algebra
 Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
GAMME DETENTE DIRECTE SOMMAIRE. X32 monosplit Inverter Page 88. X3 multisplit Inverter Page 90. Monosplits/Multisplits
 SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
SOMMAIRE GAMME DETENTE DIRECTE X32 monosplit Inverter Page 88 Page 90 87 X32 monosplit Inverter Monosplit réversible ECO Design Applications Chauffage et climatisation, dans le résidentiel ou le tertiaire
Maple Basics. K. Cooper
 Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
Lattice Boltzmann Method for ow in porous media. Samuel Corre
 Lattice Boltzmann Method for ow in porous media. avec Aziz Belmiloudi IRMAR-INSA, Rennes. Samuel.Corre@insa-rennes.fr 4 ieme école EGRIN, 25 Mai 2016. Contexte général Écoulements incompressibles en milieu
Lattice Boltzmann Method for ow in porous media. avec Aziz Belmiloudi IRMAR-INSA, Rennes. Samuel.Corre@insa-rennes.fr 4 ieme école EGRIN, 25 Mai 2016. Contexte général Écoulements incompressibles en milieu
RAPPORT DE SYNTHESE DES ACTIVITES DE LA COMMUNAUTE EUROPENNE DANS LE CHAMP DES DROITS DE L HOMME, DE LA BONNE GOUVERNANCE ET DE LA DEMOCRATIE
 RAPPORT DE SYNTHESE DES ACTIVITES DE LA COMMUNAUTE EUROPENNE DANS LE CHAMP DES DROITS DE L HOMME, DE LA BONNE GOUVERNANCE ET DE LA DEMOCRATIE Consultants pour le développement et l'environnement c:\temp\iecache\rapport
RAPPORT DE SYNTHESE DES ACTIVITES DE LA COMMUNAUTE EUROPENNE DANS LE CHAMP DES DROITS DE L HOMME, DE LA BONNE GOUVERNANCE ET DE LA DEMOCRATIE Consultants pour le développement et l'environnement c:\temp\iecache\rapport
Lie 2-Groups, Lie 2-Algebras, and Loop Groups
 Lie 2-Groups, Lie 2-Algebras, and Loop Groups Alissa S. Crans Joint work with: John Baez Urs Schreiber & Danny Stevenson in memory of Saunders Mac Lane April 8, 2006 Internalization Often a useful first
Lie 2-Groups, Lie 2-Algebras, and Loop Groups Alissa S. Crans Joint work with: John Baez Urs Schreiber & Danny Stevenson in memory of Saunders Mac Lane April 8, 2006 Internalization Often a useful first
Kommunikasjonsperm. Overvåking og undersøkelser side 1. Smerter side 2. Naturlige funksjoner, eliminasjon side 3. Sengeleie og stell side 4
 Kommunikasjonsperm Fransk Overvåking og undersøkelser side 1 Smerter side 2 Naturlige funksjoner, eliminasjon side 3 Sengeleie og stell side 4 Mat, drikke kvalme side 5 Bevegelse, syn, temperatur side
Kommunikasjonsperm Fransk Overvåking og undersøkelser side 1 Smerter side 2 Naturlige funksjoner, eliminasjon side 3 Sengeleie og stell side 4 Mat, drikke kvalme side 5 Bevegelse, syn, temperatur side
Tri sélectif de déchets. Kildesortering
 Tri sélectif de déchets Dans notre commune, on est légalement obligé de trier les déchets. Le but est de les recycler et ainsi contribuer à un meilleur environnement pour nous tous. Voici une description
Tri sélectif de déchets Dans notre commune, on est légalement obligé de trier les déchets. Le but est de les recycler et ainsi contribuer à un meilleur environnement pour nous tous. Voici une description
Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo. Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo
 Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo L HISTOIRE DU LYCEE SKOLENS HISTORIE Recherches / Etterforskning : Paul Monceyron
Bienvenue au 50 ème anniversaire du Lycée René Cassin d Oslo Velkommen til det 50. jubileumet til Den Franske Skolen i Oslo L HISTOIRE DU LYCEE SKOLENS HISTORIE Recherches / Etterforskning : Paul Monceyron
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
IUFM DE BOURGOGNE DIJON
 IUFM DE BOURGOGNE DIJON!" # # $ % & " " ' 0362024 E Introduction 1 1. Les langues étrangères à l école : 2 1.1. L historique des instructions officielles.2 1.2. Les programmes de février 2002...3 1.3.
IUFM DE BOURGOGNE DIJON!" # # $ % & " " ' 0362024 E Introduction 1 1. Les langues étrangères à l école : 2 1.1. L historique des instructions officielles.2 1.2. Les programmes de février 2002...3 1.3.
LE GENRE DU LOCUTEUR ET DE L ALLOCUTAIRE DANS LES SYSTÈMES PRONOMINAUX : GENRE GRAMMATICAL ET INDEXICALITÉ DU GENRE
 Françoise Rose Bulletin de la Société de linguistique de Paris, t. CVIII (2013), fasc. 1, p. 381-417 doi:10.2143/bsl.108.1.3019222 LE GENRE DU LOCUTEUR ET DE L ALLOCUTAIRE DANS LES SYSTÈMES PRONOMINAUX
Françoise Rose Bulletin de la Société de linguistique de Paris, t. CVIII (2013), fasc. 1, p. 381-417 doi:10.2143/bsl.108.1.3019222 LE GENRE DU LOCUTEUR ET DE L ALLOCUTAIRE DANS LES SYSTÈMES PRONOMINAUX
TECHNOLOGIE POUR CHAUDIERES DE BRUNNER. Kamin-Kessel Eck 57/67/44 Porte relevable (easy-lift) État: made in germany
 TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
TCHNOLOGI POUR CHAUDIRS D BRUNNR KaminKessel ck 57/67/44 Porte relevable (easylift) État: 01.12.2016 made in germany KaminKessel ck 57/67/44 Porte relevable (easylift) S securité départ 1/2" fil.ext. securité
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
Relative pro-l completions of mapping class groups
 Journal of Algebra 321 2009) 3335 3374 www.elsevier.com/locate/jalgebra Relative pro-l completions of mapping class groups Richard Hain a,, Makoto Matsumoto b a Department of Mathematics, Duke University,
Journal of Algebra 321 2009) 3335 3374 www.elsevier.com/locate/jalgebra Relative pro-l completions of mapping class groups Richard Hain a,, Makoto Matsumoto b a Department of Mathematics, Duke University,
m15/1/aynor/hp2/nor/tz0/xx Monday 11 May 2015 (morning) Lundi 11 mai 2015 (matin) Lunes 11 de mayo de 2015 (mañana) 2 hours / 2 heures / 2 horas
 m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
m15/1/aynor/hp2/nor/tz0/xx Norwegian A: language and literature Higher level Paper 2 Norvégien A : langue et littérature Niveau supérieur Épreuve 2 Noruego A: lengua y literatura Nivel superior Prueba
Gustave Juvet ( ) Un Pionnier Oublié desétudes Cliffordiennes
 Adv. appl. Clifford alg. 19 (2009), 547 584 c 2009 Birkhäuser Verlag Basel/Switzerland 0188-7009/030547-38, published online October 22, 2009 DOI 10.1007/s00006-009-0183-2 Advances in Applied Clifford
Adv. appl. Clifford alg. 19 (2009), 547 584 c 2009 Birkhäuser Verlag Basel/Switzerland 0188-7009/030547-38, published online October 22, 2009 DOI 10.1007/s00006-009-0183-2 Advances in Applied Clifford
Enchanté 1. Grammatikktema i kapittel 12
 Enchanté 1 Grammatikktema i kapittel 12 Repetisjon Verbtider presens, passé composé, imperativ, framtid med aller Imperativ Artikler, adjektiv, eiendomsord og preposisjoner Direkte og indirekte objektspronomen
Enchanté 1 Grammatikktema i kapittel 12 Repetisjon Verbtider presens, passé composé, imperativ, framtid med aller Imperativ Artikler, adjektiv, eiendomsord og preposisjoner Direkte og indirekte objektspronomen
Mise à jour des marges requises
 Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
Mise à jour des marges requises Table des matières 1. Mise en place... 2 1.1 Chronologie des évènements... 2 2. Marges requises... 3 2.1 Marges requises pour les comptes dénominés en USD... 3 2.2 Marges
Daniel K. Schneider - David Ott - Vivian Synteta Version: 0.4 (modifié le 15/8/01 par DKS)
 &DVFDGLQJ6W\OH6KHHWV &DVFDGLQJ6W\OH6KHHWV &RGH 2ULJLQDX[ XUOhttp://tecfa.unige.ch/guides/tie/html/css-into/css-intro.html XUOhttp://tecfa.unige.ch/guides/tie/pdf/files/css-intro.pdf $XWHXUVHWYHUVLRQ Daniel
&DVFDGLQJ6W\OH6KHHWV &DVFDGLQJ6W\OH6KHHWV &RGH 2ULJLQDX[ XUOhttp://tecfa.unige.ch/guides/tie/html/css-into/css-intro.html XUOhttp://tecfa.unige.ch/guides/tie/pdf/files/css-intro.pdf $XWHXUVHWYHUVLRQ Daniel
Bobine à noyau de fer
 1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
1 Bobne à noyau de fer Usage en contnu Bobne à noyau de fer Introducton I mpose H Pertes unquement dans les bobnages Usage en alternatf V mpose B Pertes dans le matérau 2 Bobne à noyau de fer Conventons
SVM and Complementary Slackness
 SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
St.prp. nr. 3 ( )
 St.prp. nr. 3 (1999-200) Om samtykke til å setje i kraft ein tilleggsavtale til skatteavtalen mellom Noreg og Frankrike av 19. desember 1980 med tilleggsavtalar av 14. november 1984 og 7. april 1995, underskriven
St.prp. nr. 3 (1999-200) Om samtykke til å setje i kraft ein tilleggsavtale til skatteavtalen mellom Noreg og Frankrike av 19. desember 1980 med tilleggsavtalar av 14. november 1984 og 7. april 1995, underskriven
Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2
![Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2 Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2](/thumbs/77/75859899.jpg) Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Onsdag 6. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Onsdag 6. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
Qi-Wu-Zhang model. 2D Chern insulator. León Martin. 19. November 2015
 Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Qi-Wu-Zhang model 2D Chern insulator León Martin 19. November 2015 Motivation Repeat: Rice-Mele-model Bulk behavior Edge states Layering 2D Chern insulators Robustness of edge states Motivation topological
Trust region methods: global/local convergence, approximate January methods 24, / 15
 Trust region methods: global/local convergence, approximate methods January 24, 2014 Trust region methods: global/local convergence, approximate January methods 24, 2014 1 / 15 Trust-region idea Model
Trust region methods: global/local convergence, approximate methods January 24, 2014 Trust region methods: global/local convergence, approximate January methods 24, 2014 1 / 15 Trust-region idea Model
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag 7. juni
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag 7. juni
Romansk Forum Nr
 Romansk Forum Nr. 13-2001 Forord 1 Henriksen, Turid: La mise en scène de l'article partitif 3-18 Rydning, Antin Fougner: La SYNECDOQUE - concept clé en traduction 19-41 Trandem, Beate: Å skrive det sagte
Romansk Forum Nr. 13-2001 Forord 1 Henriksen, Turid: La mise en scène de l'article partitif 3-18 Rydning, Antin Fougner: La SYNECDOQUE - concept clé en traduction 19-41 Trandem, Beate: Å skrive det sagte
Dynamic Programming Longest Common Subsequence. Class 27
 Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
Neural Network. Sensors Sorter
 CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
Årsplan for 9. klasse i Fransk (2008 2009)
 Årsplan for 9. klasse i Fransk (2008 2009) Lærer: Serge Licius Tekstbok: Chouette Nouvelle Mål for faget dem til og fransk språkbruk og egen kultur A fremme elevenes innsikt i det s evne til å ta hånd
Årsplan for 9. klasse i Fransk (2008 2009) Lærer: Serge Licius Tekstbok: Chouette Nouvelle Mål for faget dem til og fransk språkbruk og egen kultur A fremme elevenes innsikt i det s evne til å ta hånd
www.philips.com/avent
 Register your product and get support at www.philips.com/avent SCD505 EN User manual 3 DA Brugervejledning 13 DE Benutzerhandbuch 23 ES Manual del usuario 47 SV Användarhandbok 121 AR 141 Innholdsfortegnelse
Register your product and get support at www.philips.com/avent SCD505 EN User manual 3 DA Brugervejledning 13 DE Benutzerhandbuch 23 ES Manual del usuario 47 SV Användarhandbok 121 AR 141 Innholdsfortegnelse
1 Aksiomatisk definisjon av vanlige tallsystemer
 Notat XX for MAT1140 1 Aksiomatisk definisjon av vanlige tallsystemer 1.1 Aksiomer Vi betrakter en mengde R, utstyrt med to avbild- Algebraiske aksiomer. ninger: addisjon { R R R, (x, y) x + y. { R R R,
Notat XX for MAT1140 1 Aksiomatisk definisjon av vanlige tallsystemer 1.1 Aksiomer Vi betrakter en mengde R, utstyrt med to avbild- Algebraiske aksiomer. ninger: addisjon { R R R, (x, y) x + y. { R R R,
Noen tallteoretiske resultater av Fermat
 Noen tallteoretiske resultater av Fermat Arne B. Sletsjøe Universitetet i Oslo Pierre de Fermat (1601/1607-1665) Fermats lille teorem Fermats rettvinklede teorem Fermats siste teorem Cubum autem in duos
Noen tallteoretiske resultater av Fermat Arne B. Sletsjøe Universitetet i Oslo Pierre de Fermat (1601/1607-1665) Fermats lille teorem Fermats rettvinklede teorem Fermats siste teorem Cubum autem in duos
Compress Bosch Compress LW-Tx C 35 C A ++ A + A B C D E F G. db kw kw /2013
 Bosch 5000 7 LW-Tx 55 C 35 C + A B C D E F G 47 8 9 7 8 7 7 db kw kw db 2015 811/2013 Bosch 5000 7 LW-Tx ++ + + + + + A B C D E F G 2015 811/2013 Bosch 5000 7 LW-Tx Opplysningene er i samsvar med kravene
Bosch 5000 7 LW-Tx 55 C 35 C + A B C D E F G 47 8 9 7 8 7 7 db kw kw db 2015 811/2013 Bosch 5000 7 LW-Tx ++ + + + + + A B C D E F G 2015 811/2013 Bosch 5000 7 LW-Tx Opplysningene er i samsvar med kravene
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
Câble de mesure en PVC CF211
 CF211 igupur PUR TPE Câble de mesure en CF211 Pour les sollicitations moyennes Gaine extérieure en Version blindée Résistance aux huiles Non propagateur de flamme Données dynamiques Rayon de courbure chaîne
CF211 igupur PUR TPE Câble de mesure en CF211 Pour les sollicitations moyennes Gaine extérieure en Version blindée Résistance aux huiles Non propagateur de flamme Données dynamiques Rayon de courbure chaîne
BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN. Langue vivante 2
 Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
Session 2019 BACCALAURÉAT GÉNÉRAL ET TECHNOLOGIQUE NORVÉGIEN Langue vivante 2 Séries ES/S Durée de l épreuve : 2 heures coefficient : 2 Série L langue vivante obligatoire (LVO) Durée de l épreuve : 3 heures
Eksamen 21.05.2013. FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister. http://eksamensarkiv.net/
 Eksamen 21.05.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Oppgåve 1 Vous aimez voyager? Liker du å reise? Kvifor / kvifor ikkje? Skriv ein liten tekst på to til fire
Eksamen 21.05.2013 FSP5020/PSP5013 Fransk nivå I Elevar og privatistar / Elever og privatister Oppgåve 1 Vous aimez voyager? Liker du å reise? Kvifor / kvifor ikkje? Skriv ein liten tekst på to til fire
Speed Racer Theme. Theme Music: Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz. September 9, 2011 Physics 131 Prof. E. F.
 September 9, 2011 Physics 131 Prof. E. F. Redish Theme Music: Speed Racer Theme Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz 1 Reading questions Are the lines on the spatial graphs representing
September 9, 2011 Physics 131 Prof. E. F. Redish Theme Music: Speed Racer Theme Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz 1 Reading questions Are the lines on the spatial graphs representing
Rapport annuel 2012. p. 4 Reise til Frankrike?... p. 8 Felles språkdag... p. 12 Examens du BI. p. 16 Travailler du vocabulaire. p. 20 Et plus...
 Rapport annuel 2012. p. 4 Reise til Frankrike?... p. 8 Felles språkdag... p. 12 Examens du BI. p. 16 Travailler du vocabulaire. p. 20 Et plus... Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE SOMMAIRE/INNHOLD:
Rapport annuel 2012. p. 4 Reise til Frankrike?... p. 8 Felles språkdag... p. 12 Examens du BI. p. 16 Travailler du vocabulaire. p. 20 Et plus... Le bureau/ Sommaire FRANSKLÆRERFORENINGENS STYRE SOMMAIRE/INNHOLD:
Comportement du discordantiel «ne» dans six points d enquêtes du corpus PFC
 Comportement du discordantiel «ne» dans six points d enquêtes du corpus PFC Marie Therese Barkved Sous la direction de Chantal Lyche Masteroppgave i fransk språk, avlagt våren 2011 ved Det Humanistiske
Comportement du discordantiel «ne» dans six points d enquêtes du corpus PFC Marie Therese Barkved Sous la direction de Chantal Lyche Masteroppgave i fransk språk, avlagt våren 2011 ved Det Humanistiske

 LIBER BVEL MAGI SVB FIGVRÂ I $
LIBER BVEL MAGI SVB FIGVRÂ I $