Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai :00 13:00
|
|
|
- Børge Markussen
- 7 år siden
- Visninger:
Transkript
1 NTNU Side 1 av 2 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai :00 13:00 Tillatte hjelpemidler: Alternativ C Standard kalkulator (ifølge NTNU s liste). K. Rottman: Matematisk formelsamling (alle språkutgaver). Barnett & Cronin: Mathematical Formulae There is also an english version of this exam set. Dette oppgavesettet er på 2 sider. Oppgave 1. Bevegelse i et ekspanderende univers Friedmann-Lemaître-Robertson-Walker metrikken kan for k = 0 uttrykkes ved linje-elementet ds 2 = dt 2 + a(t) 2 ( dx 2 + dy 2 + dz 2), (1) når vi bruker enheter der lyshastigheten c = 1. Geodetisk bevegelse kan generelt utledes fra Lagrangefunksjonen L = 1 2 g µν(x)ẋ µ ẋ ν. (2) der startbetingelsene må oppfylle betingelsen g µν ẋ µ ẋ ν = 1 for massive partikler, og g µν ẋ µ ẋ ν = 0 for masseløse partikler (lys). Her betyr derivasjon med hensyn til egentid τ. a) Hvilke antagelser ligger bak utledningen av linje-elementet (1), og det mer generelle linjeelementet der k 0? b) Finn Euler-Lagrange ligningene for bevegelse i Friedmann-Lemaître-Robertson-Walker-geometrien når k = 0. c) De geodetiske ligningene kan generelt skrives på formen ẍ µ + Γ µ νλẋν ẋ λ = 0. (3) Bruk resultatene fra forrige punkt til å finne konneksjonskoeffisentene Γ µ νλ. d) Lagrange-funksjonen er i dette tilfellet invariant under transformasjonen x i x i + ɛ for x i = x, y, z. Bruk Nöthers teorem til å finne de tilhørende konserverte størrelsene. Vis at resultatet er konsistent med de geodetiske ligningene du har funnet. e) Lagrange-funksjonen er invariant under transformasjonen τ τ + ɛ. Hva er den tilhörende konserverte störrelsen (som kan utledes ved bruk av Nöthers teorem)? f) Bruk resultatene over til å finne dxi dt uttrykt ved startverdien ved t = t 0, og funksjonen a.
2 Eksamen i FY3452 Gravitasjon og kosmologi, Side 2 av 2 Oppgave 2. Friedmann-ligningene med konsekvenser Friedmann s to ligninger for universets dynamikk kan (i enheter der c = 1) formuleres som G = + k a a 2 = 8π 3 G N ε, (4) G = + k a a 2 + 2a a = 8πG N p, (5) der betyr derivasjon med hensyn på kosmisk tid t, og G N er Newtons konstant. Vi har antatt en energy-impuls tensor av formen ε T µ ν = 0 p p 0. (6) p a) Konsistens av Einstein-ligningene G µ ν = 8πG N T µ ν setter generelt en betingelse på energiimpuls tensoren T µ ν. Hvilken betingelse er det? b) I denne oppgaven skal du utlede denne betingelsen ved direkte manipulasjon av ligningene (4) og (5): Deriver ligning (4) med hensyn på t, og bruk deretter ligning (4) og (5) til å eliminere alle ledd som involverer a a og k a 2 fra resultatet. c) Vis at uttrykket fra forrige punkt kan skrives på formen d dt εa3 + p d dt a3 = 0. (7) Hva er den fysiske tolkningen av denne ligningen? d) Anta tilstandsligningen p = wε, der w er en konstant. Vis at ligning (7) da kan brukes til å finne en sammenheng mellom ε(t)/ε(t 0 ) og a(t)/a(t 0 ). Gi denne sammenhengen. e) Bruk sammenhengen du fant i forrige punkt til å erstatte høyresiden av ligning (4), slik at du får en ligning der a(t) er den eneste tidsavhengige størrelsen som inngår. f) Sett tilslutt k = 0 og finn den eksplisitte løsningen av ligningen du fant i forrige punkt. Se spesielt på tilfellene w = 1 3, w = 0, og w = 1. Oppgave 3. Noen astronomiske fakta a) Hva er avstanden fra jorda til sola? b) Hva er jordas hastighet rundt sola? c) Hva er avstanden fra Jupiter til sola? d) Hva er solas radius? e) Hvor er massesenteret til solsystemet? f) Hva er den astronomiske enheten (a.u)? g) Hvor langt er et lysår? h) Hvor langt er et parsec? i) Hva er avstanden til vår nærmeste (nest etter sola) stjerne? j) Hva er avstanden fra sola til sentrum av vår galakse? k) Hva er størrelsen på vår galakse? l) Hva er avstanden til vår nærmeste spiralgalakse? m) Hva er universets alder?
3 Some expressions which may be of use Euler-Lagrange equations The Euler-Lagrange equations for a field theory described by the Lagrangian L = L(ϕ a, µ ϕ a, x) are ( ) L µ = L. (8) ( µ ϕ a ) ϕ a The corresponding equations for point particle mechanics is obtained by restricting µ to only a time derivative d/dt. Nöther s theorem Assume the action is invariant under the continuous transformations ϕ a ϕ a + ε δϕ a + O(ε 2 ), more precisely that L L + ε µ Λ µ + O(ɛ 2 ) under this transformation. Then there is an associated conserved current, J µ = L ( µ ϕ a ) δϕ a Λ µ. (9) I.e., µ J µ = 0. The corresponding expression for point particle mechanics is obtained by restricting µ to only a time derivative d/dt.
4 NTNU Page 1 of 3 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: Exam in FY3452 GRAVITATION AND COSMOLOGY Saturday May 19, :00 13:00 Allowed help: Alternativ C Standard calculator (according to list by NTNU). K. Rottman: Matematisk formelsamling (all language editions). Barnett & Cronin: Mathematical Formulae Det finnes også en norsk versjon av dette eksamenssettet. This problemset consists of 3 pages. Problem 1. Motion in an expanding universe The Friedmann-Lemaître-Robertson-Walker metric can for k = 0 be expressed by the line element ds 2 = dt 2 + a(t) 2 ( dx 2 + dy 2 + dz 2), (1) when we use units where the speed of light c = 1. Geodetic motion can in general be derived from the Lagrange function L = 1 2 g µν(x)ẋ µ ẋ ν. (2) where the initial conditions must satisfy the condition g µν ẋ µ ẋ ν = 1 for massive particles, and g µν ẋ µ ẋ ν = 0 for massless particles (light). Here means differensiation with respect to egentime τ. a) Which assumptions are behind the derivation of the line element (1), and the more general line element where k 0? b) Find the Euler-Lagrange equations for motion in the Friedmann-Lemaître-Robertson-Walker geometry when k = 0. c) The geodetic equation can in general be written in the form ẍ µ + Γ µ νλẋν ẋ λ = 0. (3) Use the results of the previous point to find the connection coefficients Γ µ νλ. d) The Lagrange function is in this case invariant under the transformation x i x i + ɛ for x i = x, y, z. Use the Nöther theorem to find the corresponding conserved quantities. Show that the result is consistent with the geodetic equations you have found. e) The Lagrange function is invariant under the transformation τ τ + ɛ. What is the corresponding conserved quantity (which can be derived by use of the Nöther theorem)? f) Use the results above to find dxi dt a. expressed by the starting values at t = t 0, and the function
5 Exam in FY3452 Gravitation and cosmology, Page 2 of 3 Problem 2. The Friedmann equations and consequences The two Friedmann equations describing the dynamics of the universe can (in units where c = 1) be formulated as G = + k a a 2 = 8π 3 G N ε, (4) G = + k a a 2 + 2a a = 8πG N p, (5) where means differentiation with respect to cosmic time t, and G N is Newton s constant. We have assumed an energy-momentum tensor of the form ε T µ ν = 0 p p 0. (6) p a) Consistency of the Einstein equations G µ ν = 8πG N T µ ν in general impose a condition on the energy momentum tensor T µ ν. Which condition is it? b) In this problem you shall derive the condition by direct manipulation of equations (4) and (5): Differentiate equation (4) with respect to t, and next use equations (4) and (5) to eliminate all terms which involve a a and k a 2 from the result. c) Show that the expression from the previous point can be written on the form What is the physical interpretation of this equation? d dt εa3 + p d dt a3 = 0. (7) d) Assume the equation of state p = wε, where w is a constant. Show that we then may use (7) to find a connection between ε(t)/ε(t 0 ) and a(t)/a(t 0 ). Give this connection. e) Use the connection you found in the previous point to replace the right hand side of equation (4), to obtain an equation where a(t) is the only time dependent quantity. f) Finally set k = 0 and find the explicit solution of the equation you found in the previous point. Consider in particular the cases w = 1 3, w = 0, and w = 1. Problem 3. Some astronomical facts a) What is the distance from the earth to the Sun? b) What is the speed of the earth around the Sun? c) What is the distance from Jupiter to the Sun? d) What is the radius of the Sun? e) Where is the center-of-mass of the solar system? f) What is the astronomical unit (a.u)? g) How long is a lightyear? h) How long is a parsec? i) What is the distance to the closest (next to the sun) star?
6 Exam in FY3452 Gravitation and cosmology, Page 3 of 3 j) What is the distance from the sun to the center of our galaxy? k) What is the size of our galaxy? l) What is the distance to the nearest spiral galaxy? m) What is the age of the universe?
7 Some expressions which may be of use Euler-Lagrange equations The Euler-Lagrange equations for a field theory described by the Lagrangian L = L(ϕ a, µ ϕ a, x) are ( ) L µ = L. (8) ( µ ϕ a ) ϕ a The corresponding equations for point particle mechanics is obtained by restricting µ to only a time derivative d/dt. Nöther s theorem Assume the action is invariant under the continuous transformations ϕ a ϕ a + ε δϕ a + O(ε 2 ), more precisely that L L + ε µ Λ µ + O(ɛ 2 ) under this transformation. Then there is an associated conserved current, J µ = L ( µ ϕ a ) δϕ a Λ µ. (9) I.e., µ J µ = 0. The corresponding expression for point particle mechanics is obtained by restricting µ to only a time derivative d/dt.
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august :00 13:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
Eksamen i FY3466 KVANTEFELTTEORI II Tirsdag 20. mai :00 13:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 71 70 Eksamen i FY3466 KVANTEFELTTEORI II Tirsdag 20. mai 2008 09:00 13:00 Tillatte
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 71 70 Eksamen i FY3466 KVANTEFELTTEORI II Tirsdag 20. mai 2008 09:00 13:00 Tillatte
Eksamen i TFY4230 STATISTISK FYSIKK Onsdag 21. desember, :00 19:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 71 70 Eksamen i TFY4230 STATISTISK FYSIKK Onsdag 21. desember, 2011 15:00 19:00
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 71 70 Eksamen i TFY4230 STATISTISK FYSIKK Onsdag 21. desember, 2011 15:00 19:00
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
Løsningsforslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Torsdag 8. august 2013
 NTNU Sie 1 av 6 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY345 GRAVITASJON OG KOSMOLOGI Torsag 8. august 013 Dette løsningsforslaget er på 6 sier.
NTNU Sie 1 av 6 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY345 GRAVITASJON OG KOSMOLOGI Torsag 8. august 013 Dette løsningsforslaget er på 6 sier.
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fredag 24. mai :00 13:00
 NTNU Side 1 av 2 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Kåe Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 09:00 13:00 Tillatte hjelpemidle:
NTNU Side 1 av 2 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Kåe Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 09:00 13:00 Tillatte hjelpemidle:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Onsdag 6. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Onsdag 6. desember
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Utsatt eksamen i: ECON2915 Vekst og næringsstruktur Eksamensdag: 07.12.2012 Tid for eksamen: kl. 09:00-12:00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
1 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Utsatt eksamen i: ECON2915 Vekst og næringsstruktur Eksamensdag: 07.12.2012 Tid for eksamen: kl. 09:00-12:00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Physical origin of the Gouy phase shift by Simin Feng, Herbert G. Winful Opt. Lett. 26, (2001)
 by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON20/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Fredag 2. mai
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON20/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Fredag 2. mai
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag 8. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag 8. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Date of exam: Friday, May
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Date of exam: Friday, May
FYSMEK1110 Eksamensverksted 23. Mai :15-18:00 Oppgave 1 (maks. 45 minutt)
 FYSMEK1110 Eksamensverksted 23. Mai 2018 14:15-18:00 Oppgave 1 (maks. 45 minutt) Page 1 of 9 Svar, eksempler, diskusjon og gode råd fra studenter (30 min) Hva får dere poeng for? Gode råd fra forelesere
FYSMEK1110 Eksamensverksted 23. Mai 2018 14:15-18:00 Oppgave 1 (maks. 45 minutt) Page 1 of 9 Svar, eksempler, diskusjon og gode råd fra studenter (30 min) Hva får dere poeng for? Gode råd fra forelesere
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSIEE I OSLO ØKONOMISK INSIU Eksamen i: ECON320/420 Mathematics 2: Calculus and Linear Algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag:. desember 207 Sensur kunngjøres:
UNIVERSIEE I OSLO ØKONOMISK INSIU Eksamen i: ECON320/420 Mathematics 2: Calculus and Linear Algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag:. desember 207 Sensur kunngjøres:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl.
 1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
Exam in Quantum Mechanics (phys201), 2010, Allowed: Calculator, standard formula book and up to 5 pages of own handwritten notes.
 Exam in Quantum Mechanics (phys01), 010, There are 3 problems, 1 3. Each problem has several sub problems. The number of points for each subproblem is marked. Allowed: Calculator, standard formula book
Exam in Quantum Mechanics (phys01), 010, There are 3 problems, 1 3. Each problem has several sub problems. The number of points for each subproblem is marked. Allowed: Calculator, standard formula book
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, :00 13:00
 NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
Gradient. Masahiro Yamamoto. last update on February 29, 2012 (1) (2) (3) (4) (5)
 Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill
Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag 7. juni
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag 7. juni
EKSAMENSOPPGAVE I SØK 1002 INNFØRING I MIKROØKONOMISK ANALYSE
 Norges teknisk-naturvitenskapelige universitet Institutt for samfunnsøkonomi EKSAMENSOPPGAVE I SØK 1002 INNFØRING I MIKROØKONOMISK ANALYSE Faglig kontakt under eksamen: Hans Bonesrønning Tlf.: 9 17 64
Norges teknisk-naturvitenskapelige universitet Institutt for samfunnsøkonomi EKSAMENSOPPGAVE I SØK 1002 INNFØRING I MIKROØKONOMISK ANALYSE Faglig kontakt under eksamen: Hans Bonesrønning Tlf.: 9 17 64
Slope-Intercept Formula
 LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON420 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON420 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON3120/4120 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON3120/4120 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Tirsdag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag:
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON1410 - Internasjonal økonomi Exam: ECON1410 - International economics Eksamensdag: 18.06.2013 Date of exam: 18.06.2013 Tid for eksamen: kl.
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON1410 - Internasjonal økonomi Exam: ECON1410 - International economics Eksamensdag: 18.06.2013 Date of exam: 18.06.2013 Tid for eksamen: kl.
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
ECON3120/4120 Mathematics 2, spring 2004 Problem solutions for the seminar on 5 May Old exam problems
 Department of Economics May 004 Arne Strøm ECON0/40 Mathematics, spring 004 Problem solutions for the seminar on 5 May 004 (For practical reasons (read laziness, most of the solutions this time are in
Department of Economics May 004 Arne Strøm ECON0/40 Mathematics, spring 004 Problem solutions for the seminar on 5 May 004 (For practical reasons (read laziness, most of the solutions this time are in
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS English Exam: ECON2915 Economic Growth Date of exam: 25.11.2014 Grades will be given: 16.12.2014 Time for exam: 09.00 12.00 The problem set covers 3 pages Resources
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS English Exam: ECON2915 Economic Growth Date of exam: 25.11.2014 Grades will be given: 16.12.2014 Time for exam: 09.00 12.00 The problem set covers 3 pages Resources
0:7 0:2 0:1 0:3 0:5 0:2 0:1 0:4 0:5 P = 0:56 0:28 0:16 0:38 0:39 0:23
 UTKAST ENGLISH VERSION EKSAMEN I: MOT100A STOKASTISKE PROSESSER VARIGHET: 4 TIMER DATO: 16. februar 2006 TILLATTE HJELPEMIDLER: Kalkulator; Tabeller og formler i statistikk (Tapir forlag): Rottman: Matematisk
UTKAST ENGLISH VERSION EKSAMEN I: MOT100A STOKASTISKE PROSESSER VARIGHET: 4 TIMER DATO: 16. februar 2006 TILLATTE HJELPEMIDLER: Kalkulator; Tabeller og formler i statistikk (Tapir forlag): Rottman: Matematisk
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON420 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt eksamen i: ECON420 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Mandag
Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with.
![Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with. Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with.](/thumbs/80/81672304.jpg) Solutions #1 1. a Show that the path γ : [, π] R 3 defined by γt : cost ı sint j sint k lies on the surface z xy. b valuate y 3 cosx dx siny z dy xdz where is the closed curve parametrized by γ. Solution.
Solutions #1 1. a Show that the path γ : [, π] R 3 defined by γt : cost ı sint j sint k lies on the surface z xy. b valuate y 3 cosx dx siny z dy xdz where is the closed curve parametrized by γ. Solution.
Unit Relational Algebra 1 1. Relational Algebra 1. Unit 3.3
 Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
EKSAMENSOPPGAVE I FAG TKP 4105
 EKSAMENSOPPGAVE I FAG TKP 4105 Faglig kontakt under eksamen: Sigurd Skogestad Tlf: 913 71669 (May-Britt Hägg Tlf: 930 80834) Eksamensdato: 08.12.11 Eksamenstid: 09:00 13:00 7,5 studiepoeng Tillatte hjelpemidler:
EKSAMENSOPPGAVE I FAG TKP 4105 Faglig kontakt under eksamen: Sigurd Skogestad Tlf: 913 71669 (May-Britt Hägg Tlf: 930 80834) Eksamensdato: 08.12.11 Eksamenstid: 09:00 13:00 7,5 studiepoeng Tillatte hjelpemidler:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Mathematics 2: Calculus and linear algebra Exam: ECON320/420 Mathematics 2: Calculus and linear algebra Eksamensdag: Tirsdag 30. mai 207
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON320/420 Mathematics 2: Calculus and linear algebra Exam: ECON320/420 Mathematics 2: Calculus and linear algebra Eksamensdag: Tirsdag 30. mai 207
Løsningsforslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fredag 24. mai 2013
 NTNU Side 1 av 4 Institutt fo fysikk Fakultet fo fysikk, infomatikk og matematikk Løsningsfoslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 Dette løsningsfoslaget e på 4 side. Oppgave
NTNU Side 1 av 4 Institutt fo fysikk Fakultet fo fysikk, infomatikk og matematikk Løsningsfoslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 Dette løsningsfoslaget e på 4 side. Oppgave
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON2200 Matematikk 1/Mikroøkonomi 1 Exam: ECON2200 Mathematics 1/Microeconomics 1 Eksamensdag: Fredag 26. mai 2006 Sensur kunngjøres: Fredag 16. juni
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON2200 Matematikk 1/Mikroøkonomi 1 Exam: ECON2200 Mathematics 1/Microeconomics 1 Eksamensdag: Fredag 26. mai 2006 Sensur kunngjøres: Fredag 16. juni
Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni :00 13:00
 NTNU Side av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 7 70 Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006 09:00 3:00 Tillatte hjelpemidler:
NTNU Side av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 7 70 Eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006 09:00 3:00 Tillatte hjelpemidler:
SVM and Complementary Slackness
 SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
Oppgavesett kap. 6 (3 av..) GEF2200
 Oppgavesett kap. 6 (3 av..) GEF2200 s.m.blichner@geo.uio.no Exercise 1 - Denitions ect What do we call droplets in the liquid phase with temperatures below 0 C? What changes when an embryo of ice exceeds
Oppgavesett kap. 6 (3 av..) GEF2200 s.m.blichner@geo.uio.no Exercise 1 - Denitions ect What do we call droplets in the liquid phase with temperatures below 0 C? What changes when an embryo of ice exceeds
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1910 Poverty and distribution in developing countries Exam: ECON1910 Poverty and distribution in developing countries Eksamensdag: 1. juni 2011 Sensur
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1910 Poverty and distribution in developing countries Exam: ECON1910 Poverty and distribution in developing countries Eksamensdag: 1. juni 2011 Sensur
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Lørdag 26. mai 2001
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 8 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF407 KLASSISK FELTTEORI Lørdag 6. mai
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 8 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF407 KLASSISK FELTTEORI Lørdag 6. mai
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Mathematics : Calculus and Linear Algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Fredag 30. november 08 Sensur
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Mathematics : Calculus and Linear Algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Fredag 30. november 08 Sensur
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsdag 8. august 2002
 NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
TFY4170 Fysikk 2 Justin Wells
 TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
Oppgave 1. ( xφ) φ x t, hvis t er substituerbar for x i φ.
 Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
Oppgave 1 Beviskalklen i læreboka inneholder sluttningsregelen QR: {ψ φ}, ψ ( xφ). En betingelse for å anvende regelen er at det ikke finnes frie forekomste av x i ψ. Videre så inneholder beviskalklen
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger
 Institutt for matematiske fag Eksamensoppgave i TMA432 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 453 163 Eksamensdato: 8. august 217 Eksamenstid (fra
Institutt for matematiske fag Eksamensoppgave i TMA432 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 453 163 Eksamensdato: 8. august 217 Eksamenstid (fra
HØGSKOLEN I NARVIK - SIVILINGENIØRUTDANNINGEN
 HØGSKOLEN I NARVIK - SIVILINGENIØRUTDANNINGEN EKSAMEN I FAGET STE 6243 MODERNE MATERIALER KLASSE: 5ID DATO: 7 Oktober 2005 TID: 900-200, 3 timer ANTALL SIDER: 7 (inklusiv Appendix: tabell og formler) TILLATTE
HØGSKOLEN I NARVIK - SIVILINGENIØRUTDANNINGEN EKSAMEN I FAGET STE 6243 MODERNE MATERIALER KLASSE: 5ID DATO: 7 Oktober 2005 TID: 900-200, 3 timer ANTALL SIDER: 7 (inklusiv Appendix: tabell og formler) TILLATTE
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20 Forbruker, bedrift og marked, høsten 2004 Exam: ECON20 - Consumer behavior, firm behavior and markets, autumn 2004 Eksamensdag: Onsdag 24. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20 Forbruker, bedrift og marked, høsten 2004 Exam: ECON20 - Consumer behavior, firm behavior and markets, autumn 2004 Eksamensdag: Onsdag 24. november
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
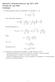 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Trigonometric Substitution
 Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Generalization of age-structured models in theory and practice
 Generalization of age-structured models in theory and practice Stein Ivar Steinshamn, stein.steinshamn@snf.no 25.10.11 www.snf.no Outline How age-structured models can be generalized. What this generalization
Generalization of age-structured models in theory and practice Stein Ivar Steinshamn, stein.steinshamn@snf.no 25.10.11 www.snf.no Outline How age-structured models can be generalized. What this generalization
Graphs similar to strongly regular graphs
 Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Joint work with Martin Ma aj 5th June 2014 Degree/diameter problem Denition The degree/diameter problem is the problem of nding the largest possible graph with given diameter d and given maximum degree
Konstanter og formelsamling finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side en selve oppgaven
 UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Midtveis -eksamen i AST1100, 7. oktober 2008, 15.00 18.00 Oppgavesettet inkludert formelsamling er på 8 sider Konstanter og formelsamling
UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Midtveis -eksamen i AST1100, 7. oktober 2008, 15.00 18.00 Oppgavesettet inkludert formelsamling er på 8 sider Konstanter og formelsamling
The exam consists of 2 problems. Both must be answered. English
 The exam consists of 2 problems. Both must be answered. English Problem 1 (60%) Consider two polluting firms, 1 and 2, each of which emits Q units of pollution so that a total of 2Q units are released
The exam consists of 2 problems. Both must be answered. English Problem 1 (60%) Consider two polluting firms, 1 and 2, each of which emits Q units of pollution so that a total of 2Q units are released
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON60/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON60/460 - Resource Allocation and Economic Policy Eksamensdag: Mandag 8. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON60/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON60/460 - Resource Allocation and Economic Policy Eksamensdag: Mandag 8. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON2915 Vekst og næringsstruktur Eksamensdag: 2.12.2013 Sensur kunngjøres: 3.1.2014 Tid for eksamen: kl. 14:00-17:00 Oppgavesettet er på 7 sider
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON2915 Vekst og næringsstruktur Eksamensdag: 2.12.2013 Sensur kunngjøres: 3.1.2014 Tid for eksamen: kl. 14:00-17:00 Oppgavesettet er på 7 sider
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1310 Økonomisk aktivitet og økonomisk politikk Exam: ECON1310 Macroeconomic theory and policy Eksamensdag: 18.05.01 Sensur blir annonsert: 07.06.01
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1310 Økonomisk aktivitet og økonomisk politikk Exam: ECON1310 Macroeconomic theory and policy Eksamensdag: 18.05.01 Sensur blir annonsert: 07.06.01
EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK og FY2045 Kvantefysikk Tirsdag 13. desember 2005 kl
 ENGLISH TEXT (and NORWEGIAN) Page 1 of 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I TFY450
ENGLISH TEXT (and NORWEGIAN) Page 1 of 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I TFY450
Stationary Phase Monte Carlo Methods
 Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS English Postponed exam: ECON2915 Economic growth Date of exam: 11.12.2014 Time for exam: 09:00 a.m. 12:00 noon The problem set covers 4 pages Resources allowed:
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS English Postponed exam: ECON2915 Economic growth Date of exam: 11.12.2014 Time for exam: 09:00 a.m. 12:00 noon The problem set covers 4 pages Resources allowed:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Bokmål Eksamen i: ECON1210 Forbruker, bedrift og marked Exam: ECON1210 Consumer Behaviour, Firm behaviour and Markets Eksamensdag: 12.12.2014 Sensur kunngjøres:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Bokmål Eksamen i: ECON1210 Forbruker, bedrift og marked Exam: ECON1210 Consumer Behaviour, Firm behaviour and Markets Eksamensdag: 12.12.2014 Sensur kunngjøres:
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Side 1 av 5 INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK
 NORGES TEKNISK-NATURVITENSKAPEIGE UNIVERSITET Side 1 av 5 INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Faglig kontakt under eksamen: Reidar Kristoffersen, tlf.: 73 59 35 67 EKSAMEN I TEP 4110 FUIDMEKANIKK Bokmål/Nnorsk/English
NORGES TEKNISK-NATURVITENSKAPEIGE UNIVERSITET Side 1 av 5 INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Faglig kontakt under eksamen: Reidar Kristoffersen, tlf.: 73 59 35 67 EKSAMEN I TEP 4110 FUIDMEKANIKK Bokmål/Nnorsk/English
LISTE OVER TILLATTE HJELPEMIDLER EKSAMEN I NOVEMBER OG DESEMBER 2014
 1 LISTE OVER TILLATTE HJELPEMIDLER EKSAMEN I NOVEMBER OG DESEMBER 2014 REGLEMENT FOR BRUK AV KALKULATOR OG ORDBOK SE SISTE SIDE 1. STUDIEÅR (ØKAD/REV): Finansregnskap m/ikt (ØABED1000) Markedsføring og
1 LISTE OVER TILLATTE HJELPEMIDLER EKSAMEN I NOVEMBER OG DESEMBER 2014 REGLEMENT FOR BRUK AV KALKULATOR OG ORDBOK SE SISTE SIDE 1. STUDIEÅR (ØKAD/REV): Finansregnskap m/ikt (ØABED1000) Markedsføring og
Examination paper for SØK2009 International Macroeconomics
 Department of Economics Examination paper for SØK2009 International Macroeconomics Academic contact during examination: Joakim Prestmo Phone: 73 59 83 37 Examination date: 04.12.2015 Examination time (from-to):
Department of Economics Examination paper for SØK2009 International Macroeconomics Academic contact during examination: Joakim Prestmo Phone: 73 59 83 37 Examination date: 04.12.2015 Examination time (from-to):
Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2
![Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2 Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2](/thumbs/77/75859899.jpg) Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Siste seminar: Foreslåtte oppgaver basert på ønsker.
 Siste seminar: Foreslåtte oppgaver basert på ønsker.!!! Siste seminar er i utgangspunktet åpent for repetisjon. Hvis seminargruppen har planlagt andre temaer for gjennomgang med seminarleder, kan det være
Siste seminar: Foreslåtte oppgaver basert på ønsker.!!! Siste seminar er i utgangspunktet åpent for repetisjon. Hvis seminargruppen har planlagt andre temaer for gjennomgang med seminarleder, kan det være
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 1 UNIVERSITETET I OSO ØKONOMISK INSTITUTT Eksamen i: ECON915 Vekst og næringgstruktur Exam: ECON915 Growth and business structure Eksamensdag: Torsdag 6. november 009 Sensur kunngjøres: 18. desember ca
1 UNIVERSITETET I OSO ØKONOMISK INSTITUTT Eksamen i: ECON915 Vekst og næringgstruktur Exam: ECON915 Growth and business structure Eksamensdag: Torsdag 6. november 009 Sensur kunngjøres: 18. desember ca
Moving Objects. We need to move our objects in 3D space.
 Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
Oppgave 1. Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk EKSAMEN I: MNFFY 245 INNFØRING I KVANTEMEKANIKK
 Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk EKSAMEN I: MNFFY 45 INNFØRING I KVANTEMEKANIKK DATO: Fredag 4 desember TID: 9 5 Antall vekttall: 4 Antall sider: 5 Tillatte hjelpemidler:
Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk EKSAMEN I: MNFFY 45 INNFØRING I KVANTEMEKANIKK DATO: Fredag 4 desember TID: 9 5 Antall vekttall: 4 Antall sider: 5 Tillatte hjelpemidler:
Bokmål / Nynorsk / English NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK. Eksamen TFY4185 Måleteknikk
 Bokmål / Nynorsk / English Side 1 av 5 NORGES TEKNISK- NATURITENSKAPELIGE UNIERSITET INSTITUTT FOR FYSIKK Steinar Raaen tel. 482 96 758 Eksamen TFY4185 Måleteknikk Mandag 17. desember 2012 Tid: 09.00-13.00
Bokmål / Nynorsk / English Side 1 av 5 NORGES TEKNISK- NATURITENSKAPELIGE UNIERSITET INSTITUTT FOR FYSIKK Steinar Raaen tel. 482 96 758 Eksamen TFY4185 Måleteknikk Mandag 17. desember 2012 Tid: 09.00-13.00
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON1210 - Forbruker, bedrift og marked Eksamensdag: 26.11.2013 Sensur kunngjøres: 18.12.2013 Tid for eksamen: kl. 14:30-17:30 Oppgavesettet er
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON1210 - Forbruker, bedrift og marked Eksamensdag: 26.11.2013 Sensur kunngjøres: 18.12.2013 Tid for eksamen: kl. 14:30-17:30 Oppgavesettet er
SCE1106 Control Theory
 Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, October 26, 2006 SCE1106 Control Theory Exercise 6 Task 1 a) The poles of the open loop system is
Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, October 26, 2006 SCE1106 Control Theory Exercise 6 Task 1 a) The poles of the open loop system is
Speed Racer Theme. Theme Music: Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz. September 9, 2011 Physics 131 Prof. E. F.
 September 9, 2011 Physics 131 Prof. E. F. Redish Theme Music: Speed Racer Theme Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz 1 Reading questions Are the lines on the spatial graphs representing
September 9, 2011 Physics 131 Prof. E. F. Redish Theme Music: Speed Racer Theme Cartoon: Charles Schultz / Jef Mallett Peanuts / Frazz 1 Reading questions Are the lines on the spatial graphs representing
KROPPEN LEDER STRØM. Sett en finger på hvert av kontaktpunktene på modellen. Da får du et lydsignal.
 KROPPEN LEDER STRØM Sett en finger på hvert av kontaktpunktene på modellen. Da får du et lydsignal. Hva forteller dette signalet? Gå flere sammen. Ta hverandre i hendene, og la de to ytterste personene
KROPPEN LEDER STRØM Sett en finger på hvert av kontaktpunktene på modellen. Da får du et lydsignal. Hva forteller dette signalet? Gå flere sammen. Ta hverandre i hendene, og la de to ytterste personene
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON2915 Vekst og næringsstruktur Exam: ECON2915 - Growth and business structure Eksamensdag: Fredag 2. desember 2005 Sensur kunngjøres: 20. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON2915 Vekst og næringsstruktur Exam: ECON2915 - Growth and business structure Eksamensdag: Fredag 2. desember 2005 Sensur kunngjøres: 20. desember
Smart High-Side Power Switch BTS730
 PG-DSO20 RoHS compliant (green product) AEC qualified 1 Ω Ω µ Data Sheet 1 V1.0, 2007-12-17 Data Sheet 2 V1.0, 2007-12-17 Ω µ µ Data Sheet 3 V1.0, 2007-12-17 µ µ Data Sheet 4 V1.0, 2007-12-17 Data Sheet
PG-DSO20 RoHS compliant (green product) AEC qualified 1 Ω Ω µ Data Sheet 1 V1.0, 2007-12-17 Data Sheet 2 V1.0, 2007-12-17 Ω µ µ Data Sheet 3 V1.0, 2007-12-17 µ µ Data Sheet 4 V1.0, 2007-12-17 Data Sheet
Second Order ODE's (2P) Young Won Lim 7/1/14
 Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Second Order ODE's (2P) Copyright (c) 2011-2014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or
Information search for the research protocol in IIC/IID
 Information search for the research protocol in IIC/IID 1 Medical Library, 2013 Library services for students working with the research protocol and thesis (hovedoppgaven) Open library courses: http://www.ntnu.no/ub/fagside/medisin/medbiblkurs
Information search for the research protocol in IIC/IID 1 Medical Library, 2013 Library services for students working with the research protocol and thesis (hovedoppgaven) Open library courses: http://www.ntnu.no/ub/fagside/medisin/medbiblkurs
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON00 Matematikk / Mikro Exam: ECON00 Mathematics / Microeconomics Eksamensdag: Onsdag 5 mai 005 Sensur kunngjøres: Onsdag 5 juni Date of exam: Weesday,
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON00 Matematikk / Mikro Exam: ECON00 Mathematics / Microeconomics Eksamensdag: Onsdag 5 mai 005 Sensur kunngjøres: Onsdag 5 juni Date of exam: Weesday,
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1220 Velferd og økonomisk politikk Exam: ECON1220 Welfare and politics Eksamensdag: 29.11.2010 Sensur kunngjøres: 21.12.2010 Date of exam: 29.11.2010
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1220 Velferd og økonomisk politikk Exam: ECON1220 Welfare and politics Eksamensdag: 29.11.2010 Sensur kunngjøres: 21.12.2010 Date of exam: 29.11.2010
Utsatt eksamen ECON2915
 Utsatt eksamen ECON2915 Oppgave 1 Betrakt en Solow vekstmodell for en lukket økonomi. Vi har følgende relasjoner: Y = AK α L 1 α (1) K = γy δk, 0 < γ < 1, 0 < δ < 1 (2) der Y er brutto nasjonalprodukt,
Utsatt eksamen ECON2915 Oppgave 1 Betrakt en Solow vekstmodell for en lukket økonomi. Vi har følgende relasjoner: Y = AK α L 1 α (1) K = γy δk, 0 < γ < 1, 0 < δ < 1 (2) der Y er brutto nasjonalprodukt,
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON00 Matematikk / Mikro Eam: ECON00 Mathematics / Microeconomics Eksamensdag: 3050 Sensur kunngjøres: 0060 Date of eam: 3050 Grades will be given:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON00 Matematikk / Mikro Eam: ECON00 Mathematics / Microeconomics Eksamensdag: 3050 Sensur kunngjøres: 0060 Date of eam: 3050 Grades will be given:
Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye)
 INF247 Er du? Er du? - Annet Ph.D. Student Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen,
INF247 Er du? Er du? - Annet Ph.D. Student Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen,
Ma Flerdimensjonal Analyse Øving 1
 Ma1203 - Flerdimensjonal Analyse Øving 1 Øistein Søvik Brukernavn: Oistes 23.01.2012 Oppgaver 10.1 6. Show that the triangle with verticies (1, 2, 3), (4, 0, 5) and (3, 6, 4) has a right angle. z y x Utifra
Ma1203 - Flerdimensjonal Analyse Øving 1 Øistein Søvik Brukernavn: Oistes 23.01.2012 Oppgaver 10.1 6. Show that the triangle with verticies (1, 2, 3), (4, 0, 5) and (3, 6, 4) has a right angle. z y x Utifra
Eksamensoppgave i SØK1002 Mikroøkonomisk analyse
 Institutt for samfunnsøkonomi Eksamensoppgave i SØK00 Mikroøkonomisk analyse Faglig kontakt under eksamen: Lars-Erik Borge Tlf.: 73 59 9 4 Eksamensdato: 9. mai 07 Eksamenstid (fra-til): 4 timer (09.00-3.00)
Institutt for samfunnsøkonomi Eksamensoppgave i SØK00 Mikroøkonomisk analyse Faglig kontakt under eksamen: Lars-Erik Borge Tlf.: 73 59 9 4 Eksamensdato: 9. mai 07 Eksamenstid (fra-til): 4 timer (09.00-3.00)
Neural Network. Sensors Sorter
 CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
EKSAMENSOPPGAVE I SØK3004 VIDEREGÅENDE MATEMATISK ANALYSE ADVANCED MATHEMATICS
 NTNU Norges teknisk-naturvitenskapelige universitet Institutt for samfunnsøkonomi EKSAMENSOPPGAVE I SØK3004 VIDEREGÅENDE MATEMATISK ANALYSE ADVANCED MATHEMATICS Faglig kontakt under eksamen: Snorre Lindset,
NTNU Norges teknisk-naturvitenskapelige universitet Institutt for samfunnsøkonomi EKSAMENSOPPGAVE I SØK3004 VIDEREGÅENDE MATEMATISK ANALYSE ADVANCED MATHEMATICS Faglig kontakt under eksamen: Snorre Lindset,
FINAL EXAM IN STA-2001
 Page 1 of 3 pages FINAL EXAM IN STA-2001 Exam in: STA-2001 Stochastic processes. Date: Tuesday the 21. of February, 2012. Time: 09:00 13:00. Place: Aud.max. Approved aids: 4 pages of your own notes. Approved
Page 1 of 3 pages FINAL EXAM IN STA-2001 Exam in: STA-2001 Stochastic processes. Date: Tuesday the 21. of February, 2012. Time: 09:00 13:00. Place: Aud.max. Approved aids: 4 pages of your own notes. Approved
Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012
 NTNU Fakultet for Naturvitskap og Teknologi Institutt for fysikk Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012 Faglærar: Førsteamanuensis John Ove Fjærestad Institutt for fysikk Telefon:
NTNU Fakultet for Naturvitskap og Teknologi Institutt for fysikk Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem, våren 2012 Faglærar: Førsteamanuensis John Ove Fjærestad Institutt for fysikk Telefon:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON00 - Matematikk 1/Mikro 1 Eam: ECON00 Mathematics 1/Microeconomics 1 Eksamensdag: Fredag 1. mai 010 Sensur kunngjøres: Fredag 11.06.010 Date of eam:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON00 - Matematikk 1/Mikro 1 Eam: ECON00 Mathematics 1/Microeconomics 1 Eksamensdag: Fredag 1. mai 010 Sensur kunngjøres: Fredag 11.06.010 Date of eam:
5 E Lesson: Solving Monohybrid Punnett Squares with Coding
 5 E Lesson: Solving Monohybrid Punnett Squares with Coding Genetics Fill in the Brown colour Blank Options Hair texture A field of biology that studies heredity, or the passing of traits from parents to
5 E Lesson: Solving Monohybrid Punnett Squares with Coding Genetics Fill in the Brown colour Blank Options Hair texture A field of biology that studies heredity, or the passing of traits from parents to
