Løsningsforslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Torsdag 8. august 2013
|
|
|
- Margit Slettebakk
- 8 år siden
- Visninger:
Transkript
1 NTNU Sie 1 av 6 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY345 GRAVITASJON OG KOSMOLOGI Torsag 8. august 013 Dette løsningsforslaget er på 6 sier. Oppgave 1. Aspekter ve stanarmoellen for kosmologi I stanarmoellen for kosmologi (Friemann-Lemaître-Robertson-Walker moellen) innfører man forskjellige former for materie eller energi. Forklar hva man i enne forbinelsen mener me a) Mørk energi eller kvintessens (ark energy or quintessence). Mørk energi er energiform er et assosierte trykket P er relatert til energitettheten ε ve formelen P = ε. (1) I stanarmoellen for kosmologi er mørk energi nøvenig for å forklare universets akselererene ekspansjon e siste (ca. fem) milliarer år. Kommentar: Mørk henspiller i enne forbinelse på at man er litt i mørke når et gjeler kunnskap om enne energiformen, spesielt når et gjeler uavhengige observasjoner av enne, men noen alternativer er vakuumenergi og kosmologisk konstant. b) Mørk materie (ark matter). Mørk materie er ikke-relativistisk materie som ikke er irekte synlig som lysgivene objekter, vs. stjerner og galakser. Den er nøvenig i stanarmoellen for å forklare galakseynamikk og universets struktur på stor skala, og observerte gravitasjonlinse-effekter. Kommentar: Mørk henspiller her først og fremst på at enne materien ikke er synlig i teleskoper, og ikke ser ut til å påvirke lysene materie på annen måte enn gjennom gravitasjonspåvirkning. Men man er også noe i mørke me hensyn til hva enne materien består av. c) Kal materie (col matter). Kal materie kan er materie som beveger seg ikke-relativistisk, slik at et kinetiske energibiraget er mye minre enn biraget fra hvilemassen. Dette betyr at vi kan neglisjere effekter av trykket P i stanarmoellen, P 0. () Kal materie består av båe mørk og normal lysene (av kjent form) materie. Kommentar: Stjerner, me temperatur på noen tusen graer, regnes altså som kal materie i enne sammenhengen.
2 Løsning FY345 Gravitasjon og kosmologi, Sie av 6 ) Varm materie (hot matter) Varm materie er relativistisk materie, er et kinetiske energibiraget er mye større enn biraget fra en eventuell hvilemasse. I stanarmoellen betyr ette at vi har sammenhengen P = 1 ε. (3) 3 e) Omtrent hvor stor anel (i prosent) av en total energitettheten utgjør hver av isse energiformene i ag (ifølge beste tilpasning til kosmologiske ata)? Ifølge siste tilpassning utgjør mørk energi ca. 68% og kal materie ca. 3% (ca. 7% mørk pluss ca. 5% normal materie) av energitettheten i universet. Biraget fra en varme materien er altså neglisjerbar iag. f) Hvoran skalerer tettheten av isse energiformene me universet ekspansjon, vs. me skalafaktoren a(t)? Energitettheten til mørk energi er uavhengig av ekspansjonen, ε a 0. Energitettheten til kal materie er omvent proporsjonal me universets volum, ε a 3. Dette kan tolkes som at antallet massive partikler, og eres masse, er konstant. Energitettheten til varm materie skalerer som ε a 4. Dette kan tolkes som at antallet masseløse partikler er konstant, men at eres energi avtar som a 1 pga. røforskyvning. Matematisk kan Friemann-Lemaître-Robertson-Walker moellen, me kun én form for energi eller materie (når man også betrakter kosmologisk konstant og krumningseffekter som energiformer), oppsummeres ve Friemanns første ligning, H = 8π G N ε, (4) 3 c konserveringsloven ε + 3H(ε + P ) = 0 (5) (er betyr erivasjon me hensyn på tien t), og tilstansligningen P = wε. (6) Her er H H(t) = a(t) 1 a(t) Hubble-parameteren, er a(t) skalafaktorer i moellen. t g) Anta at w er en konstant, og bruk ligningene (5-6) til å finne hvoran ε varier me skalafaktoren a. Dvs. vis at ε(t) a(t) µ, og bestem konstanten µ. Vi setter (6) inn i (5) og eler på ε, Dette kan omskrives som ε + 3(1 + w)ȧ ε a = 0. t [log ε(t) + 3(1 + w) log a(t)] = [ t log ε(t)a(t) 3(1+w] = 0. Dvs. at ε(t) a(t) 3(1+w) er tisuavhengig, ε(t) a(t) 3(1+w). (7) h) Bruk resultatet fra forrige punkt sammen me ligning (4) til å finne hvoran a(t) varierer me tien t. Dvs. vis at a(t) t ν (unntatt en spesiell veri av w), og bestem konstanten ν. Ligning (7) innsatt i (4) impliserer at er K er en ukjent konstant. I spesialtifellet w = 1 gir ette ȧ a = K a 3 (1+w), (8) ȧ(t) = K a(t),
3 Løsning FY345 Gravitasjon og kosmologi, Sie 3 av 6 me løsning For w 1 omskriver vi ligningen til Dvs. at a 1 (1+3w) a = Vi har valgt et passene nullpunkt for tien t. Oppgave. Forenklet Ranall-Sunrum moell Se på geometrien efinert av linje-elementet a(t) = e Kt a(0). (9) 3(1 + w) a 3 (1+w) = Kt a(t) t 3(1+w). (10) τ = e k u ( t x y z ) u, (11) vs. et univers me en ekstra romimensjon (u-retningen). Bevegelsen til en punktpartikkel (me masse m = 1 i passene enheter) i enne geometrien er bestemt av Lagrangefunksjonen, via Hamiltons prinsipp. Her løper µ, ν over fem tirom inekser, og betyr erivasjon me hensyn til egenti τ. L = 1 gµνẋµ ẋ ν, (1) x µ ( x 0, x 1, x, x 3, x 4) = (t, x, y, z, u), (13) a) Finn Euler-Lagrange ligningene for bevegelse i enne geometrien. Fra e generelle Euler-Lagrange ligningene τ ( L ẋ σ ) = L x σ finner vi Her er θ(u) stepfunksjonen, τ ek u ṫ = 0, τ ek u ẋ = 0, τ ek u ẏ = 0, τ ek u ż = 0, τ ek u u = 1 θ(u) k ( ek u ṫ ẋ ẏ ż ). (14a) (14b) (14c) (14) (14e) θ(u) = { 1 for u > 0, 1 for u < 0. b) Sammenlign resultatene fra forrige punkt me e geoesiske ligningene på generell form, og bruk ette til å finne alle ikke-forsvinnene Christoffel-symboler Γ µ νλ for enne geometrien. For å sammenligne me e generelle geoesiske ligningene, ẍ µ + Γ µ νλ ẋν ẋ λ = 0,
4 Løsning FY345 Gravitasjon og kosmologi, Sie 4 av 6 utfører vi erivasjonen på venstresiene av (14), og multipliserer me e k u. Vi har at slik at (14) blir e k u τ ek u = θ(u) k u, ẗ + g(u) u ṫ = 0, ẍ + g(u) u ẋ = 0, ÿ + g(u) u ẏ = 0, z + g(u) u ż = 0, ü + g(u) ( ṫṫ + ẋẋ + ẏẏ + żż + u u ) = 0, (15a) (15b) (15c) (15) (15e) er g(u) = 1 θ(u) k. Fra ette leser vi ut alle Christoffel-symboler som ikke er null: Γ t ut = Γ t tu = Γ x ux = Γ x xu = Γ y uy = Γ y yu = Γ z uz = Γ z zu = g(u), Γ u tt = Γ u xx = Γ u yy = Γ u zz = g(u), Γ u uu = g(u). (16a) (16b) (16c) c) Lagrangefunksjonen L avhenger ikke eksplisitt av t. Hvilken konservert størrelse gir ette opphav til? Ifølge Nöthers teorem blir en konserverte størrelsen, ε = L ṫ = ek u ṫ, (17) som vi normalt vil inentifisere me systemets energi (eller noe proporsjonalt me enne). Vi kan også lese ut enne konserveringsloven irekte fra ligning (14a). ) Lagrangefunksjonen L avhenger ikke eksplisitt av r = (x, y, z). Hvilke konserverte størrelser gir ette opphav til? Ifølge Nöthers teorem blir e konserverte størrelsene, p = L ṙ = ek u ṙ, (18) som vi normalt vil inentifisere me systemets bevegelsesmenge (eller noe proporsjonalt me enne). Vi kan også lese ut isse konserveringslovene irekte fra ligningene (14b-14). e) Lagrangefunksjonen L avhenger ikke eksplisitt av τ. Hvilken konservert størrelse gir ette opphav til? Ifølge Nöthers teorem blir konserveringsloven L ẋ µ ẋµ L = L. (19) Dette sier bare at partikkelens femmer-hastighet 1 har konstant lenge; egentien τ er valgt slik at g µν ẋ µ ẋ ν = 1, (0) slik man kan lese ut av ligning (11) etter ivisjon me τ. De ynamiske ligningene er konsistent me enne normaliseringsbetingelsen. Her finner vi altså konserveringsloven (eller normaliseringsbetingelsen) 1 Normalt (i et fireimensjonalt tirom) kalt firer-hastighet. e k u ( ṫ ẋ ẏ ż ) u = 1. (1)
5 Løsning FY345 Gravitasjon og kosmologi, Sie 5 av 6 En massiv partikkel starter i punktet r = 0, u = 0 ve tien t = 0, me hastighetene ṙ = (v 0, 0, 0) og u = v 1 > 0. f) Hva er tiens hastighet, ṫ, ve starttispunket? Ifølge ligning (1) må vi ha ṫ = e k u + ẋ + ẏ + ż = 1 + v0 + v1, vs. for ṫ(0) ṫ 0, ṫ 0 = 1 + v 0 + v 1. () g) Finn ṫ, ẋ, ẏ og ż uttrykt ve u, u og startveriene. Fra konserveringslovene for energi og bevegelsesmenge finner vi at ṫ = e k u ṫ 0, ẋ = e k u v 0, ẏ = 0, ż = 0. (3a) (3b) (3c) (3) h) Finn en største absoluttverien som u kan anta. Ligning (3) innsatt i ligning (1) gir u = (1 + v1)e k u 1. (4) Sien venstresien må være ikke-negativ har vi at (1 + v1) e k u 1, eller u log(1 + v 1) k u max. (5) i) Beregn så langt u kan banen x µ (τ) til enne partikkelen. Vi antar først at u 0 og u 0. Ligning (4) kan a skrives på formen u = τ. (6) (1 + v 1 ) e ku 1 Ve å innføre ρ = (1 + v 1 ) e ku 1 kan ette omskrives som Dette kan integreres til Ve inversjon finnes så at ρ 1 + ρ = arctan ρ = 1 k τ. (7) arctan ρ = φ 0 1 kτ. ρ(τ) = tan ( φ 0 1 kτ). (8) Her er φ 0 en konstant bestemt slik at tan φ 0 = ρ(0) = v 1. Fra ette finner vi for u > 0, e ku = 1 + ρ 1 + v 1 1 = (1 + v1 ) cos (φ 0 1 (9) kτ).
6 Løsning FY345 Gravitasjon og kosmologi, Sie 6 av 6 Ve innsetting i ligningene (3) kan isse integreres til 1 + v t(τ) = 0 + v1 τ τ 1 + v1 0 cos (φ 0 1 kτ ) = 1 + v 0 + v [ 1 k 1 + v1 tan(φ0 ) tan(φ 0 1 kτ)], x(τ) = v τ 0 τ 1 + v1 0 cos (φ 0 1 kτ ) (30a) = v 0 [ k 1 + v1 tan(φ0 ) tan(φ 0 1 kτ)], (30b) y(τ) = 0, (30c) z(τ) = 0. Den siste koorinaten er alleree gitt av ligning (9), (30) u(τ) = 1 k log [ (1 + v 1) cos (φ 0 1 kτ)]. (31)
7 Some expressions which may be of use Geoesic equations The geoesic equations in a geometry with connection coefficients Γ µ νλ are Euler-Lagrange equations ẍ µ + Γ µ νλ ẋν ẋ λ = 0. (3) The Euler-Lagrange equations for a fiel theory escribe by the Lagrangian L = L(ϕ a, µ ϕ a, x) are ( ) L µ = L. (33) ( µ ϕ a ) ϕ a The corresponing equations for point particle mechanics is obtaine by restricting µ to only a time erivative /t. Nöther s theorem Assume the action is invariant uner the continuous transformations ϕ a ϕ a + ε δϕ a + O(ε ), more precisely that L L + ε µ Λ µ + O(ɛ ) uner this transformation. Then there is an associate conserve current, J µ = L ( µ ϕ a ) δϕ a Λ µ. (34) I.e., µ J µ = 0. The corresponing expression for point particle mechanics is obtaine by restricting µ to only a time erivative /t.
8
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai :00 13:00
 NTNU Side 1 av 2 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 2 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai 2012 09:00 13:00 Tillatte hjelpemidler:
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsdag 8. august 2002
 NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
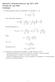 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
1b) Schwarzschil-metrikken er iagonal, og vi har at g tt = 1, c = r, c ; g rr =, r r r r, =,1, r, ; g =,r ; g '' =,r sin : (9) At raielle baner eksist
 Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Institutt for fysikk Fakultet for fysikk, informatikk og matematikk. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 31.
 NTNU Side av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 3. mai 007 Oppgave.
NTNU Side av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 3. mai 007 Oppgave.
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august :00 13:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
Løsningsforslag til eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006
 NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK Mandag 10. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
Løsningsforslag til eksamen i TFY4230 STATISTISK FYSIKK Tirsdag 9. aug 2011
 NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 5 sider. Løsningsforslag til eksamen i TFY430 STATISTISK FYSIKK Tirsdag 9. aug 011 Oppgave 1.
NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 5 sider. Løsningsforslag til eksamen i TFY430 STATISTISK FYSIKK Tirsdag 9. aug 011 Oppgave 1.
Eksamen i Ikkelineær dynamikk, fag TFY 4305 Onsdag 30. november 2005 Løsninger
 Eksamen i Ikkelineær ynamikk, fag TFY 4305 Onsag 30. november 2005 Løsninger 1) Den generelle løsningen av ligningen u t + cu x =0eru(x, t) =f(x ct), er f er en vilkårlig funksjon av en variabel. Hvoran
Eksamen i Ikkelineær ynamikk, fag TFY 4305 Onsag 30. november 2005 Løsninger 1) Den generelle løsningen av ligningen u t + cu x =0eru(x, t) =f(x ct), er f er en vilkårlig funksjon av en variabel. Hvoran
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Løsningsforslag Eksamen 9. desember 2006 TFY4250 Atom- og molekylfysikk /FY2045 Kvantefysikk
 Eksamen TFY450/FY045 9. esember 006 - løsningsforslag 1 Løsningsforslag Eksamen 9. esember 006 TFY450 Atom- og molekylfysikk /FY045 Kvantefysikk Oppgave 1 a. Grunntilstanen ψ 1 (x) har ingen nullpunkter.
Eksamen TFY450/FY045 9. esember 006 - løsningsforslag 1 Løsningsforslag Eksamen 9. esember 006 TFY450 Atom- og molekylfysikk /FY045 Kvantefysikk Oppgave 1 a. Grunntilstanen ψ 1 (x) har ingen nullpunkter.
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007
 Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løsningsforslag eksamen MAT111 Grunnkurs i Matematikk I høsten 2009
 Løsningsforslag eksamen MAT Grunnkurs i Matematikk I høsten 9 OPPGAVE (a) Vi har w = + ( ) =. I et komplekse plan ligger w i 4. kvarant og vinkelen θ mellom tallet og en relle aksen har tan θ =, vs. at
Løsningsforslag eksamen MAT Grunnkurs i Matematikk I høsten 9 OPPGAVE (a) Vi har w = + ( ) =. I et komplekse plan ligger w i 4. kvarant og vinkelen θ mellom tallet og en relle aksen har tan θ =, vs. at
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
Eksamen i FY3466 KVANTEFELTTEORI II Tirsdag 20. mai :00 13:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 71 70 Eksamen i FY3466 KVANTEFELTTEORI II Tirsdag 20. mai 2008 09:00 13:00 Tillatte
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 52 eller 45 43 71 70 Eksamen i FY3466 KVANTEFELTTEORI II Tirsdag 20. mai 2008 09:00 13:00 Tillatte
UNIVERSITETET I OSLO
 Side 1 UNIVERSITETET I OSO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: mars 017 Tid for eksamen: 14:30 17:30 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Side 1 UNIVERSITETET I OSO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: mars 017 Tid for eksamen: 14:30 17:30 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
TMA4100 Matematikk 1 Høst 2014
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 014 Løsningsforslag Øving 03.7. Økningen i uksen, F, kan approksimeres som se sie 131 i boka F F =
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 014 Løsningsforslag Øving 03.7. Økningen i uksen, F, kan approksimeres som se sie 131 i boka F F =
Løsningsforslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag 26. mai 2005
 NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 2014 2.8.2 Vi merker oss først at funksjonen f er båe kontinuerlig og eriverbar på intervallet [1,2],
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 2014 2.8.2 Vi merker oss først at funksjonen f er båe kontinuerlig og eriverbar på intervallet [1,2],
til eksamen i SIF5036 Matematisk modellering 14. desember 2002.
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Sie av 8 Løsningsforslag til eksamen i SIF5036 Matematisk moellering 4. esember 2002. Oppgave (a) Hvilke aksiomer om naturen
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Sie av 8 Løsningsforslag til eksamen i SIF5036 Matematisk moellering 4. esember 2002. Oppgave (a) Hvilke aksiomer om naturen
Løsningsforslag til prøve i fysikk
 Løsningsforslag til prøve i fysikk Dato: 17/4-2015 Tema: Kap 11 Kosmologi og kap 12 Elektrisitet Kap 11 Kosmologi: 1. Hva menes med rødforskyvning av lys fra stjerner? Fungerer på samme måte som Doppler-effekt
Løsningsforslag til prøve i fysikk Dato: 17/4-2015 Tema: Kap 11 Kosmologi og kap 12 Elektrisitet Kap 11 Kosmologi: 1. Hva menes med rødforskyvning av lys fra stjerner? Fungerer på samme måte som Doppler-effekt
AST1010 En kosmisk reise. Forelesning 19: Kosmologi
 AST1010 En kosmisk reise Forelesning 19: Kosmologi Hubble og Big Bang Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman og bakgrunnsstrålingen Oppdagelsen av bakgrunnsstrålingen Universets historie
AST1010 En kosmisk reise Forelesning 19: Kosmologi Hubble og Big Bang Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman og bakgrunnsstrålingen Oppdagelsen av bakgrunnsstrålingen Universets historie
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
TMA4100 Matematikk 1 Høst 2014
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 sforslag forkunnskapstest Faktoriser, hvis mulig, uttrkket +. (A) ( + 5)( ) (B) ( 5)( + ) (C) ( + )( )
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 sforslag forkunnskapstest Faktoriser, hvis mulig, uttrkket +. (A) ( + 5)( ) (B) ( 5)( + ) (C) ( + )( )
AST1010 En kosmisk reise. Forelesning 20: Kosmologi, del 2
 AST1010 En kosmisk reise Forelesning 20: Kosmologi, del 2 Temaer Mørk energi Inflasjon Hvordan startet det hele? Universet akselerer Ytterligere evidens for mørk energi fra avansert matematikk 1 0.32
AST1010 En kosmisk reise Forelesning 20: Kosmologi, del 2 Temaer Mørk energi Inflasjon Hvordan startet det hele? Universet akselerer Ytterligere evidens for mørk energi fra avansert matematikk 1 0.32
LØSNINGSFORSLAG TIL EKSAMEN I TEP4145 KLASSISK MEKANIKK Mandag 21. mai 2007 kl Løsningsforslaget er på i alt 9 sider.
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Løsningsforslag til øving 5
 FY1001/TFY4145 Mekanisk fysikk. Institutt for fysikk, NTNU. Høsten 011. Løsningsforslag til øving 5 Oppgave 1 a) Energibevarelse E A = E B gir U A + K A = U B + K B Innsetting av r = L x i ligningen gir
FY1001/TFY4145 Mekanisk fysikk. Institutt for fysikk, NTNU. Høsten 011. Løsningsforslag til øving 5 Oppgave 1 a) Energibevarelse E A = E B gir U A + K A = U B + K B Innsetting av r = L x i ligningen gir
Eksamen i FY3403/TFY4290 PARTIKKELFYSIKK Mandag 12. desember :00 13:00
 NTNU Side 1 av 6 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 5 eller 45 43 71 70 Eksamen i FY3403/TFY490 PARTIKKELFYSIKK Mandag 1. desember 005 09:00 13:00
NTNU Side 1 av 6 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 5 eller 45 43 71 70 Eksamen i FY3403/TFY490 PARTIKKELFYSIKK Mandag 1. desember 005 09:00 13:00
AST1010 En kosmisk reise. Forelesning 20: Kosmologi, del 2
 AST1010 En kosmisk reise Forelesning 20: Kosmologi, del 2 Akselerasjon Observasjonene viser at universet ser flatt ut. Men: observasjoner av supernovaer (type Ia) viser at universet utvider seg fortere
AST1010 En kosmisk reise Forelesning 20: Kosmologi, del 2 Akselerasjon Observasjonene viser at universet ser flatt ut. Men: observasjoner av supernovaer (type Ia) viser at universet utvider seg fortere
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Lørdag 26. mai 2001
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 8 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF407 KLASSISK FELTTEORI Lørdag 6. mai
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 8 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF407 KLASSISK FELTTEORI Lørdag 6. mai
Løsningsforslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fredag 24. mai 2013
 NTNU Side 1 av 4 Institutt fo fysikk Fakultet fo fysikk, infomatikk og matematikk Løsningsfoslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 Dette løsningsfoslaget e på 4 side. Oppgave
NTNU Side 1 av 4 Institutt fo fysikk Fakultet fo fysikk, infomatikk og matematikk Løsningsfoslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 Dette løsningsfoslaget e på 4 side. Oppgave
UNIVERSITETET I OSLO
 Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
AST1010 En kosmisk reise
 AST1010 En kosmisk reise Forelesning 21: Kosmologi, del 2 https://www.youtube.com/watch? v=xbr4gkrny04 1 Ca. 68% frastøtende energi Akselerasjon Observasjonene viser at universet ser flatt ut. Men: observasjoner
AST1010 En kosmisk reise Forelesning 21: Kosmologi, del 2 https://www.youtube.com/watch? v=xbr4gkrny04 1 Ca. 68% frastøtende energi Akselerasjon Observasjonene viser at universet ser flatt ut. Men: observasjoner
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fredag 24. mai :00 13:00
 NTNU Side 1 av 2 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Kåe Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 09:00 13:00 Tillatte hjelpemidle:
NTNU Side 1 av 2 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Kåe Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Fedag 24. mai 2013 09:00 13:00 Tillatte hjelpemidle:
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
Matematikk 4 M/N - Vår 2008 Kort Introduksjon
 Matematikk 4 M/N - Vår 2008 Kort Introduksjon Januar 7. 2008 Matematikk 4 M/N Januar 7. 2008 1 / 5 Fourier rekker Joseph Fourier (1768-1830) Fransk matematikker og fysikker. Fourier var den første å bruke
Matematikk 4 M/N - Vår 2008 Kort Introduksjon Januar 7. 2008 Matematikk 4 M/N Januar 7. 2008 1 / 5 Fourier rekker Joseph Fourier (1768-1830) Fransk matematikker og fysikker. Fourier var den første å bruke
Løsningsforslag til eksamen i FY3404 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 2004
 NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag 3. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
v(t) = r (t) = (2, 2t) v(t) = t 2 T(t) = 1 v(t) v(t) = (1 + t 2 ), t 2 (1 + t 2 ) t = 2(1 + t 2 ) 3/2.
 NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
Løysingsframlegg TFY4305 Ikkjelineær dynamikk Haust 2012
 NTNU Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Løysingsframlegg TFY4305 Ikkjelineær dynamikk Haust 01 Faglærar: Professor Jens O. Andersen Institutt for Fysikk, NTNU Telefon: 73593131
NTNU Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Løysingsframlegg TFY4305 Ikkjelineær dynamikk Haust 01 Faglærar: Professor Jens O. Andersen Institutt for Fysikk, NTNU Telefon: 73593131
Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006
 NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
EKSAMEN I FAG SIF4062 FASTSTOFFYSIKK VK Fakultet for fysikk, informatikk og matematikk Tirsdag 8. mai 2001 Tid: Sensur faller 29.
 Side 1 av 4 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Ola Hunderi Tlf.: 93411 EKSAMEN I FAG SIF406 FASTSTOFFYSIKK VK Fakultet for fysikk, informatikk
Side 1 av 4 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Ola Hunderi Tlf.: 93411 EKSAMEN I FAG SIF406 FASTSTOFFYSIKK VK Fakultet for fysikk, informatikk
EKSAMEN I FY2045 KVANTEFYSIKK Mandag 2. juni 2008 kl
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
EKSAMEN I NUMERISK MATEMATIKK(TMA4215) Lørdag 20. desember 2003 Tid: 09:00 14:00, Sensur:
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
Eksamen i fag FY2450 Astrofysikk Onsdag 20. mai 2009 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 93653, mobil 90 07 51 72 Eksamen i fag FY2450 Astrofysikk Onsdag
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 93653, mobil 90 07 51 72 Eksamen i fag FY2450 Astrofysikk Onsdag
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
Konstanter og formelsamling finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side en selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
Anbefalte oppgaver uke 36
 Anbefalte oppgaver uke 36 Høsten 2017 Løsningsforslag 1 Vi begynner me å skrive om ligningen litt, først til x y x + y = x2 + y, (1) y og så eller Nå eriverer vi, og får slik at xy y 2 = x 3 + xy + x 2
Anbefalte oppgaver uke 36 Høsten 2017 Løsningsforslag 1 Vi begynner me å skrive om ligningen litt, først til x y x + y = x2 + y, (1) y og så eller Nå eriverer vi, og får slik at xy y 2 = x 3 + xy + x 2
EKSAMEN I FY2045 KVANTEFYSIKK Onsdag 30. mai 2007 kl
 NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
Midtsemesterprøve fredag 10. mars kl
 Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
Institutt for fysikk, NTNU FY1003 Elektrisitet og magnetisme TFY4155 Elektromagnetisme Vår 2006 Midtsemesterprøve fredag 10. mars kl 0830 1130. Løsningsforslag 1) A. (Andel som svarte riktig: 83%) Det
Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: Løsningsforslag. Oppgave 1
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: 09.00 12.00 Løsningsforslag Oppgave 1 Robertson-Walker metrikken
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: 09.00 12.00 Løsningsforslag Oppgave 1 Robertson-Walker metrikken
TFY4115: Løsningsforslag til oppgaver gitt
 Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
AST1010 En kosmisk reise
 AST1010 En kosmisk reise Forelesning 19: Kosmologi Einsteins universmodell Friedmann, Lemaitre, Hubble og Big Bang Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman og bakgrunnsstrålingen Oppdagelsen
AST1010 En kosmisk reise Forelesning 19: Kosmologi Einsteins universmodell Friedmann, Lemaitre, Hubble og Big Bang Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman og bakgrunnsstrålingen Oppdagelsen
UNIVERSITETET I OSLO
 Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 22 mars 2017 Tid for eksamen: 14:30 17:30 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 22 mars 2017 Tid for eksamen: 14:30 17:30 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
UNIVERSITETET I OSLO
 Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
Side 1 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 16 mars 2016 Tid for eksamen: 15:00 18:00 (3 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark
UNIVERSITETET I BERGEN
 Bokmål UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. Løsningsforslag til Eksamen i emnet MAT - Grunnkurs i matematikk I Torsdag 22. mai 28, kl. 9-4. Dette er kun et løsningsforslag.
Bokmål UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. Løsningsforslag til Eksamen i emnet MAT - Grunnkurs i matematikk I Torsdag 22. mai 28, kl. 9-4. Dette er kun et løsningsforslag.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: AST1010 - Astronomi - en kosmisk reise Eksamensdag: Tirsdag 22. mai 2018 Tid for eksamen:1430-1730 Oppgavesettet er på 2 sider
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: AST1010 - Astronomi - en kosmisk reise Eksamensdag: Tirsdag 22. mai 2018 Tid for eksamen:1430-1730 Oppgavesettet er på 2 sider
AST1010 En kosmisk reise. Astronomiske avstander https://www.youtube.com/watch? v=vsl-jncjak0. Forelesning 20: Kosmologi, del I
 AST1010 En kosmisk reise Forelesning 20: Kosmologi, del I Astronomiske avstander Hvordan vet vi at nærmeste stjerne er 4 lysår unna? Parallakse (kun nære stjerner) Hvordan vet vi at galaksen vår er 100
AST1010 En kosmisk reise Forelesning 20: Kosmologi, del I Astronomiske avstander Hvordan vet vi at nærmeste stjerne er 4 lysår unna? Parallakse (kun nære stjerner) Hvordan vet vi at galaksen vår er 100
Oppgave 1 OPPGAVER OG LØSNINGSFORSLAG KONTINUASJONSEKSAMEN I FAG SMN 6147 OG SMN 6195 KOMPLEKS ANALYSE STED: HØGSKOLEN I NARVIK. KLASSE:4EL,4RTog5ID
 OPPGAVER OG LØSNINGSFORSLAG KONTINUASJONSEKSAMEN I FAG SMN 647 OG SMN 695 KOMPLEKS ANALYSE STED: HØGSKOLEN I NARVIK KLASSE:4EL,4RTog5ID DATO: 8 januar 004 TID: 9.00-.00 ANTALL SIDER: 0 (inklusiv formler)
OPPGAVER OG LØSNINGSFORSLAG KONTINUASJONSEKSAMEN I FAG SMN 647 OG SMN 695 KOMPLEKS ANALYSE STED: HØGSKOLEN I NARVIK KLASSE:4EL,4RTog5ID DATO: 8 januar 004 TID: 9.00-.00 ANTALL SIDER: 0 (inklusiv formler)
Løsningsforslag til eksamen i TFY4170 Fysikk august 2004
 NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
Formelsamling. ξ(r, t) = ξ 0 sin(k r ωt + φ) 2 ξ(x, t) = 1 2 ξ(x, t) t 2. 2 ξ. x ξ. z 2. y ξ. v = ω k. v g = dω dk
 Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
Formelsamling Side 7 av 16 Fete symboler angir vektorer. Symboler med hatt over angir enhetsvektorer. Formlenes gyldighet og symbolenes betydning antas å være kjent. Harmonisk plan bølge: Bølgeligning:
x, og du dx = w dy (cosh u) = sinh u H sinh w H x = sinh w H x. dx = H w w > 0, så h har ikke flere lokale ekstremverdier.
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 00 Løsningsforslag - Øving 3 Avsnitt 3. u 49 a) Fra tabell 3.4 på sie i boka: (cosh u) = sinh u. Her har vi at u = w H, og u = w y H. Det følger
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 00 Løsningsforslag - Øving 3 Avsnitt 3. u 49 a) Fra tabell 3.4 på sie i boka: (cosh u) = sinh u. Her har vi at u = w H, og u = w y H. Det følger
EKSAMEN I NUMERISK LINEÆR ALGEBRA (TMA4205)
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, :00 13:00
 NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
Løsningsforslag til oppgavene 1 8 fra spesiell relativitetsteori.
 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Desember 008. Løsningsforslag til oppgavene 1 8 fra spesiell relativitetsteori. Oppgave 1 Vi lar x 1 = x være posisjonen for hendelsene i inertialsystemet
FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Desember 008. Løsningsforslag til oppgavene 1 8 fra spesiell relativitetsteori. Oppgave 1 Vi lar x 1 = x være posisjonen for hendelsene i inertialsystemet
Litt mer om kjeglesnitt og Keplers lover om planetbanene
 Litt mer om kjeglesnitt og Keplers lover om planetbanene Det er ikke meningen at enne teksten skal stå for seg selv. Den er ment som en hjelp mens u leser 11.6 og eler av kapittel 8 i læreboka. Hvis u
Litt mer om kjeglesnitt og Keplers lover om planetbanene Det er ikke meningen at enne teksten skal stå for seg selv. Den er ment som en hjelp mens u leser 11.6 og eler av kapittel 8 i læreboka. Hvis u
UNIVERSITETET I OSLO. Konstanter og formelsamling finner du bakerst
 UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Avsluttende eksamen i AST1100, 4 desember 2007, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 14 sider Konstanter og formelsamling
UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Avsluttende eksamen i AST1100, 4 desember 2007, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 14 sider Konstanter og formelsamling
En samling av mer eller mindre relevante formler (uten nærmere forklaring) er gitt til slutt i oppgavesettet.
 Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
Norges teknisk-naturvitenskapelige universitet NTNU Institutt for fysikk Lade EKSAMEN I: MNF FY 44 KVANTEMEKANIKK I DATO: Tirsdag 4. desember 999 TID: 9.00 5.00 Antall vekttall: 4 Antall sider: 3 Sensurdato:
UNIVERSITETET I OSLO
 Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
Determinanter. Kapittel 6. Determinanter for 2 2-matriser. La oss beregne arealet av dette parallellogrammet. Vi tegner på noen hjelpelinjer:
 Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
Løsningsforslag til øving 5
 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2009. Løsningsforslag til øving 5 Oppgave 1 a) var C er korrekt. Fasehastigheten er gitt ved v ω k og vi ser fra figuren at dette forholdet
FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2009. Løsningsforslag til øving 5 Oppgave 1 a) var C er korrekt. Fasehastigheten er gitt ved v ω k og vi ser fra figuren at dette forholdet
Det matetmatisk-naturvitenskapelige fakultet Midtveis -eksamen i AST1100, 10 oktober 2007, Oppgavesettet er på 6 sider
 UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Midtveis -eksamen i AST1100, 10 oktober 2007, 14.30 17.30 Oppgavesettet er på 6 sider Konstanter og uttrykk som kan være nyttige: Lyshastigheten:
UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Midtveis -eksamen i AST1100, 10 oktober 2007, 14.30 17.30 Oppgavesettet er på 6 sider Konstanter og uttrykk som kan være nyttige: Lyshastigheten:
Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011
 Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011 Oppgave 1. a) Vi velger her, og i resten av oppgaven, positiv retning oppover. Dermed gir energibevaring m 1 gh = 1 2 m 1v 2 0 v 0 = 2gh. Rett
Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011 Oppgave 1. a) Vi velger her, og i resten av oppgaven, positiv retning oppover. Dermed gir energibevaring m 1 gh = 1 2 m 1v 2 0 v 0 = 2gh. Rett
Løsningsforslag. b) Hva er den totale admittansen til parallellkoblingen i figuren over? Oppgi både modul og fasevinkel.
 Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Kapittel 23 KURSREGNING, FORHOLD OG PROPORSJONER
 Valuta Kjøp Antall AUD Australske ollar 4,1050 1 CAD Canaiske ollar 4,6630 1 CHF Sveitsiske franc 493,5000 100 CYP Kypriotiske pun 1,3950 1 DKK Danske kroner 97,8700 100 EUR Euro 7,785 1 GBP Pun sterling
Valuta Kjøp Antall AUD Australske ollar 4,1050 1 CAD Canaiske ollar 4,6630 1 CHF Sveitsiske franc 493,5000 100 CYP Kypriotiske pun 1,3950 1 DKK Danske kroner 97,8700 100 EUR Euro 7,785 1 GBP Pun sterling
Løsningsforslag til utvalgte oppgaver i kapittel 10
 Løsningsforslag til utvalgte oppgaver i kapittel 0 I kapittel 0 får du trening i å løse ulike typer differensialligninger, og her får du bruk for integrasjonsteknikkene du lærte i forrige kapittel. Men
Løsningsforslag til utvalgte oppgaver i kapittel 0 I kapittel 0 får du trening i å løse ulike typer differensialligninger, og her får du bruk for integrasjonsteknikkene du lærte i forrige kapittel. Men
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
Prøveeksamen i MAT 1100, H-03 Løsningsforslag
 Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Det matetmatisk-naturvitenskapelige fakultet Prøveeksamen i AST1100 Oppgavesettet inkludert formelsamling er på 13 sider
 UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Prøveeksamen i AST1100 Oppgavesettet inkludert formelsamling er på 13 sider Konstanter og formelsamling finner du bakerst Vær nøye med
UNIVERSITETET I OSLO Det matetmatisk-naturvitenskapelige fakultet Prøveeksamen i AST1100 Oppgavesettet inkludert formelsamling er på 13 sider Konstanter og formelsamling finner du bakerst Vær nøye med
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
AST1010 En kosmisk reise
 AST1010 En kosmisk reise Forelesning 19: Kosmologi, del I Innhold Einsteins universmodell Friedmann, Lemaitre, Hubble og Big Bang AvstandssCgen Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman
AST1010 En kosmisk reise Forelesning 19: Kosmologi, del I Innhold Einsteins universmodell Friedmann, Lemaitre, Hubble og Big Bang AvstandssCgen Bondi, Gold, Hoyle og Steady State Gamow, Alpher, Herman
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: AST1010 - Astronomi - en kosmisk reise Eksamensdag: Onsdag 12. november 2014 Tid for eksamen:0900-1200 Oppgavesettet er på 2
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: AST1010 - Astronomi - en kosmisk reise Eksamensdag: Onsdag 12. november 2014 Tid for eksamen:0900-1200 Oppgavesettet er på 2
Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl.
 1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
AST1010 En kosmisk reise
 AST1010 En kosmisk reise Forelesning 20: Kosmologi, del 2 Temaer Mørk energi Inflasjon Hvordan startet det hele? Universet akselerer 1 Expansion History of the Universe Perlmutter, Physics Today (2003)
AST1010 En kosmisk reise Forelesning 20: Kosmologi, del 2 Temaer Mørk energi Inflasjon Hvordan startet det hele? Universet akselerer 1 Expansion History of the Universe Perlmutter, Physics Today (2003)
Grensesjikts approksimasjon. P.-Å. Krogstad
 Norges teknisk- naturvitenskapelige universitet (NTNU) Fakultetet for ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk N-749 Tronheim - NTNU Grensesjikts approksimasjon P.-Å. Krogsta
Norges teknisk- naturvitenskapelige universitet (NTNU) Fakultetet for ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk N-749 Tronheim - NTNU Grensesjikts approksimasjon P.-Å. Krogsta
LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF5045 NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
Teknisk appendiks ECON 2915 Vekst og næringsstruktur
 Teknisk appeniks ECON 2915 Vekst og næringsstruktur KÅRE BÆVRE Høsten 2005 Versjon 1 Dette notatet er ment som en støtte for stuenter som tar kurset ECON 2915 - Vekst og utvikling. Her behanles en el sentrale
Teknisk appeniks ECON 2915 Vekst og næringsstruktur KÅRE BÆVRE Høsten 2005 Versjon 1 Dette notatet er ment som en støtte for stuenter som tar kurset ECON 2915 - Vekst og utvikling. Her behanles en el sentrale
Kap. 5: Numeriske løsningsmetoder
 MEK4510 p. 3 Kap. 5: Numeriske løsningsmetoder Tidsintegrasjon for problemer med én frihetsgrad Analytisk løsning av differensiallikningen for enkle problemer Fourier-analyse for generelle, periodiske
MEK4510 p. 3 Kap. 5: Numeriske løsningsmetoder Tidsintegrasjon for problemer med én frihetsgrad Analytisk løsning av differensiallikningen for enkle problemer Fourier-analyse for generelle, periodiske
FYS2140 Kvantefysikk, Oblig 3. Sindre Rannem Bilden,Gruppe 4
 FYS40 Kvantefysikk, Oblig 3 Sindre Rannem Bilden,Gruppe 4. februar 05 Obliger i FYS40 merkes med navn og gruppenummer! Dette oppgavesettet sveiper innom siste rest av Del I av pensum, med tre oppgaver
FYS40 Kvantefysikk, Oblig 3 Sindre Rannem Bilden,Gruppe 4. februar 05 Obliger i FYS40 merkes med navn og gruppenummer! Dette oppgavesettet sveiper innom siste rest av Del I av pensum, med tre oppgaver
