Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Lørdag 26. mai 2001
|
|
|
- Asbjørg Kristiansen
- 7 år siden
- Visninger:
Transkript
1 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 8 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF407 KLASSISK FELTTEORI Lørdag 6. mai 001 Oppgavesettet gitt av Kåre Olaussen. Dette løsningsforslaget er på 8 sider. Oppgave 1 I denne oppgaven skal du se på noen aspekter ved modellen definert ved Klein-Gordon) Lagrangetettheten L = µϕ) µ ϕ) λ ϕ ϕ) n, 1) der λ > 0 og n > 1. a) Skriv ned, eller utled, feltligningene for denne modellen. Euler-Lagrange ligningene er på generell form µ µ ϕ a ) = ϕ a. ) I dette tilfellet får vi, for henholdsvis ϕ a = ϕ og ϕ a = ϕ, µ µ ϕ + nλ ϕ ϕ) n 1 ϕ = 0, 3) µ µ ϕ + nλ ϕ ϕ) n 1 ϕ = 0. 4) Kommentar: En fallgrube her og i en tilsvarende utregning av Nötherstrømmer) er at man setter istedet for µϕ) = µϕ, µϕ) = µϕ, µϕ ) = µϕ, µϕ ) = µϕ. NB! Feil! b) Anta en løsning av formen ϕx) = A e iωt, der A er en positiv, reell konstant. Finn sammenhengen mellom ω og A. Vi setter den foreslåtte løsningen inn i 3) og finner, siden 0 = [ ω ) + nλa n ] A e iωt = 0, c c t,
2 Løsning SIF407 Klassisk feltteori, 6. mai 001 Side av 8 med løsning ω = c nλ A n 1. 5) Kommentar: Det er mange ekvivalente måter å skrive denne sammenhengen på, men i) det må ikke være noen gjenværende tidsavhengighet i denne sammenhengen for da har man ikke vist eksistens av løsning) og ii) en imaginær ω bør få alle varsellamper til å blinke! c) Lagrangetettheten 1) er invariant under fasetransformasjoner ϕx) e iɛ ϕx), ϕ x) e iɛ ϕ x). 6) Skriv ned, eller utled, den konserverte strømmen, j µ, som opptrer som konsekvens av denne kontinuerlige symmetrien. I dette tilfellet har vi ϕ = iϕ, ϕ = iϕ og L = 0, så vi får j µ = µ ϕ) ϕ + µ ϕ ) ϕ = i µ ϕ ϕ ϕ µ ϕ). 7) d) Vi definerer en antallstetthet ρ 1 c j0. Finn, for løsningen fra punkt b), sammenhengen mellom ρ og A. Ved bruk av overstående fås ρ = ω c c A = nλa n+1. 8) c Kommentar: Prefaktoren 1 i definisjonen av ρ kan virke umotivert det var, fornuftig nok, ingen c som hadde bekymret seg over dette på eksamen). Den er tatt med for å at ρ skal bli dimensjonsmessig korrekt for en antallstetthet, [ρ] = m 3. Vi kan se dette av følgende analyse som ikke var forventet av kandidatene): For at virkningen S = dt d 3 r L skal få riktig dimensjon, [S] = kg m /s, må dimensjonen til ϕ-feltet tilfredstille [ϕ] = kg m/s som vi finner ut ved å se på µϕ µ ϕ-leddet i L). Da blir [ j 0] = m 1 [ϕ] = kg/s, så vi må dele med en størrelse som har dimensjon kg m 3 /s for å få et dimensjonsmessig riktig uttrykk. Kombinasjonen c oppfyller denne betingelsen. e) Virkningen S = 1 c d 4 x L definert fra Lagrangetettheten 1) er invariant under translasjoner i tid og rom, ϕx) ϕx + ɛe ν) ), ϕ x) ϕ x + ɛe ν) ), 9) der e ν) er en enhetsvektor i ν-retningen, e µ ν) = ηµ ν. Skriv ned, eller utled, den konserverte tensoren, T µ ν, som opptrer som konsekvens av disse kontinuerlige symmetriene. I dette tilfellet har vi ϕ = e µ ν) µϕ = ν ϕ, ϕ = e µ ν) µϕ = ν ϕ, L = e µ ν) µl = µ η µ ν L. Vi finner en konservert strøm for hver indeks ν. Tilsammen danner de energi-impuls tensoren T µ ν = µ ϕ ν ϕ + ν ϕ ν ϕ η µ ν L, 10)
3 Løsning SIF407 Klassisk feltteori, 6. mai 001 Side 3 av 8 med L er gitt av ligning 1). Kommentar: Skuffende mange får problemer her; det straffer seg også på de neste punktene. Men energi-impuls tensoren er et av de mest sentrale begrepene i feltteori, så det er ikke urimelig at man skal få til noe å jobbe videre med her selv om det ikke nødvendigvis er helt riktig). f) Trykket p i systemet er gitt ved p = 1 3 T i i. 11) Finn, for løsningen fra punkt b), tilstandsligningen sammenhengen mellom p og ρ). I dette tilfellet avhenger ikke feltene av posisjonen, så vi har Tj i = ηi j L = δi jl, dvs at trykket er lik Lagrangetettheten p = 1 ω ) 3 δi i L = L = ϕ ϕ λ ϕ ϕ) n = n 1) λ ϕ ϕ) n = n 1) λa n. c Vi eliminerer A til fordel for tettheten ρ, og finner en tilstandsligning ) c n/n+1) p = n 1) λ ρ n/n+1). 1) nλ Kommentar: Ligning 1) regnes her som fullgodt svar. Men for praktisk bruk vil det være mer hensiktsmessig å formulere den på en dimensjonsmessig mer opplagt form, nemlig p = k BT 0 ρa 3 ) η ρ, 13) der η = n 1) / n + 1), a er en karakteristisk lengde for modellen slik at ρa 3 blir dimensjonsløs) og k BT 0 er en karakteristisk energi for modellen. Størrelsene a og k BT 0 må konstrueres fra, c og λ. Et mulig valg er a = λ c) n 1) 1/n 4), 14) k BT 0 = n 1) 4n) n/n+1) c a. 15) For å verifisere at disse størrelsene er dimensjonsmessig korrekte observerer vi at [ λ ϕ ϕ) n 1] = ) n 1 [ [ µ µ ] = m, dvs. at [λ] = ] 1 kgm og derfor at λ c) n 1 = m n 4). Merk at dette ikke fungerer når n =. I dette tilfellet har ikke modellen noen naturlig tilordnet lengde den er skalainvariant. m g) Energitettheten u i systemet er gitt ved s u = T ) Finn, for løsningen fra punkt b), sammenhengen mellom energitetthet u og trykk p. Vi finner ω ) u = T0 0 = ϕ ϕ η 0 c 0L = n + 1) λ ϕ ϕ) n = n + 1 p. 17) n 1 Kommentar: Alternativt hvis man ikke har funnet uttrykket for T µ ν) kan man her benytte det faktum at T0 0 er lik Hamiltontettheten, T 0 0 = H = ϕ ϕ + ϕ ϕ L. Merk forøvrig at vi får u = 3p når n = skala-invariant teori); den samme relasjonen gjelder for elektromagnetiske felter. Dette betyr at energi-impuls tensoren er sporløs, T µ µ = 0, en karakteristisk egenskap for skalainvariante modeller.
4 Løsning SIF407 Klassisk feltteori, 6. mai 001 Side 4 av 8 Oppgave I denne oppgaven skal du studere bevegelse av punktpartikler i et statisk, rotasjonssymmetrisk rom med linjeelement ds = Ar)c dt Br)dr r sin ϑdϑ + dϕ ). 18) Bevegelsesligningene kan utledes fra Lagrangefunksjonen der τ er proposjonal med) egentiden. L = 1 dxµ dx ν gµνx) dτ dτ, 19) a) Anta at bevegelsen skjer i ekvator-planet, ϑ = π/, og utled bevegelsesligningene for tτ), rτ) og ϕτ). Det eksplisitte uttrykket for Lagrangefunksjonen blir når ϑ = 0) L = 1 Ar)c ṫ Br) ṙ r ϕ ). 0) Merk at denne Lagrangefunksjonen egentlig må multipliseres med en uttrykk med dimensjon kg f. eks. massen m til partikkelen) for at virkningen skal bli dimensjonsmessig korrekt. Men dette er uten betydning for bevegelsesligningene, som har formen d dτ ẋ µ = x µ, for x µ henholdsvis r, t og ϕ, der ẋ µ = dx µ /dτ. For Lagrangefunksjonen 0) gir dette der betyr derivasjon med hensyn på r. d dτ Br) ṙ = 1 A r)c ṫ 1 B r) ṙ r ϕ, 1) d dτ Ar)c ṫ = 0, ) d dτ r ϕ = 0, 3) Kommentar: Dette er et tilfelle der mere arbeid ikke nødvendigvis er bedre. Det har ingen hensikt å utføre τ-derivasjonene på venstre side av 1 3); det fører bare til mindre gjennomskuelige uttrykk. Spesielt ) og 3) viser jo meget eksplisitt at Ar)c ṫ og r b) Lagrangefunksjonen 19) er invariant under transformasjonene t t + ɛ, ϕ ϕ + ɛ. ϕ er konserverte størrelser. Hvilke konserverte størrelser kan utledes fra disse kontinuerlige symmetriene? Kall de tilhørende bevegelseskonstantene for henholdsvis K t og K ϕ. Verifiser også konserveringslovene direkte fra bevegelsesligningene du fant i forrige punkt. Vi har henholdsvis t = 1 og ϕ = 1, så konserveringslovene blir K t = ṫ = Ar)c ṫ 4) K ϕ = ϕ = r ϕ 5) Vi observerer at ligning,3) nettopp har formen d dτ K t = 0, d dτ K ϕ = 0.
5 Løsning SIF407 Klassisk feltteori, 6. mai 001 Side 5 av 8 Kommentar: Mange oppdager at vi har henholdsvis tidstranslasjons symmetri og rotasjonssymmetri, slik at de konserverte størrelsene må være proprosjonale med) energi og dreieimpuls, men glemmer helt å gjøre rutinemessig bruk av Nöthers teorem. Noen finner konserveringslover ekvivalente med at ṫ og ϕ er konstante. Dette er generelt ikke korrekt, men det blir riktig når man spesialiserer til sirkulær bevegelse som i de siste deloppgavene. c) Anta nå at bevegelsen er en rent sirkulær, med radius r. Vis at dette setter en betingelse på forholdet mellom K ϕ og K t, av formen ) Kϕ = F r), 6) og bestem F r) uttrykt ved størrelser fra ligning 18). K t Vi kan bruke konserveringslovene 4,5) til å eliminere ṫ og ϕ. Innsatt i ligning 1) gir dette d dτ Br)c ṙ = 1 A r) Ar) c K t 1 B r) ṙ 1 r 3 K ϕ. 7) For en sirkelbevegelse er ṙ = r = 0, så ligningen over reduserer seg til med løsning 1 A r) Ar) c K t 1 r 3 K ϕ = 0, Kt K ϕ ) = Ar) c r 3 A r) Ved å ta kvadratroten av dette uttrykket fås to mulige fortegn; disse svarer til to mulige retninger for rotasjonen. d) Målt i koordinat-tiden t har partikkelen en hastighet v = r dϕ dt. Bestem hvordan v må avhenge av r for en sirkelbevegelse, og skriv ut dette mer eksplisitt for Schwarzschild-metrikken, Ar) = 1 RM r ), Br) = 1 RM r 8) ) 1, R M = MG c. 9) Hastigheten for en ren sirkelbevegelse) blir v = r dϕ dt = r dϕ/dτ) dt/dτ) = Ar)c r K ϕ ra = r) c. 30) K t Innsatt for Schwarzschild-metrikken gir dette RM MG v = r c = r, 31) nøyaktig det samme uttrykket som for ikke-relativistisk bevegelse i svakt gravitasjonsfelt og i overensstemmelse med Keplers tredje lov). e) En observatør som er i ro ved radius r måler partikkelens hastighet til v r = r dϕ dt r, der t r er tiden målt med lokal klokke altså egentiden til observatøren). Bestem hvordan v r må avhenge av r for en sirkelbevegelse i Schwarzschild-metrikken.
6 Løsning SIF407 Klassisk feltteori, 6. mai 001 Side 6 av 8 Vi må finne sammenhengen mellom t r og t. Fra linjeelementet 18) følger det at ds = c dt r = Ar)c dt 3) siden dr = dϕ = dϑ = 0 langs verdenslinjen til en observatør i ro. Altså er dt/dt r = Ar) 1/, så vi får i Schwarzschild-metrikken v r = dt r RM v = v = c. 33) dt r r R M r R M Kommentar: Merk at denne deloppgaven er uavhengig av de øvrige; den er bare et lett forkledd) spørsmål om beregning av egentid langs en spesifisert verdenslinje. f) Ved hvilken radius vil lyset kunne gå i sirkelbane i Schwarzschild-metrikken? Den lokale observatøren vil observere lyshastigheten korrekt, så lyset går i sirkelbane når v r = c, dvs. når R M /r R M ) = 1. Altså når r = 3 R M. 34) Alternativt for dem som ikke stoler på at den lokale observatøren måler lyshastigheten riktig) kan man bruke at ds = 0 langs lyskurver. Sirkulære lyskurver må derfor oppfylle betingelsen Ar)c ṫ = r ϕ. Eliminasjon av ṫ og ϕ til fordel for K t og K ϕ gir betingelsen ) Kt = Ar)c r, K ϕ som må være oppfylt sammen med ligning 8). Løsningen for Schwarzschild-metrikken er som før gitt ved ligning 34), så mistroen til den lokale observatøren er helt ubegrunnet. Kommentarer: Her forslo alle som foreslo noe) løsningen r = R M, men den er altså ikke riktig. Avslutningsvis kan det være grunn til å kommentere oppgavetekstens formulering om at τ er proporsjonal med) egentiden. Innsatt for en sirkelbevegelse finner vi sammenhengen ) ) d K s = t Ar)c K ϕ Ar) K d ) τ = r ra r) 1 ϕ r 3RM r d τ = K r ϕ d τ. 35) R M Her har vi i siste overgang satt inn for Schwarzschild-metrikken. Sålenge r > 3R M kan vi alltid velge K ϕ slik at d s = c d τ, så da blir τ lik egentiden. Men for lysbaner er jo d s = 0, så da er det ikke særlig praktisk å pålegge en slik identitet. Merk at hvis vi pålegger d s = c d τ så blir K ϕ = r K t = RM r 3R M c = 1 RM r r v r 1 v r/c), 36) c 1 v r/c). 37) Vi gjenkjenner 36) som det relativistiske uttrykket for dreieimpuls pr. masseenhet, mens den mindre gjenkjennbare ligningen 37) ser ut til å være det relativistiske energiuttrykket pr. masseenhet inkludert gravitasjonsenergien). I den ikke-relativistiske, svak felt grensen reduserer K t seg til et velkjent uttrykk, K t = c + 1 v G r + Oc ) Den relativistiske svak felt grensen av 37) forteller oss at også den kinetiske energien kobler til gravitasjon, og derfor bidrar til gravitasjonspotensialet.
7 Løsning SIF407 Klassisk feltteori, 6. mai 001 Side 7 av 8 Oppgave 3 I denne oppgave skal du se på noen aspekter av Einstein s gravitasjonsligninger i svak felt grensen. Dette vil si at man utvikler den metriske tensoren som g µνx) = η µν + h µνx), 38) og bare regner til første orden i den symmetriske tensoren h og dens deriverte). I denne oppgaven merker vi oss at alle størrelsene som skal beregnes avhenger av minst en gangs deriverte av metrikken, dvs. deriverte av tensoren h. Dette betyr at vi bruker opp en orden av h til dette, og dermed kan sette g = η når indekser skal heves eller senkes. For selve utregningen bruker vi de vedlagte generelle uttrykkene, med de forenklingene som kan gjøres fordi vi bare skal regne til første orden i h. a) Beregn konneksjonskoeffisientene Γ α βγ til første orden i h. Γ α βγ = 1 ηαµ h µβ,γ + h µγ,β h βγ,µ ). 39) b) Beregn Riemanntensoren R αβγδ til første orden i h. Siden Γ er av første orden i h tar vi ikke med Γ Γ-bidragene til R: R αβγδ = Γ αβδ,γ Γ αβγ,δ = 1 h αδ,βγ + h βγ,αδ h αγ,βδ h βδ,αγ ). 40) Kommentar: Siden h er en symmetrisk tensor, og derivasjonsrekkefølgen ikke spiller rolle, er det lett å verifisere at 40) oppfyller symmetriene R αβγδ = R γδαβ = R βαγδ, og med litt mere arbeid) at R αβγδ + R αγδβ + R αδβγ = 0. c) Vis at et felt av formen h µνx) = µλ νx) + νλ µx), 41) der Λ µx) er et vilkårlig to ganger deriverbart vektorfelt, ikke gir noe bidrag til Riemanntensoren. Vi setter ligning 41) inn i 40) og får åtte ledd R αβγδ = 1 Λ α,δβγ Λ α,γβδ + Λ β,γαδ Λ β,δαγ + Λ γ,βαδ Λ γ,αβδ + Λ δ,αβγ Λ δ,βαγ ). Disse kansellerer fordi derivasjonsrekkefølgen ikke spiller rolle. d) Beregn Riccitensoren R βδ til første orden i h. R βδ = 1 ) h α δ,αβ + hα β,αδ hα α,βδ h α βδ, α. 4) e) Anta at µ h µν = 0 vi kan alltid oppnå en slik situasjon ved gauge transformasjonen, h µν h µν + µλ ν + νλ µ, for passende Λ µ). Beregn i dette tilfellet Einsteintensoren G βδ til første orden i h. Med betingelsen µ h µν = 0 forenkles Riccitensoren til R βδ = 1 h α α,βδ + h α βδ, α ),
8 Løsning SIF407 Klassisk feltteori, 6. mai 001 Side 8 av 8 så skalar krumning blir R = h α β α, β = hα α. Einsteintensoren kan da skrives G βδ = 1 η βδ β δ ) h α α 1 h βδ. 43) f) Vis at konserveringsloven α G αβ = 0 alltid er oppfylt for det uttrykket du fant i forrige punkt. Vi finner α G αβ = 1 α η αβ α β ) h γ γ 1 α h αβ = 0, 44) fordi α η αβ α β ) = β β = 0, og fordi vi har pålagt betingelsen α h αβ = 0. Kommentarer: Her kom selvsagt!) alle som prøvde seg fram til svaret 0, men ikke alle helt uten å svindle med indekser. Hvis vi ikke pålegger betingelsen α h αβ = 0 finner vi ved litt mere regning G αβ = 1 K αβ η γδ K αγ η βδ + β γ η αδ γ δ η αβ) h γδ, 45) der K αβ = η αβ α β. Fordi αk αβ = 0, og α β γ η αδ γ δ η αβ) = δ γ β β γ δ = 0, vil 45) tilfredsstille αg αβ = 0 for alle tilstrekkelig deriverbare) h γδ. Det er videre praktisk å innføre tensoren h αβ = h αβ 1 η αβh λ λ, slik at h αβ = h αβ 1 η αβ h λ λ. Innsatt i 45) fås da G αβ = 1 h ) αβ αβ αγ + η hγδ,γδ h,γ β βγ α h,γ, 46) som hvis vi pålegger betingelsen h αβ,β = 0 vi kan alltid gjøre det) reduserer seg til Gαβ = 1 h αβ. Einsteins gravitasjonsligninger i svak felt grensen blir da Oppgitt: Denne ligningen kan enkelt løses ved Fourier transformasjon. Nöther s teorem: h αβ = 16πG c 4 T αβ. 47) J µ = µ ϕ a ) ϕa M µ, når 48) L = µ M µ, der X d dɛ X for X lik ϕ a og L. 49) ɛ=0 Noen relasjoner fra differensialgeometri: Γ α βγ = 1 gαµ g µβ,γ + g µγ,β g βγ,µ ), 50) R α βγδ = Γα βδ,γ Γα βγ,δ + Γα µγγ µ βδ Γα µδ Γµ βγ, 51) R βδ = R α βαδ, 5) G βδ = R βδ 1 g βδr. 53)
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsdag 8. august 2002
 NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
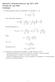 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i fag RELATIVISTISK KVANTEMEKANIKK Fredag 26. mai 2000 Tid: 09:00 14:00
 Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
Side 1 av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Navn: Kåre Olaussen Telefon: 9 36 52 Eksamen i fag 74327 RELATIVISTISK KVANTEMEKANIKK Fredag
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (bokmål) L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q i ; i = 1,
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
FYS 3120: Klassisk mekanikk og elektrodynamikk Formelsamling (bokmål) Våren 2014 1 Analytisk mekanikk Lagrangefunksjonen L = L(q, q, t), (1) er en funksjon av systemets generaliserte koordinater q = {q
Løsningsforslag til eksamen i FY8306 KVANTEFELTTEORI Fredag 9. juni 2006
 NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
NTNU Side av 3 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY836 KVANTEFELTTEORI Fredag 9. juni 6 Dette løsningsforslaget er på 3 sider, pluss et vedlegg
Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006
 NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
NTNU Side 1 av 4 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY3404/FY8307 RELATIVISTISK KVANTEMEKANIKK Fredag 9. juni 2006 Dette løsningsforslaget
FYS 3120: Klassisk mekanikk og elektrodynamikk
 FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
FYS 3120: Klassisk mekanikk og elektrodynamikk 1 Analytisk mekanikk Lagrangefunksjonen Formelsamling (nynorsk) L = L(q, q, t), (1) til eit fysisk system er ein funksjon av dei generaliserte koordinatane
Løsningsforslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag 26. mai 2005
 NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
NTNU Side av 5 Institutt or ysikk Fakultet or ysikk, inormatikk og matematikk Eksamen gitt av Kåre Olaussen Dette løsningsorslaget er på 5 sider. Løsningsorslag til eksamen i FY3464 KVANTEFELTTEORI Torsdag
LØSNINGSFORSLAG TIL EKSAMEN I TEP4145 KLASSISK MEKANIKK Mandag 21. mai 2007 kl Løsningsforslaget er på i alt 9 sider.
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I TEP4145
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai :00 13:00
 NTNU Side 1 av 2 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 2 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 19. mai 2012 09:00 13:00 Tillatte hjelpemidler:
Løsningsforslag til eksamen i FY3404 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 2004
 NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
NTNU Side av 7 Institutt for fysikk Løsningsforslag til eksamen i FY30 RELATIVISTISK KVANTEMEKANIKK Tirsdag 30. november 200 Dette løsningsforslaget er på 7 sider. Oppgave. Prosesser i QED Tegn, i de tilfeller
En kort introduksjon til generell relativitetsteori
 En kort introduksjon til generell relativitetsteori Generell relativitetsteori (GR) representerer vår mest fundamentale forståelse av tid, rom og gravitasjon, og er helt nødvendig for å formulere konsistente
En kort introduksjon til generell relativitetsteori Generell relativitetsteori (GR) representerer vår mest fundamentale forståelse av tid, rom og gravitasjon, og er helt nødvendig for å formulere konsistente
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Eksamen i fag FY1004 Innføring i kvantemekanikk Fredag 30. mai 2008 Tid: a 0 = 4πǫ 0 h 2 /(e 2 m e ) = 5, m
 Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
Side av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 5 7 Sensurfrist: Fredag 0 juni 008 Eksamen
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007
 Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK1110 Eksamensdag: Onsdag 6. juni 2012 Tid for eksamen: Kl. 0900-1300 Oppgavesettet er på 4 sider + formelark
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Eksamen i SIF5036 Matematisk modellering Onsdag 12. desember 2001 Kl
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Eksamen i fag FY1004 Innføring i kvantemekanikk Tirsdag 22. mai 2007 Tid:
 Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
Side 1 av 6 Norges teknisk-naturvitenskapelige universitet Institutt for fysikk Faglig kontakt under eksamen: Navn: Jan Myrheim Telefon: 73 59 36 53 (mobil 90 07 51 72) Sensurfrist: Tirsdag 12. juni 2007
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
(1 + x 2 + y 2 ) 2 = 1 x2 + y 2. (1 + x 2 + y 2 ) 2, x 2y
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
UNIVERSITETET I OSLO
 Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
Side av 5 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Onsdag. juni 2 Tid for eksamen: Kl. 9-3 Oppgavesettet er på 5 sider + formelark Tillatte hjelpemidler:
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
Løsningsforslag til eksamen i TFY4170 Fysikk 2 Fysikk 2 Lørdag 8. august 2005
 NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
NTNU Side 1 av 5 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i TFY4170 Fysikk Fysikk Lørdag 8. august 005 Merk: Hver del-oppgave teller like mye. Dette løsningsforslaget
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
Løsningsforslag til øving 3
 Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
FYS 3120/4120: Klassisk mekanikk og elektromagnetisme. Midtterminevaluering våren 2004 Obligatorisk sett innleveringsoppgaver
 FYS 3120/4120: Klassisk mekanikk og elektromagnetisme Midtterminevaluering våren 2004 Obligatorisk sett innleveringsoppgaver Godkjent besvarelse er nødvendig for å kunne avlegge eksamen. Besvarelsen teller
FYS 3120/4120: Klassisk mekanikk og elektromagnetisme Midtterminevaluering våren 2004 Obligatorisk sett innleveringsoppgaver Godkjent besvarelse er nødvendig for å kunne avlegge eksamen. Besvarelsen teller
KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME Onsdag 17. august 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 KONTINUASJONSEKSAMEN TFY4155 ELEKTROMAGNETISME
Løsningsforslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Torsdag 8. august 2013
 NTNU Sie 1 av 6 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY345 GRAVITASJON OG KOSMOLOGI Torsag 8. august 013 Dette løsningsforslaget er på 6 sier.
NTNU Sie 1 av 6 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY345 GRAVITASJON OG KOSMOLOGI Torsag 8. august 013 Dette løsningsforslaget er på 6 sier.
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 6. august 2003
 Noges teknisk natuvitenskapelige univesitet NTNU Side av 9 Institutt fo fysikk Fakultet fo natuvitenskap og teknologi Løsningsfoslag til eksamen i SIF47 KLASSISK FELTTEORI Onsdag 6. august 3 Dette løsningsfoslaget
Noges teknisk natuvitenskapelige univesitet NTNU Side av 9 Institutt fo fysikk Fakultet fo natuvitenskap og teknologi Løsningsfoslag til eksamen i SIF47 KLASSISK FELTTEORI Onsdag 6. august 3 Dette løsningsfoslaget
KORT INTRODUKSJON TIL TENSORER
 KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
KORT INTRODUKSJON TIL TENSORER Tensorer har vi allerede møtt i form av skalarer (tall) og vektorer. En skalar kan betraktes som en tensor av rang null (en komponent), mens en vektor er en tensor av rang
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011
 Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
Løysingsframlegg/skisse Eksamen TFY 4210 Kvanteteorien for mangepartikkelsystem 24. mai 2011 May 24, 2011 Oppgave 1 1) Ein global fasetransformasjon er på forma ψ ψe iα ψ ψ e iα, (1) der α er ein konstant.
1b) Schwarzschil-metrikken er iagonal, og vi har at g tt = 1, c = r, c ; g rr =, r r r r, =,1, r, ; g =,r ; g '' =,r sin : (9) At raielle baner eksist
 Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Løsningsforslag for FYS2140 Kvantemekanikk, Torsdag 16. august 2018
 Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
Institutt for fysikk Fakultet for fysikk, informatikk og matematikk. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 31.
 NTNU Side av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 3. mai 007 Oppgave.
NTNU Side av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i FY3403 PARTIKKELFYSIKK Torsdag 3. mai 007 Oppgave.
Løsningsforslag til eksamen i SIF4022 Fysikk 2 Tirsdag 3. desember 2002
 NTNU Side 1 av 6 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF40 Fysikk Tirsdag 3. desember 00 Dette løsningsforslaget er på 6 sider. Oppgave 1. a) Amplituden
NTNU Side 1 av 6 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF40 Fysikk Tirsdag 3. desember 00 Dette løsningsforslaget er på 6 sider. Oppgave 1. a) Amplituden
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK Mandag 10. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 BØLGEFYSIKK
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 10.2.27 a) Vi skal vise at u + v 2 = u 2 + 2u v + v 2. (1) Som boka nevner på side 581,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA1102 Grunnkurs i analyse II Vår 2019 10.2.27 a) Vi skal vise at u + v 2 = u 2 + 2u v + v 2. (1) Som boka nevner på side 581,
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, 8.juni 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober :15 16:00
 NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
NTNU Side 1 av 6 Institutt for fysikk Midtsemesterprøve i FY3403 PARTIKKELFYSIKK Onsdag 22. oktober 2008 14:15 16:00 Tillatte hjelpemidler: Vanlig kalkulator Husk å skrive studentnummeret ditt på hvert
FY1006/TFY Løsning øving 9 1 LØSNING ØVING 9
 FY1006/TFY415 - Løsning øving 9 1 Løsning oppgave Numerisk løsning av den tidsuavhengige Schrödingerligningen LØSNING ØVING 9 a. Alle leddene i (1) har selvsagt samme dimensjon. Ved å dividere ligningen
FY1006/TFY415 - Løsning øving 9 1 Løsning oppgave Numerisk løsning av den tidsuavhengige Schrödingerligningen LØSNING ØVING 9 a. Alle leddene i (1) har selvsagt samme dimensjon. Ved å dividere ligningen
FYS307 - V03 OPPGAVEARK A. Oppgave A1: Tidekraftpendel
 FYS307 - V03 OPPGAVEARK A Oppgave A1: Tidekraftpendel a) Utled uttrykket for perioden til en matematisk pendel med lengde l i et område der tyngdens akselerasjon er g. Hva er perioden til en matematisk
FYS307 - V03 OPPGAVEARK A Oppgave A1: Tidekraftpendel a) Utled uttrykket for perioden til en matematisk pendel med lengde l i et område der tyngdens akselerasjon er g. Hva er perioden til en matematisk
LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160 BØLGEFYSIKK Onsdag 20. desember 2006 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY1002 og TFY4160
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 6 juni 2017 Tid for eksamen: 14:30 18:30 (4 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK 1110 Eksamensdag: 6 juni 2017 Tid for eksamen: 14:30 18:30 (4 timer) Oppgavesettet er på 4 sider Vedlegg: Formelark Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
Eksamen i FY3403/TFY4290 PARTIKKELFYSIKK Mandag 12. desember :00 13:00
 NTNU Side 1 av 6 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 5 eller 45 43 71 70 Eksamen i FY3403/TFY490 PARTIKKELFYSIKK Mandag 1. desember 005 09:00 13:00
NTNU Side 1 av 6 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 9 36 5 eller 45 43 71 70 Eksamen i FY3403/TFY490 PARTIKKELFYSIKK Mandag 1. desember 005 09:00 13:00
LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF5045 NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
EKSAMEN I SIF4018 MATEMATISK FYSIKK mandag 28. mai 2001 kl
 Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPEIGE UNIVERSITET Institutt for fysikk og Institutt for matematiske fag Faglig kontakt under eksamen: Professor Per Hemmer, tel. 73 59 36 48 Professor Helge Holden,
Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPEIGE UNIVERSITET Institutt for fysikk og Institutt for matematiske fag Faglig kontakt under eksamen: Professor Per Hemmer, tel. 73 59 36 48 Professor Helge Holden,
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Faglig kontakt under eksamen: Navn: Bård Skaflestad (946867) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Faglig kontakt under eksamen: Navn: Bård Skaflestad (946867) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
EKSAMEN I NUMERISK MATEMATIKK(TMA4215) Lørdag 20. desember 2003 Tid: 09:00 14:00, Sensur:
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].
![Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm]. Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].](/thumbs/58/41840831.jpg) Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Obligatorisk oppgave nr 4 FYS Lars Kristian Henriksen UiO
 Obligatorisk oppgave nr 4 FYS-13 Lars Kristian Henriksen UiO. februar 15 Oppgave 1 Vi betrakter bølgefunksjonen Ψ(x, t) Ae λ x e iωt hvor A, λ og ω er positive reelle konstanter. a) Finn normaliseringen
Obligatorisk oppgave nr 4 FYS-13 Lars Kristian Henriksen UiO. februar 15 Oppgave 1 Vi betrakter bølgefunksjonen Ψ(x, t) Ae λ x e iωt hvor A, λ og ω er positive reelle konstanter. a) Finn normaliseringen
a) Bruk en passende Gaussflate og bestem feltstyrken E i rommet mellom de 2 kuleskallene.
 Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
v(t) = r (t) = (2, 2t) v(t) = t 2 T(t) = 1 v(t) v(t) = (1 + t 2 ), t 2 (1 + t 2 ) t = 2(1 + t 2 ) 3/2.
 NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
NTNU Institutt for matematiske fag TMA40 Matematikk, øving, vår 0 Løsningsforslag Notasjon og merknader Hvis boken skriver en vektor som ai + bj + ck hender det at jeg skriver den som a, b, c). Jeg benytter
Løsningsforslag til øving 5
 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2009. Løsningsforslag til øving 5 Oppgave 1 a) var C er korrekt. Fasehastigheten er gitt ved v ω k og vi ser fra figuren at dette forholdet
FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2009. Løsningsforslag til øving 5 Oppgave 1 a) var C er korrekt. Fasehastigheten er gitt ved v ω k og vi ser fra figuren at dette forholdet
Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, :00 13:00
 NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
NTNU Page 1 of 4 Institutt for fysikk Contact during the exam: Professor Kåre Olaussen Telephone: 9 36 52 or 45 43 71 70 Exam in FY3464 QUANTUM FIELD THEORY I Friday november 30th, 2007 09:00 13:00 Allowed
EKSAMEN I: BIT260 Fluidmekanikk DATO: 15. mai TILLATTE HJELPEMIDDEL: Kalkulator, én valgfri standard formelsamling. I h c A.
 DET TEKNISK-NATURVITENSKAPELIGE FAKULTET EKSAMEN I: BIT60 Fluidmekanikk DATO: 15. mai 006 TID FOR EKSAMEN: kl. 09-13 (4 timer) TILLATTE HJELPEMIDDEL: Kalkulator, én valgfri standard formelsamling OPPGAVESETTET
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET EKSAMEN I: BIT60 Fluidmekanikk DATO: 15. mai 006 TID FOR EKSAMEN: kl. 09-13 (4 timer) TILLATTE HJELPEMIDDEL: Kalkulator, én valgfri standard formelsamling OPPGAVESETTET
Oppgavesettet har 10 punkter 1, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen.
 NTNU Institutt for matematiske fag SIF55 Matematikk 2 4. mai 999 Løsningsforslag Oppgavesettet har punkter, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen. i alternativ (3, ii alternativ (2. 2 a For
NTNU Institutt for matematiske fag SIF55 Matematikk 2 4. mai 999 Løsningsforslag Oppgavesettet har punkter, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen. i alternativ (3, ii alternativ (2. 2 a For
EKSAMENSOPPGAVE. Fys-1002 Elektromagnetisme. Adm.bygget B154 Kalkulator med tomt dataminne, Rottmann: Matematisk formelsamling
 Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
Fakultet for naturvitenskap og teknologi EKSAMENSOPPGAE Eksamen i: Fys-1002 Elektromagnetisme Dato: Onsdag 26. september 2018 Klokkeslett: Kl. 9:00-13:00 Sted: Tillatte hjelpemidler: Adm.bygget B154 Kalkulator
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Tirsdag 27. mai 2008 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
Eksamen, høsten 14 i Matematikk 3 Løsningsforslag
 Oppgave 1. Fra ligningen Eksamen, høsten 14 i Matematikk 3 Løsningsforslag x 2 64 y2 36 1 finner vi a 64 8 og b 36 6. Fokus til senter avstanden er da gitt ved c a 2 + b 2 64 + 36 1 1. Dermed er fokuspunktene
Oppgave 1. Fra ligningen Eksamen, høsten 14 i Matematikk 3 Løsningsforslag x 2 64 y2 36 1 finner vi a 64 8 og b 36 6. Fokus til senter avstanden er da gitt ved c a 2 + b 2 64 + 36 1 1. Dermed er fokuspunktene
Øving 4. a) Verifiser at en transversal bølge som forplanter seg langs x-aksen med utsving D med komponentene
 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 010. Veiledning: Tirsdag 1. og onsdag. september. Innleveringsfrist: Mandag 7. september kl 1:00. Øving 4 Oppgave 1 a) Verifiser at en transversal
FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 010. Veiledning: Tirsdag 1. og onsdag. september. Innleveringsfrist: Mandag 7. september kl 1:00. Øving 4 Oppgave 1 a) Verifiser at en transversal
Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011
 Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011 Oppgave 1. a) Vi velger her, og i resten av oppgaven, positiv retning oppover. Dermed gir energibevaring m 1 gh = 1 2 m 1v 2 0 v 0 = 2gh. Rett
Løsningsforslag EKSAMEN TFY4102 FYSIKK Fredag 10. juni 2011 Oppgave 1. a) Vi velger her, og i resten av oppgaven, positiv retning oppover. Dermed gir energibevaring m 1 gh = 1 2 m 1v 2 0 v 0 = 2gh. Rett
Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: Løsningsforslag. Oppgave 1
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: 09.00 12.00 Løsningsforslag Oppgave 1 Robertson-Walker metrikken
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST2110 Universet Eksamensdag: Fredag 9. juni 2006 Tid for eksamen: 09.00 12.00 Løsningsforslag Oppgave 1 Robertson-Walker metrikken
Anbefalte oppgaver - Løsningsforslag
 TMA405 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 6 3..9: Vi starter med å finne de kritiske punktene. De deriverte blir T x (x, y) = ( x xy)e x y T y (x, y) = ( y xy)e x y, slik at de kritiske
TMA405 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 6 3..9: Vi starter med å finne de kritiske punktene. De deriverte blir T x (x, y) = ( x xy)e x y T y (x, y) = ( y xy)e x y, slik at de kritiske
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME Mandag 4. desember 2006 kl
 NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
NOGES TEKNSK- NATUVTENSKAPELGE UNVESTET NSTTUTT FO FYSKK Side 1 av 5 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 EKSAMEN FY1003 ELEKTSTET OG MAGNETSME Mandag 4. desember
Løsningsforslag til eksamen i TFY4170 Fysikk august 2004
 NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
LØSNINGSFORSLAG TIL EKSAMEN I TFY4155 ELEKTROMAGNETISME FY1003 ELEKTRISITET OG MAGNETISME Tirsdag 31. mai 2005 kl
 NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
NORGES TEKNISK- NATURVITENSKAPEIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 ØSNINGSFORSAG TI EKSAMEN I TFY4155 EEKTROMAGNETISME
LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag 3. desember 2007 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 7 59 6 6 / 45 45 55 LØSNINGSFORSLAG TIL EKSAMEN I TFY4160 BØLGEFYSIKK Mandag.
EKSAMENSOPPGAVE I FYS-1001
 side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august :00 13:00
 NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
NTNU Side 1 av 3 Institutt for fysikk Faglig kontakt under eksamen: Professor Kåre Olaussen Telefon: 45 43 71 70 Eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Lørdag 11. august 2012 09:00 13:00 Tillatte hjelpemidler:
Konstanter og formelsamling finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side en selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Konteeksamen i AST1100, 8.januar 2009, 14.30 17.30 Oppgavesettet inkludert formelsamling er på 10 sider Tillatte hjelpemidler: medbrakt
Løsningsforslag til eksamen i TMA4105 matematikk 2,
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
Eksamen i: FYS145 - Kvantefysikk og relativitetsteori Eksamensdag: Mandag 10. mai 2004, kl. 14.00-17.00 (3 timer)
 1 NORGES LANDBRUKSHØGSKOLE Institutt for matematiske realfag og teknologi Eksamen i: FYS145 - Kvantefysikk og relativitetsteori Eksamensdag: Mandag 1. mai 24, kl. 14.-17. (3 timer) Tillatte hjelpemidler:
1 NORGES LANDBRUKSHØGSKOLE Institutt for matematiske realfag og teknologi Eksamen i: FYS145 - Kvantefysikk og relativitetsteori Eksamensdag: Mandag 1. mai 24, kl. 14.-17. (3 timer) Tillatte hjelpemidler:
FYS2140 Kvantefysikk, Løsningsforslag for Oblig 1
 FYS4 Kvantefysikk, Løsningsforslag for Oblig. januar 8 Her er løsningsforslag for Oblig som dreide seg om å friske opp en del grunnleggende matematikk. I tillegg finner dere til slutt et løsningsforslag
FYS4 Kvantefysikk, Løsningsforslag for Oblig. januar 8 Her er løsningsforslag for Oblig som dreide seg om å friske opp en del grunnleggende matematikk. I tillegg finner dere til slutt et løsningsforslag
SIF5005 Matematikk 2, 13. mai 2002 Løsningsforslag
 SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
TFY Øving 8 1 ØVING 8
 TFY4215 - Øving 8 1 ØVING 8 Mye av poenget med oppgave 2 er å øke fortroligheten med orbitaler, som er bølgefunksjoner i tre dimensjoner. Fordi spørsmålene/oppdragene er spredt litt rundt omkring, markeres
TFY4215 - Øving 8 1 ØVING 8 Mye av poenget med oppgave 2 er å øke fortroligheten med orbitaler, som er bølgefunksjoner i tre dimensjoner. Fordi spørsmålene/oppdragene er spredt litt rundt omkring, markeres
Oppgave 2 Vi ser på et éndimensjonalt system hvor en av de stasjonære tilstandene ψ(x) er gitt som { 0 for x < 0, ψ(x) = Ne ax (1 e ax (1)
 Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
Oppgave Gjør kort rede for hva den fotoelektriske effekt er, hva slags konklusjoner man kunne trekke fra observasjoner av denne i kvantefysikkens fødsel, og beskriv et eksperiment som kan observere og
FY1006/TFY Løsning øving 8 1 LØSNING ØVING 8. a. (a1): Ved kontroll av egenverdiene kan vi se bort fra normeringsfaktorene.
 FY16/TFY415 - Løsning øving 8 1 Løsning oppgave 3 Vinkelfunksjoner, radialfunksjoner og orbitaler for hydrogenlignende system LØSNING ØVING 8 a. (a1: Ved kontroll av egenverdiene kan vi se bort fra normeringsfaktorene.
FY16/TFY415 - Løsning øving 8 1 Løsning oppgave 3 Vinkelfunksjoner, radialfunksjoner og orbitaler for hydrogenlignende system LØSNING ØVING 8 a. (a1: Ved kontroll av egenverdiene kan vi se bort fra normeringsfaktorene.
EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Side 1 av 6 Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 41 43 39 30 EKSAMEN FY1003 ELEKTRISITET OG MAGNETISME
Løsningsforslag Matematisk modellering Øving 2, høst 2005
 Løsningsforslag Matematisk modellering Øving 2, høst 2005 Arne Morten Kvarving / Harald Hanche-Olsen 18. september 2005 Oppgave 3 The Boussinesq transformation: Vi skal se på ligningen ( Pe u T x + v T
Løsningsforslag Matematisk modellering Øving 2, høst 2005 Arne Morten Kvarving / Harald Hanche-Olsen 18. september 2005 Oppgave 3 The Boussinesq transformation: Vi skal se på ligningen ( Pe u T x + v T
Løsningsforslag til øving 5
 FY1001/TFY4145 Mekanisk fysikk. Institutt for fysikk, NTNU. Høsten 011. Løsningsforslag til øving 5 Oppgave 1 a) Energibevarelse E A = E B gir U A + K A = U B + K B Innsetting av r = L x i ligningen gir
FY1001/TFY4145 Mekanisk fysikk. Institutt for fysikk, NTNU. Høsten 011. Løsningsforslag til øving 5 Oppgave 1 a) Energibevarelse E A = E B gir U A + K A = U B + K B Innsetting av r = L x i ligningen gir
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
TFY4215 Innføring i kvantefysikk - Løsning øving 1 1 LØSNING ØVING 1
 TFY425 Innføring i kvantefysikk - Løsning øving Løsning oppgave a. LØSNING ØVING Vi merker oss at sannsynlighetstettheten, Ψ(x, t) 2 = A 2 e 2λ x, er symmetrisk med hensyn på origo. For normeringsintegralet
TFY425 Innføring i kvantefysikk - Løsning øving Løsning oppgave a. LØSNING ØVING Vi merker oss at sannsynlighetstettheten, Ψ(x, t) 2 = A 2 e 2λ x, er symmetrisk med hensyn på origo. For normeringsintegralet
Løsningsforslag Eksamen 28. mai 2003 SIF4048 Kjemisk fysikk og kvantemekanikk
 Eksamen SIF4048 8.05.03 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 8. mai 003 SIF4048 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, 0) = β/π exp( βx ) er symmetrisk med
Eksamen SIF4048 8.05.03 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 8. mai 003 SIF4048 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, 0) = β/π exp( βx ) er symmetrisk med
Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt.
 Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
Lørdagsverksted i fysikk. Institutt for fysikk, NTNU. Høsten 27. Veiledning: 29. september kl 12:15 15:. Løsningsforslag til øving 4: Coulombs lov. Elektrisk felt. Magnetfelt. Oppgave 1 a) C. Elektrisk
Løsningsforslag Eksamen 1. desember 2009 TFY4250/FY2045
 Eksamen TFY45/FY45 1. desember 9 - løsningsforslag 1 Oppgave 1 a. For n = 3j er Løsningsforslag Eksamen 1. desember 9 TFY45/FY45 ψ () 3j (L/3) = A sin(jπ) = og ψ () 3j (L/3) = A sin(jπ) =. Vi kan da konstatere
Eksamen TFY45/FY45 1. desember 9 - løsningsforslag 1 Oppgave 1 a. For n = 3j er Løsningsforslag Eksamen 1. desember 9 TFY45/FY45 ψ () 3j (L/3) = A sin(jπ) = og ψ () 3j (L/3) = A sin(jπ) =. Vi kan da konstatere
Løsningsforslag Eksamen 26. mai 2008 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY415 6. mai 8 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. mai 8 TFY415 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
Eksamen TFY415 6. mai 8 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. mai 8 TFY415 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
10 6 (for λ 500 nm); minste størrelse av
 Sensorveiledning Eksamen FYS130 Oppgave 1 ( poeng) a) Brytningdeksen er forholdet mellom lyshastigheten i vakuum og lyshastigheten i mediet; siden lyshastigheten i et medium er alltid mindre enn i vakuum,
Sensorveiledning Eksamen FYS130 Oppgave 1 ( poeng) a) Brytningdeksen er forholdet mellom lyshastigheten i vakuum og lyshastigheten i mediet; siden lyshastigheten i et medium er alltid mindre enn i vakuum,
Løsningsforslag til eksamen i klassisk mekanikk våren e N. R ρ m
 Løsningsforsag ti eksamen i kassisk mekanikk våren 010 Oppgave 1 ω v e T θ R ρ m e N Figure 1: a Lagrangefunksjonen er gitt ved: L = T V der T V er den kinetiske potensiee energien ti systemet. Finner
Løsningsforsag ti eksamen i kassisk mekanikk våren 010 Oppgave 1 ω v e T θ R ρ m e N Figure 1: a Lagrangefunksjonen er gitt ved: L = T V der T V er den kinetiske potensiee energien ti systemet. Finner
FYS1120 Elektromagnetisme, vekesoppgåvesett 9 Løsningsforslag
 FYS1120 Elektromagnetisme, vekesoppgåvesett 9 Løsningsforslag 16. november 2016 I FYS1120-undervisninga legg vi meir vekt på matematikk og numeriske metoder enn det oppgåvene i læreboka gjer. Det gjeld
FYS1120 Elektromagnetisme, vekesoppgåvesett 9 Løsningsforslag 16. november 2016 I FYS1120-undervisninga legg vi meir vekt på matematikk og numeriske metoder enn det oppgåvene i læreboka gjer. Det gjeld
LØSNINGSFORSLAG EKSAMEN FYS120 VÅR 2017
 LØSNINGSFORSLAG EKSAMEN FYS120 VÅR 2017 Oppgave 1 a) Bruker bevaring av bevegelsesmengde i - og y-retning og velger positiv -akse mot høyre og positiv y-akse oppover, og lar vinkelen være = 24. Dekomponerer
LØSNINGSFORSLAG EKSAMEN FYS120 VÅR 2017 Oppgave 1 a) Bruker bevaring av bevegelsesmengde i - og y-retning og velger positiv -akse mot høyre og positiv y-akse oppover, og lar vinkelen være = 24. Dekomponerer
