til eksamen i SIF5036 Matematisk modellering 14. desember 2002.
|
|
|
- Oscar Viken
- 7 år siden
- Visninger:
Transkript
1 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Sie av 8 Løsningsforslag til eksamen i SIF5036 Matematisk moellering 4. esember Oppgave (a) Hvilke aksiomer om naturen ligger til grunn for imensjonsanalysen? Hva sier Buckingham s Pi-teorem, og hvoran kan en bruke teoremet til å vise at perioen for en penel må være uavhengig av ens masse? Alle relasjoner må være imensjonsmessig korrekte Ingen relasjon kan avhenge av tilfelig valgte enheter Hvis et fins en relasjon fins et også en ekvivalent relasjon Φ (R,, R N ) = 0 Ψ (π,, π N r ) = 0 er π,, π N r imensjonsløse kombinasjoner laget ve hjelp av r kjernevariable me uavhengig imensjon, er r er også rangen til imensjonsmatrisen. (b) Ve bestansvurering av skog ønsker en å estimere kubikkinnholet (volumet v) av et tre ve å måle imeteren ( ) ve bakken og høyen ( h) (et siste ve triangulering). I et eksempel i Minitab har en kommet fram vil følgee regressjonsmoell for kubikkinnholet i amerikansk kirsebærtre v /3 = β 0 + β + β 2 h + β 3 2, ( β i, i = 0,, 3 er regressjonskoeffisienter). Vis at imensjonsanalyse i steet anbefaler en relasjon på formen π = φ (π 2 ). Gi eksempel på hva φ kan være for iealiserte trær. Vi går ut fra en relasjon Φ (v,, h) = 0 Inngår bare en enhet (meter) i alle størrelsene, slik at et må være 3 = 2 imensjonsløse kombinasjoner π og π 2, og en relasjon π = φ (π 2 ). Vi kan velge som kjernevariabel slik at π = v/ 3 og π 2 = h/. Da får vi v 3 = φ ( h ). For et kjegleformet tre uten grener er v = πh 2 /2 slik at v = π h 3 2.
2 Sie 2 av 8 Oppgave 2 Ei elv renner ut et havbasseng. Elva bringer me seg san og leire, slik at bassenget etterhvert fylles opp. Vi skal sette opp en enkel enimensjonal moell for hvoran bassenget fylles, og vi antar at bassenget strekker seg fra x = 0 til + og har et konstant yp h ve t = 0. Vi antar at forholene på tvers (i y-retningen) er konstante. Mengen av san og leire som legger seg på bunnen pr. ti og flateenhet betegnes me Q (x, t). Vi beskriver vannypet ve z = b (x, t), x 0, t 0, og regner b (x, t) 0. Hvis bunnen skråner, vil partiklene på bunnen fortsette å bevege seg, og et har vist seg at enne forflytingen er proposjonal me hvor bratt bunnen er, vs. at volumfluksen har formen () j = k b x. (a) Still opp bevarelsesloven på integralform for et utsnitt av bunnen, a x b, og vis at vi på ifferensialform kommer fram til ei ligning for b (x, t) som i form er ientisk me varmeleningsligningen, (2) b t = k 2 b x + q. 2 Vi regner me et utsnitt me bree B og innfører først tetthet, fluks og kile. Her kan vi go la tettheten være en konstant massetetthet ρ. Fluksen blir a ρj og kile-funksjonen blir ρq (x, t). Vårt kontrollvolum har bree B, og går fra x = x 0 til x = x. Da får vi fra en generelle bevarelsesloven x x 0 ( ρb (b (x, t) h) x+ k b x (x, t) + k b ) x (x 0, t) ρb = Etter å ha forkortet me ρb gir ette x x 0 (b (x, t) h) x + ( k b x (x, t) + k b ) x (x 0, t) = x x 0 x x 0 q (x, t) (ρb) x. q (x, t) x, som blir bevarelsesloven på integralform. Hvis vi lar x x 0 og ivierer me (x x 0 ) blir ette på vanlig måte b (b h) = t t = k 2 b x + q. 2 (b) Anta at all grus og leire kommer inn ve x = 0, og tilførselen allti er tilstrekkelig til at ligning 2 holer og b (0, t) = 0 for t > 0. Gjør ree for at løsningen til 2 i ette tilfelle vil være en similaritetsløsning, og finn b (x, t) for x 0 og t > 0. Det oppgis at ligningen 2 y η + η y 2 2 η = 0
3 Sie 3 av 8 har generell løsning A + B erf (η/2), er erf (x) = 2 π x 0 exp ( s2 ) s. I ette tilfelle er alså kilen lokalisert til x = 0, slik at ligningen for x > 0 blir b t = kb xx. Vi skalerer b me h og kan a skrive løsningen b = hf (x, t, k) Det er ellers ikke umielbart opplagt at vi vil ha en similaritetsløsning sien yben h jo er en lengeskala. Men problemet er helt ekvivalent til en varmeleningssituasjon er temperaturen er konstant lik T 0 ve x = 0, og T når x. I ette tilfelle vil temperaturen kunne skrives T (x, t) = T 0 + (T T 0 ) τ (x, t, k), og a får vi en similaritetsløsning. Som for temperaturen må vi her erfor kunne skrive løsningen som ( ) x b = hβ = hβ (η) kt er β (0) = 0 og β (η) når η. Vi fører inn ette i ligningen etter å ha iviert me h: eller β t kβ xx = x 2 k t 3/2 β k kt β = 0, β + η 2 β = 0. Dette er oppgitt ligning, og vi ser umielbart at løsningen blir ( ) x b (x, t) = h erf. kt (c) Et mer realistisk scenario er at etterhvert som tien går (geologisk tisskala), vil strankanten s (t) flytte seg utover. Anta at vi har en konstant volumstrøm q 0 ut i bassengent pr. tis- og breeenhet ve strankanten, og at all san og leire tilføres på enne måten. Løsningen for b (x, t) blir a stasjonær i forhol til strana, vs. at b (x, t) kan skrives på formen { 0 x s (t) = Ut + x b (x, t) = 0 b 0 (x Ut x 0 ) x > Ut + x 0 Bestem hastigheten U og funksjonen b 0. Hvis vi kan gå ut fra en oppgitte formen på b, vil mengen av san og leire mellom s (t) og x = være konstant. Dette betyr at hastigheten som strana avanserer me, s/ = U, må matche q 0, vs. eller hb U = q 0 B, U = q 0 h. Vi lar nå η = x Ut x 0 og setter inn for b i ligningen er x > Ut + x 0 Ub 0 = kb 0
4 Sie 4 av 8 Ligningen for b 0 blir følgelig me generell løsning Her vil i tillegg b 0 + U k b 0 = 0 b 0 (η) = A + B exp ( Uk ) η b 0 (0) = 0, b 0 ( ) = h slik at en spesielle løsningen her blir ( b 0 (η) = h exp ( Uk ) η Vi setter inn i uttrykket for b og finner { b (x, t) = ) 0 x s (t) = Ut + x 0 h ( exp ( U k (x Ut x 0) ) ) x > Ut + x 0 Oppgave 3 Det er foreslått å moellere forekomsten av Kongekrabbe, K (t), i Varangerfjoren ve hjelp av følgene ifferensialligning K = rk ( K M ) ( K m ), 0 < m < M. (a) Hvilke egenskaper prøver moellen å beskrive og hvilke likevektspopulasjoner har vi? Vis hvoran en kan bruke lineær stabilitetsanalyse til å avgjøre stabiliteten av likevektspopulasjonene, og lag kvalitative skisser for utviklingen av K (t) for t > 0. Vi observerer først at bestanen vil vokse kun hvis Likevektspunktene er gitt ve m < K < M. K = 0, m, M, og ve å skissere trejegraspolynomet f (K) som utgjør høyresien, finner vi f (0) < 0, f (m) > 0, f (M) < 0. Vi utelater et enkle argumentet som avgjør stabilitet/ustabilitet, og ser altså her at 0 og M er stabile, mens m er ustabilt. Hvis bestanen er minre enn m, vil en ø ut.
5 Sie 5 av 8 Skisse inn her (b) En forenklet moell, som også omfatter fiskere, F (t), har etter skalering formen (3) F = F 2 + KF, K = K ( K) F Hvilke kvalitative egenskaper er byg inn i enne moellen? Det oppgis at banen F = 3K ( K) /2, 0 K <, er en løsning av lign. 3, og at enne banen eler første (F, K)-kvarant i to separate eler. Hva skjer når systemet befinner seg i en ubegrensee elen? Vi ser at hvis vi ikke har fiskere, vil veksten av Kongekrabbe følge en logisisk moell fiske vil minske veksten i Kongekrabbe hvis bestanen K < /2 er et lite interesse for fiske, slik at antall fiskere avtar hvis K > /2 øker antallet fiskere. Utenfor en oppgitte banen vil F > max (0, 3K ( K) /2), og ette betyr at < 0. Følgelig vil krabbebestanen allti ø ut. K (c) Bestem likevektspunktene for moellen i lign. 3 og finn ut hva e representerer. Hva ser ut til å skje i områet 0 K og 0 F 3K ( K) /2? De singulære punktene er gitt fra F 2 + KF = 0 K ( K) F = 0 me løsninger {F = 0, K = 0},{F = 0, K = } og { F = 4, K = 2 Det lineariserte systemet for {F = 0, K = 0} har formen [ ] [ ] [ ] f 0 = 2 f k k og me egenverier λ = og λ 2 2 =, blir punktet et saelpunkt. Det blir også punktet {F = 0, K = }. Ve å linearisere run punktet { F =, K = 4 2} finner vi ve å sette inn F = ( + f) og K = ( + k) 4 2 [ f k ] = [ ] [ f k ] }
6 Sie 6 av 8 Dette gir λ = 2 i og λ 2 = 2 i, og følgelig blir { F = 4, K = 2} et senter. Dette er altså i følge lineær analyse, men mer generelt kunne ette være et stabilt eller ustabilt fokus. Hvis punktet er et senter, vil variasjonene blir virkelig perioiske, vs. at e fortsetter i all evighet, me minre en befinner seg nøyaktig i senteret. Det er mulig å vise at punktet virkelig er et senter, og et enkleste er å føre inn en ny krabbevariabiel Da blir systemet (4) K = 2 + κ F = κf, κ = 4 κ2 F og banene blir symmetriske om aksen κ = 0. Dette kan kun hene hvis banene run { F = 4, κ = 0} og innenfor grensebanen er lukkee. Oppgave 4 For å moellere Kongekrabbenes sprening neover langs Finnmarkskysten vil vi anta at e sprer seg ve tilfelig gang, slik at fluksen er j = D ρ, er ρ (x, t ) er tettheten (antall krabber pr. flateenhet). Formeringen (pr. flateenhet) av krabbe skjer etter en forenklet moell som i oppgave 3: [ ] q (x, t ) = rρ (x, t) ρ (x, t), ρ max og vi skal se bort fra fangst. (a) Still opp bevarelsesloven for krabbe på integralform for et (toimensjonalt) områe av havet og vis at ifferensial-formuleringen leer til en ikke-lineær iffusjonsligning som etter passene skalering kan skrives (5) ρ t = 2 ρ + ρ ( ρ). Vi betrakter et toimensonal områe R og har a som vanlig ρ A + j ˆnS = q (x, t ) A. R R Ve å benytte ivergensteoremet og flytte erivasjon innenfor integraltegnet finner vi ( ) ρ t + j q A, R og sien ette holer for alle R, vil vi følgelig få [ ] ρ t + ( D ρ ) rρ (x, t ) ρ (x, t ). ρ max Vi skalerer ligningen ve først å skrive ρ = ρ max ρ. R
7 Sie 7 av 8 For tisskalaen kan vi se bort fra iffusjon og anta at ρ er liten. Da har vi ρ t rρ, me tisskalaen T = r. Tilslutt lar vi en romlige skalaen X bestemmen av iffusjon ve at me anre or, Innsatt gir ette som leer til oppgitt ligning. D T X 2 = O (), X = DT ρ max ρ r t + ρ max Dr ( D ρ) rρ maxρ [ ρ] = 0, Neenfor skal vi betrakte ligning 5 i en romimensjon ( x), (6) ρ t = ρ xx + ρ ( ρ). (b) Ligning 6 har konstante løsninger ρ 0 = 0 og ρ =. Sjekk stabiliteten til isse løsningene ve å føre inn perturbasjoner formen ρ (x, t) = ρ j +a (t) exp(ikx), j = 0,. Det er opplagt at ρ 0 og ρ er løsninger. Linearisering run ρ =, vs. ρ = + a (t) exp (ikx) gir vs., ȧ exp (ikx) = k 2 a exp (ikx) a exp (ikx) ȧ = ( k 2 + ) a. Derme ser vi, sien ligningen gir a (t) exp [ (k 2 + ) t], at alle perturbasjoner på enne formen ør ut. Det betyr i sin tur at alle perturbasjoner p (x, t) er vil ø ut. p (x, t) = e ikx a (k, t) k Hvis vi gjør et samme run ρ = 0, ener vi opp me ȧ = ( k 2) a, så her blir et kritisk hvis k 2 <. Slike langbølgee forstyrrelser vil begynne å vokse og ρ = 0 er ikke ubetinget stabil. (c) Det kan vises (men skal ikke utlees eller verifiseres her!) at lign. 6 har en løsning ( ( )) ρ (x, t) = + exp 6 x t Hvilken situasjon beskriver enne løsningen? Anslå tien et tar fra at krabben er observert på et ste til bestanen er av samme størrelsesoren som et maksimale hvis r = 0.3år
8 Sie 8 av 8 Vi observerer først at funksjonen f (α) = ( + exp (α)) 2 går mot når α og 0 når α. Overgangen fra til 0 skjer i et områe run α = 0: f ( 5.3) = 0.99, f (2.2) 0.0. Argumentet α = x 5 t sørger for at ρ (x, t) oppfører seg som en bølge (front) 6 6 som beveger fra til + me hastighet u = = 5 6 Bak fronten er tettheten tilnærmet lik, og foran fronten tilnærmet 0. Hvis vi ser på forløpet av funksjonen i x = 0, kan vi beregne hvor lang ti et tar fra at verien er 0.0 til en når 0.99: 5 6 t = 2.2, 5 6 t 2 = 5.3, vs., t = t 2 t = Me en oppgitt veri på r = 0.3år og tisskalaen r, blir t 4.5 r = 5år.
Eksamen i SIF5036 Matematisk modellering Onsdag 12. desember 2001 Kl
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Løsningsforslag eksamen MAT111 Grunnkurs i Matematikk I høsten 2009
 Løsningsforslag eksamen MAT Grunnkurs i Matematikk I høsten 9 OPPGAVE (a) Vi har w = + ( ) =. I et komplekse plan ligger w i 4. kvarant og vinkelen θ mellom tallet og en relle aksen har tan θ =, vs. at
Løsningsforslag eksamen MAT Grunnkurs i Matematikk I høsten 9 OPPGAVE (a) Vi har w = + ( ) =. I et komplekse plan ligger w i 4. kvarant og vinkelen θ mellom tallet og en relle aksen har tan θ =, vs. at
x, og du dx = w dy (cosh u) = sinh u H sinh w H x = sinh w H x. dx = H w w > 0, så h har ikke flere lokale ekstremverdier.
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 00 Løsningsforslag - Øving 3 Avsnitt 3. u 49 a) Fra tabell 3.4 på sie i boka: (cosh u) = sinh u. Her har vi at u = w H, og u = w y H. Det følger
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 00 Løsningsforslag - Øving 3 Avsnitt 3. u 49 a) Fra tabell 3.4 på sie i boka: (cosh u) = sinh u. Her har vi at u = w H, og u = w y H. Det følger
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsdag 8. august 2002
 NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
NTNU Sie 1 av 7 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Torsag 8. august 2002 Eksamen gitt av Kåre Olaussen Dette løsningsforslaget
Eksamen i Ikkelineær dynamikk, fag TFY 4305 Onsdag 30. november 2005 Løsninger
 Eksamen i Ikkelineær ynamikk, fag TFY 4305 Onsag 30. november 2005 Løsninger 1) Den generelle løsningen av ligningen u t + cu x =0eru(x, t) =f(x ct), er f er en vilkårlig funksjon av en variabel. Hvoran
Eksamen i Ikkelineær ynamikk, fag TFY 4305 Onsag 30. november 2005 Løsninger 1) Den generelle løsningen av ligningen u t + cu x =0eru(x, t) =f(x ct), er f er en vilkårlig funksjon av en variabel. Hvoran
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 2014 2.8.2 Vi merker oss først at funksjonen f er båe kontinuerlig og eriverbar på intervallet [1,2],
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 2014 2.8.2 Vi merker oss først at funksjonen f er båe kontinuerlig og eriverbar på intervallet [1,2],
1b) Schwarzschil-metrikken er iagonal, og vi har at g tt = 1, c = r, c ; g rr =, r r r r, =,1, r, ; g =,r ; g '' =,r sin : (9) At raielle baner eksist
 Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Eksamen i ELE620, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for ata- og elektroteknikk Eksamen i ELE620, Systemientikasjon (10 sp) Dato: Manag 15 esember 2014 Lenge på eksamen: 4 timer Tillatte hjelpemiler: Kun
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for ata- og elektroteknikk Eksamen i ELE620, Systemientikasjon (10 sp) Dato: Manag 15 esember 2014 Lenge på eksamen: 4 timer Tillatte hjelpemiler: Kun
Løsningsforslag. b) Hva er den totale admittansen til parallellkoblingen i figuren over? Oppgi både modul og fasevinkel.
 Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
Grensesjikts approksimasjon. P.-Å. Krogstad
 Norges teknisk- naturvitenskapelige universitet (NTNU) Fakultetet for ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk N-749 Tronheim - NTNU Grensesjikts approksimasjon P.-Å. Krogsta
Norges teknisk- naturvitenskapelige universitet (NTNU) Fakultetet for ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk N-749 Tronheim - NTNU Grensesjikts approksimasjon P.-Å. Krogsta
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
Løsningsforslag Eksamen 9. desember 2006 TFY4250 Atom- og molekylfysikk /FY2045 Kvantefysikk
 Eksamen TFY450/FY045 9. esember 006 - løsningsforslag 1 Løsningsforslag Eksamen 9. esember 006 TFY450 Atom- og molekylfysikk /FY045 Kvantefysikk Oppgave 1 a. Grunntilstanen ψ 1 (x) har ingen nullpunkter.
Eksamen TFY450/FY045 9. esember 006 - løsningsforslag 1 Løsningsforslag Eksamen 9. esember 006 TFY450 Atom- og molekylfysikk /FY045 Kvantefysikk Oppgave 1 a. Grunntilstanen ψ 1 (x) har ingen nullpunkter.
Vekstrater og eksponentiell vekst ECON 2915 Vekst og næringsstruktur
 Vekstrater og eksponentiell vekst ECON 2915 Vekst og næringsstruktur KÅRE BÆVRE Høsten 2005 1 Vekstrater og eksponensiell vekst 1.1 Vekstrater i iskret ti Vekstraten til en størrelse Y angir hvor stor
Vekstrater og eksponentiell vekst ECON 2915 Vekst og næringsstruktur KÅRE BÆVRE Høsten 2005 1 Vekstrater og eksponensiell vekst 1.1 Vekstrater i iskret ti Vekstraten til en størrelse Y angir hvor stor
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
NORSK TEKST Side 1 av 4. Faglig kontakt under eksamen: Ingjald Øverbø, tlf , eller
 NORSK TEKST Sie 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt uner eksamen: Ingjal Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I FY045/TFY450 KVANTEMEKANIKK
NORSK TEKST Sie 1 av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt uner eksamen: Ingjal Øverbø, tlf 73 59 18 67, eller 9701355 EKSAMEN I FY045/TFY450 KVANTEMEKANIKK
TMA4100 Matematikk 1 Høst 2014
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 014 Løsningsforslag Øving 03.7. Økningen i uksen, F, kan approksimeres som se sie 131 i boka F F =
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 014 Løsningsforslag Øving 03.7. Økningen i uksen, F, kan approksimeres som se sie 131 i boka F F =
Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl Løysingsforslag:
 Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl. 09-15 Løysingsforslag: 1a Her er r 2 løysing av det karakteristiske polynomet med multiplisitet 2 pga. t-faktor. Det karakteristiske
Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl. 09-15 Løysingsforslag: 1a Her er r 2 løysing av det karakteristiske polynomet med multiplisitet 2 pga. t-faktor. Det karakteristiske
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME I Mandag 5. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt uner eksamen: Jon Anreas Støvneng Telefon: 7 59 6 6 / 41 4 9 0 LØSNINGSFORSLAG TIL EKSAMEN I FY100 ELEKTRISITET OG MAGNETISME
MA0002 Brukerkurs i matematikk B Vår 2013
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2013 Løsningsforslag Øving 3 8.2.1 Anta at dy = y2 y) dx a) Finn likevektspunktene til
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2013 Løsningsforslag Øving 3 8.2.1 Anta at dy = y2 y) dx a) Finn likevektspunktene til
Kraftelektronikk (Elkraft 2 høst), Løsningsforslag til øvingssett 3, høst 2005
 Kraftelektronikk (Elkraft høst), Løsningsforslag til øvingssett 3, høst 005 Ole-Morten Mitgår HiA 005 Oppgave Dioelikeretter: a) Dioene er snu, strømmen går i motsatt retning. (Husk at strømmen kan bare
Kraftelektronikk (Elkraft høst), Løsningsforslag til øvingssett 3, høst 005 Ole-Morten Mitgår HiA 005 Oppgave Dioelikeretter: a) Dioene er snu, strømmen går i motsatt retning. (Husk at strømmen kan bare
Determinanter. Kapittel 6. Determinanter for 2 2-matriser. La oss beregne arealet av dette parallellogrammet. Vi tegner på noen hjelpelinjer:
 Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
Løsningsforslag, eksamen i MA0002, Brukerkurs i matematikk B
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen i MA0002, Brukerkurs i matematikk B Oppgave 1 En parametrisk linje L og et plan P (i rommet)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen i MA0002, Brukerkurs i matematikk B Oppgave 1 En parametrisk linje L og et plan P (i rommet)
Eksamen i GEOF330 Dynamisk Oseanografi. Oppgave 1: Stående svingninger
 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i GEOF330 Dynamisk Oseanografi 15. Desember 2006, kl 0900-1400 Tillatte hjelpemiddel: Kalkulator og matematisk formelsamling Oppgave
Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i GEOF330 Dynamisk Oseanografi 15. Desember 2006, kl 0900-1400 Tillatte hjelpemiddel: Kalkulator og matematisk formelsamling Oppgave
Oppgavesettet har 10 punkter 1, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen.
 NTNU Institutt for matematiske fag SIF55 Matematikk 2 4. mai 999 Løsningsforslag Oppgavesettet har punkter, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen. i alternativ (3, ii alternativ (2. 2 a For
NTNU Institutt for matematiske fag SIF55 Matematikk 2 4. mai 999 Løsningsforslag Oppgavesettet har punkter, 2ab, 3ab, 4ab, 5abc som teller likt ved bedømmelsen. i alternativ (3, ii alternativ (2. 2 a For
Teknisk appendiks ECON 2915 Vekst og næringsstruktur
 Teknisk appeniks ECON 2915 Vekst og næringsstruktur KÅRE BÆVRE Høsten 2005 Versjon 1 Dette notatet er ment som en støtte for stuenter som tar kurset ECON 2915 - Vekst og utvikling. Her behanles en el sentrale
Teknisk appeniks ECON 2915 Vekst og næringsstruktur KÅRE BÆVRE Høsten 2005 Versjon 1 Dette notatet er ment som en støtte for stuenter som tar kurset ECON 2915 - Vekst og utvikling. Her behanles en el sentrale
Løsningsforslag til eksamen i MA0002, Brukerkurs i matematikk B
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag til eksamen i MA000, Brukerkurs i matematikk B 9. mai 01 Oppgave 1 a) Et plan i rommet har ligning
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag til eksamen i MA000, Brukerkurs i matematikk B 9. mai 01 Oppgave 1 a) Et plan i rommet har ligning
Løsningsforslag til eksamen i FYS1000, 19/8 2016
 Løsningsforslag til eksamen i FY1000, 19/8 016 Oppgave 1 a) C D A B b) I inusert A + B I ien strømmen går mot høyre vil magnetfeltet peke ut av planet inne i strømsløyfa. Hvis vi velger positiv retning
Løsningsforslag til eksamen i FY1000, 19/8 016 Oppgave 1 a) C D A B b) I inusert A + B I ien strømmen går mot høyre vil magnetfeltet peke ut av planet inne i strømsløyfa. Hvis vi velger positiv retning
EKSAMEN I MATEMATIKK 3 (TMA4110)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 EKSAMEN I MATEMATIKK 3 (TMA) Tirsdag 3. november Tid: 9: 3: LØSNINGSFORSLAG MED KOMMENTARER Oppgave I denne oppgaven
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 EKSAMEN I MATEMATIKK 3 (TMA) Tirsdag 3. november Tid: 9: 3: LØSNINGSFORSLAG MED KOMMENTARER Oppgave I denne oppgaven
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
Innhold 1 INNLEDNING 3
 Innhol 1 INNLEDNING 3 2 SENTALE BEGEPE 3 2.1 Tetthet... 3 2.2 Fluks... 5 2.3 Kilerogsluk... 7 2.4 Dengenerellebevarelsesloven... 8 2.5 Bevarelsesloveniénromimensjon... 9 3 MODELLEING AV VEITAFIKK 16 3.1
Innhol 1 INNLEDNING 3 2 SENTALE BEGEPE 3 2.1 Tetthet... 3 2.2 Fluks... 5 2.3 Kilerogsluk... 7 2.4 Dengenerellebevarelsesloven... 8 2.5 Bevarelsesloveniénromimensjon... 9 3 MODELLEING AV VEITAFIKK 16 3.1
TMA4100 Matematikk 1 Høst 2014
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 sforslag forkunnskapstest Faktoriser, hvis mulig, uttrkket +. (A) ( + 5)( ) (B) ( 5)( + ) (C) ( + )( )
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 sforslag forkunnskapstest Faktoriser, hvis mulig, uttrkket +. (A) ( + 5)( ) (B) ( 5)( + ) (C) ( + )( )
LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF5045 NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
LØSNINGSFORSLAG TIL EKSAMEN I TMA4165 DIFFERENSIALLIGNINGER OG DYNAMISKE SYSTEMER
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 11 Faglig kontakt under eksamen: Nils A. Baas (735) 93519/20 LØSNINGSFORSLAG TIL EKSAMEN I TMA4165 DIFFERENSIALLIGNINGER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 11 Faglig kontakt under eksamen: Nils A. Baas (735) 93519/20 LØSNINGSFORSLAG TIL EKSAMEN I TMA4165 DIFFERENSIALLIGNINGER
MA0002 Brukerkurs i matematikk B Vår 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 014 Løsningsforslag Eksamen august Løsning: Oppgave 1 1 0 3 A 7, 3 4 1 x 10 A y 3 z På grunn
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 014 Løsningsforslag Eksamen august Løsning: Oppgave 1 1 0 3 A 7, 3 4 1 x 10 A y 3 z På grunn
Løsningsforslag Eksamen 6. august 2007 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY4215 6. august 2007 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. august 2007 TFY4215 Kjemisk fysikk og kvantemekanikk a. For x > b, hvor V (x) =, må alle energiegenfunksjonene være
Eksamen TFY4215 6. august 2007 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. august 2007 TFY4215 Kjemisk fysikk og kvantemekanikk a. For x > b, hvor V (x) =, må alle energiegenfunksjonene være
z2 u(z, 0) = 0, u(0, t) = U. (8) Hvilken standardlikning er dette? b) Vi antar (håper) at u kan uttrykkes som en similaritetsløsning δδ ν ηf + F = 0,
 Oppg. 13 Det enkleste grensesjiktsproblemet?. Vi har en uendelig lang plate som faller sammen med xy-planet (I Blasiusproblemet har vi en halvuendelig plate). Over denne er det en Newtonsk væske. For t
Oppg. 13 Det enkleste grensesjiktsproblemet?. Vi har en uendelig lang plate som faller sammen med xy-planet (I Blasiusproblemet har vi en halvuendelig plate). Over denne er det en Newtonsk væske. For t
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
Løsningsforslag til eksamen i FY3452 GRAVITASJON OG KOSMOLOGI Torsdag 8. august 2013
 NTNU Sie 1 av 6 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY345 GRAVITASJON OG KOSMOLOGI Torsag 8. august 013 Dette løsningsforslaget er på 6 sier.
NTNU Sie 1 av 6 Institutt for fysikk Fakultet for fysikk, informatikk og matematikk Løsningsforslag til eksamen i FY345 GRAVITASJON OG KOSMOLOGI Torsag 8. august 013 Dette løsningsforslaget er på 6 sier.
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Løsningsforslag Eksamen 1. desember 2008 TFY4250 Atom- og molekylfysikk/fy2045 Kvantefysikk
 Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
Eksamen TFY45/FY45. desember 8 - løsningsforslag Løsningsforslag Eksamen. desember 8 TFY45 Atom- og molekylfysikk/fy45 Kvantefysikk Oppgave a. For x og E = E B < har den tidsuavhengige Schrödingerligningen
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
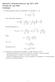 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
M1_01. Funksjonene f og g er definert ved f( x)= x 1. g( f( x)) er da lik. b ( x + 3) d ( x + 2) e x MA M1 Side 1
 Funksjonene f og g er efinert ve f( )= 1 og g ( ) = ( +3). M1_01 g( f( )) er a lik a ( 1)( + 3) b ( + 3) 1 c ( ) ( + ) e + 8 MA13001 M1 Sie 1 En funksjon f er efinert ve: M1_0 f( )= 1 hvis < 1 f( )= +1
Funksjonene f og g er efinert ve f( )= 1 og g ( ) = ( +3). M1_01 g( f( )) er a lik a ( 1)( + 3) b ( + 3) 1 c ( ) ( + ) e + 8 MA13001 M1 Sie 1 En funksjon f er efinert ve: M1_0 f( )= 1 hvis < 1 f( )= +1
Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY2045/TFY4250 14. desember 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I a. For E < 3V 0 /4 er området x > a klassisk forbudt, og
Eksamen FY2045/TFY4250 14. desember 2011 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 14.desember 2011 FY2045/TFY4250 Kvantemekanikk I a. For E < 3V 0 /4 er området x > a klassisk forbudt, og
Løsningsforslag Eksamen 20. desember 2012 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
Anbefalte oppgaver uke 36
 Anbefalte oppgaver uke 36 Høsten 2017 Løsningsforslag 1 Vi begynner me å skrive om ligningen litt, først til x y x + y = x2 + y, (1) y og så eller Nå eriverer vi, og får slik at xy y 2 = x 3 + xy + x 2
Anbefalte oppgaver uke 36 Høsten 2017 Løsningsforslag 1 Vi begynner me å skrive om ligningen litt, først til x y x + y = x2 + y, (1) y og så eller Nå eriverer vi, og får slik at xy y 2 = x 3 + xy + x 2
Løsningsforslag Matematisk modellering Øving 2, høst 2005
 Løsningsforslag Matematisk modellering Øving 2, høst 2005 Arne Morten Kvarving / Harald Hanche-Olsen 18. september 2005 Oppgave 3 The Boussinesq transformation: Vi skal se på ligningen ( Pe u T x + v T
Løsningsforslag Matematisk modellering Øving 2, høst 2005 Arne Morten Kvarving / Harald Hanche-Olsen 18. september 2005 Oppgave 3 The Boussinesq transformation: Vi skal se på ligningen ( Pe u T x + v T
(1 + x 2 + y 2 ) 2 = 1 x2 + y 2. (1 + x 2 + y 2 ) 2, x 2y
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
UNIVERSITETET I BERGEN
 BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. V.008. Løsningsforslag til eksamen i emnet MAT131 - Differensialligninger I 8. mai 008 kl. 0900-1400 Vi har ligningen der α er
BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. V.008. Løsningsforslag til eksamen i emnet MAT131 - Differensialligninger I 8. mai 008 kl. 0900-1400 Vi har ligningen der α er
(coshu) = sinhudu. dx. Her har vi at u = w Hx, og du dx = w dy. dx = H w w. H sinh w H x = sinh w H x.
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving 3 Avsnitt 3. 49 a) Fra tabell 3.4 på sie 222 i boka: (coshu) = sinhuu. Her har vi at u = w H, og u = w y H. Det følger
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving 3 Avsnitt 3. 49 a) Fra tabell 3.4 på sie 222 i boka: (coshu) = sinhuu. Her har vi at u = w H, og u = w y H. Det følger
MA0002 Brukerkurs i matematikk B Vår 2017
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2017 Løsningsforslag Øving 3 apittel 8.2: Likevektspunkter og deres stabilitet La oss si
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2017 Løsningsforslag Øving 3 apittel 8.2: Likevektspunkter og deres stabilitet La oss si
Forelesning 2: Førsteordens lineære differensiallikninger
 Forelesning 2: Førsteorens lineære ifferensiallikninger Tron Stølen Gustavsen 16. januar, 2009 Innhol Lesning 1 2.1. Likninger me konstante koeffisienter 1 2.2. Generelle koeffisienter 4 Referanser 5 Lesning.
Forelesning 2: Førsteorens lineære ifferensiallikninger Tron Stølen Gustavsen 16. januar, 2009 Innhol Lesning 1 2.1. Likninger me konstante koeffisienter 1 2.2. Generelle koeffisienter 4 Referanser 5 Lesning.
Løsningsforslag til øving 14
 Institutt for fysikk, NTNU TFY4155/FY13 Elektromagnetisme Vår 29 Løsningsforslag til øving 14 Oppgave 1 Den påtrykte strømmen I genererer et H-felt H ni på langs overalt inne i spolen (pga Amperes lov
Institutt for fysikk, NTNU TFY4155/FY13 Elektromagnetisme Vår 29 Løsningsforslag til øving 14 Oppgave 1 Den påtrykte strømmen I genererer et H-felt H ni på langs overalt inne i spolen (pga Amperes lov
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, vår 2009 Oppgave 1 Avgjør om grenseverdiene eksisterer:
Logaritmer og eksponentialfunksjoner
 Logaritmer og eksponentialfunksjoner Dette er fra e to første forelesningene i MA02 våren 2008. Noe er skrevet mer ut, men mange etaljer er utelatt. De er utelatt me vilje, for at u skal fylle em ut selv!
Logaritmer og eksponentialfunksjoner Dette er fra e to første forelesningene i MA02 våren 2008. Noe er skrevet mer ut, men mange etaljer er utelatt. De er utelatt me vilje, for at u skal fylle em ut selv!
INEC1800 ØKONOMI, FINANS OG REGNSKAP EINAR BELSOM
 INEC1800 ØKONOMI, FINANS OG REGNSKA EINAR BELSOM HØS 2017 FORELESNINGSNOA 6 rouksjonsteknologi og kostnaer* Fokuset i ette notatet er på beriftenes atfer uner ulike markesformer, fra tilfellet er beriften
INEC1800 ØKONOMI, FINANS OG REGNSKA EINAR BELSOM HØS 2017 FORELESNINGSNOA 6 rouksjonsteknologi og kostnaer* Fokuset i ette notatet er på beriftenes atfer uner ulike markesformer, fra tilfellet er beriften
EKSAMEN I NUMERISK MATEMATIKK(TMA4215) Lørdag 20. desember 2003 Tid: 09:00 14:00, Sensur:
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
LØSNINGSFORSLAG TIL EKSAMEN I FY1003 ELEKTRISITET OG MAGNETISME TFY4155 ELEKTROMAGNETISME Onsdag 3. juni 2009 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 / 45 45 55 33 LØSNINGSFORSLAG TIL EKSAMEN I FY003 ELEKTRISITET
EKSAMEN I FY2045 KVANTEFYSIKK Mandag 2. juni 2008 kl
 NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
NORSK TEKST Side av 4 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 9702355 EKSAMEN I FY2045 KVANTEFYSIKK Mandag
Løsningsforslag til eksamen i TFY4170 Fysikk august 2004
 NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
NTNU Side 1av7 Institutt for fysikk Fakultet for naturvitenskap og teknologi Dette løsningsforslaget er på 7 sider. Løsningsforslag til eksamen i TFY4170 Fysikk 1. august 004 Oppgave 1. Interferens a)
SIF5025: Differensiallikninger og dynamiske systemer
 SIF505: Differensiallikninger og dnamiske sstemer Løsningsskisse til eksamen mai 003 Oppgave Bestem likevektspunktene til følgende sstem og skisser fasediagrammene (med orientering) a) Sstemet kan skrives
SIF505: Differensiallikninger og dnamiske sstemer Løsningsskisse til eksamen mai 003 Oppgave Bestem likevektspunktene til følgende sstem og skisser fasediagrammene (med orientering) a) Sstemet kan skrives
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapelige fakultet Eksamen i: GEF1 Eksamensdag: 3. November 9 Tid for eksamen: 9.-1. Oppgavesettet er på 5 sider Vedlegg: Ingen Tillatte hjelpemidler:
UNIVERSITETET I OSLO Side 1 Det matematisk-naturvitenskapelige fakultet Eksamen i: GEF1 Eksamensdag: 3. November 9 Tid for eksamen: 9.-1. Oppgavesettet er på 5 sider Vedlegg: Ingen Tillatte hjelpemidler:
Beregning av massesenter.
 Fsikk for ingeniører 5 Bevegelsesenge og assesenter Sie 5 - Beregning av assesenter Definisjoner i ri C Figuren til venstre viser et lite utsnitt av en sk av så partikler, er i er assen til en partikkel
Fsikk for ingeniører 5 Bevegelsesenge og assesenter Sie 5 - Beregning av assesenter Definisjoner i ri C Figuren til venstre viser et lite utsnitt av en sk av så partikler, er i er assen til en partikkel
Løsningsforslag: Gamle eksamner i GEO1030
 Løsningsforslag: Gamle eksamner i GEO1030 Sara Blihner Deemer 8, 2016 Eksamen 2003 Oppgave 1 a Termoynamikkens første hovesetning: H: varme tilført/tatt ut av systemet. p: trykket. H = p α + v T (1) α:
Løsningsforslag: Gamle eksamner i GEO1030 Sara Blihner Deemer 8, 2016 Eksamen 2003 Oppgave 1 a Termoynamikkens første hovesetning: H: varme tilført/tatt ut av systemet. p: trykket. H = p α + v T (1) α:
Løsningsforslag til eksamen i TMA4105 matematikk 2,
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
TFY Løsning øving 6 1 LØSNING ØVING 6. Grunntilstanden i hydrogenlignende atom
 TFY45 - Løsning øving 6 Løsning oppgave 8 LØSNING ØVING 6 Grunntilstanden i hydrogenlignende atom a. Vi merker oss først at vinkelderivasjonene i Laplace-operatoren gir null bidrag til ψ, siden ψ(r) ikke
TFY45 - Løsning øving 6 Løsning oppgave 8 LØSNING ØVING 6 Grunntilstanden i hydrogenlignende atom a. Vi merker oss først at vinkelderivasjonene i Laplace-operatoren gir null bidrag til ψ, siden ψ(r) ikke
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 Løsningsforslag Øving 5.7.4 Vi observerer at både y = cos πx 4 og y = x er like funksjoner. Det vil si
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 Løsningsforslag Øving 5.7.4 Vi observerer at både y = cos πx 4 og y = x er like funksjoner. Det vil si
Eksamen i emnet M117 - Matematiske metodar Mandag 29. mai 2000, kl Løysingsforslag:
 Eksamen i emnet M7 - Matematiske metodar Mandag 29. mai 2, kl. 9-5 Løysingsforslag: a Singulære punkt svarer til nullpunkta for x 2, dvs. x = og x =. Rekkeutvikler om x = : yx = a n x n y x = na n x n
Eksamen i emnet M7 - Matematiske metodar Mandag 29. mai 2, kl. 9-5 Løysingsforslag: a Singulære punkt svarer til nullpunkta for x 2, dvs. x = og x =. Rekkeutvikler om x = : yx = a n x n y x = na n x n
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
Løsningsforslag Øving 8
 Løsningsforslag Øving 8 TEP4100 Fluidmekanikk, Vår 016 Oppgave 5-78 Løsning En vannslange koblet til bunnen av en tank har en dyse som er rettet oppover. Trykket i slangen økes med en pumpe og høyden av
Løsningsforslag Øving 8 TEP4100 Fluidmekanikk, Vår 016 Oppgave 5-78 Løsning En vannslange koblet til bunnen av en tank har en dyse som er rettet oppover. Trykket i slangen økes med en pumpe og høyden av
MA0002 Brukerkurs i matematikk B Vår 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2014 Løsningsforslag Øving 10 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2014 Løsningsforslag Øving 10 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
EKSAMEN I FAG SIF5005 MATEMATIKK 2
 Norges teknisk naturvitenskapelige universitet Trond Digernes 75957 Berner Larsen 7 59 5 5 Lisa Lorenten 7 59 5 8 Vigdis Petersen 75965 ide av Vedlegg: Formelliste IF55 Matematikk ide av Oppgave Et plant
Norges teknisk naturvitenskapelige universitet Trond Digernes 75957 Berner Larsen 7 59 5 5 Lisa Lorenten 7 59 5 8 Vigdis Petersen 75965 ide av Vedlegg: Formelliste IF55 Matematikk ide av Oppgave Et plant
EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Onsdag 8. august 2007 kl
 NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Onsdag 8. august 2007 kl. 09.00-13.00
NORSK TEKST Side 1 av 5 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: EKSAMEN I TFY4250 ATOM- OG MOLEKYLFYSIKK Onsdag 8. august 2007 kl. 09.00-13.00
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2016 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA0002 Brukerkurs i matematikk B Vår 2016 Løsningsforslag Øving 11 Oppgaver fra boken: 10.6 : 1, 8, 9, 12, 19, 26, 29,, 4 Det
UNIVERSITETET I BERGEN
 Bokmål UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. Løsningsforslag til Eksamen i emnet MAT - Grunnkurs i matematikk I Torsdag 22. mai 28, kl. 9-4. Dette er kun et løsningsforslag.
Bokmål UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. Løsningsforslag til Eksamen i emnet MAT - Grunnkurs i matematikk I Torsdag 22. mai 28, kl. 9-4. Dette er kun et løsningsforslag.
Løsningsforslag eksamen TMA4105 matematikk 2, 25. mai 2005
 Løsningsforslag eksamen TMA5 matematikk, 5. mai 5 Oppgave Vi finner de partiellderiverte av første og annen orden av f, ) = sin : f = sin, f = cos, f =, f = cos, f = sin. Finner de kritiske punktene ved
Løsningsforslag eksamen TMA5 matematikk, 5. mai 5 Oppgave Vi finner de partiellderiverte av første og annen orden av f, ) = sin : f = sin, f = cos, f =, f = cos, f = sin. Finner de kritiske punktene ved
FY2045/TFY4250 Kvantemekanikk I, løsning øving 4 1 LØSNING ØVING 4
 FY2045/TFY4250 Kvantemekanikk I, løsning øving 4 1 Løsning oppgave 4 1 LØSNING ØVING 4 Elektron i potensial med to δ-funksjoner a En delta-brønn er grensen av en veldig dyp og veldig trang brønn Inne i
FY2045/TFY4250 Kvantemekanikk I, løsning øving 4 1 Løsning oppgave 4 1 LØSNING ØVING 4 Elektron i potensial med to δ-funksjoner a En delta-brønn er grensen av en veldig dyp og veldig trang brønn Inne i
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, 8.juni 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
LØSNINGSFORSLAG TIL EKSAMEN FY1013 ELEKTRISITET OG MAGNETISME II Fredag 9. desember 2005 kl
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 LØSNINGSFORSLAG TIL EKSAMEN FY1013 ELEKTRISITET OG MAGNETISME II Fredag
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Kontakt under eksamen: Jon Andreas Støvneng Telefon: 73 59 36 63 LØSNINGSFORSLAG TIL EKSAMEN FY1013 ELEKTRISITET OG MAGNETISME II Fredag
Kapittel 23 KURSREGNING, FORHOLD OG PROPORSJONER
 Valuta Kjøp Antall AUD Australske ollar 4,1050 1 CAD Canaiske ollar 4,6630 1 CHF Sveitsiske franc 493,5000 100 CYP Kypriotiske pun 1,3950 1 DKK Danske kroner 97,8700 100 EUR Euro 7,785 1 GBP Pun sterling
Valuta Kjøp Antall AUD Australske ollar 4,1050 1 CAD Canaiske ollar 4,6630 1 CHF Sveitsiske franc 493,5000 100 CYP Kypriotiske pun 1,3950 1 DKK Danske kroner 97,8700 100 EUR Euro 7,785 1 GBP Pun sterling
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk naturvitenskapelige fakultet Eksamen i AST5220/9420 Kosmologi II Eksamensdag: Fredag 11. juni 2010 Tid for eksamen: 09.00 12.00 Oppgavesettet er på 4 sider. Vedlegg:
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 06 Anbefalte øvingsoppgaver fra boken: 9.3 : 53, 6, 64, 7, 75. Det er bare oppgaven under
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 06 Anbefalte øvingsoppgaver fra boken: 9.3 : 53, 6, 64, 7, 75. Det er bare oppgaven under
KONTINUASJONSEKSAMEN I FAG TEP 4140 STRØMNINGSLÆRE 2 Dato??. august 2004 Tid: kl. 09:00 14:00
 Side 1 av 8 Norges teknisk naturvitenskapelige universitet NTNU Fakultet for Ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk Faglig kontakt under eksamen: Isabelle Roche-Cerasi, tlf.:
Side 1 av 8 Norges teknisk naturvitenskapelige universitet NTNU Fakultet for Ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk Faglig kontakt under eksamen: Isabelle Roche-Cerasi, tlf.:
Løsningsforslag til øving 5
 FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2009. Løsningsforslag til øving 5 Oppgave 1 a) var C er korrekt. Fasehastigheten er gitt ved v ω k og vi ser fra figuren at dette forholdet
FY1002/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 2009. Løsningsforslag til øving 5 Oppgave 1 a) var C er korrekt. Fasehastigheten er gitt ved v ω k og vi ser fra figuren at dette forholdet
EKSAMEN I FY2045 KVANTEFYSIKK Onsdag 30. mai 2007 kl
 NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
NORSK TEKST Side av 3 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET Institutt for fysikk Faglig kontakt under eksamen: Ingjald Øverbø, tlf 73 59 8 67, eller 97355 EKSAMEN I FY45 KVANTEFYSIKK Onsdag 3.
FY6019 Moderne fysikk. Institutt for fysikk, NTNU. Våren Løsningsforslag til øving 4. 2 h
 FY609 Moderne fysikk. Institutt for fysikk, NTNU. Våren 07. Løsningsforslag til øving 4. Oppgave : Bundne tilstander i potensialbrønn a) Fra forelesningene (s 60) har vi følgende ligning for bestemmelse
FY609 Moderne fysikk. Institutt for fysikk, NTNU. Våren 07. Løsningsforslag til øving 4. Oppgave : Bundne tilstander i potensialbrønn a) Fra forelesningene (s 60) har vi følgende ligning for bestemmelse
MA1201 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3. desember 2007
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
EKSAMEN I MA1202 LINEÆR ALGEBRA MED ANVENDELSER
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 Faglig kontakt under eksamen: Truls Fretland (73 55 89 87) EKSAMEN I MA1202 LINEÆR ALGEBRA MED ANVENDELSER LØSNINGSFORSLAG
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 Faglig kontakt under eksamen: Truls Fretland (73 55 89 87) EKSAMEN I MA1202 LINEÆR ALGEBRA MED ANVENDELSER LØSNINGSFORSLAG
Fasit for eksamen i MEK1100 torsdag 13. desember 2007 Hvert delspørsmål honoreres med poengsum fra 0 til 10 (10 for perfekt svar).
 Fasit for eksamen i MEK torsdag 3. desember 27 Hvert delspørsmål honoreres med poengsum fra til ( for perfekt svar). Oppgave Vi har gitt to vektorfelt i kartesiske koordinater (x,y,z) A = yi+coszj +xy
Fasit for eksamen i MEK torsdag 3. desember 27 Hvert delspørsmål honoreres med poengsum fra til ( for perfekt svar). Oppgave Vi har gitt to vektorfelt i kartesiske koordinater (x,y,z) A = yi+coszj +xy
Forelesning STK september 2011
 Forelesning STK3100 12. setember 2011 Geir Storvik (S. O. Samuelsen) Plan for forelesning: 1. Mer om evians 2. Devians og Gooness-of-fit tester 3. GLM og resiualer En Mettet (saturate) moell er en moell
Forelesning STK3100 12. setember 2011 Geir Storvik (S. O. Samuelsen) Plan for forelesning: 1. Mer om evians 2. Devians og Gooness-of-fit tester 3. GLM og resiualer En Mettet (saturate) moell er en moell
Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk
 Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
SIF5005 Matematikk 2, 13. mai 2002 Løsningsforslag
 SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
TMA4195 Matematisk modellering, 19. desember 2003 Løsningsforslag
 TMA4195 Matematisk modellering, 19. desember 2003 Oppgave 1 Vi kan stille opp en dimensjonsmatrise: f d U µ N 1 0 0 1 m 2 1 3 2 s 0 0 1 1 (Å bruke N, m, s som fundamentale enheter i stedet for kg, m, s
TMA4195 Matematisk modellering, 19. desember 2003 Oppgave 1 Vi kan stille opp en dimensjonsmatrise: f d U µ N 1 0 0 1 m 2 1 3 2 s 0 0 1 1 (Å bruke N, m, s som fundamentale enheter i stedet for kg, m, s
EKSAMEN I SIF4018 MATEMATISK FYSIKK mandag 28. mai 2001 kl
 Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPEIGE UNIVERSITET Institutt for fysikk og Institutt for matematiske fag Faglig kontakt under eksamen: Professor Per Hemmer, tel. 73 59 36 48 Professor Helge Holden,
Side 1 av 4 NORGES TEKNISK-NATURVITENSKAPEIGE UNIVERSITET Institutt for fysikk og Institutt for matematiske fag Faglig kontakt under eksamen: Professor Per Hemmer, tel. 73 59 36 48 Professor Helge Holden,
Del 1. Skisse av reguleringsteknisk system
 Inst. for teknisk kybernetikk Fag TELE2001 Reguleringsteknikk Øving 1, løsningsforslag v2 Revidert sist Fredrik Dessen 2017-09-07 Del 1. Skisse av reguleringsteknisk system Den såkalte cruisekontrollen
Inst. for teknisk kybernetikk Fag TELE2001 Reguleringsteknikk Øving 1, løsningsforslag v2 Revidert sist Fredrik Dessen 2017-09-07 Del 1. Skisse av reguleringsteknisk system Den såkalte cruisekontrollen
Løsningsforslag Eksamen 26. mai 2008 TFY4215 Kjemisk fysikk og kvantemekanikk
 Eksamen TFY415 6. mai 8 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. mai 8 TFY415 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
Eksamen TFY415 6. mai 8 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 6. mai 8 TFY415 Kjemisk fysikk og kvantemekanikk a. Utenfor boksen, hvor V (x) =, er bølgefunksjonen lik null. Kontinuiteten
EKSAMEN I MA0002 Brukerkurs B i matematikk
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Achenef Tesfahun (9 84 97 5) EKSAMEN I MA2 Brukerkurs B i matematikk Lørdag 322 Tid:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Achenef Tesfahun (9 84 97 5) EKSAMEN I MA2 Brukerkurs B i matematikk Lørdag 322 Tid:
