z2 u(z, 0) = 0, u(0, t) = U. (8) Hvilken standardlikning er dette? b) Vi antar (håper) at u kan uttrykkes som en similaritetsløsning δδ ν ηf + F = 0,
|
|
|
- Merethe Mathisen
- 6 år siden
- Visninger:
Transkript
1 Oppg. 13 Det enkleste grensesjiktsproblemet?. Vi har en uendelig lang plate som faller sammen med xy-planet (I Blasiusproblemet har vi en halvuendelig plate). Over denne er det en Newtonsk væske. For t = er væsken i ro, men deretter settes platen i bevegelse med konstant hastighet i i x-retning. Over tid vil det da vokse opp et viskøst grensesjikt ved platen. I motsetning til Blasius-grensesjiktet har dette ingen variasjon i x-retning og strømmen er også parallell med x-aksen. Derimot er ikke strømmen stasjonær. Det er ingen trykkgradient langs platen. a) Vi retter z-aksen normalt platen og antar v = u(z, t)i. Vis at u må oppfylle randverdiproblemet u ν 2 u =, z2 u(z, ) =, u(, t) =. (8) Hvilken standardlikning er dette? b) Vi antar (håper) at u kan uttrykkes som en similaritetsløsning u = F (η), der η = z δ(t). Dette kan kalles en similaritetsløsning fordi vi har samme form på profiler langs for alle t, men profilene strekkes når t (og δ) øker. Vis at differensiallikningen i (8) nå gir og forklar at en løsning er mulig dersom δδ ν ηf + F =, δ(t) = C νt, der C er en konstant som, feks., kan velges lik 2 slik at Forklar at randbetingelser for F blir F (η) + 2ηF (η) =. (9) F () = 1, F ( ) =. c) Vis at når du løser differensiallikningen (9) og bruker den ene randbetingelsen får du η F = 1 + A e s2 ds, der A er en konstant som ennå ikke er bestemt. Du bør ikke prøve å løse ut dette integralet i formel. d) Bruk (uten bevis!) at slik at du kan skrive løsningen som e s2 ds = 1 2 π, F = 1 erf (η) = 1 erf 8 z, (1) δ(t)
2 der erf er feilfunksjonen definert ved erf(x) = 2 π t e t2 dt. e) Matlab har ferdige rutiner for å beregne erf(x) (skriv doc erf). Bruk Matlabs, eller et annet egnet verktøys, rutine for erf(x) til å plotte F som funksjon av η. f) Vi skal nå sammenlikne grensesjiktet i denne oppgaven med Blasius-grensesjiktet. Vi har vist at grensesjiktstykkelsen vokser med tiden som δ(t) = C νt. For Blasiusprofilet kan vi tenke oss at denne tiden svarer til tiden den ytre strømmen har følt plata, dvs. tiden en partikkel i den ytre strømmen bruker fra forkant av plata til x. Bruk dette og uttrykket for δ ovenfor til å anslå hvordan tykkelsen for Blasius-grensesjiktet varier med x. Er resultatet korrekt? Oppg. 14 Regnskap for bevegelsesmengde. Vi skal se på momentumlikningen for et endelig volum og knytte denne til bevegelseslikningen. Først en knapp innledning. For et system av partikler er bevegelsesmengden Massemiddelpunktsatsen kan da uttrykkes som I = mv. di dt = F, der F er summen av ytre krefter. Dersom de ytre kreftene er null i sum sier denne likningen at bevegelsesmengden er bevart. For et endelig volum, τ, med overflate σ kan vi tilsvarende sette opp en bevaringssats for bevegelsesmengde Tidsendring av bevegelsesmengde i τ = spenningskraft på σ + resultant av volumkrefter på τ - (utstrømsrate av bevegelsesmengde gjennom σ) Satsen kan brukes på vektorform, eller for hver av komponentene. Vi holder oss til vektorformen i denne oppgaven, mens komponentformenbrukes for grensesjikt i en senere oppgave. a) Forklar hvorfor utstrømsrate av bevegelsesmengden gjennom et flatelement kan skrives ρvv n dσ. Vi kan tolke ρvv som en momentumtransport-tensor skrevet på dyadeform. Forklar videre hvorfor tidsendringsraten av bevegelsesmengde i et volumelement er b) Sett opp integraler for alle bidrag til bevaringssatsen for bevegelsesmengde og vis at dette fører til dτ = n Pdσ + ρgdτ ρvv ndσ, (11) τ σ τ σ der P er spenningstensoren og g er ytre volumkrefter regnet per masse. Denne relasjonen kan være utgangspunkt for integrerte betrakninger av bevegelsesmengde i en væske, feks. for grensesjikt. 9 dτ
3 c) Vis at den integrerte likningen for bevegelsesmengde i forrige delpunkt medfører + (ρvv) = P + ρg. d) tled bevegelseslikningen, på standard form, fra resultatet i det forrige delspørsmålet. Hint: du må bruke kontinuitetslikningen og kan ha fordel av å se på oppgave 4. Oppg. 15 Integrerte likninger brukt på grensesjikt. I Blasius -problemet har vi en halvuendelig plate fra x = til x = og en ytre potensialstrøm i. Vi definerer et kontrollområde i xz planet som begrenses av (i): en linje normalt x-aksen med z H for x = a < (oppstrøms for plata); (ii) av x-aksen fra x = a til en fritt valgbar x-verdi; (iv) en øvre begrensning Z(x) = H + Δ(x) som er strømlinjen gjennom x = a og z = H; (iii) en begrensning normalt x-aksen ved den valgte x som går fra z = til z = Z(x). Det er en forutsetning at z = H er langt utenfor grensesjiktet. Tegn området. a) Vi ser først på masseregnskapet. Siden ρ er konstant er dette ensbetydende med å se på et regnskap for volum. Forklar hvorfor det ikke er noen volumtransport gjennom (ii) og (iv) og hvorfor transporten inn ved (i) da er lik transporten ut ved (iii). b) Vis at det forrige punkt fører til Vis videre at dette fører til Δ(x) = Δ kalles ofte fortrengningstykkelsen. = H H Z(x) 1 u dz u(x, z)dz. (12) 1 u dz. (13) c) Så ser vi på x-komponenten av bevegelsesmengden. Vi tar da utgangspunkt i at venstresiden i (11) forsvinner (hvorfor?). Forklar hvorfor vi ikke får betydelige bidrag til spenningsleddet fra (i), (iii) eller (iv). Forklar videre hvorfor momentum ikke fraktes med strømmen gjennom (ii) og (iv). d) Vis at (11) gir = x τ (ˆx)dˆx + ρh 2 der τ (x) = p xz (x, ) er skjærspenningen på platen. Z(x) e) Bruk (12) til å skrive om relasjonen fra forrige punkt til x τ (ˆx)dˆx = Z(x) f) Forklar hvorfor skjærspenningen kan skrives som τ (x) = x b ρu ( u) dz ρ(u(x, z)) 2 dz, (14) ρu ( u) dz. (15) b [ρu ( u)] dz, (16) x der b kan være, feks., Z, eller en korrekt definert grensesjiktstykkelse δ u, slik at u(x, δ u ). 1
4 g) Anta at hastighetsprofilet er gitt som z hvis z δ u, u = δ u hvis z > δ u. Bruk (16) til å finne δ u (x) og sammenlikn med resultatet i kompendiet. Oppg. 16 Numerisk beregning av Blasiusprofilet. For Blasiusprofilet kan hastigheten i x-retning skrives som u = f (ζ), ζ = z δ(x), der Funksjonen f oppfyller likningen med randbetingelser δ(x) = νx. f + ff =, (17) f() = f () =, lim f = 1. (18) a) Skriv om (17) og (18) til et sett av førsteordenslikninger slik at du får y1 = y 2, y2 = y 3, y3 = y 1 y 3, og randbetingelser y 1 () = y 2 () =, Problemet her er at vi har to betingelser ved ζ = og en ved ζ =. (19) lim y 2 = 1. (2) b) En enkel løsningsteknikk for et ikkelineært randverdiproblem som (19) og (2) er skytemetoden som bygger på løsning av initialverdiproblemer. Hadde vi hatt en betingelse på y 3 (), i stedet for en på y 2 i uendelig, ville en kunne integrert steg for steg fram i ζ vha. feks. Runge- Kuttas metode. I skytemetoden forsøker en å tilpasse en startverdi, y 3 () = a, slik at vi treffer betingelsen ved den andre randa ved å integrere framover ved Runge-Kuttas metode. Betingelsen i ζ = tilnærmer vi med y 2 (ζ ) = 1, der ζ er stor nok i dette problemet er ζ = 1 greit, mens en generelt må prøve seg fram, eller bruke en asymptotisk analyse (dvs. tilnærmelse for store ζ). I vårt tilfelle kan du følge prosedyren 1. Kod en løsningsteknikk for likningssettet i Matlab, eller et annet system du heller bruker, slik at a enkelt kan varieres og at y 2 (ζ ) skrives ut. 2. Velg et par verdier for a feks. 1 og 2 og beregn y 2 (ζ ) for disse. 3. Anta at y 2 (ζ ) varierer monotont med a og juster inn a manuelt til du har y 2 (ζ ) 1 <.1. Sjekk at oppløsning er fin nok og at ζ er stor nok. 4. Tegn ut hastighetsprofilet slik som i figur 1. 11
5 u z/δ(x) Figur 1: Profil beregnet vha. numerisk integrasjon c) Fortrengningstykkelsen er gitt som Δ = 1 u dz. Vis at denne blir Δ = lim (ζ F ) δ(x), og beregn konstanten foran δ med den numeriske løsningen funnet ovenfor. 12
Oppgaver for Mek 3220
 Oppgaver for Mek 322 Geir Pedersen Høst 213 Oppgavene som følger kommer i tillegg til oppgaver i kompendiet og gamle eksamensoppgaver på nettet. Nye oppgaver vil kunne komme til i løpet av semesteret og
Oppgaver for Mek 322 Geir Pedersen Høst 213 Oppgavene som følger kommer i tillegg til oppgaver i kompendiet og gamle eksamensoppgaver på nettet. Nye oppgaver vil kunne komme til i løpet av semesteret og
Oppgaver for Mek 3220
 Oppgaver for Mek 322 Geir Pedersen Høst 213 Oppgavene som følger kommer i tillegg til oppgaver i kompendiet og gamle eksamensoppgaver på nettet. Nye oppgaver vil kunne komme til i løpet av semesteret og
Oppgaver for Mek 322 Geir Pedersen Høst 213 Oppgavene som følger kommer i tillegg til oppgaver i kompendiet og gamle eksamensoppgaver på nettet. Nye oppgaver vil kunne komme til i løpet av semesteret og
- trykk-krefter. µ. u u u x. u venstre side. Det siste forsvinner fordi vi nettopp har vist x. r, der A er en integrasjonskonstant.
 Løsningsforslag, MPT 1 Fluiddynamikk, vår 7 Oppgave 1 1. Bevarelse av impuls, massefart,..; k ma. Venstre side er ma og høyre side kreftene (pr. volumenhet). Substansielt deriverte: Akselerasjon av fluidpartikkel,
Løsningsforslag, MPT 1 Fluiddynamikk, vår 7 Oppgave 1 1. Bevarelse av impuls, massefart,..; k ma. Venstre side er ma og høyre side kreftene (pr. volumenhet). Substansielt deriverte: Akselerasjon av fluidpartikkel,
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 11 Feltteori og vektoranalyse. Eksamensdag: Torsdag 1 desember 29. Tid for eksamen: 14:3 17:3. Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Torsdag 11 desember 2008. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Torsdag 11 desember 2008. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
Feltlikninger for fluider
 Kapittel 10 Feltlikninger for fluider Oppgave 1 Gitt et to-dimensjonalt strømfelt v = ωyi+ωxj. a) Den konvektive akselerasjonen for et to-dimensjonalt felt er gitt ved b) Bevegelseslikninga (Euler-likninga):
Kapittel 10 Feltlikninger for fluider Oppgave 1 Gitt et to-dimensjonalt strømfelt v = ωyi+ωxj. a) Den konvektive akselerasjonen for et to-dimensjonalt felt er gitt ved b) Bevegelseslikninga (Euler-likninga):
Oppgavehefte for Mek 1100
 Oppgavehefte for Mek 1100 Geir Pedersen Høst 2009 Oppg. 1 Normal til bane i planet. Vi har gitt en posisjonsvektor som funksjon av t på dimensjonsløs form r(t) = (5 + t)i + t 2 j. a) Finn hastigheten,
Oppgavehefte for Mek 1100 Geir Pedersen Høst 2009 Oppg. 1 Normal til bane i planet. Vi har gitt en posisjonsvektor som funksjon av t på dimensjonsløs form r(t) = (5 + t)i + t 2 j. a) Finn hastigheten,
Anbefalte oppgaver - Løsningsforslag
 TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
HAVBØLGER. Her skal vi gjennomgå den enkleste teorien for bølger på vannoverflaten:
 HAVBØLGER Her skal vi gjennomgå den enkleste teorien for bølger på vannoverflaten: Airy teori, også kalt lineær bølgeteori eller bølger av første orden Fremstillingen her vil temmelig nøyaktig følge kompendiet
HAVBØLGER Her skal vi gjennomgå den enkleste teorien for bølger på vannoverflaten: Airy teori, også kalt lineær bølgeteori eller bølger av første orden Fremstillingen her vil temmelig nøyaktig følge kompendiet
Virvelfrihet, potensialer, Laplacelikningen
 Virvelfrihet, potensialer, Laplacelikningen Kap 10 og 9 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE Forelesninger NYTT TEMA Hvorfor snakker vi om virvelfri bevegelse? Forelesninger Todimensjonal
Virvelfrihet, potensialer, Laplacelikningen Kap 10 og 9 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE Forelesninger NYTT TEMA Hvorfor snakker vi om virvelfri bevegelse? Forelesninger Todimensjonal
(1 + x 2 + y 2 ) 2 = 1 x2 + y 2. (1 + x 2 + y 2 ) 2, x 2y
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA45 Matematikk vår 9 Løsningsforslag til eksamen.5.9 Gitt f(, y) = + +y. a) Vi regner ut f = f y = + + y ( + + y ) = + + y
Fasit for eksamen i MEK1100 torsdag 13. desember 2007 Hvert delspørsmål honoreres med poengsum fra 0 til 10 (10 for perfekt svar).
 Fasit for eksamen i MEK torsdag 3. desember 27 Hvert delspørsmål honoreres med poengsum fra til ( for perfekt svar). Oppgave Vi har gitt to vektorfelt i kartesiske koordinater (x,y,z) A = yi+coszj +xy
Fasit for eksamen i MEK torsdag 3. desember 27 Hvert delspørsmål honoreres med poengsum fra til ( for perfekt svar). Oppgave Vi har gitt to vektorfelt i kartesiske koordinater (x,y,z) A = yi+coszj +xy
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Fredag 7. desember 27. Tid for eksamen: 9: 12:. Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Fredag 7. desember 27. Tid for eksamen: 9: 12:. Oppgavesettet er på 8 sider.
y = x y, y 2 x 2 = c,
 TMA415 Matematikk Vår 17 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 9 Alle oppgavenummer referer til 8. utgave av Adams & Essex alculus: A omplete
TMA415 Matematikk Vår 17 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 9 Alle oppgavenummer referer til 8. utgave av Adams & Essex alculus: A omplete
Løsning IM
 Løsning IM 6 Oppgave x + y Grensen lim er ubestemt da både teller og nevner blir Vi skal vise at grensen ( xy, ) (,) x + y ikke eksisterer og bruker rette linjer inn mot origo De enkleste linjene er koordinataksene
Løsning IM 6 Oppgave x + y Grensen lim er ubestemt da både teller og nevner blir Vi skal vise at grensen ( xy, ) (,) x + y ikke eksisterer og bruker rette linjer inn mot origo De enkleste linjene er koordinataksene
Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen
 Kapittel 4 Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen Oppgave Gitt et vektorfelt v = ui+vj +wk. Divergensen til v er definert som v = u x + v y + w z og virvlingen er gitt ved determinanten
Kapittel 4 Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen Oppgave Gitt et vektorfelt v = ui+vj +wk. Divergensen til v er definert som v = u x + v y + w z og virvlingen er gitt ved determinanten
Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3
![Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3 Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3](/thumbs/55/37240043.jpg) Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
NTNU. MA1103 Flerdimensjonal Analyse våren Maple-øving 2. Viktig informasjon. Institutt for matematiske fag. maple02 28.
 NTNU Institutt for matematiske fag MA1103 Flerdimensjonal Analyse våren 2011 Maple-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
NTNU Institutt for matematiske fag MA1103 Flerdimensjonal Analyse våren 2011 Maple-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
Fasit til eksamen i MEK1100 høst 2006
 Fasit til eksamen i MEK11 høst 26 Det er tilsammen 1 delspørsmål. Hvert delspørsmål honoreres med poengsum fra til 1 (1 for fullstendig svar, for blank). Maksimal oppnåelig poengsum er 1. Kontroller at
Fasit til eksamen i MEK11 høst 26 Det er tilsammen 1 delspørsmål. Hvert delspørsmål honoreres med poengsum fra til 1 (1 for fullstendig svar, for blank). Maksimal oppnåelig poengsum er 1. Kontroller at
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
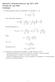 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Oppgaver og fasit til seksjon
 1 Oppgaver og fasit til seksjon 3.1-3.3 Oppgaver til seksjon 3.1 1. Regn ut a b når a) a = ( 1, 3, 2) b = ( 2, 1, 7) b) a = (4, 3, 1) b = ( 6, 1, 0) 2. Finn arealet til parallellogrammet utspent av a =
1 Oppgaver og fasit til seksjon 3.1-3.3 Oppgaver til seksjon 3.1 1. Regn ut a b når a) a = ( 1, 3, 2) b = ( 2, 1, 7) b) a = (4, 3, 1) b = ( 6, 1, 0) 2. Finn arealet til parallellogrammet utspent av a =
Tillegg om flateintegraler
 Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
Kapittel 6 Tillegg om flateintegraler 6.1 Litt ekstra om flateintegraler I kompendiet har vi definert flateintegraler som grenseoverganger for diskretiseringer. Har vi en flate kan vi representere den
Løsningsforslag Øving 5
 Løsningsforslag Øving 5 TEP41 Fluidmekanikk, Vår 216 Oppgave til forberedning til Lab x dx y y Figure 1 a) Oppdriftskraften på kvartsirkelen er F B = γu = γ π2 4 L der γ = ρg er den spesifikke vekten av
Løsningsforslag Øving 5 TEP41 Fluidmekanikk, Vår 216 Oppgave til forberedning til Lab x dx y y Figure 1 a) Oppdriftskraften på kvartsirkelen er F B = γu = γ π2 4 L der γ = ρg er den spesifikke vekten av
NTNU. MA1103 Flerdimensjonal analyse våren Maple/Matlab-øving 2. Viktig informasjon. Institutt for matematiske fag
 NTNU Institutt for matematiske fag MA1103 Flerdimensjonal analyse våren 2012 Maple/Matlab-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
NTNU Institutt for matematiske fag MA1103 Flerdimensjonal analyse våren 2012 Maple/Matlab-øving 2 Fyll inn studieprogram: Fyll inn navn: 1. 2. 3. 4. Viktig informasjon Besvarelsen kan leveres som gruppearbeid
Fasit MAT102 juni 2016
 Fasit MAT02 juni 206. (a) Finn egenverdiene og egenvektorene til matrisen ( ) 6 A = 2 7 Svar: λ = 8 og ( ) x = y y ( ) /2, λ = 5 og ( ) x = y y ( ) for alle y 0. (b) Finn den generelle løsningen på systemet
Fasit MAT02 juni 206. (a) Finn egenverdiene og egenvektorene til matrisen ( ) 6 A = 2 7 Svar: λ = 8 og ( ) x = y y ( ) /2, λ = 5 og ( ) x = y y ( ) for alle y 0. (b) Finn den generelle løsningen på systemet
Tillegg om strømfunksjon og potensialstrøm
 Kapittel 9 Tillegg om strømfunksjon og potensialstrøm 9.1 Divergensfri strøm 9.1.1 Strømfunksjonen I kompendiet, kap. 4.6 og kap. 9, er det påstått at dersom et todimensjonalt strømfelt v(x y) = v x (x
Kapittel 9 Tillegg om strømfunksjon og potensialstrøm 9.1 Divergensfri strøm 9.1.1 Strømfunksjonen I kompendiet, kap. 4.6 og kap. 9, er det påstått at dersom et todimensjonalt strømfelt v(x y) = v x (x
Eksamen i GEOF330 Dynamisk Oseanografi. Oppgave 1: Stående svingninger
 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i GEOF330 Dynamisk Oseanografi 15. Desember 2006, kl 0900-1400 Tillatte hjelpemiddel: Kalkulator og matematisk formelsamling Oppgave
Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i GEOF330 Dynamisk Oseanografi 15. Desember 2006, kl 0900-1400 Tillatte hjelpemiddel: Kalkulator og matematisk formelsamling Oppgave
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter.
 Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Løsningsforslag R2 Eksamen Nebuchadnezzar Matematikk.net Øistein Søvik
 Løsningsforslag R2 Eksamen 6 Vår 3.05.20 Nebuchadnezzar Matematikk.net Øistein Søvik Sammendrag De fleste forlagene som gir ut lærebøker til den videregående skolen, gir ut løsningsforslag til tidligere
Løsningsforslag R2 Eksamen 6 Vår 3.05.20 Nebuchadnezzar Matematikk.net Øistein Søvik Sammendrag De fleste forlagene som gir ut lærebøker til den videregående skolen, gir ut løsningsforslag til tidligere
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter.
 Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Kap. 8 Bevegelsesmengde. Kollisjoner. Massesenter. Vi skal se på: Newtons 2. lov på ny: Definisjon bevegelsesmengde Kollisjoner: Kraftstøt, impuls. Impulsloven Elastisk, uelastisk, fullstendig uelastisk
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007
 Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
Løysingsforslag (Skisse) Eksamen FY3452 Gravitasjon og Kosmologi Våren 2007 May 24, 2007 Oppgave 1 a) Lorentztransformasjonane er x = γ(x V t), t = γ(t V x), der γ = 1/ 1 V 2 Vi tar differensiala av desse
FYS1120 Elektromagnetisme, Ukesoppgavesett 1
 FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
FYS1120 Elektromagnetisme, Ukesoppgavesett 1 22. august 2016 I FYS1120-undervisningen legg vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene som
EKSAMENSOPPGAVE I FYS-1001
 side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
side 1 av 6 sider FAKULTET FOR NATURVITENSKAP OG TEKNOLOGI EKSAMENSOPPGAVE I FYS-1001 Eksamen i : Fys-1001 Mekanikk Eksamensdato : 06.12.2012 Tid : 09.00-13.00 Sted : Åsgårdvegen 9 Tillatte hjelpemidler
Arne B. Sletsjøe. Oppgaver, MAT 1012
 Arne B. Sletsjøe Oppgaver, MAT 101 1 En-variabel kalkulus 1.1 I de følgende oppgavene, i) finn alle kritiske punkter til f(x), ii) beskriv monotoniegenskapene til funksjonene ved å se på fortegnet til
Arne B. Sletsjøe Oppgaver, MAT 101 1 En-variabel kalkulus 1.1 I de følgende oppgavene, i) finn alle kritiske punkter til f(x), ii) beskriv monotoniegenskapene til funksjonene ved å se på fortegnet til
Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Obligatorisk oppgave 2
 MEK Obligatorisk oppgave 2 Nicolai Kristen Solheim Obligatorisk oppgave 2 Oppgave a) Vi kan beregne vektorfluksen Q = F ndσ gjennom en kuleflate σ gitt vektorfeltet σ F = xi + 2y + z j + z + x 2 k. Ved
MEK Obligatorisk oppgave 2 Nicolai Kristen Solheim Obligatorisk oppgave 2 Oppgave a) Vi kan beregne vektorfluksen Q = F ndσ gjennom en kuleflate σ gitt vektorfeltet σ F = xi + 2y + z j + z + x 2 k. Ved
Numerisk løsning av differensiallikninger Eulers metode,eulers m
 Numerisk løsning av differensiallikninger Eulers metode, Eulers midtpunktmetode, Runge Kuttas metode, Taylorrekkeutvikling* og Likninger av andre orden MAT-INF1100 Diskretsering Utgangspunkt: differensiallikning
Numerisk løsning av differensiallikninger Eulers metode, Eulers midtpunktmetode, Runge Kuttas metode, Taylorrekkeutvikling* og Likninger av andre orden MAT-INF1100 Diskretsering Utgangspunkt: differensiallikning
Auditorieøving 6, Fluidmekanikk
 Auditorieøving 6, Fluidmekanikk Utført av (alle i gruppen): Oppgave 1 En beholder er åpen i ene enden og har et hull i bunnen, påsatt et innadrettet rør av lengde l og med sirkulært tverrsnitt A 0. Beholderen,
Auditorieøving 6, Fluidmekanikk Utført av (alle i gruppen): Oppgave 1 En beholder er åpen i ene enden og har et hull i bunnen, påsatt et innadrettet rør av lengde l og med sirkulært tverrsnitt A 0. Beholderen,
Løsningsforslag til øving 3
 Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Institutt for fysikk, NTNU TFY455/FY003 Elektromagnetisme Vår 2009 Løsningsforslag til øving 3 Oppgave a) C V = E dl = 0 dersom dl E b) B På samme måte som et legeme med null starthastighet faller i gravitasjonsfeltet
Løsningsforslag Øving 12
 Løsningsforslag Øving 1 TEP4100 Fluidmekanikk, Vår 013 Oppgave 9-89 Løsning Vi skal finne et uttrykk for trykket som funksjon av x og y i et gitt hastighetsfelt. Antagelser 1 Strømningen er stasjonær.
Løsningsforslag Øving 1 TEP4100 Fluidmekanikk, Vår 013 Oppgave 9-89 Løsning Vi skal finne et uttrykk for trykket som funksjon av x og y i et gitt hastighetsfelt. Antagelser 1 Strømningen er stasjonær.
Løsningsforslag til eksamen i MAT 1100, H06
 Løsningsforslag til eksamen i MAT, H6 DEL. poeng Hva er den partiellderiverte f z xyz cosxyz x sinyz + xyz cosyz xy cosyz x sinyz + xz cosyz cosyz xyz sinyz når fx, y, z = xz sinyz? Riktig svar b: x sinyz
Løsningsforslag til eksamen i MAT, H6 DEL. poeng Hva er den partiellderiverte f z xyz cosxyz x sinyz + xyz cosyz xy cosyz x sinyz + xz cosyz cosyz xyz sinyz når fx, y, z = xz sinyz? Riktig svar b: x sinyz
Løsningsforslag til Øving 6 Høst 2016
 TEP4105: Fluidmekanikk Løsningsforslag til Øving 6 Høst 016 Oppgave 3.13 Skal finne utløpshastigheten fra røret i eksempel 3. når vi tar hensyn til friksjon Hvis vi antar at røret er m langt er friksjonen
TEP4105: Fluidmekanikk Løsningsforslag til Øving 6 Høst 016 Oppgave 3.13 Skal finne utløpshastigheten fra røret i eksempel 3. når vi tar hensyn til friksjon Hvis vi antar at røret er m langt er friksjonen
MA1101 Grunnkurs Analyse I Høst 2017
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA Grunnkurs Analyse I Høst 7 9.5. a) Har at + x b arctan b = π + x [arctan x]b (arctan b arctan ) f) La oss først finne en
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA Grunnkurs Analyse I Høst 7 9.5. a) Har at + x b arctan b = π + x [arctan x]b (arctan b arctan ) f) La oss først finne en
Differensiallikninger definisjoner, eksempler og litt om løsning
 Differensiallikninger definisjoner, eksempler og litt om løsning MAT-INF1100 Differensiallikninger i MAT-INF1100 Definsjon, litt om generelle egenskaper Noen få anvendte eksempler Teknikker for løsning
Differensiallikninger definisjoner, eksempler og litt om løsning MAT-INF1100 Differensiallikninger i MAT-INF1100 Definsjon, litt om generelle egenskaper Noen få anvendte eksempler Teknikker for løsning
Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].
![Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm]. Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen Q ligger i punktet ( 3, 0) [mm].](/thumbs/58/41840831.jpg) Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Oppgave 1 Finn løsningen til følgende 1.ordens differensialligninger: a) y = x e y, y(0) = 0 b) dy dt + a y = b, a og b er konstanter. Oppgave 2 Punktladningen Q ligger i punktet (3, 0) [mm] og punktladningen
Prøveeksamen i MAT 1100, H-03 Løsningsforslag
 Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Matlab-tips til Oppgave 2
 Matlab-tips til Oppgave 2 Numerisk integrasjon (a) Velg ut maks 10 passende punkter fra øvre og nedre del av hysteresekurven. Bruk punktene som input til Matlab og lag et plot. Vi definerer tre vektorer
Matlab-tips til Oppgave 2 Numerisk integrasjon (a) Velg ut maks 10 passende punkter fra øvre og nedre del av hysteresekurven. Bruk punktene som input til Matlab og lag et plot. Vi definerer tre vektorer
Eksamen R2, Våren 2011 Løsning
 R Eksamen, Våren 0 Løsning Eksamen R, Våren 0 Løsning Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (8 poeng) a) Deriver funksjonene
R Eksamen, Våren 0 Løsning Eksamen R, Våren 0 Løsning Del Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (8 poeng) a) Deriver funksjonene
x 2 = x 1 f(x 1) (x 0 ) 3 = 2 x 2 n n x 1 n 0 0, , , , , , , , , , , 7124
 NTNU Institutt for matematiske fag TMA4100 Matematikk 1 høsten 011 Løsningsforslag - Øving 4 Avsnitt 47 3 La f(x) = x 4 +x 3 med f (x) = 4x 3 +1 Med x 0 = 1 får ein med Newtons metode at Med x 0 = 1 får
NTNU Institutt for matematiske fag TMA4100 Matematikk 1 høsten 011 Løsningsforslag - Øving 4 Avsnitt 47 3 La f(x) = x 4 +x 3 med f (x) = 4x 3 +1 Med x 0 = 1 får ein med Newtons metode at Med x 0 = 1 får
Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen
 Kapittel 4 Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen Oppgave Gitt et vektorfelt Divergensen til v er definert som v = ui+vj +wk. v = u x + v y + w og virvlingen er gitt ved determinanten
Kapittel 4 Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen Oppgave Gitt et vektorfelt Divergensen til v er definert som v = ui+vj +wk. v = u x + v y + w og virvlingen er gitt ved determinanten
Grensebetingelse for trykk der hvor vann møter luft
 Forelesning 5/4 019 ved Karsten Trulsen Grensebetingelse for trykk der hvor vann møter luft Vi skal utlede en betingelse for trykket på grenseflaten der hvor vann er i kontakt med luft. Vi gjør dette ved
Forelesning 5/4 019 ved Karsten Trulsen Grensebetingelse for trykk der hvor vann møter luft Vi skal utlede en betingelse for trykket på grenseflaten der hvor vann er i kontakt med luft. Vi gjør dette ved
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 Løsningsforslag Øving 5.7.4 Vi observerer at både y = cos πx 4 og y = x er like funksjoner. Det vil si
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4 Matematikk Høst 4 Løsningsforslag Øving 5.7.4 Vi observerer at både y = cos πx 4 og y = x er like funksjoner. Det vil si
Eksamensoppgave i TMA4135 Matematikk 4D
 Institutt for matematiske fag Eksamensoppgave i TMA4135 Matematikk 4D Faglig kontakt under eksamen: Gunnar Taraldsen Tlf: 46432506 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4135 Matematikk 4D Faglig kontakt under eksamen: Gunnar Taraldsen Tlf: 46432506 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00 13:00 Hjelpemiddelkode/Tillatte
MEK1100, vår Obligatorisk oppgave 1 av 2.
 9. februar 2017 Innleveringsfrist MEK1100, vår 2017 Obligatorisk oppgave 1 av 2 Torsdag 2. mars 2017, klokken 14:30 i obligkassen, som står i gangen utenfor ekspedisjonen i 7. etasje i Niels Henrik Abels
9. februar 2017 Innleveringsfrist MEK1100, vår 2017 Obligatorisk oppgave 1 av 2 Torsdag 2. mars 2017, klokken 14:30 i obligkassen, som står i gangen utenfor ekspedisjonen i 7. etasje i Niels Henrik Abels
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
Løsningsforslag for FYS2140 Kvantemekanikk, Torsdag 16. august 2018
 Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
Løsningsforslag for FYS140 Kvantemekanikk, Torsdag 16. august 018 Oppgave 1: Materiens bølgeegenskaper a) De Broglie fikk Nobelprisen i 199 for sin hypotese. Beskriv med noen setninger hva den går ut på.
EKSAMEN. Ingeniør- og Fleksibel ingeniørutdanning.
 KANDIDATNUMMER: EKSAMEN EMNENAVN: Matematikk. EMNENUMMER: REA42/REA42F EKSAMENSDATO: Mandag 9. august 2 KLASSE: Ingeniør- og Fleksibel ingeniørutdanning. TID: kl. 9. 3.. FAGANSVARLIG: Hans Petter Hornæs
KANDIDATNUMMER: EKSAMEN EMNENAVN: Matematikk. EMNENUMMER: REA42/REA42F EKSAMENSDATO: Mandag 9. august 2 KLASSE: Ingeniør- og Fleksibel ingeniørutdanning. TID: kl. 9. 3.. FAGANSVARLIG: Hans Petter Hornæs
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MEK 1100 Feltteori og vektoranalyse. Eksamensdag: Fredag 29 mai 2009. Tid for eksamen: 14:30 17:30. Oppgavesettet er på 6 sider.
Kurve-, flate- og volumintegraler, beregning av trykkraft
 Kapittel 6 Kurve-, flate- og volumintegraler, beregning av trykkraft Oppgave 1 Vi skal regne ut kurveintegralet λ v dr langs kurven λ: y x3 når 1 x 2 og v xyi+x 2 j. Vi kan parametrisere med x som parameter,
Kapittel 6 Kurve-, flate- og volumintegraler, beregning av trykkraft Oppgave 1 Vi skal regne ut kurveintegralet λ v dr langs kurven λ: y x3 når 1 x 2 og v xyi+x 2 j. Vi kan parametrisere med x som parameter,
1 MAT100 Obligatorisk innlevering 1. 1 Regn ut i) iii) ii) Regn ut i) ii)
 1 MAT1 Obligatorisk innlevering 1 1 Regn ut 3 7 + 1 2. i) 13 14 ii) 11 14 iii) 9 14 2 Regn ut 8 9 + 3 4. i) 57 36 ii) 59 36 iii) 61 36 3 Regn ut 1 4 + 1 8. i) 3 16 ii) 3 8 iii) 5 8 4 Regn ut 1 8 + 1 16.
1 MAT1 Obligatorisk innlevering 1 1 Regn ut 3 7 + 1 2. i) 13 14 ii) 11 14 iii) 9 14 2 Regn ut 8 9 + 3 4. i) 57 36 ii) 59 36 iii) 61 36 3 Regn ut 1 4 + 1 8. i) 3 16 ii) 3 8 iii) 5 8 4 Regn ut 1 8 + 1 16.
Løsningsforslag MAT 120B, høsten 2001
 Løsningsforslag MAT B, høsten Sett A = ( ) (a) Finn egenverdiene og egenvektorene til A ( ) λ =, e = ( λ =, e = ) (b) Finn matrisen e ta og den generelle løsningen på initialverdiproblemet Ẋ = AX, X()
Løsningsforslag MAT B, høsten Sett A = ( ) (a) Finn egenverdiene og egenvektorene til A ( ) λ =, e = ( λ =, e = ) (b) Finn matrisen e ta og den generelle løsningen på initialverdiproblemet Ẋ = AX, X()
Repetisjon
 Repetisjon 18.05.017 Eksamensverksted: Mandag, 9.5., kl. 1 16, Origo Onsdag, 31.5., kl. 1 16, Origo FYS-MEK 1110 18.05.017 1 Lorentz transformasjon ( ut) y z y z u t c t 1 u 1 c transformasjon tilbake:
Repetisjon 18.05.017 Eksamensverksted: Mandag, 9.5., kl. 1 16, Origo Onsdag, 31.5., kl. 1 16, Origo FYS-MEK 1110 18.05.017 1 Lorentz transformasjon ( ut) y z y z u t c t 1 u 1 c transformasjon tilbake:
Eksamen R2 Høsten 2013 Løsning
 Eksamen R Høsten 03 Løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (3 poeng) Deriver funksjonene a) f 5cos Vi bruker produktregelen
Eksamen R Høsten 03 Løsning Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (3 poeng) Deriver funksjonene a) f 5cos Vi bruker produktregelen
Løsningsforslag, eksamen MA1101/MA
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Løsningsforslag, eksamen MA0/MA60 07.2.09 Oppgave La f() = e 4 2 2 8. a) Finn alle ekstremalpunktene til funksjonen
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Løsningsforslag, eksamen MA0/MA60 07.2.09 Oppgave La f() = e 4 2 2 8. a) Finn alle ekstremalpunktene til funksjonen
Forelesning 23 den 18/4 2017
 Forelesning 3 den 18/4 017 Eksperiment Toricelli hvor fort renner vann ut av et kar? Vi navngir eksperimentet til ære for Evangelista Torricelli (1608 1647) som oppdaget Toricellis lov i 1643. Toricelli
Forelesning 3 den 18/4 017 Eksperiment Toricelli hvor fort renner vann ut av et kar? Vi navngir eksperimentet til ære for Evangelista Torricelli (1608 1647) som oppdaget Toricellis lov i 1643. Toricelli
Γ = u dl = u φ adφ = 2πωa 2 = 6.28m 2 /s. r = 1 (ru r )
 À ËÃÇÄ Æ Á ËÌ Î Æ Ê ÁÒ Ø ØÙØØ ÓÖ Ñ Ø Ñ Ø Ó Ò ØÙÖÚ Ø Ò Ô Ä Ò Ò ÓÖ Ð Ñ Ò Ì ÐÙ ÝÒ Ñ ¾¼¼½ Î ÇÔÔ Ú ½ I hele oppgaven er u z = 0, og vi har ingen z-avhengighet, så u(r,φ) = u r (r,φ)e r +u φ (r,φ)e φ. a) For
À ËÃÇÄ Æ Á ËÌ Î Æ Ê ÁÒ Ø ØÙØØ ÓÖ Ñ Ø Ñ Ø Ó Ò ØÙÖÚ Ø Ò Ô Ä Ò Ò ÓÖ Ð Ñ Ò Ì ÐÙ ÝÒ Ñ ¾¼¼½ Î ÇÔÔ Ú ½ I hele oppgaven er u z = 0, og vi har ingen z-avhengighet, så u(r,φ) = u r (r,φ)e r +u φ (r,φ)e φ. a) For
Kurve-, flate- og volumintegraler, beregning av trykkraft
 Kapittel 6 Kurve-, flate- og volumintegraler, beregning av trykkraft Oppgave 1 Vi skal regne ut kurveintegralet λ v dr langs kurven λ: y x3 når 1 x 2 og v xyi+x 2 j. Vi kan parametrisere med x som parameter,
Kapittel 6 Kurve-, flate- og volumintegraler, beregning av trykkraft Oppgave 1 Vi skal regne ut kurveintegralet λ v dr langs kurven λ: y x3 når 1 x 2 og v xyi+x 2 j. Vi kan parametrisere med x som parameter,
Løsningsforslag for MAT-0001, desember 2009, UiT
 Løsningsforslag for MAT-1, desember 29, UiT av Kristian Hindberg Oppgave 1 a) Bestem grenseverdien e x 1 x lim x x 2 e x 1 x lim x x 2 = lim x e x 1 2x e = x lim x 2 = 1 2 b) Finn det ubestemte integralet
Løsningsforslag for MAT-1, desember 29, UiT av Kristian Hindberg Oppgave 1 a) Bestem grenseverdien e x 1 x lim x x 2 e x 1 x lim x x 2 = lim x e x 1 2x e = x lim x 2 = 1 2 b) Finn det ubestemte integralet
MA2501 Numeriske metoder
 MA501 Numeriske metoder Vår 009 Øving 9 Oppgave 1 Bruk vedlagte matlab-program skyt.m til å løse randverdiproblemet x + e x = 0, x(0) = x(1) = 0 Oppgave Gitt startverdiproblemet x = t(x ), x(0) = 1, x
MA501 Numeriske metoder Vår 009 Øving 9 Oppgave 1 Bruk vedlagte matlab-program skyt.m til å løse randverdiproblemet x + e x = 0, x(0) = x(1) = 0 Oppgave Gitt startverdiproblemet x = t(x ), x(0) = 1, x
GEF Løsningsforslag til oppgaver fra kapittel 6
 GEF1100 - Løsningsforslag til oppgaver fra kapittel 6 i.h.h.karset@geo.uio.no Oppgave 1 a) Hva er forskjellen mellom Lagrangesk og Eulersk representasjon av en væskebevegelse? Gi et eksempel på hver av
GEF1100 - Løsningsforslag til oppgaver fra kapittel 6 i.h.h.karset@geo.uio.no Oppgave 1 a) Hva er forskjellen mellom Lagrangesk og Eulersk representasjon av en væskebevegelse? Gi et eksempel på hver av
Kap. 3 Arbeid og energi. Energibevaring.
 Kap. 3 Arbeid og energi. Energibevaring. Definisjon arbeid, W Kinetisk energi, E k Potensiell energi, E p. Konservative krefter Energibevaring Energibevaring når friksjon. Arbeid = areal under kurve F(x)
Kap. 3 Arbeid og energi. Energibevaring. Definisjon arbeid, W Kinetisk energi, E k Potensiell energi, E p. Konservative krefter Energibevaring Energibevaring når friksjon. Arbeid = areal under kurve F(x)
SIF5005 Matematikk 2, 13. mai 2002 Løsningsforslag
 SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
Impuls, bevegelsesmengde, energi. Bevaringslover.
 Impuls, bevegelsesmengde, energi. Bevaringslover. Kathrin Flisnes 19. september 2007 Bevegelsesmengde ( massefart ) Når et legeme har masse og hastighet, viser det seg fornuftig å definere legemets bevegelsesmengde
Impuls, bevegelsesmengde, energi. Bevaringslover. Kathrin Flisnes 19. september 2007 Bevegelsesmengde ( massefart ) Når et legeme har masse og hastighet, viser det seg fornuftig å definere legemets bevegelsesmengde
1 Mandag 1. februar 2010
 Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen
 Kapittel 4 Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen Oppgave Gitt et vektorfelt v = ui + vj + wk. Divergensen til v er definert som v = u + v + w z og virvlingen er gitt ved determinanten
Kapittel 4 Vektorfluks og sirkulasjon, divergens, virvling, strømfunksjonen Oppgave Gitt et vektorfelt v = ui + vj + wk. Divergensen til v er definert som v = u + v + w z og virvlingen er gitt ved determinanten
a 2 x 2 dy dx = e r r dr dθ =
 NTNU Institutt for matematiske fag TMA4 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk
NTNU Institutt for matematiske fag TMA4 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon, språk
UNIVERSITETET I OSLO
 Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Side 1 av 4 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS-MEK111 Eksamensdag: Mandag 22. mars 21 Tid for eksamen: Kl. 15-18 Oppgavesettet er på 4 sider + formelark Tillatte
Øving 3. Oppgave 1 (oppvarming med noen enkle oppgaver fra tidligere midtsemesterprøver)
 Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Institutt for fysikk, NTNU TFY455/FY003: Elektrisitet og magnetisme Vår 2008 Veiledning: Fredag 25. og mandag 28. januar Innleveringsfrist: Fredag. februar kl 2.00 Øving 3 Oppgave (oppvarming med noen
Eksamen i SIF5036 Matematisk modellering Onsdag 12. desember 2001 Kl
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Harald E Krogstad, tlf: 9 35 36/ mobil:416 51 817 Sensur: uke 1, 2002 Tillatte hjelpemidler:
Løsningsforslag øving 4
 TTK405 Reguleringsteknikk, Vår 206 Oppgave Løsningsforslag øving 4 Når k 50, m 0, f 20, blir tilstandsromformen (fra innsetting i likning (3.8) i boka) Og (si A) blir: (si A) [ ] [ ] 0 0 ẋ x + u 5 2 0.
TTK405 Reguleringsteknikk, Vår 206 Oppgave Løsningsforslag øving 4 Når k 50, m 0, f 20, blir tilstandsromformen (fra innsetting i likning (3.8) i boka) Og (si A) blir: (si A) [ ] [ ] 0 0 ẋ x + u 5 2 0.
Løsningsforslag til eksamen i TMA4105 matematikk 2,
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av Løsningsforslag til eksamen i TMA45 matematikk, 9.5.4 Oppgave La fx, y, z) xy + arctanxz). La P være punktet,, ). a)
Eksamen REA3024 Matematikk R2. Nynorsk/Bokmål
 Eksamen 3.05.0 REA304 Matematikk R Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del : Hjelpemiddel på Del : 5 timar: Del skal leverast inn etter timar. Del skal leverast inn
Eksamen 3.05.0 REA304 Matematikk R Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del : Hjelpemiddel på Del : 5 timar: Del skal leverast inn etter timar. Del skal leverast inn
Løsningsforslag Eksamen i Fys-mek1110 våren 2010
 Side av Løsningsforslag Eksamen i Fys-mek våren Oppgave (Denne oppgaven teller dobbelt) Ole og Mari vil prøve om lengdekontraksjon virkelig finner sted. Mari setter seg i sitt romskip og kjører forbi Ole,
Side av Løsningsforslag Eksamen i Fys-mek våren Oppgave (Denne oppgaven teller dobbelt) Ole og Mari vil prøve om lengdekontraksjon virkelig finner sted. Mari setter seg i sitt romskip og kjører forbi Ole,
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 00 Modellering og beregninger. Eksamensdag: Torsdag 6. desember 202. Tid for eksamen: 9:00 3:00. Oppgavesettet er på 8
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 00 Modellering og beregninger. Eksamensdag: Torsdag 6. desember 202. Tid for eksamen: 9:00 3:00. Oppgavesettet er på 8
Partieltderiverte og gradient
 Partieltderiverte og gradient Kap 2 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE våren 2009 Framstilling Kommentarer, relasjon til andre kurs Struktur Mye er repitisjon fra MAT1100, litt
Partieltderiverte og gradient Kap 2 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE våren 2009 Framstilling Kommentarer, relasjon til andre kurs Struktur Mye er repitisjon fra MAT1100, litt
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. Obligatorisk innlevering 3 i emnet MAT111, høsten 2016
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Obligatorisk innlevering 3 i emnet MAT, høsten 206 Innleveringsfrist: Mandag 2. november 206, kl. 4, i Infosenterskranken i inngangsetasjen
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Obligatorisk innlevering 3 i emnet MAT, høsten 206 Innleveringsfrist: Mandag 2. november 206, kl. 4, i Infosenterskranken i inngangsetasjen
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
a) Bruk en passende Gaussflate og bestem feltstyrken E i rommet mellom de 2 kuleskallene.
 Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
Oppgave 1 Bestem løsningen av differensialligningen Oppgave 2 dy dx + y = e x, y(1) = 1 e Du skal beregne en kulekondensator som består av 2 kuleskall av metall med samme sentrum. Det indre skallet har
LØSNINGSFORSLAG EKSAMEN I MATEMATIKK 4N/D (TMA4125 TMA4130 TMA4135) Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 EKSAMEN I MATEMATIKK N/D (TMA25 TMA3 TMA35 3. August 27 LØSNINGSFORSLAG Oppgave a Løsning: fouriersinusrekken til
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 EKSAMEN I MATEMATIKK N/D (TMA25 TMA3 TMA35 3. August 27 LØSNINGSFORSLAG Oppgave a Løsning: fouriersinusrekken til
= (2 6y) da. = πa 2 3
 TMA45 Matematikk Vår 7 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavenummer referer til 8. utgave av Adams & Essex alculus: A omplete ourse.
TMA45 Matematikk Vår 7 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving Alle oppgavenummer referer til 8. utgave av Adams & Essex alculus: A omplete ourse.
FYS1120 Elektromagnetisme - Ukesoppgavesett 2
 FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
FYS1120 Elektromagnetisme - Ukesoppgavesett 2 7. september 2016 I FYS1120-undervisningen legger vi mer vekt på matematikk og numeriske metoder enn det oppgavene i læreboka gjør. Det gjelder også oppgavene
Kap. 22. Gauss lov. Vi skal se på: Fluksen til elektrisk felt E Gauss lov. Elektrisk ledere. Integralform og differensialform
 Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
Kap. 22. Gauss lov Vi skal se på: Fluksen til elektrisk felt E Gauss lov Integralform og differensialform Elektrisk ledere. E-felt fra Coulombs lov: E k q r 2 r E k n q r n 2 0n r 0n dq E k r 2 r tot.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 00 Kalkulus. Eksamensdag: Mandag,. desember 006. Tid for eksamen:.30 8.30. Oppgavesettet er på sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 00 Kalkulus. Eksamensdag: Mandag,. desember 006. Tid for eksamen:.30 8.30. Oppgavesettet er på sider. Vedlegg: Tillatte hjelpemidler:
Repetisjonsoppgaver kapittel 0 og 1 løsningsforslag
 Repetisjonsoppgaver kapittel 0 og løsningsforslag Kapittel 0 Oppgave a) Gjennomsnittet er summen av måleverdiene delt på antallet målinger. Summen av målingene er,79 s. t sum av måleverdiene antallet målinger,79
Repetisjonsoppgaver kapittel 0 og løsningsforslag Kapittel 0 Oppgave a) Gjennomsnittet er summen av måleverdiene delt på antallet målinger. Summen av målingene er,79 s. t sum av måleverdiene antallet målinger,79
Mål og innhold i Matte 1
 Mål og innhold i Institutt for matematiske fag 1. november 2013 Målet med denne oversikten er at vi skal se hvor vi er i pensum, og at du skal kunne finne hva du kan/ikke kan. Jeg vil i tillegg vise hva
Mål og innhold i Institutt for matematiske fag 1. november 2013 Målet med denne oversikten er at vi skal se hvor vi er i pensum, og at du skal kunne finne hva du kan/ikke kan. Jeg vil i tillegg vise hva
EKSAMEN I FAG SIO 1043 STRØMNINGSLÆRE Lørdag 1. juni 2002 Tid: kl. 09:00 15:00
 Side 1 av 10 Norges teknisk natrvitenskapelige niversitet NTNU Fakltet for Ingeniørvitenskap og teknologi Instittt for Mekanikk, Termo og Fliddynamikk Faglig kontakt nder eksamen: Per-Åge Krogstad, tlf.:
Side 1 av 10 Norges teknisk natrvitenskapelige niversitet NTNU Fakltet for Ingeniørvitenskap og teknologi Instittt for Mekanikk, Termo og Fliddynamikk Faglig kontakt nder eksamen: Per-Åge Krogstad, tlf.:
HØGSKOLEN I BERGEN Avdeling for Ingeniørutdanning
 HØGSKOLEN I BERGEN Avdeling for Ingeniørutdanning EKSAMEN I Matematisk analyse og vektoralgebra, FOA150 KLASSE : Alle DATO : 11. august 006 TID: : Kl. 0900-100 (4 timer) ANTALL OPPGAVER : 5 VARIGHET ANTALL
HØGSKOLEN I BERGEN Avdeling for Ingeniørutdanning EKSAMEN I Matematisk analyse og vektoralgebra, FOA150 KLASSE : Alle DATO : 11. august 006 TID: : Kl. 0900-100 (4 timer) ANTALL OPPGAVER : 5 VARIGHET ANTALL
EKSAMEN I NUMERISK MATEMATIKK(TMA4215) Lørdag 20. desember 2003 Tid: 09:00 14:00, Sensur:
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (9264) EKSAMEN I NUMERISK MATEMATIKK(TMA425) Lørdag 2. desember
Oppgave 1 OPPGAVER OG LØSNINGSFORSLAG KONTINUASJONSEKSAMEN I FAG SMN 6147 OG SMN 6195 KOMPLEKS ANALYSE STED: HØGSKOLEN I NARVIK. KLASSE:4EL,4RTog5ID
 OPPGAVER OG LØSNINGSFORSLAG KONTINUASJONSEKSAMEN I FAG SMN 647 OG SMN 695 KOMPLEKS ANALYSE STED: HØGSKOLEN I NARVIK KLASSE:4EL,4RTog5ID DATO: 8 januar 004 TID: 9.00-.00 ANTALL SIDER: 0 (inklusiv formler)
OPPGAVER OG LØSNINGSFORSLAG KONTINUASJONSEKSAMEN I FAG SMN 647 OG SMN 695 KOMPLEKS ANALYSE STED: HØGSKOLEN I NARVIK KLASSE:4EL,4RTog5ID DATO: 8 januar 004 TID: 9.00-.00 ANTALL SIDER: 0 (inklusiv formler)
