Eksamen i ELE620, Systemidentikasjon (10 sp)
|
|
|
- Monica Esther Holen
- 5 år siden
- Visninger:
Transkript
1 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentikasjon (10 sp) Dato: Fredag 15 desember 2017 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun standard enkel kalkulator. Bokmål Utkast med løsningsforslag, 28. november Merk at faglærer ikke vil gå en runde i eksamenslokalet under eksamen. Er det ting i oppgaven du synes er uklart eller tvetydig så gjør fornuftige, faglig baserte antakelser. Husk å ta de med i besvarelsen. Max oppnåelige poeng er gitt for hver oppgave, totalt kan en få 100 poeng. Med 240 minutt totalt kan en fornuftig tidsbruk være å bruke ca 10 minutt for hver 5 poeng, da har en 20 minutt til pauser og 20 minutt ekstra. Merk at oppgavene eller deloppgavene ikke er sortert etter forventet vanskelighetsgrad. Oppgavesettet er på 4 oppgaver, i tillegg er det med noen nyttige formler i del 5 side 15. Oppgavesettet med løsningsforslag er totalt 15 sider (inkludert denne forsida).
2 1 Dobbelintegrator (Antall poeng for denne oppgaven er 25) Diskretisering av tilstandsrommodell (TRM) er å gå fra den kontinuerlige TRM til den diskrete TRM som vist her ẋ = Ax + Bu y = Dx + Eu x(k + 1) = Φx(k) + Γu(k) y(k) = Dx(k) + Eu(k) (1.1) Eksakt diskretisering med nullteordens holdeelement gir følgende sammenheng Γ = T 0 Φ = e AT = L 1{ (si A) 1} t=t (1.2) e Aτ dτ B = L 1 {(si A) 1 1 s B } t=t (1.3) Gitt følgende tidskontinuerlige modell for en dobbelintegrator: der K er en konstant. ÿ = Ku (1.4) a. Forklar hvordan en går fra dierensialligningen (1.4) til en kontinuerlig TRM med matrisene A, B, D og E som nedenfor A = [ [ 0, B = K D = [ 1 0, og E = 0. Ved å sette en tilstand lik y og en tilstand lik y derivert får en ẋ 2 x 1 = y (1.5) x 2 = ẏ = ẋ 1 (1.6) ẋ 1 = ẏ = x 2 (1.7) ẋ 2 = ẍ 1 = ÿ = Ku (1.8) Disse ligningene kan skrives på matriseform med matriser som i oppgaven. [ [ [ ẋ ẋ = = x + u = Ax + Bu 0 0 K y = [ 1 0 x = Dx, og E = 0. 2
3 b. Finn matrisene Φ, Γ, D og E i den diskrete TRM med eksakt diskretisering og nullteordens holdeelement. Samplingsintervallet (tidssteget) er T [sek. Eksakt diskretisering av TRM gir { [ Φ = L 1{ (si A) 1} } 1 s 1 t=t = L 1 0 s t=t {[ } 1/s 1/s = L 1 2 [ [ 1 t 1 T = = 0 1/s t=t t=t (1.9) Γ = L 1 { (si A) 1 1 s B } t=t = L 1 {[ 1/s 1/s 2 = L 1 {[ K/s 3 K/s 2 } t=t = [ KT 2 /2 KT 0 1/s 1 s [ 0 K } t=t (1.10) Dette gir altså den diskrete tilstandsrommodellen med matrisene [ [ 1 T KT Φ =, Γ = 2 /2. (1.11) 0 1 KT D og E matrisene i diskret TRM, (1.1), er som i kontinuerlig TRM. D = [ 1 0, og E = 0. c. Finn z-transferfunksjonen, h(z) = y(z) u(z) for systemet med eksakt diskretisering. Hint: h(z) kan kanskje enklest nnes med å ta z-transformasjon av diskret TRM, men den kan også nnes ved å gå via s-transferfunksjonen, som igjen kan nnes fra dierensialligningen (1.4). z-transferfunksjonen, h(z) = y(z) av diskret TRM. u(z) for systemet kan nnes ved å ta z-transformasjon zx(z) = Φx(z) + Γu(z) (zi Φ)x(z) = Γu(z) x(z) = (zi Φ) 1 Γu(z) 3
4 og setter inn for x(z) i y(z) y(z) = Dx(z) + Eu(z) = D(zI Φ) 1 Γu(z) + Eu(z) y(z) = ( D(zI Φ) 1 Γ + E ) u(z) h(z) = y(z) u(z) = D(zI Φ) 1 Γ + E Vi nner videre at og zi Φ = (zi Φ) 1 = [ z 0 0 z [ z 1 T 0 z 1 [ 1 T = = [ z 1 T 0 z 1. 1 [ z 1 T (z 1) 2 0 z 1 h(z) = D(zI Φ) 1 Γ + E [ [ 1 z 1 T KT = [1, 0 2 /2 + 0 (z 1) 2 0 z 1 KT [ K (z 1)T = [1, 0 2 /2 + T 2 (z 1) 2 (z 1)T K = (z 1) (zt 2 /2 T 2 /2 + T 2 ) = K T 2 (z + 1) 2 2 (z 1) 2 Alternativet er å gå via s-transferfunksjonen ÿ = Ku s 2 y(s) = Ku(s) G(s) = K/s 2. og bruke ligninger fra formelarket [ { G(s) } { K } h(z) = (1 z 1 )Z L 1 = (1 z s t=kt 1 )Z [L 1 t=kt s 3 = (1 z 1 )Z [(Kt 2 /2) t=kt = K(1 z 1 )/2 Z [ T 2 k 2 = K T 2 (1 z 1 )/2 Z [ k 2 = K T 2 (1 z 1 )/2 h(z) = K T 2 (z 1)/2 z + 1 (z 1) = K T 2 (z + 1) 3 2 (z 1) 2 z(z + 1) (z 1) 3 4
5 2 Smelteovn (Antall poeng for denne oppgaven er 25) En kan her tenke seg at prosessen er en smelteovn som i gur 1 side 6. Energibalansen for et system sier at endringen i energi er lik netto sum av energi til og fra systemet. Som formel skrives dette du dt = u inn u ut + Q W u inn og u ut er energi som følger masseyt. Q er varmeenergiyt til systemet uten at masse følger med. Her er utført arbeid W = 0 for både smelte- og kjølevannsystem. Formelen fo energiinnholdet i et system i enheten [J er U = m c p T Energi-innholdet til et sto som strømmer inn i/ut av et system i enhetene [J/s er u = F c p T En modell av varmetransport i enhetene [J/s gjennom en vegg er Q = (T 1 T 2 ) I tillegg til symbolene brukt i gur 1 kan også følgende symboler brukes: v 1 - prosesstøy for T s, [K/s v 2 - prosesstøy for T kv, [K/s y - måling [K w - målestøy [K Bruk følgende antagelser: mengden kjølevann er konstant, dvs. kjølekappen er hele tiden full av vann varmekapasiteten til kjølevann og smelte er konstant (varierer ikke med temperatur) ideell blanding i kjølevann og smelte mengden smelte er konstant 5
6 Q s T i F kv T kv F kv T s m s c p,s T kv hvor: T s - temperatur i smelten [K (tilstand1/måling1) T kv - Kjølevannstemperatur [K (tilstand2/måling2) T i - Temperatur på kjølevann inn [K c p,s - Spesikk varmekapasitet i smelte [J/K kg c p,kv - Spesikk varmekapasitet i kjølevann [J/K kg - Produktet av varmeoverføringskoesient og areal mellom smelte og kjølevann [J/K s Q s - Eektpådrag i smelten [J/s F kv - ow av kjølevann [kg/s m kv - mengde kjølevann i kappen [kg m s - mengde smelte [kg Figur 1: Prinsippskisse av smelteovn. 6
7 ingen tilsats eller uttak av smelte kjølevannstemperaturen måles det er 2 pådrag, Q s og T i (mao. så har vi f.eks. en varmeveklser foran kjølevannsinntaket til reaktoren som vi kan styre temperaturen inn med). a. Gå via energibalansen for smelte og kjølevann og vis at kontinuerlig tilstandsrommodell blir ẋ = Ax + Bu + Cv y = Dx + w (2.1) der matrisene er A = [ ha ( C = + F kv [ ) m kv, B =, D = [ 0 1. [ 1 0 F 0 kv m kv. For smelten er det ingen masseyt, det er varmetap til kjølevannet og varme fra eektpådraget. uinn = 0, U = m s c p,s T s uut = 0, W = 0 Q = Qs (T s T kv ) Energibalansen blir da d(m s c p,s T s ) dt m s c p,s dt s dt T s = dt s dt = Q s (T s T kv ) = Q s T s + T kv = T s + T kv + 1 Q s (2.2) m s c p,s m s c p,s m s c p,s For kjølevannet er det masseyt inn og ut, og varme overføres fra smelten til kjølevannet. U = m kv c p,kv T kv uinn = F kv c p,kv T i uut = F kv c p,kv T kv Q = ha (T s T kv ) 7
8 Energibalansen blir da d( T kv ) dt dt kv dt T kv = dt kv dt = F kv c p,kv T i F kv c p,kv T kv + (T s T kv ) = F kv c p,kv T i F kv c p,kv T kv + T s T kv = h ( A T s + F ) kv T kv + F kv T i m kv m kv (2.3) Støyen er ennå ikke lagt til modellen men det kan enkelt gjøres ved å legge v 1 til på høyre side i ligning 2.2 og ved å legge v 2 til på høyre side i ligning 2.3. En måler kjølevannet og får da måleligningen (med støy) y = T kv + w. (2.4) Systemet har da følgende dierensialligninger T s = dt s dt = m s c p,s T s + T kv = dt kv dt = T s T kv + 1 m s c p,s ( m s c p,s Q s + v 1 (2.5) + F ) kv T kv + F kv T i + v 2 (2.6) m kv m kv y = T kv + w. (2.7) Signalvektorene i tilstandsrommodellen (2.1) er [ [ Ts T x =, ẋ = s T kv T, u = kv [ Qs T i [ v1, v = v 2. Dierensialligningene (2.2) og (2.3) skrives på matriseform som ẋ = [ ha ( ) + F kv m kv x + [ 1 0 F 0 kv m kv u. Dette mangler bare støyen og måleligningen for å få ønsket form som i ligningssystemet i oppgaven, C som identitetsmatrisen og D = [0, 1. b. Utvikle en diskret tilstandsrommodell som svarer til Euler-forover-diskretisering av modellen funnet i oppgave a. Bruk samplingsintervall T som ikke må forveksles med noen av temperaturene, alle temperaturene har subskript. Skriv den diskrete tilstandsrommodellen på formen det vil si skriv uttrykkene for Φ og Γ. x(k + 1) = Φx(k) + Γu(k) (2.8) 8
9 Diskretisering med Eulers forovermetode er å sette Φ = I + AT og Γ = BT. Her får vi da Φ = [ 1 T T 1 ( T ) + F kv m kv T, Γ = [ T 0 F 0 kv T m kv. c. En håndregel angir hvor stor øvre grense for valg av tidsteg er. I denne regelen inngår største egenverdi for ei matrise. Hvordan er denne håndregelen? Håndregelen står i læreboka, hos Haugen i ADC ligning (8.8) side 97, og i mitt notat1 (kap ). Den ble også brukt i øving 6, håndregelen er T 0.1 {eig(a)} max. (2.9) Vi ser at det er (den største av) egenverdiene for matrisa A som er viktige. 9
10 3 Kalman-lter for parameterestimering (Antall poeng for denne oppgaven er 30) Modellen som ofte brukes for parameterestimering er y(k) = ϕ T (k)θ + e(k) (3.1) Kalman-lteret er basert på en tilstandsrommodell x(k + 1) = Φ(k)x(k) + Γ(k)u(k) + Ω(k)v(k) (3.2) y(k) = D(k)x(k) + w(k). (3.3) a. Forklar hvordan en kan overføre modellen i ligning 3.1 til tilstandsrommodellen i ligningene 3.2 og 3.3. Overgangen til tilstandsrommodell er som beskrevet i kap 3.5 i notat 4 (2017). Det er de ukjente parametrene, θ, som en ønsker å estimere med ˆθ. Parametrene θ i ligning 3.1 blir da tilstanden x i ligning 3.2. En har ingen pådrag som påvirker parametrene direkte, men en må tillate litt endring av parametrene fra et tidssteg til neste, altså x(k + 1) = x(k) + v(k). Φ matrisa er altså identitetsmatrisa. Når en får tilgjengelig ei ekstra ligning, så tilsvarer dette ei ny måling, en får da y(k) = D(k)x(k) + w(k) med parameterestimeringsvariabler y(k) = ϕ T (k)ˆθ(k) + w(k). Vi ser da at vi får D(k) = ϕ T (k). En skal estimere disse for hvert tidssteg, basert på estimat for forrige tidssteg og ny ligning (ny datavektor). Tilstandsrommodell av ligning 3.1 er da θ(k + 1) = θ(k) + v(k) (3.4) y(k) = ϕ T (k)θ(k) + e(k). (3.5) Støyen e(k) er hvit støy, den samme som w(k) i ligning 3.3. Legg merke til at en her har et tidsvarierende Kalman-lter, det nytter altså ikke med noe stasjonært Kalman-lter for parameterestimering. Viktig for implementering her er størrelsen en velger for matrisene Q og R, tuningsparametrene. b. Viktig ved implementering av et Kalman-lter, ligningene 5.2 til 5.6, er matrisene Q og R. Forklar hvordan disse er denert. Forklar også hvordan de kan brukes som tuningsparametre for Kalman-lteret. Q og R er autokovariansmatriser for prosesstøy v(k) og målestøy w(k) henholdsvis. Denisjon er i kap 1.4 i notat3 (2017). E[v(k + τ)v T (k) = R v (τ, k) = δ(τ)r v (0, k) = Q(k) = Q, (3.6) E[w(k + τ)w T (k) = R w (τ, k) = δ(τ)r w (0, k) = R(k) = R. (3.7) 10
11 En antar ofte at de er konstante, men de kan i noen tilfeller variere med tiden/tidssteg k. Støy er hvit og derfor har en δ(τ) med ovenfor. Q matrisa angir variansen på prosesstøy, stor Q svarer til mye støy og dermed tillates mye endringer i tilstandene i hvert steg, og en legger da ikke så mye vekt på forrige tilstand som hvis Q er liten. R matrisa angir variansen på målestøy, stor R svarer til mye støy og dermed er det stor usikkerhet i måling og en legger mindre vekt på målingen. Forholdet mellom Q og R er det som teller og avgjør hvor mye vekt en legger på forrige tilstand i forhold til måling. En av de laåse, gjerne R som kan være gitt ut fra datablad for måleinstrumenter, mens den andre, oftest Q, brukes som tuningsparameter. c. Kalman-lter kan gjerne brukes i stedet for RLS ved parameterestimering. Forklar fordeler og ulemper med å bruke Kalman-lter i forhold til RLS. 1. Kalman-lter er mer eksibelt enn RLS. Tilstandsrommodell gir mer eksibel modellering enn den lineære regresjonsligningen. 2. Hvis en låser R og bruker Q for tuning av Kalman-lteret har en likevel mer frihet i tuning, en kan gi hver tilstand ulik tuningsparameter. I RLS har en kun en glemmefaktor. 3. Kalman-lter kan enklere utvides enn RLS, augmentert Kalman-lter, eller ekstra måling ved enkelte tidssteg. 4. Linearisering av ulineære modeller kan gjøres med Kalman-lter. 5. Kalman-lter har ingen ulemper, unntatt hvis en misliker å forholde seg til stokastiske varaibler. Noen synes RLS er enklere siden det da klarere (?) kommer fram hva en minimerer. d. I implemeteringen av Kalman-lteret, ligningene 5.2 til 5.6, har en både P og ˆP, mens en i RLS har kun ei P matrise. Hva er denisjonen for hver av disse tre matrisene. Forklar en viktig forskjell, og en viktig forbindelse (sammenheng eller likhet) mellom P og ˆP på den ene siden og P på den andre siden. I Kalman-lteret er P og ˆP denert som estimat av kovariansmatrisa for estimeringsavvikene Cov(θ θ(k)) og Cov(θ ˆθ(k)) henholdsvis. Hvis en fortrekker 11
12 å bruke tilstand x(k) i stedet for parametervektoren θ blir det P (k) = E[(x(k) x(k))(x(k) x(k)) T (3.8) ˆP (k) = E[(x(k) ˆx(k))(x(k) ˆx(k)) T (3.9) Her er x(k) som apriori, før måling y(k), estimat av tilstand og ˆx(k) som aposteriori, etter måling y(k), estimat av tilstand. I RLS er P denert via den inverse av sum av ytreprodukter av regresjonsvektorer, eventuelt vektet med glemmefaktor opphøyd i potens (k i). P 1 (k) = k λ k i ϕ(i)ϕ T (i) = λp 1 (k 1) + ϕ(k)ϕ T (k). (3.10) i=1 I RLS er ikke P stokastisk. P er deterministisk, regnet ut basert på de observerte verdiene for hvert tidssteg, ϕ(i). Likevel er det en sammenheng med kovariansmatrisene brukt i Kalman-lteret, P (k) er et estimat av variansen for parameterestimatene, og dermed også for avviket, når variansen for målestøyen σ 2 = 1, (i Kalman-lteret R = 1). 12
13 4 Statistiske egenskaper for ARMA-prosess (Antall poeng for denne oppgaven er 20) Følgende er et eksempel på en ARMA-prosess: x(k) = ax(k 1) + e(k) + ce(k 1), a < 1 (4.1) der x(k) = 0 for k < 0 og e(k) er en sekvens av normalfordelte, statistisk uavhengige tilfeldige variabler der E[e(k) = 0 { σ 2 R e (l) = E[e(k)e(k l) = e l = 0 0 l 0 Vi kan regne prosessen for stasjonær i det området vi ser på her, det vil si E[f(x(k)) = E[f(x(k l)), og f( ) er en funksjon. a. Finn forventningsverdien (middelverdien) til x(k). Denne oppgaven er lik øving 4.3 som de este av dere kk til bra tidligere i høst. Middelverdien for x(k) blir m x(k) = m x og blir E[x(k) = E[ax(k 1) + e(k) + ce(k 1) m x = am x + m e + cm e (1 a)m x = (1 + c)m e = 0 m x = 0 b. Vis at 0 for l < 0 R xe (l) = E[x(k)e(k l) = σe 2 for l = 0 a l 1 (a + c)σe 2 for l > 0 (4.2) En starter med å slå fast at støy på framtidige tidspunkt er ukorrelert med signalet nå eller tidligere. Altså R xe (l) = 0 for l < 0. Dermed kan en sette 13
14 R xe (l) = E[x(k)e(k l) (4.3) = E[ ( ax(k 1) + e(k) + ce(k 1) ) e(k l) = E[ax(k 1)e(k l) + e(k)e(k l) + ce(k 1)e(k l) = ar xe (l 1) + R e (l) + cr e (l 1) R xe (l) = 0 for l < 0 (4.4) R xe (0) = ar xe ( 1) + R e (0) + cr e ( 1) = σe 2 (4.5) R xe (1) = ar xe (0) + R e (1) + cr e (0) = aσe 2 + cσe 2 = (a + c)σe 2 (4.6) R xe (2) = ar xe (1) + R e (2) + cr e (1) = a(a + c)σe 2 (4.7) R xe (l) = ar xe (l 1) for l 2 (4.8) R xe (l) = a l 1 (a + c)σe 2 for l 1 (4.9) c. Finn variansen til x(k), altså σ 2 x = R x (0) = E[x 2 (k). Og variansen for x nnes så med σ 2 x = E[x(k)x(k) = R x (0) (4.10) = E[ ( ax(k 1) + e(k) + ce(k 1) )( ax(k 1) + e(k) + ce(k 1) ) = E[ ax(k 1)ax(k 1) + e(k)ax(k 1) + ce(k 1)ax(k 1) +ax(k 1)e(k) + e(k)e(k) + ce(k 1)e(k) +ax(k 1)ce(k 1) + e(k)ce(k 1) + ce(k 1)ce(k 1) = a 2 R x (0) + ar xe ( 1) + acr xe (0) +ar xe ( 1) + R e (0) + cr e (1) +acr xe (0) + cr e (1) + c 2 R e (0) = a 2 σx acσe σe acσe c 2 σe 2 σx ac + c2 = σ 1 a e. 2 2 (4.11) 14
15 5 Formler og ligninger Diskretisering z-transferfunksjon for kontinuerlige prosesser med nullteordens sample- og holdeelement på inngangen: [ h(z) = (1 z 1 )Z L 1 { G(s) s } t=kt. (5.1) Tranformasjonspar, δ( ) er enhetsimpuls og u( ) er enhetssteg. L { e at} = 1 s a (n 1)! s n 1 L { δ(t a) } = e as L { u(t a) } = e as (s a) 2 s L{1} = 1 s, L{t} = 1 s 2 og generelt L{t n 1 } = L { te at} = Z { δ(k) } = 1 Z { δ(k n) } = z n Z { a k u(k) } = z z a Z { ka k u(k) } = az (z a) 2 Z { k 2 a k u(k) } = az(z + a) (z a) 3 Kalman-lter I vår utledning av Kalman-lteret kom vi fram til følgende ligninger som oppsummerer hovedløkka, det er det som gjøres for hvert tidssteg k. x(k) = Φˆx(k 1) + Γu(k 1) (5.2) P (k) = Φ ˆP (k 1)Φ T + Q (5.3) K(k) = P (k)d T (DP (k)d T + R) 1 (5.4) ˆx(k) = x(k) + K(k)[y(k) Dx(k) (5.5) ˆP (k) = (I K(k)D) P (k) (5.6) Matriser Ei 2 2 matrise og den inverse er [ a b A = c d, A 1 = 1 ad bc [ d b c a. (5.7) Determinanten er: det(a) = ad bc. Egenverdier for ei matrise er verdier λ slik at det(λi A) = 0. Derivasjon d d sin x = cos x dx x = [ x1 x 2, f = d cos x = sin x dx [ f1 ( ) gir f 2 ( ) f x = dx log x = 1 x [ f1 x 1 f 2 x 2 f 2 f 1 x 1 x 2 (5.8). (5.9) 15
Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: Mandag 8 desember 2008 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: Mandag 8 desember 2008 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: onsdag 24 november 2010 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon (10 sp) Dato: onsdag 24 november 2010 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Løsningsforslag Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: Mandag 8 desember 28 Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: Mandag 8 desember 28 Lengde på eksamen: 4 timer Tillatte
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK30, Systemidentifikasjon Dato: Fredag 4. desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen
Eksamen i ELE620, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentifikasjon (10 sp) Dato: tirsdag 17 desember 2013 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentifikasjon (10 sp) Dato: tirsdag 17 desember 2013 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: 21 februar 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen Bokmål
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: 21 februar 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen Bokmål
Dato: fredag 14 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler: ingen. 1 Diskret tilstandsrommodell 2. 2 Stående pendel 4
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK30, Systemidentifikasjon Dato: fredag 4 desember 2007 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksaen i MIK130, Systeidentifikasjon (10 sp) Dato: Torsdag 17 deseber 2009 Lengde på eksaen: 4 tier Tillatte hjelpeidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksaen i MIK130, Systeidentifikasjon (10 sp) Dato: Torsdag 17 deseber 2009 Lengde på eksaen: 4 tier Tillatte hjelpeidler:
Eksamen i MIK130, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun
4.1 Diskretisering av masse-fjær-demper-system. K f m. x m u m y = x 1. x m 1 K d. Dette kan skrives på matriseform som i oppgaven med 0 1 A =
 Stavanger, 5. september 08 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 08. Innhold 4 Løsningsforslag og kommentarer, noen regneoppgaver. 4. Diskretisering av masse-fjær-demper-system...........
Stavanger, 5. september 08 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 08. Innhold 4 Løsningsforslag og kommentarer, noen regneoppgaver. 4. Diskretisering av masse-fjær-demper-system...........
Løsningsforslag Eksamen i MIK130, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentikasjon ( sp) Dato: onsdag 23 november 2 Lengde på eksamen: 4 timer Tillatte
Eksamen i ELE620, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentikasjon (0 sp) Dato: Tirsdag 5 desember 205 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentikasjon (0 sp) Dato: Tirsdag 5 desember 205 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
MIK-130 Systemidentifikasjon Løsningsforslag eksamen 28 mai 2004
 MIK-130 Systemidentifikasjon Løsningsforslag eksamen 28 mai 2004 Oppgave 1 a Energibalanse: Endring i energi = sum av tilført energi - sum av avgitt energi. Her får en da for vannet E t = (m vc pv T v
MIK-130 Systemidentifikasjon Løsningsforslag eksamen 28 mai 2004 Oppgave 1 a Energibalanse: Endring i energi = sum av tilført energi - sum av avgitt energi. Her får en da for vannet E t = (m vc pv T v
6 Modellering av smelteovn Modellering Tilstandsromform Diskretisering Observerbarthet Tidssteg...
 Stavanger, 28. mai 2019 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2019. Innhold 6 Modellering av smelteovn. 1 6.1 Modellering............................. 1 6.2 Tilstandsromform..........................
Stavanger, 28. mai 2019 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2019. Innhold 6 Modellering av smelteovn. 1 6.1 Modellering............................. 1 6.2 Tilstandsromform..........................
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas.
 Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Eksamen i ELE620, Systemidentikasjon (10 sp)
 DE EKNISK - NAURVIENSKAPEIGE FAKUE Institutt for data- og elektroteknikk Eksamen i EE620, Systemidentikasjon (0 sp) Dato: Fredag 3 mars 207 engde på eksamen: 4 timer illatte hjelpemidler: Kun standard
DE EKNISK - NAURVIENSKAPEIGE FAKUE Institutt for data- og elektroteknikk Eksamen i EE620, Systemidentikasjon (0 sp) Dato: Fredag 3 mars 207 engde på eksamen: 4 timer illatte hjelpemidler: Kun standard
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk. Løsningsforslag Eksamen i MIK130, Systemidentifikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: torsdag 6 desember Lengde på eksamen: 4 timer Tillatte
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Løsningsforslag Eksamen i MIK3, Systemidentifikasjon ( sp) Dato: torsdag 6 desember Lengde på eksamen: 4 timer Tillatte
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for elektroteknikk og databehandling Eksamen i MIK130, Systemidentifikasjon Dato: Mandag 28. november 2005 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for elektroteknikk og databehandling Eksamen i MIK130, Systemidentifikasjon Dato: Mandag 28. november 2005 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Eksamen i ELE620, Systemidentikasjon (10 sp)
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for ata- og elektroteknikk Eksamen i ELE620, Systemientikasjon (10 sp) Dato: Manag 15 esember 2014 Lenge på eksamen: 4 timer Tillatte hjelpemiler: Kun
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for ata- og elektroteknikk Eksamen i ELE620, Systemientikasjon (10 sp) Dato: Manag 15 esember 2014 Lenge på eksamen: 4 timer Tillatte hjelpemiler: Kun
Eksamen i ELE620, Systemidentikasjon (10 sp)
 DE EKNISK - NAURVIENSKAPELIGE FAKULE Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentikasjon (0 sp) Dato: Onsdag 4 desember 206 Lengde på eksamen: 4 timer illatte hjelpemidler: Kun standard
DE EKNISK - NAURVIENSKAPELIGE FAKULE Institutt for data- og elektroteknikk Eksamen i ELE620, Systemidentikasjon (0 sp) Dato: Onsdag 4 desember 206 Lengde på eksamen: 4 timer illatte hjelpemidler: Kun standard
Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler: Kun standard enkel kalkulator, HP 30S
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Eksamen i MIK130, Systemidentifikasjon
 DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
DET TEKNISK - NATURVITENSKAPELIGE FAKULTET Institutt for data- og elektroteknikk Eksamen i MIK130, Systemidentifikasjon Dato: Tirsdag 28. november 2006 Lengde på eksamen: 4 timer Tillatte hjelpemidler:
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
 Stavanger, 7. november 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 7. november 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
2 Utledning av Kalman-filter Forventningsrett estimator Kovariansmatriser Minimum varians estimator... 9
 Stavanger, 3. august 2018 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2018. Innhold 1 Tilstands- og parameterestimering med Kalman-filter 2 1.1 Observerbarhet...........................
Stavanger, 3. august 2018 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2018. Innhold 1 Tilstands- og parameterestimering med Kalman-filter 2 1.1 Observerbarhet...........................
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning. 1 Parameterestimering med LS og RLS 2
 Stavanger, 3 november 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016 Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning
Stavanger, 3 november 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016 Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning. 1 Stokastiske system og prosesser 2
 Stavanger, 4. august 016 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 4. august 016 Det teknisknaturvitenskapelige fakultet ELE60 Systemidentifikasjon, 016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Generell informasjon om faget er tilgjengelig fra It s learning. 1 En kort oppsummering Adaptiv filtrering 2. 3 Prediksjon 4
 Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas.
 Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Stavanger, 26. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
7 Tilstandsestimering for smelteovn.
 Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning. med Kalman-filter og RLS.
 Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 9. august 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Kalmanfilter på svingende pendel
 Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
Kalmanfilter på svingende pendel Rolf Henriksen og Torbjørn Houge Institutt for teknisk kybernetikk NTNU 2005 Vi skal se på hvordan Kalmanfilteret fungerer på et velkjent eksempel, den svingende pendel
SLUTTPRØVE (Teller 60% av sluttkarakteren)
 Høgskolen i Telemark Avdeling for teknologiske fag SLUTTPRØVE (Teller 60% av sluttkarakteren) EMNE: EE4209 Modellbasert regulering LÆRERE Kjell - Erik Wolden og Hans - Petter Halvorsen KLASSE(R): 2IA DATO:
Høgskolen i Telemark Avdeling for teknologiske fag SLUTTPRØVE (Teller 60% av sluttkarakteren) EMNE: EE4209 Modellbasert regulering LÆRERE Kjell - Erik Wolden og Hans - Petter Halvorsen KLASSE(R): 2IA DATO:
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. 1 Adaptiv filtrering 2.
 Stavanger, 23. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Stavanger, 23. juni 2017 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2017. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Tilstandsestimering Oppgaver
 University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
University College of Southeast Norway Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
 Stavanger, 30. juni 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 30. juni 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag 7. desember 2012 Tid: 09:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 8 Bokmål Faglig kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKEMODELLER Fredag
TTK4180 Stokastiske og adaptive systemer. Datamaskinøving 2 - Parameterestimering
 Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
Institutt for teknisk kybernetikk Norges teknisk-naturvitenskapelige universitet 27.10.98 EWR TTK4180 Stokastiske og adaptive systemer Datamaskinøving 2 - Parameterestimering Tid og sted: -Utdeling av
Litt generelt om systemidentifikasjon.
 Stavanger, 29. juni 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Stavanger, 29. juni 2016 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2016. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes It s learning.
Litt generelt om systemidentifikasjon.
 Stavanger, 31. juli 2018 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2018. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Stavanger, 31. juli 2018 Det teknisknaturvitenskapelige fakultet ELE620 Systemidentifikasjon, 2018. Generell informasjon om faget er tilgjengelig fra fagets nettside, og for øvinger brukes canvas. Innhold
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Tilstandsestimering Oppgaver
 Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks 203,
Telemark University College Department of Electrical Engineering, Information Technology and Cybernetics Tilstandsestimering Oppgaver HANS-PETTER HALVORSEN, 2012.01.27 Faculty of Technology, Postboks 203,
EKSAMEN I NUMERISK LINEÆR ALGEBRA (TMA4205)
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE. Forfatter: Atle Gjengedal (signatur forfatter)
 DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Kybernetikk/signalbehandling Vårsemesteret, 2009 Åpen / Konfidensiell Forfatter: Atle Gjengedal (signatur forfatter)
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Kybernetikk/signalbehandling Vårsemesteret, 2009 Åpen / Konfidensiell Forfatter: Atle Gjengedal (signatur forfatter)
Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 227 Numerisk lineær algebra Eksamensdag: 5. desember 2001 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 5 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i IN 227 Numerisk lineær algebra Eksamensdag: 5. desember 2001 Tid for eksamen: 9.00 15.00 Oppgavesettet er på 5 sider. Vedlegg:
TMA4240 Statistikk Høst 2015
 TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
LØSNINGSFORSLAG TIL EKSAMEN STE 6219 Digital signalbehandling
 Side 1 av 4 HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi MSc-studiet EL/RT LØSNINGSFORSLAG TIL EKSAMEN STE 6219 Digital signalbehandling Tid: Fredag 11.03.2005, kl: 09:00-12:00 Tillatte
Side 1 av 4 HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi MSc-studiet EL/RT LØSNINGSFORSLAG TIL EKSAMEN STE 6219 Digital signalbehandling Tid: Fredag 11.03.2005, kl: 09:00-12:00 Tillatte
Generell informasjon om faget er tilgjengelig fra It s learning. 7.1 Stokastisk prosess Lineær prediktor AR-3 prosess...
 Stavanger, 1. september 013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 7.1 Stokastisk prosess..........................
Stavanger, 1. september 013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 7.1 Stokastisk prosess..........................
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Oppgave 1. e rt = 120e. = 240 e
 Løsning MET 803 Matematikk Dato 5. desember 05 kl 0900-00 Oppgave. (a) Dersom vi selger eiendommen etter t år, med t > 0, så er nåverdien av salgssummen med r = 0,0. Da får vi N(t) = V (t)e rt = 0 e e
Løsning MET 803 Matematikk Dato 5. desember 05 kl 0900-00 Oppgave. (a) Dersom vi selger eiendommen etter t år, med t > 0, så er nåverdien av salgssummen med r = 0,0. Da får vi N(t) = V (t)e rt = 0 e e
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Lørdag 25. Mai 29. Tid for eksamen: :5 4:5. Oppgavesettet er på 7 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Lørdag 25. Mai 29. Tid for eksamen: :5 4:5. Oppgavesettet er på 7 sider. Vedlegg:
Løsningsforslag MAT102 Vår 2018
 Løsningsforslag MAT102 Vår 2018 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT102 Tirsdag 12 juni 2018, kl 0900-1400 Oppgavesettet har fem oppgaver Hver deloppgave
Løsningsforslag MAT102 Vår 2018 Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT102 Tirsdag 12 juni 2018, kl 0900-1400 Oppgavesettet har fem oppgaver Hver deloppgave
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Mandag 6. desember 21. Tid for eksamen: 9: 13:. Oppgavesettet er på 5 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Mandag 6. desember 21. Tid for eksamen: 9: 13:. Oppgavesettet er på 5 sider.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK2120 Statistiske metoder og dataanalyse 2. Eksamensdag: Fredag 7. juni 2013. Tid for eksamen: 14.30 18.30. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK2120 Statistiske metoder og dataanalyse 2. Eksamensdag: Fredag 7. juni 2013. Tid for eksamen: 14.30 18.30. Oppgavesettet er
Eksamensoppgave i ST1201/ST6201 Statistiske metoder
 Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 20. desember 2016 Eksamenstid (fra til): 09:00
Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 20. desember 2016 Eksamenstid (fra til): 09:00
EKSAMEN STE 6219 Digital signalbehandling
 HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi Masterstudiet EL/RT Side 1 av 4 EKSAMEN STE 6219 Digital signalbehandling Tid: Tirsdag 07.03.2006, kl: 09:00-12:00 Tillatte hjelpemidler:
HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi Masterstudiet EL/RT Side 1 av 4 EKSAMEN STE 6219 Digital signalbehandling Tid: Tirsdag 07.03.2006, kl: 09:00-12:00 Tillatte hjelpemidler:
Eksamensoppgave i Løsningsskisse TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
EKSAMEN I FAG 75510/75515 STATISTIKK 1 Tirsdag 20. mai 1997 Tid: 09:00 14:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: 12. desember 2003 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: 12. desember 2003 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 7 sider.
TMA4245 Statistikk. Innlevering 3. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT1100 Kalkulus. Eksamensdag: Fredag 9. desember 011. Tid for eksamen: 09.00 1.00. Oppgavesettet er på 5 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT1100 Kalkulus. Eksamensdag: Fredag 9. desember 011. Tid for eksamen: 09.00 1.00. Oppgavesettet er på 5 sider. Vedlegg: Tillatte
Tilstandsestimering Løsninger
 University College of Southeast Norway Tilstandsestimering Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
University College of Southeast Norway Tilstandsestimering Løsninger HANS-PETTER HALVORSEN http://home.hit.no/~hansha Innholdsfortegnelse 1 Grunnlag... 3 1.1 Statistikk og Stokastiske systemer... 3 1.2
EKSAMEN. 1 Om eksamen. EMNE: MA-109 FAGLÆRER: Svein Olav Nyberg, Turid Knutsen, Øystein Alvik
 EKSAMEN EMNE: MA- FAGLÆRER: Svein Olav Nyberg, Turid Knutsen, Øystein Alvik Klasser: (div) Dato: mai Eksamenstid: Eksamensoppgaven består av følgende: Antall sider (ink forside): Antall oppgaver: Antall
EKSAMEN EMNE: MA- FAGLÆRER: Svein Olav Nyberg, Turid Knutsen, Øystein Alvik Klasser: (div) Dato: mai Eksamenstid: Eksamensoppgaven består av følgende: Antall sider (ink forside): Antall oppgaver: Antall
EKSAMEN. 1 Om eksamen. EMNE: MA2610 FAGLÆRER: Svein Olav Nyberg, Trond Stølen Gustavsen. Klasser: (div) Dato: 24. mai 2004 Eksamenstid:
 EKSAMEN EMNE: MA6 FAGLÆRER: Svein Olav Nyberg, Trond Stølen Gustavsen Klasser: (div) Dato: mai Eksamenstid: Eksamensoppgaven består av følgende: Antall sider (ink forside): 5 Antall oppgaver: Antall vedlegg:
EKSAMEN EMNE: MA6 FAGLÆRER: Svein Olav Nyberg, Trond Stølen Gustavsen Klasser: (div) Dato: mai Eksamenstid: Eksamensoppgaven består av følgende: Antall sider (ink forside): 5 Antall oppgaver: Antall vedlegg:
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 10 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4240 STATISTIKK Mandag 12. desember 2011 Oppgave 1 Oljeleting a) Siden P(A
Prøve i Matte 1000 ELFE KJFE MAFE 1000 Dato: 02. desember 2015 Hjelpemiddel: Kalkulator og formelark
 Prøve i Matte ELFE KJFE MAFE Dato: 2. desember 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave Gitt matrisene A = 2 2 3 5 og B = [ 5 7 2 ] Regn
Prøve i Matte ELFE KJFE MAFE Dato: 2. desember 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave Gitt matrisene A = 2 2 3 5 og B = [ 5 7 2 ] Regn
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1 Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30 18.00. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1 Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30 18.00. Oppgavesettet
Språkform: Bokmål Navn: Truls Gundersen, Energi og Prosessteknikk Tlf.: (direkte) / (mobil) / (sekretær)
 Side 1 av 9 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK Faglig kontakt under eksamen: Språkform: Bokmål Navn: Truls Gundersen, Energi og Prosessteknikk
Side 1 av 9 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK Faglig kontakt under eksamen: Språkform: Bokmål Navn: Truls Gundersen, Energi og Prosessteknikk
UNIVERSITETET I BERGEN
 BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3440/4440 Signalbehandling Eksamensdag: 11. desember 006 Tid for eksamen: 15.30 18.30 Oppgavesettet er på 7 sider. Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF3440/4440 Signalbehandling Eksamensdag: 11. desember 006 Tid for eksamen: 15.30 18.30 Oppgavesettet er på 7 sider. Vedlegg:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF347/447 Digital signalbehandling Eksamensdag:. desember 5 Tid for eksamen: 9. 3. Oppgavesettet er på 7 sider. Vedlegg: Ingen
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF347/447 Digital signalbehandling Eksamensdag:. desember 5 Tid for eksamen: 9. 3. Oppgavesettet er på 7 sider. Vedlegg: Ingen
Løsningsforslag Eksamen M001 Våren 2002
 Løsningsforslag Eksamen M Våren Oppgave f(x) = (x )e x Bruker produktregelen i derivasjonen f (x) = e x + (x ) (e x ) For å derivere e x velges kjernen u = x, og vi får (e x ) = e u. f (x) = e x + (x )
Løsningsforslag Eksamen M Våren Oppgave f(x) = (x )e x Bruker produktregelen i derivasjonen f (x) = e x + (x ) (e x ) For å derivere e x velges kjernen u = x, og vi får (e x ) = e u. f (x) = e x + (x )
HØGSKOLEN I STAVANGER
 EKSAMEN I: MOT0 STATISTISKE METODER VARIGHET: TIMER DATO:. NOVEMBER 00 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV OPPGAVER PÅ 7 SIDER HØGSKOLEN
EKSAMEN I: MOT0 STATISTISKE METODER VARIGHET: TIMER DATO:. NOVEMBER 00 TILLATTE HJELPEMIDLER: KALKULATOR, TABELLER OG FORMLER I STATISTIKK (TAPIR FORLAG) OPPGAVESETTET BESTÅR AV OPPGAVER PÅ 7 SIDER HØGSKOLEN
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Eksamensdag: Torsdag 2. juni 24 Tid for eksamen: 4.3 8.3 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler: STK429
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Eksamensdag: Torsdag 2. juni 24 Tid for eksamen: 4.3 8.3 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler: STK429
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
Eksamensoppgave i ST1201/ST6201 Statistiske metoder
 Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Tlf: Eksamensdato: august 2015 Eksamenstid (fra til): Hjelpemiddelkode/Tillatte hjelpemidler:
Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Tlf: Eksamensdato: august 2015 Eksamenstid (fra til): Hjelpemiddelkode/Tillatte hjelpemidler:
Eksamensoppgave i ST1201/ST6201 Statistiske metoder
 Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 04. desember 2015 Eksamenstid (fra til): 09:00
Institutt for matematiske fag Eksamensoppgave i ST1201/ST6201 Statistiske metoder Faglig kontakt under eksamen: Nikolai Ushakov Tlf: 45128897 Eksamensdato: 04. desember 2015 Eksamenstid (fra til): 09:00
Side av 5 fra matriseteori har vi at en symmetrisk matrise alltid er ortogonalt diagonaliserbar. Det vil si at X kan skrives på formen X = M M (6) der
 Side av 5 Norges teknisk- naturvitenskapelige universitet Institutt for teknisk kybernetikk SIE38 Stokastiske og adaptive systemer Fasit til ving Oppgave Gitt at den stokastiske vektoren v er normalfordelt
Side av 5 Norges teknisk- naturvitenskapelige universitet Institutt for teknisk kybernetikk SIE38 Stokastiske og adaptive systemer Fasit til ving Oppgave Gitt at den stokastiske vektoren v er normalfordelt
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter!
 Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
Vær OBS på at svarene på mange av oppgavene kan skrives på flere ulike måter! Oppgave.. a x y = x + y = r r r +r r x y = y fri x y = y fri Vi får én fri variabel, og løsningens har følgelig dimensjon.
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7. desember 2012 Tid: 09:00 13:00
 Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag Side 1 av 8 Nynorsk Fagleg kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7.
Noregs teknisk naturvitskaplege universitet Institutt for matematiske fag Side 1 av 8 Nynorsk Fagleg kontakt under eksamen: John Tyssedal 73593534/41645376 EKSAMEN I TMA4285 TIDSREKKJEMODELLAR Fredag 7.
Alle svar skal grunngis. Alle deloppgaver har lik vekt.
 Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave Vi denerer matrisene A, B, og C som A = [ ] 3, B = 5 9, C = 3 3. a) Regn ut følgende matrisesummer og matriseprodukter, om mulig. Dersom
Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave Vi denerer matrisene A, B, og C som A = [ ] 3, B = 5 9, C = 3 3. a) Regn ut følgende matrisesummer og matriseprodukter, om mulig. Dersom
Løsningsforslag. og B =
 Prøve i Matte EMFE DAFE ELFE BYFE Dato: august 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave a) Gitt matrisene A = 2 3 2 4 2 Løsningsforslag og
Prøve i Matte EMFE DAFE ELFE BYFE Dato: august 25 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Oppgave a) Gitt matrisene A = 2 3 2 4 2 Løsningsforslag og
LØSNINGSFORSLAG EKSAMEN MA0002, V08
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 LØSNINGSFORSLAG EKSAMEN MA000, V08 Oppgave 1 Litt av hvert. a) (10%) Løs initialverdiproblemet gitt ved differensialligningen
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 LØSNINGSFORSLAG EKSAMEN MA000, V08 Oppgave 1 Litt av hvert. a) (10%) Løs initialverdiproblemet gitt ved differensialligningen
STE 6219 Digital signalbehandling Løsningsforslag
 HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi Masterstudiet EL/RT Side 1 av 3 STE 6219 Digital signalbehandling Løsningsforslag Tid: Fredag 20.04.2007, kl: 09:00-12:00 Tillatte hjelpemidler:
HØGSKOLEN I NARVIK Institutt for data-, elektro-, og romteknologi Masterstudiet EL/RT Side 1 av 3 STE 6219 Digital signalbehandling Løsningsforslag Tid: Fredag 20.04.2007, kl: 09:00-12:00 Tillatte hjelpemidler:
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1. Oppgave 1. Oppgave 2. Oppgave 3
 Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1 Oppgave 1 For AR(2)-modellen: X t = 0.4X t 1 + 0.45X t 2 + Z t (der {Z t } er hvit søy med varians 1), finn γ(3), γ(4)
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Oppgavesett 5, s. 1 Oppgave 1 For AR(2)-modellen: X t = 0.4X t 1 + 0.45X t 2 + Z t (der {Z t } er hvit søy med varians 1), finn γ(3), γ(4)
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
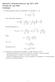 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
HØGSKOLEN I STAVANGER
 EKSAMEN I TE 335 Termodynamikk VARIGHET: 9.00 14.00 (5 timer). DATO: 24/2 2001 TILLATTE HJELPEMIDLER: Lommekalkulator OPPGAVESETTET BESTÅR AV 2 oppgaver på 5 sider (inklusive tabeller) HØGSKOLEN I STAVANGER
EKSAMEN I TE 335 Termodynamikk VARIGHET: 9.00 14.00 (5 timer). DATO: 24/2 2001 TILLATTE HJELPEMIDLER: Lommekalkulator OPPGAVESETTET BESTÅR AV 2 oppgaver på 5 sider (inklusive tabeller) HØGSKOLEN I STAVANGER
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT Kalkulus. Eksamensdag: Fredag 9. desember 2. Tid for eksamen: 9.. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT Kalkulus. Eksamensdag: Fredag 9. desember 2. Tid for eksamen: 9.. Oppgavesettet er på 8 sider. Vedlegg: Tillatte hjelpemidler:
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Løsninger til oppgavesett 5, s. 1. Oppgave 1
 Matematisk statistikk og stokastiske prosesser B, høsten 2006 Løsninger til oppgavesett 5, s AR2-modell: Oppgave X t φ X t φ 2 X t 2 Z t Antas å være kausal slik at X t ψ j Z t j er ukorrelert med Z t+,
Matematisk statistikk og stokastiske prosesser B, høsten 2006 Løsninger til oppgavesett 5, s AR2-modell: Oppgave X t φ X t φ 2 X t 2 Z t Antas å være kausal slik at X t ψ j Z t j er ukorrelert med Z t+,
Bedømmelse: Ved bedømmelse vektlegges oppgavene I, II og III likt.
 Side 1 av 5 + 2 sider vedlegg NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR TELETEKNIKK Signalbehandling Faglig kontakt under eksamen: Navn: Tor A. Ramstad Tlf.: 94314 KONTINUASJONSEKSAMEN
Side 1 av 5 + 2 sider vedlegg NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR TELETEKNIKK Signalbehandling Faglig kontakt under eksamen: Navn: Tor A. Ramstad Tlf.: 94314 KONTINUASJONSEKSAMEN
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE. Forfatter: Duy Viet Nguyen (signatur forfatter)
 DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Automatisering og signalbehandling Vårsemesteret, 2017 Åpen / Konfidensiell Forfatter: Duy Viet Nguyen (signatur forfatter)
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET MASTEROPPGAVE Studieprogram/spesialisering: Automatisering og signalbehandling Vårsemesteret, 2017 Åpen / Konfidensiell Forfatter: Duy Viet Nguyen (signatur forfatter)
MA1201 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3. desember 2007
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag MA101 Lineær algebra og geometri Løsningsforslag for eksamen gitt 3 desember 007 Oppgave 1 a) Vi ser på ligningssystemet x +
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Ny/Utsatt eksamen i: MAT1001 Matematikk 1 Eksamensdag: Torsdag 15 januar 2015 Tid for eksamen: 14:30 18:30 Oppgavesettet er på 5 sider Vedlegg:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Ny/Utsatt eksamen i: MAT1001 Matematikk 1 Eksamensdag: Torsdag 15 januar 2015 Tid for eksamen: 14:30 18:30 Oppgavesettet er på 5 sider Vedlegg:
Spesial-Oppsummering Høsten 2009 basert på Innspill fra Studenter
 Spesial- Høsten 2009 basert på Innspill fra Studenter på Hjemmesiden (fra 2008) - formidler kvintessensen av TEP4120 - omhandler Kap. 1-6, Eksergi Light og Kap. 8-9 - mangler altså (fortsatt) Kap. 10 -
Spesial- Høsten 2009 basert på Innspill fra Studenter på Hjemmesiden (fra 2008) - formidler kvintessensen av TEP4120 - omhandler Kap. 1-6, Eksergi Light og Kap. 8-9 - mangler altså (fortsatt) Kap. 10 -
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Fredag 7. desember 27. Tid for eksamen: 9: 12:. Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Fredag 7. desember 27. Tid for eksamen: 9: 12:. Oppgavesettet er på 8 sider.
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave X er kontinuerlig fordelt med sannsynlighetstetthet f X (x) = { x exp( x ) x
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave X er kontinuerlig fordelt med sannsynlighetstetthet f X (x) = { x exp( x ) x
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 11. desember 2015 Tid for eksamen: 09.00 13.00. Oppgavesettet er på 5 sider. Vedlegg: Svarark,
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 11. desember 2015 Tid for eksamen: 09.00 13.00. Oppgavesettet er på 5 sider. Vedlegg: Svarark,
EKSAMEN. Oppgavesettet består av 3 oppgaver. Alle spørsmål på oppgavene skal besvares, og alle spørsmål teller likt til eksamen.
 EKSAMEN Emnekode: ITD12011 Emne: Fysikk og kjemi Dato: 29. April 2015 Eksamenstid: kl.: 9:00 til kl.: 13:00 Hjelpemidler: 4 sider (A4) (2 ark) med egne notater. Ikke-kommuniserende kalkulator. Gruppebesvarelse,
EKSAMEN Emnekode: ITD12011 Emne: Fysikk og kjemi Dato: 29. April 2015 Eksamenstid: kl.: 9:00 til kl.: 13:00 Hjelpemidler: 4 sider (A4) (2 ark) med egne notater. Ikke-kommuniserende kalkulator. Gruppebesvarelse,

 I c;'1 høgskolen i oslo lemne: I I Gruppe(r) Kvbem~ti!
I c;'1 høgskolen i oslo lemne: I I Gruppe(r) Kvbem~ti!