Spørretime TEP Våren Spørretime TEP Våren 2008
|
|
|
- Bendik Bjørnstad
- 7 år siden
- Visninger:
Transkript
1 Søetime EP Våen 28 Fotegnskonvensjonen og Ka.9 (& OB s slides) Q: ilsynelatende uoveensstemmelse mellom det Olav Bolland esentete fo Otto/Diesel og det som stå i læeboka nå det gjelde fotegn i likninge. A: Boka svinge mellom å benytte emodynamikkens fotegnskonvensjon (vame inn e ositivt, abeid utføt e ositivt), og (gjelde tyisk fo sykliske osesse) å benytte ile fo å vise etning å abeid/vame, slik at alle støelse (Q og W) få ositive tallvedie. Dette foenkle f.eks. uttykkene fo vikningsgad. Se foøvig de 2 neste slides som vise h.h.v. Olav B s slide fo Otto syklus, samt en scannet vesjon av dele av side 376 i Moan & Shaio. Q/A-1 Søetime EP Våen 28 Olav Bolland: Q/A-2
2 Søetime EP Våen 28 Q/A-3 Søetime EP Våen 28 Stemelmotoe: Otto vs. Diesel (fa flee) Q: Hvofo bukes entali (h) og inde enegi (u) om hveande i en dieselmoto, mens man i bensinmoto (Otto) kun benytte inde enegi (u) A: Sva ved illustasjon å tavla, heunde Lukket vs. Åent System, samt sesifikt tinn 2-3 i Dieselsyklus. Gamle betegnelse innen Kjøleteknikken Q: På Øving 12, ogave 1.21 skal Q ogis både i kw og tonn; hvafonoe..?? A: Pette Nekså, SEfAS, sie: ton of efigeation e kuldeytelsen som skal til fo å fyse et tonn is i timen. Bukes i dag kun av tege ameikanee og delvis jaanee, men slike enhete godtas ikke i dag å konfeanse og i ublikasjone. E definet som 2 Btu/min elle omlag 211 kj/min. Q/A-4
3 Søetime EP Våen 28 Dokumentet Likninge og Uttykk som må beheskes (huske/fostå/anvende) ved Eksamen Q: Vil ikke disse (2) akene følge med Eksamensogavene? Det vike da meningsløst å kunne alle disse å ams? I Fysikk og Fluid e det Fomelak! A: Mange av Likningene e ikke fomle men balanselikninge som vise foståelse av hvilke masse, vame og entoistømme vi må foholde oss til i emodynamikken. På de neste 2 slides vises eksemle fa disse akene i emo-1 og Fluid. otale vs. Patielle Diffeensiale Q: Entoilikningene 6.22 og 6.23 i fohold til at vi ha konstant tykk elle volum med hhv C og Cv Q/A-5 Utdag fa Likninge og Uttykk dm dt = m m Δ E =Δ Ek +Δ E +Δ U = Q W i i e e de Vi Ve = Q W mi ( hi g zi) me ( he g ze) dt i 2 e 2 δq ds = ds dt int ev 2 δq S2 S1 = + σ 1 b Q = + + j m i si m e se σ j j i e C Vamekaftosess: η = 1 η = W / m t H ( W / m ) s Q/A-6
4 Utdag fa Fomelak i Fluid Q/A-7 Eksamensogave med Løsningsfoslag Om tidligee Eksamensogave Q: Finne ikke Des. 7 og Kont 6 å hjemmesiden. Det mangle også endel LF e fa 23 og juni 24. A: Des. 7: Kjell Eik Rian. Kont 6: Jeg ha bestemt at kun Hovedeksamen skal legges ut. Nå det gjelde tidligee ogave e foklaingene mange (og gode ). 27-Mai: Ogavetekst Løsningsfoslag 26-Desembe: Ogavetekst Løsningsfoslag 26-Juni: Ogavetekst med Løsningsfoslag 25-August: Ogavetekst Løsningsfoslag 25-Mai: Ogavetekst Løsningsfoslag 24-Desembe: Ogavetekst Løsningsfoslag 24-August: Ogavetekst Løsningsfoslag 24-Juni: Ogavetekst Løsningsfoslag 23-Desembe: Ogavetekst Løsningsfoslag 23-August: Ogavetekst Løsningsfoslag 23-Mai: Ogavetekst Løsningsfoslag Q/A-8
5 Søetime EP Våen 28 Ideell Gass og Isentoiske Posesse Q: I noen ogave benyttes v k, mens i ande ogave benyttes, hva e sammenhengen og hvofo få vi foskjellige sva? A: Foskjellen ligge i hvovidt vamekaasitetene e konstante elle ikke (se utledning/diskusjon å tavle). Kontinuasjonseksamen 25, ogave 2 Q: Hvofo sies det at det kun e ovehetet dam i sylindeen ved slutt-tilstanden (stemlet e helt oe) og tykket e blitt 3 ba? A: Se diskusjon å neste slide. Damkaftosesse med Reheat Q: I noen ogave gå man inn i tofase-omådet ette 1. tinn, i ande skje dette føst i 2. tinn, hvodan kan man vite om man e i tofase-omådet? A: Se diskusjon 2 slides fam Q/A-9 Eksamen August 25 Ogave cm 1 cm Q ilstand 1 e entydig gitt av at damkvaliteten x =.25 samt at tykket e lik utetykket luss tykket som stemlet utøve. Ved ovaming vil det fiksjonsfie stemlet bevege seg oove, og den økte enegien i systemet føe til et økt volum ved konstant tykk. ilstand a e gitt av at volumet e 4.5 gange statvolumet (vi nå øve gense fo sylindevolum, stemlet hindes videe bevegelse). Ved å sammenlikne det (sesifikke) volumet med sesifikt volum fo mettet væske og mettet dam finne vi at vi e utenfo tofase-omådet (v > v f ). Ytteligee ovaming vil selvsagt øke ovehetingen (uansett vei ) 1 a v Q/A-1
6 Øving 11 - Ogave 8.18 Q/A-11 Søetime EP Våen 28 ansient Analyse (ikke Stasjonæe osesse) Q: Vil gjene at ansient Analyse bli gjennomgått A: ok et eksemel fa Øving 6 (Ogave 4.61) å en, det e en litt vanskeligee ogave å samme Øving 6 (Ogave 4.65). A: Vet ikke hva me jeg kan gjøe? Foskjellen e jo i insiet kun at akkumuleingsleddene (fo masse, enegi og entoi) ikke e null. De fleste ogavene ha betydelige foenklinge, slik at likningene enkelt kan integees. OK? Det e ennå langt fam til Eksamensdagen Q: Kan vi sende flee søsmål til faglæe? A: Ja, det e lov å øve, men: Ingen PC til Koatia... Ved hjemkomst søndag 1.6 ioitees Løing... Q/A-12
7 Buk av elle v k ved Isentoiske Posesse 1 Entoiending geneelt (alle osesse og systeme) 1 a) ds = du + dv Δ s = s2 s1 = du + dv 1 v a) ds = dh vd Δ s = s2 s1 = dh d 2 Entoiending fo Ideell Gass (alle osesse) du = c ( ) d og dh = c d og v = R v Fo tilfelle (b) gi dette: Δ = = ( ) d s s2 s1 c d R Q/A-13 Buk av elle v k (fotsettelse) Benytte følgende tiks: c ( ) d = c ( ) d c ( ) d 1 Definee tabulet støelse: ( ) ( ) s = c d Δ s = s(, ) s(, ) = s ( ) s ( ) Rln Isentoisk Posess (og Ideell Gass) Δ s = s ( ) = s ( ) + Rln (benyttet i Øving) He: ex s ( 2 2) / R = 1 ex s ( 1 ) / R Q/A-14
8 Buk av elle v k (fotsettelse) 4 Sesialtilfellet Luft (som ideell gass) og Isentoisk s ( ) Definee Relativt ykk: = ex R 2 2 Dette gi da: = 1 1 Poeng: e tabulet fo Luft som Ideell Gass (A-22) Definee Relativt Volum: v R v v v = som gi: = v v e også tabulet fo Luft som Ideell Gass (A-22) v i Otto/Diesel, i Bayton Q/A-15 Buk av elle v k (fotsettelse) 5 Konstante Vamekaasitete, Ideell Gass og Isentoisk = k R ln ln = k 1 = v R ln + ln = v k 1 c R c R He falle gasskonstanten R, og vi ende o med uttykk som kombinee v,, og k: k 1 k 2 1 v = = v2 k 1 k 2 v 1 k k k = elle v = v = v = konstant 1 v2 Q/A-16
3. Termodynamikk. Energi og systemer. Total energi og indre energi. Systemer. 3 Termodynamikk
 3. Temodynamikk 3 Temodynamikk I mange mekaniske og fysiske osesse (som de vi behandlet i foige kaittel) og i kjemiske eaksjone ha vi utveksling av enegi, og ofte ovaming elle avkjøling. Vi kan gjene si
3. Temodynamikk 3 Temodynamikk I mange mekaniske og fysiske osesse (som de vi behandlet i foige kaittel) og i kjemiske eaksjone ha vi utveksling av enegi, og ofte ovaming elle avkjøling. Vi kan gjene si
LØSNINGSFORSLAG EKSAMEN TEP 4115 TERMODYNAMIKK 1 Lørdag 21. mai 2011 Tid: kl. 09:00-13:00
 Side a 7 NORGES EKNISK-NAURVIENSKAPELIGE UNIVERSIE (NNU) - RONDHEIM INSIU FOR ENERGI OG PROSESSEKNIKK OPPGAVE (3%) LØSNINGSFORSLAG EKSAMEN EP 45 ERMODYNAMIKK Lørdag. mai id: kl. 9: - 3: a) ermodynamikkens.
Side a 7 NORGES EKNISK-NAURVIENSKAPELIGE UNIVERSIE (NNU) - RONDHEIM INSIU FOR ENERGI OG PROSESSEKNIKK OPPGAVE (3%) LØSNINGSFORSLAG EKSAMEN EP 45 ERMODYNAMIKK Lørdag. mai id: kl. 9: - 3: a) ermodynamikkens.
Notat i FYS-MEK/F 1110 våren 2006
 1 Notat i FYS-MEK/F 1110 våen 2006 Rulling og skliing av kule og sylinde Foelest 24. mai 2006 av Ant Inge Vistnes Geneelt Rotasjonsdynamikk e en svæt viktig del av mekanikkuset våt. Dette e nytt stoff
1 Notat i FYS-MEK/F 1110 våen 2006 Rulling og skliing av kule og sylinde Foelest 24. mai 2006 av Ant Inge Vistnes Geneelt Rotasjonsdynamikk e en svæt viktig del av mekanikkuset våt. Dette e nytt stoff
Løsningsforslag Eksamen i fag TEP4110 Fluidmekanikk
 Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
Løsningsforslag TEP 4110 FLUIDMEKANIKK 18.desember ρ = = = m / s m / s 0.1
 Løsningsfoslag TEP 40 FLUIDMEKNIKK 8.desembe 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d
Løsningsfoslag TEP 40 FLUIDMEKNIKK 8.desembe 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
Spørretime TEP Høsten 2012
 Vi hadde noen spørsmål i forbindelse med eksergi og utledning av ΔS likningen Spørsmålene om Eksergi kom aldri? Ser derfor på utledningen av ΔS likningen Q (fra meg): Hvilken ΔS likning? u u Entropibalansen
Vi hadde noen spørsmål i forbindelse med eksergi og utledning av ΔS likningen Spørsmålene om Eksergi kom aldri? Ser derfor på utledningen av ΔS likningen Q (fra meg): Hvilken ΔS likning? u u Entropibalansen
At energi ikke kan gå tapt, må bety at den er bevart. Derav betegnelsen bevaringslov.
 Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
Side av 8 LØSNINGSFORSLAG KONINUASJONSEKSAMEN 006 SMN694 VARMELÆRE DAO: 04. Mai 007 ID: KL. 09.00 -.00 OPPGAVE (Vekt: 40%) a) emodynamikkens. hovedsats:. hovedsetning: Enegi kan hveken oppstå elle fosvinne,
Spesial-Oppsummering Høsten 2009 basert på Innspill fra Studenter
 Spesial- Høsten 2009 basert på Innspill fra Studenter på Hjemmesiden (fra 2008) - formidler kvintessensen av TEP4120 - omhandler Kap. 1-6, Eksergi Light og Kap. 8-9 - mangler altså (fortsatt) Kap. 10 -
Spesial- Høsten 2009 basert på Innspill fra Studenter på Hjemmesiden (fra 2008) - formidler kvintessensen av TEP4120 - omhandler Kap. 1-6, Eksergi Light og Kap. 8-9 - mangler altså (fortsatt) Kap. 10 -
LØSNINGSFORSLAG EKSAMEN TEP 4120 TERMODYNAMIKK 1 Tirsdag 9. desember 2008 Tid: kl. 09:00-13:00
 Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK LØSNINGSFORSLAG EKSAMEN TEP 410 TERMODYNAMIKK 1 Tirsdag 9. desember 008 Tid: kl. 09:00-13:00
Side 1 av 6 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK LØSNINGSFORSLAG EKSAMEN TEP 410 TERMODYNAMIKK 1 Tirsdag 9. desember 008 Tid: kl. 09:00-13:00
Betinget bevegelse
 Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Hesteveddeløp i 8. klasse
 Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
ρ = = = m / s m / s Ok! 0.1
 Løsningsfoslag TEP 00 FLUIDMEKNIKK.juni 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d g 6
Løsningsfoslag TEP 00 FLUIDMEKNIKK.juni 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d g 6
FAG: MA-209 Matematikk 3 LÆRER: Per Henrik Hogstad KANDIDATEN MÅ SELV KONTROLLERE AT OPPGAVESETTET ER FULLSTENDIG
 UNIVERITETET I AGDER Gimstad E K A M E N O P P G A V E : FAG: MA-9 Matematikk ÆRER: Pe enik ogstad Klasse: Dato:.6. Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende Antall side: 5 inkl. foside
UNIVERITETET I AGDER Gimstad E K A M E N O P P G A V E : FAG: MA-9 Matematikk ÆRER: Pe enik ogstad Klasse: Dato:.6. Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende Antall side: 5 inkl. foside
Oppgave 8.12 Gitt en potensialhvirvel med styrke K i origo. Bestem sirkulasjonen ' langs kurven C. Sirkulasjonen er definert som: ' /
 Løsning øving 3 Oppgve 8. Gitt en potensilhvivel med styke i oigo. Bestem sikulsjonen ' lngs kuven C. C y (I oppgven stå det t vi skl gå med klokk, men he h vi gått mot klokk i oveensstemmelse med definisjonen
Løsning øving 3 Oppgve 8. Gitt en potensilhvivel med styke i oigo. Bestem sikulsjonen ' lngs kuven C. C y (I oppgven stå det t vi skl gå med klokk, men he h vi gått mot klokk i oveensstemmelse med definisjonen
Løsning midtveiseksamen H12 AST1100
 Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
Spørretime TEP Høsten Spørretime TEP Høsten 2009
 Spørsmål knyttet til en Kjølekrets (Oppgave 3 på Eksamen August 2005) T 44ºC 3 11.6 bar 4 4 bar 2 1 15ºC 12 bar pv 1.01 = k s 3 4 Kjølevann 20ºC 30ºC Kondenser R134a Q C Fordamper Q inn =35 kw 2 1 W C
Spørsmål knyttet til en Kjølekrets (Oppgave 3 på Eksamen August 2005) T 44ºC 3 11.6 bar 4 4 bar 2 1 15ºC 12 bar pv 1.01 = k s 3 4 Kjølevann 20ºC 30ºC Kondenser R134a Q C Fordamper Q inn =35 kw 2 1 W C
Mandag E = V. y ŷ + V ẑ (kartesiske koordinater) r sin θ φ ˆφ (kulekoordinater)
 Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Løsningsforslag for eksamen i FY101 Elektromagnetisme torsdag 12. desember 2002
 Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
sosiale behov FASE 2: Haug barnehage 2011-2012
 : Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
: Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
Oppsummering - Kap. 5 Termodynamikkens 2. Lov
 EP 410 ermodynamikk 1 Spontane Prosesser Varmeoverføring ( > omg ), Ekspansjon (P > P omg ), og Frigjort Masse i Gravitasjonsfelt er Eksempler Energibalanser kan ikke prediktere Retning Hva kan ermodynamikkens.
EP 410 ermodynamikk 1 Spontane Prosesser Varmeoverføring ( > omg ), Ekspansjon (P > P omg ), og Frigjort Masse i Gravitasjonsfelt er Eksempler Energibalanser kan ikke prediktere Retning Hva kan ermodynamikkens.
Eksamen TFY 4240: Elektromagnetisk teori
 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
Forelesning 9/ ved Karsten Trulsen
 Foelesning 9/2 218 ved Kasten Tulsen Husk fa sist våe to spøsmål om kuveintegale: Desom vi skal beegne et kuveintegal som state i et punkt og ende opp i et annet punkt 1, så kan det væe mange veie fo å
Foelesning 9/2 218 ved Kasten Tulsen Husk fa sist våe to spøsmål om kuveintegale: Desom vi skal beegne et kuveintegal som state i et punkt og ende opp i et annet punkt 1, så kan det væe mange veie fo å
Løsningsforslag til ukeoppgave 11
 Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
UNIVERSITETET I OSLO
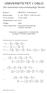 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
Newtons lover i én dimensjon
 Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Om bevegelsesligningene
 Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
Fysikk-OL Norsk finale 2005
 Univesitetet i Oslo Nosk Fysikklæefoening Fysikk-OL Nosk finale 005 3. uttakingsunde Tid: Fedag 5. apil kl 09.00.00 Hjelpemidle: Tabell/fomelsamling, gafisk lommeegne Oppgavesettet bestå av 7 oppgave på
Univesitetet i Oslo Nosk Fysikklæefoening Fysikk-OL Nosk finale 005 3. uttakingsunde Tid: Fedag 5. apil kl 09.00.00 Hjelpemidle: Tabell/fomelsamling, gafisk lommeegne Oppgavesettet bestå av 7 oppgave på
b) C Det elektriske feltet går radielt ut fra en positivt ladd partikkel.
 Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Løsningsfoslag Fysikk 2 Høst 203 Løsningsfoslag Fysikk 2 Høst 203 Opp Sva Foklaing gave a) B Fomelen fo bevegelsesmengde p = mv gi enheten kg m. s Dette kan igjen skives som: kg m = kg m s s2 s = Ns b)
Fysikk for ingeniører. 11. Termiske egenskaper. Løsninger på blandede oppgaver. Side 11-1
 Fysikk for ingeniører ermiske egenskaer Løsninger å landede ogaver Side - Ogave : a) Forutsetter at stemelet står i ro etrakter kreftene å undersiden av stemelet: = + mg mg kg 98m/s = + = Pa + = 6 Pa m
Fysikk for ingeniører ermiske egenskaer Løsninger å landede ogaver Side - Ogave : a) Forutsetter at stemelet står i ro etrakter kreftene å undersiden av stemelet: = + mg mg kg 98m/s = + = Pa + = 6 Pa m
UNIVERSITETET I OSLO
 Side av 5 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Mandag 9. juni 28 Tid fo eksamen: Kl. 9-2 Oppgavesettet e på 5 side inkludet fomelaket. Tillatte
Side av 5 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Mandag 9. juni 28 Tid fo eksamen: Kl. 9-2 Oppgavesettet e på 5 side inkludet fomelaket. Tillatte
Matematikk 3MX AA6524 / AA6526 Elever / privatister Oktober 2002
 E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
Løsning øving 12 N L. Fra Faradays induksjonslov får vi da en indusert elektromotorisk spenning:
 nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
Newtons lover i én dimensjon (2)
 Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Newtons love i én dimensjon () 9.1.13 husk: data lab fedag 1-16 FYS-MEK 111 9.1.13 1 Identifikasjon av keftene: 1. Del poblemet inn i system og omgivelse.. Tegn figu av objektet og alt som beøe det. 3.
Øving 8. Dersom ikke annet er oppgitt, antas det at systemet er i elektrostatisk likevekt.
 Institutt fo fysikk, NTNU TFY455/FY003: lektisitet og magnetisme Vå 2008 Øving 8 Veiledning: 04.03 i R2 25-400, 05.03 i R2 25-400 Innleveingsfist: Fedag 7. mas kl. 200 (Svatabell på siste side.) Opplysninge:
Institutt fo fysikk, NTNU TFY455/FY003: lektisitet og magnetisme Vå 2008 Øving 8 Veiledning: 04.03 i R2 25-400, 05.03 i R2 25-400 Innleveingsfist: Fedag 7. mas kl. 200 (Svatabell på siste side.) Opplysninge:
Sammendrag, uke 14 (5. og 6. april)
 Institutt fo fysikk, NTNU TFY4155/FY1003: Elektisitet og magnetisme Vå 2005 Sammendag, uke 14 (5. og 6. apil) Magnetisk vekselvikning [FGT 28, 29; YF 27, 28; TM 26, 27; AF 22, 24B; H 23; DJG 5] Magnetisme
Institutt fo fysikk, NTNU TFY4155/FY1003: Elektisitet og magnetisme Vå 2005 Sammendag, uke 14 (5. og 6. apil) Magnetisk vekselvikning [FGT 28, 29; YF 27, 28; TM 26, 27; AF 22, 24B; H 23; DJG 5] Magnetisme
Typisk T-v Diagram. Fasediagrammer & Projeksjoner. p-v p-t T-v. TEP 4120 Termodynamikk 1. Beregning av Egenskaper. TEP 4120 Termodynamikk 1
 Fasediagrammer & Projeksjoner p-v p-t T-v 3-1 Typisk T-v Diagram 3-2 T-v Diagram for H 2 O 3-3 Lineær Interpolasjon i en Dimensjon Tabeller og Linearitet?? TABLE A-4 (Continued) T v u h s C m 3 /kg kj/kg
Fasediagrammer & Projeksjoner p-v p-t T-v 3-1 Typisk T-v Diagram 3-2 T-v Diagram for H 2 O 3-3 Lineær Interpolasjon i en Dimensjon Tabeller og Linearitet?? TABLE A-4 (Continued) T v u h s C m 3 /kg kj/kg
1 Virtuelt arbeid for stive legemer
 1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Tre klasser kollisjoner (eksempel: kast mot vegg)
 kap8 2.09.204 Kap. 8 Bevegelsesmengde. Kollisjone. assesente. Vi skal se på: ewtons 2. lov på ny: Definisjon bevegelsesmengde Kaftstøt, impuls. Impulsloven Kollisjone: Elastisk, uelastisk, fullstendig
kap8 2.09.204 Kap. 8 Bevegelsesmengde. Kollisjone. assesente. Vi skal se på: ewtons 2. lov på ny: Definisjon bevegelsesmengde Kaftstøt, impuls. Impulsloven Kollisjone: Elastisk, uelastisk, fullstendig
Oppsummering Fysikkprosjekt
 Tekno-/Realstat høsten 011 MTFYMA, BFY, LUR Oppsummeing Fysikkposjekt m? F? v m p a F v? a? p? Lineæ bevegelse Rotasjonsbevegelse Navn: Symbol: Navn: Symbol: distanse masse hastighet akseleasjon kaft bevegelsesmengde,
Tekno-/Realstat høsten 011 MTFYMA, BFY, LUR Oppsummeing Fysikkposjekt m? F? v m p a F v? a? p? Lineæ bevegelse Rotasjonsbevegelse Navn: Symbol: Navn: Symbol: distanse masse hastighet akseleasjon kaft bevegelsesmengde,
Fysikkolympiaden 1. runde 25. oktober 5. november 2004
 Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning Fysikkolympiaden 1. unde 5. oktobe 5. novembe 004 Hjelpemidle: abell og fomelsamlinge i fysikk og matematikk Lommeegne id: 100 minutte
Nosk Fysikklæefoening Nosk Fysisk Selskaps fagguppe fo undevisning Fysikkolympiaden 1. unde 5. oktobe 5. novembe 004 Hjelpemidle: abell og fomelsamlinge i fysikk og matematikk Lommeegne id: 100 minutte
Newtons lover i to og tre dimensjoner
 Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
LØSNINGSFORSLAG EKSAMEN TEP 4120 TERMODYNAMIKK 1 Mandag 17. desember 2012 Tid: kl. 09:00-13:00
 Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK LØSNINGSFORSLAG EKSAMEN TEP 4120 TERMODYNAMIKK 1 Mandag 17. desember 2012 Tid: kl. 09:00-13:00
Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET (NTNU) - TRONDHEIM INSTITUTT FOR ENERGI OG PROSESSTEKNIKK LØSNINGSFORSLAG EKSAMEN TEP 4120 TERMODYNAMIKK 1 Mandag 17. desember 2012 Tid: kl. 09:00-13:00
Termofysikk: Ekstraoppgaver om varmekapasitet for gasser og termodynamikkens 1. lov uke 47-48
 1. Finn hastigheten til rgon atomer i en gass som har temeraturen 1. kt RT v eller der m er masen til et ekyl m og massen til et. N! begge størrelsene må angis i, ellers stemmer ikke enhetene. v 8.1 0.0
1. Finn hastigheten til rgon atomer i en gass som har temeraturen 1. kt RT v eller der m er masen til et ekyl m og massen til et. N! begge størrelsene må angis i, ellers stemmer ikke enhetene. v 8.1 0.0
Billige arboresenser og matchinger
 Billige aboesense og matchinge Magnus Lie Hetland 16. jan 009 Dette e foelesningsnotate til føste foelesning i faget Algoitmekonstuksjon, videegående kus, ved Institutt fo datateknikk og infomasjonsvitenskap,
Billige aboesense og matchinge Magnus Lie Hetland 16. jan 009 Dette e foelesningsnotate til føste foelesning i faget Algoitmekonstuksjon, videegående kus, ved Institutt fo datateknikk og infomasjonsvitenskap,
Løsningsforslag til eksempeloppgave 2 i fysikk 2, 2009
 Fysikk Eksempeloppgae Løsningsfoslag il eksempeloppgae i fysikk, 9 Del Oppgae Rikige sa på flealgsoppgaene a x e: a) C b) D c) B d) C e) C f) D g) C h) D i) B j) C k) A l) B m) A n) D o) B p) D q) D )
Fysikk Eksempeloppgae Løsningsfoslag il eksempeloppgae i fysikk, 9 Del Oppgae Rikige sa på flealgsoppgaene a x e: a) C b) D c) B d) C e) C f) D g) C h) D i) B j) C k) A l) B m) A n) D o) B p) D q) D )
Utvalg med tilbakelegging
 Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Fysikkolympiaden Norsk finale 2010
 Uniesitetet i Oslo Nosk Fysikklæefoening Fysikkolympiaden Nosk finale. ttakingsnde Fedag 6. mas kl 9. til. Hjelpemidle: abell/fomelsamling, lommeegne og tdelt fomelak Oppgaesettet bestå a 6 oppgae på side
Uniesitetet i Oslo Nosk Fysikklæefoening Fysikkolympiaden Nosk finale. ttakingsnde Fedag 6. mas kl 9. til. Hjelpemidle: abell/fomelsamling, lommeegne og tdelt fomelak Oppgaesettet bestå a 6 oppgae på side
Typisk T-v Diagram. Fasediagrammer & Projeksjoner. p-v p-t T-v. TEP 4120 Termodynamikk 1. Beregning av Egenskaper. Beregning av Egenskaper
 Fasediagrammer & Projeksjoner p-v p-t T-v T. Gundersen 3-1 Typisk T-v Diagram T. Gundersen 3-2 T-v Diagram for H 2 O T. Gundersen 3-3 Lineær Interpolasjon i en Dimensjon Tabeller og Linearitet?? T. Gundersen
Fasediagrammer & Projeksjoner p-v p-t T-v T. Gundersen 3-1 Typisk T-v Diagram T. Gundersen 3-2 T-v Diagram for H 2 O T. Gundersen 3-3 Lineær Interpolasjon i en Dimensjon Tabeller og Linearitet?? T. Gundersen
Side 1 av 3/nyn. Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735) EKSAMEN I FAG TEP4125 TERMODYNAMIKK juni 2016 Tid:
 Side 1 av 3/nyn. NOREGS TEKNISK-NATURVITSKAPLEGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735)93839 EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 11. juni
Side 1 av 3/nyn. NOREGS TEKNISK-NATURVITSKAPLEGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735)93839 EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 11. juni
TFY4104 Fysikk. Institutt for fysikk, NTNU. Høsten Øving 9. Veiledning: 18. oktober. Innleveringsfrist: 23. oktober kl 14.
 TFY404 Fysikk. Institutt fo fysikk, NTNU. Høsten 203. Øving 9. Veiledning: 8. oktobe. Innleveingsfist: 23. oktobe kl 4. Oppgve ) Figuen vise et unifomt elektisk felt (heltukne linje). Lngs hvilken stiplet
TFY404 Fysikk. Institutt fo fysikk, NTNU. Høsten 203. Øving 9. Veiledning: 8. oktobe. Innleveingsfist: 23. oktobe kl 4. Oppgve ) Figuen vise et unifomt elektisk felt (heltukne linje). Lngs hvilken stiplet
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET
 DET TEKNISK-NATURVITENSKAPELIGE FAKULTET EKSAMEN I BIT 130 Termodynamikk VARIGHET: 9.00 13.00 (4 timer). DATO: 1/12 2005 TILLATTE HJELPEMIDLER: Lommekalkulator OPPGAVESETTET BESTÅR AV: 2 oppgaver på 5
DET TEKNISK-NATURVITENSKAPELIGE FAKULTET EKSAMEN I BIT 130 Termodynamikk VARIGHET: 9.00 13.00 (4 timer). DATO: 1/12 2005 TILLATTE HJELPEMIDLER: Lommekalkulator OPPGAVESETTET BESTÅR AV: 2 oppgaver på 5
Eksamen 16. des Løsningsforslag
 Institutt fo fysikk TFY44/FY Mekanisk fysikk Eksamen 6. des.. Løsningsfoslag Dette løsningsfoslaget e spesielt fyldig med flee altenative løsninge, som ukt av flee studente i eksamensesvaelsen. Det e også
Institutt fo fysikk TFY44/FY Mekanisk fysikk Eksamen 6. des.. Løsningsfoslag Dette løsningsfoslaget e spesielt fyldig med flee altenative løsninge, som ukt av flee studente i eksamensesvaelsen. Det e også
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST1100, 13. desembe 2016, 9.00 13.00 Oppgavesettet inkludet fomelsamling e på 7 side Tillatte hjelpemidle: 1) Angel/Øgim
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST1100, 13. desembe 2016, 9.00 13.00 Oppgavesettet inkludet fomelsamling e på 7 side Tillatte hjelpemidle: 1) Angel/Øgim
Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2
 1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
KONTINUASJONSEKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
 Noges teknisk natuvitenskapelige univesitet Institutt fo elektonikk og telekommunikasjon ide 1 av 8 Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Jon Olav Gepstad 41044764) Hjelpemidle: C - pesifisete
Noges teknisk natuvitenskapelige univesitet Institutt fo elektonikk og telekommunikasjon ide 1 av 8 Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Jon Olav Gepstad 41044764) Hjelpemidle: C - pesifisete
Eksamensoppgave i TEP4105 FLUIDMEKANIKK
 Institutt fo enegi- og posessteknikk Eksamensoppgave i TEP45 FLUIDMEKANIKK Faglig kontakt unde eksamen: Ive Bevik Tlf.: 7359 3555 Eksamensdato: 7. august 23 Eksamenstid : 9. 3. Hjelpemiddelkode/Tillatte
Institutt fo enegi- og posessteknikk Eksamensoppgave i TEP45 FLUIDMEKANIKK Faglig kontakt unde eksamen: Ive Bevik Tlf.: 7359 3555 Eksamensdato: 7. august 23 Eksamenstid : 9. 3. Hjelpemiddelkode/Tillatte
LØSNINGSFORSLAG EKSAMEN TEP 4120 TERMODYNAMIKK 1 Mandag 6. desember 2010 Tid: kl. 09:00-13:00
 Side av 8 NORGES EKNISK-NAURVIENSKAPELIGE UNIVERSIE (NNU) - RONDHEIM INSIU FOR ENERGI OG PROSESSEKNIKK LØSNINGSFORSLAG EKSAMEN EP 40 ERMODYNAMIKK Mandag 6. desember 00 id: kl. 09:00 - :00 OPPGAVE (40%)
Side av 8 NORGES EKNISK-NAURVIENSKAPELIGE UNIVERSIE (NNU) - RONDHEIM INSIU FOR ENERGI OG PROSESSEKNIKK LØSNINGSFORSLAG EKSAMEN EP 40 ERMODYNAMIKK Mandag 6. desember 00 id: kl. 09:00 - :00 OPPGAVE (40%)
Newtons lover i to og tre dimensjoner
 Newtons love i to og te dimensjone 9..17 Oblig e lagt ut. Innleveing: Mandag,.. FYS-MEK 111 9..17 1 Skått kast med luftmotstand F net F D G D v v mg ˆj hoisontal og vetikal bevegelse ikke lenge uavhengig:
Newtons love i to og te dimensjone 9..17 Oblig e lagt ut. Innleveing: Mandag,.. FYS-MEK 111 9..17 1 Skått kast med luftmotstand F net F D G D v v mg ˆj hoisontal og vetikal bevegelse ikke lenge uavhengig:
HØGSKOLEN I STAVANGER
 EKSAMEN I TE 335 Termodynamikk VARIGHET: 9.00 14.00 (5 timer). DATO: 24/2 2001 TILLATTE HJELPEMIDLER: Lommekalkulator OPPGAVESETTET BESTÅR AV 2 oppgaver på 5 sider (inklusive tabeller) HØGSKOLEN I STAVANGER
EKSAMEN I TE 335 Termodynamikk VARIGHET: 9.00 14.00 (5 timer). DATO: 24/2 2001 TILLATTE HJELPEMIDLER: Lommekalkulator OPPGAVESETTET BESTÅR AV 2 oppgaver på 5 sider (inklusive tabeller) HØGSKOLEN I STAVANGER
Side 1 av 3/nyn. Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735)93839. EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 Onsdag 22. mai 2013 Tid: 09.00 13.
 Side 1 av 3/nyn. NOREGS TEKNISK-NATURVITSKAPLEGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735)93839 EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 Onsdag
Side 1 av 3/nyn. NOREGS TEKNISK-NATURVITSKAPLEGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735)93839 EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 Onsdag
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST2000, 17. desembe 2018, 09.00 13.00 Oppgavesettet inkludet fomelsamling e på 8 side Tillatte hjelpemidle: 1) Angel/Øgim
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST2000, 17. desembe 2018, 09.00 13.00 Oppgavesettet inkludet fomelsamling e på 8 side Tillatte hjelpemidle: 1) Angel/Øgim
Kap. 1 Fysiske størrelser og enheter
 Fysikk for Fagskolen, Ekern og Guldahl samling (kapitler 1, 2, 3, 4, 6) Kap. 1 Fysiske størrelser og enheter Størrelse Symbol SI-enhet Andre enheter masse m kg (kilogram) g (gram) mg (milligram) tid t
Fysikk for Fagskolen, Ekern og Guldahl samling (kapitler 1, 2, 3, 4, 6) Kap. 1 Fysiske størrelser og enheter Størrelse Symbol SI-enhet Andre enheter masse m kg (kilogram) g (gram) mg (milligram) tid t
Løsningsforslag sist oppdatert
 Løsningsfoslag sist oppdatet.. BOKMÅL Oppgave En funksjon f e definet i intevallet ved f ( ) ( ) e a) Finn f ( ). Avgjø hvo funksjonen e stigende og hvo funksjonen e avtagende. Bestem funksjonens eventuelle
Løsningsfoslag sist oppdatet.. BOKMÅL Oppgave En funksjon f e definet i intevallet ved f ( ) ( ) e a) Finn f ( ). Avgjø hvo funksjonen e stigende og hvo funksjonen e avtagende. Bestem funksjonens eventuelle
b) 3 MATEMATISKE METODER I 1 ( ) ( ) ( ) ( ) ( ) ( ) Repetisjonsoppgaver Bruk av regneregler: 1 Regn ut: e) 0 x ) 4 3 d) 4 x f) 5y
 MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG
 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG Tisdag 18. desembe 01 kl. 0900-100 Oppgave 1. Ti flevalgsspøsmål. (Telle
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG Tisdag 18. desembe 01 kl. 0900-100 Oppgave 1. Ti flevalgsspøsmål. (Telle
Side 1 av 6 NORGES TEKNISK-NATUR- VITENSKAPELIGE UNIVERSITETET INSTITUTT FOR KJEMISK PROSESSTEKNOLOGI
 NORGES TEKNISK-NATUR- VITENSKAPELIGE UNIVERSITETET INSTITUTT FOR KJEMISK PROSESSTEKNOLOGI Side 1 av 6 Faglig kontakt unde eksamen/fagleg kontakt unde eksamen: Pofesso Edd A. Blekkan, tlf.73594157 (Oppgave
NORGES TEKNISK-NATUR- VITENSKAPELIGE UNIVERSITETET INSTITUTT FOR KJEMISK PROSESSTEKNOLOGI Side 1 av 6 Faglig kontakt unde eksamen/fagleg kontakt unde eksamen: Pofesso Edd A. Blekkan, tlf.73594157 (Oppgave
Løsningsforslag Fysikk 2 Høst 2014
 Løsningsfoslag Fysikk Høst 014 Løsningsfoslag Fysikk Høst 014 Opp Sva Foklaing gave a) D Det elektiske feltet gå adielt ut fa en positivt ladet patikkel. Til høye fo elektonet lage elektonet en feltstyke
Løsningsfoslag Fysikk Høst 014 Løsningsfoslag Fysikk Høst 014 Opp Sva Foklaing gave a) D Det elektiske feltet gå adielt ut fa en positivt ladet patikkel. Til høye fo elektonet lage elektonet en feltstyke
Tips for prosjektoppgaven i FYS-MEK/F 1110 V2006
 1 Tips fo posjektoppgaven i FYS-MEK/F 1110 V2006 Utfosking av et telegeme-system Ant Inge Vistnes, vesjon 0605141330 Det e ikke nødvendig å lese dette skivet fo å løse posjektoppgaven, men de fleste vil
1 Tips fo posjektoppgaven i FYS-MEK/F 1110 V2006 Utfosking av et telegeme-system Ant Inge Vistnes, vesjon 0605141330 Det e ikke nødvendig å lese dette skivet fo å løse posjektoppgaven, men de fleste vil
14.1 Doble og itererte integraler over rektangler
 Kapittel Mltiple Integals I dette apitlet sal i se på integale a fnsjone a to aiable f og a te aiable f z.. Doble og iteete integale oe etangle Vi ønse å integee en ontinelig fnsjon f oe et etangel. :
Kapittel Mltiple Integals I dette apitlet sal i se på integale a fnsjone a to aiable f og a te aiable f z.. Doble og iteete integale oe etangle Vi ønse å integee en ontinelig fnsjon f oe et etangel. :
Magnetisk hysterese. 1. Beregn magnetfeltet fra en strømførende spole med kjent vindingstall.
 FY33 Elektisitet og magnetisme II Institutt fo fysikk, TU FY33 Elektisitet og magnetisme II, høst 7 Laboatoieøvelse Magnetisk hysteese Hensikt Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske
FY33 Elektisitet og magnetisme II Institutt fo fysikk, TU FY33 Elektisitet og magnetisme II, høst 7 Laboatoieøvelse Magnetisk hysteese Hensikt Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske
Eksamen TFY4165 Termisk fysikk kl torsdag 15. desember 2016 Bokmål
 FY4165 15. desember 2016 Side 1 av 7 Eksamen FY4165 ermisk fysikk kl 09.00-13.00 torsdag 15. desember 2016 Bokmål Ogave 1. (armeledning. Poeng: 10+10+10=30) Kontinuitetsligningen for energitetthet u og
FY4165 15. desember 2016 Side 1 av 7 Eksamen FY4165 ermisk fysikk kl 09.00-13.00 torsdag 15. desember 2016 Bokmål Ogave 1. (armeledning. Poeng: 10+10+10=30) Kontinuitetsligningen for energitetthet u og
8 Eksamens trening. E2 (Kapittel 1) På figuren er det tegnet grafene til funksjonene f og g gitt ved
 84 8 Eksamenstening 8 Eksamens tening Uten hjelpemidle E1 (Kapittel 1) Polynomfunksjonen P e gitt ved P ( ) = 7 + 14 8, DP = R. a Det kan vises at alle heltallige løsninge av P() = 0 gå opp i konstantleddet
84 8 Eksamenstening 8 Eksamens tening Uten hjelpemidle E1 (Kapittel 1) Polynomfunksjonen P e gitt ved P ( ) = 7 + 14 8, DP = R. a Det kan vises at alle heltallige løsninge av P() = 0 gå opp i konstantleddet
SIO 1027 Termodynamikk I Noen formler og uttrykk som er viktige, samt noen stikkord fra de forskjellige kapitler,, Versjon 25/
 SIO 1027 Termodynamikk I Noen formler og uttrykk som er viktige, samt noen stikkord fra de forskjellige kapitler,, Versjon 25/11-2001 Geir Owren November 25, 2001 Som avtalt med referansegruppen, er det
SIO 1027 Termodynamikk I Noen formler og uttrykk som er viktige, samt noen stikkord fra de forskjellige kapitler,, Versjon 25/11-2001 Geir Owren November 25, 2001 Som avtalt med referansegruppen, er det
EKSAMEN I FY1005 og TFY4165 TERMISK FYSIKK: LØSNINGSFORSLAG
 NORGES TEKNISK-NATURITENSKAPELIGE UNIERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1005 og TFY4165 TERMISK FYSIKK: LØSNINGSFORSLAG Mandag 11. august 2014 kl. 0900-1300 Ogave 1. 25 flervalgsogaver. (Poeng: 2
NORGES TEKNISK-NATURITENSKAPELIGE UNIERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1005 og TFY4165 TERMISK FYSIKK: LØSNINGSFORSLAG Mandag 11. august 2014 kl. 0900-1300 Ogave 1. 25 flervalgsogaver. (Poeng: 2
Slik bruker du pakken
 Slik buke du pakken Kompetanseutviklingspakken Lesestategie og leseengasjement Dette e infomasjon til deg/dee som skal lede femdiften i kollegiet. He finne du en ovesikt ove pakkens innhold til hjelp i
Slik buke du pakken Kompetanseutviklingspakken Lesestategie og leseengasjement Dette e infomasjon til deg/dee som skal lede femdiften i kollegiet. He finne du en ovesikt ove pakkens innhold til hjelp i
Pytagoreiske tripler og Fibonacci-tall
 Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a. 585 500 f.k.) og Leonado
Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a. 585 500 f.k.) og Leonado
a) C Det elektriske feltet går radielt ut fra en positivt ladet partikkel og radielt innover mot en negativt ladd partikkel.
 Løsningsfoslag Fysikk 2 Vå 2015 Løsningsfoslag Fysikk 2 Vå 2015 Oppgav e Sva Foklaing a) C Det elektiske feltet gå adielt ut fa en positivt ladet patikkel og adielt innove mot en negativt ladd patikkel.
Løsningsfoslag Fysikk 2 Vå 2015 Løsningsfoslag Fysikk 2 Vå 2015 Oppgav e Sva Foklaing a) C Det elektiske feltet gå adielt ut fa en positivt ladet patikkel og adielt innove mot en negativt ladd patikkel.
Laboratorieøvelse i MNFFY1303-Elektromagnetisme Institutt for Fysikk, NTNU MAGNETISK HYSTERESE
 Laboatoieøvelse i MNFFY33-Elektomagnetisme Institutt fo Fysikk, NTNU Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske felte og målinge av slike. Det innebæe måling av magnetfelt fa enkle
Laboatoieøvelse i MNFFY33-Elektomagnetisme Institutt fo Fysikk, NTNU Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske felte og målinge av slike. Det innebæe måling av magnetfelt fa enkle
LØSNINGSFORSLAG TIL EKSAMEN I FAG TEP4170 VARME- OG FORBRENNINGSTEKNIKK 18. mai 2007 Tid:
 av 4 Noges teknisk-natuvitenskapelige univesitet Initutt fo enegi- og poseseknikk Kontakt unde eksamen: Toleif Weydahl, tlf. 7359634 / 945 ØSNINGSFORSAG TI EKSAMEN I FAG TEP47 VARME- OG FORBRENNINGSTEKNIKK
av 4 Noges teknisk-natuvitenskapelige univesitet Initutt fo enegi- og poseseknikk Kontakt unde eksamen: Toleif Weydahl, tlf. 7359634 / 945 ØSNINGSFORSAG TI EKSAMEN I FAG TEP47 VARME- OG FORBRENNINGSTEKNIKK
Midtsemesterprøve onsdag 7. mars 2007 kl
 Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 2007 Midtsemestepøve onsdag 7. mas 2007 kl 1300 1500. Svatabellen stå på side 11. Sett tydelige kyss. Husk å skive
Institutt fo fysikk, NTNU FY1003 lektisitet og magnetisme I TFY4155 lektomagnetisme Vå 2007 Midtsemestepøve onsdag 7. mas 2007 kl 1300 1500. Svatabellen stå på side 11. Sett tydelige kyss. Husk å skive
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskaelige fakultet Eksamen i: Fys6 Eksamensdag: Fredag 6. desember 3 Tid for eksamen: 43 83 Ogavesettet er å: 4 sider Vedlegg: ingen Tilatte hjelemidler Elektronisk
UNIVERSITETET I OSLO Det matematisk-naturvitenskaelige fakultet Eksamen i: Fys6 Eksamensdag: Fredag 6. desember 3 Tid for eksamen: 43 83 Ogavesettet er å: 4 sider Vedlegg: ingen Tilatte hjelemidler Elektronisk
AGENDA: Faste saker: Saksdokumente r
 FAU-møte, tisdag 12.desembe 2017 kl. 18.00 20.30 Sted: Pesonalommet, Bjønsletta skole Møtelede: Cathine Foss Stene ( FAU-lede) Refeent: Anne Lise Stosand Caolina, Øyvind, Tine, Ragnhild, Heniette, Monica,
FAU-møte, tisdag 12.desembe 2017 kl. 18.00 20.30 Sted: Pesonalommet, Bjønsletta skole Møtelede: Cathine Foss Stene ( FAU-lede) Refeent: Anne Lise Stosand Caolina, Øyvind, Tine, Ragnhild, Heniette, Monica,
Løsningsforslag Fysikk 2 V2016
 Løsningsfoslag Fysikk V016 Oppgave Sva Foklaing a) B Faadays induksjonslov: ε = Φ, so gi at Φ = ε t t Det bety at Φ åles i V s b) D L in = 0,99 10 = 9,9 L aks = 1,04 10 = 10,4 L snitt = (L in + L aks )
Løsningsfoslag Fysikk V016 Oppgave Sva Foklaing a) B Faadays induksjonslov: ε = Φ, so gi at Φ = ε t t Det bety at Φ åles i V s b) D L in = 0,99 10 = 9,9 L aks = 1,04 10 = 10,4 L snitt = (L in + L aks )
trygghet FASE 1: barnehage
 tygghet banehage De voksnes olle Banemøte Leikeguppe Guppeaktivitet Hjemmebesøk Samlinge Måltid Påkledning Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 tygghet tygghet «Banehagen skal bistå
tygghet banehage De voksnes olle Banemøte Leikeguppe Guppeaktivitet Hjemmebesøk Samlinge Måltid Påkledning Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 tygghet tygghet «Banehagen skal bistå
Realstart og Teknostart ROTASJONSFYSIKK. PROSJEKTOPPGAVE for BFY, MLREAL og MTFYMA
 FY1001 og TFY4145 Mekanisk fysikk Institutt fo fysikk, august 2014 Realstat og Teknostat ROTASJONSFYSIKK PROSJEKTOPPGAVE fo BFY, MLREAL og MTFYMA Mål Dee skal i denne posjektoppgaen utfoske egenskape til
FY1001 og TFY4145 Mekanisk fysikk Institutt fo fysikk, august 2014 Realstat og Teknostat ROTASJONSFYSIKK PROSJEKTOPPGAVE fo BFY, MLREAL og MTFYMA Mål Dee skal i denne posjektoppgaen utfoske egenskape til
Løysingsframlegg kontinuasjonseksamen TFY 4104 Fysikk august 2011
 NTNU Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Løysingsframlegg kontinuasjonseksamen TFY 4104 Fysikk august 011 Faglærar: Professor Jens O Andersen Institutt for Fysikk, NTNU Telefon:
NTNU Fakultet for Naturvitskap og Teknologi Institutt for Fysikk Løysingsframlegg kontinuasjonseksamen TFY 4104 Fysikk august 011 Faglærar: Professor Jens O Andersen Institutt for Fysikk, NTNU Telefon:
STUDIESPESIALISERENDE
 STUDIESPESIALISERENDE Utdanningspogammet: God allmenndanning e til glede og nytte fo alle. He vil du få opplæing som gi solid gunnlag fo videe studie. Alle vil oppnå geneell studiekompetanse og med visse
STUDIESPESIALISERENDE Utdanningspogammet: God allmenndanning e til glede og nytte fo alle. He vil du få opplæing som gi solid gunnlag fo videe studie. Alle vil oppnå geneell studiekompetanse og med visse
Rettelser til. Øistein Bjørnestad Tom Rune Kongelf Terje Myklebust. Alfa. Oppgaveløsninger
 Rettelse til Øistein Bjønestad Tom Rune Kongelf Teje Myklebust Alfa Oppgaveløsninge 007 Kapittel S. 7: Fasit til oppgave.9e): Slik oppgaven stå, skal svaet væe 065 (noe ha falt ut i oppgaveteksten). S.
Rettelse til Øistein Bjønestad Tom Rune Kongelf Teje Myklebust Alfa Oppgaveløsninge 007 Kapittel S. 7: Fasit til oppgave.9e): Slik oppgaven stå, skal svaet væe 065 (noe ha falt ut i oppgaveteksten). S.
FAG: MA-209 Matematikk 3 LÆRER: Per Henrik Hogstad KANDIDATEN MÅ SELV KONTROLLERE AT OPPGAVESETTET ER FULLSTENDIG
 UNIVERITETET I GDER Gimstad E K M E N O P P G V E : G: M-9 Matematikk LÆRER: Pe Henik Hogstad Klasse: Dato: 8..8 Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende ntall side: 6 inkl. foside vedlegg
UNIVERITETET I GDER Gimstad E K M E N O P P G V E : G: M-9 Matematikk LÆRER: Pe Henik Hogstad Klasse: Dato: 8..8 Eksamenstid fa-til: 9.. Eksamensoppgaven bestå av følgende ntall side: 6 inkl. foside vedlegg
Eksamen TFY4165 Termisk fysikk kl mandag 7. august 2017 Bokmål
 FY4165 7. august 2017 Side 1 av 7 Eksamen FY4165 ermisk fsikk kl 09.00-13.00 mandag 7. august 2017 Bokmål Ogave 1. (armeledning. Poeng: 5+10+5=20) Kontinuitetsligningen for energitetthet u og energistrømtetthet
FY4165 7. august 2017 Side 1 av 7 Eksamen FY4165 ermisk fsikk kl 09.00-13.00 mandag 7. august 2017 Bokmål Ogave 1. (armeledning. Poeng: 5+10+5=20) Kontinuitetsligningen for energitetthet u og energistrømtetthet
EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 Laurdag 18. august 2012 Tid:
 Side 1 av 3/nyn. NOREGS TEKNISK-NATURVITSKAPLEGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735)93839 EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 Laurdag
Side 1 av 3/nyn. NOREGS TEKNISK-NATURVITSKAPLEGE UNIVERSITET INSTITUTT FOR ENERGI- OG PROSESSTEKNIKK Kontakt under eksamen: Ivar S. Ertesvåg, tel. (735)93839 EKSAMEN I FAG TEP4125 TERMODYNAMIKK 2 Laurdag
(b) Ekmanstrøm: Balanse mellom friksjonskraft og Corioliskraft. der ν er den kinematiske (eddy) viskositeten.
 Oppgae 1. Fgu 6.11 læeboka se den nodgående enegfluksen atosfæen ( petawatt esus beddegad på den nodlge halkulen (opp tl 75 gade, ålg dlet. Fguen se også egne plott fo tansente edde, totalt bdag fa edde
Oppgae 1. Fgu 6.11 læeboka se den nodgående enegfluksen atosfæen ( petawatt esus beddegad på den nodlge halkulen (opp tl 75 gade, ålg dlet. Fguen se også egne plott fo tansente edde, totalt bdag fa edde
Veileder for adepter. Bruk mentor - unngå omveier
 Veilede fo adepte Buk mento - unngå omveie At eg e til, Det veit eg. Eg kjenne pusten min Og eit og anna hjeteslag. Men eg vil noko mei, enn bee å vea, eg vil vea nokon, som bety noko, i det stoe fellesskapet.
Veilede fo adepte Buk mento - unngå omveie At eg e til, Det veit eg. Eg kjenne pusten min Og eit og anna hjeteslag. Men eg vil noko mei, enn bee å vea, eg vil vea nokon, som bety noko, i det stoe fellesskapet.
Verdens Elektrisitetsproduksjon
 Verdens Elektrisitetsproduksjon 2010: Kull: 42.2% Naturgass: 20.4% Fornybare: 19.4% Atomkraft: 13.6% Andre: 4.4% 8-1 Elektrisitetsproduksjon i andre Land Norge: 98-99% fra Vannkraft USA Frankrike 8-2 Den
Verdens Elektrisitetsproduksjon 2010: Kull: 42.2% Naturgass: 20.4% Fornybare: 19.4% Atomkraft: 13.6% Andre: 4.4% 8-1 Elektrisitetsproduksjon i andre Land Norge: 98-99% fra Vannkraft USA Frankrike 8-2 Den
Øving 6, løsningsskisse.
 Inst for fysikk 202 TFY455/FY003 Elektr & magnetisme Øving 6, løsningsskisse Diol Platekondensatorer Ogave Potensial rundt diol Vi skriver først V a om til en funksjon av x og z ved å bruke relasjonene
Inst for fysikk 202 TFY455/FY003 Elektr & magnetisme Øving 6, løsningsskisse Diol Platekondensatorer Ogave Potensial rundt diol Vi skriver først V a om til en funksjon av x og z ved å bruke relasjonene
Kap. 23 Elektrisk potensial
 Kp. 3 Elektisk potensil Skl definee p gunnlg v elektisk felt E: Elektisk potensiell enegi, U Elektisk potensil, V (Ketsteknikk: El. potensilfoskjell spenning) Aeid keves fo føe smmen ldninge Pføt eid gi
Kp. 3 Elektisk potensil Skl definee p gunnlg v elektisk felt E: Elektisk potensiell enegi, U Elektisk potensil, V (Ketsteknikk: El. potensilfoskjell spenning) Aeid keves fo føe smmen ldninge Pføt eid gi
T 2. + RT 0 ln p 2 K + 0, K ln. kg K. 2) Først må vi nne massestraumen av luft frå energibalansen: 0 = ṁ 1 (h 1 h 2 ) + ṁ 3 (h 3 h 4 ) kg s
 LØYSINGSFORSLAG, eksamen 4. mai 208 i fag TEP425 TERMODYNAMIKK 2 v. Ivar S. Ertesvåg, sist endra 5. mai 208. Dette er eit UTKAST. Det kan vere skrive- og reknefeil her. Endring i spesikk eksergi konstant
LØYSINGSFORSLAG, eksamen 4. mai 208 i fag TEP425 TERMODYNAMIKK 2 v. Ivar S. Ertesvåg, sist endra 5. mai 208. Dette er eit UTKAST. Det kan vere skrive- og reknefeil her. Endring i spesikk eksergi konstant
2. Termodynamikkens lover Termodynamikkens 1. lov Energiutveksling i form av varme og arbeid Trykk-volum arbeid
 Fysikk / Termodynamikk åren 2001 2. Termodynamikkens lover 2.1. Termodynamikkens 1. lov Termodynamikkens første lov kan formuleres å mange måter. En vanlig formulering er: Energien til et isolert system
Fysikk / Termodynamikk åren 2001 2. Termodynamikkens lover 2.1. Termodynamikkens 1. lov Termodynamikkens første lov kan formuleres å mange måter. En vanlig formulering er: Energien til et isolert system
