INVERST FUNKSJONSTEOREM MAT1100 KALKULUS
|
|
|
- Ellinor Hanne Jansen
- 7 år siden
- Visninger:
Transkript
1 INVERST FUNKSJONSTEOREM MAT1100 KALKULUS Simon Foldvik 29. Oktober Introduksjon Vi skal i dette dokumentet bevise en global og en lokal versjon av inverst unksjonsteorem i én variabel. Kort oppsummert handler disse teoremene om inversunksjoner og hvordan de arver egenskaper ra de opprinnelige unksjonene, deriblant monotonisitet og deriverbarhet. Vi skal også studere hvordan, i disse tilellene, de deriverte til inversunksjonene kan uttrykkes ved de deriverte til de opprinnelige unksjonene. Med inverst unksjonsteorem som verktøy skal vi deinere og studere egenskaper ved elementærunksjonene. 1 Spesielt skal vi se hvordan potensog eksponentialunksjoner, logaritmiske og trigonometriske unksjoner remkommer, blant annet, som inversunksjoner av kjente unksjoner og deretter studere noen av deres egenskaper. Poenget her er ikke å vise egenskaper vi «allerede vet» om disse unksjonene på en mer komplisert måte; poenget er heller å gi en tilredsstillende teoretisk redegjørelse or hvordan disse unksjonene kan deineres, og hvoror de har de egenskapene de har. Dette gjøres tradisjonelt ved hjelp av rekkeutvikling, men vi skal av pedagogiske årsaker ikke benytte denne remgangsmåten. Innhold 1. Introduksjon 1 2. Inverst Funksjonsteorem Terminologi Global Formulering Lokal Formulering 8 Reeranser 9 2. Inverst Funksjonsteorem 2.1. Terminologi. I denne seksjonen skal vi utvikle den nødvendige terminologien or å kunne ormulere og bevise de versjonene av inverst unksjonsteorem som er annonsert i innledningen. 1 Materialet om elementærunksjoner vil ikke bli behandlet i dette dokumentet, som kun inngår som pedagogisk supplement i emnet MAT1100 ved Universitetet i Oslo. 1
2 INVERST FUNKSJONSTEOREM Komposisjon. Vi minner om at dersom X, Y og Z er mengder og g : X Y og : Y Z er unksjoner, så er g : X Z (komposisjonen av med g; uttales «ring g») unksjonen deinert ved ( g)(x) = ( g(x) ) (x X). Følgende diagram illustrerer situasjonen: X g Z g Y Oppgave Vis at komposisjon er assosiativt; det vil si at ( g) h = (g h) or alle unksjoner, g og h slik at komposisjonene over gir mening Injeksjoner og Bijeksjoner. La X og Y være to mengder. En unksjon : X Y kalles en injeksjon, eller sies å være injektiv, dersom det or hver y Y innes på det meste ett punkt x X slik at (x) = y. Med andre ord, er injektiv dersom det or alle u X og v X er slik at (u) = (v) medører u = v. Eksempel La : (0, ) R være unksjonen deinert ved (x) = x 2 or x > 0. Dersom 0 < u < v, er (u) = u 2 < v 2 = (v), slik at (u) < (v). Dette viser at er strengt voksende, og dermed at den er injektiv. Deinisjon (Bijeksjon). La X og Y være to mengder, og anta at : X Y er en unksjon. Man sier at er en bijeksjon, eller sies å være bijektiv, dersom det or alle y Y innes nøyaktig ett punkt x X slik at (x) = y. Bemerkning. Funksjonen ra Eksempel er injektiv men ikke bijektiv. Dette har med å gjøre at det innes punkter i R som ikke oppnås som noen unksjonsverdi av. I begrepet injektiv ligger det at «orskjellige punkter sendes til orskjellige punkter», men or at : X Y skal være en injeksjon, stilles det ikke noe krav om at det or alle y Y aktisk skal eksistere et punkt x X slik at (x) = y; det er dette som skiller injeksjoner ra bijeksjoner. Til tross or at injektive unksjoner ikke nødvendigvis er bijektive, innes det en naturlig måte å danne en bijeksjon ra en injeksjon. La oss igjen betrakte en unksjon : X Y ; vi betegner dens verdimengde med (X) = { (x): x X }. Dersom er injektiv og vi deinerer unksjonen g : X (X) ved g(x) = (x) (x X),
3 INVERST FUNKSJONSTEOREM 3 er g en bijeksjon som «opererer» på samme måte som. Vi kan med andre ord danne en bijeksjon ra en injeksjon ved å begrense kodomenet, og vi vil gjøre dette videre i dokumentet uten ytterlige kommentarer Inversunksjoner. Anta at : X Y er en bijeksjon. Da kan man deinere en unksjon g : Y X på ølgende måte: dersom y Y, la x være det entydige punktet i X slik at (x) = y (et slikt punkt x eksisterer og er entydig ettersom er bijektiv), og sett g(y) = x. Vi har ølgende likheter or alle x X og alle y Y : (1) g ( (x) ) = x og ( g(y) ) = y. Dersom vi innører unksjonene id X : X X og id Y : Y Y ved id X (x) = x og id Y (y) = y, or alle x X og alle y Y, kan likhetene i (1) uttrykkes ved g = id X og g = id Y. Av åpenbare grunner kaller man g inversunksjonen til, og man betegner den med g = 1. Følgende diagram illustrerer samspillet mellom og dens invers: X Y id X g id Y X Y Bemerkning. Det er de bijektive unksjonene som har inversunksjoner. Til tross or dette skal vi også tillate oss å snakke om inversunksjoner av injektive unksjoner. For anta at F : X Y er en injeksjon, og la : X F (X) være bijeksjonen indusert av F ved å begrense dens kodomene, slik som i siste avsnitt av Seksjon Da har en inversunksjon 1 : F (X) X, og vi skal omtale denne som inversunksjonen til F og betegne den med F 1. Oppgave Anta at X og Y er to mengder og at : X Y er en unksjon. Vis at er en bijeksjon hvis og bare hvis det innes en unksjon g : Y X slik at (2) g = id X og g = id Y. Vis videre at dersom h: Y X og k : Y X er to unksjoner som tilredsstiller (2) (erstatt g), så er h = k. Med andre ord, eksistensen av en unksjon g som tilredsstiller (2) karakteriserer bijektive unksjoner ullstendig, og disse relasjonene karakteriserer også 1. Oppgave Anta at X og Y er mengder og at : X Y er en bijeksjon. Vis at da er også 1 : Y X en bijeksjon, og ( 1 ) 1 =. Hint. Bruk Oppgave Oppgave Anta at X, Y og Z er mengder og at g : X Y og : Y Z er bijeksjoner. Vis at da er også g : X Z en bijeksjon, og Tolk dette ut ira ølgende diagram: ( g) 1 = g 1 1.
4 INVERST FUNKSJONSTEOREM 4 g X Y Z id X id Y id Z X Y Z g Dieomorier. Vi vil være spesielt interesserte i unksjoner som innehar en viss grad av «glatthet». Mer presist vil vi i hovedsak være interesserte i unksjoner som har kontinuerlige deriverte av ørste orden. Med mindre noe annet er påpekt, vil vi i resten av dokumentet la I betegne et åpent og ikke-tomt intervall i R. Vi tillater også at intervallet I er ubegrenset, or eksempel ved at det er lik R selv. Deinisjon (Kontinuerlig Deriverbar Funksjon). Anta at I R er et åpent intervall og at : I R er en unksjon deinert på I. Vi sier at er kontinuerlig deriverbar dersom er deriverbar og er en kontinuerlig unksjon på I. Vi betegner mengden av alle kontinuerlig deriverbare unksjoner på I med C 1 (I). Dersom C 1 (I), er ikke bare deriverbar, men den deriverte varierer jevnt (kontinuerlig) på I. I Seksjon 2.2 skal vi inne betingelser på C 1 (I) som sikrer at den er injektiv, at dens verdimengde (I) er et åpent intervall, og videre at 1 C 1( (I) ). En slik unksjon kalles en dieomori. Deinisjon (Dieomori). La I være et åpent intervall og anta at : I R er en unksjon. Vi sier at er en dieomori av klasse C 1 dersom den er injektiv, dersom (I) er et åpent intervall, og dersom C 1 (I) og 1 C 1( (I) ). 2 Med andre ord, en dieomori av klasse C 1 på I er en kontinuerlig deriverbar injeksjon hvis verdimengde er et åpent intervall og som har en kontinuerlig deriverbar inversunksjon. 1 Oppgave La I = R og deinér unksjonen : I R ved { x 2 sin(1/x 2 ), hvis x 0 (x) = (x R). 0, hvis x = 0 Vis at er deriverbar på I, men at ikke er kontinuerlig i punktet 0. Denne oppgaven viser at det innes deriverbare unksjoner på I som ikke er kontinuerlig deriverbare. Hint. Vis at (0) = 0, og betrakt ølgen (x n) n=1 gitt ved x n = 1/ 2πn or n 1. Vis at lim (x n) =, n og bruk dette til å orklare hvoror ikke er kontinuerlig i punktet Global Formulering. Vi har nå utviklet den nødvendige terminologien or å ormulere den globale versjonen av inverst unksjonsteorem, men vi skal ørst ormulere og bevise noen hjelperesultater. Ikke bare er disse resultatene interessante i seg selv, men de vil også vise seg nyttige or å bevise hovedteoremet i denne seksjonen. 2 Strengt talt krever man bare at I og (I) skal være åpne mengder, men vi skal av pedagogiske årsaker kun benytte begrepet i denne mer restriktive orstanden.
5 INVERST FUNKSJONSTEOREM Hjelperesultater. Vi skal ørst karakterisere verdimengden til visse type unksjoner, og deretter skal vi se hvordan visse bijeksjoner har kontinuerlige inversunksjoner. Inverst unksjonsteorem vil gi betingelser på en unksjon tilstrekkelige or å garantere at den har en kontinuerlig deriverbar inversunksjon. Proposisjon Anta at I er et åpent intervall og at : I R er en kontinuerlig og strengt monoton unksjon. Da er verdimengden (I) det åpne intervallet gitt ved (I) = (m, M), hvor m = in (I) og M = sup (I). 3 Bevis. Vi skal bevise resultatet i det tilellet hvor er strengt voksende. Resultatet or tilellet hvor er strengt avtagende overlates til leseren. Anta at er strengt voksende. Det holder å vise at vi har ølgende to inklusjoner: (I) (m, M) og (I) (m, M). (1) Anta ørst at y (I), og velg x I slik at (x) = y. La deretter u I og v I være punkter slik at u < x < v (slike punkter eksisterer ettersom intervallet I er åpent). Ettersom er strengt voksende, ølger det at m (u) < (x) < (v) M, hvor ørste og siste ulikhet ølger ra m = in (I) og M = sup (I). Dette viser at y (m, M), da (x) = y. (2) Anta nå at y (m, M). Ettersom m er den største nedre skranken til (I) og m < y, kan ikke y være en nedre skranke or (I), og vi velger deror et punkt u I slik at (u) < y. Vi velger tilsvarende et punkt v I slik at y < (v). Da (u) < y < (v) og er strengt voksende, må u < v, slik at det lukkede og begrensede intervallet [u, v], hvorpå er kontinuerlig, er inneholdt i I. Det ølger ra skjæringssetningen at det innes et punkt x (u, v) slik at (x) = y, som viser at y (I). Bemerkning. En kritisk leser vil stille spørsmål ved vår kommentar om at in (I) = og sup (I) = dersom (I) ikke er henholdsvis nedad eller oppad begrenset: hva betyr det egentlig at noe er lik eller? Første måte å komme seg rundt dette spørsmålet på er ved å dele beviset ovenor inn i tileller avhengig av hvordan (I) er begrenset eller ikke. Man kan argumentere i tilelle or tilelle at (I) = (m, ) dersom (I) er nedad og ikke oppad begrenset, at (I) = (, M) dersom (I) er oppad og ikke nedad begrenset, at (I) = R dersom (I) hverken er nedad eller oppad begrenset, og så videre. Vi synes at en slik løsning er rotete, og den vil nødvendigvis øre til repetisjon av essensielt de samme argumentene i hvert tilelle. Den andre måten å komme seg rundt dette spørsmålet på er ved å konstruere og som objekter, or deretter å danne en utvidet tallinje [, ]. Deretter kan man utvide de vanlige operasjonene og strukturene 3 Vi setter in (I) = dersom (I) ikke er nedad begrenset, og, tilsvarende, sup (I) = dersom (I) ikke er oppad begrenset.
6 INVERST FUNKSJONSTEOREM 6 ra R til denne utvidede tallinjen. En slik remgangsmåte vil øre til en mer enhetlig og økonomisk behandling av emnet vi mener at det er i denne konteksten det er riktig å gjøre kalkulus men vi skal ikke ha anledning til å gå inn på detaljene her. Proposisjon Anta at situasjonen er den samme som i Proposisjon 2.2.1, og la g : (I) I betegne inversunksjonen til. Da er g kontinuerlig og strengt monoton, og den har samme monotonisitet som. Bevis. Beviset or dette er akkurat som or [1, s. 369, Teorem 7.4.5]. Oppgave La I = (a, b) være et åpent intervall, hvor a < b, og anta at unksjonen : I R er voksende. Vis at in (I) = lim (x) og sup (I) = lim (x), x a x b hvor vi tillater at disse størrelsene kan være lik eller. (Her betyr x a at x a med a < x, og x b betyr at x b med x < b.) Formuler og bevis et tilsvarende resultat or avtagende unksjoner Inverst Funksjonsteorem. Vi skal nå ormulere og bevise den globale versjonen av inverst unksjonsteorem. Teorem (Global Inverst Funksjonsteorem). La I være et åpent intervall, og anta at : I R er en kontinuerlig deriverbar unksjon slik at ikke tar verdien null på I. Da gjelder ølgende: (1) Funksjonen bytter ikke ortegn på I, og er strengt monoton. (2) Verdimengden (I) er et åpent intervall. La g : (I) I være inversunksjonen til. Da er g kontinuerlig deriverbar, den har samme monotonisitet som, og or alle y (I) har man at det vil si g = 1/( g). g (y) = 1 ( g(y) ), Hovedpunktene i Teorem er at dersom C 1 (I) er slik at ikke tar verdien null, så er en dieomori av klasse C 1, og dens inversunksjon g C 1( (I) ) tilredsstiller g = 1/( g). Legg merke til hvordan inversunksjonen «arver» egenskapene til. Vi skal bevise teoremet i lere steg. Lemma Funksjonen bytter ikke ortegn på I. Bevis. Anta, or motsigelse, at bytter ortegn på I, og la a I og b I være punkter slik at (a) < 0 og (b) > 0. Anta uten tap av generalitet at a < b. Da er [a, b] et lukket og begrenset intervall som er inneholdt i I, og er kontinuerlig på [a, b]. Ved skjæringssetningen, anvendt på, innes det et punkt c (a, b) slik at (c) = 0, hvilket motstrider hypotesen om at ikke tar verdien null. Lemma Funksjonen er strengt monoton, og verdimengden (I) er et åpent intervall.
7 INVERST FUNKSJONSTEOREM 7 Bevis. Ettersom ikke endrer ortegn, vil enten > 0 eller < 0 på hele I, og det ølger da på samme måte som i beviset or [1, s. 293, Korollar 6.2.5] at er strengt monoton. Per antagelse er deriverbar, og dermed kontinuerlig, og det ølger ra Proposisjon at (I) er et åpent intervall. Vi har vist at er strengt monoton, slik at den må være en bijeksjon ra I til (I). Vi lar g : (I) I betegne dens inversunksjon. Det ølger ra Proposisjon at g er en kontinuerlig unksjon på (I) med samme monotonisitet som, og det gjenstår å vise at den er kontinuerlig deriverbar. Lemma Inversunksjonen g : (I) I til er kontinuerlig deriverbar og tilredsstiller (3) g 1 (y) = ( g(y) ) or alle y (I), det vil si g = 1/( g). Bevis. La y (I). Vi skal vise at g er deriverbar i y og at (3) holder. Iølge Oppgave er det tilstrekkelig å vise at g(y n ) g(y) lim = n y n y 1 ( g(y) ) or alle ølger (y n ) n=0 i (I) som er slik at y n y og lim n y n = y. Anta at (y n ) n=0 er en slik ølge som beskrevet over, og la x = g(y) I og x n = g(y n ) I. Ettersom g er en bijeksjon og y n y, må x n = g(y n ) g(y) = x, slik at (x n ) n=0 er en ølge i I med x n x. Videre, ettersom g er kontinuerlig i punktet y og lim n y n = y, ølger det ra [1, s. 237, Setning ] at lim x n = lim g(y n) = g(y) = x. n n Med andre ord, (x n ) n=0 er en ølge i I slik at x n x og lim n x n = x. Siden er deriverbar i punktet x, ølger det ra nok en anvendelse av Oppgave at (x n ) (x) (4) lim = (x) 0. n x n x Ettersom x n x og er en bijeksjon, er (x n ) (x), og vi ser at g(y n ) g(y) lim = lim n y n y n x n x (x n ) (x) 1 = lim ( n (xn ) (x) ) /(x n x) = 1 (x) = 1 ( g(y) ), hvor nest siste likhet ølger ra (4) og [1, s. 207, Setning 4.3.3]. Dette viser at g er deriverbar i y og at (3) er oppylt. Vi har nå vist at g = 1/( g). Ettersom og g er kontinuerlige, ølger det ra [1, s. 235, Setning 5.1.6] at g er kontinuerlig på (I). Ettersom ikke tar verdien null, gjelder det samme or g, og det ølger ra [1, s.
8 INVERST FUNKSJONSTEOREM 8 234, Setning 5.1.4] at g = 1/( g) er kontinuerlig på (I), som viser at g C 1( (I) ). Oppgave La I være et åpent intervall og : I R en unksjon. Anta at a I. Vis at grenseverdien lim x a (x) eksisterer og er lik α R hvis og bare hvis lim (a n) = α n or alle ølger (a n) n=0 av punkter i I som tilredsstiller a n a og lim n a n = a. Hint. Tilpass beviset or [1, s. 237, Setning ] og se bemerkningen som ølger det Lokal Formulering. Hovedresultatet i orrige seksjon, Teorem 2.2.3, er av global natur. Med dette mener vi at det garanterer at den aktuelle unksjonen har en globalt deinert inversunksjon; det vil si at den er inverterbar på hele sitt deinisjonsområde. Selv om det i mange tileller ikke eksisterer globale inversunksjoner, kan man like vel, under visse betingelser, inne lokale inversunksjoner ved å innskrenke unksjonenes deinisjonsområde Restriksjon av Funksjoner. Anta at : Y Z er en unksjon mellom to mengder Y og Z, og la X Y være en delmengde av Y. Med restriksjonen av til X mener man unksjonen X : X Z deinert ved X (x) = (x) (x X). Med andre ord, restriksjonen X av til X er den unksjonen man år ved å restriktere sitt deinisjonsområde til X. La oss deinere en unksjon ι X Y : X Y ved ι X Y (x) = x (x X). Denne unksjonen kalles inklusjonsavbildningen av X inn i Y. Vi ser at ι X Y = id Y X. Følgende diagram illustrerer situasjonen: Y Z ι X Y X X Oppgave Anta at Y og Z er to mengder og at : Y Z er en unksjon. La betegne den tomme mengden. Hvoror er Y, og hva er? Oppgave Anta at A er en delmengde av R og at : A R er en kontinuerlig unksjon. Vis at dersom B A, så er unksjonen B også kontinuerlig. Denne oppgaven viser at restriksjon bevarer kontinuitet. Vi minner om at et omegn om et punkt a R er et åpent intervall som inneholder a. Oppgave La a R, og betrakt en unksjon : R R. Vis at er kontinuerlig i punktet a hvis og bare hvis det or alle omegn I om a er slik at restriksjonen I av til I er kontinuerlig i punktet a. Denne oppgaven viser at kontinuitet er et lokalt enomen: kontinuiteten til i punktet a avhenger kun av hvordan ser ut i vilkårlig små omegn om a.
9 INVERST FUNKSJONSTEOREM 9 Oppgave La situasjonen være den samme som i Oppgave 2.3.3, og la α R. Vis at er deriverbar i punktet a med (a) = α hvis og bare hvis det or alle omegn I om a er slik at restriksjonen I av til I er deriverbar i punktet a med ( I ) (a) = α. Denne oppgaven viser at deriverbarhet er et lokalt enomen: deriverbarheten til i punktet a avhenger kun av hvordan ser ut i vilkårlig små omegn om a Lokal Inverst Funksjonsteorem. Vi skal nå ormulere og bevise den lokale versjonen av inverst unksjonsteorem. Teorem (Lokal Inverst Funksjonsteorem). Anta at A er en ikke-tom delmengde av R og at : A R er en unksjon. Anta videre at a A og at det innes et omegn om a hvorpå er kontinuerlig deriverbar og tilredsstiller (a) 0. Da innes det et åpent intervall J A som inneholder a slik at J er en dieomori av klasse C 1. Bemerkning. Dette teoremet sier at dersom er kontinuerlig deriverbar på et omegn om punktet a og (a) 0, så innes det et åpent intervall J som inneholder a slik at (J ) er et åpent intervall og : J (J ) er en kontinuerlig deriverbar bijeksjon med en kontinuerlig deriverbar inversunksjon J 1 : (J ) J. Med andre ord, under disse betingelsene har en lokalt J deinert inversunksjon i nærheten av a. Bevis. La I være et omegn om a hvorpå er kontinuerlig deriverbar. Ettersom er kontinuerlig på I og (a) 0, anvender vi Oppgave til å inne et omegn J I om a slik at ikke tar verdien null på J. Resultatet ølger ved å anvende den globale versjonen av inverst unksjonsteorem, Teorem 2.2.3, på restriksjonen av til J. J Vi overlater det til leseren å undersøke hvordan Oppgave og Oppgave er brukt i beviset ovenor. Bemerkning. Det innes versjoner av inverst unksjonsteorem som ikke orutsetter like strenge krav om kontinuitet på de deriverte til de aktuelle unksjonene, men de versjonene vi har ormulert vil være tilstrekkelige or våre anvendelser, hvor disse kontinuitetskravene alltid vil være oppylt. Oppgave Anta at I er et åpent intervall og at : I R er en unksjon. Vis at dersom a I og er kontinuerlig i punktet a med (a) 0, så innes det et omegn J om a slik at har samme ortegn som (a) på hele J. Denne oppgaven viser at dersom en kontinuerlig unksjon er orskjellig ra null i et gitt punkt, så innes det et helt omegn om dette punktet hvor unksjonen er orskjellig ra null. Hint. Anta ørst at (a) > 0, og la ɛ = (a)/2 > 0. Forklar hvoror det innes en δ > 0 slik at 0 < (a)/2 = (a) ɛ < (x) når x a < δ, og bruk dette til å bevise konklusjonen. Reeranser [1] Lindstrøm, Tom: Kalkulus, 4. utgave (2016), Universitetsorlaget.
EKSEMPLER TIL ETTERTANKE MAT1100 KALKULUS
 EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
Analysedrypp II: Kompletthet
 Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Dette krever ikke noe nytt aksiom. Hvorfor? Og hvorfor må vi anta at A ikke er tom? Merk at vi har:
 Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Aksiom 3.1 (Likhet av mengder). La A og B være mengder. Da er A og B like hvis og bare hvis de har akkurat de samme elementene.
 Notat 3 for MAT1140 3 Mengder 3.1 Mengder definert ved en egenskap Det matematiske begrepet mengde har sin opprinnelse i vår intuisjon om samlinger. Objekter kan samles sammen til et nytt objekt kalt mengde.
Notat 3 for MAT1140 3 Mengder 3.1 Mengder definert ved en egenskap Det matematiske begrepet mengde har sin opprinnelse i vår intuisjon om samlinger. Objekter kan samles sammen til et nytt objekt kalt mengde.
Notat om Peanos aksiomer for MAT1140
 Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Litt topologi. Harald Hanche-Olsen
 MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
(ii) g = (f B)^{-1} \: V \to B \subset R^m er deriverbar med Dg(f(u)) = (Df(u))^{-1} \: R^m \to R^m for alle u i B.
 MAT1300 Analyse I 5. mai 2009 13.3. Det inverse funksjonsteoremet Vi vil bruke kontraksjonsprinsippet for å bevise følgende teorem: Teorem 13.13 (Det inverse funksjonsteoremet): La U \subset R^m være åpen,
MAT1300 Analyse I 5. mai 2009 13.3. Det inverse funksjonsteoremet Vi vil bruke kontraksjonsprinsippet for å bevise følgende teorem: Teorem 13.13 (Det inverse funksjonsteoremet): La U \subset R^m være åpen,
Tillegg til kapittel 11: Mer om relasjoner
 MAT1140, H-16 Tillegg til kapittel 11: Mer om relasjoner I læreboken blir ekvivalensrelasjoner trukket frem som en viktig relasjonstype. I dette tillegget skal vi se på en annen type relasjoner som dukker
MAT1140, H-16 Tillegg til kapittel 11: Mer om relasjoner I læreboken blir ekvivalensrelasjoner trukket frem som en viktig relasjonstype. I dette tillegget skal vi se på en annen type relasjoner som dukker
Oblig 1 - MAT Oppgave 1. Fredrik Meyer. Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved. x n+1 = α + x n 1 + x n.
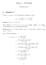 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
NOTAT OM UNIFORM KONTINUITET VEDLEGG TIL BRUK I KURSET MAT112 VED UNIVERSITETET I BERGEN
 NOTAT OM UNIFORM KONTINUITET VEDLEGG TIL BRUK I KURSET MAT2 VED UNIVERSITETET I BERGEN ANDREAS LEOPOLD KNUTSEN OG ARNE STRAY. Innledning og definisjoner Vi vil i dette notatet betrakte reelle funksjoner
NOTAT OM UNIFORM KONTINUITET VEDLEGG TIL BRUK I KURSET MAT2 VED UNIVERSITETET I BERGEN ANDREAS LEOPOLD KNUTSEN OG ARNE STRAY. Innledning og definisjoner Vi vil i dette notatet betrakte reelle funksjoner
Andre del av forelesningen om funksjoner bygger på dette notatet. Notatet bygger på læreboken og er noe mer utfyllende enn forelesningen.
 NOTAT TIL FORELESNING OM FUNKSJONER, DEL Andre del av orelesningen om unksjoner bygger på dette notatet. Notatet bygger på læreboken og er noe mer utyllende enn orelesningen. GRENSEVERDI Man kan or eksempel
NOTAT TIL FORELESNING OM FUNKSJONER, DEL Andre del av orelesningen om unksjoner bygger på dette notatet. Notatet bygger på læreboken og er noe mer utyllende enn orelesningen. GRENSEVERDI Man kan or eksempel
Notater fra forelesning i MAT1100 torsdag 27.08.09
 Notater fra forelesning i MAT1100 torsdag 27.08.09 Amandip Sangha, amandips@math.uio.no 28. august 2009 Definisjon 1.1. En delmengde A R kalles oppad begrenset dersom det finnes et tall b R slik at b x
Notater fra forelesning i MAT1100 torsdag 27.08.09 Amandip Sangha, amandips@math.uio.no 28. august 2009 Definisjon 1.1. En delmengde A R kalles oppad begrenset dersom det finnes et tall b R slik at b x
Taylorpolynom (4.8) f en funksjon a et punkt i definisjonsmengden til f f (minst) n ganger deriverbar i a Da er Taylorpolynomet til f om a
 Taylorpolynom (4.8) f en funksjon a et punkt i definisjonsmengden til f f (minst) n ganger deriverbar i a Da er Taylorpolynomet til f om a P n (x) = f (a) + f (a)(x a) + f (a) 2 (x a)2 + + f (n) (a) (x
Taylorpolynom (4.8) f en funksjon a et punkt i definisjonsmengden til f f (minst) n ganger deriverbar i a Da er Taylorpolynomet til f om a P n (x) = f (a) + f (a)(x a) + f (a) 2 (x a)2 + + f (n) (a) (x
Matematikk for IT, høsten 2016
 Matematikk or IT, høsten 016 Oblig 4 Løsningsorslag 30. setember 016.4.11 a) ( 1, 3, 5, 7, ) Her vil relasjonsmengden være slik: {(1, 1), (3, 1), (3, 3), (5, 1), (5, 3), (5, 5), (7, 1), (7, 3), (7, 5),
Matematikk or IT, høsten 016 Oblig 4 Løsningsorslag 30. setember 016.4.11 a) ( 1, 3, 5, 7, ) Her vil relasjonsmengden være slik: {(1, 1), (3, 1), (3, 3), (5, 1), (5, 3), (5, 5), (7, 1), (7, 3), (7, 5),
MAT jan jan jan MAT Våren 2010
 MAT 1012 Våren 2010 Mandag 18. januar 2010 Forelesning I denne første forelesningen skal vi friske opp litt rundt funksjoner i en variabel, se på hvordan de vokser/avtar, studere kritiske punkter og beskrive
MAT 1012 Våren 2010 Mandag 18. januar 2010 Forelesning I denne første forelesningen skal vi friske opp litt rundt funksjoner i en variabel, se på hvordan de vokser/avtar, studere kritiske punkter og beskrive
Injektive og surjektive funksjoner
 Injektive og surjektive funksjoner Christian F. Heide 5. september 07 Dette notatet forklarer begrepene injektive og surjektive funksjoner, og er tenkt brukt som et supplement til avsnitt.5 i boken «Mathem»
Injektive og surjektive funksjoner Christian F. Heide 5. september 07 Dette notatet forklarer begrepene injektive og surjektive funksjoner, og er tenkt brukt som et supplement til avsnitt.5 i boken «Mathem»
Notat med oppgaver for MAT1140
 Notat med oppgaver for MAT1140 1 Injeksjon, surjeksjon Oppgave 1.1. La f : A B være en avbildning. Vis at da er f injektiv hvis og bare hvis følgende holder: for hver mengde C og for hver g, h : C A hvis
Notat med oppgaver for MAT1140 1 Injeksjon, surjeksjon Oppgave 1.1. La f : A B være en avbildning. Vis at da er f injektiv hvis og bare hvis følgende holder: for hver mengde C og for hver g, h : C A hvis
Mer om mengder: Tillegg til Kapittel 1. 1 Regneregler for Booleske operasjoner
 MAT1140, H-16 Mer om mengder: Tillegg til Kapittel 1 Vi trenger å vite litt mer om mengder enn det som omtales i første kapittel av læreboken. I dette tillegget skal vi først se på regneregler for Booleske
MAT1140, H-16 Mer om mengder: Tillegg til Kapittel 1 Vi trenger å vite litt mer om mengder enn det som omtales i første kapittel av læreboken. I dette tillegget skal vi først se på regneregler for Booleske
Eksamensoppgave i MA1101 Grunnkurs i analyse
 Institutt for matematiske fag Eksamensoppgave i MA1101 Grunnkurs i analyse Faglig kontakt under eksamen: Kari Hag Tlf: 48 30 19 88 Eksamensdato: 15. oktober 018 Eksamenstid (fra til): 17:30 19:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i MA1101 Grunnkurs i analyse Faglig kontakt under eksamen: Kari Hag Tlf: 48 30 19 88 Eksamensdato: 15. oktober 018 Eksamenstid (fra til): 17:30 19:00 Hjelpemiddelkode/Tillatte
Notasjon i rettingen:
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 07 Notasjon i rettingen: R = Rett R = Rett, men med liten tulle)feil
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 07 Notasjon i rettingen: R = Rett R = Rett, men med liten tulle)feil
Lineærtransformasjoner
 Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Løsningsforslag til utvalgte oppgaver i kapittel 5
 Løsningsforslag til utvalgte oppgaver i kapittel 5 I kapittel 5 har mange av oppgavene et mer teoretisk preg enn du er vant til fra skolematematikken, og jeg har derfor lagt vekt på å lage løsningsforslag
Løsningsforslag til utvalgte oppgaver i kapittel 5 I kapittel 5 har mange av oppgavene et mer teoretisk preg enn du er vant til fra skolematematikken, og jeg har derfor lagt vekt på å lage løsningsforslag
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Forelesning 11 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 11 Transcendentale funksjoner Vi begynner nå på temaet transcendentale funksjoner. I dagens forelesning
TMA4100 Matematikk 1, høst 2013 Forelesning 11 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 11 Transcendentale funksjoner Vi begynner nå på temaet transcendentale funksjoner. I dagens forelesning
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09
 Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Notat om kardinalitet for MAT1140 (litt uferdig)
 Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
MAT1140 Strukturer og argumenter
 12. november 2018 MAT1140 Strukturer og argumenter Innleveringsfrist Obligatorisk oppgave 2 av 2 Torsdag 8. november 2018, klokken 14:30 i Devilry (devilry.ifi.uio.no). Instruksjoner Du velger selv om
12. november 2018 MAT1140 Strukturer og argumenter Innleveringsfrist Obligatorisk oppgave 2 av 2 Torsdag 8. november 2018, klokken 14:30 i Devilry (devilry.ifi.uio.no). Instruksjoner Du velger selv om
En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x).
 Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
9 Lineærtransformasjoner TMA4110 høsten 2018
 9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
MA oppsummering så langt
 MA1101 - oppsummering så langt Torsdag 29. september 2005 http://www.math.ntnu.no/emner/ma1101/2005h/ MA1101- oppsummering så langt p.1/21 Pensum til semesterprøven Kapittel P Kapittel 1 Kapittel 2: avsnittene
MA1101 - oppsummering så langt Torsdag 29. september 2005 http://www.math.ntnu.no/emner/ma1101/2005h/ MA1101- oppsummering så langt p.1/21 Pensum til semesterprøven Kapittel P Kapittel 1 Kapittel 2: avsnittene
Løsningsforslag til Mat112 Obligatorisk Oppgave, våren Oppgave 1
 Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Partielle ordninger, Zorns lemma og utvalgsaksiomet
 MAT1140, H-15 Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns
MAT1140, H-15 Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns
OPPGAVESETT MAT111-H16 UKE 36. Oppgaver til seminaret 9/9. Husk at seminaret finnes i to varianter, begge fredag :
 OPPGAVESETT MAT111-H16 UKE 36 Avsnitt 1.4: 17, 29, 32 Avsnitt 2.2: 12 Avsnitt 2.3: 41, 52 På settet: S.1 Oppgaver til seminaret 9/9 Husk at seminaret finnes i to varianter, begge fredag 12.15-14.00: Seminar
OPPGAVESETT MAT111-H16 UKE 36 Avsnitt 1.4: 17, 29, 32 Avsnitt 2.2: 12 Avsnitt 2.3: 41, 52 På settet: S.1 Oppgaver til seminaret 9/9 Husk at seminaret finnes i to varianter, begge fredag 12.15-14.00: Seminar
Oppsummering MA1101. Kristian Seip. 23. november 2017
 Oppsummering MA1101 Kristian Seip 23. november 2017 Forelesningen 23. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i MA1101 noen tips for eksamensperioden
Oppsummering MA1101 Kristian Seip 23. november 2017 Forelesningen 23. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i MA1101 noen tips for eksamensperioden
Analysedrypp IV: Metriske rom
 Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
OPPGAVESETT MAT111-H16 UKE 43. Oppgaver til seminaret 28/10
 OPPGAVESETT MAT111-H16 UKE 43 Avsn. 5.1: 41 Avsn. 5.3: 3, 7 Avsn. 5.4: 13, 31, 37 På settet: S.1 Oppgaver til seminaret 28/10 Oppgaver til gruppene uke 44 Merknad: Oppgavene under skal kunne løses uten
OPPGAVESETT MAT111-H16 UKE 43 Avsn. 5.1: 41 Avsn. 5.3: 3, 7 Avsn. 5.4: 13, 31, 37 På settet: S.1 Oppgaver til seminaret 28/10 Oppgaver til gruppene uke 44 Merknad: Oppgavene under skal kunne løses uten
To mengder S og T er like, S = T, hvis de inneholder de samme elementene. Notasjon. Mengden med elementene a, b, c og d skrives ofte {a, b, c, d}.
 Forelesning 0: Mengdelære, Induksjon Martin Giese - 23. januar 2008 1 Mengdelære 1.1 Mengder Mengder Definisjon 1.1. En mengde er en endelig eller uendelig samling objekter der innbyrdes rekkefølge og
Forelesning 0: Mengdelære, Induksjon Martin Giese - 23. januar 2008 1 Mengdelære 1.1 Mengder Mengder Definisjon 1.1. En mengde er en endelig eller uendelig samling objekter der innbyrdes rekkefølge og
OPPGAVESETT MAT111-H17 UKE 36. Oppgaver til seminaret 8/9. Husk at seminaret finnes i to varianter, begge fredag :
 OPPGAVESETT MAT111-H17 UKE 36 Avsnitt 1.4: 17, 29, 32 Avsnitt 2.2: 12 Avsnitt 2.3: 41, 52 På settet: S.1 Oppgaver til seminaret 8/9 Husk at seminaret finnes i to varianter, begge fredag 12.15-14.00: Seminar
OPPGAVESETT MAT111-H17 UKE 36 Avsnitt 1.4: 17, 29, 32 Avsnitt 2.2: 12 Avsnitt 2.3: 41, 52 På settet: S.1 Oppgaver til seminaret 8/9 Husk at seminaret finnes i to varianter, begge fredag 12.15-14.00: Seminar
7 Ordnede ringer, hele tall, induksjon
 Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Dagens plan. INF3170 Logikk. Mengder. Definisjon. Notasjon. Forelesning 0: Mengdelære, Induksjon. Martin Giese. 23. januar 2008.
 INF3170 Logikk Dagens plan Forelesning 0:, Induksjon Martin Giese 1 Institutt for informatikk, Universitetet i Oslo 2 23. januar 2008 Institutt for informatikk (UiO) INF3170 Logikk 23.01.2008 2 / 47 1
INF3170 Logikk Dagens plan Forelesning 0:, Induksjon Martin Giese 1 Institutt for informatikk, Universitetet i Oslo 2 23. januar 2008 Institutt for informatikk (UiO) INF3170 Logikk 23.01.2008 2 / 47 1
Ekstremverdier Mellomverdisatsen Forelesning i Matematikk 1 TMA4100
 Ekstremverdier Mellomverdisatsen Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 9. september 2011 Kapittel 4.1. Funksjoners ekseremverdier fra og med lokale ekstrema
Ekstremverdier Mellomverdisatsen Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 9. september 2011 Kapittel 4.1. Funksjoners ekseremverdier fra og med lokale ekstrema
OPPGAVESETT MAT111-H17 UKE 39. Oppgaver til seminaret 29/9
 OPPGAVESETT MAT111-H17 UKE 39 Avsnitt 3.1: 9, 23, 34 Avsnitt 3.3: 48, 61 Avsnitt 3.4: 1, 2, 9 På settet: S.1 Oppgaver til seminaret 29/9 Oppgaver til gruppene uke 40 Løs disse først så disse Mer dybde
OPPGAVESETT MAT111-H17 UKE 39 Avsnitt 3.1: 9, 23, 34 Avsnitt 3.3: 48, 61 Avsnitt 3.4: 1, 2, 9 På settet: S.1 Oppgaver til seminaret 29/9 Oppgaver til gruppene uke 40 Løs disse først så disse Mer dybde
Kleene-Kreisels funksjonaler
 Kapittel 7 Kleene-Kreisels funksjonaler 7.1 De hereditært totale funksjonalene Det er en kjent sak at hvis vi har en opplisting av beregnbare funksjoner fra N til N så vil enten opplistingen selv ikke
Kapittel 7 Kleene-Kreisels funksjonaler 7.1 De hereditært totale funksjonalene Det er en kjent sak at hvis vi har en opplisting av beregnbare funksjoner fra N til N så vil enten opplistingen selv ikke
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
Logaritmer og eksponentialfunksjoner
 Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
TMA4100: Repetisjon før midtsemesterprøven
 TMA4100: Repetisjon før midtsemesterprøven 10.10.09 Lars Sydnes sydnes@math.ntnu.no Institutt for matematiske fag October 1, 2009 L.S. (NTNU) TMA4100: Oversikt October 1, 2009 1 / 20 Kapittel 1: Funksjoner.
TMA4100: Repetisjon før midtsemesterprøven 10.10.09 Lars Sydnes sydnes@math.ntnu.no Institutt for matematiske fag October 1, 2009 L.S. (NTNU) TMA4100: Oversikt October 1, 2009 1 / 20 Kapittel 1: Funksjoner.
Funksjonsdrøfting MAT111, høsten 2017
 Funksjonsdrøfting MAT111, høsten 2017 Andreas Leopold Knutsen 11. Oktober 2017 Strengt voksende funksjon (Def. 6 i Ÿ2.8) f er strengt voksende på intervallet I dersom x 1 < x 2 i I = f (x 1 ) < f (x 2
Funksjonsdrøfting MAT111, høsten 2017 Andreas Leopold Knutsen 11. Oktober 2017 Strengt voksende funksjon (Def. 6 i Ÿ2.8) f er strengt voksende på intervallet I dersom x 1 < x 2 i I = f (x 1 ) < f (x 2
x A e x = x e = x. (2)
 Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
Funksjonsdrøfting MAT111, høsten 2016
 Funksjonsdrøfting MAT111, høsten 2016 Andreas Leopold Knutsen 11. oktober 2016 Den deriverte f Newton-kvotienten f (x+h) f (x) h er stigningen til sekantlinjen gjennom punktene (x, f (x)) og (x + h, f
Funksjonsdrøfting MAT111, høsten 2016 Andreas Leopold Knutsen 11. oktober 2016 Den deriverte f Newton-kvotienten f (x+h) f (x) h er stigningen til sekantlinjen gjennom punktene (x, f (x)) og (x + h, f
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
ANALYSEDRYPP. Et forkurs til MAT2400. av Tom Lindstrøm. Matematisk insitutt og CMA Universitetet i Oslo 2011
 1 ANALYSEDRYPP Et forkurs til MAT2400 av Tom Lindstrøm Matematisk insitutt og CMA Universitetet i Oslo 2011 2 Forord Hensikten med dette heftet er å bygge en bro mellom kalkuluskursene og det første kurset
1 ANALYSEDRYPP Et forkurs til MAT2400 av Tom Lindstrøm Matematisk insitutt og CMA Universitetet i Oslo 2011 2 Forord Hensikten med dette heftet er å bygge en bro mellom kalkuluskursene og det første kurset
Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017
 Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017 Andreas Leopold Knutsen 4. oktober 2017 Problem og hovedidé Problem: Finn løsning(er) r på en ligning
Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017 Andreas Leopold Knutsen 4. oktober 2017 Problem og hovedidé Problem: Finn løsning(er) r på en ligning
Notasjon i rettingen:
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 6: Derivasjon Eirik Hoel Høiseth Stipendiat IMF NTNU 22. august, 2012 Stigningstallet i et punkt Stigningstallet i et punkt Vi vender nå tilbake til problemet med å finne
Matematikk 1 (TMA4100) Forelesning 6: Derivasjon Eirik Hoel Høiseth Stipendiat IMF NTNU 22. august, 2012 Stigningstallet i et punkt Stigningstallet i et punkt Vi vender nå tilbake til problemet med å finne
Analysedrypp III: ɛ-δ og alt det der
 Analysedrypp III: ɛ-δ og alt det der Mange strever med ɛ-δ-argumenter. Det er flere grunner til dette: Noen har problemer med å forstå den underliggende tankegangen, mens andre sliter med de grunnleggende
Analysedrypp III: ɛ-δ og alt det der Mange strever med ɛ-δ-argumenter. Det er flere grunner til dette: Noen har problemer med å forstå den underliggende tankegangen, mens andre sliter med de grunnleggende
Løsningsforslag til noen oppgaver om Zorns lemma
 Løsningsforslag til noen oppgaver om Zorns lemma Fredrik Meyer Her er et løsningsforslag på Oppgave 3 og Oppgave 5 i notatet om Zorns lemma. De to første oppgavene ble gjort på plenum. Oppgave 1. Vi skal
Løsningsforslag til noen oppgaver om Zorns lemma Fredrik Meyer Her er et løsningsforslag på Oppgave 3 og Oppgave 5 i notatet om Zorns lemma. De to første oppgavene ble gjort på plenum. Oppgave 1. Vi skal
Den deriverte og derivasjonsregler
 Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
TMA4100 Matematikk 1, høst 2013
 TMA400 Matematikk, høst 203 Forelesning 2 www.ntnu.no TMA400 Matematikk, høst 203, Forelesning 2 Transcendentale funksjoner I dagens forelesning skal vi se på følgende: Den naturlige logaritmen. 2 Eksponensialfunksjoner.
TMA400 Matematikk, høst 203 Forelesning 2 www.ntnu.no TMA400 Matematikk, høst 203, Forelesning 2 Transcendentale funksjoner I dagens forelesning skal vi se på følgende: Den naturlige logaritmen. 2 Eksponensialfunksjoner.
Fremdriftplan. I går. I dag. 2.5 Uendelige grenser og vertikale asymptoter 2.6 Kontinuitet
 1 Fremdriftplan I går 2.5 Uendelige grenser og vertikale asymptoter 2.6 Kontinuitet I dag 2.7 Tangenter og derivasjon 3.1 Den deriverte til en funksjon 3.2 Derivasjonsregler 3.3 Den deriverte som endringsrate
1 Fremdriftplan I går 2.5 Uendelige grenser og vertikale asymptoter 2.6 Kontinuitet I dag 2.7 Tangenter og derivasjon 3.1 Den deriverte til en funksjon 3.2 Derivasjonsregler 3.3 Den deriverte som endringsrate
Zorns lemma og utvalgsaksiomet
 MAT1140, H-16 Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma bygger på det
MAT1140, H-16 Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma bygger på det
9. mai 2019 MAT Oblig 2 - Løsningsforslag
 9. mai 219 MAT 24 Oblig 2 - Løsningsforslag Oppgave 1. La X være vektorrommet X = C([ 1, 1], R utstyrt med sup-norm, og la G : X X være definert ved G(f(x = f(s m ds, for en m N. Vis at G er deriverbar
9. mai 219 MAT 24 Oblig 2 - Løsningsforslag Oppgave 1. La X være vektorrommet X = C([ 1, 1], R utstyrt med sup-norm, og la G : X X være definert ved G(f(x = f(s m ds, for en m N. Vis at G er deriverbar
MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet
 MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma
MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma
MAT1030 Diskret matematikk
 MAT1030 Diskret matematikk Forelesning 13: Funksjoner Dag Normann Matematisk Institutt, Universitetet i Oslo 25. februar 2008 Opphenting Forrige forelesning fortsatte vi innføringen av ekvivalensrelasjoner.
MAT1030 Diskret matematikk Forelesning 13: Funksjoner Dag Normann Matematisk Institutt, Universitetet i Oslo 25. februar 2008 Opphenting Forrige forelesning fortsatte vi innføringen av ekvivalensrelasjoner.
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 7: Derivasjon (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 23. august, 2012 Den deriverte som momentan endringsrate Den deriverte som momentan endringsrate Repetisjon
Matematikk 1 (TMA4100) Forelesning 7: Derivasjon (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 23. august, 2012 Den deriverte som momentan endringsrate Den deriverte som momentan endringsrate Repetisjon
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 26. november 2010 Tid for eksamen: 13:00 17:00 Oppgave 1 La A = { }. Mengdelære
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 26. november 2010 Tid for eksamen: 13:00 17:00 Oppgave 1 La A = { }. Mengdelære
Første og andrederivasjons testen Anvendt optimering Forelesning i Matematikk 1 TMA4100
 Første og andrederivasjons testen Anvendt optimering Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 13. september 2011 Kapittel 4.3. Monotone funksjoner og førstederivasjons-testen
Første og andrederivasjons testen Anvendt optimering Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 13. september 2011 Kapittel 4.3. Monotone funksjoner og førstederivasjons-testen
Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
Notater fra forelesning i MAT1100 mandag
 Notater fra forelesning i MAT00 mandag 3.08.09 Amandip Sangha, amandips@math.uio.no 8. august 009 Følger og konvergens (seksjon 4.3 i Kalkulus) Definisjon.. En følge er en uendelig sekvens av tall {a,a,a
Notater fra forelesning i MAT00 mandag 3.08.09 Amandip Sangha, amandips@math.uio.no 8. august 009 Følger og konvergens (seksjon 4.3 i Kalkulus) Definisjon.. En følge er en uendelig sekvens av tall {a,a,a
Utvalgsaksiomet, velordningsprinsippet og Zorns lemma
 Utvalgsaksiomet, velordningsprinsippet og Zorns lemma Dag Normann Universitetet i Oslo Matematisk Institutt Boks 1053 - Blindern 0316 Oslo 13. mars 2007 I dette notatet skal vi gi et bevis for ekvivalensen
Utvalgsaksiomet, velordningsprinsippet og Zorns lemma Dag Normann Universitetet i Oslo Matematisk Institutt Boks 1053 - Blindern 0316 Oslo 13. mars 2007 I dette notatet skal vi gi et bevis for ekvivalensen
Forelesning 13. Funksjoner. Dag Normann februar Opphenting. Opphenting. Opphenting. Opphenting
 Forelesning 13 Dag Normann - 25. februar 2008 Forrige forelesning fortsatte vi innføringen av ekvivalensrelasjoner. Vi definerte hva vi mener med partielle ordninger og med totale ordninger. Deretter snakket
Forelesning 13 Dag Normann - 25. februar 2008 Forrige forelesning fortsatte vi innføringen av ekvivalensrelasjoner. Vi definerte hva vi mener med partielle ordninger og med totale ordninger. Deretter snakket
Definisjoner og løsning i formel
 Dilik. p.1/24 Dierensiallikninger Deinisjoner og løsning i ormel Forelesning uke 45, 2005 MA-INF1100 Dilik. p.2/24 Dierensiallikninger Struktur i presentasjonen Lysarkene gjennomgår hovedpunkter ra alkulus
Dilik. p.1/24 Dierensiallikninger Deinisjoner og løsning i ormel Forelesning uke 45, 2005 MA-INF1100 Dilik. p.2/24 Dierensiallikninger Struktur i presentasjonen Lysarkene gjennomgår hovedpunkter ra alkulus
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 27. desember 2015 Tid for eksamen: 08.15 12:15 Oppgave 1 Grunnleggende mengdelære
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF1080 Logiske metoder for informatikk Eksamensdag: 27. desember 2015 Tid for eksamen: 08.15 12:15 Oppgave 1 Grunnleggende mengdelære
EKSAMEN I EMNET Løsning: Mat Grunnkurs i Matematikk I Mandag 14. desember 2015 Tid: 09:00 14:00
 Universitetet i Bergen Det matematisk naturvitenskapelige fakultet Matematisk institutt Side 1 av 7 BOKMÅL EKSAMEN I EMNET Mat 111 - Grunnkurs i Matematikk I Mandag 14. desember 15 Tid: 9: 14: Tillatte
Universitetet i Bergen Det matematisk naturvitenskapelige fakultet Matematisk institutt Side 1 av 7 BOKMÅL EKSAMEN I EMNET Mat 111 - Grunnkurs i Matematikk I Mandag 14. desember 15 Tid: 9: 14: Tillatte
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT00 Kalkulus Eksamensdag: Fredag 9. oktober 205 Tid for eksamen: 5.00 7.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark, formelsamling.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT00 Kalkulus Eksamensdag: Fredag 9. oktober 205 Tid for eksamen: 5.00 7.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark, formelsamling.
Oppgave: Avgjør om følgende to mengder er like: 1) (A B) C 2) A (B C)
 Mengder, fortsettelse. Tre mengder Venndiagram for tre mengder A, B og C må tegnes slik at alle muligheter blir dekket. For å få dette til må de overlappe hverandre: Oppgave: Avgjør om følgende to mengder
Mengder, fortsettelse. Tre mengder Venndiagram for tre mengder A, B og C må tegnes slik at alle muligheter blir dekket. For å få dette til må de overlappe hverandre: Oppgave: Avgjør om følgende to mengder
Fremdriftplan. Siste uke. I dag. Kap. 1 Funksjoner Grenseverdier
 1 Fremdriftplan Siste uke Kap. 1 Funksjoner 2.1-2.2 Grenseverdier I dag 2.3 Den formelle definisjonen av grenseverdi 2.4 Ensidige grenser og grenser i uendelig 2.5 Uendelige grenser og vertikale asymptoter
1 Fremdriftplan Siste uke Kap. 1 Funksjoner 2.1-2.2 Grenseverdier I dag 2.3 Den formelle definisjonen av grenseverdi 2.4 Ensidige grenser og grenser i uendelig 2.5 Uendelige grenser og vertikale asymptoter
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
Øvingsforelesning 2. Mengdelære, funksjoner, rekurrenser, osv. TMA4140 Diskret Matematikk. 10. og 12. september 2018
 Mengdelære, funksjoner, rekurrenser, osv. Øvingsforelesning 2 TMA4140 Diskret Matematikk 10. og 12. september 2018 Dagens øvingsforelesning Spørsmål til emnene i forrige uke Oppgaver fra midtsemesterprøver
Mengdelære, funksjoner, rekurrenser, osv. Øvingsforelesning 2 TMA4140 Diskret Matematikk 10. og 12. september 2018 Dagens øvingsforelesning Spørsmål til emnene i forrige uke Oppgaver fra midtsemesterprøver
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
UNIVERSITETET I OSLO. Løsningsforslag
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: MAT00 Kalkulus Eksamensdag: Fredag 4. oktober 20 Tid for eksamen: 5.00 7.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: MAT00 Kalkulus Eksamensdag: Fredag 4. oktober 20 Tid for eksamen: 5.00 7.00 Oppgavesettet er på 8 sider. Vedlegg: Tillatte
Oppgaver MAT2500 høst 2011
 Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
Repetisjonsforelesning - INF1080
 Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Deleksamen i MAT111 - Grunnkurs i Matematikk I
 Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
Oppsummering TMA4100. Kristian Seip. 26./28. november 2013
 Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Kapittel 6: Funksjoner
 MAT1030 Diskret Matematikk Forelesning 14: Mer om funksjoner Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 6: Funksjoner 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) MAT1030
MAT1030 Diskret Matematikk Forelesning 14: Mer om funksjoner Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 6: Funksjoner 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) MAT1030
UNIVERSITETET I BERGEN
 BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
MAT 1110: Bruk av redusert trappeform
 Tom Lindstrøm 10/5, 2006: MAT 1110: Bruk av redusert trappeform I Lays bok brukes den reduserte trappeformen til matriser til å løse en rekke problemer knyttet til ligningssystemer, lineærkombinasjoner,
Tom Lindstrøm 10/5, 2006: MAT 1110: Bruk av redusert trappeform I Lays bok brukes den reduserte trappeformen til matriser til å løse en rekke problemer knyttet til ligningssystemer, lineærkombinasjoner,
Løsningsforslag øving 7
 Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Grunnleggende notasjon ℕ = 1, 2, 3, 4, 5, 6, ℤ =, 3, 2, 1, 0, 1, 2, 3,
 Grunnleggende notasjon ℕ,, 3, 4, 5, 6, ℤ, 3,,, 0,,, 3, ℝ 𝑎𝑙𝑙𝑒 𝑟𝑒𝑒𝑙𝑒 𝑡𝑎𝑙𝑙 ℚ 𝑎𝑙𝑙𝑒 𝑟𝑎𝑠𝑗𝑜𝑛𝑎𝑙𝑒 𝑡𝑎𝑙𝑙 𝑎 𝑎, ℤ, 0 Induksjonsprinsippet Anta at for hver 𝑛 ℕ har vi gitt et utsagn 𝑃. Anta videre at vi vet at følgende
Grunnleggende notasjon ℕ,, 3, 4, 5, 6, ℤ, 3,,, 0,,, 3, ℝ 𝑎𝑙𝑙𝑒 𝑟𝑒𝑒𝑙𝑒 𝑡𝑎𝑙𝑙 ℚ 𝑎𝑙𝑙𝑒 𝑟𝑎𝑠𝑗𝑜𝑛𝑎𝑙𝑒 𝑡𝑎𝑙𝑙 𝑎 𝑎, ℤ, 0 Induksjonsprinsippet Anta at for hver 𝑛 ℕ har vi gitt et utsagn 𝑃. Anta videre at vi vet at følgende
MAT feb feb feb MAT Våren 2010
 MAT 1012 Våren 2010 Forelesning Vi er ferdig med en-variabel-teorien, og vi kan begynne å jobbe med funksjoner i flere variable. Det første vi skal gjøre er å gå gjennom de vanlige analysene vi gjør for
MAT 1012 Våren 2010 Forelesning Vi er ferdig med en-variabel-teorien, og vi kan begynne å jobbe med funksjoner i flere variable. Det første vi skal gjøre er å gå gjennom de vanlige analysene vi gjør for
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
Litt om forventet nytte og risikoaversjon. Eksempler på økonomisk anvendelse av forventning og varians.
 H. Goldstein Revidert januar 2008 Litt om forventet nytte og risikoaversjon. Eksempler på økonomisk anvendelse av forventning og varians. Dette notatet er ment å illustrere noen begreper fra Løvås, kapittel
H. Goldstein Revidert januar 2008 Litt om forventet nytte og risikoaversjon. Eksempler på økonomisk anvendelse av forventning og varians. Dette notatet er ment å illustrere noen begreper fra Løvås, kapittel
MAT1030 Forelesning 14
 MAT1030 Forelesning 14 Mer om funksjoner Roger Antonsen - 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) Kapittel 6: Funksjoner Surjektive funksjoner Den neste gruppen av funksjoner vi skal se på er
MAT1030 Forelesning 14 Mer om funksjoner Roger Antonsen - 10. mars 2009 (Sist oppdatert: 2009-03-10 11:34) Kapittel 6: Funksjoner Surjektive funksjoner Den neste gruppen av funksjoner vi skal se på er
Grublegruppe 19. sept. 2011: Algebra I
 Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Oppsummering TMA4100. Kristian Seip. 17./18. november 2014
 Oppsummering TMA4100 Kristian Seip 17./18. november 2014 Forelesningene 17./18. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Oppsummering TMA4100 Kristian Seip 17./18. november 2014 Forelesningene 17./18. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 14. oktober 2016 Tid for eksamen: 13.00 15.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark,
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT1100 Kalkulus Eksamensdag: Fredag 14. oktober 2016 Tid for eksamen: 13.00 15.00 Oppgavesettet er på 5 sider. Vedlegg: Svarark,
TMA4100 Matematikk 1 Høst 2014
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA400 Matematikk Høst 04 Løsningsforslag Øving 04 30 For å vise at f er en injektiv one-to-one funksjon, ser vi på den deriverte,
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 4: Grenseverdi (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 20. august, 2012 Formell definisjon av grenseverdi Formell definisjon av grenseverdi Uformell definisjon
Matematikk 1 (TMA4100) Forelesning 4: Grenseverdi (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 20. august, 2012 Formell definisjon av grenseverdi Formell definisjon av grenseverdi Uformell definisjon
Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010 Oppgave 1 Løs ulikheten x + 6 5 x + 2 Strategien er å
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Løsningsforslag, midtsemesterprøve MA1101, 5.oktober 2010 Oppgave 1 Løs ulikheten x + 6 5 x + 2 Strategien er å
