Notat i MA2201. Vegard Hagen. 27. mai La S være en mengde og la f, g, h : S S. Da er
|
|
|
- Stine Martinsen
- 8 år siden
- Visninger:
Transkript
1 Notat i MA2201 Vegard Hagen 27. mai 2012 Del I - grupper og undergrupper Seksjon 2 - Binære Operasjoner En binær operasjon på en mengde S er en funksjonsavbildning S S S. (a, b) S S betegner vi elementet ((a, b)) av S med a b. La være en binær operasjon på S og la H S. Undermengden H er lukket under hvis a, b H også har a b H. I dette tilfellet er den binære operasjonen på H gitt ved å restriktere til H kalt den induserte operasjonen av på H. En binær operasjon på en mengde S er kommutativ hvis og bare hvis a b = b a a, b S. En binær operasjon på en mengde S er assosiativ hvis (a b) c = a (b c) a, b, c S. Teorem - Assosiativitet av komposisjon: f (g h) = (f g) h. La S være en mengde og la f, g, h : S S. Da er Seksjon 3 - Isomorfe binære structurer La < S, > og < S, > være binære algebraiske strukturer. En isomorfi av S med S er en bijektiv funksjon φ : S S s.a. φ(x y) = φ(x) φ(y) x, y S homomorfiegenskap. La < S, > være en binær struktur. Et element e S er et identitetselement for hvis e s = s = s e s S Teorem - Unikhet av Identitetselementet: En binær struktur < S, > har på det meste ett identitetselement. Dvs. hvis det finnes et identitetselemet så er dette unikt. Anta < S, > her et identitetselement e for. Hvis φ : S S er en isomorfisme av < S, > med < S, >, så er φ(e) et identitetselement for på S. Seksjon 4 - Grupper En gruppe < G, > er et sett G lukket under en binær operasjon, s.a. de følgende aksiomene er tilfredsstilt: 1
2 G 1 a, b, c G har vi: (a b) c = a (b c) Assosiativitet av. G 2 e G s.a. x G har vi: e x = x e = x Identitetselement e for. G 3 a G a G s.a.: a a = a a = e Invers a av a. En gruppe G er abelsk hvis dens binære operasjon er kommutativ. Gitt < G, >, gjelder den høyre og venstre kanselleringsloven i G. dvs. a b = a c b = c og b a = c a b = c. og y i G. Gitt < G, >. a, b G vil de lineære ligningene a x = b og y a = b ha unike løsninger x I en gruppe G så!e G s.a. e x = x e = x x G og a G!a G s.a. a a = a a = e. Dvs identitetselementet og inversen av hvert elt. er unik. Korrolar: a, b G har vi (a b) = b a Seksjon 5 - Undergrupper Ordenen G til G er antall elt i G. Hvis et undersett H G er lukket under den binære operasjonen på G og hvis H med den induserte operasjonen på G sel er en gruppe, da er H en undergruppe av G. Dette betegnes med H G. G er en uekte undergruppe av seg selv. Alle ande undergrupper er ekte undergrupper av G. undergrupper e er den trivielle undergruppen. Alle andre undergrupper kalles ikke-trivielle. En undermengde H av en gruppe G er en undergruppe av G hviss: 1. H er lukket under den binære operasjonen på G. 2. Id. elt. e G er også i H. 3. a H a 1 H La a G. Da er H = {a n n Z} en undergruppe av G og er den minste undergruppen av G som inneholder a, dvs. enhver undergruppe som inneholder a må også inneholde H. La a G. Da er undergruppa {a n n Z} G kalt den sykliske undergruppa av G generert av a. Notasjon < a >. Et elt a G genererer G og er en generator for G hvis < a >= G. En gruppe G er syklisk hvis det finnes et elt a G som genererer G. Seksjon 6 - Sykliske grupper Enhver syklisk gruppe er abelsk. 2
3 Divisjonsalgoritmen for Z: Hvis m er et positivt heltall og n er et hvilket som helst heltall, så! heltall q og r s.a. n = mq + r og 0 r < m. En undergruppe av en suklisk undergruppe er også syklisk. Undergruppene av Z under addisjon er presis gruppene nz under addisjon for n Z. La r, s Z +. Den positive generatoren d av den sykliske gruppa H = {nr + ms n, m Z} under addisjon er den største felles divisor (gcd) av r og s. Vi skriver d = gcd(r, s) La G være en syklisk gruppe med generator a. Hvis G =, så er G isomorf med < Z, + >. Hvis G = n, så er G isomorfisk med < Z n, + n >. La G være syklisk med G = n og generert av a. La b G og la b = a s. Da genererer b en syklisk undergruppe H G med n/d elt., hvor d = gcd(s, n). < a s >=< a t > hviss gcd(s, n) = gcd(t, n). Hvis a er en generator for den endelige sykliske gruppa G av orden n, så er de andre generatorene av G på formen a r, hvor r og n er relativt primiske, dvs. gcd(r, n) = 1. Del II - Permutasjoner, Restklasser og Direkte Produkt Seksjon 8 - Grupper av Permutasjoner En permutasjon av en mengde A er en funksjonφ : A A som er bijektiv. La A være en ikke-tom mengde og la S A være samlingen av alla permutasjonene av A. Da er S A en gruppe under permutasjonsmultiplikasjon. La A være det endelige settet {1, 2,..., n}. Gruppen av alle permutasjonene av A er den symmetriske gruppen på n bokstaver, og er skrvet som S A. La f : A B være en funksjon og la H A. BIldet av H under f er {f(h) h H} og blir skrevet som f[h]. Lemma: La G og G være grupper og la φ : G G være en injeksjon s.a. φ(xy) = φ(x)φ(y) x, y G. Da er φ[g] en undergruppe av G og φ lager en isomorfi av G med φ[g]. Teorem - Ceyley s Enhver gruppe er isomorf med en gruppe av permutasjoner. Def 8.17 Seksjon 9 - Oribitaler, Skykler, og de Alternerende Grupper. La σ være en permutasjon av settet A. Ekvivalensklassene i A determinert av ekvivalensrelasjonen; for a, b, A, la a b hviss b = σ n (a) for en n Z, er orbitalene av σ. En permutasjon σ S er en sykel hvis den er på det meste en orbital som inneholder mer enn ett elt. Lengden av sykelen er antall elt. i dens lengste orbital. 3
4 Enhver permutasjon σ av en endelig mengde er et produkt av disjunkte sykler. En sykel av lengde 2 er en transposisjon. Enhver permutasjon av et endelig set med minst to elt. er et produkt av transposisjoner. Ingen permutasjon i S n kan uttrykkes som både et produkt av et par-antall transposisjoner og et odde-antall transposisjoner. En permutasjon av en endelig mengde er enten partall eller oddetall ettersom den kan uttrykkes som ett par-antall transposisjoner eller odde-antall transposisjoner. Hvis n 2, så vil samlingen av alle partallspermutasjoner av {1, 2, 3,..., n} lage en undergruppe av orden n!/2 av den symmetriske gruppen S n. Undergrupper av S n som inneholder partallspermutasjonene av n bokstaver er den alternerende gruppen A n på n bokstaver. Seksjon 10 - Restklasser og Lagrange teoremet. La H G. La relasjonen L være definer på G ved: a L b hviss a 1 b H, og la R være definert ved ab 1 H. Da er både L og R ekvivalensrelasjoner på G. La H G. Undermengden ah = {ah h H} av G er den venstre restklassen av H som inneholder a. Undermengden Ha = {ha h H} av G er den høyre restklassen av H som inneholder a. For en undergruppe H av en abelsk gruppe G, vil partisjonen av G til venstre restklasser av H og partisjonen til høyre restklasser være de samme. Teorem - Lagranges teorem: La G < og H G, da vil H G. Enhver gruppe av primisk orden er syklisk. Ordenen av et elt. i en endelig grupper deler ordenen av gruppa. La H G. Antallet av venstre restklasser av H i G er indeksen (G : H) av H i G. Anta H, K G s.a. K H G og anta at (H : K) og (G : H) begge er endelige. Da er (G : K) endelig og (G : K) = (G : H)(H : K) Seksjon 11 - Direkte Produkt og Endelig Genererte Abelske Grupper. Det kartesiske produktet av mengder S 1, S 2,..., S n er mengden av alle ordna n-tipler (a 1, a 2,..., a n ), hvor a i S i for i = {1, 2,..., n}. Det kartesiske produktet skrives som enten S 1 S 2... S n eller som ni=1 S i. 4
5 La G 1,..., G n være grupper. For (a 1,..., a n ) og (b 1,..., b n ) i n i=1 G i, definer (a 1,..., a n )(b 1,..., b n ) som elementet (a 1 b 1,..., a n b n ). Da er n i=1 G i en gruppe, den direkte produkt av gruppene G 1, under denne binære operasjonen. Gruppen Z m Z n er syklisk og er isomorf med Z mn hviss gcd(m, n) = 1. Gruppa n i=1 Z mi er syklisk og isomorf med Z m1 m 2 m n hviss alle m i -ene er relativt primiske. La r 1, r 2,..., r n være positive heltall. Deres minste felles multiplum (lcm) er den positive generatoren av den sykliske gruppa av alle felles multipler av r i -ene. Dvs. den sykliske gruppa av alle heltall delelig med enhver r i for i = {1, 2,..., n}. La (a 1,... a n ) n i=1 G i. Hvis a i er av endelig orden r i i G i, vil ordenen til (a 1,... a n ) i ni=1 G i være lik minste felles multiplum av alle r i -ene. Teorem - Fundamentalteoremet for Endelige Genererte Abelske Grupper: Enhver endelig generert abelsk gruppe G er isomorf med et direkte produkt av sykliske grupper på formen Z r p 1 Z r 1 p 2 2 Z p rn n Z Z Z hvor p i er primtall, og r i er positive heltall. Det direkte produkt er unikt bortsettt fra mulige ombrokkeringer av faktorene. Dvs. antallet (Betti taller av G) av faktorer Z er unikt og primtallseksponentene (p i ) r i ) er unike. En gruppe G er dekomponerbar hvis den er isomorf med et direkte produkt av to ikke-trivielle undergrupper. Ellers er G ikke-dekomponerbar. De endelige ikke-dekomponerbare abelske gruppene er nøyaktig de sykliske gruppene med orden p n hvor p er et primtall og n N. Hvis m deler ordenen av en endelig abelsk gruppe G, så har G en undergruppe av orden m. Hvis m er et kvadratfritt heltall, dvs. m er ikke delbar på kvadratet av et primtall, så vil enhver abelsk gruppe G med orden m være syklisk. Del III - Homomorfier og Faktorgrupper Seksjon 13 - Homomorfier Et kart φ : G G er en homomorfisme hvis homomorfiegenskapen, φ(ab) = φ(a)φ(b) holder a, b, G. La φ være en kartlegging av en mengde X til en mengde Y, og la A X og B Y. Bildet φ[a] av A i Y under φ er {φ(a) a A}. Mengden φ[x] er verdimengden av φ. Inversbildet φ 1 av B i X er {x X φ(x) B} La φ vøre en homomorfisme av gruppa G inn i gruppa G. 1. Hvis e er id.elt. i G, så er φ(e) id.elt. e G. 2. Hvis a G, så φ(a 1 ) = φ(a) Hvis G G, så er φ[h] G 4. Hvis K G, så er φ 1 G. 5
6 Med andre ord ivaretar φ id.elt., inverser, og undergrupper. La φ : G G være en homomorfisme av grupper. Undergruppa φ 1 [{e }] = {x G φ(x) = e } kalles kernelen til φ, og skrives ker(φ) La φ : G G være en gruppehomomorfi, og la H = ker(φ). La a G. Da vil mengden φ 1 [{φ(a)}] = {x G φ(x) = φ(a)} være den venstre restklassen ah av H, og er også den høyre restklassen Ha av H. Dette medfører at de to partisjonen av G i høyre og venstre restklasser av H er like. En gruppehomomorfi φ : G G er injektiv hviss ker(φ) = {e}. Hvordan vise at φ : G G er en isomorfi: Vis at φ er en homomorfi. Vis at ker(φ) = {e}. Vis at φ er surjektiv. En undergruppe H av en gruppe G er normal hvis dens høyre og venstre restklasser er like, dvs. gh = Hg g G, og skrives H G. Bemerk at undergrupper av abelske grupper er normale. Hvis φ : G G er en gruppehomomorfi, så er ker(φ) en normal undergruppe av G, ker(φ) G. Seksjon 14 - Faktorgrupper: LA φ : G G være en gruppehomomorfi med kernel H. Da vil restklassene av H lage en faktorgruppe, G/H, hvor (ah)(bh) = (ab)h. I tillegg vil kartet µ : G/H φ[g] definert ved (µ(ah) = φ(a) være en isomorfi. Både restklassemultiplikasjon og µ er veldefinerte, uavhengige av valgene a og b fra restklassene. La H G. Da er venstre restklassemultiplikasjon veldefinert av ligningen; (ah)(bh) = (ab)h hviss H G. La H G. Da vil restklassene til H forme en gruppe G/H under den binære operasjonen (ah)(bh) = (ab)h. Gruppa G/H er faktorgruppa (eller kvotient gruppa) av G fra H. La H G. Da vil γ : G G/H gitt med γ(x) = xh være en homomorfisme med kernel H. Teorem - Det fundamentale Homomorfismeteoremet: La φ : G G være en gruppehomomorfi med kernel H. Da er φ[g] en gruppe, og µ : G/H φ[g] gitt ved µ(gh) = φ(g) en isomorfisme. Hvis γ : G G/H homomorfien gitt vedγ(g) = gh, då er φ(g) = µγ(g) g G. Følgende er tre ekvivalente betingelser for en undergruppe H av en gruppe G for å være en normal undergruppe av G 1. ghg 1 H g G og h H. 2. ghg 1 = H g G. 6
7 3. gh = Hg g G. En isomorfi φ : G G av en gruppe G med seg selv kalles en automorfisme av G. Automorfismen i g : G G hvor i g (x) = gxg 1 x G, er den indre automorfien av G ved g. Å bruke i g på x kalles konjugeringer av x ved g. Seksjon 15 - Faktogruppeutregninger og Simple Grupper La G = H K være det direkte produktet av gruppene H og K. Da er H = {(h, e) h H en normal undergruppe av G. I tillegg er G/H isomorf med K på en naturlig måte. Likedan er G/K H på en naturlig måte. En faktorgruppe av en syklisk gruppe er syklisk. En gruppe er simpel hvis den er ikke-triviell og har ingen ekte ikke-trivielle normale undergrupper. Den alternerende gruppen A n er simpel for n 5. La φ : G G være en gruppehomomorfi. Hvis N er en normal undergruppe av G, så er φ[n] φ[g]. Videre, hvis N φ[g], så er φ 1 [N ] G. En maksimal normal undergruppe av en gruppe G er en normal undergruppe M G s.a. det ikke er noen ekte normal undergruppe N av G som ekte inneholder M. M er en maksimal normal undergruppe av G hviss G/M er simpel. La G være en gruppe. Mengden av alle kommutatorene aba 1 b 1 for a, b G genererer en undergruppe C (kommutatorundergruppen) av G. Denne undergruppen C er en normal undergruppe av G. Videre, hvis N G, så er G/N abelsk hviss C N. Seksjon 16 - Gruppehandlinger på en mengde La X være en mengde og G en gruppe. En handling av G på X er et kart : G X X s.a. 1. ex = x x X. 2. (g 1 g 2 )(x) = g 1 (g 2 x) x X og g 1, g 2 G. Under disse betingelsene er X en G-mengde. La X være en G-mengde. g G, funksjonen σ g : X X definert ved σ g = gx for x X er en permutasjon av X. I tillegg, kartet φ : G S X definert vedφ(g) = σ g er en homomorfi med egenskapen at φ(g)(g) = gx. La X være en G-mengde. Da er G x = {g G gx = x} en undergruppe av G for alle x X. La X være en G-mengde og la x X. Undergruppa G er isotropiundergruppa av X. 7
8 La X være en G-mengde. For x 1, x 2 C, la x 1 x 2 hviss g G s.a. gx 1 = x 2. Da er en ekvivalensrelasjon på X. La X være en G-mengde. Hver celle i partisjonen av denne ekvivalensrelasjonen er en orbital i X under G. Hvis x X, så er cella som inneholder x orbitalen av x. Vi kaller denne cella Gx. La X være en G-mengde og la x X. Da er Gx = (G : G x ). Hvis G er endelig, så er G x en divisor av G. Seksjon 17 - Anvendelser av G-mengder til telling Teorem - Burnsides formel: La G være en endelig gruppe og X en endelig G-mengde. Hvis r er antallet orbitaler i X under G, så gjelder: r G = g G X g. Hvis G er en endelig gruppe og X er en endelig Gmengde, så er ()Antallet orbitaler i XunderG) = (1/ G ) g G X g. Del IV - Ringer og felt En ring < R, +, > er en mengde R sammen med to binære operasjoner + og, som kalles addisjon og multiplikasjon, definer på R slik at følgende aksiom holder: R 1 < R, + > er en abelsk gruppe. R 2 Multiplikasjon er assosiativ. R 3 a, b, c R, gjelder den venstre distributiv lov, a (b + c) = (a b) + (a c) og den høyre distributiv lov, (a + b) c = (aċ) + (b c). Hvis R er en ring med additiv identitet 0, da gjelder følgende for a, b R: 1. 0a = a0 = a( b) = ( a)b = (ab). 3. ( a)( b) = ab. For ringer R og r er kartet φ : R R en homomorfi hvis følgende to krav gjelder a, b R: 1. φ(a + b) = φ(a) + φ(b). 2. φ(ab) = φ(a)φ(b). En isomorfi φ : R R er en bijektiv homomorfi. Ringene R og R er da isomorfe. I en ring hvor multiplikasjon er kommutativ er en kommutativ ring. En ring med en multiplikativ identitet er en ring med enhet. Det multiplikative identitetselementet 1 kalles enheten. La R være en ring med enhet a 0. Et elt u R er er en enhet av R hvis den har multiplikativ invers i R. Hvis alle ikke-null elt i R er en enhet, så er R en divisjonsring (eller skjevfelt). Et felt er en kommutativ divisjonsring. En ikke-kommutativ divisjonsring kalles strengt skjevfelt. 8
9 Seksjon 19 - Integraldomener Hvis a og b er to elt. ulik fra null i en ring R slik at ab = 0, da er a og b 0-divisorer. I ringen Zn er 0-divisorne presis de ikke-null elt som ikke er relativt primisk med n. Hvis p er et primtall, så har Z p ingen 0-divisorer. Kanselleringslovene gjelder i en ring R hviss R ikke har noen 0-divisorer. Et integraldomene D er en kommutativ ring med enhet 1 0 og ingen 0-divisorer. Ethvert felt F er et integraldomene. Ethvert endelig integraldomene et et felt. Hvis p er et primtall, så er Z p et felt. Hvis det for en ring R finnes et potitivt heltall n s.a. n a = 0 a R, så er det minste slikt positive heltall karakteristikken til ringen R. Hvis det ikke finnes et slikt heltall, så har R karakteristikk 0. La R være en ring med enhet. Hvis n 1 0 n Z +, så har R karakteristikk 0. Hvis n 1 = 0 for et positivt heltall, så er det minste slikt tall n karakteristikken til R. Seksjon 20 - Fermats og Eulers teorem Fermats lille teorem: Hvis a Z og p er et primtall som ikke deler a, da vil p dele a p 1 1. dvs, a p 1 1 mod p for a 0 mod p. Hvis a Z, så er a p a mod p for ethvert primtall p. modulo n. Mengden G n av ikke-null elt. av Z som ikke er 0-divisorer lager en gruppe under multiplikasjon Eulers phi-funksjon (φ(n)) er antallet positive heltall mindre enn eller lik n og relativ primisk n. Eulers teorem: Hvis a er et heltall relativt primisk til n, så er a φ(n) 1 delelig med n, dvs, a φ(n) 1 mod n. La m Z + og la a Z m være relativt primisk til m. For enhver b Z m, så vil ligningen ax = b ha en unik løsning i Z m. Hvis a og m er relativt primiske heltall, så vil kongruensen ax b mod m for hvert heltall b ha som løsninger alle heltall i presis en restklasse modulo m. 9
10 La m Z + og la a, b Z m. Videre la d = gcd(a, m). Ligningen ax = b har løsninger i Z m hviss d deler b. Når d deler b, vil ligningen ha eksakt d løsninger i Z m. La d = gcd(a, m) hvor a og m er positive heltall. Kongruensen ax b mod m har en løsning hviss d deler b. Når dette er tilfellet, er løsningene heltallene i eksakt d forskjellige restklasser modulo m. Seksjon 22 - Polynomringer La R være en ring. Et polynom f(x) med koeffisienter i R er en uendelig formell sum: a i x i = a 0 + a 1 x + + a n x n +, i=0 hvor a i R og a i = 0 for alle bortsett fra et endelig antall verdier for i. a i -ene er koeffisienter av f(x). Hvis for en i 0 det er sant at a i 0, så vil den største slik verdi av i være graden til f(x). Hvis alle a i = 0, så er graden til f(x) udefinert. Mengden R[X] av alle polynom i et indeterminant x med koeffisienter i en ring R er en ring under polynom-addisjon og -multiplikasjon. Hvis R er kommutativ, så er også R[X] kommutativ, og hvis R har unity 1 0, så er 1 også unity for R[x]. Teorem - Evalueringen av homomorfier for feltteori: La F være et underfelt av et felt E, la α være et hvilket som helts elt av E, og la x være en indeterminant. Kartet φ a : F [x] E definert ved: φ a (a 0 + a 1 x + + a n x n ) = a 0 + a 1 α + + a n α n for (a a n x n ) F [x] er en homomorfi av F [x] til E. I tillegg, φ a (x) = α, og φ a kartlegger F isomorft ved identitetskartet; dvs. φ a (a) = a for a F. Homomorfien φ a er en evaluering på α. La F være et underfelt av et felt E, og la α E. La f(x) = a 0 + +a n x n være i F [x], og la φ a : F [x] E være evalueringshomomorfien i forrige teorem. La f(α) betegne φ a (f(x)) = a 0 + +a n α n. Hvis f(α) = 0, så er α en null av f(x). Polynomet x 2 2 har ingen nuller i de rasjonelle tall. Derfor er 2 ikke et rasjonelt tall. Seksjon 23 - Faktorisering av polynomer over et felt Teorem - Divisjonsalgoritmen for F[x]: La og f(x) = a n x n + a n 1 x n a 0 g(x) = b m x m + b m 1 x m b 0 være to elt. av F [X], med a n og b n begge ikke-null elt. av F og m > 0. Da finnes det to unike polynom q(x) og r(x) i F [x] s.a. f(x) = g(x)q(x) + r(x), hvor enten r(x) = 0 eller graden av r(x) er mindre enn graden m av g(x). Korollar - Faktor teoremet: i F [X]. Et elt a F er en null av f(x) F [X] hviss x a er en faktor av f(x) 10
11 Et ikke-null polynom f(x) F [x] av grad n kan ha på det meste n nuller i et felt F. Hvis G er en endelig undergruppe av den multiplikative gruppen < F, > av et felt F, så er G syklisk. Generelt, den multiplikative gruppa av alle ikke-null elt av et endelig felt er syklisk. Et ikke-konstant polynom f(x) F [x] er irredusibelt over F eller er et irredusibelt polynom i F [x] hvis f(x) ikke kan uttrykkes som et produkt g(x)h(x) av to polynom g(x), h(x) F [x], begge av lavere grad enn f(x). Hvis f(x) F [x] er et ikkekonstant polynom som ikke er irredusibelt over F, så er f(x) redusibelt over F. La f(x) F [x], og la f(x) være av grad 2 eller 3. Da er f(x) redusibelt over F hviss den har en null i F. Hvis f(x) Z[x], så vil f(x) kunne faktoriseres til et produkt av to polynom av lavere grad r og s i Q[x] hviss det har slike faktoriseringer med polynom av samme grad r og s i Z. Hvis f(x) = x n + a n 1 x n a 0 er i Z[x] med a 0 0, og hvis f(x) har en null i Q, så har det en null m i Z, og m må dele a 0. Teorem - Eisensteinkriteriet: La p Z være et primtall. Anta at f(x) = a n x n + a 0 er i Z, og at a n 0 mod p, men a i = 0 mod p for alle i < n, med a 0 0 mod p 2. Da er f(x) irredusibelt over Q. Polynomet er irredusibelt over Q for ethvert primtall p. Φ p (x) = xp 1 x 1 = xp 1 + x p x + 1 La p(x) være et irredusibelt polynom i F [x]. Hvis p(x) deler r(x)s(x) for r(x), s(x) F [X], så deler p(x) enten r(x) eller s(x). Hvis p(x) er irredusibelt i F [x] og p(x) deler produktet r 1 (x) r n (x) for r i F [x], så deler p(x) r i (x) for minst en i. Hvis F er et felt, så kan alle ikke-konstant polynom f(x) F [x] faktoriseres i F [X] i et produkt av irredusible polynomer, de irredusible polynomene er unike bortsett fra orden og for enhet faktorer i F. Del V - Idealer og faktorringer Et kart φ av en ring R til en ring R er en homomorfi hvis for alle elt. a, b R. φ(a + b) = φ(a) + φ(b) og φ(ab) = φ(a)φ(b) 11
12 La φ være en homomorfi fra en ring R til en ring R. Hvis 0 er den additive identiteten i R, så er φ(0) = 0 den additive identiteten i R, og hvis a R, så er φ( a) = φ(a). Hvis S er en underring av R, så er φ[s] en underring av R. Dette går også den andre veien: S R φ 1 [S ] R. Hvis 1 er unity i R, så er φ(1) unity i R. La φ : R R være en ringhomomorfi. Underringen φ 1 [0 ] = {r R φ(r) = 0 } er kernelen av φ. La φ : R R igjen være en ringhomomorfi, og la H = ker(φ). La a R. Da er φ 1 [φ(a)] = a+h = H+a, hvor a + h = H + a er restklassen som inneholder a av den kommutative additive gruppen < H, + >. Korollar φ er injektiv hviss ker(φ) = {0}. φ : R R er en ringhomomorfi med kernel H. Den additive restklassen av H laget av ringen R/H. summen av to restklasser er definert ved (a + H) + (b + H) = (a + b) + H og multiplikasjonen av to restklasser er definert ved (a + H)(b + H) = (ab) + H. I tilleg er kartet µ : R/H φ[r] definert ved µ(a + H) = φ(a) en isomorfi. La H være en underring av ringen R. Multiplikasjon av additive restklasser av H er veldefinert ved ligningen (a + H)(b + H) = ab + H hviss ah H og hb H for alle a, b R og h H. En additiv undergruppe N av en ring R som tilfredsstiller egenskapene: an N og Nb N a, b R er et ideal. La N være et ideal av en ring R. Da vil de additive restklassene av N lage en ring R/N med de binære operasjonene definert ved (a + N) + (b + N) = (a + b) + N og (a + N)(b + N) = ab + N. Ringen R/N i det forrgie korollaret er faktorringen (eller kvotientringen) av R ved N. La N være et ideal av en ring R. Da er γ : R R/N gitt ved γ(x) = x+n en ringhomomorfi med kernel N Det fundamentale homomorfiteoremet: La φ : R R være en ringhomomorfi med kernel N. Da er φ[r] en ring og kartet µ : R/N φ[r] gitt ved µ(x + N) = φ(x) en isomorfi. Hvis γ : R R/N er homomorfien fitt ved γ(x) = x + N, så vil vi for alle x R ha φ(x) = µγ(x). Seksjon 27 - Primiske og maksimale ideal Hvis R er en ring med unity, og N er et ideal av R inneholdene unity, så er N = R. Et felt inneholder ingen skikkelige ikke-trivielle ideal. Et maksimalt ideal av en ring R er et ideal M forskjellige fra R s.a. det ikke er noen skikkelige ideal N av R som skikkelig inneholder M. et felt. La R være en kommutativ ring med unity. Da er M et maksimalt ideal av R hviss R/M er 12
13 En kommutativ ring med enhet er et felt hviss det har ingen skikkelige ikke-trivielle ideal. Et ideal N R i en kommutativ ring R er et primisk ideal hvis ab N impliserer at enten a N eller b N for a, b R. La R være en kommutativ ring med unity, og la N R være et ideal i R. Da er R/N et integraldomene hviss N et et primisk ideal i R. Ethvert maksimalt ideal i den kommutative ringen R med unity er et primisk ideal. For en kommutativ ring R med unity. 1. Et ideal M av R er maksimalt hviss R/M er et felt. 2. Et ideal N av R er primisk hviss R/N er et integraldomene. 3. Ethvert maksimalt ideal av R er et primisk ideal. Hvis R er en ring med unity 1, så er kartet φ : Z R gitt ved φ(n) = n 1 for n Z en homomorfi av Z inn i R. Hvis R er en ring med unity, og karakteristikk n > 1, Så inneholder R en underring isomorf med Z n. Hvis R har karakteristikk 0, så har R en underring isomorf med Z. Et felt F er enten av primisk karakteristikk p og inneholder et underfelt isomorft med Z p, eller av karakteristikk 0 og inneholdene en underring R isomorf med Q. Feltene Z p og Q er primiske felt. Hvis R er en kommutativ ring med unity og a R, så er idealet {ra r R} av alle multipler av a det prinsipielle ideal generert av a og betegnes < a >. Et ideal N av R er et prinsipielt ideal hvis N =< a > for en a R. Hvis F er et felt, så er hvert ideal i F [x] prinsipielt. Et ideal < p(x) > 0 av F [x] er maksimalt hviss p(x) er irredusibelt over F. La p(x) være et irredusibelt polynom i F [x]. Hvis p(x) deler r(x)s(x) for r(x), s(x) F [x], da vil p(x) dele enten r(x) eller s(x). Del VI - Ekstensjonsfelt Seksjon 30 - Vektorrom La F være et felt. Et vektorrom over F (eller F-vektorrom) består av en abelsk gruppe V under addisjon sammen med en operasjon av skalarmultiplikasjon av alle elt. av V med hvert elt F til venstre, s.a. for alle a, b F o α, β V holder følgende. 13
14 V 1 aα V. V 2 a(bα) = (ab)α. V 3 (a + b)α = (aα) + (bα). V 4 a(α + β) = (aα) + (aβ) V 5 1α = α. Hvis V er et vektorrom over F, da er 0α = 0, a0 = 0 og ( a)α = a( α) = (aα) for alle a F og αinv. La V være et vektorrom over F. Vektorene i en undermengde S = {α i i I} av V spenner (eller genererer) V hvis for hver β V : β = a 1 α i1 + a 2 α i2 + + a n α in for noen a j F og α ij S, j = 1,..., n. En vektor n j=1 a j α ij er en lineær kombinasjon av α ij. Et vektorrom V over et felt F er endeligdimensjonalt hvis det finnes en endelig undermengde av V som spenner V. Vektorene i undermengden S = {α i i I} av et vektorrom V over et felt F er lineært uavhengige over F hvis, det for to forskjellige vektorer α ij S, koeffisienter a j F og n Z +, vi har n j=1 a j α ij = 0 i V bare hvis a j = 0 for j = 1,..., n. Hvis vektorene ikke er lineært uavhengige over F så er de lineært avhengige over F. Hvis V er et F -vektorrom, lager vektorene i en undermengde B = {β i i I} av V en basis for V over F hvis de spenner V og er lineært uavhengige. Lemma: La V være et F -vektorrom, og la α V. Hvis α er en lineær kombinasjon av vektorene β i V for i = 1,..., m og hver β i er en lineær kombinasjon av vektorer γ j V for j = 1,... n, så er α en lineær kombinasjon av γ j -ene. I et endeligdimensjonalt vektorrom, så vil enhver mengde av vektorer som spenner rommer inneholde en undermengde som er en basis. Et endeligdimensjonalt vektorrom har en endelig basis. La S = {α 1,..., α r } være en endelig mengde av lineært uavhengige vektorer i en endeligdimensjonalt F -vektorrom V. Da kan S bli forstørret til en basis for V over F. Videre, hvis B = {β 1,..., β n } er en basis for V over F, så er r n. elementer. Hvilke som helst to basiser for et endeligdimensjonalt F -vektorrom V har det samme antall Hvis V er et endeligdimensjonalt vektorfelt, så er antallet elementer i en basis dimensjonen til V over F La E være et ekstensjonsfelt av F, og la α E være algebraisk over F. Hvis deg(α, F ) = n, så er F (α) et n-dimensjonalt vektorrom over F med basis {1, α,..., α n 1 } Videre vil hvert elt β av F (α) være algebraisk over F, og deg(β, F ) deg(α, F ) 14
15 Seksjon 33 - Endelige felt q n elt. La E være en endelig ekstensjon av grad n over et endelig felt F. Hvis F har q elt, så har E Hvis E er et endelig felt av karakteristikk p, så inneholder R eksakt p n elementer for et positivt heltall n. La E være et felt av p n elt. innehold i en algebraisk tillukning Z p av Z p. Elementene av R er presis nullene i Z p av polynomet x pn x i Z p [x]. Et element α av et felt er en n-te rot av unity hvis α n = 1. Det er en primitiv n-te rot av unity hvis α n = 1 og α m 1 for 0 < m < n. Den multiplikative gruppa < F, > av ikke-null elementer av et endelig felt F er syklisk. En endelig ekstensjon E av et endelig felt F er en simpel ekstensjon av F. Lemma: Hvis F er et felt av primisk karakteristikk p med algebraisk lukning n, så har (x pn x) p n unike nuller i F. Lemma: Hvis F er et felt av primisk karakteristikk p, så er (α + β) pn = α pn + β pn for alle α, β F og alle positive heltall n. Lemma: Et endelig felt GF(p n ) av p n elementer eksisterer for hver orden av primtallet p n. Hvis F er et endelig felt, så vil det for hvert positivt heltall n finnes et irredusibelt polynom i F [x] av grad n. La p være et primtall og la n Z +. Hvis E og E er felt av orden p n så er E E. Del VII - Avansert gruppeteori Seksjon 36 - Sylow teoremene r X = X G + Gx i. i=s+1 La G være en gruppe av orden p n og la X være en endelig G-mengde. Da er X X G mod p. La p være et primtall. En gruppe G er en p-gruppe hvis hvert elt i G har en orden en grad av primtallet p. En undergruppe av en gruppe G er en p-undergruppe av av G hvis undergruppen er en p-gruppe alene. 15
16 Cauchys teorem: La p være et primtall. La G være en endelig gruppe og la p dele G. Da har G et elt. av orden p og derfor også en undergruppe av orden p. La G være en endelig gruppe. Da er G en p-gruppe hviss G er en orden av p. La G være en gruppe og la I være samlingen av alle undergruppene til G. Vi gjør I om til en G-mengde ved å la G virke på I ved konjugering. Dvs, hvis H I så er H G og g G, så vil g virke på H gi den konjugerte undergruppa ghg 1. Det observeres at G H = {g G ghg 1 = H} er en undergruppe av G som gjør H invariant under konjugering, G H er den største undergruppa av G som har H som en normal undergruppe. Undergruppa G H kalles normalisereren av H i G og betegnes N[H]. lemma: La H være en p-undergruppe av en endelig gruppe G. Da gjelder: (N[H] : H) (G : H) mod p. La H være en p-undergruppe av en endelig gruppe G. Hvis p deler (G : H), så er N[H] H. Første Sylowteorem: m. Da gjelder: La G være en endelig gruppe og la G = p n m hvor n 1 og hvor p ikke deler 1. G inneholder en undergruppe av orden p i for hver i hvor 1 i n. 2. Enhver undergruppe H av G av orden p i er en normal undergruppe av en undergruppe av orden p i+1 for 1 i < n. En Sylow p-undergruppe P av en gruppe G er en maksimal p-undergruppe av G, dvs, en p-undergruppe ikke inneholdt i noen større p-undergruppe. Andre Sylowteorem: La P 1 og P 2 være to Sylow p-undergrupper av en endelig gruppe G. Da er P 1 og P 2 konjugerte undergruppe av G. Tredje Sylowteorem: Hvis G er en endelig gruppe og p deler G, så er antallet Sylow p-undergrupper kongruent med 1 modulo p og deler G. Seksjon 37 - Anvendelser av Sylowteori Enhver gruppe av orden en orden av et primtall (dvs, enhver endelig p-gruppe) er løsbar. La Z(G) = {x G xg = gx g G} = c (Z(G) er senteret av G), og n i = Gx i da er: G = c + n c n r Denne ligningen kalles klasseligningen for G. Enhver orbital i G under konjugering med G er en konjugertklasse i G. Senteret av en endelig ikke-triviell p-gruppe G er ikke-trivielt. La G være en gruppe og H, K G. H V kalles sammensetningen av H og K og betegner overlappingen av alle undergrupper av G som inneholder HK = {hk h H, k K}. H V er med andre ord den minste undergruppa av G som inneholder HK. 16
17 Lemma: La G være en gruppe som inneholder normale undergrupper H og K slik at H K = e og H K = G. Da er G isomorf med H K. For et primtall p er enhver gruppe G av orden p 2 abelsk. Hvis p og q er forskjellige primtall med p < q, så har enhver gruppe G av orden pq en singel undergruppe av orden q og denne undergruppen er normal i G. Derfor er G ikke simpel. Hvis q ikke er kongruent med 1 modulo p, så er G abelsk og syklisk. Lemma: Hvis H og K er endelige undergrupper av en gruppe G, så gjelder: HK = ( H )( K ) H. K Vegard Hagen Trondheim 27. mai
Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori. Ruben Spaans
 Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori Ruben Spaans August 19, 2007 2 Part I Leksikon 3 Chapter 1 Alfabetisk oppslagsverk, for alle, kvantifikator. Brukes i forbindelse med utsagn,
Et noget ukomplett oppslagsverk for TMA4150 Algebra og tallteori Ruben Spaans August 19, 2007 2 Part I Leksikon 3 Chapter 1 Alfabetisk oppslagsverk, for alle, kvantifikator. Brukes i forbindelse med utsagn,
Forslag til løsninger, TMA4150 Algebra, 29. mai 2018 Side 1 av 5
 Forslag til løsninger, TMA4150 Algebra, 29. mai 2018 Side 1 av 5 Oppgave 1 isomorfi, nemlig 24 = 2 3 3, så det finnes tre abelske grupper av orden 24 opp til Z 2 Z 2 Z 2 Z 3 ; Z 2 Z 4 Z 3 ; Z 8 Z 3. O
Forslag til løsninger, TMA4150 Algebra, 29. mai 2018 Side 1 av 5 Oppgave 1 isomorfi, nemlig 24 = 2 3 3, så det finnes tre abelske grupper av orden 24 opp til Z 2 Z 2 Z 2 Z 3 ; Z 2 Z 4 Z 3 ; Z 8 Z 3. O
Grublegruppe 19. sept. 2011: Algebra I
 Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Oblig 1 - MAT2400. Fredrik Meyer
 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Påstand 1 a). Z 5 har fire generatorer og AutZ 5 ) Z 4 Bevis. Hvert ikke-null-element i Z 5 genererer en undergruppe. Siden 5 er et primtall, må denne undergruppen
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Påstand 1 a). Z 5 har fire generatorer og AutZ 5 ) Z 4 Bevis. Hvert ikke-null-element i Z 5 genererer en undergruppe. Siden 5 er et primtall, må denne undergruppen
MAUMAT644 ALGEBRA vår 2016 Andre samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Andre samling Runar Ile 1 Ringer og ringhomomorfier 1.1 Hva er en ring? Avsnitt 18: Ringer og kropper Stoff: Ring, direkte produkt av ringer, ringhomomorfi og ringisomorfi, kjernen
MAUMAT644 ALGEBRA vår 2016 Andre samling Runar Ile 1 Ringer og ringhomomorfier 1.1 Hva er en ring? Avsnitt 18: Ringer og kropper Stoff: Ring, direkte produkt av ringer, ringhomomorfi og ringisomorfi, kjernen
Eksamensoppgave i TMA4150 Algebra
 Institutt for matematiske fag Eksamensoppgave i TMA4150 Algebra Faglig kontakt under eksamen: Torkil Utvik Stai Tlf: 47638459 Eksamensdato: 29. mai 2018 Eksamenstid (fra til): 15:00 19:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4150 Algebra Faglig kontakt under eksamen: Torkil Utvik Stai Tlf: 47638459 Eksamensdato: 29. mai 2018 Eksamenstid (fra til): 15:00 19:00 Hjelpemiddelkode/Tillatte
Utvidet løsningsforslag til Eksamen vår 2010
 Utvidet løsningsforslag til Eksamen vår 2010 Morten Brun og Runar Ile 1 Dette er et utvidet løsningsforslag hvor det er gitt alternativer løsninger på flere av punktene og noen tips og kommentarer. På
Utvidet løsningsforslag til Eksamen vår 2010 Morten Brun og Runar Ile 1 Dette er et utvidet løsningsforslag hvor det er gitt alternativer løsninger på flere av punktene og noen tips og kommentarer. På
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
UNIVERSITETET I BERGEN
 BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT220/MAUMAT44 - Algebra Fredag. juni 204, kl. 09-4 Tillatte hjelpemidler: Kalkulator i samsvar med fakultetets
BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT220/MAUMAT44 - Algebra Fredag. juni 204, kl. 09-4 Tillatte hjelpemidler: Kalkulator i samsvar med fakultetets
Eksamen i MNFMA205/SIF5021, 19. mai 1999-Løsningsforslag a b Oppgave 2. (a) Vi skal vise at H = 0 a b under matrisemultiplikasjon. Vi har at det.
 Eksamen i MNFMA205/SIF5021 19. mai 1999-Løsningsforslag { } Oppgave 2. a Vi skal vise at H 0 a C er en gruppe under matrisemultiplikasjon. Vi har at det aā + a 2 + 2 > 0 da enten a 0 eller 0. Dette fører
Eksamen i MNFMA205/SIF5021 19. mai 1999-Løsningsforslag { } Oppgave 2. a Vi skal vise at H 0 a C er en gruppe under matrisemultiplikasjon. Vi har at det aā + a 2 + 2 > 0 da enten a 0 eller 0. Dette fører
Algebraiske strukturer
 MAT1140, H-16 Algebraiske strukturer Vi kan legge samme og multiplisere tall, funksjoner og matriser, og vi kan bruke snitt og union til å danne nye mengder. Mange av disse operasjonene følger de samme
MAT1140, H-16 Algebraiske strukturer Vi kan legge samme og multiplisere tall, funksjoner og matriser, og vi kan bruke snitt og union til å danne nye mengder. Mange av disse operasjonene følger de samme
MA2201/TMA4150 Vår 2018
 MA2201/TMA4150 Vår 2018 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Seksjon 14 34 La G = n < og la H G være eneste undergruppe av G av orden m.
MA2201/TMA4150 Vår 2018 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Løsningsforslag Øving 6 Seksjon 14 34 La G = n < og la H G være eneste undergruppe av G av orden m.
7 Ordnede ringer, hele tall, induksjon
 Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 2 Faglig kontakt under eksamen: Dagfinn F. Vatne 901 38 621 EKSAMEN I ALGEBRA OG TALLTEORI (TMA4150) Bokmål Tillatte
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 2 Faglig kontakt under eksamen: Dagfinn F. Vatne 901 38 621 EKSAMEN I ALGEBRA OG TALLTEORI (TMA4150) Bokmål Tillatte
x A e x = x e = x. (2)
 Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
En rekke av definisjoner i algebra
 En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
En rekke av definisjoner i algebra Martin Strand, martin.strand@math.ntnu.no 11. november 2010 Definisjonene som er gitt her, kommer i MA2201 Algebra og MA3201 Ringer og moduler. Forhåpentligvis blir det
OPPGAVER FOR FORUM
 OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:
![Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene: Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:](/thumbs/64/52216522.jpg) HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. 8. november 2005 c Vladimir Oleshchuk 35. Teorem 11 (Z n, ) er en endelig abelsk gruppe.
 Endelige grupper Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. En gruppe er en mengde S sammen med en binær operasjon definert på S, betegnes (S, ), med følgende egenskaper: 1. a, b S, a b S 2. det
Endelige grupper Teorem 10 (Z n, + n ) er en endelig abelsk gruppe. En gruppe er en mengde S sammen med en binær operasjon definert på S, betegnes (S, ), med følgende egenskaper: 1. a, b S, a b S 2. det
MAUMAT644 ALGEBRA vår 2016 Fjerde samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Fjerde samling Runar Ile 1 Kroppsutvidelser og geometriske konstruksjoner 1.1 Hva har kroppsutvidelser med geometriproblemer å gjøre? Avsnitt 29: Kroppsutvidelser Stoff: Utvidelseskropper
MAUMAT644 ALGEBRA vår 2016 Fjerde samling Runar Ile 1 Kroppsutvidelser og geometriske konstruksjoner 1.1 Hva har kroppsutvidelser med geometriproblemer å gjøre? Avsnitt 29: Kroppsutvidelser Stoff: Utvidelseskropper
Direkte produkter. (a, b)(a 0,b 0 )=(ab, a 0 b 0 ).
 Direkte produkter Vi kjenner det kartesiske produktet av to mengder Y.Detbeståravallepar(x, y) av elementer x 2 og y 2 Y.OrdetkartesiskerdannetavegennavnetRenéDécartes, en fransk filosof og matematiker
Direkte produkter Vi kjenner det kartesiske produktet av to mengder Y.Detbeståravallepar(x, y) av elementer x 2 og y 2 Y.OrdetkartesiskerdannetavegennavnetRenéDécartes, en fransk filosof og matematiker
Et ekstremt ufullstendig oppslagsverk for TMA4185 Kodeteori
 Et ekstremt ufullstendig oppslagsverk for TMA4185 Kodeteori Ruben Spaans May 21, 2008 1 Pensum Pensumliste: ˆ Kapittel 1: Hele, unntatt 110 ˆ Kapittel 2: 21, 24 (singleton upper bound og MDS), 27 (Gilbert
Et ekstremt ufullstendig oppslagsverk for TMA4185 Kodeteori Ruben Spaans May 21, 2008 1 Pensum Pensumliste: ˆ Kapittel 1: Hele, unntatt 110 ˆ Kapittel 2: 21, 24 (singleton upper bound og MDS), 27 (Gilbert
Euklids algoritmen. p t 2. 2 p t n og b = p s 1. p min(t 2,s 2 )
 For å finne største felles divisor (gcd) kan vi begrense oss til N, sidenfor alle a, b Z, harvi gcd(a, b) =gcd( a, b ). I prinsippet, dersom vi vet at a = p t 1 kan vi se at 1 p t 2 2 p t n og b = p s
For å finne største felles divisor (gcd) kan vi begrense oss til N, sidenfor alle a, b Z, harvi gcd(a, b) =gcd( a, b ). I prinsippet, dersom vi vet at a = p t 1 kan vi se at 1 p t 2 2 p t n og b = p s
MAT Grublegruppen Notat 10
 MAT1100 - Grublegruppen Notat 10 Jørgen O. Lye Ringer Vi fortsetter i et lynkurs i algebraiske dyr. Først ut er ringer. En ring A (også kalt R) er en abelsk gruppe med addisjon + som operasjon. I tillegg
MAT1100 - Grublegruppen Notat 10 Jørgen O. Lye Ringer Vi fortsetter i et lynkurs i algebraiske dyr. Først ut er ringer. En ring A (også kalt R) er en abelsk gruppe med addisjon + som operasjon. I tillegg
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat med oppgaver for MAT1140
 Notat med oppgaver for MAT1140 1 Injeksjon, surjeksjon Oppgave 1.1. La f : A B være en avbildning. Vis at da er f injektiv hvis og bare hvis følgende holder: for hver mengde C og for hver g, h : C A hvis
Notat med oppgaver for MAT1140 1 Injeksjon, surjeksjon Oppgave 1.1. La f : A B være en avbildning. Vis at da er f injektiv hvis og bare hvis følgende holder: for hver mengde C og for hver g, h : C A hvis
Masteroppgave Galois-teori
 Masteroppgave Galois-teori Anders Fjogstad Universitetet i Stavanger 2011 Anders Fjogstad, Universitetet i Stavanger, 2011, Side 1 Sammendrag Problemstillingen for denne oppgaven er å sette seg inn i Galoisteorien
Masteroppgave Galois-teori Anders Fjogstad Universitetet i Stavanger 2011 Anders Fjogstad, Universitetet i Stavanger, 2011, Side 1 Sammendrag Problemstillingen for denne oppgaven er å sette seg inn i Galoisteorien
TALL. 1 De naturlige tallene. H. Fausk
 TALL H. Fausk 1 De naturlige tallene De naturlige tallene er 1, 2, 3, 4, 5,... (og så videre). Disse tallene brukes til å telle med, og de kalles også telletallene. Listen med naturlige tall stopper ikke
TALL H. Fausk 1 De naturlige tallene De naturlige tallene er 1, 2, 3, 4, 5,... (og så videre). Disse tallene brukes til å telle med, og de kalles også telletallene. Listen med naturlige tall stopper ikke
HJEMMEOPPGAVER (utgave av ):
 HJEMMEOPPGAVER (utgave av 20-5-2003): Oppgave 16 til 26 mai: La K være kroppen med 2 elementer og la A = K(t)[x]/(x 2 +t) være residuringen av polynomringen i den varibale x over den rasjonale funksjonsringen
HJEMMEOPPGAVER (utgave av 20-5-2003): Oppgave 16 til 26 mai: La K være kroppen med 2 elementer og la A = K(t)[x]/(x 2 +t) være residuringen av polynomringen i den varibale x over den rasjonale funksjonsringen
Obligatorisk oppgave MAT2200 VÅREN 2011
 Obligatorisk oppgave MAT2200 VÅREN 2011 Alle punkter teller likt. Det kreves at 50% er riktig (som betyr 10 av 19 punkter) for at oppgaven skal godkjennes. Den skal leveres i egen innleveringsboks i 7.
Obligatorisk oppgave MAT2200 VÅREN 2011 Alle punkter teller likt. Det kreves at 50% er riktig (som betyr 10 av 19 punkter) for at oppgaven skal godkjennes. Den skal leveres i egen innleveringsboks i 7.
(a) R n defineres som mengden av kolonnevektorer. a 1 a 2. a n. (b) R n defineres som mengden av radvektorer
 5 Vektorrom Et vektorrom er en mengde V med tre algebraiske operasjoner (addisjon, negasjon og skalærmultiplikasjon) som tilfredsstiller de 10 betingelsene fra Def. 4.1.1. Jeg vil ikke gi en eksamensoppgave
5 Vektorrom Et vektorrom er en mengde V med tre algebraiske operasjoner (addisjon, negasjon og skalærmultiplikasjon) som tilfredsstiller de 10 betingelsene fra Def. 4.1.1. Jeg vil ikke gi en eksamensoppgave
Lineærtransformasjoner
 Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Dette er altså et slags produkt av undermengder. Man sjekker lett at dette produktet har en assosiativitetsegenskap 1,nemlig:
 Kvotientgrupper En helt sentral konstruksjon i gruppeteorien er dannelsen av kvotienten av en gruppe G med en normal undergruppe. I et spesialtilfelle har vi allerede gjort denne konstruksjonen, nemlig
Kvotientgrupper En helt sentral konstruksjon i gruppeteorien er dannelsen av kvotienten av en gruppe G med en normal undergruppe. I et spesialtilfelle har vi allerede gjort denne konstruksjonen, nemlig
9 Lineærtransformasjoner TMA4110 høsten 2018
 9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
9 Lineærtransformasjoner MA4 høsten 8 I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen)
 Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen) Dette er smakebiter på ting som dukker opp i videregående emner (MAT2400 og MAT2200). Del I og II kan gjøres uavhengig
Julenøtter til gruppe 5&7! (IKKE eksamensrelevant, bare for gøy gjerne i romjulen) Dette er smakebiter på ting som dukker opp i videregående emner (MAT2400 og MAT2200). Del I og II kan gjøres uavhengig
MAT Grublegruppen Notat 9
 MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
MAT1100 - Grublegruppen Notat 9 Jørgen O. Lye Gruppeteori Oppvarmingseksempel La oss som vanlig ta en historisk vinkling. En klassisk måte grupper (som jeg straks skal denere) oppstod er gjennom å lete
Dette brukte vi f.eks. til å bevise binomialteoremet. n i. (a + b) n = a i b n i. i=0
 Prinsippet om matematisk induksjon: anta du har en påstand som er avhengig av et positivt heltall n. Om du kan vise to ting, nemlig at påstanden er sann for n = 1 og at om påstanden er sann for n = k,
Prinsippet om matematisk induksjon: anta du har en påstand som er avhengig av et positivt heltall n. Om du kan vise to ting, nemlig at påstanden er sann for n = 1 og at om påstanden er sann for n = k,
Emnerapport for MAUMAT vår og 2015 vår av Runar Ile 11/ Navn på emneansvarlig: Runar Ile (begge årene) Hvilke styringsorgan har
 Emnerapport for MAUMAT644 2014 vår og 2015 vår av Runar Ile 11/9 2015 Navn på emneansvarlig: Runar Ile (begge årene) Hvilke styringsorgan har behandlet evalueringen/når: Referanse til eventuelle saksforelegg
Emnerapport for MAUMAT644 2014 vår og 2015 vår av Runar Ile 11/9 2015 Navn på emneansvarlig: Runar Ile (begge årene) Hvilke styringsorgan har behandlet evalueringen/når: Referanse til eventuelle saksforelegg
Løsningsforslag øving 7
 Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
Oppgaver i kommutativ algebra
 Oppgaver i kommutativ algebra Fredrik Meyer 1 Moduler Oppgave (1). Vis at om m, n er koprimære, så er (Z/mZ) Z (Z/nZ) = 0. Proof. Siden m og n er koprimære, finnes det a, b Z slik at an + bm = 1. La x
Oppgaver i kommutativ algebra Fredrik Meyer 1 Moduler Oppgave (1). Vis at om m, n er koprimære, så er (Z/mZ) Z (Z/nZ) = 0. Proof. Siden m og n er koprimære, finnes det a, b Z slik at an + bm = 1. La x
Løsningsforslag Øving 5 TMA4140 Diskret matematikk Høsten 2010
 Løsningsforslag Øving 5 TMA4140 Diskret matematikk Høsten 2010 1. a) Ingen andre tall enn en deler en, og en deler fire, så (1, 4) = 1 b) 1 c) 7 er et primtall og 7 er ikke en faktor i 41, så største felles
Løsningsforslag Øving 5 TMA4140 Diskret matematikk Høsten 2010 1. a) Ingen andre tall enn en deler en, og en deler fire, så (1, 4) = 1 b) 1 c) 7 er et primtall og 7 er ikke en faktor i 41, så største felles
Lineær algebra. 0.1 Vektorrom
 Lineær algebra Siden dette temaet er alt for stort til å kunne gjennomgås på en halvtime, med alle de teoremene og denisjonene som skal til, har jeg laget dette notatet. Det bygger hovedsakelig på notatene
Lineær algebra Siden dette temaet er alt for stort til å kunne gjennomgås på en halvtime, med alle de teoremene og denisjonene som skal til, har jeg laget dette notatet. Det bygger hovedsakelig på notatene
MA1301 Tallteori Høsten 2014 Oversikt over pensumet
 MA1301 Tallteori Høsten 2014 Oversikt over pensumet Richard Williamson 3. desember 2014 Innhold Pensumet 2 Generelle råd 2 Hvordan bør jeg forberede meg?.......................... 2 Hva slags oppgaver
MA1301 Tallteori Høsten 2014 Oversikt over pensumet Richard Williamson 3. desember 2014 Innhold Pensumet 2 Generelle råd 2 Hvordan bør jeg forberede meg?.......................... 2 Hva slags oppgaver
Geometri på ikke-kommutative algebraer
 Geometri på ikke-kommutative algebraer Ski og matematikk 2011 Rondablikk Arne B. Sletsjøe Universitetet i Oslo January 4, 2012 Algebraiske varieteter k = k (f.eks. C), S = k[x 1,..., x n ] Affint algebraisk
Geometri på ikke-kommutative algebraer Ski og matematikk 2011 Rondablikk Arne B. Sletsjøe Universitetet i Oslo January 4, 2012 Algebraiske varieteter k = k (f.eks. C), S = k[x 1,..., x n ] Affint algebraisk
Øvingsforelesning 5. Binær-, oktal-, desimal- og heksidesimaletall, litt mer tallteori og kombinatorikk. TMA4140 Diskret Matematikk
 Binær-, oktal-, desimal- og heksidesimaletall, litt mer tallteori og kombinatorikk Øvingsforelesning 5 TMA4140 Diskret Matematikk 1. og 3. oktober 2018 Dagen i dag Repetere binære, oktale osv. heltallsrepresentasjoner,
Binær-, oktal-, desimal- og heksidesimaletall, litt mer tallteori og kombinatorikk Øvingsforelesning 5 TMA4140 Diskret Matematikk 1. og 3. oktober 2018 Dagen i dag Repetere binære, oktale osv. heltallsrepresentasjoner,
Permutasjoner og symmetriske grupper
 Permutasjoner og symmetriske grupper Verbet permutere betyr å bytte om, og ombyttinger, eller altså permutasjoner, er noe vi kjenner fra dagliglivet. I matematikk er de også flittig i bruk, de fleste har
Permutasjoner og symmetriske grupper Verbet permutere betyr å bytte om, og ombyttinger, eller altså permutasjoner, er noe vi kjenner fra dagliglivet. I matematikk er de også flittig i bruk, de fleste har
Øvingsforelesning 4. Modulo hva er nå det for no? TMA4140 Diskret Matematikk. 24. og 26. september 2018
 Modulo hva er nå det for no? Øvingsforelesning 4 TMA4140 Diskret Matematikk 24. og 26. september 2018 Dagen i dag Repetere den euklidske algoritmen, kongruensregning og annet underveis H11.3a: Inverser
Modulo hva er nå det for no? Øvingsforelesning 4 TMA4140 Diskret Matematikk 24. og 26. september 2018 Dagen i dag Repetere den euklidske algoritmen, kongruensregning og annet underveis H11.3a: Inverser
Introduksjon i tallteotri med anvendelser
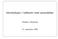 Introduksjon i tallteotri med anvendelser Vladimir Oleshchuk 15. september 2005 Delbarhet og divisorer Delbarhet og divisorer Vi skal betrakte tall fra Z = {,..., 2, 1, 0, 1, 2,...} og N = {0, 1,...} og
Introduksjon i tallteotri med anvendelser Vladimir Oleshchuk 15. september 2005 Delbarhet og divisorer Delbarhet og divisorer Vi skal betrakte tall fra Z = {,..., 2, 1, 0, 1, 2,...} og N = {0, 1,...} og
12 Lineære transformasjoner
 2 Lineære transformasjoner 2 Funksjoner Definisjon 2 En funksjon ( a function) f : A B er en regel, som tilordner en entydig bestemt verdi f (a) B til ethvert element a A Mengden A kalles domenet til f
2 Lineære transformasjoner 2 Funksjoner Definisjon 2 En funksjon ( a function) f : A B er en regel, som tilordner en entydig bestemt verdi f (a) B til ethvert element a A Mengden A kalles domenet til f
KLASSISK TALLTEORI. Erik Alfsen og Tom Lindstrøm. Matematisk Institutt, UiO, 1994
 KLASSISK TALLTEORI av Erik Alfsen og Tom Lindstrøm Matematisk Institutt, UiO, 1994 Tallene vi bruker når vi teller 1. Induksjon 1,, 3, 4, 5, kalles naturlige tall. Mengden av alle naturlige tall kalles
KLASSISK TALLTEORI av Erik Alfsen og Tom Lindstrøm Matematisk Institutt, UiO, 1994 Tallene vi bruker når vi teller 1. Induksjon 1,, 3, 4, 5, kalles naturlige tall. Mengden av alle naturlige tall kalles
STØRRELSER OG TALL Om størrelser skriver Euklid i Bok 5: 1. En størrelse er en del av en annen størrelse, den mindre av den større når den måler (går
 STØRRELSER OG TALL Om størrelser skriver Euklid i Bok 5:. En størrelse er en del av en annen størrelse, den mindre av den større når den måler (går opp i) den større.. Den større er et multiplum av den
STØRRELSER OG TALL Om størrelser skriver Euklid i Bok 5:. En størrelse er en del av en annen størrelse, den mindre av den større når den måler (går opp i) den større.. Den større er et multiplum av den
Oppgaver MAT2500. Fredrik Meyer. 29. august 2014
 Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
Oppgaver MAT500 Fredrik Meyer 9. august 04 Oppgave. Bruk cosinus-setningen til å se at definisjonen av vinkel i planet blir riktig. Løsning. Dette er en litt rar oppgave. Husk at cosinus-setningen sier
En gruppeteoretisk analyse av vri- og flyttespill. Alexander Lorenzo Masteroppgave, våren 2017
 En gruppeteoretisk analyse av vri- og flyttespill Alexander Lorenzo Masteroppgave, våren 2017 Denne masteroppgaven er levert inn som en del av programspesialiseringen Matematikk under Lektorprogrammet
En gruppeteoretisk analyse av vri- og flyttespill Alexander Lorenzo Masteroppgave, våren 2017 Denne masteroppgaven er levert inn som en del av programspesialiseringen Matematikk under Lektorprogrammet
8 Vektorrom TMA4110 høsten 2018
 8 Vektorrom TMA4 høsten 8 I de foregående kapitlene har vi tatt en lang vandring gjennom den lineære algebraens jungel. Nå skal vi gå opp på en fjelltopp og skue ut over landskapet vi har vandret gjennom.
8 Vektorrom TMA4 høsten 8 I de foregående kapitlene har vi tatt en lang vandring gjennom den lineære algebraens jungel. Nå skal vi gå opp på en fjelltopp og skue ut over landskapet vi har vandret gjennom.
Gauss-Jordan eliminasjon; redusert echelonform. Forelesning, TMA4110 Fredag 18/9. Reduserte echelonmatriser. Reduserte echelonmatriser (forts.
 Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
Gauss-Jordan eliminasjon; redusert echelonform Forelesning, TMA4110 Fredag 18/9 Martin Wanvik, IMF MartinWanvik@mathntnuno En matrise vil normalt være radekvivalent med flere echelonmatriser; med andre
MA1301 Tallteori Høsten 2014
 MA1301 Tallteori Høsten 014 Richard Williamson 1. august 015 Innhold Forord 7 1 Induksjon og rekursjon 9 1.1 Naturlige tall og heltall............................ 9 1. Bevis.......................................
MA1301 Tallteori Høsten 014 Richard Williamson 1. august 015 Innhold Forord 7 1 Induksjon og rekursjon 9 1.1 Naturlige tall og heltall............................ 9 1. Bevis.......................................
Permutasjoner og symmetriske grupper
 4. Del Permutasjoner og symmetriske grupper Verbet permutere kommer av det latinske verbet permutare og betyr å bytte om, og ombyttinger,elleraltsåpermutasjoner,ernoevikjennerfradagliglivet.imatematikker
4. Del Permutasjoner og symmetriske grupper Verbet permutere kommer av det latinske verbet permutare og betyr å bytte om, og ombyttinger,elleraltsåpermutasjoner,ernoevikjennerfradagliglivet.imatematikker
Vektorrom. Kapittel 7. Hva kan vi gjøre med vektorer?
 Kapittel 7 Vektorrom Vårt mål i dette kapitlet og det neste er å generalisere og abstrahere ideene vi har jobbet med til nå Især skal vi stille spørsmålet Hva er en vektor? Svaret vi skal gi, vil virke
Kapittel 7 Vektorrom Vårt mål i dette kapitlet og det neste er å generalisere og abstrahere ideene vi har jobbet med til nå Især skal vi stille spørsmålet Hva er en vektor? Svaret vi skal gi, vil virke
MAUMAT644 ALGEBRA vår 2016 Andre samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Andre samling Runar Ile 1 Når er to grupper strukturlike? Avsnitt 13: Homomorfier av grupper Stoff: Gruppehomomorfi (en-til-en og på), gruppeisomorfi, kjernen og bildet til en
MAUMAT644 ALGEBRA vår 2016 Andre samling Runar Ile 1 Når er to grupper strukturlike? Avsnitt 13: Homomorfier av grupper Stoff: Gruppehomomorfi (en-til-en og på), gruppeisomorfi, kjernen og bildet til en
KOMPENDIUM FOR FORKURS I MATEMATIKK FOR MASTERSTUDIET I INFORMASJONSSIKKERHET VED HØGSKOLEN I GJØVIK SOMMEREN 2004.
 KOMPENDIUM FOR FORKURS I MATEMATIKK FOR MASTERSTUDIET I INFORMASJONSSIKKERHET VED HØGSKOLEN I GJØVIK SOMMEREN 2004 av Hans Engenes 18. august 2004 2 Innhold 1 Tallteori 3 1.1 Innledning...............................
KOMPENDIUM FOR FORKURS I MATEMATIKK FOR MASTERSTUDIET I INFORMASJONSSIKKERHET VED HØGSKOLEN I GJØVIK SOMMEREN 2004 av Hans Engenes 18. august 2004 2 Innhold 1 Tallteori 3 1.1 Innledning...............................
QED 1 7. Matematikk for grunnskolelærerutdanningen. Bind 2. Fasit kapittel 1 Tallenes hemmeligheter
 QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 1 Tallenes hemmeligheter Kapittel 1 Oppgave 8. Nei Oppgave 9. Det nnes ikke nødvendigvis et minste element i mengden. Et eksempel
QED 1 7 Matematikk for grunnskolelærerutdanningen Bind 2 Fasit kapittel 1 Tallenes hemmeligheter Kapittel 1 Oppgave 8. Nei Oppgave 9. Det nnes ikke nødvendigvis et minste element i mengden. Et eksempel
Grupper de første egenskaper
 Grupper de første egenskaper Definisjonen av en gruppe Da vi studerte symmetriene til et kvadrat, så vi at det var enkelte karakteristiske trekk ved symmetrier; De kunne settes sammen og de kunne inverteres.
Grupper de første egenskaper Definisjonen av en gruppe Da vi studerte symmetriene til et kvadrat, så vi at det var enkelte karakteristiske trekk ved symmetrier; De kunne settes sammen og de kunne inverteres.
INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]
![INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng] INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]](/thumbs/57/40971904.jpg) INF1080 Logiske metoder for informatikk Digital eksamen Tid: Onsdag 7. desember 2016 kl. 14.30 18.30 (4 timer) Tillatte hjelpemidler: Ingen Eksamen består av to deler som er verdt omtrent like mye. Den
INF1080 Logiske metoder for informatikk Digital eksamen Tid: Onsdag 7. desember 2016 kl. 14.30 18.30 (4 timer) Tillatte hjelpemidler: Ingen Eksamen består av to deler som er verdt omtrent like mye. Den
Syklotome heltall og Kummers bevis for Fermats siste teorem. Paul Mathias Høglend Masteroppgave, våren 2017
 Syklotome heltall og Kummers bevis for Fermats siste teorem Paul Mathias Høglend Masteroppgave, våren 2017 Denne masteroppgaven er levert inn under masterprogrammet Matematikk, studieretning Matematikk,
Syklotome heltall og Kummers bevis for Fermats siste teorem Paul Mathias Høglend Masteroppgave, våren 2017 Denne masteroppgaven er levert inn under masterprogrammet Matematikk, studieretning Matematikk,
4-torsjonspunkter på elliptiske romkurver
 4-torsjonspunkter på elliptiske romkurver Astri Strand Lindbæck Masteroppgave, våren 2015 Innledning I denne oppgaven ønsker vi å undersøke punkter på kurver der det tangerende hyperplanet snitter kurven
4-torsjonspunkter på elliptiske romkurver Astri Strand Lindbæck Masteroppgave, våren 2015 Innledning I denne oppgaven ønsker vi å undersøke punkter på kurver der det tangerende hyperplanet snitter kurven
INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]
![INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng] INF1080 Logiske metoder for informatikk. 1 Små oppgaver [70 poeng] 1.1 Grunnleggende mengdelære [3 poeng] 1.2 Utsagnslogikk [3 poeng]](/thumbs/60/44567099.jpg) INF1080 Logiske metoder for informatikk Digital eksamen (med løsningsforslag) Dette er et utkast til løsningsforslag til eksamen i INF1080, og feil kan forekomme. Hvis du finner noen feil, si ifra til
INF1080 Logiske metoder for informatikk Digital eksamen (med løsningsforslag) Dette er et utkast til løsningsforslag til eksamen i INF1080, og feil kan forekomme. Hvis du finner noen feil, si ifra til
HJEMMEOPPGAVER (utgave av 12-7-2005):
 HJEMMEOPPGAVER (utgave av 12-7-2005: Ogave 1 til 31. januar: La f 1, f 2,... være Fibonacci tallene, det vil si f 1 f 2 1 og f n f n 1 + f n 2 for n 3. Vis: (1 f 1 + f 2 + + f n f n+2 1. (2 f n+1 f n 1
HJEMMEOPPGAVER (utgave av 12-7-2005: Ogave 1 til 31. januar: La f 1, f 2,... være Fibonacci tallene, det vil si f 1 f 2 1 og f n f n 1 + f n 2 for n 3. Vis: (1 f 1 + f 2 + + f n f n+2 1. (2 f n+1 f n 1
Repetisjonsforelesning - INF1080
 Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x).
 Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
MAT 4000 Innføring i klassisk tallteori
 MAT 4000 Innføring i klassisk tallteori Dette heftet i tallteori baserer seg i stor grad på tidligere forelesningsnotater av Karl Egil Aubert, som senere er blitt bearbeidet videre av Erik Alfsen, Tom
MAT 4000 Innføring i klassisk tallteori Dette heftet i tallteori baserer seg i stor grad på tidligere forelesningsnotater av Karl Egil Aubert, som senere er blitt bearbeidet videre av Erik Alfsen, Tom
TMA 4140 Diskret Matematikk, 4. forelesning
 TMA 4140 Diskret Matematikk, 4. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 9, 2011 Haaken Annfelt Moe (NTNU) TMA
TMA 4140 Diskret Matematikk, 4. forelesning Haaken Annfelt Moe Department of Mathematical Sciences Norwegian University of Science and Technology (NTNU) September 9, 2011 Haaken Annfelt Moe (NTNU) TMA
KONTINUASJONSEKSAMEN I TMA4140 LØSNINGSFORSLAG
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 KONTINUASJONSEKSAMEN I TMA440 LØSNINGSFORSLAG Oppgave Sannhetsverditabell for det logiske utsagnet ( (p q) ) ( q r
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 KONTINUASJONSEKSAMEN I TMA440 LØSNINGSFORSLAG Oppgave Sannhetsverditabell for det logiske utsagnet ( (p q) ) ( q r
Eksamen MAT H Løsninger
 Eksamen MAT1140 - H2014 - Løsninger Oppgave 1 Vi setter opp en vanlig sannhetsverditabell. La Φ betegne formelen i oppgaven. Tabellen vil bli som følger: A B C A B A C Φ T T T T T T T T F T T T T F T F
Eksamen MAT1140 - H2014 - Løsninger Oppgave 1 Vi setter opp en vanlig sannhetsverditabell. La Φ betegne formelen i oppgaven. Tabellen vil bli som følger: A B C A B A C Φ T T T T T T T T F T T T T F T F
Oppfriskningskurs i matematikk Dag 3
 Oppfriskningskurs i matematikk Dag 3 Petter Nyland Institutt for matematiske fag Onsdag 8. august 2018 Dagen i dag Tema 4 Polynomer: Faktorisering, røtter, polynomdivisjon, kvadratiske ligninger og rasjonale
Oppfriskningskurs i matematikk Dag 3 Petter Nyland Institutt for matematiske fag Onsdag 8. august 2018 Dagen i dag Tema 4 Polynomer: Faktorisering, røtter, polynomdivisjon, kvadratiske ligninger og rasjonale
Oppgaver MAT2500 høst 2011
 Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
Oppgaver MAT2500 høst 2011 31. oktober 2011 Oppgaver avsnitt 1 Oppgave 1. Bruk cosinussetningen til å se at definisjonen av vinkel i planet blir riktig. Oppgave 2. Vis at d(x, y) = 0 hvis og bare hvis
MAT 1140 Innføring i klassisk tallteori
 MAT1140, H15 MAT 1140 Innføring i klassisk tallteori Dette heftet er basert på forelesningsnotater av Karl Egil Aubert som senere er blitt bearbeidet av Erik Alfsen, Tom Lindstrøm, Arne B. Sletsjøe og
MAT1140, H15 MAT 1140 Innføring i klassisk tallteori Dette heftet er basert på forelesningsnotater av Karl Egil Aubert som senere er blitt bearbeidet av Erik Alfsen, Tom Lindstrøm, Arne B. Sletsjøe og
Notat om Peanos aksiomer for MAT1140
 Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Vi viser denne ekvivalensen ved å vise begge implikasjoner. " "Anta at G virker trofast på X og anta at g, h G er slik at gx = hx for alle
 TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
TMA4150 Algebra Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Seksjon 16 2 Fasit: G 1 = {ρ 0, δ 2 } = G 3 = G P1 = G P3 G S1 = {ρ 0, µ 1 } = G S3 G m1 = {ρ 0, ρ 2, µ 1, µ
= 3 11 = = 6 4 = 1.
 MAT3000/4000 Eksamen V3 Løsningsforslag Oppgave [0 poeng] Sjekk at 3 er en kvadratisk rest i Z/(3) og finn løsningene av likningen x = 3 i Z/(3) (uten å lage en tabell for x ) Du får lov til å bruke at
MAT3000/4000 Eksamen V3 Løsningsforslag Oppgave [0 poeng] Sjekk at 3 er en kvadratisk rest i Z/(3) og finn løsningene av likningen x = 3 i Z/(3) (uten å lage en tabell for x ) Du får lov til å bruke at
KAPITTEL 10. EUKLIDS ALGORITME OG DIOFANTISKE LIGNINGER
 KAPITTEL 10. EUKLIDS ALGORITME OG DIOFANTISKE LIGNINGER Euklids algoritme Euklid s setning 1, divisjonslemmaet, fra Bok 7 Gitt to ulike tall. Det minste trekkes så fra det største så mange ganger dette
KAPITTEL 10. EUKLIDS ALGORITME OG DIOFANTISKE LIGNINGER Euklids algoritme Euklid s setning 1, divisjonslemmaet, fra Bok 7 Gitt to ulike tall. Det minste trekkes så fra det største så mange ganger dette
x 1 x 2 x = x n b 1 b 2 b = b m Det kan være vanskelig (beregningsmessig) og bearbeide utrykk som inneholder
 4 Noen merknader 4. Lineære systemer Ax = b Gitt systemet Ax = b, A = [a i,j ] i=,,...,m, j=,,...,n x = b = Det kan være vanskelig (beregningsmessig) og bearbeide utrykk som inneholder b i. Med det finnes
4 Noen merknader 4. Lineære systemer Ax = b Gitt systemet Ax = b, A = [a i,j ] i=,,...,m, j=,,...,n x = b = Det kan være vanskelig (beregningsmessig) og bearbeide utrykk som inneholder b i. Med det finnes
LF, KONTINUASJONSEKSAMEN TMA
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Haaken A. Moe 92650655 Bokmål LF, KONTINUASJONSEKSAMEN TMA4140 2008 Oppgave 1 (10%)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Haaken A. Moe 92650655 Bokmål LF, KONTINUASJONSEKSAMEN TMA4140 2008 Oppgave 1 (10%)
Største felles divisor. (eng: greatest common divisors)
 Største felles divisor. (eng: greatest common divisors) La a og b være to tall der ikke begge er 0. Største felles divisor (eller faktor) for a og b er det største heltallet som går opp i både a og b.
Største felles divisor. (eng: greatest common divisors) La a og b være to tall der ikke begge er 0. Største felles divisor (eller faktor) for a og b er det største heltallet som går opp i både a og b.
Relativt primiske tall
 Relativt primiske tall To heltall a og b (der ikke begge er 0) kalles relativt primiske hvis gcd(a, b) = 1, dvs. de har ingen felles faktorer utenom 1. NB! a og b trenger ikke være primtall for at de skal
Relativt primiske tall To heltall a og b (der ikke begge er 0) kalles relativt primiske hvis gcd(a, b) = 1, dvs. de har ingen felles faktorer utenom 1. NB! a og b trenger ikke være primtall for at de skal
Matriser. Kapittel 4. Definisjoner og notasjon
 Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
Kapittel Matriser Vi har lært å løse et lineært ligningssystem ved å sette opp totalmatrisen til systemet gausseliminere den ved hjelp av radoperasjoner på matrisen Vi skal nå se nærmere på egenskaper
TMA4140 Diskret Matematikk Høst 2018
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4140 Diskret Matematikk Høst 2018 Seksjon 4.1 6 Dersom a c og b d, betyr dette at det eksisterer heltall s og t slik at c
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4140 Diskret Matematikk Høst 2018 Seksjon 4.1 6 Dersom a c og b d, betyr dette at det eksisterer heltall s og t slik at c
R for alle a A. (, så er a, En relasjon R på en mengde A er en Ekvivalensrelasjon hvis den er refleksiv, symmetrisk og transitiv.
 Repetisjon fra siste uke: Relasjoner En relasjon R på en mengde A er en delmengde av produktmengden A A. La R være en relasjon på en mengde A. R er refleksiv hvis R er symmetrisk hvis R er antisymmetrisk
Repetisjon fra siste uke: Relasjoner En relasjon R på en mengde A er en delmengde av produktmengden A A. La R være en relasjon på en mengde A. R er refleksiv hvis R er symmetrisk hvis R er antisymmetrisk
GRUPPETEORI VIA MATRISER. Dan Laksov KTH, Stockholm. matematikk/laksov/bokprosjekt/forum/gruppeteori/september 1, 2006
 GRUPPETEORI VIA MATRISER Dan Laksov KTH, Stockholm matematikk/laksov/bokprosjekt/forum/gruppeteori/september 1, 2006 GRUPPETEORI VIA MATRISER Gruppeteori via Matriser Dan Laksov Notater for Forum för Matematiklärare.
GRUPPETEORI VIA MATRISER Dan Laksov KTH, Stockholm matematikk/laksov/bokprosjekt/forum/gruppeteori/september 1, 2006 GRUPPETEORI VIA MATRISER Gruppeteori via Matriser Dan Laksov Notater for Forum för Matematiklärare.
LO118D Forelesning 5 (DM)
 LO118D Forelesning 5 (DM) Relasjoner 03.09.2007 1 Relasjoner 2 Ekvivalensrelasjoner 3 Matriser av relasjoner 4 Relasjonsdatabaser Relasjon Relasjoner er en generalisering av funksjoner En relasjon er en
LO118D Forelesning 5 (DM) Relasjoner 03.09.2007 1 Relasjoner 2 Ekvivalensrelasjoner 3 Matriser av relasjoner 4 Relasjonsdatabaser Relasjon Relasjoner er en generalisering av funksjoner En relasjon er en
Oppfriskningskurs i Matematikk
 Oppfriskningskurs i Matematikk Dag 3 Stine M. Berge 07.08.19 Stine M. Berge (NTNU) Oppfriskningskurs i Matematikk 07.08.19 1 / 19 Polynomer Polynomer er de enkleste funksjonene Definert og kontinuerlig
Oppfriskningskurs i Matematikk Dag 3 Stine M. Berge 07.08.19 Stine M. Berge (NTNU) Oppfriskningskurs i Matematikk 07.08.19 1 / 19 Polynomer Polynomer er de enkleste funksjonene Definert og kontinuerlig
4.1 Vektorrom og underrom
 4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
4.1 Vektorrom og underrom Vektorrom er en abstraksjon av R n. De kan brukes til å utlede egenskaper, resultater og metoder for tilsynelatende svært ulike klasser av objekter : n-tupler, følger, funksjoner,
Cauchys sats og Abels bevis for uløsbarheten av 5. gradslikningen
 Cauchys sats og Abels bevis for uløsbarheten av 5. gradslikningen Faglig-pedagogisk dag, 3. januar 2006 Arne B. Sletsjøe Matematisk institutt Universitetet i Oslo Cauchys sats (Journal de L école polytechnique,
Cauchys sats og Abels bevis for uløsbarheten av 5. gradslikningen Faglig-pedagogisk dag, 3. januar 2006 Arne B. Sletsjøe Matematisk institutt Universitetet i Oslo Cauchys sats (Journal de L école polytechnique,
Seksjonene : Vektorer
 Seksjonene 10.2-3: Vektorer Andreas Leopold Knutsen 22. mars 2010 Vektorer i R 3 Vektor = objekt med både størrelse (lengde) og retning. Lengden til en vektor v betegnes med v Nullvektoren 0 er vektoren
Seksjonene 10.2-3: Vektorer Andreas Leopold Knutsen 22. mars 2010 Vektorer i R 3 Vektor = objekt med både størrelse (lengde) og retning. Lengden til en vektor v betegnes med v Nullvektoren 0 er vektoren
For æresdoktoratet i Bergen 28 august 2008
 ITERERTE LINEÆRE REKURSJONER OG SCHUBERT REGNING For æresdoktoratet i Bergen 28 august 2008 1. Adjunksjon av røtter 1.1 Notasjon. La A være en ring. For en A-algebra B betrakter vi Hom A (B, A) som en
ITERERTE LINEÆRE REKURSJONER OG SCHUBERT REGNING For æresdoktoratet i Bergen 28 august 2008 1. Adjunksjon av røtter 1.1 Notasjon. La A være en ring. For en A-algebra B betrakter vi Hom A (B, A) som en
Løsningsforslag til noen oppgaver om Zorns lemma
 Løsningsforslag til noen oppgaver om Zorns lemma Fredrik Meyer Her er et løsningsforslag på Oppgave 3 og Oppgave 5 i notatet om Zorns lemma. De to første oppgavene ble gjort på plenum. Oppgave 1. Vi skal
Løsningsforslag til noen oppgaver om Zorns lemma Fredrik Meyer Her er et løsningsforslag på Oppgave 3 og Oppgave 5 i notatet om Zorns lemma. De to første oppgavene ble gjort på plenum. Oppgave 1. Vi skal
Zorns lemma og utvalgsaksiomet
 MAT1140, H-16 Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma bygger på det
MAT1140, H-16 Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma bygger på det
Eliminasjon av ubetsemthet
 1. Del Eliminasjon av ubetsemthet Warning: En svært midlertidig versjon som er ikke er ferdig. Den er rotete og sikkert full av feil. Forbedring følger etterhvert! versjon 0.3 last update: 10/21/15 2:48:38
1. Del Eliminasjon av ubetsemthet Warning: En svært midlertidig versjon som er ikke er ferdig. Den er rotete og sikkert full av feil. Forbedring følger etterhvert! versjon 0.3 last update: 10/21/15 2:48:38
Dette krever ikke noe nytt aksiom. Hvorfor? Og hvorfor må vi anta at A ikke er tom? Merk at vi har:
 Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
