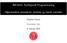
x as U == if P (x) th x qua U el fi

Transkript

1 endmodule Typemoduler 1: Oppramstype type T == {a,b,...,c} svarer til: Oppramstype: T == module type a,b,...,c: T genbas a,b,...,c 1-1 succ, pred : T T ^<^, ^ ^, ^>^, ^ ^ : T T Bool succ(x) == case x of a b... c fo pred(x) == case x of a b a... fo x<y == case (x, y) of (a, a) f (a, b) t... fo x y == x<y x=y 1

2 2: Semantisk subtype Typemoduler U == {x : T P (x)} (hvor P : T Bool) type module ^as U : T U (coercion fra T til U) x as U == if P (x) th x qua U el fi T -funksjoner og nye funksjoner] [redenerte endmodule av U innebærer U T, (U semantisk subtype til T ). Denisjonen redenisjon av T -funksjon f skal alle T i prolen erstattes Ved U. Det forlanges: u : U U'f(...,u,...) == T 'f(...,u,...) av observator, og u : U U'f(...,u,...) == T 'f(...,u,...) as U for produsent. Dermed vil teoremer for T -funksjoner uten T - for holde for tilsvarende U-funksjoner (eller bli udenerte). kvantorer U som ovenfor og V == {x:t Q(x)}. da gjelder: La ( x:t Q) P U og V x:t (P Q)) U. V 2

3 Intervall-type: {a..b} == {x : T a x b}, type Typemoduler 3: Intervall-type hvor T er typen til a og b, og T har (reeksiv) ordningsrelasjon ^ ^, samt traverseringsfunksjoner succ, pred, hvor b=succ n (a), n 0, alle automatisk redenert i subtypen. Vi har: a 1 a 2 b 2 b 1 {a 2..b 2 } {a 1..b 1 } og: b 1 <a 2 b 2 <a 1 {a 1..b 1 } {a 2..b 2 }. La U = {a 1..b 1 }, V = {a 2..b 2 }, V U. Da gjelder: xv' y == xu' y og V 'succ(x) U'succ(x), for alle x, y :V. 3

4 endmodule Typemoduler 4: Int Int by Zero, Nat1, Neg1 type Nat as Zero, with Neg as Zero Neg1, Nzo as Nat1 == module Neg1 0 : Zero; S^ : Nat Nat1 ; N^ : Nat1 Neg1 genbas 0, S^, N^ 1-1 1, 2,...: Nat1 ; ^, succ, pred : Int Int abs : Int Nat; sgn : Int { 1..1} ^<^, ^ ^, ^>^, ^ ^ : Int Int Bool ^+^, ^ ^, ^ ^ : Int Int Int; ^/^ : Int Nzo Int ^ ^ : Nat Nat Nat; ^mod^ : Int Nat1 Int x == case x of 0 0 Sx NSx Nx x fo 4

5 n = 0 får vi det tomme Kartesiske produkt, {}, som er en For med den ene verdien (). singelton-type Typemoduler 5: Kartesisk produkt produkt med n 0 navngitte komponenter: Kartesisk T == s 1 : T 1 s 2 : T 2... s type n T : n til: svarer type T == module (^, ^,...,^) : T 1 T 2... T n T (n-tuppel) genbas (^, ^,...,^) 1-1 ^.s 1 : T T 1 ;...; ^.s n T T : n (selektorer) (x 1,x 2,...,x n ).s == 1 x 1 (x 1,x 2,...,x n ).s == 2 x (x 1,x 2,...,x n ).s n x == n endmodule 5

6 Typemoduler 6: Disjunkt union union av n 2 navngitte alternativer: Disjunkt T == a 1 : T 1 + a 2 : T a type n T : n til: svarer type T == module a 1 : T 1 T ;...; a n : T n T (injektorer) 1-1 genbas a 1,a 2,...,a n endmodule alternativ er å denere T 1,...,T Et n under ett med,t T 1,...,T n syntaktiske subtyper. Fordelen med disjunkt union er at som er tidligere denerte typer, ikke nødvendigvis innbyrdes alternativene forskjellige. Fordelen med subtyper er bl.a. at injektorer implisitte. For x : T kan vi i begge tilfeller bruke funksjonene casexof til forgrening....fo Eksempel: type INT == 0 : {} + pos : Nat1 + neg : Nat1. 6

7 Typemoduler 7: Set set T by Eset, set1 == type module : Eset add : set T set1, add genbas ^ɛ^ : T set Bool mengde) (tom element) (adder (medlemskap) xɛs == case s of f add(s,y) x=y xɛsfo ^ɛ^ obsbas ^ ^ : set set Bool (inklusjon) s t == case s of t add(s,x) xɛt s tfo s, t : set T s=t s t t s s : set T, x : T add(add(s, x),x) = add(s, x) s : set T, x,y : T add(add(s, x),y) = add(add(s, y),x) endmodule 7

8 Typemoduler 8: Bag bag T by Ebag, bag1 == module type / : Ebag adb : bag T bag1 /, adb genbas mpc : bag T Nat bag) (tom element) (adder (multiplisitet) mpc(b, x) == case b of / 0 adb(b,y) if = x y th S mpc(b el mpc(b,x) fifo,x) mpc obsbas ^ ^ : bag bag Bool (inklusjon) b c == case b of / t adb(b,x) mpc(b <mpc(c, x) b c fo,x) b, c : bag b=c b c c b b : bag, x,y : T adb(adb(b, x),y) = adb(adb(b, y),x) endmodule - 8

9 seq T by Eseq, seq1 == type module Typemoduler 9: Seq ε : Eseq ^ ^ : seq T seq1 (tom sekvens) (høyre-pluss) genbas ε, ^ ^ 1-1 ^ ^ : T seq seq1 ^ ^ : seq seq seq x q == case q of ε ε x q y (x q ) y fo q r == case r of ε q r x (q r ) x fo q : seq ε q = q q, r, s : seq q (r s) = (q r) s q, r : seq, x : T q (x r) = (q x) r (venstre-pluss) (konkatener) endmodule 9

10 Typemoduler 10 Sekvenser: projeksjon og dominering ^/^ : seq T set T seq T (projiser inn i set) ^\^ : seq T set T seq T (projiser vekk fra set) ^dom^ : seq T set T Bool (er dominert av) q/s == caseqof ε ε q x if xɛsth(q /s) xelq /sfifo q\s == caseqof ε ε q x if xɛsthq \sel(q \s) xfifo q dom s == case q of ε t q x q dom s (#(q /s) = #(q \s) xɛs) fo q, r: seq T, s: set T q dom s r head q #(r/s) #(r\s) 10

11 Typemoduler 11: File type file T == module new file : file put : file T file adv : file file rew : file file get : file T new file,put,adv,rew genbas lp, rp : file seq T l) (tom post) (skriv lesehodet) (ytt (rewind) post) (nåværende (venstredel, høyredel) (lp, rp)(f ) == case F of new file (ε, ε) x) put(f, (lp(f ε) ) x, lp, rp obsbas get(f) == lt(rp(f)) adv(f ) (lp(f ) lt(rp(f)),rr(rp(f))) rew(f) (ε, lp(f ) rp(f)) fo endmodule 11

12 rew(file(q, r)) == file(ε, q r) get(file(q, r)) == lt(r) Typemoduler 12: File (1-1 genbas) type file T == module new file : file put : file T file adv : file file rew : file file get : file T file : seq T seq T file genbas file 1-1 new file == file(ε, ε) l) (tom post) (skriv lesehodet) (ytt (rewind) post) (nåværende (l-generator) put(file(q, r), x) == file(q x, ε) adv(file(q, r)) == file(q lt(r),rr(r)) endmodule 12

13 Typemoduler 13: Map Map{U, T } == type module init: Map (tomt map) ^[^ ^]: Map U T Map (oppdater map) init, ^[^ ^] genbas ^[^]: Map U T map) (appliser M[u] == case M of init M [u t] if u=u th t el M [u] fifo : Map U Bool (denerthet) (M,u) == case M of init f M [u t] u=u (M,u) fo del(m,u) == case M of init M M [u t] if u=u th del(m,u) el del(m,u)[u t] fifo M 1 =M 2 == case M 1 of init case M 2 of init t others ffo M 1 [u v] (M 2,u) M 2 [u]=v del(m 1,u)=del(M 2,u) fo del : Map U Map (fjern alle oppdateringer på gitt sted) obsbas ^[^] M :Map, u 1,u 2 :U, t 1,t 2 :T M[u 1 t 1 ][u 2 t 2 ] = if u 1 =u 2 th M[u 2 t ] 2 el M[u 2 t 2 ][u 1 t ] 1 fi endmodule 13

14 Typemoduler 14: Initialisert map Imap{U, T } == module type init : T Imap ^[^ ^]: Imap U T Imap (initialisert map) init, ^[^ ^] genbas ^[^]: Imap U T (oppdater map) (appliser map) M[u] == case M of init(t) t M [u t] if u=u th t el M [u] fifo ^[^] obsbas M :Imap, u 1,u 2 :U, t 1,t 2 :T M[u 1 t 1 ][u 2 t 2 ] = if u 1 =u 2 th M[u 2 t ] 2 el M[u 2 t 2 ][u 1 t ] 1 fi endmodule Merknad 1: Likhet på Map er ikke TGI i syntaktisk forstand, likevel terminerer termomskriving her. Det følger av et induktivt resonnement om at funksjonen del bare kan fjerne ^[^ ^]-applikasjoner fra Map-argumentet. Merknad 2: Imap{U, T } er et vanskeligere begrep, forsåvidt som likhet ikke kan deneres konstruktivt i det hele tatt for uspesisert type U. Denisjonen gitt for likhet på Map{U, T } fungerer her bare for uendelig type U. 14

15 * Generatorinduksjon over subtyper 1 typen T være subtype til U, T U, U maksimal. For å vise La : x T induktivt kan vi bruke følgende generelle teknikk: Vis P y :U med induksjon over U, hvor Q er slik at Q Q yisat Py x. Ofte kan Q settes til å være y isa T P x y (for y:u). Det svarer til følgende induksjonsregel: y j isa T P x y j, j s.a.t[y j ] T - g(...,y j,...) isa T P x g(...,y j,...) ; gɛg U SGIND T : - x: T P Her betyr T 1 T 2 at T 1 og T 2 er ikke-disjunkte, og T [y] betyr typen til y. 15

16 * Generatorinduksjon over subtyper 2 Hvis T er en syntaktisk subtype til U, gjelder g(...) isa T hvis og bare hvis gɛg T : SGIND T : y j isa T P x y j, j s.a.t[y j ] T - P x g (...,y j,...) ; gɛg T - x: T P Eksempel: Nat1 er denert som syntaktisk subtype til Nat. Vi har G Nat = {0, S^} og G Nat1 = {S^}. Vi får: SGIND Nat1 : y 0 P x y - P x Sy - x : Nat1 P 16

17 * Generatorinduksjon over subtyper 3 S^ er eneste generator for Nat1, innser vi uformelt at Siden : x Nat1 er det samme som P : y Nat PSy x Dermed bør. SGIND Nat1 kunne erstattes av følgende regel: GSIND Nat1 : - P x S0 ; P x Sz - P x SSz - x : Nat1 P Premissen SGIND i Psevdobevis: Nat1 er: y Py x PSy x 0-0 case y of f Sz tfo Py x Px Sy - case y of f Py x Sz t Py x fo PSy x case - y of t PSy x Sz P y x P Sy x fo - case - y of P x Sz Px Sz Px SSz fo S0 0 P x P - Sz x P SSz x - og - S0 17

18 y 0 Py x - PSy x (premiss, y:nat) 1. (y 0 Py x ) PSy x (1, I) P x S0 * Generatorinduksjon over subtyper 4 GSIND Nat1 bevisskritt: (P x P Sz x -P SSz x )= inneholder egentlig to S0 - y:nat PSy x = ; hvor siste skritt forlanger som, x:nat1 - P premiss et bevis for P x Sy uten induksjonshypotese. Vi viser formelt at GSIND Nat1 likevel er like sterk som SGIND Nat1 : - y (y Py x PSy x 3. ) (2, I) 0 0 P x P x 0 ) S0 (3, E) (0-4. (4,forenkl.) - 0 (Sz PSz x P SSz x (3, E) 6. ) PSz x P SSz x (6,forenkl.) P x Sz - P x Sz 9. P x Sz - P x SSz (triv.) (7,8, E) x : Nat1 P (5,9,GSIND Nat1 ) 18

19 en maksimal type T vet vi at alle argumenttyper til hver T - For enten er disjunkte med T eller er inkludert i T. Denne generator egenskapen kalles konveksitet. subtype T er ikke nødvendigvis konveks; da kan en argumenttype En til en T -generator overlappe T uten å være inkludert T. Eksempel: Nat1 er ikke-konveks, for generatoren S^ har i Nat. Derimot er Nat konveks, selv om den deneres domenet * Generatorinduksjon over subtyper 5 en syntaktisk subtype av Int. For en konveks type T, enten som eller en syntaktisk subtype, gjelder følgende generalis- maksimal erte versjon av GIND (boka s. 158): P x y j, j s.a. T[y j ] T - P x g(...,y j,...) ; gɛg T GGIND T : - x: T P 19

20 * Generatorinduksjon over subtyper 6 vise teoremet x : Nat1 x<x+ x. Det er det samme som Skal vise y : Nat Sy <Sy+ Sy, som i to TGI-skritt omskrives til: å : y Nat y<sy+ y. 0 < S < S0 t Vis y<sy+ yvis Sy <SSy + Sy Sy<S(SSy + y) Anta y<ssy + y Det går ikke! heller y, z : Nat y<sz+ y Viser 0 < Sz < Sz t Vis IH: z : Nat y<sz+ y Anta Sy <Sz+ Sy Sy<S(Sz+ y) y<sz+ y Vis er en instans av IH som 20