Øving nr. 7. LØSNINGSFORSLAG
|
|
|
- Thorbjørn Gundersen
- 7 år siden
- Visninger:
Transkript
1 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving n. 7. LØSNINGSFORSLAG Tilstandsdiagam: : Begge enhete i funksjon µ : En av enhetene feile Mek: seiell epaasjon innebæe at ovegangsintensiteten µ, ikkeµ µ : Begge enhetene feile Tilstandsligninge: µ ( µ + µ µ P P P P + P + P Løsning: P o --P µ P P µ M:\fame\4-ov-los\løsning789.fm
2 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. P µ µ -- P µ -- + µ N P µ N --- P o µ N Utilgjengelighet: q P µ N µ Foventet nedetid: θ -- 5time µ Foventet tid mellomsvikt: T f time qµ q f o M:\fame\4-ov-los\løsning789.fm
3 3 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving n. 8. LØSNINGSFORSLAG Løsningen finnes ved hjelp av lign. (7., 7. og 7.3 i læeboken, side a. Seiestuktu. Tilgjengelighet: p P 3 p Sviktfekvens: f ν 3 P 3 ( + p ( + Sviktintensitet: f p + Foentet epaasjonstid (nedetid: ( p f ( p ( p ( + p p p q + q p + q q µ + µ p µ µ + + l Foventet epaasjonstid: b. Paallellstuktu. Utilgjengelighet: q P o q q Sviktfekvens: f ν o P o ( µ + µ q q ( µ + µ Sviktintensitet: q q ( µ µ f p q q q q ( µ p + p q + p + µ q q p + p q + q µ µ + µ + µ Sviktintensitet: ( ( + M:\fame\4-ov-los\løsning789.fm
4 4 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Foventet epaasjonstid: q q q f q q ( µ + µ a. Seiestuktu, n komponente. Fo n 3: I 3 Vi danne en modul av og og benytte fomlene fa pkt. a: I + + I Fo systemet med 3 komponente: I I I I Ved gjentatt buk av slik modulaiseing få en fo n komponente i seie (fotsatt uavhengighet: i ( i i i ( i i q i i M:\fame\4-ov-los\løsning789.fm
5 5 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. b. Paallellstuktu, n komponente Fo n3: I 3 Vi benytte fomlene fa pkt. b på modul I og komponent 3: I ( + I I 3 ( I ( ( ( 3 ( M:\fame\4-ov-los\løsning789.fm
6 6 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS I I Ved gjentatt buk av slik modulaiseing få en fo n komponente i paallell (foutsatt uavhengighet: ( i i [ ( i ] ( i q ( i i [ ( i i ] 3. III I II 4 Nettveket deles opp i module, og en benytte fomlene fa pkt. og : I pe å M:\fame\4-ov-los\løsning789.fm
7 7 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS I time II + 4 I.5 pe å II I time 4 III I II ( I + II pe å III I II I II 6 time Fo hele nettveket: Antall avbudd/å: 5 + III pe å Foventet avbuddstid p. avbudd III III time p. avbudd Akkumulet avbuddstid p. å: T q time/å M:\fame\4-ov-los\løsning789.fm
8 8 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving n. 9. LØSNINGSFORSLAG Tilstandsdiagam fo poblemstillingen, pkt. 3.. ; Nomal dift p : Nettavbudd batteidift : Feil på system A, vellykket omkopling til nettdift (B. Funksjon Feil A (-p (q +q Tilstandsligninge: ( + p ( ( + P o P P Foventet tid til svikt: ET ( m P o + P + P M:\fame\4-ov-los\løsning789.fm
9 9 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. P P + µ B P p ( ( + P p P ( ( + p ( P B ( + m Ette mellomegning fås: ( + P N N [( ( ( p ] Løsningen bli: m ( + ( + ( + + p ( [( ( ( p ] Dette gi: ET ( m 6, 84 å Vi benytte: «, «, q, q «Nevne: B + µa p p Telle: p +p M:\fame\4-ov-los\løsning789.fm
10 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Multiplisee med i telle og nevne og få: A B B B p p A m B A A A p A p A µ B Fokote alle.gads ledd i telle og nevne. Buke at og «. Anta samtidig at og «m B A ( p B p ( q ( q q + q + q q q + q siden q, q «Dette gi: m ( q + q A ( q + q + q B + q A M:\fame\4-ov-los\løsning789.fm
11 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Fotolkning: Foutsetningene endes fo feilmekanismen som e knyttet til ovevåkingsutstyet. Feil på ove A q B antall gange A-enheten svikte mens det e nettavbudd (q B nettets utilgjengelighet B. q A antall gange nettet falle ut mens A-enheten e ute fo epaasjon. (q A A A-enhetens utilgjengelighet. ( q + q antall gange omkobling til nettdift (fobikobling mislykkes, enten på gunn av feil på ovevåkingsutsty elle på gunn av byteutsty. Disse te bidagene e antall ovegange fa henholdsvis tilstand, og til feiltilstand, og dette kunne en fosåvidt satt opp diekte ut fa tilstandsdiagammet. Numeiske vedie: 4 q B B q A A , q B 788, 4 pe å q A. 3 pe å ( q + q pe å m å Systemet e altså meget pålitelig med de antatte data.. M:\fame\4-ov-los\løsning789.fm
12 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. våkingsutstyet bli ikke oppdaget fø det innteffe en situasjon som keve omkopling til nettdift (, og da få vi svikt fodi omkopling ikke finne sted. Tilstandsdiagammet bli: : Nomal dift ettavbudd tteidift : Feil på system A, vellykket omkobling 3: Sovende feil, ovevåkingsutsty e defekt 4: Defekt ovevåkingsuts Nettavbudd. q Tilstandsligninge: ( + + P o - ( P ( + P ( + P 3 ( P 4 Addisjon av de to siste ligningene bli: P ( P 3 + P 4 Foventet tid til svikt: m P o + P + P + ( P 3 + P 4 M:\fame\4-ov-los\løsning789.fm
13 3 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. P P P P + ( P 3 + P P m P + P +P + P 3 +P 4 P p Fa føste ligning: P ( + + ( ( + ( + + ( ( ( + ( ( + P N Tekke minustegnet utenfo og få: Nevne: N ( + + ( ( + ( + ( Dele opp ledd og sette sammen: N ( ( + ( + ( ( ( + + ( ( + M:\fame\4-ov-los\løsning789.fm
14 4 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Slå sammen de siste te leddene ved å sette ( + utenfo. N ( ( + ( + ( + ( ( ( + q + ( + ( + ( m P ( A ( + + ( + + ( A + ( ( + ( ( + Slå sammen føste og siste ledd i telle og sette inn fo. P Løsningen bli: m ( + ( ( + + ( ( + + ( [ ( ( + q + ( + ( + ( ] Vi benytte: «, «, q «Multiplisee med i telle og nevne.fokote alle 3. gadsledd. I telleen vil ( + dominee ove de øvige ledd (.gadsledd. + m A B A q A Dividee med i telle og nevne og benytte at A og B. q A q B M:\fame\4-ov-los\løsning789.fm
15 5 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS m q q B q A q A q B Numeiske vedie: å q q B q A q A B A q B B m å Vi legge meke til at med foutsetningen:.5 feil/å bli m eduset fa m6 å til m å. Med denne vedien fo ha vi i ealiteten: m dvs. foventet tid til svikt e i hovedsak bestemt av sovende feil på ovevåkingsutstyet. M:\fame\4-ov-los\løsning789.fm
16 6 FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Anta at vedien av e slik at: q Innsatt i fomelen fo m: q m A q A q B B q A B q q q q q A B + q ( q + q + q B + q A A ( q + q + q B + q A + q A q q B q Dette e esultatet vi fant fo analysen unde pkt. 3.. Vi se altså at sammenhengen: q gi oss to ekvivalente måte å modellee feilmekanisme fo en sovende feil. M:\fame\4-ov-los\løsning789.fm
Norges teknisk-naturvitenskapelige universitet (NTNU) Institutt for elkraftteknikk FAG PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving nr. 7.
Øving nr. 7. Formål: Bli kjent med de grunnleggende begreper i en stasjonær Markovmodell: (u) tilgjengelighet, forventet oppholdstid, besøksfrekvens m.fl. En prosess styres av to styreenheter (datamaskiner).
EKSAMEN FAG TFY4160 BØLGEFYSIKK OG FAG FY1002/MNFFY101 GENERELL FYSIKK II Lørdag 6. desember 2003 kl Bokmål
ide av 0 NORGE TEKNIK- NATURVITENKAPELIGE UNIVERITET INTITUTT FOR FYIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane tand Telefon: 73 59 34 6 EKAMEN FAG TFY460 ØLGEFYIKK OG FAG FY00/MNFFY0 GENERELL
Øving nr. 4. LØSNINGSFORSLAG
FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Øving nr. 4. LØSNINGSFORSLAG Avhengig av hvordan man definerer basishendelsene og hvilken struktur man velger, vil dette gi forskjellige feiltre i form.
Utvalg med tilbakelegging
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
Laboratorieøvelse i MNFFY1303-Elektromagnetisme Institutt for Fysikk, NTNU MAGNETISK HYSTERESE
Laboatoieøvelse i MNFFY33-Elektomagnetisme Institutt fo Fysikk, NTNU Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske felte og målinge av slike. Det innebæe måling av magnetfelt fa enkle
Utvalg med tilbakelegging
Utvalg med tilbakelegging Gitt n foskjellige objekte. Vi skal velge objekte på en slik måte at fo hvet objekt vi velge, notee vi hvilket det e og legge det tilbake. Det bety at vi kan velge det samme objektet
UNIVERSITETET I OSLO
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: MEK3220/MEK4220 Kontinuumsmekanikk Eksamensdag: Onsdag 2. desembe 2015. Tid fo eksamen: 09.00 13.00. Oppgavesettet e på 7 side.
Formelsamling i medisinsk statistikk
Fomelsamling i medisinsk statistikk Vesjon av 5. juni 2009 Dette e en fomelsamling til O. O. Aalen (ed.): Statistiske metode i medisin og helsefag, Gyldendal, 2006. Mek at boken ha en nettside de det e
Forelesning 9/ ved Karsten Trulsen
Foelesning 9/2 218 ved Kasten Tulsen Husk fa sist våe to spøsmål om kuveintegale: Desom vi skal beegne et kuveintegal som state i et punkt og ende opp i et annet punkt 1, så kan det væe mange veie fo å
EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK EKSAMEN I FY1001 og TFY4145 MEKANISK FYSIKK: LØSNINGSFORSLAG Tisdag 18. desembe 01 kl. 0900-100 Oppgave 1. Ti flevalgsspøsmål. (Telle
Magnetisk hysterese. 1. Beregn magnetfeltet fra en strømførende spole med kjent vindingstall.
FY33 Elektisitet og magnetisme II Institutt fo fysikk, TU FY33 Elektisitet og magnetisme II, høst 7 Laboatoieøvelse Magnetisk hysteese Hensikt Hensikten med oppgave å gjøe seg kjent med opphavet til magnetiske
( 6z + 3z 2 ) dz = = 4. (xi + zj) 3 i + 2 ) 3 x x 4 9 y. 3 (6 2y) (6 2y)2 4 y(6 2y)
TMA415 Matematikk 2 Vå 215 Noges teknisk natuvitenskapelige univesitet Institutt fo matematiske fag Løsningsfoslag Øving 11 Alle oppgavenumme efeee til 8. utgave av Adams & Essex Calculus: A Complete Couse.
"Kapittel 5 i et nøtteskall"
Ulve "Kapittel 5 i et øtteskall" (Vesjo 9.01.0 ) Jeg gå he i gjeom alle tekikke/fomle som e elevate i dette kapitlet ved å buke et eksempel side 198 som utgagspukt fo alle tekikkee. Ovesikt ove fomle og
UNIVERSITETET I OSLO
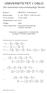UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: Eksamensdag: Tid fo eksamen: 14.30 18.30 Oppgavesettet e på 5 side. Vedlegg: Tillatte hjelpemidle: MEK3230 Fluidmekanikk 6. Juni,
Hesteveddeløp i 8. klasse
Andeas Loange Hesteveddeløp i 8. klasse Spillbettet. Gå det an å ha det gøy, utfoske algebaens mysteie og samtidig læe noe? Vi befinne oss i 8. klasse på Kykjekinsen skole i Begen. Jeg ha nettopp blitt
b) 3 MATEMATISKE METODER I 1 ( ) ( ) ( ) ( ) ( ) ( ) Repetisjonsoppgaver Bruk av regneregler: 1 Regn ut: e) 0 x ) 4 3 d) 4 x f) 5y
MATEMATISKE METODER I Buk av egneegle: Regn ut: a ( ( b 7 c ( 7 y 8 d 8 e f 5y y Regn ut og tekk sammen: a 5a b a b a + b b y + y + + y c t t + 6 ( 6t t + 8 d s+ s + s ( s + s Multiplise ut og odne a (
Norges teknisk-naturvitenskapelige universitet (NTNU) Institutt for elkraftteknikk FAG PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS.
FAG 4 PÅLITELIGHET I ELKRAFTSYSTEMER - GRUNNKURS. Formål: Øving nr. 0. Bli kjent med begreper og metode for å analysere avbruddsforhold i fordelingsnett. L a L b c Tegnforklaring: -- Effektbryter L --
Mot 5: Støy i bipolare transistorer
1/34 Mot 5: Støy i bipolae tansistoe Vi ha tidligee unnet Eni, En, og n o en osteke. Vi vil nå gjøe dette o en bipola tansisto. Vi vil se at støyen e både avhengig av opeasjonspunktet (støm og spenning)
Eksamen i TFY4205 Kvantemekanikk Mandag 8. august :00 13:00
NTNU Side 1 av 9 Institutt fo fysikk Faglig kontakt unde eksamen: Pofesso Ane Bataas Telefon: 73593647 Eksamen i TFY405 Kvantemekanikk Mandag 8. august 005 9:00 13:00 Tillatte hjelpemidle: Altenativ C
Mandag E = V. y ŷ + V ẑ (kartesiske koordinater) r sin θ φ ˆφ (kulekoordinater)
Institutt fo fysikk, NTNU TFY4155/FY13: Elektisitet og magnetisme Vå 26, uke 6 Mandag 6.2.6 Beegning av E fa V [FGT 24.4; YF 23.5; TM 23.3; F 21.1; LHL 19.9; DJG 2.3.1, 1.2.2] Gadientopeatoen : V = V V
Rettelser til. Øistein Bjørnestad Tom Rune Kongelf Terje Myklebust. Alfa. Oppgaveløsninger
Rettelse til Øistein Bjønestad Tom Rune Kongelf Teje Myklebust Alfa Oppgaveløsninge 007 Kapittel S. 7: Fasit til oppgave.9e): Slik oppgaven stå, skal svaet væe 065 (noe ha falt ut i oppgaveteksten). S.
Formelsamling i medisinsk statistikk
Fomelsamling i medisinsk statistikk Dette e fomelsamling til O. O. Aalen: Innføing i statistikk med medisinske eksemple, 2. utg., Ad Notam Gyldendal, 998. Fomelsamlingen e utabeidet i okt. 2000, med små
Energi Norge v/ingvar Solberg og Magne Fauli THEMA Consulting Group v/åsmund Jenssen og Jacob Koren Brekke 5. februar 2019
Til: Enegi Noge v/ingva Solbeg og agne Fauli Fa: v/åsmund Jenssen og Jacob Koen Bekke Dato: 5. febua 219 Refeanse: ENO-18-1 Analyse av povenyvikninge av skatteendinge siden 27 Noske vannkaftvek ha siden
Billige arboresenser og matchinger
Billige aboesense og matchinge Magnus Lie Hetland 16. jan 009 Dette e foelesningsnotate til føste foelesning i faget Algoitmekonstuksjon, videegående kus, ved Institutt fo datateknikk og infomasjonsvitenskap,
Newtons lover i to og tre dimensjoner
Newtons love i to og te dimensjone 7..13 innleveing: buk iktige boks! FYS-MEK 111 7..13 1 Skått kast kontaktkaft: luftmotstand langtekkende kaft: gavitasjon initialbetingelse: () v() v v cos( α ) iˆ +
Kombinatorikk. MAT0100V Sannsynlighetsregning og kombinatorikk. Multiplikasjonssetningen
MAT000V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
Problemet. Datamaskinbaserte doseberegninger. Usikkerheter i dose konsekvenser 1 Usikkerheter i dose konsekvenser 2
Poblemet Datamaskinbasete dosebeegninge Beegne dosefodeling i en pasient helst med gunnlag i CT-bilde Eiik Malinen Sentale kilde: T. Knöös (http://www.clin.adfys.lu.se/downloads.htm) A. Ahnesjö (div. publikasjone)
EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING LØSNINGSFORSLAG. Mandag 14. desember 2005 Tid: 09:00 13:00
Norges teknisk naturvitenskapelige universitet Institutt for telematikk Side 1 av 10 Faglig kontakt under eksamen: Poul Heegaard (73 594321) EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING
Eksamensoppgave i TEP4105 FLUIDMEKANIKK
Institutt fo enegi- og posessteknikk Eksamensoppgave i TEP45 FLUIDMEKANIKK Faglig kontakt unde eksamen: Ive Bevik Tlf.: 7359 3555 Eksamensdato: 7. august 23 Eksamenstid : 9. 3. Hjelpemiddelkode/Tillatte
LØSNINGSFORSLAG ) = Dvs
LØSNINGSFORSLAG 12 OPPGAVE 1 D j er differansen mellom måling j med metode A og metode B. D j N(µ D, 0.1 2 ). H 0 : µ D = 0 mot alternativet H 1 : µ D > 0. Vi forkaster om ˆµ D > k Under H 0 er ˆµ D =
Tillatte hjelpemidler: Lærebok og kalkulator i samsvar med fakultetet sine regler Oppgave 1 En funksjon f er gitt ved f ( x) ( x 2) e x.
UNIVERSITETET I BERGEN De maemaisk-nauvienskapelige fakule Eksamen i emne MAT Bukekus i maemaikk Fedag 8 febua, kl 9-4 BOKMÅL Tillae hjelpemidle: Læebok og kalkulao i samsva med fakulee sine egle Oppgave
c) etingelsen fo at det elektiske feltet E e otasjonsinvaiant om x-aksen e, med E og ee som denet ovenfo, at e E = E. Dette skal gjelde fo en vilkalig
Eksamen i klassisk feltteoi, fag 74 5, 4. august 995 Lsninge a) Koodinatene x; y; z tansfomees slik x 7 bx = x; y 7 by = y cos, z sin ; z 7 by = y sin + z cos Den invese tansfomasjonen e en otasjon en
Introduksjon til pålitelighetsanalyse. Jørn Vatn NTNU
Introduksjon til pålitelighetsanalyse Jørn Vatn NTNU jorn.vatn@ntnu.no Trondheim Gjøvik Ålesund Pålitelighet av hva? Komponent- og systempålitelighet Fokus i denne presentasjonen Terminologi Metoder og
Løsning midtveiseksamen H12 AST1100
Løsning midtveiseksamen H AST00 Aleksande Seland Setembe 5, 04 Ogave Vi se at kuven fo adiell hastighet e eiodisk og minne om en hamonisk funksjon. Vi kan defo anta at denne stjenen gå i bane undt et felles
UNIVERSITETET I OSLO
Side av 5 UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Eksamen i: FYS-MEK Eksamensdag: Mandag 9. juni 28 Tid fo eksamen: Kl. 9-2 Oppgavesettet e på 5 side inkludet fomelaket. Tillatte
Notat i FYS-MEK/F 1110 våren 2006
1 Notat i FYS-MEK/F 1110 våen 2006 Rulling og skliing av kule og sylinde Foelest 24. mai 2006 av Ant Inge Vistnes Geneelt Rotasjonsdynamikk e en svæt viktig del av mekanikkuset våt. Dette e nytt stoff
Løsningsforslag for eksamen i FY101 Elektromagnetisme torsdag 12. desember 2002
Løsningsfoslag fo eksamen i FY Elektomagnetisme tosdag. desembe Ved sensueing vil alle delspøsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenumme), men vi fobeholde oss etten til justeinge.
3.0 FORDELINGSNETT MED PARALLELLE FORSYNINGSVEIER.
3.0 FORDELIGETT MED PARALLELLE FORYIGVEIER. Med unntak for de generelle formlene for parallellstrukturer, kap. 2.2, er analysemetoden som er beskrevet i kapittel 2 beregnet på radielle strukturer. I dette
Matematikk 3MX AA6524 / AA6526 Elever / privatister Oktober 2002
E K S A M E N LÆRINGSSENTERET Matematikk 3MX AA6524 / AA6526 Eleve / pivatiste Bokmål Eksempeloppgave ette læeplan godkjent juli 2000 Videegående kus II Studieetning fo allmenne, økonomiske og administative
Transistorkonfigurasjoner: Det er tre hovedmåter å plassere en FET/BJT i en arkitektur:
/3 0. Fosteke akitektue Nå e tasisto skal bukes til e fosteke, oscillato, filte, seso, etc. så vil det væe behov fo passive elemete som motstade, kodesatoe og spole udt tasistoe. Disse vil søge fo biasig
Eksamensoppgave i Løsningsskisse TMA4240 Statistikk
Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Oppgave 8.12 Gitt en potensialhvirvel med styrke K i origo. Bestem sirkulasjonen ' langs kurven C. Sirkulasjonen er definert som: ' /
Løsning øving 3 Oppgve 8. Gitt en potensilhvivel med styke i oigo. Bestem sikulsjonen ' lngs kuven C. C y (I oppgven stå det t vi skl gå med klokk, men he h vi gått mot klokk i oveensstemmelse med definisjonen
ρ = = = m / s m / s Ok! 0.1
Løsningsfoslag TEP 00 FLUIDMEKNIKK.juni 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d g 6
Eksamen i MA-104 Geometri Løsningsforslag
Eksamen i M-04 Geometi 4.0.007 Løsningsfoslag Oppgave Et kvadat ha side lik s, som du velge selv. E e midtpunktet på og F e midtpunktet på. iagonalen skjæe F i H. E skjæe F i G. I oppgaven skal du buke
NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK
Side 1 av 8 NORGES TEKNISK-NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKALSK ELEKTRONIKK Faglig/fagleg kontakt unde eksamen: Navn: Helge E. Engan Tlf.: 944 EKSAMEN I EMNE SIE415 BØLGEFORPLANTNING
Løsningsforslag Eksamen i fag TEP4110 Fluidmekanikk
Oppgave Løsningsfoslag Eksamen i fag TEP40 Fluidmekanikk Onsdag 8 desembe 00 kl 500 900 Hastighetspotensialet fo en todimensjonal potensialstømning av en inkompessibel fluid e gitt som: (, ) Acos ln ()
KONTINUASJONSEKSAMEN I EMNE TFE 4120 ELEKTROMAGNETISME
Noges teknisk natuvitenskapelige univesitet Institutt fo elektonikk og telekommunikasjon ide 1 av 8 Bokmål/Nynosk Faglig/fagleg kontakt unde eksamen: Jon Olav Gepstad 41044764) Hjelpemidle: C - pesifisete
Løsningsforslag TEP 4110 FLUIDMEKANIKK 18.desember ρ = = = m / s m / s 0.1
Løsningsfoslag TEP 40 FLUIDMEKNIKK 8.desembe 007 Oppgave a) Foskjellen i vekt e oppdiftskaften på kula nå den e neddykket i olje (oppdiften i luft neglisjees). Oppdift =ρ Volum g olje π =ρvann SGolje d
8 Eksamens trening. E2 (Kapittel 1) På figuren er det tegnet grafene til funksjonene f og g gitt ved
84 8 Eksamenstening 8 Eksamens tening Uten hjelpemidle E1 (Kapittel 1) Polynomfunksjonen P e gitt ved P ( ) = 7 + 14 8, DP = R. a Det kan vises at alle heltallige løsninge av P() = 0 gå opp i konstantleddet
Måling av gravitasjonskonstanten
Måling av gavitasjonskonstanten Aeea Aka, Jako Gehad Matinussen & Ingeog Ullaland Oktoe 014 Sammendag Gavitasjonskonstantens vedi, som anvendes i Newtons univeselle gavitasjonslov, kan eegnes ved å foeta
DEN NORSKE MEDIEFESTIVAL. TV-dekning av Tippeligaen LANDSOMFATTENDE OMNIBUSS 8. - 10. APRIL 2002
DEN NORSKE MEDEFESTVAL TV-dekning av Tippeligaen LANDSOMFATTENDE OMNBUSS 8. - 10. APRL 2002 n i \ 1 fl i! : \. \, l Begen: Tlf5554 1050 Fax 55541051 Postadesse: Pb 714, Sentum 5807 Begen Besøksadesse:
Løsningsforslag til ukeoppgave 11
Oppgave FYS1001 Vå 2018 1 Løsningsfoslag til ukeoppgave 11 Oppgave 23.04 B F m qv = F m 2eV = 6, 3 10 3 T Kaft, magnetfelt og fat stå vinkelett på hveande. Se læebok s. 690. Oppgave 23.09 a) F = qvb =
Eksamen TFY 4240: Elektromagnetisk teori
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Ola Hundei, tlf. 93411 (mobil: 95143671) Eksamen TFY 4240: Elektomagnetisk teoi 8 desembe 2007 kl. 09.00-13.00
Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2
1 Løsningsfoslag EMC-eksamen 24.5. Oppgave 1 a)1 b)3 c)2 d)3 e)3 f)2 g)3 h)2 i)1 j)2 k)1 l)2 Oppgave 2 a) En geneisk standad e en geneell standad som bukes nå det ikke foeligge en poduktstandad. EN581
RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS
![RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS](/thumbs/62/46972182.jpg "RAPPORT. Endring E014 Flomvurdering eksisterende E6 STATENS VEGVESEN OPPDRAGSNUMMER [ R01] 29/05/2015 SWECO NORGE AS")
RAPPORT STATENS VEGVESEN Ending E014 Flomvudeing eksisteende E6 OPPDRAGSNUMMER 12143214 [12143214-R01] 29/05/2015 SWECO NORGE AS SAMUEL VINGERHAGEN epo002.docx 2013-06-14 Sweco epo002.docx 2013-06-14
Løsning, eksamen 3FY juni 1999
Løsning, eksamen 3FY juni 1999 Oppgae 1 km/s a) Hubbles lo sie at H, de H. 10 lyså Faten til galaksen e: 3 10 m/s H 5,0 10 7 lyså 1,10 10 m/s 10 lyså b) Dopplefomelen gi oss λ, de c e lysfaten og λ 0 e
Løsningsforslag sist oppdatert
Løsningsfoslag sist oppdatet.. BOKMÅL Oppgave En funksjon f e definet i intevallet ved f ( ) ( ) e a) Finn f ( ). Avgjø hvo funksjonen e stigende og hvo funksjonen e avtagende. Bestem funksjonens eventuelle
Kombinatorikk. MAT0100V Sannsynlighetsregning og kombinatorikk. Multiplikasjonssetningen
MAT0100V Sasylighetsegig og kombiatoikk Kombiatoikk Odede utvalg med og ute tilbakeleggig Uodede utvalg ute tilbakeleggig Pascals talltekat og biomialkoeffisietee Øulf Boga Matematisk istitutt Uivesitetet
Eksamen STK2400, 6/ Løsningsforslag
Eksamen STK2400, 6/12-07 - Løsningsforslag Arne ang Huseby December 19, 2007 Oppgave 1 I denne oppgaven skal vi se på et binært monotont system (C, φ) med komponentmengde C = {1,..., 5} og strukturfunksjon
sosiale behov FASE 2: Haug barnehage 2011-2012
: Hva kjennetegne bana i denne fasen? De voksnes olle Banemøte Påkledning Samlinge Måltid Posjekte Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 «Omsog, oppdagelse og læing i banehagen skal femme
trygghet FASE 1: barnehage
tygghet banehage De voksnes olle Banemøte Leikeguppe Guppeaktivitet Hjemmebesøk Samlinge Måltid Påkledning Uteleik Konfliktløsning Vudeing Haug banehage 2011-2012 tygghet tygghet «Banehagen skal bistå
Kapittel 9: Estimering
Kapittel 9: Estimeing TMA445 Statistikk 9.8,9.9: Estimeing, to utvalg. 9.6: Pediksjonsintevall Tuid.Follestad@math.ntnu.no p.1/13 Repetisjon: Punkt-og intevall-estimeing, eitt utvalg La X 1, X,..., X n
1 Virtuelt arbeid for stive legemer
1 Vituelt abeid fo stive legeme Innhold: Abeidsbegepet i mekanikk Pinsippet om vituelt abeid fo stive legeme Litteatu: Igens, Statikk, kap. 10.1 10.2 Hibbele, Statics, kap. 11.1 11.3 Bell, Konstuksjonsmekanikk
Konstanter og formelsamling for kurset finner du bakerst Merk: Figurene til oppgavene er ofte på en annen side enn selve oppgaven
UNIVERSITETET I OSLO Det matematisk-natuvitenskapelige fakultet Avsluttende eksamen i AST2000, 17. desembe 2018, 09.00 13.00 Oppgavesettet inkludet fomelsamling e på 8 side Tillatte hjelpemidle: 1) Angel/Øgim
EKSAMENSOPPGAVE - Skoleeksamen. Institutt for Samfunnsøkonomi. Utlevering: 17.12.2014 Kl. 09.00 Innlevering: 17.12.2014 Kl. 14.00
EKSAMENSOPPGAVE - Skoleeksamen MET 11803 Matematikk Institutt fo Samfunnsøkonomi Utleveing: 17122014 Kl 0900 Innleveing: 17122014 Kl 1400 Vekt: 70% av MET 1180 Antall side i oppgaven: Antall vedleggsfile:
Pytagoreiske tripler og Fibonacci-tall
Johan F. Aanes Pytagoeiske tiple og Fibonai-tall Pytagoas og Fibonai siamesiske tvillinge? Me enn 700 å skille dem i tid, men matematisk e de på en måte uadskillelige. Pytagoas (a. 585 500 f.k.) og Leonado
informasjon GENERELL barnehage
maianne@futuia.no «Det e at å ha 5 finge på hve hånd og 5 tæ på hve fot. Jeg kunne like gjene hatt 13 elle 30 sammenlagt. Og så ble det tilfeldigvis 20». Inge Hageup banehage Åpningstid Tilvenning av nye
EKSAMENSOPPGAVE I SIE5025-PÅLITELIGE SYSTEMER
Norges teknisk-naturvitenskapelige universitet Institutt for telematikk EKSAMENSOPPGAVE I SIE5025-PÅLITELIGE SYSTEMER Faglig kontakt under eksamen: Bjarne E. Helvik Telefon.: 92667 Eksamensdato: 24. mai
informasjon GENERELL barnehage
2011 maianne@fuedesign.no «Det e at å ha 5 finge på hve hånd og 5 tæ på hve fot. Jeg kunne like gjene hatt 13 elle 30 sammenlagt. Og så ble det tilfeldigvis 20». Inge Hageup banehage Åpningstid Tilvenning
Realavkastning. Investeringsanalyse og inflasjon. Realavkastning av finansinvesteringer
Ivesteigsaalyse og iflasjo Nomiell avkastig og ealavkastig Reell låeete (ealete) Realivesteige og iflasjo Kotatstøm i omielle og faste pise Iflasjo og skatt Omløpsmidle og iflasjo Joh-Eik Adeasse 1 Høgskole
Sammendrag, uke 14 (5. og 6. april)
Institutt fo fysikk, NTNU TFY4155/FY1003: Elektisitet og magnetisme Vå 2005 Sammendag, uke 14 (5. og 6. apil) Magnetisk vekselvikning [FGT 28, 29; YF 27, 28; TM 26, 27; AF 22, 24B; H 23; DJG 5] Magnetisme
Emnenavn: Finansiering og investering. Eksamenstid: 4 timer. Faglærer: Tor Arne Moxheim
EKSAMEN Emnekode: SFB6 Dato: 3. mai 9 Hjelpemidle: Godkjent kalkulato, vedlagte fomelsamling og entetabelle. Emnenavn: Finansieing og investeing Eksamenstid: 4 time Faglæe: o Ane Moxheim Om eksamensoppgaven
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Løsning øving 12 N L. Fra Faradays induksjonslov får vi da en indusert elektromotorisk spenning:
nstitutt fo fysikk, NTNU Fg SF 4 Elektognetise og MNFFY 3 Elektisitet og gnetise Høst øsning øving Oppgve Mgnetfeltet inne i solenoiden e : ( H( (N/) ( (dvs fo < R). Utenfo solenoiden: ( > R) Fo å eegne
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 6. august 2003
Noges teknisk natuvitenskapelige univesitet NTNU Side av 9 Institutt fo fysikk Fakultet fo natuvitenskap og teknologi Løsningsfoslag til eksamen i SIF47 KLASSISK FELTTEORI Onsdag 6. august 3 Dette løsningsfoslaget
Open #2. løp i norges største rc anlegg, stavanger Raceway
e g n Stv Open #2 s m. 0 g d lø s m. G A D N Ø S :0 Elekto Touing stock - Blinky3,5 MODIFIED :0 Elekto Touing Stndd - blinky eg. 2,5t M - Chssis Fomel :0 Offod 2WD :0 Offod 4WD :0 Stdium Tuck 2WD Shot
LØSNINGSFORSLAG TIL EKSAMEN I FAG TEP4170 VARME- OG FORBRENNINGSTEKNIKK 18. mai 2007 Tid:
av 4 Noges teknisk-natuvitenskapelige univesitet Initutt fo enegi- og poseseknikk Kontakt unde eksamen: Toleif Weydahl, tlf. 7359634 / 945 ØSNINGSFORSAG TI EKSAMEN I FAG TEP47 VARME- OG FORBRENNINGSTEKNIKK
Obj104. Ukentlige lekser med oppgaver knyttet til de fire regneartene, tid, omgjøring mellom ulike enheter, brøk, algebra og problemløsning
Obj104 RENDALEN KOMMUNE Fagetun skole Åsplan i matematikk fo 6. tinn 2014/15 Ukentlige lekse med oppgave knyttet til de fie egneatene, tid, omgjøing mellom ulike enhete, bøk, algeba poblemløsning TID TEMA
KJM Radiokjemidelen
Patikke i boks - en dimensjon KJM 1060 - Radiokjemideen Foeesning : Skamodeen d ψ m + E ψ 0 dx h n π h En V0 + m ψ n nπ( x + ) sin n 45 de n 1,,,... Sannsynigheten fo å finne patikkeen meom x og x+dx e:
FAG: MA-209 Matematikk 3 LÆRER: Per Henrik Hogstad KANDIDATEN MÅ SELV KONTROLLERE AT OPPGAVESETTET ER FULLSTENDIG
UNIVESIEE I AGDE Gimsa E K S A M E N S O P P G A V E : FAG: MA-9 Maemaikk LÆE: Pe Henik Hogsa Klasse: Dao:..5 Eksamensi a-il: 9.. Eksamensoppgaven beså av ølgene Anall sie: 5 inkl. osie velegg Anall oppgave:
Om bevegelsesligningene
Inst. fo Mekanikk, Temo- og Fluiddynamikk Om bevegelsesligningene (Repetisjon av utledninge fa IO 1008 Fluidmekanikk) P.-Å. Kogstad I det ettefølgende epetees kot utledningene av de fundamentale bevegelsesligninge,
Kapittel 2: Krumlinjet bevegelse
Kapittel : Kumlinjet bevegelse Vannett kast v = v v = gt x 0 1 x = vt 0 y= gt y Skått kast v = v v = v gt x 0x y 0y 1 x = v0 t y = v x 0 t gt y Sving uten dosseing U+ G = ma N = G v R = m R = μn = μmg
Eksamen TTM4120 Pålitelige systemer 18. mai 2004 LØSNINGSSKISSE
Side 1 av 6 Eksamen TTM4120 Pålitelige systemer 18. mai 2004 LØSNINGSSKISSE a Det skal etableres en transportforbindelse fra node 1 til node 3. Anta at C [ ij, ] = for alle [ i, j] Ω L. Denne forbindelsen
Newtons lover i én dimensjon
Newtons love i én dimensjon 4.01.013 kaft akseleasjon hastighet posisjon YS-MEK 1110 4.01.013 1 Hva e kaft? Vi ha en intuitivt idé om hva kaft e. Vi kan kvantifisee en kaft med elongasjon av en fjæ. Hva
Betinget bevegelse
Betinget bevegelse 1.0.013 innleveing på fonte FYS-MEK 1110 1.0.013 1 Innleveinge aksenavn! enhete! kommente esultatene utegninge: skitt fo skitt, ikke bae esultatet vi tenge å fostå hva du ha gjot sett
Slik bruker du pakken
Slik buke du pakken Kompetanseutviklingspakken Lesestategie og leseengasjement Dette e infomasjon til deg/dee som skal lede femdiften i kollegiet. He finne du en ovesikt ove pakkens innhold til hjelp i
ROSSELAND SKOLE LÆREPLAN I RLE 7. TRINN
Åstimetallet i faget: _38 Kistendom Hovedomådet kistendom omfatte kistendommen i histoisk pespektiv og hvodan kistendommen bli fostått og paktiset i veden og i Noge i dag, Bibelen som kilde til kultufoståelse
Oslo kommune Bydel Østensjø Bydelsadministrasjonen. Protokoll 07/14
Oslo kommune Bydel Østensjø Bydelsadministasjonen Potokoll 07/14 Møte: Bydelsutvikling, Miljø- og Kultukomite Møtested: Kafe X, Oppsal Samfunnshus, Vetlandsveien 99/101 Møtetid: Mandag 10. novembe 2014
Betraktninger rundt det klassiske elektronet.
Betaktninge undt det klassiske elektonet. Kistian Beland Matteus Häge - 1 - - - Innholdsfotegnelse: 1. Sammendag - 5 -. Innledning - 6 -. Innledende betaktninge - 7-4. Vå elektonmodell - 8-5. Enegi i feltene
NARF årsmøte 2012. 14. - 15. juni Radisson Blu Atlantic Hotel Stavanger
NARF åsøte 2012 14. - 15. juni Rdisson Blu Atlntic Hotel Stvnge T e Velkoen til åsøte 2012 Vi skl utvikle oss ot en stekee, e synlig og ttktiv bnsje. NARFs Åsøte 2012 sette ed disse odene søkelyset på
Vektreduksjon - Livsstilskurs kr. 1200,- pr. mnd
Livea - livsstil - vekteduksjon n 1-2015 Vekteduksjon - Livsstilskus k. 1200,- p. mnd kusplan 2015 Kus state nå! Les me s. 3 Gikk ned 26 kg på 16 uke "Nå føle jeg at jeg vikelig nyte mat - fo føste gang"
EKSAMEN I EMNE TKT 4125 MEKANIKK I GEOFAG OG PETROLEUMSTEKNOLOGI
NORGES EKNISK-NAURVIENSKAPELIGE UNIVERSIE INSIU FOR KONSRUKSJONSEKNIKK Faglig konak unde eksamen: Eling Nado Dahl lf. 75 977 Rune Main Hol lf. 75 97 Chalie Chunlien Li lf. 75 944 EKSAMEN I EMNE K 45 MEKANIKK
Løsning øving 9 ( ) ( ) sin ( )
nsttutt fo fskk, NTNU Fg SF 4 Elektomgnetsme og MNFFY Elektstet og mgnetsme Høst Løsnng øvng 9 Oppgve Ktesske koodnte: Enhetsvektoen stå nomlt på, som dnne en vnkel med -ksen. Det et t dnne en vnkel med
EKSAMEN I FAG SIF 4008 FYSIKK Mandag 7. mai 2001 kl Bokmål. K. Rottmann: Matematisk formelsamling
Side 1 av 1 NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR FYSIKK Faglig kontakt unde eksamen: Føsteamanuensis Knut Ane Stand Telefon: 73 59 34 61 EKSAMEN I FAG SIF 48 FYSIKK Mandag 7. mai
Løsningsforslag øving 7
Løsningsforslag øving 7 8 Husk at en funksjon er injektiv dersom x y gir f(x) f(y), men her ser vi at f(3) 9 f( 3), eller generelt at f(z) z f( z) for alle z C, som betyr at f ikke er injektiv Vi ser også
TMA4240 Statistikk Høst 2015
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 55 2. Ved bruk av formelheftet finner
Hydrostatisk ligevægt
Hyosaisk ligevæg F g F P Gaviy ynge Pesse yk F g F P Hyosaisk ligevæg P Gm. μ P k m m Gm P B π Sjene amosfæe μ P k m m Gm P B π Sjene amosfæe H P g GM B m g k H μ ~ konsan isoem ykskalahøjen 3 H h H h
Årsplan i matematikk 6. årstrinn 2016/2017
Åsplan i matematikk 6. åstinn 2016/2017 Åsplanen ta utgaspunkt i kunnskapsløftet. I planen ta vi utgaspunkt i kompetansemålene fo 7.klasse. I matematikk læe en litt av et tema på 5.åstinn, litt me om samme
Løsningsforslag Fysikk 2 Høst 2015
Løsningsfoslag Fysikk Høst 015 Oppgave Sva Foklaing a) A Vi pøve oss fa ed noen kjente fole: ε vbl B ε Φ vl t vl Nå vi nå egne ed enhete på denne foelen få vi Wb B s s Wb Magnetfeltet kan altså åles i
Løsningsforslag eksamen 2. august 2003 SIF 4005 Fysikk for kjemi og materialteknologi
Løsningsfslag eksamen. august SF 5 Fysikk f kjemi g mateialteknlgi Oppgave lektstatikk a) Sylineens ttale laning pe lengeenhet finnes ve å integee laningsfelingen ( ) ve aealelementet A= e sylineens aius