Cantors mengde og andre paradokser
|
|
|
- Edvin Steffen Larssen
- 6 år siden
- Visninger:
Transkript
1 Cantors mengde og andre paradokser På disse få sidene vil jeg presentere enkelte fenomener fra teorien for relle funksjoner av en variabel. De er alle eksempel langt fra den strake landevei, og illustrer hva som faktisk kan skje. Man kunne være fristet til å kalle eksemplene for patologier, et standpunkt som imidlertid ville være utrykk for en alt for smal horisont. Vi skal innom tre grupper av eksempler. For det første Cantormengden, og den skal vi bruke mest tid på. Det er en overtellbar mengde av mål null. Denne berømte mengden hjemme i et hvert kurs i målteori, eller for den saks skyld, også andre kurs som behandler undermengder av reelle tallene. Den ble beskrevet av Georg Cantor i 1881, imidlertdig skal både H. J. S. Smith og Vito Volterra vært innom mengden i sine arbeider, henholdsvis i 1875 og Cantormengden er en blant en rekke lignende mengder hvis egenskaper utfordrer vår intuisjon og illustrerer uventede fenomer. Om ikke annet er de en viktig motivasjon for å gi formell, vanntette beviser også for setninger som kan synes opplagte! Man vet aldri om det lurer et paradoks rundt hjørnet! Ved hjelp av Cantormengden kan man komstruere en kontinuerlig funksjon på [0, 1] som vokser (dog ikke strengt) fra 0 til 1, men som er deriverbar med deriverert er lik null nesten overalt (det vil si på en mengde hvis komplement er av mål null). Vi skal også gi eksempel på såkalte fete Cantormengder. De har alle Cantormengdens topologiske egenskaper, men er ikke lenger av mål null. Ved hjelp av slike fete mengder, skal vi så lage en funksjon som er deriverbar i [0, 1], men hvis derivert ikke er Riemann-integrerbar! Det må være en god motivasjon for å innføre Lebesque-integralet. Tilslutt skal vi gi eksemplet på en undermengde av [0, 1] som ikke er målbar. En kanskje mer vitenskapelig motivasjon enn den pedagogiske vi ga ovenfor er følgende: Om ikke undermengder av intervallet [0, 1] og kontinuerlige funksjoner på det samme intervallet skulle være av primær og basal interesse i matematikken, hva da? Det synes opplagt at dette er studieobjekter av første rang. Dessuten har Cantormengdenen og alle dxens fettere og kusiner en rekke anvendelser både i matematikk, statistikk og fysikk. Cantormengden Konstruksjon av Cantors mengde Så til Cantormengden. Vi starter med å definere en nedstigende følge av undermengder C n av intervallet [0, 1]. Hverav disse er en union av endelig mange lukkede intervaller; for å være presis er de unionen av 2 n
2 intervaller. Definisjonen av undermengdene C n er rekursiv. Vi begynner med å la C 0 = [0, 1]. For å danne C 1 fra C 0 deler vi C 0 i tre like lange intervaller og fjerner det åpne, midterse intervallet. Det betyr at C 1 = [0, 1/3] [2/3, ], og det vi fjerner, er intervallet (1/3, 2/3): 0 1 1/3 2/3 Om nå C n er konstruert, lager vi C n+1 på en tilsvarende måte. Hvert av delintervallene i C n deler vi i tre like deler, og så kaster vi vekk det åpne, midterste intervallet. For eksempel blir C 2 = [0, 1/9] [2/9, 3/9] [6/9, 7/9] [8/9, 9/9]: 0 1 1/9 2/9 1/3 2/3 7/9 8/3 På denne måten konstruerer vi en nedstigende kjede av lukkede mengder C n,ogvi lar Cantormengden, som vi skal betegne med C, være snittet av dem; altså C = ν 0 C ν. Cantormengden er av mål null. I hvert av de rekursive skrittene i konstruksjonen av Cantormengden der vi dannet C n fra C n 1 fordoblet vi antall delintervaller. Vi delte jo hvert delintervall ti C n 1 i tre og kastet bort et av dem. Ved induksjon følger det at C n består av 2 n delintervaller. De er alle lukkede, siden intervallene vi fjerner er åpne. Hvert av dem har en lengde som er en tredjedel av lengden til de foregående, og det betyr at alle delintevallene til C n er av lengde 3 n. Vi oppsummerer dette i følgende lemma: Lemma 1 i) Mengdene C n er alle lukkede, og de danner en nedstigende kjede; det vil si at C n+1 C n. ii) Mengden C n består av 2 n parvis disjunkte, lukkede intervaller som hvert er av lengde 3 n. iii) Målet av C n er gitt ved µc n =(2/3) n. Det er klart at C er lukket (snitt av lukkede er lukket), og siden målet av en nedstigende kjede av målbare mengder er lik grensen for målet av mengdene, finner vi: µc = µ( n 1 C n ) = lim n µc n = lim n (2/3) n =0. 2
3 Vi har bevist: Setning 1 Cantormengden er av mål null. Cantormengden er selvsimilær. Cantormengden har en egenskap som vi kunne omtale som å være selvsimilær. I klartekst betyr det at hvert delintervall I ienav mengdene C n snitter C i en mengde som er ekvivalent med hele Cantormengden der vi med å si at mengdene er ekvivalente, mener at de er ekvivalente som metriske rom. Vi gjenfinner altså en kopi riktig nok forminsket av Cantormengden i hvert av delintervallene. Denne selvrsimilariteten kan vises ved bruk av en ganske enkel funksjon. For å beskrive denne, lar vi I betegne et av delintervallene til C n. Det er av lengde 3 n, og det har et venstre endepunkt e og et høyre endepunkt f. Altså er I =[e, f] der f = e+3 n. Avbildningen φ som etablere selvrsimilariteten, er gitt på [0, 1] ved φ(x) =e +3 n x. Den tar opplagt verdier I, og den er invertibel, med ψ(x) =3 n (x e) som invers. Vi finner φ(x) φ(y) =3 n x y, såφ er nesten en isometri. Den bevarer ikke avstander, men forminsker alle avstander med den samme faktoren 3 n. Deres relative størrelse bevares dermed. La oss kalle en slik avbildning for en kvasiisometri. Avbildningen φ bevarer altså forholdet mellom størrelser. Det betyr at en tredeling av et intervall [0, 1] blir gjenspeilet i en tredeling av intervallet I. Det følger lett og burde være intutivt klart at φ avbilder Cantormengden C på snittet C I, ogat restriksjonen av φ til C er invertibel med restriksjonen av ψ til C I som invers. Dette betyr ar C og C I er kvasiisometriske. De er altså ekvivalente som metriske rom og har nøyaktig de samme egenskapen, bortsett fra de rent numeriske. For eksempel har de samme kardinalitet, og de er homeomorfe. Vi har etablert følgende setning: Setning 2 For hvert delintervaller I er C og C I ekvivalente metriske rom. Cantor mengden er ingensteds tett. En undermengde A X av et metrisk rom X sies å være ingensteds tett nowhere dense på engelsk dersom det indre av tillukningen av X er tomt. En annen måte å si dette på er å si at tillukningen av X ikke inneholder noen åpen mengde. I vårt tilfelle, når A [0, 1] og A er lukket, betyr dette at A ikke inneholder noe intervall. Setning 3 Cantormengden har ingen indre punkter: i.e., den inneholder ingen intervaller. Bevis. Anta at J [0, 1] er et intervall og la a være lengden av det. La n være et så stort naturlig tall at 3 n <a.dakanj ikke være inneholdt i noen av delintervallene 3
4 til C n siden disse alle har lengde 3 n som er mindre enn lengde av J. Følgelig kan ikke J ligge i C = n 0 C n. Setning 4 Cantormengden har ingen isolerte punkter, eller sagt noe annerledes, alle dens punkter er opphopningspunkter. Bevis. La x C, og la I være et intervall omkring x. Vi må vise at I inneholder punkter fra C som er forskjellig fra x. Laa være avstanden fra x til det nærmeste endepunktet til I. Velg et så stort naturlig tall n at 3 n <a. Delintervallet til C n der x ligger, må da være inneholdt i I. Men siden C er selvsimilær, vet vi at det finnes uendelig mange punkter fra C i hvert delintervall, og og følgelig også i I. Spesielt finnes det punkter fra C som er forskjellig fra x der. Cantormengden er ikke tellbar Vi skal nå gi en beskrivelse av punktene i Cantormengden ved hjelp av endepunktene til delintervallene i mengdene C n. Den vil blant annet ha som følge at Cantormengden ikke er tellbar. La nå x C. På hvert nivå altså for hver n vil x ligge i nøyaktig ett av delintervallene til C n. Selvsagt må x ligge i et siden C = n 1 C n, og like selvsagt kan x bare ligge i ett siden delintervalene er disjunkte. Vi finner således en entydig gitt nedstigende følge av delindervaller I n slik at x n 1 I n. Videre er x det eneste elementet i dette snittet; for var det et annet element der, la oss si y, ville lengden av I n være mindre enn x y for n tilstrekkelig stor, og da kunne ikke I n inneholde både x og y. Vi konkluderer med at n 1 I n = {x}. Det naturlige spørsmålet er nå om det gjelder for alle slike følger av delintervaller at snittet deres består av nøyaktig ett element? At det ikke kan ha to eller flere følger, slik vi nettopp så, av at lengden til delintervallene nærmer seg null når n, men a priori kunne det tenkes at snittet var tomt. Imidlertid er det ikke det: Lemma 2 Anta at {I n } n=1 er en følge av intervaller som oppfyller følgende to betingelser: 1. I n er et av delintevallene i C n, 2. Følgen er nedstigende; i.e., I n+1 I n. Da består n 1 I n av nøyaktig ett element. Omvendt, om x C, så finnes en entydig slik følge av intervaller hvis snitt er lik {x}. 4
5 Bevis. Vi trenger bare vise at snittet er ikketomt, resten har vi allerede bevist. For hvert intervall I n, lar vi e n være et av endepunktene (fritt valg). Følgen {e n } er en Cauchy-følge fordi e n e m 3 n for alle n m siden både e m og e n ligger i I m.det betyr at følgen {e n } konvergerer mot en x. La oss sjekke at x ligger i alle intervallene I m.lam være gitt; vi skal vise at x I m.dersome n = e m fra et visst n av, er x = e m, og vi er fremme. Tilsvarende gjelder om e n fra et visst n av er lik det andre endepunktet e m til I m. Vi kan altså anta at det finnes en n slik at e n ikke er et av de to endepunktene til I m og så stor at x e n < 1 2 max { x e m, x e m }. Siden e n I m, følger det at x I m. Underveis i dette beviset fortok vi flere valg av endepunkter. Vi skal se at dette valget kan standardiseres, slik at vi får en entydig følge av endepunkter tilordnet x C. Vi sier at en følge {e n } er god dersom: 1. Hver e n er et av endepunkene til et av delintervallene til C n 2. For hver n 1ere n 1 og e n endepunkt i det samme delintervallet til C n. I en nedstigende følge {I n } av delintevaller er I n ett av to delintervaller som er oppstått ved en tredeling av I n 1. Følgelig og det er poenget har I n ett og bare ett felles endepunkt med I n 1. Vi lar e n 1 være dette felles endepunktet. Da er det klart at følgen {e n } er en god endepunktsfølge. Omvendt, til hver slik gode følge av endepunkter, kan vi lage en nedstigende følge av delintervaller. Vi lar naturligvis I 0 = C 0,ogforn 1, lar vi I n være det delintervallet av C n som har både e n 1 og e n som endepunkt. Det er klart at I n I n 1 siden de har et felles endepunkt.vi har dermed vist: Setning 5 Det er en-en tydig korrespondanser mellom Cantormengden og følgende to mengder: i) Mengden av gode endepunktesfølger {e n }. ii) Mengden av nedstigende følger {I n } av delintervaller til C n. En slike følge av endepunkter eller delintervaller kan beskrives ved en serie binære valg. Naturligvis er alltid I 0 = C 0, og der kan vi velge e 0 på to måter; enten er e 0 lik 0, eller så er er e 0 lik 1. I det videre skal vi heller si at vi velger det venstre endepunktet det valget betegnes med v eller det høyre som betegnes med h. Siden e 0 må ligge i I 1 bestemmes I 1 av dette valget. Tilsvarende, vil vi ha to muligheter for e 1. Vi kan la e 1 = e 0 og da holder vi oss til venstre, og valget betegnes med vv eller vi kan la e 0 være det andre endepunktet til I 1 og da betegnes valget med vh. 5
6 Generelt, dersom vi har valgt e 0,e 1,...,e n 1 har vi nøyaktig to muligheter for e n. Vi tredeler jo I n 1, og kaster bort midtdelen. Det betyr at e n 1 ligger i ett av de to nye delintervallene, og vi har valget mellom å la e n = e n 1 eller å la e n være det andre endepunktet til I n valg som vi bokfører ved å føye henholdsvis en v eller en h til listen av v-er og h-er. Setning 6 Det er en-en-tydig korrespondanse mellom punkter i C og sekvenser {w n } n=1 der hver w i enten er en v eller en h. Bevis. Dette følger av hva vi nettopp sa, og korrespondansen mellom punkter i C og sekvenser av endepunkter fra setning 5. Som et umiddelbart korollar får vi: Korollar 1 Cantormengden er ikke tellbar, men har samme kardinalitet som R. Bevis. Cantors diagonalmetode som brukes til å vise at mengden av følger av nuller og enere er overtellbar gir dette. Vi kunne selvsagt bruke en vilkårlig mengde med to elementer i beskrivelsen ovenfor, for eksempel A = {0, 2} som gir en treadisk0 utvikling av tall. En annen mulighet ville vært å bruke mengden { kron, mynt }. Da ville Cantormengden vært rommet av alle mulig utfall for tellbare myntkastsekvenser. Eksempel. Endepunktene i delintervallene ligger alle i Camtormengden, og de tilsvarer valgsekvenser som til slutt stabiliserer seg med bare venstrevalg eller høyrevalg. Eller sagt anneledes, sekvenser som etterhvert kun består av v-er eller h-er. De med bare v-er i sekvensen er det minste endepunktet i et delintervall, og de med bare h-er er det største. Eksempelvis er 7/81 Cetendepunkt, som tilsvarer sekvensen vhvhvhhhhhh.... Sammenheng med den ternære utviklingen av tall På samme måte som ethvert tall x [0, 1] har en desimalutvikling, har enhver x også en ternær utvikling eller en tresimal utvikling kunne man være fristet til å si. Vi kan skrive x som en uendelig sum x = ν=1 a ν3 ν der koeffisientene a ν enten er 0, 1 eller 2. En annen måte å fremstille x på, som kanskje er mer i stil med hvordan vi vanligvis skriver desimaltall, er å skrive x =0.a 1 a 2 a 3. Der altså tresimalene a ν er blant tallene 0, 1og2. En slik fremstilling er entydig, dog med ett unntak. En uendelig tresimalhale bestående av en null etterfulgt av toere er ekvivalent med en en ener etterfulgt av 6
7 en hale av bare nuller helt i overenstemmelse med hva vi er vant til med desimaltall, nemlig at = For eksempel har vi likheten 0, = , der de to ekvivalente halene er rødfarget. La oss vende tilbake til Cantormengden, der vi nå kan karakterisere endepunkten til delintervallene i C n ved hjelp av deres ternære utvikling. De venstre endepunkten er på formen x =0.a 1 a 2 a n 000, der a ν alle enten er null eller to, mens de høyre er karakterisert ved å være på formen x =0.a 1 a 2 a n 0222, der også a ν alle enten er null eller to. Dette sjekker man lett ved induksjon: Hvis e er et ventstreendepunkt vil det enten bevares, eller så får det et tillegg på 3 (n+1) som endrere halen fra...a n 000 til...a n =...a n Om det er høyre endepunkt blir det enten bevart, eller får et fradrag på 3 (n+1) som altså endrer halen fra...a n til...a n 000. Cantormengden er grensen av følger av endepunkter, ser vi at: Setning 7 Cantormengden består av de tallene x [0, 1] med en ternær utvikling på formen x = a 1 a 2 a n der hver a ν enten er null eller to. Cantormengden er totalt usammenhengende Et topologisk rom (eller et metriske rom) kalles sammenhengende dersom det ikke kan skrives som en union av to ikke-tomme disjunkte, åpne mengder. Om dette var tilfellet og X = U 1 U 2 med U 1 U 2 = og begge mengdene U og U 2 åpne, ville jo både U 1 og U 2 begge også være lukkede siden den ene er komplementet til den andre. Defor er sammenheng ekvivalent med at det ikke finnes andre undermengder enn og X selv som både er lukkede ogåpne. Fra vår vante forestillinsverden er f.eks R og R 2 sammenhengende. Cantormengden er langti fra sammenhengende. Den er til og med det vi kaller for totalt usammenhengende. Det betyr at de eneste sammenhengende undermengdene den har, enten er ettpunktsmengdene eller den tomme mengden. Med andre ord, om x 1 og x 2 er to forskjellige punkter fra C, så finnes det to disjunkte mengder U 1 og U 2 som begge er åpne og lukkede i C med x 1 U 1 og x 2 U 2 og slik at U 1 U 2 = X. La oss nå se på C. Velg to forskjellige punkter x og y med x<y. La a være avstanden mellom dem, og velg n så stor at 3 n <a. Da kan ikke x og y ligge i samme delintervall til C n (de kan ikke begge ligge i noe intervall av lengde 3 n ). Derfor finnes en z C n med x<z<y. Vi lar U =(,z] C og V = C [z, ). Det er da to disjunkte mengder som både er åpne og lukkede i C. Mengden U er lukket i C siden den er snittet av C med en lukket mengde, og at den er åpen, følger siden U også er lik (,z) C siden z ikke ligger i C. Tilsvarenede gjelder for V. Mengdene U og V er disjunkte (siden z C) og deres union er lik hele C (siden 7
8 allerede C n er inneholdt i unionen). Dette viser at Cantormengden er totalt usammenhengende. Djeveltrappen Alfred Hitchcocks klassiske filmgrøsser The Thirty-Nine steps fra 1935 er ingen ting imot Cantors djeveltrapp med sitt overtellbart antall trinn! Den er en riktig grøsser i funksjonenes verden: En kontinuerlig funksjon på [0, 1] som vokser fra 0 til 1, men som allikevel nesten over alt har en derivert som er lik null! Djeveltrappfunksjonen kan selvsagt ikke være deriverbar over alt, og det er nettopp på Cantormengen dens deriverte ikke eksisterer. Det er der funksjonen vokser, går fra trinn til trinn for å holde oss til trappeanalogien. Imotsetning til en Hitchcockfilm som det formodentlig ligger mye arbeid bak er djeveltrappen ikke voldsomt arbeidskrevende å lage, særlig ikke når vi allerede har konstruert Cantormengden. Vi starter med å la χ n betegne den karakteristiske funksjonen til mengden C n.den tilfredstiller χ n (x) =1nårx C n og χ n (x) =0nårx C n. Vi lar så g n =(3/2) n χ n. Det er en funksjon som er konstant på C n med verdien (3/2) n, og som er identisk lik null utenfor. Vi integrerer g n og lar f n (x) = x 0 g n (t) dt. Disse funksjonenen er alle stykkevis lineær funksjon. I hvert av delintervallene til C n vokser de med stigningskoeffisient lik (3/2) n, så de blir brattere og brattere jo større n bli, mens utenfor C n er de konstante se figur 1, der vi har tegnet to suksessive slik funsksjoner /9 2/9 1/3 2/3 7/9 8/3 Figur 1: To av funskjonene f n og f n+1 som konverger mot djeveltrappen. Når x gjennom løper et av delintervallene til C n, la oss kalle det I, får funksjonsverdien til f n en viss økning. Siden stigningskoeffisienten er (3/2) n, og lengden av 8
9 delintervallet er 3 n, blir økningen (3/2) n 3 n =2 n. Vi ser nå på f n+1 over det samme delintervallet. Mengden C n+1 har to delintervaller inneholdt i I. Over det første vokser f n+1 med 2 (n+1), den er konstant i intervallet mellom de to delintervallene for så igjen å vokse med 2 (n+1) over det andre delintervallet. Totalt vokser altså f n+1 med 2 2 (n+1) =2 n over intervallet I, og det er den samme veksten som f n har. Det betyr at om f n og f n+1 tar samme verdi i det venstre endepunktet til I, tar de også samme verdi i det høyre. Siden f n (0) = f n+1 (0) = 0 følger det ved en enkel induksjon at f n (e) =f n+1 (e) for alle endepunktene til C n+1. Dermed har vi Lemma 3 Dersom m n så er f n (x) =f m (x) for alle x C m, spesielt gjelder dette for alle x C. Videre skal vi vise: Lemma 4 Vi har for alle x [0, 1]. f n+1 (x) f n (x) < 2 n Bevis. For å etablere dette ser vi på ulikheten ( 3 2 )n+1 t ( 3 2 )n t =( 3 2 )n t ( 1 2 )n, som er gyldig for 0 t ( 1 3 )n.omi er et av delintervallene til C n med venstre endepunkt e, såerf n (x) =( 3 2 )n (x e) nårx I, mens f n+1 (x) ( 3 2 )n+1 (x e) med likhet når x ligger i den venstre tredjedelen av I. Lemmaet følger da av ulikheten ovenfor siden lengden av I er lik ( 1 3 )n. Det vanlige trikset med en telskoperende sum og en geometrisk rekke gir oss at {f n (x)} er uniformt Cauchy: f m (x) f n (x) m 2 i 2 (n 1). Det betyr at følgen {f n } kovegerer uniformt og grensefunksjonen er nettopp djeveltrappen! Vi betegner den med f. Som integraler av begrensede funksjoner er f n (x) alle kontinuerlige, og siden {f n } konvergerer uniformt, er f er kontinuerlig. Videre er f konstant over hvert av delintervallene til komplementet til Cantormengden, og følgelig er f deriverbar der med derivert lik null. Vi har: i=n 9
10 Setning 8 Funksjonen f(x) = lim n f n (x) er kontinuerlig og monoton i [0, 1], den vokser fra 0 til 1, men dens deriverte er 0 nesten over alt. Fete Cantormengder Hovedelementet i Cantors konstruksjon er hva man kunne kalle en sukssesiv trichotomi eller en gjentatt tredeling på godt norsk av et intervall. I den konstruksjonen ble intervallene hele tiden delt i tre like store deler, men man kan jo tenke seg endre forhold mellom delene. Hvis intervallene som kastes vekk blir kortere og kortere i forhold til delintervallene de kastes vekk fra, kan man oppnå fete Cantormengder. Det er mengder med Cantormengdens topologiske egenskaper, men som er av positivt mål. Vi skal i det følgende konstruere slike fete Cantormengder med med mål så nær oppunder én vi vil. De vil altså målmessig utgjøre en så stor del av [0, 1] som vi måtte ønske, men de vil fortsatt ha Cantormengdens topologiske egenskaper, for eksempel vil de være ingensteds tette. Konstruksjonen er nærmest en kopi av konstruksjonen av Cantormengden, men vi skal som sagt, kaste vekk mindre og minder deler av intervallene. I konstruksjonen er det en parameter λ, et reelt tall med λ>2. Som med Cantormengden tar vi utgangspunkt i C 0 = [0, 1], og vi lar D 1 være det åpne intervallet i C 0 som er symmetrisk om midten av C 0, og som har lengde 1 λ, i.e., D 1 =(1/2 1/2λ, 1/2+1/2λ). Vi setter C 1 = C 0 \ D 1. Da har D 1 to delintervaller, og neste skritt i prosessen er å kaste vekk fra hvert av dem et åpent intervall, symmetrisk om midtpunkte deres, men denne gang av lengde 1/2λ 2, og la C 2 være det gjenstående. Det er en union av fire lukkede intervaller. I det rekursive steget antar vi at C n er konstruert og har 2 n delintervaller. Fra hvert av dem fjerner vi et åpent delintervall, symmetrisk om midten, og av lengde 2 n λ (n+1), og vi lar C n+1 være unionen av alle intervallene som står igjen. At C n+1 har 2 n+1 delintervaller er klart. Strengt tatt må vi argumentere for at det er plass nok til å fjerne slike intervaller, men når det gikk bra å fjerne en tredjedel i hvert steg slik vi gjorde da vi konstruerte Cantormengden, går det også bra å fjerne mindre. Vi lar den generaliserte Cantormengden C λ være definert ved: Vi skal vise følgende: C λ = C n. n=0 Setning 9 C λ er en lukket, og ingensteds tett undermengde av [0, 1]. Den er en fet 10
11 Cantormengde av mål gitt ved µ(c λ )= λ 2 λ 1. Før beviset bemerker vi at λ 2 går mot 1 når λ, så denne konstruksjonen gir λ 1 fete Cantormengder av mål vilkårlig nær 1. Bevis. Vi beregner målet av mengden vi har fjernet, altså av komplementet Cλ c til den generaliserte Cantormengden. Denne er lik n=1 Cc n der unionen er disjunkt. Da vi laget C n+1 fra C n, fjernet vi et intervall av lengde 2 n λ (n+1) fra hvert av de 2 n delintervallene til C n. Til sammen har disse intervallene mål 2 n 2 n λ (n+1) = λ (n+1). Summerer vi dette over alle n, finner vi µ(c c λ)= λ (n+1) = λ 1 (1 λ 1 ) 1 =(λ 1) 1, n=0 som gir setningen siden µ(c λ )=1 µ(c λ c ). En deriverbar funksjon hvis derivert ikke er integrerbar. Kostruksjonen av denne funksjonen ble gjort av den italienske matematikeren Vito Volterra i Den baserer seg på to ting. Det ene er de fete Cantormengden vi nettopp konstruerte, og det andre er funksjonen x 2 sin 1 om x = 0 x f(x) = 0 om x =0. Denne er deriverbare over alt, også i origo, der den deriverte er null det ser man lett siden (f(h) f(0))h 1 = h sin 1 som går mot null med h. Derimot er den ikke h kontinuerlig deriverbar i origo, fordi grensen av den deriverete som er 2x sin 1 cos 1 x x ikke eksisterer. La nå J =[a, b] være er et intervall. Vi skal tilpasse f(x) til J. Vi lar to funksjoner være definert ved f 1 (x) = f(x a) ogf 2 (x) = f(b x). Det betyr at vi har flyttet det singulære punktet respektivt til a og til b, ogforf 2 s vedkommende, har vi for forskyvningen speilet f gjenom y aksen. Funksjonen f(x) har et tellbart uendelig antall maksimumspunkter. De danner en følge som konvegerer mot origo. Det samme gjelder da f 1, med unntak av at maksimumspunktene hoper seg opp mot a. Velg ett av dem kall det ξ som ligger nærmere a en (b a)/2; det vil si at det ligger i venstre halvdelen av intervallet [a, b]. Da vil ξ = b a + ξ ligge symmetrisk til ξ om midtpunktet til [a, b]. Siden f 2 er 11
12 fremkommet ved å speile f gjennom y-aksen også forskyve origo til b, vil ξ være maksimumspunkt for f 2,ogf 2 (ξ )=f 1 (ξ). Vi lar nå f 1 (x) a x ξ f 1 (ξ) ξ<x<ξ f J (x) = f 2 (x) ξ <x b 0 for alle andre verdier av x Vi har altså kappet f 1 ved ξ og f 2 ved ξ og lagt en horisontal bro mellom de to maksimumspunktene. Da er f J deriverbar overalt. I punktene ξ og ξ fordi både den horisontale broen og f 1 respektive f 2 har derivert null i disse punkten, i endepunktene til J fordi til syvende og sist f er deriverbar i origo, mens i alle andre punkter er det opplagt. direkte av definisjonen av f J og av at sin x < 1 Lemma 5 La x [0, 1] og la δ J (x) betegne avstanden fra x til det nærmeste endepunktet til intervallet J. Da gjelder det at f J (x) δ J (x) 2 Vi lar nå I betegne mengden som består av alle de delintervallene vi fjernet da vi konstruerte den fete Cantormengden C. Funksjonen vi er på jakt etter er gitt ved F (x) = I I f I. Intervallene fra I er parvis disjunkte, så for hver x [0, 1] er det maksimalt ett av leddene i summen som ikke forsvinner i x. Ligger x i C, forsvinner alle leddene der, og F (x) = 0. Er derimot x inneholdt i et intervall I blant dem vi kastet vekk, er F (x) =f I (x). Vi sjekket ovenfor at f I var deriverbar, og det betyr at F er deriverbar i alle punkten i I I I. Den er altså deriverbar utenfor den fete Cantormengden. Vi skal vise følgende: Setning 10 F er deriverbar over alt. Om x C, så er F (x) = 0 og F kontinuerlig i x. er ikke La x C, det er der problemene er. Vi så at F (x) = 0, så differentialkvotienten til F i x blir: 12
13 F (x + h) F (x) h = F (x + h) h = f I (x + h)/h 0 x + h C om x + h I for en I I Anta at x + h I =[a, b], og la k = δ I (x + h). Da er h k siden x ikke ligger i I, og etter lemma 5 ovenfor finner vi: F (x + h) F (x) h f I(x + h)/h δ I (x + h) 2 / h = k 2 /h h som viser at F er deriverbar med derivert lik 0 i x. At F ikke er kontinuerlig i x følger av at enhver omegn om x innholder intervaller fra I, og i slike tar F verdiene ±1 (uendelig mange ganger). Setning 11 Volterra-funksjonen F er deriverbar over alt, men dens deriverte er ikke Riemann-integrerbar. Bevis. Vi har sett at F eksiterer over alt, og at den er diskontinuerlig i alle punktene i en fet Cantor mengde; som altså er av mål ekte større enn null. Nå er det slik at en funksjon er Riemann-intergrerbar hvis og bare hvis den er kontinuerlig nesten over alt; det vil si at mengden av dens diskontinuitetspunkter er av mål null. Det følger av dette at F ikke er Riemann-integrerbar. En mengde som ikke er Lebesgue-målbar Det finnes et klassisk eksempel på en ikke målbar undermengde av R som blir presentert i de fleste lærebøker i målteori så, altså, nå også her! Eksemplet baserer seg på en oppdeling av de reelle tallene ved hjelp av translater av de rasjonale tallene. Vi lar Q x = x + Q for x R; i.e., Q x = {x + q : q Q}. Disse mengdene danner en partisjon eller en oppdeling av R, som vi burde si på norsk. Det betyr at unionen av dem er lik R (som er opplagt siden x Q x ), og at to av dem enten er like eller disjunkte. Altså: Lemma 6 La x, y R. Dersom Q x Q y =, så er Q x = Q y. Bevis. Anta at z Q x Q y. Da kan vi skrive z = x + q = y + r der q og r er rasjonale tall. Det betyr at for et hvert rasjonalt tall s, såerx + s = y + r q + s Q y siden 13
14 summen av rasjonale tall er rasjonal. Vi har dermed vist at Q x Q y. Ved symmetri finner vi Q x = Q y. Vi lar P betegene mengden av disse translatene. Med andre ord er P = {Q x : x R}. For hvert element P Pvelger 1 vi en a P P, og siden vi kan addere rasjonale tall til a P uten å forlate P, kan vi passe på å velge a P slik at a P [0, 1]. Vi lar A = {a P : P P}, og vi skal vise at A ikke er målbar. Anta fra nå av at A er målbar; det skal vise seg at det fører til en motsigelse. Lemma 7 Dersom q og r er to rasjonale tall, og A + q A + r =, så er q = r. Bevis. Et element z som ligger både i A + q og i A + r kan skrives som z = a P + q = a P + r. Men da er a P = a P + r q P, som ikke er tilfelle når a P = a P, siden de forskjellige a P -ene ble plukket fra forskjellige P -er. Derfor er a P = a P, og følgelig q = r. Den mengden vi skal bruke til å få en motsigelse er følgende: E = q [ 1,1] Q A + q. Siden translater av målbare mengder er målbare, følger det at E er målbar dersom A er det, og etter lemma 7 ovenfor er unionen disjunkt. Da gir additivitet til Lebesgue-målet oss at µ(e) = µ(a + q) = µ(a), q [ 1,1] Q q [ 1,1] Q siden µ er translasjonsinvariant. Summen tilhøyre er en tellbart uendelig sum med alle addender like. For at det skal gi mening, må enten alle addendene være null og altså µ(e) = 0 eller så er µ(e) =. Men nå er E [ 1, 2] (siden 0 a 1og 1 q 1 gir 1 a + q 2) og det er klart at [0, 1] E (siden 0 a, a 1 gir 1 q 1 der q = a a ). Derfor er 1 µ(e) 3, og det gir oss motsigelsen vi trenger. Konklusjonen er at A ikke er målbar. Versjon: Monday, May 14, :52:55 AM 1 Her bruker vi det såkalte utvalgs aksiomet fra mengdelæren. 14
Analysedrypp II: Kompletthet
 Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Notat om kardinalitet for MAT1140 (litt uferdig)
 Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
Notat om kardinalitet for MAT1140 (litt uferdig) Poenget med tall kan man kanskje si er det å telle. In mengdeteorien ønsker man å telle antall elementer i en mengde, og det tallet man oppnår kalles da
Analysedrypp IV: Metriske rom
 Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
NOTAT OM UNIFORM KONTINUITET VEDLEGG TIL BRUK I KURSET MAT112 VED UNIVERSITETET I BERGEN
 NOTAT OM UNIFORM KONTINUITET VEDLEGG TIL BRUK I KURSET MAT2 VED UNIVERSITETET I BERGEN ANDREAS LEOPOLD KNUTSEN OG ARNE STRAY. Innledning og definisjoner Vi vil i dette notatet betrakte reelle funksjoner
NOTAT OM UNIFORM KONTINUITET VEDLEGG TIL BRUK I KURSET MAT2 VED UNIVERSITETET I BERGEN ANDREAS LEOPOLD KNUTSEN OG ARNE STRAY. Innledning og definisjoner Vi vil i dette notatet betrakte reelle funksjoner
To nyttige begreper. Ekvivalensrelasjoner
 To nyttige begreper Det er to begreper fra mengdelæren som til stadighet vil bli brukt i dette kurset, og som vi av erfaring vet kan være tungt fordøyelig for endel studender. For å få en skikkelig forståelse
To nyttige begreper Det er to begreper fra mengdelæren som til stadighet vil bli brukt i dette kurset, og som vi av erfaring vet kan være tungt fordøyelig for endel studender. For å få en skikkelig forståelse
Litt topologi. Harald Hanche-Olsen
 MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
Grunnleggende notasjon ℕ = 1, 2, 3, 4, 5, 6, ℤ =, 3, 2, 1, 0, 1, 2, 3,
 Grunnleggende notasjon ℕ,, 3, 4, 5, 6, ℤ, 3,,, 0,,, 3, ℝ 𝑎𝑙𝑙𝑒 𝑟𝑒𝑒𝑙𝑒 𝑡𝑎𝑙𝑙 ℚ 𝑎𝑙𝑙𝑒 𝑟𝑎𝑠𝑗𝑜𝑛𝑎𝑙𝑒 𝑡𝑎𝑙𝑙 𝑎 𝑎, ℤ, 0 Induksjonsprinsippet Anta at for hver 𝑛 ℕ har vi gitt et utsagn 𝑃. Anta videre at vi vet at følgende
Grunnleggende notasjon ℕ,, 3, 4, 5, 6, ℤ, 3,,, 0,,, 3, ℝ 𝑎𝑙𝑙𝑒 𝑟𝑒𝑒𝑙𝑒 𝑡𝑎𝑙𝑙 ℚ 𝑎𝑙𝑙𝑒 𝑟𝑎𝑠𝑗𝑜𝑛𝑎𝑙𝑒 𝑡𝑎𝑙𝑙 𝑎 𝑎, ℤ, 0 Induksjonsprinsippet Anta at for hver 𝑛 ℕ har vi gitt et utsagn 𝑃. Anta videre at vi vet at følgende
Analysedrypp I: Bevis, mengder og funksjoner
 Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
Analysedrypp I: Bevis, mengder og funksjoner Hensikten med Analysedrypp er å bygge en bro mellom MAT1100 og MAT1110 på den ene siden og MAT2400 på den andre. Egentlig burde det være unødvendig med en slik
TOPOLOGI. Dan Laksov
 Forum för matematiklärare TOPOLOGI Dan Laksov Institutionen för Matematik, 2009 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Topologi Dan Laksov Notater for Forum för Matematiklärare. Høst
Forum för matematiklärare TOPOLOGI Dan Laksov Institutionen för Matematik, 2009 Finansierat av Marianne och Marcus Wallenbergs Stiftelse Topologi Dan Laksov Notater for Forum för Matematiklärare. Høst
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11)
 Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Karakteriseringen av like mengder. Mengder definert ved en egenskap.
 Notat 2 for MAT1140 2 Bevis La oss si at vi er overbevist om at utsagn P er sant, og at vi ønsker å kommunisere denne innsikten. Eller la oss si vi er ganske sikre på at P er sant, men ønsker, overfor
Notat 2 for MAT1140 2 Bevis La oss si at vi er overbevist om at utsagn P er sant, og at vi ønsker å kommunisere denne innsikten. Eller la oss si vi er ganske sikre på at P er sant, men ønsker, overfor
Mer om mengder: Tillegg til Kapittel 1. 1 Regneregler for Booleske operasjoner
 MAT1140, H-16 Mer om mengder: Tillegg til Kapittel 1 Vi trenger å vite litt mer om mengder enn det som omtales i første kapittel av læreboken. I dette tillegget skal vi først se på regneregler for Booleske
MAT1140, H-16 Mer om mengder: Tillegg til Kapittel 1 Vi trenger å vite litt mer om mengder enn det som omtales i første kapittel av læreboken. I dette tillegget skal vi først se på regneregler for Booleske
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
TMA4100 Matematikk 1, høst 2013 Teknostart forelesning 6 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Teknostart forelesning 6 Grenseverdier I dagens forelesning skal vi se på følgende: 1 En formell definisjon
1 Mandag 1. februar 2010
 Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Løsningsforslag til utvalgte oppgaver i kapittel 5
 Løsningsforslag til utvalgte oppgaver i kapittel 5 I kapittel 5 har mange av oppgavene et mer teoretisk preg enn du er vant til fra skolematematikken, og jeg har derfor lagt vekt på å lage løsningsforslag
Løsningsforslag til utvalgte oppgaver i kapittel 5 I kapittel 5 har mange av oppgavene et mer teoretisk preg enn du er vant til fra skolematematikken, og jeg har derfor lagt vekt på å lage løsningsforslag
Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 2009
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Løsningsforslag, eksamen MA1101/MA6101 Grunnkurs i analyse I, vår 009 Oppgave 1 Funksjonen g er definert ved g(x)
INVERST FUNKSJONSTEOREM MAT1100 KALKULUS
 INVERST FUNKSJONSTEOREM MAT1100 KALKULUS Simon Foldvik 29. Oktober 2017 1. Introduksjon Vi skal i dette dokumentet bevise en global og en lokal versjon av inverst unksjonsteorem i én variabel. Kort oppsummert
INVERST FUNKSJONSTEOREM MAT1100 KALKULUS Simon Foldvik 29. Oktober 2017 1. Introduksjon Vi skal i dette dokumentet bevise en global og en lokal versjon av inverst unksjonsteorem i én variabel. Kort oppsummert
x A e x = x e = x. (2)
 Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
Notat om Algebra for MAT1140 1 Algebra 1.1 Operasjoner Definisjon 1.1. En operasjon på en mengde A er en avbildning fra A A til A. Bemerkning 1.1. Mer generelt kan man snakke om n-ære operasjoner på A,
En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x).
 Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Aksiom 3.1 (Likhet av mengder). La A og B være mengder. Da er A og B like hvis og bare hvis de har akkurat de samme elementene.
 Notat 3 for MAT1140 3 Mengder 3.1 Mengder definert ved en egenskap Det matematiske begrepet mengde har sin opprinnelse i vår intuisjon om samlinger. Objekter kan samles sammen til et nytt objekt kalt mengde.
Notat 3 for MAT1140 3 Mengder 3.1 Mengder definert ved en egenskap Det matematiske begrepet mengde har sin opprinnelse i vår intuisjon om samlinger. Objekter kan samles sammen til et nytt objekt kalt mengde.
Prøveunderveiseksamen i MAT-INF 1100, H-03
 Prøveunderveiseksamen i MAT-INF 1100, H-03 Denne prøveeksamenen har samme format som den virkelige underveiseksamenen, og inneholder oppgaver av samme type og vanskelighetsgrad. De 15 første oppgavene
Prøveunderveiseksamen i MAT-INF 1100, H-03 Denne prøveeksamenen har samme format som den virkelige underveiseksamenen, og inneholder oppgaver av samme type og vanskelighetsgrad. De 15 første oppgavene
Løsningsforslag til Mat112 Obligatorisk Oppgave, våren Oppgave 1
 Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
7 Ordnede ringer, hele tall, induksjon
 Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
To mengder S og T er like, S = T, hvis de inneholder de samme elementene. Notasjon. Mengden med elementene a, b, c og d skrives ofte {a, b, c, d}.
 Forelesning 0: Mengdelære, Induksjon Martin Giese - 23. januar 2008 1 Mengdelære 1.1 Mengder Mengder Definisjon 1.1. En mengde er en endelig eller uendelig samling objekter der innbyrdes rekkefølge og
Forelesning 0: Mengdelære, Induksjon Martin Giese - 23. januar 2008 1 Mengdelære 1.1 Mengder Mengder Definisjon 1.1. En mengde er en endelig eller uendelig samling objekter der innbyrdes rekkefølge og
Tillegg til kapittel 11: Mer om relasjoner
 MAT1140, H-16 Tillegg til kapittel 11: Mer om relasjoner I læreboken blir ekvivalensrelasjoner trukket frem som en viktig relasjonstype. I dette tillegget skal vi se på en annen type relasjoner som dukker
MAT1140, H-16 Tillegg til kapittel 11: Mer om relasjoner I læreboken blir ekvivalensrelasjoner trukket frem som en viktig relasjonstype. I dette tillegget skal vi se på en annen type relasjoner som dukker
Partielle ordninger, Zorns lemma og utvalgsaksiomet
 MAT1140, H-15 Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns
MAT1140, H-15 Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns
Notasjon i rettingen:
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
Oppsummering TMA4100. Kristian Seip. 26./28. november 2013
 Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09
 Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Oppgaveark Uke 37 (07/09-11/09) MAT111 - H09 Oppgave 1 Du ar fått deg en jobb i et firma og skal kjøre til en konferanse med overnatting. Du drar jemmefra på mandag kl 07:15 og ankommer 11:07. Du overnatter
Løsning til prøveeksamen i MAT2400, V-11
 Løsning til prøveeksamen i MAT400, V-11 Oppgave 1 a) Vi ser at den deriverte f (x) = 1 1+x alltid er mindre enn eller lik 1 i tallverdi. Gitt to punkter x, y R, finnes det ifølge middelverdisetningen en
Løsning til prøveeksamen i MAT400, V-11 Oppgave 1 a) Vi ser at den deriverte f (x) = 1 1+x alltid er mindre enn eller lik 1 i tallverdi. Gitt to punkter x, y R, finnes det ifølge middelverdisetningen en
Litt mer mengdelære. INF3170 Logikk. Multimengder. Definisjon (Multimengde) Eksempel
 INF3170 Logikk Forelesning 2: Mengdelære, induktive definisjoner og utsagnslogikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo Litt mer mengdelære 2. februar 2010 (Sist oppdatert: 2010-02-02
INF3170 Logikk Forelesning 2: Mengdelære, induktive definisjoner og utsagnslogikk Roger Antonsen Institutt for informatikk, Universitetet i Oslo Litt mer mengdelære 2. februar 2010 (Sist oppdatert: 2010-02-02
Deleksamen i MAT111 - Grunnkurs i Matematikk I
 Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
Bergen, oktober. 2004. Løsningsforslag til Deleksamen i MAT - Grunnkurs i Matematikk I Mandag. oktober 2004, kl. 09-2. Oppgave Beregn grensen f.eks. ved hjelp av l Hôpitals regel. lim x ln x x Vi ser at
INF3170 Forelesning 2
 INF3170 Forelesning 2 Mengdelære, induktive definisjoner og utsagnslogikk Roger Antonsen - 2. februar 2010 (Sist oppdatert: 2010-02-02 14:26) Dagens plan Innhold Litt mer mengdelære 1 Multimengder.........................................
INF3170 Forelesning 2 Mengdelære, induktive definisjoner og utsagnslogikk Roger Antonsen - 2. februar 2010 (Sist oppdatert: 2010-02-02 14:26) Dagens plan Innhold Litt mer mengdelære 1 Multimengder.........................................
Løsningsforslag eksamen 18/ MA1102
 Løsningsforslag eksamen 8/5 009 MA0. Dette er en alternerende rekke, der leddene i størrelse går monotont mot null, så alternerenderekketesten gir oss konvergens. (Vi kan også vise konvergens ved å vise
Løsningsforslag eksamen 8/5 009 MA0. Dette er en alternerende rekke, der leddene i størrelse går monotont mot null, så alternerenderekketesten gir oss konvergens. (Vi kan også vise konvergens ved å vise
Oppsummering TMA4100. Kristian Seip. 16./17. november 2015
 Oppsummering TMA4100 Kristian Seip 16./17. november 2015 Forelesningene 17./18. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 noen tips for
Oppsummering TMA4100 Kristian Seip 16./17. november 2015 Forelesningene 17./18. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 noen tips for
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker
 Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 14. februar 2012 Funksjonsrekker En rekke på formen fn(x) der fn er en funksjon, kalles en n=1 funksjonsrekke. For alle
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 14. februar 2012 Funksjonsrekker En rekke på formen fn(x) der fn er en funksjon, kalles en n=1 funksjonsrekke. For alle
MAT1140: Kort sammendrag av grafteorien
 MAT1140, H-15 MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oppsummering av grafteorien i MAT1140. Vekten er på den logiske oppbygningen, og jeg har utelatt all motivasjon og (nesten)
MAT1140, H-15 MAT1140: Kort sammendrag av grafteorien Dette notatet gir en kort oppsummering av grafteorien i MAT1140. Vekten er på den logiske oppbygningen, og jeg har utelatt all motivasjon og (nesten)
UNIVERSITETET I BERGEN
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT - Grunnkurs i Matematikk II Torsdag 4. juni 05, kl. 09:00-4:00 Bokmål Tillatte hjelpemiddel: Enkel kalkulator i samsvar
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT - Grunnkurs i Matematikk II Torsdag 4. juni 05, kl. 09:00-4:00 Bokmål Tillatte hjelpemiddel: Enkel kalkulator i samsvar
Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3
![Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3 Løsningsforslag. Oppgave 1 Gitt matrisene ] [ og C = A = 4 1 B = 2 1 3](/thumbs/55/37240043.jpg) Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Prøve i Matematikk BYFE DAFE Dato: 27. mai 26 Hjelpemiddel: Kalkulator og formelark Alle svar skal grunngis. Alle deloppgaver har lik vekt. Løsningsforslag Oppgave Gitt matrisene [ 2 A 4 B [ 2 og C [ 2
Oppsummering TMA4100. Kristian Seip. 17./18. november 2014
 Oppsummering TMA4100 Kristian Seip 17./18. november 2014 Forelesningene 17./18. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Oppsummering TMA4100 Kristian Seip 17./18. november 2014 Forelesningene 17./18. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Dedekind introduserer nå en spesiell klasse snitt som han kaller rasjonale snitt:
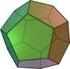 DE IRRASJONALE TALLENE EUDOXUS TESTAMENTE. Dedekind s snitt. Vi så tidligere at de greske matmatikerene kom til klarhet over at ikke alle forhold kunne beskrives som de vi kaller rasjonale tall dvs at
DE IRRASJONALE TALLENE EUDOXUS TESTAMENTE. Dedekind s snitt. Vi så tidligere at de greske matmatikerene kom til klarhet over at ikke alle forhold kunne beskrives som de vi kaller rasjonale tall dvs at
OPPGAVER FOR FORUM
 OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
OPPGAVER FOR FORUM 2006-2007 MERK!: Du skal først skrive hele oppgaveteksten for hver oppgave, og deretter svaret på oppgaven. Hvert svar skal være detajert, og skrevet i et klart og tydelig matematisk
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Forelesning 11 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 11 Transcendentale funksjoner Vi begynner nå på temaet transcendentale funksjoner. I dagens forelesning
TMA4100 Matematikk 1, høst 2013 Forelesning 11 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 11 Transcendentale funksjoner Vi begynner nå på temaet transcendentale funksjoner. I dagens forelesning
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker
 Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 15. februar 2010 Funksjonsrekker En rekke på formen f n (x) der f n er en funksjon, kalles en funksjonsrekke. For alle x
Seksjonene 9.6-7: Potensrekker og Taylor/Maclaurinrekker Andreas Leopold Knutsen 15. februar 2010 Funksjonsrekker En rekke på formen f n (x) der f n er en funksjon, kalles en funksjonsrekke. For alle x
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente Oppvarming Her er et eksempel på et
Løsningsforslag til prøveunderveiseksamen i MAT-INF 1100, H-03
 Løsningsforslag til prøveunderveiseksamen i MAT-INF 1100, H-03 Denne prøveeksamenen har samme format som den virkelige underveiseksamenen, og inneholder oppgaver av samme type og vanskelighetsgrad. De
Løsningsforslag til prøveunderveiseksamen i MAT-INF 1100, H-03 Denne prøveeksamenen har samme format som den virkelige underveiseksamenen, og inneholder oppgaver av samme type og vanskelighetsgrad. De
Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017
 Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017 Andreas Leopold Knutsen 4. oktober 2017 Problem og hovedidé Problem: Finn løsning(er) r på en ligning
Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017 Andreas Leopold Knutsen 4. oktober 2017 Problem og hovedidé Problem: Finn løsning(er) r på en ligning
Eliminasjon av ubetsemthet
 1. Del Eliminasjon av ubetsemthet Warning: En svært midlertidig versjon som er ikke er ferdig. Den er rotete og sikkert full av feil. Forbedring følger etterhvert! versjon 0.3 last update: 10/21/15 2:48:38
1. Del Eliminasjon av ubetsemthet Warning: En svært midlertidig versjon som er ikke er ferdig. Den er rotete og sikkert full av feil. Forbedring følger etterhvert! versjon 0.3 last update: 10/21/15 2:48:38
TMA4240 Statistikk Høst 2008
 TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
MAT jan jan jan MAT Våren 2010
 MAT 1012 Våren 2010 Mandag 18. januar 2010 Forelesning I denne første forelesningen skal vi friske opp litt rundt funksjoner i en variabel, se på hvordan de vokser/avtar, studere kritiske punkter og beskrive
MAT 1012 Våren 2010 Mandag 18. januar 2010 Forelesning I denne første forelesningen skal vi friske opp litt rundt funksjoner i en variabel, se på hvordan de vokser/avtar, studere kritiske punkter og beskrive
Forelesning 1 mandag den 18. august
 Forelesning 1 mandag den 18 august 11 Naturlige tall og heltall Definisjon 111 Et naturlig tall er et av tallene: 1,, Merknad 11 Legg spesielt merke til at i dette kurset teller vi ikke 0 iblant de naturlige
Forelesning 1 mandag den 18 august 11 Naturlige tall og heltall Definisjon 111 Et naturlig tall er et av tallene: 1,, Merknad 11 Legg spesielt merke til at i dette kurset teller vi ikke 0 iblant de naturlige
MAT Grublegruppen Uke 37
 MAT00 - Grublegruppen Uke 37 Jørgen O. Lye Bemerkning: Mye av stoffet i dette notatet er å finne i Kalkulus, kapittel. Dette kapittelet er leselig etter man vet hva følger er, men er ikke pensum før i
MAT00 - Grublegruppen Uke 37 Jørgen O. Lye Bemerkning: Mye av stoffet i dette notatet er å finne i Kalkulus, kapittel. Dette kapittelet er leselig etter man vet hva følger er, men er ikke pensum før i
MA1102 Grunnkurs i Analyse II Vår 2015
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet
 MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma
MAT1140: Partielle ordninger, Zorns lemma og utvalgsaksiomet I dette notatet skal vi se på Zorns lemma, som er et kraftig redskap for å bevise eksistensen av matematiske objekter. Beviset for Zorns lemma
Komplekse tall og komplekse funksjoner
 KAPITTEL Komplekse tall og komplekse funksjoner. Komplekse tall.. Definisjon av komplekse tall. De komplekse tallene er en utvidelse av de reelle tallene. Dvs at de komplekse tallene er en tallmengde som
KAPITTEL Komplekse tall og komplekse funksjoner. Komplekse tall.. Definisjon av komplekse tall. De komplekse tallene er en utvidelse av de reelle tallene. Dvs at de komplekse tallene er en tallmengde som
Sannsynlighetsbegrepet
 Sannsynlighetsbegrepet Notat til STK1100 Ørnulf Borgan Matematisk institutt Universitetet i Oslo Januar 2004 Formål Dette notatet er et supplement til kapittel 1 i Mathematical Statistics and Data Analysis
Sannsynlighetsbegrepet Notat til STK1100 Ørnulf Borgan Matematisk institutt Universitetet i Oslo Januar 2004 Formål Dette notatet er et supplement til kapittel 1 i Mathematical Statistics and Data Analysis
ANDREAS LEOPOLD KNUTSEN
 NOTAT OM FUNKSJONER AV FLERE VARIABLE VEDLEGG TIL BRUK I KURSET MAT112 VED UNIVERSITETET I BERGEN ANDREAS LEOPOLD KNUTSEN Dette notatet inneholder ikke noe nytt pensum i kurset MAT112 i forhold til læreboken
NOTAT OM FUNKSJONER AV FLERE VARIABLE VEDLEGG TIL BRUK I KURSET MAT112 VED UNIVERSITETET I BERGEN ANDREAS LEOPOLD KNUTSEN Dette notatet inneholder ikke noe nytt pensum i kurset MAT112 i forhold til læreboken
ANALYSEDRYPP. Et forkurs til MAT2400. av Tom Lindstrøm. Matematisk insitutt og CMA Universitetet i Oslo 2011
 1 ANALYSEDRYPP Et forkurs til MAT2400 av Tom Lindstrøm Matematisk insitutt og CMA Universitetet i Oslo 2011 2 Forord Hensikten med dette heftet er å bygge en bro mellom kalkuluskursene og det første kurset
1 ANALYSEDRYPP Et forkurs til MAT2400 av Tom Lindstrøm Matematisk insitutt og CMA Universitetet i Oslo 2011 2 Forord Hensikten med dette heftet er å bygge en bro mellom kalkuluskursene og det første kurset
Repetisjonsforelesning - INF1080
 Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Repetisjonsforelesning - INF1080 Mengder, relasjoner og funksjoner 18. november 2015 1 Grunnleggende mengdelære 1.1 Elementært om mengder 1.1.1 Hva er en mengde? Definisjon 1.1 (Mengde). En mengde er en
Dagens plan. INF3170 Logikk. Mengder. Definisjon. Notasjon. Forelesning 0: Mengdelære, Induksjon. Martin Giese. 23. januar 2008.
 INF3170 Logikk Dagens plan Forelesning 0:, Induksjon Martin Giese 1 Institutt for informatikk, Universitetet i Oslo 2 23. januar 2008 Institutt for informatikk (UiO) INF3170 Logikk 23.01.2008 2 / 47 1
INF3170 Logikk Dagens plan Forelesning 0:, Induksjon Martin Giese 1 Institutt for informatikk, Universitetet i Oslo 2 23. januar 2008 Institutt for informatikk (UiO) INF3170 Logikk 23.01.2008 2 / 47 1
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: 12. desember 2003 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 7 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: 12. desember 2003 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 7 sider.
Tallfølger er noe av det første vi treffer i matematikken, for eksempel når vi lærer å telle.
 Kapittel 1 Tallfølger 1, 2, 3, 4, 5, 6, 7, 8,... Det andre temaet i kurset MAT1001 er differenslikninger. I en differenslikning er den ukjente en tallfølge. I dette kapittelet skal vi legge grunnlaget
Kapittel 1 Tallfølger 1, 2, 3, 4, 5, 6, 7, 8,... Det andre temaet i kurset MAT1001 er differenslikninger. I en differenslikning er den ukjente en tallfølge. I dette kapittelet skal vi legge grunnlaget
Grublegruppe 19. sept. 2011: Algebra I
 Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Grublegruppe 19. sept. 2011: Algebra I Ivar Staurseth ivarsta@math.uio.no Innledning, definisjoner Vi har så langt jobbet med mengder, X, hvor vi har hatt et avstandsbegrep og hvor vi har vært i stand
Ekstremverdier Mellomverdisatsen Forelesning i Matematikk 1 TMA4100
 Ekstremverdier Mellomverdisatsen Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 9. september 2011 Kapittel 4.1. Funksjoners ekseremverdier fra og med lokale ekstrema
Ekstremverdier Mellomverdisatsen Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 9. september 2011 Kapittel 4.1. Funksjoners ekseremverdier fra og med lokale ekstrema
Notat om Peanos aksiomer for MAT1140
 Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
INF3170 / INF4171. Intuisjonistisk logikk: Kripke-modeller, sunnhet, kompletthet. Andreas Nakkerud. 15. september 2015
 INF3170 / INF4171 Intuisjonistisk logikk: Kripke-modeller, sunnhet, kompletthet Andreas Nakkerud 15. september 2015 Kripke-modeller Vi ser på modeller for et språk L. Definisjon En Kripke-modell er et
INF3170 / INF4171 Intuisjonistisk logikk: Kripke-modeller, sunnhet, kompletthet Andreas Nakkerud 15. september 2015 Kripke-modeller Vi ser på modeller for et språk L. Definisjon En Kripke-modell er et
Logaritmer og eksponentialfunksjoner
 Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger del 1 Eksamensdag: Tirsdag 7. desember 2004 Tid for eksamen: 14:30 17:30 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger del 1 Eksamensdag: Tirsdag 7. desember 2004 Tid for eksamen: 14:30 17:30 Oppgavesettet
Eksamen MAT H Løsninger
 Eksamen MAT1140 - H2014 - Løsninger Oppgave 1 Vi setter opp en vanlig sannhetsverditabell. La Φ betegne formelen i oppgaven. Tabellen vil bli som følger: A B C A B A C Φ T T T T T T T T F T T T T F T F
Eksamen MAT1140 - H2014 - Løsninger Oppgave 1 Vi setter opp en vanlig sannhetsverditabell. La Φ betegne formelen i oppgaven. Tabellen vil bli som følger: A B C A B A C Φ T T T T T T T T F T T T T F T F
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
5.8 Iterative estimater på egenverdier
 5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
7 Egenverdier og egenvektorer TMA4110 høsten 2018
 7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
7 Egenverdier og egenvektorer TMA4 høsten 8 Det er ofte hensiktsmessig å tenke på en matrise ikke bare som en tabell med tall, men som en transformasjon av vektorer. Hvis A er en m n-matrise, så gir A
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile
 MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
MAUMAT644 ALGEBRA vår 2016 Første samling Runar Ile 1 Introduksjon: Grupper og ringer Ringer En ring er et sted hvor du kan addere, subtrahere og multiplisere. Hvis du også kan dividere kalles ringen for
Løsningsforslag, eksamen MA1101/MA
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Løsningsforslag, eksamen MA0/MA60 07.2.09 Oppgave La f() = e 4 2 2 8. a) Finn alle ekstremalpunktene til funksjonen
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Løsningsforslag, eksamen MA0/MA60 07.2.09 Oppgave La f() = e 4 2 2 8. a) Finn alle ekstremalpunktene til funksjonen
Terningkast. Utfallsrommet S for et terningskast med en vanlig spillterning med 6 sider er veldefinert 1, 2, 3, 4, 5, 6
 Terningkast Halvor Aarnes, UiO, 2014 Innhold Ett terningkast og utfallsrom... 1 Union og snitt... 4 Betinget sannsynlighet... 5 Forventningsverdi E(X) og varianse Var(X)... 5 Konfidensintervall for proporsjoner...
Terningkast Halvor Aarnes, UiO, 2014 Innhold Ett terningkast og utfallsrom... 1 Union og snitt... 4 Betinget sannsynlighet... 5 Forventningsverdi E(X) og varianse Var(X)... 5 Konfidensintervall for proporsjoner...
Dette krever ikke noe nytt aksiom. Hvorfor? Og hvorfor må vi anta at A ikke er tom? Merk at vi har:
 Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
Notat 4 for MAT1140 4 Mer om mengder 4.1 Familier av mengder Union og snitt. Aksiom 4.1. Dersom A er en mengde bestående av mengder, kan de sistnevnte føyes sammen til en stor mengde, kalt unionen til
MAT1030 Forelesning 10
 MAT1030 Forelesning 10 Mengdelære Roger Antonsen - 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) Kapittel 5: Mengdelære Oversikt Vi har nå innført de Boolske operasjonene, union snitt komplement
MAT1030 Forelesning 10 Mengdelære Roger Antonsen - 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) Kapittel 5: Mengdelære Oversikt Vi har nå innført de Boolske operasjonene, union snitt komplement
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 10: Mengdelære Roger Antonsen Institutt for informatikk, Universitetet i Oslo 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) Kapittel 5: Mengdelære MAT1030 Diskret
MAT1030 Diskret Matematikk Forelesning 10: Mengdelære Roger Antonsen Institutt for informatikk, Universitetet i Oslo 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) Kapittel 5: Mengdelære MAT1030 Diskret
Løsning til øving 23 for FY1004, våren 2008
 Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
Kapittel 5: Mengdelære
 MAT1030 Diskret Matematikk Forelesning 10: Mengdelære Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 5: Mengdelære 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) MAT1030 Diskret
MAT1030 Diskret Matematikk Forelesning 10: Mengdelære Roger Antonsen Institutt for informatikk, Universitetet i Oslo Kapittel 5: Mengdelære 24. februar 2009 (Sist oppdatert: 2009-02-25 08:27) MAT1030 Diskret
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Torsdag 1. oktober 2005. Tid for eksamen: 9:00 11:00. Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Torsdag 1. oktober 2005. Tid for eksamen: 9:00 11:00. Oppgavesettet er på
Oppfriskningskurs i Matematikk
 Oppfriskningskurs i Matematikk Dag 2 Stine M. Berge 06.07.19 Stine M. Berge (NTNU) Oppfriskningskurs i Matematikk 06.07.19 1 / 16 Funksjoner Definisjon En funksjon f er en prosses som ett element i en
Oppfriskningskurs i Matematikk Dag 2 Stine M. Berge 06.07.19 Stine M. Berge (NTNU) Oppfriskningskurs i Matematikk 06.07.19 1 / 16 Funksjoner Definisjon En funksjon f er en prosses som ett element i en
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
Sannsynlighetsregning og Statistikk
 Sannsynlighetsregning og Statistikk Leksjon 2. Leksjon 2 omhandler begreper og regneregler for sannsynligheter. Dette er behandlet i kapittel 3.1 og 3.2 i læreboka. Du bør når du har fullført leksjon 2
Sannsynlighetsregning og Statistikk Leksjon 2. Leksjon 2 omhandler begreper og regneregler for sannsynligheter. Dette er behandlet i kapittel 3.1 og 3.2 i læreboka. Du bør når du har fullført leksjon 2
9 + 4 (kan bli endringer)
 Innlevering DAFE ELFE Matematikk HIOA Obligatorisk innlevering 4 Innleveringsfrist Onsdag 29. april 25 Antall oppgaver: 9 + 4 (kan bli endringer) Finn de ubestemte integralene a) 2x 3 4/x dx b) c) 2 5
Innlevering DAFE ELFE Matematikk HIOA Obligatorisk innlevering 4 Innleveringsfrist Onsdag 29. april 25 Antall oppgaver: 9 + 4 (kan bli endringer) Finn de ubestemte integralene a) 2x 3 4/x dx b) c) 2 5
Oppsummering MA1101. Kristian Seip. 23. november 2017
 Oppsummering MA1101 Kristian Seip 23. november 2017 Forelesningen 23. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i MA1101 noen tips for eksamensperioden
Oppsummering MA1101 Kristian Seip 23. november 2017 Forelesningen 23. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i MA1101 noen tips for eksamensperioden
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010
 ÅM0 Sannsynlighetsregning med statistikk, våren 00 Kp. Sannsynlighetsregning (sannsynlighetsteori).5 (kp..5) - innledning Eks.: Et terningkast; {,, 3, 4, 5, 6}. Ved bruk av uniform modell: hvert utfall
ÅM0 Sannsynlighetsregning med statistikk, våren 00 Kp. Sannsynlighetsregning (sannsynlighetsteori).5 (kp..5) - innledning Eks.: Et terningkast; {,, 3, 4, 5, 6}. Ved bruk av uniform modell: hvert utfall
Potensrekker Forelesning i Matematikk 1 TMA4100
 Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.7. Potensrekker (fra konvergens av) 3 Konvergens av potensrekker Eksempel For
Potensrekker Forelesning i Matematikk 1 TMA4100 Hans Jakob Rivertz Institutt for matematiske fag 1. november 2011 Kapittel 8.7. Potensrekker (fra konvergens av) 3 Konvergens av potensrekker Eksempel For
De hele tall har addisjon, multiplikasjon, subtraksjon og lineær ordning, men ikke divisjon.
 Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Innledning til Matematikk Hans Petter Hornæs, hans.hornaes@hig.no Det er ofte vanskelig å komme i gang et fag. Innledningsvis er det gjerne en del grunnleggende begreper som må på plass. Mange studenter
Notasjon i rettingen:
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 07 Notasjon i rettingen: R = Rett R = Rett, men med liten tulle)feil
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 07 Notasjon i rettingen: R = Rett R = Rett, men med liten tulle)feil
Derivasjonen som grenseverdi
 Gitt graf. Start/stopp. Fra sekant til tangent. Veien til formelen for den deriverte til funksjon f i et punkt Animasjonens jem: ttp://ome.ia.no/~cornelib/animasjon/ matematikk/mate-online-at/ablgrenz/
Gitt graf. Start/stopp. Fra sekant til tangent. Veien til formelen for den deriverte til funksjon f i et punkt Animasjonens jem: ttp://ome.ia.no/~cornelib/animasjon/ matematikk/mate-online-at/ablgrenz/
EKSAMEN I EMNET Løsning: Mat Grunnkurs i Matematikk I Mandag 14. desember 2015 Tid: 09:00 14:00
 Universitetet i Bergen Det matematisk naturvitenskapelige fakultet Matematisk institutt Side 1 av 7 BOKMÅL EKSAMEN I EMNET Mat 111 - Grunnkurs i Matematikk I Mandag 14. desember 15 Tid: 9: 14: Tillatte
Universitetet i Bergen Det matematisk naturvitenskapelige fakultet Matematisk institutt Side 1 av 7 BOKMÅL EKSAMEN I EMNET Mat 111 - Grunnkurs i Matematikk I Mandag 14. desember 15 Tid: 9: 14: Tillatte
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: Torsdag 10 januar 2008 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 6
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: Torsdag 10 januar 2008 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 6
Løsningsforslag oblig. innlevering 1
 Løsningsforslag oblig. innlevering 1 IN1150 Logiske metoder Høsten 2017 Oppgave 1 - Mengdelære (10 poeng) a) Ut fra opplysningene under, angi hvilke mengder A og B er. A B = {1, 2, 3, 4, 5, 6} A B = {2,
Løsningsforslag oblig. innlevering 1 IN1150 Logiske metoder Høsten 2017 Oppgave 1 - Mengdelære (10 poeng) a) Ut fra opplysningene under, angi hvilke mengder A og B er. A B = {1, 2, 3, 4, 5, 6} A B = {2,
Eksamensoppgave i MA1101 Grunnkurs i analyse
 Institutt for matematiske fag Eksamensoppgave i MA1101 Grunnkurs i analyse Faglig kontakt under eksamen: Kari Hag Tlf: 48 30 19 88 Eksamensdato: 15. oktober 018 Eksamenstid (fra til): 17:30 19:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i MA1101 Grunnkurs i analyse Faglig kontakt under eksamen: Kari Hag Tlf: 48 30 19 88 Eksamensdato: 15. oktober 018 Eksamenstid (fra til): 17:30 19:00 Hjelpemiddelkode/Tillatte
Lineærtransformasjoner
 Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Kapittel 8 Lineærtransformasjoner I forrige kapittel begynte vi å formulere lineær algebra på en generell måte, ved å gi en abstrakt definisjon av vektorrom For å beskrive sammenhenger mellom forskjellige
Løsningsforslag eksamen i TMA4100 Matematikk desember Side 1 av 7
 Løsningsforslag eksamen i TMA4 Matematikk 2. desember 23. Side av 7 Oppgave Løs initialverdiproblemet y (2/x)y, y() 2. Løsning: y (2/x)y er en førsteordens lineær differensialligning. Vi finner en løsning
Løsningsforslag eksamen i TMA4 Matematikk 2. desember 23. Side av 7 Oppgave Løs initialverdiproblemet y (2/x)y, y() 2. Løsning: y (2/x)y er en førsteordens lineær differensialligning. Vi finner en løsning
