Bootstrapping og stokatisk simulering Tilleggslitteratur for STK1100
|
|
|
- Asle Amundsen
- 6 år siden
- Visninger:
Transkript
1 Bootstrapping og stokatisk simulering Tilleggslitteratur for STK1100 Geir Storvik April Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor statistikk men også mer generelt. Dette notatet er et supplement til STK1100. Læreboka [Devore and Berk, 011] diskuterer bootstrapping, men stoffet er fordelt over ulike kapitler og avsnitt og er noe overfladisk. Tilsvarende er stokastisk simulering stort sett kun diskutert gjennom oppgaver. Dette notatet er ment å samle hovedideene bak bootstrapping og samtidig si noe mer om potensialet for stokastisk simulering. Samtidig gir den eksempler på hvordan bootstrapping og stokastisk simulering kan utføres i Matlab. Alle koder er tilgjengelige fra kursets hjemmeside. Bootstrapping Anta vi har observert x 1,..., x n F der F er den kumulative fordelingsfunksjon 1. Vi ønsker å estimere en ukjent parameter θ med ˆθ = ˆθ(x) der x = (x 1,..., x n ). Noen av de spørsmål vi gjerne stiller er: 1. Er ˆθ forventningsrett, og hvis ikke hva er skjevheten til estimatet?. Hva er usikkerheten til ˆθ? 1 Det er litt enklere å snakke om F istedet for p eller f da vi med F ikke behøver å skille mellom diskrete og kontinuerlige fordelinger 1
2 Disse er knyttet til fordelingsegenskapene til ˆθ som avhenger av F. Med dette mener vi oppførselen til ˆθ hvis vi gjentar vårt eksperiment med å samle inn data x fra fordelingen beskrevet F. Et problem her er at F er ukjent, noe som medfører at også fordelingsegenskapene til ˆθ er ukjente. For å kunne gi noen svar på spørsmålene ovenfor, må vi derfor gjøre noen tilnærminger. I kapitlene 6 og 7 i Devore and Berk [011] diskuteres at normaltilnærming (begrunnet gjennom sentralgrenseteoremet) ofte kan benyttes. Men hva hvis antagelsene som ligger til grunn for disse tilnærmingene ikke er tilstede? Bootstrapping er da et alternativ..1 Bootstrapping og standard feil Ideen bak bootstrapping [Efron, 198] kan illustreres gjennom et eksempel. La X i, i = 1,..., n være levetidene til n komponenter. Anta vi har observert [Devore and Berk, 011, eksempel 7.1 i] En ofte brukt modell for levetider er den eksponensielle fordeling, f(x; λ) = λe λx. Innenfor denne modellen er E(X i ) = µ = 1/λ. Dermed er E[ X] = µ og en rimelig estimator for λ er ˆλ = 1/ X For observasjonene ovenfor får vi estimatet ˆλ = 1/ = Hva er så standard feilen til denne estimatoren? La oss først se på variansen til ˆλ. Merk at variansen er et må på variasjonen i ˆλ ved gjentatte eksperimenter der vi samler inn n = 10 observasjoner i hvert eksperiment. Hvis vi kunne repetere eksperimentet mange ganger ville vi derfor kunne estimere variansen til ˆλ ved den empiriske variansen over disse repeterte eksperimentene. Standard feilen kan så fås ved å ta kvadratroten av den empiriske variansen. Problemet ligger i at vi ikke klarer å repetere eksperimentene i virkeligheten. Men: Vi kan simulere tilsvarende eksperimenter på datamaskinen. Anta den eksponensielle fordeling er den riktige fordeling og vi kjenner λ. Vi kan da gjennomføre B = 1000 simuleringseksperimenter med følgende Matlab kode: B = 1000; f o r b=1:b x s t a r = exprnd (1/ lambda, 1, n ) ; lambdasim ( b ) = 1/mean( x s t a r ) ; end SE=s q r t ( var ( lambdasim ) )
3 Vi vil da få ut standard feilen til de simulerte ˆλ-ene (vektoren lambdasim). Merk at vi selv kan bestemme B slik at ved å gjøre B stor nok får vi så stor nøyaktighet som vi vil. Et ekstra problem er imidlertid at vi ikke kjenner den riktige fordeling til observasjonene våre. Anta vi er villige til å anta modellen om at de er eksponensielt fordelte slik at kun λ er ukjent. Fra data har vi imidlertid et estimat på λ. En tilnærming er da å bruke f(x; ˆλ) istedet for f(x; λ). Matlab kode for dette blir da x = [ ] ; n = 1 0 ; mu hat = mean( x ) lambda hat = 1/ mu hat B = 10000; lambdasim = z e r o s (1,B) ; f o r b=1:b x s t a r = exprnd (1/ mu hat, 1, n ) ; lambdasim ( b ) = 1/mean( x s t a r ) ; end SE = s q r t ( var ( lambdasim ) ) 5 kjøringer av disse komandoene gir standard feil verdiene Merk at vi får litt forskjellige verdier hver gang vi kjører. Dette kommer av tilfeldighetene som ligger i simuleringene våre. En økning av B til ga tallene Vi ser nå at vi får et mye mer nøyaktig resultat. Merk imidlertid at det nå er to kilder til usikkerhet Usikkerhet i de opprinnelige observasjoner x 1,..., x n Usikkerhet i våre simuleringer I praksis vil usikkerheten som ligger i data være lagt større enn usikkerheten i våre simuleringer slik at B = 1000 typisk vil være nok. Prosedyren vi har gjennomført i eksempelet ovenfor kalles for parametrisk bootstrapping. Generelt går denne prosedyren ut på at hvis data er generert fra en modell med kumulativ fordelingsfunksjon F (x; θ) og vi har en estimator ˆθ = ˆθ(x) så kan vi estimere standard feilen til ˆθ ved følgende trinn: 3
4 1. Repeter for b = 1,..., B (a) Simuler x 1,..., x n uif fra F (x; ˆθ) (b) Sett θ b = ˆθ(x ) der x = (x 1,..., x n) 1. Estimer σˆθ ved B B 1 b=1 (θ b θ ) der θ = 1 B B b=1 θ b. I parametrisk bootstrapping estimerer vi standard feilen under antagelsen om at modellen F (x; θ) er riktig. Hvis modellen ikke er alt for forskjellig fra F (x; θ) vil svarene vi får være fornuftige. Hvis vi er usikre på dette kan ikke-parametrisk bootstrapping være et alternativ. Idéen i dette tilfellet er å gjøre minimale antagelser på F i utgangspunktet. Merk at F (x) = P (X x) En mulig estimator for F i det tilfellet er den empirisk kumulative fordelingsfunksjon som er gitt ved F (x) = 1 n (#x i x) (1) Merk at under F så er Pr(X = x i ) = 1 n for i = 1,..., n. og at trekking fra F svarer til å trekke fra x 1,..., x n med tilbakelegging. Dette er en viktig egenskap ved F som vi vil utnytte når vi skal utføre de nødvendige beregninger involvert i bootstrapping. La oss igjen se på eksemplet vårt med levetider av komponenter. Nedenfor følger Matlab kode for å utføre ikke-parametrisk bootstrapping: B = 1000; lambdasim = z e r o s (1,B) ; f o r b=1:b x s t a r = randsample ( x, n, true ) ; lambdasim ( b ) = 1/mean( x s t a r ) ; end SE = s q r t ( var ( lambdasim ) ) 5 gjentatte kjøringer av disse kommandoene ga standard feil Vi ser nå at standard feilen har økt noe. Dette kan tyde på at dataene ikke helt passer i forhold til den ekspoensielle fordeling (hvis modell-antagelsene er riktige vil resultatene fra ikke-parametrisk og parametrisk bootstrapping være rimelig like). 4
5 . Bootstrapping og forventningsskjevhet Simuleringene av ˆθ vi får gjennom Bootstrapping kan imidlertid brukes til mer enn bare å estimere standard feil. Figuren nedenfor viser histogrammer av de simulerte ˆθ-ene, parametrisk bootstrapping til venstre og ikke-parametrisk bootstrapping til høyre. Her ser vi at fordelingene er ganske skjeve. Dette tyder på at sentralgrenseteoremet ikke gjelder her. Det er to grunner til dette: Det er få observasjoner (n = 10). ˆλ er ikke et gjennomsnitt Her kan et alternativ være å se på ˆµ = X istedet. Plottet nedenfor viser Bootstrap simuleringer av denne. Vi får nå noe som ligner mer på normalfordeling men fremdeles er det noe ikke-symmetri som indikerer at n = 10 er noe lite i dette tilfellet der vi starter med en ganske skjev fordeling på dataene selv. La oss imidlertid gå tilbake til ˆλ men nå konsentrere oss om forventningsskjevhet. Vi er altså interesser i å si noe om Bias(ˆθ) = E[ˆθ] θ 5
6 Denne forventningsskjevheten kan estimeres fra Bootstrap simuleringene våre ved Bias(ˆθ) = θ ˆθ For vårt tidligere eksempel så kan dette utføres ved Matlab kommandoene b i a s = mean( lambdasim) lambdahat En simulering med parametrisk bootstrapping ga Bias(ˆθ) = mens ikke-parametrisk bootstrapping ga Vi kan nå oppsummere våre resultater i følgende tabell (basert på første kjøring med B = 1000): Bootstrapping Estimat SE Bias Parametrisk Ikke-parametrisk Dette kan nå brukes til å anslå forventet kvadratis feil for ˆθ. For parametrisk bootstrapping blir dette MSE = = [ ] 10 5 = mens for ikke-parametrisk bootstrapping er de tilsvarende tallene MSE = = [ ] 10 4 = I begge tilfeller ser vi at forventningsskjevheten bidrar svært lite til den totale feilen noe som tilsier at forventingsskjevheten er liten i dette tilfelle. 3 Stokastisk simulering og Monte Carlo integrasjon I forbindelse med Bootstrapping brukte vi simulering av tilfeldige variable som verktøy for å få ut de svar vi ønsket. Når tilfeldighet inngår i simuleringer kalles det ofte for stokastisk simulering. To aktuelle faktorer er interessante å diskutere videre i den forbindelse: Hvordan kan en datamaskin utføre simuleringer fra en vilkårlig fordeling? Hva annet kan vi bruke stokastisk simulering til? 6
7 3.1 Simulering fra en vilkårlig fordeling Formelt er datamaskinen en deterministisk boks (selv om det kanskje ikke alltid virker slik). Det beste vi derfor kan gjøre er å konstruere algoritmer som kan få datamaskinen til å simulere hva vi kaller pseudotilfeldige tall, dvs de tall vi får ut ligner på den fordeling vi er ute etter. Utgangspunktet for all stokastisk simulering er simulering av variable fra den uniforme fordeling på intervallet [0, 1]. De fleste datamaskiner og tilhørende software har idag ferdige funksjoner som generer pseudotilfeldige tall som for alle praktiske formål ligner nok på tilfeldige tall fra uniforme fordeling. Kommandoene nedenfor viser hvordan dette kan gjøres i Matlab, innkludert plotting av et histogram for dette. u = rand ( ) ; x = 0 : : 1 n = h i s t c (u, x ) ; bar ( x, n/(sum( n ) ), 1 ) ; Figuren nedenfor viser histogrammet av de genererte variable og illustrerer at vi får variable som passer godt med den uniforme fordeling. Anta nå vi ønsker å simulere fra en generell fordeling med kumulativ fordelingsfunksjon F. La U uniform[0, 1] og la X = F 1 (U). Da er P (X x) =P (F 1 (U) x) =P (U F (x)) = F (x) som viser at X da har kumulativ fordelingsfunksjon X. 3. Inversjonsmetoden Eksempel Anta vi ønsker å trekke fra den eksponensielle fordeling f(x; λ) = λe λx. Da er F (x; λ) = 1 e λx og F 1 (u) = λ 1 log(1 u). Dermed kan vi bruke følgende algoritme for å generere en variabel fra den eksponensielle fordeling 7
8 1. Generer u Uniform[0, 1].. Sett x = λ 1 log(1 u) I Matlab med λ = 1.5 kan flere variable genereres simultant ved kommandoene lambda = 1. 5 ; u = rand ( 1, ) ; x = l o g (1 u)/ lambda ; Nedenfor er et histogram av de simulerte x-ene sammen med plot av den sanne sannsynlighetstetthet f(x; λ). For de fleste kjente fordelinger vil det imidlertid finnes ferdige funksjoner som gjør dette for oss, for den eksponensielle fordeling så vi tidligere at vi i Matlab kan bruke funksjonen exprnd. Det er imidlertid andre fordelinger der ikke slike funksjoner er tilgjengelige Eksempel Cauchy fordeling f(x) = 1 π(1 + x ) Cauchy fordelingen er definert ved Det ser ikke ut til å være noen ferdig implementerte funksjoner i standard Matlab for å generere variable fra denne fordelingen. Vi har imidlertid at som gir F (x) = 1 + π 1 tan 1 (x) F 1 (u) = tan[π(u 1 )] Dermed kan vi generere tilfeldige variable fra Cauchy fordelingen ved følgende Matlab kommandoer: 8
9 u = rand ( 1, ) ; x = tan ( pi (u 0.5)) Nedenfor er et histogram av de simulerte x-ene sammen med plot av den sanne sannsynlighetstetthet f(x). 3.3 Forkastningsmetoden Anta nå vi ønsker å simulere fra en fordeling f(x) = 0x(1 x 3 ), 0 < x < 1 Dette er et spesialtilfelle av Beta fordelingen som er en mye brukt fordeling for observasjoner som er begrenset til intervallet [0, 1]. Et problem her er at den kumulative fordelingsfunksjonen F (x) ikke har noe analytisk uttrykk, noe som gjør inversjonsmetoden vanskelig å benytte. Et alternativ da er forkastningsmetoden. Forkastningsmetoden trenger en forslagsfordeling G(x) med tilhørende sannsynlighetstetthetsfunksjon g(x) slik at f(x)/g(x) < c for alle x. Metoden er da definert gjennom følgende algoritme: 1. Simuler y G( ).. Generer u Uniform[0, 1] 3. Hvis u f(x)/(cg(x)), sett x = y, hvis ikke returner til trinn 1 Proposisjon 1 Variabelen som kommer ut av forkastningsmetoden vil ha sannsynlighetstetthet f(x). Sannsynligheten for å akseptere en generert y er 1/c. 9
10 Bevis Se oppgave 5.85 i Devore and Berk [011] Merk at c er et mål på hvor effektiv algoritmen er. Jo større c er, jo mindre er sannsynligheten for å akseptere og jo flere forsøk må vi gjøre. Vi ønsker derfor at c skal være minst mulig. Samtidig har vi begrensningen c > f(x)/g(x). Et vanlig valg er derfor å velge c = min x f(x) g(x) Merk spesielt at vi må ha at g(x) > 0 for alle verdier der f(x) > 0. Eksempel Betrakt igjen eksemplet f(x) = 0x(1 x 3 ), 0 < x < 1 Siden vi her har en fordeling over intervallet [0, 1] kan en mulig forslagsfordeling være den uniforme fordeling. I det tilfellet er c = min x f(x) g(x) = min 0x(1 x)3 x Her får vi den minste verdi for x = 1/4 som gir c = 135 = I Matlab kan algoritmen 64 implementeres på følgende måte: n = 10000; x = z e r o s (1, n ) ; cinv = 64/135; f o r i =1:n y = rand ( 1 ) ; u = rand ( 1 ) ; while ( u > 0 y (1 y) (1 y) (1 y ) cinv ) y = rand ( 1 ) ; u = rand ( 1 ) ; end x ( i ) = y ; end Figuren nedenfor viser til venstre histogram av de simulerte x-er sammen med den sanne f(x). Vi ser også her at det er godt samsvar mellom de simulerte verdier og den modell de skal være simulert ifra. Til høyre er et histogram over antall simuleringer som måtte gjennomføres før en verdi ble akseptert. 10
11 3.4 Monte Carlo integrasjon Vi vil nå se på hvordan stokastisk simulering kan brukes til å løse et matematisk problem. Anta vi er interessert i å beregne θ = cos(x)e x / dx. Merk at vi kan omskrive integralet til θ = = 1 π cos(x) / π e x dx π cos(x)f(x)dx der f(x) nå er sannsynlighetstetthetsfunksjonen til standard normal fordelingen. Dermed er θ = E[ π cos(x)] der X nå er en tilfeldig variabel som følger standard normal fordelingen. Anta nå vi kan simulere X 1,..., X M fra f(x). Vi kan da bruke vår sannsynlighetsteori til å konstruere en estimator for θ ved θ = 1 M M π cos(xi ) i=1 I Matlab kan vi nå få ut et estimat på θ ved følgende kommandoer: M = 10000; x = normrnd ( 0, 1, 1,M) ; y = s q r t ( pi ) cos ( x ) thetahat = mean( y ) ; 11
12 Fem kjøringer av disse kommandoene ga verdiene Hver av disse verdiene er et estimat på θ. Disse kan så sammenliknes med hva man får ut av en numerisk integrasjonsmetode, 1.503, som i dette tilfellet kan ses på som en fasit. Merk at estimatene ligger i nærheten av denne verdien, men varierer noe. Vi kan øke M til Da ender vi opp med verdiene Vi ser nå at estimatene varierer mye mindre rundt den riktige verdien. Fra standard regler har vi at og V ( θ) = 1 M V (Y i) σ θ = 1 M σ Yi σ Yi vil være vanskelig å beregne, men kan også estimeres fra våre simuleringer: Sy = s q r t ( var ( y ) ) En ny kjøring med M = ga θ = og s cos(xi ) = For å vurdere nøyaktigheten på estimatet har vi følgende: P ( θ σ θ θ θ + σ θ) =P ( σ θ θ θ σ θ) =P ( θ θ σ θ =P ( θ θ σ θ ) ). Fra sentralgrenseteoremet har vi at θ θ σ θ er tilnærmet (standard) normal fordelt. Dermed er P ( θ θ σ θ ) P ( Z ) = Φ() Φ( ) = som da altså gir at P ( θ σ θ θ θ + σ θ)
13 For å komme helt i mål, må vi bruke nok en tilnærming ved at s θ σ θ der s θ = 1 M s Yi. Setter vi så inn våre estimater θ og s Yi får vi at med 95.4% sannsynlighet så vil intervallet [ θ σ θ, θ + σ θ)] = [1.5199, 1.513] inneholde den sanne verdi av θ. Eksempelet ovenfor illustrerer en generell prosedyre kalt Monte Carlo integrasjon eller Monte Carlo metoden: Anta vi er interessert i et integral θ = g(x)dx Dette kan vi skrive om til θ = g(x) f(x) f(x)dx der vi krever at f(x) > 0 hvis g(x) > 0. Denne omskrivningen gjelder for enhver funksjon f(x) med disse begrensningene. Vi vil imidlertid begrense oss ytterligere til å anta at f(x) er en sannsynlighetstetthetsfunksjon, dvs f(x) 0 og f(x)dx = 1. Under denne antagelsen er ) θ = E ( g(x) f(x) der X nå er en tilfeldig variabel med sannsynlighetstetthetsfunksjon f(x). Anta nå vi kan simulere X 1,..., X M uif (uavhengig og identisk fordelt) fra f(x) og la Y = g(x). Da kan vi f(x) estimere θ ved M θ = 1 M i=1 Y i Vi har direkte at E( θ) = θ. Videre har vi at og V ( θ) = 1 M V (Y ) σ θ = 1 M σ Y Vi kan dermed styre usikkerheten i estimatet ved å velge passende antall simuleringer M. Et annet aspekt ved denne metoden er at vi også kan velge f(x), som ofte blir kalt forslagsfordelingen. Ulike valg av denne vil gi ulike verdier av σ g(x)/f(x). Noen ganger kan usikkerheten reduseres kraftig ved smarte valg av forslagsfordeling. 13
14 Eksempel θ = Anta vi er interessert i 1 dx π(1+x ) Merk at f(x) = 1 π(1+x ) θ = P (X ) er sannsynlighetstettheten til Cauchy fordelingen slik at hvis X er en tilfeldig variabel fra Cauchy fordelingen. Den opplagte metode for å estimere θ gjennom Monte Carlo integrasjon er dermed å simulere X 1,..., X M uif fra Cauchyfordelingen, la Y i = 1 hvis X i og 0 ellers og så la ˆθ 1 = 1 S M i=1 Y i Merk at Y i er en Bernouilli variabel med sannynlighet for suksess lik θ. Dermed er Y = M i=1 Y i binomisk fordelt med S forsøk og suksess sannsynlighet θ. Det gir da at E[ˆθ 1 ] = θ, V [ˆθ 1 ] = 1 θ(1 θ). S For å kunne bruke denne estimatoren, trenger vi å simulere fra Cauchy fordelingen. Det er ikke noen direkte rutiner for dette i Matlab, men vi kan bruke inversjonsmetoden: Vi har at F (x) = P (X x) = 1 π arctan(x) + 1 som gir at F 1 (u) = tan(π(u 1)). Dermed kan vi generere X ved X = tan(π(u 1 )) der U Uniform[0, 1]. I Matlab kan dette utføres med følgende kommandoer: S = ; u = unifrnd ( 0, 1, 1, S ) ; x = tan ( pi (u 0. 5 ) ) ; y = x>; thetahat1 = mean( y ) V1 = var ( y ) Dette ga et estimat på θ lik og et variansestimat på /S. Det er dog mulig å konstruere bedre estimatorer. Merk at f(x) er symmetrisk om 0 slik at θ = P (X ) = P (X ) = 1 P ( X ). La nå Z i = 1 hvis X i og 0 ellers og definer ˆθ = 1 S M i=1 Z i 14
15 Vi har nå ta Z i er en Bernouilli variabel med sannynlighet for suksess lik θ. Dermed er Z = M i=1 Z i binomisk fordelt med S forsøk og suksess sannsynlighet θ. Det gir da at E[ˆθ ] = θ, V [ˆθ ] = 1 1 θ(1 θ) = 4S S θ(1 θ) < V [ˆθ 1 ] I Matlab kan denne estimatoren brukes med følgende kommandoer: S = ; u = unifrnd ( 0, 1, 1, S ) ; x = tan ( pi (u 0. 5 ) ) ; z = abs ( x) >; thetahat = 0.5 mean( z ) V = var ( z )/4 Dette ga et estimat på θ lik og et variansestimat på /S. Man kan imidlertid gjøre ytterligere forbedringer. Definer V Uniform[0, ]. Da er E(V ) = 0 [ 1 f(u)] 1 du = 1 f(u)du 0 = 1 P (0 X ) = 1 [P (X ) P (X 0)] = 1 [1 θ 1 ] = θ Vi kan nå lage oss en tredje estimator for θ: = 1 f(u) der U ˆθ 3 = 1 S S [ 1 f(u uif i)], U i Uniform[0, ] i=1 Av beregningene ovenfor er ˆθ 3 forventningsrett. De nødvendige Matlab kommandoene i dette tilfellet er S = ; u = unifrnd ( 0,, 1, S ) ; v = 0.5./( pi. (1+u. ˆ ) ) ; thetahat3 = mean( v ) V3 = var ( v ) 15
16 Dette ga et estimat på θ lik og et variansestimat på /S. Tilslutt, se på W = 1 f(u) der U Uniform[0, 1/]. Da er 1/ 1 E(W ) = f(u)du = = = = 0 1 f(1/v) 1 v dv π(1+ 1 v ) 1 1 π(v +1 v dv f(v)dv = θ Vi kan nå lage oss en fjerde estimator for θ: ˆθ 4 = 1 S S i=1 1 f(u uif i), U i Uniform[0, 1/] Av beregningene ovenfor er ˆθ 4 forventningsrett. Matlab kommandoene i dette tilfellet er S = ; u = unifrnd ( 0, 0. 5, 1, S ) ; w = / ( pi. (1+u. ˆ ) ) ; thetahat4 = mean(w) V4 = var (w) Dette ga et estimat på θ lik og et variansestimat på /S. Referanser Jay L Devore and Kenneth N Berk. Modern Mathematical Statistics with Applications. Springer, 011. B. Efron. The Jackknife, the Bootstrap, and Other Resampling Plans. Number 38 in CBMS-NSF Regional Conference Series in Applied Mathematics. Siam, Philadelphia,
Bootstrapping og simulering Tilleggslitteratur for STK1100
 Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 (oppdatert April 2016) 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor
Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 (oppdatert April 2016) 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor
Bootstrapping og simulering
 Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor statistikk, men
Bootstrapping og simulering Tilleggslitteratur for STK1100 Geir Storvik April 2014 1 Introduksjon Simulering av tilfeldige variable (stokastisk simulering) er et nyttig verktøy innenfor statistikk, men
Punktestimator. STK Bootstrapping og simulering - Kap 7 og eget notat. Bootstrapping - eksempel Hovedide: Siden λ er ukjent, bruk ˆλ:
 Punktestimator STK00 - Bootstrapping og simulering - Kap 7 og eget notat Geir Storvik 8. april 206 Trekke ut informasjon om parametre fra data x,..., x n Parameter av interesse: θ Punktestimator: Observator,
Punktestimator STK00 - Bootstrapping og simulering - Kap 7 og eget notat Geir Storvik 8. april 206 Trekke ut informasjon om parametre fra data x,..., x n Parameter av interesse: θ Punktestimator: Observator,
Inferens. STK Repetisjon av relevant stoff fra STK1100. Eksempler. Punktestimering - "Fornuftig verdi"
 Inferens STK1110 - Repetisjon av relevant stoff fra STK1100 Geir Storvik 12. august 2015 Data x 1,..., x n evt også y 1,..., y n Ukjente parametre θ kan være flere Vi ønsker å si noe om θ basert på data.
Inferens STK1110 - Repetisjon av relevant stoff fra STK1100 Geir Storvik 12. august 2015 Data x 1,..., x n evt også y 1,..., y n Ukjente parametre θ kan være flere Vi ønsker å si noe om θ basert på data.
STK Oppsummering
 STK1100 - Oppsummering Geir Storvik 6. Mai 2014 STK1100 Tre temaer Deskriptiv/beskrivende statistikk Sannsynlighetsteori Statistisk inferens Sannsynlighetsregning Hva Matematisk verktøy for å studere tilfeldigheter
STK1100 - Oppsummering Geir Storvik 6. Mai 2014 STK1100 Tre temaer Deskriptiv/beskrivende statistikk Sannsynlighetsteori Statistisk inferens Sannsynlighetsregning Hva Matematisk verktøy for å studere tilfeldigheter
STK Oppsummering
 STK1110 - Oppsummering Geir Storvik 11. November 2015 STK1110 To hovedtemaer Introduksjon til inferensmetoder Punktestimering Konfidensintervall Hypotesetesting Inferens innen spesifikke modeller/problemer
STK1110 - Oppsummering Geir Storvik 11. November 2015 STK1110 To hovedtemaer Introduksjon til inferensmetoder Punktestimering Konfidensintervall Hypotesetesting Inferens innen spesifikke modeller/problemer
Notat 3 - ST februar 2005
 Notat 3 - ST1301 1. februar 2005 1 Simulering fra modell Når vi skal analysere et gitt konkret innsamlet datasett vil vi gjøre dette med utgangspunkt i en statistisk modell. Vi kan si at en slik statistisk
Notat 3 - ST1301 1. februar 2005 1 Simulering fra modell Når vi skal analysere et gitt konkret innsamlet datasett vil vi gjøre dette med utgangspunkt i en statistisk modell. Vi kan si at en slik statistisk
Estimatorar. Torstein Fjeldstad Institutt for matematiske fag, NTNU
 Estimatorar Torstein Fjeldstad Institutt for matematiske fag, NTNU 11.10.2018 I dag Repetisjon Er dataa mine normalfordelt? Estimatorar Eigenskapar til S 2 Kahoot 2 Repetisjon Obervator Ein observator
Estimatorar Torstein Fjeldstad Institutt for matematiske fag, NTNU 11.10.2018 I dag Repetisjon Er dataa mine normalfordelt? Estimatorar Eigenskapar til S 2 Kahoot 2 Repetisjon Obervator Ein observator
Ekstraoppgaver for STK2120
 Ekstraoppgaver for STK2120 Geir Storvik Vår 2011 Ekstraoppgave 1 Anta X 1 og X 2 er uavhengige med X 1 N(1.0, 1.0) og X 2 N(2.0, 1.5). La X = (X 1, X 2 ) T. Definer c = ( ) 2.0 3.0, A = ( ) 1.0 0.5 0.0
Ekstraoppgaver for STK2120 Geir Storvik Vår 2011 Ekstraoppgave 1 Anta X 1 og X 2 er uavhengige med X 1 N(1.0, 1.0) og X 2 N(2.0, 1.5). La X = (X 1, X 2 ) T. Definer c = ( ) 2.0 3.0, A = ( ) 1.0 0.5 0.0
Oblig 1 i MAT2400. Oppgave 1. Tor Hedin Brønner. a) Vi tar integralet av f X (x) fra til x: = 1. Medianen, µ, finner vi ved å sette.
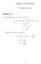 Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
Oblig 1 i MAT24 Tor Hedin Brønner Oppgave 1. a) Vi tar integralet av f X (x) fra til x: x f X (x) dy = Medianen, µ, finner vi ved å sette.5 = µ dy + x = [ θ y θ] x = θ x θ + θ θ ( θ = 1 x) µ θ = θ.5 µ
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent) Mette Langaas Foreleses mandag 11.oktober,
TMA4240 Statistikk H2010 Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent) Mette Langaas Foreleses mandag 11.oktober,
Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent)
 TMA440 Statistikk H010 Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent) Mette Langaas Foreleses mandag 11.oktober,
TMA440 Statistikk H010 Statistisk inferens: 9.14: Sannsynlighetsmaksimeringsestimatoren 8.5: Fordeling til gjennomsnittet 9.4: Konfidensintervall for µ (σ kjent) Mette Langaas Foreleses mandag 11.oktober,
Første sett med obligatoriske oppgaver i STK1110 høsten 2015
 Første sett med obligatoriske oppgaver i STK1110 høsten 2015 Dette er det første obligatoriske oppgavesettet i STK1110 høsten 2015. Oppgavesettet består av fire oppgaver. Du må bruke Matematisk institutts
Første sett med obligatoriske oppgaver i STK1110 høsten 2015 Dette er det første obligatoriske oppgavesettet i STK1110 høsten 2015. Oppgavesettet består av fire oppgaver. Du må bruke Matematisk institutts
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
Utfordring. TMA4240 Statistikk H2010. Mette Langaas. Foreleses uke 40, 2010
 TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
TMA4240 Statistikk H2010 Statistisk inferens: 8.1: Tilfeldig utvalg 9.1-9.3: Estimering Mette Langaas Foreleses uke 40, 2010 2 Utfordring Ved en bedrift produseres en elektrisk komponent. Komponenten må
TMA4240 Statistikk Høst 2015
 TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
TMA4245 Statistikk Høst 2016
 TMA5 Statistikk Høst 6 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving Løsningsskisse Oppgave a) Den tilfeldige variabelen X er kontinuerlig fordelt med sannsynlighetstetthet
TMA5 Statistikk Høst 6 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving Løsningsskisse Oppgave a) Den tilfeldige variabelen X er kontinuerlig fordelt med sannsynlighetstetthet
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen. Jo Thori Lind
 Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
Medisinsk statistikk Del I høsten 2009:
 Medisinsk statistikk Del I høsten 2009: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Beregning av sannsynlighet i en binomisk forsøksrekke generelt Sannsynligheten for at suksess intreffer X
Medisinsk statistikk Del I høsten 2009: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Beregning av sannsynlighet i en binomisk forsøksrekke generelt Sannsynligheten for at suksess intreffer X
Observatorer. STK Observatorer - Kap 6. Utgangspunkt. Eksempel høyde Oxford studenter
 Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
Observatorer STK00 - Observatorer - Kap 6 Geir Storvik 4. april 206 Så langt: Sannsynlighetsteori Stokastiske modeller Nå: Data Knytte data til stokastiske modeller Utgangspunkt Eksempel høyde Oxford studenter
Utvalgsfordelinger. Utvalg er en tilfeldig mekanisme. Sannsynlighetsregning dreier seg om tilfeldige mekanismer.
 Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en statistikk (observator) er fordelingen av verdiene statistikken tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg
Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en statistikk (observator) er fordelingen av verdiene statistikken tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg
TMA4240 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Ekstreme bølger. Geir Storvik Matematisk institutt, Universitetet i Oslo. 5. mars 2014
 Ekstreme bølger Geir Storvik Matematisk institutt, Universitetet i Oslo 5. mars 2014 Bølger Timesvise max-bølger ved bøye utenfor østkyst av USA (17/12/1991-23/2-1992) Størrelse på bølger varierer sterkt
Ekstreme bølger Geir Storvik Matematisk institutt, Universitetet i Oslo 5. mars 2014 Bølger Timesvise max-bølger ved bøye utenfor østkyst av USA (17/12/1991-23/2-1992) Størrelse på bølger varierer sterkt
Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010
 Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Oppgave 1 a Forventet antall dødsulykker i år i er E(X i λ i. Dermed er θ i λ i E(X i forventet antall dødsulykker per 100
Løsningsforslag til andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Oppgave 1 a Forventet antall dødsulykker i år i er E(X i λ i. Dermed er θ i λ i E(X i forventet antall dødsulykker per 100
TMA4245 Statistikk. Innlevering 3. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
STK1100 våren Normalfordelingen. Normalfordelingen er den viktigste av alle sannsynlighetsfordelinger
 STK00 våren 206 Normalfordelingen Svarer til avsnitt 4.3 i læreboka Geir Storvik Matematisk institutt Universitetet i Oslo Normalfordelingen er den viktigste av alle sannsynlighetsfordelinger Normalfordelingen
STK00 våren 206 Normalfordelingen Svarer til avsnitt 4.3 i læreboka Geir Storvik Matematisk institutt Universitetet i Oslo Normalfordelingen er den viktigste av alle sannsynlighetsfordelinger Normalfordelingen
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST 101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 30. november 1992. Tid for eksamen: 09.00 15.00.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST 101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 30. november 1992. Tid for eksamen: 09.00 15.00.
Løsningsforslag oblig 1 STK1110 høsten 2014
 Løsningsforslag oblig STK høsten 4 Oppgave I forbindelse med en studie av antioksidanter og antocyanider, ble innholdet av antocyan i 5 beger med blåbær målt. De målte verdiene var (i mg per gram): 55
Løsningsforslag oblig STK høsten 4 Oppgave I forbindelse med en studie av antioksidanter og antocyanider, ble innholdet av antocyan i 5 beger med blåbær målt. De målte verdiene var (i mg per gram): 55
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i STK2120 Statistiske metoder og dataanalyse 2 Eksamensdag: Mandag 6. juni 2011. Tid for eksamen: 14.30 18.30. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i STK2120 Statistiske metoder og dataanalyse 2 Eksamensdag: Mandag 6. juni 2011. Tid for eksamen: 14.30 18.30. Oppgavesettet er
Kap. 8: Utvalsfordelingar og databeskrivelse
 Kap. 8: Utvalsfordelingar og databeskrivelse Utvalsfordelingar Utvalsfordeling for gjennomsnitt (med kjent varians) ( X ) Sentralgrenseteoremet (SGT) Utvalsfordeling for varians (normalfordeling) Utvalfordeling
Kap. 8: Utvalsfordelingar og databeskrivelse Utvalsfordelingar Utvalsfordeling for gjennomsnitt (med kjent varians) ( X ) Sentralgrenseteoremet (SGT) Utvalsfordeling for varians (normalfordeling) Utvalfordeling
Gammafordelingen og χ 2 -fordelingen
 Gammafordelingen og χ 2 -fordelingen Gammafunksjonen Gammafunksjonen er en funksjon som brukes ofte i sannsynlighetsregning. I mange fordelinger dukker den opp i konstantleddet. Hvis man plotter n-fakultet
Gammafordelingen og χ 2 -fordelingen Gammafunksjonen Gammafunksjonen er en funksjon som brukes ofte i sannsynlighetsregning. I mange fordelinger dukker den opp i konstantleddet. Hvis man plotter n-fakultet
Oppfriskning av blokk 1 i TMA4240
 Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Forelesning 7: Store talls lov, sentralgrenseteoremet. Jo Thori Lind
 Forelesning 7: Store talls lov, sentralgrenseteoremet Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Estimering av variansen 2. Asymptotisk teori 3. Store talls lov 4. Sentralgrenseteoremet 1.Estimering
Forelesning 7: Store talls lov, sentralgrenseteoremet Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Estimering av variansen 2. Asymptotisk teori 3. Store talls lov 4. Sentralgrenseteoremet 1.Estimering
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1100 Statistiske metoder og dataanalyse 1 - Løsningsforslag Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1100 Statistiske metoder og dataanalyse 1 - Løsningsforslag Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30
x λe λt dt = 1 e λx for x > 0 uavh = P (X 1 v)p (X 2 v) = F X (v) 2 = (1 e λv ) 2 = 1 2e λv + e 2λv = 2 1 λ 1 2λ = 3
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 7 Løsningsskisse Oppgave 1 a) Regner først ut den kumulative fordelingsfunksjonen til X: F X (x) = x λe λt dt
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 7 Løsningsskisse Oppgave 1 a) Regner først ut den kumulative fordelingsfunksjonen til X: F X (x) = x λe λt dt
Oppsummering av STK2120. Geir Storvik
 Oppsummering av STK2120 Geir Storvik Vår 2011 Hovedtemaer Generelle inferensmetoder Spesielle modeller/metoder Bruk av R Vil ikke bli testet på kommandoer, men må forstå generelle utskrifter Generelle
Oppsummering av STK2120 Geir Storvik Vår 2011 Hovedtemaer Generelle inferensmetoder Spesielle modeller/metoder Bruk av R Vil ikke bli testet på kommandoer, men må forstå generelle utskrifter Generelle
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 8, blokk II Løsningsskisse Oppgave 1 Da komponentene danner et parallellsystem, vil systemet fungere dersom minst
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 8, blokk II Løsningsskisse Oppgave 1 Da komponentene danner et parallellsystem, vil systemet fungere dersom minst
Forslag til endringar
 Forslag til endringar Bakgrunn: Vi har ingen forelesningar veka etter påske. Eg skal bort 18. og 19. april. Eksamen er 30.mai Forslag til endringar: Ekstra forelesningar onsdag 16.mars og onsdag 30 mars
Forslag til endringar Bakgrunn: Vi har ingen forelesningar veka etter påske. Eg skal bort 18. og 19. april. Eksamen er 30.mai Forslag til endringar: Ekstra forelesningar onsdag 16.mars og onsdag 30 mars
Forelesning 3. april, 2017
 Forelesning 3. april, 2017 APPENDIX TIL KAP. 6 Sentralgrenseteoremet AVSNITT 6.3 Anvendelser av sentralgrenseteoremet Histogrammer S-kurver Q-Q-plot Diverse eksempler MGF for følger av uavhengige identisk
Forelesning 3. april, 2017 APPENDIX TIL KAP. 6 Sentralgrenseteoremet AVSNITT 6.3 Anvendelser av sentralgrenseteoremet Histogrammer S-kurver Q-Q-plot Diverse eksempler MGF for følger av uavhengige identisk
Kapittel 8: Tilfeldige utvalg, databeskrivelse og fordeling til observatorar, Kapittel 9: Estimering
 Kapittel 8: Tilfeldige utvalg, databeskrivelse og fordeling til observatorar, Kapittel 9: Estimering TMA4245 Statistikk Kapittel 8.1-8.5. Kapittel 9.1-9.3+9.15 Turid.Follestad@math.ntnu.no p.1/21 Har sett
Kapittel 8: Tilfeldige utvalg, databeskrivelse og fordeling til observatorar, Kapittel 9: Estimering TMA4245 Statistikk Kapittel 8.1-8.5. Kapittel 9.1-9.3+9.15 Turid.Follestad@math.ntnu.no p.1/21 Har sett
ÅMA110 Sannsynlighetsregning med statistikk, våren
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
Siden vi her har brukt første momentet i fordelingen (EX = EX 1 ) til å konstruere estimatoren kalles denne metoden for momentmetoden.
 Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
ECON2130 Kommentarer til oblig
 ECON2130 Kommentarer til oblig Her har jeg skrevet ganske utfyllende kommentarer til en del oppgaver som mange slet med. Har noen steder gått en del utover det som det strengt tatt ble spurt om i oppgaven,
ECON2130 Kommentarer til oblig Her har jeg skrevet ganske utfyllende kommentarer til en del oppgaver som mange slet med. Har noen steder gått en del utover det som det strengt tatt ble spurt om i oppgaven,
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1 Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30 18.00. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Statistiske metoder og dataanalyse 1 Eksamensdag: Mandag 30. november 2015. Tid for eksamen: 14.30 18.00. Oppgavesettet
for x 0 F X (x) = 0 ellers Figur 1: Parallellsystem med to komponenter Figur 2: Seriesystem med n komponenter
 TMA4245 Statistikk Vår 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3, blokk II Dette er den første av to innleveringer i blokk 2. Denne øvingen skal oppsummere
TMA4245 Statistikk Vår 2016 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3, blokk II Dette er den første av to innleveringer i blokk 2. Denne øvingen skal oppsummere
TMA4240 Statistikk H2017 [15]
![TMA4240 Statistikk H2017 [15] TMA4240 Statistikk H2017 [15]](/thumbs/104/162215320.jpg) TMA4240 Statistikk H207 [5] Del 2: Statistisk inferens Populasjon og utvalg [8.] Observatorer og utvalgsfordelinger [8.2-8.3] Fordeling til gjennomsnittet og sentralgrenseteoremet [8.4] Normalplott [8.8]
TMA4240 Statistikk H207 [5] Del 2: Statistisk inferens Populasjon og utvalg [8.] Observatorer og utvalgsfordelinger [8.2-8.3] Fordeling til gjennomsnittet og sentralgrenseteoremet [8.4] Normalplott [8.8]
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Ferdig før tiden 4 7 Ferdig til avtalt tid 12 7 Forsinket 1 måned 2 6 Forsinket 2 måneder 4 4 Forsinket 3 måneder 6 2 Forsinket 4 måneder 0 2
 Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
Besvar alle oppgavene. Hver deloppgave har lik vekt. Oppgave I En kommune skal bygge ny idrettshall og vurderer to entreprenører, A og B. Begge gir samme pristilbud, men kommunen er bekymret for forsinkelser.
STK1100 våren Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner
 STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
Høgskolen i Telemark. Institutt for økonomi og informatikk FORMELSAMLING Statistikk I. Til bruk ved eksamen. Per Chr. Hagen
 Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag Situasjonen er som i quiz-eksempelet: n = 4, p = 1/3 ( suksess betyr å gjette riktig alternativ), q = 2/3. Oppgave: Finn
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag Situasjonen er som i quiz-eksempelet: n = 4, p = 1/3 ( suksess betyr å gjette riktig alternativ), q = 2/3. Oppgave: Finn
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 21. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 21. april Bjørn H. Auestad Oppsummering våren
L12-Dataanalyse. Introduksjon. Nelson Aalen plott. Page 76 of Introduksjon til dataanalyse. Levetider og sensurerte tider
 Page 76 of 80 L12-Dataanalyse Introduksjon Introduksjon til dataanalyse Presentasjonen her fokuserer på dataanalyseteknikker med formål å estimere parametere (MTTF,, osv) i modeller vi benytter for vedlikeholdsoptimering
Page 76 of 80 L12-Dataanalyse Introduksjon Introduksjon til dataanalyse Presentasjonen her fokuserer på dataanalyseteknikker med formål å estimere parametere (MTTF,, osv) i modeller vi benytter for vedlikeholdsoptimering
ST0103 Brukerkurs i statistikk Høsten Momentestimatoren og sannsynlighetsmaksimeringsestimatoren
 ST0103 Brukerkurs i statistikk Høsten 2016 Momentestimatoren og sannsynlighetsmaksimeringsestimatoren (SME) Boka har bare ett eksempel med sannsynlighetsmaksimeringsestimatoren. Vi gjengir dette nedenfor,
ST0103 Brukerkurs i statistikk Høsten 2016 Momentestimatoren og sannsynlighetsmaksimeringsestimatoren (SME) Boka har bare ett eksempel med sannsynlighetsmaksimeringsestimatoren. Vi gjengir dette nedenfor,
TMA4240 Statistikk Eksamen desember 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Løsningsforslag, eksamen statistikk, juni 2015
 Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 29. november 1993. Tid for eksamen: 09.00 15.00. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 29. november 1993. Tid for eksamen: 09.00 15.00. Oppgavesettet
Kapittel 4.4: Forventning og varians til stokastiske variable
 Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Kapittel 4.4: Forventning og varians til stokastiske variable Forventning og varians til stokastiske variable Histogrammer for observerte data: Sannsynlighets-histogrammer og tetthetskurver for stokastiske
Modeller og parametre. STK Punktestimering - Kap 7. Eksempel støtfangere. Statistisk inferens. Binomisk fordeling. p X (x) = p x (1 p) n x
 STK1100 - Puktestimerig - Kap 7 Geir Storvik Modeller og parametre Biomisk fordelig ( ) p X (x) = p x (1 p) x x Parameter: p Normalfordelig f X (x) = 1 2πσ e 1 2σ 2 (x µ) 2 11. april 2016 Parametre: µ,
STK1100 - Puktestimerig - Kap 7 Geir Storvik Modeller og parametre Biomisk fordelig ( ) p X (x) = p x (1 p) x x Parameter: p Normalfordelig f X (x) = 1 2πσ e 1 2σ 2 (x µ) 2 11. april 2016 Parametre: µ,
Kapittel 2: Hendelser
 Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Øvingsforelesning i Matlab TDT4105
 Øvingsforelesning i Matlab TDT4105 Øving 6. Tema: funksjoner med vektorer, plotting, while Benjamin A. Bjørnseth 12. oktober 2015 2 Oversikt Funksjoner av vektorer Gjennomgang av øving 5 Plotting Preallokering
Øvingsforelesning i Matlab TDT4105 Øving 6. Tema: funksjoner med vektorer, plotting, while Benjamin A. Bjørnseth 12. oktober 2015 2 Oversikt Funksjoner av vektorer Gjennomgang av øving 5 Plotting Preallokering
Andre sett med obligatoriske oppgaver i STK1110 høsten 2010
 Andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Dette er det andre settet med obligatoriske oppgaver i STK1110 høsten 2010. Oppgavesettet består av fire oppgaver. Det er valgfritt om du vil
Andre sett med obligatoriske oppgaver i STK1110 høsten 2010 Dette er det andre settet med obligatoriske oppgaver i STK1110 høsten 2010. Oppgavesettet består av fire oppgaver. Det er valgfritt om du vil
STK Statistiske metoder og dataanalyse høsten 2019 Løsningsforslag til oppgaver i læreboka for uke 38
 STK1110 - Statistiske metoder og dataanalyse høsten 2019 Løsningsforslag til oppgaver i læreboka for uke 38 Vinnie Ko & Ørnulf Borgan September 21, 2019 Lærebok: Modern Mathematical Statistics with Applications
STK1110 - Statistiske metoder og dataanalyse høsten 2019 Løsningsforslag til oppgaver i læreboka for uke 38 Vinnie Ko & Ørnulf Borgan September 21, 2019 Lærebok: Modern Mathematical Statistics with Applications
ECON Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger. Jo Thori Lind
 ECON2130 - Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Betinget sannsynlighet 2. Stokastiske variable 3. Forventning og varians 4. Regneregler
ECON2130 - Statistikk 1 Forelesning 4: Stokastiske variable, fordelinger Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Betinget sannsynlighet 2. Stokastiske variable 3. Forventning og varians 4. Regneregler
Forelesning 27. mars, 2017
 Forelesning 27. mars, 2017 AVSNITT 5.5 Ordningsobservatorene AVSNITT 6.1 Observatorer og deres fordelinger Ordningsobservatorene La X 1,..., X n være n uavhengige stokastiske variable som alle har samme
Forelesning 27. mars, 2017 AVSNITT 5.5 Ordningsobservatorene AVSNITT 6.1 Observatorer og deres fordelinger Ordningsobservatorene La X 1,..., X n være n uavhengige stokastiske variable som alle har samme
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST0 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Torsdag 9. mai 994. Tid for eksamen: 09.00 5.00. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST0 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Torsdag 9. mai 994. Tid for eksamen: 09.00 5.00. Oppgavesettet
Dekkes av kap , 9.10, 9.12 og forelesingsnotatene.
 Estimering 2 -Konfidensintervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesingsnotatene. En (punkt-)estimator ˆΘ gir oss et anslag på en ukjent parameterverdi, men gir oss ikke noen direkte informasjon
Estimering 2 -Konfidensintervall Dekkes av kap. 9.4-9.5, 9.10, 9.12 og forelesingsnotatene. En (punkt-)estimator ˆΘ gir oss et anslag på en ukjent parameterverdi, men gir oss ikke noen direkte informasjon
Forelesning 6: Punktestimering, usikkerhet i estimering. Jo Thori Lind
 Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
Forelesning 6: Punktestimering, usikkerhet i estimering Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Trekke utvalg 2. Estimatorer og observatorer som stokastiske variable 3. Egenskapene til en estimator
STK1100 våren 2019 Mere om konfidensintevaller
 STK1100 våren 2019 Mere om konfidensintevaller Svarer til avsnitt 8.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 Konfidensintervall for µ i store utvalg Anta at de stokastiske
STK1100 våren 2019 Mere om konfidensintevaller Svarer til avsnitt 8.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 Konfidensintervall for µ i store utvalg Anta at de stokastiske
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave Scriptet run confds.m simulerer n data x,..., x n fra en normalfordeling med
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave Scriptet run confds.m simulerer n data x,..., x n fra en normalfordeling med
Merk at vi for enkelthets skyld antar at alle som befinner seg i Roma sentrum enten er italienere eller utenlandske turister.
 ECON230: EKSAMEN 20 VÅR - UTSATT PRØVE 2 TALLSVAR. Oppgave Da Anne var på besøk i Roma, fikk hun raskt problemer med språket. Anne snakker engelsk, men ikke italiensk, og kun av 5 italienere behersker
ECON230: EKSAMEN 20 VÅR - UTSATT PRØVE 2 TALLSVAR. Oppgave Da Anne var på besøk i Roma, fikk hun raskt problemer med språket. Anne snakker engelsk, men ikke italiensk, og kun av 5 italienere behersker
Programmering i R - del 2
 Programmering i R - del 2 14. februar 2004 1 Simulering fra modell Når vi skal analysere et gitt konkret innsamlet datasett vil vi gjøre dette med utgangspunkt i en statistisk modell. Vi kan si at en slik
Programmering i R - del 2 14. februar 2004 1 Simulering fra modell Når vi skal analysere et gitt konkret innsamlet datasett vil vi gjøre dette med utgangspunkt i en statistisk modell. Vi kan si at en slik
Løsningsforslag ECON 2130 Obligatorisk semesteroppgave 2017 vår
 Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
Løsningsforslag ECON 130 Obligatorisk semesteroppgave 017 vår Andreas Myhre Oppgave 1 1. (i) Siden X og Z er uavhengige, vil den simultane fordelingen mellom X og Z kunne skrives som: f(x, z) = P(X = x
TMA4240 Statistikk Høst 2008
 TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
Regneøvelse 22/5, 2017
 Regneøvelse 22/5, 217 Arne Bang Huseby Eksamen STK11 212: oppgave 1 og 2 Eksamen STK11 28: oppgave 1) og 2 Eksamen 212, oppgave 1 Ved en bestemt butikk i en større dagligvarekjede viser langvarige data
Regneøvelse 22/5, 217 Arne Bang Huseby Eksamen STK11 212: oppgave 1 og 2 Eksamen STK11 28: oppgave 1) og 2 Eksamen 212, oppgave 1 Ved en bestemt butikk i en større dagligvarekjede viser langvarige data
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
Utvalgsfordelinger. Utvalg er en tilfeldig mekanisme. Sannsynlighetsregning dreier seg om tilfeldige mekanismer.
 Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en observator er fordelingen av verdiene observatoren tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg er en tilfeldig
Utvalgsfordelinger Vi har sett at utvalgsfordelinger til en observator er fordelingen av verdiene observatoren tar ved mange gjenttatte utvalg av samme størrelse fra samme populasjon. Utvalg er en tilfeldig
FORMELSAMLING TIL STK1100 OG STK1110
 FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 16. november 2009) 1. Sannsynlighet La A, B, A 1, A 2,...,B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 16. november 2009) 1. Sannsynlighet La A, B, A 1, A 2,...,B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
TMA4240 Statistikk Høst 2018
 TMA4240 Statistikk Høst 2018 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 5 Dette er andre av tre innleveringer i blokk 2. Denne øvingen skal oppsummere pensum
TMA4240 Statistikk Høst 2018 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 5 Dette er andre av tre innleveringer i blokk 2. Denne øvingen skal oppsummere pensum
Løsningsforslag til eksamen i TMA4245 Statistikk 7. juni 2007
 Løsningsforslag til eksamen i TMA4245 Statistikk 7. juni 2007 Oppgave 1: Pengespill a) For hver deltaker har vi følgende situasjon: Deltakeren får en serie oppgaver. Hver runde har to mulige utfall: Deltakeren
Løsningsforslag til eksamen i TMA4245 Statistikk 7. juni 2007 Oppgave 1: Pengespill a) For hver deltaker har vi følgende situasjon: Deltakeren får en serie oppgaver. Hver runde har to mulige utfall: Deltakeren
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 Ei bedrift produserer elektriske komponentar. Komponentane kan ha to typar
Eksamensoppgave i TMA4240 / TMA4245 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 / TMA4245 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland Tlf: 48 22 18 96 Eksamensdato: 10. august 2017 Eksamenstid (fra til): 09.00-13.00
Institutt for matematiske fag Eksamensoppgave i TMA4240 / TMA4245 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland Tlf: 48 22 18 96 Eksamensdato: 10. august 2017 Eksamenstid (fra til): 09.00-13.00
Utvalgsfordelinger (Kapittel 5)
 Utvalgsfordelinger (Kapittel 5) Observator En observator er en funksjon av data for mange individer, for eksempel Gjennomsnitt Andel Stigningstall i regresjonslinje En observator er en tilfeldig variabel
Utvalgsfordelinger (Kapittel 5) Observator En observator er en funksjon av data for mange individer, for eksempel Gjennomsnitt Andel Stigningstall i regresjonslinje En observator er en tilfeldig variabel
Statistikk og dataanalyse
 Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
Njål Foldnes, Steffen Grønneberg og Gudmund Horn Hermansen Statistikk og dataanalyse En moderne innføring Kapitteloversikt del 1 INTRODUKSJON TIL STATISTIKK Kapittel 1 Populasjon og utvalg 19 Kapittel
j=1 (Y ij Ȳ ) 2 kan skrives som SST = i=1 (J i 1) frihetsgrader.
 FORMELSAMLING TIL STK2120 (Versjon av 30. mai 2012) 1 Enveis variansanalyse Anta at Y ij = µ + α i + ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; der ɛ ij -ene er uavhengige og N(0, σ 2 )-fordelte. Da
FORMELSAMLING TIL STK2120 (Versjon av 30. mai 2012) 1 Enveis variansanalyse Anta at Y ij = µ + α i + ɛ ij ; j = 1, 2,..., J i ; i = 1, 2,..., I ; der ɛ ij -ene er uavhengige og N(0, σ 2 )-fordelte. Da
Om eksamen. Never, never, never give up!
 I dag I dag Rekning av eksamensoppgåver Eksamen Mai 2014, oppgåve 2 (inkl normal fordeling, lin.reg. og deskriptiv statistikk) Eksamen August 2012, oppgåve 3 a og b (inkl SME) Om eksamen (Truleg) 10 punkt.
I dag I dag Rekning av eksamensoppgåver Eksamen Mai 2014, oppgåve 2 (inkl normal fordeling, lin.reg. og deskriptiv statistikk) Eksamen August 2012, oppgåve 3 a og b (inkl SME) Om eksamen (Truleg) 10 punkt.
Kap. 6.1: Fordelingen til en observator og stok. simulering
 Kap. 6.1: Fordelingen til en observator og stok. simulering Data, observatorer og relaterte fordelinger. Stokastisk simulering. Illustrasjon: - Sammenligning av jury bedømmelser i idrett. Fra data til
Kap. 6.1: Fordelingen til en observator og stok. simulering Data, observatorer og relaterte fordelinger. Stokastisk simulering. Illustrasjon: - Sammenligning av jury bedømmelser i idrett. Fra data til
TMA4240 Statistikk Høst 2007
 TMA4240 Statistikk Høst 2007 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b4 Løsningsskisse Oppgave 1 Eksamen juni 1999, oppgave 3 av 3 a) µ populasjonsgjennomsnitt,
TMA4240 Statistikk Høst 2007 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b4 Løsningsskisse Oppgave 1 Eksamen juni 1999, oppgave 3 av 3 a) µ populasjonsgjennomsnitt,
Observatorar og utvalsfordeling. Torstein Fjeldstad Institutt for matematiske fag, NTNU
 Observatorar og utvalsfordeling Torstein Fjeldstad Institutt for matematiske fag, NTNU 08.10.2018 I dag Til no i emnet Observatorar Utvalsfordelingar Sentralgrenseteoremet 2 Til no i emnet definisjon av
Observatorar og utvalsfordeling Torstein Fjeldstad Institutt for matematiske fag, NTNU 08.10.2018 I dag Til no i emnet Observatorar Utvalsfordelingar Sentralgrenseteoremet 2 Til no i emnet definisjon av
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
Løsningsforslag øving 8, ST1301
 Løsningsforslag øving 8, ST3 Oppgave Hva gjør følgende funksjon? Hvilken fordeling har variabelen n som returneres som funksjonsverdi? Forklar hvorfor. Forutsett at to enkle positive tall blir oppgitt
Løsningsforslag øving 8, ST3 Oppgave Hva gjør følgende funksjon? Hvilken fordeling har variabelen n som returneres som funksjonsverdi? Forklar hvorfor. Forutsett at to enkle positive tall blir oppgitt
Prøveeksamen STK2100 (fasit) - vår 2018
 Prøveeksamen STK2100 (fasit) - vår 2018 Geir Storvik Vår 2018 Oppgave 1 (a) Vi har at E = Y Ŷ =Xβ + ε X(XT X) 1 X T (Xβ + ε) =[I X(X T X) 1 X T ]ε Dette gir direkte at E[E] = 0. Vi får at kovariansmatrisen
Prøveeksamen STK2100 (fasit) - vår 2018 Geir Storvik Vår 2018 Oppgave 1 (a) Vi har at E = Y Ŷ =Xβ + ε X(XT X) 1 X T (Xβ + ε) =[I X(X T X) 1 X T ]ε Dette gir direkte at E[E] = 0. Vi får at kovariansmatrisen
Bernoulli forsøksrekke og binomisk fordeling
 Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
DEL 1 GRUNNLEGGENDE STATISTIKK
 INNHOLD 1 INNLEDNING 15 1.1 Parallelle verdener........................... 18 1.2 Telle gunstige.............................. 20 1.3 Regneverktøy og webstøtte....................... 22 1.4 Oppgaver................................
INNHOLD 1 INNLEDNING 15 1.1 Parallelle verdener........................... 18 1.2 Telle gunstige.............................. 20 1.3 Regneverktøy og webstøtte....................... 22 1.4 Oppgaver................................
Om eksamen. Never, never, never give up!
 Plan vidare Onsdag Gjere ferdig kap 11 + repetisjon Fredag Rekning av eksamensoppgåver Eksamen Mai 2014, oppgåve 2 (inkl normal fordeling, lin.reg. og deskriptiv statistikk) Eksamen August 2012, oppgåve
Plan vidare Onsdag Gjere ferdig kap 11 + repetisjon Fredag Rekning av eksamensoppgåver Eksamen Mai 2014, oppgåve 2 (inkl normal fordeling, lin.reg. og deskriptiv statistikk) Eksamen August 2012, oppgåve
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 Statistisk inferens: 9.4: Konfidensintervall for µ 8.7: Student-t fordeling 8.6: Fordeling til S 2 Mette Langaas Foreleses onsdag 13.oktober, 2010 2 Estimering Mål: finne sannheten
TMA4240 Statistikk H2010 Statistisk inferens: 9.4: Konfidensintervall for µ 8.7: Student-t fordeling 8.6: Fordeling til S 2 Mette Langaas Foreleses onsdag 13.oktober, 2010 2 Estimering Mål: finne sannheten
STK1100 våren Generell introduksjon. Omhandler delvis stoffet i avsnitt 1.1 i læreboka (resten av kapittel 1 blir gjennomgått ved behov)
 STK1100 våren 2017 Generell introduksjon Omhandler delvis stoffet i avsnitt 1.1 i læreboka (resten av kapittel 1 blir gjennomgått ved behov) Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 «Overalt»
STK1100 våren 2017 Generell introduksjon Omhandler delvis stoffet i avsnitt 1.1 i læreboka (resten av kapittel 1 blir gjennomgått ved behov) Ørnulf Borgan Matematisk institutt Universitetet i Oslo 1 «Overalt»
STK1100 Oblig 2. Øyvind Kolbu Gruppe februar 2007
 STK1100 Oblig 2 Øyvind Kolbu Gruppe 3 oyvink@math.uio.no 16. februar 2007 Oppgave A Vis at E(X n ) = µ: X n = 1 n n X i = 1 n (X 1 + X 2 +... + X n ) i=1 ( n ) E(X n ) = 1 n E X i = 1 n E (X 1 + X 2 +...
STK1100 Oblig 2 Øyvind Kolbu Gruppe 3 oyvink@math.uio.no 16. februar 2007 Oppgave A Vis at E(X n ) = µ: X n = 1 n n X i = 1 n (X 1 + X 2 +... + X n ) i=1 ( n ) E(X n ) = 1 n E X i = 1 n E (X 1 + X 2 +...
