TMA4245 Statistikk Vår 2007
|
|
|
- Theodor Gjertsen
- 7 år siden
- Visninger:
Transkript
1 TMA4245 Statistikk Vår 2007 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har lært. Oppgavene skal besvares uten å bruke læreboka eller tabellen. Bestem det/de riktige svaret/svarene for hvert spørsmål. a) Hendelse Hva er en hendelse?. Et utfall som inntreffer sjelden 2. En mengde av enkeltutfall 3. Konvergens av relative hyppigheter 4. Et stokastisk forsøk som ikke kan gjentas under samme betingelser b) Disjunkte hendelser To disjunkte hendelser er. To hendelser som ikke kan inntreffe samtidig 2. To hendelser som bare kan inntreffe samtidig 3. To umulige hendelser 4. To hendelser som har minst ett enkeltutfall felles c) Kast en mynt to ganger. Da er det (når en ikke tar hensyn til rekkefølgen). mer sannsynlig å få to kron enn å få en mynt og en kron 2. mindre sannsynlig å få to kron enn å få en mynt og en kron 3. like sannsynlig å få to kron som å få en mynt og en kron d) Hvor mange tre-sifrede tall av tallene,2,3,4,5 fins det? a. Trekker med tilbakelegging, ordnet: b. Trekker uten tilbakelegging, ordnet: e) Betinget sannsynlighet La A og B være to disjunkte hendelser. Hva er da P (A B)? Ikke definert 4. P (A) + P (B) 5. 2 oving7-oppg-b 4. februar 2007 Side
2 f) Total sannsynlighet Setningen om total sannsynlighet sier: La A,... A r være en oppdeling av utfallsrommet S (dvs. at hendelsene A j er parvis disjunkte og tilsammen oppfyller hele utfallsrommet) og la B være en vilkårlig hendelse. Da gjelder:. P (B) = r j= P (A j)p (B A j ) 2. P (B) = r j= P (A j)p (A j B) 3. P (B) = r j= P (B j)p (A B j ) 4. P (B) = r j= P (A j)p (B A j ) 5. P (B A j ) = r j= P (A j)p (B A j ) g) Uavhengighet Hva vil det si at to hendelser A og B er uavhengige?. At de ikke kan inntreffe samtidig 2. At de ikke er disjunkte 3. At de er disjunkte 4. At P (A B) = P (A)P (B A) 5. At P (A B) = P (A)P (B) 6. At de forekommer i atskilte stokastiske forsøk 7. At A er inneholdt i B eller omvendt h) Diskret variabel En stokastisk variable sies å være diskret fordelt dersom:. Den har bare endelig mange mulige verdier 2. Den har endelig eller tellbart uendelig mange mulige verdier 3. De mulige verdier er tallene,2,3, De mulige verdier er mengden av alle reelle tall 5. De mulige verdier er et intervall [a, b] på tallinjen, der vi kan ha a = og/eller b = i) Kontinuerlig variabel En stokastisk variable sies å være kontinuerlig fordelt dersom:. Den har bare endelig mange mulige verdier 2. Den har endelig eller tellbart uendelig mange mulige verdier 3. De mulige verdier er tallene, 2, 3, De mulige verdier er mengden av alle reelle tall 5. De mulige verdier er et intervall [a, b] på tallinjen, der vi kan ha a = og/eller b = j) Punktsannsynlighet diskret variabel Punktsannsynligheten p(x) for en diskret stokastisk variabel X tilfredsstiller:
3 . p(x) > 0 for alle reelle tall x 2. p(x) > 0 for alle mulige verdier for X 3. p(x) > 0 for x =, 2, p(x) er en strengt voksende funksjon av x 5. p(x) er overalt ikke-avtagende som funksjon av x 6. x p(x) = k) Fordelingsfunksjon diskret variabel Fordelingsfunskjonen F (x) for en diskret stokastisk variabel X tilfredsstiller:. F (x) er definert for alle reelle tall x 2. F (x) > 0 for alle reelle tall x 3. F (x) > 0 for alle mulige verdier for X 4. F (x) > 0 for x =, 2, F (x) er en strengt voksende funksjon av x 6. F (x) er overalt ikke-avtagende som funksjon av x 7. x F (x) = 8. lim x F (x) = 9. F (0) = 0 l) Forventning og varians En stokastisk variabel X har punktsannsynlighet: p( ) = 0.5, p() = 0.5. En stokastisk variabel Y har punktsannsynlighet: p( 2) = 0.5, p(2) = X har mindre forventingsverdi enn Y 2. X har større forventingsverdi enn Y 3. X og Y har samme forventningsverdi, nemlig 0 4. X har mindre varians enn Y 5. X har større varians enn Y 6. X og Y har samme varians 7. SD(X) =, SD(Y ) = 2 m) Ved innføringen av bomringen i Trondheim vil 80% av bilistene ha køfri- brikke. For en gruppe på 0 bilister, hva er sannsynligheten for at alle har køfri-brikke? /0 = 0.08 n) En urne inneholder 7 røde og 5 grønne kuler. Trekk 3 kuler - og la X være antall grønne blant de 3. Mulige sannsynlighetsfordelinger for X kan være:. X er binomisk fordelt. 2. X er poissonfordelt. 3. X er hypergeometrisk fordelt. Skriv riktig tall (,2 eller 3) for fordeling i situasjonene nedenfor.
4 a.... De 3 kulene trekkes med tilbakelegging. b.... De 3 kulene trekkes uten tilbakelegging. o) Kontinuerlige variable La X være en kontinuerlig stokastisk variabel med sannsynlighetstetthet f(x) og fordelingsfunksjon F (x). Sett ring rundt de utsagn nedenfor som er korrekte.. 0 f(x) for alle x. 2. f(x) 0 for alle x F (x) for alle x. 4. F (x) > 0 for alle x. 5. F (x) er en ikke-avtagende funksjon. 6. f(x) er en ikke-avtagende funksjon. 7. f(x) er stykkevis kontinuerlig 8. f (x) = F (x) for alle unntatt muligens endelig mange x. 9. F (x) = f(x) for alle unntatt muligens endelig mange x. 0. P (X = x) = 0 for alle verdier av x.. P (X = x) > 0 for alle unntatt muligens endelig mange x. 2. F (x) = x f(u)du. 3. f(x) = x F (u)du. 4. P (a < X b) = b a f(u)du. 5. P (a X b) = b a f(u)du. 6. P (a < X b) = F (b) F (a). p) Forventningsverdi og varians La X være en kontinuerlig stokastisk variabel med sannsynlighetstetthet f(x) og fordelingsfunksjon F (x). Sett ring rundt de utsagn nedenfor som er korrekte.. E(X) = xf(x)dx 2. E(X) = x2 f(x)dx 3. E(X) = xf (x)dx 4. E(X) er alltid lik den verdi av x der f(x) er størst 5. Var(X) = x2 f(x)dx 6. Var(X) = x2 f(x)dx hvis E(X) = 0 7. Var(X) = (x E(X))2 f(x)dx 8. Var(X) = x2 f(x)dx [E(X)] 2 q) Eksponensialfordelingen Hva mener en med at eksponensialfordelingen ikke har hukommelse? (T eksp(λ)). Den er vanskelig å huske.
5 2. La T være levetiden til en lyspære. En ny lyspære har like stor sannsynlighet for å leve i 0 timer som en lyspære som virker etter 00 timer har å leve i 0 timer til. 3. P (T > y) = P (T > x + y T > x) 4. Parameteren λ endrer seg hele tiden. Eksponensialfordelingen husker ikke sin verdi av λ. r) Funksjon av stokastisk variabel La X være kontinuerlig fordelt med sannsynlighetstetthet f X (x), og la Y = e X. Da blir sannsynlighetstettheten til Y:. f Y (y) = f X (e y )e y 2. f Y (y) = f X (ln y)e y 3. f Y (y) = f X (ln y) y s) La X være normalfordelt med forventningsverdi µ og varians σ 2. La Y = ax + b for gitte konstanter a og b. Sett ring rundt de riktige utsagn nedenfor.. Y er ikke nødvendigvis normalfordelt 2. Y er normalfordelt 3. Hvis a = /σ og b = µ/σ, så er Y standard normalfordelt 4. E(Y ) = aσ + b 5. E(Y ) = aµ + b 6. Var(Y ) = aσ 7. Var(Y ) = a 2 σ 2 8. Var(Y ) = aσ 2 + b 2 t) La X være normalfordelt med forventningsverdi µ og varians σ 2. Hvilken av følgende transformasjoner av X gir en standard normalfordeling (dvs. N(0,))?. Z = X µ σ 2. Z = X µ σ 2 3. Z = X µ µ 4. Z = X µσ u) La Φ(x) være fordelingsfunksjonen i standard normalfordelingen. Sett ring rundt de riktige utsagnene nedenfor.. Φ(x) = 2π e x Φ( x) = Φ(x) 7. Φ( x) = Φ(x) 2. Φ(x) = Φ( x) 5. Φ( x) = Φ(x) 8. Φ(0) = 0 3. Φ(0) = Φ(0) = 9. lim x Φ(x) = 0 v) La X og X 2 være diskrete stokastiske variable, hver med mulige verdier 0,, 2, 3,.... Sett ring rundt det riktige utsagnet nedenfor.. P (X 2 = 0 X = 0) + P (X 2 = X = 0) + P (X 2 = 2 X = 0) + P (X 2 = 3 X = 0) +... = 2. P (X 2 = 0 X = 0) + P (X 2 = 0 X = ) + P (X 2 = 0 X = 2) + P (X 2 = 0 X = 3) +... = w) La X og X 2 være to stokastiske variable, diskrete eller kontinuerlige. Sett ring rundt de korrekte utsagnene nedenfor.. Var(X + X 2 ) = Var(X ) + Var(X 2 )
6 2. Var(X + X 2 ) = Var(X ) + Var(X 2 ) + Cov(X, X 2 ) 3. Var(X + X 2 ) = Var(X ) + Var(X 2 ) + 2Cov(X, X 2 ) 4. Var(X + X 2 ) = Var(X ) + Var(X 2 ) 2Cov(X, X 2 ) 5. Var(X + X 2 ) = Var(X ) + Var(X 2 ) hvis X og X 2 er stokastisk uavhengige 6. Cov(X, X 2 ) = E(X X 2 ) E(X )E(X 2 ) 7. Cov(X, X 2 ) = E(X X 2 ) hvis X og X 2 er stokastisk uavhengige 8. Cov(X, X 2 ) = E(X )E(X 2 ) hvis X og X 2 er stokastisk uavhengige 9. E(X X 2 ) = E(X )E(X 2 ) hvis X og X 2 er stokastisk uavhengige x) La X og X 2 være uavhengige stokastiske variable. La Y = X X 2 og Z = 2 (X +X 2 ). Sett ring rundt de riktige svarene nedenfor:. Var(Y ) = Var(X ) Var(X 2 ) 2. Var(Y ) = Var(X ) + Var(X 2 ) 3. Var(Z) = 2 (Var(X ) + Var(X 2 )) 4. Var(Z) = 4 (Var(X ) + Var(X 2 )) 5. Var(Z) = 4 Var(Y ) 6. Var(2Z) = Var(Y ) Oppgave 2 Simultanfordeling - Eksamen august 2006, oppgave 4 av 4 Simultanfordelingen, f(x, y), til de to diskrete stokastiske variablene X og Y er gitt i flgende tabell: y=0 y= y=2 x= x= x= Finn marginalfordelingen til X og til Y, og beregn forventning og varians til X og til Y. Beregn kovariansen mellom X og Y, Cov(X, Y ). Er X og Y uavhengige? Svaret skal begrunnes. Oppgave 3 a-d Oljeutslipp Eksamen 6. august 2004, oppgave 2 av 3, punkt a av
7 Oljeselskaper som er operatører på norsk kontinentalsokkel må hvert år rapportere forurensende utslipp til myndighetene. Under de fleste reservoarer ligger det en vannsone som etter noen tids produksjon trekkes opp i brønnene og blir en del av væsken som produseres på feltene. Vannet skilles fra oljen under produksjonen, men en del olje blir igjen i produksjonsvannet som slippes ut i sjøen. Myndighetene krever at oljekonsentrasjonen i produksjonsvann som slippes ut i sjøen skal være mindre enn 40 mg/l. Basert på dagens teknologi kan det antas at oljekonsentrasjonen i et tilfeldig valgt utslipp av produksjonsvann er normalfordelt med forventing µ = 2.6 mg/l og standardavvik σ = 3.4 mg/l. a) Finn sannsynligheten for at oljekonsentrasjonen i et tilfeldig valgt utslipp av produksjonsvann er mindre enn 30 mg/l. Hva er sannsynligheten for at oljekonsentrasjonen i et tilfeldig valgt utslipp overskrider myndighetenes krav? Finn sannsynligheten for at oljekonsentrasjonen i et tilfeldig valgt utslipp ligger innenfor [µ 3σ, µ + 3σ]. Oppgave 4 Sykehjemmet Eksamen 5. august 2004, oppgave 2 av 3 Vi ser på dødsfall om natten ved sykehjemmet Aftensol. Ved sykehjemmet er det tre sykepleiere i rene nattevaktstillinger, Anne, Bernt og Cecilie. Hver natt er en av dem på vakt gjennom hele natten, og det er da ingen andre ansatte tilstede ved hjemmet. Anne jobber i 00% nattevaktstilling, mens Bernt og Cecilie jobber i 50% nattevaktstillinger. Vi ser på en tilfeldig valgt natt og definerer følgende hendelser: A = Anne er på vakt, B = Bernt er på vakt, C = Cecilie er på vakt, D = det skjer et dødsfall. Anta at alle dødsfall er naturlige. Det er da rimelig å gå ut fra at sannsynligheten for dødsfall er den samme uansett hvilken sykepleier som er på vakt, dvs. at P (D A) = P (D B) = P (D C). Anta at den felles verdi for disse er a) Tegn de 4 hendelsene definert ovenfor i et venndiagram. Hva er sannsynlighetene P (A), P (B) og P (C)? Finn P (D). Er hendelsene D og C uavhengige? Begrunn svaret. I den siste tiden har det vært 0 dødsfall om natten ved sykehjemmet, og hele 7 av disse har skjedd når Cecilie har vært på vakt. Det er derfor satt igang etterforskning for eventuelt å avdekke om Cecilie har noe med dødsfallene å gjøre. Anta i det følgende at alle dødsfallene er naturlige, og at de har skjedd på forskjellige netter. La X være en stokastisk variabel som beskriver antall av n = 0 naturlige dødsfall som skjer på Cecilies vakter.
8 b) Forklar hvorfor det kan antas at X er binomisk fordelt med n = 0 og p = (Det er ikke tilstrekkelig å skrive opp de generelle forutsetningene for en binomisk fordeling, betingelsene må relateres direkte til situasjonen som er beskrevet.) Hva er sannsynligheten for at 7 eller flere av 0 dødsfall om natten skjer på Cecilies vakter? La oss tenke oss at det rundt om på sykehjem i Norge jobber 300 andre sykepleiere i tilsvarende stilling som Cecilie. Hva er sannsynligheten for at minst en av de 300 sykepleierne opplever at 7 eller flere av 0 naturlige dødsfall skjer på sine vakter? Gir svarene i dette punktet grunn til å styrke mistanken mot Cecilie? Begrunn svaret. Oppgave 5 Transport av masse Eksamen mai 2006, oppgave 2 av 4 En entreprenør har leid inn et transportfirma til å transportere masse bort fra en byggeplass. Det er to mulige veivalg fra byggeplassen til stedet der massen skal deponeres, gjennom eller utenom bykjernen. Av helse, miljø og sikkerhetshensyn velger entreprenøren at massen skal transporteres utenom bykjernen. Når oppdraget er ferdig har transportfirmaet kjørt 000 turer, og transportfirmaet informerer entreprenøren om at av de 000 turene har 5 blitt kjørt gjennom bykjernen og 995 er blitt kjørt utenom bykjernen. I løpet av transportperioden har entreprenøren ved 5 tilfeldig valgte transporter sjekket om transporten har skjedd gjennom bykjernen. La X være antall ganger, av de 5 transportene som ble sjekket, entreprenøren finner at massen er blitt transportert gjennom bykjernen. Hvilken fordeling har X? Begrunn svaret. Hvilken verdi av X har høyest punktsannsynlighet? Nå viser det seg at entreprenøren fant at i 5 av de 5 tilfellene han sjekket så ble massen transportert gjennom bykjernen. Hva er sannsynligheten for dette, dvs. P (X = 5)? Oppgave 6 Levetid til elektroniske komponenter Eksamen desember 999, oppgave 4 av 5, punkt a,b (av a-e) Levetiden (målt i måneder), X, til en del typer elektroniske komponenter har vist seg å følge en fordeling med sannsynlighetstetthet { x e x θ for x > 0 f(x) = 2θ 0 ellers, der θ er en parameter som beskriver kvaliteten til komponentene. Tilhørende kumulative fordelingsfunksjon er gitt ved { F (x) = e x θ for x > 0 0 ellers. I hele denne oppgaven antar vi at levetider til ulike komponenter er uavhengige. (6.)
9 [Hint: Du kan i denne oppgaven uten bevis benytte at 0 x α e x θ dx = 2θ 2α+2 Γ(2α + 2), for α >, θ > 0, der Γ(α) er gamma-funksjonen (se også tabell).] a) For θ = 2.0, finn sannsynligheten for at en elektronisk komponent av denne typen fremdeles skal funksjonere etter 0 måneder. Gitt at en komponent fremdeles funksjonerer etter 0 måneder, hva er sannsynligheten for at den også vil funksjonere etter 20 måneder dersom θ = 2.0? Vis at E(X) = 2θ 2. b) Et bestemt instrument inneholder to elektroniske komponenter, komponent A og komponent B. For at instrumentet skal funksjonere må begge de to elektroniske komponentene funksjonere. La X A betegne levetiden til komponent A og la X B være levetiden til komponent B. Levetiden til instrumentet blir dermed U = min(x A, X B ). Levetidene for begge komponentene er på formen gitt i ligning (6.), men med ulik kvalitetsparameter θ, dvs. komponent A har kvalitetsparameter θ A, mens komponent B har kvalitetsparameter θ B. Finn sannsynlighetstettheten for instrumentets levetid (uttrykt ved θ A og θ B ). Hva blir forventet levetid for instrumentet? Oppgave 7 Eksamen mai 2003, oppgave 3 av 3, punkt a,b av a-e Et apparat inneholder k like komponenter og fungerer bare dersom alle disse er i orden. Komponentenes levetider T, T 2,... T k er uavhengige og eksponensielt fordelte med parameter β (> 0), dvs. sannsynlighetstettheten er f(t) = β e t/β for t 0, 0 for t < 0. a) Finn den kumulative fordelingsfunksjonen for levetiden til en komponent. Hva blir P (T < 3) og P (2 < T < 4) når β = 5? b) La X betegne apparatets levetid. Vis at X er eksponensielt fordelt med parameter β/k. Hva blir apparatets forventede levetid når k = 4 og β = 5? Oppgave 8 X er kontinuerlig fordelt med sannsynlighetstetthet Finn sannsynlighetsfordelingen til f(x) = { 2xe x 2 for x 0 0 ellers
10 a) U = X 2 b) V = 2X c) W = X 2 Oppgave 9 Levetid for lyspærer Eksamen august 2002, oppgave 3 av 3 To typer lyspærer, A og B, har levetider henholdsvis X og Y, der X og Y antas uavhengige. Videre antas at X har sannsynlighetstetthet f (x) og Y har sannsynlighetstetthet f 2 (y), der { f (x) = β e x/β for x 0 0 ellers, f 2 (y) = { β 2 e y/β 2 for y 0 0 ellers og β, β 2 > 0. a) Vis at forholdet mellom forventet levetid for pære A og forventet levetid for pære B er β /β 2. La U = X/Y være forholdet mellom levetidene og la V = Y. b) Finn simultan sannsynlighetstetthet for U og V. (Å finne simultanfordelingen er ikke pensum, men for de som vil prøve seg er teorem 7.4 et godt tips. Svaret er f U,V (u, v) = v β β 2 e u v β + β 2 u, v > 0 0 ellers. Resten av oppgaven er pensum, bruk f U,V (u, v) som oppgitt.) Vis at marginal sannsynlighetstetthet for U er { β β 2 g(u) = (β +β 2 for u 0, u) 2 0 ellers. c) Vis at E(U) er uendelig. Oppgave 0 Eksamen desember 999, oppgave 5 av 5 I en poissonprosess med intensitet λ, la X betegne tiden frem til første hendelse og la X 2 betegne tiden mellom første og andre hendelse. Som kjent er da X og X 2 uavhengige og eksponensialfordelte med forventning /λ (dette trenger ikke du vise). La Y betegne tiden frem til andre hendelse, dvs. Y = X + X 2. Vis at da er Y gamma-fordelt med parametre α = 2 og β = /λ, dvs. vis at sannsynlighetstettheten for Y er { λ f(y) = 2 ye λy for y > 0, 0 ellers.
11 Oppgave Oppgave 7. fra læreboka. Oppgave 2 Oppgave 7.3 fra læreboka. Oppgave 3 Oppgave 7.5 fra læreboka. Fasit 3. a) , 0, a) P(D)=0.06 b) 0.004, P (X = 5) = a) 0.206, 0.59 b) f(u) = (/θ A + /θ B )exp( u /2 (/θ A + /θ B ))/(2u /2 ), E(U) = 2(θ A θ B / (θ A + θ B )) 2 7. a) 0.452, b).25
TMA4240 Statistikk Høst 2008
 TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
TMA4240 Statistikk Høst 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave 1 Tippekonkurranse Denne oppgaven er ment som en kjapp test på hva du har
TMA4240 Statistikk. Øving nummer 7. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4240 Statistikk Vår 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave Blandet drops a) Tippekupong På en tippekupong er det gitt 2 fotballkamper.
TMA4240 Statistikk Vår 2008 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 7 Oppgave Blandet drops a) Tippekupong På en tippekupong er det gitt 2 fotballkamper.
A) B) 400 C) 120 D) 60 E) 10. Rett svar: C. Fasit: ( 5 6 = 60. Hvis A, B, C er en partisjon av utfallsrommet S, så er P (A B) lik.
 Oppgave 1 Det skal velges en komité bestående av 2 menn og 1 kvinne. Komitéen skal velges fra totalt 5 menn og 6 kvinner. Hvor mange ulike komitéer kan dannes? A) 86400 B) 400 C) 120 D) 60 E) 10 Rett svar:
Oppgave 1 Det skal velges en komité bestående av 2 menn og 1 kvinne. Komitéen skal velges fra totalt 5 menn og 6 kvinner. Hvor mange ulike komitéer kan dannes? A) 86400 B) 400 C) 120 D) 60 E) 10 Rett svar:
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x er sannsynlighetstettheten til en kontinuerlig X dersom:. f(x 0 for alle x R 2. f(xdx = 3. P (a
Høgskolen i Telemark. Institutt for økonomi og informatikk FORMELSAMLING Statistikk I. Til bruk ved eksamen. Per Chr. Hagen
 Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
Høgskolen i Telemark Institutt for økonomi og informatikk FORMELSAMLING 6005 Statistikk I Til bruk ved eksamen Per Chr. Hagen . Sannsynlighetsregning. Regneregler Komplementsetningen: Addisjonssetningen:
TMA4240 Statistikk Høst 2015
 TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
Oppfriskning av blokk 1 i TMA4240
 Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Oppfriskning av blokk 1 i TMA4240 Geir-Arne Fuglstad November 21, 2016 2 Hva har vi gjort i dette kurset? Vi har studert to sterkt relaterte grener av matematikk Sannsynlighetsteori: matematisk teori for
Bernoulli forsøksrekke og binomisk fordeling
 Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
Bernoulli forsøksrekke og binomisk fordeling Bernoulli forsøksrekke i) gjentar et forsøk n ganger ii) hvert forsøk gir enten suksess eller fiasko iii) sannsynligheten for suksess er p i alle forsøkene
Togforsinkelsen (Eksamen Des2003.1a) I denne oppgaven kan du bruke uten å vise det at
 Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4245 V2007: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF 4.1: La X være
Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4245 V2007: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF 4.1: La X være
6 x P (X = x) = x=1 = P (X 2 = 6)P (X 2 = 6)P (X 3 = 6) =
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 4, blokk I Løsningsskisse Oppgave 1 a) Utfallsrommet til X 1 er {1, 2,, 4, 5, }. Sannsynlighetsfordelingen
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 4, blokk I Løsningsskisse Oppgave 1 a) Utfallsrommet til X 1 er {1, 2,, 4, 5, }. Sannsynlighetsfordelingen
Litt mer om eksponensialfordelingen
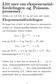 Litt mer om eksponensialfordelingen og Poissonprosesser. Dekkes av 5.6, 6.6, 6.7 og det som står under. Eksponensialfordelingen Så langt har vi lært at det finnes to parametriseringer av eksponensialfordelingen
Litt mer om eksponensialfordelingen og Poissonprosesser. Dekkes av 5.6, 6.6, 6.7 og det som står under. Eksponensialfordelingen Så langt har vi lært at det finnes to parametriseringer av eksponensialfordelingen
FORMELSAMLING TIL STK1100 OG STK1110
 FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 16. november 2009) 1. Sannsynlighet La A, B, A 1, A 2,...,B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 16. november 2009) 1. Sannsynlighet La A, B, A 1, A 2,...,B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
6.2 Normalfordeling. Høyde kvinner og menn. 6.1 Kontinuerlig uniform fordeling. Kapittel 6
 3 6.2 Normalfordeling Kapittel 6 Noen kontinuerlige sannsynlighetsfordelinger TMA4245 V2007: Eirik Mo Normalfordeling: Sannsynlighetstettheten til en normalfordelt stokastisk variabel, X, med forventning
3 6.2 Normalfordeling Kapittel 6 Noen kontinuerlige sannsynlighetsfordelinger TMA4245 V2007: Eirik Mo Normalfordeling: Sannsynlighetstettheten til en normalfordelt stokastisk variabel, X, med forventning
TMA4240 Statistikk Høst 2009
 TMA44 Statistikk Høst 9 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b Løsningsskisse Oppgave X er en stokastisk variabel med sannsynlighetstetthet { f(x),
TMA44 Statistikk Høst 9 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b Løsningsskisse Oppgave X er en stokastisk variabel med sannsynlighetstetthet { f(x),
Eksempel: kast med to terninger
 Kapittel 3 TMA4245 V2007: Eirik Mo 2 Eksempel: kast med to terninger I et eksperiment kaster vi to terninger og registerer antall øyne på hver terning. Utfallsrom S={(,),(,2),(,3),...,(,), (2,),...,(2,),...,(,)}
Kapittel 3 TMA4245 V2007: Eirik Mo 2 Eksempel: kast med to terninger I et eksperiment kaster vi to terninger og registerer antall øyne på hver terning. Utfallsrom S={(,),(,2),(,3),...,(,), (2,),...,(2,),...,(,)}
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 3.3: Kontinuerlige sannsynlighetsfordelinger 4.1: Matematisk forventing (univariat del) Mette Langaas Foreleses mandag 6. september 2010 2 3.1 Stokastisk variabel (repetisjon)
TMA4240 Statistikk H2010 3.3: Kontinuerlige sannsynlighetsfordelinger 4.1: Matematisk forventing (univariat del) Mette Langaas Foreleses mandag 6. september 2010 2 3.1 Stokastisk variabel (repetisjon)
3.1 Stokastisk variabel (repetisjon)
 TMA4240 Statistikk H2010 3.3: Kontinuerlige sannsynlighetsfordelinger 4.1: Matematisk forventing (univariat del) Mette Langaas Foreleses mandag 6. september 2010 2 3.1 Stokastisk variabel (repetisjon)
TMA4240 Statistikk H2010 3.3: Kontinuerlige sannsynlighetsfordelinger 4.1: Matematisk forventing (univariat del) Mette Langaas Foreleses mandag 6. september 2010 2 3.1 Stokastisk variabel (repetisjon)
Formelsamling V-2014 MAT110. Statistikk 1. Per Kristian Rekdal
 Formelsamling V-2014 MAT110 Statistikk 1 Per Kristian Rekdal 2 Forord Dette er formelsamlingen i emnet MAT110 Statistikk 1 ved høgskolen i Molde. Formlene i denne formelsamlingen er stort sett de formlene
Formelsamling V-2014 MAT110 Statistikk 1 Per Kristian Rekdal 2 Forord Dette er formelsamlingen i emnet MAT110 Statistikk 1 ved høgskolen i Molde. Formlene i denne formelsamlingen er stort sett de formlene
Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger
 f(x,y) NTNU Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger TMA4240 Statistikk (F2 og E7) 3.4: Foreleses mandag 30.august y=hoyde x=vekt Ole.Petter.Lodoen@math.ntnu.no p.1/18 Oppsummering
f(x,y) NTNU Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger TMA4240 Statistikk (F2 og E7) 3.4: Foreleses mandag 30.august y=hoyde x=vekt Ole.Petter.Lodoen@math.ntnu.no p.1/18 Oppsummering
Foreleses onsdag 8. september 2010
 TMA4240 Statistikk H200 4.2: Varians (univariat del) 4.4: Chebyshevs teorem 3.4: Simultanfordelinger Mette Langaas Foreleses onsdag 8. september 200 Mette.Langaas@math.ntnu.no, TMA4240H200 2 4.2 Varians
TMA4240 Statistikk H200 4.2: Varians (univariat del) 4.4: Chebyshevs teorem 3.4: Simultanfordelinger Mette Langaas Foreleses onsdag 8. september 200 Mette.Langaas@math.ntnu.no, TMA4240H200 2 4.2 Varians
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5, blokk I Løsningsskisse Oppgave 1 X og Y er uavhengige Poisson-fordelte stokastiske variable, X p(x;5 og Y p(y;1.
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5, blokk I Løsningsskisse Oppgave 1 X og Y er uavhengige Poisson-fordelte stokastiske variable, X p(x;5 og Y p(y;1.
Tyngdepunkt. Togforsinkelsen (Eksamen Des2003.1a) I denne oppgaven kan du bruke uten å vise det at. Kapittel 4
 3 Tyngdepunkt Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4240 H2006: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF
3 Tyngdepunkt Kapittel 4 Forventningsverdi, varians, kovarians for én stokastisk variabel og funksjoner av stokastiske variabler TMA4240 H2006: Eirik Mo 2 4.1 Forventing til en stokastisk variabel DEF
MULTIPLE CHOICE ST0103 BRUKERKURS I STATISTIKK September 2016
 MULTIPLE CHOICE ST0103 BRUKERKURS I STATISTIKK September 2016 SETT RING RUNDT DET RIKTIGE SVARET FOR HVER OPPGAVE. Oppgave 1 Stokastisk forsøk Stokastiske forsøk karakteriseres ved to av følgende egenskaper.
MULTIPLE CHOICE ST0103 BRUKERKURS I STATISTIKK September 2016 SETT RING RUNDT DET RIKTIGE SVARET FOR HVER OPPGAVE. Oppgave 1 Stokastisk forsøk Stokastiske forsøk karakteriseres ved to av følgende egenskaper.
Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger
 Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger TMA4245 Statistikk (B, K1, I) 3.1, 3.2, 3.3 foreleses torsdag 15.januar 0.00 0.02 0.04 0.06 0.08 160 170 180 190 hoyde i cm Mette.Langaas@math.ntnu.no
Kapittel 3: Stokastiske variable og sannsynlighetsfordelinger TMA4245 Statistikk (B, K1, I) 3.1, 3.2, 3.3 foreleses torsdag 15.januar 0.00 0.02 0.04 0.06 0.08 160 170 180 190 hoyde i cm Mette.Langaas@math.ntnu.no
3.4: Simultanfordelinger (siste rest) 4.1,4.2,4.3: Multivariat del (ferdig med kapittel 3 og 4 etter denne forelesningen)
 TMA4240 Statistikk H200 3.4: Simultanfordelinger (siste rest) 4.,4.2,4.3: Multivariat del (ferdig med kapittel 3 og 4 etter denne forelesningen) Mette Langaas Foreleses mandag 3. september 200 2 f (x,
TMA4240 Statistikk H200 3.4: Simultanfordelinger (siste rest) 4.,4.2,4.3: Multivariat del (ferdig med kapittel 3 og 4 etter denne forelesningen) Mette Langaas Foreleses mandag 3. september 200 2 f (x,
TMA4240/TMA4245 Statistikk: Oppsummering kontinuerlige sannsynlighetsfordelinger
 TMA4240/TMA4245 Statistikk: Oppsummering kontinuerlige sannsynlighetsfordelinger Kontinuerlig uniform fordeling f() = B A, A B. En kontinuerlig størrelse (vekt, lengde, tid), som aldri kan bli mindre enn
TMA4240/TMA4245 Statistikk: Oppsummering kontinuerlige sannsynlighetsfordelinger Kontinuerlig uniform fordeling f() = B A, A B. En kontinuerlig størrelse (vekt, lengde, tid), som aldri kan bli mindre enn
To-dimensjonale kontinuerlige fordelinger
 To-dimensjonale kontinuerlige fordelinger Noen resultater for diskrete fordelinger Vi har tidligere definert punktsannsynligheten p(x, y) for en todimensjonal variabel (X, Y ) som p(x, y) = P ({X = x}
To-dimensjonale kontinuerlige fordelinger Noen resultater for diskrete fordelinger Vi har tidligere definert punktsannsynligheten p(x, y) for en todimensjonal variabel (X, Y ) som p(x, y) = P ({X = x}
TMA4240 Statistikk Høst 2009
 TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b7 Oppgave 1 Automatisert laboratorium Eksamen november 2002, oppgave 3 av 3 I eit
TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b7 Oppgave 1 Automatisert laboratorium Eksamen november 2002, oppgave 3 av 3 I eit
Sum to terninger forts. Eksempel: kast med to terninger. Sum to terninger forts. Kapittel 3. TMA4240 H2006: Eirik Mo
 3 Sum to terninger forts. Kapittel 3 TMA4240 H200: Eirik Mo 2 3 4 5,,2,3,4,5, 2 2, 2,2 2,3 2,4 2,5 2, Andre 3 3, 3,2 3,3 3,4 3,5 3, terning 4 4, 4,2 4,3 4,4 4,5 4, 5 5, 5,2 5,3 5,4 5,5 5,,,2,3,4,5, Med
3 Sum to terninger forts. Kapittel 3 TMA4240 H200: Eirik Mo 2 3 4 5,,2,3,4,5, 2 2, 2,2 2,3 2,4 2,5 2, Andre 3 3, 3,2 3,3 3,4 3,5 3, terning 4 4, 4,2 4,3 4,4 4,5 4, 5 5, 5,2 5,3 5,4 5,5 5,,,2,3,4,5, Med
STK1100 våren Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner
 STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
STK1100 våren 2017 Kontinuerlige stokastiske variabler Forventning og varians Momentgenererende funksjoner Svarer til avsnittene 4.1 og 4.2 i læreboka Ørnulf Borgan Matematisk institutt Universitetet i
Eksamensoppgave i Løsningsskisse TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Institutt for matematiske fag Eksamensoppgave i Løsningsskisse TMA440 Statistikk Faglig kontakt under eksamen: Håkon Tjelmeland a, Sara Martino b Tlf: a 48 18 96, b 99 40 33 30 Eksamensdato: 30. november
Kapittel 2: Hendelser
 Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Kapittel 2: Hendelser FENOMEN Eksperiment Utfall Utfallsrom Eksperiment. Utfall. Eksperiment Utfall Hendelse Sannsynlighet: egenskaper, gunstige vs. mulige, relativ frekvens Sannsynlighet for mer enn en
Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma.
 TMA4240 Statistikk H2010 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma. Mette Langaas Foreleses mandag 27. september 2010 2
TMA4240 Statistikk H2010 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma. Mette Langaas Foreleses mandag 27. september 2010 2
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Deleksamen i: STK Sannsynlighetsregning og statistisk modellering Eksamensdag: Mandag 4. mars 26 Tid for eksamen: 5. 7. Oppgavesettet er
ST0202 Statistikk for samfunnsvitere Kapittel 6: Normalfordelingen
 ST0202 Statistikk for samfunnsvitere Kapittel 6: Normalfordelingen Bo Lindqvist Institutt for matematiske fag 2 Kap. 6: Normalfordelingen Normalfordelingen regnes som den viktigste statistiske fordelingen!
ST0202 Statistikk for samfunnsvitere Kapittel 6: Normalfordelingen Bo Lindqvist Institutt for matematiske fag 2 Kap. 6: Normalfordelingen Normalfordelingen regnes som den viktigste statistiske fordelingen!
Løsningsforslag, eksamen statistikk, juni 2015
 Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
TMA4245 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 4 Løsningsskisse Oppgave 1 Mureren La X være mengden mørtel mureren bruker i løpet av en tilfeldig valgt arbeidsdag.
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 4 Løsningsskisse Oppgave 1 Mureren La X være mengden mørtel mureren bruker i løpet av en tilfeldig valgt arbeidsdag.
TMA4240 Statistikk H2015
 TMA4240 Statistikk H2015 Kapittel 4: Matematisk forventning [4.1+start 4.3] Quiz kjørt med Kahoot! fra kahoot.it. Mette Langaas wiki.math.ntnu.no/emner/tma4240/2015h/start/ 2 Høyde, kvinner Frequency
TMA4240 Statistikk H2015 Kapittel 4: Matematisk forventning [4.1+start 4.3] Quiz kjørt med Kahoot! fra kahoot.it. Mette Langaas wiki.math.ntnu.no/emner/tma4240/2015h/start/ 2 Høyde, kvinner Frequency
Kontinuerlige sannsynlighetsfordelinger.
 Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
Kontinuerlige sannsynlighetsfordelinger. Dekkes av kap. 6 og deler av kap. 8.5 i boka. Husk: f(x) er sannsynlighetstettheten til en kontinuerlig X dersom: 1. f(x) 0 for alle x R 2. f(x)dx =1 3. P (a
MAT4010 PROSJEKTOPPGAVE: Statistikk i S2. Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem
 MAT400 PROSJEKTOPPGAVE: Statistikk i S2 Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem 20. mai 205 Innhold. Stokastisk Variabel.. Stokastiske variable som funksjoner 3 2. Forventningsverdi
MAT400 PROSJEKTOPPGAVE: Statistikk i S2 Olai Sveine Johannessen, Vegar Klem Hafnor & Torstein Mellem 20. mai 205 Innhold. Stokastisk Variabel.. Stokastiske variable som funksjoner 3 2. Forventningsverdi
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave X er kontinuerlig fordelt med sannsynlighetstetthet f X (x) = { x exp( x ) x
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Løsningsskisse Oppgave X er kontinuerlig fordelt med sannsynlighetstetthet f X (x) = { x exp( x ) x
ÅMA110 Sannsynlighetsregning med statistikk, våren 2010. ÅMA110 Sannsynlighetsregning med statistikk, våren 2010
 ÅMA Sannsynlighetsregning med statistikk, våren Kp. Diskrete tilfeldige variable ÅMA Sannsynlighetsregning med statistikk, våren Kp. Diskrete tilfeldige variable Diskrete tilfeldige variable, innledning
ÅMA Sannsynlighetsregning med statistikk, våren Kp. Diskrete tilfeldige variable ÅMA Sannsynlighetsregning med statistikk, våren Kp. Diskrete tilfeldige variable Diskrete tilfeldige variable, innledning
FORMELSAMLING TIL STK1100 OG STK1110
 FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 11. november 2017) 1. Sannsynlighet La A, B, A 1, A 2,..., B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
FORMELSAMLING TIL STK1100 OG STK1110 (Versjon av 11. november 2017) 1. Sannsynlighet La A, B, A 1, A 2,..., B 1, B 2,... være begivenheter, dvs. delmengder av et utfallsrom Ω. a) Aksiomene: Et sannsynlighetsmål
Forelesing 27 Oppsummering. Torstein Fjeldstad Institutt for matematiske fag, NTNU
 Forelesing 27 Oppsummering Torstein Fjeldstad Institutt for matematiske fag, NTNU 18.04.2018 I dag Lineær regresjon (sjekk av modellantagelser) Praktisk informasjon Andre statistikk-kurs Oversikt over
Forelesing 27 Oppsummering Torstein Fjeldstad Institutt for matematiske fag, NTNU 18.04.2018 I dag Lineær regresjon (sjekk av modellantagelser) Praktisk informasjon Andre statistikk-kurs Oversikt over
Oppgave 1 Vi lar X være antall tankskip som ankommer havnen i løpet av en dag. Vi har fått oppgitt at X poisson(λ) med
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 5, blokk I Løsningsskisse Oppgave 1 Vi lar X være antall tankskip som ankommer havnen i løpet av en dag.
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalte oppgaver 5, blokk I Løsningsskisse Oppgave 1 Vi lar X være antall tankskip som ankommer havnen i løpet av en dag.
EKSAMEN I TMA4245 Statistikk
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Turid Follestad (98 06 68 80/73 59 35 37) Hugo Hammer (45 21 01 84/73 59 77 74) Eirik
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Turid Follestad (98 06 68 80/73 59 35 37) Hugo Hammer (45 21 01 84/73 59 77 74) Eirik
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 29. november 1993. Tid for eksamen: 09.00 15.00. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: ST101 Innføring i statistikk og sannsynlighetsregning. Eksamensdag: Mandag 29. november 1993. Tid for eksamen: 09.00 15.00. Oppgavesettet
Løsningsforslag til seminar 4 Undervisningsfri uke
 Løsningsforslag til seminar 4 Undervisningsfri uke Iman Ghayoornia February 22, 2016 Oppgave 2.1 Se Excel-filen som er tilgjengelig på emnesiden. Hvis du lurer på hvordan jeg fikk verdiene i cellene så
Løsningsforslag til seminar 4 Undervisningsfri uke Iman Ghayoornia February 22, 2016 Oppgave 2.1 Se Excel-filen som er tilgjengelig på emnesiden. Hvis du lurer på hvordan jeg fikk verdiene i cellene så
Binomisk fordeling. Tilfeldige variabler. MAT0100V Sannsynlighetsregning og kombinatorikk
 MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilfeldige variabler Når vi kaster to terninger er det 36 utfall Vi ser på X = «sum antall øyne» De mulige verdiene
MAT0100V Sannsynlighetsregning og kombinatorikk Forventning, varians og standardavvik Tilfeldige variabler Når vi kaster to terninger er det 36 utfall Vi ser på X = «sum antall øyne» De mulige verdiene
Forelesning 13. mars, 2017
 Forelesning 13. mars, 217 AVSNITT 5.2 Kovariansen mellom to variable Korrelasjon mellom to variable AVSNITT 5.3 Betingede fordelinger Kovariansen mellom to stokastiske variable Kovariansen mellom to stokastiske
Forelesning 13. mars, 217 AVSNITT 5.2 Kovariansen mellom to variable Korrelasjon mellom to variable AVSNITT 5.3 Betingede fordelinger Kovariansen mellom to stokastiske variable Kovariansen mellom to stokastiske
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 5. JUNI 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform Onsdag Normal Onsdag Eksponensial I dag Gamma I dag Kji-kvadrat I dag Student-T (Kap
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform Onsdag Normal Onsdag Eksponensial I dag Gamma I dag Kji-kvadrat I dag Student-T (Kap
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Stokastisk variabel. Eksempel augefarge
 Dagens tekst Kap 3: Stokastiske variable og sannsynsfordelingar Stokastisk variabel: Diskret sannsynsfordeling: Kontinuerleg sannsynsfordeling: Kummulativ sannsynsfordeling: Diskret simultanfordeling Kontinuerleg
Dagens tekst Kap 3: Stokastiske variable og sannsynsfordelingar Stokastisk variabel: Diskret sannsynsfordeling: Kontinuerleg sannsynsfordeling: Kummulativ sannsynsfordeling: Diskret simultanfordeling Kontinuerleg
a ) Forventningen estimeres med gjennomsnittet: x = 1 12 (x 1 + + x 12 ) = 1 (755 + 708 + + 748) = 8813/12 = 734.4
 ÅMA110 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 011, s. 1 (Det tas forbehold om feil i løsningsforslaget. Oppgave 1 Vi betrakter dataene x 1,..., x 1 somutfall av n = 1 u.i.f.
ÅMA110 Sannsylighetsregning og statistikk Løsningsforslag til eksamen høst 011, s. 1 (Det tas forbehold om feil i løsningsforslaget. Oppgave 1 Vi betrakter dataene x 1,..., x 1 somutfall av n = 1 u.i.f.
TMA4240 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
1.1.1 Rekke med konstante ledd. En rekke med konstante ledd er gitt som. a n (1) n=m
 Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma. Mette Langaas Foreleses mandag 27. september 2010 2
TMA4240 Statistikk H2010 Kapittel 6: Kontinuerlige sannsynlighetsfordelinger 6.4-5.7: Normalfordelingen, normalapproksimasjon, eksponensial og gamma. Mette Langaas Foreleses mandag 27. september 2010 2
TMA4240 Statistikk Høst 2009
 TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5 Løsningsskisse Oppgave 1 En lottorekke kan oppfattes som et ikke-ordnet utvalg på
TMA4240 Statistikk Høst 2009 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 5 Løsningsskisse Oppgave 1 En lottorekke kan oppfattes som et ikke-ordnet utvalg på
TMA4240 Statistikk 2014
 TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
TMA4240 Statistikk 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 12, blokk II Oppgave 1 På ein av vegane inn til Trondheim er UP interessert i å måle effekten
TMA4240 Statistikk Eksamen desember 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4240 Statistikk Eksamen desember 15 Oppgave 1 La den kontinuerlige stokastiske variabelen X ha fordelingsfunksjon (sannsynlighetstetthet
Statistikk 1 kapittel 4
 Statistikk 1 kapittel 4 Nico Keilman ECON 2130 Vår 2015 Kapittel 4 Stokastiske (tilfeldige) variabler Anta 1) Vi kjenner sannsynligheter for ulike utfall knyttet til et forsøk 2) Hvert utfall har en (meningsfull)
Statistikk 1 kapittel 4 Nico Keilman ECON 2130 Vår 2015 Kapittel 4 Stokastiske (tilfeldige) variabler Anta 1) Vi kjenner sannsynligheter for ulike utfall knyttet til et forsøk 2) Hvert utfall har en (meningsfull)
Kap. 6, Kontinuerlege Sannsynsfordelingar
 Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
Kapittel 6, Kontinuerlege Sannsynsfordelingar Sjå på eit utval av ofte brukte kontinuerlege sannsynsfordelingar Uniform I går Normal I går Eksponensial I dag Gamma I dag Kji-kvadrat I dag Nokre eigenskapar
TMA4240 Statistikk Høst 2012
 TMA424 Statistikk Høst 212 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving blokk II Oppgave 1 Oppgave 11.3 fra læreboka. Oppgave 2 Oppgave 11.19 fra læreboka. Oppgave
TMA424 Statistikk Høst 212 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving blokk II Oppgave 1 Oppgave 11.3 fra læreboka. Oppgave 2 Oppgave 11.19 fra læreboka. Oppgave
Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte
 Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
Hypotesetesting. 10 og fore- Dekkes av pensumsidene i kap. lesingsnotatene. Hypotesetesting er en systematisk fremgangsmåte for å undersøke hypoteser (påstander) knyttet til parametre i sannsynlighetsfordelinger.
TMA4240 Statistikk H2015
 TMA4240 Statistikk H2015 Funksjoner av stokastiske variabler (kapittel 7+notat) Fokus på start med kumulativ fordeling 7.2 Funksjon av en SV (inkludert en-entydighet). Fordeling til max/min (fra notat).
TMA4240 Statistikk H2015 Funksjoner av stokastiske variabler (kapittel 7+notat) Fokus på start med kumulativ fordeling 7.2 Funksjon av en SV (inkludert en-entydighet). Fordeling til max/min (fra notat).
Betinget sannsynlighet
 Betinget sannsynlighet Multiplikasjonsloven for sannsynligheter (s. 49 i bok): P( AB ) = P( A B ) P(B) Veldig viktig verktøy for å finne sannsynligheter for snitt. (Bevises ved rett fram manipulering av
Betinget sannsynlighet Multiplikasjonsloven for sannsynligheter (s. 49 i bok): P( AB ) = P( A B ) P(B) Veldig viktig verktøy for å finne sannsynligheter for snitt. (Bevises ved rett fram manipulering av
TMA4240 Statistikk H2010
 TMA4240 Statistikk H2010 2.8: Bayes regel 3.1: Stokastisk variabel 3.2: Diskrete sannsynlighetsfordelinger 3.3: Kontinuerlige sannsynlighetsfordelinger Mette Langaas Foreleses onsdag 1. september 2010
TMA4240 Statistikk H2010 2.8: Bayes regel 3.1: Stokastisk variabel 3.2: Diskrete sannsynlighetsfordelinger 3.3: Kontinuerlige sannsynlighetsfordelinger Mette Langaas Foreleses onsdag 1. september 2010
Kapittel 2: Sannsynlighet [ ]
![Kapittel 2: Sannsynlighet [ ] Kapittel 2: Sannsynlighet [ ]](/thumbs/91/105500625.jpg) Kapittel 2: Sannsynlighet [2.3-2.5] TMA4240 Statistikk (F2 og E7) 2.3, 2.4, 2.5: Kombinatorikk og sannsynlighet [18.august 2004] Ole.Petter.Lodoen@math.ntnu.no p.1/21 Produktregel for valgprosess TEO 2.1
Kapittel 2: Sannsynlighet [2.3-2.5] TMA4240 Statistikk (F2 og E7) 2.3, 2.4, 2.5: Kombinatorikk og sannsynlighet [18.august 2004] Ole.Petter.Lodoen@math.ntnu.no p.1/21 Produktregel for valgprosess TEO 2.1
Forelening 1, kapittel 4 Stokastiske variable
 Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
Forelening 1, kapittel 4 Stokastiske variable Eksempel X = "antall kron på kast med to mynter (før de er kastet)" Uniformt utfallsrom {MM, MK, KM, KK}. X = x beskriver hendelsen "antall kron på kast med
6.1 Kontinuerlig uniform fordeling
 Kapittel 6 Noen kontinuerlige sannsynlighetsfordelinger TMA4240 H2006: Eirik Mo 2 6.1 Kontinuerlig uniform fordeling Kontinuerlig uniform fordeling: Sannsynlighetstettheten til den kontinuerlige uniforme
Kapittel 6 Noen kontinuerlige sannsynlighetsfordelinger TMA4240 H2006: Eirik Mo 2 6.1 Kontinuerlig uniform fordeling Kontinuerlig uniform fordeling: Sannsynlighetstettheten til den kontinuerlige uniforme
Statistikk 1 kapittel 4
 Statistikk 1 kapittel 4 Nico Keilman ECON 2130 Vår 2017 Kapittel 4 Stokastiske (tilfeldige) variabler Anta 1) Vi kjenner sannsynligheter for ulike utfall knyttet til et forsøk 2) Hvert utfall har en (meningsfull)
Statistikk 1 kapittel 4 Nico Keilman ECON 2130 Vår 2017 Kapittel 4 Stokastiske (tilfeldige) variabler Anta 1) Vi kjenner sannsynligheter for ulike utfall knyttet til et forsøk 2) Hvert utfall har en (meningsfull)
Siden vi her har brukt første momentet i fordelingen (EX = EX 1 ) til å konstruere estimatoren kalles denne metoden for momentmetoden.
 Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Estimeringsmetoder Momentmetoden La X, X 2,..., X n være uavhengige variable som er rektangulært fordelte på intervallet [0, θ]. Vi vet da at forventningsverdiene til hver observasjon og forventningen
Oppgave 1: Feil på mobiltelefoner
 Oppgave 1: Feil på mobiltelefoner a) Sannsynlighetene i oppgaven blir P (F 1 F 2 ) P (F 1 ) + P (F 2 ) P (F 1 F 2 ) P (F 1 ) + 1 P (F2 C ) P (F 1 F 2 ) 0.080 + 0.075 0.006 0.149 P (F 1 F 2 ) P (F 1 F 2
Oppgave 1: Feil på mobiltelefoner a) Sannsynlighetene i oppgaven blir P (F 1 F 2 ) P (F 1 ) + P (F 2 ) P (F 1 F 2 ) P (F 1 ) + 1 P (F2 C ) P (F 1 F 2 ) 0.080 + 0.075 0.006 0.149 P (F 1 F 2 ) P (F 1 F 2
TMA4245 Statistikk Høst 2016
 TMA5 Statistikk Høst 6 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving Løsningsskisse Oppgave a) Den tilfeldige variabelen X er kontinuerlig fordelt med sannsynlighetstetthet
TMA5 Statistikk Høst 6 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving Løsningsskisse Oppgave a) Den tilfeldige variabelen X er kontinuerlig fordelt med sannsynlighetstetthet
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Regler i statistikk STAT 100
 TORIL FJELDAAS RYGG - VÅREN 2010 Regler i statistikk STAT 100 Innhold side Sannsynlighetsregning 3 - Uttrykk 3 - Betinget sannsynlighet 4 - Regler for sannsynlighet 4 - Bayes teorem 4 - Uavhengige begivenheter
TORIL FJELDAAS RYGG - VÅREN 2010 Regler i statistikk STAT 100 Innhold side Sannsynlighetsregning 3 - Uttrykk 3 - Betinget sannsynlighet 4 - Regler for sannsynlighet 4 - Bayes teorem 4 - Uavhengige begivenheter
statistikk, våren 2011
 ÅMA110 Sannsynlighetsregning med statistikk, våren 011 Kp. 3 Diskrete tilfeldige variable 1 Diskrete tilfeldige variable, innledning Hva er en tilfeldig variabel (stokastisk variabel)? Diskret tilfeldig
ÅMA110 Sannsynlighetsregning med statistikk, våren 011 Kp. 3 Diskrete tilfeldige variable 1 Diskrete tilfeldige variable, innledning Hva er en tilfeldig variabel (stokastisk variabel)? Diskret tilfeldig
ST1101/ST6101 Sannsynlighetsregning og statistikk Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag ST/ST Sannsynlighetsregning og statistikk Vår 9 Oppgaver fra boka 3..9 Ved et terningkast anses utfallet antall øyne lik for
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag ST/ST Sannsynlighetsregning og statistikk Vår 9 Oppgaver fra boka 3..9 Ved et terningkast anses utfallet antall øyne lik for
Motivasjon for kurset. ÅMA110 Sannsynlighetsregning med statistikk, våren 2008. Oppsummering. ÅMA110 Sannsynlighetsregning med statistikk våren 2008
 ÅMA0 Sannsynlighetsregning med statistikk, våren 008 Oppsummering ÅMA0 Sannsynlighetsregning med statistikk våren 008 Pensum: Pensumbok: Per Chr. Hagen: "Innføring i sannsynlighetsregning og statistikk",
ÅMA0 Sannsynlighetsregning med statistikk, våren 008 Oppsummering ÅMA0 Sannsynlighetsregning med statistikk våren 008 Pensum: Pensumbok: Per Chr. Hagen: "Innføring i sannsynlighetsregning og statistikk",
Regneøvelse 22/5, 2017
 Regneøvelse 22/5, 217 Arne Bang Huseby Eksamen STK11 212: oppgave 1 og 2 Eksamen STK11 28: oppgave 1) og 2 Eksamen 212, oppgave 1 Ved en bestemt butikk i en større dagligvarekjede viser langvarige data
Regneøvelse 22/5, 217 Arne Bang Huseby Eksamen STK11 212: oppgave 1 og 2 Eksamen STK11 28: oppgave 1) og 2 Eksamen 212, oppgave 1 Ved en bestemt butikk i en større dagligvarekjede viser langvarige data
ÅMA110 Sannsynlighetsregning med statistikk, våren 2008
 ÅMA0 Sannsynlighetsregning med statistikk, våren 008 Kp. Sannsynlighetsregning (sannsynlighetsteori).5 Betinget sannsynlighet Betinget sannsynlighet (kp..5) - innledning Eks.: Et terningkast; {,, 3, 4,
ÅMA0 Sannsynlighetsregning med statistikk, våren 008 Kp. Sannsynlighetsregning (sannsynlighetsteori).5 Betinget sannsynlighet Betinget sannsynlighet (kp..5) - innledning Eks.: Et terningkast; {,, 3, 4,
HØGSKOLEN I STAVANGER
 HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 30. AUGUST 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
HØGSKOLEN I STAVANGER Avdeling for TEKNISK NATURVITEN- EKSAMEN I: TE199 SANNSYNLIGHETSREGNING MED STATISTIKK SKAPELIGE FAG VARIGHET: 4 TIMER DATO: 30. AUGUST 2003 TILLATTE HJELPEMIDLER: KALKULATOR OPPGAVESETTET
Dagens tekst. Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon
 Dagens tekst Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
Dagens tekst Kap 7: Funksjonar av stokastiske variable Transformasjon av variable Moment Momentgenererande funksjon Notat: Ordningsvariable og ekstremvariable Ordnings variable Maksimum Minumum Transformasjon
Emnenavn: Eksamenstid: 4 timer. Faglærer: Hans Kristian Bekkevard
 EKSAMEN Emnekode: SFB107111 Emnenavn: Metode 1, statistikk deleksamen Dato: 16. mai 2017 Hjelpemidler: Godkjent kalkulator og vedlagt formelsamling m/tabeller Eksamenstid: 4 timer Faglærer: Hans Kristian
EKSAMEN Emnekode: SFB107111 Emnenavn: Metode 1, statistikk deleksamen Dato: 16. mai 2017 Hjelpemidler: Godkjent kalkulator og vedlagt formelsamling m/tabeller Eksamenstid: 4 timer Faglærer: Hans Kristian
ØVINGER 2017 Løsninger til oppgaver. Lineærkombinasjonen Z = 5X + 8Y har forventningsverdi
 ØVINGER 27 Løsninger til oppgaver Øving 6 4. (7). Fra oppgave 4.5 (øving 4) har vi forventningsverdien variansen til X, E[X] =.92, V ar[x] =.3. Lineærkombinasjonen Z = 5X + 8Y har forventningsverdi E[Z]
ØVINGER 27 Løsninger til oppgaver Øving 6 4. (7). Fra oppgave 4.5 (øving 4) har vi forventningsverdien variansen til X, E[X] =.92, V ar[x] =.3. Lineærkombinasjonen Z = 5X + 8Y har forventningsverdi E[Z]
TMA4245 Statistikk. Innlevering 3. Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag
 TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
TMA4245 Statistikk Vår 2017 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Innlevering 3 Dette er den første av to innleveringer i blokk 2 Denne øvingen skal oppsummere pensum
ÅMA110 Sannsynlighetsregning med statistikk, våren
 ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
ÅMA110 Sannsynlighetsregning med statistikk, våren 2006 Oppsummering Bjørn H. Auestad Institutt for matematikk og naturvitenskap Universitetet i Stavanger 24. april Bjørn H. Auestad Oppsummering våren
Oppgave 1. og t α/2,n 1 = 2.262, så er et 95% konfidensintervall for µ D (se kap 9.9 i læreboka): = ( 0.12, 3.32).
 Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 16. november 2009 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir
Løsningsforslag til eksamen i MOT310 STATISTISKE METODER 1 VARIGHET: 4 TIMER DATO: 16. november 2009 TILLATTE HJELPEMIDLER: Kalkulator: HP30S, Casio FX82 eller TI-30 Tabeller og formler i statistikk (Tapir
Diskrete sannsynlighetsfordelinger.
 Diskrete sannsynlighetsfordelinger. Dekkes av kapittel 5 i læreboka. Husk: f(x) er punktsannsynligheten til en diskret X dersom: 1. f(x) 0 2. x f(x) =1 3. f(x) =P (X = x) Vi skal nå sepå situasjoner der
Diskrete sannsynlighetsfordelinger. Dekkes av kapittel 5 i læreboka. Husk: f(x) er punktsannsynligheten til en diskret X dersom: 1. f(x) 0 2. x f(x) =1 3. f(x) =P (X = x) Vi skal nå sepå situasjoner der
Forventning og varians.
 Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
Forventning og varians. Dekkes av kapittel 4 i læreboka. Forventning (4.) Forventningsverdi gjennomsnitt i det lange løp. Defininsjon: Forventningsverdien til en stokastisk variabel X er: E(X) f(),x diskret
EKSAMEN I FAG 75510/75515 STATISTIKK 1 Tirsdag 20. mai 1997 Tid: 09:00 14:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Håvard Rue 73 59 35 20 Håkon Tjelmeland 73 59 35 20 Bjørn Kåre Hegstad 73 59 35 20
Oppgave 1 a) La X være massen til et tilfeldig valgt egg, målt i gram. Sannsynligheten for at et tilfeldig valgt egg veier mer enn 60 g er
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 5 Løsningsskisse Oppgave 1 a La X være massen til et tilfeldig valgt egg, målt i gram. Sannsynligheten for at
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 5 Løsningsskisse Oppgave 1 a La X være massen til et tilfeldig valgt egg, målt i gram. Sannsynligheten for at
Poissonprosesser og levetidsfordelinger
 Poissonprosesser og levetidsfordelinger Poissonfordeling som grensetilfelle for binomisk fordeling La X være binomisk fordelt med fordeling P (X = x) = ( ) n p x (1 p) n x, for x = 0, 1,... n. (1) x Forventningsverdien
Poissonprosesser og levetidsfordelinger Poissonfordeling som grensetilfelle for binomisk fordeling La X være binomisk fordelt med fordeling P (X = x) = ( ) n p x (1 p) n x, for x = 0, 1,... n. (1) x Forventningsverdien
ÅMA110 Sannsynlighetsregning med statistikk, våren Kp. 3 Diskrete tilfeldige variable. Diskrete tilfeldige variable, varians (kp. 3.
 ÅMA Sannsynlighetsregning med statistikk, våren 8 Kp. Diskrete tilfeldige variable Kp. Diskrete tilfeldige variable Har sett på (tidligere: begrep/definisjoner; tilfeldig (stokastisk variabel sannsynlighetsfordeling
ÅMA Sannsynlighetsregning med statistikk, våren 8 Kp. Diskrete tilfeldige variable Kp. Diskrete tilfeldige variable Har sett på (tidligere: begrep/definisjoner; tilfeldig (stokastisk variabel sannsynlighetsfordeling
TMA4240 Statistikk Høst 2015
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 55 2. Ved bruk av formelheftet finner
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 55 2. Ved bruk av formelheftet finner
TMA4245 Statistikk Eksamen august 2014
 TMA4245 Statistikk Eksamen august 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Oppgave 1 En bedrift produserer en type medisin i pulverform Medisinen selges på flasker
TMA4245 Statistikk Eksamen august 2014 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Oppgave 1 En bedrift produserer en type medisin i pulverform Medisinen selges på flasker
TMA4240 Statistikk Høst 2007
 TMA4240 Statistikk Høst 2007 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b4 Løsningsskisse Oppgave 1 Eksamen juni 1999, oppgave 3 av 3 a) µ populasjonsgjennomsnitt,
TMA4240 Statistikk Høst 2007 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer b4 Løsningsskisse Oppgave 1 Eksamen juni 1999, oppgave 3 av 3 a) µ populasjonsgjennomsnitt,
Medisinsk statistikk Del I høsten 2008:
 Medisinsk statistikk Del I høsten 2008: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Noen tips Boka Summary etter hvert kapittel forteller hvor dere har vært og hva som er sentralt Øvingene Overdriv
Medisinsk statistikk Del I høsten 2008: Kontinuerlige sannsynlighetsfordelinger Pål Romundstad Noen tips Boka Summary etter hvert kapittel forteller hvor dere har vært og hva som er sentralt Øvingene Overdriv
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen. Jo Thori Lind
 Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
Forelesning 5: Kontinuerlige fordelinger, normalfordelingen Jo Thori Lind j.t.lind@econ.uio.no Oversikt 1. Kontinuerlige fordelinger 2. Uniform fordeling 3. Normal-fordelingen 1. Kontinuerlige fordelinger
