Viskositetsløsninger
|
|
|
- Elisabeth Hanssen
- 7 år siden
- Visninger:
Transkript
1 Viskositetsløsninger Problem: F x, u, Du, D 2 u = 0, x Ω R n. 1 Her blir F = F Ω, R, R n, Sn R, der Sn er mengden av symmetriske n n reelle matriser. Vi skriver F x, r, p, X. F kalles degenerert elliptisk dersom F x, r, p, X F x, r, p, Y for X Y. 2 Hvis F er degenerert elliptisk kalles F proper hvis den er ikke avtagende i r, F x, r, p, X F x, s, p, X for r s. 3 Det fins mange eksempler, både lineære og ikkelinære, på slike ligninger. Dersom F er ikkelinær kan vi ikke vente oss at løsningene er deriverbare Siden karakteristikker vil møtes. For å definere et løsningsbegrep trenger vi noen begreper. u { } x = lim sup uy x y r 4 r 0 u x = lim inf r 0 { uy x y r } 5 Dersom u = u kalles u øvre semikontinuerlig, og hvis u = u kalles u nedre semikontinuerlig. Hvis u er kontinuerlig, så er u = u = u. Definisjon Subløsning, u kalles en subløsning av 1 dersom u = u og for alle testfunksjoner ϕ C 2 Ω, og ˆx et lokalt maksimum for u ϕ, så har vi at F ˆx, uˆx, Dϕˆx, D 2 ϕˆx 0. 6 Supløsning, v kalles en supløsning av 1 dersom u = u, og for alle ϕ C 2 Ω, og ˆx et lokalt minimum for u ϕ, så har vi at F ˆx, uˆx, Dϕˆx, D 2 ϕˆx 0. 7 Viskositetsløsning, u kalles en viskositesløsning av 1 dersom u er både en supløsning og en subløsning. Lemma 1. Anta at O R n og ω, Ψ er funksjoner fra O til R, Ψ 0, og ω og Ψ er øvre semikontinuerlige, anta videre at og sup O ωz Ψz <. Sett Dersom z er slik at N = { z O Ψz = 0 }, M = sup ωz Ψz. O M ωz Ψz 0, så har vi at Ψz 0. Videre blir alle opphopningspunkter for {z } når 0 med i N, og hvis ẑ er et slikt opphopningspunkt, så blir ωz ωẑ for z N. 1
2 Bevis. Siden Ψ 0 blir M avtagende i for 0 < 1. Videre får vi at sup N ω M M 1 <, som medfører at lim 0 M = M 0 fins. Ved definisjonen av M µ er q.e.d. og vi definerer g ved ωz Ψz µ M µ, 8 ωz Ψz = M g. Observer at g 0 når 0. Vi trekker den siste likheten fra 8 og får at 1 1 Ψz M µ M + g. µ Setter vi µ = 2 gir dette at Ψz 2M 2 M + g 0, når 0. Anta nå at z ẑ, da har vi at 0 = lim sup 0 Ψz Ψẑ ved semikontinuitet. Dette medfører at ẑ N. Men siden ω er øvre semikontinuerlig, ωẑ lim ωz Ψz = M 0 sup ωz. 0 N Merk at dersom vi har at en subløsning alltid er mindre eller lik en supløsning, så vil dette medføre entydighet av viskositetsløsninger. Vi sier at et problem av typen 1 har et sammenligninsprinsipp dersom u er en subløsning og v en supløsning, så har vi at u v. Vi skal nå vise at noen problemer har et sammenligningsprinsipp. Dirichlet problemet Entydighet for første ordens ligninger Hx, u, Du = 0, for x Ω, u = g på Ω, 9 der Ω er en åpen begrenset mengde. Nå har vi at ved definisjonen av en sup- og en subløsning ux gx vx på Ω. Uten antagelser på H eller g kan dette problemet både ha mange løsninger eller ingen. Vi velger en tesfunksjon ϕx, y slik at Φx, y := ux vy ϕx, y har et lokalt maksimum i Ω. Dette kan vi oppnå dersom u og v er begrenset ovenifra. Vi setter ϕx, y = 1 x y 2 2 Nå kan vi bruke Lemma 1 med O = Ω Ω, ω = u v og Ψ = x y 2 /2. La ˆx, ŷ være et maksimumspunkt for ω ϕ. Da har vi at ˆx ŷ 2 0 2
3 når 0. Det vil si at alle grenser for {ˆx, ŷ } vil være på formen ˆx, ˆx. Dersom ˆx Ω så har vi at uˆx gˆx vˆx som viser at lim sup Φ ˆx, ŷ 0. 0 Hvis ˆx Ω så har vi at siden u er subløsning og v er supløsning at H ˆx, uˆx, ˆx ŷ H ŷ, vŷ, ˆx ŷ For å komme videre må vi anta noe om H. Hvis vi f.eks. antar at og at H er strengt proper, m.a.o., Hx, r, p Hy, r, p L x y 1 + p, 11 Hx, u, p Hx, v, p γu v, 12 for en konstant γ > 0, så har vi et sammenligningsprinsipp. Vi får nå at H ˆx, uˆx, ˆx ŷ H ŷ, vŷ, ˆx ŷ = H ˆx, uˆx, ˆx ŷ H ˆx, vŷ, ˆx ŷ + H ˆx, vŷ, ˆx ŷ H Ved å bruke antagelsene 11 og 12, får vi at γ uˆx vŷ H ˆx, uˆx, ˆx ŷ L ˆx ŷ ŷ, vŷ, ˆx ŷ H 1 + ˆx ŷ.. ˆx, vŷ, ˆx ŷ Nå kan vi sende 0 og får at Ved det siste utsagned i Lemma 1 uˆx vˆx 0. og vi får et sammenligningsprinsipp. ux vx uˆx vˆx 0, Et problem på et ubegrenset område Vi prøver å finne et sammenligningsprinsipp for problemet Hx, u, Du = 0, x in R n. 13 Som før antar vi at u er en begrenset subløsning og v en begrenset supsløsning av 13. For å sikre at vi har maksima av den typen vi fant i eksempelet over, må vi modifisere testfunksjonen. Sett Φx, y = ux vy 1 2 x y 2 δ x 2 + y 2. 2 Siden Φ er begrenset ovenifra, så må den ha et maksimum i ˆx, ŷ. Vi har at ˆx og ŷ avhenger av og δ men vi noterer ikke dette. Som før får vi at H ˆx, uˆx, ˆx ŷ δˆx H 3 ŷ, vŷ, ˆx ŷ δŷ 0.
4 Vi skriver dette som H ˆx, uˆx, ˆx ŷ δˆx H ˆx, vŷ, ˆx ŷ δˆx H ˆx, vŷ, ˆx ŷ L ˆx ŷ 1 + δˆx ˆx ŷ H dersom vi har de samme antagelsene på H som før, og i tillegg antar at Hx, u, p Hx, u, q L p q. ŷ, vŷ, ˆx ŷ + Lδ ˆx ŷ, δŷ Siden u og v er begrenset vil sup ux vy 12 x y 2 <. x,y Ved bruk av Lemma 1 får vi nå at der lim 0 ˆx ŷ 2 C δ,, lim sup C δ, = 0. δ 0 Vi har også at for 0 < 1 er u0 v0 Φˆx, ŷ, det vil si at 1 ˆx 2 + ŷ 2 v0 u0 + uˆx vˆx ˆx ŷ C 1. Derfor blir δ ˆx + ŷ 2 C 1 δ. Vi får også at ˆx ŷ ˆx ŷ 2 = 1/2, ˆx ŷ C δ,. Hvis H er strengt proper, og tilfredstiller Lipschitz betingelsene så får vi γu ˆx v ŷ H ˆx, uˆx, ˆx ŷ δˆx H ˆx, vŷ, ˆx ŷ δˆx L 1 + δ C δ, + C δ,, Hvis vi sender δ og til 0, og bruker at H er proper og kontinuerlig så følger det at lim 0 Nå kan vi fortsette med å observere at lim sup uˆx vŷ 0. δ 0 ux vy x y 2 2 = lim Φx, y lim Φˆx, ŷ lim lim sup δ 0 δ 0 0 δ 0 uˆx vŷ 0. Hvis vi setter x = y til venstre får vi sammenligningsprinsippet. Et hyperbolsk problem Vi kan nå bruke disse teknikkene på problemet u t + Ht, x, u, Du = 0, x, t R n 0, ux, 0 = u 0 x. 14 4
5 Her er u 0 x en begrenset og absolutt kontinuerlig funksjon. Her søker vi en løsning som er en begrenset funksjon av x og t. En subløsning u er defninert ved at dersom u ϕ har et maksimum i ˆx, ˆt så er ϕ t ˆx, ˆt + H ˆt, ˆx, uˆx, ˆt, Dϕˆx, ˆt 0. En supløsning er definert tilsvarende. Det blir nå en smal sak å adaptere argumentene fra de to tidligere eksemplene til å gjelde for dette eksemplet. Vi setter Φx, t, y, s = ux, t vy, s 1 2 Ved argumentene over følger det at ux, t vx, t. x y 2 + s t 2 δ x 2 + y 2 + t 2 + s 2. 2 Ny definisjon av viskositetsløsning Anta at ϕ er kontinuerlig deriverbar og at u ϕ har et lokalt maksimum i ˆx. For x nær ˆx så har vi at og hvis ϕ er C 2 ux uˆx + ϕx ϕˆx = uˆx + p, x ˆx + o x ˆx. 15 ux uˆx + p, x ˆx Xx ˆx, x ˆx + o x ˆx 2, 16 der p = Dϕˆx og X = D 2 ϕˆx. Omvendt har vi at dersom 15 holder for en p R n, så fins det en ϕ C 1 med Dϕˆx = p slik at u ϕ har et lokalt strengt maksimum i ˆx. Dersom 16 holder så kan vi finne en ϕ C 2 slik at p = Dϕˆx og X = D 2 ϕˆx og u ϕ har et lokalt maksimum i ˆx. Vi setter J 1,+ uˆx = { p R n } slik at 15 gjelder 17 og J 2,+ uˆx = { p R n, X Sn slik at 16 gjelder. } 18 Vi definerer J 1, u og J 2, u ˆx ved at de motsatte ulikhetene av 15 og 16. r, p, X J 2,+ ux tillukningen dersom Nå sier vi at x n x, ux n, p n, X n J 2,+ ux n, og ux n, p n, X n r, p, X. Tillukningen J 2, ux defineres på samme måte. Nå kan vi reformulere definisjonen av en sub/supløsning. Vi sier at en øvre semikontinuerlig funksjon u er en subløsning av F x, u, Du, D 2 u = 0 dersom det for alle r, p, X i J 2,+ ux er slik at F x, r, p, X 0. Tilsvarende sier vi at en nedre semikontinuerlig v er en supløsning dersom det for alle r, p, X i J 2, vx er slik at F x, r, p, X 0. En kontinuerlig funksjon u er en viskositetsløsning av F = 0 dersom den er både en sup- og en subløsning. For å dra nytte av denne definisjonen trenger vi et teknisk resultat: Lemma 2. La O R n være et lokalkompakt område og U : O R øvre semikontinuerlig, z O og Uz, p, X J 2,+ Uz. Anta videre at {u n } er en samling øvre semikontinuerlige funksjoner på O slik at 1. x n, u n x n z, Uz, 5
6 2. z n O, z n x O og lim sup n u n z n Ux. Da har vi at det fins {ˆx n } O og uˆx n, p n, X n J 2,+ u n ˆx n slik at ˆx n, u n ˆx n, p n, X n z, Uz, p, X. Bevis. Sett z = 0, vi finner r > 0 slik at N r = B r O er kompakt, og en ϕ C 2 slik at Ux ϕx U0 ϕ0, for x N r. Videre blir 0 et strengt maksimum for U ϕ. Ved 1 så har vi at x n, u n x n 0, U0. Sett ˆx n til et maksimum for u n ϕ i N r, slik at u n x ϕx u n ˆx n ϕˆx n. Siden N r er kompakt vil en delfølge av {ˆx n } gå mot ŷ når n. Vi har at u n 0 ϕ0 lim inf n u nˆx n ϕˆx n. Ved 2 vil nå lim inf n u n ˆx n Uŷ. Det vil si at ŷ = 0. Derfor har vi at ˆx n, u n ˆx n 0, U0 for alle delfølger, dvs. at denne konvergensen holder for følgen {ˆx n } selv. Altså har vi at U0, Dϕ0, D 2 ϕ0 u n ˆx n, Dϕ ˆx n, D 2 ϕ ˆx n J 2,+ u n ˆx n. q.e.d. Dette kan vi bruke med en gang Lemma 3. Anta at F er en samling subløsninger av F = 0 på Ω, sett Ux = sup F {ux}. Hvis U er endelig, er U en løsning av F 0. Bevis. La z Ω og U, p, X J 2,+ U z. Vi finner x n Ω og u n F slik at x n, u n x n z, U z. Nå holder antagelsene i lemma 2, og vi velger ˆx n, p n og X n slik at ˆx n, u n ˆx n, p n, X n z, U z, p, X, og slik at u n ˆx n, p n, X n J 2,+ u n ˆx n og F ˆx n, u n ˆx n, p n, X n 0. Dette medfører ved kontinuitet av F at F z, U z, p, X 0. q.e.d. Hvis vi har en samling funksjoner {u n } definert på O så kan vi finne den minste funksjonen U slik at lim sup n u n x n Ux der x n x. U blir definert slik Ux = lim sup { u n y = lim sup un y n m, x y 1/m }. 19 n,y x m Vi skriver at og definerer lim slik lim n U = lim n u n, u n = lim u n. n Hvis U = lim u n, så kan vi alltid finne en delfølge av {u n } slik at xnj, u nj xnj x, Ux. Vi har nå følgende nyttige og viktige resultat: Teorem 1. Anta at u n løser F n 0, og sett U = lim u n. Hvis F lim inf n F n, og U er endelig, så løser U F 0. Spesiellt dersom u n U og F n F uniformt, så løser U F 0. 6
7 Bevis. La Uz, p, X J 2,+ Uz, da kan vi bruke lemma 2 til å finne en delfølge slik at Ved antagelsen på F så finner vi at x n, u n x n, p n, X n x, U, p, X. F x, Ux, p, X lim inf n F nx n, u n x n, p n, X n 0. q.e.d. Som et eksempel kan la u n være en begrenset klassisk løsning av u n + HDu n u n n = Da er u n både en sub- og en supløsning. At u n er en subløsning medfører at u = lim u n eksisterer, siden u n er endelig, så vil også u være endelig. Her har vi at F = F r, p = r + Hp og F n r, p, X = r + Hp TrX/n, slik at F = lim n F n uniformt. Da blir u en løsning av F 0. Sett v = lim u n, ved samme argument blir v en løsning av F 0. Ved sammenligningsprinsippet har vi at u v, ved konstruksjon har vi at u v, altså er u = v og er en viskositetsløsning av u + HDu = 0. Eksistens av løsninger. Hittil har vi sett på entydighet for første ordens ligninger, nå skal vi vise et viktig teorem metode for å få eksistens av løsninger. Anta at u løser F 0 og u ikke løser F 0 i et område Ω. Vi kan f.eks. anta at F 0, u 0, Dϕ0, D 2 ϕ0 < 0 og u x ϕx > u 0 ϕ0 + hr, der h 0 og r = x. Videre er hr > 0 og h > 0 for r > 0. Denne ulikheten skal gjelde for r x 0 r 0. Vi kan anta at u 0 = ϕ0, ved kontinuitet av F får vi at F x, ϕx + δ, Dϕx, D 2 ϕx < 0 for x r 0. Mao. er ϕx + δ en klassisk løsning av F < 0 for små x. Men vi har at ux u x ϕx + hr for x < r 0. Sett nå δ < hr 0 /2/2. Da blir ux > u δ x = ϕx + δ for r 0 /2 < x r 0. Sett { max ux, u δ x x < r 0 Ux = ux ellers. Da blir U en løsning av F 0, og supu u δ > 0. Ved definisjonen av u har vi en følge {x n } slik at x n, ux n 0, u 0. Da får vi at lim Ux n ux n = u δ 0 u 0 = δ > 0. n Mao. i enhver omegn om 0 fins det punkter der U > u, og U er en subløsning. Altså er ikke u den maksimale subløsningen. Vi har altså vist at dersom u løser F 0 i et åpent område Ω, og u ikke løser F 0 i et punkt ˆx, altså det fins u ˆx, p, X J 2,+ u ˆx slik at F ˆx, u ˆx, p, X < 0. Da fins det for enhver liten δ, en subløsning U δ slik at { U δ x ux sup Ω U δ u > 0, U δ x = ux for x ˆx δ. Denne konstruksjonen kan vi bruke til å vise følgende viktige resultat: 7
8 Teorem 2 Ishiis teorem. Anta at g er kontinuerlig og at problemet F x, u, Du, D 2 u = 0, x Ω, u = g på Ω, har et sammenligningsprinsipp. Anta videre at det fins en subløsning u og en supløsning ū slik at u = ū = g på Ω, da vil en viskositetsløsning av F = 0 i Ω. W x = sup { wx u w ū og w løser F 0 }, Bevis. Observer at u W W W ū, og spesiellt at W = W = W = g på Ω. Vi har at W er en subløsning ved lemma 3. Derfor vil sammenligningsprinsippet medføre at W ū. Derfor får vi at W = W ved definisjonen av W og W. Dersom W ikke er en supløsning i ˆx, så kan vi finne en U δ som over. Da blir u W < U δ ū, men siden W er den største subløsningen får vi ut U δ W. Altså blir W en supløsning, og ved sammenligning blir W W = W, men da blir W = W = W og dette viser at W blir kontinuerlig og en viskositetsløsning. q.e.d. Et eksempel på bruk av dette får vi ved å se på u + Du fx = 0 x Ω, u = 0 på Ω, der f 0 og kontinuerlig. Her har vi et sammenligningsprinsipp, og u = 0 blir en subløsning som tilfredstiller randkravet. For å vise eksistens må vi finne en supløsning som er 0 på randen. Sett vx = distx, Ω. Da har vi at Dv = 1 i Ω. Dersom M sup Ω f, så kan vi sette u = Mv. Da er Du = M, og u tilfredstiller randkravet. Videre får vi at u + Du f u + M f Mdistx, Ω 0, dvs. u blir en supløsning som tilfredstiller randkravene. Altså fins det en entydig viskositetsløsning. Nå prøver vi å vise eksistens av en viskositetsløsning av F x, u, Du, D 2 u = fx, x Ω, u = 0 på Ω. For å gjøre dette trenger vi et ekstra krav på F. For en matrise X i Sn setter vi X = µ EigX der egenverdiene blir regnet med multiplisitet. En funksjon F kalles uniformt elliptisk dersom der 0 < λ Λ. Dette er ekvivalent med at µ, F x, r, p, X + Z F x, r, p, X λtrz og F x, r, p, X F x, r, p, Z Λ X Z, F x, r, p, X ΛTrZ F x, r, p, X + Z F x, r, p, X λtrz. Vi kan uten tap av generalitet anta at F x, 0, 0, 0 = 0, noe som medfører at u = 0 blir en subløsning dersom f 0. Vi skal nå konstruere supløsninger av F = 0 x Ω, u = 0 x Ω. For å gjøre dette antar vi at alle punkter x b på Ω er slik at det fins en z b in R n \ Ω, slik at x b er slik at min Ω x z b er oppnådd for x = x b. Vi søker en supløsning på formen Ux = Gr, der r = x z b, slik at Ux b = 0. For alle slike G har vi at xj xigr = xj G r x z b i = G r G r r r x zb i x z b j 8 r 2 + G r δ i,j. r 21
9 Vi får at D 2 Gx har n 1 egenvektorer som er x z b med egenverdi G r/r, og x z b er en egenvektor med egenverdi G r. Vi setter P til å betegne projeksjonen på x z b. Med denne notasjonen blir D 2 G x z b = G rp + G r I P. r Nå kan vi definere Gr = 1 r σ 0 1 r σ, der r 0 = x b z b. Da har vi at G 0 i Ω og Gx b = 0. Videre blir G r > 0 og G r < 0 for r > r 0. Nå får vi at F x, G, DG, D 2 G F x, 0, DG, D 2 G F x, 0, 0, D 2 G F x, 0, 0, D 2 G F x, 0, DG, D 2 G F x, 0, 0, D 2 G γ DG F x, 0, 0, G P Λ r G rtri P γg r F x, 0, 0, 0 λg Λn 1 r G r γg r r σσ + 1 σλn 1 = λ r σ+2 r σ+2 γ σ r σ+1 = σ λσ + 1 Λσn 1 γr rσ+2 κ > 0, for tilstrekkelig stor σ. Altså har vi at for stor nok σ at F x, G, DG, D 2 G κ > 0. Siden f er begrenset så kan vi finne M slik at M sup Ω f +. κ Vi indikerer x b avhengigheten til G ved å skrive G xb = G. Ved regningen over får vi at U xb = MG xb løser F x, U xb, DU xb, D 2 U xb Mκ > f på Ω. Vi har at U xb blir en supløsning som ikke tilfredstiller randkravene untatt i x b!. Nå kan vi bruke at Ux = inf {U x b x} x b Ω en supløsning og U Ω = 0. Siden 0 U så får vi eksistens av en viskositetsløsning. Vi ser først på ligningen Sammenligning for 2. gradsligninger. u + F Du, D 2 u = fx i Ω, u = ψ på Ω. Vi antar at F p, X er degenerert elliptisk og Ω begrenset i R n. La u og v være en sub- og en superløsning som før. Sett x y 2 Φx, y = ux vy. 2 Vi regner som før og får at ˆx ŷ u ˆx + F, I f ˆx ˆx ŷ v ŷ + F, I f ŷ. 9
10 Vi trekker fra og får at ˆx ŷ u ˆx v ŷ + F, I ˆx ŷ F, I f ˆx f ŷ. Siden I > I så kommer vi ikke videre! Merk imidlertid at dersom u og v er to ganger deriverbare så kan vi vite mer om et maksimum for Φ, nemlig at D 2 Φˆx, ŷ 0, altså at D 2 uˆx 0 0 D 2 1 I I. vŷ I I Dette ville ha hjulpet oss. Vi trenger derfor noe lignende informasjon dersom u og v ikke er deriverbare. Denne informasjonen får vi fra Teorem 3 Summeteoremet. Gitt O R n lokalkompakt, og funksjoner u, v fra O R slik at u og v er øvre semikontinuerlige. La ϕ C 2 R n R n. Anta at ux vy ϕx, y har et maksimum i ˆx, ŷ. For alle κ > 0 slik at κd 2 ϕ ˆx, ŷ < I så fins det X og Y i Sn slik at slik at uˆx, D x ϕˆx, ŷ, X J 2,+ O uˆx og vŷ, D yϕˆx, ŷ, Y I X 0 κ I κd 2 ϕˆx, ŷ 1 D 2 ϕˆx, ŷ. 0 Y 2, J O vŷ Nå kan vi vise et sammenligningsprinsipp. La Φ være som før, og sett A = 1 2 D2 x y 2 ˆx,ŷ = 1 I I. I I Vi har at A 2I/, og for 2κ/ 1 har vi at I κa 1 A = 1 2κ I I I I. Ved summeteoremet kan vi finne X og Y slik at uˆx, ˆx ŷ, X J 2,+ uˆx, og vŷ, ˆx ŷ, Y J 2, vŷ, slik at Vi multipliserer med ξ, ξ og får at altså er X Y. Dette medfører at 1 X 0 κ I 1 0 Y 2κ ξxξ ξy ξ 0. F p, X F p, Y, I I I I siden F er degenerert elliptisk. Som før fører dette til at vi får et sammenligningsprinsipp. Vi kan lett utvide et slik ressonement til å gjelde for ligninger av typen F x, u, Du, D 2 u = 0. dersom F tilfredstiller F x, r, p, X F x, s, p, X γr s 10
11 for r s og en γ > 0, og F x, r, p, X F y, r, p, X L x y 1 + p. Parabolske ligninger. Ofte treffer vi på problemer av typen u t + F x, t, u, Du, D 2 u = 0, for x Ω 0, T, ux, t = 0, for x Ω [0, T, ux, 0 = gx, for x Ω. 22 For slike problemer kan vi definere semijetter P 2,± istedenfor J 2,± som følger: For en øvre semikontinuerlig funksjon ux, t sier vi at ux, t, a, p, X P 2,+ ux, t dersom ux, t uy, s + at s + p, x y + 1 x 2 Xx y, x y + o y 2 + t s når y, s x, t. Vi har at P 2, = P 2,+ u. En subløsning er nå en øvre semikontinuerlig funksjon u slik at for alle a, p, X slik at ux, t, a, p, X P 2,+ ux, t har vi at a + F x, t, ux, t, p, X 0. Vi får en tilsvarende definisjon av en subløsning av 22. For å vise et sammenligningsprinsipp trenger vi Teorem 4 Parabolsk summeteorem. La O R n være lokaltkompakt, og u og v være øvre semikontinuerlige funksjoner O 0, T. La ϕx, y, t være i C 2,2,1 O O 0, T, og ˆx, ŷ, ˆt være et globalt maksimum for wx, y, t = ux, t vy, t ϕx, y, t i O O 0, T. Anta også at det fins r > 0 slik at det for alle M > 0 fins en C slik at b C når ux, t, b, q, X P 2,+ ux, t og x ˆx + t ˆt r og ux, t + q + X M. Anta at også v tilfredstiller dette. Da fins det for alle κ > 0 slik at κd 2 ϕˆx, ŷ, ˆt < I, X og Y i Sn, b 1 og b 2 i R slik at uˆx, ˆt, b 1, D x ϕˆx, ŷ, ˆt, X P 2,+ O uˆx, ˆt og vˆx, ˆt, b 1, D y ϕˆx, ŷ, ˆt, Y 2,+ P O vŷ, ˆt, og og 1 X 0 κ I I κd 2 ϕˆx, ŷ, ˆt 1 D 2 ϕˆx, ŷ, ˆt 0 Y b 1 b 2 = ϕ t ˆx, ŷ, ˆt. Med dette kan vi fortsette. Vi kan anta at u og v er begrenset ovenifra. La c og være positive og sett ũ = u ct T t. Da vil ũ tilfredstille ũ t + F x, t, ũ, Dũ, D 2 ũ c T t 2. 11
12 Dersom vi viser at ũ v så følger det at u v. Altså kan vi anta at u tilfredstiller { u t + F x, t, u, Du, D 2 u c < 0 og lim t T ux, t = uniformt i x. Med disse antagelsene får vi at det fins et maksimumspunkt ˆx, ŷ, ˆt for ux, t vy, t x y 2, 2 i Ω Ω [0, T, og hvor ˆx ŷ 2 / 0. Sett z = x, x, t til å være en grense for ˆx, ˆx, ˆt når 0. Hvis z er på randen eller t = 0 gir randkravene eller initialbetingelsen at ˆx ŷ 2 ux, t vx, t lim inf uˆx, ˆt vŷ, ˆt 0. 0 Hvis t > 0 og x Ω, så kan vi anta at ˆx og ŷ er i Ω og bruke summeteoremet. Da finner vi a, b, X og Y slik at uˆx, ˆt, a, ˆx ŷ, X Videre har vi at a b = 0 og P 2,+ uˆx, ˆt og 3 X 0 I 3 0 Y vŷ, ˆt, b, ˆx ŷ, Y I I I I P 2, vŷ, ˆt.. 23 Den første ulikheten får vi ved å velge κ = /3. Siden vŷ, ˆt uˆx, ˆt medfører at u v, kan vi anta at vŷ, ˆt < uˆx, ˆt. Da har vi a + F ˆx, ˆt, uˆx, ˆt, ˆx ŷ, X c, og b + F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, Y 0. Dette impliserer at c F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, Y F ˆx, ˆt, uˆx, ˆt ˆx ŷ, X F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, Y F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, X + F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, X F ŷ, ˆt, uˆx, ˆt, ˆx ŷ, X + F ŷ, ˆt, uˆx, ˆt, ˆx ŷ, X F ˆx, ˆt, uˆx, ˆt, ˆx ŷ, X. Fra den første ulikheten i 23 får vi at X Y som medfører at F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, Y F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, X Videre er F proper, så F ŷ, ˆt, vŷ, ˆt, ˆx ŷ, X Nå ender vi opp med at c L F ˆx ŷ 1 + ŷ, ˆt, uˆx, ˆt, ˆx ŷ, X som fører til en selvmotsigelse. Altså blir uˆx, ˆt vŷ, ˆt. 0. γu ˆx, ˆt vŷ, ˆt. ˆx ŷ γu ˆx, ˆt vŷ, ˆt 12
13 Beregning av viskositetsløsninger I denne delen skal vi ta for oss noen metoder for å regne ut tilnærmede løsninger av Hamilton- Jacobi ligninger. Slike numeriske metoder, og den tilhørende teorien, er ofte basert på numeriske metoder for konserveringslover. Vi starter derfor med en diskusjon av sammenhengen mellom skalare konserveringslover og Hamilton-Jacobi ligninger i én romdimensjon. For å gjøre dette vil vi begynne med å presentere frontfølgingsmetoden for konserveringslover og Hamilton-Jacobi ligninger i én romdimensjon. Frontfølging. typen Dette er en numerisk metode for å finne løsninger på initialverdiproblemer av p t + Gp x = 0, px, 0 = p 0 x, 24 der G er en stykkevis lineær og Lipschitz kontinuerlig funksjon. Videre er p 0 en stykkevis konstant funksjon med et endelig antall sprangdiskontinuiteter. Med en entropiløsning på problemer av denne typen der G ikke nødvendigvis er stykkevis lineær eller p 0 ikke nødvendigvis stykkevis konstant menes en funksjon p som tilfredstiller R [0,T ] p k ϕ t + sign p k Gp Gkϕ x dxdt + R p k t=t t=0 dx 0, 25 for alle ikke-negative testfunksjoner ϕ C0R 1 2 og alle konstanter k R. Det er dette kravet, som kalles Kružkovs entropibetingelse, som skal vise seg å bli analogt til viskositetsløsningsbegrepet. Som med Hamilton-Jacobi ligninger har heller ikke konserverigslover alltid glatte løsninger, og derfor blir slike betingelser nødvendige for å definere en generalisert løsning. De punktene der G er diskontiuerlig kaller vi knekkpunktene til G. For å finne løsningen på 24 starter vi med å løse Riemannproblemet, dvs. initialverdiproblemet der { p l x 0, p 0 x = 26 p r x > 0, der p l og p r er to konstanter. Nå setter vi G til å være den konvekse envelopen til G mellom p l og p r, G p; p l, p r = sup {gp } g er konveks, og gp Gp, mellom pl og p r. 27 På samme måte kan vi definere Ḡ til å være den øvre konkave envelopen ved at Ḡ p; p l, p r = G p; p l, p r. Så setter vi Gp; p l, p r = { Gp; p l, p r Ḡp; p l, p r p l p r ellers. Siden G er stykkevis lineær og kontinuerlig, så vil G også være det. Sett p1 = p l og anta at G har N 1 knekkpunkter mellom p l og p r, vi kaller disse p 2,..., p N 1, og setter p N = p r, slik at p i < p i+1 hvis p l < p r og p i > p i+1 hvis p l > p l. Sett σ 0 =, σ N =, og σ i = G i G i+1 p i p i+1, for i = 1,..., N 1, der G i = Gp i ; p l, p r = Gp i. Nå setter vi Ω i til Ω i = {x, t } 0 t T, tσi 1 < x tσ i. Da har vi 13
14 Lemma 4. Definer px, t = p i for x Ω i. Da er p en entropiløsning av 24. Bevis. Vi viser dette for p l p r. Definisjonen av den nedre envelopen medfører at for alle konstanter k [p i, p i+1 ], Gk G i + k p i σ i Vi har også at G i+1 + k p i+1 σ i G i + G i σ i k p i + p i+1. 2 sign p k Gp Gk = G p k G p k =: qp, k, der p k = min{p, k} og p k = max{p, k}. Dobbeltintegralet i 25 kan nå skrives som N i=1 Ω i p i k ϕ t + q p i, k ϕ x dxdt = N 1 i=1 T 0 R px, T k ϕx, T p 0 x k ϕx, 0 dx {σ i p i+1 k p i k [q p i+1, k q p i, k] ϕ σ i t, t} dt, ved Greens formel anvendt på hver Ω i. Dersom k [p i, p i+1 ] så har vi at σ i p i+1 k p i k [G p i+1 k G p i+1 k G p i k + G p i k] = 0, ellers har vi at σ i p i+1 k p i k [G p i+1 k G p i+1 k G p i k + G p i k] = Gk σ i k p i+1 + p i + G i+1 + G i 2 2 ved regningen over. Altså blir p en entropiløsning. q.e.d. Nå kan vi bruke dette lemmaet til å konstruere den entydige entropiløsningen på 24. Hver diskontinuitet i p 0 er et Riemannproblem, som vi kan løse ved metoden over. Merk at siden G er Lipschitz kontinuerlig, så vil alle diskontinuitetene, heretter kalt fronter, i løsningene ha endelig hastighet. Dette medfører at vi kan finne den løsningen fram til den første kollisjonen mellom to fronter. Denne kollisjonen definerer et nytt Riemannproblem som vi kan løse på samme måte, og derved har vi konstruert løsningen fram til den andre kollisjonen. Det viser seg at vi kan fortsette denne prosedyren så lenge vi vil, derved er entropiløsningen px, t definert for alle t > 0. Vi kaller denne konstruksjonen for frontfølging. Spesiellt så har vi at Teorem 5. Anta at Gp er en Lipschitz kontinuerlig og stykkevis lineær funksjon med et endelig antall knekkpunkter for p i [ M, M]. Anta videre at p 0 er en stykkevis konstant funksjon, med et endelig antall sprangdiskontinuiteter, slik at p 0 x M for alle x. Da har initialverdiproblemet 24 en entydig entropiløsning px, t, som kan finnes ved frontfølging. Videre har vi at p er en stykkevis konstant funksjon av x for hver t, og p tar verdier i mengden { } { } p 0 x knekkpunktene til G. Det er også slik at frontene i p bare vil kollidere et endelig antall ganger for alle t > 0. Dersom Ĝ er en annen stykkevis lineær og Lipschitz kontinuerlig funksjon, og ˆp 0 en annen stykkevis konstant funksjon med verdier i [ M, M], og ˆp er entropiløsningen til ˆp t + Ĝˆp x = 0, ˆpx, 0 = ˆp 0, 0, 14
15 så har vi at hvis p 0 og ˆp 0 er i L 1 R B.V.R, p, T ˆp, T L1 R p 0 ˆp 0 L1 R + T p 0 B.V. ˆp 0 B.V. G Ĝ. 28 Lip[ M,M] Vi kan altså finne løsningen på initialverdiproblemer der fluksfunksjonen G og intialverdiene p 0 ligger i { } D flux = stykkevis lineær og Lipschitz kontinuerlig { } D init = stykkevis konstant L 1 R B.V.R. Ved å ta Lip. norm tillukningen av D flux og L 1 tillukningen av D init, så får vi eksistens av løsning for en større klasse problemer. La δ og x være små positive tall. Anta først at H er en C 2 funksjon og definér H δ p = Hiδ + p iδ H i+1 H i, for p [iδ, i + 1δ], δ der H i = Hiδ og i er et heltall. For η > δ får vi at H η H δ Lip[ M,M] sup p [ M,M] sup p q η p sup p q η q Altså blir { H δ} en Cauchyfølge i Lip. normen. Sett p x 0 x = 1 x i+1 x i x H η p H δ p H p H q H s ds H L [ M,M] η. p 0 x dx, Vi får at også { p 0 x } blir en Cauchy følge i L 1, siden p x 0 p L1 0 = i+1 x R i i x p 0x 1 x i i 1 x 1 x i+1 x i x i+1 x for x [i x, i + 1 x. i+1 x i x i x i x i+1 x x i i x x p 0 B.V.R. i+1 x x i+1 x i x p 0 z dz dx p 0 x p 0 z dxdz z p 0y dy p 0y dydxdz La p δ, x betegne løsningen av 24 med G = H δ og px, 0 = p 0 x. Ved å bruke stabilitetsestimatet 28 følger det at p = lim δ, x 0 pδ, x eksisterer. Videre, siden p p k og p qp, k er kontinuerlige, blir p en entropiløsning av p t + Hp x = 0, px, 0 = p 0 x
16 Vi kan komme oss unna restriksjonen med at H begrenset, ved å bruke 28 som nå gjelder for en større klasse og et approximasjonsargument. Herved får vi eksistens, og konvergens av frontfølging, for H Lipschitz kontinuerlig. Hvis vi har en Hamilton-Jacobi ligning u t + Hu x = 0, ux, 0 = u 0 x, så kan vi formellt sette p = u x, derivere m.h.p. x og få en konserveringslov p t + Hp x = 0, px, 0 = u 0x. Siden løsningsbegrepene for disse to ligningene er forskjellige viskositet/entropi så er det ikke gitt at den deriverte til en viskositetsløsning blir en entropiløsning av en konserveringslov. Men dersom H er stykkevis lineær og u 0 /p 0 er stykkevis lineære/konstante, så kan vi gjennomføre denne overgangen rigorøst. La derfor G være stykkevis lineær som over, og u 0 en stykkevis lineær og Lipschitz kontinuerlig funksjon. Vi ønsker å løse u t + Gu x = 0, ux, 0 = u 0 x, 30 ved hjelp av frontfølging. Vi starter med Riemannproblemet { p l x x 0, u 0 x = u p r x x 0, der p l og p r er to konstanter. Vi setter px, t til å betegne løsningen på det tilsvarende Riemannproblemet for konserveringsloven 24. Nå har vi at u er gitt ved ux, t = u xpx, t tgpx, t. 31 Siden p er diskontinuerlig, kan det se ut som om u blir diskontinuerlig, men siden p tilfredstiller Rankine-Hugoniot betingelsen, σ i p i p i+1 = G i G i+1 over en diskontinuitet, blir u Lipschitz kontinuerlig, og for hver t blir ux, t stykkevis lineær i x med knekkpunkter i frontene til p. Når man skal beregne u, må man bare holde rede på hvordan u forandrer seg i frontene til p. Langs en front med hastighet σ i har vi at u σ i t, t = u t σ i p i Gp i = u t σ i p i+1 G p i+1. Vi kan nå bruke frontfølgingsmetoden til å definere en funksjon ux, t til initialverdiproblemet 30 der u 0 er stykkevis lineær. Vi har at ux, t definert ved denne metoden blir stykkevis lineær i x for hver t, og kan defineres for enhver t > 0. Videre har vi Lemma 5. Den stykkevis lineære og kontinuerlige funksjonen ux, t definert ved frontfølging er en viskositetsløsning av 30, og er lineær på et endelig antall polygoner i R R + 0. Hvis Ĝ er en annen stykkevis lineær funksjon, og û 0 en annen begrenset og absolutt kontinuerlig funksjon, og û er viskositetsløsningen av û t + Ĝ û x = 0, ûx, 0 = û 0 x, så har vi at G u, T û, T L R u 0 û 0 L R + T Ĝ L [ M,M], 32 dersom u 0 og û 0 er begrenset av M. 16
17 Bevis. Vi viser at u blir en viskositetsløsning. Merk at u er bestemt av løsningen på et endelig antall Riemannproblemer i punktene x j, t j. Gitt et punkt x, t der t > 0, så kan vi finne en j slik at ux, t er bestemt av Riemannproblemet i x j, t j. Sett p = u x, og anta at u ϕ har et maksimum i ˆx, ˆt, og at u ˆx, ˆt er bestemt av Riemannproblemet i x j, t j. Da u er stykkevis lineær, kan vi definere p l = lim u x x, ˆt, og p r = lim u x x, ˆt. x ˆx x ˆx + Vi får også at Definér p l ϕ x ˆx, ˆt p r. σ = G p l G p r p l p r, dersom p l p r, og sett σ = G p l,r dersom p l = p r. Nå er p l p r og vi må bruke den øvre envelopen for å løse Riemannproblemet, derfor har vi at Velg x, t i nærheten av ˆx, ˆt slik at G ϕ x ˆx, ˆt G p l + σ ϕ x ˆx, ˆt p l. σ = x ˆx t ˆt, og slik t < ˆt og at ux, t også er bestemt av løsningen på Riemannproblemet i x j, t j. Dersom ˆt > 0 kan vi alltid gjøre dette. Nå får vi at Ved definisjonen av ux, t blir Derfor kan vi la t ˆt og får at u ˆx, ˆt ux, t ˆt t ϕ ˆx, ˆt ϕx, t. ˆt t u ˆx, ˆt = ux, t + ˆx x p l ˆt t G p l. σp l G p l ϕ t ˆx, ˆt + σϕ x ˆx, ˆt ϕ t ˆx, ˆt + G ϕ x ˆx, ˆt + σp l G p l. Dersom ˆt = 0, så kan vi velge t > 0 og σ definert som før, men nå blir ux, t = u ˆx, ˆt x ˆx p l tg p l. Denne ligningen gir samme konklusjon, nemlig at 0 ϕ t ˆx, ˆt + G ϕ x ˆx, ˆt, altså er u subløsning. Et tilsvarende argument gir at u også er en supløsning. Stabilitetsestimatet følger nå fra et generellt stabilitetsestimat for viskositetsløsninger som vi kanskje får tid til å vise. q.e.d. Som før ønsker vi nå å sjekke at dersom vi interpolerer en H med en stykkevis lineær H δ og initialdata med stykkevis lineære u x, så konvergerer de tilsvarende viskositetsløsningene u δ, x. La H δ være som før, og sett u x 0 = 1 u 0 i xi + 1 x x + u 0 i + 1 xx i x x La u δ, x være viskositetsløsningene til u δ, x t + H δ u δ, x x = 0, u δ, x x, 0 = u x for x [i x, i + 1 x]
18 Da har vi at u δ, x, T u η, y L R u x 0 u y 0 L R + T sup p M y u 0 Lip + T η H Lip, H δ p H η p dersom y x og η δ. Siden H δ konvergerer uniformt mot H på [ M, M] så har vi at er en viskositetsløsning av ux, t = lim δ, x 0 uδ, x x, t u t + H u x = 0, ux, 0 = u 0 x. 33 Dette følger fra Teorem 1. Nå kan vi bruke dette til å vise forbindelsen mellom entropiløsninger av konserveringslover og viskositetsløsninger av Hamilton-Jacobi ligninger. Teorem 6. La u være den entydige viskositetsløsningen av 33 og la p være entropiløsningen av Da har vi at for nesten alle x, at px, t = x ux, t. p t + Hp x = 0, px, 0 = u 0x. 34 Bevis. Velg en z, og observér at vi har u δ, x x, t = u δ, x z, t + x z p δ, x y, t dy når δ, x 0, ux, t = uz, t + x z py, t dy. q.e.d. Nå har vi vist sammenhengen mellom løsningen av endimensjonale konserveringslover, og løsningen av en Hamilton-Jacobi ligning. Vi har også definert en numerisk metode for denne Hamilton-Jacobi ligningen, og vist at denne er konvergent. Vi fortsetter nå med å presentere andre numeriske metoder for initialverdiproblemer av typen 33, men vi trenger ikke begrense oss til én romdimension. Vi skal atså se på u t + HDu = 0, x, t R d 0, T ux, 0 = u 0 x. 35 For å undersøke konvergensen til disse metodene er det nyttig å kjenne noen egenskaper til viskositetsløsningene. I resten av dette notatet skriver vi for supnormen, og setter α + = α 0 og α = α 0. Her har vi et meget nyttig generellt lemma som hjelper oss. Lemma 6 Crandall-Tartar. La C L Ω være slik at dersom f og g er i C, så er g + f g + i C, og la T være en avbildning fra C til C som kommuterer med addisjon av konstanter, dvs. at T f + k = T f + k. Da er følgende ekvivalent for f og g i C, i Hvis f g nesten overalt så er T f T g nesten overalt. ii T f T g + f g +. iii T f T g f g. 18
19 Bevis. Anta at i holder, siden g + f g + er i C og antagelsen sier at g + f g + f g. Derfor får vi at T f T g + T g + f g + T g = f g +. At ii impliserer iii er lett å vise. Anta derfor at iii holder og sett k = g f +. Siden f g så har vi at k = g f. Altså T f T g + k = T f + k T g f g + k k. Det vil si at T f T g 0. q.e.d. Ved hjelp av dette lemmaet kan vi vise følgende om viskositetsløsningen av 33. Teorem 7. Anta at u er viskositetsløsningen av 6. Vi skriver ux, t = S t u 0 x. Da har løsningsoperatoren S følgende egenskaper: i S t u 0 S t v 0 + u0 v 0 +. ii S t u 0 S t v 0 u 0 v 0. iii inf x u 0 th0 + S t u 0 sup x u 0. iv S t u 0 + y S t u 0 sup x u 0 x + y u 0 x. v Du 0 L DS t u 0 L vi S t u 0 S τ u 0 t τ sup p L Hp. Bevis. Først ønsker vi å vise at dersom u 0 v 0 så er S t u 0 S t v 0. Sett Hp = Hp H0, og S t u 0 til å være viskositetsløsningen av u t + HDu = 0, ux, 0 = u Da vil St u 0 + k = S t u 0 + k, siden H0 = 0. Dersom u 0 v 0, blir S t u 0 en subløsning av ligningen med v 0 som initialdata. Da gir sammenligningsprinsippet at S t u 0 S t v 0. Nå har vi at ux, t = S t u 0 th0 blir en viskositetsløning av 35. Derfor blir også S t u 0 S t v 0. Derfor får vi at i og ii holder. Sett k = sup x u 0 x. Da er S t u 0 k th0. På samme måte blir S t u 0 inf x u 0 th0, og iii holder. Påstanden iv følger fra ii siden u + y, t er løsningen med u 0 + y som initialdata. Påstanden v følger fra iv. For å vise vi anta at u 0 er kontinuerlig deriverbar, og sett Da har vi at ūx, t = u 0 x + t sup Hp. p L ū t + HDū 0, og ū blir en supløsning, dvs. u ū. Resultatet for u begrenset og absolutt kontinuerlig følger ved et approximasjonsargument. q.e.d. Fra beviset ser vi at dersom ũ løser 36, så vil u = ũ + th0 løse 35. Derfor vil vi heretter anta at H0 = 0. Nå skal vi vise et nyttig resultat om sammenligning av to begrensede og absolutt kontinuerlige funksjoner. Dette er mer en teknikk, som kan brukes og modifiseres i flere sammenhenger, enn et enkeltresultat, og det kan sees på som en paralell til Kružkovs/Kuznetsovs måte å sammenligne entropiløsninger av konserveringslover. La derfor u og v være to begrensede og uniformt kontinuerlige funksjoner på Π T = R d [0, T. Vi ønkser å få et estimat på u v, men siden u og v ikke nødvendigvis er deriverbare, kan vi ikke derivere. Definér M ± = sup Π T ux, t vx, t ±. 19
20 Det er klart at u v = max M +, M. Vi vil estimere M = M +, og det vil bli klart at samme teknikk kan brukes til å estimere M. Vi kan anta at M > 0, og at u og v er mindre enn R. Vi velger først to testfunksjoner, β og γ som er slik at og Vi setter så Så setter vi og definerer β : R d R, βx = 1 x 2, for x 3/2,, 0 βx < 1/4, for x > 3/2, og βx = 0 for x > 1, Dβ 2, og D 2 β 4, γ : R R, γτ = 1 τ 2, for τ 3/2, 0 γτ < 1/4, for τ > 3/2, og γτ = 0 for τ > 1, γ 2, og γ 4. β x = βx/, γ τ = γτ/. Ex, t, y, s = ux, t vy, s +, Φx, t, y, s = Ex, t, y, s + 3R + 1β x y + 3R + 1γ t s t + s 4T M. Siden Φ er begrenset i Π T Π T, kan vi finne punkter x 1, t 1, y 1, s 1 slik at Φ nesten antar sin supremumsverdi i et slikt punkt, mer presist, for alle δ > 0 kan vi finne et punkt x 1, t 1, y 1, s 1 slik at Φ x 1, t 1, y 1, s 1 > sup Φx, t, y, s δ. Π T Π T Nå velger vi en ξ in C 0 R d R d slik at 0 ξ 1, ξx 1, y 1 = 1, Dξ 1 og D 2 ξ 1, og sett Ψ = Φ + 2δξ. Poenget med dette er at nå har Ψ et globalt maksimumspunkt, selv om ikke Φ har det. Altså fins et punkt x 0, t 0, y 0, s 0 i Π T Π T, slik at Ψ x 0, t 0, y 0, s 0 Ψx, y, t, s i hele Π T Π T. Videre har vi at dersom δ < 1/2 og enten x 0 y 0 eller t 0 s 0 større enn, så har vi at 2R R δ Ψ x 0, t 0, y 0, s 0 Ψx, t, x, t Ex, t, x, t + 6R + 1 M 2. Ved å ta supremum over x, t til høyre får vi at som motsier at δ < 1/2. Videre får vi at δ R M/2, Ψ x 0, t 0, y 0, s 0 6R M/2, slik at Derfor, hvis δ < M/8, har vi at E x 0, t 0, y 0, s 0 + 2δ M/2. E x 0, t 0, y 0, s 0 M/4 >
21 Vi har også at 2R R + 1β x 0 y 0 + 3R δ Ψ x 0, t 0, y 0, s 0 Ψx, t, x, t M/2 + 6R + 1, altså blir dersom δ R + 1/8. Da har vi at β x 0 y δ 3R , og vi får på samme måte at Dette gir også at β x 0 y 0 = 1 x 0 y 0 2 2, 38 γ t 0 s 0 = 1 t 0 s x 0 y 0 Vi har også at y 0 er et globalt minimum for avbildningen Derfor, for alle y R d, , og t 0 s y vy, s 0 3R + 1β x 0 y 2δξ x 0, y. 3R + 1 β x 0 y β x 0 y 0 + 2δ ξx 0, y ξx 0, y 0 der Dv betegner Lipschitz seminormen i y til v. Dette medfører at Siden Dξ 1 og ved 38 får vi at 3R + 1Dβ x 0 y 0 + 2δD y ξx 0, y 0 Dv. vy, s 0 vy 0, s 0 Dv y y 0, 6R + 1 x 0 y 0 Dv + 2δ På samme måte så får vi at 6R + 1 t 0 s 0 t v + M T Nå kan vi bruke dette til å sammenligne viskositetsløsninger med andre viskositetsløsninger eller med andre funksjoner. En klasse numeriske skjemaer. Istedenfor å ta for oss et konkret skjema, så skal vi se på en klasse av skjemaer som tilfredstiller en rekke betingelser. På denne måten blir estimatene lettere, og kanskje mer generelle. På samme måte som vi har definert en løsningsoperator S t, så definerer vi en omtrentlig løsningsoperator S t. Her er ideén at når diskretiseringen blir liten, er S t S t. Definisjon. For hver t er St funksjoner, som tilfredstiller er en avbildning definert for begrensede og uniformt kontinuerlige i S 0 u = u ii u S t u er kontinuerlig i. 21
22 iii Dersom u v så så er S t u S t v. iv S t u + k = S t u + k for alle konstanter k. v S t u u C1 t, der C 1 = C 1 Du. vi DS t u Du + tc2 for en konstant C 2 som bare avhenger av u. vii For alle begrensede testfunksjoner ϕ C 2 R d, og for tilstrekkelig små t har vi at St ϕ ϕ + HDϕ t C Dϕ + D 2 ϕ for en konstant C 4. Merk at iv holder for den eksakte løsningsoperatoren dersom H0 = 0, og vi har sett at vi kan anta dette. For konserveringslover i én romdimensjon er ofte Lax-Friedrichs skjemaet det første vi støter på. For Hamilton-Jacobi ligninger blir blir dette skjemaet u n+1 i = 1 2 u n i+1 + u n i 1 th u n i+1 u n i 1 2 x, 43 der jeg håper at notasjonen er kjent. Fra dette kan vi definere en omtrentlig løsningsoperator. Sett λ = t/ x, og for u begrenset og absolutt kontinuerlig definér u x + x u x x St ux = ux t H 1 u x + x 2ux + u x x. 2 x 2λ x 44 Setter vi D + ux + x ux xux =, og D ux ux x xux =, x x kan vi skrive dette som D St + x ux = ux t H ux + D x ux 1 D + x 2 2λ ux D x ux. 45 La oss sjekke om dette skjemaet tilfredstiller kravene. Først er i åpenbar. Vi har sett at vi godt kan anta at H0 = 0, da kommuterer St med addisjon av konstanter, og dersom iii og Crandall-Tartar lemmaet gir at St u St v u v. Altså er ii en konsekvens av iii. Dette medfører at S t u + y St u u + y u, som igjen medfører vi. Vi har at St ux er en funksjon av ux, ux x. Vi deriverer og får S t ux ux = 1 t t 0, dersom t t. Videre St ux ux ± x = t 1 u x + x u x x 2 x λ H 0, 2 x hvis λ max p Du H p 1. Fra dette får vi iii. Fra 45 ser vi at v holder med C 1 = λ + 1 λ Du. 22
23 Det siste kravet, vii, er det som skal sikre oss at St har noe med ligningen å gjøre. Dersom ϕx er glatt, så er D + x ϕx + D x ϕx = ϕ x + x ϕ 2 og D + x ϕx D+ x ϕx x ϕ Da får vi at og Derfor blir D + H x ϕx + D+ x ϕx Hϕ x 2 sup H p x ϕ. p ϕ 1 D + x 2λ ϕx D x ϕx x 2λ ϕ. St ϕx ϕx + Hϕ x t C x ϕ, Altså fins det minst ett skjema som passer med det generelle oppsettet. Det er ikke vanskelig å vise at dersom H > 0, så passer også oppstrømsskjemaet. Vi kan tilogmed vise at implisitte skjemaer, f.eks. implisitt Lax-Friedrichs passer inn i oppsettet. Nå fortsetter vi den generelle diskusjonen. La den tilnærmede løsningen, u, være definert ved { u x, 0 = u 0 x u x, t = St t 46 n u, t n x t t n, t n+1, der t n = n 1 t. Vi setter nå u = u og v = u der u er en viskositetsløsning av 35 med u 0 som initialdata. Vi skal altså begrense M, og vi må diskutere tre tilfeller, a t 0 = 0, s 0 0, b t 0 0, s 0 = 0, og c t 0 > 0, s 0 > 0. Vi begynner med a Her har vi at E x 0, 0, y 0, s 0 + 3R + 1β x 0 y 0 + 3R s δξx 0, y 0 som gir at Ψx 0, 0, y 0, s 0 Ψx 0, 0, y 0, 0 = u 0 x 0 u 0 y 0 + 3R + 1β x 0 y 0 + 3R δξx 0, y 0 uy 0, s 0 uy s Vi har at t u er begrenset av sup p Du0 Hp =: H, så da får vi Trekantulikheten gir at s H s 0, dvs. s 0 H 2. u 0 x 0 u 0 y 0 + u 0 y 0 uy 0, t 0 + 6R δ Ψ x 0, 0, y 0, s 0 M 2 + 6R + 1, mao. M 4 H 2 + Du 0 Du 0 + 2δ
24 b Nå er s 0 = 0, på samme måte som i forrige tilfelle observerer vi at E x 0, t 0, y 0, 0 + 3R + 1β x 0 y 0 + 3R t δξx 0, y 0 Ψ x 0, t 0, y 0, s 0 Ψx 0, 0, y 0, 0 = u 0 x 0 u 0 y 0 + 3R + 1β x 0 y 0 + 3R δξx 0, y 0, som gir at Ved v får vi at Nå gir trekantulikheten at u x 0, t 0 u 0 x t C 1 t 0 t2 0 2, eller t 0 C 1 2. u x 0, t 0 u 0 x 0 + u 0 x 0 u 0 y 0 + 6R δ Ψ x 0, t 0, y 0, 0 M 2 + 6R + 1, mao. M 4 C Du 0 Du 0 + 2δ c Til nå har vi hverken brukt at u er en viskositetsløsning, og nesten ikke at u nesten er det. Derfor burde tilfellene a og b bli nesten identiske for alle begrensede og uniformt kontinuerlige funksjoner. Vi har at y 0, s 0 er et globalt minimum for uy, s 3R + 1β x 0 y + 3R + 1γ t 0 s + 2δξx 0, y t 0 + s 4T M, }{{} =:θy,s og siden u er en supløsning, så får vi at Altså har vi θ t y 0, s 0 + HDθx 0, y 0 0. γ t 0 s 0 M 3R 4T + H + 1Dβ x 0 y 0 + 2δD y ξ x 0, y 0 0, eller M 4T γ t 0 s 0 + H 3R + 1Dβ x 0 y 0 + 2δD y ξ x 0, y Videre er x 0, t 0 et globalt maksimum for u x, t 3R + 1β x y 0 3R + 1γ t s 0 2δξx, y 0 + t + s 0 4T M. }{{} =:ψx,t Nå har vi at t 0 t n, t n+1 ] for en n, ved definisjon har vi da at u x 0, t 0 = S t t n u, t n x 0. Videre er u x, t n ψx, t n + u x 0, t 0 ψx 0, t 0. Det siste leddet er en konstant, og vi bruker iv og iii og får S t t n u, t n x S t t n ψ, t n x + u x 0, t 0 ψx 0, t 0. 24
25 Setter vi x = x 0 får vi at altså at Vi har at 0 S t t n ψ, t n x 0 ψx 0, t 0 0 S t t n ψ, t n x 0 ψx 0, t n t 0 t n + ψx 0, t n ψx 0, t 0 t 0 t n. ψx 0, t n ψx 0, t 0 t 0 t n for en τ i intervallet [t n, t 0 ]. Fra vii får vi Nå er Derfor blir og = 3R + 1γ t 0 s 0 1 3R + 1γ τ t 0 t n M 2 4T, S t t n ψ, t n x 0 ψx 0, t n t 0 t n H Dψx 0, t n 1 + C Dψ + D 2 ψ. Bruker vi dette får vi at M 4T Dψx, t = 3R + 1Dβ x y 0 2δD x ξx, y 0, D 2 ψx, t = 3R + 1D 2 β x y 0 2δD 2 xξx, y 0. Dψ 6R δ og D 2 ψ 12R δ, Dψx 0, t n = 3R + 1Dβ x 0 y 0 2δD x ξx 0, y 0. 3R + 1γ t 0 s 0 3R γ τt 0 t n Legger vi sammen 49 og 50 får vi at [ M 4T 12R + 1 t 0 t n H 3R + 1Dβ x 0 y 0 + 2δD y ξ x 0, y 0 Vi bruker argumentet før 41 og 40 og får at H 3R + 1Dβ x 0 y 0 2δD x ξ x 0, y 0 6R R C δ. 50 H 3R + 1Dβ x 0 y 0 2δD x ξ x 0, y 0 ] 6R R C δ 3R + 1Dβ x 0 y 0 2δD x ξ x 0, y 0 Du 0 Derfor har vi at H 3R + 1Dβ x 0 y 0 + 2δD y ξ x 0, y 0 H 3R + 1Dβ x 0 y 0 2δD x ξ x 0, y 0 sup H p 4δ. p Du 0 og 25
26 Vi sender δ til null og får [ t0 t n M 24R + 1T C ] 2 51 fra 47, 48 og 51 at { M min 4 H 2 + Du 0 2 2, C1 2 + Du 0 2 2, 24R + 1T [ t C ]} 2. Det virker vanskelig å finne den optimale fra dette utrykket, men setter vi t = c, og = 1/4, så får vi at M O. Vi viser at M er begrenset på samme måte. Altså har vi vist Teorem 8. Anta at u er definert ved 46 der St tilfredstiller kravene i-vii. La u være viskositetsløsningen til 35. Da har vi at det fins en konstant C som bare avhenger av u 0, Du 0 og T slik at u, t u, t C. All denne regningen kan vi lett få mer ut av. Hvis vi istedenfor u lar u være û, der û er viskositetsløsningen av û t + ĤDû = 0, ûx, 0 = u 0x, så får vi en beregnet u û. Estimatet 49 holder som før, og vi har fremdeles at u ψ har et maksimum i x 0, t 0. Siden û er en subløsning så vil ψ t x 0, t 0 + Ĥ Dψ x 0, t 0 0, eller 3R + 1γ t 0 s 0 + M 4T + Ĥ 3R + 1Dβ x 0 y 0 2δD x ξx 0, y 0 0. Hvis vi rydder og legger sammen med 49 så får vi at M 4T 3R H + 1Dβ x 0 y 0 + 2δD y ξx 0, y 0 Ĥ 3R + 1Dβ x 0 y 0 2δD x ξx 0, y 0. Vi sender δ til null, og bruker at 3R + 1Dβ x 0 y 0 Du 0 for å få M 4T sup Hp Ĥp. Dette medfører spesiellt at for alle T 0 p Du 0 u, T û, T 4T sup p Du 0 Hp Ĥp, 52 som jo nesten er estimatet 32. Hadde vi vært litt smartere kunne vi kvittet oss med faktoren 4. Vi kan også sette u = u µ, der u µ løser ligningen med viskositet u µ t + H Du µ = µ u µ, u µ x, 0 = u 0 x, 26
27 der = TrD 2. Siden u µ er en subløsning får vi nå at 3R + 1γ t 0 s 0 + M 3R 4T + H + 1Dβ x 0 y 0 2δD x ξx 0, y 0 µtr 3R + 1D 2 β x 0 y 0 2δD 2 ξx 0, y 0. Vi rydder litt, legger resultatet sammen med 49, sender δ til null, og får at M 4T µ 2. Siden 47 og 48 fortsatt gjelder, så får vi at for alle T 0, der C bare avhenger av u 0 og Du 0. Hvis d = 1, og H 0, så vil ux, t = u 0. Sett u, T u µ, T C T µ, 53 u 0 x = 1 x, for x [ 1, 1], og u 0 x = 0, for x > 1. Nå har vi at Nå kan vi regne ut u µ x, t = 1 1 4πµt 1 e x y2 4µt 1 y dy. u µ 1, t u1, t = 1 0 4πµt µt π µt = π µt 4π 1 1 e 1 y2 4µt 0 1 e 1 4µt e 1 y2 4µt 1 + y dy y 2µt dy for µt 1/4 ln2. Dette viser at estimatet 53 er optimalt. 4πµt 1 0 e 1 y2 4µt 1 y dy Alt som står i disse notatene er hentet fra følgende kilder, spesiellt anbefaler jeg Bardi et al. og User s guide for å få et visst intrykk. For skjemaer er Souganidis arbeide et godt utgangspunkt. Jeg vil understreke at viskositetsløsninger er et felt i rivende utvikling, og det utgis stadig nye og viktige resultater. M. Bardi, M.G. Crandall, L.C. Evans, M. Soner, P.E. Souganidis Viscosity solutions and applications, Lecture Notes, Springer M.G. Crandall, H. Ishii, P.L. Lions User s guide to viscosity solutions of second order partial differential equations, Bull. AMS, 27, 1, M.G. Crandall, L.C. Evans, P.L. Lions Some properties of viscosity solutions of Hamilton- Jacobi equations, Trans. AMS, 282, 2, M.G. Crandall, P.L. Lions Viscosity solutions of Hamilton-Jacobi equations, Trans. AMS, 277, M.G. Crandall, P.L. Lions Two approximations of solutions of Hamilton-Jacobi equations, 27
28 Math. Comp., 43, M.G. Crandall, L. Tartar Some relations between nonexpansive and order preserving mappings, Proc. AMS, 78, 3, P.E. Souganidis Approximation schemes for viscosity solutions of Hamilton-Jacobi equations, J. Diff. Eqn., 59, K.H. Karlsen, N.H. Risebro A note on front tracking and the equivalence between viscosity solutions of Hamilton-Jacobi equations and entropy solutions of scalar conservation laws, URL: G. Barles, P.E. Souganidis Convergence of approximation schemes for fully nonlinear second order equations, Asympt. Anal., 4,
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT111 Prøveeksamen Eksamensdag: 5. juni 21. Tid for eksamen: 1. 13.3. Oppgavesettet er på 9 sider. Vedlegg: Tillatte hjelpemidler:
Oblig 1 - MAT Oppgave 1. Fredrik Meyer. Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved. x n+1 = α + x n 1 + x n.
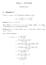 Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
Oblig 1 - MAT2400 Fredrik Meyer 1 Oppgave 1 Vi lar α > 1 og x 1 > α. Vi definerer en følge (x n ) ved Lemma 1 (a). x n > 1 n N x n+1 = α + x n = x n + α x2 n Bevis. Siden α > 1 er α + x n >, så 1 = 1+xn
Litt topologi. Harald Hanche-Olsen
 MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
MA2104 2006 Litt topologi Harald Hanche-Olsen hanche@math.ntnu.no De reelle tall En grunnleggende egenskap ved de reelle tall, som skiller dem fra de rasjonale tall, er kompletthetsaksiomet. Det har flere
dg = ( g P0 u)ds = ( ) = 0
 NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
NTNU Institutt for matematiske fag TMA4105 Matematikk 2, øving 8, vår 2011 Løsningsforslag Notasjon og merknader Som vanlig er enkelte oppgaver kopiert fra tidligere års løsningsforslag. Derfor kan notasjon,
Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
 Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Norges teknisk naturvitenskapelige universitet NTNU Side 1 av 9 Institutt for fysikk Fakultet for naturvitenskap og teknologi Løsningsforslag til eksamen i SIF4072 KLASSISK FELTTEORI Onsdag 28. mai 2003
Løsning til øving 23 for FY1004, våren 2008
 Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
Løsning til øving 23 for FY1004, våren 2008 Diracs δ-funksjon kan defineres ved at δ(x) = 0 for x 0, og dx δ(x) = 1. Vi vil bruke δ-funksjonen som et potensial for en partikkel i en dimensjon. Vi setter
TMA4100 Matematikk 1, høst 2013
 TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
TMA4100 Matematikk 1, høst 2013 Forelesning 9 www.ntnu.no TMA4100 Matematikk 1, høst 2013, Forelesning 9 Derivasjon I dagens forelesning skal vi se på følgende: 1 Tilnærminger til små endringer. 2 Vekstfart.
UNIVERSITETET I BERGEN
 BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. V.008. Løsningsforslag til eksamen i emnet MAT131 - Differensialligninger I 8. mai 008 kl. 0900-1400 Vi har ligningen der α er
BOKMÅL UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. V.008. Løsningsforslag til eksamen i emnet MAT131 - Differensialligninger I 8. mai 008 kl. 0900-1400 Vi har ligningen der α er
LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF5045 NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 8 Faglig kontakt under eksamen: Syvert P. Nørsett 7 59 5 45 LØSNINGSFORSLAG TIL EKSAMEN I FAG SIF545 NUMERISK LØSNING
Fasit til utvalgte oppgaver MAT1110, uka 28/4-2/5
 Fasit til utvalgte oppgaver MAT1110, uka 8/4-/5 Tom Lindstrøm (lindstro@math.uio.no) 5..5 a) Alle punktene i B har avstand til origo større enn 1, så d(0, B) må være minst 1. Ved å velge punkter på x-aksen
Fasit til utvalgte oppgaver MAT1110, uka 8/4-/5 Tom Lindstrøm (lindstro@math.uio.no) 5..5 a) Alle punktene i B har avstand til origo større enn 1, så d(0, B) må være minst 1. Ved å velge punkter på x-aksen
UNIVERSITETET I BERGEN
 LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. H.007. Eksamen i emnet MAT131 - Differensialligninger I 8. september 007 kl. 0900-100 Tillatte hjelpemidler: Ingen (heller
LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. H.007. Eksamen i emnet MAT131 - Differensialligninger I 8. september 007 kl. 0900-100 Tillatte hjelpemidler: Ingen (heller
TFY4215 Innføring i kvantefysikk - Løsning øving 1 1 LØSNING ØVING 1
 TFY425 Innføring i kvantefysikk - Løsning øving Løsning oppgave a. LØSNING ØVING Vi merker oss at sannsynlighetstettheten, Ψ(x, t) 2 = A 2 e 2λ x, er symmetrisk med hensyn på origo. For normeringsintegralet
TFY425 Innføring i kvantefysikk - Løsning øving Løsning oppgave a. LØSNING ØVING Vi merker oss at sannsynlighetstettheten, Ψ(x, t) 2 = A 2 e 2λ x, er symmetrisk med hensyn på origo. For normeringsintegralet
Analysedrypp II: Kompletthet
 Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
Analysedrypp II: Kompletthet Kompletthet er et begrep som står sentralt i både MAT1100 og MAT1110, og som vil stå enda mer sentralt i MAT2400. I de tidligere kursene fremstår begrepet på litt forskjellig
EKSAMEN I NUMERISK LINEÆR ALGEBRA (TMA4205)
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren 93064 EKSAMEN I NUMERISK LINEÆR ALGEBRA TMA405 Fredag 5 desember
= x lim n n 2 + 2n + 4
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving Avsnitt 8.7 6 Potensrekken konvergerer opplagt for x = 0, så i drøftingen nedenfor antar vi x 0. Vi vil bruke forholdstesten
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving Avsnitt 8.7 6 Potensrekken konvergerer opplagt for x = 0, så i drøftingen nedenfor antar vi x 0. Vi vil bruke forholdstesten
Løsningsforslag til Mat112 Obligatorisk Oppgave, våren Oppgave 1
 Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
Løsningsforslag til Mat2 Obligatorisk Oppgave, våren 206 Oppgave Avgjør om følgende rekker er konvergente: (a) n + n n + n + Løsning: rekken lim : n n + n n + n + Vi bruker grensesammenligningstesten mhp.
5.8 Iterative estimater på egenverdier
 5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
5.8 Iterative estimater på egenverdier Det finnes ingen eksplisitt formel for beregning av egenverdiene til en kvadratisk matrise. Iterative metoder som finner (ofte) en (meget god) approksimasjon til
Analysedrypp IV: Metriske rom
 Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
Analysedrypp IV: Metriske rom Vi har tidligere sett at begreper som konvergens og kontinuitet har med avstand å gjøre at f er kontinuerlig i punktet a, betyr f. eks. at det for enhver ɛ > 0, finnes en
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Separable og førsteordens lineære differensialligninger En differensialligning er separabel
MA1102 Grunnkurs i analyse II Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i analyse II Vår 219 8.4.1 Vi skal finne lengden til kurven x = 3t 2, y = 2t 3 der t 1. Som boka beskriver på
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i analyse II Vår 219 8.4.1 Vi skal finne lengden til kurven x = 3t 2, y = 2t 3 der t 1. Som boka beskriver på
Eksamensoppgave i MA1103 Flerdimensjonal analyse
 Institutt for matematiske fag Eksamensoppgave i MA113 Flerdimensjonal analyse Faglig kontakt under eksamen: Tlf: Eksamensdato: 5. Juni 19 Eksamenstid (fra til): 9: 13: Hjelpemiddelkode/Tillatte hjelpemidler:
Institutt for matematiske fag Eksamensoppgave i MA113 Flerdimensjonal analyse Faglig kontakt under eksamen: Tlf: Eksamensdato: 5. Juni 19 Eksamenstid (fra til): 9: 13: Hjelpemiddelkode/Tillatte hjelpemidler:
Et forsøk på et oppslagsverk for TMA4145 Lineære metoder
 Et forsøk på et oppslagsverk for TMA4145 Lineære metoder Ruben Spaans May 21, 2009 1 Oppslagsverk Adjungert Ball, la (X, d) være et metrisk rom og la ɛ > 0. Da er for x 0 X: 1. B(x 0 ; ɛ) = {x x X d(x,
Et forsøk på et oppslagsverk for TMA4145 Lineære metoder Ruben Spaans May 21, 2009 1 Oppslagsverk Adjungert Ball, la (X, d) være et metrisk rom og la ɛ > 0. Da er for x 0 X: 1. B(x 0 ; ɛ) = {x x X d(x,
Eksamen i Klassisk feltteori, fag TFY 4270 Onsdag 26. mai 2004 Løsninger
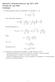 Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
Eksamen i Klassisk feltteori, fag TFY 470 Onsdag 6. mai 004 Løsninger 1a) Sammenhengen mellom koordinattiden t og egentiden τ er at Den relativistiske impulsen er Hamiltonfunksjonen er Siden har vi at
ECON2200: Oppgaver til for plenumsregninger
 University of Oslo / Department of Economics / Nils Framstad 9. mars 2011 ECON2200: Oppgaver til for plenumsregninger Revisjoner 9. mars 2011: Nye oppgavesett til 15. og 22. mars. Har benyttet sjansen
University of Oslo / Department of Economics / Nils Framstad 9. mars 2011 ECON2200: Oppgaver til for plenumsregninger Revisjoner 9. mars 2011: Nye oppgavesett til 15. og 22. mars. Har benyttet sjansen
1.1.1 Rekke med konstante ledd. En rekke med konstante ledd er gitt som. a n (1) n=m
 Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
Formelsamling og tabeller FO020E Matte 2000 for elektroprogrammet 1 Matematikk 1.1 Denisjoner av ulike typer polynomer og rekker 1.1.1 Rekke med konstante ledd En rekke med konstante ledd er gitt som a
Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener.
 NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
NTNU Institutt for matematiske fag TMA45 Matematikk, øving, vår Løsningsforslag Notasjon og merknader Oppgavene er hentet fra fagets lærebok, Hass, Weir og Thomas, samt gamle eksamener. Oppgaver fra kapittel
Tillegg om strømfunksjon og potensialstrøm
 Kapittel 9 Tillegg om strømfunksjon og potensialstrøm 9.1 Divergensfri strøm 9.1.1 Strømfunksjonen I kompendiet, kap. 4.6 og kap. 9, er det påstått at dersom et todimensjonalt strømfelt v(x y) = v x (x
Kapittel 9 Tillegg om strømfunksjon og potensialstrøm 9.1 Divergensfri strøm 9.1.1 Strømfunksjonen I kompendiet, kap. 4.6 og kap. 9, er det påstått at dersom et todimensjonalt strømfelt v(x y) = v x (x
Løsningsforslag Eksamen M100 Høsten 1998
 Løsningsforslag Eksamen M00 Høsten 998 Oppgave { x y = f(x) = + x + a hvis x ln( + x ) x hvis < x lim f(x) = f( ) = + a = a x lim f(x) = ln( + x ( ) ) ( ) = ln + For at f(x) skal være kont. i x = må lim
Løsningsforslag Eksamen M00 Høsten 998 Oppgave { x y = f(x) = + x + a hvis x ln( + x ) x hvis < x lim f(x) = f( ) = + a = a x lim f(x) = ln( + x ( ) ) ( ) = ln + For at f(x) skal være kont. i x = må lim
Forberedelse Kompletthet Kompakthet INF3170 / INF4171. Predikatlogikk: kompletthet, kompakthet. Andreas Nakkerud. 8.
 INF3170 / INF4171 Predikatlogikk: kompletthet, kompakthet Andreas Nakkerud 8. september 2015 Forberedelse Theorem La x være en variabel som ikke forekommer i Γ eller i φ. (i) Γ φ Γ[x/c] Γ[x/c]. (ii) Hvis
INF3170 / INF4171 Predikatlogikk: kompletthet, kompakthet Andreas Nakkerud 8. september 2015 Forberedelse Theorem La x være en variabel som ikke forekommer i Γ eller i φ. (i) Γ φ Γ[x/c] Γ[x/c]. (ii) Hvis
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (964) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER
LØSNINGSFORSLAG TMA4105 Matematikk 2 8. August 2005
 LØSNINGSFORSLAG TMA45 Matematikk 8. August 5 Oppgave Vi introduserer funksjonen g(x, y, z) x +y z slik at flaten z x + y er gitt ved g(x, y, z). I dette tilfellet utgjør gradienten til g en normalvektor
LØSNINGSFORSLAG TMA45 Matematikk 8. August 5 Oppgave Vi introduserer funksjonen g(x, y, z) x +y z slik at flaten z x + y er gitt ved g(x, y, z). I dette tilfellet utgjør gradienten til g en normalvektor
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11)
 Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Litt om numerisk integrasjon og derivasjon og løsningsforslag til noen ekstraoppgaver MAT-INF 1100 uke 48 (22/11-26/11) Knut Mørken 22. november 2004 Vi har tidligere i kurset sett litt på numerisk derivasjon
Løsning til prøveeksamen i MAT2400, V-11
 Løsning til prøveeksamen i MAT400, V-11 Oppgave 1 a) Vi ser at den deriverte f (x) = 1 1+x alltid er mindre enn eller lik 1 i tallverdi. Gitt to punkter x, y R, finnes det ifølge middelverdisetningen en
Løsning til prøveeksamen i MAT400, V-11 Oppgave 1 a) Vi ser at den deriverte f (x) = 1 1+x alltid er mindre enn eller lik 1 i tallverdi. Gitt to punkter x, y R, finnes det ifølge middelverdisetningen en
LP. Kap. 17: indrepunktsmetoder
 LP. Kap. 17: indrepunktsmetoder simpleksalgoritmen går langs randen av polyedret P av tillatte løsninger et alternativ er indrepunktsmetoder de finner en vei i det indre av P fram til en optimal løsning
LP. Kap. 17: indrepunktsmetoder simpleksalgoritmen går langs randen av polyedret P av tillatte løsninger et alternativ er indrepunktsmetoder de finner en vei i det indre av P fram til en optimal løsning
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger del 1 Eksamensdag: Tirsdag 7. desember 2004 Tid for eksamen: 14:30 17:30 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger del 1 Eksamensdag: Tirsdag 7. desember 2004 Tid for eksamen: 14:30 17:30 Oppgavesettet
UNIVERSITETET I BERGEN
 BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
BOKMÅL MAT - Høst 03 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i emnet MAT Grunnkurs i Matematikk I Mandag 6. desember 03, kl. 09- Tillatte hjelpemidler: Lærebok ( Calculus
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT Kalkulus og lineær algebra Eksamensdag: Onsdag 9 mai 9 Tid for eksamen: 4:3 8:3 Oppgavesettet er på 7 sider Vedlegg: Tillatte
Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:
![Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene: Oppgave 14 til 9. desember: I polynomiringen K[x, y] i de to variable x og y over kroppen K definerer vi undermengdene:](/thumbs/64/52216522.jpg) HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
HJEMMEOPPGAVER utgave av 8-12-2002): Oppgave 15 til 16 desember: La H være mengden av alle matriser på formen A = a 1 a 12 a 13 a 1n 0 a 2 0 0 0 0 a 3 0 0 0 a n der a 1 a 2 a n 0 Videre la SH være matrisene
Notat om Peanos aksiomer for MAT1140
 Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Notat om Peanos aksiomer for MAT1140 1 Tall Hva er egentlig tall? Tanken her, er ikke å si hva tall er, hva deres interne struktur muligens kan være, men å si hva vi kan gjøre med dem, sett utenifra. Vi
Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl Løysingsforslag:
 Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl. 09-15 Løysingsforslag: 1a Her er r 2 løysing av det karakteristiske polynomet med multiplisitet 2 pga. t-faktor. Det karakteristiske
Eksamen i emnet M117 - Matematiske metodar Onsdag 7. september 2001, kl. 09-15 Løysingsforslag: 1a Her er r 2 løysing av det karakteristiske polynomet med multiplisitet 2 pga. t-faktor. Det karakteristiske
Notat 05 for MAT Relasjoner, operasjoner, ringer. 5.1 Relasjoner
 Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
Notat 05 for MAT1140 5 Relasjoner, operasjoner, ringer 5.1 Relasjoner Når R er en relasjon som er veldefinert på A B, slik at R(x, y) er en påstand når x A og B B, tenker vi på relasjonen som noe som lever
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: FYS14, Kvantefysikk Eksamensdag: 17. august 17 4 timer Lovlige hjelpemidler: Rottmann: Matematisk formelsamling, Øgrim og Lian:
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 7: Derivasjon (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 23. august, 2012 Den deriverte som momentan endringsrate Den deriverte som momentan endringsrate Repetisjon
Matematikk 1 (TMA4100) Forelesning 7: Derivasjon (fortsettelse) Eirik Hoel Høiseth Stipendiat IMF NTNU 23. august, 2012 Den deriverte som momentan endringsrate Den deriverte som momentan endringsrate Repetisjon
EKSEMPLER TIL ETTERTANKE MAT1100 KALKULUS
 EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
EKSEMPLER TIL ETTERTANKE MAT00 KALKULUS Simon Foldvik. Oktober 207 Dette dokumentet inneholder eksempler på hvor «ting går galt» og har til hensikt å vise eksempler på hva man ikke kan konkludere. Alle
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
Prøveeksamen i MAT 1100, H-03 Løsningsforslag
 Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
Prøveeksamen i MAT, H- Løsningsforslag. Integralet cos x dx er lik: +sin x Riktig svar: c) arctan(sin x) + C. Begrunnelse: Sett u = sin x, da er du = cos x dx og vi får: cos x + sin x dx = du du = arctan
MA2501, Vårsemestre 2019, Numeriske metoder for lineære systemer
 MA5 Vårsemestre 9 Numeriske metoder for lineære systemer Introduksjon Vi vil approksimere løsningen av lineære systemet av n ligningene og n ukjente: a x + a x + + a n x n b a x + a x + + a n x n b ()
MA5 Vårsemestre 9 Numeriske metoder for lineære systemer Introduksjon Vi vil approksimere løsningen av lineære systemet av n ligningene og n ukjente: a x + a x + + a n x n b a x + a x + + a n x n b ()
EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER MED DIFFERANSEMETODER (TMA4212)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Faglig kontakt under eksamen: Navn: Bård Skaflestad (946867) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Faglig kontakt under eksamen: Navn: Bård Skaflestad (946867) EKSAMEN I NUMERISK LØSNING AV DIFFERENSIALLIGNINGER
MA1102 Grunnkurs i Analyse II Vår 2015
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA112 Grunnkurs i Analyse II Vår 215 Løsningsforslag Øving 5 11.3:3 f n (x) = 2n+1 x? = x 1 2n+1. (Det er muligens en forskjell
Løsningsforslag til øving 4
 1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
1 FY100/TFY4160 Bølgefysikk. Institutt for fysikk, NTNU. Høsten 01. Løsningsforslag til øving 4 Oppgave 1 a) D = D 0 [ cos (kx ωt) + sin (kx ωt) ] 1/ = D 0 for alle x og t. Med andre ord, vi har overalt
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjoner (også kalt koordinatmatriser) av lineære avbildninger mellom endeligdimensjonale vektorrom En slik
FY1006/TFY Løsning øving 9 1 LØSNING ØVING 9
 FY1006/TFY415 - Løsning øving 9 1 Løsning oppgave Numerisk løsning av den tidsuavhengige Schrödingerligningen LØSNING ØVING 9 a. Alle leddene i (1) har selvsagt samme dimensjon. Ved å dividere ligningen
FY1006/TFY415 - Løsning øving 9 1 Løsning oppgave Numerisk løsning av den tidsuavhengige Schrödingerligningen LØSNING ØVING 9 a. Alle leddene i (1) har selvsagt samme dimensjon. Ved å dividere ligningen
Anbefalte oppgaver - Løsningsforslag
 Anbefalte oppgaver - Løsningsforslag Uke 6 12.6.4: Vi finner først lineariseringen i punktet (2, 2). Vi har at Lineariseringen er derfor 2x + y f x (x, y) = 24 (x 2 + xy + y 2 ) 2 2y + x f y (x, y) = 24
Anbefalte oppgaver - Løsningsforslag Uke 6 12.6.4: Vi finner først lineariseringen i punktet (2, 2). Vi har at Lineariseringen er derfor 2x + y f x (x, y) = 24 (x 2 + xy + y 2 ) 2 2y + x f y (x, y) = 24
Matematikk 1 (TMA4100)
 Matematikk 1 (TMA4100) Forelesning 6: Derivasjon Eirik Hoel Høiseth Stipendiat IMF NTNU 22. august, 2012 Stigningstallet i et punkt Stigningstallet i et punkt Vi vender nå tilbake til problemet med å finne
Matematikk 1 (TMA4100) Forelesning 6: Derivasjon Eirik Hoel Høiseth Stipendiat IMF NTNU 22. august, 2012 Stigningstallet i et punkt Stigningstallet i et punkt Vi vender nå tilbake til problemet med å finne
Oppsummering TMA4100. Kristian Seip. 26./28. november 2013
 Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Oppsummering TMA4100 Kristian Seip 26./28. november 2013 Forelesningene 26./28. november Disse forelesningene er et forsøk på å se de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 delvis
Flere anvendelser av derivasjon
 Flere anvendelser av derivasjon Department of Mathematical Sciences, NTNU, Norway September 30, 2014 Forelesning 17.09.2014 Fikspunkt-iterasjon Newtons metode Metoder for å finne nullpunkter av funksjoner:
Flere anvendelser av derivasjon Department of Mathematical Sciences, NTNU, Norway September 30, 2014 Forelesning 17.09.2014 Fikspunkt-iterasjon Newtons metode Metoder for å finne nullpunkter av funksjoner:
LØSNINGSFORSLAG EKSAMEN, MAT 1001, HØSTEN (x + 1) 2 dx = u 2 du = u 1 = (x + 1) 1 = 1 x + 1. ln x
 LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
LØSNINGSFORSLAG EKSAMEN, MAT 00, HØSTEN 06 DEL.. Hvilken av funksjonene gir en anti-derivert for f(x) = (x + )? Løsning. Vi setter u = x +, som gir du = dx, (x + ) dx = u du = u = (x + ) = x + a) x+ b)
INF-MAT5370. Delaunay-trianguleringer og Voronoi-diagram
 INF-MAT5370 Delaunay-trianguleringer og Voronoi-diagram Øyvind Hjelle oyvindhj@simula.no, +47 67 82 82 75 Simula Research Laboratory, www.simula.no September 7, 2009 Innhold Klassisk teori Optimale trianguleringer
INF-MAT5370 Delaunay-trianguleringer og Voronoi-diagram Øyvind Hjelle oyvindhj@simula.no, +47 67 82 82 75 Simula Research Laboratory, www.simula.no September 7, 2009 Innhold Klassisk teori Optimale trianguleringer
Eksamensoppgave i MA1103 Flerdimensjonal analyse
 Institutt for matematiske fag Eksamensoppgave i MA3 Flerdimensjonal analyse Faglig kontakt under eksamen: Mats Ehrnstrøm Tlf: 735 97 44 Eksamensdato: 22. mai 28 Eksamenstid (fra til): 9: 3: Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i MA3 Flerdimensjonal analyse Faglig kontakt under eksamen: Mats Ehrnstrøm Tlf: 735 97 44 Eksamensdato: 22. mai 28 Eksamenstid (fra til): 9: 3: Hjelpemiddelkode/Tillatte
Løsningsforslag Konte-eksamen 13. august 2002 SIF4048 Kjemisk fysikk og kvantemekanikk
 ppgave Løsningsforslag Konte-eksamen 3. august SIF8 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, ) mω/π h exp( mωx / h) er symmetrisk med hensyn på origo, er forventningsverdien
ppgave Løsningsforslag Konte-eksamen 3. august SIF8 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, ) mω/π h exp( mωx / h) er symmetrisk med hensyn på origo, er forventningsverdien
Løsningsforslag Konte-eksamen 2. august 2003 SIF4048 Kjemisk fysikk og kvantemekanikk
 Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
Partieltderiverte og gradient
 Partieltderiverte og gradient Kap 2 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE våren 2009 Framstilling Kommentarer, relasjon til andre kurs Struktur Mye er repitisjon fra MAT1100, litt
Partieltderiverte og gradient Kap 2 Matematisk Institutt, UiO MEK1100, FELTTEORI OG VEKTORANALYSE våren 2009 Framstilling Kommentarer, relasjon til andre kurs Struktur Mye er repitisjon fra MAT1100, litt
Den deriverte og derivasjonsregler
 Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
Den deriverte og derivasjonsregler Department of Mathematical Sciences, NTNU, Norway September 3, 2014 Tangenten til en funksjon i et punkt (kap. 2.1) Sekant til en funksjon gjennom to punkter 25 20 f(c+h)
1 Mandag 1. februar 2010
 Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
Mandag. februar 200 I dag skal vi fortsette med rekkeutviklinger som vi begynte med forrige uke. Vi skal se på litt mer generell rekker og vurdere når de konvergerer, bl.a. gi et enkelt kriterium. Dette
TMA4240 Statistikk H2015
 TMA4240 Statistikk H2015 Funksjoner av stokastiske variabler (kapittel 7+notat) Fokus på start med kumulativ fordeling 7.2 Funksjon av en SV (inkludert en-entydighet). Fordeling til max/min (fra notat).
TMA4240 Statistikk H2015 Funksjoner av stokastiske variabler (kapittel 7+notat) Fokus på start med kumulativ fordeling 7.2 Funksjon av en SV (inkludert en-entydighet). Fordeling til max/min (fra notat).
MAT1100 - Grublegruppen Uke 36
 MAT - Grublegruppen Uke 36 Jørgen O. Lye Partiell derivasjon Hvis f : R 2 R er en kontinuerlig funksjon, så kaller man følgende dens partiellderiverte (gitt at de finnes!) f f(x + h, y) f(x, y) (x, y)
MAT - Grublegruppen Uke 36 Jørgen O. Lye Partiell derivasjon Hvis f : R 2 R er en kontinuerlig funksjon, så kaller man følgende dens partiellderiverte (gitt at de finnes!) f f(x + h, y) f(x, y) (x, y)
Løsningsforslag Matematisk fysikk, 28. mai 2001
 Løsningsforslag Matematisk fysikk, 8. mai Oppgave a) Det er trykkfeil i oppgaven. Riktig uttrykk er Vi har sin n θ = π cosx sin θ) = π π = n= n= n= = J x). π n n!). ) n x sin θ) n n= ) n x n ) n x n )
Løsningsforslag Matematisk fysikk, 8. mai Oppgave a) Det er trykkfeil i oppgaven. Riktig uttrykk er Vi har sin n θ = π cosx sin θ) = π π = n= n= n= = J x). π n n!). ) n x sin θ) n n= ) n x n ) n x n )
Løsningsforslag Eksamen 28. mai 2003 SIF4048 Kjemisk fysikk og kvantemekanikk
 Eksamen SIF4048 8.05.03 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 8. mai 003 SIF4048 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, 0) = β/π exp( βx ) er symmetrisk med
Eksamen SIF4048 8.05.03 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 8. mai 003 SIF4048 Kjemisk fysikk og kvantemekanikk a. Da sannsynlighetstettheten Ψ(x, 0) = β/π exp( βx ) er symmetrisk med
Løsningsforslag, eksamen MA1103 Flerdimensjonal analyse, 8.juni 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 7 Løsningsforslag, eksamen MA11 Flerdimensjonal analyse, 8.juni 21 Oppgave 1 a) Finn og klassifiser alle kritiske
Litt matematikk som er nyttig for teorien bak spillteorien.
 Litt matematikk som er nyttig for teorien bak spillteorien.. John von Neumanns min-max teorem For å vise dette resultatet trenger vi et lite hjelperesultat. For p R m så sier vi at p er en sannsynlighetsvektor
Litt matematikk som er nyttig for teorien bak spillteorien.. John von Neumanns min-max teorem For å vise dette resultatet trenger vi et lite hjelperesultat. For p R m så sier vi at p er en sannsynlighetsvektor
Anbefalte oppgaver - Løsningsforslag
 TMA405 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 6 3..9: Vi starter med å finne de kritiske punktene. De deriverte blir T x (x, y) = ( x xy)e x y T y (x, y) = ( y xy)e x y, slik at de kritiske
TMA405 Matematikk Anbefalte oppgaver - Løsningsforslag Uke 6 3..9: Vi starter med å finne de kritiske punktene. De deriverte blir T x (x, y) = ( x xy)e x y T y (x, y) = ( y xy)e x y, slik at de kritiske
MAT jan jan jan MAT Våren 2010
 MAT 1012 Våren 2010 Mandag 18. januar 2010 Forelesning I denne første forelesningen skal vi friske opp litt rundt funksjoner i en variabel, se på hvordan de vokser/avtar, studere kritiske punkter og beskrive
MAT 1012 Våren 2010 Mandag 18. januar 2010 Forelesning I denne første forelesningen skal vi friske opp litt rundt funksjoner i en variabel, se på hvordan de vokser/avtar, studere kritiske punkter og beskrive
TFY4115: Løsningsforslag til oppgaver gitt
 Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
Institutt for fysikk, NTNU. Høsten. TFY45: Løsningsforslag til oppgaver gitt 6.8.9. OPPGAVER 6.8. Vi skal estemme Taylorrekkene til noen kjente funksjoner: a c d sin x sin + x cos x sin 3 x3 cos +... x
FY2045/TFY4250 Kvantemekanikk I, løsning øving 13 1 LØSNING ØVING 13. V (x, t) = xf (t) = xf 0 e t2 /τ 2.
 FY045/TFY450 Kvantemekanikk I, løsning øving 13 1 Løsning Oppgave 13 1 LØSNING ØVING 13 Transient perturbasjon av harmonisk oscillator a. Med kraften F (t) = qe(t) = F 0 exp( t /τ ) og sammenhengen F (t)
FY045/TFY450 Kvantemekanikk I, løsning øving 13 1 Løsning Oppgave 13 1 LØSNING ØVING 13 Transient perturbasjon av harmonisk oscillator a. Med kraften F (t) = qe(t) = F 0 exp( t /τ ) og sammenhengen F (t)
En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x).
 Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Funksjoner En (reell) funksjon f fra en (reell) mengde D er en regel som til hvert element x D tilordner en unik verdi y = f (x). Mengden D kalles definisjonsmengden (eng.: domain) til f. Merknad Dersom
Oppsummering TMA4100. Kristian Seip. 16./17. november 2015
 Oppsummering TMA4100 Kristian Seip 16./17. november 2015 Forelesningene 17./18. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 noen tips for
Oppsummering TMA4100 Kristian Seip 16./17. november 2015 Forelesningene 17./18. november Denne forelesningen beskriver de store linjer og sammenhengen mellom de ulike deltemaene i TMA4100 noen tips for
Institutionen för Matematik, KTH
 Institutionen för Matematik, KTH Lösningsforslag till tentamen, 200-2-7, kl. 8.00-.00. 5B04, Envariabel. Uppgift. Den karakteristiske ligningen r 2 r + 2 0 kan omskrives som (r )(r 2) 0. Den generelle
Institutionen för Matematik, KTH Lösningsforslag till tentamen, 200-2-7, kl. 8.00-.00. 5B04, Envariabel. Uppgift. Den karakteristiske ligningen r 2 r + 2 0 kan omskrives som (r )(r 2) 0. Den generelle
Løsningsforslag til eksamen i MAT 1100, H06
 Løsningsforslag til eksamen i MAT, H6 DEL. poeng Hva er den partiellderiverte f z xyz cosxyz x sinyz + xyz cosyz xy cosyz x sinyz + xz cosyz cosyz xyz sinyz når fx, y, z = xz sinyz? Riktig svar b: x sinyz
Løsningsforslag til eksamen i MAT, H6 DEL. poeng Hva er den partiellderiverte f z xyz cosxyz x sinyz + xyz cosyz xy cosyz x sinyz + xz cosyz cosyz xyz sinyz når fx, y, z = xz sinyz? Riktig svar b: x sinyz
Fraktaler og kaos Harald Hanche-Olsen
 TMA4165 Dynamiske systemer 2007 Fraktaler og kaos 2 Fraktaler og kaos Harald Hanche-Olsen hanche@math.ntnu.no Sammendrag. Tillegg til dynamiske systemer 2007. Etter notater av Nils A. Baas. Notatet gir
TMA4165 Dynamiske systemer 2007 Fraktaler og kaos 2 Fraktaler og kaos Harald Hanche-Olsen hanche@math.ntnu.no Sammendrag. Tillegg til dynamiske systemer 2007. Etter notater av Nils A. Baas. Notatet gir
Iterasjon og optimering
 Innhold 5 Iterasjon og optimering 3 5.1 Litt topologi i R m........................ 4 5. Kompletthet av R m....................... 13 5.3 Noen konsekvenser av kompletthet............... 18 5.4 Iterasjon
Innhold 5 Iterasjon og optimering 3 5.1 Litt topologi i R m........................ 4 5. Kompletthet av R m....................... 13 5.3 Noen konsekvenser av kompletthet............... 18 5.4 Iterasjon
Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk
 Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
Eksamen FY2045 27. mai 2005 - løsningsforslag 1 Oppgave 1 Løsningsforslag Eksamen 27. mai 2005 FY2045 Kvantefysikk a. Ifølge den tidsuavhengige Shrödingerligningen, Ĥψ = Eψ, har vi for x < 0 : E = Ĥψ ψ
EKSAMEN I MA0002 Brukerkurs B i matematikk
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Achenef Tesfahun (9 84 97 5) EKSAMEN I MA2 Brukerkurs B i matematikk Lørdag 322 Tid:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Achenef Tesfahun (9 84 97 5) EKSAMEN I MA2 Brukerkurs B i matematikk Lørdag 322 Tid:
MAT jan jan feb MAT Våren 2010
 MAT 1012 Våren 2010 Mandag 25. januar 2010 Forelesning Vi fortsetter med å se på det bestemte integralet, bl.a. på hvordan vi kan bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis
MAT 1012 Våren 2010 Mandag 25. januar 2010 Forelesning Vi fortsetter med å se på det bestemte integralet, bl.a. på hvordan vi kan bruke numeriske beregninger til å bestemme verdien når vi ikke nødvendigvis
EKSAMEN I EMNET Løsning: Mat Grunnkurs i Matematikk I Mandag 14. desember 2015 Tid: 09:00 14:00
 Universitetet i Bergen Det matematisk naturvitenskapelige fakultet Matematisk institutt Side 1 av 7 BOKMÅL EKSAMEN I EMNET Mat 111 - Grunnkurs i Matematikk I Mandag 14. desember 15 Tid: 9: 14: Tillatte
Universitetet i Bergen Det matematisk naturvitenskapelige fakultet Matematisk institutt Side 1 av 7 BOKMÅL EKSAMEN I EMNET Mat 111 - Grunnkurs i Matematikk I Mandag 14. desember 15 Tid: 9: 14: Tillatte
Løsningsforslag øving 6
 Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Løsningsforslag øving 6 7 Husk Teorem 79 i notatet: En delmengde U av et vektorrom V er et underrom hvis ) nullvektoren er i U, ) summen av to vektorer i U er i U igjen, og 3) et skalarmultiplum av en
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag. Side 1 av 6. Faglig kontakt under eksamen: Navn: Brynjulf Owren (93518)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (93518) EKSAMEN I NUMERISK LØSNING AV DIFFERENISALLIGNINGER (75316)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 6 Faglig kontakt under eksamen: Navn: Brynjulf Owren (93518) EKSAMEN I NUMERISK LØSNING AV DIFFERENISALLIGNINGER (75316)
Løsningsforslag Eksamen 8. august 2011 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
Notasjon i rettingen:
 UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Løsningsforslag med kommentarer) til Innlevering /4 i emnet MAT, høsten 207 Notasjon i rettingen: R Rett R Rett, men med liten tulle)feil
Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017
 Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017 Andreas Leopold Knutsen 4. oktober 2017 Problem og hovedidé Problem: Finn løsning(er) r på en ligning
Finne løsninger på ligninger numerisk: Newton-Raphson metoden og Fikspunktiterasjon MAT111, høsten 2017 Andreas Leopold Knutsen 4. oktober 2017 Problem og hovedidé Problem: Finn løsning(er) r på en ligning
SIF5005 Matematikk 2, 13. mai 2002 Løsningsforslag
 SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
SIF55 Matematikk, 3. mai Oppgave Alternativ : At de to ligningene skjærer hverandre vil si at det finnes parameterverdier u og v som, innsatt i de to parametriseringene, gir samme punkt: Vi løser hver
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Fredag 7. desember 27. Tid for eksamen: 9: 12:. Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 11 Modellering og beregninger. Eksamensdag: Fredag 7. desember 27. Tid for eksamen: 9: 12:. Oppgavesettet er på 8 sider.
Fremdriftplan. I går. I dag. 2.5 Uendelige grenser og vertikale asymptoter 2.6 Kontinuitet
 1 Fremdriftplan I går 2.5 Uendelige grenser og vertikale asymptoter 2.6 Kontinuitet I dag 2.7 Tangenter og derivasjon 3.1 Den deriverte til en funksjon 3.2 Derivasjonsregler 3.3 Den deriverte som endringsrate
1 Fremdriftplan I går 2.5 Uendelige grenser og vertikale asymptoter 2.6 Kontinuitet I dag 2.7 Tangenter og derivasjon 3.1 Den deriverte til en funksjon 3.2 Derivasjonsregler 3.3 Den deriverte som endringsrate
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Fredag 7. januar 2005. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger. Eksamensdag: Fredag 7. januar 2005. Tid for eksamen: 14:30 17:30. Oppgavesettet er på
Logaritmer og eksponentialfunksjoner
 Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
Logaritmer og eksponentialfunksjoner Harald Hanche-Olsen og Marius Irgens 20-02-02 Dette notatet ble først laget for MA02 våren 2008. Denne versjonen er omskrevet for MA02 våren 20. Du vil oppdage at mange
SIF 5005 Matematikk 2 våren 2001
 IF 55 Matematikk våren Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Diverse løsningsforslag 75 Matematikk B, mai 994 (side 77 79) 6 a) Vi finner en potensialfunksjon φ(x,
IF 55 Matematikk våren Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Diverse løsningsforslag 75 Matematikk B, mai 994 (side 77 79) 6 a) Vi finner en potensialfunksjon φ(x,
Eksamen i emnet M117 - Matematiske metodar Mandag 29. mai 2000, kl Løysingsforslag:
 Eksamen i emnet M7 - Matematiske metodar Mandag 29. mai 2, kl. 9-5 Løysingsforslag: a Singulære punkt svarer til nullpunkta for x 2, dvs. x = og x =. Rekkeutvikler om x = : yx = a n x n y x = na n x n
Eksamen i emnet M7 - Matematiske metodar Mandag 29. mai 2, kl. 9-5 Løysingsforslag: a Singulære punkt svarer til nullpunkta for x 2, dvs. x = og x =. Rekkeutvikler om x = : yx = a n x n y x = na n x n
MA oppsummering så langt
 MA1101 - oppsummering så langt Torsdag 29. september 2005 http://www.math.ntnu.no/emner/ma1101/2005h/ MA1101- oppsummering så langt p.1/21 Pensum til semesterprøven Kapittel P Kapittel 1 Kapittel 2: avsnittene
MA1101 - oppsummering så langt Torsdag 29. september 2005 http://www.math.ntnu.no/emner/ma1101/2005h/ MA1101- oppsummering så langt p.1/21 Pensum til semesterprøven Kapittel P Kapittel 1 Kapittel 2: avsnittene
Anbefalte oppgaver - Løsningsforslag
 TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
TMA415 Matematikk 2 Anbefalte oppgaver - Løsningsforslag Uke 7 15.1.3: Siden vektorfeltet er gitt ved F(x, y) = yi + xj må feltlinjene tilfredstille differensiallikningen eller y = x y, ( ) 1 2 y2 = x.
OPPGAVE 1 LØSNINGSFORSLAG
 LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i MAT - Grunnkurs i matematikk I torsdag 5.desember 20 kl. 09:00-4:00 OPPGAVE a Modulus: w = 2 + 3 2 = 2. Argument
LØSNINGSFORSLAG UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet Eksamen i MAT - Grunnkurs i matematikk I torsdag 5.desember 20 kl. 09:00-4:00 OPPGAVE a Modulus: w = 2 + 3 2 = 2. Argument
7 Ordnede ringer, hele tall, induksjon
 Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
Notat 07 for MAT1140 7 Ordnede ringer, hele tall, induksjon Definition 7.1. La R være utstyrt med addisjon og multiplikasjon slik at vi har å gjøre med en kommutativ ring. Anta videre at R er utstyrt med
