Hvordan lære matematikk gjennom teknologi og design?
|
|
|
- Irene Espeland
- 8 år siden
- Visninger:
Transkript
1 Mona Røsseland Hvordan lære matematikk gjennom teknologi og design? Det å innlemme emnet teknologi og design (T&D) i matematikkundervisningen innebærer en rekke utfordringer. Emnet er ikke et eget fag med egne kompetansemål, men det skal inngå i blant annet matematikkopplæringen med sikte på å gi elevene økt kompetanse i matematikk. I den felles beskrivelsen av emnet i den nye læreplanen omtales teknologi og design som en prosess knyttet til det å planlegge og til å framstille produkter. Det er ikke vanskelig å finne en tydelig tråd til bestemte kompetansemål i naturfag og kunst og håndverk. Så er ikke tilfellet i forhold til kompetansemål i matematikk. Matematikkfagets rolle beskrives i stedet som et redskapsfag, og det blir knyttet direkte til arbeidet med konkret produktutvikling. Noe som gir matematikk et minimalt bidrag til teknologi og design sammenlignet med naturfagene og kunst og håndverk. Dette er veldig synd, for jeg tror det er mulig å finne matematikken igjen i alle delene av arbeidsprosessen i et teknologi og design-prosjekt. Gjennom T&D-opplegg kan en forholdsvis enkelt sette fokus på matematiske prosesser, som utforsking, undersøkelser, problemløsning, representasjon, modellering, fremfor kun på resultater. Lærerens oppgave vil variere fra 2 Mona Røsseland, Matematikksenteret mona@fiboline.no prosjekt til prosjekt, men han vil fortsatt være viktig for elevenes læringsutbytte. Det vil være han som legger til rette for at elevene får tid til tilstrekkelig refleksjon, det er han som ser når det er noe stoff som må undervises spesielt i. Det er ikke sikkert elevene klarer å se de grunnleggende naturvitenskaplig eller matematiske prinsippene i en teknologisk løsning på egenhånd. Svært ofte trenger de læreren som brobygger og oversetter. For å finne mer ut av hvordan en kan lære matematikk gjennom T&D gjennomførte jeg i samarbeid med klasselærer Mariann Tallis Sandvik et Tekologi og Design prosjekt på tredje trinn ved Gjerde skole i Samnanger. Elevene skulle i løpet av en hel skoleuke designe og lage et kjøkken/allrom av ulike materialer. Vi valgte å gi elevene en stor grad av selvbestemmelse i dette T&D prosjektet. Det vil si at elevene var forholdsvis frie i forhold til hva de ville lage, hvilke materialer de valgte å bruke og hvordan produktene ble seende ut. Det var et viktig poeng for oss å skape rom for utforsking og at elevene skulle få prøve seg i forhold til de ulike elementene i T&D. Vi ville at de skulle være aktive, handlende og selvstendige, for på denne måten å skaffe seg viktig erfaringer og ny kunnskap. I denne prosessen frem mot ny kunnskap arbeidet elevene i grupper, slik at de kunne dra nytte av hverandre sin kompetanse. Men selv 4/2006 tangenten
2 om de løste mange oppgaver sammen, var det også rom for individuelt arbeid i sluttførelsen av de ulike produktene. Vi hadde også felles økter, spesielt i starten, etter hver arbeidsøkt og på slutten av prosjektet, der hele klassen var sammen om å komme med ideer og refleksjon. Siden dette var et T&D prosjekt ville selvsagt de faglige målene være knyttet opp mot kjernen i T&D. Vi ønsket å gi elevene økte kunnskaper og erfaringer med design, teknologiske prinsipper, materialkunnskap, teknologiske ferdigheter og til dels teknologi sett i sammenheng med samfunnet for øvrig. Men vi ønsket også en klar fokusering på de matematiske kompetansemålene for prosjektet. For å styrke det matematikkfaglige perspektivet la vi også opp til noen oppgaver underveis som var til dels styrende. Elevene fikk blant annet i oppgave å fliselegge gulvet i rommet deres, og hver gruppe fikk 1000 kr til å handle fliser for. Hver gruppe på 4 elever fikk utdelt en tykk papplate på cm. Dette var grunnflaten på kjøkkenet / allrommet i målestokk 1 : 10. Elevene måtte nå planlegge og diskutere hva som er på et kjøkken, hvordan deres rom skulle se ut og hvilke materialer de ville velge for å lage de ulike komponentene. Vi hadde et godt utvalg av materialer som for eksempel papp i ulike tykkelser, blomsterpinner, ulike typer plast og tekstiler. Papplaten på cm var det eneste materiellet som var felles for alle. Vi brukte god tid til å gå gjennom hva vi hadde av utstyr, og vi diskuterte med elevene de ulike bruksområdene for hvert av materialene. Som verktøy hadde vi blant annet limpistoler og tapetkniv, så vi måtte også gå igjennom en del forsiktighetsregler. Da vi satte i gang prosjektet var det ikke innlysende for elevene hva et kjøkken inneholdt. I felles klasse diskuterte vi hva et kjøkken inneholder, og det tok overraskende lang tid før alle de vanligste produktene kom opp på tavlen. Etter hvert hadde hver gruppe laget seg en skisse som inneholdt de tingene som de ville ha med i sitt rom. I det videre arbeidet brukte elevene et dataprogram som vi hadde lastet ned fra IKEA sine nettsider. Programmet heter IKEA kitchen planner, og her kunne de sette inn kjøkkenskap og hvitevarer og lage både 2- og 3 dimensjonale tegninger. Romplanleggeren hadde også en annen funksjon som gjorde at elevene måtte forholde seg til rotasjon. For etter at de hadde valgt ut hvilke møbler de skulle ha på tegningen i programmet måtte de få dem til å ligge inntil hverandre. Det gjorde de ikke automatisk, og da var det to knapper med rotasjonspiler elevene kunne styre dem på plass med. Elevene fikk en god erfaring med hvordan rotasjon fungerte. Neste utfordring var å sette riktige mål på tingene de hadde laget skisse på. De fleste hadde ganske enkelt ikke peiling på hvor høy en komfyr er, eller hvor lang en kjøkkenbenk kan tangenten 4/2006 3
3 4 være. Vi spurte dem hvordan de kunne finne dette ut. Noen foreslo at de kunne tippe og bare sette et mål, andre mente de kunne se på meterstokken og anslå, noen mente de måtte hjem å sjekke, men så var det et lyst hode som foreslo at vi kunne gå på skolekjøkkenet og ta mål der. Gruppene fikk beskjed om å ta med seg det utstyret de trengte, uten at vi sa noe mer enn det. Ganske mange fór av gårde med linjalen de hadde i pennalhuset, selv om vi hadde lagt frem både meterstokk og måleband på rull. Mange kom og hentet dette utstyret etter å ha gjort noen erfaringer med linjalen. De fleste elevene hadde kunnskaper om lengdemåling, og det var en forutsetning for denne aktiviteten. Mange klarte også å regne om fra centimeter til meter, og de på gruppen som kunne dette forklarte greit til de andre. På tegningen ser vi en skisse der eleven har vært på kjøkkenet og målt og skrevet på målene. Som vi ser, har han målt alle sidene på bordet. Det kan tyde på at han ennå ikke har automatisert egenskapene ved en rektangulær figur. Den lærdomen kom etter hvert da de skulle lage skapene, og de ikke var nøyaktige nok med målene på de ulike sidene slik at skapet ble skakt. De hadde stadig behov for hjelpetegninger og skisser, som da de skulle finne ut hvor stort bord de trengte. De ville at det skulle være plass til 12 personer, men visste ikke hvor stort bord det krevde. De diskuterte seg frem til at hver person måtte ha 50 cm plass, og så lagde de seg en hjelpetegning der de skrev på 50 cm + 50 cm + 50 cm + 50 cm + 50 cm på den ene siden av bordet, det samme på andre siden og til slutt 50 cm på hver av endene. Bordet måtte da være minst 250 cm langt og 50 cm bredt. Neste steg var nå å lage de ulike møblene og utstyret, og de skulle arbeide med målestokken 1:10, og dette var vanskelig for 3.klassingene. Vi måtte gå grundig gjennom det med felles klasse, og vi følte at mange av elevene fikk det med seg. De var med da vi forklarte at 50 cm på modellen representerte 5 m i virkeligheten, og mange hadde opp hånda og svarte at langsiden på papplaten deres var 7 m i virkeligheten. Vi skrittet også opp 5 m 7 m i klasserommet, slik at de skulle få en føling med hvor stor 35 m 2 egentlig er. Ja, ja, det er jo i grunn enkelt, tenkte jeg, de skal jo bare gange med 10 eller dele på 10. Det var likevel bare 3 4 elever i klassen som forsto målestokk og brukte det bevisst i det videre arbeidet. De andre elevene måtte ha hjelp til utregningene, men de viste tydelig at de hadde forstått grunnprinsippene i målestokk. De hadde ingen problemer med å skjønne at tingene de lagde var en forminsket modell av virkeligheten, men derifra til å forstå sammenhengen mellom de ulike målene var noe annet. De elevene som ikke fikk den fulle forståelsen for målestokk fikk smakebiter av hva det betydde, og laget seg noen mentale knagger til neste gang de møter det. Et eksempel på dette var Christian som hadde laget en TV, og de andre på gruppen ville ikke ha det med i rommet fordi de mente det var for lite. Christian var en av dem som ikke hadde forstått dette med målestokk så godt, men til min store overraskelse sier han: Kan du hjelpe meg å finne ut hvor stort TV blir i virkeligheten, jeg vet ikke hvordan jeg kan finne det ut. Sammen kom vi frem til at han måtte finne målene på TV-en han hadde laget. Så forklarte jeg ham at 4/2006 tangenten
4 i virkeligheten blir den ti ganger større. Med litt hjelp klarte han å beregne hvor stort TV-en ville bli, og vi kunne slå fast at det var på størrelse med en liten reise-tv, som passet godt opp på et kjøkkenskap. Det oppsto flere lignende episoder, der vi så at flere og flere elever skjønte målestokk da de jobbet med modellene sine og gjerne ville vite hvor store de ble i virkeligheten. Jeg mener dette underbygger det Dewey [1] poengterer når han sier at det er viktig at elevene først får erfare et fenomen, for så å lære seg de underliggende teoriene. Ved at elevene får kjenne problemet på kroppen gjennom det praktiske, vil de være mer mottakelige og knytte sterkere bånd til teorien. Dess viktigere det praktiske er for dem, jo mer motiverte vil de være for en teoretisk forklaring. Elevene fikk også mye erfaring i løpet av uken med å gjenkjenne, navngi, tegne, bygge, sammenligne og sortere 2- og 3-dimensjonale figurer. For at skapene og de andre produktene skulle bli minst mulig skakke og skjeve måtte de ta hensyn til figurenes egenskaper i forhold til hjørner, sider, kanter og flater, når de skulle sette dem sammen. Vi så mye god refleksjon etter hvert som det ene skakkjørte kjøkkenskapet etter det andre så dagens lys. Refleksjonen gav frukter og etter hvert ble skapene mer og mer strømlinjeformet, med korrekt størrelse på alle sidene. Kreativitet begynte også å spre seg, og skapene fikk etter hvert hyller og dører som kunne åpnes og lukkes. Kjøkkenbenkene fikk nedsunkne vasker med kraner. Lærer er med å styre Som et ledd i å få mer matematikk inn i prosjektet hadde vi som sagt laget til oppgaven med flisene. Vi hadde priset flisene med 7 kr for kvadratiske og 4 kr for trekantete, men først måtte elevene lage et geometriske mønster. Deretter måtte de beregne hvor mange fliser de trengte for å dekke hele gulvet. Til sist måtte de regne ut hva de skulle betale for alle flisene. Her fikk vi mange spennende refleksjoner og måter å finne ut av problemet på. Noen elever begynte å telle antall ruter, mens andre fant ut at det var ti i ene rekke og så talte de ti om gangen 14 ganger til de kom til 140. Andre gikk motsatt vei og fant ut at det ble 14 i den lengste rekken, så talte de ti ruter opp og ganget Det ble i grunnen vanskeligere å finne ut hva de skulle betale for flisene. De visste nå at de hadde behov for 140 kvadratiske fliser og at disse kostet 7 kr stykke, men hva gjorde en for å finne svaret. Vi hadde i oppstarten av prosjektet vist dem hvordan en kan bruke lommeregner til de fire regneartene, og hver gruppe hadde fått utdelt hver sin lommeregner. Men den var ikke til hjelp med det første, for hva skulle de gjøre med den? Som en liten ledetråd gjorde vi tallene enklere: Hva om du bare skulle kjøpe fem fliser, hvordan ville du regnet da? Jo, da ville de ha plusset 7 fem ganger. Kunne du ha regnet det på en annen måte også? spurte vi videre. Tina vet det; du kunne ganget, sier hun. Det var den utløsende faktoren, nå kaster elevene seg over lommeregnerne og etter litt leting på knappene finner alle gruppene ut prisen for sine fliser. Da er det bare å levere bestillingslisten til læreren og be han gå og lage flisene. En elev skriver senere i loggen sin at det viktigste han hadde lært den dagen var å gange med store tall. Denne oppgaven var som tidligere nevnt konstruert fra vår side, for vi ønsket å legge til rette for enda mer matematisk aktivitet. Dette kunne slå begge veier, for ville elevene godta oppgaven som en del av leken eller ville de oppleve det som et brudd i deres aktivitet? Dewey understreker betydningen at formidlingen må leveres på elevenes premisser, at læringen skjer i tilknytning til det som har betydning for dem. Nå viste det seg heldigvis at dette ble en av de mest vellykka aktivitetene hele uken. Jeg tror elevene opplevde vår inngripen som ubetinget positivt, og at de følte at vi ble med på leken. Vi ble fliseforhandlere og lagde fliser på bestilling. Pengene var veldig motiverende for elevene, og i etterkant ser vi at hadde tangenten 4/2006 5
5 vi beregnet litt mer tid til prosjektet kunne vi med fordel har brukt samme konsept på alle materialene. Vi fikk inn veldig mye regning på disse aktivitetene, og jeg er ikke i tvil om at beregningene elevene gjorde i disse oppgavene blant annet førte til økt forståelse for multiplikasjon. Elevene hadde frem til nå arbeidet med multiplikasjon som gjentatt addisjon, og her fikk de se multiplikasjon som rekke. De fikk også erfaring med å regne med større tall enn de hadde gjort frem til nå i matematikkboken. Refleksjon det handler om å se matematikken Et viktig poeng i læringssammenheng er den tiden vi brukte til felles refleksjon underveis i prosjektet. På slutten av hver økt snakket vi om hva elevene hadde lært i dag, hvilke oppdagelser de hadde gjort og hvilken matematikk de hadde hatt brukt for i løpet av dagen. Da vi gjorde dette etter første dag fikk vi nesten ingen hender i været når vi spurte om de hadde brukt noe matematikk. Ingenting, svarte flere. Hva gjorde dere nede på skolekjøkkenet da, spurte vi. Nei, vi målte bare der, var svaret! Den første refleksjonsøkten endte med at vi 6 omtrent måtte nevne opp alle situasjonene vi hadde sett de bruke matematikk. I løpet av uken skjedde det en markant forandring i forhold til deres bevissthetsforhold til hva matematikk er og når de hadde bruk for det. Da vi hadde siste evalueringsøkt var det 21 hender i været når vi spurte etter matematikken de hadde brukt den dagen og ellers i prosjektet. Men selv om de nå så det klarere at det var matematikk de brukte, så betyr ikke det at de ikke brukte matematikk før den tid. Det var bare det at de ikke reflekterte over hva de gjorde og hva de lærte. Selv om den forenklede Dewey tolkningen: «learning by doing» antyder noe annet, var Dewey opptatt av at barn må lære abstraksjon. Utgangspunktet hans var at elevene starter med en aktivitetssituasjon som er basert på forholdet mellom deres erfaringer, interesser og samspillet med miljøet rundt. Så skulle elevene arbeide seg fremover mot et stadig høyere abstraksjonsnivå gjennom en kunnskapsprosess som skjer mellom elev og lærestoff. Jeg mener at denne refleksjonen som en må gjøre med barna, for at de skal kunne oversette fra praktiske aktiviteter til et høyere abstraksjonsnivå, er et av de elementene som gjør at T&D også kan føre til 4/2006 tangenten
6 matematisk læring. Custer [2] sier at teknologisk kunnskap må forankres i praksis og at det er fundamentet for en mer analytisk og abstrakt forståelse. En forutsetning da vil selvsagt være at læreren klarer å bygge bro mellom den praktiske erfaringen som elevene får gjennom T&D til den påfølgende matematikkundervisningen. Elevene har nå fått noen verdifulle erfaringer eller knagger som kan danne grunnlag for videre forståelse i tallenes og geometriens verden frem mot en mer abstrakt forståelse, men det skjer sjelden automatisk uten et oversettende ledd; nemlig læreren! Avslutning Gjennom T&D har vi en unik mulighet til å ta utgangspunkt i elevenes interesser og erfaringer gjennom elevaktivitet. Hvis vi igjen går til Dewey så påpeker han verdien av å utvikle elevenes praktiske evne til å beherske ulike forhold og gi dem innsikt og forståelse for hvordan ting henger sammen. Det er et viktig poeng at vi klarer å gjøre elevene bedre rustet og stadig dyktigere i å mestre dagliglivets utfordringer. Her finner vi et av hovedargumentene for T&D, nemlig å anvende kunnskap på en systematisk måte i praktiske sammenhenger, og utvikle fremgangsmåter for å nå våre mål som enkeltindivid og samfunn. Jeg vil våge å påstå at i T&D-prosjekt har læreren en svært viktig rolle. Ikke bare som veileder, men også den som kan generere matematiske utfordringer. Vi skal ikke være redde for å gripe inn i aktiviteten, men heller prøve å bli en del av den med våre innspill. På denne måten kan T&D bli et enda større supplement i forhold til den vanlige matematikkundervisningen. Vi kan nemlig ta inn oppgaver med temaer som vi ønsker de skal få trening eller erfaring med. Dermed kan vi styre det matematiske læringsutbytte i langt større grad enn ved at T&D prosjekter får drive dit elevene fører dem. T&D kan aldri erstatte matematikken eller realfagene, men heller være et supplement som kan vise hvordan matematikk brukes i praksis. Elevene trenger å se forbindelsen mellom teori og praktisk anvendelse. Målet med all teori er at den kan anvendes praktisk. Elevene trenger derfor en arena der den teoretiske kunnskapen nettopp kan brukes i praksis. Til slutt vil jeg understreke betydningen av at en hele tiden må ha kompetansemålene blinkende i fremgrunnen under aktivitetene Hva vil jeg elevene skal lære gjennom dette prosjektet? Hva kan jeg gjøre for at jeg sikrer meg at de lærer disse målene? I tillegg må en til stadighet ha på seg matematikkbrillene som klarer å fange opp de uforutsette matematiske momentene som dukker opp underveis. Det er utrolig spennende å følge elever på en slik reise mot stadig høyere kompetansenivå, men det krever at læreren innehar stor nok faglig kompetanse i matematikk. Tatt i betraktning at under 60 % av norske grunnskolelærerne har den nødvendige matematikkutdanningen, er det viktig å stille seg sunt tvilende til læringseffekten i matematikk gjennom T&D prosjekter i stor utstrekning. Det kan fort bli mye aktivitet for aktiviteten sin skyld. Jeg vil derfor konkludere med at det går an å lære mye matematikk gjennom Teknologi og design-prosjekter, men at det er svært læreravhengig! Litteraturliste [1] Imsen, Gunn: Lærerens verden Innføring i generell didaktikk, Tano-Aschehoug, 1997 [2] Hansen, Pål J. Kirkeby: Teknologi i skolen og i NSM, HiO-notat nr. 13, 2000 (fortsatt fra side 1) oppgave for noen lærere, men en spennende og utfordrende en. I dette heftet har vi prøvd å samle en rekke eksempler der matematikken står sentralt i teknologi og designprosjekter. Vi prøver å sette søkelyset på de grepene lærerne har gjort for at matematikken skal bli synlig og viktig for elevene og håper at mange lykkes med denne nye utfordringen. tangenten 4/2006 7
Inspirasjon og motivasjon for matematikk
 Inspirasjon og motivasjon for matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? Bjørnar Alseth Høgskolen i Oslo Styremedlem i Lamis Lærebokforfatter; MULTI Mona Røsseland
Inspirasjon og motivasjon for matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? Bjørnar Alseth Høgskolen i Oslo Styremedlem i Lamis Lærebokforfatter; MULTI Mona Røsseland
tangenten 4/2006 1 (fortsettes side 7)
 Teknologi og design, en mulighet eller en felle for matematikkfaget? Med Kunnskapsløftet har også emnet teknologi og design entret skolearenaen. Det ble ikke et eget skolefag som mange trodde men det ble
Teknologi og design, en mulighet eller en felle for matematikkfaget? Med Kunnskapsløftet har også emnet teknologi og design entret skolearenaen. Det ble ikke et eget skolefag som mange trodde men det ble
OVERFLATE FRA A TIL Å
 OVERFLATE FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overflate... 2 2 Grunnleggende om overflate.. 2 3 Overflate til:.. 3 3 3a Kube. 3 3b Rett Prisme... 5 3c
OVERFLATE FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overflate... 2 2 Grunnleggende om overflate.. 2 3 Overflate til:.. 3 3 3a Kube. 3 3b Rett Prisme... 5 3c
Nyheter fra Fang. Den Hellige Ånd falt. To uker før pinse hadde vi en pinseopplevelse med staben vår.
 Nyheter fra Fang Den Hellige Ånd falt To uker før pinse hadde vi en pinseopplevelse med staben vår. Denne uken hadde vi først et amerikansk ektepar som underviste. Da de skulle be for staben vår spurte
Nyheter fra Fang Den Hellige Ånd falt To uker før pinse hadde vi en pinseopplevelse med staben vår. Denne uken hadde vi først et amerikansk ektepar som underviste. Da de skulle be for staben vår spurte
ADDISJON FRA A TIL Å
 ADDISJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til addisjon 2 2 Grunnleggende om addisjon 3 3 Ulike tenkemåter 4 4 Hjelpemidler i addisjoner 9 4.1 Bruk av tegninger
ADDISJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til addisjon 2 2 Grunnleggende om addisjon 3 3 Ulike tenkemåter 4 4 Hjelpemidler i addisjoner 9 4.1 Bruk av tegninger
Lengdemål, areal og volum
 Lengdemål, areal og volum Lengdemål Elever bør tidlig få erfaring med å vurdere ulike avstander og lengdemål. De kommer ofte opp i situasjoner i hverdagen hvor det er en stor ulempe å ikke ha begrep om
Lengdemål, areal og volum Lengdemål Elever bør tidlig få erfaring med å vurdere ulike avstander og lengdemål. De kommer ofte opp i situasjoner i hverdagen hvor det er en stor ulempe å ikke ha begrep om
Regning i alle fag. Hva er å kunne regne? Prinsipper for god regneopplæring. 1.Sett klare mål, og form undervisningen deretter
 Regning i alle fag Hva er å kunne regne? Å kunne regne er å bruke matematikk på en rekke livsområder. Å kunne regne innebærer å resonnere og bruke matematiske begreper, fremgangsmåter, fakta og verktøy
Regning i alle fag Hva er å kunne regne? Å kunne regne er å bruke matematikk på en rekke livsområder. Å kunne regne innebærer å resonnere og bruke matematiske begreper, fremgangsmåter, fakta og verktøy
24.11.2010. Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre?
 Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Inspirasjon og motivasjon for matematikk
 oversikt Inspirasjon og motivasjon for matematikk Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Ny læreplan, nye utfordringer for undervisningen i matematikk
oversikt Inspirasjon og motivasjon for matematikk Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Ny læreplan, nye utfordringer for undervisningen i matematikk
L06. Den gode matematikkundervisning. - hva er det? Hvordan bli en motiverende lærer? Intensjonene med den nye læreplanen
 Den gode matematikkundervisning Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? - hva er det? Mona Røsseland Nasjonalt senter for matematikk i opplæringen 1-May-06 1-May-06
Den gode matematikkundervisning Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? - hva er det? Mona Røsseland Nasjonalt senter for matematikk i opplæringen 1-May-06 1-May-06
Elevaktiv matematikk. hvorfor og hvordan? Retningslinjer for undervisningen. Intensjoner med ny læreplan. Hvilke utfordringer gir dette lærerne?
 Elevaktiv matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? hvorfor og hvordan? Mona Røsseland Leder i Lamis Nasjonalt senter for matematikk i opplæringen Lærebokforfatter
Elevaktiv matematikk Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? hvorfor og hvordan? Mona Røsseland Leder i Lamis Nasjonalt senter for matematikk i opplæringen Lærebokforfatter
Anne-Cath. Vestly. Åtte små, to store og en lastebil
 Anne-Cath. Vestly Åtte små, to store og en lastebil Åtte små, to store og en lastebil Det var en gang en stor familie. Det var mor og far og åtte unger, og de åtte ungene het Maren, Martin, Marte, Mads,
Anne-Cath. Vestly Åtte små, to store og en lastebil Åtte små, to store og en lastebil Det var en gang en stor familie. Det var mor og far og åtte unger, og de åtte ungene het Maren, Martin, Marte, Mads,
Læreplanene for Kunnskapsløftet
 Læreplanene for Kunnskapsløftet Hvordan få samsvar mellom intensjon og praksis? Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i Lamis Lærebokforfatter; MULTI 21-Mar-06 Intensjoner
Læreplanene for Kunnskapsløftet Hvordan få samsvar mellom intensjon og praksis? Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i Lamis Lærebokforfatter; MULTI 21-Mar-06 Intensjoner
Å styrke leseforståelsen til flerspråklige elever på 3. trinn. Delt av Eli-Margrethe Uglem, student Lesing 2. Lesesenteret Universitetet i Stavanger
 Å styrke leseforståelsen til flerspråklige elever på 3. trinn Delt av Eli-Margrethe Uglem, student Lesing 2 Lesesenteret Universitetet i Stavanger Bakgrunn og mål Med utgangspunkt i at alle elever har
Å styrke leseforståelsen til flerspråklige elever på 3. trinn Delt av Eli-Margrethe Uglem, student Lesing 2 Lesesenteret Universitetet i Stavanger Bakgrunn og mål Med utgangspunkt i at alle elever har
Velkommen til presentasjon av Multi!
 Velkommen til presentasjon av Multi! Bjørnar Alseth Høgskolen i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg, Høgskolen i Oslo Dagsoversikt Ny læreplan,
Velkommen til presentasjon av Multi! Bjørnar Alseth Høgskolen i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg, Høgskolen i Oslo Dagsoversikt Ny læreplan,
Posisjonsystemet FRA A TIL Å
 Posisjonsystemet FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til posisjonsystemet P - 2 2 Grunnleggende om posisjonsystemet P - 2 3 Titallsystemet P - 3 4 Posisjonsystemet
Posisjonsystemet FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til posisjonsystemet P - 2 2 Grunnleggende om posisjonsystemet P - 2 3 Titallsystemet P - 3 4 Posisjonsystemet
"Hva er god. matematikkundervisning. Mål at alle matematikklærerne skal: Resultat i matematikk på kunnskapsnivåer, 8.trinn
 "Hva er god matematikkundervisning? Mål at alle matematikklærerne skal: en felles forståelse for hva god matematikkundervisning er. Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter,
"Hva er god matematikkundervisning? Mål at alle matematikklærerne skal: en felles forståelse for hva god matematikkundervisning er. Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter,
Arbeid med geometriske figurer på 1. trinn
 Bjørg Skråmestø Arbeid med geometriske figurer på 1. trinn På 1. trinn har vi jobbet med geometriske figurer på forskjellige måter. Vi har lagt vekt på at barna skulle få bli kjent med figurene gjennom
Bjørg Skråmestø Arbeid med geometriske figurer på 1. trinn På 1. trinn har vi jobbet med geometriske figurer på forskjellige måter. Vi har lagt vekt på at barna skulle få bli kjent med figurene gjennom
10.03.2011. Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre?
 Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Hvorfor får elevene problemer med tekstoppgaver? Hva kan vi gjøre for at elevene skal mestre tekstoppgaver bedre? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI
Den gode matematikkundervisning
 Den gode matematikkundervisning Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? - hva er det? Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i LAMIS Lærebokforfatter;
Den gode matematikkundervisning Hvordan får vi aktive, engasjerte og motiverte elever og lærere i matematikk? - hva er det? Mona Røsseland Nasjonalt senter for matematikk i opplæringen Leder i LAMIS Lærebokforfatter;
Overslag FRA A TIL Å
 Overslag FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overslag 2 2 Grunnleggende om overslag 2 3 Å gjøre overslag 6 4 Forsiktighetsregler 7 4.1 Når overslaget ikke
Overslag FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til overslag 2 2 Grunnleggende om overslag 2 3 Å gjøre overslag 6 4 Forsiktighetsregler 7 4.1 Når overslaget ikke
DA MIRJAM MÅTTE FLYTTE TIL KAIRO
 DA MIRJAM MÅTTE FLYTTE TIL KAIRO Bilde 1 Hei! Jeg heter Mirjam. Jeg er seks år og bor i Kairo. Bilde 2 Kairo er en by i Egypt. Hvis du skal til Egypt, må du reise med fly i syv timer. Bilde 3 Det er et
DA MIRJAM MÅTTE FLYTTE TIL KAIRO Bilde 1 Hei! Jeg heter Mirjam. Jeg er seks år og bor i Kairo. Bilde 2 Kairo er en by i Egypt. Hvis du skal til Egypt, må du reise med fly i syv timer. Bilde 3 Det er et
Leker gutter mest med gutter og jenter mest med jenter? Et nysgjerrigpersprosjekt av 2. klasse, Hedemarken Friskole 2016
 Leker gutter mest med gutter og jenter mest med jenter? Et nysgjerrigpersprosjekt av 2. klasse, Hedemarken Friskole 2016 1 Forord 2. klasse ved Hedemarken friskole har hatt mange spennende og morsomme
Leker gutter mest med gutter og jenter mest med jenter? Et nysgjerrigpersprosjekt av 2. klasse, Hedemarken Friskole 2016 1 Forord 2. klasse ved Hedemarken friskole har hatt mange spennende og morsomme
23.10.2011. Mona Røsseland www.fiboline.no www.gyldendal.no/multi
 Dersom elevene skal utvikle en bred matematisk kompetanse, må de gjennom undervisningen få muligheter til å å oppdage, resonnere og kommunisere matematikk gjennom ulike typer oppgaver, aktiviteter og diskusjoner.
Dersom elevene skal utvikle en bred matematisk kompetanse, må de gjennom undervisningen få muligheter til å å oppdage, resonnere og kommunisere matematikk gjennom ulike typer oppgaver, aktiviteter og diskusjoner.
PROGRESJONS DOKUMENT. Barnehagens fagområder. Barns læringsprosesser
 PROGRESJONS DOKUMENT Barnehagene i SiT jobber ut fra en felles pedagogisk plattform. Den pedagogiske plattformen er beskrevet i barnehagenes årsplaner. Dette dokumentet viser mer detaljer hvordan vi jobber
PROGRESJONS DOKUMENT Barnehagene i SiT jobber ut fra en felles pedagogisk plattform. Den pedagogiske plattformen er beskrevet i barnehagenes årsplaner. Dette dokumentet viser mer detaljer hvordan vi jobber
Årets nysgjerrigper 2009
 Årets nysgjerrigper 2009 Prosjekttittel: Hvorfor kommer det støv? Klasse: 6. trinn Skole: Gjerpen Barneskole (Skien, Telemark) Antall deltagere (elever): 2 Dato: 29.04.2009 Side 1 Vi er to jenter fra 6a
Årets nysgjerrigper 2009 Prosjekttittel: Hvorfor kommer det støv? Klasse: 6. trinn Skole: Gjerpen Barneskole (Skien, Telemark) Antall deltagere (elever): 2 Dato: 29.04.2009 Side 1 Vi er to jenter fra 6a
"Hva er god matematikkundervisning?
 "Hva er god matematikkundervisning? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI 14-Sep-10 Innhold Hvordan skal vi få elevene våre til å bli varm i hodet i matematikken?
"Hva er god matematikkundervisning? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI 14-Sep-10 Innhold Hvordan skal vi få elevene våre til å bli varm i hodet i matematikken?
Elevenes egenvurdring,
 Elevenes egenvurdring, knyttet til arbeidet med TFO-1 (november 2014) Hva tenker du om din framføring av oppgavearbeidet? Hva var bra? Hva kan bli bedre? Jeg syns jeg hadde med mye bra detaljer. Fremføringen
Elevenes egenvurdring, knyttet til arbeidet med TFO-1 (november 2014) Hva tenker du om din framføring av oppgavearbeidet? Hva var bra? Hva kan bli bedre? Jeg syns jeg hadde med mye bra detaljer. Fremføringen
Kvikkbilde 8 6. Mål. Gjennomføring. Planleggingsdokument Kvikkbilde 8 6
 Kvikkbilde 8 6 Mål Generelt: Sammenligne og diskutere ulike måter å se et antall på. Utfordre elevene på å resonnere omkring tallenes struktur og egenskaper, samt egenskaper ved regneoperasjoner. Spesielt:
Kvikkbilde 8 6 Mål Generelt: Sammenligne og diskutere ulike måter å se et antall på. Utfordre elevene på å resonnere omkring tallenes struktur og egenskaper, samt egenskaper ved regneoperasjoner. Spesielt:
09.02.2013. Gjett tre kort. Mastermind. www.fiboline.no. Resultat i matematikk på kunnskapsnivåer, 8.trinn. Mona Røsseland Lærebokforfatter, MULTI
 Foreldrene betyr all verden! Mona Røsseland Lærebokforfatter, MULTI www.fiboline.no Utstyr En kortstokk Gjett tre kort Regler Et spill for 2 3 spillere eller for en stor gruppe En person trekker tre kort
Foreldrene betyr all verden! Mona Røsseland Lærebokforfatter, MULTI www.fiboline.no Utstyr En kortstokk Gjett tre kort Regler Et spill for 2 3 spillere eller for en stor gruppe En person trekker tre kort
Periodeevaluering 2014
 Periodeevaluering 2014 Prosjekt denne perioden: Bokstaver. Periode: uke3-11. Hvordan startet det, bakgrunn for prosjektet. Vi brukte de første ukene etter jul til samtaler og observasjoner, for å finne
Periodeevaluering 2014 Prosjekt denne perioden: Bokstaver. Periode: uke3-11. Hvordan startet det, bakgrunn for prosjektet. Vi brukte de første ukene etter jul til samtaler og observasjoner, for å finne
09.05.2011 12:20 QuestBack eksport - Evaluering av PSY-2577/PSY-3008, Multivariate metoder
 Evaluering av PSY-2577/PSY-3008, Multivariate metoder Publisert fra 28.04.2011 til 05.05.2011 25 respondenter (25 unike) 1. Alder 1 19-29 79,2 % 19 2 30-39 12,5 % 3 3 30-49 8,3 % 2 4 49-59 0,0 % 0 Total
Evaluering av PSY-2577/PSY-3008, Multivariate metoder Publisert fra 28.04.2011 til 05.05.2011 25 respondenter (25 unike) 1. Alder 1 19-29 79,2 % 19 2 30-39 12,5 % 3 3 30-49 8,3 % 2 4 49-59 0,0 % 0 Total
Desimaltall FRA A TIL Å
 Desimaltall FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side Innledning til desimaltall D - 2 2 Grunnleggende om desimaltall D - 2 2. Tideler, hundredeler og tusendeler D - 6 3 Å regne
Desimaltall FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side Innledning til desimaltall D - 2 2 Grunnleggende om desimaltall D - 2 2. Tideler, hundredeler og tusendeler D - 6 3 Å regne
Skolesekken: Elevers og læreres erfaringer. Catharina Christophersen Førsteamanuensis, Høgskolen i Bergen
 Skolesekken: Elevers og læreres erfaringer Catharina Christophersen Førsteamanuensis, Høgskolen i Bergen Elever og læreres ytringer og synspunkter Hvordan kan de gode kunstmøtene iscenesette elever og
Skolesekken: Elevers og læreres erfaringer Catharina Christophersen Førsteamanuensis, Høgskolen i Bergen Elever og læreres ytringer og synspunkter Hvordan kan de gode kunstmøtene iscenesette elever og
DEN GODE HYRDE / DEN GODE GJETEREN
 DEN GODE HYRDE / DEN GODE GJETEREN TIL DENNE LEKSJONEN Fokus: Gjeteren og sauene hans Tekster: Matteus 18:12-14; Lukas 15:1-7 (Salme 23; Joh.10) Lignelse Kjernepresentasjon Materiellet: Plassering: Lignelseshylla
DEN GODE HYRDE / DEN GODE GJETEREN TIL DENNE LEKSJONEN Fokus: Gjeteren og sauene hans Tekster: Matteus 18:12-14; Lukas 15:1-7 (Salme 23; Joh.10) Lignelse Kjernepresentasjon Materiellet: Plassering: Lignelseshylla
Et lite svev av hjernens lek
 Et lite svev av hjernens lek Jeg fikk beskjed om at jeg var lavmål av deg. At jeg bare gjorde feil, ikke tenkte på ditt beste eller hva du ville sette pris på. Etter at du gikk din vei og ikke ville se
Et lite svev av hjernens lek Jeg fikk beskjed om at jeg var lavmål av deg. At jeg bare gjorde feil, ikke tenkte på ditt beste eller hva du ville sette pris på. Etter at du gikk din vei og ikke ville se
KURS FOR SPRÅKHJELPERE. Innhold og gjennomføring
 KURS FOR SPRÅKHJELPERE Innhold og gjennomføring Organisering Spor 1-deltakernes timeplan Språkhjelperne Organisering Språkhjelperne i aksjon Hvem er språkhjelperne? Viderekomne spor 2-deltakere På nivå
KURS FOR SPRÅKHJELPERE Innhold og gjennomføring Organisering Spor 1-deltakernes timeplan Språkhjelperne Organisering Språkhjelperne i aksjon Hvem er språkhjelperne? Viderekomne spor 2-deltakere På nivå
MANN Jeg snakker om den gangen ved elva. MANN Den første gangen. På brua. Det begynte på brua.
 NATT En enakter av Harold Pinter INT. KJØKKEN. NATT Jeg snakker om den gangen ved elva. Hva for en gang? Den første gangen. På brua. Det begynte på brua. Jeg husker ikke. På brua. Vi stansa og så på vannet.
NATT En enakter av Harold Pinter INT. KJØKKEN. NATT Jeg snakker om den gangen ved elva. Hva for en gang? Den første gangen. På brua. Det begynte på brua. Jeg husker ikke. På brua. Vi stansa og så på vannet.
ConTre. Teknologi og Design. En introduksjon. Utdrag fra læreplaner. Tekst og foto: JJJ Consult As
 ConTre Teknologi og Design En introduksjon Utdrag fra læreplaner Tekst og foto: JJJ Consult As Teknologi i skolen Teknologi på timeplanen Teknologi utgjør en stadig større del av folks hverdag. Derfor
ConTre Teknologi og Design En introduksjon Utdrag fra læreplaner Tekst og foto: JJJ Consult As Teknologi i skolen Teknologi på timeplanen Teknologi utgjør en stadig større del av folks hverdag. Derfor
Nye læreplaner, nye utfordringer i matematikk!
 Oversikt Nye læreplaner, nye utfordringer i matematikk! Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Ny læreplan, nye utfordringer for undervisningen
Oversikt Nye læreplaner, nye utfordringer i matematikk! Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Ny læreplan, nye utfordringer for undervisningen
Kvinne 30, Berit eksempler på globale skårer
 Kvinne 30, Berit eksempler på globale skårer Demonstrasjon av tre stiler i rådgivning - Målatferd er ikke definert. 1. Sykepleieren: Ja velkommen hit, fint å se at du kom. Berit: Takk. 2. Sykepleieren:
Kvinne 30, Berit eksempler på globale skårer Demonstrasjon av tre stiler i rådgivning - Målatferd er ikke definert. 1. Sykepleieren: Ja velkommen hit, fint å se at du kom. Berit: Takk. 2. Sykepleieren:
Vurdering og progresjon i kunst og håndverk
 Vurdering og progresjon i kunst og håndverk Kontinuerlige veilednings- og vurderingssamtaler med elevene er kjernen i faget. Her finner du eksempel på vurderingssamtaler og oversikt over progresjonen i
Vurdering og progresjon i kunst og håndverk Kontinuerlige veilednings- og vurderingssamtaler med elevene er kjernen i faget. Her finner du eksempel på vurderingssamtaler og oversikt over progresjonen i
Læreplanene for Kunnskapsløftet
 Læreplanene for Kunnskapsløftet Hvordan få samsvar mellom intensjon og praksis? Mona Røsseland Leder i Lamis Nasjonalt senter for matematikk i opplæringen Lærebokforfatter; MULTI 12-Mar-06 Intensjoner
Læreplanene for Kunnskapsløftet Hvordan få samsvar mellom intensjon og praksis? Mona Røsseland Leder i Lamis Nasjonalt senter for matematikk i opplæringen Lærebokforfatter; MULTI 12-Mar-06 Intensjoner
2.3 Delelighetsregler
 2.3 Delelighetsregler Begrepene multiplikasjon og divisjon og regneferdigheter med disse operasjonene utgjør sentralt lærestoff på barnetrinnet. Det er mange tabellfakta å huske og operasjonene skal kunne
2.3 Delelighetsregler Begrepene multiplikasjon og divisjon og regneferdigheter med disse operasjonene utgjør sentralt lærestoff på barnetrinnet. Det er mange tabellfakta å huske og operasjonene skal kunne
ANITA forteller. om søndagsskolen og de sinte mennene
 ANITA forteller om søndagsskolen og de sinte mennene Tekst og foto: Marianne Haugerud (Fortellingen bygger på virkelige hendelser, men er lagt i Anitas munn av Stefanusalliansen.) 1 Hei! Jeg heter Anita,
ANITA forteller om søndagsskolen og de sinte mennene Tekst og foto: Marianne Haugerud (Fortellingen bygger på virkelige hendelser, men er lagt i Anitas munn av Stefanusalliansen.) 1 Hei! Jeg heter Anita,
Gjennom lydmuren. Jeg har alltid folt meg litt i min egen lille boble. Om a leve med nedsatt horsel. Forsiden
 Om a leve med nedsatt horsel Forsiden Mangler forsidebildet Må ikke ha det. Snakker vi om på tlf. Jeg har alltid folt meg litt i min egen lille boble Innledning Moren Vi blir også kjent med Joakims mor
Om a leve med nedsatt horsel Forsiden Mangler forsidebildet Må ikke ha det. Snakker vi om på tlf. Jeg har alltid folt meg litt i min egen lille boble Innledning Moren Vi blir også kjent med Joakims mor
Stegark i matematikk PRAKTISK BRUK AV STEGARKENE
 Stegark i matematikk PRAKTISK BRUK AV STEGARKENE OM STEGMETODEN Stegmetodens styrke Stegarkene angir en stige hvor eleven selv kan ta et medansvar for hva han/hun bør arbeide med. De fleste lærere har
Stegark i matematikk PRAKTISK BRUK AV STEGARKENE OM STEGMETODEN Stegmetodens styrke Stegarkene angir en stige hvor eleven selv kan ta et medansvar for hva han/hun bør arbeide med. De fleste lærere har
Rapport: Undersøkelse utseendepress
 Rapport: Undersøkelse utseendepress Temaet vårt er utseendepress på Horten Videregående Skole. Hvorfor?: Det angår oss siden det er vår skole, og vi omgir oss med dette hver dag. Det er spennende å se
Rapport: Undersøkelse utseendepress Temaet vårt er utseendepress på Horten Videregående Skole. Hvorfor?: Det angår oss siden det er vår skole, og vi omgir oss med dette hver dag. Det er spennende å se
Lisa besøker pappa i fengsel
 Lisa besøker pappa i fengsel Historien om Lisa er skrevet av Foreningen for Fangers Pårørende og illustrert av Brit Mari Glomnes. Det er fint om barnet leser historien sammen med en voksen. Hei, jeg heter
Lisa besøker pappa i fengsel Historien om Lisa er skrevet av Foreningen for Fangers Pårørende og illustrert av Brit Mari Glomnes. Det er fint om barnet leser historien sammen med en voksen. Hei, jeg heter
Fire kort. Mål. Gjennomføring. Film. Problemløsing Fire kort
 Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Begynneropplæringen i matematikk. 1.-3.trinn 07.03.2012. Dagsoversikt. Tallfølelse
 07.03.2012 Begynneropplæringen i matematikk 1.-3.trinn Tillegskomponenter: Kartleggingsprøver: Halvårsprøve og årsprøve Grublishefte 1-4 og 5-7 Nettsted: www.gyldendal.no/multi Elevoppgaver Lærersider
07.03.2012 Begynneropplæringen i matematikk 1.-3.trinn Tillegskomponenter: Kartleggingsprøver: Halvårsprøve og årsprøve Grublishefte 1-4 og 5-7 Nettsted: www.gyldendal.no/multi Elevoppgaver Lærersider
Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra
 Anne-Mari Jensen Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra Innledning I ungdomsskolen kommer funksjoner inn som et av hovedområdene i læreplanen i matematikk. Arbeidet
Anne-Mari Jensen Utforsking av funksjonsuttrykk og de tilhørende grafene ved hjelp av GeoGebra Innledning I ungdomsskolen kommer funksjoner inn som et av hovedområdene i læreplanen i matematikk. Arbeidet
Fire kort. Mål. Gjennomføring. Film. Problemløsing Fire kort
 Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Inspirasjon og motivasjon for matematikk
 Inspirasjon og motivasjon for matematikk Mona Røsseland Nasjonalt senter for matematikk i Opplæringen 15-Apr-07 En visuell representasjon av de ulike matematiske kompetansene 15-Apr-07 2 Modelleringskompetanse
Inspirasjon og motivasjon for matematikk Mona Røsseland Nasjonalt senter for matematikk i Opplæringen 15-Apr-07 En visuell representasjon av de ulike matematiske kompetansene 15-Apr-07 2 Modelleringskompetanse
Gje meg eit tresifra. Hvordan skal jeg regne, lærer? 1. Arbeide både praktisk og teoretisk. Retningslinjer for undervisningen
 Hvordan skal jeg regne, lærer? Fokus på tall og utvikling av god tall forståelse Mona Røsseland Nasjonalt senter for matematikk i opplæringen Gje meg eit tresifra tal 17-Apr-06 17-Apr-06 2 Intensjoner
Hvordan skal jeg regne, lærer? Fokus på tall og utvikling av god tall forståelse Mona Røsseland Nasjonalt senter for matematikk i opplæringen Gje meg eit tresifra tal 17-Apr-06 17-Apr-06 2 Intensjoner
Utdrag fra Beate Børresen og Bo Malmhester: Filosofere i barnehagen, manus mars 2008.
 Utdrag fra Beate Børresen og Bo Malmhester: Filosofere i barnehagen, manus mars 2008. Hvorfor skal barn filosofere? Filosofiske samtaler er måte å lære på som tar utgangspunkt i barnets egne tanker, erfaring
Utdrag fra Beate Børresen og Bo Malmhester: Filosofere i barnehagen, manus mars 2008. Hvorfor skal barn filosofere? Filosofiske samtaler er måte å lære på som tar utgangspunkt i barnets egne tanker, erfaring
Digitale verktøy eller pedagogikk kan vi velge?
 Digitale verktøy eller pedagogikk kan vi velge? Førstelektor Tor Arne Wølner, Skolelederkonferansen Lillestrøm, fredag 11. november, 13:40 14:5 1 Læreren er opptatt av: Læreren at elevene skal være trygge
Digitale verktøy eller pedagogikk kan vi velge? Førstelektor Tor Arne Wølner, Skolelederkonferansen Lillestrøm, fredag 11. november, 13:40 14:5 1 Læreren er opptatt av: Læreren at elevene skal være trygge
Kortryllekunst og matematikk.
 Kortryllekunst og matematikk. Innlevert av 7. trinn, Ulsmåg skole ved Ulsmåg skole (Bergen, Hordaland) Årets nysgjerrigper 201 Kjære leser Nå skal du få lese en rapport om et korttriks og mattematikk.
Kortryllekunst og matematikk. Innlevert av 7. trinn, Ulsmåg skole ved Ulsmåg skole (Bergen, Hordaland) Årets nysgjerrigper 201 Kjære leser Nå skal du få lese en rapport om et korttriks og mattematikk.
Mann 21, Stian ukodet
 Mann 21, Stian ukodet Målatferd: Følge opp NAV-tiltak 1. Saksbehandleren: Hvordan gikk det, kom du deg på konsert? 2. Saksbehandleren: Du snakket om det sist gang at du... Stian: Jeg kom meg dit. 3. Saksbehandleren:
Mann 21, Stian ukodet Målatferd: Følge opp NAV-tiltak 1. Saksbehandleren: Hvordan gikk det, kom du deg på konsert? 2. Saksbehandleren: Du snakket om det sist gang at du... Stian: Jeg kom meg dit. 3. Saksbehandleren:
Matematisk juleverksted
 GLASSMALERI Matematisk juleverksted Mona Røsseland 1 2 GLASSMALERI GLASSMALERI Slik går du frem: Fremgangsmåte for å lage ramme Lag en ramme av svart papp. Lag strimler av svart papp, som skal brukes til
GLASSMALERI Matematisk juleverksted Mona Røsseland 1 2 GLASSMALERI GLASSMALERI Slik går du frem: Fremgangsmåte for å lage ramme Lag en ramme av svart papp. Lag strimler av svart papp, som skal brukes til
Telle i kor steg på 120 frå 120
 Telle i kor steg på 120 frå 120 Erfaringer fra utprøving Erfaringene som er beskrevet i det følgende er gjort med lærere og elever som gjennomfører denne typen aktivitet for første gang. Det var fire erfarne
Telle i kor steg på 120 frå 120 Erfaringer fra utprøving Erfaringene som er beskrevet i det følgende er gjort med lærere og elever som gjennomfører denne typen aktivitet for første gang. Det var fire erfarne
Men hvorfor trenger vi et didaktisk verktøy og hvorfor skulle vi endre eller lage oppgaver?
 DiVeLOpp - DEL 1 Didaktisk Verktøy for å Lage Oppgaver Vi vil snakke om kunnskaper og læringsaktiviteter i fire ganger. Vi begynner med å identifisere kunnskaper. Deretter ser vi på læringsaktiviteter.
DiVeLOpp - DEL 1 Didaktisk Verktøy for å Lage Oppgaver Vi vil snakke om kunnskaper og læringsaktiviteter i fire ganger. Vi begynner med å identifisere kunnskaper. Deretter ser vi på læringsaktiviteter.
DIANA Vil du hjelpe meg med matvarene? DAVID Okay. DIANA Tomatene ser fine ut... Har du sett dem? David? DAVID Hva er Gryphon?
 INDECENT PROPOSAL FORHISTORIE: Diana og David har gått langt for å ordne opp i økonomien sin. De har fått et tilbud: Diana har sex med en annen mann, mot en stor sum penger. I etterkant av dette er paret
INDECENT PROPOSAL FORHISTORIE: Diana og David har gått langt for å ordne opp i økonomien sin. De har fått et tilbud: Diana har sex med en annen mann, mot en stor sum penger. I etterkant av dette er paret
SUBTRAKSJON FRA A TIL Å
 SUBTRAKSJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til subtraksjon S - 2 2 Grunnleggende om subtraksjon S - 2 3 Ulike fremgangsmåter S - 2 3.1 Tallene under hverandre
SUBTRAKSJON FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til subtraksjon S - 2 2 Grunnleggende om subtraksjon S - 2 3 Ulike fremgangsmåter S - 2 3.1 Tallene under hverandre
Magisk Matematikk. 75 minutter. Passer for: Varighet:
 Lærerveiledning Passer for: Varighet: Magisk Matematikk 9. - 10. trinn 75 minutter Magisk Matematikk er et skoleprogram som tar utgangspunkt i «magiske» talltriks i plenum som enkelt avsløres med algebra,
Lærerveiledning Passer for: Varighet: Magisk Matematikk 9. - 10. trinn 75 minutter Magisk Matematikk er et skoleprogram som tar utgangspunkt i «magiske» talltriks i plenum som enkelt avsløres med algebra,
"Hva er god matematikkundervisning?
 "Hva er god matematikkundervisning? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI Innhold Hvordan skal vi få elevene våre til å bli varm i hodet i matematikken?
"Hva er god matematikkundervisning? Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI Innhold Hvordan skal vi få elevene våre til å bli varm i hodet i matematikken?
Hvordan lykkes med tilpasset undervisning?
 Hvordan lykkes med tilpasset undervisning? Mona Røsseland Doktorgradsstipendiat Universitetet i Agder www.fiboline.no Oversikt 10-11.30: Makronivå: Hva er god matematikkundervisning og hvordan legger det
Hvordan lykkes med tilpasset undervisning? Mona Røsseland Doktorgradsstipendiat Universitetet i Agder www.fiboline.no Oversikt 10-11.30: Makronivå: Hva er god matematikkundervisning og hvordan legger det
Telle med 0,3 fra 0,3
 Telle med 0,3 fra 0,3 Mål Generelt: Søke etter mønster og sammenhenger. Gi grunner for at mønstrene oppstår. Lage nye mønstre ved å utnytte mønstre en allerede har funnet. Utfordre elevene på å resonnere
Telle med 0,3 fra 0,3 Mål Generelt: Søke etter mønster og sammenhenger. Gi grunner for at mønstrene oppstår. Lage nye mønstre ved å utnytte mønstre en allerede har funnet. Utfordre elevene på å resonnere
Cellegruppeopplegg. IMI Kirken høsten 2014
 Cellegruppeopplegg IMI Kirken høsten 2014 SEPTEMBER Godhet - neste steg Samtaleopplegg september 2014 Kjære deg, Denne høsten vil vi igjen sette et sterkt fokus på Guds godhet i IMI Kirken. Vi tror Gud
Cellegruppeopplegg IMI Kirken høsten 2014 SEPTEMBER Godhet - neste steg Samtaleopplegg september 2014 Kjære deg, Denne høsten vil vi igjen sette et sterkt fokus på Guds godhet i IMI Kirken. Vi tror Gud
Felles klasseundervisning og tilpasset opplæring kan det forenes?
 Felles klasseundervisning og tilpasset opplæring kan det forenes? 1.-4.trinn Innhold Hvordan skal vi klare å få alle elevene til å oppleve mestring og samtidig bli utfordret nok og få mulighet til å strekke
Felles klasseundervisning og tilpasset opplæring kan det forenes? 1.-4.trinn Innhold Hvordan skal vi klare å få alle elevene til å oppleve mestring og samtidig bli utfordret nok og få mulighet til å strekke
Skriftlig innlevering
 2011 Skriftlig innlevering Spørre undersøkelse VG2 sosiologi Vi valgte temaet kantinebruk og ville finne ut hvem som handlet oftest i kantinen av første-, andre- og tredje klasse. Dette var en problem
2011 Skriftlig innlevering Spørre undersøkelse VG2 sosiologi Vi valgte temaet kantinebruk og ville finne ut hvem som handlet oftest i kantinen av første-, andre- og tredje klasse. Dette var en problem
De kastet fra seg garna, og så var de i gang, og Peter fulgte Jesus i tre år, fram til den siste påska i Jerusalem.
 Preken 15. April 2012 i Fjellhamar kirke 2. s i påsketiden Kapellan Elisabeth Lund Hva er vi opptatt av? I dag får vi høre om Simon Peter. En av disiplene til Jesus. Alle som har lest litt i Bibelen kjenner
Preken 15. April 2012 i Fjellhamar kirke 2. s i påsketiden Kapellan Elisabeth Lund Hva er vi opptatt av? I dag får vi høre om Simon Peter. En av disiplene til Jesus. Alle som har lest litt i Bibelen kjenner
Inspirasjon og motivasjon for matematikk
 Mona Røsseland Matematikksenteret, NTNU Leder i Lamis Lærebokforfatter, MULTI Inspirasjon og motivasjon for matematikk God matematikkundervisning... hva er det? for hvem? 15-Oct-06 15-Oct-06 Matte er bare
Mona Røsseland Matematikksenteret, NTNU Leder i Lamis Lærebokforfatter, MULTI Inspirasjon og motivasjon for matematikk God matematikkundervisning... hva er det? for hvem? 15-Oct-06 15-Oct-06 Matte er bare
Karriereveiledning tilfredshet, utbytte og behov
 Karriereveiledning tilfredshet, utbytte og behov Fagsamling Tromsø november 2014 Avdelingsdirektør Ingjerd E. Gaarder Temaer som blir belyst: Hvem er brukerne? Hvorfor går de til karriereveiledning? Hvordan
Karriereveiledning tilfredshet, utbytte og behov Fagsamling Tromsø november 2014 Avdelingsdirektør Ingjerd E. Gaarder Temaer som blir belyst: Hvem er brukerne? Hvorfor går de til karriereveiledning? Hvordan
Tallinjen FRA A TIL Å
 Tallinjen FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til tallinjen T - 2 2 Grunnleggende om tallinjen T - 2 3 Hvordan vi kan bruke en tallinje T - 4 3.1 Tallinjen
Tallinjen FRA A TIL Å VEILEDER FOR FORELDRE MED BARN I 5. 7. KLASSE EMNER Side 1 Innledning til tallinjen T - 2 2 Grunnleggende om tallinjen T - 2 3 Hvordan vi kan bruke en tallinje T - 4 3.1 Tallinjen
Ny Giv. Grunnleggende regneferdighet. Brynhild Farbrot Foosnæs
 Ny Giv Grunnleggende regneferdighet Brynhild Farbrot Foosnæs Læring innebærer endring Hva har du endret siden sist? Læring innebærer at du blir utfordret og at du tør å ta utfordringen. Hvilke utfordringer
Ny Giv Grunnleggende regneferdighet Brynhild Farbrot Foosnæs Læring innebærer endring Hva har du endret siden sist? Læring innebærer at du blir utfordret og at du tør å ta utfordringen. Hvilke utfordringer
På vei til ungdomsskolen
 Oslo kommune Utdanningsetaten Til deg som8s.tkrainl n begynne på På vei til ungdomsskolen P.S. Kan tryg anbefales fot r voksne ogsa! På vei til ungdomsskolen Oslo kommune Utdanningsetaten 1 » Du har mye
Oslo kommune Utdanningsetaten Til deg som8s.tkrainl n begynne på På vei til ungdomsskolen P.S. Kan tryg anbefales fot r voksne ogsa! På vei til ungdomsskolen Oslo kommune Utdanningsetaten 1 » Du har mye
HELHETLIG PLAN I REGNING VED OLSVIK SKOLE.
 HELHETLIG PLAN I REGNING VED OLSVIK SKOLE. Prinsipper og strategier ved Olsvik skole. FORORD Olsvik skole har utarbeidet en helhetlig plan i regning som viser hvilke mål og arbeidsmåter som er forventet
HELHETLIG PLAN I REGNING VED OLSVIK SKOLE. Prinsipper og strategier ved Olsvik skole. FORORD Olsvik skole har utarbeidet en helhetlig plan i regning som viser hvilke mål og arbeidsmåter som er forventet
Grafisk løsning av ligninger i GeoGebra
 Grafisk løsning av ligninger i GeoGebra Arbeidskrav 2 Læring med digitale medier 2013 Magne Svendsen, Universitetet i Nordland Innholdsfortegnelse INNLEDNING... 3 GRAFISK LØSNING AV LIGNINGER I GEOGEBRA...
Grafisk løsning av ligninger i GeoGebra Arbeidskrav 2 Læring med digitale medier 2013 Magne Svendsen, Universitetet i Nordland Innholdsfortegnelse INNLEDNING... 3 GRAFISK LØSNING AV LIGNINGER I GEOGEBRA...
Faget teknologi og design
 Tore Fagerli Faget teknologi og design Teknologi og design (T&D) er et nytt fag som på forsøksbasis utprøves i norsk skole. I svært mange andre land i den vestlige verden har imidlertid teknologi som fagområde
Tore Fagerli Faget teknologi og design Teknologi og design (T&D) er et nytt fag som på forsøksbasis utprøves i norsk skole. I svært mange andre land i den vestlige verden har imidlertid teknologi som fagområde
Geometri Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI Geometri i skolen Geometri etter 4.
 Geometri Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI 15-Apr-07 Geometri i skolen dreier seg blant annet om å analysere egenskaper ved to- og tredimensjonale
Geometri Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Leder i LAMIS Lærebokforfatter, MULTI 15-Apr-07 Geometri i skolen dreier seg blant annet om å analysere egenskaper ved to- og tredimensjonale
7.4 Eksempler på misoppfatninger/mistolkinger
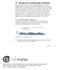 Verdier som parvis hører sammen. Nedbør som samsvarer med dagen vi velger. Utviklingen eller forandringen. Har nedbørsmengden steget eller sunket, har det gått opp og ned? Måleverdien har forandret seg
Verdier som parvis hører sammen. Nedbør som samsvarer med dagen vi velger. Utviklingen eller forandringen. Har nedbørsmengden steget eller sunket, har det gått opp og ned? Måleverdien har forandret seg
Ingar Skaug. Levende lederskap. En personlig oppdagelsesferd
 Ingar Skaug Levende lederskap En personlig oppdagelsesferd Om forfatteren: INGAR SKAUG er en av Norges få toppledere av internasjonalt format. Han hadde sentrale lederroller i de store snuoperasjonene
Ingar Skaug Levende lederskap En personlig oppdagelsesferd Om forfatteren: INGAR SKAUG er en av Norges få toppledere av internasjonalt format. Han hadde sentrale lederroller i de store snuoperasjonene
Tangenten: tidsskrift for matematikkundervisning. Nordheim Proporsjoner i kjempenes land
 Nordheim Proporsjoner i kjempenes land Ideen til dette undervisningsopplegget på 2. trinn fikk jeg da vi skulle jobbe med Roald Dahls bok SVK Store Vennlige Kjempe fra 1999 etter at trinnet hadde sett
Nordheim Proporsjoner i kjempenes land Ideen til dette undervisningsopplegget på 2. trinn fikk jeg da vi skulle jobbe med Roald Dahls bok SVK Store Vennlige Kjempe fra 1999 etter at trinnet hadde sett
"Matte er kjedelig, fordi det er så lett"
 "Matte er kjedelig, fordi det er så lett" Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI Innhold Hvordan gi utfordringer til alle elevene? Tilpasset undervisning
"Matte er kjedelig, fordi det er så lett" Mona Røsseland Matematikksenteret (for tiden i studiepermisjon) Lærebokforfatter, MULTI Innhold Hvordan gi utfordringer til alle elevene? Tilpasset undervisning
Forfatterne bak Multi: Multi i praksis. 5.-7.trinn. En bred matematisk kompetanse. Oppbyggingen av Multi. Grunntanken bak Multi
 Forfatterne bak Multi: Multi i praksis 5.-7.trinn Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg, Høgskolen i Oslo Grunntanken
Forfatterne bak Multi: Multi i praksis 5.-7.trinn Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg, Høgskolen i Oslo Grunntanken
Fire kort. Mål. Gjennomføring. Film. Problemløsing Fire kort Planleggingsdokument
 Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Fire kort Mål Generelt: Søke etter mønster og sammenhenger. Gjennomføre undersøkelse og begrunne resultat. Utfordre elevene på å resonnere og kommunisere. Spesielt: Finne alle kombinasjoner når de adderer
Å være i fysisk aktivitet er å leve. Når du er i bevegelse sier du ja til livet. Det er den som sitter stille, som lever farlig.
 Liv er bevegelse Å være i fysisk aktivitet er å leve. Når du er i bevegelse sier du ja til livet. Det er den som sitter stille, som lever farlig. Idrettsutøvere i verdensklasse kan være inspirerende. Selv
Liv er bevegelse Å være i fysisk aktivitet er å leve. Når du er i bevegelse sier du ja til livet. Det er den som sitter stille, som lever farlig. Idrettsutøvere i verdensklasse kan være inspirerende. Selv
Hvorfor knuser glass?
 Hvorfor knuser glass? Innlevert av 3. trinn ved Sylling skole (Lier, Buskerud) Årets nysgjerrigper 2013 Ansvarlig veileder: Magnhild Alsos Antall deltagere (elever): 7 Innlevert dato: 30.04.2013 Deltagere:
Hvorfor knuser glass? Innlevert av 3. trinn ved Sylling skole (Lier, Buskerud) Årets nysgjerrigper 2013 Ansvarlig veileder: Magnhild Alsos Antall deltagere (elever): 7 Innlevert dato: 30.04.2013 Deltagere:
Utvalg År Prikket Sist oppdatert Stokkan ungdomsskole (Høst 2014) Høst 2014 24.01.2015
 Utvalg År Prikket Sist oppdatert Stokkan ungdomsskole (Høst 2014) Høst 2014 24.01.2015 Lærerundersøkelsen Bakgrunn Er du mann eller kvinne? 16 32 Mann Kvinne Hvilke faggrupper underviser du i? Sett ett
Utvalg År Prikket Sist oppdatert Stokkan ungdomsskole (Høst 2014) Høst 2014 24.01.2015 Lærerundersøkelsen Bakgrunn Er du mann eller kvinne? 16 32 Mann Kvinne Hvilke faggrupper underviser du i? Sett ett
ÅRSPLAN I MATEMATIKK FOR 4. TRINN 2015/2016 (høst)
 ÅRSPLAN I MATEMATIKK FOR 4. TRINN 2015/2016 (høst) Læreverk: Multi Lærer: Mona Haukås Olsen og Anne Marte Urdal/Ruben Elias Austnes 34-36 37-40 MÅL (K06) TEMA ARBEIDSFORM VURDERING lese avlassere og beskrive
ÅRSPLAN I MATEMATIKK FOR 4. TRINN 2015/2016 (høst) Læreverk: Multi Lærer: Mona Haukås Olsen og Anne Marte Urdal/Ruben Elias Austnes 34-36 37-40 MÅL (K06) TEMA ARBEIDSFORM VURDERING lese avlassere og beskrive
Ordenes makt. Første kapittel
 Første kapittel Ordenes makt De sier et ord i fjernsynet, et ord jeg ikke forstår. Det er en kvinne som sier det, langsomt og tydelig, sånn at alle skal være med. Det gjør det bare verre, for det hun sier,
Første kapittel Ordenes makt De sier et ord i fjernsynet, et ord jeg ikke forstår. Det er en kvinne som sier det, langsomt og tydelig, sånn at alle skal være med. Det gjør det bare verre, for det hun sier,
Matematikk i lys av Kunnskapsløftet
 Matematikk i lys av Kunnskapsløftet Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Intensjoner med den nye læreplanen 1. Større handlingsrom for lærerne: Organisering, metoder, arbeidsmåter
Matematikk i lys av Kunnskapsløftet Mona Røsseland Nasjonalt senter for matematikk i Opplæringen Intensjoner med den nye læreplanen 1. Større handlingsrom for lærerne: Organisering, metoder, arbeidsmåter
La oss starte med et høvelig forsøk. Kjent fra før? Det er ikke bare å gjøre et forsøk Vi må også utnytte læringsarenaen som skapes
 La oss starte med et høvelig forsøk Kjent fra før? Det er ikke bare å gjøre et forsøk Vi må også utnytte læringsarenaen som skapes Arbeidsmåter Forskerspiren i praksis Barnetrinnet Anders Isnes Bergen
La oss starte med et høvelig forsøk Kjent fra før? Det er ikke bare å gjøre et forsøk Vi må også utnytte læringsarenaen som skapes Arbeidsmåter Forskerspiren i praksis Barnetrinnet Anders Isnes Bergen
Vi lager ma lestokklinjaler
 Vi lager ma lestokklinjaler En målestokklinjal er en linjal som viser virkelig lengde når vi måler en lengde på tegningen Fremgangsmåten 1) Start med en samtale om en linjal i målestokk 1:100. Tallen blir
Vi lager ma lestokklinjaler En målestokklinjal er en linjal som viser virkelig lengde når vi måler en lengde på tegningen Fremgangsmåten 1) Start med en samtale om en linjal i målestokk 1:100. Tallen blir
Hva kan bidra til å styrke vår emosjonelle utvikling, psykiske helse og positive identitet?
 Hva kan bidra til å styrke vår emosjonelle utvikling, psykiske helse og positive identitet? Hva trenger vi alle? Hva trenger barn spesielt? Hva trenger barn som har synsnedsettelse spesielt? Viktigste
Hva kan bidra til å styrke vår emosjonelle utvikling, psykiske helse og positive identitet? Hva trenger vi alle? Hva trenger barn spesielt? Hva trenger barn som har synsnedsettelse spesielt? Viktigste
Refleksjoner omkring hverdagsmatematikk
 Reidar Mosvold Refleksjoner omkring hverdagsmatematikk Matematikk i dagliglivet kom inn som eget emne i norske læreplaner med L97. En undersøkelse av tidligere læreplaner viser at en praktisk tilknytning
Reidar Mosvold Refleksjoner omkring hverdagsmatematikk Matematikk i dagliglivet kom inn som eget emne i norske læreplaner med L97. En undersøkelse av tidligere læreplaner viser at en praktisk tilknytning
Forfatterne bak Multi!
 Multi i praktisk bruk Forfatterne bak Multi! Tilpasset opplæring Forfatterteam: Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg,
Multi i praktisk bruk Forfatterne bak Multi! Tilpasset opplæring Forfatterteam: Bjørnar Alseth Universitetet i Oslo Henrik Kirkegaard, Flisnes skole, Ålesund Mona Røsseland, Matematikksenteret Gunnar Nordberg,
Hvorfor kiler det ikke når vi kiler oss selv?
 Hvorfor kiler det ikke når vi kiler oss selv? Innlevert av 7.trinn ved Bispehaugen skole (Trondheim, Sør-Trøndelag) Årets nysgjerrigper 2011 Da sjuende trinn startet skoleåret med naturfag, ble ideen om
Hvorfor kiler det ikke når vi kiler oss selv? Innlevert av 7.trinn ved Bispehaugen skole (Trondheim, Sør-Trøndelag) Årets nysgjerrigper 2011 Da sjuende trinn startet skoleåret med naturfag, ble ideen om
