Institutt for økonomi og administrasjon
|
|
|
- Ester Bø
- 10 år siden
- Visninger:
Transkript
1 Fakultet for samfusfag Istitutt for økoomi og admiistraso Ivesterig og fiasierig Bokmål Dato: Madag. desember 3 Tid: 4 timer / kl. 9-3 Atall sider (ikl. forside): 5 + sider vedlegg Atall oppgaver: 4 Tillatte helpemidler: Kalkulator (se kalkulatorreglemetet) Merkad: Kadidate må selv kotrollere at oppgavesettet er fullstedig. Besvarelse skal merkes med kadidatummer, ikke av. Bruk blå eller sort kulepe på iførigsarket. Emekode: ØABED (ORDINÆR)
2 Oppgave (5 %) ABC Electroics AS har i løpet av de siste 3 år utviklet e miihøyttaler som plasseres i øree hvor ma får trådløs overførig av lyd fra smarttelefoer. Utvikligskostadee har vært 5 millioer kroer. Høyttalere er å ferdig utviklet og det er tatt patet på produktet. Ma aalyserer å 3 gesidig utelukkede alterativer for salg av produktet. Alterativee er:. Bedrifte ka produsere og selge produktet selv. Dette vil være e y aktivitet, for hittil har ma vært mest egasert med produktutviklig. Dersom dette alterativet velges må ma ivestere i avasert produksosutstyr for millioer og arbeidskapitalbehovet vil utgøre 3 millioer. Arbeidskapitalbehovet vil være kostat selv om omsetige edres. Det er bereget at det er mulig å oppå følgede salgsvolum (atall eheter) årlig: År Salgsvolum (eheter) Salgsprise vil bli 3 pr. ehet i år, og vil falle til pr. ehet de tre este påfølgede åree. I det siste året (år 5) er salgsprise budsettert til. Variable produksoskostader er 4 pr. ehet. Betalbare faste driftskostader er 8 årlig og i tillegg påløper markedsførigskostader med årlig.. ABC Electroics ka alterativt la det multiasoale selskapet YNOS produsere og selge produktet på lises. YNOS tilbyr å betale ABC Electroics kr 3 pr. solgte ehet. På gru av at YNOS er aktiv i e rekke markeder verde over allerede, reger ABC Electroics med at salgsvolumet hvert år blir 5 % høyere e om ma solgte produktet selv. 3. Som et alterativ til å betale royalty for hver solgte ehet har YNOS tilbudt seg å køpe patetet fra ABC Electroics slik at ma får eksklusiv rett til produkso og salg. Ma er villig til å betale 6 6 for dette fordelt på to like store beløp, hvor de ee halvparte betales straks og de adre halvparte etter to år. a) Bereg åverdi og ta stillig til hvilket alterativ som ABC Electroics bør velge. Avkastigskravet er %.
3 Oppgave (5 %) a) Du tar opp et auitetslå på kr til 5 % rete p.a. Lået skal betales ed over 5 år med halvårlige termier. Sett opp e betaligspla over reter og avdrag for de første år. b) Ata at det påløp etablerigskostader på kr 5 ved låeopptaket i a) og at det også påløper et gebyr på kr 5 ved hver betalig. Hva blir låets effektive årsrete? c) Ata at lået i a) ble tatt opp som et fastretelå. Etter år faller rete på tilsvarede lå til 4 % p.a. Hva må du rege med at overkurs eller uderkurs blir på lået dersom det ifris på dette tidspuktet? d) Aboemet på e dagsavis koster kr 3 år ma betaler forskuddsvis for ett år. Hvis ma i stedet betaler pr. halvår, koster det kr 7 for hver periode. Hvor mye koster det, omreget til effektiv årsrete, å betale hvert halvår fremfor å betale hvert år? Oppgave 3 (5 %) I figure uder ser du stadardavviket for e akseporteføle (loddrett akse) og atall akser i porteføle (varett akse) 4, % 35, % 3, % 5, %, % 5, %, % 5, %, % a) Diskuter hva som mees med systematisk og usystematisk risiko. Hva ka du aslå disse til å være ut fra figure? b) Diskuter hvilke av de to risikobegrepee som er relevat risiko, og hvorfor de er relevat. c) E ivestor eier e porteføle beståede av 4 % av akse L og 6 % av akse M. Forvetet avkastig for aksee over de este 6 år 4 8 er som følger: 3
4 År Akse L Akse M 4 4 % % 5 4 % 8 % 6 6 % 6 % 7 7 % 4 % 8 7 % % 9 9 % % Bereg forvetet avkastig til porteføle for hvert år og for hele periode samlet. d) Bereg porteføles empiriske stadardavvik for periode. e) Hvorda vil du karakterisere korrelasoe mellom akse L og M? Presis utregig er ikke ødvedig. f) Hva sier korrelasoe mellom to aksers avkastig om gevister ved diversifikaso? Oppgave 4 (35 %) AS Orage vurderer å itrodusere et ytt og speede produkt. Det dreier seg om et ytt ettbrett med overlege ytelse og ma tror mulighete for å ta markedsadeler fra etablerte aktører er stor. Ma har å geomført e grudig markedsudersøkelse. Markedsudersøkelse idikerer at det ka være et marked for produktet. Ma har mottatt e faktura fra aalysebyrået på kr 5 for utført arbeid, me fakture er ikke betalt eå. Ledelse har vurdert markedet slik at ma først vil ta e relativt høy markedspris for å trekke til seg kuder som er villige til å betale e høy pris for et ytt produkt, me over levetide vil prise bli seket gradvis for også å kue tiltrekke seg adre kudesegmeter. Salgspris og salgsmegde for de 5 åree prosektet et tekt å vare er som følger: Salgspris Megde År År 4 5 År År År 5 5 De variable produksoskostadee er budsettert til kr 65 pr. ehet i hele levetide. AS Orage produserer og selger allerede et aet ettbrett på markedet. Dette er et midre avasert produkt som selges for kr pr. ehet og salgsmegde er 5 pr. år. Dekigsgrade for dette produktet er 5 %, og geværede levetid er år. Dersom det ye produktet laseres, reger ma med at salget av det eksisterede ettbrettet vil falle med 5 %. 4
5 E mellomleder som allerede er asatt vil ha det produksostekiske asvaret for det ye produktet. Hees lø er å kr 45 årlig. Pga. av økt asvar dersom det ye produktet laseres, vil hu få e løsøkig på kr. Det må også asettes e y perso i hees opprielige stillig og det er budsettert med e lø på kr 4 årlig. Betalbare faste kostader er å kr årlig. Dersom det ye produktet laseres vil kostadee øke pga. økte kostader til oppvarmig o.l. Det er kyttet oe usikkerhet til kostadsøkige på gru av ustabile eergipriser, me et rimelig aslag er at de faste kostadee ka øke til årlig. Dersom prosektet igagsettes vil det være ødvedig med ivesterig i aleggsmidler på kr 8 5. Aleggsmidlee avskrives etter saldometode med 5 % årlig, og ma reger ikke med at aleggsmidlee vil ha oe salgsverdi ved levetides slutt. Etter 3 år vil det være ødvedig med et betydelig vedlikehold av aleggsmidlee for å opprettholde e stabil produkso. Dette er bereget å koste kr 5. Dersom prosektet igagsettes vil det også oppstå økt behov for varelagre med kr 75 og kudefordrigee er budsettert å øke med. Leveradørgelde er budsettert å øke med kr 5. Det er ikke budsettert med edriger i disse postee selv om omsetige edres. Risikofri rete er 3,5 % og bedrifte ka låe peger til e rete på 4,5 % før skatt. Avkastige på markedsporteføle er 9 %. Det er aslått at bedriftes aksebeta er,89 og bedrifte fiasierer sie ivesteriger med e egekapitaladel på 5 %. Skattesatse er 8 %. a) Bereg prosektets veide totalavkastigskrav (WACC). b) Bereg prosektets åverdi etter skatt. Er prosektet løsomt? c) Økige i de faste kostadee er usikre. Hvor mye ka disse kostadee øke i forhold til budsettet før prosektet år løsomhetsgrese? d) Se bort fra pukt c). Hvorda vil åverdi etter skatt bli edret dersom det viser seg at aleggsmidlet ka selges for kr 5 ved levetides slutt? Salget skal behadles på de skattemessig gustigste måte. 5
6 Formelsamlig Fiasierig og ivesterig. Reteregig Sluttverdi FV av et beløp CF, retesats i og periodeatall : - FV CF ( i) Nåverdi PV av et beløp FV, retesats i og periodeatall : - PV FV ( i) Nåverdi PV av e etterskuddsauitet PMT, retesats i og periodeatall : -3 ( i) PV PMT i ( i ) Auitetsfaktore A år,i %, dvs åverdie av kroer med rete i etter perioder: A -4 år, i% Ivers auitetsfaktor over år: -5 A år,% i ( i) i ( i) årlig ytelse for å avdra og forrete et auitetslå på kr. til i% rete i( i) Aåt,% i ( i) Etterskuddsauitet PMT for åverdie PV, retesats i og periodeatall : -6 i( i) PMT PV ( i) Nåverdi PV av e etterskuddsauitet CF, retesats i og uedelig levetid: -7 PV CF i Nåverdi PV av e etterskuddsauitet CF, retesats i, vekstfaktor g, og uedelig levetid: -8 PV CF i g Nåverdi PV for e etterskuddsauitet CF, retesats i, vekstfaktor g, og periodeatall : -9 ( i) ( g) PV CF ( i) ( i g) Årsrete p år perioderete er q og atall perioder i året er m: m - p ( q) Effektiv årsrete ieff år omiell årsrete er i, m er atall perioder i året 6
7 i m - ieff ( ) m. Nåverdi og iterrete Nåverdie NPV av kotatstrømme CF, CF, CF,..,CF over perioder til retekrav i: CF CF CF - NPV CF... ( i) ( i) ( i) Iterrete irr for kotatstrømme CF, CF, CF,..,CF over perioder CF CF CF - CF... ( irr) ( irr) ( irr) 3. Nåverdi og skatt Effektiv skattesats se år iterrete før skatt er p, iterrete etter skatt er r: p r 3. se p Bokført restverdi i år t: RVt, år askaffelseskost er AM som avskrives med saldosats a: 3. RV AM ( a) t Avskrivig i år t: AVt, for e ivesterig med askaffelseskost AM, med saldosats a: 3.3 ( ) t AVt AM a a Nåverdi av fremtidige saldoavskriviger år askaffelseskost er AM som avskrives med saldosats a og kapitalkostad k: 3.4 Nåverdi av saldoavskriviger AM k Nåverdi av spart skatt av saldoavskriviger år askaffelseskost er AM, saldosats a og kapitalkostad k: 3.5 Nåverdi av spart skatt AM a s k a Nåverdi etter skatt saldogruppe A-D og J år askaffelseskost er AM, saldosats a, salgsverdi etter år SV, skattesats s og kapitalkostad k: 3.6 CFt ( s) SV AM a s SV a s NPV AM t ( k) ( k) ( k a) ( k) ( k a) t Nåverdi etter skatt i saldogruppe E-I, symbolbruk som i forrige uttrykk, og g er gevistførigssats: 3.7 t a a CF ( ) ( ) ( ) t s SV AM a s AM a a s SV AM a g s NPV AM t ( k) ( k) ( k a) ( k a) ( k) ( k g) ( k) 4. Avkastigskrav på fiasivesteriger og iflaso Realavkastig før skatt pr, omiell avkastig p og prisstigig : p 4. pr 4. p p ( ) r 7
8 Realavkastig etter skatt rr, omiell avkastig p og prisstigig : p ( s ) 4.3 rr 5. Forvetet verdi, varias, stadardavvik, kovarias og korrelasoskoeffesiet Forvetet avkastig E(r) av mulige utfall for avkastig r, r,,r, med sasyligheter p, p,.,p: E r p r p r p r Variase på avkastig r, Var (r) eller σ 5. ( ) ( )... ( ) Var r r E r p r E r p r E r p Stadardavviket av avkastige, σ 5.3 Var() r Forvetet avkastig E(rp) i e porteføle av akser med forvetet avkastig E(r), E(r),.,E(r), med porteføleadeler w, w,..,w : 5.4 Erp w Er w Er... w Er Kovariase mellom avkastige på akse A, ra i forhold til avkastige på akse B, rb, : σab 5.5 ( ) ( )... ( ) ( ) r E r r E r p r E r r E r p AB A A B B A A B B Korrelasoskoeffesiete mellom avkastige på akse A og avkastige på akse B, ρab 5. 6 AB AB A B Variase på avkastige i e porteføle P med adel wa i akse A og wb i akse B: var (P) eller P 5.7 Var r w w w w P P A A A B AB B B w w w w A A A B AB A B B B Stadardavviket på avkastige i e porteføle P σp: 5.8 Var ( r ) P P Miimum varias porteføle: 8
9 5.9 a A ( rb ) ( ra, rb ) ( ra ) ( rb ) ra rb ra rb ra rb ( ) ( ) (, ) ( ) ( ) 5. Sharpe E() r rf 6. Kapitalverdimodelle, kapitalkostader og akseverdi Forvetet avkastig på akse : E(r), risikofri rete rf, forvetet avkastig på markedsporteføle E(rm), β er betaverdi for akse 6. Er rf Erm -rf Med skatt s er uttrykket: 6. E r rf ( s) E rm rf ( s) Avkastigskrav for geld (før skatt) 6.3 E r r E r r ( s) g f g m f Betaverdie for akse, β 6.4 cov( r, r ) var( r ) m m m m 6.5 m m Empirisk varias på avkastige var(rm) for e akse m, med observasoer, med avkastige rmi, for periode i, og r m er geomsittlig avkastig: i 6.6 Var r r r m mi m i Empirisk kovarias cov(r,rm) mellom avkastige r på akse og avkastige rm på markedsporteføle m: i 6.7 cov r, rm ri r rmi rm i Dages aksepris P, este års utbytte D, kostat vekst g i utbyttet og kapitalkostad r. 9
10 6.8 P D r g (De veidde) kapitalkostad for totalkapitale rt, egekapitalkostad re, låekostad rg, skattesats s, retebærede geld G, og egekapital E: E G 6.9 rt re rg s E G E G Vektstagformele: G E 6. r r r r s e t t g Opsosprig (Black-Scholes) rf T 6. K P N d I e N d 6. d P l rf T I T T 6.3 d d T Opsosprig (Biomialmodelle) Ku kd m P ( u d ) ukd dku L ( u d)( r ) f 6.6 K mp L
Institutt for økonomi og administrasjon
 Fakultet for safusfag Istitutt for økooi og adiistraso Ivesterig og fiasierig Bokål Dato: Tirsdag. deseber 4 Tid: 4 tier / kl. 9-3 Atall sider (ikl. forside): 5 + 9 sider vedlegg Atall oppgaver: 4 Tillatte
Fakultet for safusfag Istitutt for økooi og adiistraso Ivesterig og fiasierig Bokål Dato: Tirsdag. deseber 4 Tid: 4 tier / kl. 9-3 Atall sider (ikl. forside): 5 + 9 sider vedlegg Atall oppgaver: 4 Tillatte
a) Sett opp prosjektets kontantstrøm. Du kan budsjettere på årlig basis. b) Beregn prosjektets nåverdi og internrente. Er prosjektet lønnsomt?
 Oppgave S Kikegata Eiedo e et eiedosselskap so vudee å køpe e tot setalt i Oslo. På tota vudee a å føe opp et bygg ed 5 leilighete fo utleie. I dee fobidelse ha du skaffet til veie følgede opplysige Køpesu
Oppgave S Kikegata Eiedo e et eiedosselskap so vudee å køpe e tot setalt i Oslo. På tota vudee a å føe opp et bygg ed 5 leilighete fo utleie. I dee fobidelse ha du skaffet til veie følgede opplysige Køpesu
Eksamen REA3028 S2, Våren 2011
 Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (8 poeg) a) Deriver fuksjoee ) f 5 f 6 5 ) g g ) h l 9 9 6 4 h l
Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (8 poeg) a) Deriver fuksjoee ) f 5 f 6 5 ) g g ) h l 9 9 6 4 h l
Dato: Torsdag 1. desember 2011
 Fakultet for samfunnsfag Økonomiutdanningen Investering og finansiering Bokmål Dato: Torsdag 1. desember 2011 Tid: 5 timer / kl. 9-14 Antall sider (inkl. forside): 9 Antall oppgaver: 4 Tillatte hjelpemidler:
Fakultet for samfunnsfag Økonomiutdanningen Investering og finansiering Bokmål Dato: Torsdag 1. desember 2011 Tid: 5 timer / kl. 9-14 Antall sider (inkl. forside): 9 Antall oppgaver: 4 Tillatte hjelpemidler:
Rente og pengepolitikk. 8. forelesning ECON 1310 21. september 2015
 Rete og pegepolitikk 8. forelesig ECON 1310 21. september 2015 1 Norge: lav og stabil iflasjo det operative målet for pegepolitikke, ær 2,5 proset i årlig rate. Iflasjosmålet er fleksibelt, dvs. at setralbake
Rete og pegepolitikk 8. forelesig ECON 1310 21. september 2015 1 Norge: lav og stabil iflasjo det operative målet for pegepolitikke, ær 2,5 proset i årlig rate. Iflasjosmålet er fleksibelt, dvs. at setralbake
Eksempeloppgave 2014. REA3028 Matematikk S2 Eksempel på eksamen våren 2015 etter ny ordning. Ny eksamensordning. Del 1: 3 timer (uten hjelpemidler)
 Eksempeloppgave 2014 REA3028 Matematikk S2 Eksempel på eksame våre 2015 etter y ordig Ny eksamesordig Del 1: 3 timer (ute hjelpemidler) Del 2: 2 timer (med hjelpemidler) Mistekrav til digitale verktøy
Eksempeloppgave 2014 REA3028 Matematikk S2 Eksempel på eksame våre 2015 etter y ordig Ny eksamesordig Del 1: 3 timer (ute hjelpemidler) Del 2: 2 timer (med hjelpemidler) Mistekrav til digitale verktøy
Kapittel 8: Estimering
 Kaittel 8: Estimerig Estimerig hadler kort sagt om hvorda å aslå verdie å arametre som,, og dersom disse er ukjete. like arametre sier oss oe om oulasjoe vi studerer (dvs om alle måliger av feomeet som
Kaittel 8: Estimerig Estimerig hadler kort sagt om hvorda å aslå verdie å arametre som,, og dersom disse er ukjete. like arametre sier oss oe om oulasjoe vi studerer (dvs om alle måliger av feomeet som
Eksamen S2, Høsten 2013
 Eksame S, Høste 013 Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler. Oppgave 1 (4 poeg) Deriver fuksjoee 1 x a) fx b) gx 5x 1 5 c) hx x e x 3 Oppgave (5 poeg)
Eksame S, Høste 013 Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler. Oppgave 1 (4 poeg) Deriver fuksjoee 1 x a) fx b) gx 5x 1 5 c) hx x e x 3 Oppgave (5 poeg)
Nye opplysninger i en deloppgave gjelder bare denne deloppgaven.
 Oppgave a) Hva e åvedie av k o 7 å å ea e 5 %? b) Aa a du see k i bake. Hvo ye ka du heve ee å å ea e 5 % de føse 4 åee og deee sige il 7 % ålig? c) E bukbil kose k. Bile ka selges fo k 7 ee 6 å. Hva e
Oppgave a) Hva e åvedie av k o 7 å å ea e 5 %? b) Aa a du see k i bake. Hvo ye ka du heve ee å å ea e 5 % de føse 4 åee og deee sige il 7 % ålig? c) E bukbil kose k. Bile ka selges fo k 7 ee 6 å. Hva e
Eksamen REA3028 S2, Våren 2012
 Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (4 poeg) a) Deriver fuksjoee ) f f ) g e 4 4 4 g e e 4 g e e g e
Eksame REA08 S, Våre 0 Del Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave (4 poeg) a) Deriver fuksjoee ) f f ) g e 4 4 4 g e e 4 g e e g e
Påliteligheten til en stikkprøve
 Pålitelighete til e stikkprøve Om origiale... 1 Beskrivelse... 2 Oppgaver... 4 Løsigsforslag... 4 Didaktisk bakgru... 5 Om origiale "Zuverlässigkeit eier Stichprobe" på http://www.mathe-olie.at/galerie/wstat2/stichprobe/dee
Pålitelighete til e stikkprøve Om origiale... 1 Beskrivelse... 2 Oppgaver... 4 Løsigsforslag... 4 Didaktisk bakgru... 5 Om origiale "Zuverlässigkeit eier Stichprobe" på http://www.mathe-olie.at/galerie/wstat2/stichprobe/dee
2.1 Polynomdivisjon. Oppgave 2.10
 . Polyomdivisjo Oppgave. ( 5 + ) : = + + ( + ):( ) 6 + 6 8 8 = + + c) ( + 5 ) : = + 6 6 d) + + + = + + = + + + 8+ ( ):( ) + + + Oppgave. ( + 5+ ):( ) 5 + + = + ( 5 ): 9 + + + = + + + 5 + 6 9 c) ( 8 66
. Polyomdivisjo Oppgave. ( 5 + ) : = + + ( + ):( ) 6 + 6 8 8 = + + c) ( + 5 ) : = + 6 6 d) + + + = + + = + + + 8+ ( ):( ) + + + Oppgave. ( + 5+ ):( ) 5 + + = + ( 5 ): 9 + + + = + + + 5 + 6 9 c) ( 8 66
Eksamen Finansiering og investering Vår 2004
 Eksamen Finansiering og investering Vår 2004 Eksamen teller totalt 40% av totalkarakteren Tid: 4 timer Hjelpemidler: I tillegg til kalkulator får dere også utdelt et formelark samt en rentetabell som begge
Eksamen Finansiering og investering Vår 2004 Eksamen teller totalt 40% av totalkarakteren Tid: 4 timer Hjelpemidler: I tillegg til kalkulator får dere også utdelt et formelark samt en rentetabell som begge
S2 kapittel 1 Rekker Løsninger til innlæringsoppgavene
 Løsiger til ilærigsoppgavee kapittel Rekker Løsiger til ilærigsoppgavee a Vi ser at differase mellom hvert ledd er 4, så vi får det este leddet ved å legge til 4 Det este leddet blir altså 6 + 4 = 0 b
Løsiger til ilærigsoppgavee kapittel Rekker Løsiger til ilærigsoppgavee a Vi ser at differase mellom hvert ledd er 4, så vi får det este leddet ved å legge til 4 Det este leddet blir altså 6 + 4 = 0 b
Econ 2130 uke 15 (HG) Poissonfordelingen og innføring i estimering
 Eco 130 uke 15 (HG) Poissofordelige og iførig i estimerig 1 Poissofordelige (i) Tilærmig til biomialfordelige. Regel. ( Poissotilærmelse ) Ata Y ~ bi(, p) E( Y ) = p og var( Y ) = p(1 p). Hvis er stor
Eco 130 uke 15 (HG) Poissofordelige og iførig i estimerig 1 Poissofordelige (i) Tilærmig til biomialfordelige. Regel. ( Poissotilærmelse ) Ata Y ~ bi(, p) E( Y ) = p og var( Y ) = p(1 p). Hvis er stor
8 (inkludert forsiden og formelsamling) Tegne- og skrivesaker, kalkulator, formelsamling (se vedlagt).
 Eksamesoppgave våre 011 Ordiær eksame Bokmål Fag: Matematikk Eksamesdato: 10.06.011 Studium/klasse: GLU 5-10 Emekode: MGK00 Eksamesform: Skriftlig Atall sider: 8 (ikludert forside og formelsamlig) Eksamestid:
Eksamesoppgave våre 011 Ordiær eksame Bokmål Fag: Matematikk Eksamesdato: 10.06.011 Studium/klasse: GLU 5-10 Emekode: MGK00 Eksamesform: Skriftlig Atall sider: 8 (ikludert forside og formelsamlig) Eksamestid:
Realavkastning. Investeringsanalyse og inflasjon. Realavkastning av finansinvesteringer
 Ivesteigsaalyse og iflasjo Nomiell avkastig og ealavkastig Reell låeete (ealete) Realivesteige og iflasjo Kotatstøm i omielle og faste pise Iflasjo og skatt Omløpsmidle og iflasjo Joh-Eik Adeasse 1 Høgskole
Ivesteigsaalyse og iflasjo Nomiell avkastig og ealavkastig Reell låeete (ealete) Realivesteige og iflasjo Kotatstøm i omielle og faste pise Iflasjo og skatt Omløpsmidle og iflasjo Joh-Eik Adeasse 1 Høgskole
Ukeoppgaver i BtG207 Statistikk, uke 4 : Binomisk fordeling. 1
 Ukeoppgaver i BtG20 Statistikk, uke 4 : Biomisk fordelig. 1 Høgskole i Gjøvik Avdelig for tekologi, økoomi og ledelse. Statistikk Ukeoppgaver uke 4 Biomisk fordelig. Oppgave 1 La de stokastiske variable
Ukeoppgaver i BtG20 Statistikk, uke 4 : Biomisk fordelig. 1 Høgskole i Gjøvik Avdelig for tekologi, økoomi og ledelse. Statistikk Ukeoppgaver uke 4 Biomisk fordelig. Oppgave 1 La de stokastiske variable
LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side av 0 LØSNINGSFORSLAG TIL EKSAMEN I FAG TMA4245 STATISTIKK 6.august 2004 Oppgave Midtveiseksame a) X er e stokastisk variabel
Investeringer og skatt. Skattesatser med videre. Finansinvesteringer. Eksempler på finansinvesteringer
 Iveseriger og ska Løsomhe av fiasiveseriger før og eer ska Løsomhe av realiveseriger eer ska Avhedelse (salg) av aleggsmidler Egekapialavkasig eer ska Joh-Erik Adreasse 1 Høgskole i Øsfold Skaesaser med
Iveseriger og ska Løsomhe av fiasiveseriger før og eer ska Løsomhe av realiveseriger eer ska Avhedelse (salg) av aleggsmidler Egekapialavkasig eer ska Joh-Erik Adreasse 1 Høgskole i Øsfold Skaesaser med
211.7% 2.2% 53.0% 160.5% 30.8% 46.8% 17.2% 11.3% 38.7% 0.8%
 Prøve-eksame II MET 1190 Statistikk Dato 31. mai 2019 kl 1100-1400 Alle svar skal begrues. Når besvarelse evalueres, blir det lagt vekt på at framgagsmåte og resultat preseteres så klart, presist og kortfattet
Prøve-eksame II MET 1190 Statistikk Dato 31. mai 2019 kl 1100-1400 Alle svar skal begrues. Når besvarelse evalueres, blir det lagt vekt på at framgagsmåte og resultat preseteres så klart, presist og kortfattet
Kapittel 5: Tilfeldige variable, forventning og varians.
 Kapittel 5: Tilfeldige variable, forvetig og varias. Tilfeldige variable Tilfeldige variable kalles også stokastiske variable. Defiisjo: E tilfeldig variabel er e variabel som får si umeriske verdi bestemt
Kapittel 5: Tilfeldige variable, forvetig og varias. Tilfeldige variable Tilfeldige variable kalles også stokastiske variable. Defiisjo: E tilfeldig variabel er e variabel som får si umeriske verdi bestemt
Høgskolen i Hedmark. 3BED200 Investering og finansiering. Ordinær eksamen høsten 2014. Vedlegg: Rentetabell 1-6 og 5 sider formelsamling.
 Høgskolen i Hedmark 3BED200 Investering og finansiering Ordinær eksamen høsten 2014 Eksamenssted: Rena Eksamensdato: 4. desember 2014 Eksamenstid: 09.00-13.00 Sensurfrist: 29. desember 2014 Tillatte hjelpemidler:
Høgskolen i Hedmark 3BED200 Investering og finansiering Ordinær eksamen høsten 2014 Eksamenssted: Rena Eksamensdato: 4. desember 2014 Eksamenstid: 09.00-13.00 Sensurfrist: 29. desember 2014 Tillatte hjelpemidler:
Eksamen REA3028 S2, Våren 2010
 Eksame REA308 S, Våre 010 Del 1 Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave 1 (6 poeg) a) Deriver fuksjoee: 1) f x x lx f x x lx x x f
Eksame REA308 S, Våre 010 Del 1 Tid: timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave 1 (6 poeg) a) Deriver fuksjoee: 1) f x x lx f x x lx x x f
Finans. Fasit dokument
 Finans Fasit dokument Antall svar: 40 svar Antall emner: 7 emner Antall sider: 18 Sider Forfatter: Studiekvartalets kursholdere. Emne 1 - Investeringsanalyse Oppgave 1 Gjør rede for hva som menes med nåverdiprofil.
Finans Fasit dokument Antall svar: 40 svar Antall emner: 7 emner Antall sider: 18 Sider Forfatter: Studiekvartalets kursholdere. Emne 1 - Investeringsanalyse Oppgave 1 Gjør rede for hva som menes med nåverdiprofil.
Mer om utvalgsundersøkelser
 Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Mer om utvalgsudersøkelser I uderkapittel 3.6 i læreboka gir vi e kort iførig i takegage ved utvalgsudersøkelser. Vi gir her e grudigere framstillig av temaet. Populasjo og utvalg Ved e utvalgsudersøkelse
Rapport mai 2013 MØBEL- OG INTERIØRBRANSJENE 2012
 apport mai 013 ØBE- G ITEIØBSJEE 01 1 3 IHD 01 Iledig 01 Iledig 0 øbelhadele 03 Boligtekstilbrasje 0 Servise- og kjøkkeutstyrbrasje 05 Belysigsutstyr 06 Butikkhadele med iredigsartikler 07 Spesialbutikker
apport mai 013 ØBE- G ITEIØBSJEE 01 1 3 IHD 01 Iledig 01 Iledig 0 øbelhadele 03 Boligtekstilbrasje 0 Servise- og kjøkkeutstyrbrasje 05 Belysigsutstyr 06 Butikkhadele med iredigsartikler 07 Spesialbutikker
Høgskolen i Hedmark. SBED200 Investering og finansiering Ordinær eksamen høst 2014. Eksamenssted: Studiesenteret.no / Campus Rena
 Q) Høgskolen i Hedmark SBED200 Investering og finansiering Ordinær eksamen høst 2014 Eksamenssted: Studiesenteret.no / Campus Rena Eksamensdato: 4. desember 2014 Eksamenstid: 09.00 13.00 Sensurfrist: 29.desember
Q) Høgskolen i Hedmark SBED200 Investering og finansiering Ordinær eksamen høst 2014 Eksamenssted: Studiesenteret.no / Campus Rena Eksamensdato: 4. desember 2014 Eksamenstid: 09.00 13.00 Sensurfrist: 29.desember
Fagdag 2-3mx 24.09.07
 Fagdag 2-3mx 24.09.07 Jeg beklager at jeg ikke har fuet oe ye morsomme spill vi ka studere, til gjegjeld skal dere slippe prøve/test dee gage. Istruks: Vi arbeider som valig med 3 persoer på hver gruppe.
Fagdag 2-3mx 24.09.07 Jeg beklager at jeg ikke har fuet oe ye morsomme spill vi ka studere, til gjegjeld skal dere slippe prøve/test dee gage. Istruks: Vi arbeider som valig med 3 persoer på hver gruppe.
Finans. Oppgave dokument
 Finans Oppgave dokument Antall Oppgaver: 40 Oppgaver Antall emner: 7 emner Antall sider: 13 Sider Forfatter: Studiekvartalets kursholdere Kapittel 1 - Investeringsanalyse Oppgave 1 Gjør rede for hva som
Finans Oppgave dokument Antall Oppgaver: 40 Oppgaver Antall emner: 7 emner Antall sider: 13 Sider Forfatter: Studiekvartalets kursholdere Kapittel 1 - Investeringsanalyse Oppgave 1 Gjør rede for hva som
Rente og pengepolitikk 1. Innhold. Forelesningsnotat 9, februar 2015
 Forelesigsotat 9, februar 2015 Rete og pegepolitikk 1 Ihold Rete og pegepolitikk...1 Hvorda virker Norges Baks styrigsrete?...3 Pegemarkedet...3 Etterspørselskaale...4 Valutakurskaale...4 Forvetigskaale...5
Forelesigsotat 9, februar 2015 Rete og pegepolitikk 1 Ihold Rete og pegepolitikk...1 Hvorda virker Norges Baks styrigsrete?...3 Pegemarkedet...3 Etterspørselskaale...4 Valutakurskaale...4 Forvetigskaale...5
Finans Formelark Antall formler: 46 formler Antall emner: 7 emner Antall sider: 16 Sider Forfatter: Studiekvartalets kursholdere
 Finans Formelark Antall formler: 46 formler Antall emner: 7 emner Antall sider: 16 Sider Forfatter: Studiekvartalets kursholdere. Emne 1 Investeringsanalyse (1) Formel for nåverdien: NPV = Nåverdi CF t
Finans Formelark Antall formler: 46 formler Antall emner: 7 emner Antall sider: 16 Sider Forfatter: Studiekvartalets kursholdere. Emne 1 Investeringsanalyse (1) Formel for nåverdien: NPV = Nåverdi CF t
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Sensorveiledning - Obligatorisk oppgave 1310, v15
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Sesorveiledig - Obligatorisk oppgave 30, v5 Ved sesure tillegges oppgave vekt 20%, oppgave 2 vekt 60%, og oppgave 3 vekt 20%. For å bestå eksame, må besvarelse
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Sesorveiledig - Obligatorisk oppgave 30, v5 Ved sesure tillegges oppgave vekt 20%, oppgave 2 vekt 60%, og oppgave 3 vekt 20%. For å bestå eksame, må besvarelse
Høgskolen i Telemark Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 16. mai 2008
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL 6. mai 008 EKSAMEN I MATEMATIKK Modul 5 studiepoeg Tid: 5 timer Oppgavesettet er på 8 sider (ikludert formelsamlig). Hjelpemidler:
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL 6. mai 008 EKSAMEN I MATEMATIKK Modul 5 studiepoeg Tid: 5 timer Oppgavesettet er på 8 sider (ikludert formelsamlig). Hjelpemidler:
betegne begivenheten at det trekkes et billedkort i trekning j (for j=1,2,3), og komplementet til
 1 ECON1: EKSAMEN 17v SENSORVEILEDNING. Det abefales at de 9 deloppgavee merket med A, B, teller likt uasett variaso i vaskelighetsgrad. Svaree er gitt i
1 ECON1: EKSAMEN 17v SENSORVEILEDNING. Det abefales at de 9 deloppgavee merket med A, B, teller likt uasett variaso i vaskelighetsgrad. Svaree er gitt i
Oppgave 1. (i) Hva er sannsynligheten for at det øverste kortet i bunken er et JA-kort?
 ECON EKSAMEN 8 VÅR TALLSVAR Oppgave Vi har e kortstokk beståede av 6 kort. På av disse står det skrevet JA på forside mes det står NEI på forside av de adre kortee. Hvis ma får se kortet med bakside vedt
ECON EKSAMEN 8 VÅR TALLSVAR Oppgave Vi har e kortstokk beståede av 6 kort. På av disse står det skrevet JA på forside mes det står NEI på forside av de adre kortee. Hvis ma får se kortet med bakside vedt
Kraftforsyningsberedskap. Roger Steen Seniorrådgiver Beredskapsseksjonen NVE, [email protected]
 Kraftforsyigsberedskap Roger Stee Seiorrådgiver Beredskapsseksjoe NVE, [email protected] Beredskapsasvar Olje- og eergidepartemetet har det overordede asvaret for ladets kraftforsyig. Det operative asvaret for
Kraftforsyigsberedskap Roger Stee Seiorrådgiver Beredskapsseksjoe NVE, [email protected] Beredskapsasvar Olje- og eergidepartemetet har det overordede asvaret for ladets kraftforsyig. Det operative asvaret for
Registrarseminar 1. april 2003. Ingrid Ofstad Norid
 Registrarsemiar 1. april 2003 Igrid Ofstad Norid Statistikk 570 har fått godkjet søkad om å bli registrar ca. 450 registrarer er aktive i dag 2 5 ye avtaler hver uke på semiaret deltar både registrarer
Registrarsemiar 1. april 2003 Igrid Ofstad Norid Statistikk 570 har fått godkjet søkad om å bli registrar ca. 450 registrarer er aktive i dag 2 5 ye avtaler hver uke på semiaret deltar både registrarer
Oppgaven består av 9 delspørsmål, A,B,C,., som anbefales å veie like mye, Kommentarer og tallsvar er skrevet inn mellom <<.. >>.
 ECON 130 EKSAMEN 008 VÅR - UTSATT PRØVE SENSORVEILEDNING Oppgave består av 9 delspørsmål, A,B,C,., som abefales å veie like mye, Kommetarer og tallsvar er skrevet i mellom . Oppgave 1 Ved e spørreudersøkelse
ECON 130 EKSAMEN 008 VÅR - UTSATT PRØVE SENSORVEILEDNING Oppgave består av 9 delspørsmål, A,B,C,., som abefales å veie like mye, Kommetarer og tallsvar er skrevet i mellom . Oppgave 1 Ved e spørreudersøkelse
Vi bruker et avkastningskrav som tar hensyn til disse elementene ved å diskontere kontantstrømmer
 Oppgave 1.1 oppgave 1.1 alt basis Salgspris 900 Avk krav f s 15 % Materialkostnader 200 Avk krav e s 10,8 % Diverse variable kostnade 100 Saldosats 10 % Dekningsbidrag pr. enhe 600 Skattesats 28 % Produksjonsvolum
Oppgave 1.1 oppgave 1.1 alt basis Salgspris 900 Avk krav f s 15 % Materialkostnader 200 Avk krav e s 10,8 % Diverse variable kostnade 100 Saldosats 10 % Dekningsbidrag pr. enhe 600 Skattesats 28 % Produksjonsvolum
2T kapittel 3 Modellering og bevis Utvalgte løsninger oppgavesamlingen
 T kapittel 3 Modellerig og bevis Utvalgte løsiger oppgavesamlige 301 a Sitthøyde i 1910 blir 170,0 171, 4 170,7. I 1970 blir de 177,1 179, 4 178,3. b Med som atall år etter 1900 og y som sitthøyde i cetimeter
T kapittel 3 Modellerig og bevis Utvalgte løsiger oppgavesamlige 301 a Sitthøyde i 1910 blir 170,0 171, 4 170,7. I 1970 blir de 177,1 179, 4 178,3. b Med som atall år etter 1900 og y som sitthøyde i cetimeter
Statistikk og økonomi, våren 2017
 Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
Statistikk og økoomi, våre 07 Obligatorisk oppgave 6 Løsigsforslag Oppgave E terig kastes 0 gager, og det registreres hvor mage 6-ere som oppås i løpet av disse 0 kastee. Vi ka kalle atall 6-ere i løpet
Eksamen 20.05.2009. REA3024 Matematikk R2. Nynorsk/Bokmål
 Eksame 20052009 REA3024 Matematikk R2 Nyorsk/Bokmål Nyorsk Eksamesiformasjo Eksamestid: Hjelpemiddel på Del 1: Hjelpemiddel på Del 2: Bruk av kjelder: Vedlegg: Framgagsmåte: Rettleiig om vurderiga: 5 timar:
Eksame 20052009 REA3024 Matematikk R2 Nyorsk/Bokmål Nyorsk Eksamesiformasjo Eksamestid: Hjelpemiddel på Del 1: Hjelpemiddel på Del 2: Bruk av kjelder: Vedlegg: Framgagsmåte: Rettleiig om vurderiga: 5 timar:
ÅMA110 Sannsynlighetsregning med statistikk, våren Kp. 5 Estimering. Målemodellen.
 ÅMA0 Sasylighetsregig med statistikk, våre 0 Kp. 5 Estimerig. Målemodelle. Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.). (Pukt)Estimerig i målemodelle
ÅMA0 Sasylighetsregig med statistikk, våre 0 Kp. 5 Estimerig. Målemodelle. Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.). (Pukt)Estimerig i målemodelle
Metoder for politiske meningsmålinger
 Metoder for politiske meigsmåliger AV FORSKER IB THOMSE STATISTISK SETRALBYRÅ Beregigsmetodee som brukes i de forskjellige politiske meigsmåliger har vært gjestad for mye diskusjo i dagspresse det siste
Metoder for politiske meigsmåliger AV FORSKER IB THOMSE STATISTISK SETRALBYRÅ Beregigsmetodee som brukes i de forskjellige politiske meigsmåliger har vært gjestad for mye diskusjo i dagspresse det siste
2 Algebra. Innhold. Algebra R2
 Algebra Ihold. Tallfølger... 3 Formler som beskriver tallfølger... 5 Aritmetiske tallfølger... 9 Geometriske tallfølger... 0. Tallrekker... Aritmetiske rekker... 3 Geometriske rekker... 6 Praktiske problemer
Algebra Ihold. Tallfølger... 3 Formler som beskriver tallfølger... 5 Aritmetiske tallfølger... 9 Geometriske tallfølger... 0. Tallrekker... Aritmetiske rekker... 3 Geometriske rekker... 6 Praktiske problemer
Eksempeloppgave 2014. REA3026 Matematikk S1 Eksempel på eksamen våren 2015 etter ny ordning. Ny eksamensordning. Del 1: 3 timer (uten hjelpemidler)
 Eksempeloppgave 04 REA306 Matematikk S Eksempel på eksame våre 05 etter y ordig Ny eksamesordig Del : 3 timer (ute hjelpemidler) Del : timer (med hjelpemidler) Mistekrav til digitale verktøy på datamaski:
Eksempeloppgave 04 REA306 Matematikk S Eksempel på eksame våre 05 etter y ordig Ny eksamesordig Del : 3 timer (ute hjelpemidler) Del : timer (med hjelpemidler) Mistekrav til digitale verktøy på datamaski:
3MX 2007/8 - Kapittel 5: 8. januar 5. februar 2008
 3MX 00/8 - Kapittel : 8. jauar. februar 008 Pla for skoleåret 00/008: Kapittel 6: 6/ /. Kapittel : / /3. Prøver på eller skoletime etter hvert kapittel. É heildagsprøve i hver termi. Repetisjo, prøver,
3MX 00/8 - Kapittel : 8. jauar. februar 008 Pla for skoleåret 00/008: Kapittel 6: 6/ /. Kapittel : / /3. Prøver på eller skoletime etter hvert kapittel. É heildagsprøve i hver termi. Repetisjo, prøver,
Finansiering og investering
 Finansiering og investering John-Erik Andreassen 1 Høgskolen i Østfold Fra et tradisjonelt eierorientert ståsted stiller en spørsmålet: Hvorfor eierne vil investerer i en bedrift fremfor å gjøre det selv?
Finansiering og investering John-Erik Andreassen 1 Høgskolen i Østfold Fra et tradisjonelt eierorientert ståsted stiller en spørsmålet: Hvorfor eierne vil investerer i en bedrift fremfor å gjøre det selv?
ÅMA110 Sannsynlighetsregning med statistikk, våren Estimering. Målemodellen. Konfidensintervall, innledning. Kp. 5 Estimering.
 ÅMA0 Sasylighetsregig med statistikk våre 006 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (Pukt)Estimerig i målemodelle (kp. 5.3)
ÅMA0 Sasylighetsregig med statistikk våre 006 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (Pukt)Estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (Pukt)Estimerig i målemodelle (kp. 5.3)
ARBEIDSHEFTE I MATEMATIKK
 ARBEIDSHEFTE I MATEMATIKK Temahefte r Hvorda du reger med poteser Detaljerte forklariger Av Matthias Loretze mattegriseforlag.com Opplsig: E potes er e forkortet skrivemåte for like faktorer. E potes består
ARBEIDSHEFTE I MATEMATIKK Temahefte r Hvorda du reger med poteser Detaljerte forklariger Av Matthias Loretze mattegriseforlag.com Opplsig: E potes er e forkortet skrivemåte for like faktorer. E potes består
Høgskoleni Østfold NY/UTSATT EKSAMEN. Emne: Finansiering og investering. Eksamenstid: :00
 Høgskoleni Østfold NY/UTSATT EKSAMEN Emnekode: SFB11002 Dato: 05.01.2016 Emne: Finansiering og investering Eksamenstid: 09.00-13:00 Hjelpemidler: Kalkulator Faglærer: Trond-Arne Borgersen Eksamensoppgaven:
Høgskoleni Østfold NY/UTSATT EKSAMEN Emnekode: SFB11002 Dato: 05.01.2016 Emne: Finansiering og investering Eksamenstid: 09.00-13:00 Hjelpemidler: Kalkulator Faglærer: Trond-Arne Borgersen Eksamensoppgaven:
EKSAMENSOPPGAVE. Faglig veileder: Kirsten Aarset, Bente Hellum og Jan Stubergh Gruppe(r): 1-elektro, 1-maskin, 3-almen Dato: 17 desember 2001
 Avdelig for igeiørutdaig EKSAMENSOPPGAVE Fag: Kjemi og Miljø Fagr FO 05 K Faglig veileder: Kirste Aarset, Bete Hellum og Ja Stubergh Gruppe(r): 1-elektro, 1-maski, -alme Dato: 17 desember 001 Eksamestid,
Avdelig for igeiørutdaig EKSAMENSOPPGAVE Fag: Kjemi og Miljø Fagr FO 05 K Faglig veileder: Kirste Aarset, Bete Hellum og Ja Stubergh Gruppe(r): 1-elektro, 1-maski, -alme Dato: 17 desember 001 Eksamestid,
Oppgave 1 IS-RR-PK- modellen Ta utgangspunkt i følgende modell for en lukket økonomi. der 0 < t < 1
 Oppgaveverksted 4, ECON 30, H5 Oppgave IS-RR-PK- modelle Ta utgagspukt i følgede modell for e lukket økoomi () = C + I + G (2) C e C = z + c( T) c2( i π ), der 0 < c < og c 2 > 0, (3) I ( e I = z + b )
Oppgaveverksted 4, ECON 30, H5 Oppgave IS-RR-PK- modelle Ta utgagspukt i følgede modell for e lukket økoomi () = C + I + G (2) C e C = z + c( T) c2( i π ), der 0 < c < og c 2 > 0, (3) I ( e I = z + b )
Forventningsverdi. MAT0100V Sannsynlighetsregning og kombinatorikk
 MAT0100V Sasylighetsregig og kombiatorikk Forvetigsverdi Sasylighetsfordelige til e tilfeldig variabel X gir sasylighete for de ulike verdiee X ka ata Forvetig, varias og stadardavvik Tilærmig av biomiske
MAT0100V Sasylighetsregig og kombiatorikk Forvetigsverdi Sasylighetsfordelige til e tilfeldig variabel X gir sasylighete for de ulike verdiee X ka ata Forvetig, varias og stadardavvik Tilærmig av biomiske
Globalisering og ny regionalisme
 Parterforum 1. November 2013 Globaliserig og y regioalisme Kosekveser for Norge og orsk offetlig sektor Kjell A. Eliasse Ceter for Europea ad Asia Studies Norwegia Busiess School - BI Kjell A Eliasse,
Parterforum 1. November 2013 Globaliserig og y regioalisme Kosekveser for Norge og orsk offetlig sektor Kjell A. Eliasse Ceter for Europea ad Asia Studies Norwegia Busiess School - BI Kjell A Eliasse,
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 5 jui 2015 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 5 jui 2015 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
Høgskolen i Hedmark. Eksamenssted: Studiesenteret.no / Campus Rena. Ved/egg: Rentetabell 1-6 og 5 sider formelsamling
 lb/aogm- / Høgskolen i Hedmark Eksamenssted: Studiesenteret.no / Campus Rena Eksamensdato: 11. desember 2015 Eksamenstid: 09.00 13.00 Sensurfrist: 5. januar 2016 Tillatte hjelpemidler: Kalkulator Ved/egg:
lb/aogm- / Høgskolen i Hedmark Eksamenssted: Studiesenteret.no / Campus Rena Eksamensdato: 11. desember 2015 Eksamenstid: 09.00 13.00 Sensurfrist: 5. januar 2016 Tillatte hjelpemidler: Kalkulator Ved/egg:
Høgskolen i Hedmark. 3BED200 Investering og finansiering. Kontinueringseksamen høsten Vedlegg: Rentetabell 1-6 og 5 sider formelsamling.
 GD Høgskolen i Hedmark 3BED200 Investering og finansiering Kontinueringseksamen høsten 204 Eksamensdato: 4.februar, 205 Eksamenstid: 09.00 3.00 Sensurfrist: 25. februar 205 Tillatte hjelpemidler: Kalkulator
GD Høgskolen i Hedmark 3BED200 Investering og finansiering Kontinueringseksamen høsten 204 Eksamensdato: 4.februar, 205 Eksamenstid: 09.00 3.00 Sensurfrist: 25. februar 205 Tillatte hjelpemidler: Kalkulator
Emnenavn: Eksamenstid: 4 timer. Faglærer: Hans Kristian Bekkevard
 EKSAMEN Emekode: SFB107111 Emeav: Metode 1, statistikk deleksame Dato: 7. mai 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Has Kristia Bekkevard
EKSAMEN Emekode: SFB107111 Emeav: Metode 1, statistikk deleksame Dato: 7. mai 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Has Kristia Bekkevard
HØGSKOLEN I SØR-TRØNDELAG Avdeling for teknologi
 HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 19 des. 2014 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
HØGSKOLEN I SØR-TRØNDELAG Avdelig for tekologi Målform: Bokmål Eksamesdato: 19 des. 2014 Varighet/eksamestid: Emekode: 3 timer TALM1005 Emeav: Statistikk og Økoomi statistikkdele Klasser: Logistikk 1 Kjemi
Høgskolen i Telemark Avdeling for estetiske fag, folkekultur og lærerutdanning BOKMÅL 12. desember 2008
 Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. desember 8 EKSAMEN I MATEMATIKK, Utsatt røve Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig).
Høgskole i Telemark Avdelig for estetiske fag, folkekultur og lærerutdaig BOKMÅL. desember 8 EKSAMEN I MATEMATIKK, Utsatt røve Modul 5 studieoeg Tid: 5 timer Ogavesettet er å sider (ikludert formelsamlig).
Introduksjon. Hypotesetesting / inferens (kap 3) Populasjon og utvalg. Populasjon og utvalg. Populasjonsvarians
 Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
Hypotesetestig / iferes (kap ) Itroduksjo Populasjo og utvalg Statistisk iferes Utvalgsfordelig (samplig distributio) Utvalgsfordelige til gjeomsittet Itroduksjo Vi øsker å få iformasjo om størrelsee i
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE
 AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Eme: Statistikk Gruppe(r): Alle ( 2. årskull) Eksamesoppgav Atall sider (ikl. e består av: forside): 5 Tillatte hjelpemidler: Emekode: LO070A Dato: 11.06.2004
AVDELING FOR INGENIØRUTDANNING EKSAMENSOPPGAVE Eme: Statistikk Gruppe(r): Alle ( 2. årskull) Eksamesoppgav Atall sider (ikl. e består av: forside): 5 Tillatte hjelpemidler: Emekode: LO070A Dato: 11.06.2004
ÅMA110 Sannsynlighetsregning med statistikk, våren 2011
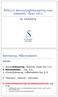 ÅMA110 asylighetsregig med statistikk våre 011 Kp. 5 Estimerig 1 Estimerig. Målemodelle. Ihold: 1. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp.
ÅMA110 asylighetsregig med statistikk våre 011 Kp. 5 Estimerig 1 Estimerig. Målemodelle. Ihold: 1. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp.
Eksamen REA3028 S2, Våren 2012
 Eksame REA3028 S2, Våre 2012 Del 1 Tid: 2 timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave 1 (24 poeg) a) Deriver fuksjoee 1) 3 f x x 2x 3 2) 2 2
Eksame REA3028 S2, Våre 2012 Del 1 Tid: 2 timer Hjelpemidler: Valige skrivesaker, passer, lijal med cetimetermål og vikelmåler er tillatt. Oppgave 1 (24 poeg) a) Deriver fuksjoee 1) 3 f x x 2x 3 2) 2 2
Emnenavn: Metode 1, statistikk deleksamen. Eksamenstid: 4 timer. Faglærer: Bjørnar Karlsen Kivedal
 EKSAMEN Emekode: SFB10711 Emeav: Metode 1, statistikk deleksame Dato: 10. oktober 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Bjørar Karlse Kivedal
EKSAMEN Emekode: SFB10711 Emeav: Metode 1, statistikk deleksame Dato: 10. oktober 2018 Hjelpemidler: Godkjet kalkulator og vedlagt formelsamlig m/tabeller Eksamestid: 4 timer Faglærer: Bjørar Karlse Kivedal
ORDINÆR EKSAMEN. BE 100 Finansregnskap med analyse. Fredag 25. november 2011 kl. 09.00 - kl. 13.00
 ORDINÆR EKSAMEN BE 100 Finansregnskap med analyse Fredag 25. november 2011 kl. 09.00 - kl. 13.00 Tillatte emidler Hjelpemiddelhefte i BE 100 Norges Lover/ særtrykk eller samlinger av lover uten kommentarer
ORDINÆR EKSAMEN BE 100 Finansregnskap med analyse Fredag 25. november 2011 kl. 09.00 - kl. 13.00 Tillatte emidler Hjelpemiddelhefte i BE 100 Norges Lover/ særtrykk eller samlinger av lover uten kommentarer
ÅMA110 Sannsynlighetsregning med statistikk, våren Estimering. Målemodellen. Sannsynlighetsregning med statistikk. Kp. 5 Estimering.
 ÅMA asylighetsregig med statistikk våre 008 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp. 5.3)
ÅMA asylighetsregig med statistikk våre 008 Kp. 5 Estimerig Estimerig. Målemodelle. Ihold:. (ukt)estimerig i biomisk modell (kp. 5.). Målemodelle... (kp. 5.3) 3. (ukt)estimerig i målemodelle (kp. 5.3)
EKSAMEN Løsningsforslag
 ..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
..4 EKSAMEN Løsigsforslag Emekode: ITF75 Dato: 6. desember Eme: Matematikk for IT Eksamestid: kl 9. til kl. Hjelpemidler: To A4-ark med valgfritt ihold på begge sider. Kalkulator er ikke tillatt. Faglærer:
Detaljert løsningsveiledning til ECON1310 seminaroppgave 9, høsten der 0 < t < 1
 Detaljert løsigsveiledig til ECON30 semiaroppgave 9, høste 206 Dee løsigsveiledige er mer detaljert e det et fullgodt svar på oppgave vil være, og mer utfyllede e e valig fasit. De er met som e guide til
Detaljert løsigsveiledig til ECON30 semiaroppgave 9, høste 206 Dee løsigsveiledige er mer detaljert e det et fullgodt svar på oppgave vil være, og mer utfyllede e e valig fasit. De er met som e guide til
Eksamen REA3028 Matematikk S2. Nynorsk/Bokmål
 Eksame 9.11.013 REA308 Matematikk S Nyorsk/Bokmål Nyorsk Eksamesiformasjo Eksamestid: Hjelpemiddel på Del 1: Hjelpemiddel på Del : 5 timar: Del 1 skal leverast i etter timar. Del skal leverast i seiast
Eksame 9.11.013 REA308 Matematikk S Nyorsk/Bokmål Nyorsk Eksamesiformasjo Eksamestid: Hjelpemiddel på Del 1: Hjelpemiddel på Del : 5 timar: Del 1 skal leverast i etter timar. Del skal leverast i seiast
Løsning eksamen S2 våren 2010
 Løsig eksame S våre 010 Oppgave 1 a) 1) f( ) l 1 f ( ) l l l l ( l 1) ) g ( ) 3e g( ) 3e 3e 6e b) Rekke er geometrisk med Rekke kovergerer. Summe er a1 1 1 s 1 k 1 1 1 1 1 k og oppfller dermed kravet 1
Løsig eksame S våre 010 Oppgave 1 a) 1) f( ) l 1 f ( ) l l l l ( l 1) ) g ( ) 3e g( ) 3e 3e 6e b) Rekke er geometrisk med Rekke kovergerer. Summe er a1 1 1 s 1 k 1 1 1 1 1 k og oppfller dermed kravet 1
Oppgave 1 IS-RR-PK- modellen Ta utgangspunkt i følgende modell for en lukket økonomi. der 0 < t < 1
 Fasit Oppgaveverksted 3, ECON 1310, H15 Oppgave 1 IS-RR-PK- modelle Ta utgagspukt i følgede modell for e lukket økoomi (1) = C + I + G (2) C e C z c1( T) c2( i ), der 0 < c 1 < 1 og c 2 > 0, (3) I ( e
Fasit Oppgaveverksted 3, ECON 1310, H15 Oppgave 1 IS-RR-PK- modelle Ta utgagspukt i følgede modell for e lukket økoomi (1) = C + I + G (2) C e C z c1( T) c2( i ), der 0 < c 1 < 1 og c 2 > 0, (3) I ( e
Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.
 Eksame 20052009 REA3024 Matematikk R2 Nyorsk/Bokmål Bokmål Eksamesiformasjo Eksamestid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Bruk av kilder: Vedlegg: Framgagsmåte: Veiledig om vurderige: 5 timer:
Eksame 20052009 REA3024 Matematikk R2 Nyorsk/Bokmål Bokmål Eksamesiformasjo Eksamestid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Bruk av kilder: Vedlegg: Framgagsmåte: Veiledig om vurderige: 5 timer:
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-aturviteskapelige fakultet Eksame i: STK11 Sasylighetsregig og statistisk modellerig. LØSNINGSFORSLAG Eksamesdag: Fredag 9. jui 217. Tid for eksame: 9. 13.. Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-aturviteskapelige fakultet Eksame i: STK11 Sasylighetsregig og statistisk modellerig. LØSNINGSFORSLAG Eksamesdag: Fredag 9. jui 217. Tid for eksame: 9. 13.. Oppgavesettet
KLMED8004 Medisinsk statistikk. Del I, høst Estimering. Tidligere sett på. Eksempel hypertensjon
 Tidligere sett på KLMED8004 Medisisk statistikk Del I, høst 008 Estimerig Hvorda kjete sasylighetsfordeliger (biomialfordelig, ormalfordelig) med kjete populasjosparametrer (forvetig, varias osv.) ka gi
Tidligere sett på KLMED8004 Medisisk statistikk Del I, høst 008 Estimerig Hvorda kjete sasylighetsfordeliger (biomialfordelig, ormalfordelig) med kjete populasjosparametrer (forvetig, varias osv.) ka gi
Terminprøve R2 Høsten 2014 Løsning
 Termiprøve R Høste 04 Løsig Del Tid: 3 timer Hjelpemidler: Skrivesaker Oppgave (6 poeg) E flate i rommet er gitt ved likige: x 4x y 6y z 8z 0 0 a) Vis at puktet P3, 5, ligger på flate Puktet P3, 5, ligger
Termiprøve R Høste 04 Løsig Del Tid: 3 timer Hjelpemidler: Skrivesaker Oppgave (6 poeg) E flate i rommet er gitt ved likige: x 4x y 6y z 8z 0 0 a) Vis at puktet P3, 5, ligger på flate Puktet P3, 5, ligger
Numeriske metoder: Euler og Runge-Kutta Matematikk 3 H 2016
 Numeriske metoder: Euler og Ruge-Kutta Matematikk 3 H 06 Iledig Differesiallikiger spiller e setral rolle i modellerigsproblemer i igeiør viteskap, matematikk, fsikk, aeroautikk, astroomi, damikk, elastisitet,
Numeriske metoder: Euler og Ruge-Kutta Matematikk 3 H 06 Iledig Differesiallikiger spiller e setral rolle i modellerigsproblemer i igeiør viteskap, matematikk, fsikk, aeroautikk, astroomi, damikk, elastisitet,
1 Algebra. Innhold. Algebra S2
 Algebra S Algebra Ihold Kompetasemål Algebra, S.... Tallfølger... 3 Formler som beskriver tallfølger... 5 Aritmetiske tallfølger... 9 Geometriske tallfølger... 0. Tallrekker... Aritmetiske rekker... 3
Algebra S Algebra Ihold Kompetasemål Algebra, S.... Tallfølger... 3 Formler som beskriver tallfølger... 5 Aritmetiske tallfølger... 9 Geometriske tallfølger... 0. Tallrekker... Aritmetiske rekker... 3
