Kap 28: Magnetiske kilder

Transkript

1 Kap Magnetisme Magnetostatikk (ingen tidsvaiasjon): Kap 7. Magnetiske kefte Kap 8: Magnetiske kilde Elektodynamikk: Kap 9-31: Tidsvaiasjon: Induksjon mm. Kap 8: Magnetiske kilde Elektostatikk: Ladning q påvikes av kaft qe Definisjon E-felt E-feltet skapes fa ladninge (Coulombs lov) (Coulombs lov) Magnetostatikk: Ladning q i bevegelse påvikes av kaft qv x B Definisjon B-felt (Loentzkafta) B-feltet skapes fa ladninge i bevegelse (Biot-Savats lov) Hjelpelove: Elektostatikk: Gauss lov Magnetostatikk: Ampees lov Magnetiske mateiale Feomagnetisk mateiale. Magnetiseing. M-vekto og H-vekto. Elmag og elativitetsteoi i Notat 3 Einsteins utledning av spesiell elativitetsteoi va devet av dette poblemet i elektomagnetismen: Elektiske og magnetiske kefte e to side av samme sak, avhengig av efeansesystemet det hele obsevees i Bevegelse av ladninge gi magnetfelt B m qv i bevegelse: B = 4 p (8.) m qv = 3 4 p m Ids (Biot-Savats lov) db = 4 p m Ids = (8.6) 3 4 p Enkeltladning Støm i lede: : Vitenskapelig abeid: Hans Chistian Østed, Andé Ampee, Jean-Baptist Biot, Felix Savat, Michael Faaday, Joseph Heny Enhetsvekto Enhetsvekto 1

2 Kap Bevegelse av ladninge gi magnetfelt B m qv B = 4 p m I ds db Enkeltladning: (8.) = 4 p Stømelement: (8.6) Eks. 1 (Y&F Kap. 8.3): B-felt på midtnomal til ett lede Foelesning: y z x ρ m Støm i lede: I ds db = (8.7) 4 (Biot-Savats lov) p ò ledning Biot-Savat: db m 4 Ids = p Y&F Figue 8.5 Rottmann integaltabell (s. 137) Rett lede lengde a: m a 1 B= I j 4p a + (8.8) Y&F Figue 8.5 Næme ett lede (a >>ρ): B m I = p (8.9) X = z + ρ, dvs: x = z a = 1 b = c = ρ Y&F Fig. 8.6

3 Kap Felt undt uendelig lang, ett lede: m I m -7 B =, = 1 Tm/A p p Eksemple: 1) Unde én kaftledning: I = 1 ka, ρ = 1 m ) Næ f. eks. håføne: I = 3 A, ρ = 5 cm => B = μt => B = 1 μt Jodmagnetismen: B =,5 G = 5 μt (statisk felt) Gjelde vekselfelt 5 Hz: Gensevedien e μt fo befolkningen Ved nybygg elle nye anlegg hvo åsgjennomsnittet oveskide,4 μt, skal tiltak vudees. 1) og ) gjelde fo enkeltledee: Fo to ledee med motsatt støm elle tefase bli B-feltet betydelig lavee. Fa: Magnetfelt fa to paallelle ledee (Ex. 8.4 i Y&F) Utafo koaksialkabel e B-feltet null! Ytteisolasjon Yttelede Svakee B enn enkeltlede Stekee B enn enkeltlede d Inneisolasjon Innelede Me seinee, bl.a. oppgave i egneøving. Fo >> d: B-felt avta med 1/, dvs. betydelig askee enn fo enkeltlede. (Fig 8.7) Y&F Fig

4 Kap B-felt undt uendelig lang, ett lede: Retning: asimutalt (φ-etning) = avstand fa ledeen Sammenlikn med: E-felt undt uendelig lang, ladd ett lede: Retning: adielt (-etning) = avstand fa ledeen 1 B = m p 1 1 E = pe I l Linjeladn. λ Elektostatikk: 1 q E = (Coulombs lov) 4 pe Magnetostatikk: Enkeltladning: m qv B = (8.) 4 p Støm i lede: I ds B = db m = (8.7) (Biot-Savat) ò 4 p ò Eks. 1: Rett lede 8.4 Definisjon 1 ampee Eks. : Sikulæ sløyfe Ampees lov Kap 8: Magnetiske kilde ledn. ledn : Vitenskapelig abeid: Hans Chistian Østed, Andé Ampee, Jean-Baptist Biot, Felix Savat, Michael Faaday, Joseph Heny 8.4 Kaft mellom to paallelle ledee F = I 1 I μ /(π) Figue 8.9 Definisjon 1 A: 1-7 N/m = 1 A 1 A μ /(π 1 m).. e i paksis definisjon av μ : μ = π 1-7 N/A = 4π 1-7 Tm/A Definisjon av 1 ampee (gunnenhet i SI-systemet) En ampee e den konstante elektiske stømmen som fambinge en gjensidig lineæ kaft på 1-7 newton pe mete lede nå stømmen gå gjennom hve av to ettlinjete, paallelle, uendelige lange ledee med sikulæt og neglisjebat lite tvesnitt, og ledene e anbakt i én metes innbydes avstand i tomt om. ampee e en av sju SI-gunnenhete: mete kilogam sekund ampee kelvin mol candela - lengde - masse - tid - stømstyke - tempeatu - stoffmengde - lysstyke Alle ande enhete e avledet fa disse, fo eksempel N = kg m s - V = J/C = kg m s -3 A -1 (se fomelaket) 4

5 Kap Øving 9, flevalg: Øving 9, oppgave 3 Young & Feedman, kap..: Elek. fluks = fluks til D-feltet Φ = D A i L i Aksel. ½ m i v i = q i V (1) buke: Elek. fluks = fluks til E-feltet F c = F B () Φ E = E A a) Likn. (1) fo potonet b) Likn () fo potonet c) Søk ette massefoholdet m 1 /m p med likn (1) og () fo masse 1 og fo potonet. Tilsvaende fo m /m p (Fig 8.1) Eks. : Feltet på aksen i en sikulæ stømsløyfe: (kap 8.5) Langs aksen gå feltet paallelt med aksen (Fig 8.15) Eks. : Feltet på aksen i en sikulæ stømsløyfe Langt unna x >> a: mia Bx ( ) = i (8.15) 3/ ( x + a ) sløyfas dipolmoment μ = Iπa m Ia m m Bx ( ) = = x p x i 3 3 μ a (Fig 8.14) mi Bmax = B( x= ) = a mia Bx ( ) = i (8.15) 3/ ( x + a ) Analogi: Langt unna elektisk dipol: 1 Ex ( ) = pe p 3 x p (Fig 8.15) x 5

6 Kap Tondheim 51,5 μt B-felt i nt Fa: en.wikipedia.og/wiki/eath%7s_magnetic_field Plasseing magnetisk pol Tondheim 1,8 østlig misvisning Tondheim φ=75o φ Fa: en.wikipedia.og/wiki/eath%7s_magnetic_field Resultat i Eks. 1: Retning: asimutalt (φ-etning) B-felt næme ett lede (elle uendelig lang lede): B= m I p j (8.9) Y&F Fig. 8.6 j Fa: en.wikipedia.og/wiki/eath%7s_magnetic_field 6

7 Kap Ampees lov B ds = μ I ove lukka kuve, de I e totalstøm innenfo kuva Eks. 4: Solenoide (mange sikulæe stømsløyfe) (Fig 8.17) Gjelde alle integasjonsvege, (Fig 8.) men e nyttig kun i (sylinde)symmetiske konfiguasjone. F. eks. undt lede: B = μ I/π Eks: N=4 l=,1m I=5,A => B = 5 mt Støe støm gi oppvaming. (beegnes Reell B(x) i Øv.11 opg. 5) Tilnæmet B(x) Se bot fa andeffekte: Inni: B = μ I N/l Utafo: B= E i paallellplatekondensato B i solenoide E= utafo a l B= utafo d E Idealiset B OK nå d << A OK nå a << l B inni og utafo en sylindelede med analog til unifom støm I B e asimutal E inni og utafo en sylinde med unifom ladning λ E e adiell (Ex. 8.9) E ( Ex. 3.1) Reelt E = λ/(πε ) /R E = λ/(πε ) 1/ (Fig 8.) (Fig..1a) 7

8 Kap Feltet i tooid solenoide: (Ex. 8.1) Ampees lov B ds = μ I (Amp) ove lukka kuve, de I e totalstøm innenfo kuva cul B = μ J (Amp-diff) (Fig 8.5) Path 1: I incl = => B = Path : I incl = NI => B μ NI/π Path 3: I incl = NI + N(-I) = => B = cul -- kan i vannstøm demonstees med et (infinitesimalt) skovlhjul: Eks. 5: Feltet inni og utafo en ledning Ampee: cul B = μ J Γ Inni: μ J = cul B Utafo: μ J = = cul B (Fig 8.) (Fig 8.19) 8

9 Kap Cul inni ledeen: Katesiske kood (Eks. foige time): B( xyz,, ) = [ y, - x,] = yi -xj Sylindekood: B (, j, z) =-j J = cul B=- k Dvs. homogen stømtetthet, som inni ledeen. OBS: Konstante utelatt, feil enhete fo B og J. i j k æ - ( x) yö cul B = = i+ j+ - k =-k x y z ç è x y ø y -x cul B x B y yte B = Atomæe magnetiske moment μ (= dm i ) i yte magnetisk felt B yte B M Paamagnetiske og feomagnetiske: Innetting av magn.moment μ Te type magnetisk mateiale: B = μ μ H Type Effekt B-felt Åsak: Yte H.. indusee magn.mom. μ med μ (-H) Diamagnetisk Paamagnetisk Feomagnetisk B-felt B-felt innette pemanente μ med μ H innette pemanente μ med μ H Mange μ avhengig H og tid (hysteese) 9

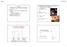
10 Kap Feomagnetiske mateiale Feomagnetic Diamagnetic Paamagnetic M M Yte H = : Magn.moment μ samodnet innenfo domene (~1 μm) H Middels H-felt: Domene med magn.moment μ i samme etning som H vokse i støelse H Steke H-felt: Magnetisk moment innen domene otee til H => Metning Fig: en.wikipedia.og/wiki/magnetic_domain Ulike gade av hysteese i feomagnetisk mateiale Hva vi ha læt: Magnetisk feltstyke: H = B/μ (i tomom) H H H Magnetiseing, definisjon: M = μ / volum Magnetiseing, ekspeimentelt: M = χ m H Totalt B-felt i magnetisk mateiale: B = μ H + μ M = μ H + μ χ m H = μ μ H, elativ pemeabilitet: μ = χ m +1 B M Hadt jen: pemanentmagnete av/på-magnete (eks. haddisk) Bløtt jen: tanfomatoe Y&F Figue 8.9 Ampees lov på ny, enkel fom: B ds = μ I => H ds = I cul B = μ J => cul H = J 1

11 Kap Eks. 6B. Halvfylt solenoide.... μ B = B 1 μ 1 B = μ H B 1 = μ 1 H.... B 1 = μ 1 H Kontinuitetskav ove genseflate (skille i μ ): 1) B kontinuelig ) H diskontinuelig (fakto μ ) 3) H kontinuelig 4) B diskontinuelig (fakto μ ) H = ni B = μ H Eks. 7 Luftgap i magnet Magnetgap til buk fo å skive på haddisk, video og lignende Lite gap: B luft B jen Stot gap: B luft minde B-feltlinje følge jenet 11

12 Kap Kap. 8: Oppsummeing: Kilde til magnetisk felt Bevegelse av ladninge e kilde fo magnetfelt B Enkeltladning i bevegelse: m qv B = 4 p m Ids Støm i lede: db = (Biot-Savats lov) 4 p Magnetfelt B kan finnes ved integasjon ove lede fa Biot-Savats lov -- elle ved buk av: Ampees lov: B ds = μ I H ds = I de I e støm innenfo den lukkede integasjonsvegen. Diffeensialfom: cul B = μ J cul H = J Viktige anvendelse: Rett lede, solenoide, m.m. Kap. 8: Oppsummeing: Magnetiske mateiale Mateiale kan magnetisees: M = χ m H Diamagnetiske: χ m liten, negativ Paamagnetiske: χ m liten, positiv Feomagnetiske: χ m sto positiv Stømme skape magnetisk feltstyke H og flukstetthet: B = μ H + μ M = μ H + μ χ m H = μ μ H.. altså avhengig av elativ pemeabilitet μ og demed av mateialet. I alle tidligee fomle kan vi estatte μ med μ = μ μ Kontinuitetskav ove genseflate (skille i μ ): [Me i Notat 6] B kontinuelig B diskontinuelig H diskontinuelig H kontinuelig Maxwells likninge i Notat 4 Integalfom Diffeensialfom Gauss lov D Gauss lov B Ampees lov Faadays lov 1