MA2501 Numerical methods
|
|
|
- Rune Caspersen
- 7 år siden
- Visninger:
Transkript
1 MA250 Numerical methods Solutions to problem set Problem a) The function f (x) = x 3 3x + satisfies the following relations f (0) = > 0, f () = < 0 and there must consequently be at least one zero for f (x) in the interval (0, ). Moreover, as f (x) = 3x 2 3 = 3( x 2 ) < 0 for x (0, ), the function is strictly decreasing in (0, ) and there can thus be at most one zero in (0, ). The zero of f (x) in [0, ] is consequently unique. The function f 2 (x) = cos(x) cos(3x) satsifies the following relations f 2 () = cos() cos(3) > 0, f 2 (2) = cos(2) cos(6) < 0 and there must consequently be at least one zero for f 2 (x) in the interval (, 2). Moreover, as f 2(x) = 3 sin(3x) sin(x) < 0 for x (, 2) the function can have at most one zero in (, 2). The zero of f 2 (x) in [, 2] is thus unique. Alternatively one can use the trigonometric identity at page 92 in the textbok and rewrite f 2 in the form f 2 (x) = 4 sin(x) 2 cos(x). The zero of this function in the interval (, 2) is at x = π/2.
2 With a little bit of inspection we see that f 3 (x) = x 3 6x 2 + 2x 8 = (x 2) 3 which means that the zero of f 3 (x) in [.5, 3] is unique (x = 2) and of multiplicity 3. b) We will apply the bisection method (intervallhalvvering) to locate the zero of f 2 (x) in [, 2]. Starting with we find i) ii) iii) iv) a 0 =, f 2 (a 0 ) > 0 b 0 = 2, f 2 (b 0 ) < 0 c 0 = 2 (a 0 + b 0 ) =.5, f 2 (c 0 ) > 0. The zero of f 2 (x) is thus in the interval (c 0, b 0 ), so we set a = c 0 =.5, b = b 0 = 2 and start over. c = 2 (a + b ) =.75, f 2 (c ) < 0. The zero of f 2 (x) is thus in the interval (a, c ), so we set a 2 = a =.5, b 2 = c =.75 and start over. c 2 = 2 (a 2 + b 2 ) =.625, f 2 (c 2 ) < 0. The zero of f 2 (x) is thus in the interval (a 2, c 2 ), so we set a 3 = a 2 =.5, b 3 = c 2 =.625 and start over. c 3 = 2 (a 3 + b 3 ) =.5625, f 2 (c 3 ) > 0. The zero of f 2 (x) is thus in the interval (c 3, b 3 ). We may continue the process, but accurately locating the zero by means of the bisection method is too tedious for hand calculation. Four iterations of the bisection method thus locates the zero of f 2 (x) on [, 2] to the more narrow interval (.5625,.625). Newton s method, however, is in this case defined by the scheme x n+ = x n f 2(x n ) f 2 (x n) = x n cos(x n) cos(3x n ) 3 sin(3x n ) sin(x n ) () 2
3 Table : Newton iterates () from x 0 =.5 n x n for all n 0. Choosing x 0 =.5 and performing four iterations of () we find the iterates in Table. In fact, as may be seen by inspection, the exact solution to f 2 (x) = 0 is x = π We thus see that merely four iterations of () is sufficient to compute the exact solution to f 2 (x) = 0 to at least 6 significant digits. This is an example of the rapid convergence often exhibited by Newton s method when started sufficiently close to the exact solution. c) Not shown here. d) A suggested improvement is available as a function newton_improved (in newton_improved.m) from the course homepage. e) The zero of f (x) on [0, ] may be found using fzero by implementing a function f (in f.m) as function y = f(x) % f -- Implement function f from problem set, MA250. y = x.^3-3*x + ; and then calling fzero as >> x = fzero( f, [0, ]) x = The same procedure may be applied to functions f 2 (x) and f 3 (x). 3
4 Oppgave a) Vi vet at r = Ae e = A r. La være en vektornorm på R n med en tilhørende avledet (subordinat) matrisenorm på R n n. Siden blir Ax A = sup Ax A x, x 0 x e x = A r A r x x = r A A A x som var det vi skulle vise. A A r Ax = A A r r = κ(a) b b b) «Problem» Vi finner at [ ] [ ] r =, ẽ =, [ ] [ ] ˆr =, ê = Vi observerer altså at løsningen med størst residual ( r = ) har klart minst feil ( ẽ = 0.00). Dette skyldes at matrisen A er dårlig kondisjonert. Spesielt finner vi at κ (A) = A A Videre er x =, ê = 0.93, ˆr = og b = Dermed er feilestimatet oppfylt for både ẽ og ê. Eksemplet viser altså at man må være forsiktig med å bruke residualet som eneste indikator på feilen hvis koeffisientmatrisen er dårlig kondisjonert. c) Vi velger eksaktløsning x = [,,..., ] T. For n = 0 kan vi da løse problemet ved matlab-setningene n = 0; x = ones([n, ]); A = hilb(n); b = A * x; xt = A \ b; e = norm(x - xt, inf) k = cond(a, inf) 4
5 n x x κ (A) Table 2: Feil og kondisjonstall for system basert på Hilbertmatrisen. n x x κ (A) Table 3: Feil og kondisjonstall for system basert på en tilfeldig matrise. Resultatene er oppsummert i Tabell 2. De samme eksperimentene med utgangspunkt i en tilfeldig matrise av tilfeldige tall, definert i matlab som A = rand(n), gir derimot resultatene i Tabell 3. Dine egne resultater vil sannsynligvis variere noe fra disse. Dette viser imidlertid at kondisjonstallet for Hilbertmatrisen er ganske ekstremt. På den annen side vil vi normalt måtte forvente at kondisjonstallet vokser med økende dimensjon på matrisen. Oppgave 2 Kincaid & Cheney, «Problem» Vi skal løse ligningssystemet 2x + 3x 2 = 8 x + 2x 2 x 3 = 0 3x + 2x 3 = 9 ved help av Gausseliminasjon med skalert delvis pivotering. Denne metoden er beskrevet i boka på side 280 og utover. 5
6 Vi skriver ligningssystemet på formen Ax = b og får x x 2 = 8 0. (2) x 3 9 Først beregner vi skaleringsfaktoren til hver rad i A. Skaleringsfaktoren er den største absoluttverdien i hver rad, det vil si s i = max j n a ij for hver rad i n. Skaleringsfaktorene beregnes kun én gang. Vi får s = 3, s 2 = 2, s 3 = 3. I skritt k velger vi som pivotligning den rad i A der forholdet a ik / s i, i I er størst. I er her mengden av «gjenværende» pivotrader. I skritt finner vi a s = 2/3, a 2 s 2 = /2, a 3 s 3 =, så vi velger ligning 3 som pivotrad. Ett skritt i Gaussprosessen gir da x /3 x 2 2 x 2 = /3 x 2 = x x 3 9 I skritt 2 beregner vi for de gjenværende radene i I = {, 2} a 2 s = 3/3 =, a 22 s 2 = så vi velger rad som pivotrad fordi den har lavest indeks. Ett skritt i Gaussprosessen gir da 0 3 4/3 x /3 x /3 x 2 = /9 x 2 = 5/ x x 3 9 Den siste pivotraden som vi ikke gjør noe med blir rad 2. Vi gjør tilbakesubstituering i samme motsatt rekkefølge av den rekkefølgen vi fikk for pivotradene, altså 2,, 3. Det gir x 3 = 5/9 5/3 = 3, x 2 = 3 (4/ ) = 2, x = 3 (9 2 3) =. 6
7 Kincaid & Cheney, «Problem» 8..4 Vi er gitt matrisen 2 2 A =. 3 2 a) Vi skal vise at A ikke kan LU-faktoriseres, det vil si A kan ikke skrives som et produkt av en nedre enhetstriangulær matrise L og en øvre triangulær matrise U. En matrise kan LU-faktoriseres hvis og bare hvis naiv Gausseliminasjon ikke stopper opp på grunn av null som pivotelement (se forøvrig side 38 i C & K). Vi utfører et skritt med naiv Gausseliminasjon: /2 0 /2 Vi ser at a 22 = 0. Matrisen A har dermed ingen LU-faktorisering. b) Vi skal vise at vi ved å bytte om radene i matrisen A kan produsere en matrise som har en LU-faktorisering. Vi ser at problemet med A er at a = a 2 og a 2 = a 22. Det betyr at eliminasjon av a 2 ved hjelp av a også vil eliminere a 22 ved «hjelp» av a 2. Ved å bytte om radene som rad 2, rad 3 og rad 3 2 får vi da B = Dermed gir ett skritt med Gausseliminasjon Matrisen B, oppnådd ved å permutere radene til A, har altså en LUfaktorisering. 7
MA2501 Numeriske metoder
 MA2501 Numeriske metoder Løsningsforslag, øving 7 Oppgave 1 a) Vi vet at r = Ae e = A 1 r. La være en vektornorm på R n med en tilhørende avledet (subordinat) matrisenorm på R n n. Siden blir Ax A = sup
MA2501 Numeriske metoder Løsningsforslag, øving 7 Oppgave 1 a) Vi vet at r = Ae e = A 1 r. La være en vektornorm på R n med en tilhørende avledet (subordinat) matrisenorm på R n n. Siden blir Ax A = sup
MA2501 Numeriske metoder
 MA250 Numeriske metoder Oppgave Løsningsforslag, øving 7 a) Vi vet at r = Ae e = A r. La være en vektornorm på R n med en tilhørende avledet (subordinat) matrisenorm på R n n. Siden blir Ax A = sup Ax
MA250 Numeriske metoder Oppgave Løsningsforslag, øving 7 a) Vi vet at r = Ae e = A r. La være en vektornorm på R n med en tilhørende avledet (subordinat) matrisenorm på R n n. Siden blir Ax A = sup Ax
Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl.
 1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
1 MAT131 Bokmål Universitetet i Bergen Det matematisk-naturvitenskapelige fakultet Eksamen i emnet Mat131 - Differensiallikningar I Onsdag 25. mai 2016, kl. 09-14 Oppgavesettet er 4 oppgaver fordelt på
TMA4329 Intro til vitensk. beregn. V2017
 Norges teknisk naturvitenskapelige universitet Institutt for Matematiske Fag TMA439 Intro til vitensk. beregn. V17 ving 4 [S]T. Sauer, Numerical Analysis, Second International Edition, Pearson, 14 Teorioppgaver
Norges teknisk naturvitenskapelige universitet Institutt for Matematiske Fag TMA439 Intro til vitensk. beregn. V17 ving 4 [S]T. Sauer, Numerical Analysis, Second International Edition, Pearson, 14 Teorioppgaver
Trigonometric Substitution
 Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
Trigonometric Substitution Alvin Lin Calculus II: August 06 - December 06 Trigonometric Substitution sin 4 (x) cos (x) dx When you have a product of sin and cos of different powers, you have three different
TMA4122/TMA4130 Matematikk 4M/4N Høsten 2010
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4122/TMA410 Matematikk 4M/4N Høsten 2010 1 Oppgave: Løs følgende ligningssystemer ved hjelp av Gauss-eliminasjon med delvis
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA4122/TMA410 Matematikk 4M/4N Høsten 2010 1 Oppgave: Løs følgende ligningssystemer ved hjelp av Gauss-eliminasjon med delvis
Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger
 Institutt for matematiske fag Eksamensoppgave i TMA432 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 453 163 Eksamensdato: 8. august 217 Eksamenstid (fra
Institutt for matematiske fag Eksamensoppgave i TMA432 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 453 163 Eksamensdato: 8. august 217 Eksamenstid (fra
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT2400 Analyse 1. Eksamensdag: Onsdag 15. juni 2011. Tid for eksamen: 09.00 13.00 Oppgavesettet er på 6 sider. Vedlegg: Tillatte
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postponed exam: ECON420 Mathematics 2: Calculus and linear algebra Date of exam: Tuesday, June 8, 203 Time for exam: 09:00 a.m. 2:00 noon The problem set covers
Eksamensoppgave i TMA4135 Matematikk 4D
 Institutt for matematiske fag Eksamensoppgave i TMA435 Matematikk 4D Faglig kontakt under eksamen: Helge Holden a, Gard Spreemann b Tlf: a 92038625, b 93838503 Eksamensdato: 0. desember 205 Eksamenstid
Institutt for matematiske fag Eksamensoppgave i TMA435 Matematikk 4D Faglig kontakt under eksamen: Helge Holden a, Gard Spreemann b Tlf: a 92038625, b 93838503 Eksamensdato: 0. desember 205 Eksamenstid
Slope-Intercept Formula
 LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
LESSON 7 Slope Intercept Formula LESSON 7 Slope-Intercept Formula Here are two new words that describe lines slope and intercept. The slope is given by m (a mountain has slope and starts with m), and intercept
SVM and Complementary Slackness
 SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
SVM and Complementary Slackness David Rosenberg New York University February 21, 2017 David Rosenberg (New York University) DS-GA 1003 February 21, 2017 1 / 20 SVM Review: Primal and Dual Formulations
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Utsatt ksamen i: ECON3120/4120 Matematikk 2: Matematisk analyse og lineær algebra Postponed exam: ECON3120/4120 Mathematics 2: Calculus and linear algebra Eksamensdag:
ECON3120/4120 Mathematics 2, spring 2004 Problem solutions for the seminar on 5 May Old exam problems
 Department of Economics May 004 Arne Strøm ECON0/40 Mathematics, spring 004 Problem solutions for the seminar on 5 May 004 (For practical reasons (read laziness, most of the solutions this time are in
Department of Economics May 004 Arne Strøm ECON0/40 Mathematics, spring 004 Problem solutions for the seminar on 5 May 004 (For practical reasons (read laziness, most of the solutions this time are in
Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger
 Institutt for matematiske fag Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 4503 0163 Eksamensdato: 30. mai 2017 Eksamenstid (fra
Institutt for matematiske fag Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 4503 0163 Eksamensdato: 30. mai 2017 Eksamenstid (fra
Lineære likningssystemer
 Lineære likningssystemer Mange fysiske problemer kan formuleres som lineære likningssystemer i vektorrommet, 1/19 Lu = f Lineær: betyr at virkningen av L på u + v er L(u + v) = Lu + Lv, og skaleres som
Lineære likningssystemer Mange fysiske problemer kan formuleres som lineære likningssystemer i vektorrommet, 1/19 Lu = f Lineær: betyr at virkningen av L på u + v er L(u + v) = Lu + Lv, og skaleres som
Unit Relational Algebra 1 1. Relational Algebra 1. Unit 3.3
 Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
Relational Algebra 1 Unit 3.3 Unit 3.3 - Relational Algebra 1 1 Relational Algebra Relational Algebra is : the formal description of how a relational database operates the mathematics which underpin SQL
Eksamensoppgave i TMA4123/TMA4125 Matematikk 4M/4N
 Institutt for matematiske fag Eksamensoppgave i TMA4123/TMA4125 Matematikk 4M/4N Faglig kontakt under eksamen: Dag Wessel-Berg Tlf: 924 48 828 Eksamensdato: 1. juni 216 Eksamenstid (fra til): 9: 13: Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i TMA4123/TMA4125 Matematikk 4M/4N Faglig kontakt under eksamen: Dag Wessel-Berg Tlf: 924 48 828 Eksamensdato: 1. juni 216 Eksamenstid (fra til): 9: 13: Hjelpemiddelkode/Tillatte
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON360/460 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON360/460 - Resource allocation and economic policy Eksamensdag: Fredag 2. november
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. juni 2010 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3120/4120 Mathematics 2: Calculus an linear algebra Exam: ECON3120/4120 Mathematics 2: Calculus an linear algebra Eksamensag: Tirsag 3. juni 2008
Elementære eliminasjonsmatriser
 Elementære eliminasjonsmatriser Gitt en vektor a = [a 1,..., a n ] T, en matrise 1 0 0 0.......... M k = 0 1 0 0 0 a k+1 a k 1 0, a k 0,.......... 0 an a k 0 1 kalles elementære eliminasjonsmatriser eller
Elementære eliminasjonsmatriser Gitt en vektor a = [a 1,..., a n ] T, en matrise 1 0 0 0.......... M k = 0 1 0 0 0 a k+1 a k 1 0, a k 0,.......... 0 an a k 0 1 kalles elementære eliminasjonsmatriser eller
Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2
![Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2 Mathematics 114Q Integration Practice Problems SOLUTIONS. = 1 8 (x2 +5x) 8 + C. [u = x 2 +5x] = 1 11 (3 x)11 + C. [u =3 x] = 2 (7x + 9)3/2](/thumbs/77/75859899.jpg) Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Mathematics 4Q Name: SOLUTIONS. (x + 5)(x +5x) 7 8 (x +5x) 8 + C [u x +5x]. (3 x) (3 x) + C [u 3 x] 3. 7x +9 (7x + 9)3/ [u 7x + 9] 4. x 3 ( + x 4 ) /3 3 8 ( + x4 ) /3 + C [u + x 4 ] 5. e 5x+ 5 e5x+ + C
Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with.
![Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with. Solutions #12 ( M. y 3 + cos(x) ) dx + ( sin(y) + z 2) dy + xdz = 3π 4. The surface M is parametrized by σ : [0, 1] [0, 2π] R 3 with.](/thumbs/80/81672304.jpg) Solutions #1 1. a Show that the path γ : [, π] R 3 defined by γt : cost ı sint j sint k lies on the surface z xy. b valuate y 3 cosx dx siny z dy xdz where is the closed curve parametrized by γ. Solution.
Solutions #1 1. a Show that the path γ : [, π] R 3 defined by γt : cost ı sint j sint k lies on the surface z xy. b valuate y 3 cosx dx siny z dy xdz where is the closed curve parametrized by γ. Solution.
TMA4240 Statistikk 2014
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Fremgangsmetode: P X 1 < 6.8 Denne kan finnes ved å sette opp integralet over
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Fremgangsmetode: P X 1 < 6.8 Denne kan finnes ved å sette opp integralet over
TFY4170 Fysikk 2 Justin Wells
 TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
TFY4170 Fysikk 2 Justin Wells Forelesning 5: Wave Physics Interference, Diffraction, Young s double slit, many slits. Mansfield & O Sullivan: 12.6, 12.7, 19.4,19.5 Waves! Wave phenomena! Wave equation
Moving Objects. We need to move our objects in 3D space.
 Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
Transformations Moving Objects We need to move our objects in 3D space. Moving Objects We need to move our objects in 3D space. An object/model (box, car, building, character,... ) is defined in one position
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1220 Velferd og økonomisk politikk Exam: ECON1220 Welfare and politics Eksamensdag: 29.11.2010 Sensur kunngjøres: 21.12.2010 Date of exam: 29.11.2010
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1220 Velferd og økonomisk politikk Exam: ECON1220 Welfare and politics Eksamensdag: 29.11.2010 Sensur kunngjøres: 21.12.2010 Date of exam: 29.11.2010
Stationary Phase Monte Carlo Methods
 Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Stationary Phase Monte Carlo Methods Daniel Doro Ferrante G. S. Guralnik, J. D. Doll and D. Sabo HET Physics Dept, Brown University, USA. danieldf@het.brown.edu www.het.brown.edu Introduction: Motivations
Trådløsnett med. Wireless network. MacOSX 10.5 Leopard. with MacOSX 10.5 Leopard
 Trådløsnett med MacOSX 10.5 Leopard Wireless network with MacOSX 10.5 Leopard April 2010 Slå på Airport ved å velge symbolet for trådløst nettverk øverst til høyre på skjermen. Hvis symbolet mangler må
Trådløsnett med MacOSX 10.5 Leopard Wireless network with MacOSX 10.5 Leopard April 2010 Slå på Airport ved å velge symbolet for trådløst nettverk øverst til høyre på skjermen. Hvis symbolet mangler må
Gradient. Masahiro Yamamoto. last update on February 29, 2012 (1) (2) (3) (4) (5)
 Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill
Gradient Masahiro Yamamoto last update on February 9, 0 definition of grad The gradient of the scalar function φr) is defined by gradφ = φr) = i φ x + j φ y + k φ ) φ= φ=0 ) ) 3) 4) 5) uphill contour downhill
Matematikk Øvingsoppgaver i numerikk leksjon 2 Løsningsforslag
 Matematikk 1000 Øvingsoppgaver i numerikk leksjon 2 Løsningsforslag Oppgave 1 Vektorer a) Variablene i MATLAB kan være tall, vektorer eller matriser. Vi kan for eksempel gi vektoren x = [1, 0, 3] på denne
Matematikk 1000 Øvingsoppgaver i numerikk leksjon 2 Løsningsforslag Oppgave 1 Vektorer a) Variablene i MATLAB kan være tall, vektorer eller matriser. Vi kan for eksempel gi vektoren x = [1, 0, 3] på denne
Dynamic Programming Longest Common Subsequence. Class 27
 Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
Dynamic Programming Longest Common Subsequence Class 27 Protein a protein is a complex molecule composed of long single-strand chains of amino acid molecules there are 20 amino acids that make up proteins
SCE1106 Control Theory
 Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, October 26, 2006 SCE1106 Control Theory Exercise 6 Task 1 a) The poles of the open loop system is
Master study Systems and Control Engineering Department of Technology Telemark University College DDiR, October 26, 2006 SCE1106 Control Theory Exercise 6 Task 1 a) The poles of the open loop system is
Numerical Simulation of Shock Waves and Nonlinear PDE
 Numerical Simulation of Shock Waves and Nonlinear PDE Kenneth H. Karlsen (CMA) Partial differential equations A partial differential equation (PDE for short) is an equation involving functions and their
Numerical Simulation of Shock Waves and Nonlinear PDE Kenneth H. Karlsen (CMA) Partial differential equations A partial differential equation (PDE for short) is an equation involving functions and their
Databases 1. Extended Relational Algebra
 Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
Databases 1 Extended Relational Algebra Relational Algebra What is an Algebra? Mathematical system consisting of: Operands --- variables or values from which new values can be constructed. Operators ---
Perpetuum (im)mobile
 Perpetuum (im)mobile Sett hjulet i bevegelse og se hva som skjer! Hva tror du er hensikten med armene som slår ut når hjulet snurrer mot høyre? Hva tror du ordet Perpetuum mobile betyr? Modell 170, Rev.
Perpetuum (im)mobile Sett hjulet i bevegelse og se hva som skjer! Hva tror du er hensikten med armene som slår ut når hjulet snurrer mot høyre? Hva tror du ordet Perpetuum mobile betyr? Modell 170, Rev.
Eksamensoppgave i MA2501 Numeriske metoder
 Institutt for matematiske fag Eksamensoppgave i MA50 Numeriske metoder Faglig kontakt under eksamen: Trond Kvamsdal Tlf: 9305870 Eksamensdato: 3. mai 08 Eksamenstid (fra til): 09:00 3:00 Hjelpemiddelkode/Tillatte
Institutt for matematiske fag Eksamensoppgave i MA50 Numeriske metoder Faglig kontakt under eksamen: Trond Kvamsdal Tlf: 9305870 Eksamensdato: 3. mai 08 Eksamenstid (fra til): 09:00 3:00 Hjelpemiddelkode/Tillatte
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MoD200 Eksamensdag: 15. desember 2003 Tid for eksamen: 14.30 17.30 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MoD200 Eksamensdag: 15. desember 2003 Tid for eksamen: 14.30 17.30 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler:
Matematikk Øvingsoppgaver i numerikk leksjon 2 Løsningsforslag
 Matematikk 1000 Øvingsoppgaver i numerikk leksjon Løsningsforslag Oppgave 1 Vektorer a) Variablene i MATLAB kan være tall, vektorer eller matriser. Vi kan for eksempel gi vektoren x = [1, 0, 3] på denne
Matematikk 1000 Øvingsoppgaver i numerikk leksjon Løsningsforslag Oppgave 1 Vektorer a) Variablene i MATLAB kan være tall, vektorer eller matriser. Vi kan for eksempel gi vektoren x = [1, 0, 3] på denne
Information search for the research protocol in IIC/IID
 Information search for the research protocol in IIC/IID 1 Medical Library, 2013 Library services for students working with the research protocol and thesis (hovedoppgaven) Open library courses: http://www.ntnu.no/ub/fagside/medisin/medbiblkurs
Information search for the research protocol in IIC/IID 1 Medical Library, 2013 Library services for students working with the research protocol and thesis (hovedoppgaven) Open library courses: http://www.ntnu.no/ub/fagside/medisin/medbiblkurs
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON30/40 Matematikk : Matematisk analyse og lineær algebra Exam: ECON30/40 Mathematics : Calculus and Linear Algebra Eksamensdag: Tirsdag 0. desember
Trust region methods: global/local convergence, approximate January methods 24, / 15
 Trust region methods: global/local convergence, approximate methods January 24, 2014 Trust region methods: global/local convergence, approximate January methods 24, 2014 1 / 15 Trust-region idea Model
Trust region methods: global/local convergence, approximate methods January 24, 2014 Trust region methods: global/local convergence, approximate January methods 24, 2014 1 / 15 Trust-region idea Model
Eksamen i TMA4123/TMA4125 Matematikk 4M/N
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Anne Kværnø: mobil 92663824 Eksamen i TMA423/TMA425 Matematikk 4M/N Bokmål Mandag 2.
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Anne Kværnø: mobil 92663824 Eksamen i TMA423/TMA425 Matematikk 4M/N Bokmål Mandag 2.
Kurskategori 2: Læring og undervisning i et IKT-miljø. vår
 Kurskategori 2: Læring og undervisning i et IKT-miljø vår Kurs i denne kategorien skal gi pedagogisk og didaktisk kompetanse for å arbeide kritisk og konstruktivt med IKT-baserte, spesielt nettbaserte,
Kurskategori 2: Læring og undervisning i et IKT-miljø vår Kurs i denne kategorien skal gi pedagogisk og didaktisk kompetanse for å arbeide kritisk og konstruktivt med IKT-baserte, spesielt nettbaserte,
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Date of exam: Friday, May
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Exam: ECON320/420 Mathematics 2: Calculus and Linear Algebra Eksamen i: ECON320/420 Matematikk 2: Matematisk analyse og lineær algebra Date of exam: Friday, May
FYSMEK1110 Eksamensverksted 23. Mai :15-18:00 Oppgave 1 (maks. 45 minutt)
 FYSMEK1110 Eksamensverksted 23. Mai 2018 14:15-18:00 Oppgave 1 (maks. 45 minutt) Page 1 of 9 Svar, eksempler, diskusjon og gode råd fra studenter (30 min) Hva får dere poeng for? Gode råd fra forelesere
FYSMEK1110 Eksamensverksted 23. Mai 2018 14:15-18:00 Oppgave 1 (maks. 45 minutt) Page 1 of 9 Svar, eksempler, diskusjon og gode råd fra studenter (30 min) Hva får dere poeng for? Gode råd fra forelesere
Øving 5 - Fouriertransform - LF
 Øving 5 - Fouriertransform - LF Obligatoriske oppgaver See the notes Matlab: %x og t aksen x=:.:pi; t=:pi/:*pi; %sette opp funksjon og plotte hver frame for j=:length(t) %funksjonsverdier p innev rende
Øving 5 - Fouriertransform - LF Obligatoriske oppgaver See the notes Matlab: %x og t aksen x=:.:pi; t=:pi/:*pi; %sette opp funksjon og plotte hver frame for j=:length(t) %funksjonsverdier p innev rende
EKSAMEN I NUMERISK LINEÆR ALGEBRA (TMA4205)
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Kontakt under eksamen Navn: Bawfeh Kingsley Kometa kontor: 7359975, mobil: 936 24 483) Sensur: 06.0.20 EKSAMEN I NUMERISK
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 Kontakt under eksamen Navn: Bawfeh Kingsley Kometa kontor: 7359975, mobil: 936 24 483) Sensur: 06.0.20 EKSAMEN I NUMERISK
TMA4240 Statistikk Høst 2013
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 575 2 ). Ved bruk av tabell A.3 finner
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 6, blokk I Løsningsskisse Oppgave 1 Vi antar X er normalfordelt, X N(3315, 575 2 ). Ved bruk av tabell A.3 finner
Oppgave. føden)? i tråd med
 Oppgaver Sigurd Skogestad, Eksamen septek 16. des. 2013 Oppgave 2. Destillasjon En destillasjonskolonne har 7 teoretiske trinn (koker + 3 ideelle plater under føden + 2 ideellee plater over føden + partielll
Oppgaver Sigurd Skogestad, Eksamen septek 16. des. 2013 Oppgave 2. Destillasjon En destillasjonskolonne har 7 teoretiske trinn (koker + 3 ideelle plater under føden + 2 ideellee plater over føden + partielll
GEOV219. Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet postbachelor phd
 GEOV219 Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet postbachelor phd Mener du at de anbefalte forkunnskaper var nødvendig? Er det forkunnskaper du har savnet? Er det forkunnskaper
GEOV219 Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet postbachelor phd Mener du at de anbefalte forkunnskaper var nødvendig? Er det forkunnskaper du har savnet? Er det forkunnskaper
Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger
 Institutt for matematiske fag Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 4503 0163 Eksamensdato: 30. mai 2017 Eksamenstid (fra
Institutt for matematiske fag Eksamensoppgave i TMA4320 Introduksjon til vitenskapelige beregninger Faglig kontakt under eksamen: Anton Evgrafov Tlf: 4503 0163 Eksamensdato: 30. mai 2017 Eksamenstid (fra
32.2. Linear Multistep Methods. Introduction. Prerequisites. Learning Outcomes
 Linear Multistep Methods 32.2 Introduction In the previous Section we saw two methods (Euler and trapezium) for approximating the solutions of certain initial value problems. In this Section we will see
Linear Multistep Methods 32.2 Introduction In the previous Section we saw two methods (Euler and trapezium) for approximating the solutions of certain initial value problems. In this Section we will see
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON20/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Fredag 2. mai
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON20/420 Matematikk 2: Matematisk analyse og lineær algebra Exam: ECON20/420 Mathematics 2: Calculus and Linear Algebra Eksamensdag: Fredag 2. mai
Ma Linær Algebra og Geometri Øving 1
 Ma0 - Linær Algebra og Geometri Øving Øistein Søvik 0. september 0 Excercise Set. = 4 x6 x x = x 6 4 x x = x 4 4 4 x x. In each part, determine whether the equation is linear in x, x and x Før vi begynner
Ma0 - Linær Algebra og Geometri Øving Øistein Søvik 0. september 0 Excercise Set. = 4 x6 x x = x 6 4 x x = x 4 4 4 x x. In each part, determine whether the equation is linear in x, x and x Før vi begynner
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF 3230 Formell modellering og analyse av kommuniserende systemer Eksamensdag: 4. april 2008 Tid for eksamen: 9.00 12.00 Oppgavesettet
x(x 1)(x 2) p(x) = 3,0 1( 1 1)( 1 2) Newtons interpolasjonsformel: Tabellen over dividerte differenser er gitt ved
 NTNU Institutt for matematiske fag TMA35 Matematikk D eksamen 20. desember 200 Løsningsforslag Oppgaven kan, for eksempel, løses ved hjelp av Lagrange-interpolasjon eller Newtons interpolasjonsformel.
NTNU Institutt for matematiske fag TMA35 Matematikk D eksamen 20. desember 200 Løsningsforslag Oppgaven kan, for eksempel, løses ved hjelp av Lagrange-interpolasjon eller Newtons interpolasjonsformel.
f (x) = a 0 + a n cosn π 2 x. xdx. En gangs delvisintegrasjon viser at 1 + w 2 eixw dw, 4 (1 + w 2 ) 2 eixw dw.
 NTNU Institutt for matematiske fag Eksamen i TMA Matematikk M høsten 008 Løsningsforslag a Cosinusrekka til f blir av formen - 0 6 f (x a 0 + n0 a n cosn π x Vi har a 0 0, og a n R 0 f (xcosnπ xdx En gangs
NTNU Institutt for matematiske fag Eksamen i TMA Matematikk M høsten 008 Løsningsforslag a Cosinusrekka til f blir av formen - 0 6 f (x a 0 + n0 a n cosn π x Vi har a 0 0, og a n R 0 f (xcosnπ xdx En gangs
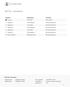
1 Oppgave 1 Skriveoppgave Manuell poengsum. 2 Oppgave 2 Code editor Manuell poengsum. 3 Oppgave 3 Skriveoppgave Manuell poengsum
 MAT102 - Demoprøve Oppgaver Oppgavetype Vurdering Forside Dokument Ikke vurdert 1 Oppgave 1 Skriveoppgave Manuell poengsum 2 Oppgave 2 Code editor Manuell poengsum 3 Oppgave 3 Skriveoppgave Manuell poengsum
MAT102 - Demoprøve Oppgaver Oppgavetype Vurdering Forside Dokument Ikke vurdert 1 Oppgave 1 Skriveoppgave Manuell poengsum 2 Oppgave 2 Code editor Manuell poengsum 3 Oppgave 3 Skriveoppgave Manuell poengsum
Verifiable Secret-Sharing Schemes
 Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Aarhus University Verifiable Secret-Sharing Schemes Irene Giacomelli joint work with Ivan Damgård, Bernardo David and Jesper B. Nielsen Aalborg, 30th June 2014 Verifiable Secret-Sharing Schemes Aalborg,
Exercise 1: Phase Splitter DC Operation
 Exercise 1: DC Operation When you have completed this exercise, you will be able to measure dc operating voltages and currents by using a typical transistor phase splitter circuit. You will verify your
Exercise 1: DC Operation When you have completed this exercise, you will be able to measure dc operating voltages and currents by using a typical transistor phase splitter circuit. You will verify your
Neural Network. Sensors Sorter
 CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
CSC 302 1.5 Neural Networks Simple Neural Nets for Pattern Recognition 1 Apple-Banana Sorter Neural Network Sensors Sorter Apples Bananas 2 Prototype Vectors Measurement vector p = [shape, texture, weight]
Fasit MAT102 juni 2016
 Fasit MAT02 juni 206. (a) Finn egenverdiene og egenvektorene til matrisen ( ) 6 A = 2 7 Svar: λ = 8 og ( ) x = y y ( ) /2, λ = 5 og ( ) x = y y ( ) for alle y 0. (b) Finn den generelle løsningen på systemet
Fasit MAT02 juni 206. (a) Finn egenverdiene og egenvektorene til matrisen ( ) 6 A = 2 7 Svar: λ = 8 og ( ) x = y y ( ) /2, λ = 5 og ( ) x = y y ( ) for alle y 0. (b) Finn den generelle løsningen på systemet
6350 Månedstabell / Month table Klasse / Class 1 Tax deduction table (tax to be withheld) 2012
 6350 Månedstabell / Month table Klasse / Class 1 Tax deduction table (tax to be withheld) 2012 100 200 3000 0 0 0 13 38 63 88 113 138 163 4000 188 213 238 263 288 313 338 363 378 386 5000 394 402 410 417
6350 Månedstabell / Month table Klasse / Class 1 Tax deduction table (tax to be withheld) 2012 100 200 3000 0 0 0 13 38 63 88 113 138 163 4000 188 213 238 263 288 313 338 363 378 386 5000 394 402 410 417
SERVICE BULLETINE 2008-4
 S e r v i c e b u l l e t i n e M a t e r i e l l Materiellsjef F/NLF kommuniserer påminnelse omkring forhold som ansees som vesentlige for å orientere om viktige materiellforhold. Målgruppen for Servicbulletinen
S e r v i c e b u l l e t i n e M a t e r i e l l Materiellsjef F/NLF kommuniserer påminnelse omkring forhold som ansees som vesentlige for å orientere om viktige materiellforhold. Målgruppen for Servicbulletinen
TMA4210 Numerisk løsning av part. diff.lign. med differansemetoder Vår 2005
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA40 Numerisk løsning av part. diff.lign. med differansemetoder Vår 005 Løsningsforslag Øving 5 a) Vi skal undersøke stabilitet
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA40 Numerisk løsning av part. diff.lign. med differansemetoder Vår 005 Løsningsforslag Øving 5 a) Vi skal undersøke stabilitet
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 14 juni 2004 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler: INF-MAT2350
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i Eksamensdag: 14 juni 2004 Tid for eksamen: 9.00 12.00 Oppgavesettet er på 5 sider. Vedlegg: Tillatte hjelpemidler: INF-MAT2350
Fagevalueringsrapport FYS Diffraksjonsmetoder og elektronmikroskopi
 Fagevalueringsrapport FYS4340 - Diffraksjonsmetoder og elektronmikroskopi Fall 08 Lecturer:Arne Olsen and Anette Eleonora Gunnæs Fysisk Fagutvalg 4. november 2008 Fagutvalgets kommentar: Fysisk fagutvalg
Fagevalueringsrapport FYS4340 - Diffraksjonsmetoder og elektronmikroskopi Fall 08 Lecturer:Arne Olsen and Anette Eleonora Gunnæs Fysisk Fagutvalg 4. november 2008 Fagutvalgets kommentar: Fysisk fagutvalg
Trådløsnett med Windows XP. Wireless network with Windows XP
 Trådløsnett med Windows XP Wireless network with Windows XP Mai 2013 Hvordan koble til trådløsnettet eduroam med Windows XP Service Pack 3? How to connect to the wireless network eduroam with Windows XP
Trådløsnett med Windows XP Wireless network with Windows XP Mai 2013 Hvordan koble til trådløsnettet eduroam med Windows XP Service Pack 3? How to connect to the wireless network eduroam with Windows XP
1. (a) Finn egenverdiene og egenvektorene til matrisen A =
 1. (a) Finn egenverdiene og egenvektorene til matrisen A = ( ) 2 3. 1 4 Svar: λ = 5 med egenvektorer [x, y] T = y[1, 1] T og λ = 1 med egenvektorer [x, y] T = y[ 3, 1] T, begge strengt tatt med y 0. (b)
1. (a) Finn egenverdiene og egenvektorene til matrisen A = ( ) 2 3. 1 4 Svar: λ = 5 med egenvektorer [x, y] T = y[1, 1] T og λ = 1 med egenvektorer [x, y] T = y[ 3, 1] T, begge strengt tatt med y 0. (b)
PSi Apollo. Technical Presentation
 PSi Apollo Spreader Control & Mapping System Technical Presentation Part 1 System Architecture PSi Apollo System Architecture PSi Customer label On/Off switch Integral SD card reader/writer MENU key Typical
PSi Apollo Spreader Control & Mapping System Technical Presentation Part 1 System Architecture PSi Apollo System Architecture PSi Customer label On/Off switch Integral SD card reader/writer MENU key Typical
Endringer i neste revisjon av EHF / Changes in the next revision of EHF 1. October 2015
 Endringer i neste revisjon av / Changes in the next revision of 1. October 2015 INFORMASJON PÅ NORSK 2 INTRODUKSJON 2 ENDRINGER FOR KATALOG 1.0.3 OG PAKKSEDDEL 1.0.2 3 ENDRINGER FOR ORDRE 1.0.3 4 ENDRINGER
Endringer i neste revisjon av / Changes in the next revision of 1. October 2015 INFORMASJON PÅ NORSK 2 INTRODUKSJON 2 ENDRINGER FOR KATALOG 1.0.3 OG PAKKSEDDEL 1.0.2 3 ENDRINGER FOR ORDRE 1.0.3 4 ENDRINGER
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1910 Poverty and distribution in developing countries Exam: ECON1910 Poverty and distribution in developing countries Eksamensdag: 1. juni 2011 Sensur
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON1910 Poverty and distribution in developing countries Exam: ECON1910 Poverty and distribution in developing countries Eksamensdag: 1. juni 2011 Sensur
FYS2140 Kvantefysikk. Løsningsforslag for Oblig 7
 FYS2140 Kvantefysikk Løsningsforslag for Oblig 7 Oppgave 2.23 Regn ut følgende intgral a) +1 3 (x 3 3x 2 + 2x 1)δ(x + 2) dx (1) Svar: For å løse dette integralet bruker vi Dirac deltafunksjonen (se seksjon
FYS2140 Kvantefysikk Løsningsforslag for Oblig 7 Oppgave 2.23 Regn ut følgende intgral a) +1 3 (x 3 3x 2 + 2x 1)δ(x + 2) dx (1) Svar: For å løse dette integralet bruker vi Dirac deltafunksjonen (se seksjon
Kneser hypergraphs. May 21th, CERMICS, Optimisation et Systèmes
 Kneser hypergraphs Frédéric Meunier May 21th, 2015 CERMICS, Optimisation et Systèmes Kneser hypergraphs m, l, r three integers s.t. m rl. Kneser hypergraph KG r (m, l): V (KG r (m, l)) = ( [m]) l { E(KG
Kneser hypergraphs Frédéric Meunier May 21th, 2015 CERMICS, Optimisation et Systèmes Kneser hypergraphs m, l, r three integers s.t. m rl. Kneser hypergraph KG r (m, l): V (KG r (m, l)) = ( [m]) l { E(KG
Endelig ikke-røyker for Kvinner! (Norwegian Edition)
 Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Click here if your download doesn"t start automatically Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Endelig ikke-røyker
Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Click here if your download doesn"t start automatically Endelig ikke-røyker for Kvinner! (Norwegian Edition) Allen Carr Endelig ikke-røyker
Numerisk lineær algebra
 Numerisk lineær algebra Arne Morten Kvarving Department of Mathematical Sciences Norwegian University of Science and Technology 29. Oktober 2007 Problem og framgangsmåte Vi vil løse A x = b, b, x R N,
Numerisk lineær algebra Arne Morten Kvarving Department of Mathematical Sciences Norwegian University of Science and Technology 29. Oktober 2007 Problem og framgangsmåte Vi vil løse A x = b, b, x R N,
IN2010: Algoritmer og Datastrukturer Series 2
 Universitetet i Oslo Institutt for Informatikk S.M. Storleer, S. Kittilsen IN2010: Algoritmer og Datastrukturer Series 2 Tema: Grafteori 1 Publisert: 02. 09. 2019 Utvalgte løsningsforslag Oppgave 1 (Fra
Universitetet i Oslo Institutt for Informatikk S.M. Storleer, S. Kittilsen IN2010: Algoritmer og Datastrukturer Series 2 Tema: Grafteori 1 Publisert: 02. 09. 2019 Utvalgte løsningsforslag Oppgave 1 (Fra
Maple Basics. K. Cooper
 Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
Basics K. Cooper 2012 History History 1982 Macsyma/MIT 1988 Mathematica/Wolfram 1988 /Waterloo Others later History Why? Prevent silly mistakes Time Complexity Plots Generate LATEX This is the 21st century;
Lineære ligningssystemer. Forelesning, TMA4110 Torsdag 17/9. Lineære ligningssystemer (forts.) Eksempler
 Lineære ligningssystemer Generell form; m ligninger i n ukjente, m n-system: Forelesning, TMA4110 Torsdag 17/9 Martin Wanvik, IMF MartinWanvik@mathntnuno a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1
Lineære ligningssystemer Generell form; m ligninger i n ukjente, m n-system: Forelesning, TMA4110 Torsdag 17/9 Martin Wanvik, IMF MartinWanvik@mathntnuno a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1
Independent Inspection
 Independent Inspection Odd Ivar Johnsen Vidar Nystad Independent Inspection Mål: Felles forståelse og utøvelse av "Independent Inspection" i forbindelse med "Critical Maintenance Task". Independent Inspection
Independent Inspection Odd Ivar Johnsen Vidar Nystad Independent Inspection Mål: Felles forståelse og utøvelse av "Independent Inspection" i forbindelse med "Critical Maintenance Task". Independent Inspection
Emneevaluering GEOV272 V17
 Emneevaluering GEOV272 V17 Studentenes evaluering av kurset Svarprosent: 36 % (5 av 14 studenter) Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet PhD Candidate Samsvaret mellom
Emneevaluering GEOV272 V17 Studentenes evaluering av kurset Svarprosent: 36 % (5 av 14 studenter) Hvilket semester er du på? Hva er ditt kjønn? Er du...? Er du...? - Annet PhD Candidate Samsvaret mellom
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON1210 - Forbruker, bedrift og marked Eksamensdag: 26.11.2013 Sensur kunngjøres: 18.12.2013 Tid for eksamen: kl. 14:30-17:30 Oppgavesettet er
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT BOKMÅL Eksamen i: ECON1210 - Forbruker, bedrift og marked Eksamensdag: 26.11.2013 Sensur kunngjøres: 18.12.2013 Tid for eksamen: kl. 14:30-17:30 Oppgavesettet er
0:7 0:2 0:1 0:3 0:5 0:2 0:1 0:4 0:5 P = 0:56 0:28 0:16 0:38 0:39 0:23
 UTKAST ENGLISH VERSION EKSAMEN I: MOT100A STOKASTISKE PROSESSER VARIGHET: 4 TIMER DATO: 16. februar 2006 TILLATTE HJELPEMIDLER: Kalkulator; Tabeller og formler i statistikk (Tapir forlag): Rottman: Matematisk
UTKAST ENGLISH VERSION EKSAMEN I: MOT100A STOKASTISKE PROSESSER VARIGHET: 4 TIMER DATO: 16. februar 2006 TILLATTE HJELPEMIDLER: Kalkulator; Tabeller og formler i statistikk (Tapir forlag): Rottman: Matematisk
Right Triangle Trigonometry
 0 Capter Trigonometry 70. f 8 7 8 Vertical asymptote: 8 0 y 7 0 7 8 9 9 ± 8 y Slant asymptote: ± 89 ;.,. y 7 8 y-intercept: 0, 8 -intercept:.8, 0 Section. Rigt Triangle Trigonometry You sould know te rigt
0 Capter Trigonometry 70. f 8 7 8 Vertical asymptote: 8 0 y 7 0 7 8 9 9 ± 8 y Slant asymptote: ± 89 ;.,. y 7 8 y-intercept: 0, 8 -intercept:.8, 0 Section. Rigt Triangle Trigonometry You sould know te rigt
Klara Hveberg, 26 sylen under pivot-elementet, ma vi na bare trekke (3; 2)=(2; 2) = 8=2 = 4 ganger andre rad fra tredje rad >> k=(3,2)/(2,2); >> (3,:)
 Lab 2: Gauss-eliminasjon av Klara Hveberg I denne laboratorievelsen skal vi se pa hvordan vi kan lage Matlab-funksjoner som utfrer Gauss-eliminasjon pa matriser, dvs som bringer dem pa trappeform ved hjelp
Lab 2: Gauss-eliminasjon av Klara Hveberg I denne laboratorievelsen skal vi se pa hvordan vi kan lage Matlab-funksjoner som utfrer Gauss-eliminasjon pa matriser, dvs som bringer dem pa trappeform ved hjelp
Gol Statlige Mottak. Modul 7. Ekteskapsloven
 Gol Statlige Mottak Modul 7 Ekteskapsloven Paragraphs in Norwegian marriage law 1.Kjønn To personer av motsatt eller samme kjønn kan inngå ekteskap. Two persons of opposite or same sex can marry 1 a. Ekteskapsalder.
Gol Statlige Mottak Modul 7 Ekteskapsloven Paragraphs in Norwegian marriage law 1.Kjønn To personer av motsatt eller samme kjønn kan inngå ekteskap. Two persons of opposite or same sex can marry 1 a. Ekteskapsalder.
1 Aksiomatisk definisjon av vanlige tallsystemer
 Notat XX for MAT1140 1 Aksiomatisk definisjon av vanlige tallsystemer 1.1 Aksiomer Vi betrakter en mengde R, utstyrt med to avbild- Algebraiske aksiomer. ninger: addisjon { R R R, (x, y) x + y. { R R R,
Notat XX for MAT1140 1 Aksiomatisk definisjon av vanlige tallsystemer 1.1 Aksiomer Vi betrakter en mengde R, utstyrt med to avbild- Algebraiske aksiomer. ninger: addisjon { R R R, (x, y) x + y. { R R R,
Dean Zollman, Kansas State University Mojgan Matloob-Haghanikar, Winona State University Sytil Murphy, Shepherd University
 Dean Zollman, Kansas State University Mojgan Matloob-Haghanikar, Winona State University Sytil Murphy, Shepherd University Investigating Impact of types of delivery of undergraduate science content courses
Dean Zollman, Kansas State University Mojgan Matloob-Haghanikar, Winona State University Sytil Murphy, Shepherd University Investigating Impact of types of delivery of undergraduate science content courses
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Bokmål Eksamen i: ECON1210 Forbruker, bedrift og marked Exam: ECON1210 Consumer Behaviour, Firm behaviour and Markets Eksamensdag: 12.12.2014 Sensur kunngjøres:
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Bokmål Eksamen i: ECON1210 Forbruker, bedrift og marked Exam: ECON1210 Consumer Behaviour, Firm behaviour and Markets Eksamensdag: 12.12.2014 Sensur kunngjøres:
Physical origin of the Gouy phase shift by Simin Feng, Herbert G. Winful Opt. Lett. 26, (2001)
 by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
by Simin Feng, Herbert G. Winful Opt. Lett. 26, 485-487 (2001) http://smos.sogang.ac.r April 18, 2014 Introduction What is the Gouy phase shift? For Gaussian beam or TEM 00 mode, ( w 0 r 2 E(r, z) = E
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3610/4610 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON3610/4610 Resource Allocation and Economic Policy Eksamensdag: Torsday 28.
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamen i: ECON3610/4610 Samfunnsøkonomisk lønnsomhet og økonomisk politikk Exam: ECON3610/4610 Resource Allocation and Economic Policy Eksamensdag: Torsday 28.
Hvordan føre reiseregninger i Unit4 Business World Forfatter:
 Hvordan føre reiseregninger i Unit4 Business World Forfatter: dag.syversen@unit4.com Denne e-guiden beskriver hvordan du registrerer en reiseregning med ulike typer utlegg. 1. Introduksjon 2. Åpne vinduet
Hvordan føre reiseregninger i Unit4 Business World Forfatter: dag.syversen@unit4.com Denne e-guiden beskriver hvordan du registrerer en reiseregning med ulike typer utlegg. 1. Introduksjon 2. Åpne vinduet
Du må håndtere disse hendelsene ved å implementere funksjonene init(), changeh(), changev() og escape(), som beskrevet nedenfor.
 6-13 July 2013 Brisbane, Australia Norwegian 1.0 Brisbane har blitt tatt over av store, muterte wombater, og du må lede folket i sikkerhet. Veiene i Brisbane danner et stort rutenett. Det finnes R horisontale
6-13 July 2013 Brisbane, Australia Norwegian 1.0 Brisbane har blitt tatt over av store, muterte wombater, og du må lede folket i sikkerhet. Veiene i Brisbane danner et stort rutenett. Det finnes R horisontale
Vedlegg 2 Dokumentasjon fra TVM leverandør
 (Step 7) Payment selection or date modification state This screen is displayed after validation of a date in the calendar screen. The customer can: - Modify again the date by pressing the Validity begin:
(Step 7) Payment selection or date modification state This screen is displayed after validation of a date in the calendar screen. The customer can: - Modify again the date by pressing the Validity begin:
Elektronisk termostat med spareprogram. Lysende LCD display øverst på ovnen for enkel betjening.
 Elektronisk termostat med spareprogram. Lysende LCD display øverst på ovnen for enkel betjening. 27.5 LCD Electronic thermostat with program setting. Bright LCD display placed at the top of the heater
Elektronisk termostat med spareprogram. Lysende LCD display øverst på ovnen for enkel betjening. 27.5 LCD Electronic thermostat with program setting. Bright LCD display placed at the top of the heater
TMA Kræsjkurs i Matlab. Oppgavesett 1/3
 TMA4123 - Kræsjkurs i Matlab. Oppgavesett 1/3 22.02.2013 Dette oppgavesettet omhandler grunnleggende Matlab-funksjonalitet, slik som variabler, matriser, matematiske funksjoner og plotting. Den aller viktigste
TMA4123 - Kræsjkurs i Matlab. Oppgavesett 1/3 22.02.2013 Dette oppgavesettet omhandler grunnleggende Matlab-funksjonalitet, slik som variabler, matriser, matematiske funksjoner og plotting. Den aller viktigste
Monteringsprosedyre for Soundstop - lydmatte
 NORSOK STANDARD PIPING AND EQUIPMENT INSULATION R-004 5.7 Guidelines for acoustic insulation The acoustic pipe insulation classes can be met by various combinations of insulation materials and jacketing
NORSOK STANDARD PIPING AND EQUIPMENT INSULATION R-004 5.7 Guidelines for acoustic insulation The acoustic pipe insulation classes can be met by various combinations of insulation materials and jacketing
Lineære ligningssystemer og gausseliminasjon
 Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
Kapittel Lineære ligningssystemer og gausseliminasjon Vi skal lære en metode for å finne og beskrive alle løsninger av systemer av m lineære ligninger med n ukjente. Oppvarming Her er et eksempel på et
