Kapittel 23 KURSREGNING, FORHOLD OG PROPORSJONER
|
|
|
- Aage Hovland
- 8 år siden
- Visninger:
Transkript
1 Valuta Kjøp Antall AUD Australske ollar 4, CAD Canaiske ollar 4, CHF Sveitsiske franc 493, CYP Kypriotiske pun 1, DKK Danske kroner 97, EUR Euro 7,785 1 GBP Pun sterling (Britiske pun) 11, HKD Hong Kong ollar 0, INR Iniske rupii 0, ISK Islanske kroner 8, JPY Japanske yen 5, MTL Maltesiske lire 17,100 1 NZD New Zealanske ollar 3, PKR Pakistanske rupi 0, SEK Svenske kroner 80, SGD Singapore ollar 4,160 1 USD Amerikanske ollar 7, ZAR Sør-Afrikanske ran 0,775 1
2 1eller 100 Norsk kurs Utenlansk eløp Norsk eløp Vi kjøper 5000 svenske kroner, vs SEK. Den norske kursen på SEK er 85, x x 85 x x x 85 x 100 x x : x x 450 Vi må etale 450 norske kroner (NOK) for 5000 svenske kroner (SEK) når en norske kursen på svenske kroner er 85.
3 1eller 100 Norsk kurs Utenlansk eløp Norsk eløp Vi kjøper SEK for NOK 450. Den norske kursen på svenske kroner x 100 Utenlansk eløp Norsk kurs Norsk eløp x x x x 85 : x x 85 Vi får 5000 svenske kroner (SEK) for 450 norske kroner (NOK) når en norske kursen på svenske kroner er 85.
4 1eller 100 Norsk kurs Utenlansk eløp Norsk eløp Hva er en norske kursen på SEK når vi får 5000 SEK for 450 NOK? Utenlansk eløp x 450 Norsk kurs Norsk eløp 100 x x x x 450 x x x : x x x x 85 Hvis vi får 5000 svenske kroner (SEK) for 450 norske kroner (NOK), så er en norske kursen på svenske kroner 85.
5 1eller 100 Norsk kurs Utenlansk eløp Norsk eløp De norske kursene på engelske pun ( -GBP), amerikanske ollar ($-USD) og euro ( -EUR) forteller hva vi må etale for ett pun, én ollar og én euro. Derme lir et lettere å omregne. Vi ivierer på kursen når vi skal omregne fra norske kroner, og multipliserer me kursen når vi skal omregne til norske kroner. Men vi kan også ruke formelen over, som nå ser slik ut: 1 Norsk kurs Utenlansk eløp Norsk eløp Spesielt for GBP og USD og EUR.
6 Kursregning i ferien Når vi er turister i utlanet og er ute og hanler, kan vi lage oss enkle omregningsregler som forteller oss omtrent hvor mange norske kroner vi må etale. Hvis vi for eksempel er på Islan og 100 islanske kroner (ISK) koster 8,045 norske kroner (NOK), kan vi lage regelen slik: 100 ISK koster 8,045 NOK. Dersom kursen hae vært 10 NOK for 100 ISK, kunne u iviert en islanske prisen på 10 (flyttet esimalkommaet én plass til venstre). Den reelle prisen i norske kroner er minre. Alternativt, ersom u synes et er OK me litt hoeregning, kan u iviere en islanske prisen på 100 (flytte esimalkommaet to plasser til venstre), gå til et nærmeste passene rune tallet og multiplisere me 8. Resultatet er tilnærmet prisen i norske kroner.
7 Forhol og proporsjoner Forholet mellom to størrelser a og er lik verien av røken a To størrelser x og y er proporsjonale ersom forholet mellom em er konstant. y x y k x k x y 1 k To størrelser x og y er omvent proporsjonale ersom prouktet av em er konstant. 1 y k y x k x y k x
8 Når to forhol er like, kaller vi et en proporsjon. c a er en proporsjon. Proporsjonen c a kan vi me kryssmultiplikasjon ( ) omskrive slik: c a Omregningen uner ekrefter et: c a c a c a c a
9 Proporsjoner møter vi i mange matematiske sammenhenger. AB AC AB BC AC BC DE DF DE EF DF EF I ette kapitlet om kursregning møtte u proporsjonen 100 utenlansk eløp norsk kurs norsk eløp Når vi regner me engelske pun (GBP), amerikanske ollar (USD) og euro (EUR), skal telleren i en første røken være 1. I et forrige kapitlet om ineks møtte u proporsjonen poeng år poeng år nr. 1 veri år nr. veri år nr. 1 nr.
10 Litt mer om proporsjonal og omvent proporsjonal Ofte kan vi lese og høre at noe er proporsjonalt eller omvent proporsjonalt me noe annet. Her er noen sitat: Det forventes at en framtiige stemmeforelingen i større gra enn i ag vil være proporsjonal me melemslanenes efolkningsmenge. (fra en hånok i EØS arei). 4π Av formelen T m kan vi se at T og m skulle være proporsjonale k størrelser. På grafen er e are et til en viss gra, men en kan se at grafen er tilnærmet lineær (fra en rapport om et elevforsøk me elastiske penler). Blant em som ønsker lukkee stuier er gjerne stuiekvalitet et kronargument. Det er imilerti ikke nøvenigvis slik at kvalitet og kvantitet er omvent proporsjonale størrelser. (fra en artikkel om lukkete stuier). Forholet mellom innkommene opprag og utgåene regninger hae hos meg en tenens til å opptre som omvent proporsjonale størrelser. Det var egentlig logisk. Jeg likte å ruke penger, ikke å tjene em. (fra romanen Det annet kinn av Jan Mehlum). Iflg. Newtons gravitasjonslov (1687) virker to legemer gjensiig på hveranre me en kraft som er proporsjonal me prouktet av legemenes masser og omvent proporsjonal me kvaratet på avstanen mellom em. (fra et leksikon). FORSLAG Skriv en forklaring til en tenkt person som spør eg hva som menes me proporsjonal og omvent proporsjonal.
11 Proporsjonale størrelser y k x
12 Et leksikon sier: Iflg. Newtons gravitasjonslov (1687) virker to legemer gjensiig på hveranre me en kraft som er proporsjonal me prouktet av legemenes masser. m m r 1 Newtons gravitasjonsligning sier et slik: F G m1 m - 1 m g m er prouktet (resultatet av en multiplikasjon er et proukt) av massene til to legemer. Enheten er kg. - r er avstanen mellom e to legemene. Enheten er meter. G r - G er en universelle konstanten 11 N m 6, kg Dersom vi vil vite hvilken etyning massene har for hvoran to legemer tiltrekkes av G hveranre, kan vi tenke oss at avstanen r i ligningen F m m er konstant. Da lir også røken slik: G r en konstant. Hvis vi kaller enne konstanten k, kan vi skrive ligningen g r 1 Fg k (m1 m ) Vi sier oss enige me leksikonet: Iflg. Newtons gravitasjonslov (1687) virker to legemer gjensiig på hveranre me en kraft som er proporsjonal me prouktet av legemenes masser. Hvis for eksempel et av legemene yttes me et som er tre ganger så tungt, vs. me et som har tre ganger så stor masse, så lir tiltrekningen mellom e to legemene tre ganger så stor. Dersom egge yttes me et som er tre ganger så tungt, lir tiltrekningen ganger sterkere. Tiltrekningen forlir en samme ersom vi halverer massen til en ene legemet og oler massen til et anre.
13 Omvent proporsjonale størrelser y k 1 x Dersom et tippelag har vunnet en gevinst, så er anelen til hver spiller og antall spillere på laget omvent proporsjonale størrelser
14 m m G : r r 1 Vi ser igjen på hvoran leksikonet forklarer ligningen Fg G m1 m Iflg. Newtons gravitasjonslov (1687) virker to legemer gjensiig på hveranre me en kraft som er omvent proporsjonal me kvaratet på avstanen mellom em. Vi lar massene til to legemer være konstante og omskriver ligningen slik: Fg 1 G m1 m r Nå er G m 1 m en konstant som vi kan kalle k. Ligningen lir a slik: Fg 1 k r Denne versjonen ekrefter at to legemer tiltrekker hveranre me en kraft som er omvent proporsjonal me avstanen mellom em opphøy i anre, vs. me kvaratet av avstanen. r står i nevneren. F g reuseres erfor kraftig når avstanen mellom legemene øker. Når r øker, øker r ena raskere. Dersom vi oler avstanen r, fireoles r og tiltrekningen lir reusert til en fjereel.
Hastigheten til bob-en er 120 km/t. Hva vil det si?
 Hastigheten til bob-en er 120 km/t. Hva vil det si? 12 Hm, ett britisk pund koster 11,45 kr! Sammensatte enheter MÅL I dette kapitlet skal du lære om fart priser lønn valuta KOPIERINGSORIGINALER 12.1 Felles
Hastigheten til bob-en er 120 km/t. Hva vil det si? 12 Hm, ett britisk pund koster 11,45 kr! Sammensatte enheter MÅL I dette kapitlet skal du lære om fart priser lønn valuta KOPIERINGSORIGINALER 12.1 Felles
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
Determinanter. Kapittel 6. Determinanter for 2 2-matriser. La oss beregne arealet av dette parallellogrammet. Vi tegner på noen hjelpelinjer:
 Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
Kapittel 6 Determinanter En matrise inneholer mange tall og erme mye informasjon så mye at et kan være litt overvelene Vi kan konensere ne all informasjonen i en kvaratisk matrise til ett enkelt tall som
2 Likninger. 2.1 Førstegradslikninger med én ukjent
 MATEMATIKK: 2 Likninger 2 Likninger 2.1 Førstegradslikninger med én ukjent Ulike problemer kan løses på ulike måter. I den gamle folkeskolen brukte man delingsregning ved løsning av enkelte oppgaver. Eksempel
MATEMATIKK: 2 Likninger 2 Likninger 2.1 Førstegradslikninger med én ukjent Ulike problemer kan løses på ulike måter. I den gamle folkeskolen brukte man delingsregning ved løsning av enkelte oppgaver. Eksempel
:á«déÿg Ò`Z äéeóÿg ( QÉ«àNG äéeóÿg òg ô ùdg ºbôdG) ó«uôdg øy QÉ ùøà S G -1 ''ó«uq'' õeôdg õeôdg ÜÉ ù G ƒf
 الخدمات المص رفية: عبر الرس اءل النص ية القص يرة راحتك على الدوام! دليل المس تخدم: يمكن لزباءننا الا عزاء القيام بمعاملاتهم المص رفية من خلال ا رس ال الرموز التالية ا لى ٩٠٣٠٠ (عمان موبايل) ا و ٩٩٢٢٤٠١٥
الخدمات المص رفية: عبر الرس اءل النص ية القص يرة راحتك على الدوام! دليل المس تخدم: يمكن لزباءننا الا عزاء القيام بمعاملاتهم المص رفية من خلال ا رس ال الرموز التالية ا لى ٩٠٣٠٠ (عمان موبايل) ا و ٩٩٢٢٤٠١٥
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
SAMMENDRAG OG FORMLER. Nye Mega 10A og 10B
 SAMMENDRAG OG FORMLER Nye Mega 10A og 10B 1 Sammendrag og formler Nye Mega 10A Kapittel A GEOMETRI Oversikt over vinkelkonstruksjoner 90 45 60 30 120 135 67 1 2 75 Den pytagoreiske læresetningen I en rettvinklet
SAMMENDRAG OG FORMLER Nye Mega 10A og 10B 1 Sammendrag og formler Nye Mega 10A Kapittel A GEOMETRI Oversikt over vinkelkonstruksjoner 90 45 60 30 120 135 67 1 2 75 Den pytagoreiske læresetningen I en rettvinklet
1T kapittel 1 Tall og algebra Løsninger til innlæringsoppgavene
 T kapittel Tall og algera Løsninger til innlæringsoppgavene. a 8 + ( ) 8 ( ) +. a Temperaturen er C. Så reuseres en me C. Da lir temperaturen C C 8 C Temperaturen er C. Så reuseres en me x. Da lir temperaturen
T kapittel Tall og algera Løsninger til innlæringsoppgavene. a 8 + ( ) 8 ( ) +. a Temperaturen er C. Så reuseres en me C. Da lir temperaturen C C 8 C Temperaturen er C. Så reuseres en me x. Da lir temperaturen
1P kapittel 1 Tall og algebra Løsninger til innlæringsoppgavene
 1P kapittel 1 Tall og algera Løsninger til innlæringsoppgavene 1.1 a 10 8 10 + ( ) 10 8 10 1 10 ( ) 10 + 1 1. a Temperaturen er C. Så reuseres en me 11 C. Da lir temperaturen C 11 C 8 C Temperaturen er
1P kapittel 1 Tall og algera Løsninger til innlæringsoppgavene 1.1 a 10 8 10 + ( ) 10 8 10 1 10 ( ) 10 + 1 1. a Temperaturen er C. Så reuseres en me 11 C. Da lir temperaturen C 11 C 8 C Temperaturen er
Løsningsforslag. b) Hva er den totale admittansen til parallellkoblingen i figuren over? Oppgi både modul og fasevinkel.
 Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
Løsningsforslag FYS / FY / FYS Elektromagnetisme, torsag 8. esember Ve sensurering vil alle elspørsmål i utgangspunktet bli gitt samme vekt (uavhengig av oppgavenummer), men vi forbeholer oss retten til
1 Tall 1.1 a 1.2 a 1.4 a 1.5 a 1.6 1.7 a 1.8 a 1.9 a 1.10 a 1.11 a 1.13 a 1.14 a 1.15 1.16 a 1.17 a 1.18 a 1.19 1.20 1.21 a
 Tall. a - - 0 - - - 0. a > < >. a - - 0 - e - f -9. a 9 C C.6-00 kr. a - e - f. a 6 - -6 e f.9 a - - -.0 a 0 - - - -, -,9 0,0 0,9,. a -6 - -. a - 6 6. a Trysil Lillehammer Oppal. a - C 96 C. a Ja.6 a =
Tall. a - - 0 - - - 0. a > < >. a - - 0 - e - f -9. a 9 C C.6-00 kr. a - e - f. a 6 - -6 e f.9 a - - -.0 a 0 - - - -, -,9 0,0 0,9,. a -6 - -. a - 6 6. a Trysil Lillehammer Oppal. a - C 96 C. a Ja.6 a =
Enkel matematikk for økonomer. Del 1 nødvendig bakgrunn. Parenteser og brøker
 Vedlegg Enkel matematikk for økonomer I dette vedlegget går vi gjennom noen grunnleggende regneregler som brukes i boka. Del går gjennom de helt nødvendige matematikk-kunnskapene. Dette må du jobbe med
Vedlegg Enkel matematikk for økonomer I dette vedlegget går vi gjennom noen grunnleggende regneregler som brukes i boka. Del går gjennom de helt nødvendige matematikk-kunnskapene. Dette må du jobbe med
Litt mer om kjeglesnitt og Keplers lover om planetbanene
 Litt mer om kjeglesnitt og Keplers lover om planetbanene Det er ikke meningen at enne teksten skal stå for seg selv. Den er ment som en hjelp mens u leser 11.6 og eler av kapittel 8 i læreboka. Hvis u
Litt mer om kjeglesnitt og Keplers lover om planetbanene Det er ikke meningen at enne teksten skal stå for seg selv. Den er ment som en hjelp mens u leser 11.6 og eler av kapittel 8 i læreboka. Hvis u
EKSAMEN TMA4100 HØST 2014 LØSNINGSFORSLAG. du/dx = e x du = e x dx, Her har vi brukt analysens fundamentalteorem til å derivere telleren.
 EKSAMEN TMA400 HØST 04 ØSNINGSFORSAG Oppgave. Uner rottegnet står et + e x, og en eriverte til ette uttrykket er e x, som står utenfor rottegnet. Sett erfor u +e x. Da får vi og vi kan løse intergralet:
EKSAMEN TMA400 HØST 04 ØSNINGSFORSAG Oppgave. Uner rottegnet står et + e x, og en eriverte til ette uttrykket er e x, som står utenfor rottegnet. Sett erfor u +e x. Da får vi og vi kan løse intergralet:
Her er C en funksjon av F
 Kapittel 9 FUNKSJONER C F 50 58 40 40 0 0 4 0 4 0 0 50 0 68 0 86 40 04 50 9 F C + 5 Her er F en funksjon av C Dette er like ra C 5 9 F 60 9 Her er C en funksjon av F Kapittel 9 FUNKSJONER Det norske oljeeventyret
Kapittel 9 FUNKSJONER C F 50 58 40 40 0 0 4 0 4 0 0 50 0 68 0 86 40 04 50 9 F C + 5 Her er F en funksjon av C Dette er like ra C 5 9 F 60 9 Her er C en funksjon av F Kapittel 9 FUNKSJONER Det norske oljeeventyret
x, og du dx = w dy (cosh u) = sinh u H sinh w H x = sinh w H x. dx = H w w > 0, så h har ikke flere lokale ekstremverdier.
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 00 Løsningsforslag - Øving 3 Avsnitt 3. u 49 a) Fra tabell 3.4 på sie i boka: (cosh u) = sinh u. Her har vi at u = w H, og u = w y H. Det følger
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 00 Løsningsforslag - Øving 3 Avsnitt 3. u 49 a) Fra tabell 3.4 på sie i boka: (cosh u) = sinh u. Her har vi at u = w H, og u = w y H. Det følger
INEC1800 ØKONOMI, FINANS OG REGNSKAP EINAR BELSOM
 INEC1800 ØKONOMI, FINANS OG REGNSKA EINAR BELSOM HØS 2017 FORELESNINGSNOA 6 rouksjonsteknologi og kostnaer* Fokuset i ette notatet er på beriftenes atfer uner ulike markesformer, fra tilfellet er beriften
INEC1800 ØKONOMI, FINANS OG REGNSKA EINAR BELSOM HØS 2017 FORELESNINGSNOA 6 rouksjonsteknologi og kostnaer* Fokuset i ette notatet er på beriftenes atfer uner ulike markesformer, fra tilfellet er beriften
SKAGEN Tellus mars 2007. Porteføljeforvalter Torgeir Høien
 SKAGEN Tellus s Porteføljeforvalter Torgeir Høien Investeringsfilosofien SKAGEN Tellus investerer i kredittsikre obligasjoner utstedt av myndigheter i land med sunn pengepolitikk, åpne kapitalkeder og
SKAGEN Tellus s Porteføljeforvalter Torgeir Høien Investeringsfilosofien SKAGEN Tellus investerer i kredittsikre obligasjoner utstedt av myndigheter i land med sunn pengepolitikk, åpne kapitalkeder og
TMA4100 Matematikk 1 Høst 2014
 Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 014 Løsningsforslag Øving 03.7. Økningen i uksen, F, kan approksimeres som se sie 131 i boka F F =
Norges teknisknaturvitenskapelige universitet Institutt for matematiske fag TMA4100 Matematikk 1 Høst 014 Løsningsforslag Øving 03.7. Økningen i uksen, F, kan approksimeres som se sie 131 i boka F F =
CMC Markets tar ikke depotgebyr, og alle sanntidskurser og ordredybder på våre instrumenter er helt kostnadsfrie.
 PRISLISTE 1. DEPOTGEBYR OG GEBYR FOR SANNTIDSKURSER CMC Markets tar ikke depotgebyr, og alle sanntidskurser og ordredybder på våre instrumenter er helt kostnadsfrie. Depotgebyr Sanntidskurser Standardkonto
PRISLISTE 1. DEPOTGEBYR OG GEBYR FOR SANNTIDSKURSER CMC Markets tar ikke depotgebyr, og alle sanntidskurser og ordredybder på våre instrumenter er helt kostnadsfrie. Depotgebyr Sanntidskurser Standardkonto
Kapittel 6. Trekanter
 Kapittel 6. Trekanter Mål for kapittel 6: Kompetansemål Mål for opplæringen er at eleven skal kunne bruke og grunngi bruk av formlikhet, målestokk og Pytagoras setning til beregninger i praktisk arbeid
Kapittel 6. Trekanter Mål for kapittel 6: Kompetansemål Mål for opplæringen er at eleven skal kunne bruke og grunngi bruk av formlikhet, målestokk og Pytagoras setning til beregninger i praktisk arbeid
Aktuell kommentar. Norske kroner ingen trygg havn. av Alexander Flatner, seniorrådgiver i Markedsoperasjons- og analyseavdelingen i Norges Bank *
 Nr. 3 2009 Aktuell kommentar Norske kroner ingen trygg havn av Alexander Flatner, seniorrådgiver i Markedsoperasjons- og analyseavdelingen i Norges Bank * * Synspunktene i denne kommentaren representerer
Nr. 3 2009 Aktuell kommentar Norske kroner ingen trygg havn av Alexander Flatner, seniorrådgiver i Markedsoperasjons- og analyseavdelingen i Norges Bank * * Synspunktene i denne kommentaren representerer
Modellering 2P, Prøve 2 løsning
 Modellering P, Prøve løsning Del Tid: 40 min Hjelpemidler: Skrivesaker Oppgave Steinar er på tur i Etiopia. Myntenheten i Etiopia er Birr. Steinar finner ut at etiopisk irr 0,70 norske kroner. a) Hvor
Modellering P, Prøve løsning Del Tid: 40 min Hjelpemidler: Skrivesaker Oppgave Steinar er på tur i Etiopia. Myntenheten i Etiopia er Birr. Steinar finner ut at etiopisk irr 0,70 norske kroner. a) Hvor
PRESSEKONFERANSE - 9. august 2013 2. KVARTAL 2013. www.nbim.no
 PRESSEKONFERANSE - 9. august 213 2. KVARTAL 213 www.nbim.no Fondets markedsverdi Kvartalstall. Milliarder kroner, 3. juni 213 4 5 4 397 4 5 4 Aktivaklasse Verdi Prosentandel fond 4 3 5 Aksjer 2 785 63,4%
PRESSEKONFERANSE - 9. august 213 2. KVARTAL 213 www.nbim.no Fondets markedsverdi Kvartalstall. Milliarder kroner, 3. juni 213 4 5 4 397 4 5 4 Aktivaklasse Verdi Prosentandel fond 4 3 5 Aksjer 2 785 63,4%
Test, Algebra (1P) 1.1 Tallregning. 1) Addere betyr x legge sammen trekke fra gange dele. 2) Subtrahere betyr legge sammen x trekke fra gange dele
 Test, Algebra (1P) 1.1 Tallregning 1) Addere betyr x legge sammen trekke fra gange dele 2) Subtrahere betyr legge sammen x trekke fra gange dele 3) Multiplisere betyr legge sammen trekke fra x gange dele
Test, Algebra (1P) 1.1 Tallregning 1) Addere betyr x legge sammen trekke fra gange dele 2) Subtrahere betyr legge sammen x trekke fra gange dele 3) Multiplisere betyr legge sammen trekke fra x gange dele
Enkel matematikk for økonomer 1. Innhold. Parenteser, brøk og potenser. Ekstranotat, februar 2015
 Ekstranotat, februar 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser, brøk og potenser... Funksjoner...4 Tilvekstform (differensialregning)...5 Nyttige tilnærminger...8
Ekstranotat, februar 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser, brøk og potenser... Funksjoner...4 Tilvekstform (differensialregning)...5 Nyttige tilnærminger...8
Innhold. Forord Symboler som brukes i boken... 11
 Innhold Forord... 5 Symboler som brukes i boken... 11 KAPITTEL 1 Finansiell risikostyring: en oversikt... 13 1.1 Hvor store er svingningene i valutakurser og råvarepriser?... 14 1.2 Kurssvingningenes mulige
Innhold Forord... 5 Symboler som brukes i boken... 11 KAPITTEL 1 Finansiell risikostyring: en oversikt... 13 1.1 Hvor store er svingningene i valutakurser og råvarepriser?... 14 1.2 Kurssvingningenes mulige
1b) Schwarzschil-metrikken er iagonal, og vi har at g tt = 1, c = r, c ; g rr =, r r r r, =,1, r, ; g =,r ; g '' =,r sin : (9) At raielle baner eksist
 Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Eksamen i klassisk feltteori, fag 74 50, 8. esember 1998 Lsninger 1a) Vi antar at x +, x x =0; (1) og at c = g x x. Sa gjr vi en koorinattransformasjon x 7 ex,ogskal vise at ex + e, ex ex =0; () er c =
Norsk Fysikklærerforening Norsk Fysisk Selskaps faggruppe for undervisning
 Norsk Fysikklærerforening Norsk Fysisk Selskaps faggruppe for unervisning FYSIKK-KONKURRANSE 00 00 Anre rune: 7/ 00 Skriv øverst: Navn, føselsato, hjeearesse og eventuell e-postaresse, skolens navn og
Norsk Fysikklærerforening Norsk Fysisk Selskaps faggruppe for unervisning FYSIKK-KONKURRANSE 00 00 Anre rune: 7/ 00 Skriv øverst: Navn, føselsato, hjeearesse og eventuell e-postaresse, skolens navn og
Landinformasjon ved betalinger til utlandet
 Landinformasjon ved betalinger til utlandet Land med IBAN-nummer Betalinger til land som har innført IBAN (International bank account number) fylles ut på samme måte. Trykk på linken under for å se om
Landinformasjon ved betalinger til utlandet Land med IBAN-nummer Betalinger til land som har innført IBAN (International bank account number) fylles ut på samme måte. Trykk på linken under for å se om
Fugletetraederet. Øistein Gjøvik
 Øistein Gjøvik Fugletetraeeret Nå skal vi lage et romlegeme u kanskje ikke har sett før. Det er ikke noe mystisk ve selve figuren, men en hører ikke til lant e mest rukte i unervisningen. Lag figuren før
Øistein Gjøvik Fugletetraeeret Nå skal vi lage et romlegeme u kanskje ikke har sett før. Det er ikke noe mystisk ve selve figuren, men en hører ikke til lant e mest rukte i unervisningen. Lag figuren før
Løsningsforslag: Gamle eksamner i GEO1030
 Løsningsforslag: Gamle eksamner i GEO1030 Sara Blihner Deemer 8, 2016 Eksamen 2003 Oppgave 1 a Termoynamikkens første hovesetning: H: varme tilført/tatt ut av systemet. p: trykket. H = p α + v T (1) α:
Løsningsforslag: Gamle eksamner i GEO1030 Sara Blihner Deemer 8, 2016 Eksamen 2003 Oppgave 1 a Termoynamikkens første hovesetning: H: varme tilført/tatt ut av systemet. p: trykket. H = p α + v T (1) α:
4. Viktige kvantemekaniske teoremer
 FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
FY1006/TFY4215 Tillegg 4 1 TILLEGG 4 4. Viktige kvantemekaniske teoremer Før vi i neste kapittel går løs på treimensjonale potensialer, skal vi i kapittel 4 i ette kurset gå gjennom noen viktige kvantemekaniske
Kapittel 1. Metoder. Mål for Kapittel 1, Metoder. Kompetansemål. Mål for opplæringen er at eleven skal kunne
 Kapittel 1. Metoder Mål for Kapittel 1, Metoder Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere resultatene
Kapittel 1. Metoder Mål for Kapittel 1, Metoder Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere resultatene
Forelesning 2: Førsteordens lineære differensiallikninger
 Forelesning 2: Førsteorens lineære ifferensiallikninger Tron Stølen Gustavsen 16. januar, 2009 Innhol Lesning 1 2.1. Likninger me konstante koeffisienter 1 2.2. Generelle koeffisienter 4 Referanser 5 Lesning.
Forelesning 2: Førsteorens lineære ifferensiallikninger Tron Stølen Gustavsen 16. januar, 2009 Innhol Lesning 1 2.1. Likninger me konstante koeffisienter 1 2.2. Generelle koeffisienter 4 Referanser 5 Lesning.
Kraftelektronikk (Elkraft 2 høst), Løsningsforslag til øvingssett 3, høst 2005
 Kraftelektronikk (Elkraft høst), Løsningsforslag til øvingssett 3, høst 005 Ole-Morten Mitgår HiA 005 Oppgave Dioelikeretter: a) Dioene er snu, strømmen går i motsatt retning. (Husk at strømmen kan bare
Kraftelektronikk (Elkraft høst), Løsningsforslag til øvingssett 3, høst 005 Ole-Morten Mitgår HiA 005 Oppgave Dioelikeretter: a) Dioene er snu, strømmen går i motsatt retning. (Husk at strømmen kan bare
Forvaltningen av Norges Banks valutareserver. Rapport for tredje kvartal 2010
 Forvaltningen av Norges Banks valutareserver Rapport for tredje kvartal 2010 November 2010 Forvaltningen av Norges Banks valutareserver Rapport for tredje kvartal 2010 Valutareservene skal kunne brukes
Forvaltningen av Norges Banks valutareserver Rapport for tredje kvartal 2010 November 2010 Forvaltningen av Norges Banks valutareserver Rapport for tredje kvartal 2010 Valutareservene skal kunne brukes
Løsningsforslag til øving 14
 Institutt for fysikk, NTNU TFY4155/FY13 Elektromagnetisme Vår 29 Løsningsforslag til øving 14 Oppgave 1 Den påtrykte strømmen I genererer et H-felt H ni på langs overalt inne i spolen (pga Amperes lov
Institutt for fysikk, NTNU TFY4155/FY13 Elektromagnetisme Vår 29 Løsningsforslag til øving 14 Oppgave 1 Den påtrykte strømmen I genererer et H-felt H ni på langs overalt inne i spolen (pga Amperes lov
Grensesjikts approksimasjon. P.-Å. Krogstad
 Norges teknisk- naturvitenskapelige universitet (NTNU) Fakultetet for ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk N-749 Tronheim - NTNU Grensesjikts approksimasjon P.-Å. Krogsta
Norges teknisk- naturvitenskapelige universitet (NTNU) Fakultetet for ingeniørvitenskap og teknologi Institutt for Energi og Prosessteknikk N-749 Tronheim - NTNU Grensesjikts approksimasjon P.-Å. Krogsta
Løsningsforslag Eksamen M1 Onsdag 14.desember 2005
 Løsningsforslag Eksamen M Onsdag.desember 005 Her følger et kort løsningsforslag, med forbehold om at det kan ha sneket seg inn enkelte feil... Oppgave (0) a) V basskasse dm 5,5dm 5,0dm 75,dm 75, l Basskassen
Løsningsforslag Eksamen M Onsdag.desember 005 Her følger et kort løsningsforslag, med forbehold om at det kan ha sneket seg inn enkelte feil... Oppgave (0) a) V basskasse dm 5,5dm 5,0dm 75,dm 75, l Basskassen
Hovedstyremøte 11. mars 2004
 Hovedstyremøte. mars Hovedstyremøte. mars BNP-vekst i USA, Japan, euroområdet og hos handelspartnerne samlet. Kvartalsvekst. Prosent. -. Sesongjustert USA Japan Euroområdet Handelspartnere - - - - Hovedstyremøte.
Hovedstyremøte. mars Hovedstyremøte. mars BNP-vekst i USA, Japan, euroområdet og hos handelspartnerne samlet. Kvartalsvekst. Prosent. -. Sesongjustert USA Japan Euroområdet Handelspartnere - - - - Hovedstyremøte.
Tall i arbeid Påbygging terminprøve våren 2013
 Tll i rei Påygging terminprøve våren 2013 DEL 1 Uten hjelpemiler Hjelpemiler: vnlige skrivesker, psser, linjl me entimetermål og vinkelmåler Oppgve 1 Skriv tllene på stnrform. 1 0,000 00015 2 19,6 millirer
Tll i rei Påygging terminprøve våren 2013 DEL 1 Uten hjelpemiler Hjelpemiler: vnlige skrivesker, psser, linjl me entimetermål og vinkelmåler Oppgve 1 Skriv tllene på stnrform. 1 0,000 00015 2 19,6 millirer
Løsningsforslag eksamen MAT111 Grunnkurs i Matematikk I høsten 2009
 Løsningsforslag eksamen MAT Grunnkurs i Matematikk I høsten 9 OPPGAVE (a) Vi har w = + ( ) =. I et komplekse plan ligger w i 4. kvarant og vinkelen θ mellom tallet og en relle aksen har tan θ =, vs. at
Løsningsforslag eksamen MAT Grunnkurs i Matematikk I høsten 9 OPPGAVE (a) Vi har w = + ( ) =. I et komplekse plan ligger w i 4. kvarant og vinkelen θ mellom tallet og en relle aksen har tan θ =, vs. at
Eksamen våren 2015 Løsninger
 DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 For et utvalg der antall oservasjoner er et partall, slik som her, er medianen gjennomsnittet
DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 For et utvalg der antall oservasjoner er et partall, slik som her, er medianen gjennomsnittet
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN
 Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene Den globale økonomien er i resesjon. Blant de utviklede økonomiene var det
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene Den globale økonomien er i resesjon. Blant de utviklede økonomiene var det
Opplysninger om markedsrisiko
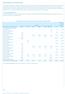 Opplysninger om markedsrisiko Når det gjelder beskrivelse av Telenors markedsrisiko henviser vi til note 20 og 21 i årsregnskapet. De følgende tabeller gir en oversikt over våre markedssensitive finansielle
Opplysninger om markedsrisiko Når det gjelder beskrivelse av Telenors markedsrisiko henviser vi til note 20 og 21 i årsregnskapet. De følgende tabeller gir en oversikt over våre markedssensitive finansielle
Løsningsforslag til Eksamen 2P vår 2008
 Løsningsforslag til Eksamen P vår 008 Delprøve 1 OPPGAVE 1 a) Avlesning av grafen viser at 50 stoler koster 40.000 kroner. Gjennomsnittskostnaden per stol blir da: 40000 = 800 kroner. 50 b) c) = = 4,46
Løsningsforslag til Eksamen P vår 008 Delprøve 1 OPPGAVE 1 a) Avlesning av grafen viser at 50 stoler koster 40.000 kroner. Gjennomsnittskostnaden per stol blir da: 40000 = 800 kroner. 50 b) c) = = 4,46
1 C z I G + + = + + 2) Multiplikasjon av et tall med en parentes foregår ved å multiplisere tallet med alle leddene i parentesen, slik at
 Ekstranotat, 7 august 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser og brøker... Funksjoner...3 Tilvekstform (differensialregning)...4 Telleregelen...7 70-regelen...8
Ekstranotat, 7 august 205 Enkel matematikk for økonomer Innhold Enkel matematikk for økonomer... Parenteser og brøker... Funksjoner...3 Tilvekstform (differensialregning)...4 Telleregelen...7 70-regelen...8
Løsningsforslag til eksamen i FYS1000, 19/8 2016
 Løsningsforslag til eksamen i FY1000, 19/8 016 Oppgave 1 a) C D A B b) I inusert A + B I ien strømmen går mot høyre vil magnetfeltet peke ut av planet inne i strømsløyfa. Hvis vi velger positiv retning
Løsningsforslag til eksamen i FY1000, 19/8 016 Oppgave 1 a) C D A B b) I inusert A + B I ien strømmen går mot høyre vil magnetfeltet peke ut av planet inne i strømsløyfa. Hvis vi velger positiv retning
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med entimetermål og vinkelmåler Oppgave 1 Økningen i salget er 1000 øker per år. Da vil den prosentvise økningen fra et år til
DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med entimetermål og vinkelmåler Oppgave 1 Økningen i salget er 1000 øker per år. Da vil den prosentvise økningen fra et år til
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN
 Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene BNP krympet trolig kraftig i de fleste utviklede land i fjerde kvartal. Aktivitetsindikatorene
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene BNP krympet trolig kraftig i de fleste utviklede land i fjerde kvartal. Aktivitetsindikatorene
Forvaltningen av Norges Banks valutareserver Rapport for andre kvartal 2012
 Forvaltningen av Norges Banks valutareserver Rapport for andre kvartal 212 Valutareservene skal kunne brukes til intervensjoner i valutamarkedet som ledd i gjennomføringen av pengepolitikken eller ut fra
Forvaltningen av Norges Banks valutareserver Rapport for andre kvartal 212 Valutareservene skal kunne brukes til intervensjoner i valutamarkedet som ledd i gjennomføringen av pengepolitikken eller ut fra
SAMMENDRAG OG FORMLER
 SAMMENDRAG OG FORMLER SAMMENDRAG OG FORMLER Nye Mega 8A Kapittel A GEOMETRI LINJE, LINJESTYKKE OG STRÅLE linje stråle linjestykke VINKLER VINKELBEIN OG TOPPUNKT En vinkel har et toppunkt. Denne vinkelen
SAMMENDRAG OG FORMLER SAMMENDRAG OG FORMLER Nye Mega 8A Kapittel A GEOMETRI LINJE, LINJESTYKKE OG STRÅLE linje stråle linjestykke VINKLER VINKELBEIN OG TOPPUNKT En vinkel har et toppunkt. Denne vinkelen
EKSAMEN Løsningsforslag
 5..7 EKSAMEN Løsningsforslag Emnekode: ITD5 Dato:. desember 7 Hjelpemidler: - To A-ark med valgfritt innhold på begge sider. - Formelhefte. - Kalkulator som deles ut samtidig med oppgaven. Emnenavn: Matematikk
5..7 EKSAMEN Løsningsforslag Emnekode: ITD5 Dato:. desember 7 Hjelpemidler: - To A-ark med valgfritt innhold på begge sider. - Formelhefte. - Kalkulator som deles ut samtidig med oppgaven. Emnenavn: Matematikk
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN
 Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene Den globale økonomien var i resesjon i fjerde kvartal 8 og første kvartal
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene Den globale økonomien var i resesjon i fjerde kvartal 8 og første kvartal
Beregning av massesenter.
 Fsikk for ingeniører 5 Bevegelsesenge og assesenter Sie 5 - Beregning av assesenter Definisjoner i ri C Figuren til venstre viser et lite utsnitt av en sk av så partikler, er i er assen til en partikkel
Fsikk for ingeniører 5 Bevegelsesenge og assesenter Sie 5 - Beregning av assesenter Definisjoner i ri C Figuren til venstre viser et lite utsnitt av en sk av så partikler, er i er assen til en partikkel
Introduksjon til Forexmarkedet
 Innholdsfortegnelse Introduksjon til Forexmarkedet... 3 Hvordan foregår Forexhandel?... 4 Fordeler ved å trade i Forexmarkedet... 6 Valutapar... 7 Leverage/giring Hva er det?... 8 Kostnader... 9 Fundamental
Innholdsfortegnelse Introduksjon til Forexmarkedet... 3 Hvordan foregår Forexhandel?... 4 Fordeler ved å trade i Forexmarkedet... 6 Valutapar... 7 Leverage/giring Hva er det?... 8 Kostnader... 9 Fundamental
Eksamen høsten Fag: MAT1006 Matematikk 1T-Y. Eksamensdato: 13. november Kunnskapsløftet. Videregående trinn 1.
 Eksamensoppgave for følgende fylker: Akershus, Oslo, Buskerud, Vestfold, Østfold, Oppland, Hedmark, Telemark, Aust-Agder, Vest-Agder, Rogaland, Hordaland, Sogn og Fjordane Eksamen høsten 013 Fag: MAT1006
Eksamensoppgave for følgende fylker: Akershus, Oslo, Buskerud, Vestfold, Østfold, Oppland, Hedmark, Telemark, Aust-Agder, Vest-Agder, Rogaland, Hordaland, Sogn og Fjordane Eksamen høsten 013 Fag: MAT1006
Anbefalte oppgaver uke 36
 Anbefalte oppgaver uke 36 Høsten 2017 Løsningsforslag 1 Vi begynner me å skrive om ligningen litt, først til x y x + y = x2 + y, (1) y og så eller Nå eriverer vi, og får slik at xy y 2 = x 3 + xy + x 2
Anbefalte oppgaver uke 36 Høsten 2017 Løsningsforslag 1 Vi begynner me å skrive om ligningen litt, først til x y x + y = x2 + y, (1) y og så eller Nå eriverer vi, og får slik at xy y 2 = x 3 + xy + x 2
3. Parlamentarikerkomiteen for EØS. Forhåndsmelding om en foretakssammenslutning (Sak COMP/M.3609 Cinven/France Télécom Câble-NC Numéricâble)...
 NORSK utgave EØS-tillegget til Den europeiske unions tidende I EØS-ORGANER 1. EØS-rådet 2. EØS-komiteen 3. Parlamentarikerkomiteen for EØS ISSN 1022-9310 Nr. 6 12. årgang 10.2.2005 4. Den rådgivende komité
NORSK utgave EØS-tillegget til Den europeiske unions tidende I EØS-ORGANER 1. EØS-rådet 2. EØS-komiteen 3. Parlamentarikerkomiteen for EØS ISSN 1022-9310 Nr. 6 12. årgang 10.2.2005 4. Den rådgivende komité
Forvaltningen av Norges Banks valutareserver. Rapport for første kvartal 2010
 Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 2010 Juni 2010 Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 2010 Valutareservene skal kunne brukes til
Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 2010 Juni 2010 Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 2010 Valutareservene skal kunne brukes til
Fasit Tall og algebra 1.1 a) 2, d) 1, b) 3, e) 2, c) 4, f) 1,3 10 6
 Tekstfarge plate (,) Tall og algebra. a), 0 d), 0, 0 e),7 0 c), 0 f), 0.,0 0 8. a), 0 d), 0 7,0 0 e),07 0 c),0 0 f) 9,0 0 9. a),0 0 d) 7, 0,0 0 e) 8, 0 c) 8,0 0 f),9 0. a),0 0 c) 8,0 0, 0 7 d), 0 0. a)
Tekstfarge plate (,) Tall og algebra. a), 0 d), 0, 0 e),7 0 c), 0 f), 0.,0 0 8. a), 0 d), 0 7,0 0 e),07 0 c),0 0 f) 9,0 0 9. a),0 0 d) 7, 0,0 0 e) 8, 0 c) 8,0 0 f),9 0. a),0 0 c) 8,0 0, 0 7 d), 0 0. a)
Eksamen høsten 2016 Løsninger
 DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 Vi fordeler malingen på de små oksene: 8 8 3 4 8 : 1 3 3 3 3 Vi trenger 1 okser. Oppgave
DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 Vi fordeler malingen på de små oksene: 8 8 3 4 8 : 1 3 3 3 3 Vi trenger 1 okser. Oppgave
(coshu) = sinhudu. dx. Her har vi at u = w Hx, og du dx = w dy. dx = H w w. H sinh w H x = sinh w H x.
 NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving 3 Avsnitt 3. 49 a) Fra tabell 3.4 på sie 222 i boka: (coshu) = sinhuu. Her har vi at u = w H, og u = w y H. Det følger
NTNU Institutt for matematiske fag TMA400 Matematikk høsten 20 Løsningsforslag - Øving 3 Avsnitt 3. 49 a) Fra tabell 3.4 på sie 222 i boka: (coshu) = sinhuu. Her har vi at u = w H, og u = w y H. Det følger
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Tenk deg at du har et spann med 8 L maling. Du vil helle malingen over i mindre bokser. I hver boks er det plass til 2 3 L. Hvor mange bokser trenger du? Oppgave
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Tenk deg at du har et spann med 8 L maling. Du vil helle malingen over i mindre bokser. I hver boks er det plass til 2 3 L. Hvor mange bokser trenger du? Oppgave
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 15 L 150 dl Til sammen 150 dl med dl i hvert glass gir: 150 glass 75 glass Oppgave Vi
DEL 1 Uten hjelpemidler Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 15 L 150 dl Til sammen 150 dl med dl i hvert glass gir: 150 glass 75 glass Oppgave Vi
= 5, forventet inntekt er 26
 Eksempel på optimal risikodeling Hevdet forrige gang at i en kontrakt mellom en risikonøytral og en risikoavers person burde den risikonøytrale bære all risiko Kan illustrere dette i en enkel situasjon,
Eksempel på optimal risikodeling Hevdet forrige gang at i en kontrakt mellom en risikonøytral og en risikoavers person burde den risikonøytrale bære all risiko Kan illustrere dette i en enkel situasjon,
Mer øving til kapittel 1
 Mer øving til kpittel 1 KAPITTEL 1 TALL OG TALLREGNING Oppgve 1 Finn svret ve hoeregning. Velg to v oppgvene og forklr hvilken strtegi u hr rukt. 27 + 38 e 160 70 i 130 4 35 + 75 f 19 5 j 6 7,5 58 + 42
Mer øving til kpittel 1 KAPITTEL 1 TALL OG TALLREGNING Oppgve 1 Finn svret ve hoeregning. Velg to v oppgvene og forklr hvilken strtegi u hr rukt. 27 + 38 e 160 70 i 130 4 35 + 75 f 19 5 j 6 7,5 58 + 42
Forvaltningen av Norges Banks valutareserver. Rapport for første kvartal 2009
 Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 29 2 mai 29 Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 29 Valutareservene skal kunne brukes til intervensjoner
Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 29 2 mai 29 Forvaltningen av Norges Banks valutareserver Rapport for første kvartal 29 Valutareservene skal kunne brukes til intervensjoner
Eksamen R2 høst 2011, løsning
 Eksamen R høst 0, løsning Oppgave (4 poeng) a) Deriver funksjonene f e ) Bruker produktregelen for derivasjon, uv uv uv f e e e e ) g sin Bruker kjerneregelen på uttrykket cos der u og g u sinu Vi har
Eksamen R høst 0, løsning Oppgave (4 poeng) a) Deriver funksjonene f e ) Bruker produktregelen for derivasjon, uv uv uv f e e e e ) g sin Bruker kjerneregelen på uttrykket cos der u og g u sinu Vi har
Kapittel 4. Algebra. Mål for kapittel 4: Kompetansemål. Mål for opplæringen er at eleven skal kunne
 Kapittel 4. Algebra Mål for kapittel 4: Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere resultatene
Kapittel 4. Algebra Mål for kapittel 4: Kompetansemål Mål for opplæringen er at eleven skal kunne gjøre overslag over svar, regne praktiske oppgaver, med og uten digitale verktøy, presentere resultatene
Kapittel 8. Potensregning og tall på standardform
 Kapittel 8. Potensregning og tall på standardform I potensregning skriver vi tall som potenser og forenkler uttrykk som inneholder potenser. Standardform er en metode som er nyttig for raskt å kunne skrive
Kapittel 8. Potensregning og tall på standardform I potensregning skriver vi tall som potenser og forenkler uttrykk som inneholder potenser. Standardform er en metode som er nyttig for raskt å kunne skrive
Forvaltningen av Norges Banks valutareserver. Rapport for fjerde kvartal 2008
 Forvaltningen av Norges Banks valutareserver Rapport for fjerde kvartal 28 13 mars 29 Valutareservene skal kunne brukes til intervensjoner i valutamarkedet som ledd i gjennomføringen av pengepolitikken
Forvaltningen av Norges Banks valutareserver Rapport for fjerde kvartal 28 13 mars 29 Valutareservene skal kunne brukes til intervensjoner i valutamarkedet som ledd i gjennomføringen av pengepolitikken
MA0002 Brukerkurs i matematikk B Vår 2016
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Løsningsforslag Øving 1 Kapittel 7.1: Substitusjon Teorem 1. Hvis u = g() så er f(g())g
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag MA000 Brukerkurs i matematikk B Vår 016 Løsningsforslag Øving 1 Kapittel 7.1: Substitusjon Teorem 1. Hvis u = g() så er f(g())g
S1 kapittel 1 Algebra Løsninger til oppgavene i læreboka
 Løsninger til oppgvene i ok S kpittel Alger Løsninger til oppgvene i læreok. 8 ( ) 5 9. e = = 9 = = 8 5 = = 0 = 0 0 0 = 000 =. e Ashehoug www.lokus.no Sie v Løsninger til oppgvene i ok..5..7 = = + 5 =
Løsninger til oppgvene i ok S kpittel Alger Løsninger til oppgvene i læreok. 8 ( ) 5 9. e = = 9 = = 8 5 = = 0 = 0 0 0 = 000 =. e Ashehoug www.lokus.no Sie v Løsninger til oppgvene i ok..5..7 = = + 5 =
Forvaltningen av Norges Banks valutareserver. Rapport for andre kvartal 2009
 Forvaltningen av Norges Banks valutareserver Rapport for andre kvartal 29 14 august 29 Forvaltningen av Norges Banks valutareserver Rapport for andre kvartal 29 Valutareservene skal kunne brukes til intervensjoner
Forvaltningen av Norges Banks valutareserver Rapport for andre kvartal 29 14 august 29 Forvaltningen av Norges Banks valutareserver Rapport for andre kvartal 29 Valutareservene skal kunne brukes til intervensjoner
Eksamen 21.05.2012. MAT0010 Matematikk Grunnskoleeksamen for voksne deltakere og privatister DEL 2. Bokmål
 Eksamen 21.05.2012 MAT0010 Matematikk Grunnskoleeksamen for voksne deltakere og privatister DEL 2 Bokmål Eksamensinformasjon for Del 2 Eksamenstid Hjelpemidler til Del 2 09.00 14.00, totalt 5 timer Del
Eksamen 21.05.2012 MAT0010 Matematikk Grunnskoleeksamen for voksne deltakere og privatister DEL 2 Bokmål Eksamensinformasjon for Del 2 Eksamenstid Hjelpemidler til Del 2 09.00 14.00, totalt 5 timer Del
Høsten 2015 Bokmål. Prøveinformasjon. Prøvetid: Hjelpemidler på Del 1 og Del 2: Framgangsmåte og forklaring: Del 1 (32,5 poeng) Del 2 (29 poeng)
 Høsten 2015 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og Del 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt samtidig. Del 1 skal du levere innen
Høsten 2015 Bokmål Navn: Gruppe: Prøveinformasjon Prøvetid: Hjelpemidler på Del 1 og Del 2: Framgangsmåte og forklaring: 5 timer totalt. Del 1 og Del 2 blir utdelt samtidig. Del 1 skal du levere innen
1. Matteoppgaver til Kapittel 2. x i x yi y. (a + bxi ),
 FRIVILLIGE MATTEOPPGAVER FOR STK1000 KAPITTEL 2 STEFFEN GRØNNEBERG Sammenrag. Følgene oppgaver er til glee for matteinteresserte STK1000- stuenter som ønsker å gå litt ypere inn i e matematiske aspektene
FRIVILLIGE MATTEOPPGAVER FOR STK1000 KAPITTEL 2 STEFFEN GRØNNEBERG Sammenrag. Følgene oppgaver er til glee for matteinteresserte STK1000- stuenter som ønsker å gå litt ypere inn i e matematiske aspektene
ANALYSER AV INDEKSER PÅ SKOLEPORTEN
 Christian Wenelborg ANALYSER AV INDEKSER PÅ SKOLEPORTEN Analyser på fylkes- og nasjonalt nivå for 7.trinn, 10. trinn og Vg1 2018 Christian Wenelborg Analyser av inekser på Skoleporten 2018 Analyser på
Christian Wenelborg ANALYSER AV INDEKSER PÅ SKOLEPORTEN Analyser på fylkes- og nasjonalt nivå for 7.trinn, 10. trinn og Vg1 2018 Christian Wenelborg Analyser av inekser på Skoleporten 2018 Analyser på
a 5 (2 + 8) d 5 (2 + 8) 4 g b 3 5 (2 + 8) e h 3 ( ) j Begrunn hvorfor du ikke får samme svar på oppgave b og g.
 Mtemtikk for ungomstrinnet KAPITTEL 4 TALL OG ALGEBRA MER ØVING Oppgve 1 Oppgve 2 Se på uttrykket A = g h. Hv forteller e ulike okstvene? Se på uttrykket O = 2π. Hv står e ulike symolene for? Forklr hv
Mtemtikk for ungomstrinnet KAPITTEL 4 TALL OG ALGEBRA MER ØVING Oppgve 1 Oppgve 2 Se på uttrykket A = g h. Hv forteller e ulike okstvene? Se på uttrykket O = 2π. Hv står e ulike symolene for? Forklr hv
4 Matematikklæreren til Kirsten gir poeng og karakterer på prøver. På de tre prøvene Kirsten har hatt, har hun fått poengene 47, 32 og 38.
 Likninger Løs likningene nedenfor og sett prøve på dem: a) + 4 b) 7 c) 4 + d) 8 5 e) 6 + + 5 f) 5 + g) + 5 h) 7( 4) 4 (5 6) Løs disse likningene: a) ( ) + 5 b) 5 (4 ) c) ( ) ( ) d) (5 ) + ( + ) 5 + 4 e)
Likninger Løs likningene nedenfor og sett prøve på dem: a) + 4 b) 7 c) 4 + d) 8 5 e) 6 + + 5 f) 5 + g) + 5 h) 7( 4) 4 (5 6) Løs disse likningene: a) ( ) + 5 b) 5 (4 ) c) ( ) ( ) d) (5 ) + ( + ) 5 + 4 e)
HOVEDENDRINGER AV VILKÅRENE FOR TRAVEL CASH-KONTOEN 16. AUGUST 2018
 HOVEDENDRINGER AV VILKÅRENE FOR TRAVEL CASH-KONTOEN 16. AUGUST 2018 Key Changes Norway 1 Hovedendringer av vilkårene for Travel Cash-kontoen som vil tre i kraft fra 16. august 2018 For de fullstendige
HOVEDENDRINGER AV VILKÅRENE FOR TRAVEL CASH-KONTOEN 16. AUGUST 2018 Key Changes Norway 1 Hovedendringer av vilkårene for Travel Cash-kontoen som vil tre i kraft fra 16. august 2018 For de fullstendige
Løsningsforslag Matematikk for ungdomstrinnet Del 1, Modul 1, 4MX130UM1-K
 Løsningsforslag Matematikk for ungdomstrinnet Del 1, Modul 1, 4MX130UM1-K ORDINÆR EKSAMEN 11.1.009 Oppgave 1 a) En følge av parallellaksiomet er at samsvarende vinkler ved parallelle linjer er like store.
Løsningsforslag Matematikk for ungdomstrinnet Del 1, Modul 1, 4MX130UM1-K ORDINÆR EKSAMEN 11.1.009 Oppgave 1 a) En følge av parallellaksiomet er at samsvarende vinkler ved parallelle linjer er like store.
Regler for: - Regning med tall! Det anbefales at man først ser på powerpoint-reglene når man skal lære seg ulike spill med kortstokkene!
 Regler for: getsmart Kids - Regning med tall! Det anbefales at man først ser på powerpoint-reglene når man skal lære seg ulike spill med kortstokkene! Sjekk hjemmesiden for flere powerpoint-presentasjoner.
Regler for: getsmart Kids - Regning med tall! Det anbefales at man først ser på powerpoint-reglene når man skal lære seg ulike spill med kortstokkene! Sjekk hjemmesiden for flere powerpoint-presentasjoner.
Løsningsforslag til del 2 av oppgavesettet Tall og algebra i Sirkel oppgavebok 10B, kapittel 6
 Tall og algera Del Løsningsforslag til del av oppgavesettet Tall og algera i Sirkel oppgaveok 10B, kapittel 6 Oppgave.1 a En pakke skinke holder til åtte horn. Sju pakker holder til 56 horn, og åtte pakker
Tall og algera Del Løsningsforslag til del av oppgavesettet Tall og algera i Sirkel oppgaveok 10B, kapittel 6 Oppgave.1 a En pakke skinke holder til åtte horn. Sju pakker holder til 56 horn, og åtte pakker
Eksamen REA3024 Matematikk R2
 Eksamen 03.1.009 REA304 Matematikk R Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del : Bruk av kilder: Vedlegg: Framgangsmåte: Veiledning om vurderingen:
Eksamen 03.1.009 REA304 Matematikk R Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del : Bruk av kilder: Vedlegg: Framgangsmåte: Veiledning om vurderingen:
UNIVERSITETET I BERGEN
 Bokmål UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. Løsningsforslag til Eksamen i emnet MAT - Grunnkurs i matematikk I Torsdag 22. mai 28, kl. 9-4. Dette er kun et løsningsforslag.
Bokmål UNIVERSITETET I BERGEN Det matematisk-naturvitenskapelige fakultet. Løsningsforslag til Eksamen i emnet MAT - Grunnkurs i matematikk I Torsdag 22. mai 28, kl. 9-4. Dette er kun et løsningsforslag.
Eksamen 27.01.2012. MAT1013 Matematikk 1T. Nynorsk/Bokmål
 Eksamen 27.01.2012 MAT1013 Matematikk 1T Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Framgangsmåte: 5 timer: Del 1 skal leveres inn etter 2 timer.
Eksamen 27.01.2012 MAT1013 Matematikk 1T Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på Del 1: Hjelpemidler på Del 2: Framgangsmåte: 5 timer: Del 1 skal leveres inn etter 2 timer.
Skriveregler for registrering i WebSak
 Skriveregler for registrering i WebSak Etnedal kommune Innholdsfortegnelse 1 Formål... 3 2 Omfang... 3 3 Ansvar/myndighet... 3 4 Definisjoner... 3 5 Beskrivelse/fremgangsmåte... 3 5.1 Språk... 3 5.2 Oppbygging
Skriveregler for registrering i WebSak Etnedal kommune Innholdsfortegnelse 1 Formål... 3 2 Omfang... 3 3 Ansvar/myndighet... 3 4 Definisjoner... 3 5 Beskrivelse/fremgangsmåte... 3 5.1 Språk... 3 5.2 Oppbygging
1P eksamen høsten Løsningsforslag
 1P eksamen høsten 2017 - Løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (2 poeng) En vare koster 640 kroner. Butikkeieren
1P eksamen høsten 2017 - Løsningsforslag Tid: 2 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (2 poeng) En vare koster 640 kroner. Butikkeieren
YF kapittel 1 Tall Løsninger til oppgavene i læreboka
 YF kpittel 1 Tll Løsninger til oppgvene i læreok Oppgve 10,, 0, 1,, 5,,, 0 Oppgve 10 Tllet 5 står til høyre for tllet på tllinj. Altså er 5>. Tllet 5 står til venstre for tllet 1 på tllinj. Altså er 5
YF kpittel 1 Tll Løsninger til oppgvene i læreok Oppgve 10,, 0, 1,, 5,,, 0 Oppgve 10 Tllet 5 står til høyre for tllet på tllinj. Altså er 5>. Tllet 5 står til venstre for tllet 1 på tllinj. Altså er 5
Dette er et sammendrag av det du har arbeidet med om tall og tallregning i Nummer 8, Nummer 9 og Nummer 10.
 SAMMENDRAG Dette er et sammendrag av det du har arbeidet med om tall og tallregning i Nummer 8, Nummer 9 og Nummer 10. Hvis du trenger mer trening utover oppgavene i Nummer 10, finner du ekstra oppgaver
SAMMENDRAG Dette er et sammendrag av det du har arbeidet med om tall og tallregning i Nummer 8, Nummer 9 og Nummer 10. Hvis du trenger mer trening utover oppgavene i Nummer 10, finner du ekstra oppgaver
Fasit. Oppgavebok. Kapittel 2. Bokmål
 Fasit 9 Oppgavebok Kapittel 2 Bokmål Kapittel 2 Lineære funksjoner rette linjer 2.1 a f (x) = 3x b f (0) = 0, f (3) = 9, f (5) = 15 2.2 a Funksjonen dobler tallet og trekker fra 1. b Funksjonen ganger
Fasit 9 Oppgavebok Kapittel 2 Bokmål Kapittel 2 Lineære funksjoner rette linjer 2.1 a f (x) = 3x b f (0) = 0, f (3) = 9, f (5) = 15 2.2 a Funksjonen dobler tallet og trekker fra 1. b Funksjonen ganger
Løsningsforslag til utsatt eksamen 2. desember 2015
 Løsningsforslag til utsatt eksamen 2. desember 2015 Oppgave 1 (vekt 20 %) a) Løs ligningen 3x 2 7x + 2 = 0 ved å bruke formelen for løsning av andregradsligninger. Løsning. 3x 2 7x + 2 = 0 x = ( 7) ( 7)2
Løsningsforslag til utsatt eksamen 2. desember 2015 Oppgave 1 (vekt 20 %) a) Løs ligningen 3x 2 7x + 2 = 0 ved å bruke formelen for løsning av andregradsligninger. Løsning. 3x 2 7x + 2 = 0 x = ( 7) ( 7)2
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN
 Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene Den globale økonomien falt kraftig i første kvartal i år, og fallet fortsatte
Kunsten å bruke sunn fornuft Verden sett fra SKAGEN Makroøkonomiske utsikter..9 Porteføljeforvalter Torgeir Høien Hovedpunktene Den globale økonomien falt kraftig i første kvartal i år, og fallet fortsatte
Høyt presterende elevers vurdering av læringsmiljøet
 Christian Wenelborg og Joakim Caspersen Høyt presterene elevers vurering av læringsmiljøet Analyser av Elevunersøkelsen 2013 og 2014 Rapport 2016 Mangfol og inkluering Christian Wenelborg og Joakim Caspersen
Christian Wenelborg og Joakim Caspersen Høyt presterene elevers vurering av læringsmiljøet Analyser av Elevunersøkelsen 2013 og 2014 Rapport 2016 Mangfol og inkluering Christian Wenelborg og Joakim Caspersen
være en rasjonal funksjon med grad p < grad q. La oss skrive p(x) (x a)q(x) = A
 MA 4: Analyse Uke 46, http://homehiano/ aasvaldl/ma4 H Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag Oppgave 73: Først skal vi delbrøkoppspalte (se Eksempel 5 side 558 i boka) 3t
MA 4: Analyse Uke 46, http://homehiano/ aasvaldl/ma4 H Høgskolen i Agder Avdeling for realfag Institutt for matematiske fag Oppgave 73: Først skal vi delbrøkoppspalte (se Eksempel 5 side 558 i boka) 3t
6.201 Badevekt i heisen
 RST 1 6 Kraft og bevegelse 27 6.201 Badevekt i heisen undersøke sammenhengen mellom normalkraften fra underlaget på et legeme og legemets akselerasjon teste hypoteser om kraft og akselerasjon Du skal undersøke
RST 1 6 Kraft og bevegelse 27 6.201 Badevekt i heisen undersøke sammenhengen mellom normalkraften fra underlaget på et legeme og legemets akselerasjon teste hypoteser om kraft og akselerasjon Du skal undersøke
