Bygge en trygg trapp LÆRERVEILEDNING. Presentasjon av sammenhengen
|
|
|
- Bent Ask
- 8 år siden
- Visninger:
Transkript
1 1 Bygge en trygg trapp LÆRERVEILEDNING Presentasjon av sammenhengen Oppgaven dreier seg om å bygge en trygg trapp for en privatbolig ved hjelp av en vanlig trekonstruksjon, slik en snekker eller tømrer vanligvis ville utføre arbeidet. Trappen kan være basert på planer fra en designer eller arkitekt som har vurdert den plassen som er tilgjengelig og skissert en utforming som er i samsvar med byggeforskriftene, men snekkeren må utføre det praktiske arbeidet med måling og bygging. Den generelle byggemåten kan vises ved hjelp av denne YouTube-videoen: Den viser hvordan en snekker i USA løser de praktiske problemene. Legg merke til at målene i denne videoen er i tommer, men prosessen er den samme når man arbeider med metriske mål, og hensikten med videoen er å gi en forståelse av prosessen. (Se gjerne videoen uten lyd for å unngå behovet for oversettelse, ettersom dette bare er en demonstrasjon av prosessen). Følgende terminologi er vanlig i byggebransjen: Gangtrinn den horisontale delen av et trinn der foten plasseres. Vange rammen som brukes til å feste gangtrinnene og stusstrinnene. Opptrinn høydeforskjellen mellom hvert trinn. Inntrinn dybden forfra og bakover for et gangtrinn, fratrukket eventuell overlapping med trinnet over. Dette målet er vanligvis noe mindre enn gangtrinnet for å gi plass til trinnese (utstikk i trinnet over). Trinndybde = trinnese + inntrinn.
2 2 Diagrammene under viser forskjellige måter å arrangere inntrinn og opptrinn, med varierende trinneser. Merk at diagram A er en åpen trapp mens B og C er mer tradisjonelle lukkede trappekonstruksjoner der trinnet stikker ut over opptrinnet eller opptrinnet er trukket tilbake for å gi ekstra plass. Det er ikke nødvendig å vurdere trinnese for de oppgavene som skal løses av elevene, men det forklarer terminologien. Kilde: I YouTube-videoen forklarer en snekker hvordan han bruker en tommelfingerregel i sine beregninger. I denne videoen bruker snekkeren tommemål, og tommelfingerregelen sier at hvert opptrinn bør være ca. 7 tommer og inntrinnene bør være ca. 10 tommer. Denne tommelfingerregelen er et praktisk hjelpemiddel som hjelper ham med å komme frem til mål som samsvarer med byggeforskriftene. Denne videoen egner seg ikke for å vise til elevene på grunn av de detaljerte beregningene i tommemål, men den kan gi nyttig bakgrunnsinformasjon for lærerne. Legg merke til snekkerens behov for å runde av tall ved hjelp av estimering, hvordan han begrunner sine valg og hvordan han i dette tilfellet regner med brøk, men bruker desimaler i målene ved den praktiske utførelsen. Det virker som om dette gjør oppgaven vanskeligere. Oppgave 1 En byggmester anbefaler denne tommelfingerregelen for å bygge en trapp: Hold høyden på opptrinnet mellom 170 mm og 185 mm dersom det er mulig, og bruk inntrinn på rundt 275 mm. Bruk denne regelen til å utforme en enkel trapp som passer for en etasjehøyde på nøyaktig mm. Tilgjengelig plass i horisontalplanet er 5 m. Hvor mange inntrinn og opptrinn vil du bruke? Hvilke mål vil du bruke for inntrinnene og opptrinnene vil du bruke, og hvorfor? Hvilke forutsetninger tar du? Hvilke andre faktorer kan det tenkes at du må vurdere ved utforming av en virkelig trapp?
3 3 Merknader til oppgave 1: Den tommelfingerregelen som brukes her vil passe for å oppfylle kravene i byggeforskriftene i flere land, og den brukes i denne oppgaven selv om forskjellige land kan ha ulike regler. Be elevene arbeide i små grupper med å utvikle et design og tegne et diagram. Elevene kan angripe denne oppgaven på forskjellige måter. Byggmesteren kan dividere totalhøyden med forskjellige opptrinnshøyder og sammenligne resultatene før svarene avrundes, og så beregne nøyaktig hvilken høyde opptrinnene må ha for passe til plassen (det må ikke finnes tomrom). Dette medfører en del avrunding av desimaler samt forutsetninger om nivået av nøyaktighet som kreves og hvilken høyde som ville være best å bruke for opptrinnene. Eksempel: / 170 = 16,76, men / 185 = 15,4 Ved å velge 16 trinn betyr det at hvert opptrinn blir 178,1 mm siden / 16 = 178, trinn betyr at hvert opptrinn blir 167,6 mm siden / 17 = 167,64 15 trinn betyr at hvert opptrinn blir 190 mm siden / 15 = trinn betyr at hvert opptrinn blir 158,3 mm siden / 18 = 158,33 Dersom det brukes 16 trinn vil høyden på opptrinnet ligge innenfor det foretrukne intervallet, og dermed ser det ut til å være det beste svaret, men: Med 16 trinn vil inntrinnet bli / 16 = mm Med 17 trinn vil inntrinnet bli / 17 = 294,12 mm Med 18 trinn vil inntrinnet bli / 18 = 277,78mm Dersom man antar at antall inntrinn og opptrinn er det samme, så vil: 17 trinn gi et inntrinn nær 275 mm, men høyden på opptrinnet blir like utenfor det akseptable intervallet. Med 16 trinn havner opptrinnet innenfor intervallet, men inntrinnet faller lengre utenfor intervallet. Med 18 trinn blir inntrinnet nærmere 275 mm, men opptrinnet faller enda lengre utenfor det foretrukne intervallet. Dersom elevene beslutter at antallet inntrinn skal være ett mindre enn antall opptrinn, vil det kunne brukes forskjellige kombinasjoner. Likevel vil ingen av kombinasjonene være ideelle i henhold til tommelfingerregelen, f.eks. 17 opptrinn og 16 inntrinn. Elevene må begrunne beslutningene sine, og de kan spørre hvorfor enkelte mål er anbefalt og om én anbefaling er viktigere enn en annen. Målene for inntrinn og opptrinn som brukes i forskriftene er teoretisk basert på gjennomsnittlig fotstørrelse og komfortabel trinnhøyde for en voksen, selv om det kan diskuteres. Dersom man avviker fra disse størrelsene, kan enkelte mennesker oppleve trappen som ubehagelig. Dette kan åpne for en interessant diskusjon av koblingen til antropometri, om årsakene til at byggeforskriftene varierer mellom ulike land, hvilke mål for "gjennomsnittlig" fotstørrelse og trinnhøyde som kan være passende og hvordan man kan finne frem til disse målene. En annen grunn som oppgis for at det er nødvendig med forskrifter, er at folk blir vant til bestemte størrelser på opptrinn og inntrinn, og det finnes indikasjoner på at det forekommer flere uhell når målene avviker betydelig fra tommelfingerregelen. Det kan forekomme dersom trinnene er for grunne eller for brede, samt i trapper som er for bratte eller har for smale trinn. (Disse årsakene som ligger bak bestemmelsene kan være et alternativt utgangspunkt for oppgaven, eller en utvidelse den. Elevene kan prøve å finne disse målene ved å undersøke data som er tilgjengelig på Internett eller ved å måle skostørrelse og trinnhøyde for et utvalg av personer og beregne et gjennomsnittsmål eller ved å måle eksisterende trapper for å beregne den gjennomsnittlige høyden for opptrinn og dybden for inntrinn i et utvalg av lokale trapper).
4 4 Noen grupper kan beslutte å måle variasjon i inntrinn og opptrinn for trinnene i en gitt trapp. Hvis de ikke velger å gjøre det, kan det være verdt å spørre elevene hvorfor de antar at trinnene har samme størrelse. Den viktigste grunnen som vanligvis angis for konsistens er sikkerhet, og byggeforskriftene vil generelt anbefale at inntrinnene og opptrinnene i en trapp har samme størrelse gjennom hele trappen for å unngå ulykker. Elevene kan tenkes å ha kommentarer til dette eller eksempler fra egen erfaring. Som svar på spørsmålet "Hvilke andre faktorer kan det tenkes at du må vurdere ved utforming av en virkelig trapp?" kan elevene foreslå at designet er avhengig av kostnader og tilgjengelighet av materialer (noen materialer for trinn leveres bare i visse bredder), behov for fri høyde på oversiden (bør vanligvis være minst mm), den ekstra gulvplassen som trengs ved bunnen og toppen av trappen (bør vanligvis være minst 900 mm), mulig plassbehov for håndløpere, rekkverkstype, praktisk plassering av trappen i bygningen etc. Med hele klassen samlet, be gruppene om å beskrive den utformingen de foreslår for trappen og forklare hvordan de tok sine beslutninger. Sammenlign de forskjellige gruppenes tilnærmingsmåter. Oppgave 2 Når du skal utforme en trapp for montering på et sted hvor en sammenhengende trapp ikke kan plasseres, blir du nødt til å vurdere hvordan du plasserer avsatser der trappen svinger, eller om du vil gjøre det på en annen måte. Anbefalt minimumstørrelse for en trappeavsats er vanligvis et kvadrat hvor sidenes lengde er lik trappens bredde. Her er noen eksempler på utforming med avsatser: Kilde: Foreslå en utforming av en trapp for en plass som måler mm ganger mm og har en høyde mellom etasjene på mm. Bruk den samme tommelfingerregelen som tidligere. Lag diagrammer for å vise utformingen din. Merknader til oppgave 2: Alternativt kan elevene måle og vurdere et faktisk sted hvor det kan være ønskelig å plassere en trapp, eller prøve å skissere et annet arrangement for en eksisterende trapp. Også denne gangen skal hver gruppe lage diagrammer for å vise sitt forslag til utforming. I denne oppgaven må elevene også beslutte hvilken bredde trappen skal ha. En bredde på 900 mm ville være typisk, men de bør ta sine egne beslutninger. Dette kan innebære diskusjoner om kroppsstørrelse og om to personer skal kunne passere hverandre i trappen eller ikke. Alternativt kan elevene bestemme seg for å måle noen eksisterende trapper for å finne ut hva som er normalt, eller de kan søke opp informasjon på Internett. (Ved måling av eksisterende trapper må man være oppmerksom på at det sannsynligvis er forskjeller mellom offentlige bygg og private boliger).
5 5 Be hver gruppe om å beskrive sitt løsningsforslag for klassen og forklare beslutningene som ligger bak utformingen. Oppgave 3 (utvidelse) En alternativ arbeidsmåte kan være å bruke de aktuelle byggeforskriftene i stedet for tommelfingerregelen som er avledet fra dem. I byggeforskrifter i Storbritannia er det for eksempel angitt tre viktige parametre i veiledningen. 1. Alle opptrinnshøyder mellom 155 mm og 220 mm kan brukes med alle inntrinnsdybder fra 245 mm til 260 mm eller alle opptrinn mellom 165 mm og 200 mm kan brukes med alle inntrinn mellom 223 mm og 300 mm. 2. Trappen må maksimalt ha en helning på 42 o (funnet ved hjelp av vertikal måling dividert med horisontal og invers tangent). 3. 2O + I må ligge mellom 550 mm og 700 mm, hvor O er høyden på opptrinn og I er dybden på inntrinn. Kilde: Merk at en helningsvinkel på 42 o kan tolkes som tan 42 o = opptrinn/inntrinn. For løsning av denne oppgaven er det ikke nødvendigvis viktig hvilket land byggeforskriftene hører til kanskje vil du tilpasse oppgaven for bruk sammen med dine egne nasjonale byggeforskrifter. Start med å diskutere med elevene hvilken betydning begrensningene kan ha, og be dem deretter be om å: Finne ut om den trappen de foreslo i første oppgave er i samsvar med regelverket eller ikke, og hvorfor det er slik. Bruke formelen og de andre begrensningene som er oppgitt til å undersøke om det er noen andre lovlige kombinasjoner som ikke ville oppstå fra metoden med tommelfingerregel, og om det ville være hensiktsmessig å bruke disse. Elevene kan velge å forskjellige tilnærminger til denne oppgaven. De kan for eksempel tabulere mulige alternativer systematisk eller de kan bruke en grafisk tilnærming. En grafisk tilnærming viser tydelig hvordan noen av opplysningene faktisk er overflødige, selv om arkitekter eksempelvis tilsynelatende bruker regelen om helningsvinkel som en praktisk sjekk på sine beregninger. Dermed kan man oppmuntre til denne tilnærmingen, eller den kan vises for gruppen senere. Det illustrerer også hvordan tommelfingerregelen passer godt innenfor det området hvor de mulige kombinasjoner av mål ligger på grafen. Diskuter med klassen hvordan de har konkludert om andre kombinasjoner av målinger, og hvorfor de kan eller hvorfor de ikke kan bruke disse. Diskuter den relative nytten av å bruke tommelfingerregelen og de mer detaljerte reglene.
1) Sette seg inn i regler som gjelder for trapper 2) Utføre målinger og beregninger 3) Utfordring: Hvordan presentere resultatene?
 TRAPPEMATEMATIKK Beskrivelse/Presentasjon Hensikten med oppgaven er at elevene skal gjøre målinger og teste ut trappeformelen på ulike trapper på egen skole for å sjekke at de tilfredsstiller kravene til
TRAPPEMATEMATIKK Beskrivelse/Presentasjon Hensikten med oppgaven er at elevene skal gjøre målinger og teste ut trappeformelen på ulike trapper på egen skole for å sjekke at de tilfredsstiller kravene til
Nasjonale prøver i lesing, regning og engelsk på 5. trinn 2015
 Nasjonale prøver i lesing, regning og engelsk på 5. trinn 2015 Resultater fra nasjonale prøver på 5. trinn høsten 2015 er nå publisert i Skoleporten. Her er et sammendrag for Nord-Trøndelag: - I snitt
Nasjonale prøver i lesing, regning og engelsk på 5. trinn 2015 Resultater fra nasjonale prøver på 5. trinn høsten 2015 er nå publisert i Skoleporten. Her er et sammendrag for Nord-Trøndelag: - I snitt
Veiledning om tekniske krav til byggverk Trapp
 12-16. Trapp Publisert dato 07.11.2011 12-16. Trapp (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport, herunder rømning ved brann. Følgende
12-16. Trapp Publisert dato 07.11.2011 12-16. Trapp (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport, herunder rømning ved brann. Følgende
Veiledning om tekniske krav til byggverk 12-16. Trapp
 12-16. Trapp Lastet ned fra Direktoratet for byggkvalitet 09.10.2013 12-16. Trapp (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport, herunder
12-16. Trapp Lastet ned fra Direktoratet for byggkvalitet 09.10.2013 12-16. Trapp (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport, herunder
Matematisk modellering. Astrid Bondø Ny GIV, februar/mars 2013
 Matematisk modellering Astrid Bondø Ny GIV, februar/mars 2013 Representasjon av funksjoner Janviers tabell Til Kontekst Tabell Graf Uttrykk Fra verbalt eller situasjon Kontekst verbalt eller situasjon
Matematisk modellering Astrid Bondø Ny GIV, februar/mars 2013 Representasjon av funksjoner Janviers tabell Til Kontekst Tabell Graf Uttrykk Fra verbalt eller situasjon Kontekst verbalt eller situasjon
Vår saksbehandler Vår referanse Vår dato R. Sand 110825_Passasjerflyt_V ossstasjon_n001_rev1209
 NOTAT Til: Fra: Kopi: John Arne Bjerknes Roald Sand Arkiv 2060 Vår saksbehandler Vår referanse Vår dato R. Sand 110825_Passasjerflyt_V ossstasjon_n001_rev1209 18. september 2012 EMNE: Vurdering av passasjerflyt
NOTAT Til: Fra: Kopi: John Arne Bjerknes Roald Sand Arkiv 2060 Vår saksbehandler Vår referanse Vår dato R. Sand 110825_Passasjerflyt_V ossstasjon_n001_rev1209 18. september 2012 EMNE: Vurdering av passasjerflyt
Teori om preferanser (en person), samfunnsmessig velferd (flere personer) og frikonkurranse
 Teori om preferanser (en person), samfunnsmessig velferd (flere personer) og frikonkurranse Flere grunner til å se på denne teorien tidlig i kurset De neste gangene skal vi bl.a. se på hva slags kontrakter
Teori om preferanser (en person), samfunnsmessig velferd (flere personer) og frikonkurranse Flere grunner til å se på denne teorien tidlig i kurset De neste gangene skal vi bl.a. se på hva slags kontrakter
b. Trapp skal ha jevn stigning og samme høyde på opptrinn i hele trappens lengde.
 12-16. Trapp (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport, herunder rømning ved brann. Følgende skal minst være oppfylt: a. Trapp skal
12-16. Trapp (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport, herunder rømning ved brann. Følgende skal minst være oppfylt: a. Trapp skal
Miljø og kjemi i et IT-perspektiv
 Miljø og kjemi i et IT-perspektiv Prosjektrapporten av Kåre Sorteberg Halden mars 2008 Side 1 av 5 Innholdsfortegnelse Innholdsfortegnelse... 2 Prosjektrapporten... 3 Rapportstruktur... 3 Forside... 3
Miljø og kjemi i et IT-perspektiv Prosjektrapporten av Kåre Sorteberg Halden mars 2008 Side 1 av 5 Innholdsfortegnelse Innholdsfortegnelse... 2 Prosjektrapporten... 3 Rapportstruktur... 3 Forside... 3
Limtre Bjelkelags- og sperretabeller
 Pb 142 2391 Moelv www.limtre.no pr juni 2005 Forutsetninger for bjelkelags- og sperretabeller Tabellene bygger på følgende norske standarder og kvaliteter: NS 3470-1, 5.utg. 1999, Prosjektering av trekonstruksjoner
Pb 142 2391 Moelv www.limtre.no pr juni 2005 Forutsetninger for bjelkelags- og sperretabeller Tabellene bygger på følgende norske standarder og kvaliteter: NS 3470-1, 5.utg. 1999, Prosjektering av trekonstruksjoner
Min Maskin! TIP 120 minutter
 Lærerveiledning Passer for: Varighet: Min Maskin! TIP 120 minutter Min Maskin! er et program hvor elevene lærer om grunnleggende bruk av hydrauliske prinsipper. Elevene skal bruke noe av det de kan om
Lærerveiledning Passer for: Varighet: Min Maskin! TIP 120 minutter Min Maskin! er et program hvor elevene lærer om grunnleggende bruk av hydrauliske prinsipper. Elevene skal bruke noe av det de kan om
Sensorveiledning for Matematikk 103 Måling, tall og algebra og funksjoner LBMAT10311
 Høst 2018 Sensorveiledning for Matematikk 103 Måling, tall og algebra og funksjoner LBMAT10311 1) Eksamensoppgaven med løsningsforslag side 3 til 11. Den inneholder fasit og forslag eller kommentarer til
Høst 2018 Sensorveiledning for Matematikk 103 Måling, tall og algebra og funksjoner LBMAT10311 1) Eksamensoppgaven med løsningsforslag side 3 til 11. Den inneholder fasit og forslag eller kommentarer til
Geometri. Mål. for opplæringen er at eleven skal kunne
 8 1 Geometri Mål for opplæringen er at eleven skal kunne bruke geometri i planet til å analysere og løse sammensatte teoretiske og praktiske problemer knyttet til lengder, vinkler og areal 1.1 Vinkelsummen
8 1 Geometri Mål for opplæringen er at eleven skal kunne bruke geometri i planet til å analysere og løse sammensatte teoretiske og praktiske problemer knyttet til lengder, vinkler og areal 1.1 Vinkelsummen
1 of 6 3/29/2016 2:03 PM
 1 of 6 3/29/2016 2:03 PM OPPRINNELIG KUNNGJORT VERSJON OPPRINNELIG KUNNGJORT VERSJON Dato FOR-2009-09-24-1245 Departement Helse- og omsorgsdepartementet Publisert I 2009 hefte 11 s 1787 Ikrafttredelse
1 of 6 3/29/2016 2:03 PM OPPRINNELIG KUNNGJORT VERSJON OPPRINNELIG KUNNGJORT VERSJON Dato FOR-2009-09-24-1245 Departement Helse- og omsorgsdepartementet Publisert I 2009 hefte 11 s 1787 Ikrafttredelse
(12) PATENT (19) NO (11) 332103 (13) B1 NORGE. (51) Int Cl. Patentstyret
 (12) PATENT (19) NO (11) 3323 (13) B1 NORGE (1) Int Cl. A01K 61/00 (06.01) G01B 11/04 (06.01) G01B 11/24 (06.01) Patentstyret (21) Søknadsnr 1736 (86) Int.inng.dag og søknadsnr (22) Inng.dag.12.13 (8)
(12) PATENT (19) NO (11) 3323 (13) B1 NORGE (1) Int Cl. A01K 61/00 (06.01) G01B 11/04 (06.01) G01B 11/24 (06.01) Patentstyret (21) Søknadsnr 1736 (86) Int.inng.dag og søknadsnr (22) Inng.dag.12.13 (8)
Stillasdagene Offentlige trappetårn STILLASENTREPRENØRENES FORENING
 Stillasdagene 2017 Offentlige trappetårn 1 Bekymringsmelding; Trappetårn Det skulle bygges et midlertidig trappetårn som rømningsvei for et kjøpesenter. Eurokode 1 del 1 har krav til slike trappetårn (rømningsvei);
Stillasdagene 2017 Offentlige trappetårn 1 Bekymringsmelding; Trappetårn Det skulle bygges et midlertidig trappetårn som rømningsvei for et kjøpesenter. Eurokode 1 del 1 har krav til slike trappetårn (rømningsvei);
Delrapport 4.4 Maritime forhold Grindjordområdet
 Narvik Havn KF Nye Narvik havn Delrapport 4.4 Maritime forhold Grindjordområdet Utdrag av Delrapport 3.3 2013-02-07 Oppdragsnr. 5125439 1 Stedlige forhold 1.1 BESKRIVELSE AV STEDET Grindjord ligger i
Narvik Havn KF Nye Narvik havn Delrapport 4.4 Maritime forhold Grindjordområdet Utdrag av Delrapport 3.3 2013-02-07 Oppdragsnr. 5125439 1 Stedlige forhold 1.1 BESKRIVELSE AV STEDET Grindjord ligger i
Utgave 01.04.2013. Rettløpstrapp, unngå svingt trapp. Trapp plassert slik at det unngås sammenstøt med underkant av trappekonstruksjon.
 1 Sjekkpunkter TEK10 med utdrag fra veiledning Anbefalte tilleggsytelser Generelt 12-16 (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport,
1 Sjekkpunkter TEK10 med utdrag fra veiledning Anbefalte tilleggsytelser Generelt 12-16 (1) Trapp skal være lett og sikker å gå i. Bredde og høyde i trapp skal tilpasses forventet ferdsel og transport,
NMCUs demokratimodell - presentasjon av rapporten fra arbeidsgruppa. Årsmøtet tar konklusjonene i rapporten fra arbeidsgruppa til etterretning
 NMCUs årsmøte 2009 Vedtektene 4, Innmeldte saker Sak 1: Forslagstiller: Forslag: Begrunnelse: Sentralstyrets kommentar: NMCUs demokratimodell - presentasjon av rapporten fra arbeidsgruppa Sentralstyret
NMCUs årsmøte 2009 Vedtektene 4, Innmeldte saker Sak 1: Forslagstiller: Forslag: Begrunnelse: Sentralstyrets kommentar: NMCUs demokratimodell - presentasjon av rapporten fra arbeidsgruppa Sentralstyret
Veiledning. Nasjonale prøver i regning for 5. trinn. Versjon: juli 2010, bokmål
 Veiledning Nasjonale prøver i regning for 5. trinn Versjon: juli 2010, bokmål Nasjonale prøver i regning for 5. trinn Her får du informasjon om nasjonale prøver i regning og hva prøven måler. Videre presenteres
Veiledning Nasjonale prøver i regning for 5. trinn Versjon: juli 2010, bokmål Nasjonale prøver i regning for 5. trinn Her får du informasjon om nasjonale prøver i regning og hva prøven måler. Videre presenteres
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) 1,0 g salt inneholder 0,4 g natrium. Helsemyndighetene anbefaler et inntak av natrium på maksimalt 2,4 g per dag. a) Hvor mange gram salt kan du maksimalt innta
DEL 1 Uten hjelpemidler Oppgave 1 (3 poeng) 1,0 g salt inneholder 0,4 g natrium. Helsemyndighetene anbefaler et inntak av natrium på maksimalt 2,4 g per dag. a) Hvor mange gram salt kan du maksimalt innta
Moro med bungyjump. Lærerveiledning. Passer for: trinn Antall elever: Maksimum 16
 Lærerveiledning Moro med bungyjump Passer for: 8. 10. trinn Antall elever: Maksimum 16 Varighet: 90 minutter Moro med bungyjump er et skoleprogram hvor elevene får erfaring med hvordan man leser informasjon
Lærerveiledning Moro med bungyjump Passer for: 8. 10. trinn Antall elever: Maksimum 16 Varighet: 90 minutter Moro med bungyjump er et skoleprogram hvor elevene får erfaring med hvordan man leser informasjon
48 tips. som gjør boligen din funksjonell
 48 tips som gjør boligen din funksjonell UNIVERSELL UTFORMING EN BOLIG TIL BRUK I ALLE LIVSFASER Den som er frisk, sprek og fleksibel, tenker kanskje ikke over det så ofte, men har nok likevel irritert
48 tips som gjør boligen din funksjonell UNIVERSELL UTFORMING EN BOLIG TIL BRUK I ALLE LIVSFASER Den som er frisk, sprek og fleksibel, tenker kanskje ikke over det så ofte, men har nok likevel irritert
Eksempeloppgave 1T, Høsten 2009
 Eksempeloppgave 1T, Høsten 009 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) a) Bruk opplysningene nedenfor til å finne
Eksempeloppgave 1T, Høsten 009 Del 1 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) a) Bruk opplysningene nedenfor til å finne
NOTAT 4. mars 2010. Norsk institutt for vannforskning (NIVA), Oslo
 NOTAT 4. mars 21 Til: Naustdal og Askvoll kommuner, ved Annlaug Kjelstad og Kjersti Sande Tveit Fra: Jarle Molvær, NIVA Kopi: Harald Sørby (KLIF) og Jan Aure (Havforskningsinstituttet) Sak: Nærmere vurdering
NOTAT 4. mars 21 Til: Naustdal og Askvoll kommuner, ved Annlaug Kjelstad og Kjersti Sande Tveit Fra: Jarle Molvær, NIVA Kopi: Harald Sørby (KLIF) og Jan Aure (Havforskningsinstituttet) Sak: Nærmere vurdering
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005 Oppgave ( poeng) Løs likningssystemet x 3y 13 4x y Oppgave 3 ( poeng) Løs ulikheten x 6x 0 Oppgave 4
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005 Oppgave ( poeng) Løs likningssystemet x 3y 13 4x y Oppgave 3 ( poeng) Løs ulikheten x 6x 0 Oppgave 4
Prøve i FO929A - Matematikk Dato: 15. november 2012 Hjelpemiddel: Kalkulator
 Prøve i FO929A - Matematikk Dato: 15. november 2012 Hjelpemiddel: Kalkulator Oppgave 1 a) Finn alle løsningene til likningen 10x 100 = 90x 1. b) Finn alle løsninger v til likningen slik at 0 v 4π. 2 cos
Prøve i FO929A - Matematikk Dato: 15. november 2012 Hjelpemiddel: Kalkulator Oppgave 1 a) Finn alle løsningene til likningen 10x 100 = 90x 1. b) Finn alle løsninger v til likningen slik at 0 v 4π. 2 cos
dyst Nærstrid er våpenøvelser mot målskiver. Øvelsene settes sammen til en bane som består av varierende våpen og teknikker.
 Hva er riddersport? Riddersport er middelalderens våpenbruk til hest gjeninnført som en moderne sport. Grener og momenter er historisk basert, og i størst mulig grad hentet fra manuskripter fra høy- og
Hva er riddersport? Riddersport er middelalderens våpenbruk til hest gjeninnført som en moderne sport. Grener og momenter er historisk basert, og i størst mulig grad hentet fra manuskripter fra høy- og
Læreplan i felles programfag i Vg1 naturbruk
 Læreplan i felles programfag i Vg1 naturbruk Fastsatt som forskrift av Utdanningsdirektoratet 16. januar 2006 etter delegasjon i brev av 26.september 2005 fra utdannings- og forskningsdepartementet med
Læreplan i felles programfag i Vg1 naturbruk Fastsatt som forskrift av Utdanningsdirektoratet 16. januar 2006 etter delegasjon i brev av 26.september 2005 fra utdannings- og forskningsdepartementet med
Gjennom denne oppgaven skal elevene lære å bruke ulike måleredskaper for å beregne volum og tetthet til kuler og vurdere om svarene virker rimelig.
 KULeMATEMATIKK Beskrivelse/Presentasjon Gjennom denne oppgaven skal elevene lære å bruke ulike måleredskaper for å beregne volum og tetthet til kuler og vurdere om svarene virker rimelig. Arbeidsoppdraget
KULeMATEMATIKK Beskrivelse/Presentasjon Gjennom denne oppgaven skal elevene lære å bruke ulike måleredskaper for å beregne volum og tetthet til kuler og vurdere om svarene virker rimelig. Arbeidsoppdraget
Romfartskarriereprosjektet 2016
 Romfartskarriereprosjektet 2016 Innledning I 2016 gjennomfører ESA-astronauten Tim Peake et lengevarende oppdrag på Den internasjonale romstasjonen (ISS). Oppdraget har fått navnet Principia. Astronauter
Romfartskarriereprosjektet 2016 Innledning I 2016 gjennomfører ESA-astronauten Tim Peake et lengevarende oppdrag på Den internasjonale romstasjonen (ISS). Oppdraget har fått navnet Principia. Astronauter
7-41 Planløsning, størrelse og utforming
 7-41 Planløsning, størrelse og utforming 1 Generelle krav Et funksjonelt godt byggverk er ulykkesforebyggende. Korte og enkle trafikklinjer som minst mulig krysser hverandre, er en forutsetning for rasjonell
7-41 Planløsning, størrelse og utforming 1 Generelle krav Et funksjonelt godt byggverk er ulykkesforebyggende. Korte og enkle trafikklinjer som minst mulig krysser hverandre, er en forutsetning for rasjonell
ESERO AKTIVITET HVILKEN EFFEKT HAR SOLEN? Lærerveiledning og elevaktivitet. Klassetrinn 7-8
 ESERO AKTIVITET Klassetrinn 7-8 Lærerveiledning og elevaktivitet Oversikt Tid Læremål Nødvendige materialer 50 min. lære at Solen dreier seg rundt sin egen akse fra vest til øst (mot urviserne) oppdage
ESERO AKTIVITET Klassetrinn 7-8 Lærerveiledning og elevaktivitet Oversikt Tid Læremål Nødvendige materialer 50 min. lære at Solen dreier seg rundt sin egen akse fra vest til øst (mot urviserne) oppdage
Generelle opplysninger om eksamen i 1T. I vurderingsveiledning fra Utdanningsdirektoratet finner vi blant annet dette:
 Forord Generelle opplysninger om eksamen i 1T I vurderingsveiledning fra Utdanningsdirektoratet finner vi blant annet dette: Eksamensordning Eksamen varer fem timer og er todelt. Del 1 og del 2 av eksamensoppgaven
Forord Generelle opplysninger om eksamen i 1T I vurderingsveiledning fra Utdanningsdirektoratet finner vi blant annet dette: Eksamensordning Eksamen varer fem timer og er todelt. Del 1 og del 2 av eksamensoppgaven
Læreplan i aktivitetslære - felles programfag i utdanningsprogram for idrettsfag
 Læreplan i aktivitetslære - felles programfag i utdanningsprogram for idrettsfag Gjelder fra 01.08.2006 http://www.udir.no/kl06/idr1-01 Formål Tradisjonelle idretter, og nyere former for idrett og aktivitet,
Læreplan i aktivitetslære - felles programfag i utdanningsprogram for idrettsfag Gjelder fra 01.08.2006 http://www.udir.no/kl06/idr1-01 Formål Tradisjonelle idretter, og nyere former for idrett og aktivitet,
Lagertelt 9 m2monteringsanvisning
 Lagertelt 9 m2monteringsanvisning BESKRIVELSE MODELLNR. 3 m x 3 m x 2,4 m Shed-in-a-Box - Grå 70333 ANBEFALT VERKTØY ELLER 11 mm Les HELE anvisningen før monteringen påbegynnes. Denne beskyttelsen MÅ forankres
Lagertelt 9 m2monteringsanvisning BESKRIVELSE MODELLNR. 3 m x 3 m x 2,4 m Shed-in-a-Box - Grå 70333 ANBEFALT VERKTØY ELLER 11 mm Les HELE anvisningen før monteringen påbegynnes. Denne beskyttelsen MÅ forankres
Analyse av nasjonale prøver i engelsk, lesing og regning på 5. trinn 2015
 Analyse av nasjonale prøver i engelsk, lesing og regning på 5. trinn 2015 Sammendrag I snitt presterer elevene likt i engelsk og regning i 2014 og 2015. Endringen i prestasjoner fra 2014 til 2015 i engelsk
Analyse av nasjonale prøver i engelsk, lesing og regning på 5. trinn 2015 Sammendrag I snitt presterer elevene likt i engelsk og regning i 2014 og 2015. Endringen i prestasjoner fra 2014 til 2015 i engelsk
Eksamensoppgave i TIØ4120 Operasjonsanalyse, gk.
 Institutt for industriell økonomi og teknologiledelse Eksamensoppgave i TIØ4120 Operasjonsanalyse, gk. Faglig kontakt under eksamen: Anders Gullhav Tlf.: 90 92 71 00 Eksamensdato: 05.08.2013 Eksamenstid
Institutt for industriell økonomi og teknologiledelse Eksamensoppgave i TIØ4120 Operasjonsanalyse, gk. Faglig kontakt under eksamen: Anders Gullhav Tlf.: 90 92 71 00 Eksamensdato: 05.08.2013 Eksamenstid
: subs x = 2, f n x end do
 Oppgave 2..5 a) Vi starter med å finne de deriverte til funksjonen av orden opp til og med 5 i punktet x = 2. Det gjør vi ved å bruke kommandoen diff f x, x$n der f x er uttrykket som skal deriveres, x
Oppgave 2..5 a) Vi starter med å finne de deriverte til funksjonen av orden opp til og med 5 i punktet x = 2. Det gjør vi ved å bruke kommandoen diff f x, x$n der f x er uttrykket som skal deriveres, x
Monteringsanvisning Skyggetaksrullegardin
 Monteringsanvisning Skyggetaksrullegardin Art nr: 61-3283 Rev.nr: 140214 Bormaskin/Skrutrekker Skrutrekker Baufil Tommestokk 61-3283 - NO Montering Skyggetaket passer under tak der avstanden mellom takstolene
Monteringsanvisning Skyggetaksrullegardin Art nr: 61-3283 Rev.nr: 140214 Bormaskin/Skrutrekker Skrutrekker Baufil Tommestokk 61-3283 - NO Montering Skyggetaket passer under tak der avstanden mellom takstolene
Matematikk 1P-Y. Bygg- og anleggsteknikk
 Matematikk 1P-Y «Å kunne regne i bygg- og anleggsteknikk innebærer å beregne tid, pris, vekt, volum, mengde, størrelser og masser. I tillegg er målestokk, måltaking og beregning av vinkler knyttet til
Matematikk 1P-Y «Å kunne regne i bygg- og anleggsteknikk innebærer å beregne tid, pris, vekt, volum, mengde, størrelser og masser. I tillegg er målestokk, måltaking og beregning av vinkler knyttet til
Anne Berit Fuglestad Elektroniske arbeidsark i Excel
 Anne Berit Fuglestad Elektroniske arbeidsark i Excel Regnearkene nevnt i denne artikkelen kan du hente via www.caspar.no/tangenten/ 2003/anneberit103.html Regneark er et av de verktøyprogram som gir mange
Anne Berit Fuglestad Elektroniske arbeidsark i Excel Regnearkene nevnt i denne artikkelen kan du hente via www.caspar.no/tangenten/ 2003/anneberit103.html Regneark er et av de verktøyprogram som gir mange
Oppfinnelsens område. Bakgrunn for oppfinnelsen
 1 Oppfinnelsens område Oppfinnelsen vedrører smelting av metall i en metallsmelteovn for støping. Oppfinnelsen er nyttig ved smelting av flere metaller og er særlig nyttig ved smelting av aluminium. Bakgrunn
1 Oppfinnelsens område Oppfinnelsen vedrører smelting av metall i en metallsmelteovn for støping. Oppfinnelsen er nyttig ved smelting av flere metaller og er særlig nyttig ved smelting av aluminium. Bakgrunn
Retningslinjer for kjellervinduer i ØTB
 Retningslinjer for kjellervinduer i ØTB ØTBs utbyggingskomite av 2004 la på ekstraordinært sameiermøte 29. november 2006 fram følgende forslag, som ble enstemmig vedtatt: 1. Komiteens forslag «Regelverk
Retningslinjer for kjellervinduer i ØTB ØTBs utbyggingskomite av 2004 la på ekstraordinært sameiermøte 29. november 2006 fram følgende forslag, som ble enstemmig vedtatt: 1. Komiteens forslag «Regelverk
7.4 Eksempler på misoppfatninger/mistolkinger
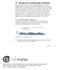 Verdier som parvis hører sammen. Nedbør som samsvarer med dagen vi velger. Utviklingen eller forandringen. Har nedbørsmengden steget eller sunket, har det gått opp og ned? Måleverdien har forandret seg
Verdier som parvis hører sammen. Nedbør som samsvarer med dagen vi velger. Utviklingen eller forandringen. Har nedbørsmengden steget eller sunket, har det gått opp og ned? Måleverdien har forandret seg
Elevens ID: Elevspørreskjema. 4. årstrinn. Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo
 Elevens ID: Elevspørreskjema 4. årstrinn Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo International Association for the Evaluation of Educational Achievement Copyright IEA, 2005
Elevens ID: Elevspørreskjema 4. årstrinn Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo International Association for the Evaluation of Educational Achievement Copyright IEA, 2005
Indekshastighet. Måling av vannføring ved hjelp av vannhastighet
 Indekshastighet. Måling av vannføring ved hjelp av vannhastighet Av Kristoffer Dybvik Kristoffer Dybvik er felthydrolog i Hydrometriseksjonen, Hydrologisk avdeling, NVE Sammendrag På de fleste av NVEs
Indekshastighet. Måling av vannføring ved hjelp av vannhastighet Av Kristoffer Dybvik Kristoffer Dybvik er felthydrolog i Hydrometriseksjonen, Hydrologisk avdeling, NVE Sammendrag På de fleste av NVEs
11.09.2013. Kursdag på NN skole om matematikkundervisning. Hva har læringseffekt? Hva har læringseffekt? Multiaden 2013. Lærerens inngripen
 God matematikkundervisning. Punktum. Multiaden 2013 Kursdag på NN skole om matematikkundervisning Hva bør dagen handle om? Ranger disse ønskene. Formativ vurdering Individorientert undervisning Nivådifferensiering
God matematikkundervisning. Punktum. Multiaden 2013 Kursdag på NN skole om matematikkundervisning Hva bør dagen handle om? Ranger disse ønskene. Formativ vurdering Individorientert undervisning Nivådifferensiering
Fra idé til virkelighet
 Typebetegnelse Fra idé til virkelighet FREKHAUG VINDUET AS FREKHAUG VINDUET AS 5918 FREKHAUG Tlf. 56 17 44 40 FAX 56 17 44 80 www.frekhaug.com med rett til å velge På de kommende sider viser vi Frekhaug
Typebetegnelse Fra idé til virkelighet FREKHAUG VINDUET AS FREKHAUG VINDUET AS 5918 FREKHAUG Tlf. 56 17 44 40 FAX 56 17 44 80 www.frekhaug.com med rett til å velge På de kommende sider viser vi Frekhaug
Eksamen 1T høsten 2015
 Eksamen 1T høsten 015 Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005
Eksamen 1T høsten 015 Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 (1 poeng) Regn ut og skriv svaret på standardform 1 1,8 10 0,0005
Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo. 4. klasse
 Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo Hovedtest Elevspørreskjema 4. klasse Veiledning I dette heftet vil du finne spørsmål om deg selv. Noen spørsmål dreier seg om fakta,
Institutt for lærerutdanning og skoleutvikling Universitetet i Oslo Hovedtest Elevspørreskjema 4. klasse Veiledning I dette heftet vil du finne spørsmål om deg selv. Noen spørsmål dreier seg om fakta,
Kapittel 4 Opplæringen i klassene B kode 96 og BE
 Kapittel 4 Opplæringen i klassene B kode 96 og BE Hovedmål for opplæring klasse B kode 96 og BE, jf 12-1 Etter å ha gjennomført føreropplæring i klasse BE, skal eleven ha den kompetansen som trengs for
Kapittel 4 Opplæringen i klassene B kode 96 og BE Hovedmål for opplæring klasse B kode 96 og BE, jf 12-1 Etter å ha gjennomført føreropplæring i klasse BE, skal eleven ha den kompetansen som trengs for
168291/S20: Transport av farlig gods på veg, sjø og bane. Jørn Vatn Prosjektleder SINTEF
 168291/S20: Transport av farlig gods på veg, sjø og bane Jørn Vatn Prosjektleder SINTEF 1 Tema for presentasjon Kan risikoanalysen benyttes som bevisføring for at en løsning er bedre enn en alternativ
168291/S20: Transport av farlig gods på veg, sjø og bane Jørn Vatn Prosjektleder SINTEF 1 Tema for presentasjon Kan risikoanalysen benyttes som bevisføring for at en løsning er bedre enn en alternativ
Sammenlikning av kostnader, BSF vs tradisjonelle løsninger
 Side 1 av 5 Typiske spørsmål vi får når det gjelder evaluering av BSF- teknologien er: - Hva er kostnadene i forhold til tradisjonelle? - eller - Hva er besparelsen i forhold til tradisjonelle konsoller?
Side 1 av 5 Typiske spørsmål vi får når det gjelder evaluering av BSF- teknologien er: - Hva er kostnadene i forhold til tradisjonelle? - eller - Hva er besparelsen i forhold til tradisjonelle konsoller?
Læreplan i breddeidrett - valgfrie programfag i utdanningsprogram for idrettsfag
 Læreplan i breddeidrett - valgfrie programfag i utdanningsprogram for idrettsfag Gjelder fra 01.08.2006 http://www.udir.no/kl06/idr6-01 Formål Ungdommens valg av idretts- og friluftsaktiviteter er i stadig
Læreplan i breddeidrett - valgfrie programfag i utdanningsprogram for idrettsfag Gjelder fra 01.08.2006 http://www.udir.no/kl06/idr6-01 Formål Ungdommens valg av idretts- og friluftsaktiviteter er i stadig
DEL 1 Uten hjelpemidler 2 timer
 DEL 1 Uten hjelpemidler timer Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 a Regn ut tallet som mangler. 1 450 cm m 0,50 m L b Else løp 400 meter på 50 sekunder.
DEL 1 Uten hjelpemidler timer Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Oppgave 1 a Regn ut tallet som mangler. 1 450 cm m 0,50 m L b Else løp 400 meter på 50 sekunder.
Turny bladvender Brukerveiledning
 Turny bladvender Brukerveiledning Generelt om Turny elektronisk bladvender...2 Tilkobling av Turny...2 Installasjon...3 Montering av bok/tidsskrift...4 Bruk av Turny...4 Aktiviser vippefunksjonen...5 Mulige
Turny bladvender Brukerveiledning Generelt om Turny elektronisk bladvender...2 Tilkobling av Turny...2 Installasjon...3 Montering av bok/tidsskrift...4 Bruk av Turny...4 Aktiviser vippefunksjonen...5 Mulige
GODE ALGORITMER. Mekanisk regneferdighet. Forskningens konklusjon. Hva kreves i læreplanen? Var alt bedre før? 17.09.2012
 Mekanisk regneferdighet GODE ALGORITMER IKKE SØRGELIG SUBTRAKSJON OG DYSTER DIVISJON Bjørnar Alseth Multi i Vest 2012 Forskningens konklusjon Hva kreves i læreplanen? Forskerne er enige om 1. Vi må ikke
Mekanisk regneferdighet GODE ALGORITMER IKKE SØRGELIG SUBTRAKSJON OG DYSTER DIVISJON Bjørnar Alseth Multi i Vest 2012 Forskningens konklusjon Hva kreves i læreplanen? Forskerne er enige om 1. Vi må ikke
Tabellen viser en serie med verdier for den uavhengige variabelen, og viser den tilhørende verdien til den avhengige variabelen.
 Kapittel 13: Tabeller 13 Oversikt over tabeller... 222 Oversikt over fremgangsmåten for å generere en en tabell... 223 Velge tabellparametre... 224 Vise en automatisk tabell... 226 Bygge en manuell tabell
Kapittel 13: Tabeller 13 Oversikt over tabeller... 222 Oversikt over fremgangsmåten for å generere en en tabell... 223 Velge tabellparametre... 224 Vise en automatisk tabell... 226 Bygge en manuell tabell
Kjønn og lesing i nasjonale og internasjonale leseundersøkelser. NOLES 5. februar 2014 Astrid Roe
 Kjønn og lesing i nasjonale og internasjonale leseundersøkelser NOLES 5. februar 2014 Astrid Roe Reading Literacy i PISA: Lesekompetanse er ikke bare et grunnlag for å lære i alle fag, det er også nødvendig
Kjønn og lesing i nasjonale og internasjonale leseundersøkelser NOLES 5. februar 2014 Astrid Roe Reading Literacy i PISA: Lesekompetanse er ikke bare et grunnlag for å lære i alle fag, det er også nødvendig
NASJONALE PRØVER. Matematikk 10. trinn delprøve 2. Skolenr. Elevnr. Oppgaver som kan løses ved hjelp av lommeregner. Tid: 90 minutter.
 Bokmål Skolenr. Elevnr. NASJONALE PRØVER Matematikk 10. trinn delprøve 2 Tid: 90 minutter 15. april 2004 Gutt Jente Oppgaver som kan løses ved hjelp av lommeregner. Tillatte hjelpemidler: lommeregner,
Bokmål Skolenr. Elevnr. NASJONALE PRØVER Matematikk 10. trinn delprøve 2 Tid: 90 minutter 15. april 2004 Gutt Jente Oppgaver som kan løses ved hjelp av lommeregner. Tillatte hjelpemidler: lommeregner,
1. COACHMODELL: GROW... 1 2. PERSONLIG VERDIANALYSE... 2 3. EGENTEST FOR MENTALE MODELLER. (Noen filtre som vi til daglig benytter)...
 Personal og lønn Coaching 1. COACHMODELL: GROW... 1 2. PERSONLIG VERDIANALYSE... 2 3. EGENTEST FOR MENTALE MODELLER. (Noen filtre som vi til daglig benytter).... 3 1. COACHMODELL: GROW Formål: GROW-modellen
Personal og lønn Coaching 1. COACHMODELL: GROW... 1 2. PERSONLIG VERDIANALYSE... 2 3. EGENTEST FOR MENTALE MODELLER. (Noen filtre som vi til daglig benytter).... 3 1. COACHMODELL: GROW Formål: GROW-modellen
Sensurveiledning Matematikk 1, 5-10, emne 1 Høsten 2013
 Sensurveiledning Matematikk 1, 5-10, emne 1 Høsten 2013 Oppgave 1 a) =2 = 5 2 =5 2 = = 25 4 = 25 8 Full uttelling gis for arealet uttrykt over. Avrundinger gis noe uttelling. b) DC blir 5 cm og bruk av
Sensurveiledning Matematikk 1, 5-10, emne 1 Høsten 2013 Oppgave 1 a) =2 = 5 2 =5 2 = = 25 4 = 25 8 Full uttelling gis for arealet uttrykt over. Avrundinger gis noe uttelling. b) DC blir 5 cm og bruk av
Prosjektering MEMO 551 EN KORT INNFØRING
 Side 1 av 7 Denne innføringen er ment å gi en liten oversikt over bruk og design av forbindelsene, uten å gå inn i alle detaljene. er et alternativ til f.eks faste eller boltede søylekonsoller. enhetene
Side 1 av 7 Denne innføringen er ment å gi en liten oversikt over bruk og design av forbindelsene, uten å gå inn i alle detaljene. er et alternativ til f.eks faste eller boltede søylekonsoller. enhetene
Mal for vurderingsbidrag
 Mal for vurderingsbidrag Fag: Naturfag Tema:Verdensrommet Trinn:6. Tidsramme: 5 undervisningsøkter (ca 5 x 45 min) Trintom Gro Sk Undervisningsplanlegging Konkretisering Kompetansemål Mål for en periode
Mal for vurderingsbidrag Fag: Naturfag Tema:Verdensrommet Trinn:6. Tidsramme: 5 undervisningsøkter (ca 5 x 45 min) Trintom Gro Sk Undervisningsplanlegging Konkretisering Kompetansemål Mål for en periode
Dusj beslag. Dette kapitelet inneholder ulike typer beslag til dusj løsninger. Hengsler 4 ulike design. Side 2-10. Aluminium hel hengsle Side 11
 Dusj beslag Dette kapitelet inneholder ulike typer beslag til dusj løsninger Hengsler 4 ulike design. Side 2-10 Aluminium hel hengsle Side 11 Knotter Side 12-13 Håndtak Side 13-14 Støtte stag Side 15-18
Dusj beslag Dette kapitelet inneholder ulike typer beslag til dusj løsninger Hengsler 4 ulike design. Side 2-10 Aluminium hel hengsle Side 11 Knotter Side 12-13 Håndtak Side 13-14 Støtte stag Side 15-18
Algebra trinn. Nord-Gudbrandsdalen Januar 2015
 Algebra 8.-10. trinn Nord-Gudbrandsdalen Januar 2015 Hva er algebra? Diskuter i grupper. Finn en enkel forklaring. Algebra i skolen Når bør vi starte algebraundervisningen? Bli enige om et synspunkt. Argumenter
Algebra 8.-10. trinn Nord-Gudbrandsdalen Januar 2015 Hva er algebra? Diskuter i grupper. Finn en enkel forklaring. Algebra i skolen Når bør vi starte algebraundervisningen? Bli enige om et synspunkt. Argumenter
MEMO 733. Søyler i front - Innfesting i stålsøyle i vegg Standard sveiser og armering
 INNHOLD BWC 50-240 Side 1 av 9 FORUTSETNINGER... 2 GENERELT... 2 TILLATT BRUDDLAST PÅ KOMPLETT ENHET... 2 TILLATT BRUDDLAST PÅ YTTERØR BRUKT I KOMBINASJON MED TSS... 2 TILLATT BRUDDLAST VED BRUK AV INNERRØR
INNHOLD BWC 50-240 Side 1 av 9 FORUTSETNINGER... 2 GENERELT... 2 TILLATT BRUDDLAST PÅ KOMPLETT ENHET... 2 TILLATT BRUDDLAST PÅ YTTERØR BRUKT I KOMBINASJON MED TSS... 2 TILLATT BRUDDLAST VED BRUK AV INNERRØR
Løsningsforslag heldagsprøve våren 2010 1T
 Løsningsforslag heldagsprøve våren 00 T DEL OPPGAVE a) Regn ut x x x x x x x x x x 9x x x x x 6x x x x 6x x 6x b) Løs likninga x x 6 x x 6 x x 6 x x 6 x x x x c) Løs likningssettet ved regning x y x y
Løsningsforslag heldagsprøve våren 00 T DEL OPPGAVE a) Regn ut x x x x x x x x x x 9x x x x x 6x x x x 6x x 6x b) Løs likninga x x 6 x x 6 x x 6 x x 6 x x x x c) Løs likningssettet ved regning x y x y
NB! Les bruksanvisningen nøye før stolen tas i bruk!
 NB! Les bruksanvisningen nøye før stolen tas i bruk! Arctic løftestoler er testet og godkjent i henhold til følgende krav og standarder: EN 12182 EN 1021-1 EN 13751 EN 1021-2 EN 1728 EN 1022 EN 60601-1
NB! Les bruksanvisningen nøye før stolen tas i bruk! Arctic løftestoler er testet og godkjent i henhold til følgende krav og standarder: EN 12182 EN 1021-1 EN 13751 EN 1021-2 EN 1728 EN 1022 EN 60601-1
Sentralverdi av dataverdi i et utvalg Vi tenker oss et utvalg med datapar. I vårt eksempel har vi 5 datapar.
 Statistisk behandling av kalibreringsresultatene Del 4. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Dennne artikkelen tar
Statistisk behandling av kalibreringsresultatene Del 4. v/ Rune Øverland, Trainor Elsikkerhet AS Denne artikkelserien handler om statistisk behandling av kalibreringsresultatene. Dennne artikkelen tar
7-41 Planløsning, størrelse og utforming
 7-41 Planløsning, størrelse og utforming 1. Generelle krav Et funksjonelt godt byggverk er ulykkesforebyggende, der fare for skade på personer må unngås. Korte og enkle trafikklinjer som minst mulig krysser
7-41 Planløsning, størrelse og utforming 1. Generelle krav Et funksjonelt godt byggverk er ulykkesforebyggende, der fare for skade på personer må unngås. Korte og enkle trafikklinjer som minst mulig krysser
Faktor. Eksamen høst 2005 SØK 1001- Innføring i matematikk for økonomer Besvarelse nr 1: -en eksamensavis utgitt av Pareto
 Faktor -en eksamensavis utgitt av Pareto Eksamen høst 005 SØK 00- Innføring i matematikk for økonomer Besvarelse nr : OBS!! Dette er en eksamensbevarelse, og ikke en fasit. Besvarelsene er uten endringer
Faktor -en eksamensavis utgitt av Pareto Eksamen høst 005 SØK 00- Innføring i matematikk for økonomer Besvarelse nr : OBS!! Dette er en eksamensbevarelse, og ikke en fasit. Besvarelsene er uten endringer
Elevene skal bygge en mekanisk målskårer etter veiledningen i LEGO WeDo -programvaren. De skal skyte på en papirball med den mekanisk målskåreren.
 Lærerveiledning - mekanisk målskårer Elevene skal bygge en mekanisk målskårer etter veiledningen i LEGO WeDo -programvaren. De skal skyte på en papirball med den mekanisk målskåreren. De skal anslå/komme
Lærerveiledning - mekanisk målskårer Elevene skal bygge en mekanisk målskårer etter veiledningen i LEGO WeDo -programvaren. De skal skyte på en papirball med den mekanisk målskåreren. De skal anslå/komme
Veiledning del 3. Oppfølging av resultater fra. nasjonal prøve i regning. 8. trinn
 Versjon 8. september 2009 Bokmål Veiledning del 3 Oppfølging av resultater fra nasjonal prøve i regning 8. trinn Høsten 2009 1 Dette heftet er del 3 av et samlet veiledningsmateriell til nasjonal prøve
Versjon 8. september 2009 Bokmål Veiledning del 3 Oppfølging av resultater fra nasjonal prøve i regning 8. trinn Høsten 2009 1 Dette heftet er del 3 av et samlet veiledningsmateriell til nasjonal prøve
Matematikk 1P-Y. Bygg- og anleggsteknikk
 Matematikk 1P-Y «Å kunne regne i bygg- og anleggsteknikk innebærer å beregne tid, pris, vekt, volum, mengde, størrelser og masser. I tillegg er målestokk, måltaking og beregning av vinkler knyttet til
Matematikk 1P-Y «Å kunne regne i bygg- og anleggsteknikk innebærer å beregne tid, pris, vekt, volum, mengde, størrelser og masser. I tillegg er målestokk, måltaking og beregning av vinkler knyttet til
Norges Blindeforbunds kvalitetskrav til bygg
 Norges Blindeforbunds kvalitetskrav til bygg Dette dokumentet skal fungere som en sjekkliste når man går rundt i byggverk og ser om kravene i henhold til lovverk og Norges Blindeforbund sine krav er oppfylt.
Norges Blindeforbunds kvalitetskrav til bygg Dette dokumentet skal fungere som en sjekkliste når man går rundt i byggverk og ser om kravene i henhold til lovverk og Norges Blindeforbund sine krav er oppfylt.
Instruksjonshefte biltilhengere
 Instruksjonshefte biltilhengere Produsent : TREDAL AS 4520 Lindesnes 1 Gratulerer med ny TREDAL biltilhenger! Tredal`s høye kvalitet og meget gode kjøreegenskaper på grunn av vårt SPIRAX fjæringssystem
Instruksjonshefte biltilhengere Produsent : TREDAL AS 4520 Lindesnes 1 Gratulerer med ny TREDAL biltilhenger! Tredal`s høye kvalitet og meget gode kjøreegenskaper på grunn av vårt SPIRAX fjæringssystem
S 33/09 Utkast til utviklingsplanen
 Interimsstyret for samorganisering og samlokalisering av NVH og UMB S 33/09 Utkast til utviklingsplanen Arbeidet med utviklingsplanen er i forsinket, og dette innebærer at interimsstyret og institusjonsstyrne
Interimsstyret for samorganisering og samlokalisering av NVH og UMB S 33/09 Utkast til utviklingsplanen Arbeidet med utviklingsplanen er i forsinket, og dette innebærer at interimsstyret og institusjonsstyrne
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Skriv som prosent a) 0,451 b) 5 25 Oppgave 2 (2 poeng) a) Forklar at de to trekantene ovenfor er formlike. b) Bestem lengden av siden BC ved regning. Eksamen
DEL 1 Uten hjelpemidler Oppgave 1 (1 poeng) Skriv som prosent a) 0,451 b) 5 25 Oppgave 2 (2 poeng) a) Forklar at de to trekantene ovenfor er formlike. b) Bestem lengden av siden BC ved regning. Eksamen
Analyse og metodikk i Calculus 1
 Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
Analyse og metodikk i Calculus 1 Fredrik Göthner og Raymi Eldby Norges teknisk-naturvitenskapelige universitet 3. desember 01 1 Innhold Forord 3 1 Vurdering av grafer og funksjoner 4 1.1 Hva er en funksjon?.........................
Garasjetelt RoundTop 23 m2 Monteringsanvisning
 Garasjetelt RoundTop 23 m2 Monteringsanvisning BESKRIVELSE MODELLNR. 3,7 x 6 x 2,4 m Garage-in-a-Box RoundTop - Grå 62780 ANBEFALT VERKTØY Les HELE anvisningen før monteringen påbegynnes. Denne beskyttelsen
Garasjetelt RoundTop 23 m2 Monteringsanvisning BESKRIVELSE MODELLNR. 3,7 x 6 x 2,4 m Garage-in-a-Box RoundTop - Grå 62780 ANBEFALT VERKTØY Les HELE anvisningen før monteringen påbegynnes. Denne beskyttelsen
Eksempeloppgåve/ Eksempeloppgave 2009
 Eksempeloppgåve/ Eksempeloppgave 2009 MAT1013 Matematikk 1T Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del 1: Hjelpemiddel på Del 2: Bruk av kjelder: Vedlegg: Framgangsmåte:
Eksempeloppgåve/ Eksempeloppgave 2009 MAT1013 Matematikk 1T Nynorsk/Bokmål Nynorsk Eksamensinformasjon Eksamenstid: Hjelpemiddel på Del 1: Hjelpemiddel på Del 2: Bruk av kjelder: Vedlegg: Framgangsmåte:
Veiledning del 3. Oppfølging av resultater fra. nasjonal prøve i regning. 5. trinn
 Versjon 8. september 2009 Bokmål Veiledning del 3 Oppfølging av resultater fra nasjonal prøve i regning 5. trinn Høsten 2009 1 Dette heftet er del 3 av et samlet veiledningsmateriell til nasjonal prøve
Versjon 8. september 2009 Bokmål Veiledning del 3 Oppfølging av resultater fra nasjonal prøve i regning 5. trinn Høsten 2009 1 Dette heftet er del 3 av et samlet veiledningsmateriell til nasjonal prøve
Støpetips Legging av skifer trinn for trinn
 LEGGING AV SKIFER I denne brosjyren finner du en enkel trinnfor-trinn beskrivelse av hvordan du legger et skifergulv. Vårt eksempel viser omlegging av et eksisterende gulv, men prinsippet er det samme
LEGGING AV SKIFER I denne brosjyren finner du en enkel trinnfor-trinn beskrivelse av hvordan du legger et skifergulv. Vårt eksempel viser omlegging av et eksisterende gulv, men prinsippet er det samme
Monterings og bruksanvisning til rustfrie rustjebaner av typen DPP og Basic
 Monterings og bruksanvisning til rustfrie rustjebaner av typen DPP og Basic Takk for di tillit. Belønningen vil være et kvalitetsprodukt og tilfredsstillelse av deres barn. Innledning Her får du informasjon
Monterings og bruksanvisning til rustfrie rustjebaner av typen DPP og Basic Takk for di tillit. Belønningen vil være et kvalitetsprodukt og tilfredsstillelse av deres barn. Innledning Her får du informasjon
SPRÅKVERKSTED. på Hagaløkka skole
 SPRÅKVERKSTED på Hagaløkka skole Språkverkstedet er en strukturert begrepslæringsmodell for barn og unge med ulike språkvansker. Modellen ble utprøvd i flere barnehager og skoler i Sør-Trøndelag i 2008/2009,
SPRÅKVERKSTED på Hagaløkka skole Språkverkstedet er en strukturert begrepslæringsmodell for barn og unge med ulike språkvansker. Modellen ble utprøvd i flere barnehager og skoler i Sør-Trøndelag i 2008/2009,
Hva holder vi på med? Læring eller opplæring eller begge deler?
 Hva holder vi på med? Læring eller opplæring eller begge deler? 1 Er det slik i norsk skole? 2 Læring er hardt individuelt arbeid! Hvordan møter vi kommentaren: «Du har ikke lært meg dette, lærer» 90%
Hva holder vi på med? Læring eller opplæring eller begge deler? 1 Er det slik i norsk skole? 2 Læring er hardt individuelt arbeid! Hvordan møter vi kommentaren: «Du har ikke lært meg dette, lærer» 90%
Fargeundersøkelser av eksteriøret
 Oppdragsrapport nr. 124/2010 B.359. Røros Kjerkgata 29 Fargeundersøkelser av eksteriøret Jon Brænne Røros. Kjerkgata. 17. mai. Trolig 1912. Kjerkgata 29 under bygging. Dato: 17.6.2010 Til: Riksantikvaren
Oppdragsrapport nr. 124/2010 B.359. Røros Kjerkgata 29 Fargeundersøkelser av eksteriøret Jon Brænne Røros. Kjerkgata. 17. mai. Trolig 1912. Kjerkgata 29 under bygging. Dato: 17.6.2010 Til: Riksantikvaren
Jernbaneverket OVERBYGNING Kap.: 14 Infrastruktur Regler for prosjektering Utgitt: 01.01.06
 Plattformer og spor på stasjoner Side: 1 av 9 1 HENSIKT OG OMFANG... 2 2 PLATTFORMER... 3 2.1 Plattformhøyder og avstand spormidt - plattformkant... 3 2.2 Plattformlengde... 5 2.3 Spor mot plattformer...
Plattformer og spor på stasjoner Side: 1 av 9 1 HENSIKT OG OMFANG... 2 2 PLATTFORMER... 3 2.1 Plattformhøyder og avstand spormidt - plattformkant... 3 2.2 Plattformlengde... 5 2.3 Spor mot plattformer...
Byggesak og tilsyn. Universell utforming. seniorrådgiver Ivar Sannerud, byggesak, Ullensaker kommune
 Byggesak og tilsyn Universell utforming seniorrådgiver Ivar Sannerud, byggesak, 1 Tilgjengelighetskrav for orienterings og bevegelseshemmede i publikumsbygg i PBL og teknisk forskrift siden sent 70-tall.
Byggesak og tilsyn Universell utforming seniorrådgiver Ivar Sannerud, byggesak, 1 Tilgjengelighetskrav for orienterings og bevegelseshemmede i publikumsbygg i PBL og teknisk forskrift siden sent 70-tall.
35 Z 3713 65. Justerbar hengsle. 7 65 For å få hengsle med forskjøvet bakplate selges platene løse og byttes ut med platen på 3711.
 Dusjbeslag Dusjbeslag for 6 10 mm herdet glass. Z 3711 Justerbar hengsle Messing 50 55 90 70 90 35 Z 3713 65 Justerbar hengsle 18 55 Messing 50 90 70 90 7 65 For å få hengsle med forskjøvet bakplate selges
Dusjbeslag Dusjbeslag for 6 10 mm herdet glass. Z 3711 Justerbar hengsle Messing 50 55 90 70 90 35 Z 3713 65 Justerbar hengsle 18 55 Messing 50 90 70 90 7 65 For å få hengsle med forskjøvet bakplate selges
Gangvei, balkong, rekkverk. Arbeidslokaler og driftsbygninger i landbruket
 3 Fallskader Hjemmeulykker utgjør i dag den største gruppen av ulykker. Mange av ulykkene skyldes uforsiktighet, skjødesløshet, fysiske svekkelser eller «hendelige uhell». Undersøkelser indikerer imidlertid
3 Fallskader Hjemmeulykker utgjør i dag den største gruppen av ulykker. Mange av ulykkene skyldes uforsiktighet, skjødesløshet, fysiske svekkelser eller «hendelige uhell». Undersøkelser indikerer imidlertid
Din bruksanvisning DYMO LABELMANAGER 420P http://no.yourpdfguides.com/dref/3645396
 Du kan lese anbefalingene i bruksanvisningen, de tekniske guide eller installasjonen guide for DYMO LABELMANAGER 420P. Du vil finne svar på alle dine spørsmål på DYMO LABELMANAGER 420P i bruksanvisningen
Du kan lese anbefalingene i bruksanvisningen, de tekniske guide eller installasjonen guide for DYMO LABELMANAGER 420P. Du vil finne svar på alle dine spørsmål på DYMO LABELMANAGER 420P i bruksanvisningen
4 Rømningsvei. Utforming av rømningsvei
 4 Rømningsvei Rømning kan deles i følgende tre faser : Forflytning innen branncellen det rømmes fra. Denne forflytningen er ikke en del av rømningsveien Forflytning i korridor Forflytning i trapperom til
4 Rømningsvei Rømning kan deles i følgende tre faser : Forflytning innen branncellen det rømmes fra. Denne forflytningen er ikke en del av rømningsveien Forflytning i korridor Forflytning i trapperom til
Kongsvinger dag 5 22.11.2013
 Kongsvinger dag 5 22.11.2013 Enda mer Ny Giv? Er det mulig? Hva i all verden skal vi gjøre i dag? Sikker noe lesegreier? Plan: Vi ser litt mer på MUNTLIGE FERDIGHETER og DIGITALE FERDIGHETER Fokus: god
Kongsvinger dag 5 22.11.2013 Enda mer Ny Giv? Er det mulig? Hva i all verden skal vi gjøre i dag? Sikker noe lesegreier? Plan: Vi ser litt mer på MUNTLIGE FERDIGHETER og DIGITALE FERDIGHETER Fokus: god
8.2.6 Supplerende informasjon
 128 A8 PROSJEKTERING MED BETONGELEMENTER Lask a) Strekkbånd på dekket b) Strekkbånd i bjelken c) Utstøpninger ved elementender d) Strekkbånd på opplegget e) Forankring til gavl 8.2.5 Rassikkerhet Et bygg
128 A8 PROSJEKTERING MED BETONGELEMENTER Lask a) Strekkbånd på dekket b) Strekkbånd i bjelken c) Utstøpninger ved elementender d) Strekkbånd på opplegget e) Forankring til gavl 8.2.5 Rassikkerhet Et bygg
my baby carrier NORSK BRUKSANVISNING OBS! OPPBEVAR BRUKSANVISNINGEN FOR SENERE BEHOV!!
 my baby carrier BRUKSANVISNING NORSK Integrert nakkestøtte OBS! OPPBEVAR BRUKSANVISNINGEN FOR SENERE BEHOV!! Integrert bærestykkeforlenger... > ADVARSLER! ADVARSEL: Du kan miste likevekten på grunn av
my baby carrier BRUKSANVISNING NORSK Integrert nakkestøtte OBS! OPPBEVAR BRUKSANVISNINGEN FOR SENERE BEHOV!! Integrert bærestykkeforlenger... > ADVARSLER! ADVARSEL: Du kan miste likevekten på grunn av
Rapport fra e-handelsanalyse [organisasjonsnavn]
![Rapport fra e-handelsanalyse [organisasjonsnavn] Rapport fra e-handelsanalyse [organisasjonsnavn]](/thumbs/29/13245092.jpg) Rapport fra e-handelsanalyse [organisasjonsnavn] INNHOLD Innhold... 2 sammendrag... 3 Bakgrunnsinformasjon... 4 1 Interessenter og rammevilkår... 5 2 Anskaffelser og praksis... 6 3 E-handelsløsning...
Rapport fra e-handelsanalyse [organisasjonsnavn] INNHOLD Innhold... 2 sammendrag... 3 Bakgrunnsinformasjon... 4 1 Interessenter og rammevilkår... 5 2 Anskaffelser og praksis... 6 3 E-handelsløsning...
