Kart og andre umodne objekter

Transkript

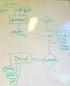
1 Figur 5-. Ogdens trekant Kart og andre umodne objekter Thoughts of Reference Begreper Person Bil Døgn Gerhard Skagestein David Skogan Fozia Jabeen Arif Shomaila Kausar DF febr. --9 Symbol Lingvistiske elementer representasjoner Referent Fenomener i interesseområdet ligmodell ligmodell Hva påvirker konseptualiseringen? Ulike typer verdier: Navn, skalar, lig verdi Hvilke begreper og forhold ser vi i lige/geografiske modeller? Påvirkning fra: o formålet? o detaljeringsgraden (målestokken)? OK objekt gnr/bnr form og beliggenhet 55/57 navn o dimensjonaliteten? spesielt: med eller uten t-akse boareal lig verdi o visualiseringen (dvs. kartet)? o representasjonen? ikke OK 5m skalar ligmodell ligmodell 4

2 Litt Ifi barnelærdom Representasjoner Fylke fylkenr {id} Fylke fylkenr {id} «identifying» Vi har standarder for representasjon o av navn (UNICODE, ASCII) o av skalarer (heltallrepresentasjoner, flyttallsrepresentasjoner IEEE 754) o --- men hvordan representerer vi lige verdier? Kommune kommunenr {id} fylkenr{fk}{id} innbyggertall Kommune kommunenr {id} innbyggertall # {id} Antall et villniss av ulike representasjoner (raster, TIN, Quadtree, splines,...) representasjon velges som oftest på grunnlag av bruksformen Samme modell på gruppert og ugruppert form ligmodell 5 ligmodell 6 Påvirker representasjonen konseptualiseringen? Dimensjonalitet i og av verdier Thoughts of Reference Begreper punkt i kurve i flate i ) volum i 4 ) punkt i flate kurve i flate ) plan flate i flate utilbørlig påvirkning? punkt på linje ) navn rett linje på linje Romlige representasjoner Rommet som opptas av huset Referent Fenomener i interesseområdet Rommets dimensjonalitet Verdiens dimensjonalitet ) Tradisjonell skalar ) Vanlig graf på papir ) Vanlig i GIS, kalt ½-dimensjonalitet 4 ) Vanlig i CAD/CAM ligmodell 7 ligmodell 8

3 Rommets dimensjonalitet 4 Dimensjonalitet i og av verdier, utvidelse med en fjerde dimensjon punkt i hyper punkt i punkt i flate punkt på linje ) navn kurve i kurve i kurve i flate ) rett linje på linje flate i hyper flate i ) plan flate i flate volum i hyper volum i hypervolum i hyper 4 Representasjon av lige verdier Romlig verdi: En tett punktmengde Umulig å representere direkte. Bruker istedenfor et utvalgt antall punkter (eller andre geometriske primitiver) + algoritmer (eksempelvis interpolasjonsregler) for å beregne andre punkter ved behov Raster, vektor og halvplan Viser eksempler i D kan generaliseres til høyere dimensjoner, og degenereres til D og D Et uendelig antall punkter, der det mellom punkter alltid kan legges inn et punkt til. Verdiens dimensjonalitet ligmodell 9 ligmodell Rasterrepresentasjon Hierarkisk raster, såkalt "Quadtree" D: punkter, D: linjestykker, D: piksler, D: voler ligmodell ligmodell

4 Vektorrepresentasjon med lineær interpolasjon, D Vektorrepresentasjon med høyere ordens interpolasjon ligmodell ligmodell 4 Vektorrepresentasjonen har for store frihetsgrader? Representasjon av krumme flater i D- Triangulated Irregular Network TIN Høydekurver ligmodell 5 ligmodell 6

5 Halvplan-representasjon Hvert halvplan kan beskrives med a + a + a + Representasjon [a, a, a ] (antall koeffisienter = dim + ) Ett halvplan for hver fasett Konveks polytope: Snittet av et endelig antall halvplan Ikke-konvekse polytoper må deles Polyhedron: Unionen av et endelig antall polytoper z Samme ide i høyere dimensjoner Et punkt, y, z ligger i kulen dersom (- ) +(y-y ) + (z-z ) r, eller X = {, y, z (- ) +(y-y ) + (z-z ) r } y Typisk CAD/CAM En union av to volumer (hvorav det ene er negativt) ligmodell 7 ligmodell 8 Uskarpe grenser "Fuzzy" verdier Mange geografiske objekter har uskarp avgrensning Eksempler: Hvor er kanten på myra? Hvor går grensen mellom Galdhøpiggen og resten av Jotunheimen? Gir behov for lige verdier med uskarpe grenser Også lige verdier med uskarpe grenser må kunne o representeres o o vises fram regnes med ("spatial algebra") ligmodell 9 ligmodell

6 Fuzzy, halvplan-representasjon Hvert halvplan kan beskrives med a + a + a + samt bredden på en overgangssone, z Representasjon [a, a, a, z] (antall koeffisienter = dim + ) Operasjoner på verdier Operasjoner Dimensjonsbevarende: Intersection (snitt), union men resultatet kan degenerere til en lavere dimensjon (eksempel: Snitt mellom to kryssende linjer) Dimensjonsøkende: Interior, eterior Dimensjonsminkende: Boundary Skalarer: Volume/area/length Boolske: Intersect, touch, Operasjoner på met Projection ligmodell ligmodell Over til modellene Objektmodeller og feltmodeller Thoughts of Reference Begreper Objektmodellen: Verden er satt sammen av avgrensede objekter med bestemte egenskaper 55/57 Romlige representasjoner Huset Rommet som opptas av huset Referent Fenomener i interesseområdet Feltmodellen: Verden er satt sammen av en rekke felt, som er noe som varierer kontinuerlig over et område ligmodell ligmodell 4

7 Objektmodell og feltmodell? La oss bli kvitt feltmodellen Feltmodellen: Gitt et punkt i og y, hvilken feltverdi har vi der? La oss oppfatte feltverdiene som verdier langs en tredje akse (som ikke behøver å være en lig z) Gråhø Da får vi en -dimensjonal verdi i et -dimensjonalt Storsjø Objekt objektid{id} felt D-verdi i D- representasjon{id} Eksempel: Skogsteig skogsteigid{id} bonitet D-verdi i D- representasjon{id} ligmodell 5 ligmodell 6 Eksplisitte og implisitte forhold Skranker mellom lige verdier Oslo S Drammen Hønefoss Nesbyen Ål Geilo Ustaoset Haugastøl forrige : Stasjon stasjonsnavn{id} avstand_fra_start : neste {derived} Assosiasjonen kan enten avledes, eller det ligger en skranke mellom assosiasjonen og attributtet avstand_fra_start Eiendom eiendomsid{id} areal Romlig verdi verdirepresentasjon{id} avgrenses av forløp Eiendomsgrense eiendomsgrenseid{id} Eiendom->Eiendomsgrense.forløp = boundary(eiendom.areal) ligmodell 7 ligmodell 8

8 Skranker mellom lige verdier Hvorfor redundans (og dermed skranker) i modellene? Bygger opp under det objektorienterte syn Topologisk modell Et modellperspektiv for eksempel det geometriske er ikke alltid tilstrekkelig Veistykke veistykkeid{id} forløp Romlig verdi verdirepresentasjon{id} går mellom beliggenhet Veikryss veikryssid{id} o ikke tilstrekkelig nøyaktig (avrunding i representasjon, måleunøyaktighet) o inneholder ikke bestandig nok opplysninger Ulike dataleverandører ulike modeller og av og til har vi behov for å integrere Geometrisk modell Veikryss.beliggenhet = boundary(veistykke.forløp) ligmodell 9 ligmodell Variant : Hvordan realisere redundans underlagt skranker Redundante representasjoner + beskrivelse av skranker + håndheving av skrankene ("spaghetti-modell") Modeller med t-akse Hvis met inkluderer t som akse på linje med, y og z, kan vi bruke de samme representasjoner og de samme operasjoner som for rene lige modeller ( men: vi kan få bruk for 4D) Variant : Utnytte skrankene til å fjerne redundante representasjoner ("topologisk modell") Modellen kan altså være objektorientert, selv om representasjonene ikke er det ligmodell ligmodell

9 Eksempel i og t: Togfremdrift på Bergensbanen Eksempel i og t: Syklisten og regnbygene km Voss Myrdal Finse Ustaoset Geilo Ål Gol Nesbyen våt vei våt syklist bakketopp regn i vente Hønefoss : : 4: t ligmodell ligmodell 4 Eksempel i, y, z og t flygelederens oppgave Tesselering og aggregering Tesselering: Å dele opp en helhet i deler med det formål å kunne beskrive hver enkelt del for seg Helhet Et fly beskriver en bane i, y, z og t Flygelederens oppgave er å sikre at baner for ulike fly ikke berører hverandre Aggregering: Å samle enkeltdeler til en helhet med det formål å kunne beskrive helheten under ett Del ligmodell 5 ligmodell 6

10 Interessante valg ved tesselering Tesselering/aggregering eller kompleksverdi? Regulært eller irregulært mønster? Måling i knutepunktene eller i tyngdepunktene? Skal målemulighetene påvirke mønsteret? Produkt Produkt volumkompleks For en oversikt over vanlige teknikker, se Vckovski avsnitt 4.4 (side 74): Cell grids Polyhedral tesselation (polygons) Simplicial complees (triangulated irregular networks) Lattice or point grids Irregular points Contour models volum Del Det avgjørende er om delene kan oppfattes som features i seg selv ligmodell 7 ligmodell 8 Fra representasjon til aggregat "Finite Element"-metoden Figur -4. Topologiske skranker, aggregering av flater Fylkegeometri må omfatte kommunegeometri for kommune som er en del av fylket Fylke Kommune Administrativ inndeling (avledet/beskranket?) fylkegeometri Geografisk inndeling Flate fylkegeometri kommunegeometri kommunegeometri Avledbar gjennom algebra Ingen overlapping i ligmodell 9 ligmodell 4

11 Tesselering i t-dimensjonen Figur -8. Aggregering i tid tilstandsendring larve puppe sommerfugl Én forekomst for hvert tidspunkt! årstall{id} t År t «identifies» Person ansattnr{id} Personår «identifies» : Kjønn kjønnskode{id} #kg{id} Vekt Lepidopter Lepidopterfase lepidopter lepidopterliv Tidsmessig inndeling Periode faseperiode faseperiode lepidopterperiode Avledbar gjennom algebra t ligmodell 4 ligmodell 4 Figur -5. Topologiske skranker, aggregering i tid Generalisering Lepidopterliv må omfatte faseperiode for samme lepidopter Lepidopter lepidopterliv Periode faseperiode lepidopterperiode generalisering Built-up area Lepidopterfase Tidsmessig inndeling Ingen overlapping i tid Kontinuitet i tid faseperiode Avledbar gjennom algebra Source dataset Target dataset Kan dette gjøres. automatisk?. inkrementelt? ligmodell 4 ligmodell 44