Løsningskisse: EKSAMEN 24. mai 2005 I EMNE TTM4120 Pålitelige systemer.
|
|
|
- Tora Aas
- 7 år siden
- Visninger:
Transkript
1 Loesning_mellomregn.nb 1 Løsningskisse: EKSAMEN 24. mai 2005 I EMNE TTM4120 Pålitelige systemer ; ; , BEH ü Generell informasjon om løsningsskissen Denne inneholder både en skisse til løsning og det mellomregninger som er gjort for å komme frem til delresultater som er gitt i oppgaveteksten. Den er (som vanlig :-) mer omstendelig og detaljert enn de som kreves ved en eksamensbesvarelse. Det er også tatt med elementer som ikke ble gitt til eksamen og alternative løsninger. ü a) Estimater fra observerte verdier MTBF = n Ho i=1 i + d i L ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ n U = n d i=1 i ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ t p Sorter de observerte oppetider i stigende rekkefølge o HiL hvor o HiL o Hi+1L, " i. Sett o H0L = 0 og o Hn+1L = (Fremgansmåte som korresponderer til øving 1.) F = i ê n ê; o HiL t o Hi+1L Alternativ løsning n F = I@o i td ê n i=1 ü b) Restlevetid F := 1 - Hg Exp@-g td + d Exp@-d tdl ü Krav til a og b <<Tentativt spørsmål, ikke med i oppgaven; mindre relevans til faget>> En fysikalsk beskrivelse krever at 0 g + d 1 Hvis mindre enn en, indikerer det umiddelbart feiling. Likhet med null, alltid umiddelbar feiling. Positivt derivert = ingen "negative sannsynligheter".
2 Loesning_mellomregn.nb 2 D@F td 0, " t -t g g g + d -t d d 0, " t ü Midlere oppetid MUT = Integrate@1 - F 8t, 0, Infinity<, Assumptions Ø Re@gD > 0 && Re@dD > 0D g ÅÅÅÅ g + ÅÅÅÅ d d ü Fordelingen av gjenværende tid til feil. Uttrykket for tetthetsfunksjon av restlevetid er gitt i pensum og bør huskes. Hvis ikke forventes at utledningen tas på relativt strak arm. I dette tilfellet finnes også en direkte utledning. f := H1 - F ê MUT Clear@RrD Rr@t_D := Rr@tD = Integrate@f 8x, t, Infinity<, Assumptions Ø Re@gD > 0 && Re@dD > 0 && Re@gD 0 && Re@dD 0D Rr@tD d -t d g + -t g g d ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ d g + g d ü Alternativt direkte resonnement, ( løsning fra student på eksamen): P@T F > td = P@T F > t» " g fordeling " ] P[ " g fordeling "D + P@T F > t» " d fordeling " ] P[ " d fordeling "D Fordelingene er gitt av sannsynligheten for å "treffe" en kort eller lang fordeling P@"g fordeling"d = g d ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ d g + g d ÅÅÅÅ g í MUT êê Simplify g Rrx@t_D = -t g g d ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ d g + g d + d g -t d ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ d g + g d êê Simplify d -t d g + -t g g d ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ d g + g d ü Diskusjon Params = 8g -> 1, d Ø 0.1, g -> 1 - d, d -> 0.6<; << Graphis`Legend`
3 Loesning_mellomregn.nb 3 Plot@Evaluate@81 - F Rr@tD< êê. ParamsD, 8t, 0, 30<, PlotRange Ø All, PlotStyle Ø 8GrayLevel@0D, Dashing@8.03<D<, PlotLegend Ø 8"Oppetid", "Tid til feil"<, LegendPosition Ø 80.2, 0.1<, LegendShadow Ø None, AxesLabel Ø 8"Tid", "Sannsynlighet"<, LegendTextSpae Ø 6D Sannsynlighet Oppetid Tid til feil Tid Ü Graphis Ü Oppetidene kan betraktes som å være negativt eksponensialfordelte, enten fra en fordeling med middelverdi 1, eller fra en fordeling med middelverdi 10. Ca 40 % av oppetidene er korte, de resterende er lange, med en typisk middelverdi på 10 (gitt av dl.ved å gå tilfeldig inn og observere systemet når det er oppe, vil en ha størst sannsynlighet for å treffe en lang oppetid. Siden fordelingen gjenværende tid i eksponensialfordelinger er lik fordelingen (hukommelsesløshet), vil sannsynligheten for at gjenværende oppetid skal være en lang (ha middelverdi større en den originale oppetid) være større. ü ) Temperaturavhengighet. Relasjonen følger fra Arrenius lov (kreves ikke) som gitt sammenhengen mellom absolutt temperatur og kjemisk reaksjonshastighet. Det antas at feilintensitet/rate følger den kjemiske reaksjonshastigheten. ü Relasjon z@t_d = C Exp@- ê TD; Her er C en ukjent konstant og = E a ê k (kreves ikke) hvor E a er aktiveringsenergien for feilprosessen og k er Boltzmanns konstant. NB! her er T den absolutte temperatur. ü Prediktering Det er gitt sammenheng mellom temperatur og feilintensitet. 8z@T1D ã a1, z@t2d ã a2<; Map@Log, %, 82<D êê Simplify 9LogAC - ÅÅÅÅÅÅ T1 E ã Log@a1D, LogAC - ÅÅÅÅÅ T2 E ã Log@a2D= linset = 9Log@CD - ÅÅÅÅÅÅÅ == Log@a1D, Log@CD - T1 ÅÅÅÅÅÅÅ == Log@a2D=; T2
4 Loesning_mellomregn.nb 4 Solve@linset, 8Log@CD, <D -T1 Log@a1D + T2 Log@a2D 99Log@CD Ø - ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ, Ø T1 - T2 T1 T2 HLog@a1D - Log@a2DL ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ == T1 - T2 Følgelig kan vi prediktere den nødvendig absolutte temperaturen T3 ved SolveALog@CD - 9T3 Ø ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ Log@CD - Log@a3D = ÅÅÅÅÅÅÅ == Log@a3D, T3E êê First T3 En alternativ "grafisk" løsning som den nedenstående godtas også med behørig forklaring. ü Usikkerhetsfaktorer Det kan være statistisk usikkerhet knyttet til observasjonene av a i og T i. Den dominerende feilmekanismen kan være ulik i ulike temperaturområder. (Avhenger av aktiveringsenergi og proposjonalitetskonstant.) ü d) Modell av maskinvaren og likninger. ü Tilstandsmodell
5 Loesning_mellomregn.nb 5 ü Ligninger << "êusersêbjarneêundervisningêmma toolsêpakages and demosêdependabilityêstatediagrams.m" MUT::shdw : Symbol MUT appears in multiple ontexts 8Dependability`StateDiagrams`, Global`<; definitions in ontext Dependability`StateDiagrams` may shadow or be shadowed by other definitions. More Setter opp transisjonsmatrisen fra figuren. (Mx = SetDiagonal[Transpose[{{xx,2 b,0},{m,xx,b},{0,0,xx}}]])//matrixform i j k -2 b m 0 2 b -b - m 0 0 b 0 y z { (Operational mode og State labels for StateDiagrams.m pakke.) WorkingQ = {True,True, False};Labels = {"OK", "1 Failed", "2 Failed"}; General::spell1 : Possible spelling error: new symbol name "Labels" is similar to existing symbol "Label". More Ligninger etableres som ordinært første orden diff lign. Vektoren med tilstandssansynnlighet kalles p@td. t p@td ã Mx.p@tD Initialbetingelse p@0d = 81, 0, 0<. Og hvor funksjonsannsynligheten er gitt av R@tD = p@td.81, 1, 0< ü Løsning; ikke endel av oppgaven. R@t_D = RelFun@Mx, WorkingQ, td I - ÅÅÅÅ 1 2 I3 b+m+è!!!!!!!!!!!!!!!! b 2 +6 b!!!!!!!!!!! m+m 2 M t II1 + è!!!!!!!!!!!!!!!! b 2 +6 b!!!!!!!!!!! m+m 2 3 b I2 I1 + è!!!!!!!!!!!!!!!! b 2 +6 b!!!!!!!!!!! m+m 2 t M b 2 + m II1 + è!!!!!!!!!!!!!!!! b 2 +6 b!!!!!!!!!!! m+m 2 Finner penere form uttrykket ved egenverdiene. 8xy, r1, r2< = Eigenvalues@MxD 90, 1 ÅÅÅÅ 2 è!!!!!!!!!!!!!!!! I-3 b - m - b b!!!!!!!!!!!!! m + m 2 M, ÅÅÅÅ 1 2 t M m + I-1 + è!!!!!!!!!!!!!!!! b 2 +6 b!!!!!!!!!!! m+m 2 t M m + I-1 + è!!!!!!!!!!!!!!!! b 2 +6 b!!!!!!!!!!! m+m 2 t M è!!!!!!!!!!!!!!!! b b!!!!!!!!!!!!! m + m 2 M + t M è!!!!!!!!!!!!!!!! b b!!!!!!!!!!!!! m + m 2 MMM ë H2 Hb b m + m 2 LL è!!!!!!!!!!!!!!!! I-3 b - m + b b!!!!!!!!!!!!! m + m 2 M= R@tD ã HRh@tD = r1 ê Hr1 - r2l Exp@r2 td - r2 ê Hr1 - r2l Exp@r1 tdl êê Simplify True ü e) MTFF med diskusjon MTFF = IntegrateARh@tD, 8t, 0, Infinity<, Assumptions Ø ReA è!!!!!!!!!!!!!!!!!!!!!!!!!!! b b m + m 2 E < 3 Re@bD + Re@mDE 3 b + m ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ 2 b 2
6 Loesning_mellomregn.nb 6 ü Håndregnet r1 ê Hr1 - r2l ê r2 - r2 ê Hr1 - r2l ê r1 Hr1^2 - r2 ^2L ê HHr1 - r2l r1 r2l Hr1 + r2l ê Hr1 r2l r1 + r2 êê Simplify -3 b - m Hr1 r2l 1 ÅÅÅÅ 4 è!!!!!!!!!!!!!!!! I-3 b - m -!!!!!!!!!!!!! Tredje og andre kvadratsetning! % êê Simplify 2 b 2 b b m + m 2 M I-3 b - m + è!!!!!!!!!!!!!!!! b!!!!!!!!!!!!! b m + m 2 M ü Diskusjon m Ø 0 svarer til ingen reparasjon. I middel vil det gå 1 ê H2 bltil den første prosessoren feiler, og 1 ê b til den andre feiler; tilsammen 3 ê H2 bl. m Ø svarer til øyeblikkelig reparasjon. To samtidige feil kan ikke inntreffe og MTFF Ø. m m p b innebærer at MTFF reduseres til ÅÅÅÅÅÅÅÅ. Systemet vil, før det feiler, pendle mellom OK og en feil. Sannsynligheten 2 b 2 for å finne det i en tilstand med en feil er tilnærmet 2 b ê m. Feilintensitet mens det er i denne tilstanden er b. Den samlede feilintensiteten blir da 2 b ê m ÿ b = 1 ê HMTFFL.
7 Loesning_mellomregn.nb 7 ü f) Tilstandsdiagram ü g) Introduserer elementer Kommentar: Dette spørsmålet er nesten likt et spørsmål som ble gitt på obligatorisk laboratorium. Eneste utvidelse er at det nå er flere klienter i stedet for bare en.vi får derfor testet om kandidatene forstår at hver klient har en egen stub. Løsning: - Introduser minst en prosessor som kjører depenable registry (DR). DR tjenesten kjøres normalt av en gruppe for feiltoleranse. -Minst en server starter og registrerer en proxy i et Dependable Registry. -Hver server har et proxy-objekt -Hver av klientene laster ned en klient-proxy fra dependable registry til sin maskin. Denne proxien brukes til å kommunisere med gruppen.
8 Loesning_mellomregn.nb 8 ü h) Typer metodekall og semantikk ü Typer metodekall Kommentar: Dette spørsmålet er innholdsmessig likt et spørsmål som ble gitt til laben..løsning: -IGMI benyttes mellom serverne,internt i gruppen; -EMGI benyttes mellom en klient og servergruppen; Disse bør være forskjellige fordi: i) Synlighet, metoder for koordinering av tilstand mellom serverne bør være gjemt for klientene ii) Transparens,klientene trenger ikke å forholde seg til at de kommuniserer med en gruppe med replikerte servere iii) effektivitet,uten skille ville klientene måtte være medlem i gruppen,noe som ville ført til problemer med skalerbarhet. ü Semantikk i kall Kommentar: Senario som likner på implementasjonen i laben, men her har ikke hver server ansvaret for en del av databasen. Flere mulige løsninger. Løsning: Fra ovenstående er det "opplagt" at EMGI skal benyttes. -Multiast ved registrering fordi nøkkelen skal være tilgjengelig på alle serverne samtidig. Replikaene av databasen holdes konsistent ved endring. -Uniast ved henting fordi nøklene er like på alle serverne.ingen endring av databasen. Multiast gjør at vi mister fordelen med lastdeling. -Multiast ved tilbaketrekking fordi nøkkelen må fjernes fra alle serverne samtidig. Replikaene av databasen holdes konsistent ved endring (Bruk av uniast ved endring og senere propagering til det andre replikaet medfører at feil kan medføre at informasjonen går tapt. Ikke akseptabel løsning.)
NY Eksamen i matematikk III, 5 studiepoeng. August 2007
 NY Eksamen i matematikk III, 5 studiepoeng. August 7 Oppgave a. Regn ut gradienten til funksjonen f(x, y) = x +y +xy. I hvilken retning øker f mest når x = og y =? b. Regn ut kurveintegralet f(x, y) ds
NY Eksamen i matematikk III, 5 studiepoeng. August 7 Oppgave a. Regn ut gradienten til funksjonen f(x, y) = x +y +xy. I hvilken retning øker f mest når x = og y =? b. Regn ut kurveintegralet f(x, y) ds
Oppgave 1. Oppgave 2. Eksamen feb 2006.nb 1. Vektorfeltet er ikke konservativt da curl F 0. F. dr der C er kurven parametrisert av r(t), 0 t 1
 Eksamen feb 6.nb Oppgave Clear@x, y, zd F@x_, y_, z_d := 8x y z, y z, x y z<
Eksamen feb 6.nb Oppgave Clear@x, y, zd F@x_, y_, z_d := 8x y z, y z, x y z<
Eksamen Ma 3 des 2004
 Eksamen Ma 3 des 4.nb Eksamen Ma 3 des 4 Initialization In[8]:= In[]:=
Eksamen Ma 3 des 4.nb Eksamen Ma 3 des 4 Initialization In[8]:= In[]:=
EKSAMENSOPPGAVE I SIE5025-PÅLITELIGE SYSTEMER
 Norges teknisk-naturvitenskapelige universitet Institutt for telematikk EKSAMENSOPPGAVE I SIE5025-PÅLITELIGE SYSTEMER Faglig kontakt under eksamen: Bjarne E. Helvik Telefon.: 92667 Eksamensdato: 24. mai
Norges teknisk-naturvitenskapelige universitet Institutt for telematikk EKSAMENSOPPGAVE I SIE5025-PÅLITELIGE SYSTEMER Faglig kontakt under eksamen: Bjarne E. Helvik Telefon.: 92667 Eksamensdato: 24. mai
EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING LØSNINGSFORSLAG. Mandag 14. desember 2005 Tid: 09:00 13:00
 Norges teknisk naturvitenskapelige universitet Institutt for telematikk Side 1 av 10 Faglig kontakt under eksamen: Poul Heegaard (73 594321) EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING
Norges teknisk naturvitenskapelige universitet Institutt for telematikk Side 1 av 10 Faglig kontakt under eksamen: Poul Heegaard (73 594321) EKSAMEN I EMNE TTM4110 PÅLITELIGHET OG YTELSE MED SIMULERING
NTNU Norges teknisk-naturvitenskapelige universitet Institutt for telematikk
 NTNU Norges teknisk-naturvitenskapelige universitet Institutt for telematikk Side 1 av 21 Faglig kontakt under eksamen: Navn: Bjarne E. Helvik Tlf: 92667 EKSAMEN I EMNE SIE5015 PÅLITELIGHET OG YTELSE MED
NTNU Norges teknisk-naturvitenskapelige universitet Institutt for telematikk Side 1 av 21 Faglig kontakt under eksamen: Navn: Bjarne E. Helvik Tlf: 92667 EKSAMEN I EMNE SIE5015 PÅLITELIGHET OG YTELSE MED
Eksamen TTM4120 Pålitelige systemer 18. mai 2004 LØSNINGSSKISSE
 Side 1 av 6 Eksamen TTM4120 Pålitelige systemer 18. mai 2004 LØSNINGSSKISSE a Det skal etableres en transportforbindelse fra node 1 til node 3. Anta at C [ ij, ] = for alle [ i, j] Ω L. Denne forbindelsen
Side 1 av 6 Eksamen TTM4120 Pålitelige systemer 18. mai 2004 LØSNINGSSKISSE a Det skal etableres en transportforbindelse fra node 1 til node 3. Anta at C [ ij, ] = for alle [ i, j] Ω L. Denne forbindelsen
I denne øvingen vil vi sammenlikne det teoretiske resultat med et grafisk bilde av konturlinjene til flaten. Vi tegner konturene der
 Øving uke 44 Kritiske punkter Se også Mathematicakompendiet, kap 3.8 En funksjon av to variable kan ha lokale maksimal- og minimalpunkter innenfor definisjonsmengden, akkurat som funksjoner av en variabel.
Øving uke 44 Kritiske punkter Se også Mathematicakompendiet, kap 3.8 En funksjon av to variable kan ha lokale maksimal- og minimalpunkter innenfor definisjonsmengden, akkurat som funksjoner av en variabel.
Flytte Lønn 5.0 fra SQL 2000 til SQL 2005 / 2008
 Flytte Lønn 5.0 fra SQL 2000 til SQL 2005 / 2008 Før du flytter databasene til Lønn 5.0 fra SQL Server 2000 til SQL Server 2005 / 2008 må du ta backup av databasene. Hvis SQL Server 2005 /2008 ikke allerede
Flytte Lønn 5.0 fra SQL 2000 til SQL 2005 / 2008 Før du flytter databasene til Lønn 5.0 fra SQL Server 2000 til SQL Server 2005 / 2008 må du ta backup av databasene. Hvis SQL Server 2005 /2008 ikke allerede
Eksamen. Fag: AA6524/AA6526 Matematikk 3MX. Eksamensdato: 6. desember 2006. Vidaregåande kurs II / Videregående kurs II
 Eksamen Fag: AA654/AA656 Matematikk 3MX Eksamensdato: 6. desember 006 Vidaregåande kurs II / Videregående kurs II Studieretning: Allmenne, økonomiske og administrative fag Elevar/Elever Privatistar/Privatister
Eksamen Fag: AA654/AA656 Matematikk 3MX Eksamensdato: 6. desember 006 Vidaregåande kurs II / Videregående kurs II Studieretning: Allmenne, økonomiske og administrative fag Elevar/Elever Privatistar/Privatister
ü Omkrets ü Rotasjonsflate oblig1 Ma 3B h 2007 fasit.nb 2 Ldq. Vi må passe på at cos H ÅÅÅÅL>0 når 0 Relasjonen cosh ÅÅÅÅ
 oblig Ma 3B h 7 fasit.nb Oblig Ma 3B h 7 fasit ü Oppgave Det er ikke umiddelbart klart hvordan vi eliminerer parameteren t, men prøv å summere de kvadrerte uttrykkene og se hva det fører til: x + y = -
oblig Ma 3B h 7 fasit.nb Oblig Ma 3B h 7 fasit ü Oppgave Det er ikke umiddelbart klart hvordan vi eliminerer parameteren t, men prøv å summere de kvadrerte uttrykkene og se hva det fører til: x + y = -
MOT310 Statistiske metoder 1, høsten 2006 Løsninger til regneøving nr. 8 (s. 1) Oppgaver fra boka:
 MOT30 Statistiske metoder, høsten 2006 Løsninger til regneøving nr. 8 (s. ) Oppgaver fra boka: Oppgave.5 (.3:5) ) Først om tolking av datautskriften. Sammendrag gir følgende informasjon: Multippel R =R,
MOT30 Statistiske metoder, høsten 2006 Løsninger til regneøving nr. 8 (s. ) Oppgaver fra boka: Oppgave.5 (.3:5) ) Først om tolking av datautskriften. Sammendrag gir følgende informasjon: Multippel R =R,
Løsningskisse seminaroppgaver uke 11 ( mars)
 HG Mars 008 Løsningskisse seminaroppgaver uke (0.-4. mars) ECON 0 EKSAMEN 004 VÅR Oppgave En gitt prøve er laget som en flervalgsprøve ( multiple choice test ). Prøven består av tre spørsmål. For hvert
HG Mars 008 Løsningskisse seminaroppgaver uke (0.-4. mars) ECON 0 EKSAMEN 004 VÅR Oppgave En gitt prøve er laget som en flervalgsprøve ( multiple choice test ). Prøven består av tre spørsmål. For hvert
KJ1042 Øving 5: Entalpi og entropi
 KJ1042 Øving 5: Entalpi og entropi Ove Øyås Sist endret: 17. mai 2011 Repetisjonsspørsmål 1. Hva er varmekapasitet og hva er forskjellen på C P og C? armekapasiteten til et stoff er en målbar fysisk størrelse
KJ1042 Øving 5: Entalpi og entropi Ove Øyås Sist endret: 17. mai 2011 Repetisjonsspørsmål 1. Hva er varmekapasitet og hva er forskjellen på C P og C? armekapasiteten til et stoff er en målbar fysisk størrelse
1T eksamen høsten 2017 løsning
 1T eksamen høsten 017 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform. 105000 0,15
1T eksamen høsten 017 løsning Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform. 105000 0,15
L12-Dataanalyse. Introduksjon. Nelson Aalen plott. Page 76 of Introduksjon til dataanalyse. Levetider og sensurerte tider
 Page 76 of 80 L12-Dataanalyse Introduksjon Introduksjon til dataanalyse Presentasjonen her fokuserer på dataanalyseteknikker med formål å estimere parametere (MTTF,, osv) i modeller vi benytter for vedlikeholdsoptimering
Page 76 of 80 L12-Dataanalyse Introduksjon Introduksjon til dataanalyse Presentasjonen her fokuserer på dataanalyseteknikker med formål å estimere parametere (MTTF,, osv) i modeller vi benytter for vedlikeholdsoptimering
eksamen-f0b-v2001.nb 1
 eksamen-f0b-v200.nb Løsningsforslag Eksamen Fysikk for forkurs Våren 200 Alle forbehold om feil og uklarheter; dette er som navnet sier et forslag. OPPGAVE a) Regn ut bølgelengden til et foton med energi
eksamen-f0b-v200.nb Løsningsforslag Eksamen Fysikk for forkurs Våren 200 Alle forbehold om feil og uklarheter; dette er som navnet sier et forslag. OPPGAVE a) Regn ut bølgelengden til et foton med energi
Oppgave 1 Ytelse i ett nettelement
 Side 1 av 14 Oppgave 1 Ytelse i ett nettelement a) Beskriv systemet ved Kendalls notasjon og lag en Markov modell av NE i hvorkun én pakke kan betjenes ad gangen og bufferet har uendelig kapasitet, B =.
Side 1 av 14 Oppgave 1 Ytelse i ett nettelement a) Beskriv systemet ved Kendalls notasjon og lag en Markov modell av NE i hvorkun én pakke kan betjenes ad gangen og bufferet har uendelig kapasitet, B =.
Del 2: Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamen i: STA-1002 Statistikk og sannsynlighet 2 Dato: Fredag 31. mai 2013 Tid: Kl 09:00 13:00 Sted: Administrasjonsbygget
 FA K U L T E T FO R NA T U R V I T E N S K A P O G TE K N O L O G I EKSAMENSOPPGAVE Eksamen i: STA-1002 Statistikk og sannsynlighet 2 Dato: Fredag 31. mai 2013 Tid: Kl 09:00 13:00 Sted: Administrasjonsbygget
FA K U L T E T FO R NA T U R V I T E N S K A P O G TE K N O L O G I EKSAMENSOPPGAVE Eksamen i: STA-1002 Statistikk og sannsynlighet 2 Dato: Fredag 31. mai 2013 Tid: Kl 09:00 13:00 Sted: Administrasjonsbygget
Løsningsforslag Konte-eksamen 2. august 2003 SIF4048 Kjemisk fysikk og kvantemekanikk
 Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
Konte-eksamen SIF448.aug. 3 - løsningsforslag 1 Oppgave 1 a. Hamilton-operatoren er Løsningsforslag Konte-eksamen. august 3 SIF448 Kjemisk fysikk og kvantemekanikk Ĥ = h m x + V (x), og den tidsuavhengige
STK juni 2016
 Løsningsforslag til eksamen i STK220 3 juni 206 Oppgave a N i er binomisk fordelt og EN i np i, der n 204 Hvis H 0 er sann, er forventningen lik E i n 204/6 34 for i, 2,, 6 6 Hvis H 0 er sann er χ 2 6
Løsningsforslag til eksamen i STK220 3 juni 206 Oppgave a N i er binomisk fordelt og EN i np i, der n 204 Hvis H 0 er sann, er forventningen lik E i n 204/6 34 for i, 2,, 6 6 Hvis H 0 er sann er χ 2 6
Chebyshev interpolasjon
 Chebyshev interpolasjon Chebyshev polynomer Vi vil studere polynomapproksimasjon på intervallet [-, ]. Målet er å minimalisere den største verdien av feilestimatet E HxL = f HxL - P HxL, hvor maksimum
Chebyshev interpolasjon Chebyshev polynomer Vi vil studere polynomapproksimasjon på intervallet [-, ]. Målet er å minimalisere den største verdien av feilestimatet E HxL = f HxL - P HxL, hvor maksimum
SIF5005 våren 2003: Maple-øving 1
 SIF våren : Maple-øving Løsningsforslag. Oppgave. Litt grunnleggende Maple Hvordan får du hjelp i Maple med en funksjon når du kjenner navnet? Det raskeste er slik: >?simplify Tips for å lese hjelpesider:
SIF våren : Maple-øving Løsningsforslag. Oppgave. Litt grunnleggende Maple Hvordan får du hjelp i Maple med en funksjon når du kjenner navnet? Det raskeste er slik: >?simplify Tips for å lese hjelpesider:
Generell informasjon om faget er tilgjengelig fra It s learning. 1 En kort oppsummering Adaptiv filtrering 2. 3 Prediksjon 4
 Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Stavanger, 13. august 2013 Det teknisknaturvitenskapelige fakultet ELE500 Signalbehandling, 2013. Generell informasjon om faget er tilgjengelig fra It s learning. Innhold 1 En kort oppsummering. 1 2 Adaptiv
Oppgaven består av to deler, del A og del B. Alle skal besvare både del A og del B, men det finnes noen valgmuligheter innenfor hver del.
 Oblig 4 INF1000-SIKT Gulbrand Grås Husleiesystem Mål: Formålet med oppgaven er å gi erfaring med å løse et større programmeringsproblem ved hjelp av klasser og objekter (og tilhørende metoder), dessuten
Oblig 4 INF1000-SIKT Gulbrand Grås Husleiesystem Mål: Formålet med oppgaven er å gi erfaring med å løse et større programmeringsproblem ved hjelp av klasser og objekter (og tilhørende metoder), dessuten
a) Blir produktet av to vilkårlige oddetall et partall eller et oddetall? Bevis det.
 Prøve i R1 04.1.15 Del 1 Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Husk å begrunne alle svar. Det skal gå klart frem av besvarelsen hvordan du har tenkt. Oppgave
Prøve i R1 04.1.15 Del 1 Hjelpemidler: vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler Husk å begrunne alle svar. Det skal gå klart frem av besvarelsen hvordan du har tenkt. Oppgave
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Sikkerhetsrisiko:lav. fare for øyeskade. HMS ruoner
 Reaksjonskinetikk. jodklokka Risiko fare Oltak Sikkerhetsrisiko:lav fare for øyeskade HMS ruoner Figur 1 :risikovurdering Innledning Hastigheten til en kjemisk reaksjon avhenger av flere faktorer: Reaksjonsmekanisme,
Reaksjonskinetikk. jodklokka Risiko fare Oltak Sikkerhetsrisiko:lav fare for øyeskade HMS ruoner Figur 1 :risikovurdering Innledning Hastigheten til en kjemisk reaksjon avhenger av flere faktorer: Reaksjonsmekanisme,
TMA4245 Statistikk Eksamen desember 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag TMA4245 Statistikk Eksamen desember 2016 Oppgave 1 En bedrift produserer elektriske komponenter. Komponentene kan ha to typer
R1 eksamen høsten 2016 løsningsforslag
 R eksamen høsten 06 løsningsforslag Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (5 poeng) Deriver funksjonene f x x 5x 6 a) fx 4x 5 b) g(
R eksamen høsten 06 løsningsforslag Tid: 3 timer Hjelpemidler: Vanlige skrivesaker, linjal med centimetermål og vinkelmåler er tillatt. Oppgave (5 poeng) Deriver funksjonene f x x 5x 6 a) fx 4x 5 b) g(
UNIVERSITETET I OSLO ØKONOMISK INSTITUTT
 Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Eksamen i: ECON30 Statistikk UNIVERSITETET I OSLO ØKONOMISK INSTITUTT Eksamensdag: 03.06.06 Sensur kunngjøres: 4.06.06 Tid for eksamen: kl. 09:00 :00 Oppgavesettet er på 5 sider Tillatte hjelpemidler:
Eksamen AA6516 Matematikk 2MX Privatistar/Privatister. Nynorsk/Bokmål
 Eksamen 04.12.2008 AA6516 Matematikk 2MX Privatistar/Privatister Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler: Vedlegg: Andre opplysninger: Framgangsmåte og forklaring: 5 timer Se
Eksamen 04.12.2008 AA6516 Matematikk 2MX Privatistar/Privatister Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler: Vedlegg: Andre opplysninger: Framgangsmåte og forklaring: 5 timer Se
Faktor. Eksamen høst 2005 SØK 1001- Innføring i matematikk for økonomer Besvarelse nr 1: -en eksamensavis utgitt av Pareto
 Faktor -en eksamensavis utgitt av Pareto Eksamen høst 005 SØK 00- Innføring i matematikk for økonomer Besvarelse nr : OBS!! Dette er en eksamensbevarelse, og ikke en fasit. Besvarelsene er uten endringer
Faktor -en eksamensavis utgitt av Pareto Eksamen høst 005 SØK 00- Innføring i matematikk for økonomer Besvarelse nr : OBS!! Dette er en eksamensbevarelse, og ikke en fasit. Besvarelsene er uten endringer
EKSAMEN I MA0002 Brukerkurs B i matematikk
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Achenef Tesfahun (9 84 97 5) EKSAMEN I MA2 Brukerkurs B i matematikk Lørdag 322 Tid:
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 7 Faglig kontakt under eksamen: Achenef Tesfahun (9 84 97 5) EKSAMEN I MA2 Brukerkurs B i matematikk Lørdag 322 Tid:
Løsningskisse for oppgaver til undervisningsfri uke 8 ( februar 2012)
 1 ECON 130 HG - februar 01 Løsningskisse for oppgaver til undervisningsfri uke 8 (0.-. februar 01) Oppg..1. Variabel: x = antall kundehenvendelser pr. dag 1. Antall observasjoner: n = 100 dager. I Excel
1 ECON 130 HG - februar 01 Løsningskisse for oppgaver til undervisningsfri uke 8 (0.-. februar 01) Oppg..1. Variabel: x = antall kundehenvendelser pr. dag 1. Antall observasjoner: n = 100 dager. I Excel
Denne labøvelsen gir en videre innføring i elementær bruk av programmet Maple.
 MAPLE-LAB 2 Denne labøvelsen gir en videre innføring i elementær bruk av programmet Maple.. Sett i gang Maple på din PC / arbeidsstasjon. Hvis du sitter på en Linux-basert maskin og opplever problemer
MAPLE-LAB 2 Denne labøvelsen gir en videre innføring i elementær bruk av programmet Maple.. Sett i gang Maple på din PC / arbeidsstasjon. Hvis du sitter på en Linux-basert maskin og opplever problemer
Exam - Friday 24. may SIE 5025 Pålitelige systemer Dependable systems. Løsningsforslag
 Side av 3 Exam - Friday 4. may 003 SIE 505 Pålitelige systemer Dependable systems Løsningsforslag Version 0.; 9 May 003; BEH Oppgave a) Fordeler: En varm reserve er hurtigere å få idriftsatt med enten
Side av 3 Exam - Friday 4. may 003 SIE 505 Pålitelige systemer Dependable systems Løsningsforslag Version 0.; 9 May 003; BEH Oppgave a) Fordeler: En varm reserve er hurtigere å få idriftsatt med enten
EKSAMEN. 1 Om eksamen. EMNE: MA2610 FAGLÆRER: Svein Olav Nyberg, Trond Stølen Gustavsen. Klasser: (div) Dato: 24. mai 2004 Eksamenstid:
 EKSAMEN EMNE: MA6 FAGLÆRER: Svein Olav Nyberg, Trond Stølen Gustavsen Klasser: (div) Dato: mai Eksamenstid: Eksamensoppgaven består av følgende: Antall sider (ink forside): 5 Antall oppgaver: Antall vedlegg:
EKSAMEN EMNE: MA6 FAGLÆRER: Svein Olav Nyberg, Trond Stølen Gustavsen Klasser: (div) Dato: mai Eksamenstid: Eksamensoppgaven består av følgende: Antall sider (ink forside): 5 Antall oppgaver: Antall vedlegg:
Løsningsforslag Eksamen 20. desember 2012 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
Eksamen FY045/TFY450 0. desember 0 - løsningsforslag Oppgave Løsningsforslag Eksamen 0. desember 0 FY045/TFY450 Kvantemekanikk I a. For x < 0 er potensialet lik null. (i) For E > 0 er da ψ E = (m e E/
LF, KONTINUASJONSEKSAMEN TMA
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Haaken A. Moe 92650655 Bokmål LF, KONTINUASJONSEKSAMEN TMA4140 2008 Oppgave 1 (10%)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: Haaken A. Moe 92650655 Bokmål LF, KONTINUASJONSEKSAMEN TMA4140 2008 Oppgave 1 (10%)
EKSAMEN I SOS1120 KVANTITATIV METODE 6. DESEMBER 2007 (4 timer)
 EKSAMEN I SOS1120 KVANTITATIV METODE 6. DESEMBER 2007 (4 timer) Bruk av ikke-programmerbar kalkulator er tillatt under eksamen. Utover det er ingen hjelpemidler tillatt. Sensur faller torsdag 3. Januar
EKSAMEN I SOS1120 KVANTITATIV METODE 6. DESEMBER 2007 (4 timer) Bruk av ikke-programmerbar kalkulator er tillatt under eksamen. Utover det er ingen hjelpemidler tillatt. Sensur faller torsdag 3. Januar
LØSNINGSFORSLAG EKSAMEN MA0002, VÅR 09
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 LØSNINGSFORSLAG EKSAMEN MA000, VÅR 09 Oppgave a) (0%) Løs initialverdiproblemet gitt ved differensialligningen med
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side av 6 LØSNINGSFORSLAG EKSAMEN MA000, VÅR 09 Oppgave a) (0%) Løs initialverdiproblemet gitt ved differensialligningen med
Løsningsforslag eksamen INF3480 vår 2011
 Løsningsforslag eksamen INF3480 vår 0 Oppgave a) A - Arbeidsrommet er en kule med radius L 3 + L 4. B - Alle rotasjonsaksene er paralelle, roboten beveger seg bare i et plan, dvs. null volum. C - Arbeidsrommet
Løsningsforslag eksamen INF3480 vår 0 Oppgave a) A - Arbeidsrommet er en kule med radius L 3 + L 4. B - Alle rotasjonsaksene er paralelle, roboten beveger seg bare i et plan, dvs. null volum. C - Arbeidsrommet
Øving 6 Tallfølger og differenslikninger
 Øving Tallfølger og differenslikninger Teori Se også Mathematicakompendiet kap. En tallfølge er en liste av elementer satt opp i en bestemt rekkefølge { a[0]a[]a[]...a[n]... } = {a[n]} 0. Vi kaller elementet
Øving Tallfølger og differenslikninger Teori Se også Mathematicakompendiet kap. En tallfølge er en liste av elementer satt opp i en bestemt rekkefølge { a[0]a[]a[]...a[n]... } = {a[n]} 0. Vi kaller elementet
DEL 1. Uten hjelpemidler. Oppgave 1 (2 poeng) Oppgave 2 (4 poeng) Oppgave 3 (4 poeng) I er en konstant. Deriver funksjonene
 DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Deriver funksjonene 3 a) f( x) 5x x 5 b) g( x) x e x Oppgave (4 poeng) Polynomfunksjonen P er gitt ved 3 P( x) x x 10x 8, DP a) Faktoriser P( x ) i førstegradsfaktorer.
DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Deriver funksjonene 3 a) f( x) 5x x 5 b) g( x) x e x Oppgave (4 poeng) Polynomfunksjonen P er gitt ved 3 P( x) x x 10x 8, DP a) Faktoriser P( x ) i førstegradsfaktorer.
Løsningskisse seminaroppgaver uke 15
 HG April 0 Løsningskisse seminaroppgaver uke 5 Oppg. 5.6 La X = antall barn i utvalget som har lærevansker. Andel barn med lærevansker i populasjonen av barn antas å være p = 0,5. Utvalgsstørrelsen er
HG April 0 Løsningskisse seminaroppgaver uke 5 Oppg. 5.6 La X = antall barn i utvalget som har lærevansker. Andel barn med lærevansker i populasjonen av barn antas å være p = 0,5. Utvalgsstørrelsen er
Eksamen R1 høsten 2014
 Eksamen R1 høsten 014 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Deriver funksjonene 3 a) f x x x x b) gxx e 5 5 Oppgave
Eksamen R1 høsten 014 Tid: timer Hjelpemidler: Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler er tillatt. Oppgave 1 ( poeng) Deriver funksjonene 3 a) f x x x x b) gxx e 5 5 Oppgave
Notater nr 9: oppsummering for uke 45-46
 Notater nr 9: oppsummering for uke 45-46 Bøkene B (læreboken): Tor Gulliksen og Arne Hole, Matematikk i Praksis, 5. utgave. K (kompendium): Amir M. Hashemi, Brukerkurs i matematikk MAT, høsten. Oppsummering
Notater nr 9: oppsummering for uke 45-46 Bøkene B (læreboken): Tor Gulliksen og Arne Hole, Matematikk i Praksis, 5. utgave. K (kompendium): Amir M. Hashemi, Brukerkurs i matematikk MAT, høsten. Oppsummering
1T eksamen hausten 2017 Løysing
 1T eksamen hausten 017 Løysing Tid: 3 timar Hjelpemiddel: Vanlege skrivesaker, linjal med centimetermål og vinkelmålar er tillatne. Oppgåve 1 ( poeng) Rekn ut og skriv svaret på standardform. 105000 0,15
1T eksamen hausten 017 Løysing Tid: 3 timar Hjelpemiddel: Vanlege skrivesaker, linjal med centimetermål og vinkelmålar er tillatne. Oppgåve 1 ( poeng) Rekn ut og skriv svaret på standardform. 105000 0,15
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT-INF 1100L Programmering, modellering, og beregninger. Prøveeksamen 2 Eksamensdag: Onsdag 14. November 2014. Tid for eksamen:
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT-INF 1100L Programmering, modellering, og beregninger. Prøveeksamen 2 Eksamensdag: Onsdag 14. November 2014. Tid for eksamen:
Eksamensoppgave i TMA4115 Matematikk 3
 Institutt for matematiske fag Eksamensoppgave i TMA45 Matematikk 3 Faglig kontakt under eksamen: Aslak Bakke Buan a, Morten Andreas Nome b, Tjerand Silde c Tlf: a mobil Aslak, b mobil Morten, c mobil Tjerand
Institutt for matematiske fag Eksamensoppgave i TMA45 Matematikk 3 Faglig kontakt under eksamen: Aslak Bakke Buan a, Morten Andreas Nome b, Tjerand Silde c Tlf: a mobil Aslak, b mobil Morten, c mobil Tjerand
Testobservator for kjikvadrattester
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 11: Anvendelser av kjikvadratfordelingen: Kjikvadrattester Situasjon: Et tilfeldig utvalg av n individer er trukket
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 11: Anvendelser av kjikvadratfordelingen: Kjikvadrattester Situasjon: Et tilfeldig utvalg av n individer er trukket
Del 2: Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.
 Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.
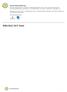
Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye)
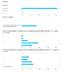 INF102 Er du? Er du? - Annet Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor
INF102 Er du? Er du? - Annet Hvor mye teoretisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor mye praktisk kunnskap har du tilegnet deg på dette emnet? (1 = ingen, 5 = mye) Hvor
Løsningsforslag, eksamen statistikk, juni 2015
 Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Løsningsforslag, eksamen statistikk, juni 0 Oppgave 1 Siden det spørres om tall fra et intervall, som oppgaven viser kan være et reelle, er det tydelig at tallene er tatt fra en kontinuerlig fordeling.
Eksamensoppgave i TMA4240 Statistikk
 Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
Institutt for matematiske fag Eksamensoppgave i TMA4240 Statistikk Faglig kontakt under eksamen: Mette Langaas a, Ingelin Steinsland b, Geir-Arne Fuglstad c Tlf: a 988 47 649, b 926 63 096, c 452 70 806
betyr begivenheten at det blir trukket en rød kule i første trekning og en hvit i andre, mens B1 B2
 ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
ECON30: EKSAMEN 06v SENSORVEILEDNING. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
Generelle opplysninger om eksamen i 1T. I vurderingsveiledning fra Utdanningsdirektoratet finner vi blant annet dette:
 Forord Generelle opplysninger om eksamen i 1T I vurderingsveiledning fra Utdanningsdirektoratet finner vi blant annet dette: Eksamensordning Eksamen varer fem timer og er todelt. Del 1 og del 2 av eksamensoppgaven
Forord Generelle opplysninger om eksamen i 1T I vurderingsveiledning fra Utdanningsdirektoratet finner vi blant annet dette: Eksamensordning Eksamen varer fem timer og er todelt. Del 1 og del 2 av eksamensoppgaven
Antall i I/O-minnet (merk! her er denne lik antall i systemet ettersom pakken ligger i minnet både mens den betjenes og venter på betjening).
 Løsningsskisse a) Anta først at sentralenhetens betjeningstid av pakker er konstant med forventning. På grunn av sanntids-trafikk settes det som krav at maksimal forsinkelse gjennom ruteren skal være 0
Løsningsskisse a) Anta først at sentralenhetens betjeningstid av pakker er konstant med forventning. På grunn av sanntids-trafikk settes det som krav at maksimal forsinkelse gjennom ruteren skal være 0
Differensiallikninger definisjoner, eksempler og litt om løsning
 Differensiallikninger definisjoner, eksempler og litt om løsning MAT-INF1100 Differensiallikninger i MAT-INF1100 Definsjon, litt om generelle egenskaper Noen få anvendte eksempler Teknikker for løsning
Differensiallikninger definisjoner, eksempler og litt om løsning MAT-INF1100 Differensiallikninger i MAT-INF1100 Definsjon, litt om generelle egenskaper Noen få anvendte eksempler Teknikker for løsning
For mer informasjon om SQL Server 2014 Express, se Microsoft sine nettsider: https://msdn.microsoft.com/en-us/sqlserver2014express.
 1 Innholdsfortegnelse Microsoft SQL Server 2014 Express... 3 Nedlastning av installasjonsfil for SQL Server 2014 Express... 3 Installasjon av SQL Server 2014 Express... 4 Installasjon av Huldt & Lillevik
1 Innholdsfortegnelse Microsoft SQL Server 2014 Express... 3 Nedlastning av installasjonsfil for SQL Server 2014 Express... 3 Installasjon av SQL Server 2014 Express... 4 Installasjon av Huldt & Lillevik
Eksamensoppgave i ST0103 Brukerkurs i statistikk
 Institutt for matematiske fag Eksamensoppgave i ST0103 Brukerkurs i statistikk Faglig kontakt under eksamen: Jarle Tufto Tlf: 99 70 55 19 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00-13:00
Institutt for matematiske fag Eksamensoppgave i ST0103 Brukerkurs i statistikk Faglig kontakt under eksamen: Jarle Tufto Tlf: 99 70 55 19 Eksamensdato: 3. desember 2016 Eksamenstid (fra til): 09:00-13:00
UNIVERSITETET I OSLO
 NIVERSIEE I OSO Det matematisk-naturvitenskapelige fakultet Eksamen i: Fys60 Eksamensdag: Fredag 6. desember 03 id for eksamen: 430 830 Oppgavesettet er på: 4 sider Vedlegg: ingen ilatte hjelpemidler Godkjente
NIVERSIEE I OSO Det matematisk-naturvitenskapelige fakultet Eksamen i: Fys60 Eksamensdag: Fredag 6. desember 03 id for eksamen: 430 830 Oppgavesettet er på: 4 sider Vedlegg: ingen ilatte hjelpemidler Godkjente
TDT4110 IT Grunnkurs Høst 2012
 TDT4110 IT Grunnkurs Høst 2012 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 7 Denne øvingen er en fellesøving laget i samarbeid med emnet TMA4100
TDT4110 IT Grunnkurs Høst 2012 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Øving 7 Denne øvingen er en fellesøving laget i samarbeid med emnet TMA4100
ST0202 Statistikk for samfunnsvitere
 ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 13: Lineær korrelasjons- og regresjonsanalyse Kap. 13.1-13.3: Lineær korrelasjonsanalyse. Disse avsnitt er ikke pensum,
ST0202 Statistikk for samfunnsvitere Bo Lindqvist Institutt for matematiske fag 2 Kap. 13: Lineær korrelasjons- og regresjonsanalyse Kap. 13.1-13.3: Lineær korrelasjonsanalyse. Disse avsnitt er ikke pensum,
FYS våren Linjetilpasning. Alex Read Universitetet i Oslo Fysisk institutt
 FYS150 - våren 019 Linjetilpasning Alex Read Universitetet i Oslo Fysisk institutt Mål Studere en alternativ linjetilpasning der vi kjenner usikkerheten per målepunkt σ i (i stedet for å hente denne usikkerheten
FYS150 - våren 019 Linjetilpasning Alex Read Universitetet i Oslo Fysisk institutt Mål Studere en alternativ linjetilpasning der vi kjenner usikkerheten per målepunkt σ i (i stedet for å hente denne usikkerheten
Figur 2: Fortegnsskjema for g (x)
 Løsningsforslag Eksamen M00 Våren 998 Oppgave a) g) = e ) = e ) Figur : Fortegnsskjema for g) g) > 0 for < 0 og > og g) < 0 for 0 <
Løsningsforslag Eksamen M00 Våren 998 Oppgave a) g) = e ) = e ) Figur : Fortegnsskjema for g) g) > 0 for < 0 og > og g) < 0 for 0 <
TMA4240 Statistikk Høst 2016
 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Anbefalt øving 9 Løsningsskisse Oppgave 1 a) Vi lar her Y være antall fugler som kolliderer med vindmølla i løpet av den gitte
INF / Kap. 5, Del 2 Stein Krogdahl, Ifi, UiO
 INF5110 12/2-2013 Kap. 5, Del 2 Stein Krogdahl, Ifi, UiO Dagens temaer: Noen foiler igjen fra forrige gang SLR(1), LR(1)- og LALR(1)-grammatikker NB: Oppgaver til kap 4 og 5 er lagt ut på undervisningsplanen
INF5110 12/2-2013 Kap. 5, Del 2 Stein Krogdahl, Ifi, UiO Dagens temaer: Noen foiler igjen fra forrige gang SLR(1), LR(1)- og LALR(1)-grammatikker NB: Oppgaver til kap 4 og 5 er lagt ut på undervisningsplanen
Emnerapport 2013 vår, KJEM202 Miljøkjemi
 Emnerapport 2013 vår, KJEM202 Miljøkjemi Faglærers vurdering av gjennomføring Praktisk gjennomføring KJEM202 er et kurs som har studenter fra en rekke institutter ved MNF. Det er totalt 24 dobbelttimer
Emnerapport 2013 vår, KJEM202 Miljøkjemi Faglærers vurdering av gjennomføring Praktisk gjennomføring KJEM202 er et kurs som har studenter fra en rekke institutter ved MNF. Det er totalt 24 dobbelttimer
Retteinstrukser for midtveiseksamen i AST2000 høst 2018
 Retteinstrukser for midtveiseksamen i AST2000 høst 2018 Nedenfor følger veiledende retteinstrukser for midtveiseksamen i AST2000 høst 2018. Retteinstruksene skal ikke følges slavisk men poengfordelingen
Retteinstrukser for midtveiseksamen i AST2000 høst 2018 Nedenfor følger veiledende retteinstrukser for midtveiseksamen i AST2000 høst 2018. Retteinstruksene skal ikke følges slavisk men poengfordelingen
Eksamensoppgave i SØK1010 Matematikk og mikroøkonomi
 Institutt for samfunnsøkonomi Eksamensoppgave i SØK1010 Matematikk og mikroøkonomi Faglig kontakt under eksamen: Hildegunn E. Stokke Tlf.: 73 59 16 65 Eksamensdato: 16.12.2013 Eksamenstid (fra-til): 5
Institutt for samfunnsøkonomi Eksamensoppgave i SØK1010 Matematikk og mikroøkonomi Faglig kontakt under eksamen: Hildegunn E. Stokke Tlf.: 73 59 16 65 Eksamensdato: 16.12.2013 Eksamenstid (fra-til): 5
Histogramprosessering
 Histogramprosessering Lars Vidar Magnusson January 22, 2018 Delkapittel 3.3 Histogram Processing Histogram i Bildeanalyse Et histogram av et digitalt bilde med intensitet i intervallet [0, L) er en diskret
Histogramprosessering Lars Vidar Magnusson January 22, 2018 Delkapittel 3.3 Histogram Processing Histogram i Bildeanalyse Et histogram av et digitalt bilde med intensitet i intervallet [0, L) er en diskret
Oppgave 1 (25 %) - Flervalgsoppgaver
 Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
Oppgaver og løsningsforslag for 4t eksamen 10.mai 006 i LO510D Lineær algebra med grafiske anvendelser. Fra og med oppgave skal alle svar begrunnes. Oppgave 1 (5 %) - Flervalgsoppgaver Denne oppgaven består
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT-INF 1100L Programmering, modellering, og beregninger. Eksamensdag: Fredag 2. Desember 2016. Tid for eksamen: 9:00 13:00.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT-INF 1100L Programmering, modellering, og beregninger. Eksamensdag: Fredag 2. Desember 2016. Tid for eksamen: 9:00 13:00.
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: Torsdag 10 januar 2008 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 6
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i MAT-INF 1100 Modellering og beregninger Eksamensdag: Torsdag 10 januar 2008 Tid for eksamen: 9:00 12:00 Oppgavesettet er på 6
ST1101/ST6101 Sannsynlighetsregning og statistikk Vår 2019
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag ST1101/ST6101 Sannsynlighetsregning og statistikk Vår 2019 Løsningsforslag Øving 8 Oppgaver fra boka.12.1 X har pdf p X (k)
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag ST1101/ST6101 Sannsynlighetsregning og statistikk Vår 2019 Løsningsforslag Øving 8 Oppgaver fra boka.12.1 X har pdf p X (k)
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Fys216 Eksamensdag: Tirsdag 8. desember 215 Tid for eksamen: 143 183 Oppgavesettet er på: 4 sider Vedlegg: ingen Tilatte hjelpemidler
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: Fys216 Eksamensdag: Tirsdag 8. desember 215 Tid for eksamen: 143 183 Oppgavesettet er på: 4 sider Vedlegg: ingen Tilatte hjelpemidler
Løsningsforsalg til andre sett med obligatoriske oppgaver i STK1110 høsten 2015
 Løsningsforsalg til andre sett med obligatoriske oppgaver i STK1110 høsten 2015 R-kode for alle oppgaver er gitt bakerst. Oppgave 1 (a) Boksplottet antyder at verdiene er høyere for kvinner enn for menn.
Løsningsforsalg til andre sett med obligatoriske oppgaver i STK1110 høsten 2015 R-kode for alle oppgaver er gitt bakerst. Oppgave 1 (a) Boksplottet antyder at verdiene er høyere for kvinner enn for menn.
TMA4240 Statistikk Høst 2015
 TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
TMA4240 Statistikk Høst 2015 Norges teknisk-naturvitenskapelige universitet Institutt for matematiske fag Øving nummer 9, blokk II Oppgave 1 X er kontinuerlig fordelt med sannsynlighetstetthet f(x) = 2xe
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK2120 Statistiske metoder og dataanalyse 2. Eksamensdag: Fredag 7. juni 2013. Tid for eksamen: 14.30 18.30. Oppgavesettet er
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK2120 Statistiske metoder og dataanalyse 2. Eksamensdag: Fredag 7. juni 2013. Tid for eksamen: 14.30 18.30. Oppgavesettet er
TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i <<< >>>.
 1 ECON213: EKSAMEN 217 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
1 ECON213: EKSAMEN 217 VÅR - UTSATT PRØVE TALLSVAR. Det anbefales at de 9 deloppgavene merket med A, B, teller likt uansett variasjon i vanskelighetsgrad. Svarene er gitt i
NITH PG4200 Algoritmer og datastrukturer Løsningsforslag Eksamen 4.juni 2013
 NITH PG4200 Algoritmer og datastrukturer Løsningsforslag Eksamen 4.juni 20 ette løsningsforslaget er til tider mer detaljert enn det man vil forvente av en eksamensbesvarelse. et er altså ikke et eksempel
NITH PG4200 Algoritmer og datastrukturer Løsningsforslag Eksamen 4.juni 20 ette løsningsforslaget er til tider mer detaljert enn det man vil forvente av en eksamensbesvarelse. et er altså ikke et eksempel
Løsningsforslag Eksamen 8. august 2011 FY2045/TFY4250 Kvantemekanikk I
 Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
Eksamen FY45/TFY45 8. august - løsningsforslag Oppgave Løsningsforslag Eksamen 8. august FY45/TFY45 Kvantemekanikk I a. For E < V blir området x > klassisk forbudt, og den tidsuavhengige Schrödingerligningen
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: MAT 0 Lineær algebra Eksamensdag: Mandag 0. desember 0 Tid for eksamen: 4.30 8.30. Oppgavesettet er på 7 sider. Vedlegg: Tillatte
Løsningsforslag. n X. n X 1 i=1 (X i X) 2 og SY 2 = 1 ny S 2 X + S2 Y
 Statistiske metoder 1 høsten 004. Løsningsforslag Oppgave 1: a) Begge normalplottene gir punkter som ligger omtrent på ei rett linje så antagelsen om normalfordeling ser ut til å holde. Konfidensintervall
Statistiske metoder 1 høsten 004. Løsningsforslag Oppgave 1: a) Begge normalplottene gir punkter som ligger omtrent på ei rett linje så antagelsen om normalfordeling ser ut til å holde. Konfidensintervall
DEL 1 Uten hjelpemidler
 DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform 10 5 000 0,15 Oppgave ( poeng) Løs likningen grafisk 1 1 9 x x Oppgave 3 ( poeng) Løs ulikheten x x 1 0 Oppgave 4 ( poeng)
DEL 1 Uten hjelpemidler Oppgave 1 ( poeng) Regn ut og skriv svaret på standardform 10 5 000 0,15 Oppgave ( poeng) Løs likningen grafisk 1 1 9 x x Oppgave 3 ( poeng) Løs ulikheten x x 1 0 Oppgave 4 ( poeng)
WISEflow brukerveiledning for deltaker
 WISEflow brukerveiledning for deltaker Version 2.9.0 1 Innholdsfortegnelse Deltaker: slik kommer du i gang... 2 Rediger din profil... 3 Flowoversikt... 5 Flowtyper... 6 Flowens tilstand... 6 Hvordan leverer
WISEflow brukerveiledning for deltaker Version 2.9.0 1 Innholdsfortegnelse Deltaker: slik kommer du i gang... 2 Rediger din profil... 3 Flowoversikt... 5 Flowtyper... 6 Flowens tilstand... 6 Hvordan leverer
Bokmål. Eksamensinformasjon
 Eksamen 27052010 REA022 Matematikk R1 Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på del 1: Hjelpemidler på del 2: Vedlegg: Framgangsmåte: Veiledning om vurderingen: 5 timer: Del
Eksamen 27052010 REA022 Matematikk R1 Nynorsk/Bokmål Bokmål Eksamensinformasjon Eksamenstid: Hjelpemidler på del 1: Hjelpemidler på del 2: Vedlegg: Framgangsmåte: Veiledning om vurderingen: 5 timer: Del
Eksamensoppgave i MA0002 Brukerkurs i matematikk B - LØSNING
 Institutt for matematiske fag Eksamensoppgave i MA0002 Brukerkurs i matematikk B - LØSNING Faglig kontakt under eksamen: Frode Rønning Tlf: 95 21 81 38 Eksamensdato: 7. august 2017 Eksamenstid (fra til):
Institutt for matematiske fag Eksamensoppgave i MA0002 Brukerkurs i matematikk B - LØSNING Faglig kontakt under eksamen: Frode Rønning Tlf: 95 21 81 38 Eksamensdato: 7. august 2017 Eksamenstid (fra til):
Kommentarer til eksempelinnleveringene
 Kommentarer til eksempelinnleveringene Det er lagt ut 4 eksempelinnleveringer, en som er nesten perfekt og får 100 poeng uten opprunding. De andre 3 er kommentert i detalj her. Merk at tilbakemeldingene
Kommentarer til eksempelinnleveringene Det er lagt ut 4 eksempelinnleveringer, en som er nesten perfekt og får 100 poeng uten opprunding. De andre 3 er kommentert i detalj her. Merk at tilbakemeldingene
EKSAMEN I FAG TMA4275 LEVETIDSANALYSE Xxxdag xx. juni 2008 Tid: 09:0013:00
 Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: NN EKSAMEN I FAG TMA4275 LEVETIDSANALYSE Xxxdag xx. juni 2008 Tid: 09:0013:00 Tillatte
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag Side 1 av 5 Faglig kontakt under eksamen: NN EKSAMEN I FAG TMA4275 LEVETIDSANALYSE Xxxdag xx. juni 2008 Tid: 09:0013:00 Tillatte
Dette kan selvfølgelig brukes direkte som en numerisk tilnærmelse til den deriverte i et gitt punkt.
 Numerisk derivasjon Anne Kværnø Problemstilling Gitt en tilstrekkelig glatt funksjon. Finn en tilnærmelse til i et gitt punkt. Den deriverte av (https://wiki.math.ntnu.no/tma4100/tema/differentiation?
Numerisk derivasjon Anne Kværnø Problemstilling Gitt en tilstrekkelig glatt funksjon. Finn en tilnærmelse til i et gitt punkt. Den deriverte av (https://wiki.math.ntnu.no/tma4100/tema/differentiation?
MAT1120 Notat 2 Tillegg til avsnitt 5.4
 MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
MAT1120 Notat 2 Tillegg til avsnitt 54 Dette notatet utfyller bokas avsnitt 54 om matriserepresentasjonen (også kalt koordinatmatrisen) til en lineær avbildning mellom to endeligdimensjonale vektorrom
Rapportskrivning, eller Hvordan ser en god labrapport* ut?
 FYS2150 - våren 2019 Rapportskrivning, eller Hvordan ser en god labrapport* ut? Alex Read Universitetet i Oslo Fysisk institutt *En labrapport er et eksempel på et skriftlig vitenskapelig arbeid Essensen
FYS2150 - våren 2019 Rapportskrivning, eller Hvordan ser en god labrapport* ut? Alex Read Universitetet i Oslo Fysisk institutt *En labrapport er et eksempel på et skriftlig vitenskapelig arbeid Essensen
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Løsningsforslag: Statistiske metoder og dataanalys Eksamensdag: Fredag 9. desember 2011 Tid for eksamen: 14.30 18.30
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i: STK1110 Løsningsforslag: Statistiske metoder og dataanalys Eksamensdag: Fredag 9. desember 2011 Tid for eksamen: 14.30 18.30
EKSAMEN. Flexibel ingeniørutdanning, 2kl. Bygg m.fl.
 KANDIDATNUMMER: EKSAMEN FAGNAVN: FAGNUMMER: Statistikk. REA 1081 og REA1081F EKSAMENSDATO: 1. juni 2011. KLASSE: Flexibel ingeniørutdanning, 2kl. Bygg m.fl. TID: kl. 9.00 12.00. FAGLÆRER: Hans Petter Hornæs
KANDIDATNUMMER: EKSAMEN FAGNAVN: FAGNUMMER: Statistikk. REA 1081 og REA1081F EKSAMENSDATO: 1. juni 2011. KLASSE: Flexibel ingeniørutdanning, 2kl. Bygg m.fl. TID: kl. 9.00 12.00. FAGLÆRER: Hans Petter Hornæs
FY1006/TFY4215 Innføring i kvantefysikk, - Ekstraøving 2 1. Ekstraøving 2. = 1 2 (3n2 l 2 l), = 1 n 2, 1 n 3 (l ), 1 n 3 l(l + 1.
 FY006/TFY45 Innføring i kvantefysikk, - Ekstraøving Frist for innlevering (Til I.Ø.): 7. mai kl 7 Oppgave 9 hydrogenlignende atom Ekstraøving I denne oppgaven ser vi på et hydrogenlignende atom, der et
FY006/TFY45 Innføring i kvantefysikk, - Ekstraøving Frist for innlevering (Til I.Ø.): 7. mai kl 7 Oppgave 9 hydrogenlignende atom Ekstraøving I denne oppgaven ser vi på et hydrogenlignende atom, der et

 Eksamen Ma B høst 6.nb Eksamen Ma red.pensum 6 Oppgave
Eksamen Ma B høst 6.nb Eksamen Ma red.pensum 6 Oppgave