Et ekstremt ufullstendig oppslagsverk for TMA4185 Kodeteori

Transkript

1 Et ekstremt ufullstendig oppslagsverk for TMA4185 Kodeteori Ruben Spaans May 21, Pensum Pensumliste: ˆ Kapittel 1: Hele, unntatt 110 ˆ Kapittel 2: 21, 24 (singleton upper bound og MDS), 27 (Gilbert lower bound), 29 (Varshamov lower bound) + tillegg gitt i undervisning og oppgaver ˆ Kapittel 3: Hele, unntatt 38 ˆ Kapittel 4: 41, 42 (unntatt fra Exercise 212 og ut), 43 (unntatt fra s136 og ut), 44 (unntatt fra s143 og ut), 45 (BCH-bound og Hartmann-Tzeng-bound tom s153), 46 (Meggitt-dekoding) ˆ Kapittel 5: 51 (unntatt fra Exercise 286 og ut, ane invariant codes ikke pensum), 52, 54 (bare Peterson-Gorenstein-Zierler-dekoding), 55, 56 2 Oppslagsverk Merk: Enkelte begreper er forklart i Oppslagsverk for TMA4150 Algebra og tallteori istedenfor i dette dokumentet BCH-kode, la δ være et heltall slik at 2 δ n En BCH-kode over F q med lengde n er en kode med denerende mengde T = C b C b+1 C b+δ 2 der C i er den q-syklotomiske restklassen modulo n som inneholder i En BCH-kode er streng (engelsk: denisjonen narrow-sense) BCH-kode hvis b = 1 i Hvis n = q t 1, så sier vi at koden er en primitiv BCH-kode 1

2 Bose-distance, la C være en BCH-kode Største δ til C kalles for Bosedistansen til C Denerende mengde, la C være en syklisk kode i R n = F q [x]/(x n 1) med generatorpolynom g(x) Ved teorem 411 (i) og teorem 421 (vii), g(x) = s M α s(x) = s i C i (x α i ), der s løper gjennom en delmengde av de representative for de q-syklotomiske restklassene modulo n La T = s C s være unionen av disse q-syklotomiske restklassene Mengden T kalles den denerende mengden til C Se eksempel 441 i boken s142 Merk Gitt C og det unike generatorpolynomet g(x) og en primitiv n-terot av 1, så er T gitt unikt Merk T = deg(g(x)), så dimensjonen til C er n T Distanse, distansen til en lineær kode C er min(d(x, y)) = min(wt(z) z 0) Divisjonsalgoritmen (polynom), la f(x), g(x) F q [x], g(x) 0 1 h(x), r(x) F q [x] slik at f(x) = g(x)h(x) + r(x) med deg(r(x)) < deg(g(x)) eller r(x) = 0 2 Hvis f(x) = g(x)h(x) + r(x), så er gcd(f(x), g(x)) = gcd(g(x), r(x)) Endelig kropp, en endelig kropp F q er en kropp med et endelig antall elementer q = p m, og hvert element i F q tilsvarer restklassene til F p [x]/ f(x), der f(x) har grad m og er irredusibelt over F p Vi kan skrive elementene som vektorer i F m p, sammenhengen er slik: g m 1 x m g 1 x + g 0 + f(x) g m 1 g 1 g 0 Eksempel Polynomet f(x) = x 3 + x + 1 er irredusibelt over F 2 F 8 = F 2 [x]/ f(x) har følgende elementer: Restklasse Vektor 0 + f(x) f(x) 001 x + f(x) 010 x f(x) 011 x 2 + f(x) 100 x f(x) 101 x 2 + x + f(x) 110 x 2 + x f(x) 111 Etterfølgende elementer, la T være en denerende mengde for en syklisk kode C med lengde n Vi sier at T inneholder s etterfølgende elementer hvis det nnes en mengde S = {b, b + 1,, b + s 1} slik at {b, b + 1,, b + s 1}(mod n) T 2

3 Eksempel 1 T = {0, 2, 6, 7, 8, 11}, S = {6, 7, 8}, s = 3(mod 15) Eksempel 2 T = {0, 3, 8, 9, 11, 12, 13, 14}, S = {11, 12, 13, 14, 0}, s = 5(mod 15) Galoisgruppe, en automor på F q er en isomor σ : F q F q La Gal(F q ) være mengden av alle automorer på F q Denne mengden er en syklisk gruppe og kalles Galoisgruppen til F q Generator (syklisk kode, la v F La S = {v, π(v), π2 (v),, π n 1 (v)} La C være koden utspent av vektorene i S Vi sier at C er koden generert av S (generert av v) Vi skriver S, og v er en generator for C C er åpenbart lineær og er den minste sykliske koden som inneholder v Generatorpolynom, la g(x) være det moniske polynomet med minst mulig grad i en syklisk kode C i F q /(x n 1) Da er g(x) generatorpolynomet til C g(x) er unikt Merk at det kan nnes andre polynomer (ikke-moniske, eller høyere grad) som genererer C Hartmann-Tzeng-bound, se teorem 456 Eksempel La C være en binær syklisk kode med lengde 17 og denerende mengde T = {1, 2, 4, 8, 9, 13, 15, 16} δ 1 = 2 d 3 La A = {1, 2} og B{jb(mod 17)} med b = 7 og s = 2 gcd(7, 17) = 1 B = {0 7, 1 7, 2 7} = {0, 7, 14} A + B = {1 + 0, 1 + 7, , 2 + 0, 2 + 7, } = {1, 8, 15, 2, 9, 16} T, så d = 5 Idempotent, la R være en ring, og e C Vi sier at e er en idempotent hvis e 2 = e Den genererende idempotenten e(x) (se teorem 432) kan man nne ut fra g(x) ved hjelp av Euklids algoritme: 1 = a(x)g(x)+b(x)h(x) der h(x) = xn 1 g(x) og sette e(x) = a(x)g(x)(mod x n 1) Idempotent generator, la C være en syklisk kode i R n = F q /(x n 1), og la e(x) være en idempotent i C e(x) er en idempotent generator hvis C = e(x) Merk at idempotent er brukt som adjektiv i frasen idempotent generator, så dette er ikke en orddelingsfeil Eksempel Se eksempel 434 og eksempel 435 i boken Irredusibel (polynom), f(x) F q [x] er irredusibelt hvis det ikke kan skrives som et produkt av to polynomer av grad 1 Karakteristikk (kropp), det minste positive heltallet n slik at n a = 0, a F kalles karakteristikken til kroppen F Skrives kar (F) = n eller char (F) = n Eksempel 1 kar (Z 2 ) = 2, kar (Z 3 ) = 3, kar (Z p ) = p (p primtall) Eksempel 2 kar (F 4 ): = 0, w + w = 0, w + w = 0 kar (F 4 ) = 2 3

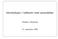
4 Kropp, en kropp F er en mengde med binære operatorer + og (addisjon og multiplikasjon) slik at: 1 F med operator + (addisjon) er en abelsk gruppe med identitet 0 2 Multiplikasjon er assosiativ: 3 a, b, c F ˆ a(b + c) = ab + ac ˆ (a + b)c = ac + bc 4 F = F \ {0} er en abelsk gruppe under multiplikasjon med identitetselement 1 Kroppsutvidelse, hvis F er en underkropp av E, så sier vi at E er en kroppsutvidelse (extension eld) av F Eksempel F 2 24 har underkroppene F 2, F 2 2, F 2 3, F 2 4, F 2 6, F 2 8 og F 2 12 Se gur 1 Figure 1: Hassediagram for underkropper til F 2 24 Maksimalt ideal, La R være en kommutativ ring med identitetselement 1 M er et maksimalt ideal hvis og bare hvis R/M er en kropp Et ideal p(x) F q [x] er maksimalt hvis og bare hvis p(x) er irredusibelt over F q Dette medfører at F p [x]/ p(x) (p primtall) er en kropp hvis og bare hvis p(x) er irredusibelt over F p Meggitt-dekoding, la C være en syklisk [n, k, d]-kode over F q med generatorpolynom g(x) La v(x) F q Vi denerer R g(x) (v(x)) til å være resten ved divisjonen v(x) : g(x) La S(v(x)) = R g(x) (x n k v(x)) være syndrompolynomet til v(x) Algoritme (mottar y(x)): 1 Finn alle syndrompolynomer til alle polynomer e(x) med wt(e(x)) t = d 1 2 og deg(e(x)) = n 1 Dette trengs bare å gjøres én gang 4

5 2 Finn S(y(x)) = R g(x) (x n k y(x)) Da har vi S(y(x)) = S(e(x)) der e(x) er feilpolynomet, dvs y(x) = c(x) + e(x), der c(x) C 3 Hvis X(y(x)) = 0 er vi ferdige, og vi kan konkludere med at y(x) ble sendt (e(x) = 0) Hvis X(y(x)) 0 og S(y(x)) er i tabellen vi fant i 1), da vet vi e(x), og vi nner c(x) = y(x) e(x) og konkluderer med at c(x) ble sendt 4 Hvis S(y(x)) ikke er i tabellen i 1), regn ut syndrompolynomet til xy(x), x 2 y(x), helt til vi nner et syndrompolynom i tabellen i 1) Hvis S(x i y(x)) er i tabellen og e (x) er tilsvarende feilpolynom, sett c(x) = y(x) x n i e (x), og konkluder med at c(x) ble sendt Minimalt polynom Hvis E er en kroppsutvidelse av F q, da er E = F q t for en t Alle elementer i E er røtter i x qt x (teorem 332), så hvis α E, så eksisterer det et monisk polynom M α (x) i F q [x] med minst mulig grad slik at α er en rot (M α (α) = 0) Et slikt polynom kalles det minimale polynomet til α over F q Se teorem 371, 372 og 373 for egenskaper Eksempel 1 La F = Q og E = R, og α = 2 M α (x) = x 2 2 Eksempel 2 La F = Q og E = R, og α = M α (x) = x 4 10x = (x 2 3)(x 2 + 3)(x 2 + 3)(x ) Nullpunkt, la C være en syklisk kode med denerende mengde T Røttene av 1, Z = {α i i T } kalles nullpunktene til C Z = {α i i / T } kalles ikkenullpunktene til C Orden, la a være minste positive heltall slik at q a 1(mod n) a er ordenen av n til q, og skrives ord n (q) La t = ord n (q) Da har vi q t 1(mod n), så F q t er den minste kroppen som inneholder en n-terot av 1 (α) Orden (kropp), ordenen til en endelig kropp F n er n, antall elementer i kroppen Peterson-Gorenstein-Zierler-dekoding av RS-koder, La C være en BCH-kode over F q av lengde m, med designert distance δ d δ kan rette minst t = δ 1 2 feil Anta at C er streng, så {1, 2,, δ 1} T α er primitiv n-terot av 1 i F q m, m = ord n (q) Anta at vi mottar y(x) og at det ikke er ere enn t feil, dvs wt(e(x)) = v t der v er antall feil som har skjedd (ukjent) y(x) = c(x) + e(x), der e(x) er feilpolynom og c(x) C Anta at feilene har oppstått i koordinatene k 1, k 2,, k v, dvs e(x) = e k1 X k e kv X kv Målet er å nne k i og e ki for alle i slik at 1 i v Husk teorem 442 (primitiv n-terot av 1) og teorem 331 5

6 For alle i slik at 1 i v, regn ut S i = y(α i ) = e(α i ) = sum v j=1 e k j (α k j ) i Vi denerer E j = e kj (koesienten til x k j i e(x) og X j = α k j (feilposisjon, posisjon k j ) På grunn av teorem 331 (α i = α k i = k), beskriver X j feilposisjonen k j unikt S i = v j=1 E jxj i Får et ikke-lineært ligningssystem: S 1 = E 1 X 1 + E 2 X E v X v S 2 = E 1 X E 2 X E v X 2 v S 2 t = E 1 X1 2t + E 2 X2 2t + + E v Xv 2t La σ(x) = (X 1 x 1)(X 2 x 1) (X v x 1) = 1+ v i=1 σ ix i Merk at røttene til σ(x) er X1 1, X 1 2,, X 1 v σ(x 1 j ) = 1 + σ 1 x 1 j + σ 2 x 2 j + + σ v x v j = 0 for alle j slik at 1 j v Gang med E j X i+v j v j=1 E jxj i+v ( v j=1 E jx i+v E j X i+v j + σ i v j=1 E jx i+v 1 j j = S i+v, v j=1 E jxj i+v 1 = S i+v 1,, v j=1 E jxj i = S i) S i+v + σ 1 S i+v σ v S i = 0 σ 1 S i+v σ v S i = S i+v + σ 1 E j X i+v 1 j S 1 S 2 S 3 S v 1 S v S 2 S 3 S 4 S v S v+1 S v S v+1 S v+2 S 2v 2 S 2v σ v E j Xj i = 0 for alle i + + v j=1 E jx i j σ v σ v 1 σ 1 = S v+1 S v+2 S 2v Så kan vi nne σ(x) Vi vet ikke antall feil, men vi antar at et minste antall feil har skjedd, så vi ønsker en løsning på systemet med minst mulig v La M µ = S 1 S 2 S µ S 2 S 3 S µ+1 S µ S µ+1 S 2µ 1 M µ er singulær (inverterbar, ligningssystemet over har løsning) hvis µ > v, der v er antall feil som har skjedd Algoritme (y(x) mottatt) 6

7 1 Regn ut syndromene S i = y(α i ), 1 i t 2 Regn ut M µ for µ = t, t 1, helt til M µ ikke er singulær Sett v = µ og løs S 1 S 2 S v σ v S v+1 S 2 S 3 S v+1 σ v 1 S v+2 S v S v+1 S 2v 1 σ 1 = S 2v 3 Finn røttene til σ(x) Inverter røttene for å nne X j (X j angir feilposisjon) 4 Løs de v første ligningene i systemet: S 1 = E 1 X 1 + E 2 X E v X v S 2 = E v X E v X E v X 2 v S v = E v X v 1 + E v X v 2 + E v X v v E i gir feil i posisjon gitt ved X Polynom (kropp), La F q være en endelig kropp F q [x] er mengden av alle polynomer av x med koesienter i F q ˆ F q [x] er en kommutativ ring med identitet ˆ F q [x] er et integraldomene (integritetsområde), dvs ab = 0 a = 0 eller b = 0 ˆ Et element (polynom) i F q [x] er generelt på formen a n x n +a n 1 x n a 1 x + a 0 = n i=0 xi, med a i F q ˆ Vi skriver deg(f(x)) for graden til f(x) (høyeste grad til alle leddene) ˆ Vi sier at f(x) er monisk hvis koesienten til leddet med høyest grad er 1 Primitiv n-terot, et element β F q er en n-terot av 1 hvis β n = 1, og er en primitiv n-terot av 1 hvis i tillegg β s 1 for 0 < s < n Et primitivt element γ i F q er derfor et primitivt (q 1)-terot av 1 Primitivt element, hvis γ er en generator for F q (dvs at F q = γ ), da sier vi at γ er et primitivt element i F q Prinsipalring (engelsk: PID, principal ideal domain), R er en ring R er PID hvis R er et integritetsområde og alle idealer er generert av ett element F q [x] er PID F q [x]/(x n 1) er PID 7

8 q-syklotomisk restklasse, la F q t være en kroppsutvidelse av F q La α F q t, og M α (x) F q [x] være minimalt polynom slik at M α (α) = 0 Da har M α (x) distinkte røtter, og alle røttene er i F q t (teorem 373 (ii)) Vi ønsker å nne alle røttene til M α (x) α, α q, α q2,, α qr er alle røtter til M α (x), og dette er alle røttene (deg(m α (x)) = r) Hvis γ er et primitivt element i F q t, da har vi α = γ s for en s Da kan vi denere q-syklotomiske restklasser av s modulo q t 1 C s = {s, sq, sq 2,, sq r 1 }mod q t 1 α, α q,, α qr 1 = γ s, γ sq,, γ sqr 1 er distinkte og er alle røttene til M α (x) = M γ s(x) Eksempel 1 De 2-syklotomiske restklassene modulo 15 er: C 0 = {0} C 1 = {1, 2, 4, 8} C 3 = {3, 6, 12, 9} C 5 = {5, 10} C 7 = {7, 14, 13, 11} Reed-Solomon-kode, En Reed-Solomon-kode (forkortes RS-kode) C over F q er en BCH-kode av lengde n = q 1 Vi har ord n (q) = 1, så alle elementer i F q er røtter i x n 1, dvs x n 1 faktoriseres fullstendig i førstegradspolynomer over F q Rotkropp, F q t kalles rotkroppen (splitting eld) til x n 1 over F q Rotkroppen inneholder alle røttene α 0, α 1,, α n til x n 1 Syklisk kode, en kode C er syklisk hvis c = c 0 c 1 c 2 c n 1 C c n 1 c 0 c 1 c n 2 C En kode C er syklisk hvis c(x) C xc(x)(mod x n 1) Sykliske koder er idealer i R n = F q [x]/(x n 1) og idealer i R n er sykliske koder Antallet sykliske koder i R n er 2 m, der m er antall q-syklotomiske restklasser modulo n Dimensjonene til de sykliske kodene i R n er alle de mulige summene av antal elementer i de q-syklotomiske restklassene modulo n Eksempel 1 Se eksempel 412 i boken der det ble vist at over F 2, x 9 1 = (1 + x)(1 + x + x 2 )(1 + x 3 + x 6 ), så derfor er det 8 binære sykliske koder C i av lengde 9 med generatorpolynom g i (x) gitt i følgende tabell: 8

9 i dim g i (x) 0 0 x 9 1(= 0) 1 1 (x 2 + x + 1)(x 6 + x 3 + 1) 2 2 (x 6 + x 3 + 1)(x + 1) 3 3 x 6 + x (x + 1)(x 2 + x + 1) 5 7 x 2 + x x Eksempel 2 på korollar 425: C 2 C 3 g 3 (x) g ( x), g 3 (x) = x 6 + x 3 + 1, g 2 (x) = (x 6 + x 3 + 1)(x + 1) Eksempel 3 Koding La G være en generatormatrise, la a F k q være ordet vi ønsker å kode Kodeordet blir da c = ag C a(x) og c(x) er polynomene som svarer til a og c Da er c(x) = a(x)g(x) der g(x) er generatorpolynom Syklisk skift, la c = c 0 c 1 c n 1 C der C er en syklisk kode Vektoren som man får ved å skifte koordinatene slik at i i + 1(mod n) c = c n 1 c 0 c 1 c n 2 C kalles et syklisk skift Et syklisk skift kan også skrives c(x) xc(x)(mod x n 1) Et syklisk skift til et ord c C skrives π(c) Syndrompolynom La v(x) C, der C er en syklisk [n, k]-kode over F q og la R g(x) (v(x)) være resten ved divisjonen v(x) : g(x) S(v(x)) = R g(x) (x n k v(x)) kalles syndrompolynomet til v(x) Vandermonde-matrise, La F være en kropp, og la α 1, α 2,, α s være elementer i F α1 0 α2 0 α 0 s α1 1 α2 1 α 1 s V = α1 s α2 s αs s kalles en Vandermonde-matrise Vekt, la A i (C) være antall kodeord i C med vekt i Alle A i (C)(0 i n kalles vektfordelingen til C 9

10 3 Regneeksempler 31 Multiplikasjon av primitive elementer La f(x) = x 3 + x + 1 F 2 [x] og irredusibelt F 2 [x]/ f(x) F 2 3 = F 8 Elementene er gitt i tabell, se stikkord Endelig kropp x 3 + x 2 + x f(x) (x f(x) )(x f(x) ) = (x 2 + 1)(x + 1) + f(x) = mod f(x) = x 2 + f(x) 32 Knytte elementer i endelig kropp mot potens av generator La p(x) = x 3 + x + 1 F 2 [x] α = x + p(x) F 2 [x]/ p(x) er en generator for α = (F 2 [x]/ p(x) ) p(α) = α 3 + α + 1 = 0 Regn ut alle aktuelle α i : α 3 = α + 1 α 4 = (α + 1)α = α 2 + α α 5 = α 3 + α 2 = α α 2 α 6 = α 2 + α + α 3 = α 2 + α + α + 1 = α Relater hver α i til elementer i kroppen: restklasse-element vektor α 0 + p(x) p(x) 001 α 0 α + p(x) 010 α α p(x) 011 α 3 α 2 + p(x) 100 α 2 α p(x) 101 α 6 α 2 + α + p(x) 110 α 4 α 2 + α p(x) 111 α 5 Multiplikasjon kan så gjøres ved å nne tilhørende α for hver faktor, multiplisere disse ( ta mod q 1 av summen av potensene) og oversette tilbake 33 Bruke q-syklotomiske restklasser til å nne alle røttene til M α (x) F 16 = F 2 4 er en kroppsutvidelse av F 2, konstruert med f(x) = x 4 + x + 1 F 2 [x] La α være en rot i f(x), α = x + f(x) Siden α er en rot i f(x), 10

11 så har vi f(α) = α 3 + α + 1 = 0 og α 3 = α + 1(modulo 2) α 4, α 5, nner man ved å multiplisere forrige likhet med α og substituere Se forrige subseksjon for eksempel Vi lager så en tabell som relaterer α i til et element i F 16 / f(x) restklasse-element (+ f(x) ) vektor α identiteter α + 1 = α α = α 8 α 0010 α α = α 14 α α 4 α = α 10 α α 2 α = α 13 α α 8 α = α 9 α 2 + α 0110 α 5 α 11 = α α 2 + α α 10 α α 3 α α 14 α 3 + α 1010 α 8 α 3 + α α 7 α 3 + α α 6 α 3 + α α 13 α 3 + α 2 + α 1110 α 11 α 3 + α 2 + α α 12 Vi nner så disse 2-syklotomiske restklassene modulo 15: C 0 = {0} C 1 = {1, 2, 4, 8} C 3 = {3, 6, 12, 9} C 5 = {5, 10} C 7 = {7, 14, 13, 11} La γ = α, siden α er et primitivt element i dette tilfellet Alle røttene til M α 1(x) er α i, i C 1 (som også er alle røttene til M α 2(x), M α 4(x) og M α 8(x), og deg(m α 1(x)) = 4) M α 3(x) α i, i C 3, deg = 4 M α 5(x) α i, i C 5, deg = 2 M α 7(x) α i, i C 7, deg = 4 Deretter regner vi ut de minimale polynomene, her kommer identitetene i tabellen over til stor hjelp for å substituere α i for i > 3 Her er detaljert 11

12 utregning for M α 1: M γ s(x) = i C s (x γ i ) M α (x) = i C s (x α i ) M α 1(x) = (x α)(x α 2 )(x α 4 )(x α 8 ) = (x 2 + (α 2 + α)x + α 3 )(x 2 + (α 8 + α 4 )x + α 12 ) = (x 2 + α 5 x + α 3 )(x 2 + α 4 αx + α 12 ) = x 4 + α 5 x 3 + α 12 x 2 + α 5 x 3 + α 10 x 2 + α 17 x + α 3 x 2 + α 8 x + α 15 = x 4 + (α 12 + α 10 + α 3 )x 2 + (α 17 + α 8 )x + α 15 = x 4 + (α 10 (α 2 + 1) + α 3 )x 2 + (α 8 (α 9 + 1))x + 1 (α = α 8, α = α 7 ) = x 4 + (α 18 + α 3 )x 2 + α 15 x + 1 (α 15 = 1) = x 4 + α 3 (α )x 2 + x + 1 (α = 0) = x 4 + 0x 2 + x + 1 = x 4 + x + 1 røtter 2-syklotomiske restklasser minimale polynomer 0 x 1 = α 0 {0} x + 1 α, α 2, α 4, α 8 {1, 2, 4, 8} x 4 + x + 1 α 3, α 6, α 12, α 9 {3, 6, 12, 9} x 4 + x 3 + x α 5, α 10 {5, 10} x 2 + x + 1 α 7, α 14, α 13, α 11 {7, 14, 13, 11} x 4 + x Finne idempotent generator Vi vil nne e 2 (x) for en syklisk kode C 2 av lengde 7 over F 2 Den kan nnes ved å løse 1 = a(x)g(x) + b(x)h(x) med Euklids algoritme, der h(x) = (x n 1)/g(x) Deretter, e(x) = a(x)g(x)(mod x n 1) La h 2 (x) = xn 1 g 2 (x) = x3 + x

13 Utfør gcd(g 2 (x), h 2 (x)) = gcd(x 4 + x 3 + x 2 + 1, x 3 + x 2 + 1): x 4 + x 3 + x = (x 3 + x 2 + 1)x + x 2 + x + 1 x 3 + x = (x 2 + x + 1)x + (x + 1) x + 1 = 1(x + 1) + 0 Da får vi: 1 = a(x)g 2 (x) + b(x)h 2 (x) = (x 2 + 1)(x 4 + x 3 + x 2 + 1) + (x 3 )(x 3 + x 2 + 1) a(x)g 2 (x) = (x 2 + 1)(x 4 + x 3 + x 2 + 1) = x 6 + x 5 + x = e 2 (x) 35 Finne generatorpolynom når man har en idempotent generator Vi vil nne g 5 (x) for en syklisk kode C 5 av lengde 7 over F 2, og e 5 (x) = x 6 + x 5 + x 3 er gitt Generatorpolynomet er gitt ved g 5 (x) = gcd(e 5 (x), x 7 1), og vi bruker Euklids algoritme: x = x 7 1 = (x 6 + x 5 + x 3 )(x + 1) + (x 5 + x 4 + x 3 + 1) gcd(e 5 (x), x 7 1 = x 3 + x Denerende mengde La C i være en syklisk kode av lengde 9 over F 2 [x]/(x 9 1), og la α være primitiv 9-rot av 1 Da har vi følgende 2-syklotomiske restklasser: restklasse i innhold Mα(x) i C 0 {0} x + 1 C 1 {1, 2, 4, 8, 7, 5} x 6 + x C 2 {3, 6} x 2 + x + 1 x 9 1 = (x + 1)(x 2 + x + 1)(x 6 + x 3 + 1) 13

14 i dim g i (x) T S δ 1 d = s 0 0 x 9 1 {0, 1, 2, 3, 4, 5, 6, 7, 8} {0, 1, 2, 3, 4, 5, 6, 7, 8} (x 2 + 1)(x 6 + x 3 + 1) {1, 2, 3, 4, 5, 6, 7, 8} {1, 2, 3, 4, 5, 6, 7, 8} (x 6 + x 3 + 1)(x + 1) {0, 1, 2, 4, 8, 7, 5} {7, 8, 0, 1, 2} (x 6 + x 3 + 1) {1, 2, 4, 8, 7, 5} {1, 2}, {4, 5}, {7, 8} (x 2 + x + 1)(x + 1) {0, 3, 6} {0}, {3}, {6} x 2 + x + 1 {3, 6} {3}, {6} x + 1 {0} {0} Teoremer 41 Kapittel 1 Teorem La G = [ I k A ] være en generatormatrise for [n, k]-koden C, på standard form Da er H = [ A T ] I n k en paritetssjekkmatrise for C Teorem La d(x, y) være funksjonen som angir Hammingdistanse mellom to kodeord x, y F n q og er antall koordinater hvor x og y er forskjellig d(x, y) har følgende egenskaper: (i) d(x, y) 0 (ii) d(x, y) = 0 x = y (iii) d(x, y) = d(x, y)- (iv) d(x, z) d(x, y) + d(y, z) Teorem La wt(x) være (Hamming)vekten til x C, dvs antall koordinater i x som er forskjellig fra 0 Da har vi at d(x, y) = wt(x y) Teorem Hvis C er en lineær kode, så er min(d(x, y)) = min(wt(z) z 0) Teorem (i) x, y F n 2 : wt(x + y) = wt(x) + wt(y) 2wt(x y) (ii) x, y F n 2 : wt(x y) = x y(mod 2) (iii) x F n 2 : wt(x) x y(mod 2) (iv) x F n 3 : wt(x) x y(mod 3) (v) x F n 4 : wt(x) x, y = x y(mod 2) Teorem La C være en [n, k, d]-kode over F q Da har vi følgende: (i) A 0 (C) + A 1 (C) + + A n (C) = q k =antall elementer i C 14

15 (ii) A 0 (C) = 1, A 1 (C) = A 2 (C) = = A d 1 (C) = 0 (iii) C kode over F 2 og 11 1 C Da har vi at A i (C) = A n i (C) for 0 i n (iv) C kode over F 2 og selvortogonal Da har alle kodeord lik vekt og C inneholder Kapittel 3 Teorem Z p er en kropp p er primtall Teorem 311 La F q være en endelig kropp med q elementer (i) q = p m for et primtall p (ii) F q inneholder underkroppen F p (iii) F q er et vektorrom over F p med dimensjon m (iv) pα = 0 for alle α F q (v) F q er unik opp til isomor Teorem 331 (i) Gruppen F q = F \ {0} er syklisk med orden q 1 under multiplikasjon under F q (ii) Hvis γ er en generator for denne sykliske gruppen (F q = γ ), da er F q = {0, 1 = γ 0, γ, γ 2,, γ q 2 } og γ i = 1 hvis og bare hvis (q 1) i Bevis Se bok s104 Teorem 332 Elementene i F q er røttene til x q 1 Teorem 333 (i) La γ være et primitivt element i F q Da nnes φ(q 1) primitive elementer Disse er på formen γ i der gcd(i, q 1) = 1 Teorem 341 La F q [x] være et unikt faktoriseringsområde La f(x) F q [x] Da kan vi skrive f(x) = p 1 (x) a1 p n (x) an der p 1 (x) er irredusibel i Polynomene p i (x) er unike opp til skalarmultiplikasjon og a i er unike i Teorem 344 For ethvert primtall p og ethvert positivt heltall m, nnes det en endelig kropp med q = p m, og denne er unik opp til isomor 15

16 Teorem 353 La q = p n (i) F q har en underkropp av orden s = p r hvis og bare hvis r n (ii) Elementene i F s er elementene i F q som er røtter i x s x (iii) For hver r n nnes bare én underkropp F p r av F q Teorem Gal(F q ) (se stikkord Galoisgruppe) er en gruppe (syklisk) Teorem 371 La F q t være en kroppsutvidelse til F q og la α være et element i F q t med minimalt polynom M α (x) i F q [x] Da har vi følgende: (i) M α (x) er irredusibelt over F q (ii) Hvis g(x) er et vilkårlig polynom i F q [x] som tilfredsstiller g(α) = 0, da er M α (x) g(x) (iii) M α (x) er unikt, det nnes bare et monisk polynom i F q [x] med minst grad som har α som rot Teorem 372 La f(x) være et monisk irredusibelt polynom over F q av grad r Da har vi følgende: (i) alle røttene i f(x) ligger i F q r og i enhver kropp som inneholder F q sammen med en rot fra f(x) (ii) f(x) = r r=1 x α i der α i F q r for i i r (iii) f(x) x qr x Bevis Se bok s113 Teorem 373 La F q t være en kroppsutvidelse av F q og la α være et element i F q t med minimalt polynom M α (x) (monisk og irredusibelt) i F q [x] Da har vi følgende: (i) M α (x) x qt x (ii) M α (x) har distinkte røtter som alle ligger i F q t (iii) Graden til M α (x) dividerer t (iv) x qt x = α M α(x), der α løper gjennom en delmengde av F q t som enumererer alle minimalpolynomene til alle elementene i F q t akkurat en gang (v) x qt x = f f(x) der f løper gjennom alle de moniske irredusible polynomene over F q der graden dividerer t Bevis Se bok s Teorem 374 La f(x) være et polynom i F q [x] og la α være rot til f(x) i en eller annen kroppsutvideldse F q t Da har vi følgende: 16

17 (i) f(x q ) = f(x) q (ii) α q er også en rot i f(x) i F q Bevis Se bok s114 Teorem 376 Hvis γ er et primitivt element i F q t, da er det minimale polynomet til γ s over F q : Bevis Se bok s115 M γ (x) = i C s (x γ i ) 43 Kapittel 4 Teorem La C være en syklisk kode over F q, og c, c C (i) π(c + c ) = π(c) + π(c ) (ii) π(ac) = aπ(c), a F q Bevis Se notat nr14 fra forelesning Korollar For å vise at en binær kode er syklisk, er det nok å vise at π(c) C for alle ord c i en basis for C Teorem x n 1 over F q har ingen repeterende faktorer hvis og bare hvis gcd(n, q) = 1 Se exercise 201 s122 Teorem 411 La gcd(n, q) = 1 og t = ord n (q) La α være primitiv n-terot av 1 i F q t Da har vi følgende: (i) M α s = i C s (x α i ), 0 < s < n, der C s er en q-syklotomisk restklasse modulo n (ii) x n 1 = s M α s(x) er en faktorisering av xn 1 i irredusible polynomer over F q (s i produktet er en representativ i hver q-syklotomiske restklasse modulo n) Teorem 421 La C være en syklisk kode (ikke null) i R n Da eksisterer det et polynom g(x) C med følgende egenskaper: (i) g(x) er det unike moniske polynomet med minst mulig grad i C (ii) C = g(x) (iii) g(x) (x n 1) La k = n deg(g(x)), og la g(x) = n k i=0 g ix i, der g n k = 1 Da har vi følgende: 17

18 (iv) dimensjonen til C er k og [g(x), xg(x),, x k 1 g(x)] er en basis for C (v) hvert element i C kan uttrykkes unikt som et produkt g(x)f(x), der f(x) = 0 eller deg(f(x)) < k g 0 g 1 g 2 g n k 0 (vi) G = 0 g 0 g 1 g n k 1 g n k 0 g 0 g n k g(x) xg(x) x k 1 g(x) (vii) Hvis α er en primitiv n-terot av 1 i en kroppsutvidelse av F q, da er g(x) = s M α s(x) det produktet løper over delmengden av representativer for q-syklotomiske restklasser modulo n Bevis Se bok s Korollar 422 La C være en syklisk kode (ikke-null) i F q /(x n 1) Følgende er ekvivalent: (i) g(x) er det moniske polynomet i C med minst grad (ii) C = g(x), g(x) monisk, og g(x) x n 1 Bevis Se bok s126 Korollar 423 Antallet sykliske koder i R n er 2 m, der m er antall q- syklotomiske restklasser modulo n Dimensjonene til de sykliske kodene i R n er alle de mulige summene av antal elementer i de q-syklotomiske restklassene modulo n Korollar 425 La C 1 og C 2 være sykliske koder over F q med generatorpolynomer g 1 (x) og g 2 (x) Da er C 1 C 2 hvis og bare hvis g 2 (x) g 1 (x) Teorem 426 Den duale koden til en syklisk kode er syklisk Teorem 427 La C være en syklisk [n, k]-kode med generatorpolynom g(x) La h(x) = (x n 1)/g(x) = k i=0 h ix i Da er generatorpolynomet til C g (x) = x k h(x 1 )/h(0) Videre, en generatormatrise for C og paritetss- 18

19 jekkmatrise for C er: h k h k 1 h k 2 h h k h k 1 h 1 h h k h 0 Teorem 432 La C være en syklisk kode i R n = F q [x]/x n 1) Da har vi følgende: (i) Det eksisterer en unik idempotent e(x) C slik at e(x) genererer C, dvs C = e(x) (ii) Hvis e(x) er en idempotent i C som ikke er 0, da er C = e(x) hvis og bare hvis e(x) er en enhet i C Bevis Se bok s Teorem 433 La C være en syklisk kode over F q med genererende idempotent e(x) Generatorpolynomet til C er da g(x) = gcd(e(x), x n 1) over F q [x] Bevis Se bok s133 Teorem 436 La C være en syklisk [n, k]-kode med idempotent generator n 1 e(x) = e i x i Da er k n-matrisen e 0 e 1 e 2 e n 2 e n 1 e n 1 e 0 e 1 e n 3 e n 2 e n k+1 e n k+2 e n k+3 e n k 1 e n k i=0 en generatormatrise for C Bevis Se bok s135 Teorem 437 La C i være en syklisk kode av lengde n over F q med generatorpolynom g i (x) og idempotent generator e i (x) for i = 1 og 2 Da har vi følgende: (i) C 1 C 2 er en syklisk kode og har generatorpolynom lcm(g 1 (x), g 2 (x)) og idempotent generator e 1 (x)e 2 (x) 19

20 (ii) C 1 + C 2 er en syklisk kode og har generatorpolynom gcd(g 1 (x), g 2 (x)) og idempotent generator e 1 (x) + e 2 (x) e 1 (x)e 2 (x) Merk C 1 + C 2 = {c 1 + c 2 c 1 C 1 og c 2 C 2 } Bevis Se bok s135 Teorem 442 La α være en primitiv n-terot av 1 i en kroppsutvidelse til F q La C være en syklisk kode med lengde n over F q med denerende mengde T og generatorpolynom g(x) Da har vi følgende: (i) T er en union av q-syklotomiske restklasser modulo n (ii) g(x) = i T x αi (iii) c(x) R n er i C hvis og bare hvis c(α i ) = 0 for alle i T (iv) Dimensjonen til C er n T Lemma 451 La V være en Vandermonde-matrise av størrelse s s Da er det V = 1 i<js α j α i Med andre ord, V er ikke-singulær (det V 0) hvis elementene α 1, α 2,, α s er distinkte Teorem 453 (BCH-bound) La C være en syklisk kode av lengde n over F q med denerende mengde T Anta at C har minste vekt d Hvis T inneholder δ 1 etterfølgende elementer, da har vi d δ Teorem 456 (Hartmann-Tzeng-bound) Først, la A, B være delmengder av heltall modulo n A + B = {a + b(mod n) a A, b B} La C være en syklisk kode av lengde n over F q med denerende mengde T La A være mengden av δ 1 etterfølgende elementer i T og B = {jb(mod n) 0 j s}, der gcd(n, b) < δ Hvis A + B T, da har vi at den minste vekten d i C tilfredsstiller d δ + s Bevis Se bok s151 Teorem 461 La C være en syklisk [n, k, d]-kode over F q med generatorpolynom g(x) Dener følgende: R g(x) (v(x)) er resten ved divisjonen v(x) : g(x) der v(x) F q La S(v(x)) = R g(x) (x n k v(x)) være syndrompolynomet til v(x) Da har vi følgende: (i) R g(x)(v(x)) = 0 hvis og bare hvis v(x)(mod x n 1) C (ii) Hvis c(x) C, da er R g g(x)(c(x) + e(x)) = R g(x) (e(x)) Merk v(x) R n S(v(x)) = 0 r(x) C) Teorem 462 La g(x) være en monisk divisor til x n 1 av grad n k Hvis R g(x) (v(x)) = s(x), da er R g(x) (xv(x)(mod x n 1)) = R g(x) (xs(x)) = xs(x) g(x)s n k 1 20

21 der s n k 1 er koesienten til x n k 1 i s(x) Bevis Se bok s Kapittel 5 Teorem 511 En BCH-kode med designert distanse δ har minste vekt på minst δ Bevis Den denerende mengden inneholder δ 1 etterfølgende elementer, og resultatet følger av BCH-bound (teorem 453) Teorem 514 La n = qr 1 q 1 der gcd(r, q 1) = 1 La C være den strenge BCH-koden med denerende mengde C 1 Da er C Hammingkoden H q,r Bevis Se bok s Korollar 515 Alle binære Hammingkoder er en streng BCH-kode Merk Det nnes Hammingkoder som ikke er en BCH-kode, se eksempel 516 i boken Teorem 517 La C være en [n, k]-bch-kode over F q med designert distanse δ Da har vi følgende: (i) k n ord n (δ 1) (ii) Hvis q = 2 og C er en streng BCH-kode, da kan δ antas å være odde Hvis q = 2w + 1, da er k n ord n (q)w Bevis Se bok s Formodning Alle binære primitive strenge BCH-koder med designert Bosedistanse δ has minste distanse ikke mer enn δ + 4 Teorem 521 La C være en RS-kode over F q med lengde n = q 1 og designert distance δ Da har vi følgende: (i) C har denerende mengde T = {b, b + 1,, b + δ 2} for et heltall b (ii) C har minste distanse δ = d og dimensjon k = n d + 1 (iii) C er MDS (maximum distance separable) Bevis Se notat nr21 fra Teorem 523 La α være et primitivt element i F q og la k være et heltall med 0 k n = q 1 La P k være mengden av alle polynomer med grad mindre enn k i F q [x], k 0 Da har vi at C = {f(1), f(α), f(α 2 ),, f(α q 2 ) f P k } 21

22 er den strenge [n, k, n k + 1]-RS-koden over F q Bevis Se bok s175 22