deeegimnoorrrsstt Sjette forelesning
|
|
|
- Benedicte Skoglund
- 7 år siden
- Visninger:
Transkript
1 deeegimnoorrrsstt Sjette forelesning 1
2 2
3 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 3
4 Bellman-Ford BFS/DFS Binære søketrær Binærsøk De gjenværende algoritmene er litt mer omfattende. (Mange av sorteringsalgoritmene Bubblesorther er ganske enkle, f.eks.) Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort 4 Sterke komponenter I tillegg: Eksempler (DP, LP) NPC-problemer Topologisk sortering
5 Gjensyn med masterteoremet 5
6 Masterteoremet 6
7 T (n) = at (n/b) + f(n) Antall «barn»: Størrelse per «barn»: «Høyde»: a n/b log b n = Θ(lg n) Rota har f(n) arbeid; hver løvnode har en konstant mengde arbeid. Hva vil dominere totalen? Det kommer an på forholdet mellom f(n) og antallet løvnoder. Antall «løvnoder»: a log b n = n log b a Husk uttrykket for antall løvnoder! 7
8 Tilfelle 1: Løvnodene dominerer Da blir kostnaden Θ(n log b a ) Det skjer når f(n) = O(n log b a ɛ ) 8
9 Tilfelle 2: «Dødt løp» Da blir kostnaden Det skjer når Θ(n log b a lg n) f(n) = Θ(n log b a ) Samme kostnad i hvert nivå (dvs. det samme som løvnodene); vi ganger med høyden. 9
10 Det finnes en c < 1 s.a. af(n/b) cf(n), for store nok verdier n Det vil intuitivt si at f-en krymper nedover i treet. 10 f(n) er da regulær
11 Tilfelle 3: Rota dominerer Da blir kostnaden Det skjer når Θ(f(n)) f(n) = Ω(n log b a+ɛ ) 11 Regulariteten innebærer, for en c < 1 og store n: a*f(n/b) c*f(n). Trenger ikke sjekkes hvis f(n) er polynomisk (dvs. n^k). f(n) må være regulær!
12 T (n) = { 1 if n = 1 2T (n/2) + n if n > 1 a = 2 b = 2 log b a = 1 n log b a = n f(n) = n = Θ(n log b a ) Her er det dødt løp, så vi får høyde * antall løvnoder = høyde * radsummen, som vi jo kjenner så godt fra treet vårt T (n) = Θ(n log b a lg n) = Θ(n lg n) 12
13 T (n) = { 1 if n = 1 2T (n/2) + n if n > 1 a = 2 b = 2 log b a = 1 n log b a = n f(n) = n = Θ(n log b a ) Her er det dødt løp, så vi får høyde * antall løvnoder = høyde * radsummen, som vi jo kjenner så godt fra treet vårt T (n) = Θ(n log b a lg n) = Θ(n lg n) 13
14 Variabelskifte 14
15 Flytter oss til «en enklere verden» Skift funksjon og variabel; går «opp i opp» T(n) = S(m) F.eks. m = lg n, S(m) = T(2m ) 15
16 T (n) = 2T ( n) + lg n [m = lg n] T (2 m ) = 2T (2 m/2 ) + m [S(m) = T (2 m )] S(m) = 2S(m/2) + m = O(m lg m) T (n) = O(lg n lg lg n) 16
17 T (n) = 2T ( n) + lg n [m = lg n] T (2 m ) = 2T (2 m/2 ) + m [S(m) = T (2 m )] S(m) = 2S(m/2) + m = O(m lg m) T (n) = O(lg n lg lg n) Legg merke til at alle venstresidene (og høyresidene, for den saks skyld) er like. 17
18 Rebus. Hva er dette? Svar: Kvadratiske sorteringsalgoritmer :-> Som vanlig relativt abstrakte beskrivelser her. Ta en titt på pseudokode i boka for mer detaljert arrayelement-skyfling. sorteri ngsalgo ritmer. Nært Brute Force, men ikke helt. Hva vil brute force (type prøv alle muligheter e.l.) være for sortering? 18
19 Merk: Samme mønster som Bellman-Ford, på sett og vis. Tilsynelatende bare overfladisk, men egentlig et generelt mønster. Bubble Sort Normalt: Sammenlign alle par i rekkefølge fra venstre til høyre. Tenk etter: Vil det fungere om du i hver iterasjon fikser parene i tilfeldig rekkefølge? Beviset blir helt klart ikke det samme, men blir det korrekt likevel? Gjenta n ganger: Sammenlign og evt. fiks alle n 1 par Utfør fra venstre til høyre i hver iterasjon. I hver iterasjon vil da det største usorterte elementet ha falt på plass. n iterasjoner gir da fullstendig sortering. 19
20 Selection Sort Gjenta n ganger: Finn det største usorterte elementet Bytt plass med det siste usorterte Nærmest en direkte implementasjon av korrekthetsbeviset til Bubble Sort!20
21 Insertion Sort Gjenta n ganger Sett inn første usorterte blant sorterte De sorterte havner i starten. Man leter etter riktig plass. Merk at man ofte lar elementet synke ned til riktig plass, så man setter det inn mens man leter. Det kan evt. gjøres ved å bare duplisere neste element hele veien, og så sette inn elementet direkte når man har funnet rett plass. 21 Oppgave : Tenk ut din egen sorteringsalgoritme med kvadratisk kjøretid. Om du ikke klarer det, prøv en med kjøretid på O(2^n) eller O(n!) :)
22 Stå på eksamen uten å lese! 22
23 23
24 And I was really impressed with how they managed to shock the Goatse guy. 24
25 Men hvor effektivt kan det bli? Ω(n lg n) 25
26 Se kap. 8 Hver sammenligning halverer antall muligheter. Vi starter med n! mulige rekkefølger. Beste «worst-case» blir lg(n!) :"+76#'391.23("391/2.,/ 91.23!391/2! /234&5673$%36##689 /,) 91.23!391/2.,)! - 91/23-391)2! - ".0/0)#.,) "/0.0)# /,)! - Nyttig: 91.23!391/23!391)2! Stirlings - approksimasjon: / )2 ".0)0/# ")0.0/# "/0)0.# ")0/0.# n! > (n/e)^n Dermed: h lg(n!) lg(n/e)^n = n lg(n/e) = n lg n - n lg e = Omega(n lg n) 26
27 Med andre ord lg n! = Ω(n lg n) 27
28 Heapsort 28
29 < D C > E = B <? <= <> A B C D > < 29
30 < D C > E = B <? <= <> A B C D > < p(i) = i/2 l(i) = 2i r(i) = 2i + 1 < D C > E = B <? <= <> A B C D > < 30
31 Heapify 31
32
33
34
35 På tavla: Kjøretid Korrekthet (invariant) Build-Heap(A, n): for i floor(n/2) downto 1 Heapify(A, i, n) 35
36 Korrekthet vises enkelt induktivt. Eksempel på tavla. Heapsort(A, n): Build-Max-Heap(A, n) for i n downto 2 exchange A[1] and A[i] Max-Heapify(A, 1, i 1) 36
37 Operasjonene forklart på tavla. Viktig: Hvordan elementer kan «flyte» oppover eller «synke» nedover til riktig plass. Insert(S, x) Maximum(S) Extract-Max(S) Increase-Key(S, x, k) 37
38 Sortering «Selection sort» med en heap In-place, enkel O(n lg n) Heapsort 38
39 M g O e rg t r o es Dårlig worst-case, men bra average-case. Lave konstantledd. Mergesort virker på en måte «omvendt». QS er in-place; MS er det ikke. MS har bedre worst-case. Quicksort 39
40 Grunn-idé Korrekthet vises induktivt. Kjøretiden gis av vårt velkjente binærtre. Del sekvensen i to Sorter hver halvdel rekursivt Kombinér etterpå (Mergesort) eller rydd litt først (Quicksort) Tegning/forklaring på tavla. 40
41 &! " # $ % & ' (. 7 &! " # $ % & ' (.62 7 & "! # $ % & ' (.62 7 & "! # $ % & ' (. 2 7 & " $ #! % & ' (. 2 7 & " $ %! # & ' (. 2 7 & " $ % & #! ' (. 2 & " $ % & #! ' (. 2 & " $ % & (! ' # Invariant: 41 8)&*+, -./01 8)7,22,&3"*+, 401,561, : 8)2;",22,73"*+, <40=4,10,>6,?,-./01 8).,22,2*+, <40=4,10,>6,!,-./01
42 &! " # $ % & ' (. 7 &! " # $ % & ' (.62 7 & "! # $ % & ' (.62 7 & "! # $ % & ' (. 2 7 & " $ #! % & ' (. 2 7 & " $ %! # & ' (. 2 7 & " $ % & #! ' (. 2 & " $ % & #! ' (. 2 & " $ % & (! ' # Invariant: 42 8)&*+, -./01 8)7,22,&3"*+, 401,561, : 8)2;",22,73"*+, <40=4,10,>6,?,-./01 8).,22,2*+, <40=4,10,>6,!,-./01
43 Merge Enkelt eksempel på tavla. Du har to sorterte (del-)sekvenser Plukk ett av sekvens-«hodene» Velg hele tiden det minste Legg det inn på neste ledige plass i resultatet 43
44 Kjøretid Worst-case for MS og Best-case for QS T(n) = 2T(n/2) + n Selv 9-til-1-split gir Θ(n log n) for QS Average-case blir også Θ(n log n) Skjev split for QS gir kvadratisk WC Randomisering: Unngår data-avhengig WC 44
45 Average-case Intuisjon: Selv om annenhvert nivå er helt skjevt vil det bare øke kjøretiden med en konstant. 6!B6C 6!B6C? 45
46 Sortering Store/små for seg Rekursivt Kjapp O(n 2 ) WC O(n lg n) Avg. Quicksort 46
47 Sortering Splitt og hersk og flett Stabil Ikke in-place O(n lg n) Mergesort 47
48 48
49 49
50 50
51 51
52 52
53 53
54 54
55 Vi slår den nedre grensen ved å «spille et annet spill» Lineær sortering 55
56 Lineær sortering Counting sort 56
57 Inn: A[1 n], der A[i] {0, 1,, k} Ut: B[1 n], sortert Ekstralager: C[0 k] Vi bruker C til å telle forekomster 57
58 Tell hvor mange vi har av hver Gjør telle-tabellen (C) kumulativ Tallet angir nå posisjonen til den siste forekomsten Gå igjennom A (baklengs) og bruk C til å finne posisjon Oppdater C etter hvert (dekrementer posisjonen) 58
59 for i = 0 to k C[i] = 0 for j = 1 to n C[A[j]] = C[A[j]] + 1 for i = 1 to k C[i] = C[i] + C[i 1] for j = n downto 1 B[C[A[j]]] = A[j] C[A[j]] = C[A[j]] 1 Her gjelder det å gå systematisk til verks Her har vi «downto» for å holde sorteringen stabil. Ser du hvorfor det må være sånn? Bonusspørsmål: Klarer du å lage en versjon som *ikke* bruker downto, men som er stabil likevel? 59
60 Kø-sortering En måte å se «koblingen» på er at vi i tellesortering først holder rede på hvor lange køene er, og deretter på En lignende sak hvor køene slutter. En forskjell er at vi henter verdier fra hver kø i tilfeldig rekkefølge. Opprett en FIFO-kø for hver mulig verdi For hvert input-element: Legg bakerst i riktig kø Slå sammen køer Fyll output med verdier fra køen Denne algoritmen er også en svært nær slektning (en slags heltallsvariant) av bøttesortering (forklares litt senere). 60 Dette kan enten ses som en konseptuell forklaring av (nesten) hva som skjer i tellesortering (det kan kreve litt tenking å se «ekvivalensen») eller som en egen, enkel, lineær-tids sorteringsalgoritme.
61 Sorter heltall Eller lignende Verdier O(n) Tell forekomster Regn ut indeks Lineær Strenge krav O(n) Tellesortering 61
62 Lineær sortering Radix sort 62
63 Sorter hvert siffer for seg Bruk en stabil sortering (f.eks. CS) for å bevare arbeidet så langt Vi må begynne med minst signifikante siffer Konstant antall siffer: Lineær kjøretid 63
64 A09>3H <:P T;< P+R R<; ];. T<; ]+T PV+ PV+ ];. T;< ]+T R<; T<; <:P P+R ]+T P+R <:P R<; T<; ];. T;< PV+ <:P T<; T;< P+R PV+ ]+T ];. R<; 64
65 A09>3H <:P T;< P+R R<; ];. T<; ]+T PV+ PV+ ];. T;< ]+T R<; T<; <:P P+R ]+T P+R <:P R<; T<; ];. T;< PV+ <:P T<; T;< P+R PV+ ]+T ];. R<; 65
66 Hva om tallene har ulikt antall siffer? Hva om det er veldig stor forskjell? Kan vi få til O(m), der m er det totale antall siffer brukt? (Det ville kunne brukes på vilkårlige strenger også.) Bryter vi i så fall den nedre grensen vår? Korrekthet kan vises ved induksjon på antall pass Kjøretid Θ(n + k) (evt. Θ((n + k)d) Hvordan bryter radix sort reglene for sammenligningssortering? Vi kan få informasjon ut over bare å sammenligne to nøkler. Vi bruker nøkler som tabellindekser! 66 Det kan vi gjøre fordi vi kjenner verdiområdet.
67 Sorter heltall Eller lignende Verdier O(n k ) Sorter siffer Stabilt Lineær Ganske strenge krav O(kn) Radikssortering 67 Evt. gruntallssortering :-)
68 Lineær sortering Bucket sort 68
69 Anta uniformt fordelte verdier i [0,1) Del [0,1) i n like store bøtter Fordél verdiene i bøttene Gå igjennom bøttene i rekkefølge Skriv ut verdiene sortert 69
70 Bøttene sorteres (med en enkel algoritme) Hver bøtte har O(1) forventet størrelse Totalt O(n) kjøretid 70
71 Sortering Uniformt [0,1) Ordnet hashing Lineær Krav O(n) Bøttesortering 71
72 Select 72
73 Seleksjon: Finn i-ende ordens statistic Eksempler: minimum, maksimum, median min/maks: enkle spesialtilfeller Vi ønsker ikke å sortere 73
74 I stedet for å sortere begge halvdeler fortsetter vi bare i den som inneholder posisjon i, som er den vi leter etter. Randomized-Select Eksempel på tavla..5 Quicksort Verste tilfelle blir som for Quicksort. Beste tilfelle blir Theta(n). Forventet kjøretid, forenklet: T(n) = T(n/2) + n 74 Regnes på tavla.
75 Select Hårete og søt 75
76 Del i grupper på 5, og finn medianen i hver Finn «medianen til medianene», rekursivt Bruk denne som pivot i Partition Select rekursivt på «halvparten» Median-av-5: Konstant tid (insertion sort, f.eks.) for hver; O(n) totalt. Median-av-medianer: T(n/5). Merk: Etter utført algoritme vil dataene allerede være partisjonerte rundt elementet vi leter etter. Så ved å kjøre select etter element k så finner vi automatisk de k minste elementene i tabellen. 76 Partition: O(n). Rekursivt kall T(7n/10 + 6), hvis T(n) er monotont stigende. Mao: Vi får en «prosent-deling» i rekursjonen.
77 Finn median Og lignende Halv Quicksort Kjapp O(n 2 ) WC O(n) Avg. Randomized Select 77
78 Finn median Og lignende Pivot = m. av m. finnes rekursivt Kjapp O(n) Select 78
79 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 79
80 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 80
deeegimnoorrrsstt Sjette forelesning
 deeegimnoorrrsstt Sjette forelesning 1 2 Rebus. Hva er dette? Svar: Kvadratiske sorteringsalgoritmer :-> Som vanlig relativt abstrakte beskrivelser her. Ta en titt på pseudokode i boka for mer detaljert
deeegimnoorrrsstt Sjette forelesning 1 2 Rebus. Hva er dette? Svar: Kvadratiske sorteringsalgoritmer :-> Som vanlig relativt abstrakte beskrivelser her. Ta en titt på pseudokode i boka for mer detaljert
n/b log b n = (lg n) a log b n = n log b a
 Masterteoremet 1 T (n) = at (n/b) + f(n) Antall «barn»: Størrelse per «barn»: «Høyde»: a n/b log b n = (lg n) Rota har f(n) arbeid; hver løvnode har en konstant mengde arbeid. Hva vil dominere totalen?
Masterteoremet 1 T (n) = at (n/b) + f(n) Antall «barn»: Størrelse per «barn»: «Høyde»: a n/b log b n = (lg n) Rota har f(n) arbeid; hver løvnode har en konstant mengde arbeid. Hva vil dominere totalen?
O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0
![O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0 O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0](/thumbs/64/51255941.jpg) O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i bwfs(u, i) for each neighbor u of v if λ[u] = 0 bwfs(u, i+1) Bacwards-first search; traverserer en graf med kvadratisk worst-casekjøretid.
O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i bwfs(u, i) for each neighbor u of v if λ[u] = 0 bwfs(u, i+1) Bacwards-first search; traverserer en graf med kvadratisk worst-casekjøretid.
Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15
 http://www.idi.ntnu.no/~algdat algdat@idi.ntnu.no Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15 b c g a f d e h The pitch drop experiment. Foreløpig kjørt fra 1927 til nå. Åtte dråper har
http://www.idi.ntnu.no/~algdat algdat@idi.ntnu.no Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15 b c g a f d e h The pitch drop experiment. Foreløpig kjørt fra 1927 til nå. Åtte dråper har
Spenntrær, oppsummert: Kruskal: Traverserer ikke. Plukker kanter i hytt og vær Prim: Legger alltid til den noden som er nærmest treet
 Spenntrær, oppsummert: Kruskal: Traverserer ikke. Plukker kanter i hytt og vær Prim: Legger alltid til den noden som er nærmest treet 1 A B D C Prim: Kruskal: AB, BD, DC DC, AB, BD 2 0 + 1 + + n 1; antall
Spenntrær, oppsummert: Kruskal: Traverserer ikke. Plukker kanter i hytt og vær Prim: Legger alltid til den noden som er nærmest treet 1 A B D C Prim: Kruskal: AB, BD, DC DC, AB, BD 2 0 + 1 + + n 1; antall
Øvingsforelesning 6. Sorteringsalgoritmer. Kristian Veøy
 Øvingsforelesning 6 Sorteringsalgoritmer Kristian Veøy veoy@stud.ntnu.no 26.09.08 1 Spørsmål fra øvingsgruppene Må jeg kunne python på eksamen? (Nei) Er det lurt å gjøre alle programmeringsøvingene? (Ikke
Øvingsforelesning 6 Sorteringsalgoritmer Kristian Veøy veoy@stud.ntnu.no 26.09.08 1 Spørsmål fra øvingsgruppene Må jeg kunne python på eksamen? (Nei) Er det lurt å gjøre alle programmeringsøvingene? (Ikke
Øvingsforelesning 6. Sorteringsalgoritmer. Martin Kirkholt Melhus Basert på foiler av Kristian Veøy 30/09/14 1
 Øvingsforelesning 6 Sorteringsalgoritmer Martin Kirkholt Melhus martme@stud.ntnu.no Basert på foiler av Kristian Veøy 30/09/14 1 Agenda l Spørsmål fra øving 4 l Sortering l Presentasjon av øving 6 30/09/14
Øvingsforelesning 6 Sorteringsalgoritmer Martin Kirkholt Melhus martme@stud.ntnu.no Basert på foiler av Kristian Veøy 30/09/14 1 Agenda l Spørsmål fra øving 4 l Sortering l Presentasjon av øving 6 30/09/14
for bare trær Andre forelesning
 Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Lineær sortering. Radix sort
 Fra forrige gang 1 Lineær sortering Radix sort 2 Sorter hvert siffer for seg Bruk en stabil sortering (f.eks. CS) for å bevare arbeidet så langt Vi må begynne med minst signifikante siffer Konstant antall
Fra forrige gang 1 Lineær sortering Radix sort 2 Sorter hvert siffer for seg Bruk en stabil sortering (f.eks. CS) for å bevare arbeidet så langt Vi må begynne med minst signifikante siffer Konstant antall
Dijkstras algoritme. Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert.
 Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Heapsort. Lars Vidar Magnusson Kapittel 6 Heaps Heapsort Prioritetskøer
 Heapsort Lars Vidar Magnusson 24.1.2014 Kapittel 6 Heaps Heapsort Prioritetskøer Sorterings Problemet Sorterings problemet er et av de mest fundementalske problemene innen informatikken. Vi sorterer typisk
Heapsort Lars Vidar Magnusson 24.1.2014 Kapittel 6 Heaps Heapsort Prioritetskøer Sorterings Problemet Sorterings problemet er et av de mest fundementalske problemene innen informatikken. Vi sorterer typisk
Ninety-nine bottles. Femte forelesning. I dagens forelesning: Mest matematiske verktøy. Først: Asymptotisk notasjon. Så: Rekurrensligninger.
 I dagens forelesning: Mest matematiske verktøy. Først: Asymptotisk notasjon. Så: Rekurrensligninger. Hva slags kjøretid har denne sangen? Hvordan kan du formulere det som en rekurrensligning? Ninety-nine
I dagens forelesning: Mest matematiske verktøy. Først: Asymptotisk notasjon. Så: Rekurrensligninger. Hva slags kjøretid har denne sangen? Hvordan kan du formulere det som en rekurrensligning? Ninety-nine
Øvingsforelesning 3: Splitt og hersk. Daniel Solberg
 Øvingsforelesning 3: Splitt og hersk Daniel Solberg Plan for dagen Vi går raskt gjennom øving 2 Splitt og hersk Algoritmer: Mergesort Quicksort Binærsøk Rekurrenser, masse rekurrenser 2 Splitt og hersk
Øvingsforelesning 3: Splitt og hersk Daniel Solberg Plan for dagen Vi går raskt gjennom øving 2 Splitt og hersk Algoritmer: Mergesort Quicksort Binærsøk Rekurrenser, masse rekurrenser 2 Splitt og hersk
INF2220: Time 12 - Sortering
 INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
Go with the. Niende forelesning. Mye matematikk i boka her ikke så komplisert, men mye å holde styr på.
 Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Innhold. Innledning 1
 Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Først litt praktisk info. Sorteringsmetoder. Nordisk mesterskap i programmering (NCPC) Agenda
 Først litt praktisk info Sorteringsmetoder Gruppeøvinger har startet http://selje.idi.ntnu.no:1234/tdt4120/gru ppeoving.php De som ikke har fått gruppe må velge en av de 4 gruppende og sende mail til algdat@idi.ntnu.no
Først litt praktisk info Sorteringsmetoder Gruppeøvinger har startet http://selje.idi.ntnu.no:1234/tdt4120/gru ppeoving.php De som ikke har fått gruppe må velge en av de 4 gruppende og sende mail til algdat@idi.ntnu.no
Ekstra ark kan legges ved om nødvendig, men det er meningen at svarene skal få plass i rutene på oppgavearkene. Lange svar teller ikke positivt.
 Side 1 av 5 Noen viktige punkter: (i) (ii) (iii) (iv) Les hele eksamenssettet nøye før du begynner! Faglærer går normalt én runde gjennom lokalet. Ha evt. spørsmål klare! Skriv svarene dine i svarrutene
Side 1 av 5 Noen viktige punkter: (i) (ii) (iii) (iv) Les hele eksamenssettet nøye før du begynner! Faglærer går normalt én runde gjennom lokalet. Ha evt. spørsmål klare! Skriv svarene dine i svarrutene
Quicksort. Lars Vidar Magnusson Kapittel 7 Quicksort Randomisert Quicksort Analyse av Quicksort
 Quicksort Lars Vidar Magnusson 29.1.2014 Kapittel 7 Quicksort Randomisert Quicksort Analyse av Quicksort Om Quicksort Quicksort er en svært populær sorteringsalgoritme. Algoritmen har i verstefall en kjøretid
Quicksort Lars Vidar Magnusson 29.1.2014 Kapittel 7 Quicksort Randomisert Quicksort Analyse av Quicksort Om Quicksort Quicksort er en svært populær sorteringsalgoritme. Algoritmen har i verstefall en kjøretid
Algdat Eksamensforelesning. Nils Barlaug
 Algdat Eksamensforelesning Nils Barlaug Eksamen Pensum Eksamen Pensum Oppgaver du har gjort og ting du har lest Eksamen Pensum Oppgave på eksamen Oppgaver du har gjort og ting du har lest Eksamen Pensum
Algdat Eksamensforelesning Nils Barlaug Eksamen Pensum Eksamen Pensum Oppgaver du har gjort og ting du har lest Eksamen Pensum Oppgave på eksamen Oppgaver du har gjort og ting du har lest Eksamen Pensum
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Sortering i Lineær Tid
 Sortering i Lineær Tid Lars Vidar Magnusson 5.2.2014 Kapittel 8 Counting Sort Radix Sort Bucket Sort Sammenligningsbasert Sortering Sorteringsalgoritmene vi har sett på så langt har alle vært sammenligningsbaserte
Sortering i Lineær Tid Lars Vidar Magnusson 5.2.2014 Kapittel 8 Counting Sort Radix Sort Bucket Sort Sammenligningsbasert Sortering Sorteringsalgoritmene vi har sett på så langt har alle vært sammenligningsbaserte
Live life and be merry
 Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk
Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk
Eksamen i tdt4120 Algoritmer og datastrukturer
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Algdat-ninja på 60 minutter: Et galskapsprosjekt. Magnus Lie Hetland
 Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
Algdat Oppsummering, eksamen-ting. Jim Frode Hoff
 Algdat Oppsummering, eksamen-ting Jim Frode Hoff November 18, 2012 1 Definisjoner 1.1 Ordliste Problem Probleminstans Iterasjon Asymtpoisk notasjon O(x) kjøretid Ω(x) kjøretid Θ(x) kjøretid T (x) kjøretid
Algdat Oppsummering, eksamen-ting Jim Frode Hoff November 18, 2012 1 Definisjoner 1.1 Ordliste Problem Probleminstans Iterasjon Asymtpoisk notasjon O(x) kjøretid Ω(x) kjøretid Θ(x) kjøretid T (x) kjøretid
INF2220: Forelesning 2
 INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Rundt og rundt og. Trettende forelesning
 Nettverksalgoritmer. Anvendelser og generaliseringer. Sirkulasjonsproblemet/ lineær programmering. (Kap. 29.1-29.2) Rundt og rundt og Trettende forelesning 1 Merk: Ikke sikkert alt dette blir gjennomgått
Nettverksalgoritmer. Anvendelser og generaliseringer. Sirkulasjonsproblemet/ lineær programmering. (Kap. 29.1-29.2) Rundt og rundt og Trettende forelesning 1 Merk: Ikke sikkert alt dette blir gjennomgått
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap LØSNINGSFORSLAG,
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap LØSNINGSFORSLAG,
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
All good things. Fjortende forelesning
 All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
Divide-and-Conquer II
 Divide-and-Conquer II Lars Vidar Magnusson 1712014 Kapittel 4 Analyse av divide-and-conquer algoritmer ved hjelp av rekursjonstrær Analyse av divide-and-conquer algoritmer ved hjelp av masterteoremet Løse
Divide-and-Conquer II Lars Vidar Magnusson 1712014 Kapittel 4 Analyse av divide-and-conquer algoritmer ved hjelp av rekursjonstrær Analyse av divide-and-conquer algoritmer ved hjelp av masterteoremet Løse
LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER (IT1105)
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
Hvor raskt klarer vi å sortere?
 Sortering Sorteringsproblemet Gitt en array med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene slik at de står i stigende (evt. avtagende) rekkefølge
Sortering Sorteringsproblemet Gitt en array med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene slik at de står i stigende (evt. avtagende) rekkefølge
TDT4105 Informasjonsteknologi, grunnkurs
 1 TDT4105 Informasjonsteknologi, grunnkurs Matlab: Sortering og søking Anders Christensen (anders@idi.ntnu.no) Rune Sætre (satre@idi.ntnu.no) TDT4105 IT Grunnkurs 2 Pensum Matlab-boka: 12.3 og 12.5 Stoffet
1 TDT4105 Informasjonsteknologi, grunnkurs Matlab: Sortering og søking Anders Christensen (anders@idi.ntnu.no) Rune Sætre (satre@idi.ntnu.no) TDT4105 IT Grunnkurs 2 Pensum Matlab-boka: 12.3 og 12.5 Stoffet
Heap* En heap er et komplett binært tre: En heap er også et monotont binært tre:
 Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Heap Heap* En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger til venstre En heap er også et
Sorteringsproblemet. Gitt en array A med n elementer som kan sammenlignes med hverandre:
 Sortering Sorteringsproblemet Gitt en array A med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene i A slik at de står i stigende (evt. avtagende) rekkefølge
Sortering Sorteringsproblemet Gitt en array A med n elementer som kan sammenlignes med hverandre: Finn en ordning (eller permutasjon) av elementene i A slik at de står i stigende (evt. avtagende) rekkefølge
Avsluttende eksamen i IT1105/TDT4120 Algoritmer og datastrukturer
 IT1105/TDT4120 2007 06 12 1/6 Avsluttende eksamen i IT1105/TDT4120 Algoritmer og datastrukturer Eksamensdato Torsdag 6. desember Eksamenstid 1500 1900 Sensurdato Torsdag 10. januar Språk/målform Bokmål
IT1105/TDT4120 2007 06 12 1/6 Avsluttende eksamen i IT1105/TDT4120 Algoritmer og datastrukturer Eksamensdato Torsdag 6. desember Eksamenstid 1500 1900 Sensurdato Torsdag 10. januar Språk/målform Bokmål
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). Innsetting og søk. Rekursjon igjen. A C E G
 TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
Alle mot alle. Åttende forelesning. (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder.
 Enkel alle-til-allealgoritme: Kjør Dijkstra (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder. Kan fungere for spinkle grafer blir dyrt ellers. Alle mot alle Åttende forelesning 1 Dijkstra
Enkel alle-til-allealgoritme: Kjør Dijkstra (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder. Kan fungere for spinkle grafer blir dyrt ellers. Alle mot alle Åttende forelesning 1 Dijkstra
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 7 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 7 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Hvorfor sortering og søking? Søking og sortering. Binære søketrær. Ordnet innsetting forbereder for mer effektiv søking og sortering INF1010 INF1010
 Hvorfor sortering og søking? Man bør ha orden i dataene umulig å leve uten i informasjonssamfunnet vi blir fort lei av å lete poleksempel internett alt er søking og sortering alternativer til sortering
Hvorfor sortering og søking? Man bør ha orden i dataene umulig å leve uten i informasjonssamfunnet vi blir fort lei av å lete poleksempel internett alt er søking og sortering alternativer til sortering
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Algoritmer og Datastrukturer IAI 21899
 Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl
 Student nr.: Side 1 av 5 Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle
Student nr.: Side 1 av 5 Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle
A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity.
 A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity. Previous studies suggest that the learning capacity of both people and
A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity. Previous studies suggest that the learning capacity of both people and
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Kjøretidsanalyse. Hogne Jørgensen
 Kjøretidsanalyse Hogne Jørgensen Program Presentasjon/tips til Øving 5 Kompleksitetsanalyse Kahoot Rekurrensligninger Kahoot 2 Øving 5 Veibygging i Ogligogo Finne dyreste kant i minimalt spenntre Prim
Kjøretidsanalyse Hogne Jørgensen Program Presentasjon/tips til Øving 5 Kompleksitetsanalyse Kahoot Rekurrensligninger Kahoot 2 Øving 5 Veibygging i Ogligogo Finne dyreste kant i minimalt spenntre Prim
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 7. desember 2013 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode Målform/språk
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 7. desember 2013 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode Målform/språk
Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer
 Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer TDT4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Forstå, og kunne bruke, algoritmer
Python: Rekursjon (og programmering av algoritmer) Python-bok: Kapittel 12 + teoribok om Algoritmer TDT4110 IT Grunnkurs Professor Guttorm Sindre Læringsmål og pensum Mål Forstå, og kunne bruke, algoritmer
Binær heap. En heap er et komplett binært tre:
 Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Heap Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle noder på nederste nivå ligger så langt til venstre som mulig
Logaritmiske sorteringsalgoritmer
 Logaritmiske sorteringsalgoritmer Logaritmisk sortering Rekursive og splitt og hersk metoder: Deler verdiene i arrayen i to (helst) omtrent like store deler i henhold til et eller annet delingskriterium
Logaritmiske sorteringsalgoritmer Logaritmisk sortering Rekursive og splitt og hersk metoder: Deler verdiene i arrayen i to (helst) omtrent like store deler i henhold til et eller annet delingskriterium
Agenda. 1 Sortering, heap og select. 2 Binære trær. 3 Grafer, BFS og DFS. 4 Spenntrær og Korteste vei. 5 Maks flyt. 6 Dynamisk programmering
 Agenda 1 Sortering, heap og select Oppsummering Ola Natvig IDI - NTNU 23. november 2007 2 Binære trær 3 Grafer, BFS og DFS 4 Spenntrær og Korteste vei 5 Maks flyt 6 Dynamisk programmering 7 Grådighet 8
Agenda 1 Sortering, heap og select Oppsummering Ola Natvig IDI - NTNU 23. november 2007 2 Binære trær 3 Grafer, BFS og DFS 4 Spenntrær og Korteste vei 5 Maks flyt 6 Dynamisk programmering 7 Grådighet 8
Heap og prioritetskø. Marjory the Trash Heap fra Fraggle Rock
 Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Heap og prioritetskø Marjory the Trash Heap fra Fraggle Rock Binær heap En heap er et komplett binært tre: Alle nivåene i treet, unntatt (muligens) det nederste, er alltid helt fylt opp med noder Alle
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 918 51 949 Eksamensdato 4. desember, 2017
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 918 51 949 Eksamensdato 4. desember, 2017
August
 None of us truly understands the P versus NP problem, we have only begun to peel the layers around this increasingly complex question. Perhaps we will see a resolution of the P versus NP problem in the
None of us truly understands the P versus NP problem, we have only begun to peel the layers around this increasingly complex question. Perhaps we will see a resolution of the P versus NP problem in the
INF2220: Forelesning 2
 INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2. Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7)
 INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
INF2220: Forelesning 2 Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) REPETISJON: BINÆRE SØKETRÆR 2 Binære søketrær 8 4 12 2 7 9 15 6 11 13 16 For enhver node i et binært søketre
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl
 SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
LO118D Forelesning 2 (DM)
 LO118D Forelesning 2 (DM) Kjøretidsanalyse, matematisk induksjon, rekursjon 22.08.2007 1 Kjøretidsanalyse 2 Matematisk induksjon 3 Rekursjon Kjøretidsanalyse Eksempel Finne antall kombinasjoner med minst
LO118D Forelesning 2 (DM) Kjøretidsanalyse, matematisk induksjon, rekursjon 22.08.2007 1 Kjøretidsanalyse 2 Matematisk induksjon 3 Rekursjon Kjøretidsanalyse Eksempel Finne antall kombinasjoner med minst
Dijkstras algoritme. Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert.
 Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl
 Student nr.: Side 1 av 7 Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Student nr.: Side 1 av 7 Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2015 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2015, forelesning
Studentnummer: Side 1 av 1. Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005
 Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
All good things. Fjortende forelesning
 All good things Fjortende forelesning 1 Reduksjons- Eksempler 2 Clique til Independent Set 3 Partition til Bin Packing 4 Partition til Subset Sum 5 CNF-SAT til Dir. Ham. Cycle 6 Dir. Ham. Cycle til Ham.
All good things Fjortende forelesning 1 Reduksjons- Eksempler 2 Clique til Independent Set 3 Partition til Bin Packing 4 Partition til Subset Sum 5 CNF-SAT til Dir. Ham. Cycle 6 Dir. Ham. Cycle til Ham.
INF1010 notat: Binærsøking og quicksort
 INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
INF1010 notat: Binærsøking og quicksort Ragnhild Kobro Runde Februar 2004 I dette notatet skal vi ta for oss ytterligere to eksempler der rekursjon har en naturlig anvendelse, nemlig binærsøking og quicksort.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Om Kurset og Analyse av Algoritmer
 Om Kurset og Analyse av Algoritmer Lars Vidar Magnusson 8.1.2014 Praktisk informasjon om kurset Hva er en algoritme? (kapittel 1) Hvordan analysere en algoritme? (kapittel 2) Praktisk Informasjon Introduction
Om Kurset og Analyse av Algoritmer Lars Vidar Magnusson 8.1.2014 Praktisk informasjon om kurset Hva er en algoritme? (kapittel 1) Hvordan analysere en algoritme? (kapittel 2) Praktisk Informasjon Introduction
Introduksjon til Algoritmeanalyse
 Introduksjon til Algoritmeanalyse 26. August, 2019 Institutt for Informatikk 1 Hvordan skal vi tenke i IN2010? Effektive løsninger Hvordan skalérer problemet og løsningen? 2 Terminologi Betegnelse Problem
Introduksjon til Algoritmeanalyse 26. August, 2019 Institutt for Informatikk 1 Hvordan skal vi tenke i IN2010? Effektive løsninger Hvordan skalérer problemet og løsningen? 2 Terminologi Betegnelse Problem
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
for bare trær Andre forelesning
 Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
NITH PG4200 Algoritmer og datastrukturer Løsningsforslag Eksamen 4.juni 2013
 NITH PG00 Algoritmer og datastrukturer Løsningsforslag Eksamen.juni 0 Dette løsningsforslaget er til tider mer detaljert enn det man vil forvente av en eksamensbesvarelse. Det er altså ikke et eksempel
NITH PG00 Algoritmer og datastrukturer Løsningsforslag Eksamen.juni 0 Dette løsningsforslaget er til tider mer detaljert enn det man vil forvente av en eksamensbesvarelse. Det er altså ikke et eksempel
SIF8010 ALGORITMER OG DATASTRUKTURER
 SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
SIF8010 ALGORITMER OG DATASTRUKTURER KONTINUASJONSEKSAMEN, 1999; LØSNINGSFORSLAG Oppgave 1 (12%) Anta at du skal lage et støtteprogram som umiddelbart skal varsle om at et ord blir skrevet feil under inntasting
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
INF2220 - Algoritmer og datastrukturer HØSTEN 2009 Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 5: Prioritetskø og Heap Bjarne Holen (Ifi, UiO) INF2220 H2009, forelesning 5 1 /
Divide-and-Conquer. Lars Vidar Magnusson 13.1.2015
 Divide-and-Conquer Lars Vidar Magnusson 13.1.2015 Kapittel 4 Maximum sub-array problemet Matrix multiplikasjon Analyse av divide-and-conquer algoritmer ved hjelp av substitusjonsmetoden Divide-and-Conquer
Divide-and-Conquer Lars Vidar Magnusson 13.1.2015 Kapittel 4 Maximum sub-array problemet Matrix multiplikasjon Analyse av divide-and-conquer algoritmer ved hjelp av substitusjonsmetoden Divide-and-Conquer
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Løsningsforslag for Obligatorisk Oppgave 2. Algoritmer og Datastrukturer ITF20006
 Løsningsforslag for Obligatorisk Oppgave 2 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.02.14 Den andre obligatoriske oppgaven tar for seg forelesning 5, 6, og 7 som dreier seg om
Løsningsforslag for Obligatorisk Oppgave 2 Algoritmer og Datastrukturer ITF20006 Lars Vidar Magnusson Frist 28.02.14 Den andre obligatoriske oppgaven tar for seg forelesning 5, 6, og 7 som dreier seg om
Teoriøving 7 + litt om Ford-Fulkerson. Magnus Lie Hetland
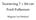 Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 1 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 1 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Fra A til B. Syvende forelesning
 Fra A til B Syvende forelesning 1 Amøbeproblemet nok en gang. Hva er 1+2+4+ +n/2? 2 Skal la være å trekke frem binærtrefiguren igjen ;-) La oss se på det på en litt annen måte, som passer dagens tema (fra
Fra A til B Syvende forelesning 1 Amøbeproblemet nok en gang. Hva er 1+2+4+ +n/2? 2 Skal la være å trekke frem binærtrefiguren igjen ;-) La oss se på det på en litt annen måte, som passer dagens tema (fra
Alg. Dat. Øvingsforelesning 3. Grafer, BFS, DFS og hashing
 Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner, hashtabeller Kollisjonshåndtering
Alg. Dat Øvingsforelesning 3 Grafer, BFS, DFS og hashing Dagens tema Grafer Terminologi Representasjon av grafer Bredde først søk (BFS) Dybde først søk (DFS) Hashing Hashfunksjoner, hashtabeller Kollisjonshåndtering
LO118D Forelesning 12 (DM)
 LO118D Forelesning 12 (DM) Trær 15.10.2007 1 Traversering av trær 2 Beslutningstrær 3 Isomorfisme i trær Preorden-traversering 1 Behandle den nåværende noden. 2 Rekursivt behandle venstre subtre. 3 Rekursivt
LO118D Forelesning 12 (DM) Trær 15.10.2007 1 Traversering av trær 2 Beslutningstrær 3 Isomorfisme i trær Preorden-traversering 1 Behandle den nåværende noden. 2 Rekursivt behandle venstre subtre. 3 Rekursivt
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl
 Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 918 51 949 Eksamensdato 12. august, 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 918 51 949 Eksamensdato 12. august, 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D.
IN Algoritmer og datastrukturer
 IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 3: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning
IN2010 - Algoritmer og datastrukturer HØSTEN 2018 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 3: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2010 H2018, forelesning
UNIVERSITETET I OSLO
 Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 14. desember 2015 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 6 sider. Vedlegg: Tillatte hjelpemidler: INF2220
Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 14. desember 2015 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 6 sider. Vedlegg: Tillatte hjelpemidler: INF2220
INF1020 Algoritmer og datastrukturer. Dagens plan
 Dagens plan Prioritetskø ADT Motivasjon Operasjoner Implementasjoner og tidsforbruk Heap-implementasjonen Strukturkravet Heap-ordningskravet Insert DeleteMin Tilleggsoperasjoner Build Heap Anvendelser
Dagens plan Prioritetskø ADT Motivasjon Operasjoner Implementasjoner og tidsforbruk Heap-implementasjonen Strukturkravet Heap-ordningskravet Insert DeleteMin Tilleggsoperasjoner Build Heap Anvendelser
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Søkeproblemet. Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke?
 Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
Søking Søkeproblemet Gitt en datastruktur med n elementer: Finnes et bestemt element (eller en bestemt verdi) x lagret i datastrukturen eller ikke? Effektiviteten til søkealgoritmer avhenger av: Om datastrukturen
