Live life and be merry
|
|
|
- Line Fosse
- 6 år siden
- Visninger:
Transkript
1 Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder]
2 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 2
3 Ek s l e p em Optimale søketrær 3
4 Optimaliseringskriteriet blir den vektede (med vekt p_i) summen av dybdene (+) til nøklene k_i. K = [k,, kn], k < k2 < < kn Vil bygge et binært søketre over K Sannsynlighet p i for søk etter ki Vil minimere forventet søkekostnad Antar at alle søk lykkes. 4
5 ; E Forventet søketid: 2.5. ; 9 ; G ; F ; H 6 0,7#8 < (; 6 ) 0,7#8 < (; 6 ) EH E I I F E 9 G 9 E H E J 99H 5
6 ;! ; " ; # Forventet søketid: 2.0. (Optimalt.) ; $ Merk: Ikke sikkert vi vil ha minimal høyde. Heller ikke sikkert den høyeste sannsynligheten ender i rota. ; % 8 &'()* < (; 8 ) &'()* < (; 8 ) 2 8 " " +!#!,, % % +"# $! +$ # " +% "+", 6 Brute force: Bygg alle mulige binære søketrær (BST), og sett inn nøklene. Beregn forventet søkekostnad. Velg beste. Men det er Ω(4 n /n 3/2 ) BST-er med n noder.
7 Hvis T inneholder nøklene ki kj så må T være optimalt for disse nøklene vises lett ved selvmotsigelse.!!" 7
8 ! " Hvis vi antar at rota inneholder kr (som en hypotese) så vil alle k<kr være til venstre (og tilsv. for høyre). Begge deltrær må (som nevnt i forrige foil) være optimale for de gitte nøklene. Hvis vi undersøker alle k = ki kj som mulige røtter, og har (og løser problemet rekursivt) så er vi garantert å finne den optimale løsningen for ki kj!! #! "!"! "#"! $ 8
9 %&'()*& +,(&-.,* /02(&*!" ' 9*,:*7786:!"# w(8, ; ) = w(8, * $) + 2* + w(* + $, ; )% Hvis j = i er treet tomt. &'()(*+)(, &-8, ;. = &-8, * $. + &-* + $, ;. + w(8, ; )% e[i, j] er forventet kostnad for optimalt BST over ki kj. &'/0 ("2#/+3 200"4(0 #'2# 5( 26)( '/:' 9(8 /0 <* % ;( 7+3<#% &)8 266 :237/72#(0, 237 =/:9 #'( >(0# } + w(i, j) /* ; = 8 $, &-8, ;. = 4/3 {&-8, * $. + &-* + $, ;. + w(8, ; )} /* 8 ;. 8 * ; A+"67 5)/#( 2 )(:")0/B( 26C+)/#'4% % %!"#$%&'() *( "$&'#*+,"+%&'"( D0 E"0"26,F 5(<66 0#+)( #'( B26"(0 /3 2 #2>6(? Vi legger til w(i, j) (dvs. alle p-ene legges til én gang) fordi høyden til alle noder i deltrærne øker med én. w(i, j) er summen av pi pj &- "$.. #$ 6 + 6%. " #$ :23 0#+)( :23 0#+)( &-6 + $, 6. 9
10 [trekk pusten dypt] 0
11 !"#$%&'()*#(!, ", #)!"# $ + $" # + + %" %,$, $ +-. w,$, $ +-.!"# & + $" # %"!"# $ + $" # & + + %" ' $ + & + %,$, '- w,$, '- w,$, ' +- +! '!"# ( $ $" ' Kubisk kjøretid. /02/3 % 435 (**) l (liten L) i hovedløkken er størrelsen på deltrærne vi beregner. i er start og j er slutt for nøklene i det aktuelle deltreet. %" ) %,$, ( +- + %,( + +, '- + w,$, '- &! ) < %,$, '- $'() %,$, '- ) (**),$, '- (
12 !"#$%&'!%(")%*+,-(.$%(!""#)!!""#/0, $ %8! 749 6:; 3<<68!"#$%&'!%(")%($'.%&==(0,! 0,!, 7>;?68,!""#)!"#$%&'!%(")%($'.%&==(! + 0, $,!, 734@:68,!""#)!"#$%&'!%(")%($'.%&==(&, ',!, (&!,!""#)!" & ' #$%& #!""#/&, ' %8 # 7498 (&! 7A:4>B <? %8!!"#$%&'!%(")%($'.%&==(&, # 0, #, 7>;?68,!""#)!"#$%&'!%(")%($'.%&==(# + 0, ', #, 734@:68,!""#) 2
13 Eksempel Longest Common Subsequence. Finner en felles subsekvens hos to sekvenser. Lengden kan brukes som et likhetsmål. Denne type algoritmer er vanlig i bioinformatikk og informasjonsg jenfinning. LCS 3
14 Noen eksempler. En Brute Forceløsning vil ha en kjøretid på (n2^m) ser du hvorfor? s p r i n g t i m e h o r s e b a c k p i o n e e r s n o w f l a k e m a e l s t r o m h e r o i c a l l y b e c a l m Merk: John Stewarteksemplet ser bare på snittet av bokstavmengdene et mye enklere problem (som lett kan løses i lineær tid vha. f.eks. hashing). 4 s c h o l a r l y
15 X i = [x,, xi], Yi = [y,, yi] X = X m, Y = Yn Z = [z,, zk] er en LCS av X og Y 5
16 Hvis de ikke deler siste element kan LCS-en utvides en selvmotsigelse. Hvis x m = yn: z k = xm = yn og Z k er en LCS av Xm og Yn Det samme gjelder her hvis Xm- og Yn- har en lenger felles subsekvens så kan vi finne en lenger total felles subsekvens enn Z igjen en selvmotsigelse. 6
17 Hvis xm yn og zk xm: I begge tilfeller må Z være en felles subsekvens. Hvis det eksisterte en som var lenger vil den også være lenger totalt en selvmotsigelse. Z er en LCS av X m og Y Hvis xm yn og zk yn: Z er en LCS av X og Y n 7
18 !" #$%%&'()* '+," -'.&+ 0.&(&+(& # + '7+ 8&9:&4*&8 *+4'3) ;(&!< 34 56# + ;(&!<&8 8&9:&4*&8" c[i,j] er lengden på en LCS av Xi og Yj.!"#$%&'(" )*%+$,-.'*/ =&!4& #>6, ;? + 56# + <6 34B = ; " C& 734' #>5, 4?" ) 6 = D +( ; = D, D ) 6, ; > D 34B >6 = 3 ;, #>6, ;? = #>6 E, ; E? + E %3<(#>6 E, ;?, #>6, ; E?) ) 6, ; > D 34B >6 " = 3 ;. FA3)42 7& *+:@B 7()'& 3 (&*:(8)G& 3@A+()'.% H38&B +4 '.)8 +(%:@3')+4" 0($ 7)'. H+I+2 H3'" J2!!2! 8 Enten er xi og yj like eller ikke. Hvis de er det skal xi=yj=zk være med. Ellers vil Z være en LCS enten av Xi- og Y eller av X og Yj-. Vi vet ikke hvilken, men prøver begge og velger den største.!2!
19 Rekursjon? Enten vi gjør det rekursivt eller iterativt: Legg svarene i en tabell. J2!!2!!2!,2!!2,!2, J2E E2!,2,,2,!2E,2,!2E!2E J2D D2! E2, E2,,2E E2,,2E,2E!2D 9
20 !"#$!%&'()(!, ", #, $)!"# % * $" # %" &+%,,-,!"# ', $" $ %" &+,, '-,!"# % * $" # %"!"# ' * $" $ %" &! ( % = ) ' $'() &+%, '- &+% *, ' *- + * *+%, '-. / (*+( &! &+% *, '- &+%, ' *- $'() &+%, '- &+% *, '- *+%, '-. / (*+( &+%, '- &+%, ' *- *+%, '-. / #($,#) & 02 * I b-tabellen lagrer vi en referanse til hvor vi «kom fra». 20
21 K L L M M * K L L M M * L L L M M * L M M M M * L M M M M * M M M M M * * * * * * * * * * * * * * * * * * * * * * * * * * + &!, & -. * & /! # - # (. 0 - &! -. 2
22 X nedover til venstre, Y bortover på toppen. Nedoverpil: Dropp en bokstav fra X vekt 0. Bortoverpil: Dropp en bokstav fra Y vekt 0. Skråpil: Ta med bokstav fra X/Y: Vekt. Finn lengste vei fra øverst t.v. til nederst t.h. Dette er rett og slett DAG Shortest Path (eller Longest Path, da som jo blir like lett for DAG-er). 22
23 !"#$%&'()(!, ", #, $)!" # = * +, $ = * #$%& '%#('&!"!-#, $. = / 0 #$%&!"#$%&'()(!, ", #, $ ) 2,345 % # %)*%!"!-#, $. = / 0 #$%&!"#$%&'()(!, ", #, $) %)*%!"#$%&'()(!, ", #, $ ) 23
24 Egenskaper bak DP Optimal substruktur: En optimal løsning bygger på optimale løsninger på delproblemer Overlappende delproblemer: Fordi flere problemer deler delproblemer lønner det seg å lagre dem 24 Korteste vei? Har begge deler. Lengste vei (uten sykler)? Har ikke optimal substruktur Hvis vi ikke har overlappende delproblemer *kan* vi bruke DP, men det er egentlig ingen vits det blir bare splitt-og-hersk med unødvendig lagring av delproblemer.
25 ! 25
26 2 C 2 D < 2 Korteste vei oppdeling i delproblemer som må optimaliseres. Korteste veier består av korteste del-veier. 26
27 A * Lengste vei. Betrakt q-r-t, en maksimal sti fra q til t. Består den av lengste vei fra q til r og fra r til t? *Nei*! Vi kan ikke bruke DP (og har ingen annen god løsning heller). - ( 27
28 Og så var det denne, da
29 for i = n for j = i if A[i] > A[j] L[i] max(l[i], L[j]+) A L For hvert element, let bakover etter lovlige forgjengere. (Å lete bakover er nyttig hvis vi vil begrense spranglengden.) Delproblemene er lengste subsekvens som slutter på en gitt posisjon, og det er disse vi bruker når vi leter bakover. (Vi kan også lagre hva vi valgte dvs. hva som er forgjengeren, altså pilene i figuren.) 29
30 Kan du finne en subkvadratisk løsning? Hint: Binærsøk 30
31 Kort om Matrisekjedemultiplikasjon 3
32 Vi vil løse ABC (AB)C kan ha en annen kostnad enn A(BC) Hvordan finner vi optimal parentes-setting? For hver splitt må hver halvdel løses optimalt Parametrisering: Start- og slutt-indeks 32
33 For hver start-indeks og hver slutt-indeks, prøv alle splitt-indekser og velg den som gir lavest kostnad. Vi bevarer beregningene for alle delproblemer, som før. Dette forklares ganske omstendelig i boka, men både problemet og løsningen er egentlig svært enkle. 33
34 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 34
35 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 35
36 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 36
37 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 37
38 38
39 g i t k i s K ort Grådighet All form for optimalisering kan jo ses som «grådig», men med grådighet mener vi hær en nærsynt, kortsiktig, «hedonistisk» form for grådighet. Vi velger det som virker bra her og nå, uten å tenke på fremtiden. Noen kjente algoritmer som er grådige? (Spenntrær, Dijkstras algoritme og løsningen på fractional knapsack, f.eks.) Det er en veldig enkel strategi, så det som er interessant er: Når kan dette *også* være optimalt globalt/på lang sikt? 39
40 Minner om dynamisk programmering Brukes til optimalisering Når vi kan velge, velg det som er best lokalt Vis at løsningen også blir globalt optimal 40
41 I DAG-SP må vi prøve alle mulige veier tilbake fra slutt-noden til start-noden for å finne den beste. Dette vil fort ta eksponensiell tid. Heldigvis består hver optimale løsning av optimale del-løsninger og disse overlapper. Ved å gjenbruke dem (mellomlagring) får vi polynomisk (lineær) kjøretid Men hva om vi vet noe mer enn at vi har en DAG? Hva om vi kunne «nøste oss bakover» og velge riktig hele veien? For eksempel ved å velge den korteste kanten i hvert trinn 2 4
42 Her ble det jammen riktig! Dette er et eksempel på en grådig strategi og et tilfelle der den fungerte. Den fungerer naturligvis ikke for DAG-SP generelt men det viser at grådighet er beslektet med DP på et eller annet vis
43 splitt-og-hersk dyn. prog. Del i uavhengige delproblemer og løs alle. Del i (potensielt overlappende) delproblemer og løs alle. grådighet Velg «nærsynt» hvilke delproblemer vi bryr oss om. Også her må vi ha optimal substruktur! 43 Dette er ingen «hardand-fast» taksonomi. Hva med binærsøk, f.eks.? Eller Dijkstras algoritme?
44 Grei metafor: Fyller ut puslespill rad for rad, med brikker av ulik pris. En grådig algoritme vil starte med den dyreste brikken, og alltid kaste dem som ikke passer. Spenntrær godt eksempel. $20 $0 $5 44
45 Eksempel Aktivitetsplukking 45
46 Vi har et sett med intervaller f.eks. tidsintervaller for aktiviteter som trenger en ekslusiv ressurs (f.eks. møter/ møterom).! &! %! #! (! *! "! $! '! )! " # $ % & ' ( ) * "! "" "# "$ "% "& "' Vi vil velge et størst mulig subsett der ingen overlapper. 46
47 Optimal substruktur Aktiviteter i Sij er kompatible med alle hendelser som er avsluttet innen fi og alle som starter etter sj. Vi legger på a_0 = [-inf, 0) og a_n+ = [inf, inf+ ) Vi har da: S = S_0,n+ Anta aktiviteter sortert etter slutt-tid. Hvis i j så S_ij = {} < := = { > < <. : - > <. > - = } = = =I=I=. : - >. > - = : > = =I=I= Trenger bare bry oss om S_ij der 0 i < j n+. Hvis S_ij inneholder a_k har vi to delproblemer: S_ik og S_kj 47 La A_ij være optimal løsning for S_ij. Vi har da: A_ij = A_ik + {a_k} + A_kj hvis vi antar at S_ij ikke er tom og at vi kjenner a_k.
48 Med andre ord: For et mulig subsett kan vi «splitte» på ulike objekter. Rekursiv definisjon av optimal løsning: Dette *kunne* vi ha løst med dynamisk programmering, *men* vi kan *forenkle* $% $" # =, #!!", # " = &'( {!!", %" +!!%, # " + )} $% $" # # =. "<%< # &% $" # Vi må altså velge en k og vi må «kvitte» oss med ett delproblem. Finnes det et gyldig «nærsynt» valg? 48
49 Det at den første «halvdelen» forsvinner er ganske opplagt; ellers måtte et element der ha startet *før* elementet (for å være til venstre) og sluttet *etter* (for ikke å bli valgt) og vi ville da ha overlapp. Elementet som slutter først kan tas med «Halvdelen» før dette forsvinner Vi sitter altså igjen med ett delproblem men hvordan kan vi være sikker på at det elementet som slutter først er trygt å ta med? 49
50 La de grå være et optimalt ut valg. Det vil alltid være trygt å bytte den første av dem med det objektet som slutter først, siden det ikke kan «overlappe lenger» enn det grå objektet som slutter først. 50
51 5
52 *, 8, =) =!"#$% 9 = &- ) 9 < * 8 K)-!,"( &'()*)(. ) > 8,=+= 5 &' = #( 9 = )"%* +%),+* {- 9 } ;DE2!E@7F7@G2HDIDE@J;(), *, 9, =) %$-% +%),+* 23).)"+ '"++ ;DE2!E@7F7@G2HDIDE@J;(), *, L, =)5 While-løkken leter etter det første lovlige elementet. Altså det elementet som starter etter f og som har tidligst slutt-tid. (Antar sortering etter slutt-tid her.) Denne er jo rekursiv, da Vi kan godt gjøre den iterativ. 52
53 *, =) 5 {- = } 8 = ('+ 9 M )' = &' #( ) 9 * 8 )"%* 5 5 {- 9 } )" $/"(,%'%( &--)()/ (/ 5 +%),+* 5 Vi har altså bevist at det er trygt å alltid velge det første (etter slutt-tid) lovlige elementet og det er jo det vi gjør her. 53
54 Eksempel! &! %! #! (! *! "! $! '! )! " # $ % & ' ( ) * "! "" "# "$ "% "& "' 54
55 Grådige strategier 55
56 . Finn optimal substruktur Vi lager gjerne substrukturen med tanke nettopp på å kunne velge grådig og på å eliminere delproblemer. 2. Lag en rekursiv løsning 3. Vis at grådig valg er trygt 4. Vis vi sitter igjen med bare ett delproblem 5. Lag rekursiv grådig løsning 6. Konverter den til en iterativ løsning 56
57 Strømlinjeformet Såkalte «set systems» er en veldig generell problemstruktur for denne typen ting (se kapitlet om matroider i boka; ikke pensum).. Formuler som problem der vi kan velge grådig og sitte igjen med ett delproblem 2. Vis at det alltid er trygt å velge grådig 3. Vis at grådig valg + optimal del-løsning gir optimal løsning De siste to punktene gjelder for generelle strukturer som matroider og greedoider. En helt eksakt karakterisering av slike strukturer er gitt ved såkalte matroid embeddings. (Ikke pensum! :-)) 57
58 Vi har altså to hovedingredienser: Greedy-choice-egenskapen Optimal substruktur (Det finnes andre måter å bevise korrekthet for grådighet på, altså ) Det står om matroider i boka. Dere kan jo evt. også google greedoids eller hvis dere er eventyrlystne, matroid embeddings. 58
59 Eksempel Huffmankoder 59
60 e = a = q = Morsekode. Vi er ute etter noe litt lignende. En effektiv, variabel kode. z = 60
61 Prefikskoder (eller prefiksfrie koder): Koder der ingen koder er prefiks av andre koder. Mao. er det aldri tvil om dekodingen. Ulike tegn får koder med ulik lengde Vi kan bruke prefiks-koder Total tekst-lengde skal minimeres Vi har kun informasjon om tegnfrekvenser 6
62 Kodene blir prefiksfrie fordi vi ikke har tegn i de interne nodene. Venstre = 0, høyre =. a = 0 0 c b = 0 a b c = Vi ønsker å minimere tegnfrekvens * tegndybde (implisitt også tekstlengde). Minner om de optimale søketrærne våre, men vi har ikke noe krav om rekkefølge. 62
63 Huffmans algoritme: Lag et tre for hvert tegn med frekvens-vekt Gjenta: Slå sammen de to letteste trærne 63
64 Prøv å tegne opp hvordan dette treet bygges helst trinn for trinn A : 8 B : 3 C : D : E : F : G : H : 64
65 A : 8 B : 3 C : D : E : F : 2 G : H : 65
66 A : 8 B : 3 C : D : 2 2 E : F : G : H : 66
67 A : 8 B : C : D : E : F : G : H : 67
68 A : 8 B : C : D : 2 2 E : F : G : H : 68
69 A : B : C : D : E : F : G : H : 69
70 A : B : C : D : E : F : G : H : 70
71 Merk: Dette minimerer forventet sti-lengde hvis vi «søker» etter en bokstav. Med andre ord er dette en mer effektiv variant av de optimale søketrærne fra forrige gang bortsett fra at søketre-egenskapen ikke er oppfylt. A : 8 7 Hvis man kan konstruere «ja/nei»- spørsmålene selv (som f.eks. ved en prosedyre for medisinsk diagnose), i stedet for å bruke søkenøkler, så kan Huffmans algoritme også brukes til denslags. 5 4 B : Dette er jo klart en grådig fremgangsmåte men hvorfor blir det optimalt? C : D : E : F : G : H : 7
72 Bevis-skisse: Hvis treet ikke er fullt kan vi kollapse stier der noder bare har ett (internt) barn. Bortkastet å ikke ha et fullt tre Det er OK for de to billigste å være søsken, nederst i treet Hvis de to billigste behandles som ett symbol må det resterende treet være optimalt Hvis vi bytter ut ett av dem med et dyrere vil det dyrere ikke komme lenger opp og det billige vil ikke komme lenger ned så det vil ikke bli billigere totalt. 72
73 Min. forv. koding Kombiner minste O(n lg n) Huffmans algoritme 73
74 74
75 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 75
76 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding Insertion sort Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Selection sort Sterke komponenter Topologisk sortering 76
77 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 77
78 D&C Bellman-Ford BFS/DFS Binære søketrær LP Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp (Par.) Floyd- Warshall Hashing Gr. Heapsort Huffmankoding Insertion sort NPC Flyt+ Kruskal Merge sort Prim Quicksort Radix sort Randomized Select Select Θ etc. Selection sort Sterke komponenter Topologisk sortering DP 78
Live life and be merry
 Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 2 g i t k i s K o rt Grådighet All form for
Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 2 g i t k i s K o rt Grådighet All form for
Live life and be merry
 Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 Litt repetisjon 2 Eksempel Longest Common Subsequence.
Om grådighet og først litt mer DP. Live life and be merry Ellevte forelesning for tomorrow you may catch some disgusting skin disease. [Edmund Blackadder] 1 Litt repetisjon 2 Eksempel Longest Common Subsequence.
Choices, choices. Tiende forelesning. Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før.
 Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity.
 A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity. Previous studies suggest that the learning capacity of both people and
A new study has found that cockroaches are morons in the morning and geniuses in the evening in terms of their learning capacity. Previous studies suggest that the learning capacity of both people and
Choices, choices. Tiende forelesning. Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før.
 Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
Choices, choices Tiende forelesning Dynamisk programmering: En serie med valg der valgmulighetene er avhengige av hva vi har valgt før. DAG- SP er erkeeksemplet (og den underliggende modellen for all DP).
Dijkstras algoritme. Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert.
 Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15
 http://www.idi.ntnu.no/~algdat algdat@idi.ntnu.no Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15 b c g a f d e h The pitch drop experiment. Foreløpig kjørt fra 1927 til nå. Åtte dråper har
http://www.idi.ntnu.no/~algdat algdat@idi.ntnu.no Pensum: 3. utg av Cormen et al. Øvingstime: I morgen, 14:15 b c g a f d e h The pitch drop experiment. Foreløpig kjørt fra 1927 til nå. Åtte dråper har
August
 None of us truly understands the P versus NP problem, we have only begun to peel the layers around this increasingly complex question. Perhaps we will see a resolution of the P versus NP problem in the
None of us truly understands the P versus NP problem, we have only begun to peel the layers around this increasingly complex question. Perhaps we will see a resolution of the P versus NP problem in the
for bare trær Andre forelesning
 Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Formler eller bevis e.l. som er uklare? Si ifra, så kan jeg gå g jennom dem. Forelesningene er ment å være en hjelp til å forstå det man leser i boka ikke «spoon-feeding» av det samme som står der for
Go with the. Niende forelesning. Mye matematikk i boka her ikke så komplisert, men mye å holde styr på.
 Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Go with the Niende forelesning Mye matematikk i boka her ikke så komplisert, men mye å holde styr på. Fokuserer på de viktigste ideene i dagens forelesning, så det forhåpentligvis blir lettere å skjønne
Rundt og rundt og. Trettende forelesning
 Nettverksalgoritmer. Anvendelser og generaliseringer. Sirkulasjonsproblemet/ lineær programmering. (Kap. 29.1-29.2) Rundt og rundt og Trettende forelesning 1 Merk: Ikke sikkert alt dette blir gjennomgått
Nettverksalgoritmer. Anvendelser og generaliseringer. Sirkulasjonsproblemet/ lineær programmering. (Kap. 29.1-29.2) Rundt og rundt og Trettende forelesning 1 Merk: Ikke sikkert alt dette blir gjennomgått
Alle mot alle. Åttende forelesning. (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder.
 Enkel alle-til-allealgoritme: Kjør Dijkstra (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder. Kan fungere for spinkle grafer blir dyrt ellers. Alle mot alle Åttende forelesning 1 Dijkstra
Enkel alle-til-allealgoritme: Kjør Dijkstra (eller eller Bellman-Ford, eller BFS, alt ettersom) fra alle noder. Kan fungere for spinkle grafer blir dyrt ellers. Alle mot alle Åttende forelesning 1 Dijkstra
deeegimnoorrrsstt Sjette forelesning
 deeegimnoorrrsstt Sjette forelesning 1 2 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding
deeegimnoorrrsstt Sjette forelesning 1 2 Bellman-Ford BFS/DFS Binære søketrær Binærsøk Bubblesort Bucket sort Counting sort Dijkstra DAGshortest-path Edmonds- Karp Floyd- Warshall Hashing Heapsort Huffmankoding
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Dijkstras algoritme. Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert.
 Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Her finnes det også (minst) en riktig rekkefølge for Relax, men den må vi oppdage litt etter hvert. Tenk vann som sprer seg i rør: Vi behandler krysningspunktene i den rekkefølgen de fylles. Det må gi
Algdat Eksamensforelesning. Nils Barlaug
 Algdat Eksamensforelesning Nils Barlaug Eksamen Pensum Eksamen Pensum Oppgaver du har gjort og ting du har lest Eksamen Pensum Oppgave på eksamen Oppgaver du har gjort og ting du har lest Eksamen Pensum
Algdat Eksamensforelesning Nils Barlaug Eksamen Pensum Eksamen Pensum Oppgaver du har gjort og ting du har lest Eksamen Pensum Oppgave på eksamen Oppgaver du har gjort og ting du har lest Eksamen Pensum
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 11: Huffman-koding & Dynamisk programmering (Ifi, UiO) INF2220 H2015, forelesning 11 1 / 32 Dagens
INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 11: Huffman-koding & Dynamisk programmering (Ifi, UiO) INF2220 H2015, forelesning 11 1 / 32 Dagens
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap LØSNINGSFORSLAG,
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap LØSNINGSFORSLAG,
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 7 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 7 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Dynamisk programmering (Ifi, UiO) INF2220 H2017, forelesning 13 1 / 30 Dagens plan Dynamisk
INF2220 - Algoritmer og datastrukturer Institutt for informatikk, Universitetet i Oslo INF2220, forelesning 13: Dynamisk programmering (Ifi, UiO) INF2220 H2017, forelesning 13 1 / 30 Dagens plan Dynamisk
Algdat-ninja på 60 minutter: Et galskapsprosjekt. Magnus Lie Hetland
 Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
Algdat-ninja på 60 minutter: Et galskapsprosjekt Magnus Lie Hetland 15. november, 2002 Advarsel: Tettpakkede og overfladiske foiler forut! 1 Algtdat i 6 punkter 1. Grunnbegreper og basisverktøy 2. Rekursjon
Grådige algoritmer. Lars Vidar Magnusson Kapittel 16. Aktivitetvelgingsproblemet Huffmankoder
 Grådige Algoritmer Lars Vidar Magnusson 12.3.2014 Kapittel 16 Grådige algoritmer Aktivitetvelgingsproblemet Huffmankoder Ideen bak Grådige Algoritmer Ideen bak grådige algoritmer er å løse optimaliseringsproblem
Grådige Algoritmer Lars Vidar Magnusson 12.3.2014 Kapittel 16 Grådige algoritmer Aktivitetvelgingsproblemet Huffmankoder Ideen bak Grådige Algoritmer Ideen bak grådige algoritmer er å løse optimaliseringsproblem
Algdat - øvingsforelesning
 Algdat - øvingsforelesning Dynamisk programmering Nils Barlaug Dagens plan 1. 2. 3. 4. Praktisk og dagens plan LF øving 8 a. Teori b. Praksis Dynamisk programmering a. Introduksjon b. Rod Cutting c. Matrise-multiplikasjon
Algdat - øvingsforelesning Dynamisk programmering Nils Barlaug Dagens plan 1. 2. 3. 4. Praktisk og dagens plan LF øving 8 a. Teori b. Praksis Dynamisk programmering a. Introduksjon b. Rod Cutting c. Matrise-multiplikasjon
ALGORITMER OG DATASTRUKTURER
 Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
Stud. nr: Side 1 av 6 NTNU Norges teknisk-naturvitenskapelige universitet BOKMÅL Fakultet for informasjonsteknologi, matematikk og elektroteknikk Institutt for datateknikk og informasjonsvitenskap AVSLUTTENDE
O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0
![O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0 O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i. bwfs(u, i+1) if λ[u] = 0](/thumbs/64/51255941.jpg) O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i bwfs(u, i) for each neighbor u of v if λ[u] = 0 bwfs(u, i+1) Bacwards-first search; traverserer en graf med kvadratisk worst-casekjøretid.
O(V 2 ) bwfs(v, i=1) λ[v] = i for each neighbor u of v if 0 < λ[u] < i bwfs(u, i) for each neighbor u of v if λ[u] = 0 bwfs(u, i+1) Bacwards-first search; traverserer en graf med kvadratisk worst-casekjøretid.
All good things. Fjortende forelesning
 All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
All good things Fjortende forelesning Div notater finnes på http://www.idi.ntnu.no/~algdat Foiler finnes på http://www.idi.ntnu.no/~mlh/algdat/latitudinary Spørsmål? algdat@idi.ntnu.no Sjekkliste Dette
Longest increasing. subsequence Betingelser. Longest. common subsequence. Knapsack Grådig vs. DP Moro: 2D-Nim Spørsmål. Forside. Repetisjon.
 :: :: Dynamisk programmering Eksamenskurs Åsmund Eldhuset asmunde *at* stud.ntnu.no folk.ntnu.no/asmunde/algdat/dp.ppt Svært rask repetisjon Noen ganger (f.eks. ved utregning av Fibonaccitall) vil en rekursiv
:: :: Dynamisk programmering Eksamenskurs Åsmund Eldhuset asmunde *at* stud.ntnu.no folk.ntnu.no/asmunde/algdat/dp.ppt Svært rask repetisjon Noen ganger (f.eks. ved utregning av Fibonaccitall) vil en rekursiv
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 14. desember 2011 Eksamenstid 1500 1900 Sensurdato 14. januar Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl
 Student nr.: Side 1 av 5 Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle
Student nr.: Side 1 av 5 Kontinuasjonseksamen i fag SIF8010 Algoritmer og Datastrukturer Torsdag 9. August 2001, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle
Dagens plan. INF Algoritmer og datastrukturer. Koding av tegn. Huffman-koding
 Grafer Dagens plan INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Avsluttende om grådige algoritmer (kap. 10.1.2) Dynamisk programmering Floyds algoritme
Grafer Dagens plan INF2220 - Algoritmer og datastrukturer HØSTEN 2007 Institutt for informatikk, Universitetet i Oslo Avsluttende om grådige algoritmer (kap. 10.1.2) Dynamisk programmering Floyds algoritme
Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist)
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Innhold. Innledning 1
 Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Innhold Innledning 1 1 Kompleksitetsanalyse 7 1.1 Innledning.............................. 8 1.2 Hva vi beregner........................... 8 1.2.1 Enkle operasjoner...................... 8 1.2.2 Kompleksitet........................
Notater til INF2220 Eksamen
 Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Notater til INF2220 Eksamen Lars Bjørlykke Kristiansen December 13, 2011 Stor O notasjon Funksjon Navn 1 Konstant log n Logaritmisk n Lineær n log n n 2 Kvadratisk n 3 Kubisk 2 n Eksponensiell n! Trær
Dynamisk programmering Undervises av Stein Krogdahl
 Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
Dynamisk programmering Undervises av Stein Krogdahl 5. september 2012 Dagens stoff er hentet fra kapittel 9 i læreboka, samt kapittel 20.5 (som vi «hoppet over» sist) Kapittel 9 er lagt ut på undervisningsplanen.
INF2220: Time 12 - Sortering
 INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
INF0: Time 1 - Sortering Mathias Lohne mathialo Noen algoritmer Vi skal nå se på noen konkrete sorteringsalgoritmer. Gjennomgående i alle eksempler vil vi sortere tall etter tallverdi, men som diskutert
Dynamisk programmering
 Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 50-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å
Eksamen i tdt4120 Algoritmer og datastrukturer
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 5 Oppgavestillere: Magnus Lie Hetland Jon Marius Venstad Kvalitetskontroll: Magnar Nedland Faglig
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Dynamisk programmering
 Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 5-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å gjøre.)
Dynamisk programmering Metoden ble formalisert av Richard Bellmann (RAND Corporation) på 5-tallet. Programmering i betydningen planlegge, ta beslutninger. (Har ikke noe med kode eller å skrive kode å gjøre.)
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl
 Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Student nr.: Side 1 av 5 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Pensum: fra boken (H-03)+ forelesninger
 Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Pensum: fra boken (H-03)+ forelesninger unntatt kursorisk tema KAP. 1 KAP. 2 KAP. 3 JAVA I-110 (ikke gjennomgått) OO + ABSTRAKSJON /GENERISK PROGRAMMERING REKURSJON ALGORITME-TIDSANALYSE; O-NOTASJON KAP.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Longest. increasing. subsequence. Betingelser. Matrise- common. Grådig vs. DP. Forside. Intro. Fibonacci-tall. Memoisering DP
 og dynamisk Matrisemultiplikasjomultiplikasjon programmering Matrise- Åsmund Eldhuset og Dette er to ganske like teknikker for å lage algoritmer De kan brukes på svært mange tilsynelatende forskjellige
og dynamisk Matrisemultiplikasjomultiplikasjon programmering Matrise- Åsmund Eldhuset og Dette er to ganske like teknikker for å lage algoritmer De kan brukes på svært mange tilsynelatende forskjellige
Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl
 SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Løsningsforslag for eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf.
Ekstra ark kan legges ved om nødvendig, men det er meningen at svarene skal få plass i rutene på oppgavearkene. Lange svar teller ikke positivt.
 Side 1 av 5 Noen viktige punkter: (i) (ii) (iii) (iv) Les hele eksamenssettet nøye før du begynner! Faglærer går normalt én runde gjennom lokalet. Ha evt. spørsmål klare! Skriv svarene dine i svarrutene
Side 1 av 5 Noen viktige punkter: (i) (ii) (iii) (iv) Les hele eksamenssettet nøye før du begynner! Faglærer går normalt én runde gjennom lokalet. Ha evt. spørsmål klare! Skriv svarene dine i svarrutene
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 9. august, 07 Eksamenstid
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf.!! 91851949 Eksamensdato! 15. august 2013 Eksamenstid (fra til)! 0900 1300 Hjelpemiddelkode D.
n/b log b n = (lg n) a log b n = n log b a
 Masterteoremet 1 T (n) = at (n/b) + f(n) Antall «barn»: Størrelse per «barn»: «Høyde»: a n/b log b n = (lg n) Rota har f(n) arbeid; hver løvnode har en konstant mengde arbeid. Hva vil dominere totalen?
Masterteoremet 1 T (n) = at (n/b) + f(n) Antall «barn»: Størrelse per «barn»: «Høyde»: a n/b log b n = (lg n) Rota har f(n) arbeid; hver løvnode har en konstant mengde arbeid. Hva vil dominere totalen?
Agenda. 1 Sortering, heap og select. 2 Binære trær. 3 Grafer, BFS og DFS. 4 Spenntrær og Korteste vei. 5 Maks flyt. 6 Dynamisk programmering
 Agenda 1 Sortering, heap og select Oppsummering Ola Natvig IDI - NTNU 23. november 2007 2 Binære trær 3 Grafer, BFS og DFS 4 Spenntrær og Korteste vei 5 Maks flyt 6 Dynamisk programmering 7 Grådighet 8
Agenda 1 Sortering, heap og select Oppsummering Ola Natvig IDI - NTNU 23. november 2007 2 Binære trær 3 Grafer, BFS og DFS 4 Spenntrær og Korteste vei 5 Maks flyt 6 Dynamisk programmering 7 Grådighet 8
Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). Innsetting og søk. Rekursjon igjen. A C E G
 TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
TLDR RTFM Innsetting og søk. Rekursjon igjen. Evt. forklar på tavla. Diskuter kjøretid (best-/ worst-case). D B F A C E G reduksjon! rekursjon dekomp. induksjon gjenbruk travers. Søk i søketre uten balansering
Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl
 SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 41661982; Magnus Lie
SIF8010 2003-08-09 Stud.-nr: Antall sider: 1 Eksamen i fag SIF8010 Algoritmer og datastrukturer Lørdag 9. august 2003, kl. 0900 1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 41661982; Magnus Lie
Heapsort. Lars Vidar Magnusson Kapittel 6 Heaps Heapsort Prioritetskøer
 Heapsort Lars Vidar Magnusson 24.1.2014 Kapittel 6 Heaps Heapsort Prioritetskøer Sorterings Problemet Sorterings problemet er et av de mest fundementalske problemene innen informatikken. Vi sorterer typisk
Heapsort Lars Vidar Magnusson 24.1.2014 Kapittel 6 Heaps Heapsort Prioritetskøer Sorterings Problemet Sorterings problemet er et av de mest fundementalske problemene innen informatikken. Vi sorterer typisk
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 91851949 Eksamensdato 11. august 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D. Ingen
Algdat Oppsummering, eksamen-ting. Jim Frode Hoff
 Algdat Oppsummering, eksamen-ting Jim Frode Hoff November 18, 2012 1 Definisjoner 1.1 Ordliste Problem Probleminstans Iterasjon Asymtpoisk notasjon O(x) kjøretid Ω(x) kjøretid Θ(x) kjøretid T (x) kjøretid
Algdat Oppsummering, eksamen-ting Jim Frode Hoff November 18, 2012 1 Definisjoner 1.1 Ordliste Problem Probleminstans Iterasjon Asymtpoisk notasjon O(x) kjøretid Ω(x) kjøretid Θ(x) kjøretid T (x) kjøretid
Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl
 Student nr.: Side 1 av 7 Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
Student nr.: Side 1 av 7 Løsningsforslag til eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler:
MAT1030 Forelesning 25
 MAT1030 Forelesning 25 Trær Dag Normann - 27. april 2010 (Sist oppdatert: 2010-04-27 14:16) Forelesning 25 Litt repetisjon Vi har snakket om grafer og trær. Av begreper vi så på var følgende: Eulerstier
MAT1030 Forelesning 25 Trær Dag Normann - 27. april 2010 (Sist oppdatert: 2010-04-27 14:16) Forelesning 25 Litt repetisjon Vi har snakket om grafer og trær. Av begreper vi så på var følgende: Eulerstier
LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER (IT1105)
 Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
Norges teknisk naturvitenskapelige universitet Institutt for datateknikk og informasjonsvitenskap Side 1 av 8 Faglig kontakt under eksamen: Magnus Lie Hetland LØSNINGSFORSLAG, EKSAMEN I ALGORITMER OG DATASTRUKTURER
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 25: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo 27. april 2010 (Sist oppdatert: 2010-04-27 14:15) Forelesning 25 MAT1030 Diskret Matematikk 27. april
MAT1030 Diskret Matematikk Forelesning 25: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo 27. april 2010 (Sist oppdatert: 2010-04-27 14:15) Forelesning 25 MAT1030 Diskret Matematikk 27. april
IN Algoritmer og datastrukturer
 IN010 - Algoritmer og datastrukturer HØSTEN 018 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer III Ingrid Chieh Yu (Ifi, UiO) IN010 0.10.018 1 / 0 Dagens plan: Dybde-først søk Biconnectivity
IN010 - Algoritmer og datastrukturer HØSTEN 018 Institutt for informatikk, Universitetet i Oslo Forelesning 6: Grafer III Ingrid Chieh Yu (Ifi, UiO) IN010 0.10.018 1 / 0 Dagens plan: Dybde-først søk Biconnectivity
Forelesningsplan. Grådighet. LF Øving 9. Hva er grådighet? Aktivitetsvelger En grådig strategi Grådig eller dynamisk? Knapsack Huffmankoding
 1 Grådighet 2 Forelesningsplan Grådighet Hva er grådighet? Aktivitetsvelger En grådig strategi Grådig eller dynamisk? Knapsack Huffmankoding LF Øving 9 Teori Praksis 3 Forelesningsplan Grådighet Hva er
1 Grådighet 2 Forelesningsplan Grådighet Hva er grådighet? Aktivitetsvelger En grådig strategi Grådig eller dynamisk? Knapsack Huffmankoding LF Øving 9 Teori Praksis 3 Forelesningsplan Grådighet Hva er
INF1020 Algoritmer og datastrukturer GRAFER
 GRAFER Dagens plan: Avsluttende om grådige algoritmer Huffman-koding (Kapittel 10.1.2) Dynamisk programmering Floyds algoritme for korteste vei alle-til-alle (Kapittel 10.3.4) Ark 1 av 16 Forelesning 22.11.2004
GRAFER Dagens plan: Avsluttende om grådige algoritmer Huffman-koding (Kapittel 10.1.2) Dynamisk programmering Floyds algoritme for korteste vei alle-til-alle (Kapittel 10.3.4) Ark 1 av 16 Forelesning 22.11.2004
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Lineær sortering. Radix sort
 Fra forrige gang 1 Lineær sortering Radix sort 2 Sorter hvert siffer for seg Bruk en stabil sortering (f.eks. CS) for å bevare arbeidet så langt Vi må begynne med minst signifikante siffer Konstant antall
Fra forrige gang 1 Lineær sortering Radix sort 2 Sorter hvert siffer for seg Bruk en stabil sortering (f.eks. CS) for å bevare arbeidet så langt Vi må begynne med minst signifikante siffer Konstant antall
deeegimnoorrrsstt Sjette forelesning
 deeegimnoorrrsstt Sjette forelesning 1 2 Rebus. Hva er dette? Svar: Kvadratiske sorteringsalgoritmer :-> Som vanlig relativt abstrakte beskrivelser her. Ta en titt på pseudokode i boka for mer detaljert
deeegimnoorrrsstt Sjette forelesning 1 2 Rebus. Hva er dette? Svar: Kvadratiske sorteringsalgoritmer :-> Som vanlig relativt abstrakte beskrivelser her. Ta en titt på pseudokode i boka for mer detaljert
INF2220: Time 4 - Heap, Huffmann
 INF0: Time 4 - Heap, Huffmann Mathias Lohne mathialo Heap (prioritetskø) En heap (også kalt prioritetskø) er en type binært tre med noen spesielle struktur- og ordningskrav. Vi har to typer heap: min-
INF0: Time 4 - Heap, Huffmann Mathias Lohne mathialo Heap (prioritetskø) En heap (også kalt prioritetskø) er en type binært tre med noen spesielle struktur- og ordningskrav. Vi har to typer heap: min-
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2017 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2017, forelesning
Løsningsforslag for utvalgte oppgaver fra kapittel 9
 Løsningsforslag for utvalgte oppgaver fra kapittel 9 9.2 1 Grafer og minne.......................... 1 9.2 4 Omvendt graf, G T......................... 2 9.2 5 Kompleksitet............................
Løsningsforslag for utvalgte oppgaver fra kapittel 9 9.2 1 Grafer og minne.......................... 1 9.2 4 Omvendt graf, G T......................... 2 9.2 5 Kompleksitet............................
Løsnings forslag i java In115, Våren 1996
 Løsnings forslag i java In115, Våren 1996 Oppgave 1a For å kunne kjøre Warshall-algoritmen, må man ha grafen på nabomatriseform, altså en boolsk matrise B, slik at B[i][j]=true hvis det går en kant fra
Løsnings forslag i java In115, Våren 1996 Oppgave 1a For å kunne kjøre Warshall-algoritmen, må man ha grafen på nabomatriseform, altså en boolsk matrise B, slik at B[i][j]=true hvis det går en kant fra
45011 Algoritmer og datastrukturer Løsningsforslag eksamen 13. januar 1992
 45011 Algoritmer og datastrukturer Løsningsforslag eksamen 13. januar 12 Oppgave 1 Idé til algoritme Benytter S n som betegn på en tallmengde med n elementer. For at et tall m skal være et majoritetstall
45011 Algoritmer og datastrukturer Løsningsforslag eksamen 13. januar 12 Oppgave 1 Idé til algoritme Benytter S n som betegn på en tallmengde med n elementer. For at et tall m skal være et majoritetstall
Hvorfor sortering og søking? Søking og sortering. Binære søketrær. Ordnet innsetting forbereder for mer effektiv søking og sortering INF1010 INF1010
 Hvorfor sortering og søking? Man bør ha orden i dataene umulig å leve uten i informasjonssamfunnet vi blir fort lei av å lete poleksempel internett alt er søking og sortering alternativer til sortering
Hvorfor sortering og søking? Man bør ha orden i dataene umulig å leve uten i informasjonssamfunnet vi blir fort lei av å lete poleksempel internett alt er søking og sortering alternativer til sortering
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 918 51 949 Eksamensdato 4. desember, 2017
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 918 51 949 Eksamensdato 4. desember, 2017
Teoriøving 7 + litt om Ford-Fulkerson. Magnus Lie Hetland
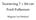 Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
Teoriøving 7 + litt om Ford-Fulkerson Magnus Lie Hetland Oppgave 1 a s 7 t 3 x 4 2 2 8 2 u 6 v 3 w Bruk DIJKSTRA eller BELLMAN-FORD og finn minste avstand fra s til de andre nodene. Svar/utregning (DIJKSTRA):
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 918 51 949 Eksamensdato 12. august, 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D.
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Tlf. 918 51 949 Eksamensdato 12. august, 2014 Eksamenstid (fra til) 0900 1300 Hjelpemiddelkode D.
Forelesning 25. MAT1030 Diskret Matematikk. Litt repetisjon. Litt repetisjon. Forelesning 25: Trær. Dag Normann
 MAT1030 Diskret Matematikk Forelesning 25: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo Forelesning 25 27. april 2010 (Sist oppdatert: 2010-04-27 14:16) MAT1030 Diskret Matematikk 27. april
MAT1030 Diskret Matematikk Forelesning 25: Trær Dag Normann Matematisk Institutt, Universitetet i Oslo Forelesning 25 27. april 2010 (Sist oppdatert: 2010-04-27 14:16) MAT1030 Diskret Matematikk 27. april
Algoritmer og Datastrukturer IAI 21899
 Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Eksamen i Algoritmer og Datastrukturer IAI 21899 Høgskolen i Østfold Avdeling for informatikk og automatisering Torsdag 30. november 2000, kl. 09.00-14.00 LØSNINGSFORSLAG 1 Del 1, Binære søketrær Totalt
Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl
 Student nr.: Side 1 av 5 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
Student nr.: Side 1 av 5 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 18. Desember 2000, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
MAT1030 Diskret Matematikk
 MAT1030 Diskret Matematikk Forelesning 26: Trær Roger Antonsen Institutt for informatikk, Universitetet i Oslo 5. mai 2009 (Sist oppdatert: 2009-05-06 22:27) Forelesning 26 MAT1030 Diskret Matematikk 5.
MAT1030 Diskret Matematikk Forelesning 26: Trær Roger Antonsen Institutt for informatikk, Universitetet i Oslo 5. mai 2009 (Sist oppdatert: 2009-05-06 22:27) Forelesning 26 MAT1030 Diskret Matematikk 5.
Øvingsforelesning Korteste vei: Alle til alle
 Øvingsforelesning Korteste vei: Alle til alle TDT4120 Algoritmer og datastrukturer Ole Kristian Pedersen 02. november, 2018 IDI, NTNU Plan for dagen Løsninger teoriøving 10 Alle til alle med Dijkstra &
Øvingsforelesning Korteste vei: Alle til alle TDT4120 Algoritmer og datastrukturer Ole Kristian Pedersen 02. november, 2018 IDI, NTNU Plan for dagen Løsninger teoriøving 10 Alle til alle med Dijkstra &
Eksamensoppgave i TDT4120 Algoritmer og datastrukturer
 Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Institutt for datateknikk og informasjonsvitenskap Eksamensoppgave i TDT0 Algoritmer og datastrukturer Faglig kontakt under eksamen Magnus Lie Hetland Telefon 98 5 99 Eksamensdato 7. desember, 06 Eksamenstid
Først litt praktisk info. Sorteringsmetoder. Nordisk mesterskap i programmering (NCPC) Agenda
 Først litt praktisk info Sorteringsmetoder Gruppeøvinger har startet http://selje.idi.ntnu.no:1234/tdt4120/gru ppeoving.php De som ikke har fått gruppe må velge en av de 4 gruppende og sende mail til algdat@idi.ntnu.no
Først litt praktisk info Sorteringsmetoder Gruppeøvinger har startet http://selje.idi.ntnu.no:1234/tdt4120/gru ppeoving.php De som ikke har fått gruppe må velge en av de 4 gruppende og sende mail til algdat@idi.ntnu.no
UNIVERSITETET I OSLO
 Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 13. desember 2011 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 7 sider. Vedlegg: INF2220 lgoritmer og datastrukturer
Eksamen i UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamensdag: 13. desember 2011 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 7 sider. Vedlegg: INF2220 lgoritmer og datastrukturer
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF2220 Algoritmer og datastrukturer Eksamensdag: 16. desember 2013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider.
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i INF2220 Algoritmer og datastrukturer Eksamensdag: 16. desember 2013 Tid for eksamen: 14.30 18.30 Oppgavesettet er på 8 sider.
All good things. Fjortende forelesning
 All good things Fjortende forelesning 1 Reduksjons- Eksempler 2 Clique til Independent Set 3 Partition til Bin Packing 4 Partition til Subset Sum 5 CNF-SAT til Dir. Ham. Cycle 6 Dir. Ham. Cycle til Ham.
All good things Fjortende forelesning 1 Reduksjons- Eksempler 2 Clique til Independent Set 3 Partition til Bin Packing 4 Partition til Subset Sum 5 CNF-SAT til Dir. Ham. Cycle 6 Dir. Ham. Cycle til Ham.
Definisjon av binært søketre
 Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Binære søketrær Definisjon av binært søketre For alle nodene i et binært søketre gjelder: Alle verdiene i nodens venstre subtre er mindre enn verdien i noden Alle verdiene i nodens høyre subtre er større
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 3. desember 2012 Eksamenstid 0900 1300 Sensurdato 3. januar 2013 Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl
 Student nr.: Side 1 av 7 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
Student nr.: Side 1 av 7 Eksamen i fag SIF8010 Algoritmer og Datastrukturer Tirsdag 14. Desember 1999, kl 0900-1500 Faglig kontakt under eksamen: Arne Halaas, tlf. 73 593442. Hjelpemidler: Alle kalkulatortyper
Grunnleggende Grafteori
 Grunnleggende Grafteori 2. September, 2019 Institutt for Informatikk 1 Dagens plan Terminologi og definisjoner Hvordan representere grafer i datamaskinen Traversering Dybde-først-søk Bredde-først-søk Topologisk
Grunnleggende Grafteori 2. September, 2019 Institutt for Informatikk 1 Dagens plan Terminologi og definisjoner Hvordan representere grafer i datamaskinen Traversering Dybde-først-søk Bredde-først-søk Topologisk
INF Algoritmer og datastrukturer
 INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
INF2220 - Algoritmer og datastrukturer HØSTEN 2016 Ingrid Chieh Yu Institutt for informatikk, Universitetet i Oslo Forelesning 4: Prioritetskø og Heap Ingrid Chieh Yu (Ifi, UiO) INF2220 H2016, forelesning
Løsnings forslag i java In115, Våren 1998
 Løsnings forslag i java In115, Våren 1998 Oppgave 1 // Inne i en eller annen klasse private char S[]; private int pardybde; private int n; public void lagalle(int i) if (i==n) bruks(); else /* Sjekker
Løsnings forslag i java In115, Våren 1998 Oppgave 1 // Inne i en eller annen klasse private char S[]; private int pardybde; private int n; public void lagalle(int i) if (i==n) bruks(); else /* Sjekker
Øvingsforelesning 6. Sorteringsalgoritmer. Kristian Veøy
 Øvingsforelesning 6 Sorteringsalgoritmer Kristian Veøy veoy@stud.ntnu.no 26.09.08 1 Spørsmål fra øvingsgruppene Må jeg kunne python på eksamen? (Nei) Er det lurt å gjøre alle programmeringsøvingene? (Ikke
Øvingsforelesning 6 Sorteringsalgoritmer Kristian Veøy veoy@stud.ntnu.no 26.09.08 1 Spørsmål fra øvingsgruppene Må jeg kunne python på eksamen? (Nei) Er det lurt å gjøre alle programmeringsøvingene? (Ikke
Studentnummer: Side 1 av 1. Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005
 Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
Studentnummer: Side 1 av 1 Løsningsforslag, Eksamen i TDT4120 Algoritmer og datastrukturer August 2005 Faglige kontakter under eksamen: Magnus Lie Hetland, Arne Halaas Tillatte hjelpemidler: Bestemt enkel
Fra A til B. Syvende forelesning
 Fra A til B Syvende forelesning 1 Amøbeproblemet nok en gang. Hva er 1+2+4+ +n/2? 2 Skal la være å trekke frem binærtrefiguren igjen ;-) La oss se på det på en litt annen måte, som passer dagens tema (fra
Fra A til B Syvende forelesning 1 Amøbeproblemet nok en gang. Hva er 1+2+4+ +n/2? 2 Skal la være å trekke frem binærtrefiguren igjen ;-) La oss se på det på en litt annen måte, som passer dagens tema (fra
INF2220: Forelesning 2
 INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
INF2220: Forelesning 2 Mer om analyse av algoritmer Analyse av binære søketrær Balanserte søketrær Rød-svarte trær (kapittel12.2) B-trær (kapittel 4.7) ANALYSE AV ALGORITMER 2 Analyse av tidsforbruk Hvor
EKSAMEN. Dato: 28. mai 2018 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 28. mai 2018 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
UNIVERSITETET I OSLO
 UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF 110 Algoritmer og datastrukturer Eksamensdag : Lørdag 8. desember 2001 Tid for eksamen : 09.00-15.00 Oppgavesettet er på
UNIVERSITETET I OSLO Det matematisk-naturvitenskapelige fakultet Eksamen i : INF 110 Algoritmer og datastrukturer Eksamensdag : Lørdag 8. desember 2001 Tid for eksamen : 09.00-15.00 Oppgavesettet er på
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer
 Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 18. august 2011 Eksamenstid 0900 1300 Sensurdato 8. september Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
Avsluttende eksamen i TDT4120 Algoritmer og datastrukturer Eksamensdato 18. august 2011 Eksamenstid 0900 1300 Sensurdato 8. september Språk/målform Bokmål Kontakt under eksamen Magnus Lie Hetland (tlf.
O, what a tangled. Fjerde forelesning. Robot-eksemplet som ikke ble gjennomgått sist blir frivillig selvstudium (ut fra foilene :-)
 Dagens oppvarming 1 O, what a tangled Fjerde forelesning Robot-eksemplet som ikke ble gjennomgått sist blir frivillig selvstudium (ut fra foilene :-) O, what a tangled web we weave / When first we practice
Dagens oppvarming 1 O, what a tangled Fjerde forelesning Robot-eksemplet som ikke ble gjennomgått sist blir frivillig selvstudium (ut fra foilene :-) O, what a tangled web we weave / When first we practice
EKSAMEN. Dato: 18. mai 2017 Eksamenstid: 09:00 13:00
 EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 18. mai 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Kalkulator Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
EKSAMEN Emnekode: ITF20006 Emne: Algoritmer og datastrukturer Dato: 18. mai 2017 Eksamenstid: 09:00 13:00 Hjelpemidler: Alle trykte og skrevne Kalkulator Faglærer: Jan Høiberg Om eksamensoppgavene: Oppgavesettet
